Overload Risk Assessment of Transmission Lines Considering Dynamic Line Rating
Abstract
1. Introduction
2. Overload Criterion of Transmission Line Based on the Dynamic Capacity Increase Calculation Model
2.1. Model Building
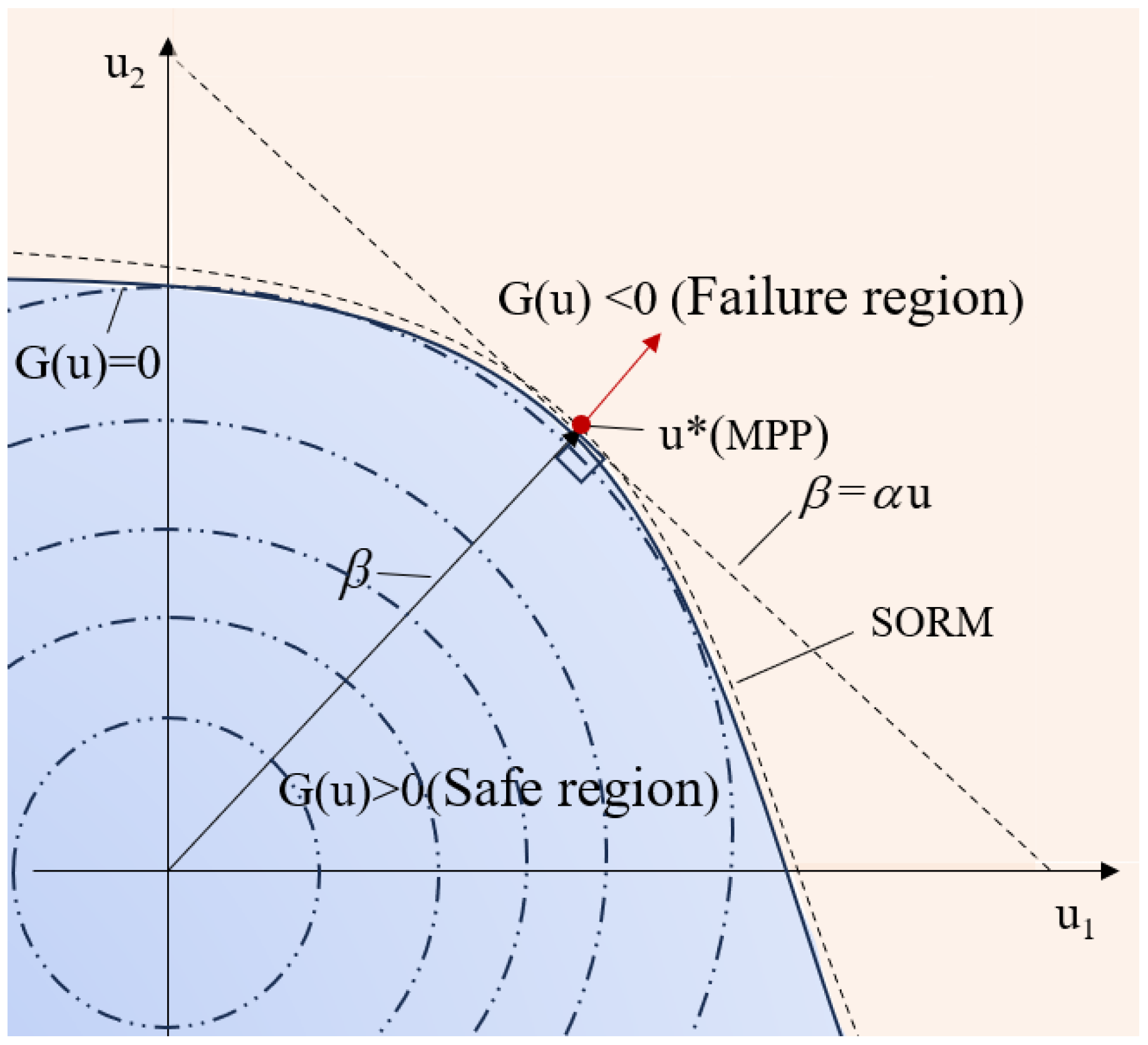
2.2. Overload Probability Solution Based on Second-Order Surface Approximation
3. Overload Risk Assessment of Transmission Lines Based on Multiscenario Stochastic Analysis
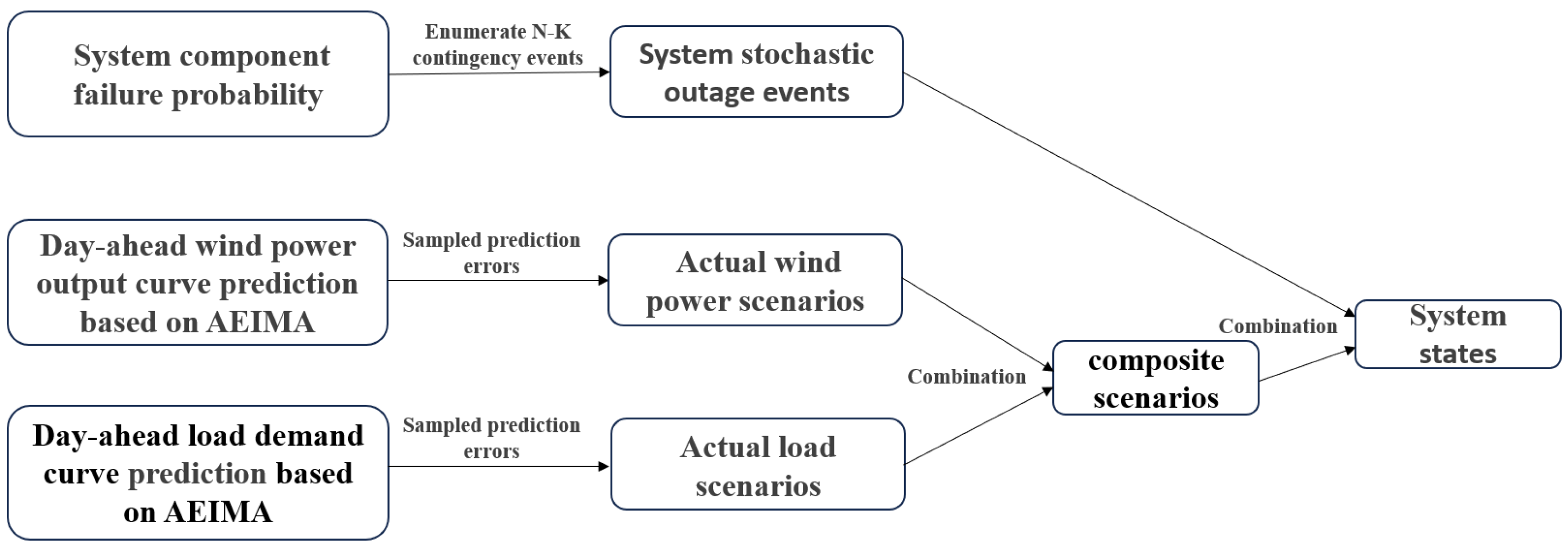
3.1. System State Generation and Uncertainty Modeling
3.2. Overload Risk Assessment Process Based on Scenario Analysis
- (1)
- Based on the predicted curves and prediction errors of renewable energy output and load, scenarios for renewable energy and load are generated.
- (2)
- Using the system component failure probability model, the outage events for system components are generated.
- (3)
- The renewable energy and load scenarios are combined with the system component outage events to generate system states and their corresponding probabilities.
- (4)
- Power flow analysis is performed based on the system states and environmental parameters along the transmission lines. Second-order reliability methods are used to analytically calculate the expected overload probability indicators for the transmission lines.
4. Case Study
4.1. Parameter Setting
4.2. IEEE RBTS6 Node System
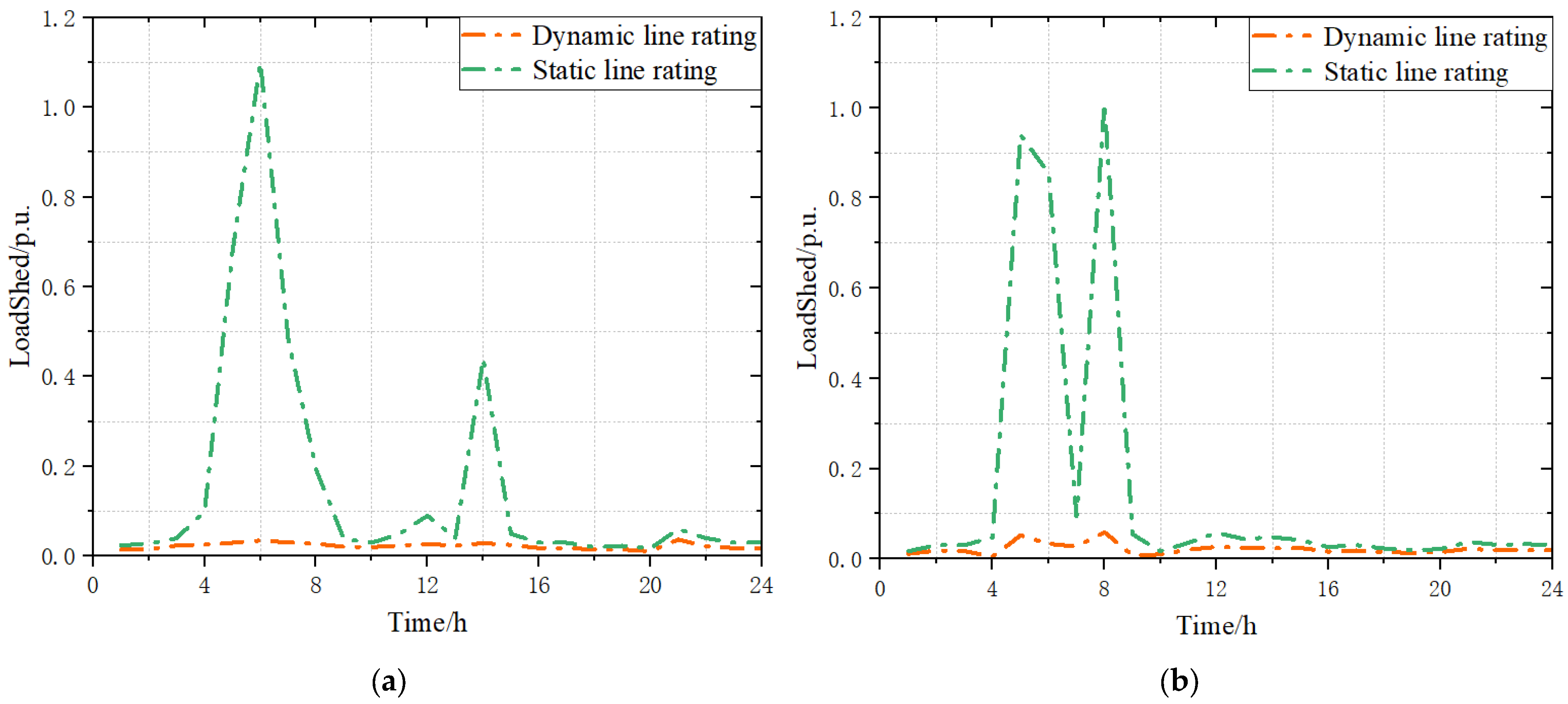
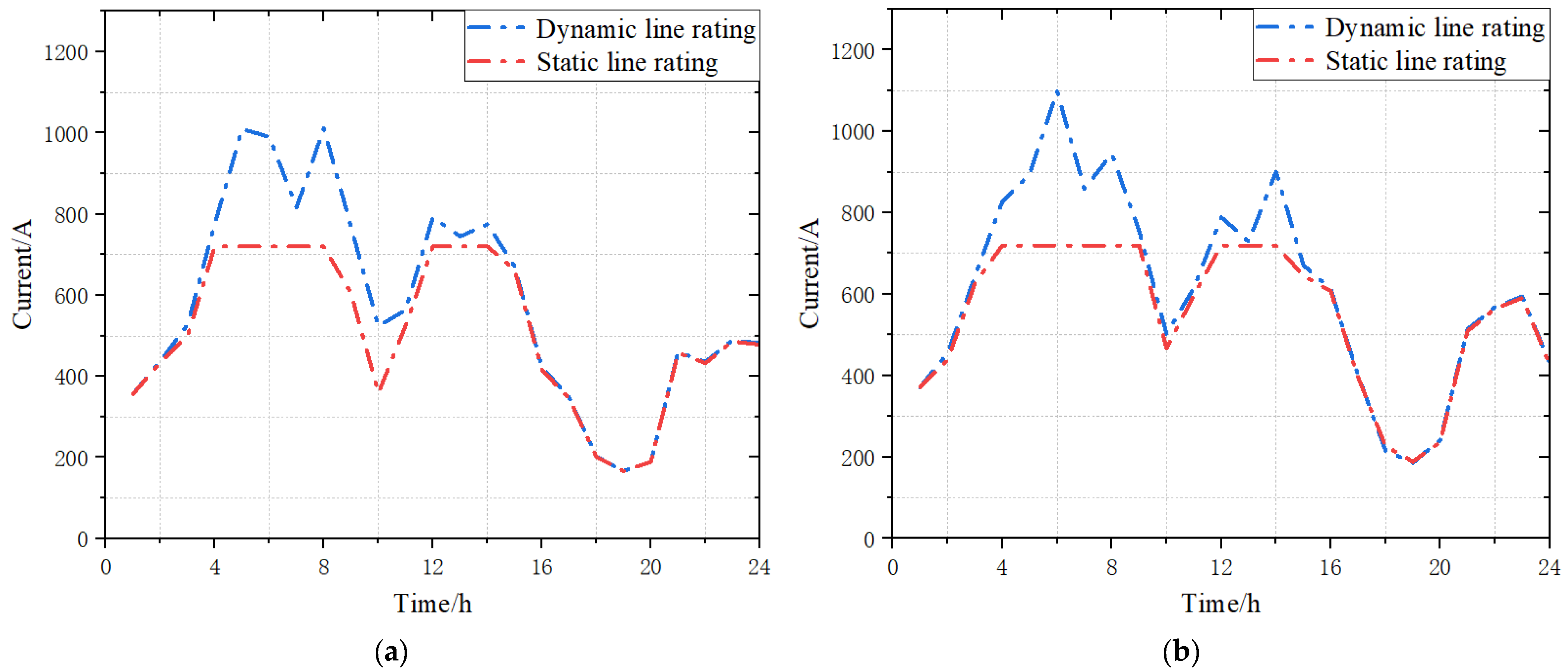
- (1)
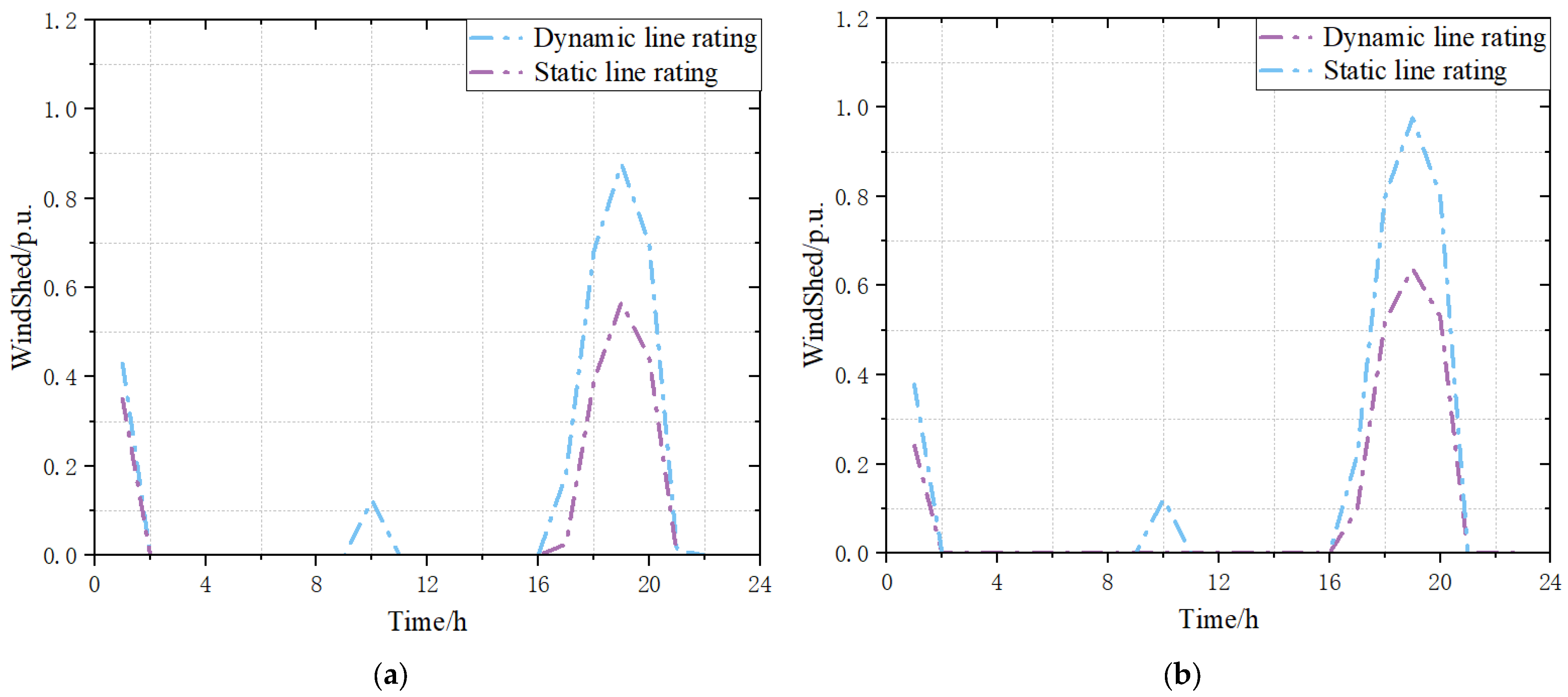
- Effectiveness analysis of the dynamic capacity increase
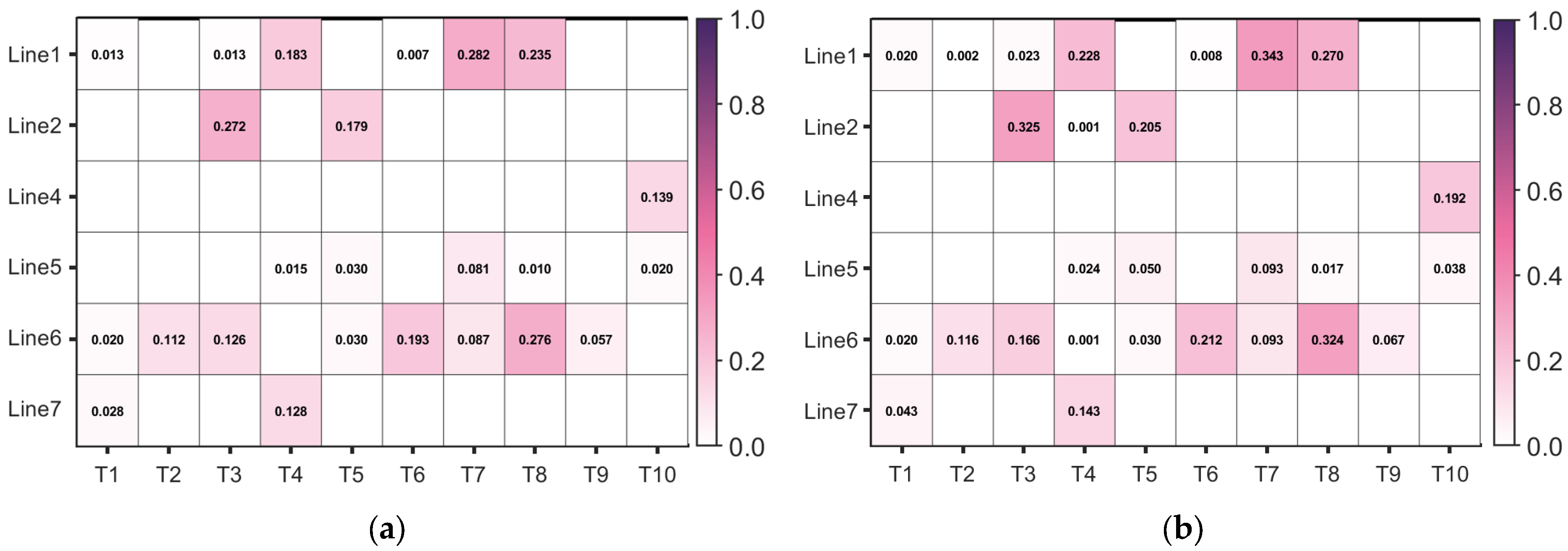
- (2)
- Analysis of overload risk assessment results considering the influence of component failure
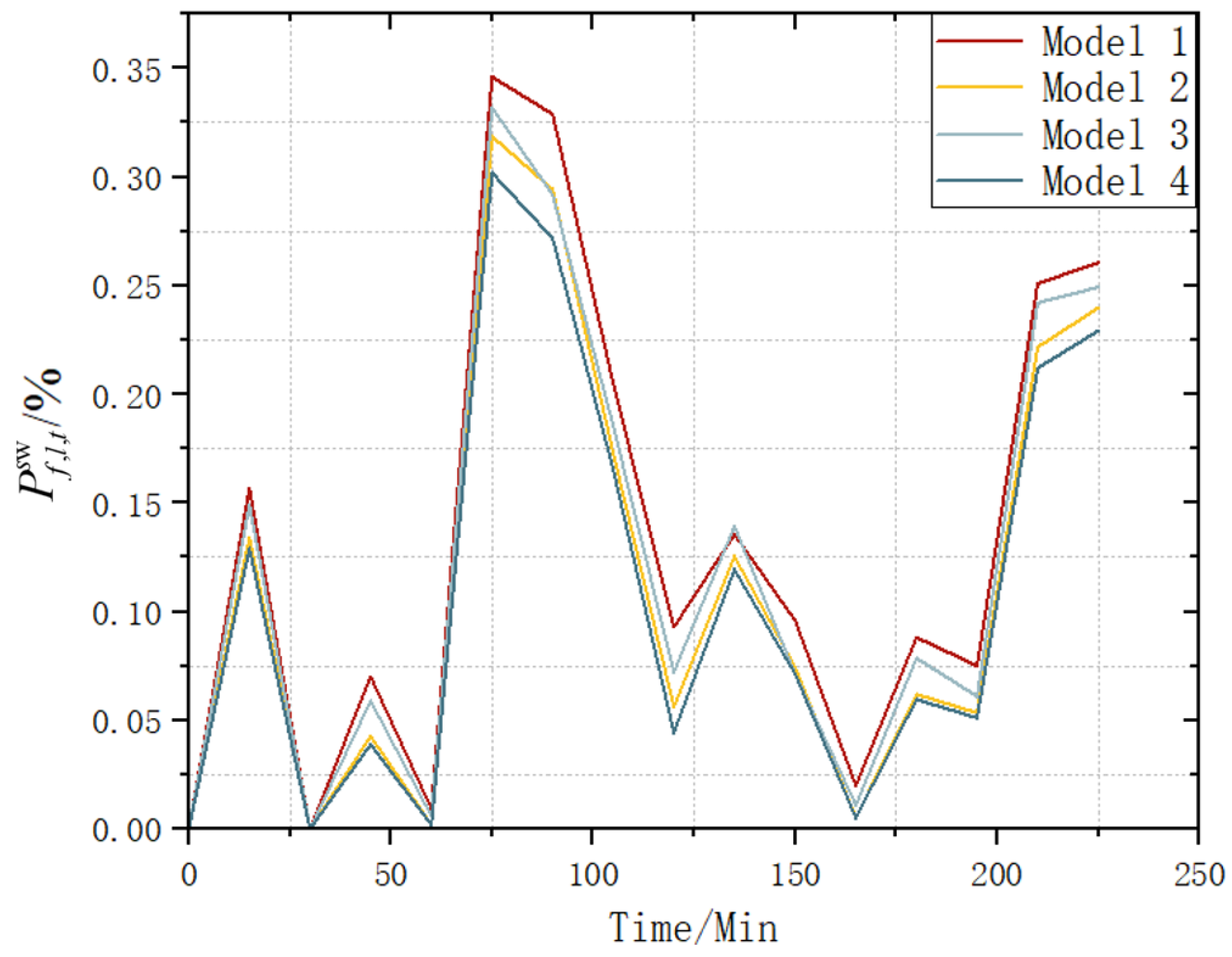
4.3. IEEE-RTS79 System
- (1)
- Influence of the different methods for the determination of the efficiency and accuracy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yu, Z.; Liu, X.; Yan, K.; Song, Y.; Zhou, K. Combination Model of Chance-constrained Security Constraint Unit with Considering the Forecast Uncertainties of DLR and Wind Power. High Volt. Eng. 2021, 47, 1204–1214. [Google Scholar] [CrossRef]
- IEEE Std 738-2006 (Revision of IEEE Std 738-1993); IEEE Standard for Calculating the Current-Temperature of Bare Overhead Conductors. IEEE Standard Association: Piscataway, NJ, USA, 2007; pp. 1–58. [CrossRef]
- Karimi, S.; Musilek, P.; Knight, A.M. Dynamic thermal rating of transmission lines: A review. Renew. Sustain. Energy Rev. 2018, 91, 600–612. [Google Scholar] [CrossRef]
- Peng, X.; Peng, R.; Wang, R.; Guo, D.; Fan, Y.; Liu, G. Equivalent Heat Transfer Transient Measurement Model for Dynamic Capacity Increase of Overhead Transmission Lines. High Volt. Technol. 2022, 48, 3975–3986. [Google Scholar]
- Wang, T.; Zhu, S.; Guo, R.; Qu, X. Study on the dynamic current carrying capacity of the parallel grid line of Baihubao wind farm in Pinglu Shanxi province. Power Syst. Technol. 2016, 40, 1400–1405. [Google Scholar]
- Hou, Y.; Wang, W.; Wei, Z.; Deng, X.; Ji, Q.; Wang, T.; Ru, X. Research and application of dynamic line rating technology. Energy Rep. 2020, 6, 716–730. [Google Scholar] [CrossRef]
- Lawal, O.A.; Teh, J. Assessment of dynamic line rating forecasting methods. Electr. Power Syst. Res. 2022, 214, 108807. [Google Scholar] [CrossRef]
- Viafora, N.; Morozovska, K.; Kazmi, S.H.H.; Laneryd, T.; Hilber, P.; Holbøll, J. Day-ahead dispatch optimization with dynamic thermal rating of transformers and overhead lines. Electr. Power Syst. Res. 2019, 171, 194–208. [Google Scholar] [CrossRef]
- Gao, Z.; Hu, S.; Jin, T.; Sun, H.; Chen, X.; Wang, Z. Day-ahead power system scheduling model considering transmission line dynamic capacity expansion risk. High Volt. Eng. 2023, 49, 3215–3226. [Google Scholar]
- Wallnerstrm, C.J.; Huang, Y.; Sder, L. Impact from Dynamic Line Rating on Wind Power Integration; IEEE Press: New York, NY, USA, 2015. [Google Scholar] [CrossRef]
- Wang, K.; Sheng, G.; Sun, X.; Wang, W.; Wang, S.; Jiang, X. Online prediction of transmission dynamic line rating based on radial basis function neural network. Dianwang Jishu/Power Syst. Technol. 2013, 37, 1719–1725. [Google Scholar] [CrossRef]
- Zhu, X.; Xue, Y.; Huang, T. Complexity of Influence of Generator Inertia on Transient Angle Stability. Autom. Electr. Power Syst. 2019, 43, 102–108. [Google Scholar]
- Wang, C.; Liu, F.; Wang, J.; Wei, W.; Mei, S. Risk-Based Admissibility Assessment of Wind Generation Integrated into a Bulk Power System. IEEE Trans. Sustain. Energy 2015, 7, 325–336. [Google Scholar] [CrossRef]
- Ding, Z.; Yu, K.; Wang, C.; Lee, W.J. Transmission Line Overload Risk Assessment Considering Dynamic Line Rating Mechanism in a High-Wind-Penetrated Power System: A Data-Driven Approach. IEEE Trans. Sustain. Energy 2022, 13, 1112–1122. [Google Scholar] [CrossRef]
- Zhaohao, D.; Kaiyuan, Y.; Cheng, W. Overload Risk Assessment of Power Transmission Line Considering Dynamic Line Rating. Autom. Electr. Power Syst. 2021, 45, 146–152. [Google Scholar]
- Cai, X.; Dang, P.; Zeng, W. Application Status and Development Trend of Capacity-Increase Technology for Overhead Transmission. Wire Cable 2023, 66, 1–6. [Google Scholar] [CrossRef]
- Xingang, Y.; Yanxue, Z.; Yajun, Z. Improved method for improving iterative convergence of short circuit calculation in new energy AC power grid. Electr. Power Autom. Equip. 2024, 44, 185192–185209. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, C.; Xie, K.; Hu, B.; Yang, H. Review on Network Transmission Flexibility of Power System and Its Evaluation. CSEE 2023, 43, 5429–5441. [Google Scholar]
- Aznarte, J.L.; Siebert, N. Dynamic Line Rating Using Numerical Weather Predictions and Machine Learning: A Case Study. IEEE Trans. Power Deliv. 2017, 32, 335–343. [Google Scholar] [CrossRef]
- Guang, M.; Yining, Z.; Zhe, C. Risk assessment method for hybrid AC/DC system with large-scale wind power Integration. Power Syst. Technol. 2019, 43, 3241–3252. [Google Scholar] [CrossRef]
- Ye, K.; Zhao, J.; Hong, M.; Maslennikov, S.; Tan, B.; Luo, X. Power System Overloading Risk Assessment Considering Topology and Renewable Uncertainties. In Proceedings of the 2024 IEEE Power & Energy Society General Meeting (PESGM), Seattle, WA, USA, 21–25 July 2024; pp. 1–5. [Google Scholar]
- Matus, M.; Saez, D.; Favley, M.; Suazo-Martinez, C.; Moya, J.; Jimenez-Estevez, G.; Palma-Behnke, R.; Olguin, G.; Jorquera, P. Identification of Critical Spans for Monitoring Systems in Dynamic Thermal Rating. IEEE Trans. Power Deliv. 2012, 27, 1002–1009. [Google Scholar] [CrossRef]
- Breitung, K. Asymptotic approximations for multinormal integrals. J. Eng. Mech. ASCE 1984, 110, 357–366. [Google Scholar] [CrossRef]
- Fu, S. Research on Probability Prediction Method of Carrying Capacity of Overhead Conductor. Master’s Thesis, Shandong University, Jinan, China, 2019. [Google Scholar]
- Chen, P.; Pedersen, T.; Bak-Jensen, B.; Chen, Z. ARIMA-Based Time Series Model of Stochastic Wind Power Generation. IEEE Trans. Power Syst. 2010, 25, 667–676. [Google Scholar] [CrossRef]
- Liu, Y.; Li, W.; Liu, C. Mixed skew distribution model for short-term wind power prediction error. Proc. CSEE 2015, 35, 2375–2382. [Google Scholar]
- Zhao, S.; Shao, C.; Ding, J.; Hu, B.; Xie, K.; Yu, X.; Zhu, Z. Unreliability Tracing of Power Systems for Identifying the Most Critical Risk Factors Considering Mixed Uncertainties in Wind Power Output. In Protection and Control of Modern Power Systems; IEEE: Piscataway, NJ, USA, 2024; Volume 9, pp. 96–111. [Google Scholar] [CrossRef]
- Long, X. A Fully Analytical Approach for the Real-Time Dynamic Reliability Evaluation of Composite Power Systems with Renewable Energy Sources. Engineering 2024, in press. [Google Scholar] [CrossRef]
- Yang, W.; Cao, M.; Ge, P.; Hu, B.; Qu, G.; Xie, K.; Cheng, X.; Peng, L.; Yan, J.; Li, Y. Risk-Oriented Renewable Energy Scenario Clustering for Power System Reliability Assessment and Tracing. IEEE Access 2020, 8, 183995–184003. [Google Scholar] [CrossRef]
- Wang, T. Research on Short-Term Current-Carrying Capacity Prediction Method of Overhead Conductor; Shandong University: Jinan, China, 2022. [Google Scholar]
- Han, H.; Gao, S.; Dai, J.; Chen, Y. A new multi-point estimate method on uncertain power flow. In Proceedings of the 2014 International Conference on Power System Technology, Chengdu, China, 20–22 October 2014; pp. 440–444. [Google Scholar]
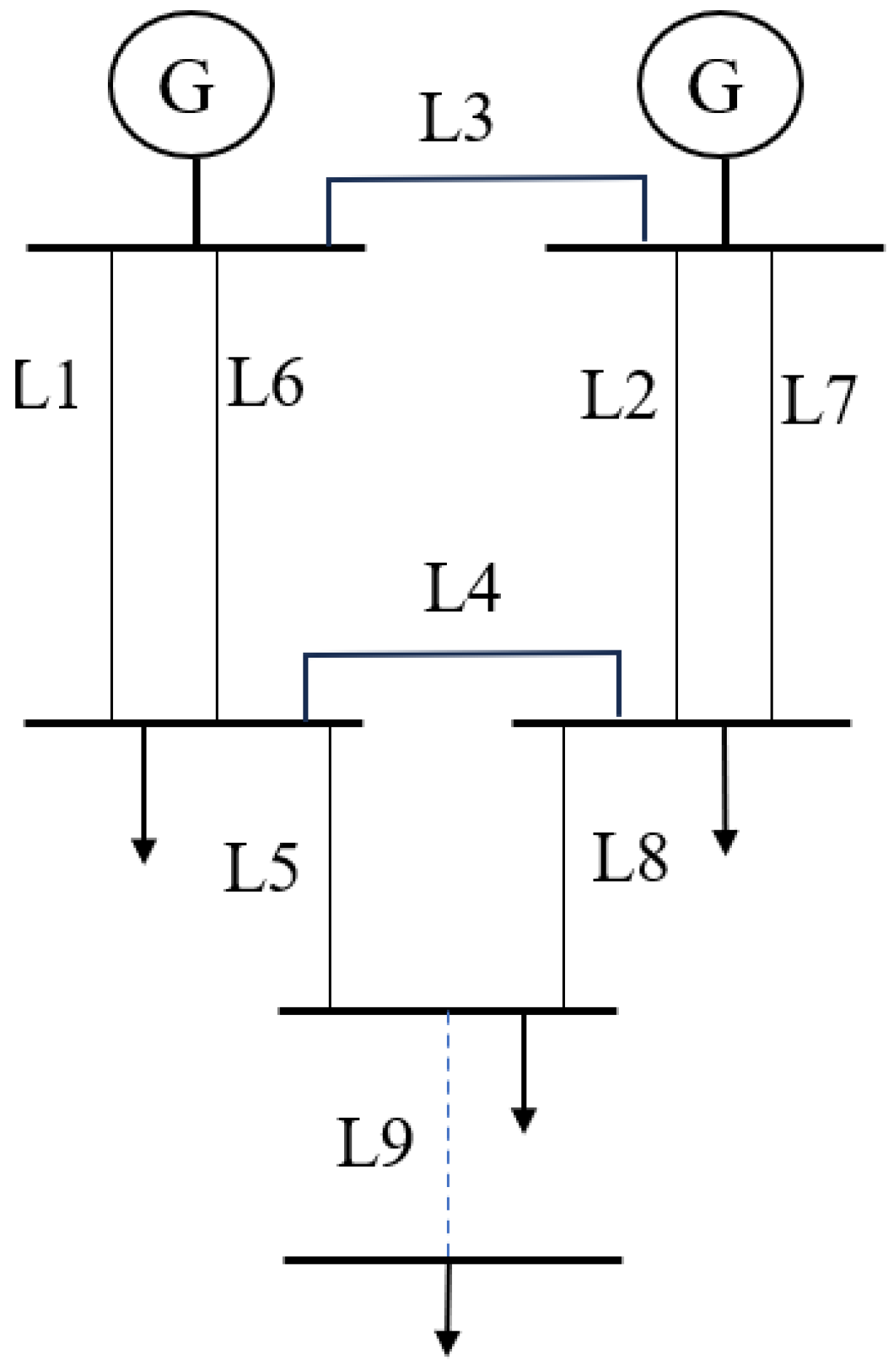
| Wind Turbine Access Node | Installed Capacity (MW) |
|---|---|
| 1 | 250 |
| 3 | 150 |
| Component | Capacity (MW) | λ (Occ./Yr) | μ (Occ./Yr) | FOR0 |
|---|---|---|---|---|
| Generator 1 | 45 | 2 | 194.67 | 0.0300 |
| Generator 2 | 45 | 2 | 194.67 | 0.0350 |
| Generator 3 | 60 | 4 | 194.67 | 0.0250 |
| Generator 4 | 60 | 2.4 | 194.67 | 0.0350 |
| Generator 5 | 60 | 1 | 219.27 | 0.0150 |
| Generator 6 | 60 | 12 | 219.27 | 0.0150 |
| Generator 7 | 45 | 2.4 | 159.27 | 0.0200 |
| Generator 8 | 60 | 5 | 194.67 | 0.0150 |
| Generator 9 | 60 | 3 | 146.00 | 0.0150 |
| Generator 10 | 60 | 6 | 194.67 | 0.0150 |
| Generator 11 | 60 | 6 | 194.67 | 0.0150 |
| Line 1 | 81 | 1.5 | 876.00 | 0.0017 |
| Line 2 | 81 | 5 | 876.00 | 0.0057 |
| Line 3 | 71 | 4 | 876.00 | 0.0045 |
| Line 4 | 71 | 1 | 876.00 | 0.0011 |
| Line 5 | 71 | 1 | 876.00 | 0.0011 |
| Line 6 | 71 | 1.5 | 876.00 | 0.0017 |
| Line 7 | 71 | 5 | 876.00 | 0.0057 |
| Line 8 | 71 | 1 | 876.00 | 0.0011 |
| Line 9 | 71 | 1 | 876.00 | 0.0011 |
| Model 1 | Model 2 | Model 3 | Model 4 | |
|---|---|---|---|---|
| Calculation time (s) | 14.8 | 39.6 | 77.9 | 1094.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Lin, J.; Han, Y.; Zhu, L.; Chang, D.; Shao, C. Overload Risk Assessment of Transmission Lines Considering Dynamic Line Rating. Energies 2025, 18, 1822. https://doi.org/10.3390/en18071822
Li J, Lin J, Han Y, Zhu L, Chang D, Shao C. Overload Risk Assessment of Transmission Lines Considering Dynamic Line Rating. Energies. 2025; 18(7):1822. https://doi.org/10.3390/en18071822
Chicago/Turabian StyleLi, Jieling, Jinming Lin, Yu Han, Lingzi Zhu, Dongxu Chang, and Changzheng Shao. 2025. "Overload Risk Assessment of Transmission Lines Considering Dynamic Line Rating" Energies 18, no. 7: 1822. https://doi.org/10.3390/en18071822
APA StyleLi, J., Lin, J., Han, Y., Zhu, L., Chang, D., & Shao, C. (2025). Overload Risk Assessment of Transmission Lines Considering Dynamic Line Rating. Energies, 18(7), 1822. https://doi.org/10.3390/en18071822






