Multi-Timescale Nested Hydropower Station Optimization Scheduling Based on the Migrating Particle Whale Optimization Algorithm
Abstract
1. Introduction
2. Multi-Timescale Nested Reservoir Optimization Scheduling
2.1. Objective Function
2.2. Constraints
- (1)
- Water balance constraintswhere and represent the reservoir storage at the end of periods and , respectively. denotes the average inflow to the reservoir during period , and represents the average outflow from the reservoir during period .
- (2)
- Water level constraintswhere and represent the minimum and maximum water level constraints of the reservoir during period , respectively.
- (3)
- Flow constraintswhere and represent the minimum and maximum outflow constraints of the reservoir during period , respectively.
- (4)
- Output constraintswhere and represent the minimum and maximum power output constraints of the power station during period , respectively.
- (5)
- Water level variation constraintswhere is the maximum variation constraint of the water level in the adjacent time period.
- (6)
- Initial and final water level constraintwhere and represent the initial and final water levels of the reservoir in the lower-level scheduling model during the scheduling period, respectively. Similarly, and represent the initial and final water levels of the upper-level scheduling model during the scheduling period. Here, one scheduling cycle of the lower-level model corresponds to one scheduling period of the upper-level model.
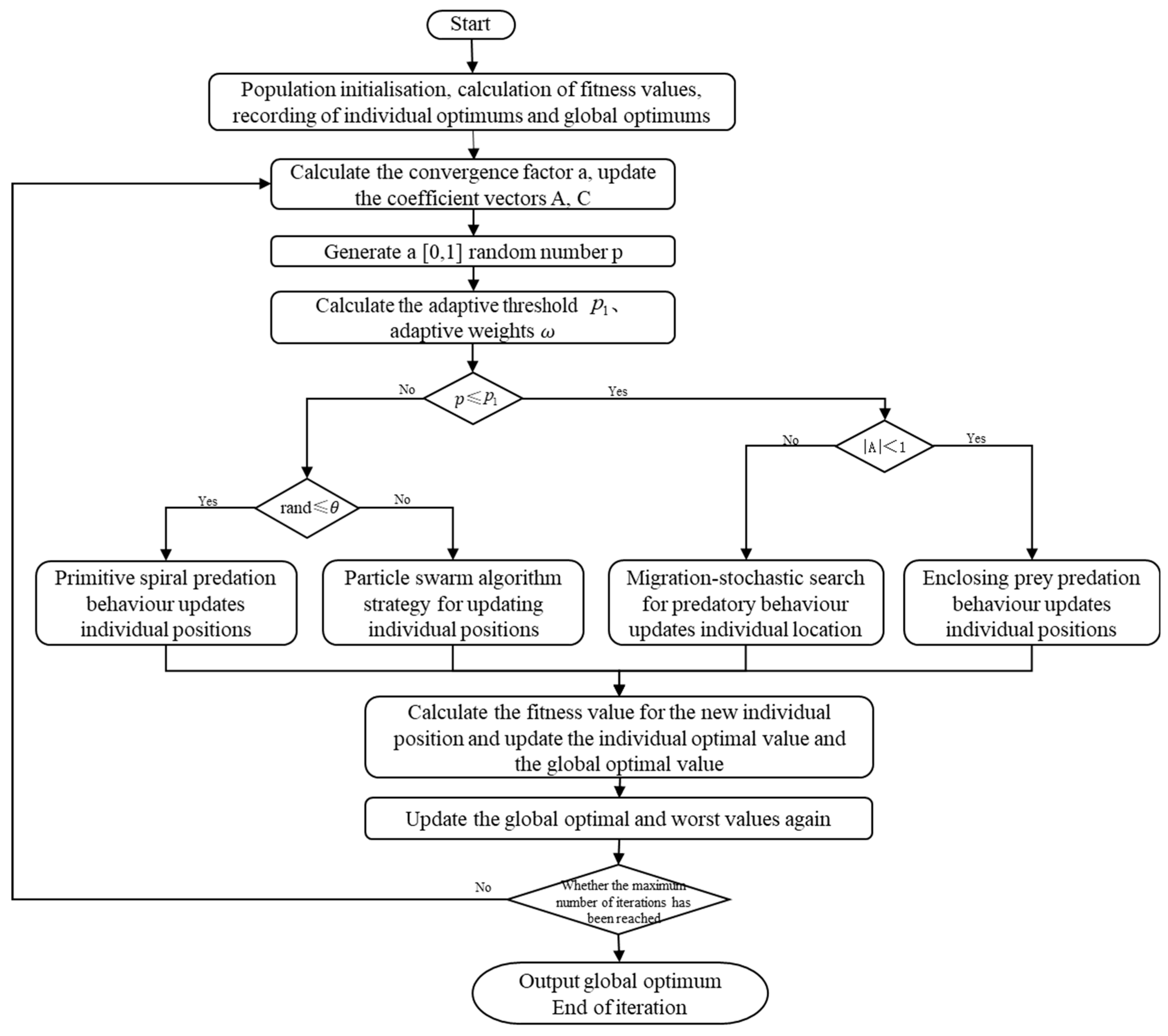
3. Improved Whale Optimization Algorithm
3.1. Chaotic Mapping Initialization
- (1)
- According to Equation (9), N individuals are generated, each with D dimensions, yielding the chaotic sequence values as follows:where represents the value of the -th dimension of the -th chaotic individual.
- (2)
- In accordance with Equation (11)The generated chaotic sequence values are mapped to the value space of decision variables to obtain the initial population. Where and represent the lower and upper bounds of the value space, respectively, and is the decision variable value in the -th dimension of the -th individual.
3.2. Encircling Prey Process
3.3. Particle-Spiral Bubble Hunting Process
3.4. Migration-Random Search
4. Discussion
4.1. Test Function Verification of the MPWOA Algorithm
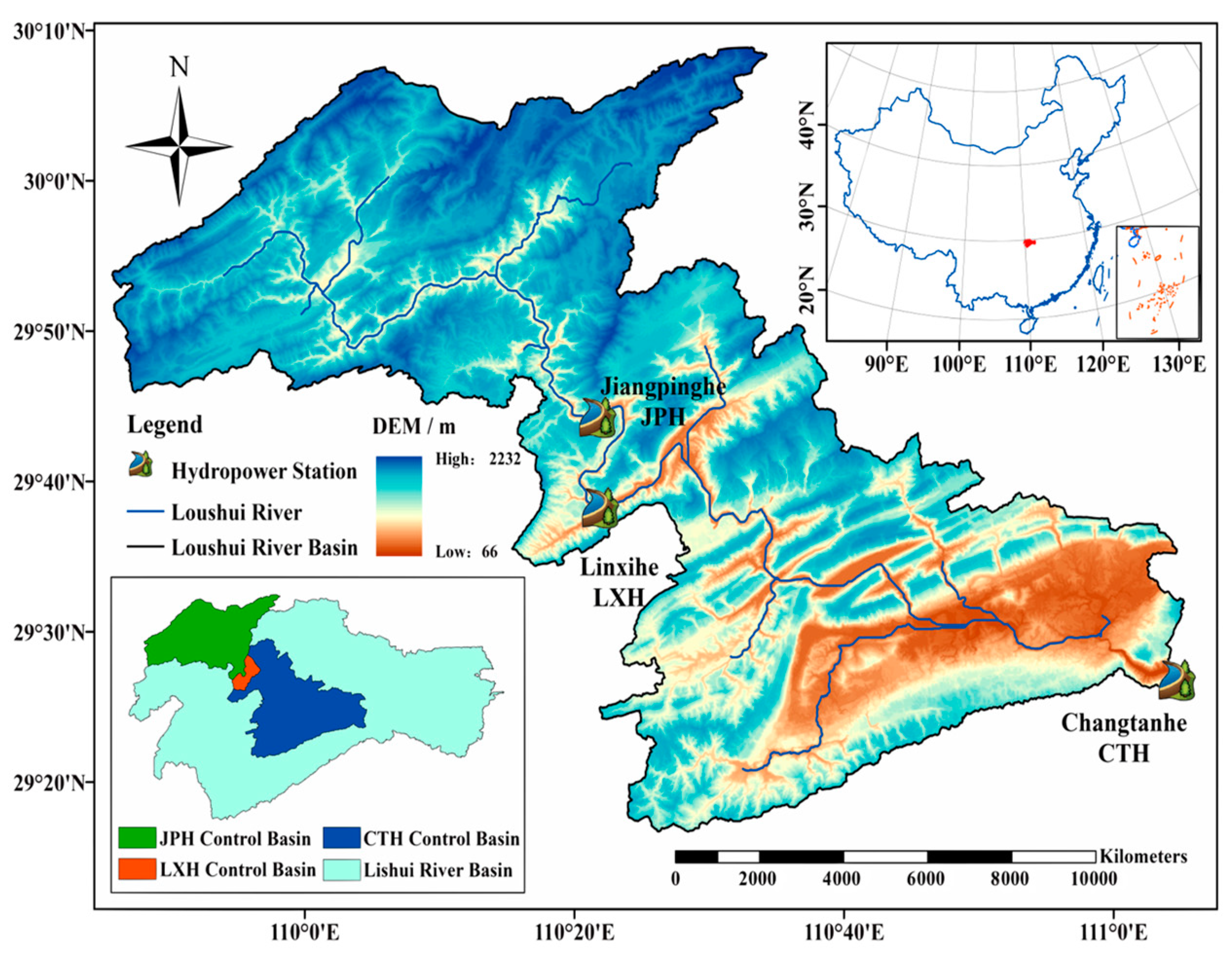
4.2. Case Overview
4.3. Case Study
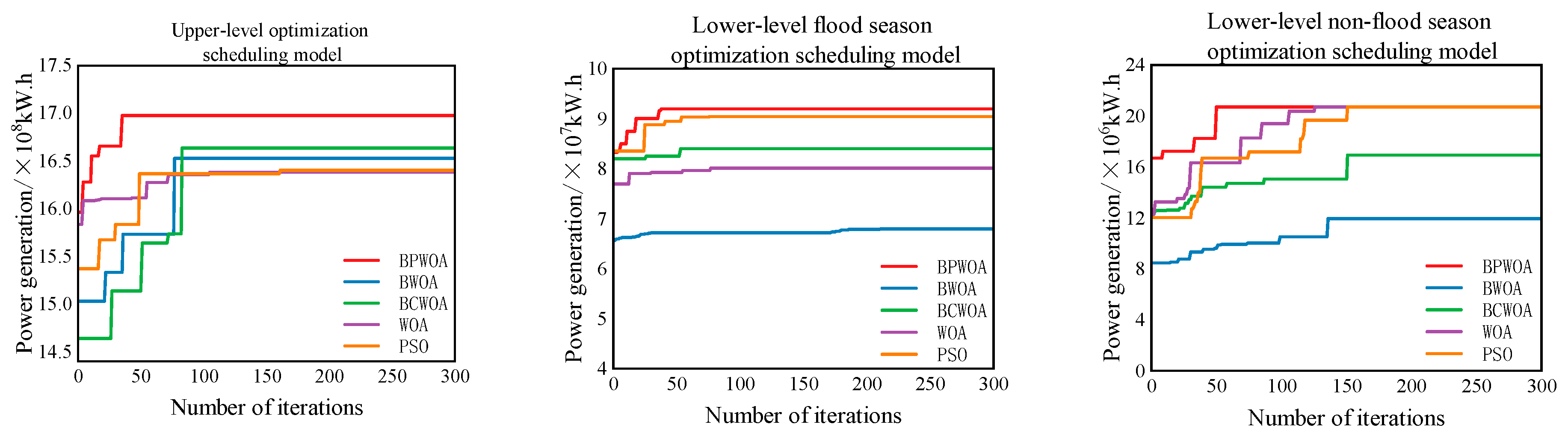
4.3.1. Practical Analysis of the MPWOA Algorithm
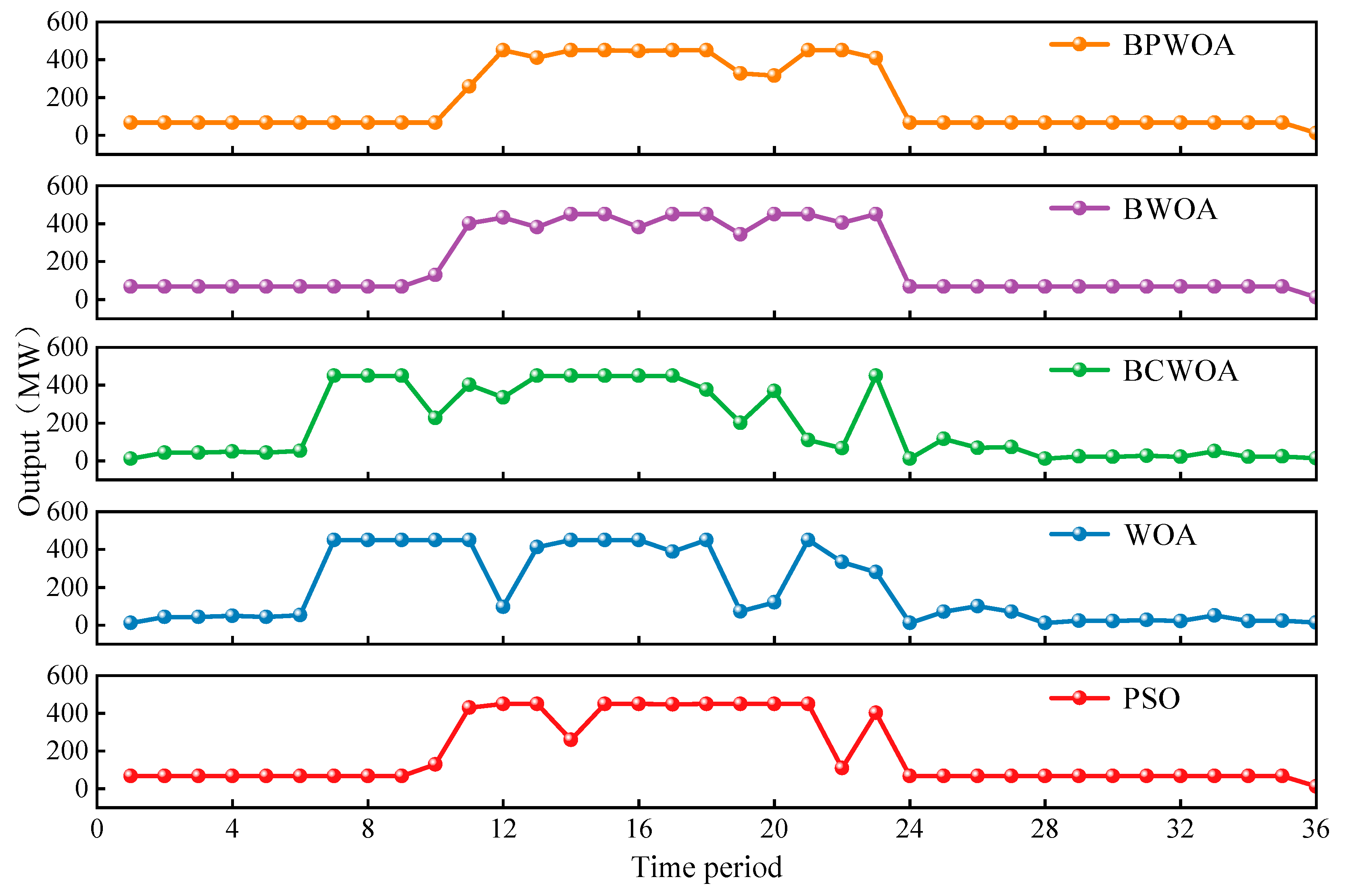
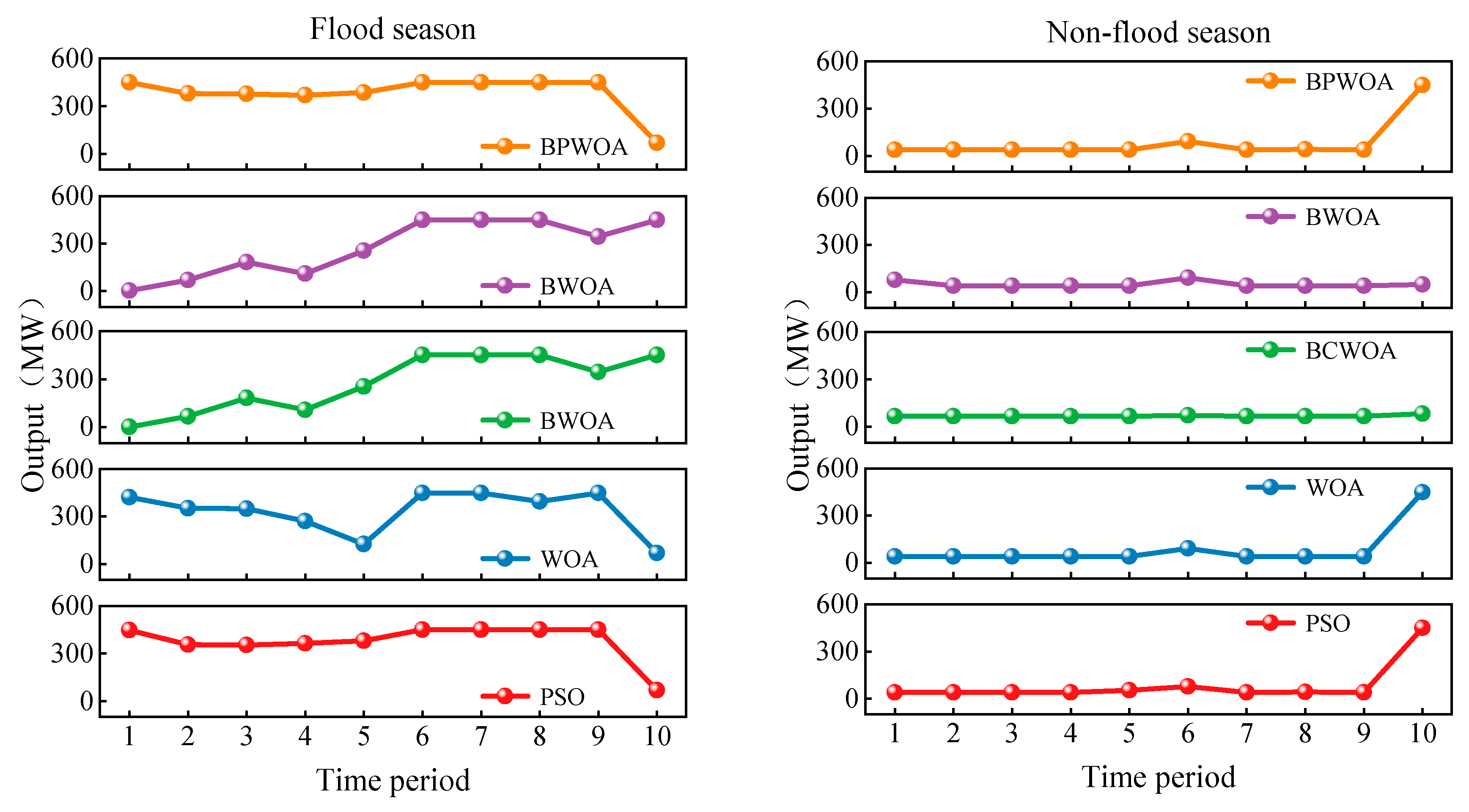
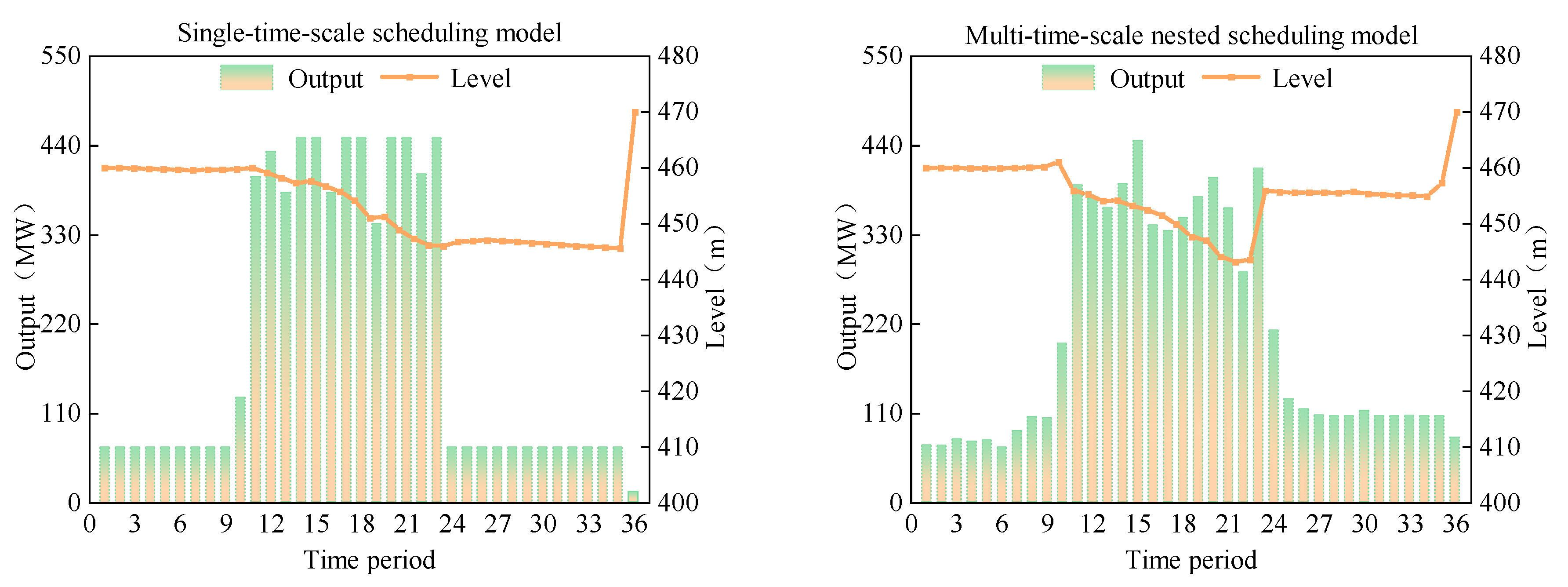
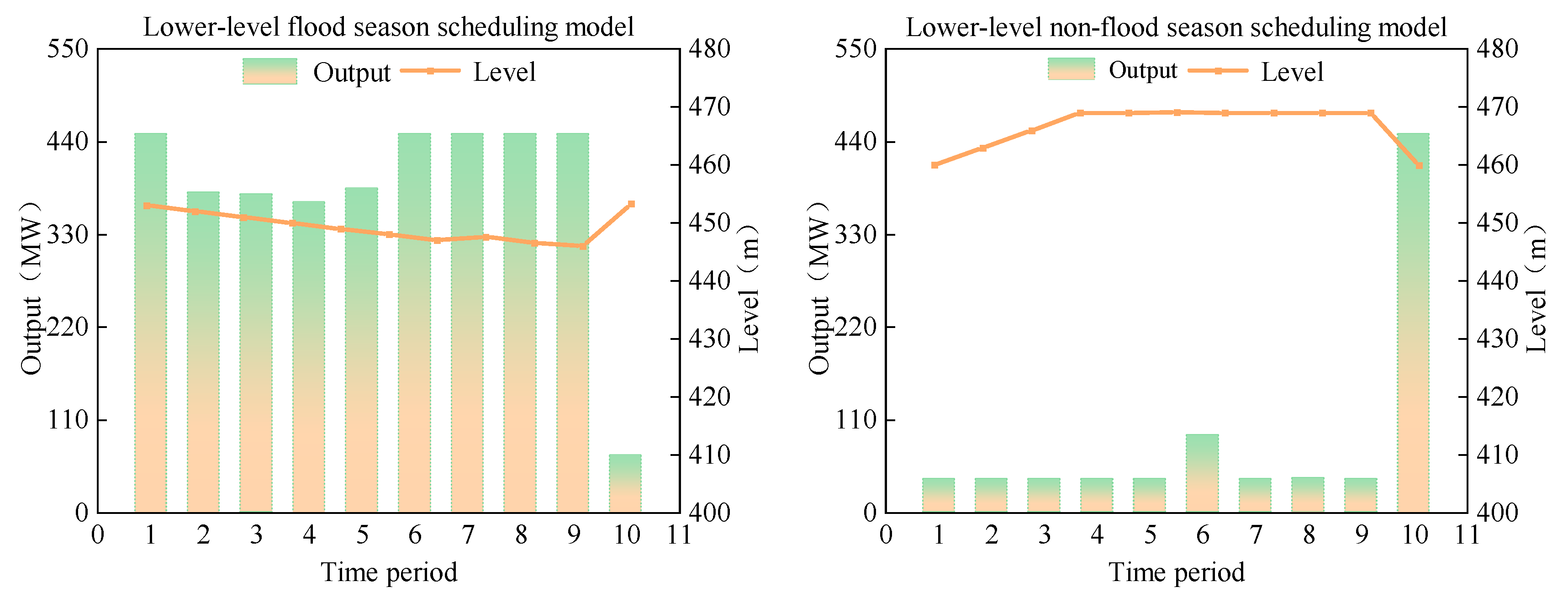
4.3.2. Analysis of Scheduling Results Under the MPWOA Algorithm
5. Conclusions
- (1)
- The Migrating Particle Whale Optimization Algorithm (MPWOA), based on the black-winged kite migration mechanism and particle swarm algorithm, showed superior optimization capabilities in both 10 test functions and hydropower generation scheduling models. Compared to MWOA, MCWOA, WOA, and PSO, MPWOA exhibited faster convergence and more stable search performance. It also significantly reduced the risk of falling into local optima. Furthermore, MPWOA demonstrated strong adaptability in solving multi-timescale, nonlinear, and multi-constraint hydropower scheduling problems. This adaptability helped improve the rational allocation and efficient use of water resources, thus providing a scientifically effective solution for hydropower station scheduling optimization.
- (2)
- The MPWOA achieved notable improvements in addressing hydropower generation scheduling problems, enhancing both long-term scheduling in the upper model and short-term scheduling in the lower model. The algorithm effectively leverages water resources, maximizes power generation efficiency, and provides a scientific, efficient solution for optimal scheduling.
- (3)
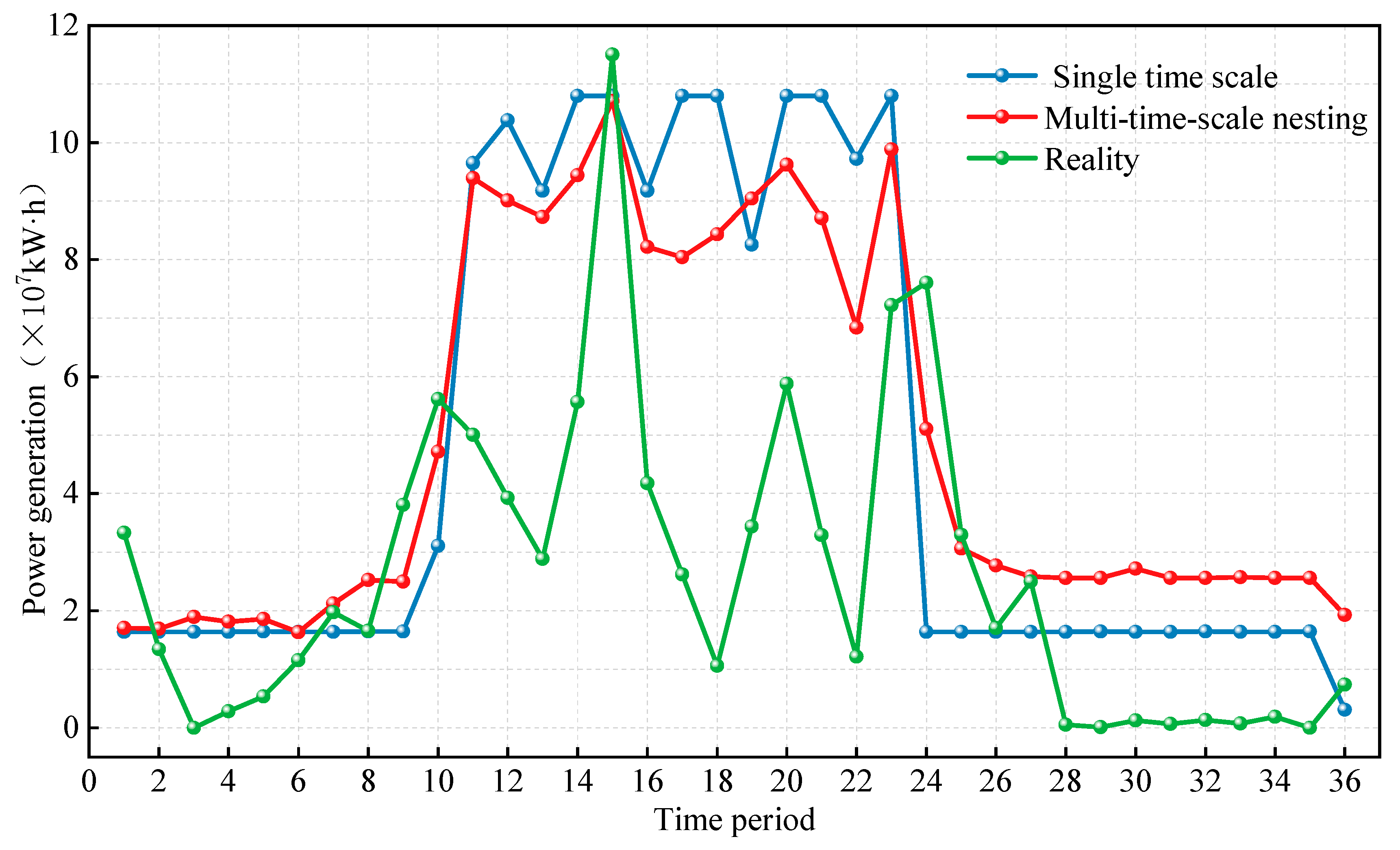
- The proposed multi-timescale nested optimal scheduling model achieved significant improvements in achieving power generation targets compared to the single-timescale scheduling model. This model can more accurately reflect actual operational characteristics, mitigate the risks of over-exploitation of resources associated with the single-timescale model, and enhance the efficient use of water resources while fostering sustainable development. It offers a more comprehensive and sound foundation for optimizing hydropower station scheduling.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MPWOA | Migrating Particle Whale Optimization Algorithm |
| MWOA | Migrating Whale Optimization Algorithm |
| MCWOA | Migrating Chaotic Whale Optimization Algorithm |
| WOA | Whale Optimization Algorithm |
| PSO | Particle Swarm Algorithm |
References
- Kosolapova, N.A.; Matveeva, L.G.; Nikitaeva, A.Y.; Molapisi, L. Modeling Resource Basis for Social and Economic Development Strategies: Water Resource Case. J. Hydrol. 2017, 553, 438–446. [Google Scholar] [CrossRef]
- Bilalova, S.; Newig, J.; Tremblay-Lévesque, L.-C.; Roux, J.; Herron, C.; Crane, S. Pathways to Water Sustainability? A Global Study Assessing the Benefits of Integrated Water Resources Management. J. Environ. Manag. 2023, 343, 118179. [Google Scholar] [CrossRef]
- Li, P.; Wu, J. Water Resources and Sustainable Development. Water 2024, 16, 134. [Google Scholar] [CrossRef]
- Niu, W.; Luo, T.; Yao, X.; Gong, J.; Huang, Q.; Gao, H.; Feng, Z. Artificial Intelligence-Based Response Surface Progressive Optimality Algorithm for Operation Optimization of Multiple Hydropower Reservoirs. Energy 2024, 291, 130449. [Google Scholar] [CrossRef]
- Wang, Z.; Tan, Q.; Wen, X.; Su, H.; Fang, G.; Wang, H. Capacity Optimization of Retrofitting Cascade Hydropower Plants with Pumping Stations for Renewable Energy Integration: A Case Study. Appl. Energy 2025, 377, 124429. [Google Scholar] [CrossRef]
- Liu, W.; Zhu, F.; Chen, J.; Wang, H.; Xu, B.; Song, P.; Zhong, P.; Lei, X.; Wang, C.; Yan, M.; et al. Multi-Objective Optimization Scheduling of Wind–Photovoltaic–Hydropower Systems Considering Riverine Ecosystem. Energy Convers. Manag. 2019, 196, 32–43. [Google Scholar] [CrossRef]
- He, J.; Tang, Y.; Guo, X.; Chen, H.; Guo, W. Research on Hybrid Reservoir Scheduling Optimization Based on Improved Walrus Optimization Algorithm with Coupling Adaptive ε Constraint and Multi-Strategy Optimization. Sci. Rep. 2024, 14, 11981. [Google Scholar] [CrossRef]
- Myateg, T.; Mitrofanov, S.; Xi, C.; Sekretarev, Y.; Safaraliev, M.; Volosatov, R.; Arestova, A.; Gulakhmadov, A. Long-Term Hydropower Plant Scheduling Considering Environmental and Economic Criteria. Sustainability 2024, 16, 10106. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, S.; Wen, X.; Yue, Z.; Zhou, Y. Optimization of Short-Term Hydropower Scheduling with Dynamic Reservoir Capacity Based on Improved Genetic Algorithm and Parallel Computing. J. Hydrol. 2024, 636, 131238. [Google Scholar] [CrossRef]
- Li, Z.; Wang, Y.; Chang, J.; Guo, A.; Wang, L.; Niu, C.; Hu, R.; He, B. Multi-Objective Double Layer Water Optimal Allocation and Scheduling Framework Combing the Integrated Surface Water—Groundwater Model. Water Res. 2024, 262, 122141. [Google Scholar] [CrossRef]
- Shang, L.; Li, X.; Shi, H.; Kong, F.; Wang, Y.; Shang, Y. Long-, Medium-, and Short-Term Nested Optimized-Scheduling Model for Cascade Hydropower Plants: Development and Practical Application. Water 2022, 14, 1586. [Google Scholar] [CrossRef]
- Subotić, I.; Groß, D.; Colombino, M.; Dörfler, F. A Lyapunov Framework for Nested Dynamical Systems on Multiple Time Scales With Application to Converter-Based Power Systems. IEEE Trans. Autom. Control. 2021, 66, 5909–5924. [Google Scholar] [CrossRef]
- Ben Alaya, A.; Souissi, A.; Tarhouni, J.; Ncib, K. Optimization of Nebhana Reservoir Water Allocation by Stochastic Dynamic Programming. Water Resour. Manag. 2003, 17, 259–272. [Google Scholar] [CrossRef]
- Jalali, M.R.; Afshar, A.; Mariño, M.A. Multi-Colony Ant Algorithm for Continuous Multi-Reservoir Operation Optimization Problem. Water Resour Manag. 2007, 21, 1429–1447. [Google Scholar] [CrossRef]
- Yi, M.; Mo, L.; Shen, Q. Study on Generation Scheduling of Cascade Hydropower Stations Based on SAPSO. J. Coast. Res. 2020, 104, 371–378. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Hu, Q.; Hu, H.; Lin, Z.; Chen, Z.; Zhang, Y. A Decision-Making Method for Reservoir Operation Schemes Based on Deep Learning and Whale Optimization Algorithm. Front. Plant Sci. 2023, 14, 1102855. [Google Scholar] [CrossRef]
- Yang, K.; Yang, K. Short-Term Hydro Generation Scheduling of the Three Gorges Hydropower Station Using Improver Binary-Coded Whale Optimization Algorithm. Water Resour. Manag. 2021, 35, 3771–3790. [Google Scholar] [CrossRef]
- Wang, W.; Wang, B.; Chau, K.; Zhao, Y.; Zang, H.; Xu, D. Monthly Runoff Prediction Using Gated Recurrent Unit Neural Network Based on Variational Modal Decomposition and Optimized by Whale Optimization Algorithm. Environ. Earth Sci. 2024, 83, 72. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Hu, X.; Qiu, L.; Zang, H. Black-Winged Kite Algorithm: A Nature-Inspired Meta-Heuristic for Solving Benchmark Functions and Engineering Problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle Swarm Optimization Algorithm: An Overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Mo, C.; Zhao, S.; Ruan, Y.; Liu, S.; Lei, X.; Lai, S.; Sun, G.; Xing, Z. Research on Reservoir Optimal Operation Based on Long-Term and Mid-Long-Term Nested Models. Water 2022, 14, 608. [Google Scholar] [CrossRef]
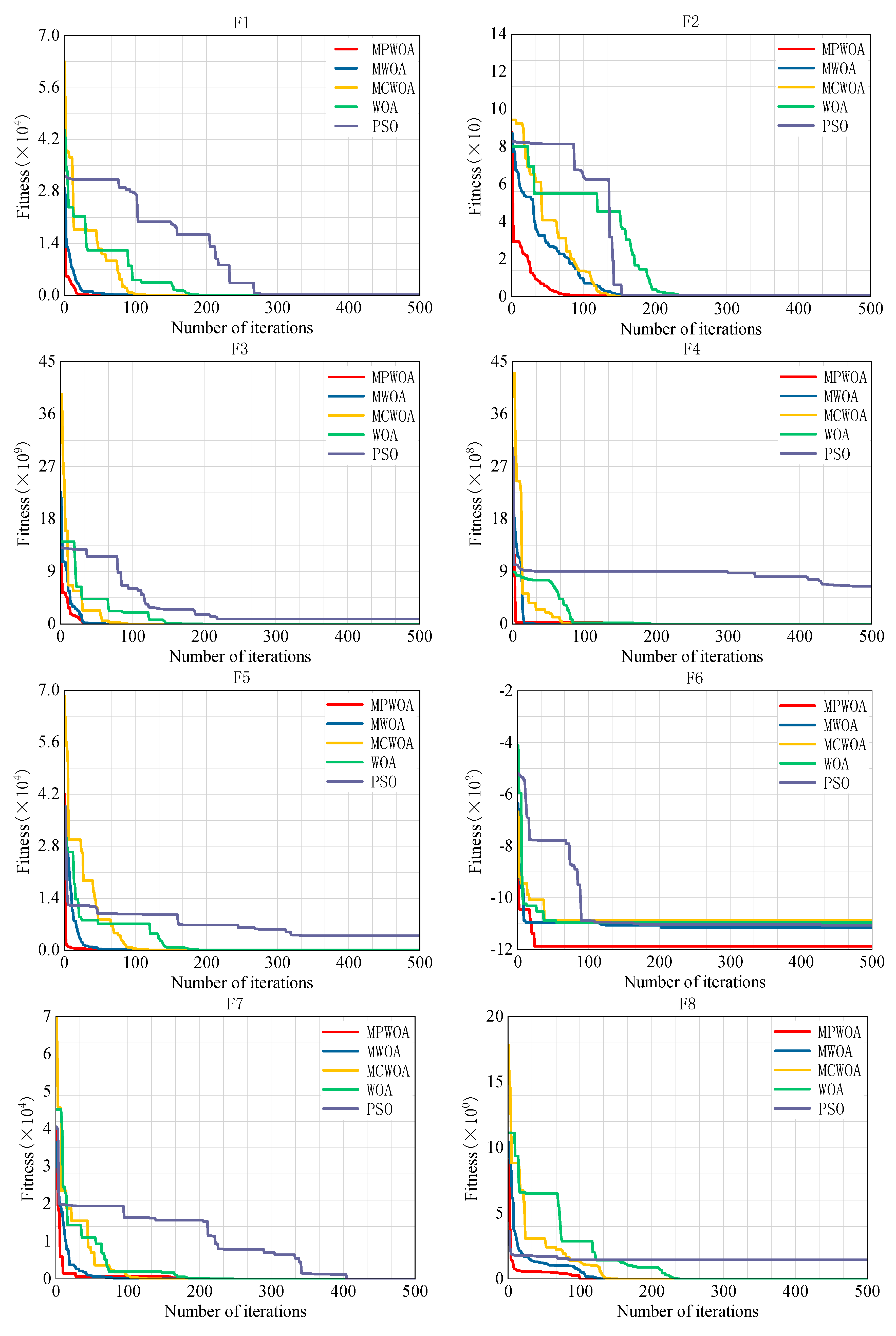
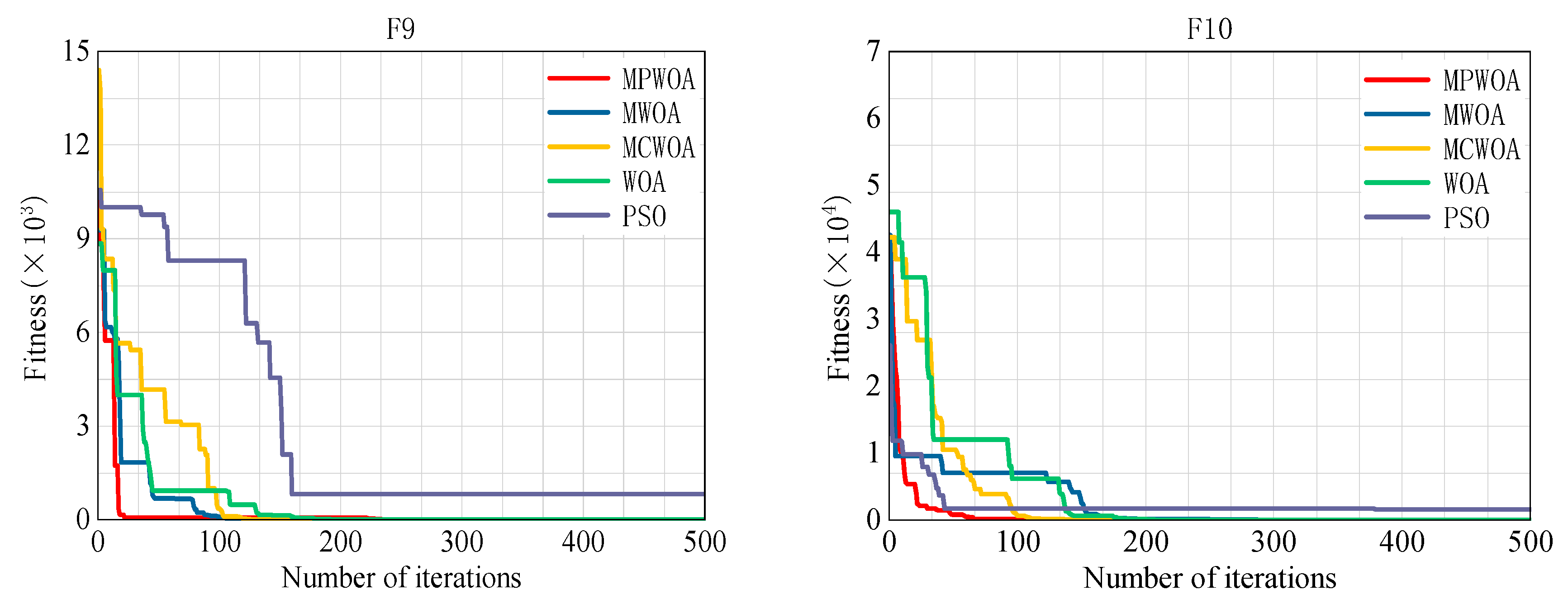
| Functions | Test Function Expression | Feasibility Domain | Optimal Value |
|---|---|---|---|
| F1 | [−100, 100] | 0 | |
| F2 | [−100, 100] | 0 | |
| F3 | [−30, 30] | 0 | |
| F4 | [−1.28, 1.28] | 0 | |
| F5 | [−100, 100] | 0 | |
| F6 | [−500, 500] | −12,569.487 | |
| F7 | [−5.12, 5.12] | 0 | |
| F8 | [−600, 600] | 0 | |
| F9 | Among them | [−50, 50] | 0 |
| F10 | [−5.12, 5.12] | 0 |
| Test Functions | Algorithmic Optimum | ||||
|---|---|---|---|---|---|
| MPWOA | MWOA | MCWOA | WOA | PSO | |
| F1 | 1.13 × 10−71 | 2.52 × 10−32 | 8.03 × 10−63 | 1.64 × 10−26 | 0.3239 |
| F2 | 5.28 × 10−23 | 4.28 × 10−5 | 7.85 × 10−3 | 5.01 × 10−7 | 0.6244 |
| F3 | 15.0864 | 16.1746 | 17.1548 | 16.9633 | 8.79 × 108 |
| F4 | 5.99 × 10−5 | 1.28 × 10−3 | 0.1176 | 8.989 × 10−5 | 6.41 × 108 |
| F5 | 0.000178 | 0.251984 | 1.33 × 10−3 | 2.26 × 10−3 | 3809.7982 |
| F6 | −1187.71 | −1114.33 | −1088.04 | −1095.59 | −1106.23 |
| F7 | 0 | 0 | 0 | 2.84 × 10−14 | 0 |
| F8 | 0 | 0 | 0 | 0 | 1.4588 |
| F9 | 0.1428 | 0.2746 | 0.7013 | 0.9088 | 820.1237 |
| F10 | 0 | 15.0585 | 0 | 0 | 1625.7943 |
| Indicator | MPWOA | MWOA | MCWOA | WOA | PSO |
|---|---|---|---|---|---|
| Average value (104 kW·h) | 168,051.21 | 164,804.43 | 164,347.42 | 166,049.07 | 166,685.63 |
| Maximum value (104 kW·h) | 172,836.05 | 172,702.91 | 172,561.43 | 171,719.24 | 170,696.97 |
| Minimum value (104 kW·h) | 162,994.47 | 159,330.34 | 157,867.30 | 159,728.75 | 160,727.26 |
| Standard deviation | 2197.72 | 3112.21 | 3942.29 | 2836.56 | 2707.31 |
| Computation time (seconds) | 7.19 | 7.71 | 7.23 | 8.07 | 7.67 |
| Indicator | MPWOA | MWOA | MCWOA | WOA | PSO |
|---|---|---|---|---|---|
| Average value (104 kW·h) | 9192.654 | 6793.043 | 8355.873 | 8045.079 | 9047.433 |
| Maximum value (104 kW·h) | 9193.198 | 6799.317 | 8401.596 | 8152.287 | 9132.499 |
| Minimum value (104 kW·h) | 9176.902 | 6768.352 | 8260.771 | 7851.573 | 9044.499 |
| Standard deviation | 2.925 | 5.042 | 61.241 | 136.059 | 15.796 |
| Computation time (seconds) | 0.4322 | 0.6134 | 0.5356 | 0.5262 | 0.5531 |
| Indicator | MPWOA | MWOA | MCWOA | WOA | PSO |
|---|---|---|---|---|---|
| Average value (104 kW·h) | 2071.464 | 1194.661 | 1691.218 | 2069.064 | 2069.145 |
| Maximum value (104 kW·h) | 2071.464 | 1194.661 | 1691.218 | 2069.169 | 2069.184 |
| Minimum value (104 kW·h) | 2071.464 | 1194.661 | 1691.218 | 2069.184 | 2069.064 |
| Standard deviation | 1.818 × 10−13 | 9.094 × 10−13 | 9.094 × 10−13 | 0.040951 | 0.056184 |
| Computation time (seconds) | 0.83 | 0.95 | 1.02 | 0.96 | 0.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Zhou, G.; Liu, B.; Huang, D.; Yu, H.; Mo, L. Multi-Timescale Nested Hydropower Station Optimization Scheduling Based on the Migrating Particle Whale Optimization Algorithm. Energies 2025, 18, 1780. https://doi.org/10.3390/en18071780
Zhang M, Zhou G, Liu B, Huang D, Yu H, Mo L. Multi-Timescale Nested Hydropower Station Optimization Scheduling Based on the Migrating Particle Whale Optimization Algorithm. Energies. 2025; 18(7):1780. https://doi.org/10.3390/en18071780
Chicago/Turabian StyleZhang, Mi, Guosheng Zhou, Bei Liu, Dajun Huang, Hao Yu, and Li Mo. 2025. "Multi-Timescale Nested Hydropower Station Optimization Scheduling Based on the Migrating Particle Whale Optimization Algorithm" Energies 18, no. 7: 1780. https://doi.org/10.3390/en18071780
APA StyleZhang, M., Zhou, G., Liu, B., Huang, D., Yu, H., & Mo, L. (2025). Multi-Timescale Nested Hydropower Station Optimization Scheduling Based on the Migrating Particle Whale Optimization Algorithm. Energies, 18(7), 1780. https://doi.org/10.3390/en18071780






