A Bi-Level Capacity Optimization Method for Hybrid Energy Storage Systems Combining the IBWO and MVMD Algorithms
Abstract
1. Introduction
- (1)
- The bi-level optimization model achieves an optimal balance between the configuration of the energy storage system and the scheduling strategy through the coordinated optimization of both the inner and outer layers. This results in an operational solution that effectively balances economic considerations with stability.
- (2)
- The IBWO incorporates the reverse elite strategy, vertical and horizontal crossover, and whirlwind scavenging strategy. These enhancements increase population diversity, facilitate global exploration, and mitigate the risk of local optima. Consequently, this method demonstrates improved speed and accuracy compared to three other widely used algorithms.
- (3)
- The electric–hydrogen hybrid storage technology is integrated with modal decomposition-based scheduling. By employing the MVMD algorithm to decompose power signals, batteries can swiftly respond to short-term load fluctuations, while the hydrogen storage offers substantial power support for large-scale, long-duration storage. This combination significantly enhances both the efficiency and the reliability of the microgrid.
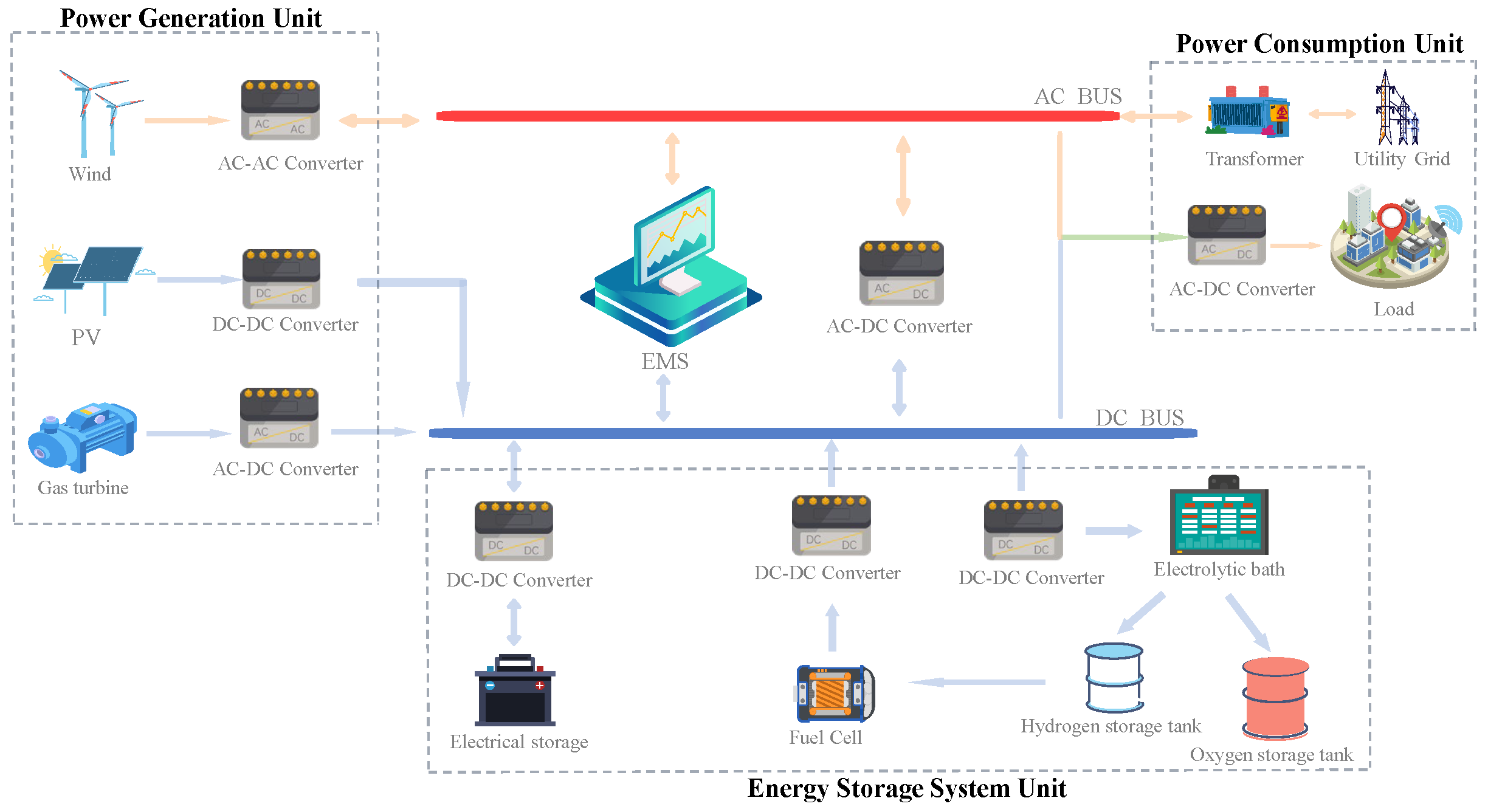
2. Wind–Solar–Hybrid Energy Storage of Microgrid Model
2.1. Wind Power Generation Model
2.2. Photovoltaic System Model
2.3. Battery Model
2.4. Hydrogen Energy Storage Model
2.5. The Model of the Microgas Turbine
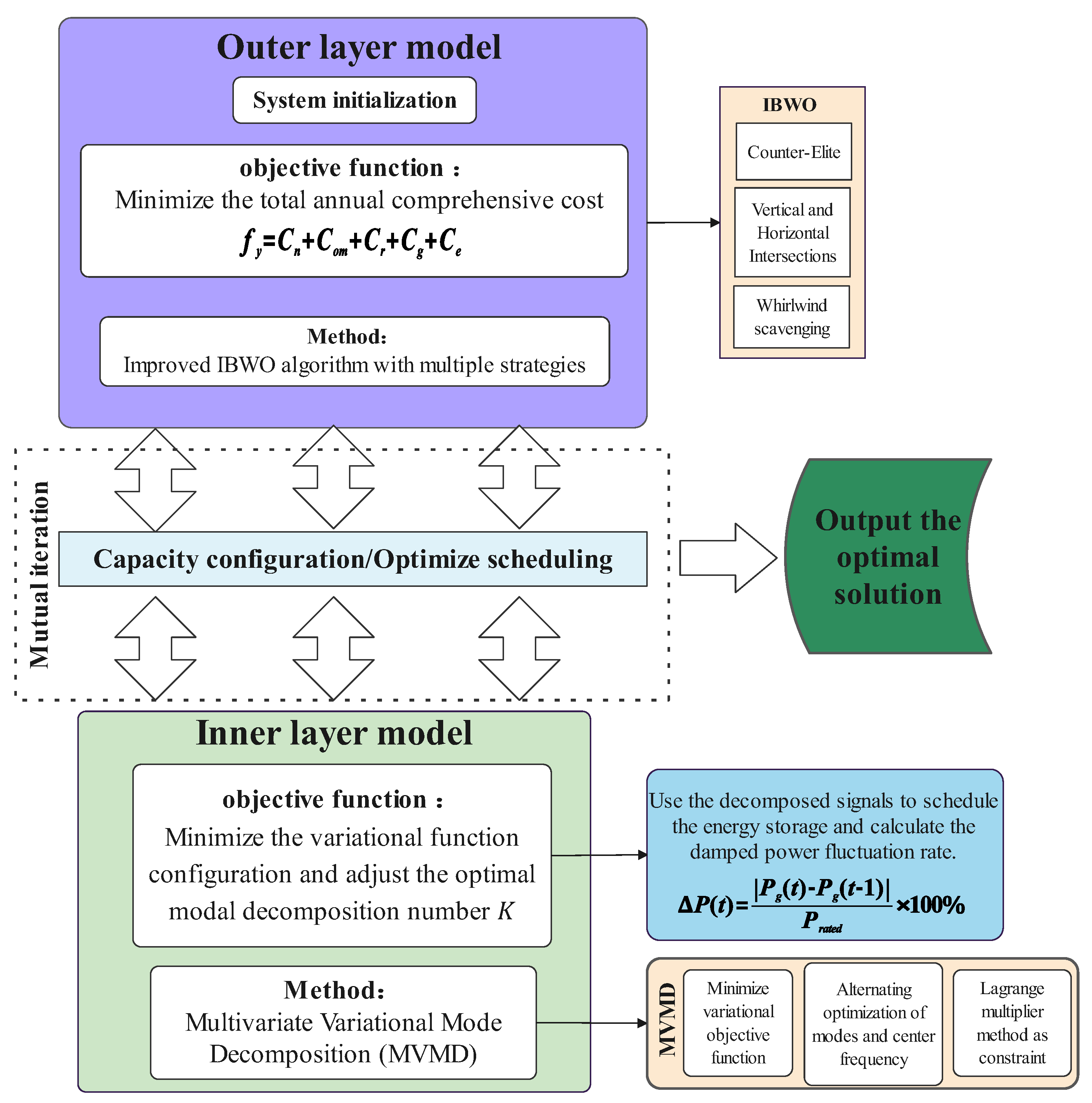
3. The Bi-Level Optimization Model for Microgrids
3.1. Outer Layer Optimization Model
3.1.1. Outer Objective Function
3.1.2. Outer Constraints
3.2. Inner Layer Optimization Model
3.2.1. Inner Objective Function
3.2.2. Inner Constraint
3.3. Evaluating Indicator
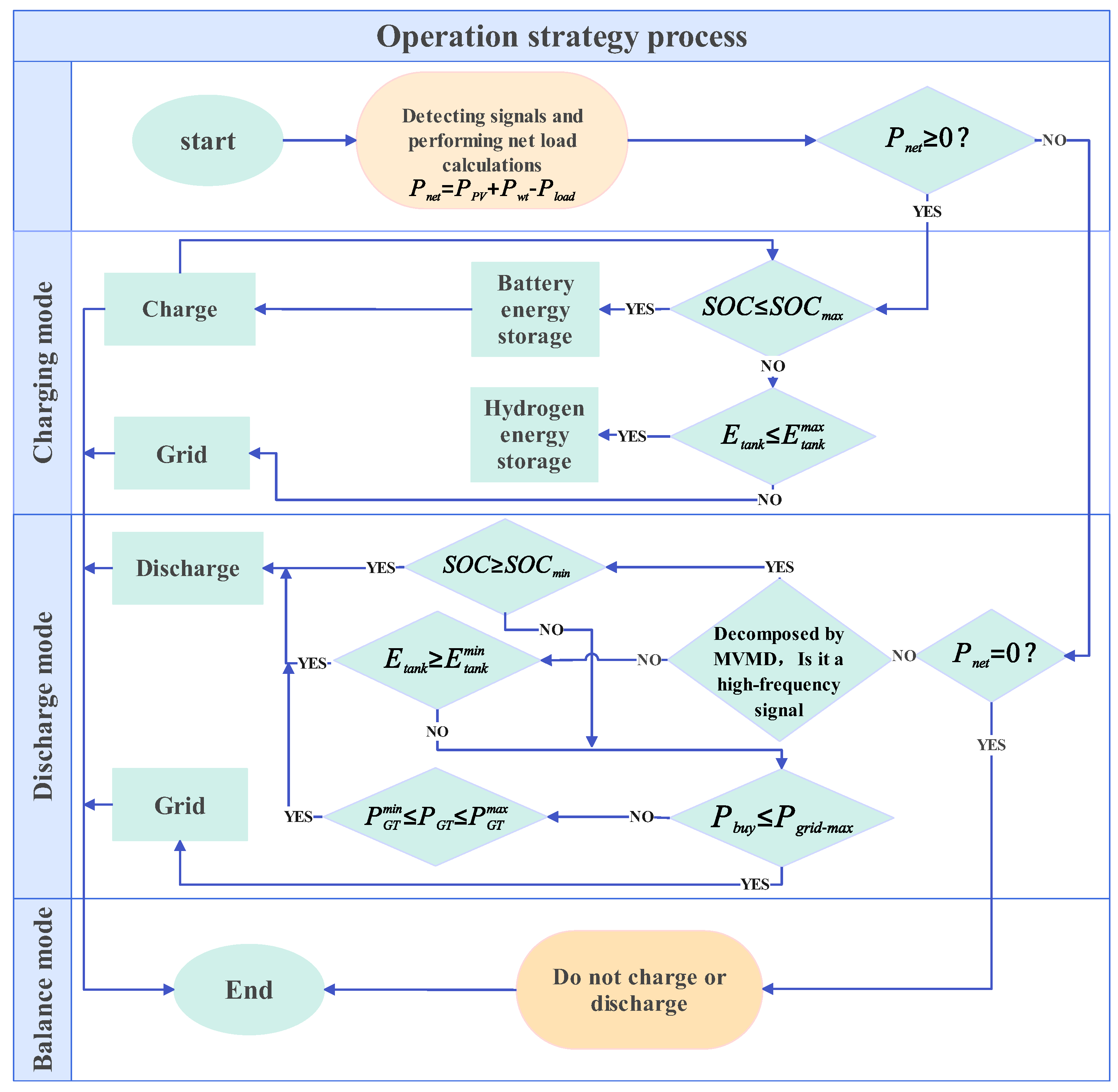
3.4. Operation Strategy
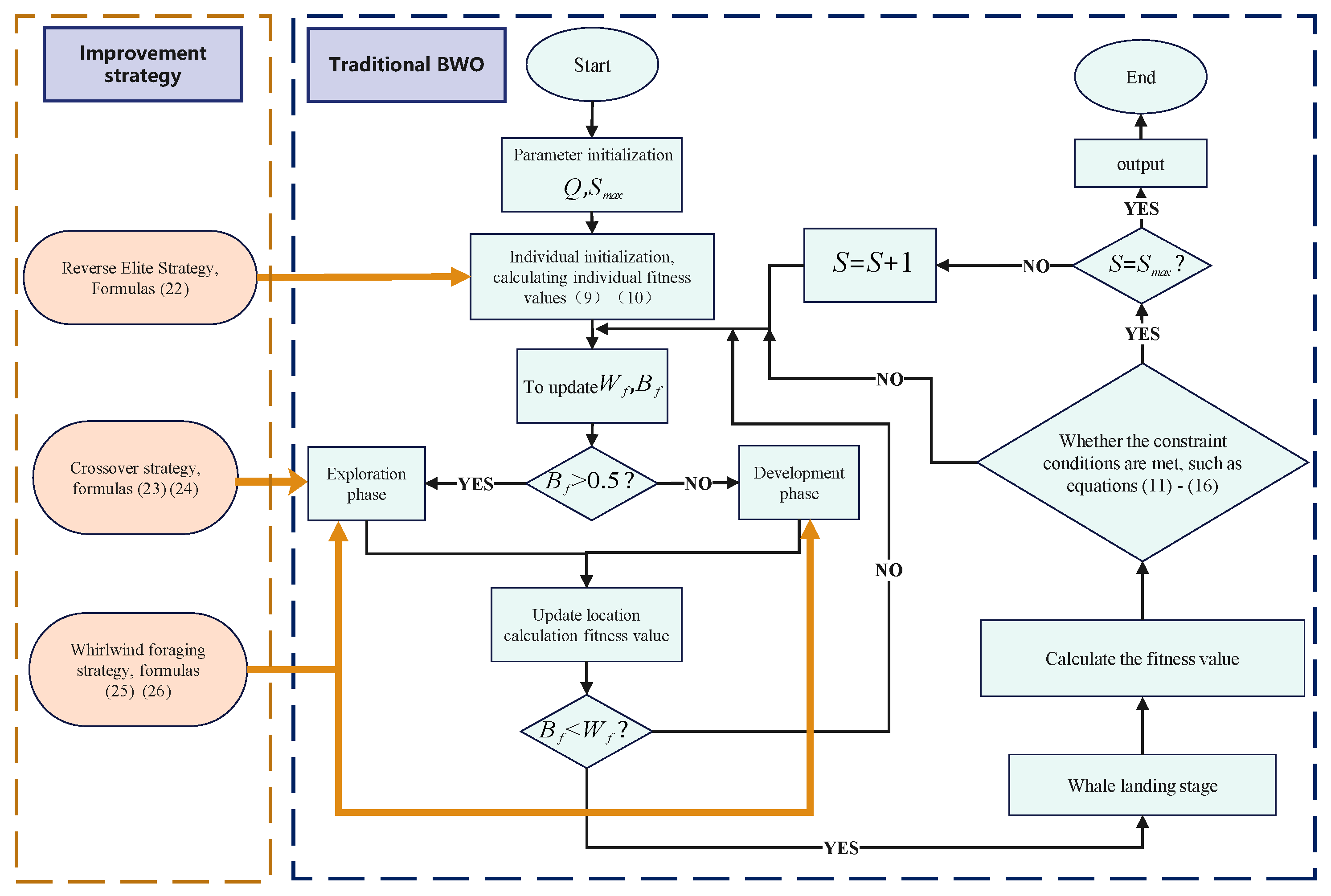
4. IBWO
4.1. Reverse Elite Strategy
4.2. Vertical and Horizontal Crossover Operation
4.2.1. Horizontal Crossover Operation
4.2.2. Vertical Crossover Operation
4.3. Whirlwind Scavenging Strategy
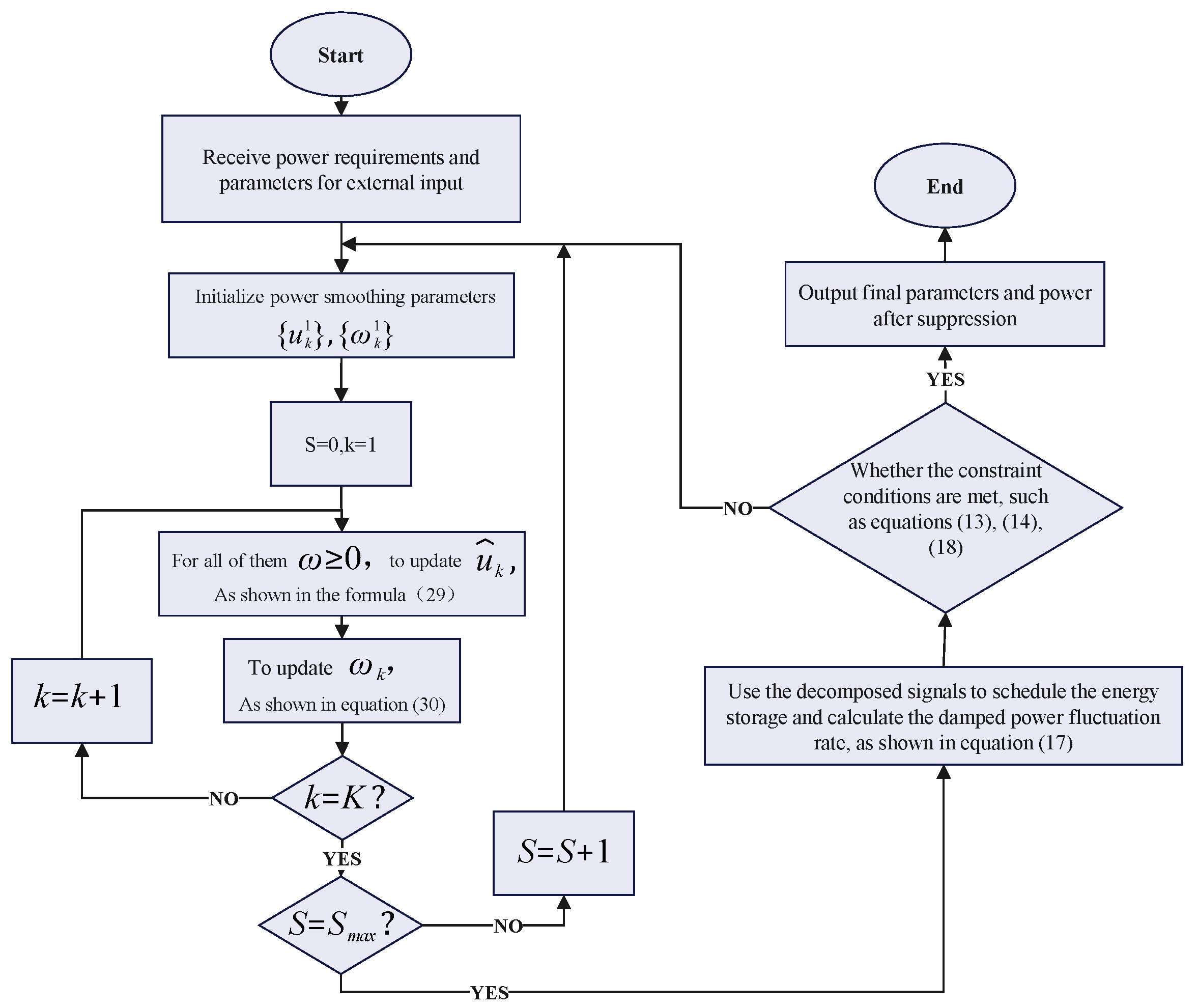
4.4. The Optimization Process of IBWO
5. MVMD
5.1. Formulation of the Variational Problem
5.2. Solution of Variational Problem
5.3. Optimization Process of MVMD
6. Example Analysis
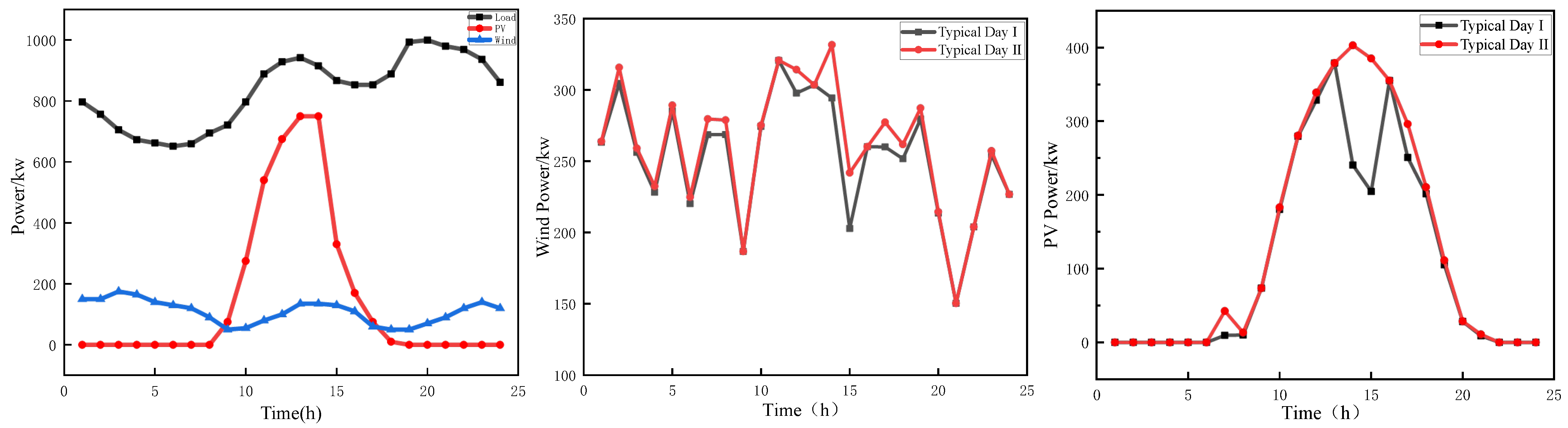
6.1. Data Preparation
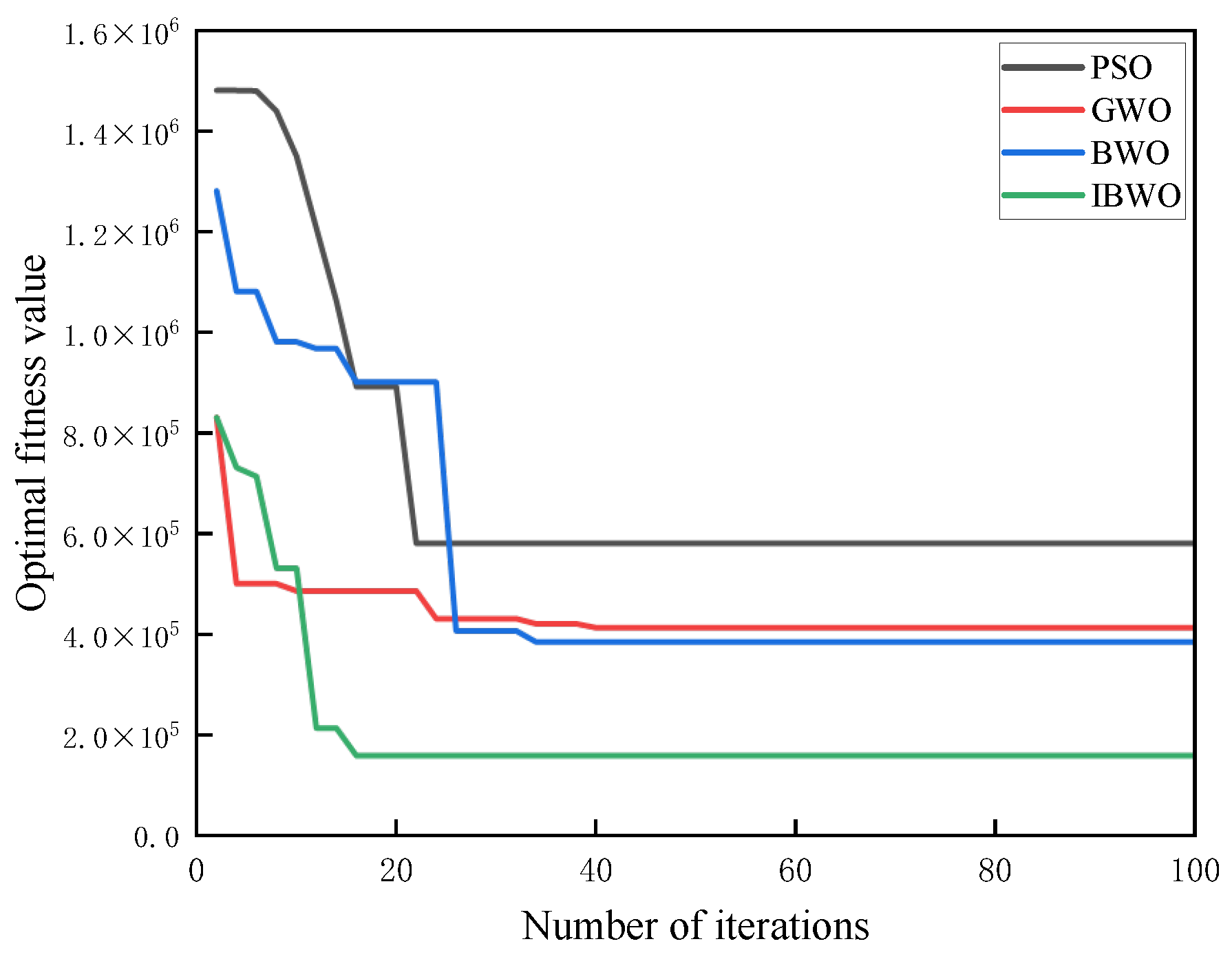
6.2. Comparison and Analysis of IBWO and Other Algorithms
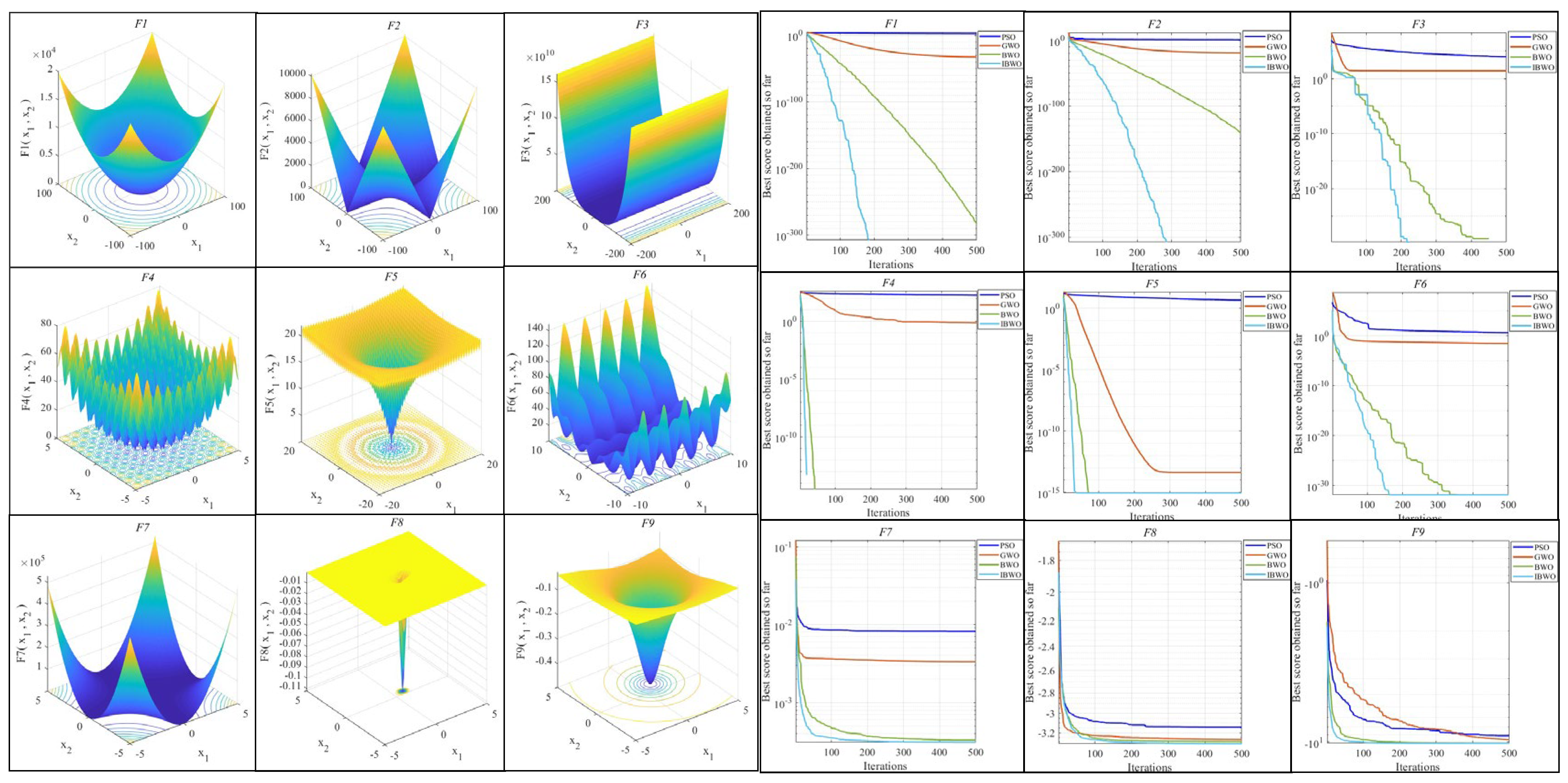
6.2.1. Verifying IBWO Algorithm Performance
6.2.2. Comparison with Other Test Functions
6.3. Comparative Analysis of MVMD Performance
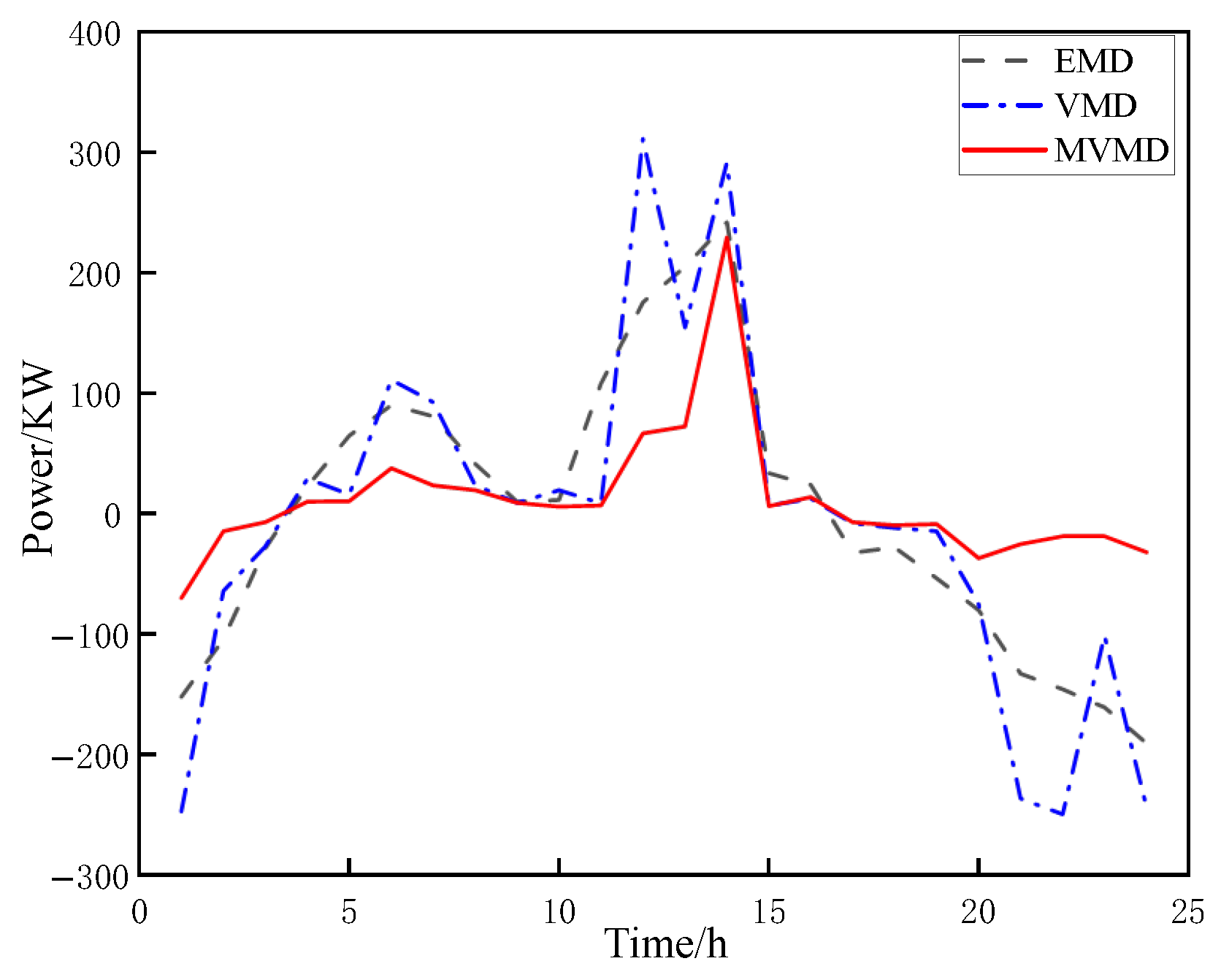
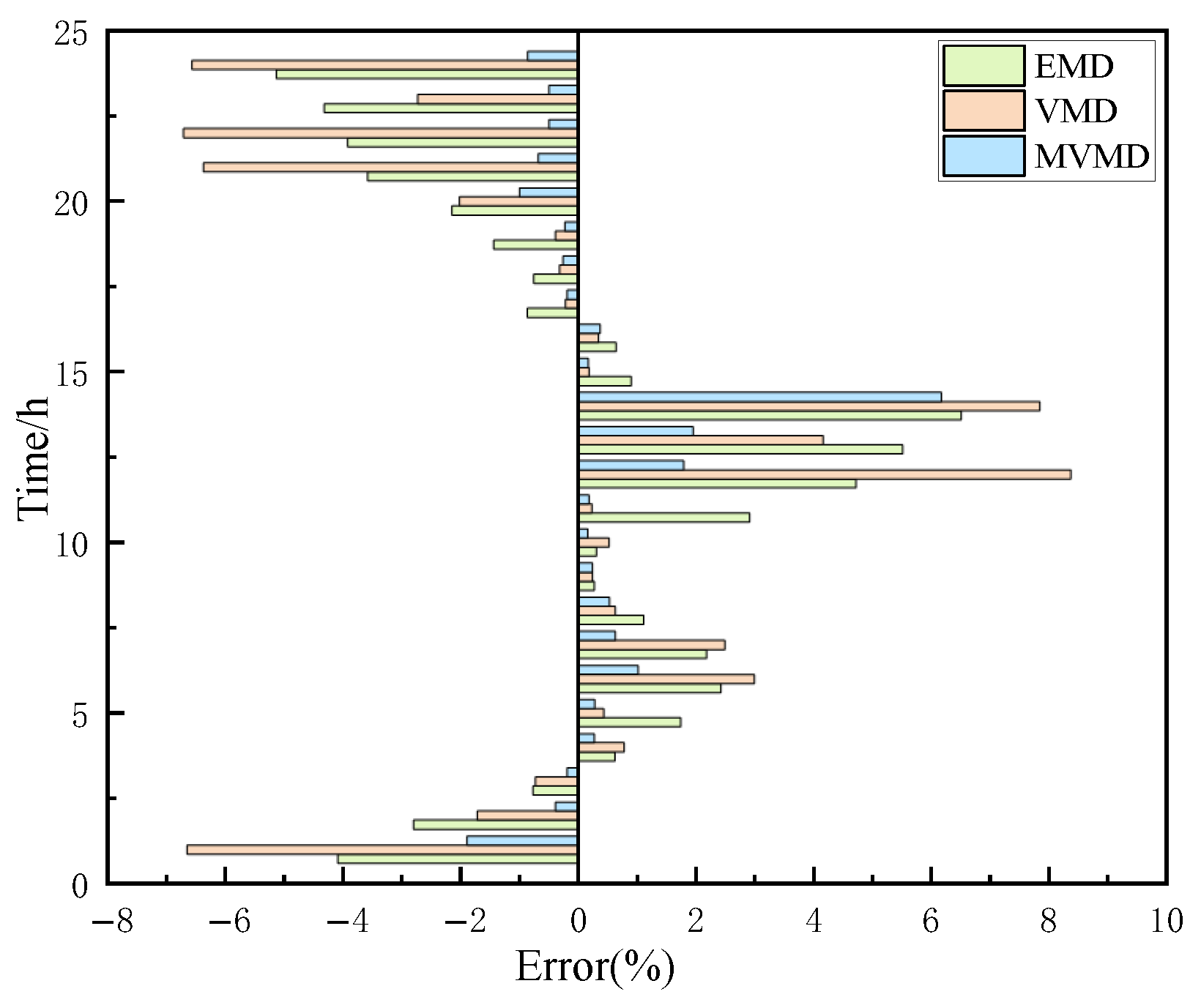
6.3.1. MVMD Compared to Other Modal Decomposition Strategies
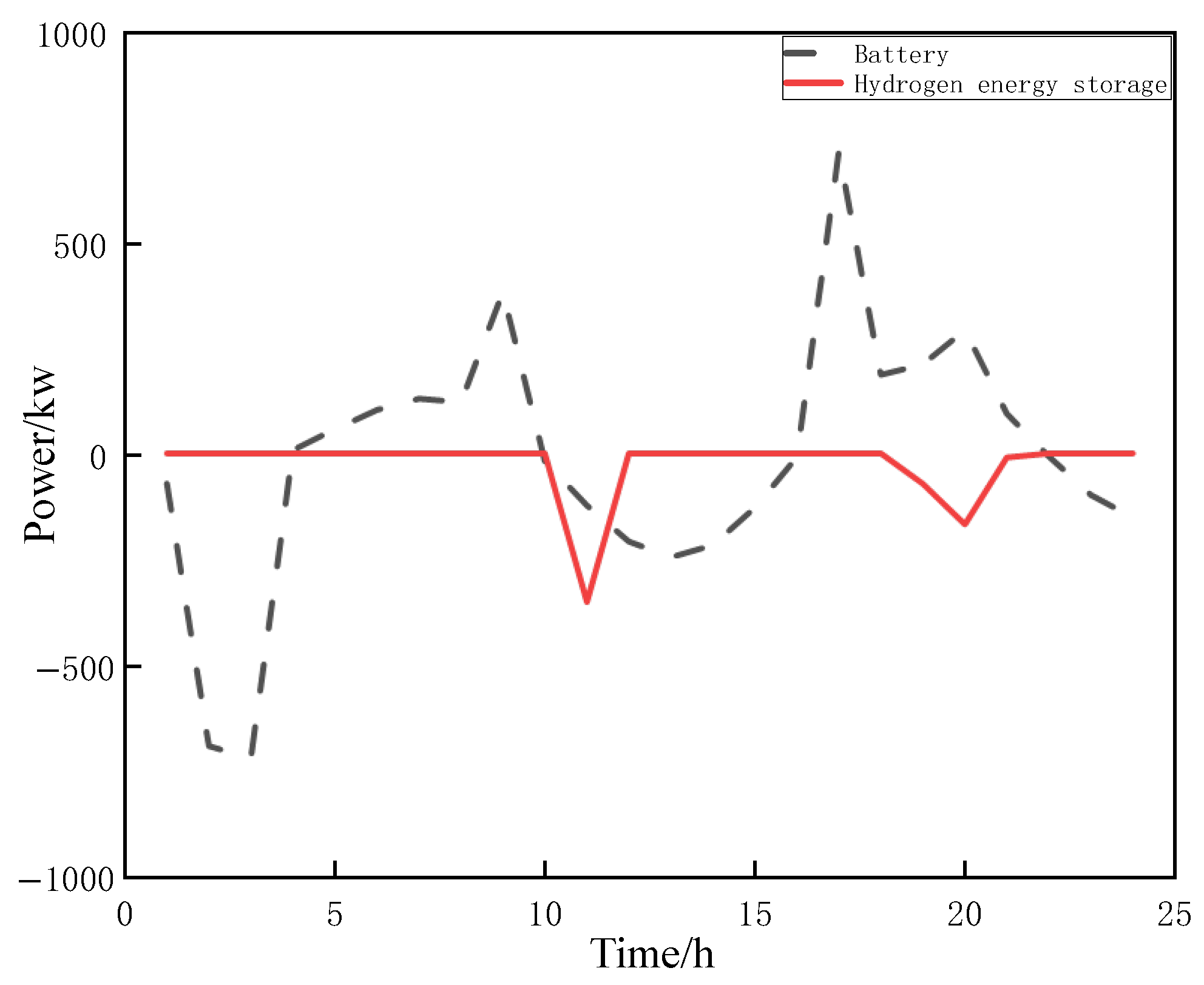
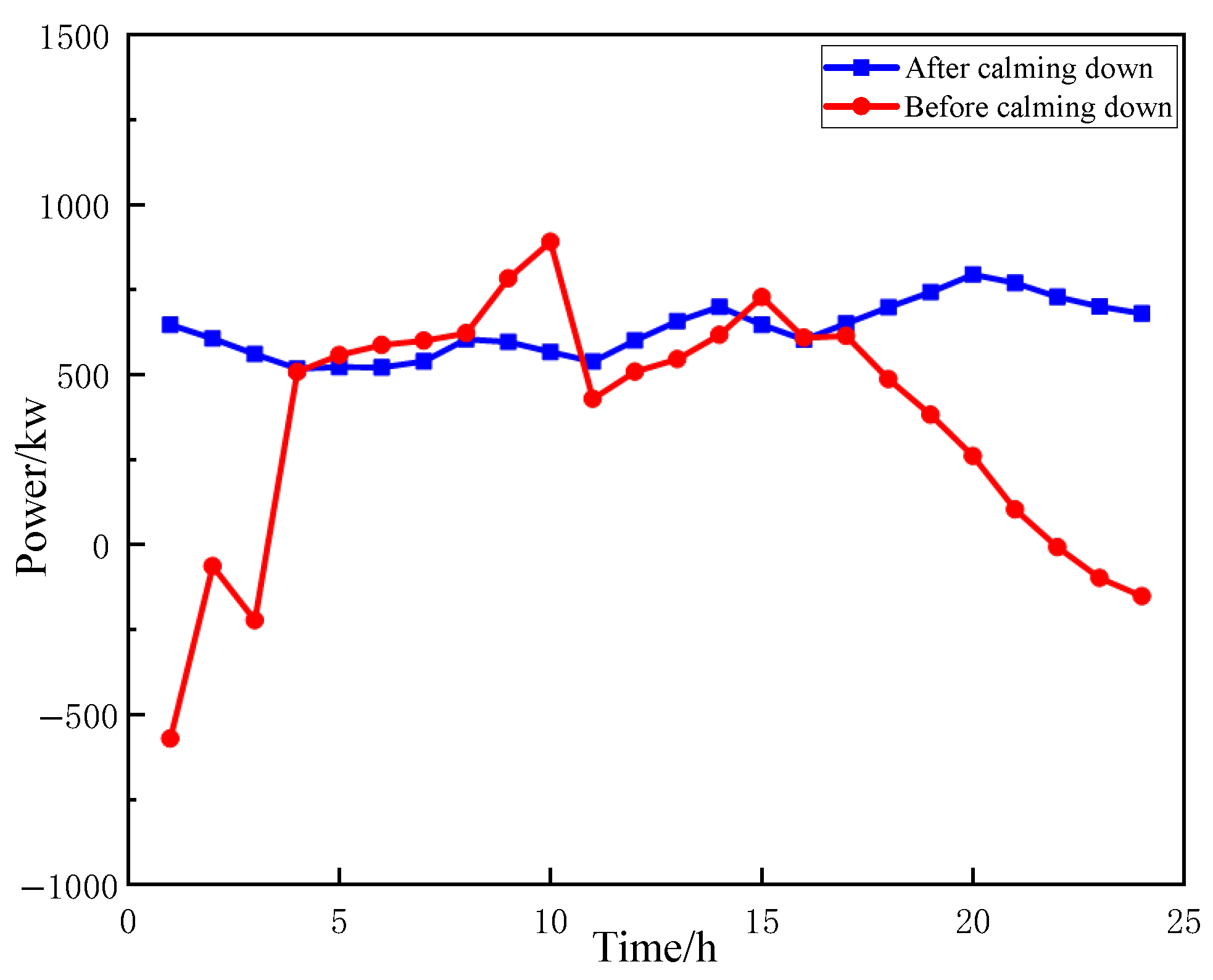
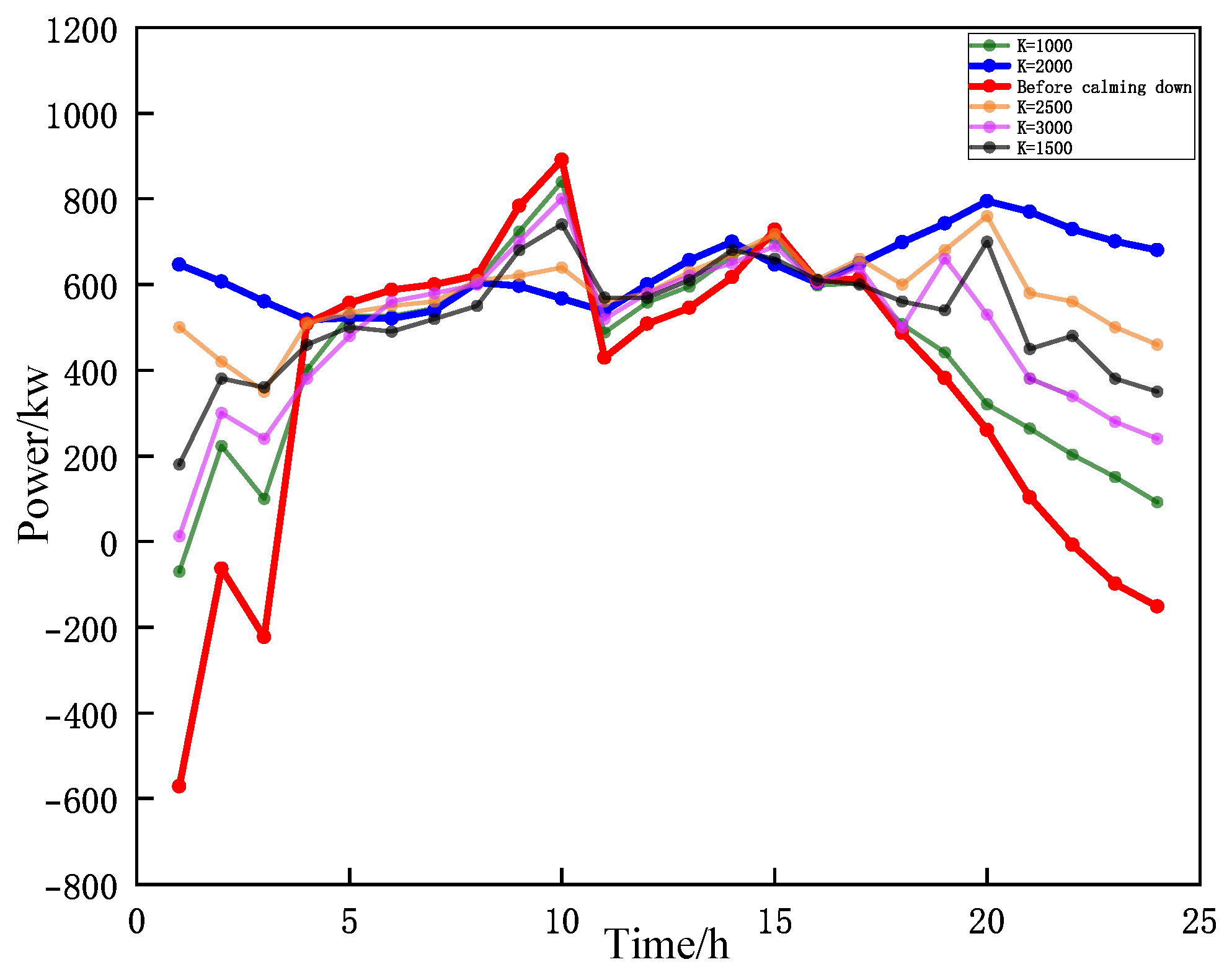
6.3.2. Analysis of Power Fluctuation Smoothing Effect and Power Allocation Results in Hybrid Energy Storage Systems
6.4. Multiscenario Comparison
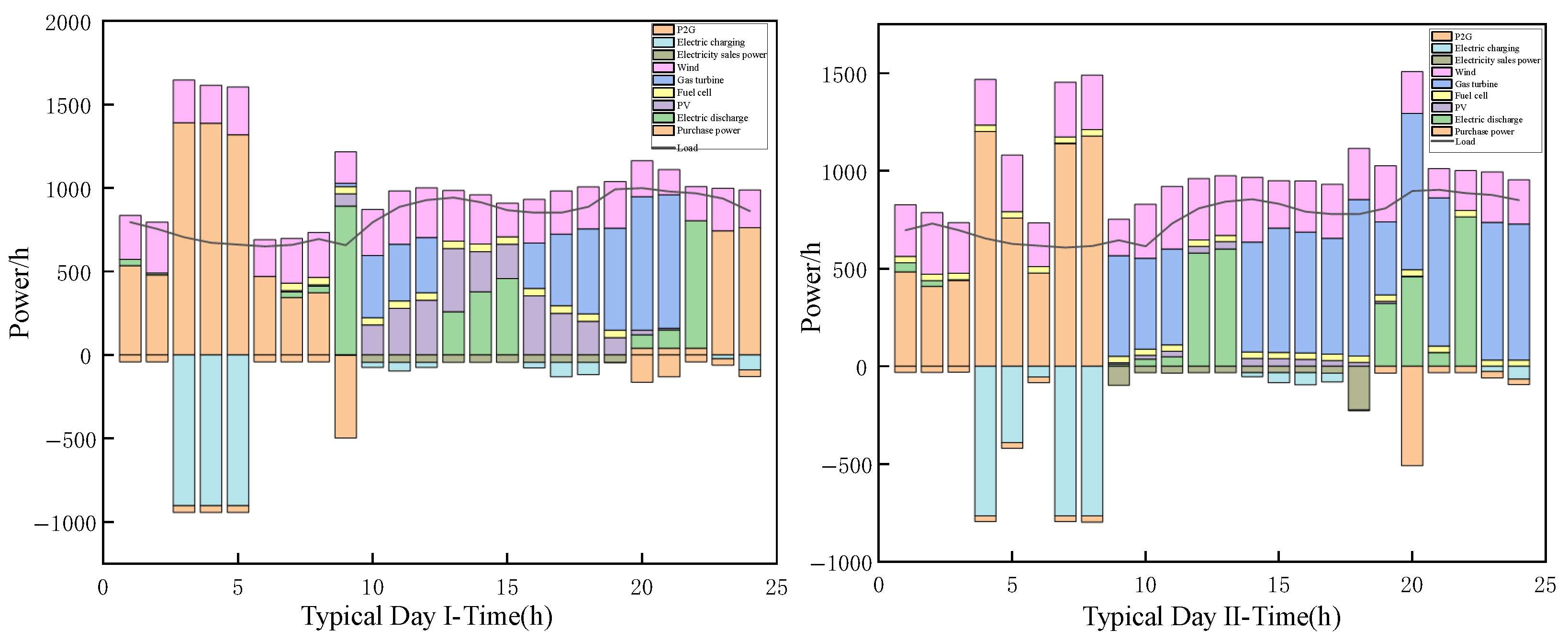
6.5. Results and Optimal Capacity Analysis
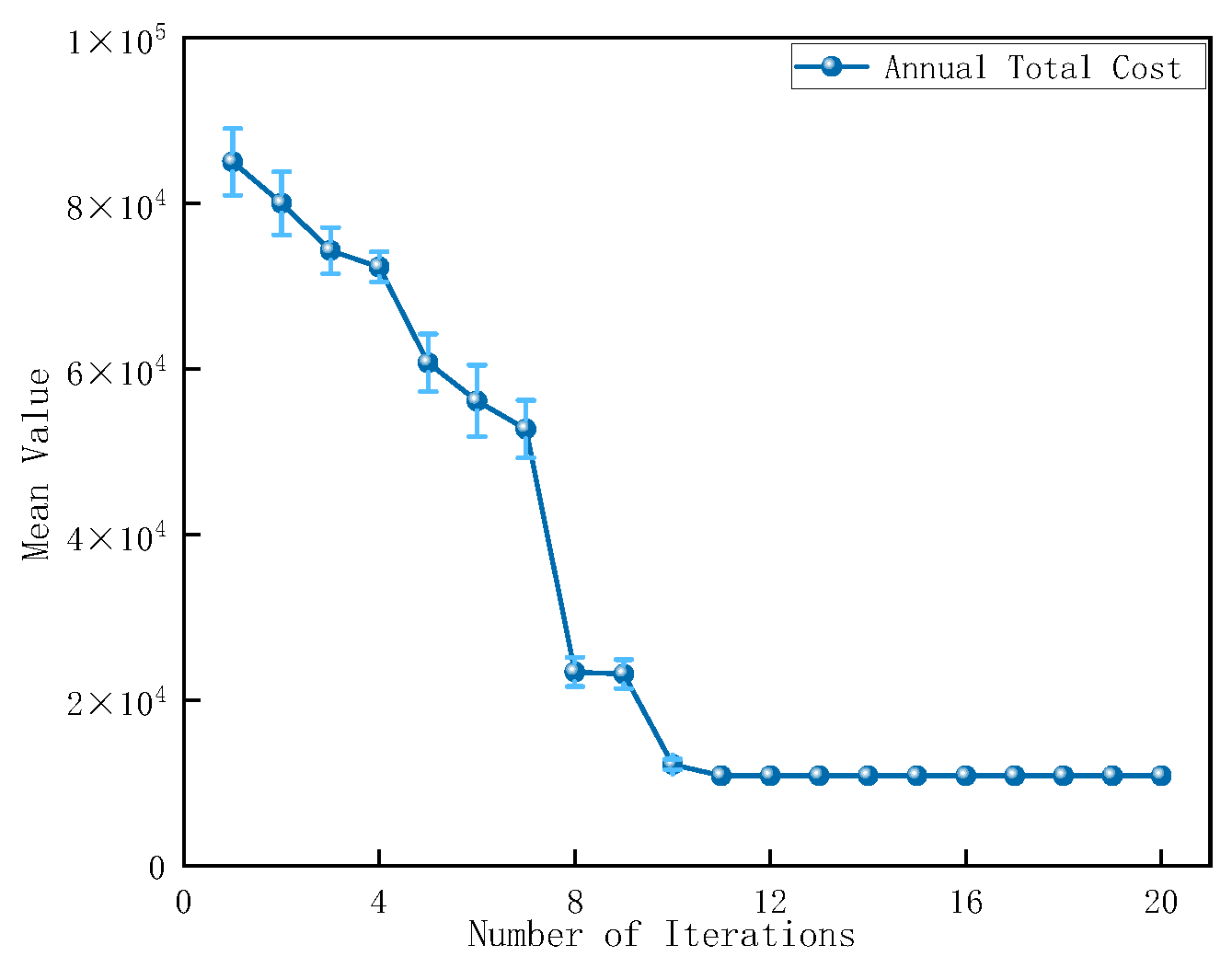
6.6. Sensitivity Testing
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gan, C.K.; Tan, Y.C.; Wong, K.H. Microgrid and its applications: A review. J. Clean. Prod. 2018, 186, 773–783. [Google Scholar]
- Mohsin, N.; Jha, S.K. Optimal design of microgrids with hybrid energy storage systems. Energies 2019, 12, 2708. [Google Scholar]
- Liang, Y.; Chen, W.; Zhang, Y. A survey on swarm intelligence algorithms. J. Comput. Sci. 2019, 30, 239–249. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Yuan, J. Swarm Intelligence Algorithms for Portfolio Optimization Problems: Overview and Recent Advances. Mob. Inf. Syst. 2022, 2022, 4241049. [Google Scholar] [CrossRef]
- Feng, Z.; Liu, H.; Zhang, Y. An adaptive particle swarm optimization algorithm based on chaotic mapping. Appl. Sci. 2020, 10, 5637. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, J.; Guo, C. Application of improved particle swarm optimization in power system optimization. Energy Rep. 2021, 7, 251–258. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J.; He, Y.; Zhang, Y.; Liu, Y.; Yan, K. Multi-objective optimization scheduling of microgrids based on improved particle swarm optimization algorithm. Electr. Power Sci. Eng. 2021, 37, 1–10. [Google Scholar]
- Liu, C.; Sun, Z. Green flexible production and intelligent factory building structure design based on improved ant colony algorithm. Therm. Sci. Eng. Prog. 2024, 53, 102753. [Google Scholar] [CrossRef]
- Fan, H.; Wu, H.; Li, S.; Han, S.; Ren, J.; Huang, S.; Zou, H. Optimal Scheduling Method of Combined Wind–Photovoltaic–Pumped Storage System Based on Improved Bat Algorithm. Processes 2025, 13, 101. [Google Scholar] [CrossRef]
- Huang, Z.; Bei, L.; Wang, B.; Xu, L. Capacity optimization configuration for a park-level hybrid energy storage system based on an improved cuckoo algorithm. Processes 2024, 12, 718. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, L. White whale optimization algorithm for optimal sizing of energy storage systems in microgrids. Renew. Energy 2020, 148, 1347–1357. [Google Scholar]
- Zhou, X.; Li, J. Application of white whale optimization algorithm in renewable energy systems. Renew. Energy 2021, 45, 57–69. [Google Scholar]
- Zhao, N.; Zhang, L.; Li, D.; Huang, W.; Xie, W.; Yang, Y. Capacity optimization configuration method for wind-solar-hydrogen-storage microgrids based on improved honey badger algorithm. J. Electr. Eng. 2025, 20, 338–351. [Google Scholar]
- Liao, X.; Lei, R.; Ouyang, S.; Huang, W. Capacity Optimization Allocation of Multi-Energy-Coupled Integrated Energy System Based on Energy Storage Priority Strategy. Energies 2024, 17, 5261. [Google Scholar] [CrossRef]
- Liu, Y.J.; Wang, J.F.; Liu, K.S. Dynamic modal analysis for power fluctuation in microgrid systems. Energy Rep. 2020, 5, 567–573. [Google Scholar]
- Farhangi, H.R. Control strategies for energy management in microgrids using modal decomposition. Renew. Energy 2021, 163, 511–520. [Google Scholar]
- Zhang, Y.; Li, M.; Wang, L. A comprehensive review of modal decomposition techniques: Emd, vmd, and their applications. IEEE Access 2020, 8, 175054–175075. [Google Scholar]
- Lei, S.; He, Y.; Zhang, J.; Deng, K. Optimal configuration of hybrid energy storage capacity in a microgrid based on variational mode decomposition. Energies 2023, 16, 4307. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, W.; Chen, J. Power oscillation damping using empirical mode decomposition and adaptive control. IEEE Trans. Power Syst. 2021, 36, 1534–1543. [Google Scholar]
- Feng, C.; Wang, Y.; Zhang, J. Multiscale variational mode decomposition for fault detection in microgrids. IEEE Access 2020, 8, 129425–129436. [Google Scholar]
- Zhang, X.; Liu, Q.; Wang, Y. Application of multiscale variational mode decomposition in microgrid stability analysis. Renew. Energy 2021, 167, 227–237. [Google Scholar]
- Li, X.; Zhang, H. Application of mvmd in power smoothing of microgrids with renewable energy integration. IEEE Trans. Sustain. Energy 2021, 12, 1590–1599. [Google Scholar]
- Zhang, Y.; Chen, L.; Wang, J. Comparison and improvement of mvmd and vmd for power smoothing in microgrids. Electr. Power Syst. Res. 2020, 189, 106742. [Google Scholar]
- Liu, Y.; Zhao, Q. Case study of mvmd in power output stabilization for photovoltaic integrated microgrids. J. Renew. Sustain. Energy 2023, 15, 043001. [Google Scholar]
- El-Sharkawy, M.M.; Shakib, A.S. Modal decomposition for energy storage optimization in microgrids. J. Energy Storage 2022, 48, 103501. [Google Scholar]
- Liu, Y.; Zhang, X.; Li, T. Energy storage systems and their applications in microgrids: A review. Renew. Sustain. Energy Rev. 2020, 121, 109738. [Google Scholar]
- Zhou, Y.; Liu, F. The role of flywheel energy storage in microgrid operations: A review. Renew. Sustain. Energy Rev. 2019, 109, 109–120. [Google Scholar]
- Yang, Y.; Zhang, X.; Chen, J. Performance analysis of lithium-ion batteries in microgrids: A case study. J. Energy Storage 2020, 28, 101198. [Google Scholar]
- Gao, H.; Zhang, Z. Optimal sizing and control of supercapacitors in microgrid applications. IEEE Trans. Power Electron. 2022, 37, 1394–1403. [Google Scholar]
- Sutikno, T.; Arsadiando, W.; Wangsupaphol, A.; Yudhana, A.; Facta, M. A review of recent advances on hybrid energy storage system for solar photovoltaics power generation. IEEE Access 2022, 10, 42346–42359. [Google Scholar]
- Zheng, Y.; Wang, J.; Zhou, L. Energy management strategies for hybrid energy storage systems in microgrids: A comprehensive review. Renew. Sustain. Energy Rev. 2019, 107, 189–205. [Google Scholar]
- Krishan, O.; Suhag, S. A novel control strategy for a hybrid energy storage system in a grid-independent hybrid renewable energy system. Int. Trans. Electr. Energy Syst. 2020, 30, e12262. [Google Scholar] [CrossRef]
- Jiang, S.; Wang, Q.; Zhang, Y. Coordinated control strategy of hybrid energy storage system for microgrids. IEEE Trans. Power Syst. 2020, 35, 1002–1013. [Google Scholar]
- Tang, Y.; Xun, Q.; Liserre, M.; Yang, H. Energy management of electric-hydrogen hybrid energy storage systems in photovoltaic microgrids. Int. J. Hydrogen Energy 2024, 80, 1–10. [Google Scholar]
- Li, J.; Xiao, Y.; Lu, S. Optimal configuration of multi microgrid electric hydrogen hybrid energy storage capacity based on distributed robustness. J. Energy Storage 2024, 76, 109762. [Google Scholar] [CrossRef]
- Liu, S.; Wu, J.; Xu, Y. A review of hybrid energy storage systems in microgrid applications. Appl. Energy 2020, 261, 114364. [Google Scholar]
- Liu, Y.; Chen, G. Optimization of hybrid energy storage systems combining battery and hydrogen storage for renewable energy applications. Appl. Energy 2021, 283, 116369. [Google Scholar]
- Zhong, C.; Li, G.; Meng, Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowl.-Based Syst. 2022, 251, 109215. [Google Scholar]
| Type | Method | Advantage | Limitation | References |
|---|---|---|---|---|
| Algorithm | PSO | Fast convergence speed and strong adaptability | Local convergence, limited accuracy | [5,6,7] |
| ACO | Slightly stronger global search | Slow convergence speed | [8] | |
| BA | Slightly stronger global search | Local convergence, slow convergence speed | [9] | |
| BWO | Strong global exploration ability and fast convergence speed | Need to finely adjust parameters | [11,12] | |
| IBWO | Superior stability and convergence speed, suitable for high uncertainty systems | More complex calculations | - | |
| Mode decomposition | EMD | High decomposition accuracy | Need to set the number of modes reasonably | [18] |
| VMD | High precision, capable of processing complex signals | Reasonably set the number of modes | [19] | |
| MVMD | Processing multidimensional signals with high accuracy and adaptive adjustment of modal numbers | The model complexity is higher and the calculation is more complex | [20,21,22,23,24] | |
| Model | Single level | Simple and fast calculation | Single scope | [5,9] |
| Bi-level | Taking into account multiple objectives, the output solution is more applicable | More complex calculations | [10,11] |
| Parameter | Meaning | Parameter | Meaning |
|---|---|---|---|
| v | Real-time wind speed | Rated cut-in speed of wind turbine | |
| Rated cut-out speed of wind turbine | Efficiency of electrolytic cell | ||
| Rated speed of wind turbine | Fuel cell output power | ||
| Power derating coefficient | Hydrogen power input to the fuel cell | ||
| Rated power of photovoltaic panel | Fuel cell conversion efficiency | ||
| Solar irradiance intensity | Hydrogen storage efficiency | ||
| Ambient temperature | Hydrogen storage tank energy | ||
| Power temperature coefficient | Real power output of gas turbine | ||
| G | Actual irradiance | Operational efficiency of gas turbine | |
| Self-discharge rate of the battery | Fuel costs of diesel generators | ||
| Charging power of the battery | Temperature of the solar panel | ||
| Discharge power of the battery | Emission of k-type pollutants produced | ||
| Rated capacity of the battery | State of charge of the battery | ||
| Charging efficiency of the battery | Adjacent time intervals | ||
| Discharge efficiency of the battery | Battery capacity | ||
| T | Temperature of the photovoltaic panel surface | Electricity generation of diesel generators | |
| Operation and maintenance cost coefficient of diesel generators | Operation and maintenance costs of diesel generators | ||
| Input electrical power of the electrolytic cell | Pollutant emission control costs of diesel generators |
| Parameter | Meaning | Parameter | Meaning |
|---|---|---|---|
| Initial construction cost | The unit price of electricity sold | ||
| Replacement cost | The unit price of electricity purchased | ||
| Grid transaction cost | The power purchased | ||
| Environmental protection cost | The power sold | ||
| Annual operation and maintenance cost | The number of distributed power sources | ||
| The emissions of pollutant type r | The cost of pollutant treatment | ||
| Replacement cost coefficient | Trading power with the power grid | ||
| Minimum value of battery capacity | Gas turbine output power | ||
| Maximum capacity of battery | Charging power of electrolytic cell | ||
| Maximum charging power of battery | Load demand power | ||
| Maximum discharge power of battery | Maximum output power of the fan | ||
| Minimum output power of gas turbine | The output power of the wind turbine | ||
| Maximum output power of gas turbine | The discharging power of the fuel cell | ||
| Maximum output power of photovoltaics | The output power of the photovoltaic panel | ||
| The rated capacity of the i-th energy source | Maximum charging power of electrolytic cell | ||
| The life cycle of the i-th energy source | Maximum discharge power of fuel cells | ||
| Grid-connected power value after stabilization | Power limit for trading with the power grid | ||
| n | Types of distributed power sources | Abandoned renewable energy generation | |
| m | The types of distributed energy resources requiring replacement | The cost coefficient for treating pollutant type r | |
| Upper limit of capacity for hydrogen storage tank | Rated installed capacity of power generation system | ||
| Lower limit of capacity for hydrogen storage tank | Total electricity generation from renewable energy sources | ||
| The investment cost coefficient of the i-th energy source | The charging and discharging power of the battery | ||
| The annual operation and maintenance cost coefficient of the i-th energy source | Rated power generation of the i-th energy device | ||
| Maximum power fluctuation allowed by the system | Actual utilization of renewable energy generation |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.95 | 0.1 | ||
| 0.95 | 0.9 | ||
| 0.95 | 0.95 | ||
| 20 | 0.01 | ||
| 20 | 0.95 | ||
| 0.95 |
| Parameter | WT | PV | Gas Turbine | Grid |
|---|---|---|---|---|
| Upper power limit (kw) | 800 | 500 | 1000 | 1500 |
| Power lower limit (kw) | 0 | 0 | 0 | 1500 |
| Upper limit of climbing power (kw/min) | - | - | 400 | 1000 |
| Type of Project | Construction Cost (CNY/k) | Operation and Maintenance Cost (CNY/kW·year) | Disposal Cost (CNY/k) | Service Life/Year |
|---|---|---|---|---|
| WT | 12,000 | 589 | 540 | 20 |
| PV | 3200 | 150 | 144 | 20 |
| Electrolytic tank | 6360 | 236 | 286.2 | 10 |
| Fuel cell | 3000 | 132 | 135 | 20 |
| Hydrogen storage unit | 3500 | 170 | 157.5 | 20 |
| Oxygen storage device | 3200 | 120 | 144 | 20 |
| Gas turbine | 1500 | 70 | 67.5 | 20 |
| Pollutant Type | Treatment Cost /(CNY)/kg | Pollutant Emission Coefficient | |||
|---|---|---|---|---|---|
| WT | PV | Gas Turbine | Grid | ||
| 0.023 | 0 | 0 | 724 | 889 | |
| 6 | 0 | 0 | 0.0036 | 1.8 | |
| 8 | 0 | 0 | 0.2 | 1.6 | |
| Classification | Period of Time | Electricity Price /(CNY/kWh) | Electricity Sales /(CNY/kWh) |
|---|---|---|---|
| Peak time period | 10:00–11:00, 18:00–22:00 | 0.9320 | 0.72 |
| Ordinary time period | 08:00–09:00, 12:00–17:00 | 0.6213 | 0.53 |
| Valley time period | 01:00–07:00, 23:00–24:00 | 0.3107 | 0.28 |
| Algorithm | Cost of Electricity Purchase and Sales | Energy Storage Cost | Gas Purchase Cost | Environmental Cost | Income from Oxygen Sales | Energy Abandonment Value | Total Cost |
|---|---|---|---|---|---|---|---|
| IBWO | 2213.591101 | 6880.081639 | 4482.360625 | 917.4613181 | 4678 | 1054 | 10,869.49468 |
| PSO | 2273.132626 | 8270.405543 | 4348.431902 | 958.8278697 | 4532 | 2545 | 13,863.79794 |
| BWO | 2068.658942 | 5640.479227 | 4633.431902 | 1078.525926 | 4406 | 2537 | 11,552.096 |
| GWO | 2184.59231 | 6510.659613 | 4272.663356 | 901.3143863 | 4235 | 2125 | 11,759.22967 |
| Algorithm | P2G | Fuel Cell | Electric Energy Storage | Hydrogen Energy Storage | Gas Turbine | P2G | Discard Rate |
|---|---|---|---|---|---|---|---|
| IBWO | 800 | 39.81576152 | 718.2345711 | 93.05151524 | 800 | 103 | 1.03% |
| PSO | 900 | 43.02271848 | 589.4736842 | 88.80429703 | 800 | 267 | 2.67% |
| BWO | 1200 | 43.02271848 | 459.7164407 | 108.9891041 | 800 | 276 | 2.76% |
| GWO | 1000 | 1118.002234 | 1096.20901 | 164.0792016 | 120 | 279 | 2.79% |
| Typical Day | Decomposition Mode Number | Grid-Connected Mode Number | Battery | Hydrogen Energy Storage | Total Cost |
|---|---|---|---|---|---|
| Typical Day I | 1500 | 1 | 750 | 180 | 8753 |
| Typical Day II | 2000 | 2 | 718 | 93 | 6880 |
| Scenario | Battery | Hydrogen Energy Storage | Single-Level | Bi-Level |
|---|---|---|---|---|
| 1 | ✓ | |||
| 2 | ✓ | ✓ | ||
| 3 | ✓ | ✓ | ||
| 4 | ✓ | ✓ | ✓ | |
| 5 | ✓ | ✓ | ✓ |
| Scenario | PV | Wind | P2G | Fuel Cell | Electric Energy Storage | Hydrogen Energy Storage | Gas Turbine |
|---|---|---|---|---|---|---|---|
| 1 | 750 | 175 | 0 | 0 | 0 | 0 | 0 |
| 2 | 750 | 175 | 0 | 0 | 1200 | 0 | 0 |
| 3 | 750 | 175 | 0 | 0 | 0 | 300 | 0 |
| 4 | 750 | 175 | 850 | 50 | 752.1 | 102 | 785 |
| 5 | 750 | 175 | 800 | 39.81576 | 718.2346 | 93.05152 | 750 |
| Scenario | Cost of Electricity Purchase and Sales | Energy Storage Cost | Gas Purchase Cost | Environmental Cost | Income from Oxygen Sales | Energy Abandonment Value | Total Cost |
|---|---|---|---|---|---|---|---|
| 1 | 20,761.06341 | 0 | 8052 | 1568 | 0 | 2015 | 32,396.06341 |
| 2 | 11,863.46481 | 11,161.1 | 5046 | 1256 | 0 | 1842 | 31,168.56974 |
| 3 | 6779.122747 | 9498.813 | 5023 | 963.3344 | 4677 | 1785 | 19,372.26984 |
| 4 | 3873.784427 | 8084.096 | 4896.2 | 963.3344 | 3985 | 1161.508 | 14,993.92274 |
| 5 | 2213.591101 | 6880.082 | 4482.361 | 917.4613 | 4678 | 1054 | 10,869.49468 |
| Typical Day | PV | Wind | P2G | Fuel Cell | Electric Energy Storage | Hydrogen Energy Storage | Gas Turbine |
|---|---|---|---|---|---|---|---|
| Day I | 40.2978 | 334.6501 | 1200 | 32.6456 | 765.2968 | 297.6342 | 800 |
| Day II | 378.9116 | 320.6967 | 1200 | 44.5213 | 902.889 | 2595.1159 | 800 |
| Cost Reduction Coefficient of Energy Storage Equipment | Electric Energy Storage | Hydrogen Energy Storage | Hybrid Energy Storage Cost | Total Cost |
|---|---|---|---|---|
| 5% | 728.6739068 | 107.0092425 | 8744.086882 | 10,652.10479 |
| 10% | 677.8947368 | 102.1249416 | 8134.736842 | 13,586.52198 |
| 15% | 812.3 | 125.3374698 | 9747.6 | 11,321.05408 |
| 20% | 832.6075 | 188.6910818 | 9991.29 | 11,524.04507 |
| 25% | 836.7705375 | 190.5779927 | 10,041.24645 | 11,662.33361 |
| 30% | 840.9543902 | 223.2 | 10,091.45268 | 11,559.70508 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Q.; Li, S.; Qiu, D.; Long, Y.; Liao, Q.; Yin, X.; Li, Y.; Qian, K. A Bi-Level Capacity Optimization Method for Hybrid Energy Storage Systems Combining the IBWO and MVMD Algorithms. Energies 2025, 18, 1777. https://doi.org/10.3390/en18071777
Xing Q, Li S, Qiu D, Long Y, Liao Q, Yin X, Li Y, Qian K. A Bi-Level Capacity Optimization Method for Hybrid Energy Storage Systems Combining the IBWO and MVMD Algorithms. Energies. 2025; 18(7):1777. https://doi.org/10.3390/en18071777
Chicago/Turabian StyleXing, Qiaoqiao, Shidong Li, Da Qiu, Yang Long, Qinyi Liao, Xiangjin Yin, Yunxiang Li, and Kai Qian. 2025. "A Bi-Level Capacity Optimization Method for Hybrid Energy Storage Systems Combining the IBWO and MVMD Algorithms" Energies 18, no. 7: 1777. https://doi.org/10.3390/en18071777
APA StyleXing, Q., Li, S., Qiu, D., Long, Y., Liao, Q., Yin, X., Li, Y., & Qian, K. (2025). A Bi-Level Capacity Optimization Method for Hybrid Energy Storage Systems Combining the IBWO and MVMD Algorithms. Energies, 18(7), 1777. https://doi.org/10.3390/en18071777






