Electrochemical–Thermal Model of a Lithium-Ion Battery
Abstract
1. Introduction
Types of Battery Modeling
2. Model Implementation
2.1. Battery Chemistry
2.2. Electrochemical–Thermal Mathematical Model
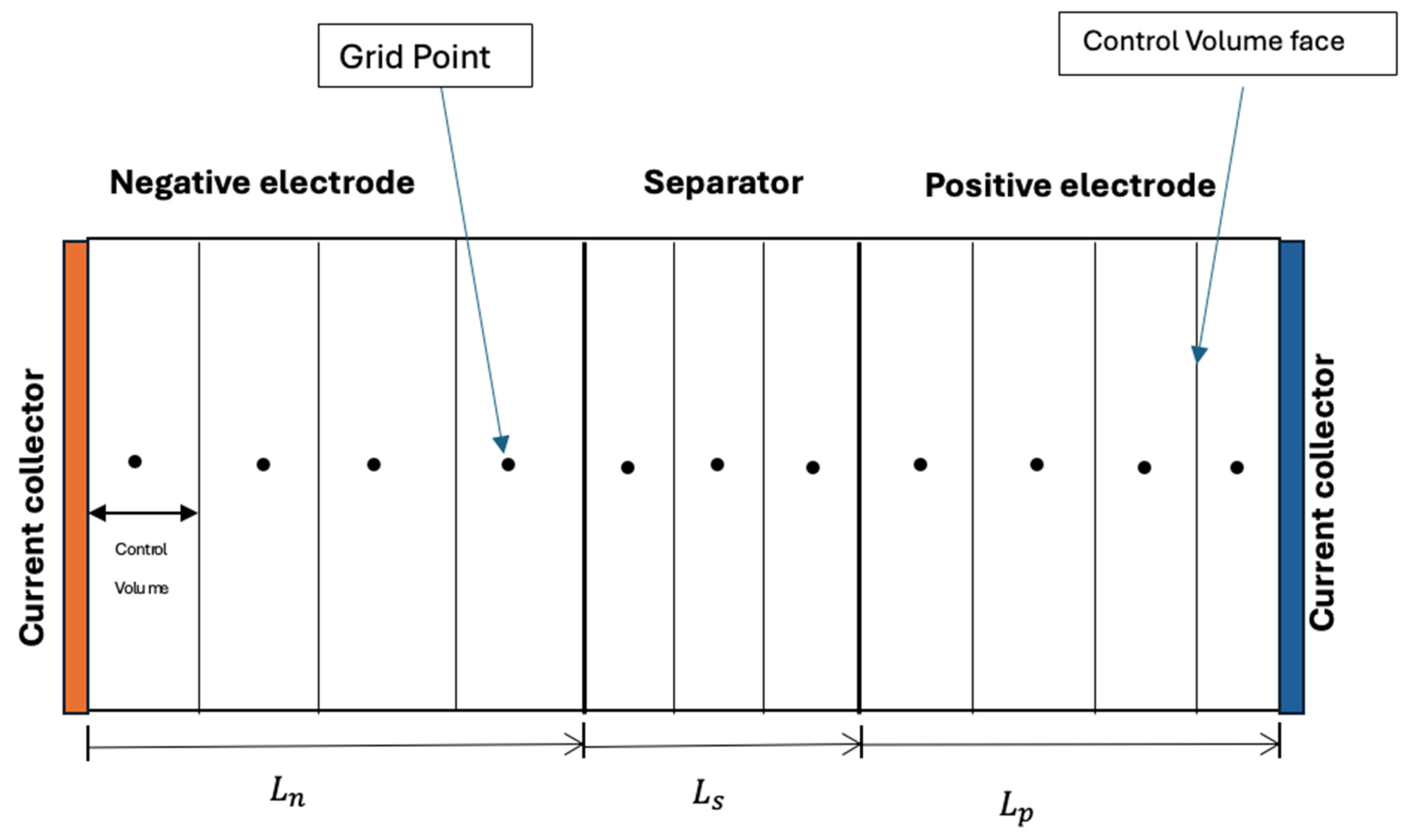
2.3. Computer Algorithm
3. Results
3.1. Electrochemical Model Verification
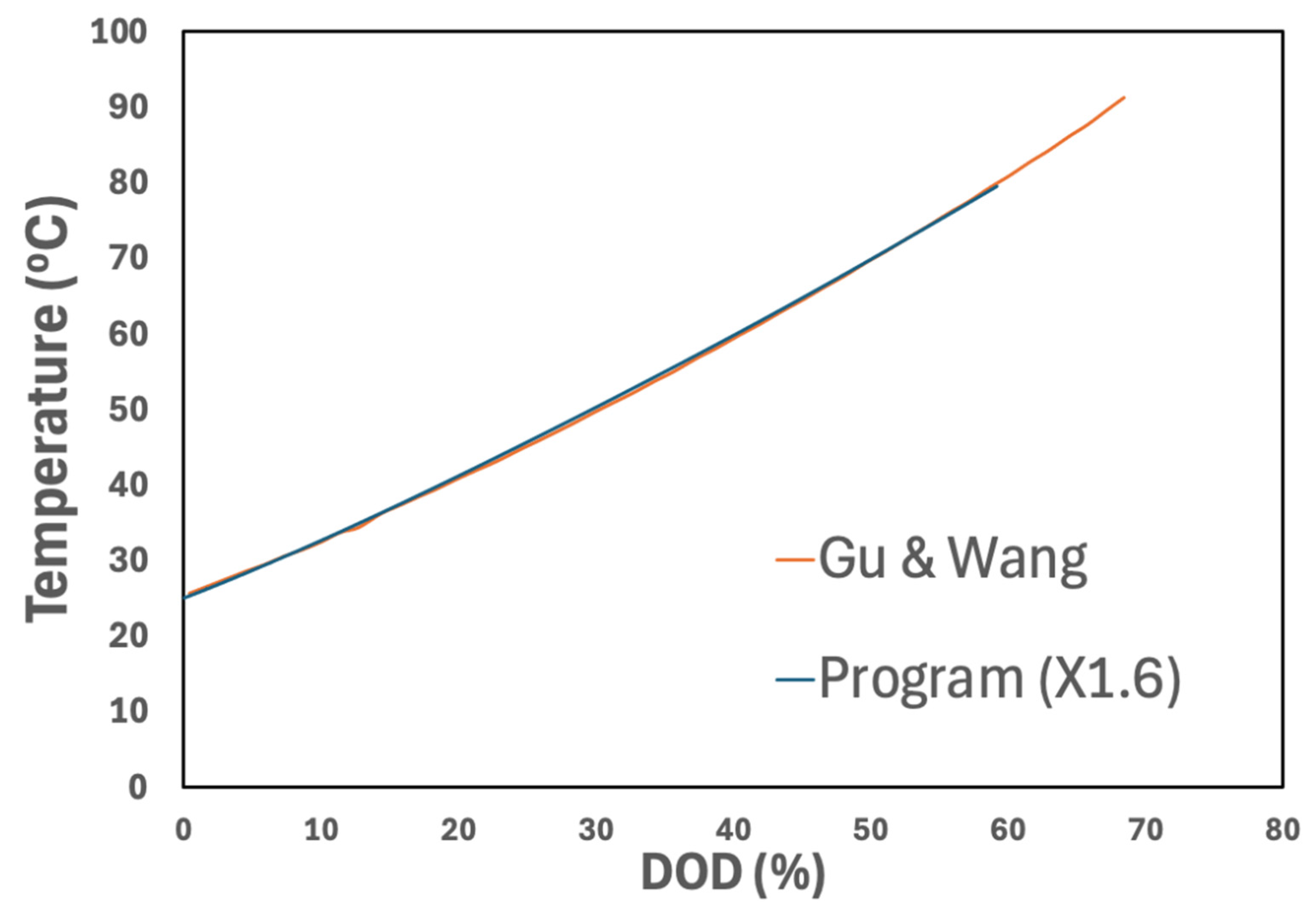
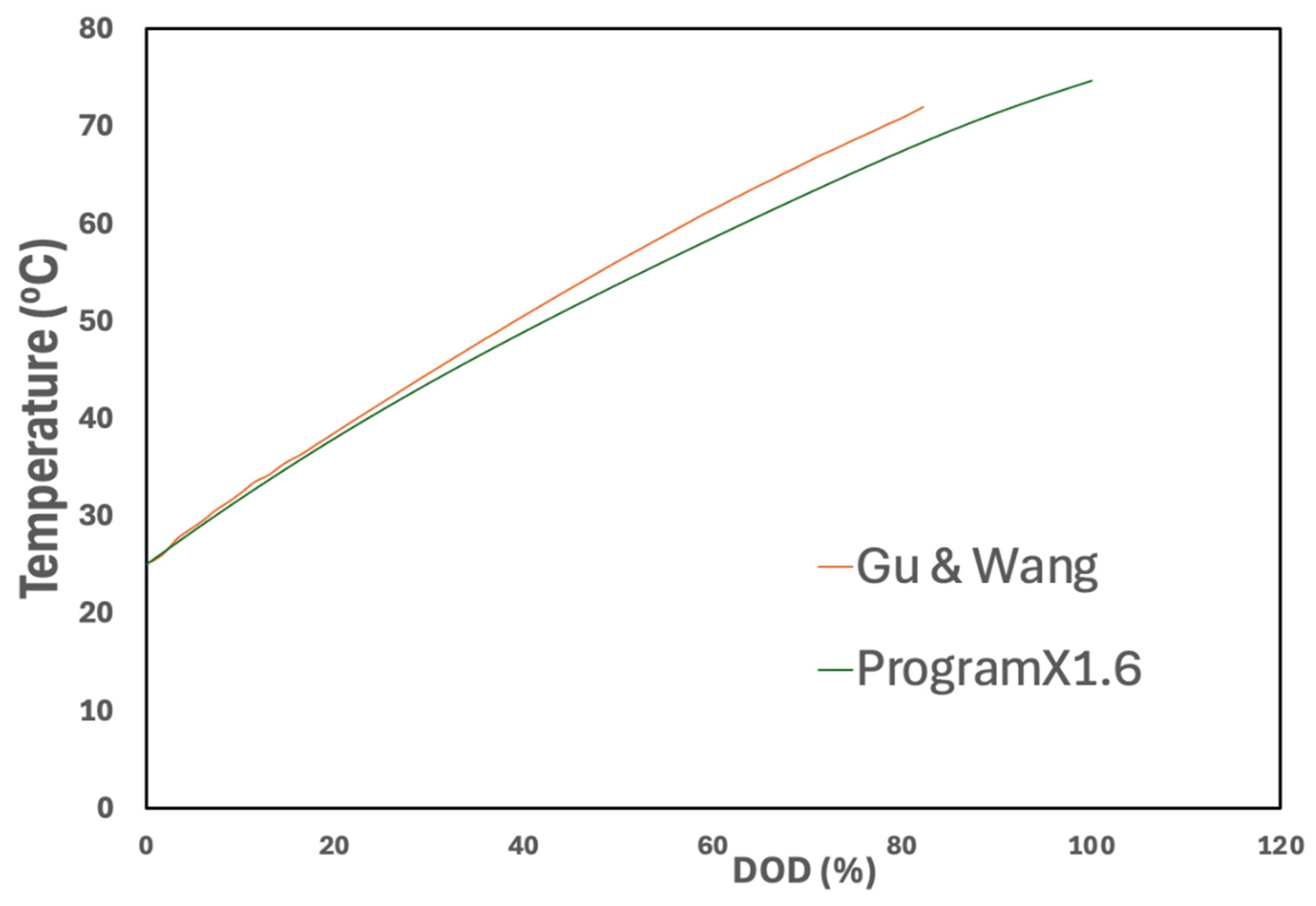
3.2. Electrochemical–Thermal Model Results
3.2.1. Cell Voltages
3.2.2. Cell Temperatures
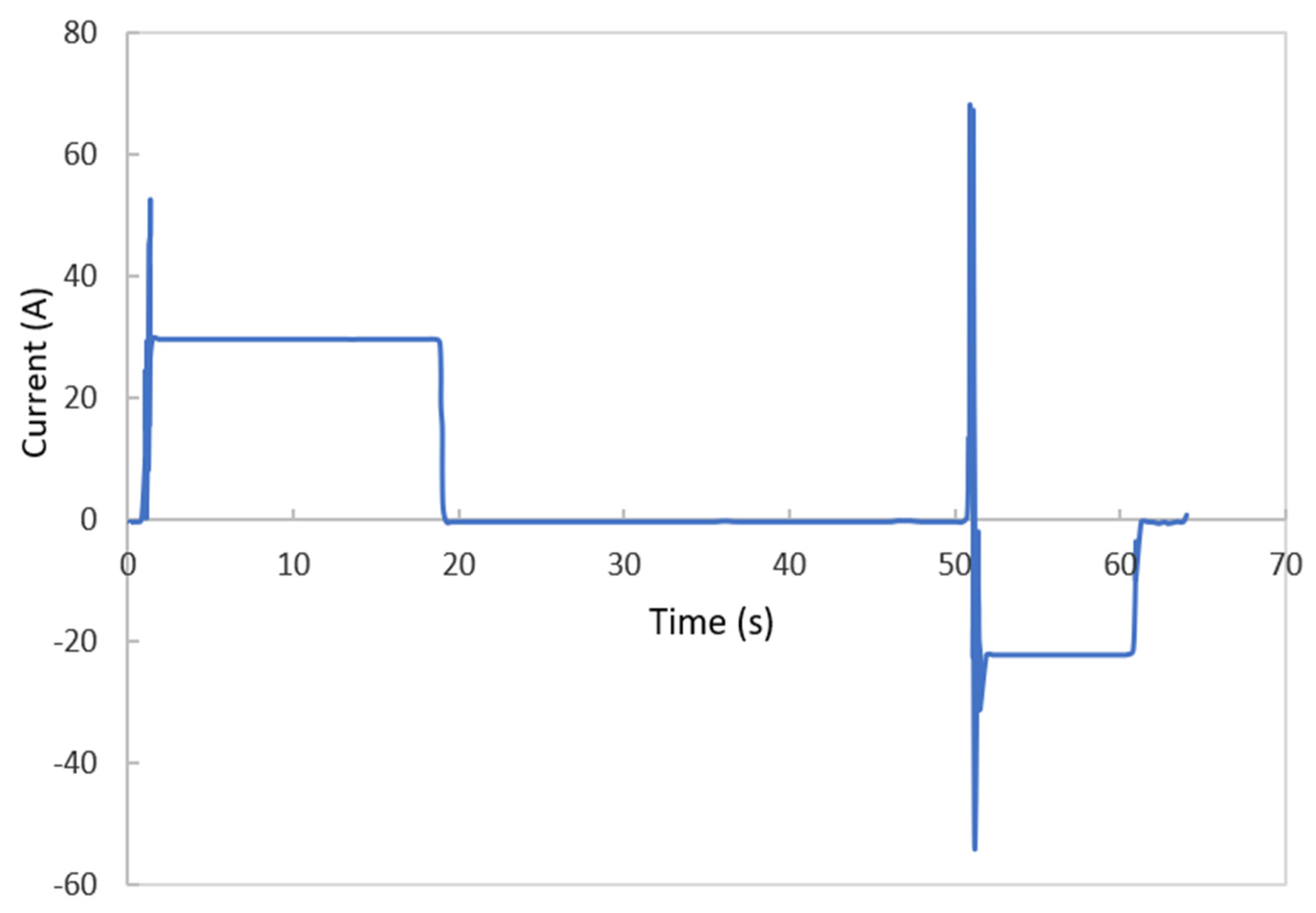
3.2.3. Effect of Current Load
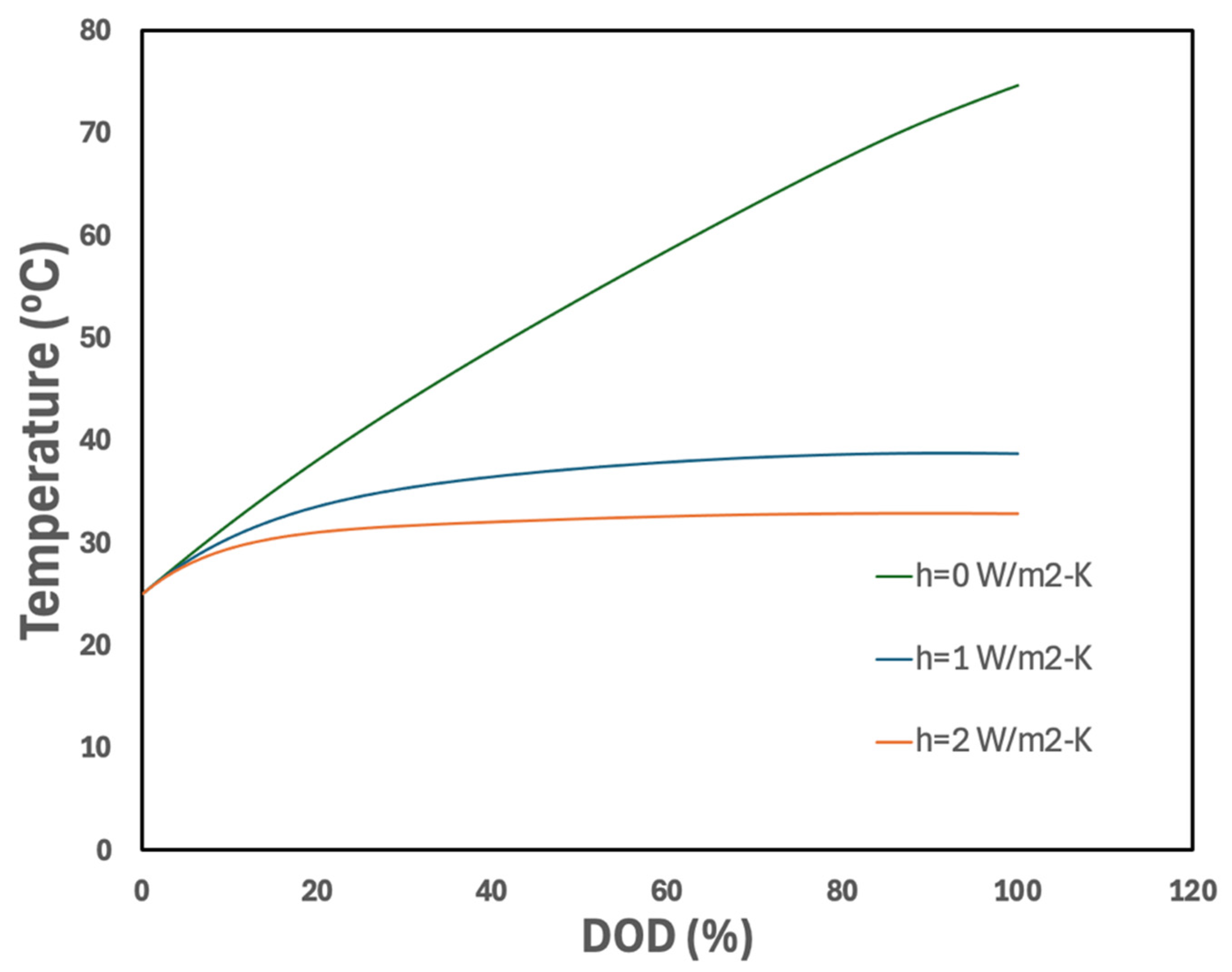
3.2.4. Effect of Boundary Heat Transfer Coefficient
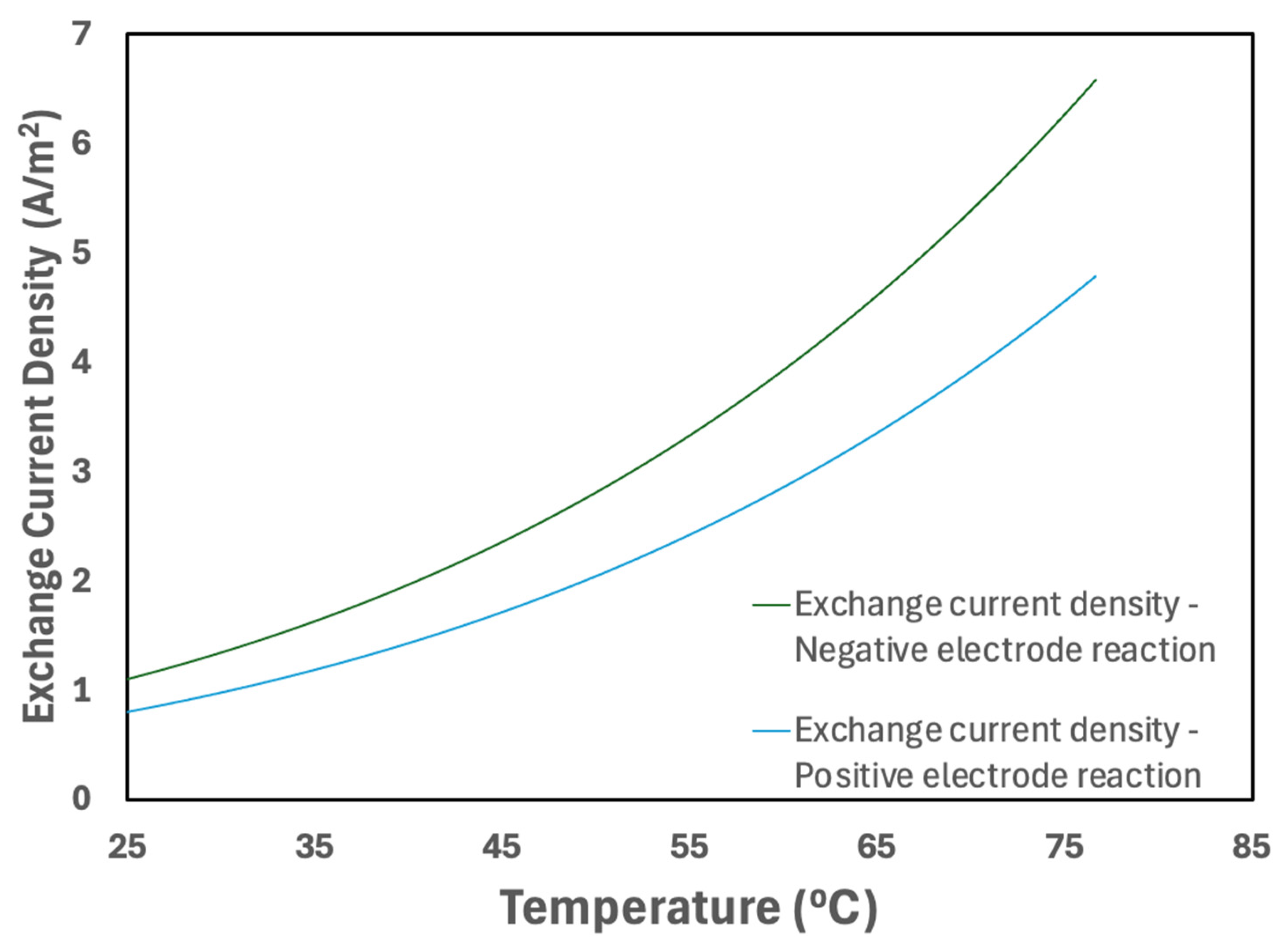
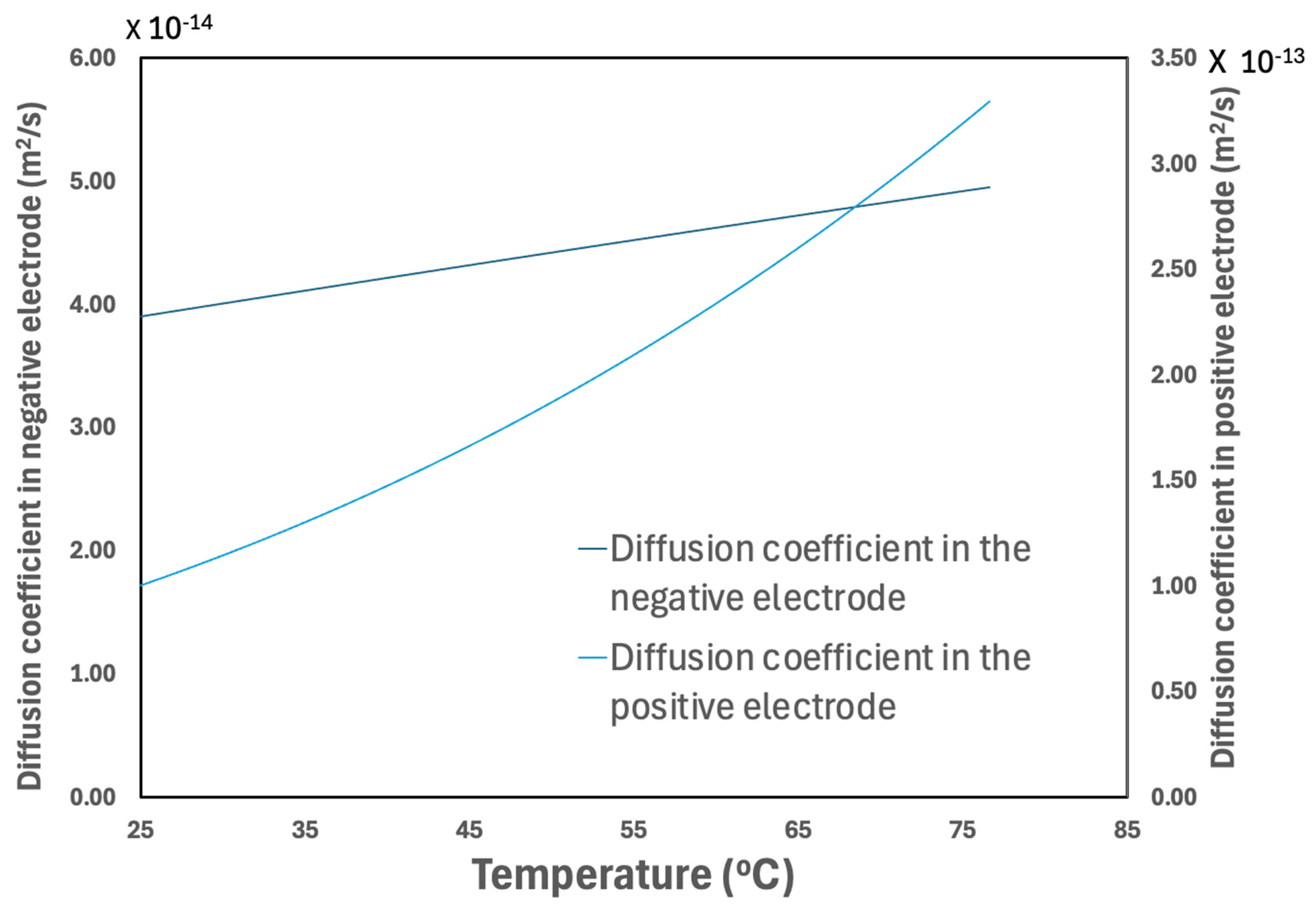
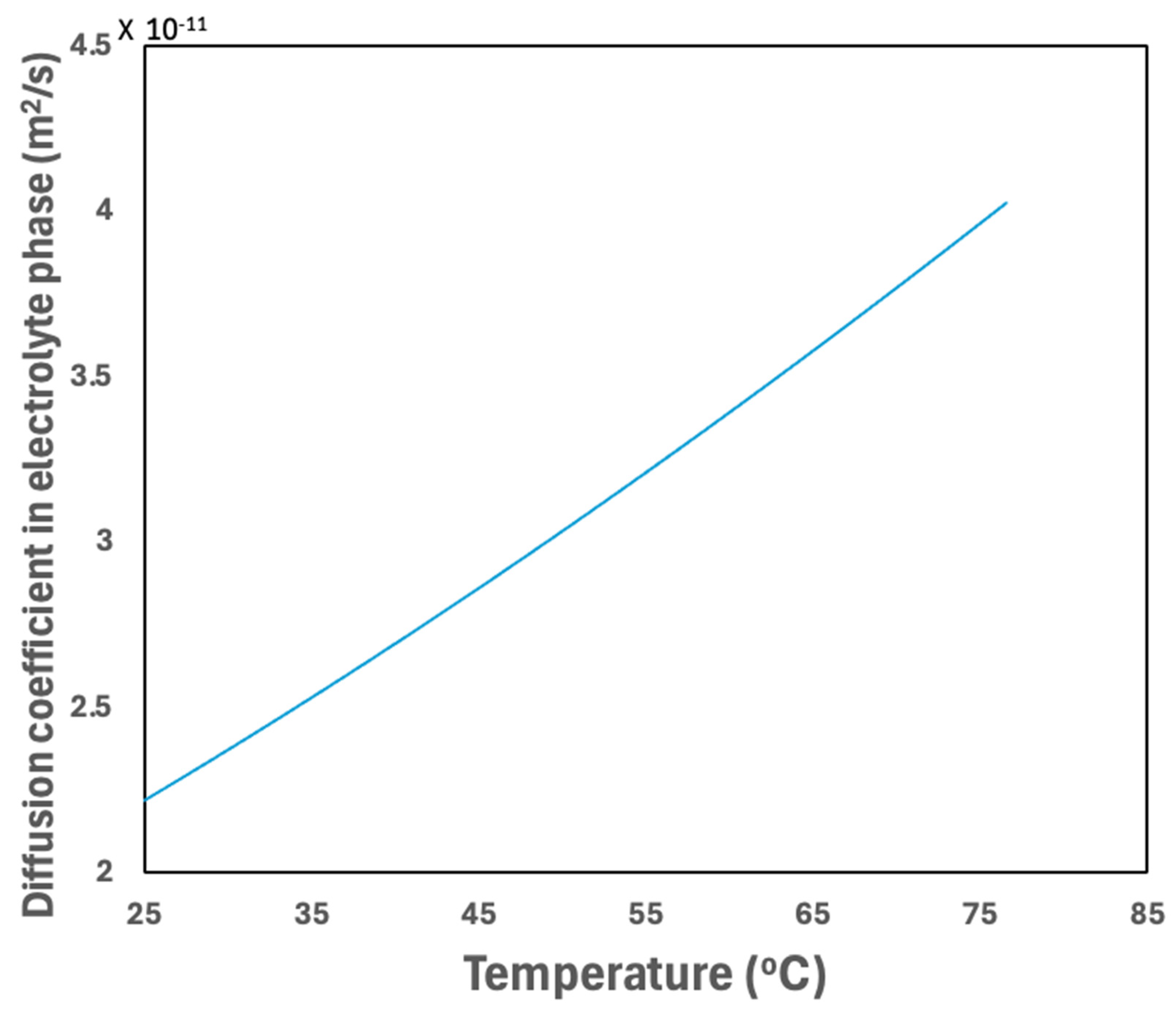
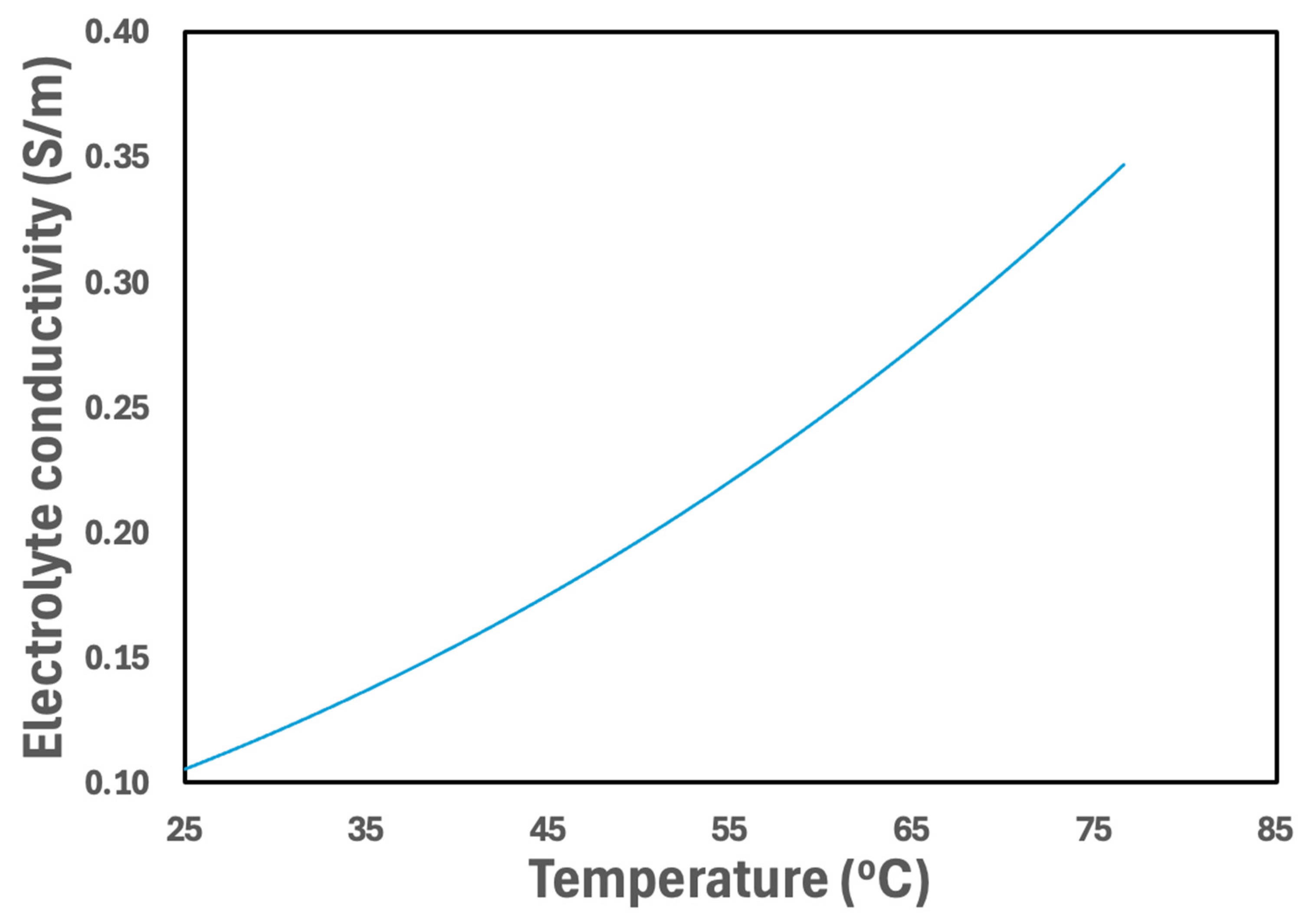
3.2.5. Temperature Effect on Material Properties
3.3. Spatial Results
3.3.1. Temperature
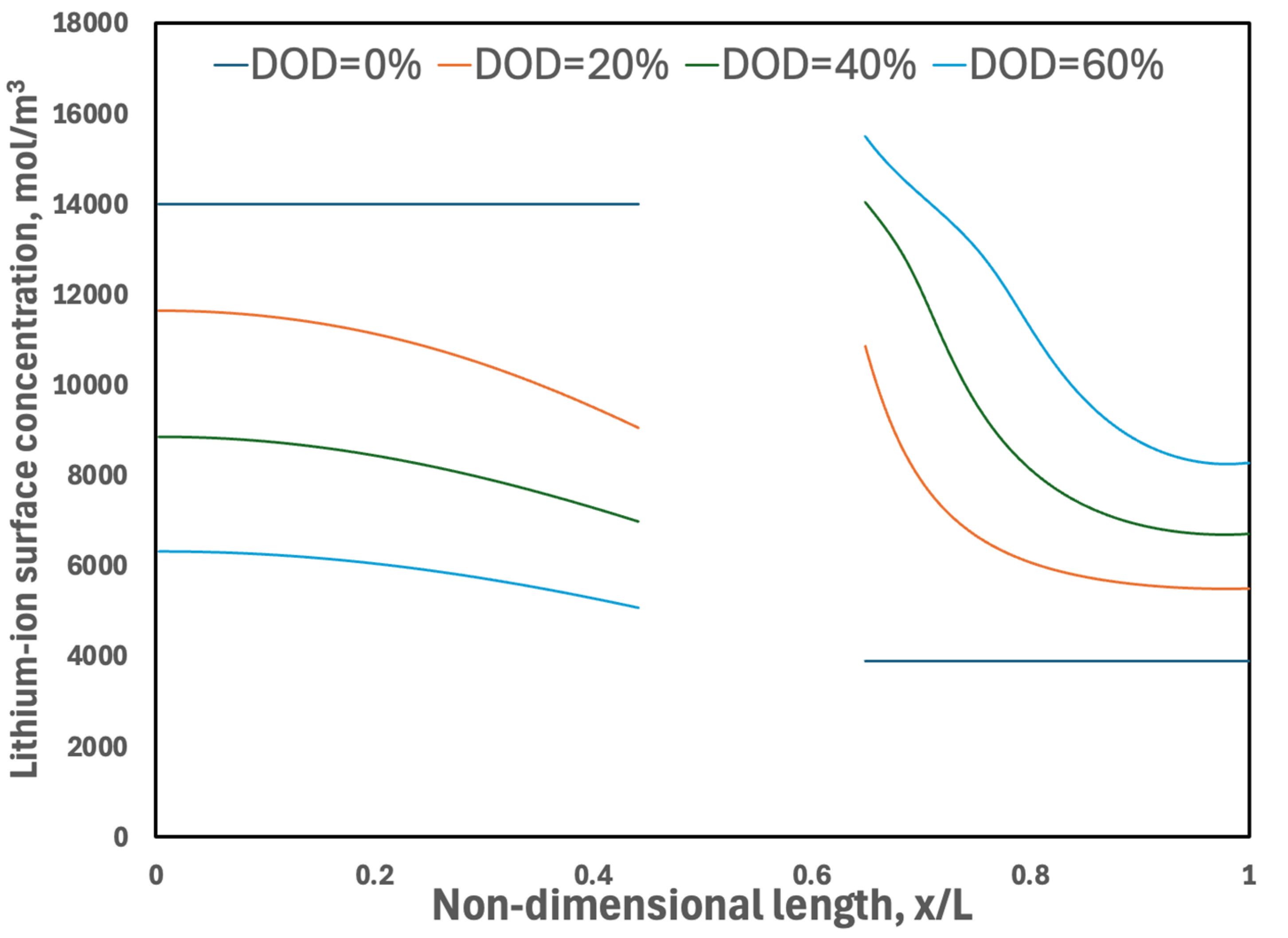
3.3.2. Surface Concentration
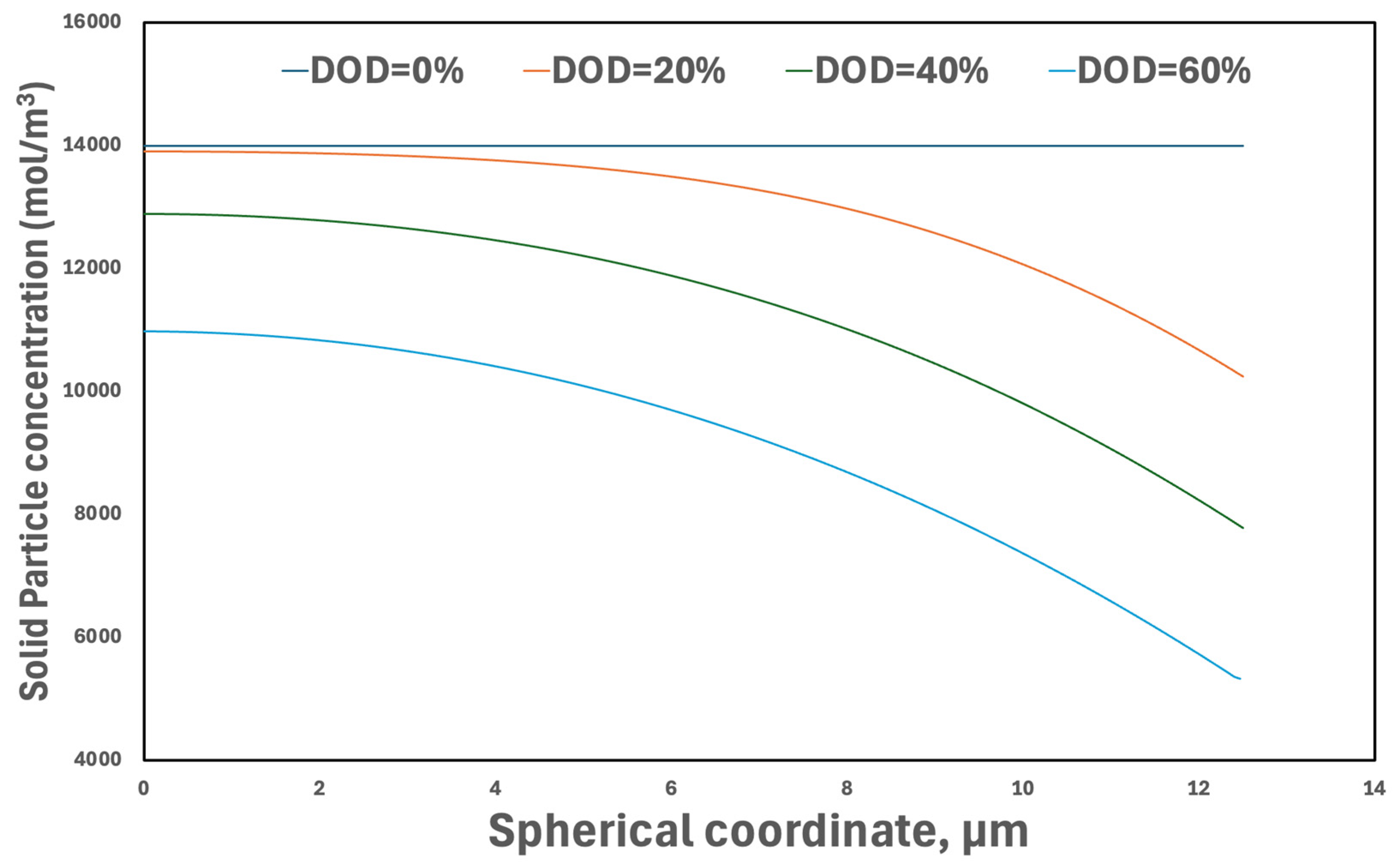
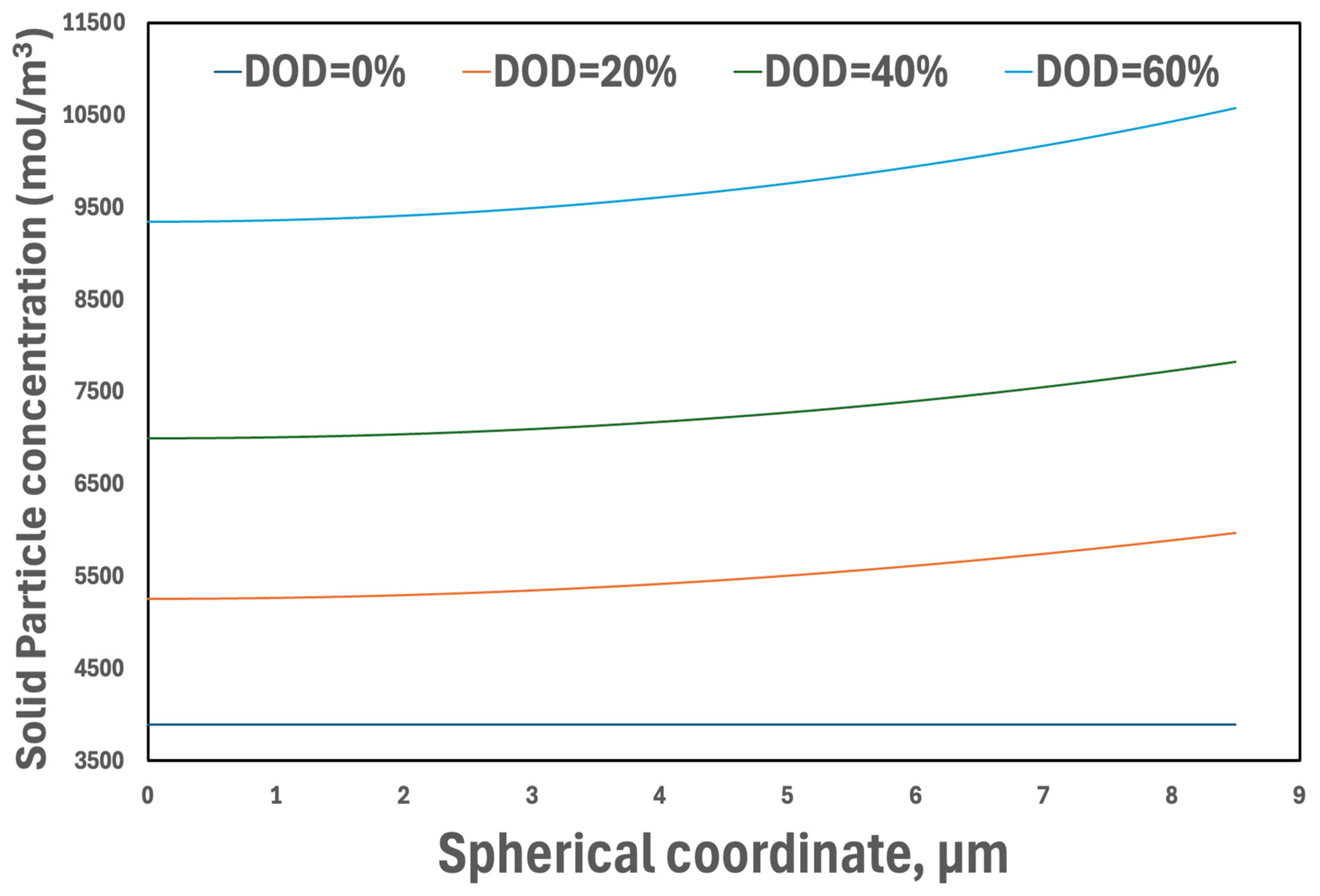
3.3.3. Concentrations in Active Particles
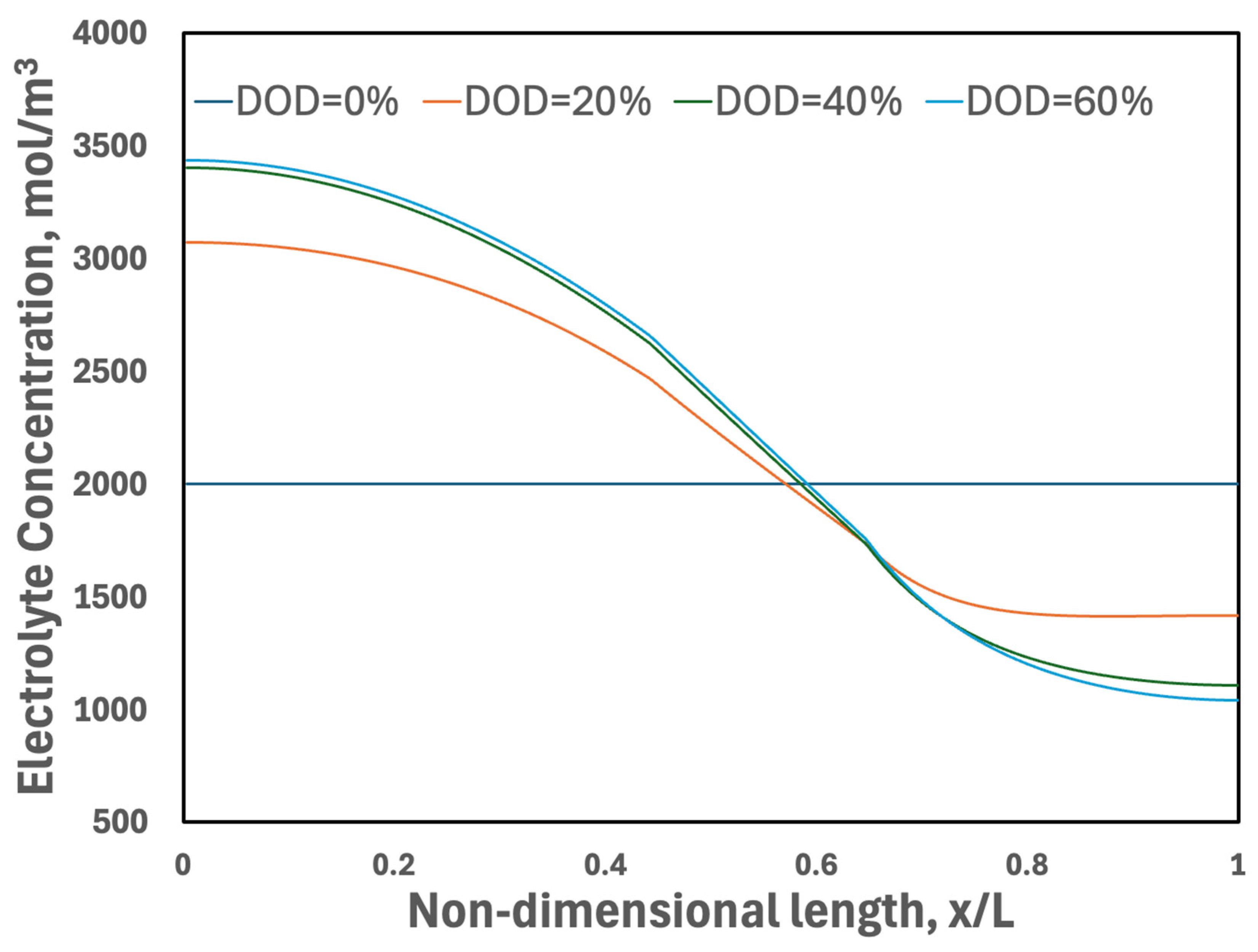
3.3.4. Electrolyte Concentration
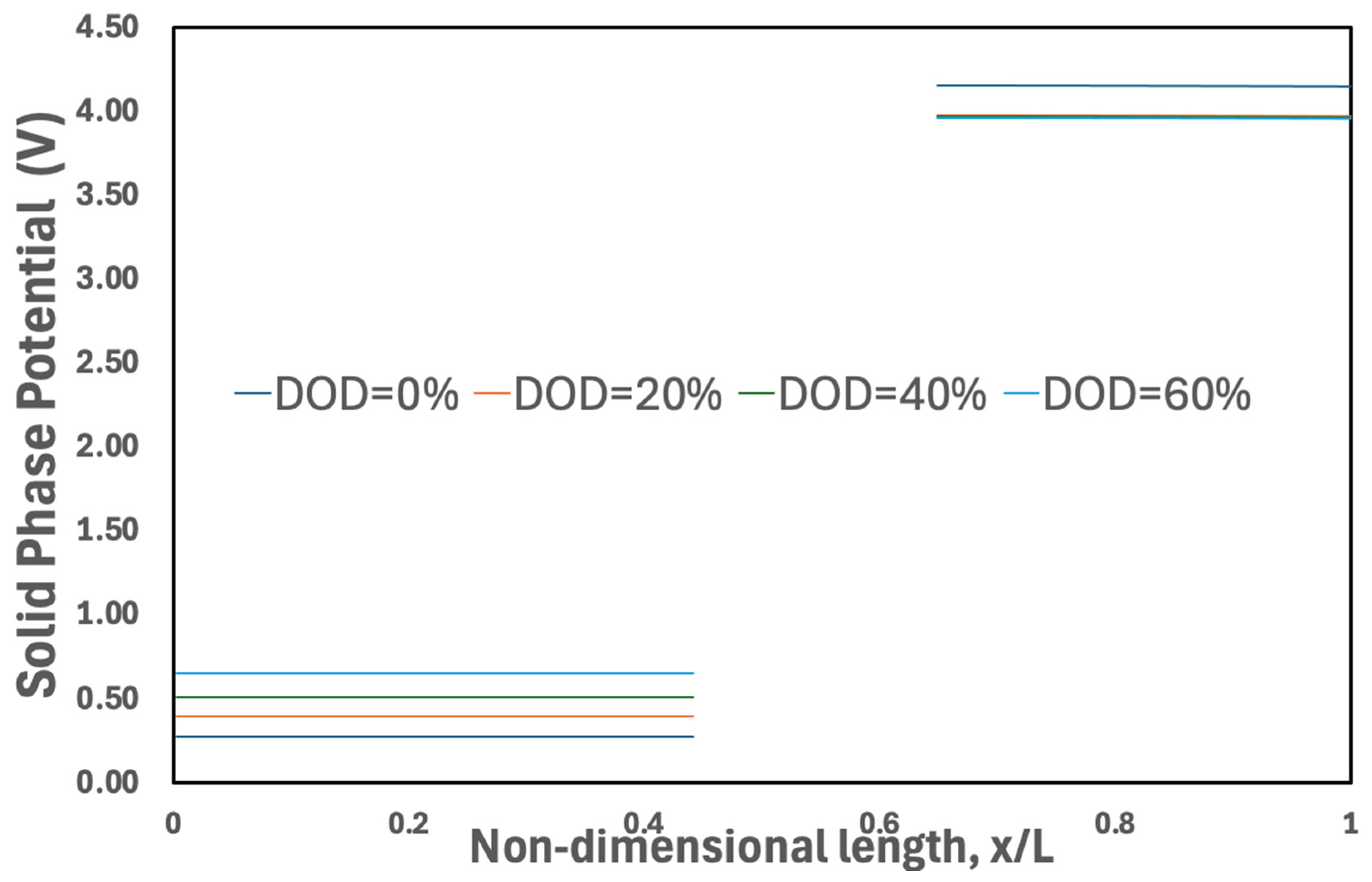
3.3.5. Solid-Phase Potential
3.3.6. Overpotential
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Letters | |
| Plate area | |
| Ah | Ampere hours |
| Lithium-ion concentration in electrolyte | |
| Specific heat capacity of material | |
| Lithium-ion concentration in solid phase | |
| Maximum lithium-ion concentration in solid phase | |
| Maximum lithium-ion concentration in positive electrode | |
| Maximum lithium-ion concentration in negative electrode | |
| Lithium-ion concentration at the surface of active spherical particle | |
| Diffusion coefficient of lithium-ions in electrolyte phase | |
| Effective diffusion coefficient of lithium-ions in electrolyte phase | |
| DOD | Depth of Discharge |
| Diffusion coefficient of lithium ions in solid phase | |
| Activation energy | |
| Molar activity coefficient | |
| Faraday’s constant | |
| HEV | Hybrid Electric Vehicle |
| HPPC | Hybrid Pulse Power Characterization |
| Applied current at current collectors | |
| Exchange current density | |
| Transfer current | |
| Ionic conductivity of the electrolyte phase | |
| Effective diffusion conductivity | |
| Effective ionic conductivity of electrolyte | |
| Reaction rate constant | |
| Coefficient of thermal conductivity | |
| Location of positive electrode–current collector boundary | |
| Thickness of the negative electrode | |
| Thickness of the positive electrode | |
| Thickness of the separator | |
| OCV | Open-Circuit Voltage |
| Bruggeman’s exponent | |
| Charge capacity of the negative electrode | |
| Charge capacity of the positive electrode | |
| Irreversible heat generated | |
| Reversible heat generated | |
| Radial location in the spherical coordinate system | |
| Film resistance | |
| Outer radius of spherical particle | |
| Resistance of electrode–electrolyte interface | |
| SOC | State of Charge |
| Temperature | |
| Ambient temperature | |
| Transference number | |
| Cell equilibrium potential | |
| Equilibrium potential at negative electrode | |
| Equilibrium potential at positive electrode | |
| Location in the cartesian coordinate system | |
| Stoichiometric coefficient of the negative electrode | |
| Stoichiometric coefficient of the negative electrode at 100% SOC | |
| Stoichiometric coefficient of the negative electrode at 0% SOC | |
| Stoichiometric coefficient of the positive electrode | |
| Stoichiometric coefficient of the positive electrode at 0% SOC | |
| Stoichiometric coefficient of the positive electrode at 100% SOC | |
| Greek Letters | |
| Anodic charge transfer coefficient | |
| Cathodic charge transfer coefficient | |
| Difference in negative electrode stoichiometry at 100% SOC and 0% SOC | |
| Difference in positive electrode stoichiometry at 100% SOC and 0% SOC | |
| Volume fraction of the electrolyte phase | |
| Volume fraction of the conductive filler | |
| Volume fraction of the polymer | |
| Volume fraction of active particles in electrode | |
| Volume fraction of active particles in negative electrode | |
| Volume fraction of active particles in positive electrode | |
| Overpotential | |
| Density of material | |
| Effective electrical conductivity of the solid phase | |
| Spatially dependent property | |
| Electrolyte-phase potential | |
| Solid-phase potential | |
References
- Gong, Q.; Wang, P.; Cheng, Z. A novel deep neural network model for estimating the state of charge of lithium-ion battery. J. Energy Storage 2022, 54, 105308. [Google Scholar] [CrossRef]
- Pillai, P.; Sundaresan, S.; Kumar, P.; Pattipati, K.R.; Balasingam, B. Open-Circuit Voltage Models for Battery Management Systems: A Review. Energies 2022, 15, 6803. [Google Scholar] [CrossRef]
- Tran, M.K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar]
- De Angelis, A.; Carbone, P.; Santoni, F.; Vitelli, M.; Ruscitti, L. On the Usage of Battery Equivalent Series Resistance for Shuntless Coulomb Counting and SOC Estimation. Batteries 2023, 9, 286. [Google Scholar] [CrossRef]
- Abaspour, M.; Pattipati, K.R.; Shahrrava, B.; Balasingam, B. Robust Approach to Battery Equivalent-Circuit-Model Parameter Extraction Using Electrochemical Impedance Spectroscopy. Energies 2022, 15, 9251. [Google Scholar] [CrossRef]
- Newman, J.; Tobias, C.W. Theoretical Analysis of Current Distribution in Porous Electrodes. J. Electrochem. Soc. 1962, 109, 1183–1191. [Google Scholar]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery State Estimation for a Single Particle Model With Electrolyte Dynamics. IEEE Trans. Control Syst. Technol. 2017, 25, 453–468. [Google Scholar] [CrossRef]
- Ma, Y.; Yin, M.; Ying, Z.; Chen, H. Establishment and simulation of an electrode averaged model for a lithium-ion battery based on kinetic reactions. RSC Adv. 2016, 6, 25435–25443. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Guo, Q.; Ramadass, P.; White, R.E. Review of models for predicting the cycling performance of lithium ion batteries. J. Power Sources 2006, 156, 620–628. [Google Scholar]
- Borakhadikar, A.S. One Dimensional Computer Modeling of a Lithium-Ion Battery. Master’s Thesis, Department of Mechanical and Materials Engineering, Wright State University, Dayton, OH, USA, 2017. Available online: http://rave.ohiolink.edu/etdc/view?acc_num=wright1496056104287962 (accessed on 6 January 2022).
- Smith, K.A.; Rahn, C.D.; Wang, C.-Y. Control oriented 1D electrochemical model of lithium ion battery. Energy Convers. Manag. 2007, 48, 2565–2578. [Google Scholar] [CrossRef]
- Smith, K.; Wang, C.Y. Solid-state diffusion limitations on pulse operation of a lithium-ion cell for hybrid electric vehicles. J. Power Sources 2006, 165, 678–686. [Google Scholar] [CrossRef]
- Białoń, T.; Niestrój, R.; Skarka, W.; Korski, W. HPPC Test Methodology Using LFP Battery Cell Identification Tests as an Example. Energies 2023, 16, 6239. [Google Scholar] [CrossRef]
- Rotas, R.; Iliadis, P.; Nikolopoulos, N.; Rakopoulos, D.; Tomboulides, A. Dynamic Battery Modeling for Electric Vehicle Applications. Batteries 2024, 10, 188. [Google Scholar] [CrossRef]
- Katrašnik, T.; Mele, I.; Zelič, K. Multi-scale modelling of Lithium-ion batteries: From transport phenomena to the outbreak of thermal runaway. Energy Convers. Manag. 2021, 236, 114036. [Google Scholar] [CrossRef]
- Kim, Y.; Mohan, S.; Siegel, J.B.; Stefanopoulou, A.G.; Ding, Y. The Estimation of Temperature Distribution in Cylindrical Battery Cells Under Unknown Cooling Conditions. IEEE Trans. Control Syst. Technol. 2014, 22, 2277–2286. [Google Scholar]
- Li, Y.; Wei, Z.; Xiong, B.; Vilathgamuwa, D.M. Adaptive Ensemble-Based Electrochemical-Thermal Degradation State Estimation of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2022, 69, 6984–6996. [Google Scholar]
- Chiew, J.; Chin, C.S.; Toh, W.D.; Zhang, C. A pseudo three-dimensional electrochemical-thermal model of a cylindrical LiFePO4/graphite battery. Appl. Therm. Eng. 2018, 147, 106. [Google Scholar] [CrossRef]
- Gu, W.B.; Wang, C.Y. Thermal and electrochemical coupled modeling of a lithium-ion cell. J. Power Sources 2000, 99, 25–37. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere: New York, NY, USA, 1980. [Google Scholar]
- Sun, J.; Kainz, J. Optimization of hybrid pulse power characterization profile for equivalent circuit model parameter identification of Li-ion battery based on Taguchi method. J. Energy Storage 2023, 70, 108034. [Google Scholar] [CrossRef]








| Governing Equations | Boundary Conditions |
|---|---|
| Charge Conservation in Negative Electrode | |
where | |
| Charge Conservation in Positive Electrode | |
| Charge Conservation in Electrolyte for Entire Battery | |
where for [13] or for [20] | |
| Mass Conservation in Solid Spherical Particles in Negative and Positive Electrodes | |
| Mass Conservation in Electrolyte for Entire Battery | |
where | |
| Energy Conservation in the Entire Battery | |
where | |
| Equilibrium Potentials for Smith and Wang’s [13] Comparisons | |
| Negative Electrode Positive Electrode where | |
| Equilibrium Potentials for Gu and Wang’s [20] Comparisons | |
| Negative Electrode Positive Electrode | |
| Bultler–Volmer Equation | |
where | |
| Cell Voltage, Sate of Charge and Depth of Discharge | |
| Temperature-Dependent Property Relationship | |
| Parameter | Unit | Negative Electrode | Separator | Positive Electrode |
|---|---|---|---|---|
| Geometry | ||||
| Thickness | μm | 128 | 76 | 190 |
| Plate area | 24 | 24 | ||
| Router | μm | 12.5 | 8.5 | |
| Material Properties | ||||
| ρ | g/cm3 | 2.5 | 1.2 | 1.5 |
| Kth | W/cm·K | 0.05 | 0.01 | 0.05 |
| CP | J/g·K | 0.7 | 0.7 | 0.7 |
| σ | S/cm | 1 | 0 | 0.038 |
| Diffusion Properties | ||||
| Ds | ||||
| De | ||||
| Concentrations | ||||
| Csmax | mol/cm3 | 0.02639 | 0.02286 | |
| mol/cm3 | ||||
| Volume fractions | ||||
| εe | 0.357 | 0.724 | 0.444 | |
| εp | 0.146 | 0.276 | 0.186 | |
| εf | 0.026 | 0 | 0.073 | |
| εs | 0.471 | 0.297 | ||
| Activation energy | ||||
| kJ/mol | 30 | 30 | ||
| kJ/mol | 4 | 20 | ||
| kJ/mol | 10 | |||
| kJ/mol | 20 | |||
| Constants | ||||
| F | C/mol | 96,485 | ||
| R | J/Kmol | 8.314 | ||
| Others | ||||
| αa, αc | 0.5 | 0.5 | ||
| i0 | ||||
| 0.363 | ||||
| p | 1.5 | |||
| h | 0 (adiabatic), 1 or 2 | |||
| K | 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kalungi, P.; Menart, J. Electrochemical–Thermal Model of a Lithium-Ion Battery. Energies 2025, 18, 1764. https://doi.org/10.3390/en18071764
Kalungi P, Menart J. Electrochemical–Thermal Model of a Lithium-Ion Battery. Energies. 2025; 18(7):1764. https://doi.org/10.3390/en18071764
Chicago/Turabian StyleKalungi, Paul, and James Menart. 2025. "Electrochemical–Thermal Model of a Lithium-Ion Battery" Energies 18, no. 7: 1764. https://doi.org/10.3390/en18071764
APA StyleKalungi, P., & Menart, J. (2025). Electrochemical–Thermal Model of a Lithium-Ion Battery. Energies, 18(7), 1764. https://doi.org/10.3390/en18071764




