Dynamic Response of a 15 MW Jacket-Supported Offshore Wind Turbine Excited by Different Loadings

Abstract

This study investigates the dynamic behavior of a jacket-supported offshore wind turbine (JOWT) by developing its substructure and controller tailored for the IEA 15 MW reference wind turbine. A fully coupled numerical model integrating the turbine, jacket, and pile is established to analyze the natural frequencies and dynamic responses of the system under wind–wave–current loading and seismic excitations. Validation studies confirm that the proposed 15 MW JOWT configuration complies with international standards regarding natural frequency constraints, bearing capacity requirements, and serviceability limit state criteria. Notably, the fixed-base assumption leads to overestimations of natural frequencies by 32.4% and 13.9% in the fore-aft third- and fourth-order modes, respectively, highlighting the necessity of soil–structure interaction (SSI) modeling. During both operational and extreme wind–wave conditions, structural responses are governed by first-mode vibrations, with the pile-head axial forces constituting the primary resistance against jacket overturning moments. In contrast, seismic excitations conversely trigger significantly higher-mode activation in the support structure, where SSI effects substantially influence response magnitudes. Comparative analysis demonstrates that neglecting SSI underestimates peak seismic responses under the BCR (Bonds Corner Record of 1979 Imperial Valley Earthquake) ground motion by 29% (nacelle acceleration), 21% (yaw-bearing bending moment), 42% (yaw-bearing shear force), and 17% (tower-base bending moment).

1. Introduction

Offshore wind energy offers substantial reserves with minimal marine ecosystem disruption [1], driving rapid growth [2]. According to the 2024 Global Wind Energy Report [3], the global new installations of offshore wind power are predicted to reach 25 GW in 2025. To reduce the levelized cost, wind turbines are increasing in size [4], requiring support structures with greater stiffness. Studies show that jacket substructures have better impact resistance and lower levelized costs in water depths over 40 m [5,6,7]. Therefore, jacket sub-structures have significant advantages in 40–60 m transitional water depths from the industrial, technical, and economic perspectives.

The bottom-fixed offshore wind turbines (OWTs), consisting of turbine generators and support structures, are subjected to long-term loading from wind, waves, currents, etc. The dynamic response [8], fatigue life [9,10,11,12], and structural design [13,14,15] of jacket-supported offshore wind turbines (JOWTs) under combined wind–wave actions have attracted significant attention from researchers. Additionally, the structural integrity of offshore wind turbines under calculated working conditions, such as extreme wind–wave conditions [16] or wind–ice loads [17], remains a key research focus in this field. The support structures of large-scale OWTs mainly adopt rigid–flexible solutions to optimize costs, positioning the system’s fundamental frequency between the 1P and 3P frequency bands of the turbine. The dynamic response analyses of JOWTs [18,19,20,21,22,23] highlight the critical role of soil–structure interaction (SSI) in these long-period structures.

The JOWTs exhibit complex dynamic responses under combined wind–wave–current loads, primarily due to multi-physics coupling effects. Although fluid–structure interaction theory has been applied across multiple disciplines [24,25], it is difficult for existing tools to simulate the influence of servo systems directly. Consequently, simplified engineering methods are predominantly adopted in the wind energy field to analyze multi-field coupling problems. For wave–current loads, the Morison equation is the most widely applied method [26], while the added mass method is the most common choice for hydrodynamic forces induced by structural vibrations [27]. For wind loads, aero-elastic analysis methods are extensively utilized in the numerical simulation software of the wind energy industry [28]. In addition to numerical simulations, small-scale model tests have been employed to investigate the hydro-elastic effects of JOWT structures [29]. These studies highlight the necessity to address the coupling effects of wind, wave, and current loads.

The commercial structural dynamics software inadequately simulates aero–servo–hydro–elastic coupling effects in running OWTs, necessitating specialized numerical tools. The commercial software GL-Bladed (V4.6) was used to analyze the dynamic and seismic response of JOWTs [26]. The open-source software OpenFAST (V3.0), developed by NREL, was used to perform dynamic analysis of a 5 MW JOWT [30,31,32,33]. In addition, the comparisons of GL-Bladed, OpenFAST, HAWC2, and Flex5 were performed by NREL in a series of research tasks [34]. The offshore wind farms in seismically prone regions encounter significant threats due to large turbine masses and long fundamental periods [35,36]. On one hand, dynamic responses of tripod and jacket OWTs under combined wind–wave–earthquake loads revealed that moderate-intensity earthquakes may induce greater internal forces than extreme wind–wave conditions [37]. On the other hand, existing research emphasized the significant influence of SSI [38] and layered soil on the seismic response of JOWTs [39].

Recently, 15 MW wind turbines have been deployed in bottom-fixed offshore wind farms and have attracted attention from researchers in the floating offshore wind energy sector [40,41,42]. The existing studies of JOWTs predominantly focus on the 5 MW model, with several studies on the 10 MW wind turbine. This study investigates the dynamic response of a site-specific 15 MW JOWT. The paper structure comprises the following: Section 2 details geotechnical and meteorological characterization, controller design, and model validation; Section 3 investigates natural frequencies, operational and extreme environmental load responses, and seismic response; Section 4 presents conclusive findings.

2. Numerical Model and Analysis Method

2.1. The 15 MW Wind Turbine

The IEA 15 MW reference wind turbine is a three-blade horizontal-axis wind turbine that employs a variable-speed and collective pitch control strategy.

Table 1. Properties of IEA 15 MW wind turbine.

Parameter (Unit)	Value
Power rating (MW)	15
Cut-in, rated, and cut-out wind speeds (m/s)	3, 10.88, 25
Rotor diameter (m)	240
Hub height (m)	150
Minimum and maximum rotor speeds (rpm)	5, 7.56
RNA mass (t)	1016.645
Nacelle center of mass from tower top (m)	(−6.476, 0.0, 4.269)
Tower mass (t)	859.8

presents the main technical parameters of this turbine model, with additional details available in Ref. [43].

2.2. Offshore Site and Soil–Pile Interaction Model

To conduct the jacket and foundation design for the 15 MW OWT, the marine soil site shown in Figure 1 was selected, where γ represents the effective saturated soil unit weight, k₀ denotes the initial foundation modulus, and Φ indicates the internal friction angle of the soil. This site has been widely used to perform dynamic response analysis of bottom-fixed OWTs, and more details can be found in the report [44]. The jacket was supported by a pile foundation measuring 82 m in length and 4.5 m in diameter, exhibiting a slenderness ratio of 18.2 that exceeds the critical threshold of 15. Following established methodologies in previous studies [45], the API p–y curve method [46] was implemented to simulate soil–pile interaction. With a pile spacing of 35 m (7.78 times the pile diameter), group effects were considered negligible. The API py curve and associated parameters are presented in Equations (1)–(4):

$$p=\mathrm{A}{p}_{u}tanh\left({\displaystyle \frac{k_0{z}_{\mathrm{s}}}{\mathrm{A}{p}_u}}y\right)$$

(1)

$$p_u=min\left\{p_{us},p_{ud}\right\}$$

(2)

$$p_{us}=\left(C_1{z}_s+C_{2}D\right)\gamma z_s$$

(3)

$$p_{ud}=C_{3}D\gamma z_{\mathrm{s}}$$

(4)

where $p$ is the constraint force exerted by the soil on the pile per unit length (N/m), the coefficient $\mathrm{A}$ is taken as 0.9, $p_u$ represents the ultimate bearing capacity of the soil (N/m), $y$ is the horizontal displacement of the pile (m), $z_{\mathrm{s}}$ is the depth of the soil layer below the mudline (m), $\gamma$ is the lateral displacement of the pile body (m), $D$ denotes the pile diameter in meters (m), and $C_1{,C}_2$, and $C_3$ are dimensionless parameters that are functions of the soil’s effective internal friction angle. For the sake of brevity, the t–z curve and Q–z curve were not elaborated in this paper. All the relevant formulas and parameters can refer to the API specification [46]. To account for energy dissipation in the foundation, a viscous damper was connected in parallel with the horizontal spring. The viscous damping coefficient can be determined according to the recommendations of Makris and Gazetas [47]:

$${\mathrm{c}}_m=2k_{\mathrm{S}}{\displaystyle \frac{{\beta }_m}{\omega }}$$

(5)

where $\omega$ is the first modal circular frequency (rad/s), $k_{\mathrm{S}}$ denotes the initial tangent modulus of the p–y curve (N/m²), and ${\beta }_m$ represents the hysteretic damping ratio of the soil, taken as 5% in this study according to the recommendation of Yang [48].

2.3. Jacket Support Structure

The JOWT is illustrated in Figure 2, where the origin of the global inertial coordinate system xyz is positioned at the intersection of the undeformed tower axis and the mean sea level. The x-axis is along the longitudinal plane of the wind field; the y-axis is oriented along the lateral of the wind field; and the z-axis is vertically upward. The measured meteo-ocean data of the K13 deep-water site with a water depth of 60 m [49], located in the North Sea of Denmark (53°13′04″ N, 3°13′13″ E), is used to design the jacket support structure and analyze the dynamic response of the IEA 15 MW wind turbine.

Table 2. The relationship between wind and wave for the K13 sit.

Average Wind Speed at Hub Height Vhub (m/s)	Significant Wave Height Hs (m)	Characteristic Period Tp (s)	Probability f
2	1.02	5.76	0.058
4	1.05	5.62	0.085
6	1.13	5.50	0.134
8	1.25	5.42	0.135
10	1.41	5.48	0.138
12	1.62	5.62	0.122
14	1.82	5.80	0.096
16	2.09	6.08	0.072
18	2.36	6.41	0.047
20	2.64	6.68	0.030
22	2.95	7.07	0.018
24	3.27	7.45	0.009
26	3.59	7.77	0.005
28	3.98	8.11	0.002
30	4.26	8.46	0.0009
32	4.57	8.71	0.0005
34~42	4.68	9.01	0.0002

presents the prevailing wind–wave parameters and their occurrence probabilities at the site, while

Table 3. Parameters of extreme wind for the K13 site.

Return Period Tr (yr)	Mean Wind Speed at Hub Height Vhub (m/s)	Significant Wave Height Hs (m)	Maximum Wave Height Hm (m)	Period T (s)
1	34.28	7.1	13.21	9.44
5	38.69	8.1	15.07	10.09
10	40.55	8.5	15.81	10.33
50	44.87	9.4	17.48	10.87
100	46.73	9.9	18.41	11.15

details the extreme wind and wave parameters along with their corresponding return periods. It should be noted that the relationship between the mean wind speed at 150 m height and wave spectral parameters was derived based on the established mean wind speed–wave parameter relationship at 80 m height from Ref. [49], combined with the site-specific wind profile.

The preliminary design methodology of JOWT support structures proposed by Jalbi and Bhattacharya [13] was employed to develop the jacket substructure and pile foundation for the IEA 15 MW wind turbine.

Table 4. Overall geometric parameters of the jacket.

Parameter (Unit)	Value
Overall height (m)	144.582
Top width (m)	16.5
Bottom width (m)	35
Main leg inclination angle (deg)	4
Layer 1 height (m)	29
Layer 2 height (m)	23
Layer 3 height (m)	18.5
Layer 4 height (m)	15
Layer 1 bottom width (m)	35.0
Layer 2 bottom width (m)	28.7
Layer 3 bottom width (m)	23.73
Layer 4 bottom width (m)	19.74

summarizes the main geometric parameters of the jacket structure for the IEA 15 MW wind turbine.

Table 5. Dimensions of members of the jacket.

Member	Diameter D (m)	Wall Thickness t (mm)
Pile	4.5	70
Leg 1	3.5	80
Leg 2	2	77
Leg 3	1.51	65
Leg 4	1.5	60
Brace 1	1	62
Brace 2	0.84	42
Brace 3	0.73	39
Brace 4	0.65	24

details the cross-sectional dimensions of structural members. It should be emphasized that the bearing capacity calculations explicitly account for variations in member internal forces at different structural positions, resulting in distinct cross-sectional dimensions for legs and braces across various layers. This design represents an improvement over the methodology documented in Ref. [13]. The proposed configuration satisfies requirements for structural component Ultimate Limit States (ULS), Serviceability Limit States (SLS) of the OWT, and natural frequency constraints.

2.4. Wind, Wave, Current Model, and Load Cases

This study employed the power law recommended by IEC 61400-3 [50] to describe the vertical variation of 10-min mean wind speed. According to the measured data of the K13 marine site [49], the surface roughness exponent was set to 0.14. Consequently, the mean wind speed U(ξ) (m/s) was formulated as follows:

$$U\left(\xi \right)=V_{\mathit{hub}}{\left({\displaystyle \frac{\xi }{{\xi }_r}}\right)}^{0.14}$$

(6)

where V_hub denotes the mean wind speed at hub height (m/s), ξ represents the elevation relative to the mean sea level (m), and ξ_r corresponds to the hub height set to 150 m. The fluctuating wind spectrum is characterized by the Kaimal spectrum:

$$S_k\left(f\right)={\displaystyle \frac{\frac{4{\sigma }_k{L}_k}{V_{hub}}}{\left(1+\frac{6f{L}_k}{V_{hub}}({)}^{\frac{5}{3}}\right)}}$$

(7)

where $f$ denotes the frequency (Hz) in the fluctuating wind power spectral density function; ${\sigma }_k$ and $L_k$ represent the standard deviation (m/s) and integral scale (m) of the respective velocity components for fluctuating wind; and k serves as the index for turbulent wind velocity components, taking values 1, 2, and 3 to correspond with the x-, y-, and z-axes, respectively. The turbulence class of the wind field was selected as IEC Class B. The turbulence intensity and other relevant parameters of the Kaimal spectrum can be determined in accordance with IEC 61400-3 [50].

The total duration of the wind field was set to 700 s to encompass the simulation period and mitigate the influence of initial conditions. The inflow wind field was defined as a vertical rectangular domain measuring 300 m × 300 m that fully covers the rotor plane. Considering both spatial resolution requirements and computational costs, both horizontal and vertical grid nodes were spaced at 15 m intervals, as shown in Figure 3.

In accordance with IEC 61400-3 [50], the cross-power spectral density function between wind field nodes i and j can be expressed as follows:

$$S_{i,j}\left(f\right)=C\left(\mathsf{\Delta }r,f\right)\sqrt{S_{i,i}\left(f\right)\cdot S_{j,j}\left(f\right)}$$

(8)

where $S_{i,i}\left(f\right)$ and $S_{j,j}\left(f\right)$ represent the power spectral density functions at nodes i and j (m²/(s²·Hz)) and $C\left(\mathsf{\Delta }r,f\right)$ denotes the coherence function:

$$C\left(\Delta r,f\right)=\exp \left[-b\sqrt{\left({\displaystyle \frac{f\Delta r}{V_{hub}}}\right)+\left({\displaystyle \frac{0.12\Delta r}{L_C}}\right)}\right]$$

(9)

where Δr denotes the distance between two nodes (m), b represents the decay coefficient (taken as 12), and $L_C$ signifies the turbulence integral scale (set to 340.2 m).

The blade element momentum theory is adopted to calculate the aerodynamic load of the blades. The Øye model was used to simulate the dynamic wake effect, and the incompressible flow Beddoes–Leishman model was employed to consider the dynamic stall effect. Meanwhile, the corrections for blade root and tip losses were also taken into account. Detailed theoretical foundations can be referenced in the GL-Bladed software (V4.8) theoretical manual [51]. The irregular wave fields were used to simulate realistic sea states. To generate the wave field, the JONSWAP spectrum was selected to describe the characteristics of the wave spectrum.

$$S\left(f\right)={\displaystyle \frac{\alpha g^2}{{\left(2\pi \right)}^4}}{f}^{-5}exp\left(-{\displaystyle \frac{5}{4}}{\left({\displaystyle \frac{f}{f_p}}\right)}^{-4}\right){\gamma }^{exp\left(-0.5{\left({\displaystyle \frac{f-f_p}{\sigma ·f_p}}\right)}^2\right)}$$

(10)

where $f$ denotes the wave spectral frequency (Hz), $f_p$ represents the peak frequency of the spectrum (Hz), $g$ is the gravitational acceleration (m/s²), $\alpha$ signifies the generalized Phillips constant, $\sigma$ denotes the spectral width parameter, and $\gamma$ is the peak enhancement factor.

The current velocity ${\mathrm{V}}_c\left(z\right)$ at varying water depths is described by a power-law distribution:

$${\mathrm{V}}_c\left(z\right)=V_0{\left({\displaystyle \frac{z+h}{h}}\right)}^{1/7}$$

(11)

where $V_0$ represents the surface current velocity (m/s), and $h$ denotes the water depth (m). For the case study in this paper, the surface current velocity $V_0$ was set to 0.55 m/s under normal sea states and 1.1 m/s under extreme sea conditions.

Under combined wind–wave–current loading, the hydrodynamic pressure acting on the JOWT can be decomposed into wave-induced forces and added hydrodynamic pressure arising from structural vibrations. The wave-induced force f is calculated using the Morison equation:

$$f=C_M\rho V\ddot{u}+{\displaystyle \frac{1}{2}}{C}_D\rho D{\left(\dot{u}\right)}^2$$

(12)

where $C_M$ and $C_D$ denote the inertia and drag coefficients, taken as 2.0 and 1.2; ρ represents seawater density, set to 1027 kg/m³; $V$ is the unit-length cylinder volume (m³/m); D is the outer diameter of the structure (m); and $\dot{u}\mathrm{a}\mathrm{n}\mathrm{d}\ddot{u}$ represent the water particle velocity (m/s) and acceleration (m/s²), respectively. The added hydrodynamic pressure $\tilde{f}$ (N/m) induced by structural vibrations is calculated using the added mass model proposed by Li et al. [52].

$$\tilde{f}=-c_{mi}\left(\rho \pi D\right){\ddot{u}}_t$$

(13)

where π is taken as 3.14, $c_{mi}$ denotes the added mass coefficient, and ${\ddot{u}}_t$ represents the pile acceleration (m/s²).

2.5. Mechanical Control and Numerical Model of 15 MW JOWT

This study employed the GL-Bladed software (V4.8) to establish a numerical model of the 15 MW JOWT, utilizing Euler–Bernoulli beam elements to simulate the dynamic behavior of flexible components including blades, tower, and jacket. The blade stiffness parameters were derived from the IEA 15 MW wind turbine user manual [49]. The support structure was constructed using steel with a strength grade of 533 MPa, and their primary mechanical properties are summarized in

Table 6. Material parameters of support structure for a 15 MW JOWT.

Density (kg/m3)	Young’s Modulus (GPa)	Yield Strength (MPa)
8000	200	533

. The element length was set as 2 m for tower and jacket members and 1 m for pile segments. The parametric analysis confirms that the accuracy of the structural discretized model satisfies the requirements for engineering analysis.

The mechanical controller of this JOWT incorporates variable-speed and pitch-regulated technologies. When the mean wind speed at hub height is below the rated wind speed, the generator torque is modulated to maintain optimal tip–speed ratio for maximum energy capture by adjusting rotor speed. When the mean wind speed at hub height exceeds rated wind speed, the blade pitch angles are increased to regulate rotor speed and stabilize output power. Controller parameters for the 15 MW JOWT were tuned using the ROSCO (V2.6) [53] software developed by NREL, with natural frequencies of 0.18 Hz specified for both generator and pitch control systems, thereby determining proportional and integral controller gain parameters. The dynamic link library (DLL) file of the controller was integrated into the 15 MW JOWT model through GL-Bladed’s external controller interface. Selected controller parameters are presented in

Table 7. Parameters of controller for a 15 MW JOWT.

Parameter	Value	Description
PC_Max Pit	1.570	Maximum physical pitch limit, [rad].
PC_Max Rat	0.06978	Maximum pitch rate (in absolute value) in pitch controller, [rad/s].
PC_Ref Speed	0.79168	Desired (reference) HSS speed for pitch controller, [rad/s].
PC_Switch	0.01745	Angle above lowest minimum pitch angle for switch, [rad].
SD_Max Pit	0.6981	Maximum blade pitch angle to initiate shutdown, [rad].
SD_CornerFreq	0.41888	Cut-off frequency for first order low-pass filter for blade pitch angle, [rad/s].

.

The dynamic analyses of OWT involve thousands of load cases. Consequently, simulation tools such as GL-Bladed and OpenFAST employ modal superposition methods for dynamic characterization of flexible components [51]. The computational platform utilized in this work features a 16-core i9-12900K processor and 128 GB RAM. The analysis reveals that employing all blade and support structure modes leads to excessively low computational efficiency. Considering the objective of the present study, this section investigated the influence of modal truncation on seismic response predictions. Figure 4 compares results between a benchmark model (retaining all blade and support structure modes, ‘All modes’ in this figure) and a simplified model (retaining 10 blade modes and 30 support structure modes, ‘Partial modes’ in this figure), with seismic input derived from the 1994 Northridge earthquake Rinaldi Receiving Station (RRS) ground motion record.

According to Figure 4, it is demonstrated that there is excellent agreement between the two models in predicting nacelle acceleration, tower-base bending moment, and shear force, as well as the pile-head axial force. The simplified model demonstrates adequate precision for all input ground motions adopted in this study (Section 3.4). In the interest of simplicity, corresponding validation results are not presented here. To achieve a balance between computational efficiency and analytical precision, this study adopted 10 blade modes and 30 support structure modes in the dynamic response analysis. The operational wind speed range of the wind turbine (3–25 m/s) was partitioned into 2 m/s bins, with the hub-height mean wind speed assigned as the bin midpoints.

3. Result and Discussion

To investigate the dynamic behavior of the 15 MW JOWT, this section analyzes the natural frequency, dynamic response, and seismic response of the system. To evaluate the influence of SSI, this study analyzed the dynamic response of the 15 MW JOWT using two distinct modeling approaches: one incorporating SSI and the other neglecting it. For brevity, the models are referred to as the SSI model and no-SSI model, respectively. In the SSI model, the methodology described in Section 2.2 was adopted, while in the no-SSI model, all nodal degrees of freedom at the pile foundations were fully restrained.

3.1. Natural Frequency Analysis of the System

The GL-Bladed software (V4.8) adopts two critical modeling premises in its natural frequency analysis of support structures: (a) utilization of linear soil spring stiffness coefficients and (b) rigid-body idealization of the rotor–nacelle assembly (RNA). These two assumptions were solely employed for the natural frequency analysis in this subsection, while in the subsequent numerical simulations of this paper, the pile–soil interaction adopted the nonlinear model presented in Section 2.2, with the blades being treated as flexible components.

Table 8. Natural frequencies of fore-aft modes for a 15 MW JOWT.

Mode	Description	SSI Frequency	No-SSI Frequency	Relative Error
1	1st fore-aft mode	0.2058	0.2113	2.67%
2	2nd fore-aft mode	1.254	1.321	5.34%
3	3rd fore-aft mode	1.453	1.924	32.41%
4	4th fore-aft mode	2.784	3.172	13.94%
5	5th fore-aft mode	3.196	3.245	1.53%
6	6th fore-aft mode	3.226	3.385	4.93%
7	7th fore-aft mode	4.008	4.02	0.3%
8	8th fore-aft mode	4.181	4.192	0.26%

presents the first 8 modal frequencies of the 15 MW JOWT in the fore-aft (FA) direction. For the first and second FA modes, neglecting SSI overestimates the natural frequency by 2.7% and 5.3%, respectively. The third and fourth fore-aft modes exhibit SSI-induced frequency overestimations of 32.4% and 13.9%, respectively. For fifth to eighth fore-aft modes, SSI effects become significantly smaller than that of the previous modes.

As presented in

Table 9. Natural frequencies of side-to-side modes for a 15 MW JOWT.

Mode	Description	SSI Frequency	No-SSI Frequency	Relative Error
1	1st side–side mode	0.2048	0.2103	2.69%
2	2nd side–side mode	1.135	1.188	4.67%
3	3rd side–side mode	1.453	1.924	32.41%
4	4th side–side mode	2.784	3.124	12.21%
5	5th side–side mode	3.117	3.172	1.76%
6	6th side–side mode	3.196	3.385	5.91%
7	7th side–side mode	3.783	3.793	0.26%
8	8th side–side mode	4.008	4.02	0.3%

, the first eight side–side (SS) modal natural frequencies demonstrate similar SSI effects to those observed in FA modes. Notably, the second-mode natural frequencies exhibit a 10.5% relative deviation between FA and SS directions, attributable to rotational inertia disparities in the rotor–nacelle assembly. This structural anisotropy may introduce directional dependence in the dynamic response of the 15 MW JOWT under external excitations. The turbine’s 1P and 3P excitation frequency ranges (0.126–0.378 Hz) are strategically separated from the system’s fundamental modal frequencies of 0.2058 Hz (FA) and 0.2048 Hz (SS). This frequency decoupling confirms that the support structure design successfully satisfies the required frequency exclusion criteria, effectively avoiding resonance conditions during normal turbine operations.

3.2. Dynamic Response of 15 MW OWT Excited by Common Wind, Wave, and Current

The dynamic response of the 15 MW JOWT under the combined wind––wave–current excitation was analyzed in this section, with a focus on SSI effects. To account for wind field stochasticity, six statistically independent three-dimensional turbulent wind fields were generated via different random seeds for each mean wind speed. Additionally, to eliminate transient effects caused by initial conditions (e.g., turbine start-up), numerical results of the first 100 s were discarded.

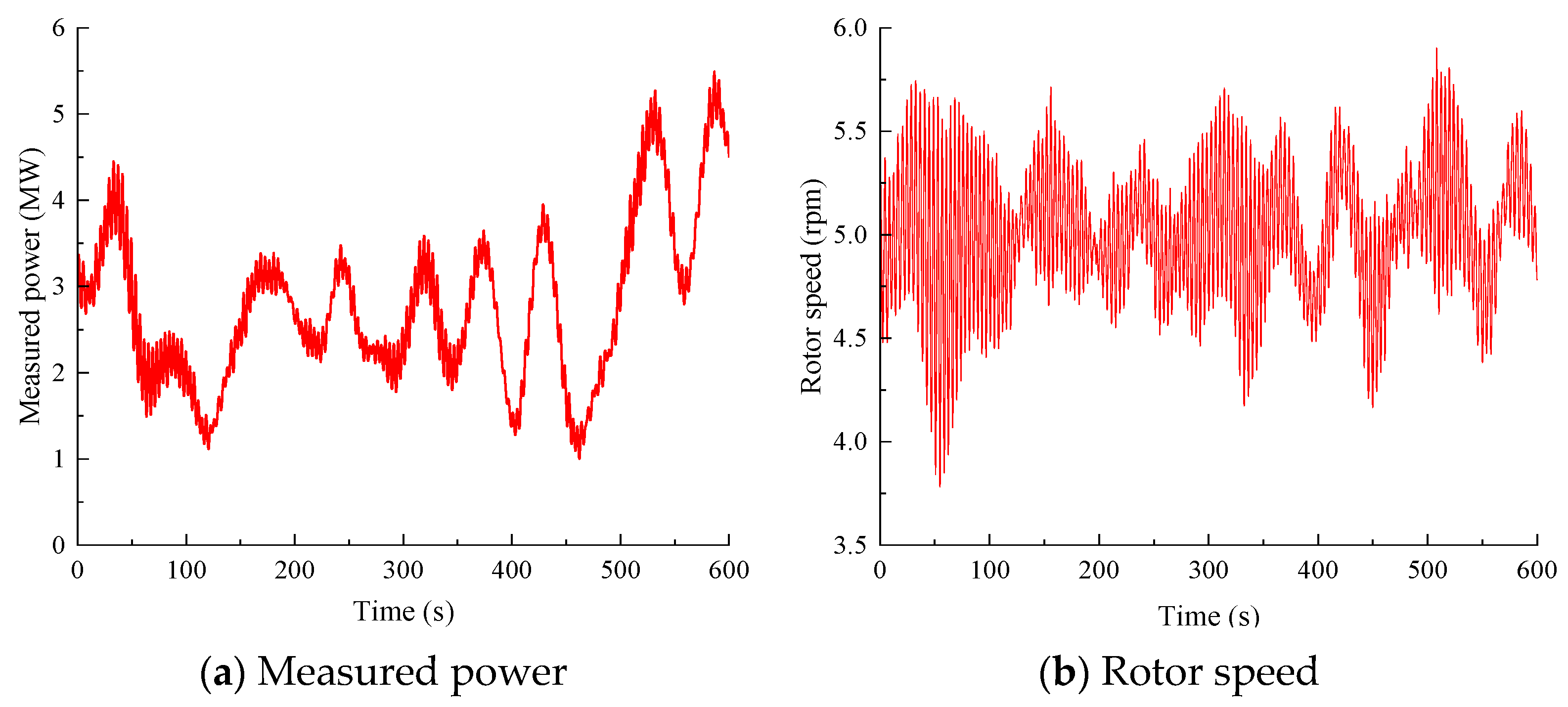
Figure 5 presents the power output and rotor speed when the hub-height mean wind speed is 6 m/s. Below the rated wind speed, the controller regulates rotor speed between 4 and 5.5 rpm by adjusting generator torque, maintaining a tip–speed ratio (ratio of blade tip tangential velocity to inflow wind speed) near 10 to optimize energy capture, with power outputs ranging from 1 to 5.5 MW.

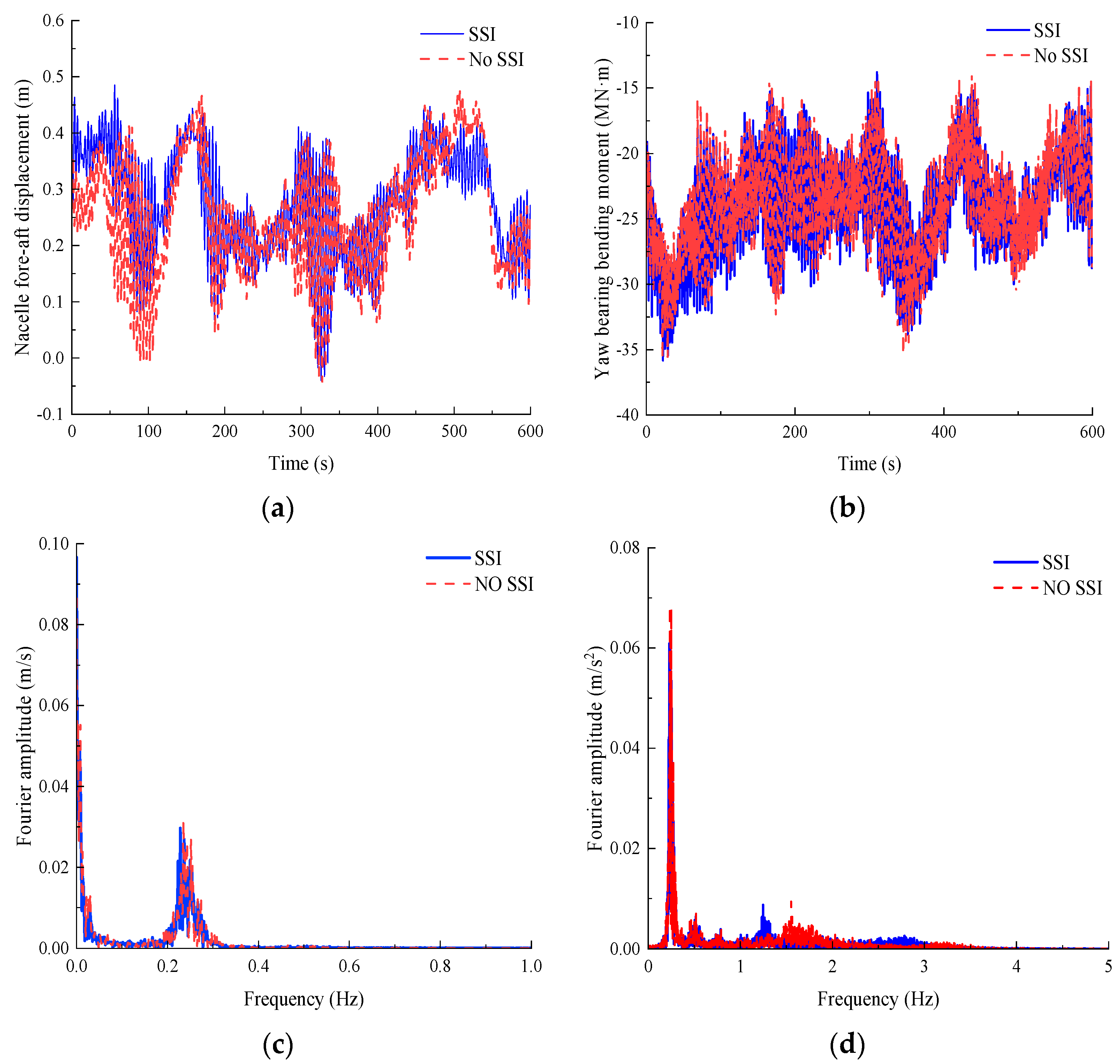
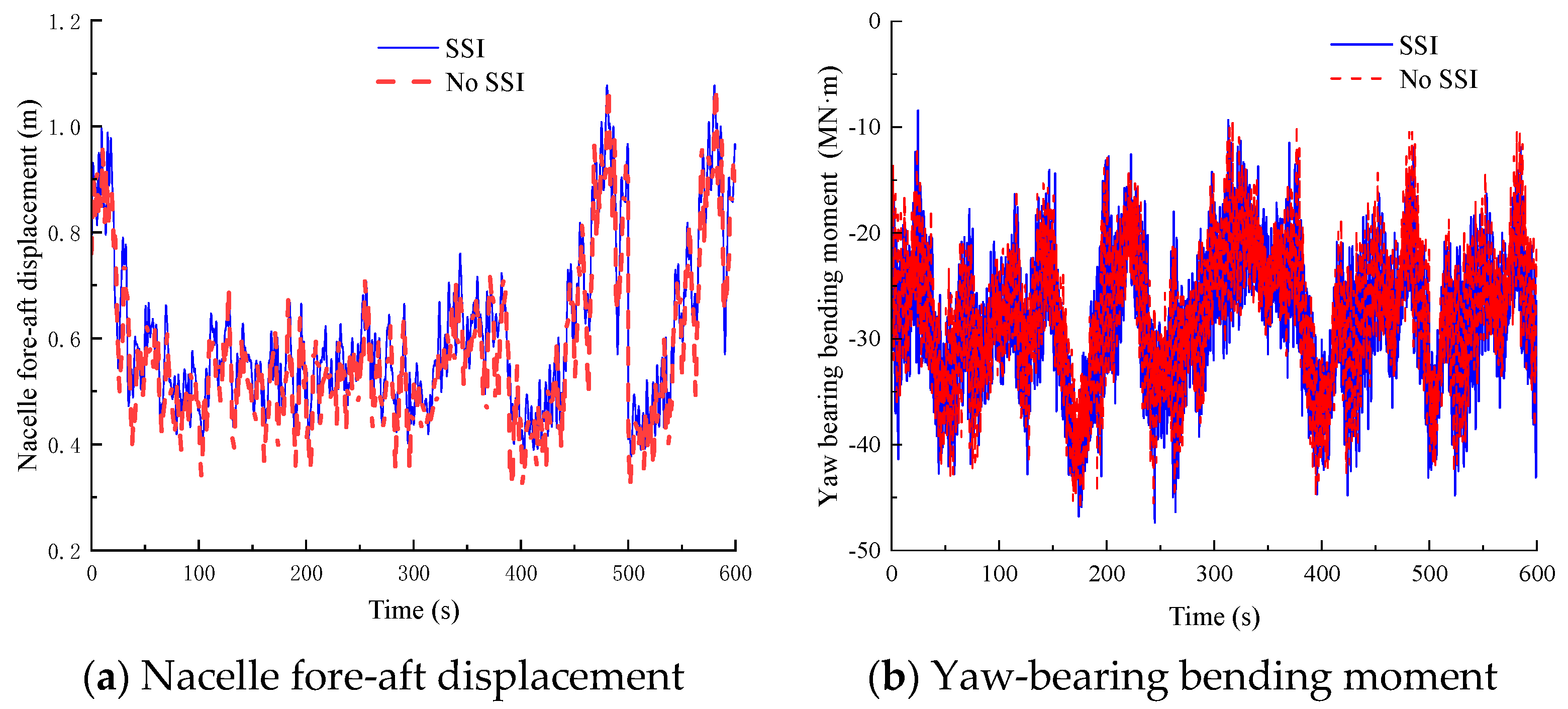
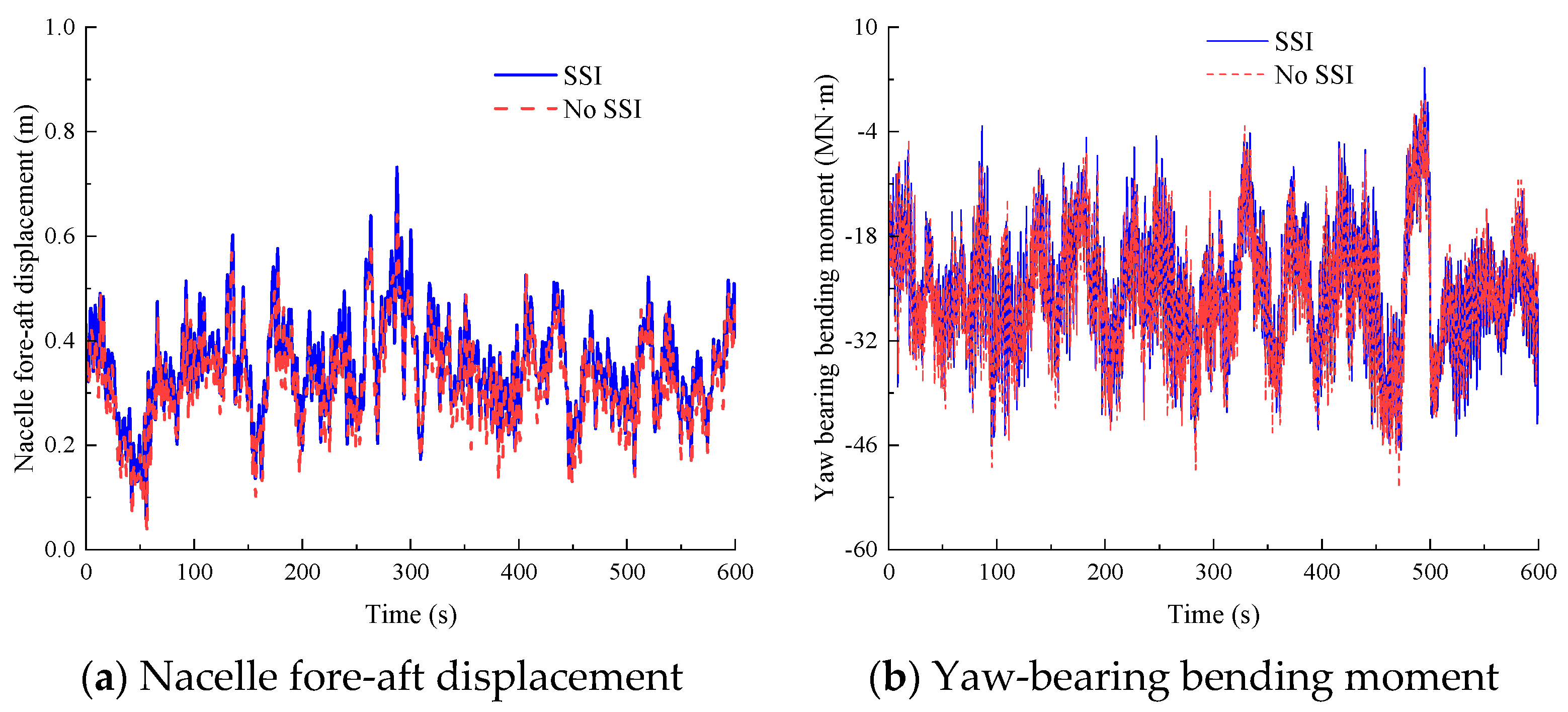
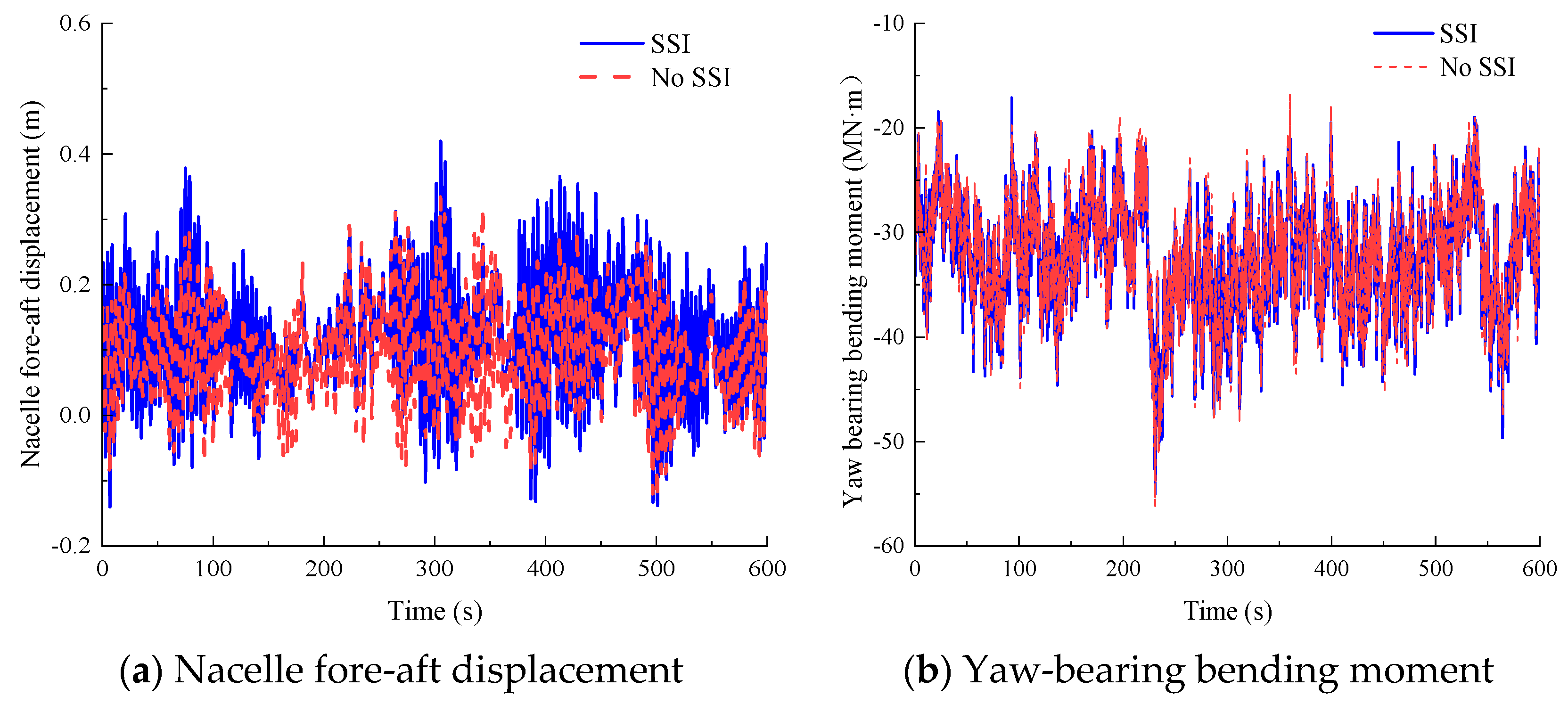
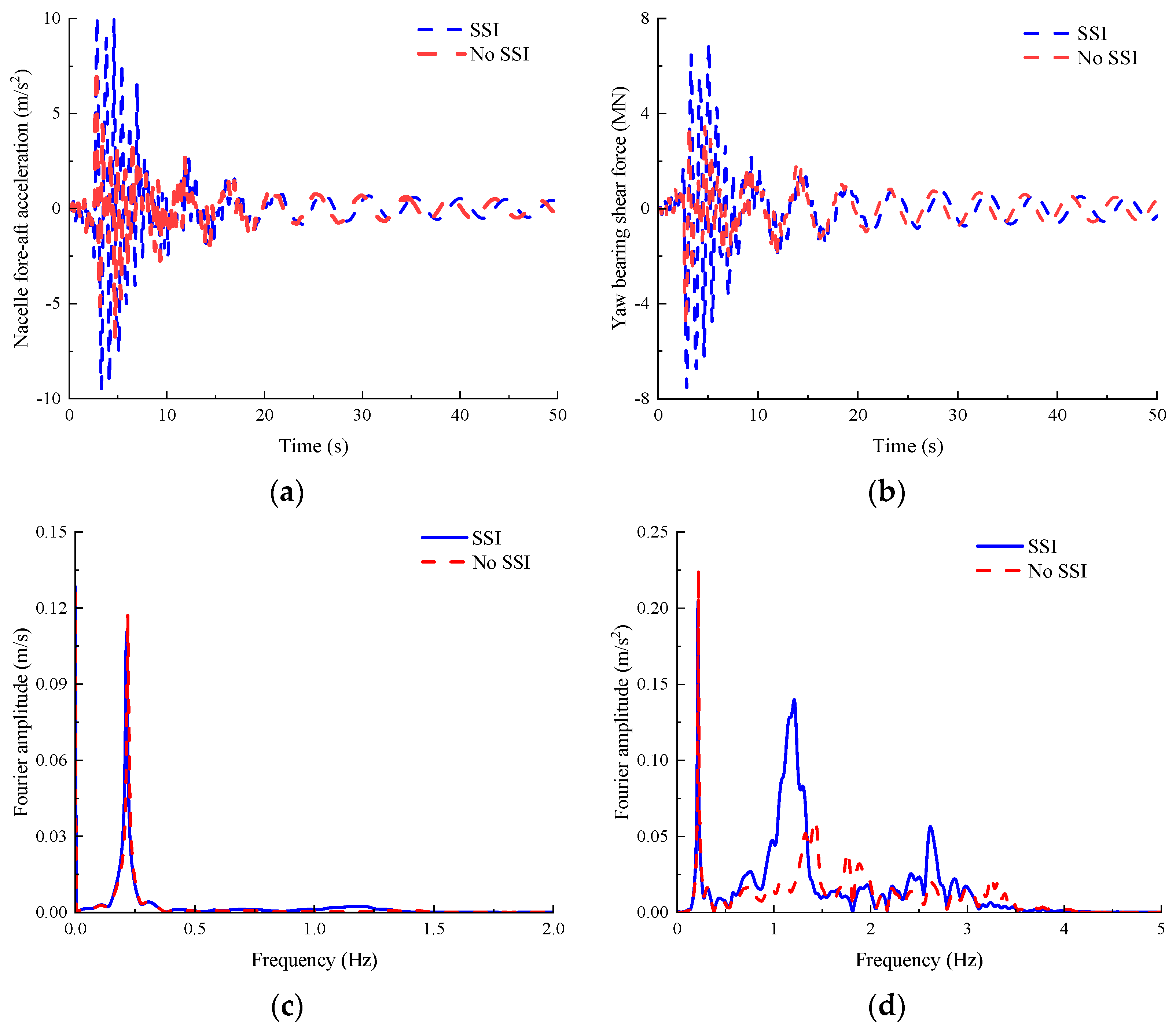
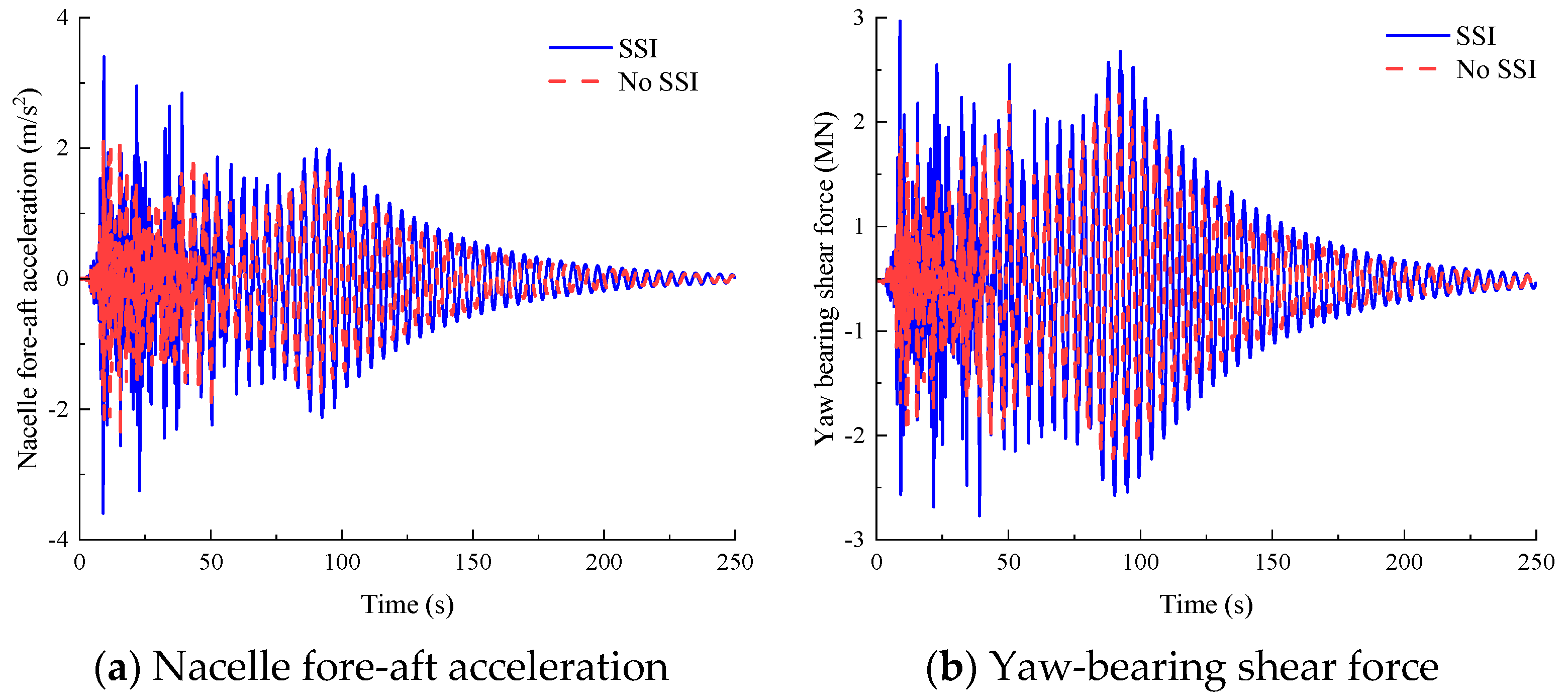
Figure 6a,b present the dynamic responses of the 15 MW JOWT under a mean wind speed of 6 m/s at the hub height, including the nacelle displacement in the x-axis and yaw-bearing bending moment about the y-axis. When SSI is considered, the peak values reach 0.485 m for nacelle displacement and 35.83 MN·m for yaw-bearing bending moment. Figure 6c,d display the Fourier amplitude spectra of nacelle displacement and acceleration, respectively. As shown in these figures, the displacement response is dominated by static displacement and the first mode of the system, while the acceleration response primarily reflects the first mode with measurable contributions from higher-order modes.

Table 10. Analysis error of a mechanical system for a 15 MW JOWT neglecting SSI with a mean wind speed of 6 m/s.

Statistics	Nacelle Fore-Aft Response		Yaw-Bearing Internal Force
	Displacement	Acceleration	Bending Moment	Shear Forces
Max	−2.08%	2.12%	−0.42%	4.42%
Average	−7.29%	–	−1.55%	−2.43%
Standard deviation	9.31%	–	−0.54%	12.36%

quantifies relative deviations between SSI and no-SSI models across statistical parameters. Notably, SSI effects remain moderate, with relative errors for all parameters except yaw mechanism shear force standard deviation confined within (−10%, 10%).

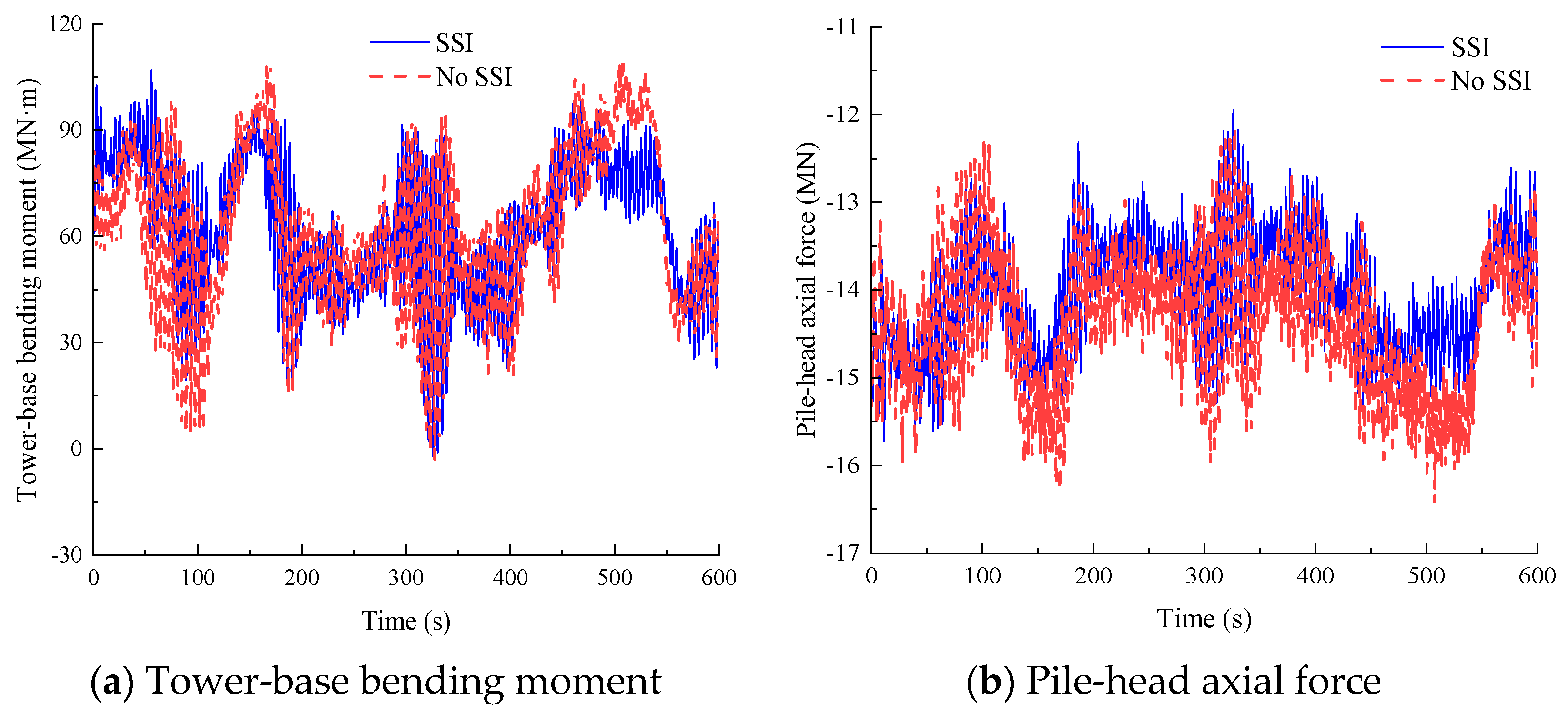
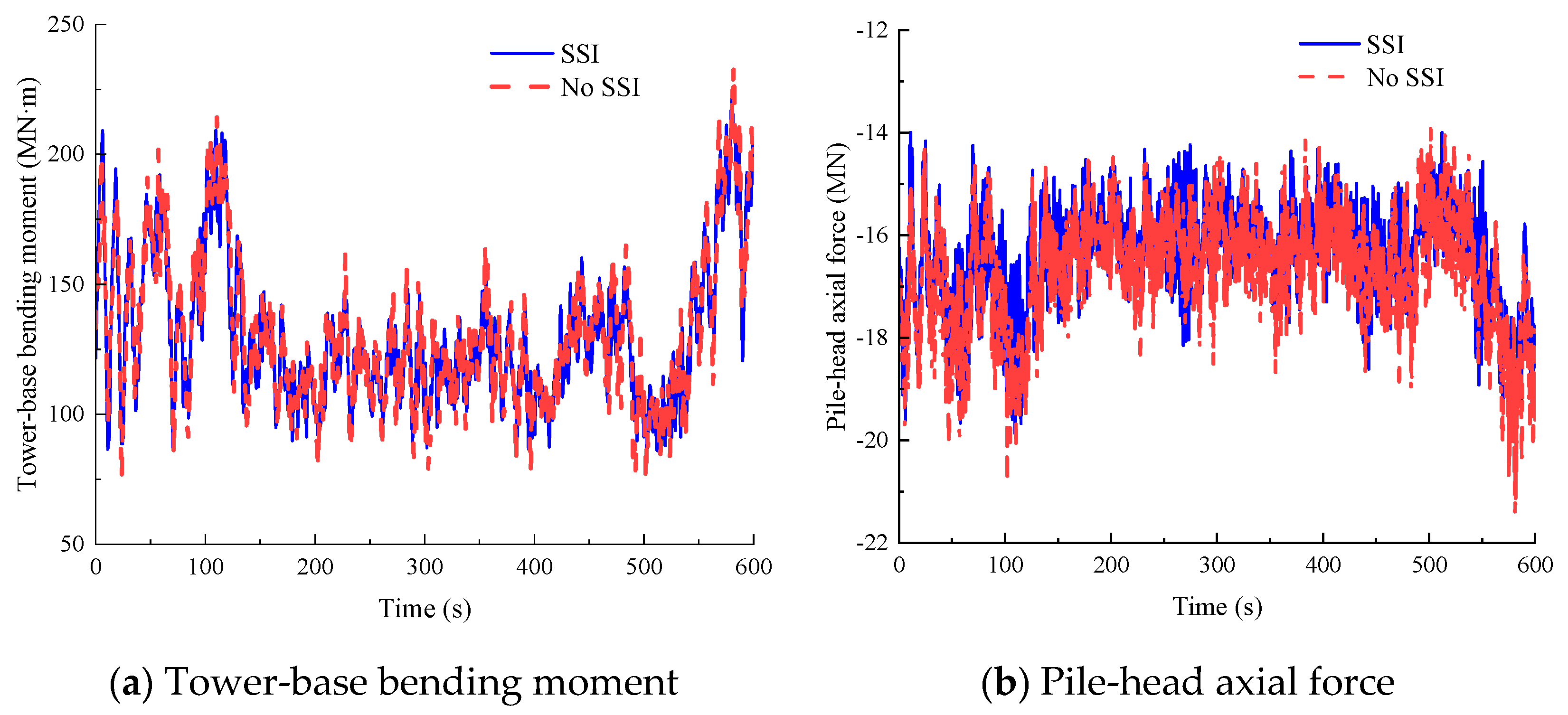
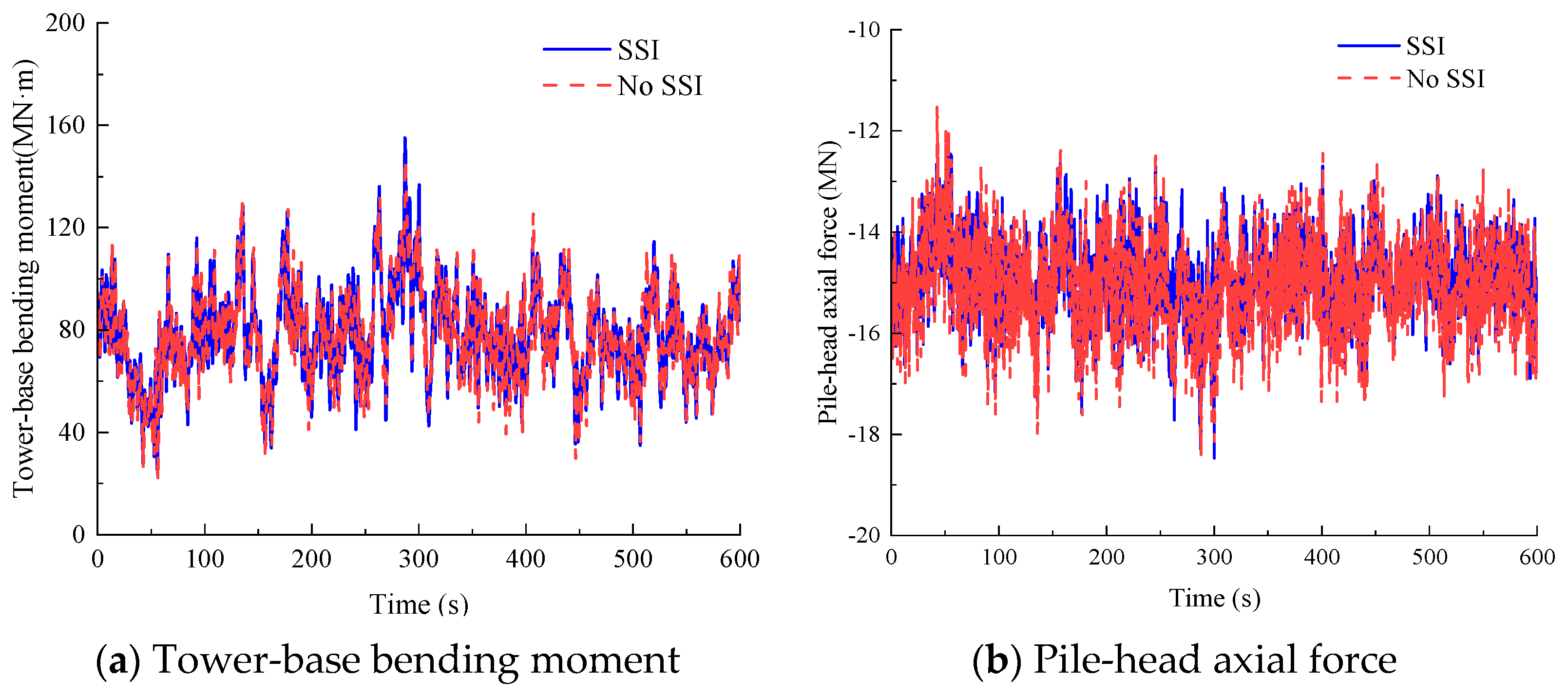
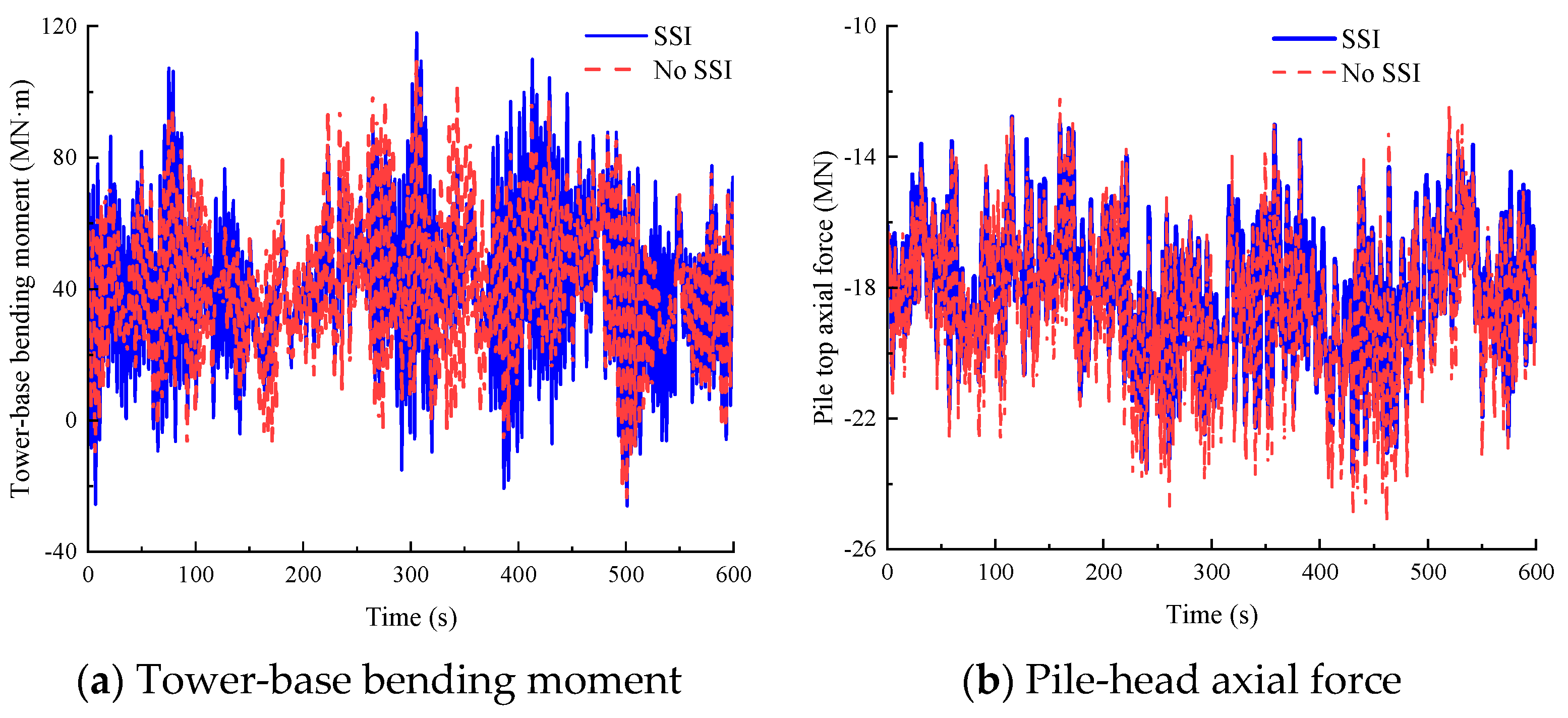
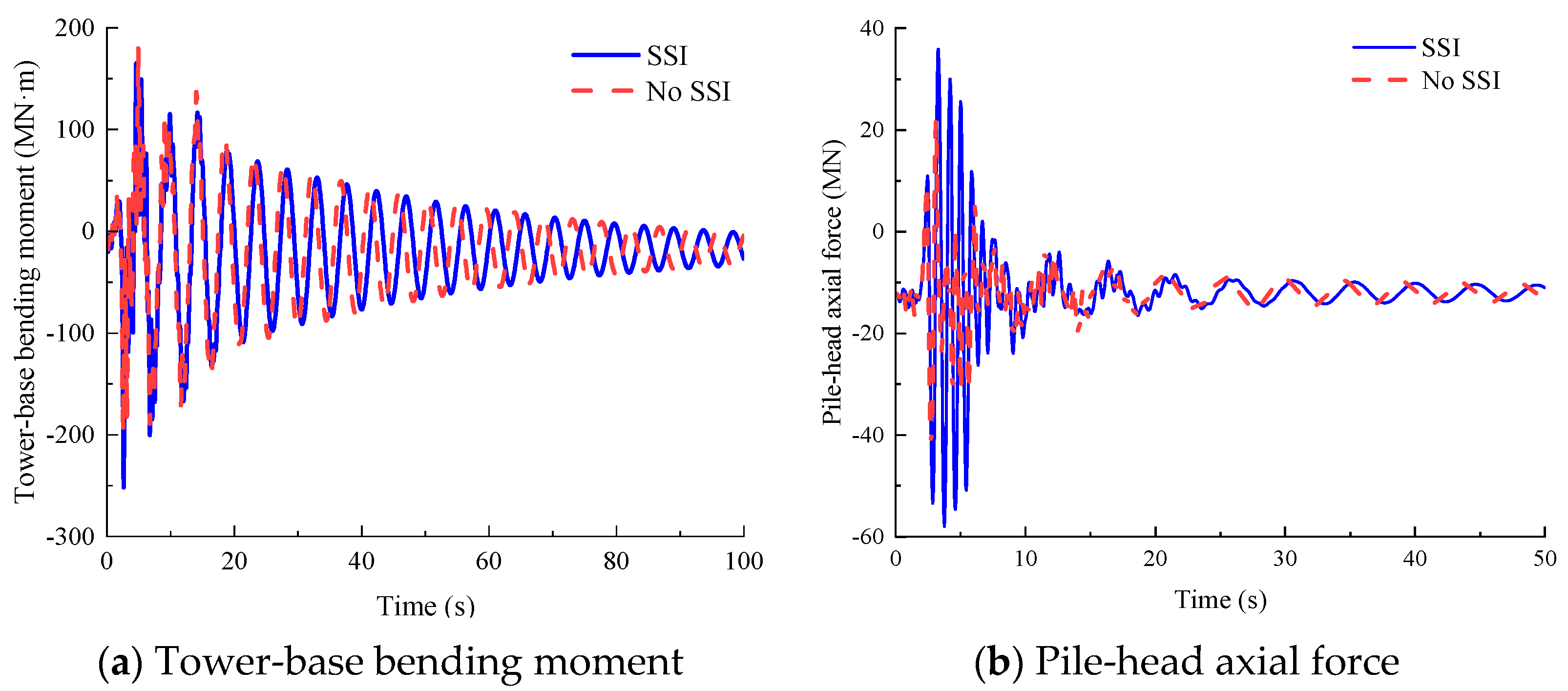
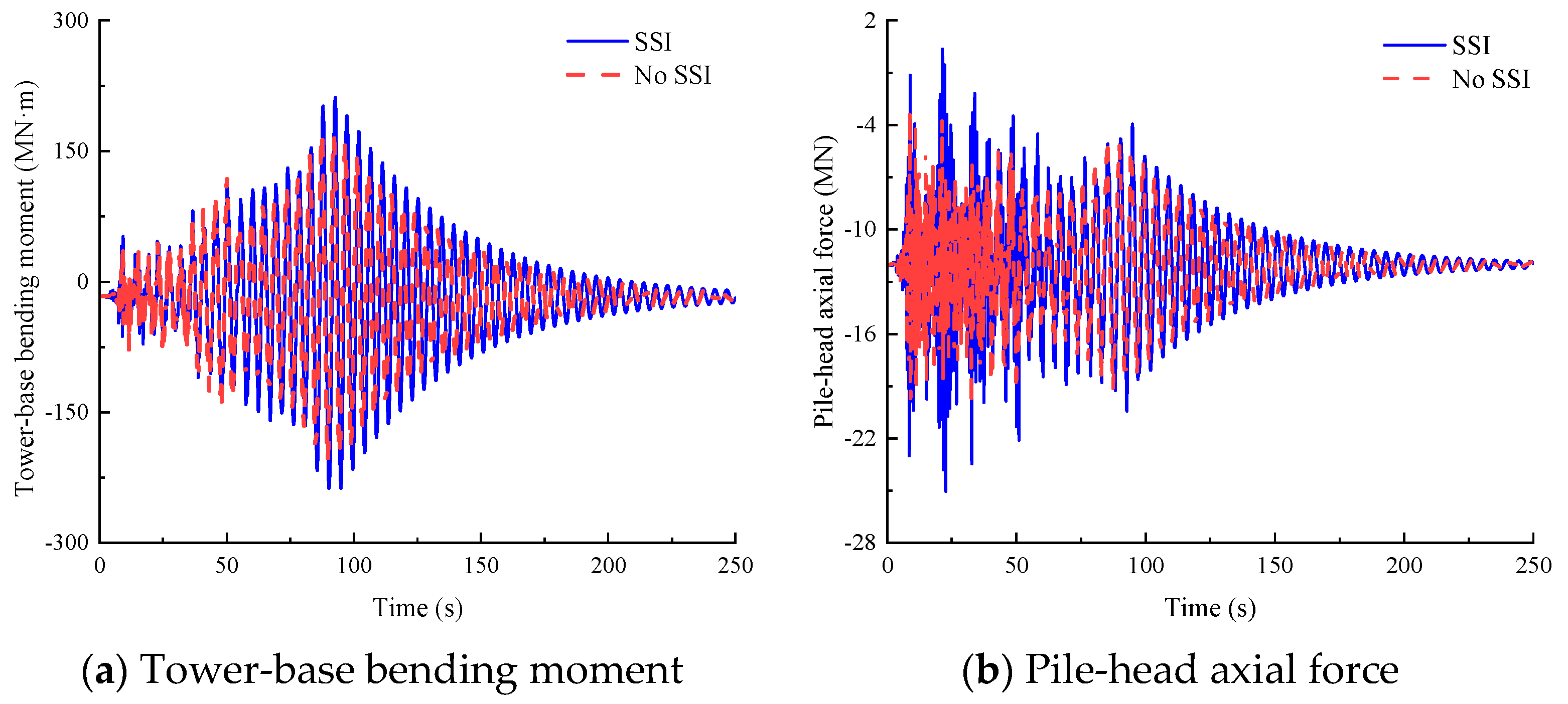
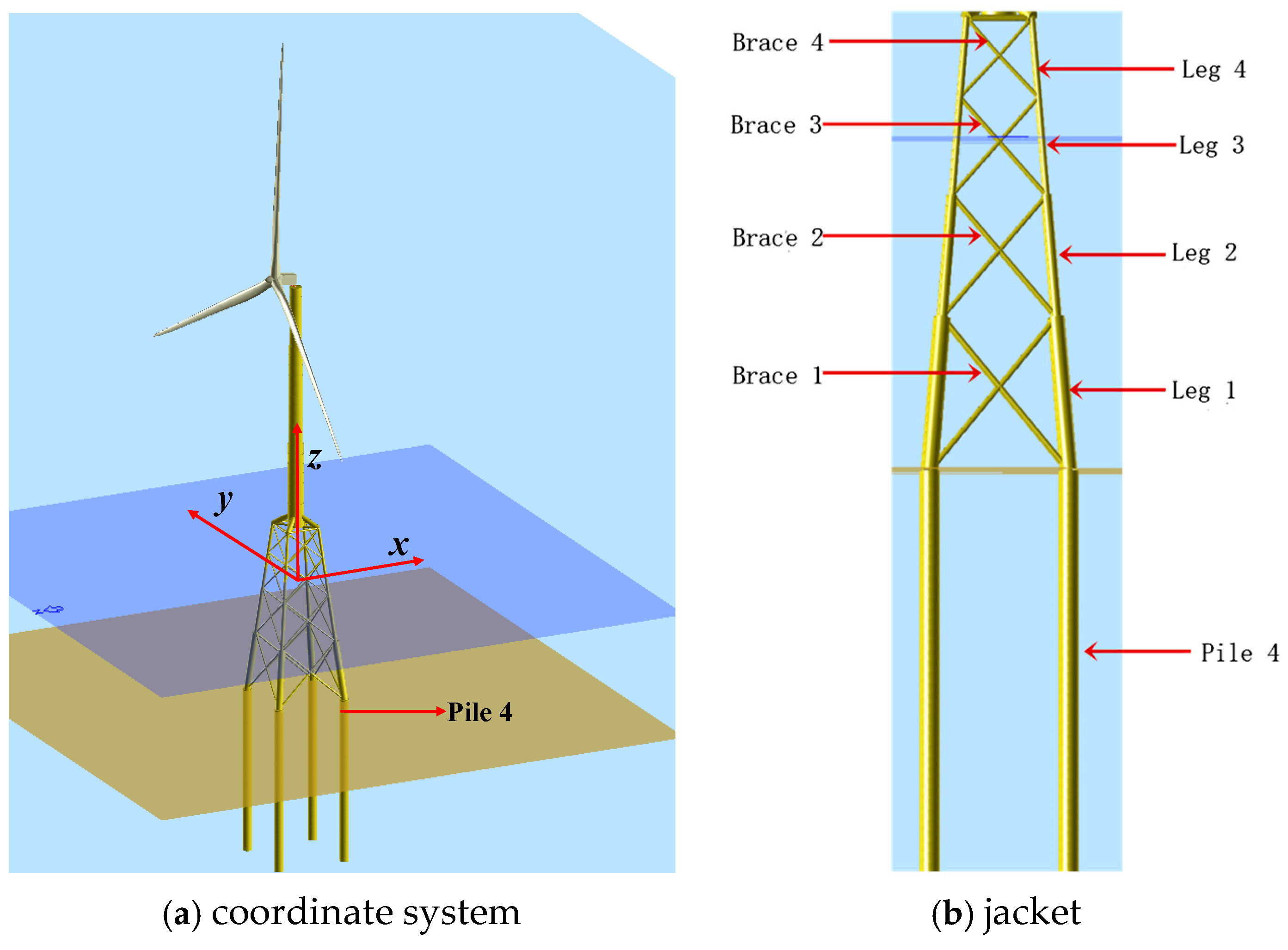
Figure 7 presents time–history responses of critical structural components under a mean wind speed of 6 m/s at the hub height: tower-base bending moment about the y-axis and pile-head axial force of pile 4 (Figure 2a). When SSI is considered, the peak values reach 107.09 MN·m for tower-base bending moment and 15.72 MN for pile-head axial force.

Table 11. Analysis error of structure for a 15 MW JOWT neglecting SSI with a mean wind speed of 6 m/s.

Statistics	Pile-Head Internal Force		Tower-Base Internal Force
	Axial Force	Bending Moment	Bending Moment	Shear Force
Max	4.38%	−84.48%	3.15%	3.23%
Average	2.28%	−87.87%	−1.06%	−1.02%
Standard deviation	18.95%	−65.04%	14.43%	14.46%

quantifies the relative errors in statistical parameters when neglecting SSI. The pile-head bending moment demonstrates the highest sensitivity to foundation modeling, with neglecting SSI resulting in underestimations of its peak, mean, and standard deviation by 84.48%, 87.87%, and 65.04%, respectively. Additionally, neglecting SSI introduces relative errors of 18.95% in pile-head axial force standard deviation, 14.43% in tower-base bending moment standard deviation, and 14.46% in tower-base shear force standard deviation. The relative errors for the remaining (e.g., peak of tower-base shear force) parameters remain within the (−5%, 5%) range.

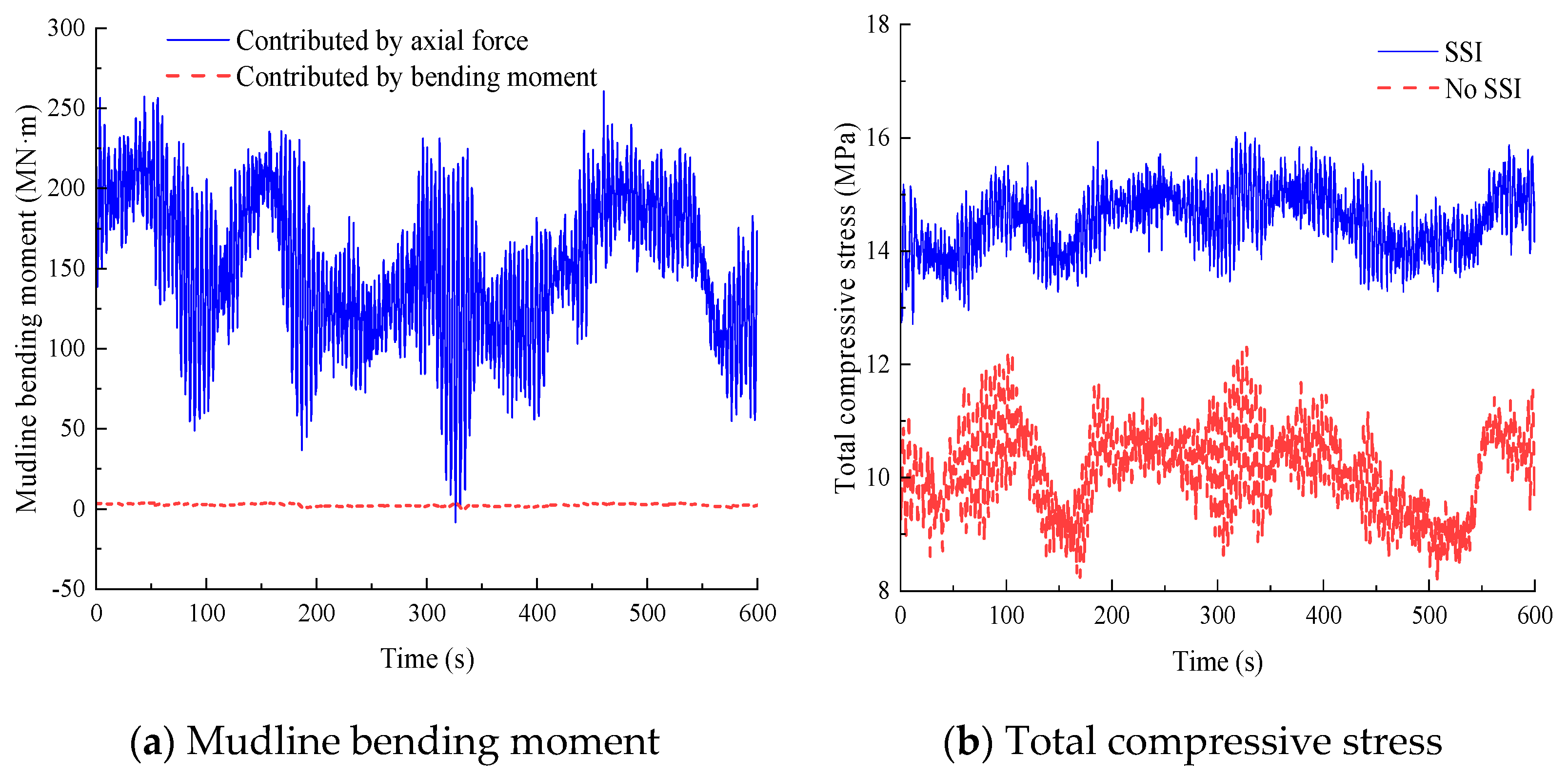
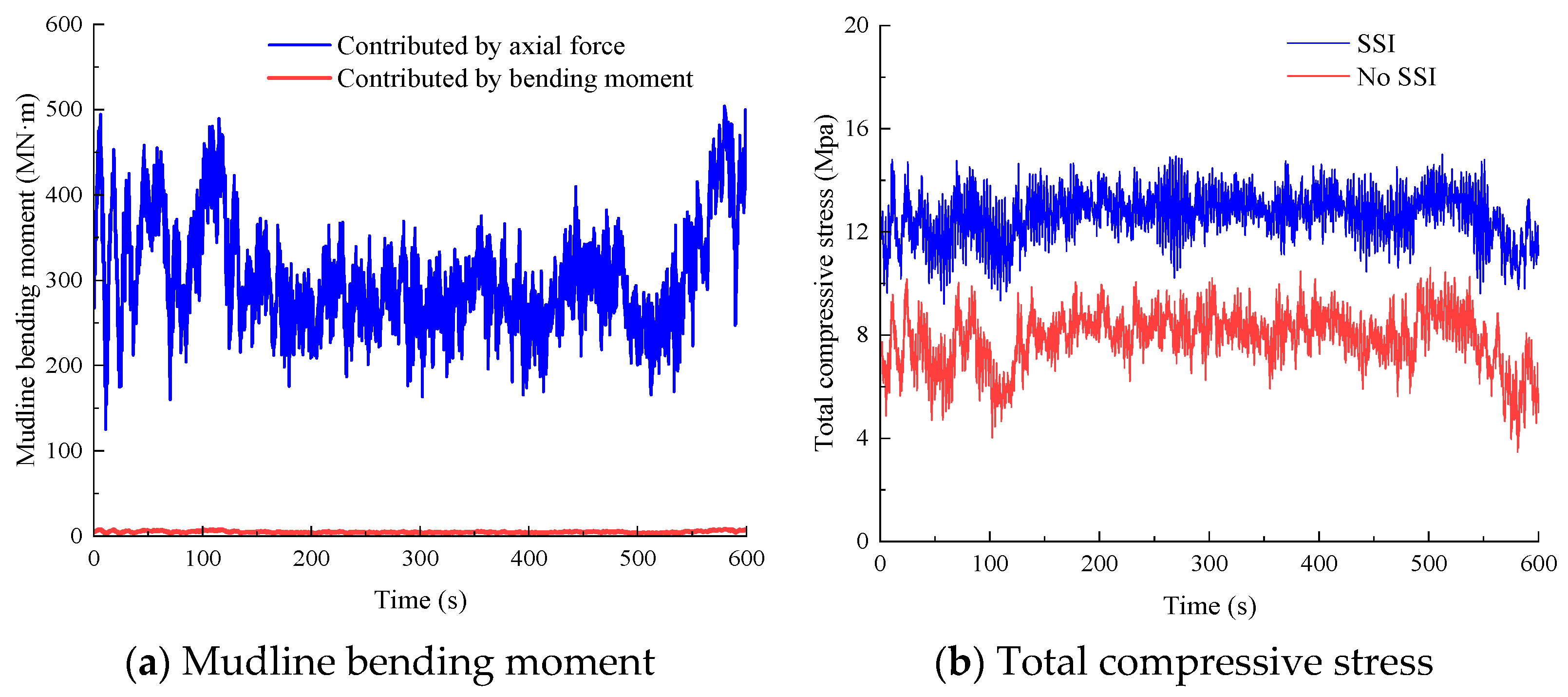
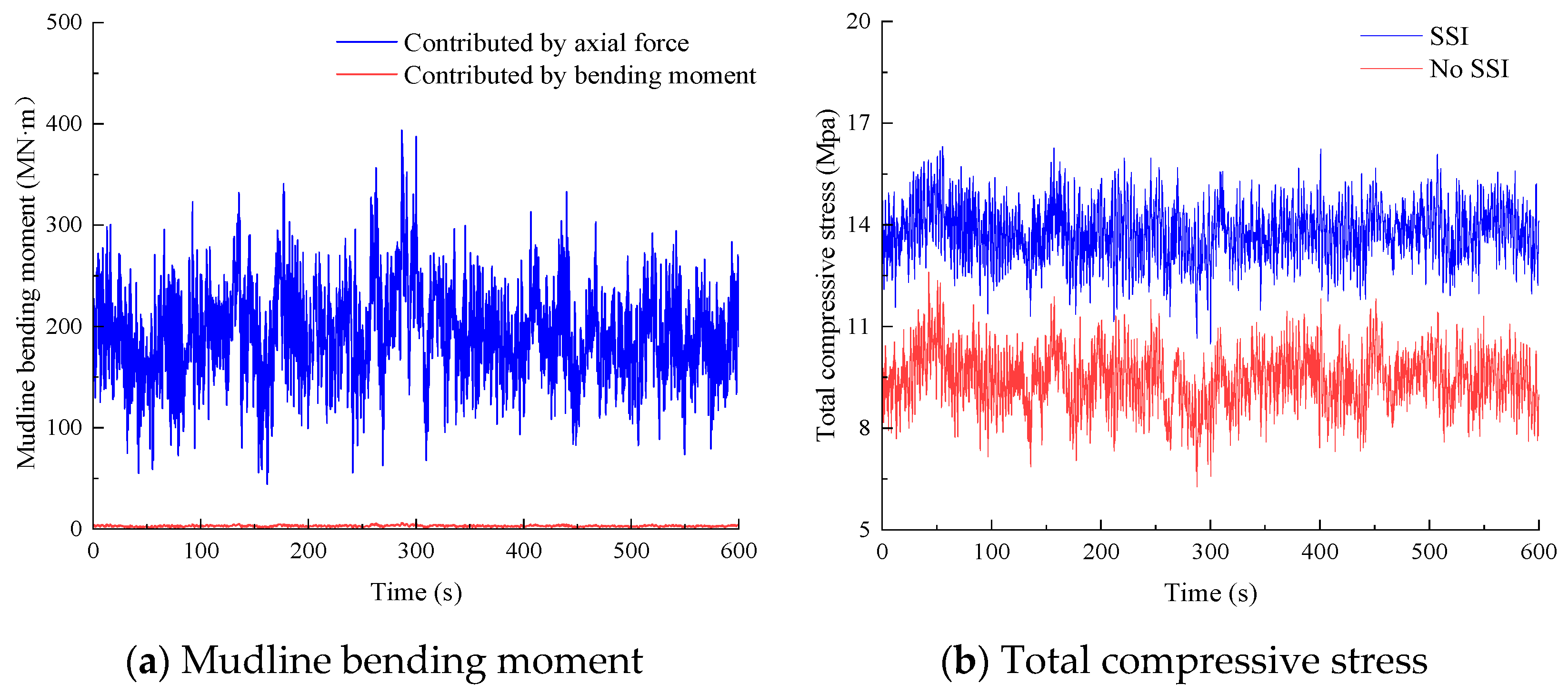
As high-rise flexible structures, the OWTs experience aerodynamic loadings acting on the wind rotor and wave–current forces on the substructures. Consequently, bottom-fixed OWTs are subjected to a large overturning moment, with pile foundations providing anti-overturning resistance through constrained forces at their interface. Based on moment equilibrium analysis at the mudline, the overturning resistance can be decomposed into axial-force-induced and bending-moment-induced components. Figure 8a quantifies these resistance mechanisms, revealing axial forces dominate overturning resistance with minimal bending moment effects. For graphical clarity, total overturning moment curves are omitted, as their values deviate from axial resistance components by less than 2%. This confirms the piles primarily function as vertical load-bearing elements under operational conditions. Figure 8b presents time histories of maximum compressive stress at the pile head, showing compressive stress levels of 16.2 MPa in the SSI model, 30% higher than the 12.1 MPa observed in the no-SSI model.

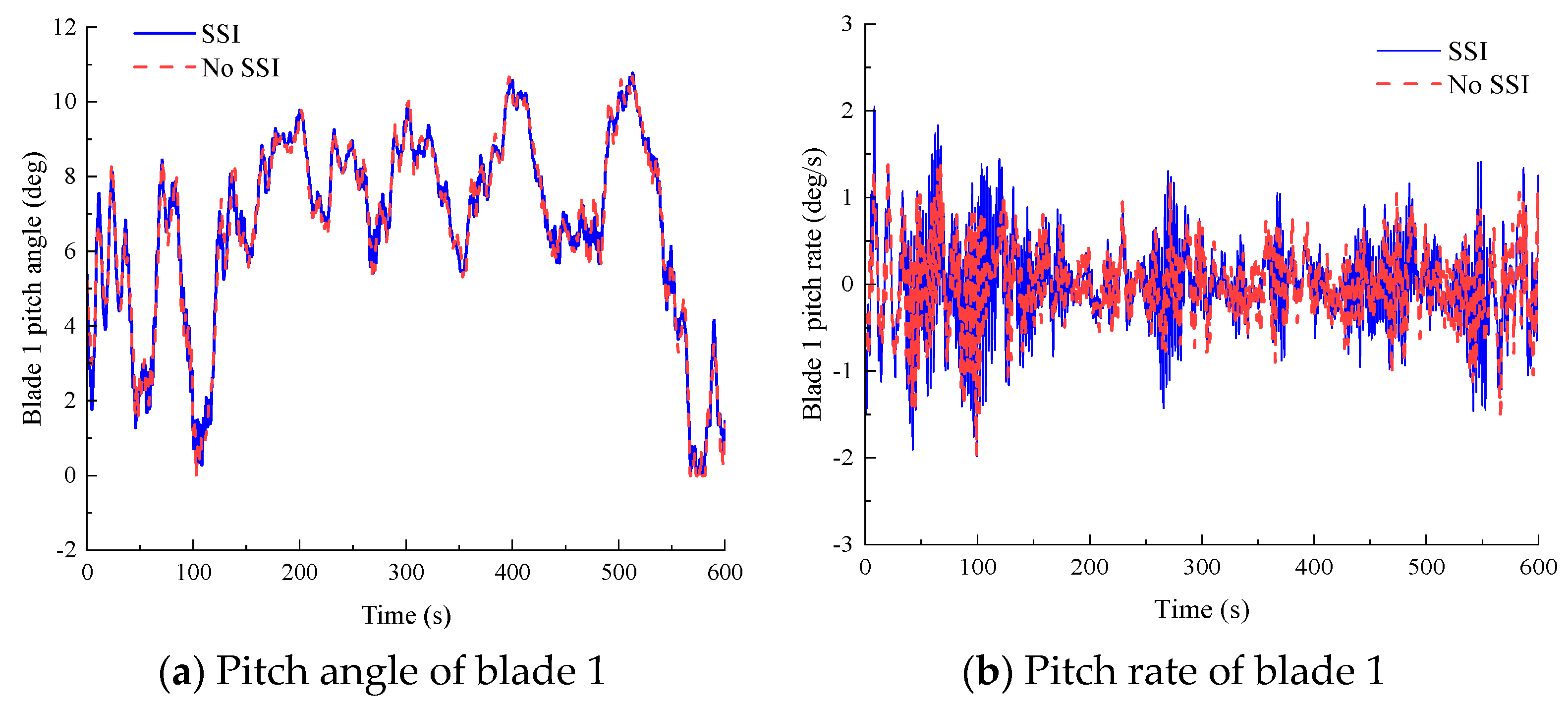
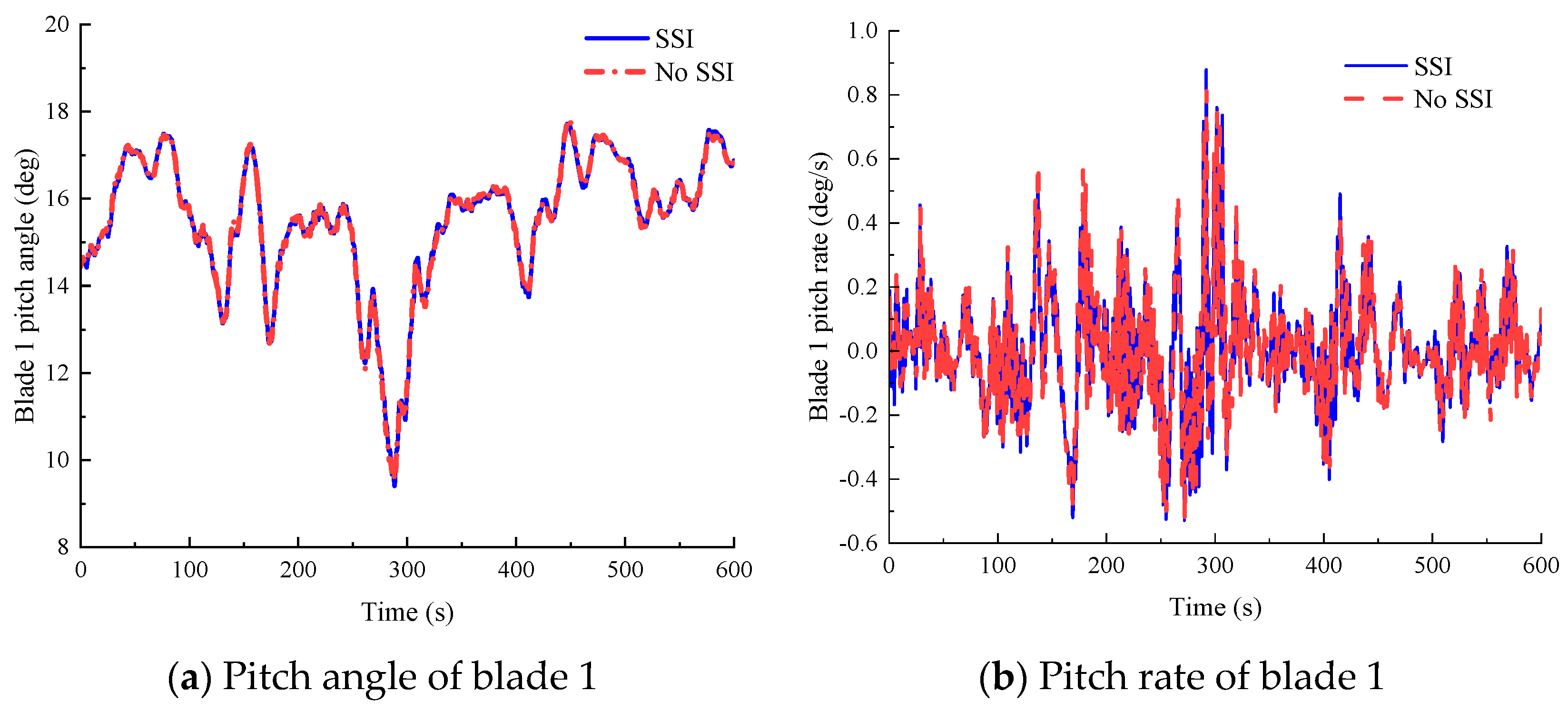
As the mean wind speed exceeds the rated wind speed, the controller increases blade pitch angles to mitigate aerodynamic torque. The power output ranges between 13 and 17.5 MW with rotor speeds maintained at 6.5 to 8.5 rpm. Figure 9a,b compare blade 1 pitch angles and pitch rates between SSI and no-SSI analyses. At a wind speed bin of 11–13 m/s (near-rated operation), pitch angle discrepancies between models are less than 0.5°, with both satisfying controller pitch rate constraints.

Figure 10a,b present the nacelle displacement in the x-axis and yaw-bearing bending moment about the y-axis when the mean wind speed of hub height is 12 m/s. When SSI is considered, peak values reach 1.08 m for nacelle displacement and 47.34 MN·m for yaw-bearing bending moment. The Fourier amplitude spectra of nacelle displacement and acceleration reveal that the first mode dominates the dynamic response of 15 MW JOWT excited by this load case.

Table 12. Analysis error of mechanical system for a 15 MW JOWT neglecting SSI with a mean wind speed of 12 m/s.

Statistics	Nacelle Fore-Aft Response		Yaw-Bearing Response
	Displacement	Acceleration	Bending Moment	Shear Forces
Max	−0.07%	14.96%	−2.75%	4.54%
Average	−4.83%	–	−2.48%	−0.98%
Standard deviation	−0.78%	–	−1.19%	1.25%

quantifies relative errors induced by SSI exclusion, revealing a 15% overestimation of nacelle acceleration peaks in no-SSI analyses. Relative errors for other parameters (e.g., peak, mean, and standard deviation of yaw-bearing shear force and bending moment) remain within the (−5%, 5%) range.

Figure 11 presents time histories of critical structural responses under a mean wind speed of 12 m/s at hub height: tower-base bending moment about the y-axis and pile-head axial force of pile 4. When SSI is considered, peak values reach 222.65 MN·m for tower-base bending moment and 19.95 MN for pile-head axial force.

Table 13. Analysis error of structure for a 15 MW JOWT neglecting SSI with a mean wind speed of 12 m/s.

Statistics	Pile-Head Response		Tower-Base Response
	Axial Force	Bending Moment	Bending Moment	Shear Force
Max	7.44%	−91.62%	4.93%	5.00%
Average	1.88%	−96.47%	0.71%	0.75%
Standard deviation	11.41%	−57.77%	3.65%	3.67%

quantifies relative errors when neglecting the SSI, revealing greater influence on these parameters compared with nacelle motion characteristics and yaw-bearing internal forces. Specifically, the pile-head bending moment exhibits the highest sensitivity to foundation modeling, with the no-SSI model causing underestimations of 91.62% in peak value, 96.47% in mean value, and 57.77% in standard deviation. Additionally, the relative error in pile-head axial force standard deviation reaches 11.4%, while other parameters (e.g., peak, mean, and standard deviation of the tower-base shear force and bending moment) demonstrate relative errors within the (−10%, 10%) range.

Figure 12a illustrates the anti-overturning moments contributed by pile-head axial forces and bending moments under a mean wind speed of 12 m/s at hub height. The analysis confirms that anti-overturning resistance is predominantly provided by pile-head axial forces, with bending moment contributions remaining statistically negligible. This demonstrates that the jacket foundation piles primarily function as vertical load-bearing members under this operational condition, resisting overturning moments through axial forces. Figure 12b reveals that the SSI model yields 40% higher maximum compressive stresses at the pile head compared to the no-SSI case.

Figure 13a,b compare blade 1 pitch angles and pitch rates between SSI and no-SSI models when the mean wind speed of hub height is 18 m/s. Overall, the pitch angle exhibits a substantial increase compared to the previous load case. The mean pitch angle reaches 15.7° under current conditions, contrasting with 6.6° observed in the scenario with a 12 m/s hub-height mean wind speed. While both models exhibit minimal discrepancies in pitch-angle time histories, the SSI model demonstrates marginally reduced pitch rate variations compared to the no-SSI model.

Figure 14 presents the dynamic responses of the 15 MW JOWT under a mean wind speed of 18 m/s at hub height, including time histories of nacelle displacement in the x-axis and yaw-bearing bending moment about the y-axis. The Fourier amplitude spectra of nacelle displacement and acceleration reveal that the first mode dominates the dynamic response of the 15 MW JOWT excited by this load case.

Table 14. Analysis error of a 15 MW JOWT mechanism without SSI with the mean wind speed of 18 m/s.

Statistics	Nacelle Fore-Aft Response		Yaw-Bearing Response
	Displacement	Acceleration	Bending Moment	Shear Forces
Max	−0.07%	7.96%	10.98%	−3.69%
Average	−6.62%	–	2.54%	−1.17%
Standard deviation	−1.09%	–	0.25%	1.20%

quantifies relative errors induced by the no-SSI model, revealing a 10.98% error in peak yaw-bearing bending moment. Relative errors for other parameters (e.g., peak, mean, and standard deviation of yaw-bearing shear force) remain within the (−10%, 10%) range, demonstrating moderate SSI effects under this load case.

Figure 15 presents time histories of critical structural responses under a mean wind speed of 18 m/s at the hub height, including the tower-base bending moment about the y-axis and pile-head axial force of pile 4. When SSI is considered, the peak responses reach 155.162 MN·m for tower-base bending moment and −18.47 MN for pile-head axial force.

Table 15. Analysis error of structure for a 15 MW JOWT neglecting SSI with a mean wind speed of 18 m/s.

Statistics	Pile-Head Response		Tower-Base Response
	Axial Force	Bending Moment	Bending Moment	Shear Force
Max	−0.12%	−86.50%	−6.19%	−6.08%
Average	0.93%	−91.11%	−0.77%	−0.73%
Standard deviation	11.97%	−54.84%	1.93%	1.98%

details the effects of no-SSI on these parameters. Specifically, the analysis reveals extreme sensitivity of pile-head bending moment to foundation modeling, with no-SSI causing underestimations of 86.50% in peak value, 91.11% in mean value, and 54.84% in standard deviation. The relative errors for other parameters (e.g., peak, mean, and standard deviation of yaw-bearing shear force and bending moment) remain within (−10%, 10%) except for the pile-head axial force standard deviation (11.97%).

Figure 16a illustrates that the anti-overturning moment is predominantly resisted by pile-head axial forces, while the contribution from bending moment is negligible in comparison. Figure 16b quantifies maximum compressive stresses at the pile head, revealing that the no-SSI model results in a 38% underestimation of the maximum compressive stress.

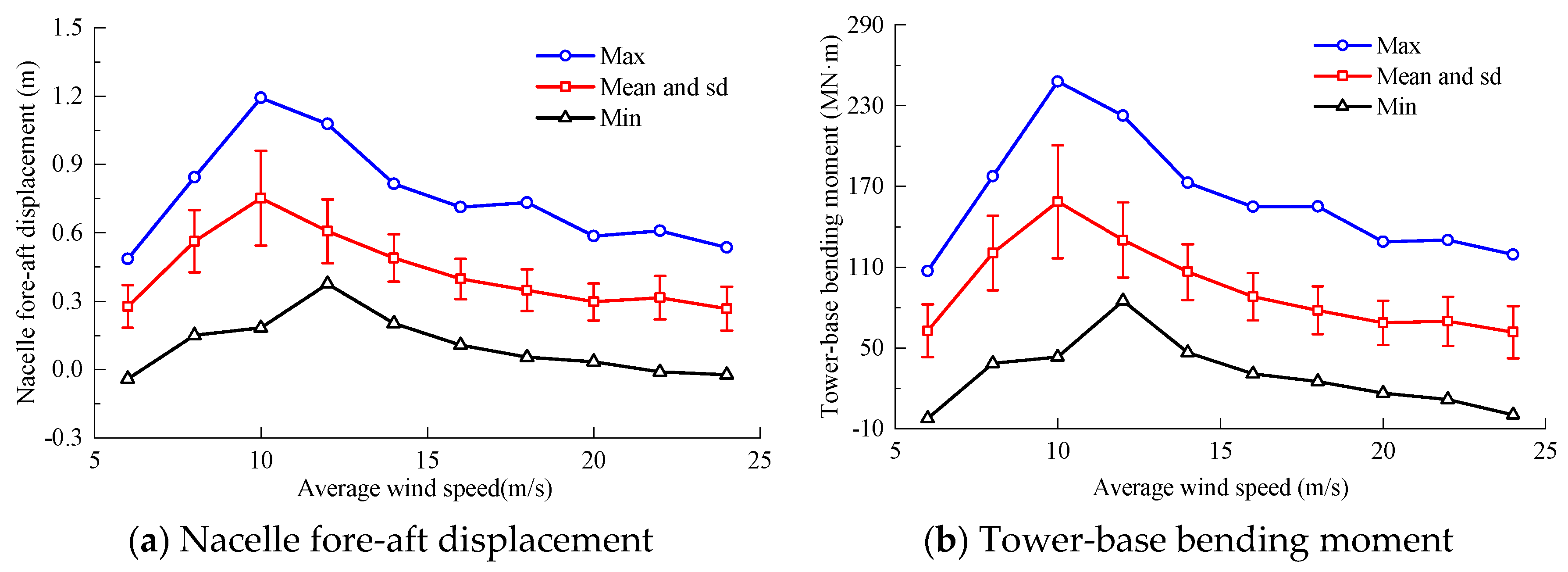
Figure 17 compares peak values, minima, and standard deviations (SD) of nacelle displacement in the x-axis and tower-base bending moment about the y-axis for the 15 MW JOWT with SSI considered. The peak values for these statistical parameters consistently occur under load case 3 or 4, which aligns with the rated wind speed of 10.8 m/s. According to the dynamic response of JOWT, the controller described in Section 2.5 effectively maintains the operational stability of the 15 MW JOWT, thereby demonstrating its suitability for integrated dynamic analyses of running OWTs.

3.3. Dynamic Response of 15 MW OWT Excited by Extreme Wind, Wave and Current

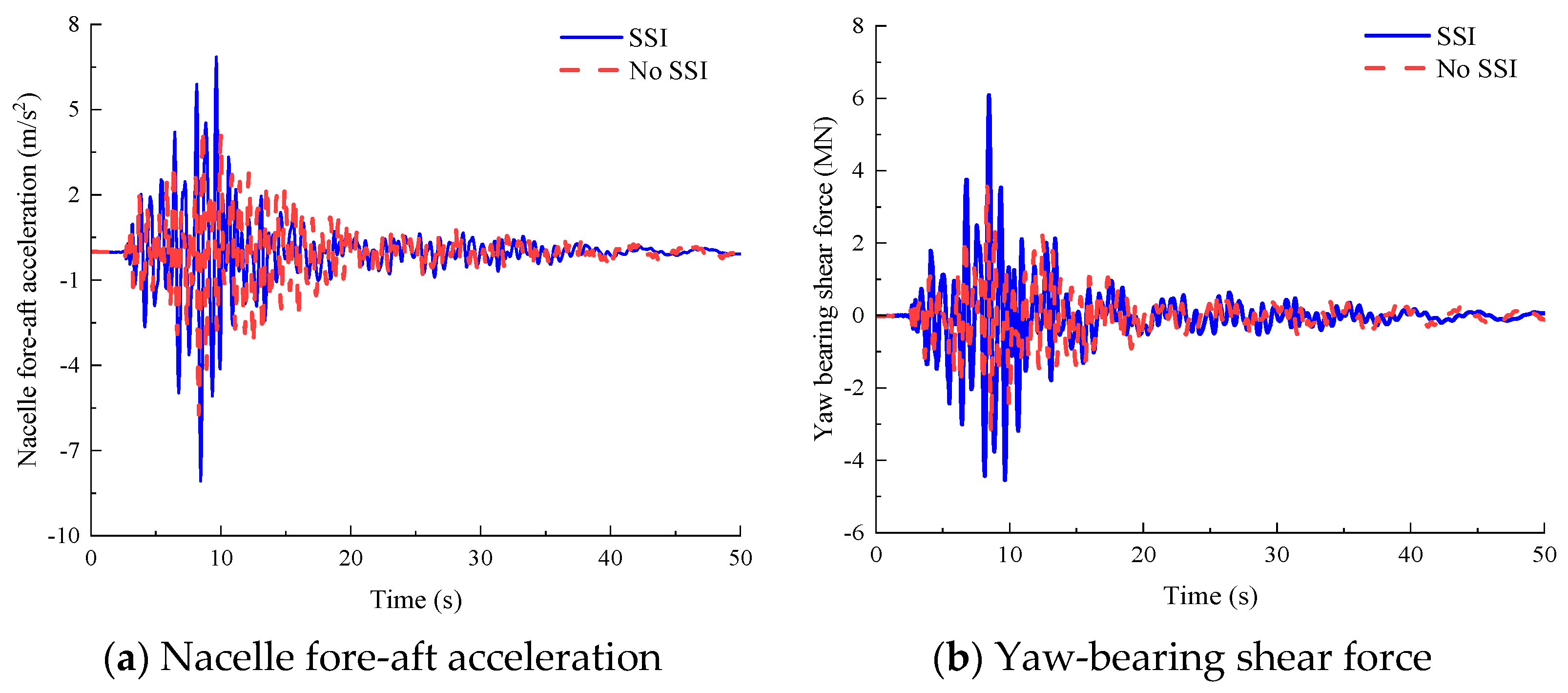
Under extreme wind conditions with a mean wind speed of 50 m/s at the hub height, the JOWT enters the parked condition with blades pitched to 90°. Figure 18a,b present the dynamic responses of the 15 MW JOWT at this wind speed, including nacelle displacement in the x-axis and yaw-bearing bending moment about the y-axis. When SSI is considered, the peak values reach 0.421 m for nacelle displacement and 54.97 MN·m for yaw-bearing bending moment. The Fourier amplitude spectra of nacelle displacement and acceleration reveal that the first mode dominates the dynamic response of 15 MW JOWT excited by this load case.

Table 16. Analysis error of a mechanical system for a 15 MW JOWT neglecting SSI with a mean wind speed of 50 m/s.

Statistics	Nacelle Fore-Aft Response		Yaw-Bearing Response
	Displacement	Acceleration	Bending Moment	Shear Forces
Max	−20.33%	−3.28%	2.24%	−6.94%
Average	−19.46%	–	−0.77%	−6.39%
Standard deviation	−18.09%	–	0.71%	−12.46%

quantifies the relative errors induced by the no-SSI model, revealing significant underestimation of nacelle displacement parameters: 20.33% in peak value, 19.46% in mean value, and 18.09% in standard deviation. The standard deviation of the yaw mechanism shear force is underestimated by 12.46%, while relative errors for other parameters (e.g., peak, mean, and standard deviation of the yaw-bearing bending moment) remain within the range of (−10%, 10%).

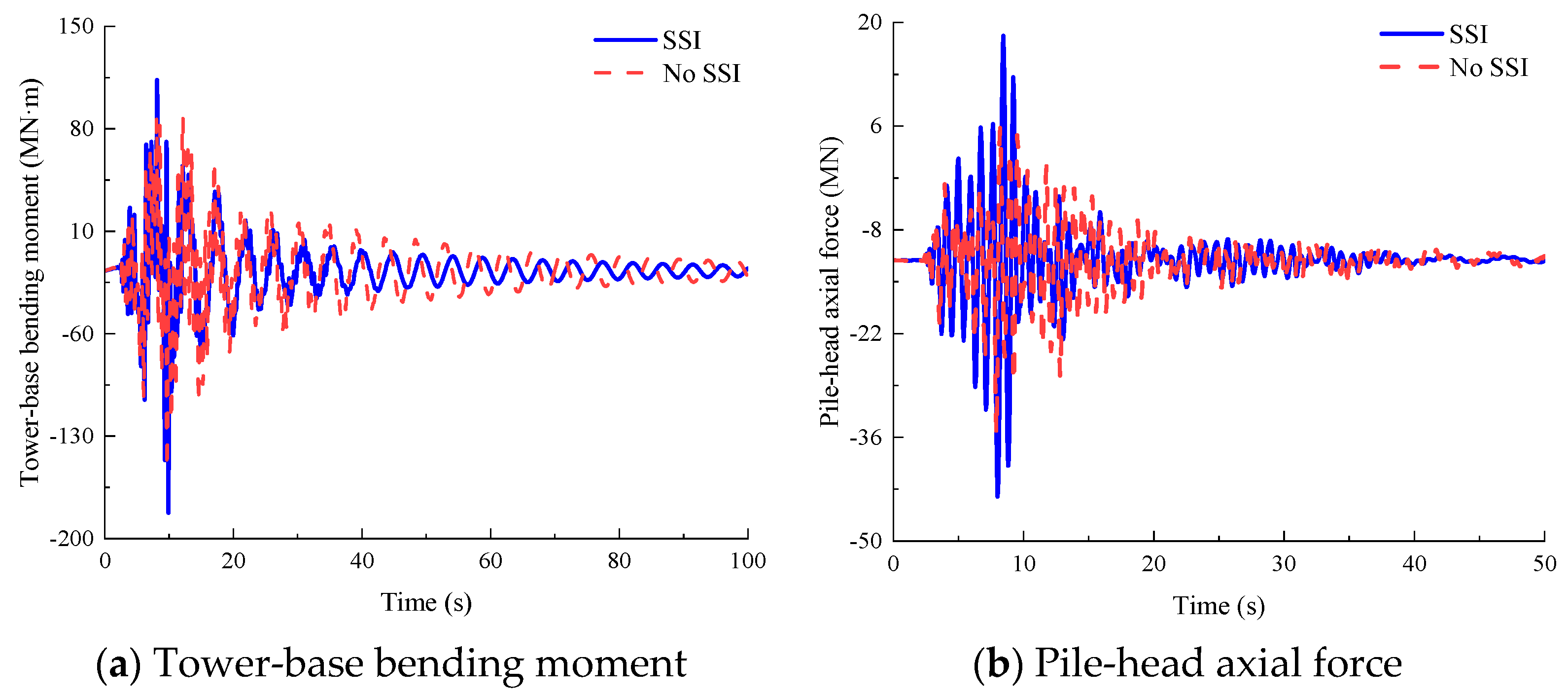
Figure 19 shows time histories of critical structural responses under a mean wind speed of 18 m/s at hub height, including the tower-base bending moment about the y-axis and pile-head axial force of pile 4. When SSI is considered, the peak values reach 117.897 MN·m for tower-base bending moment and −23.65 MN for pile-head axial force.

Table 17. Analysis error of the structure for a 15 MW JOWT neglecting SSI with a mean wind speed of 50 m/s.

Statistics	Pile-Head Response		Tower-Base Response
	Axial Force	Bending Moment	Bending Moment	Shear Force
Max	6.27%	−82.69%	−7.23%	−7.19%
Average	2.69%	−88.79%	1.13%	1.21%
Standard deviation	10.79%	−73.10%	−10.18%	−10.14%

summarizes the significant effects of SSI on these parameters. Specifically, this table indicates significant underestimations by the no-SSI model: pile-head bending moment peak, mean, and standard deviation are reduced by 82.69%, 88.79%, and 73.10%, respectively. In addition, relative errors for the pile-head axial force, tower-base bending moment, and shear force standard deviations reach 10.79%, −10.18%, and −10.14%, while other parameters exhibit errors within the range of (−10%, 10%). In general, under extreme conditions, wave loads increase significantly, leading to more pronounced participation of higher-order modes in the structural dynamic response. The nacelle acceleration and peak yaw mechanism bending moment exceed those under the running condition of OWT.

3.4. Seismic Response of 15 MW OWT

Given the predominant influence of SSI on the higher-order natural frequencies of OWTs and the growing deployment of offshore wind farms in seismically active regions (e.g., Japan or Taiwan of China), this section investigates the seismic response of the 15 MW JOWT. The wind turbine was modeled in a parked condition, excluding wind–wave–current loads, with hydrodynamic effects restricted to added mass pressures induced by structural vibrations. To minimize the impact of initial conditions, the seismic excitation is applied at 150 s, and the total simulation duration is set to 400 s.

The site depicted in Figure 1 lacks measured shear wave velocity data. Based on statistical correlations between the sand internal friction angle and shear wave velocity, the 30-m equivalent shear wave velocity at this site ranges from 220 to 290 m/s. Three strong ground motion records with equivalent shear wave velocities comparable to this range, as shown in

Table 18. Information on input ground motion.

ID No.	Abbreviation of the Record	Year	Name	Recording Station	Vs30 (m/s)
1	RRS	1994	Northridge-01	Rinaldi Receiving Station	282
2	BCR	1979	Imperial Valley-06	Bonds Corner	223
3	DLT	1979	Imperial Valley	Delta	275

, were selected from the PEER Strong Motion Database as input ground motions for this study. Figure 20 presents the acceleration time histories and 5% damped absolute acceleration response spectra of the selected ground motion components.

3.4.1. Seismic Response of JOWT Excited by RRS Record

Figure 21a,b show the time histories of the nacelle acceleration and shear force in the x-axis under the RRS ground motion. With SSI, the peak nacelle x-axis displacement and acceleration reach 0.761 m and 10.11 m/s², while the yaw mechanism exhibits peak bending moment and shear force values of 114.58 MN·m and 6.99 MN, respectively. The Fourier amplitude spectra of nacelle displacement and acceleration (Figure 21c,d) reveal stronger higher-mode participation compared with those in Section 3.2 and Section 3.3. Since SSI predominantly modifies higher-order modes of the 15 MW JOWT, these parameters are significantly amplified during seismic excitation.

Table 19. Analysis error of a mechanical system for a 15 MW JOWT neglecting SSI excited by the RRS record.

Statistics	Nacelle Fore-Aft Response		Yaw-Bearing Response
	Displacement	Acceleration	Bending Moment	Shear Forces
Max	−16.82%	−26.31%	3.64%	−50.71%
Average	−1.90%	–	0.14%	−4.72%
Standard deviation	−2.95%	–	−16.45%	−39.13%

summarizes the analysis errors induced by neglecting SSI. Specifically, peak nacelle displacement (−16.82%), acceleration (−26.31%), and yaw shear force (−50.71%) are substantially underestimated, with standard deviation errors of −16.45% (bending moment) and −39.13% (shear force). Collectively, the impact of SSI on the seismic responses of the JOWT exceeds the impacts observed under wind–wave–current excitations.

Figure 22 presents the time histories of the tower-base bending moment about the y-axis and pile-head axial force. When SSI is considered, the peak values reach 251.67 MN·m for tower-base bending moment and −57.99 MN for pile-head axial force. In general, neglecting SSI results in more pronounced effects on these structural response parameters compared to the nacelle motion and yaw mechanism internal forces, as shown in

Table 20. Analysis error of a 15 MW JOWT structure without SSI excited by RRS record.

Statistics	Pile-Head Response		Tower-Base Response
	Axial Force	Bending Moment	Bending Moment	Shear Force
Max	−27.64%	−82.35%	−21.74%	−21.48%
Average	0.07%	−83.70%	0.27%	0.29%
Standard deviation	−46.56%	−87.54%	1.60%	1.56%

. Specifically, neglecting SSI underestimates peak values by 27.64% (pile-head axial force), 82.35% (pile-head bending moment), 21.74% (tower-base bending moment), and 21.48% (tower-base shear force). Additionally, the mean pile bending moment, its standard deviation, and the pile-head axial force standard deviation are underestimated by 83.70%, 46.56%, and 87.54%, respectively. The results demonstrate that neglecting SSI may introduce significant errors in statistical metrics of these structural responses.

3.4.2. Seismic Response of JOWT Excited by BCR Record

Figure 23a,b present the time histories of the nacelle acceleration and yaw-bearing shear force on the x-axis. When SSI is considered, the nacelle peak displacement and yaw-bearing shear force are 0.45 m and 6.08 MN, respectively. The Fourier amplitude spectra of nacelle displacement and acceleration reveal stronger higher-mode participation, similar to sub-Section 3.4.1. This excitation significantly activates higher-order vibration modes, thereby amplifying the SSI influences on structural seismic responses.

Table 21. Analysis error of a mechanical system for a 15 MW JOWT neglecting SSI excited by the BCR record.

Statistics	Nacelle Fore-Aft Response		Yaw-Bearing Response
	Displacement	Acceleration	Bending Moment	Shear Forces
Max	−2.12%	−29.07%	−20.91%	−41.45%
Average	−0.52%	–	0.001%	0.26%
Standard deviation	−1.92%	–	−2.94%	−29.51%

quantifies the relative errors of seismic response induced by neglecting SSI. Specifically, the peak nacelle acceleration, yaw mechanism bending moment, and shear force are underestimated by 29.07%, 20.91%, and 41.45%, respectively. The yaw mechanism shear force standard deviation is underestimated by 29.51%. These results underscore the critical importance of considering SSI for seismic performance evaluations under high-mode-dominant excitations due to its amplified effects.

Figure 24 displays the time histories of the tower-base bending moment about the y-axis and pile-head axial force. When SSI is considered, the peak values reach 163.51 MN·m for tower-base bending moment and 44.03 MN for pile-head axial force.

Table 22. Analysis error of a 15 MW JOWT structure without SSI excited by BCR record.

Statistics	Pile-Top Response		Tower-Base Response
	Axial Force	Bending Moment	Bending Moment	Shear Force
Max	−19.37%	−70.37%	−16.65%	−16.22%
Average	0.07%	−83.68%	0.09%	0.11%
Standard deviation	−22.56%	−63.95%	12.80%	−13.11%

reveals that the no-SSI analysis model underestimates peak values by 19.37% (pile-head axial force), 70.37% (pile-head bending moment), 16.65% (tower-base bending moment), and 16.22% (tower-base shear force). Additionally, the mean pile bending moment is underestimated by 83.68%, while the standard deviations of pile-head axial force, pile-head bending moment, tower-base bending moment, and tower-base shear force are reduced by 22.56%, 63.95%, 12.80%, and 13.11%. The results demonstrate that neglecting SSI introduces significant errors in statistical metrics of these structural responses.

3.4.3. Seismic Response of JOWT Excited by DLT Record

Figure 25a,b present the time histories of nacelle displacement and yaw-bearing shear force in the x-axis under the BCR ground motion. When SSI is considered, the nacelle peak acceleration and yaw-bearing shear force in the x-axis are 1.25 m and 2.47 MN, respectively. The Fourier amplitude spectra of nacelle displacement and acceleration reveal stronger higher-mode participation, similar to Section 3.4.1 and Section 3.4.2.

Table 23. Analysis error of a mechanical system for a 15 MW JOWT neglecting SSI excited by the DLT record.

Statistics	Nacelle Fore-Aft Response		Yaw-Bearing Response
	Displacement	Acceleration	Bending Moment	Shear Forces
Max	−17.59%	−32.01%	−6.12%	−28.07%
Average	−1.91%	–	0.02%	−0.24%
Standard deviation	−16.65%	–	−3.02%	−18.72%

summarizes the relative errors of structural response parameters resulting from neglecting SSI. The results demonstrate that disregarding SSI leads to underestimations of 17.59%, 32.01%, and 28.07% for peak nacelle displacement, nacelle acceleration, and yaw mechanism shear force, respectively. The standard deviations of nacelle displacement and yaw mechanism shear force are underestimated by 16.65% and 18.72%.

Figure 26 displays the time histories of the tower-base bending moment about the y-axis and pile-head axial force. When SSI is considered, the peak values reach 237.52 MN·m for tower-base bending moment and 25.04 MN for pile-head axial force.

Table 24. Analysis error of a 15 MW JOWT structure without SSI excited by the DLT record.

Statistics	Pile-Top Response		Tower-Base Response
	Axial Force	Bending Moment	Bending Moment	Shear Force
Max	−19.98%	−74.87%	−14.75%	−14.70%
Average	0.08%	−86.64%	0.08%	0.10%
Standard deviation	−18.01%	−66.69%	−14.12%	−14.09%

reveals that the no-SSI analysis model underestimates peak values by 19.98% (pile-head axial force), 74.87% (pile-head bending moment), 14.75% (tower-base bending moment), and 14.7% (tower-base shear force). Additionally, the mean pile bending moment is underestimated by 86.64%, while the standard deviations of pile-head axial force, pile-head bending moment, tower-base bending moment, and tower-base shear force are reduced by 18.01%, 66.69%, 14.12%, and 14.09%. These results demonstrate that neglecting SSI introduces significant errors in statistical metrics of these structural responses.

The modal analysis demonstrates that the SSI predominantly influences the second-, third-, and fourth-order FA and SS modes of the 15 MW JOWT. During the seismic excitation, these higher-order modes are strongly excited, resulting in SSI effects that have significantly greater impacts on structural seismic responses compared to those induced by wind–wave–current loading.

Table 25. Analysis error of 15 MW JOWT without SSI excited by different load cases.

Load Cases	Nacelle Acceleration	Yaw-Bearing Shear Force	Tower-Base Bending Moment	Pile-Head Axial Force
Wind–wave–current	14.96%	−6.94%	−7.23%	7.44%
Seismic	−32.01%	−50.71%	−21.74%	−27.64%

compares the maximum prediction errors of peak values for selected 15 MW JOWT parameters under two loading scenarios in non-SSI models. The results demonstrate significantly larger errors in dynamic response peaks induced by seismic excitation when neglecting SSI effects, compared to those observed under combined wind–wave–current loading conditions. Consequently, SSI plays a critical role in determining the seismic performance of the 15 MW JOWT, necessitating rigorous modeling in seismic risk assessments to ensure accuracy.

4. Conclusions and Outlooks

This study designed a jacket substructure and a variable-speed and pitch-collective controller for the IEA 15 MW wind turbine based on measured meteo-ocean data from a deep-water site in the North Sea of Denmark (53°13′04″ N, 3°13′13″ E). The natural frequencies of the system were analyzed with and without soil–structure interaction, followed by investigations of dynamic responses under combined wind–wave–current loads and seismic actions. The following conclusions are drawn:

• A preliminary design of the jacket substructure and pile foundation, along with a mechanical controller, for the IEA 15 MW turbine was proposed. The case studies demonstrate that this JOWT satisfies industry standards regarding natural frequency constraints and ultimate/serviceability limit states. The controller tuned with the ROSCO tool effectively regulates the generator torque and blade pitch of the 15 MW JOWT.
• The modal analysis reveals that the natural frequencies of 15 MW JOWT are related to the SSI effect and vibration direction. Specifically, neglecting the SSI effect overestimates the third and fourth FA modal frequencies by 32.4% and 13.9%, respectively. Due to differences in RNA rotational inertia between different directions, the second-order modal frequencies of this JOWT are 1.254 Hz (FA) and 1.135 Hz (SS), respectively, showing a relative deviation of 10.5%.
• The numerical simulation demonstrates that parameters such as tower-top displacement and tower-base bending moment reach maximum amplitudes when the hub-height mean wind speed approaches the rated value. Moreover, the structural responses under wind–wave–current loads are dominated by their fundamental modes, with significant overturning moments on the jacket primarily resisted by axial forces at pile heads.
• The seismic analyses of this JOWT using selected strong motion records reveal pronounced higher-mode excitations, evidenced by high-frequency spectral components in nacelle accelerations. The SSI effect substantially influences seismic responses: under the BCR record excitation, neglecting this interaction results in underestimation of peak nacelle accelerations, yaw mechanism moments, and shear forces by 29%, 21%, and 42%, respectively.

Due to GL-Bladed software simplifying RNA as a rigid body in modal analysis, neglecting the blade modes and potentially affecting the values of system natural frequencies, future studies should conduct modal analysis of the 15 MW JOWT under flexible blade conditions. In addition, under operational wind–wave conditions, the SSI significantly influences the internal force standard deviations at the tower base and pile head, potentially affecting fatigue life predictions at these critical locations.