Optimizing Electric Cold-Chain Vehicle Scheduling for Sustainable Urban Logistics: A Novel Framework Balancing Freshness and Vehicle Charging

Abstract

Cold-chain logistics, characterized by high energy consumption and significant emissions, pose a critical challenge for the green transformation of global transportation. Electric cold-chain vehicles have emerged as a promising solution to reduce carbon emissions in urban logistics. However, their scheduling is highly complex due to the need to balance freshness and charging requirements, presenting operational challenges for cold-chain companies. To address this issue, this paper proposes an optimization model and algorithm for the efficient scheduling of these innovative electric cold-chain vehicles. First, we define the unique features of these vehicles and establishes an operational framework tailored to cold-chain logistics. Subsequently, we develop a mixed-integer programming model to optimize freshness preservation. Additionally, we design a state-of-the-art algorithm based on an improved genetic algorithm to solve the scheduling model effectively. Numerical experiments conducted using operational data from Shanghai, China, validate the proposed method and algorithm. This study provides valuable insights and tools to support the green transformation of urban cold-chain logistics and contributes to the reduction of urban carbon emissions.

1. Introduction

With the rise in residents’ living standards, customers now have higher expectations for the quantity and quality of cold-chain products [1,2]. However, traditional fuel-powered cold-chain vehicles face restrictions in many cities due to their high pollution emissions, excessive noise, and other drawbacks, which limit their operating time and range [3]. Notably, fuel-powered refrigerated vehicles are substantial energy consumers, which not only results in considerable carbon emissions but also poses significant challenges for pollution control. As a result, the management of these high-emission vehicles has become a priority for governments worldwide [4,5]. Hence, these limitations generate significant challenges for delivering time-sensitive cold-chain products. Fortunately, the emergence of electric cold-chain vehicles has accelerated the integration and development of cleaner and more efficient solutions in this field.

Electric vehicles offer numerous advantages, such as low noise, zero emissions, and environmental friendliness [6,7], enabling them to conduct cold-chain distribution at any time and in any area of the city. These benefits are significant for building green cities and reducing urban air pollution [8]. At the same time, as customer expectations for cold-chain services grow, there is a demand for both refrigerated and frozen goods to be delivered in a single shipment to minimize unloading time and enhance operational efficiency. However, traditional single-temperature electric cold-chain vehicles cannot meet these evolving needs. Therefore, optimizing the distribution and charging scheduling of electric cold-chain vehicles to achieve multi-temperature co-distribution has become a critical focus for cold-chain company managers.

Compared with traditional cold-chain logistics research, the main contributions of this study are as follows. Firstly, this paper addresses the business needs of an intercity cold-chain delivery company in Shanghai by proposing the use of two-compartment electric cold-chain vehicles for cold-chain distribution. Secondly, considering the constraints of compartment capacity and vehicle battery capacity, a mixed-integer programming (MIP) model is constructed to minimize freshness loss. To solve this model, a state-of-the-art genetic algorithm is employed, taking into account the complexity of integrating vehicle delivery routes and charging schedules in a multi-temperature co-distribution environment. During the chromosome decoding process, a rollback strategy is introduced to enhance the feasibility of infeasible solutions, and a comparative study is conducted with mainstream penalty strategies.

This study holds both practical significance and theoretical contributions, offering efficient decision-making support for cold-chain company managers and providing a new research framework for scholars in the field of sustainable cold-chain logistics. The remainder of this paper is organized as follows: Section 2 reviews the related works. Section 3 defines the optimization problem and proposes the model. Section 4 develops the novel algorithm to solve the model. Section 5 conducts the case study in Shanghai. Section 6 proposes the managerial insights derived from the above experiment. Section 7 summarizes the paper and proposes future research directions.

2. Literature Review

2.1. Electric Vehicle Scheduling

Nowadays, electric vehicles (EVs) have become very popular for eco-friendly transportation [9,10]. In this field, most scholars mainly focus on vehicle path optimization and optimal scheduling strategies for vehicle charging and swapping. In terms of vehicle path optimization, Seyfi et al. [11] handled the problem of electric vehicle path optimization in multi-objections. They constructed a MIP model and used a large-scale search algorithm to solve the model. Hermann et al. [12] studied the routing optimization problem of EVs and made improvements to the genetic algorithm, which improved its performance in local search and global optimization. Wang et al. [13] researched the routing optimization issue of electric vehicles in multi-yard collaboration, incorporating time window constraints and shared electric pile features into the model construction, and developed effective algorithms to solve the model.

EV scheduling strategies for charging and swapping are also hot topics for researchers [14,15]. Hof et al. [16] introduced the battery-swapping process of electric vehicles into the scheduling model and used an adaptive variable neighborhood search algorithm for model solving. Basso et al. [17] considered the energy prediction problem in the path optimization process and applied machine learning methods to the path optimization modeling process of electric vehicles. Bezzi et al. [18] researched the routing optimization issue of EVs under multiple technology integration modes and proposed an improved branch pricing algorithm. The experimental results verified the progressiveness of the proposed model. Montoy et al. [19] considered the nonlinear relationship between the quantity and time during charging and constructed a heuristic algorithm to handle the model. Jie et al. [20] considered battery replacement, taking into account the electric vehicle load, battery capacity, and replacement cost. They constructed an integer programming mathematical model and used a hybrid-heuristic algorithm to get the solutions. Schiffer et al. [21] analyzed the charging behavior of pure electric logistics fleets and constructed a multi-objective MIP model to minimize fleets’ total distance and total charging cost. At the same time, the influence of charging station location on vehicle path optimization was also considered.

2.2. Cold-Chain Logistics

Cold-chain logistics is a significant topic in academia, focusing on the transportation of vaccines, food, and other products closely tied to people’s daily lives [22,23]. Scholars primarily concentrate on supply chain coordination for cold-chain products and the environmental impact of cold-chain transportation. In recent years, the multi-temperature coordination problem has emerged as a key research hotspot. Regarding supply chain coordination, Awad et al. [24] explored collaborative distribution within cold-chain transportation, systematically analyzing existing models, processes, and methods for supply chain transportation and distribution management, thereby laying a foundation for subsequent research. Shi et al. [25] investigated vehicle collaborative optimization in cold-chain supply chains, developing a multi-objective optimization model validated with real-world data. Zhang et al. [26] addressed the green transformation of cold-chain transportation by constructing a site selection optimization model for urban cold-chain logistics under carbon emission constraints. Their case study analysis provided policy recommendations and scientific support for government departments to optimize urban cold-chain transportation systems.

2.3. Optimization Model and Methodology

High-quality optimization models and methods are essential tools for enhancing the operational efficiency of enterprises [27,28]. Wei et al. [29] proposed a cold-chain network collaborative delivery model based on consumer demand and solved it using a genetic algorithm, verifying the applicability of the model. Considering the environmental impact of cold-chain transportation, Saif et al. [30] considered the impact of greenhouse gases generated during cold-chain transportation on the environment, constructed a mathematical model to minimize greenhouse gas emissions, and proposed a new hybrid simulation optimization algorithm for problem-solving. Hariga et al. [31] considered the carbon emissions on the social environment during the whole lifecycle of transportation and storage and constructed a cold-chain transportation model that takes into account carbon tax regulatory policies. Zheng et al. [32] studied the truck scheduling issue in cold-chain transportation scenarios and solved the cold-chain truck scheduling model with the heuristic algorithms.

Supply chain optimization management is a critical application scenario of optimization methodology, and many scholars have made significant contributions [33,34]. Ren et al. [35] studied the collaborative optimization issue of a large-scale cold-chain transportation supply chain, analyzed and optimized the e-commerce cold-chain operations using LNS methods, and verified the algorithm through practical cases. While studying the optimization of the cold-chain distribution aspect, Chen et al. [36] used a large-scale neighborhood search algorithm based on the actual problem background to solve the scheduling optimization problem of multi-compartment cold-chain vehicles. Wu et al. [37] studied the dynamic optimization problem of cold-chain vehicles, solved the transportation scheduling with a mixed ant colony algorithm, and obtained an effective and reliable method in polynomial time.

2.4. Research Gap

From the literature reviewed, it is evident that existing studies have primarily focused on the characteristics of cold-chain logistics and electric vehicles (EVs) separately. Only a limited number of studies have integrated the analysis of multi-temperature cold-chain logistics with the unique features of electric vehicles. However, as the industry evolves, the multi-temperature requirements in cold-chain logistics have become an urgent issue that demands resolution. Additionally, the complexity of route optimization for multi-temperature cold-chain vehicles presents a significant opportunity for advancing the theoretical development of vehicle routing optimization. Therefore, this study will investigate the optimization of multi-temperature EV cold-chain vehicle routing to address the existing research gap.

3. Problem Description and Modeling

3.1. Model Specification

In this paper, a distribution path optimization problem for pure electric cold-chain vehicles is proposed, taking into account the capacity constraints, charging costs, refrigeration costs, and transportation costs of vehicles. 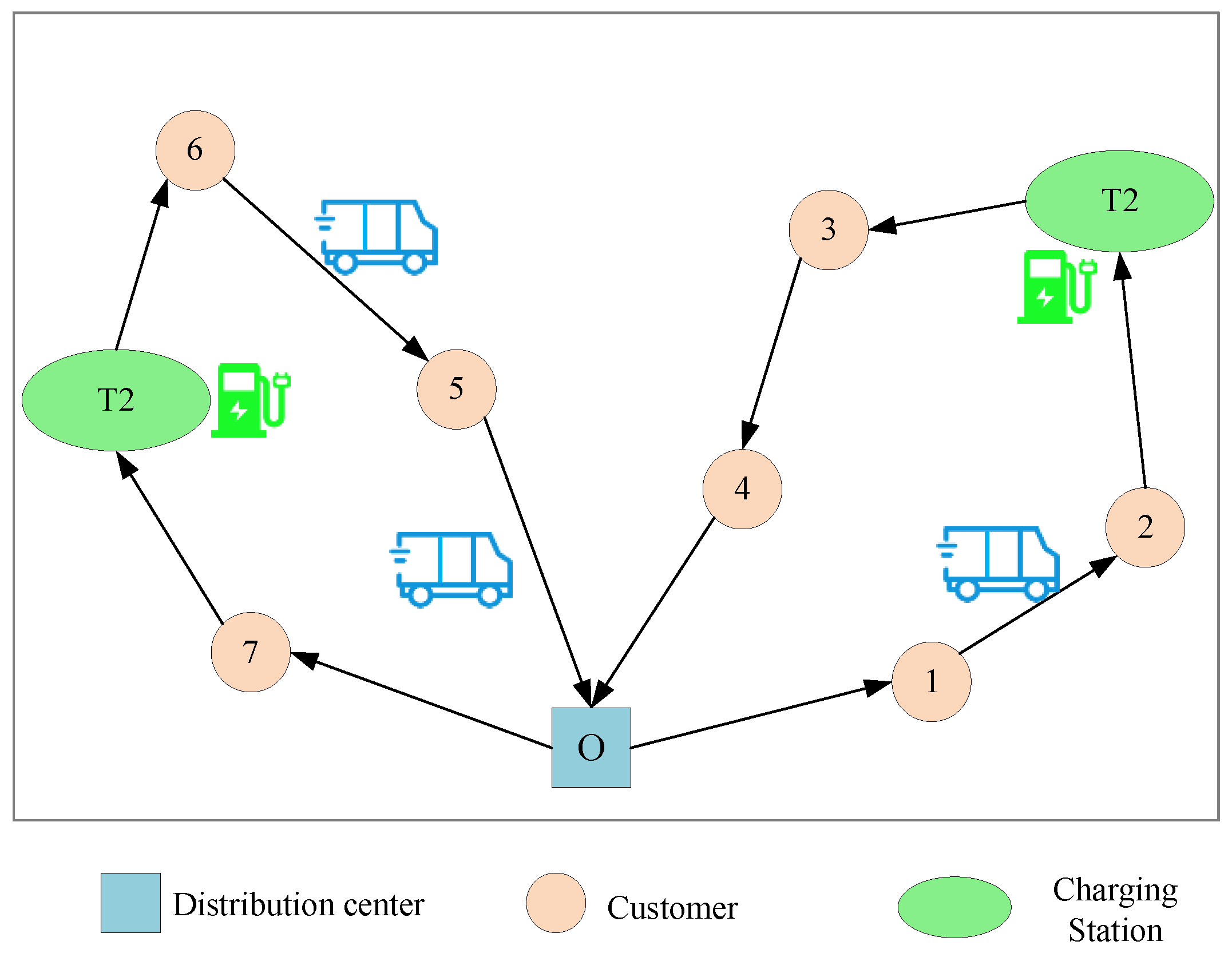Cold-chain logistics is a door-to-door logistics service that involves the coordinated operation of vehicles and service points, thus presenting a certain level of complexity [38]. As shown in Figure 1, N = {1, 2, 3…, n} is the set of customer points, T is the set of charging stations, and O is the starting point. Then, the problem can be defined as the existence of a directed graph G = (V,S), where V = N ∪ T ∪ O represents the set of all points, and (i,j) ∈ S represents the set of all arcs in the graph, where i ≠ j. Cold-chain vehicles start from the distribution center, travel between different points while meeting capacity constraints, and complete the distribution works of all customer points. Each customer point has at least one type of goods demand (refrigerated or frozen goods) and is only served once. During the service process, the vehicle can be charged multiple times [39]. The two compartments of the vehicle have their maximum capacity limits, and each vehicle does not restock midway, with no returns occurring. The number of vehicles at the delivery station is fixed.

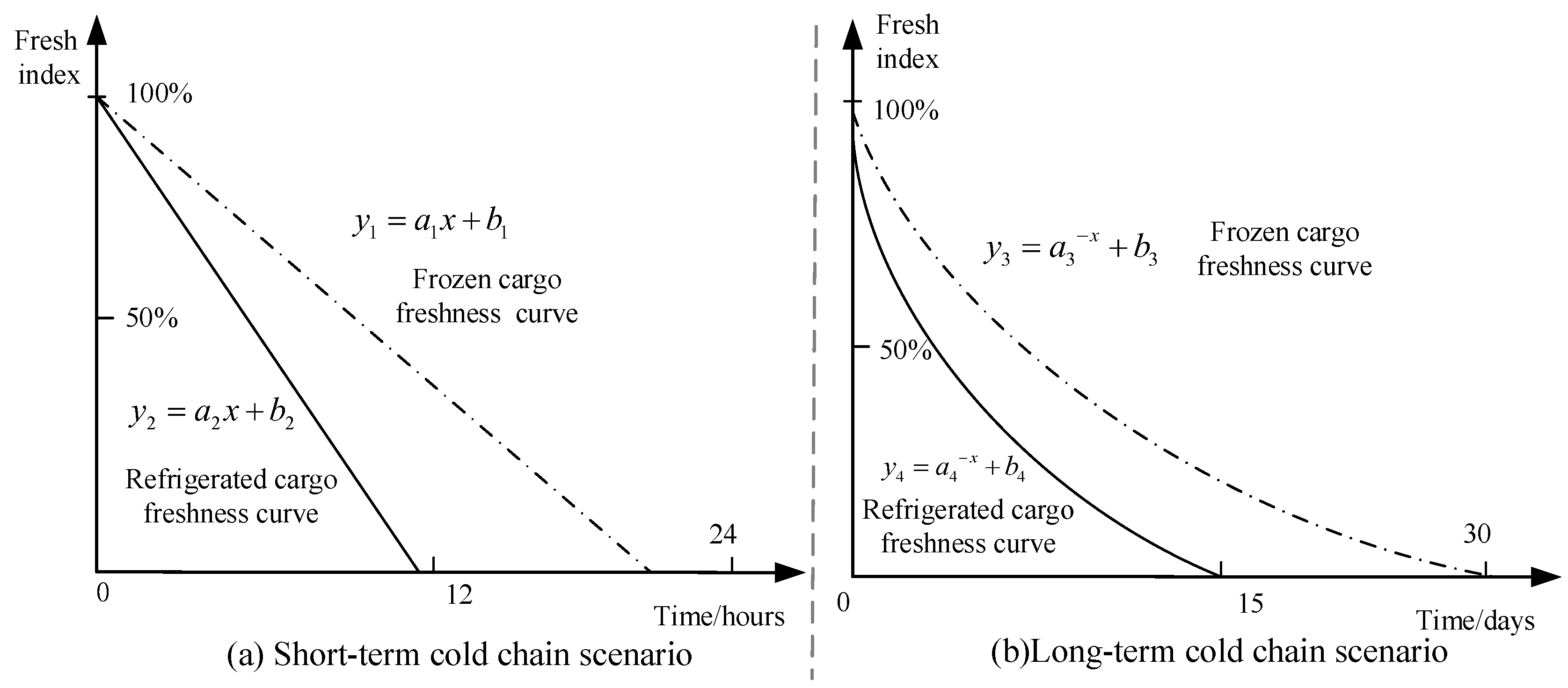
Meanwhile, due to the high requirement for freshness in cold-chain transportation goods, we also considered the variation of goods’ freshness over time. Figure 2 shows the example decrease curve in the freshness of cold-chain goods in short-term cold-chain logistics and long-term cold-chain logistics ($a_1<a_2<0, a_3{>a}_4>1$, $b_1,b_2,b_3,b_4 \mathrm{i}\mathrm{s} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t} \mathrm{v}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e}$). Short-term cold-chain delivery (e.g., urban daily delivery) could be set as linear, but in long-term cold-chain delivery (e.g., shipping cold-chain logistics) the decrease could be set as nonlinear [40,41]. This paper investigated the daily cold-chain delivery, which falls under the category of short-term cold-chain delivery. Hence, a linear degradation (Figure 2a) was adopted.

It is noteworthy that the determination of the freshness degradation curve is inherently complex, involving multiple factors, such as cold-chain delivery distance, product type, and seasonal temperatures, etc. Hence, the linear degradation employed in this study serves merely as an example. In practical applications, it is essential to design the degradation curve function according to specific scenarios.

3.2. Mathematic Model Proposed

In the process of model construction, this paper follows the basic assumptions:

(1)

The electricity consumption of vehicles is constant per kilometer.

(2)

Cold-chain vehicles have the same unloading time at different customer points.

(3)

When a cold-chain vehicle is charging at a charging station, the refrigeration system needs to work properly.

(4)

The driver strictly follows the established delivery plan route.

(5)

The demand for goods of customer nodes could be known in advance.

(6)

No returns occur during the delivery process.

3.2.1. Notations

(1)

Sets

• N denotes the set of customer points,
• T denotes the set of charging stations,
• O denotes the starting point,
• K denotes the set of cold-chain vehicles,
• V denotes the set of all points in the directed graph, $V=N\cup T\cup O$

(2)

Variables and parameters

• d_ij is the distance between nodes i and j,
• $q_i^1$ is the demand for refrigerated goods at site i,
• $q_i^2$ is the demand for frozen goods at site i,
• ${\mathrm{g}}_{jk}$ is the cumulative electricity consumption of the k-th vehicle at the station,
• $e_1$ is the electricity consumption per unit distance,
• $e_2$ is the electricity consumption per unit of time in the refrigerated compartment,
• $e_3$ is the electricity consumption per unit of time in the frozen compartment,
• C is the total battery capacity of cold-chain vehicles,
• v is the average speed of cold-chain vehicles,
• $Q_1$ is the capacity of the vehicle’s refrigerated compartment,
• $Q_2$ is the capacity of the vehicle’s frozen compartment,
• ${\mathsf{\alpha }}_1$ is the freshness sensitivity factor of refrigerated goods,
• ${\mathsf{\alpha }}_2$ is the freshness sensitivity factor of frozen goods,
• ${\mathrm{T}}_1$ is the freshness date of refrigerated goods,
• ${\mathrm{T}}_2$ is the freshness date of frozen goods,
• $f_{kj}^1$ is the freshness of refrigerated goods delivered to customer j on the k-th EV,
• $f_{kj}^2$ is the freshness of frozen goods delivered to customer j on the k-th EV,
• $w_i$ is the dwell time of the vehicle at point i.

(3)

Decision variables

• $x_{ijk}$ is the 0, 1 variable. If EVs k pass through arc $(i,j)$, it is 1; otherwise, it is 0.
• $t_{ki}$ is the time when vehicle k reaches node $i$.

3.2.2. Mathematical Model

Due to this paper primarily focusing on the impact of introducing electric vehicles in cold-chain logistics distribution, the objective function was established to minimize the loss of freshness in cold-chain products.

Equation (1) shows the optimization objection, which represents minimizing the freshness loss when customers receive goods at their points:

$$Min{\displaystyle \sum _{\in V}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{k\in K}{x}_{ijk}{q}_j^1(1-f_{kj}^1)}}}+{\displaystyle \sum _{i\in V}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{k\in K}{x}_{ijk}{q}_j^2(1-f_{kj}^2)}}}$$

(1)

Equation (2) shows the relationship between the freshness of refrigerated goods and time:

$$f_{kj}^1=1-{\displaystyle \frac{{\alpha }_1{t}_{ki}}{T}}\hspace{1em}\forall i,j\in N$$

(2)

Equation (3) is the function relationship between the freshness of frozen products and time:

$$f_{kj}^2=1-{\displaystyle \frac{{\alpha }_2{t}_{ki}}{T}}$$

(3)

Equation (4) is the maximum capacity constraint for compartment 1 (refrigerated) of the vehicle:

$${\displaystyle \sum _{i\in V}{\displaystyle \sum _{j\in V}q{1}_i{x}_{ijk}\le Q_1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\forall k\in K}}$$

(4)

Equation (5) represents the maximum capacity constraint for compartment 2 (frozen) of the vehicle:

$${\displaystyle \sum _{i\in V}{\displaystyle \sum _{j\in V}q{2}_i{x}_{ijk}\le Q_2\hspace{0.33em}\hspace{0.33em}\forall k\in K}}$$

(5)

Equation (6) indicates that the customers are only served by one vehicle and served once:

$${\displaystyle \sum _{i\in V}{\displaystyle \sum _{k\in K}{x}_{ijk}=1\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\forall j\in N}}$$

(6)

Equation (7) is a constraint on the number of vehicles, indicating that there are m EVs participating in the delivery operation:

$${\displaystyle \sum _{i\in \left\{O\right\}}{\displaystyle \sum _{j\in V}{\displaystyle \sum _{k\in K}{x}_{ijk}}=}}{\displaystyle \sum _{i\in V}{\displaystyle \sum _{j\in \left\{O\right\}}{\displaystyle \sum _{k\in K}{x}_{ijk}}}}$$

(7)

Equation (8) represents the cumulative quantity of electricity consumption of the k-th cold-chain vehicle, and specifies that when the vehicle is at the starting point or after leaving the charging station, it is fully charged:

$$g_{jk}=\left\{\begin{array}{c}{g}_{ik}+{\displaystyle \sum _{i\in N}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{k\in K}{e}_0{d}_{ij}{x}_{ijk}+{\displaystyle \sum _{i\in N}{\displaystyle \sum _{j\in N}{\displaystyle \sum _{k\in K}(\frac{x_{ijk}}{v}+w_{kj})·(e_1+e_2),\forall i,j\in N,k\in K,i\ne j\hspace{0.33em}}}}}}}\\ 0,\forall j\in T\cup \left\{O\right\},k\in K\end{array}\right.$$

(8)

Equation (9) represents the quantity constraint of electricity consumption during driving:

$$g_{jk}+e_0{d}_{ij}{x}_{ijk}+{\displaystyle \frac{x_{ijk}}{v}}(e_1+e_2)\le C\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\forall i\in N,j\in T\cup \left\{O\right\},k\in K$$

(9)

Equations (10) and (11) represent the range of values for decision variables:

$$x_{ijk}=\left\{\begin{array}{l}1,\hspace{0.33em}\mathrm{vehicle}\hspace{0.33em}\mathrm{k}\hspace{0.33em}\mathrm{passes}\hspace{0.33em}\mathrm{through}\hspace{0.33em}arc\left(i,j\right)\hspace{0.33em}\\ 0,\hspace{0.33em}\mathrm{otherwise}\end{array}\right.$$

(10)

$$t_{ki}\ge 0$$

(11)

Equation (12) represents the range of values for other variables:

$$0\le i,j\le n,1\le t\le T,1\le k\le m$$

(12)

4. Algorithm Framework

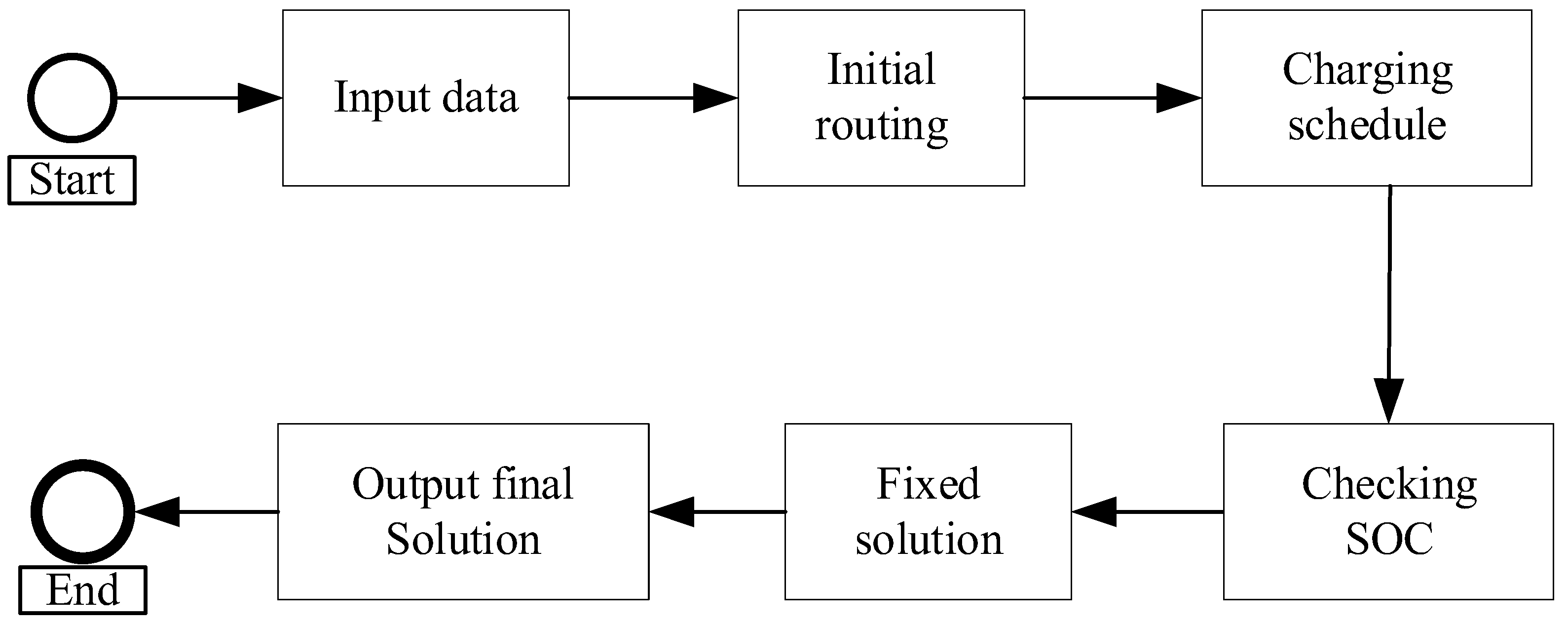
Considering that this problem is an MIP problem, the selection of charging stations also needs to be considered. Therefore, the optimization scope of the problem was quite big, and the complexity was high, making it an NP-hard problem. Therefore, constructing an effective algorithm is crucial to get the perfect solutions. The genetic algorithm is widely used to address NP-hard problems for its great parallelism and clear coding logic. Therefore, we also adopted a genetic algorithm for model solving. To improve the computational performance and problem adaptability of the algorithm, a rollback strategy was adopted for the processing of some infeasible solutions in the chromosome decoding process, thereby transforming infeasible solutions into feasible solutions and improving the searchability of the algorithm, as shown in Figure 3.

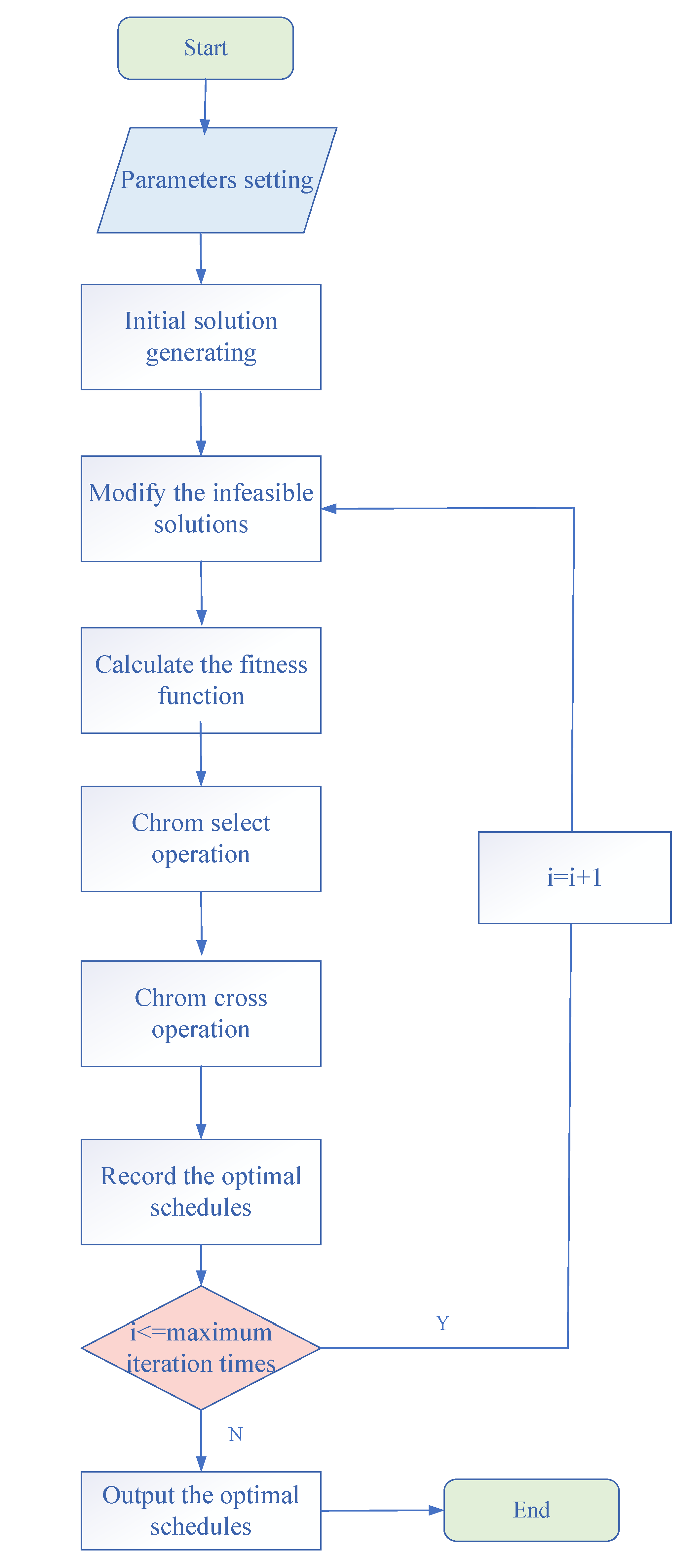
4.1. Algorithm Step Process

In practical applications, it is essential to encode the solution to the problem in a manner that enables computer recognition and facilitates efficient computational processing. The initial solution to this problem is represented as a sequence of numbers. During the encoding process, relevant constraints must be taken into account, such as the capacity limits of the two compartments and the vehicle’s energy consumption constraints. The details are shown in Figure 4.

Step 1. Generate the initial solution. According to the capacity constraint of each compartment, divide the specific customer points served by different vehicles. If any storage space exceeds the capacity limit, the current customer point will be allocated to the next vehicle.

Step 2. Calculate the charging location. Calculate the location ${\mathsf{\xi }}_i,\{i=\mathrm{1,2},3\dots n\}$ of charging demand generation based on the vehicle quantity constraint of electricity consumption.

Step 3. Modify the infeasible solutions. Based on the location ${\mathsf{\xi }}_i$ of charging demand generation, determine whether the vehicle can travel from this point to the nearest charging station. If the remaining battery cannot support reaching the nearest charging station, execute a rollback strategy, adjust the charging position, and generate a feasible solution.

Step 4. Calculate the fitness function. Based on the path results of Step 3, calculate the freshness loss values of the current refrigerated and frozen goods, respectively, and sum them to obtain the total freshness loss.

Step 5. Perform selected operation. Adopt a roulette wheel strategy for selection of operations, select a scheduling strategy with high adaptability, and enter the next round of operations.

Step 6. Perform cross-operation. Adopt a two-point crossover mechanism to exchange genes in the crossover region, followed by conflict detection operations.

Step 7. Solution mutation. Perform mutation operation with a certain probability and randomly select two positions in the chromosome for exchange operation.

Step 8. Record the optimal schedules. Select and record the vehicle delivery plan, charging location, and total freshness loss value for the best fitness individual.

Step 9. Determine termination conditions. Determine whether the current genetic algebra meets the set maximum genetic algebra. If it does not meet the stopping condition, return to Step 5.

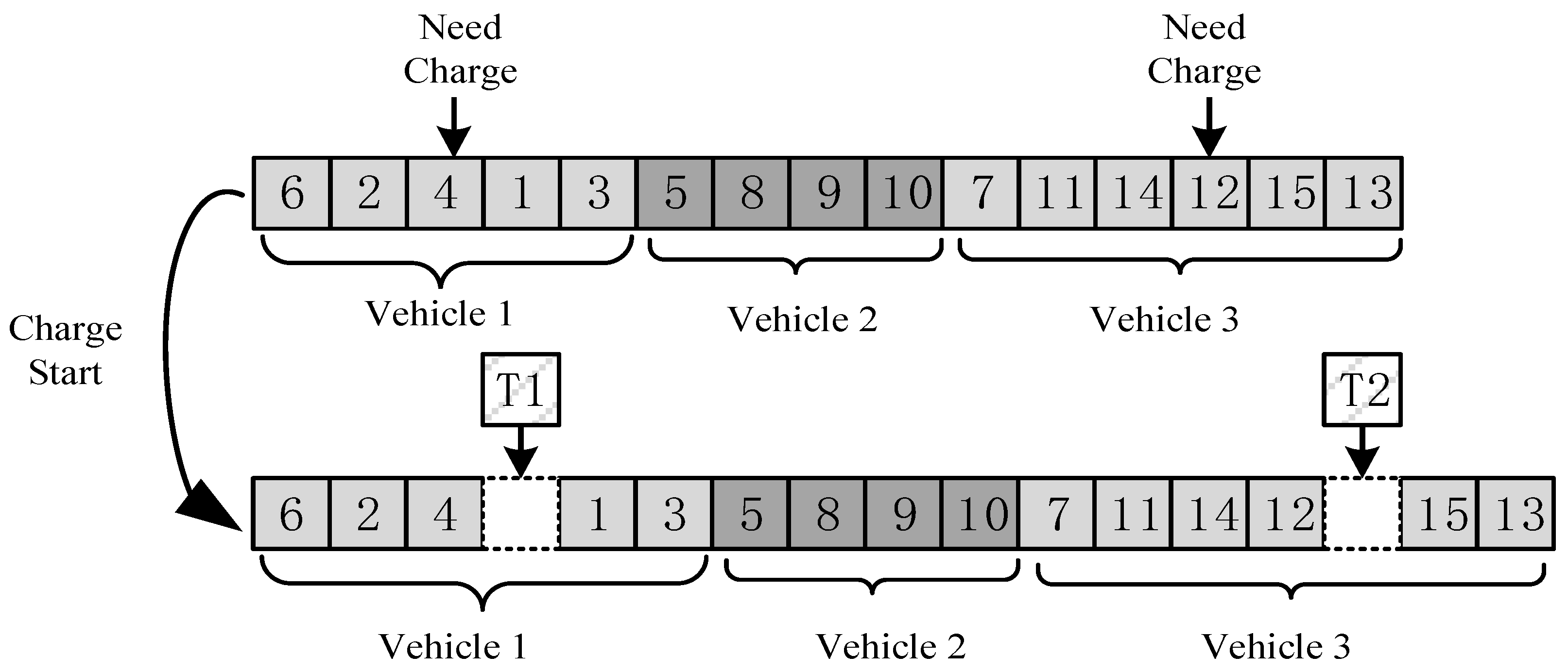
4.2. Algorithm Decoding Process

The decoding process of chromosomes is a crucial step in enabling genetic algorithm solutions. This process can be broken down into three key components. First, customer points are grouped based on their demands and the compartment’s capacity constraints, with each vehicle assigned to one group. Next, following the delivery sequence derived from the grouping results, the algorithm identifies the necessary charging points for the electric vehicles (EVs) and inserts them into the route. Finally, using the established delivery and charging routes, the fitness values of the chromosomes are calculated, completing the decoding process.

(1)

Demand nodes classification

As shown in Figure 5, the algorithm utilizes the demand point number as chromosome encoding information, where the numbers represent the demand points. By using this encoding method, it can effectively ensure that each customer point is only served once. Meanwhile, we should ensure that the refrigerated and frozen compartments of each vehicle do not exceed their respective maximum capacity constraint (Constraints 4 and 5), to sequentially allocate different demand points to different vehicles and complete the initial correspondence between vehicles and customer points.

(2)

Insert charging station

Calculate the charging positions $i\in N$ of different vehicles based on their battery capacity constraints. After completing the service at node i, the remaining battery of the vehicle is no longer able to support its journey to the next destination (customer point or distribution center). The vehicle needs to drive to the nearest charging station, wait for the charging to be completed, and then continue with the operation, as shown in Figure 6. Unlike electric passenger vehicles, which only need to consider the electricity consumption of driving, we comprehensively considered the consumption of the driving and cooling systems during the vehicle’s driving process when calculating the cumulative electricity consumption ${\mathrm{g}}_{ik}$ of the k cold-chain vehicle.

The detailed processes for selecting the EVs’ charging station are as follows:

Step 1. Initialize the cumulative electricity consumption of each vehicle, ${\mathrm{g}}_{ik}=0,\forall k\in K$.

Step 2. Calculate the charging position. Accumulate the driving distance and cooling time of the vehicle, calculate the cumulative electricity consumption ${\mathrm{g}}_{(i+1)k}$ from the position $i$ to the next target point $i+1$, and determine whether the cumulative electricity consumption exceeds the battery capacity ${\mathrm{g}}_{(i+1)k}>C$. If it is met, execute Step 3. If it is not met, continue to accumulate electricity consumption.

Step 3. Select the most suitable charging station. According to the charging location provided in Step 2, calculate the closest charging station to that point. Determine whether the current remaining battery can support the vehicle to reach the charging station. If it cannot be reached, move the charging position back by one point until a charging station that meets the conditions is found.

Step 4. After the charging process, the cumulative electricity consumption is reset to zero, ${\mathrm{g}}_{(i+1)k}=0$, indicating that it is fully charged.

Step 5. Return to Step 2 and select the charging station for the later stage of charging.

(3)

Calculate fitness value

Based on the results of vehicle distribution grouping and the charging schedule, calculate the time $t_{ki}$ for different vehicles to go to the customer node. With the time sequence, we could calculate the freshness loss for the current refrigerated and frozen goods. As it is a loss minimization problem, we assigned the reciprocal of the loss value ${\displaystyle \frac{1}{loss}}$ to the fitness of the corresponding chromosome. The smaller the loss value, the greater the fitness, and the better the individual can enter the next iteration process.

5. Case Study

5.1. Case Background

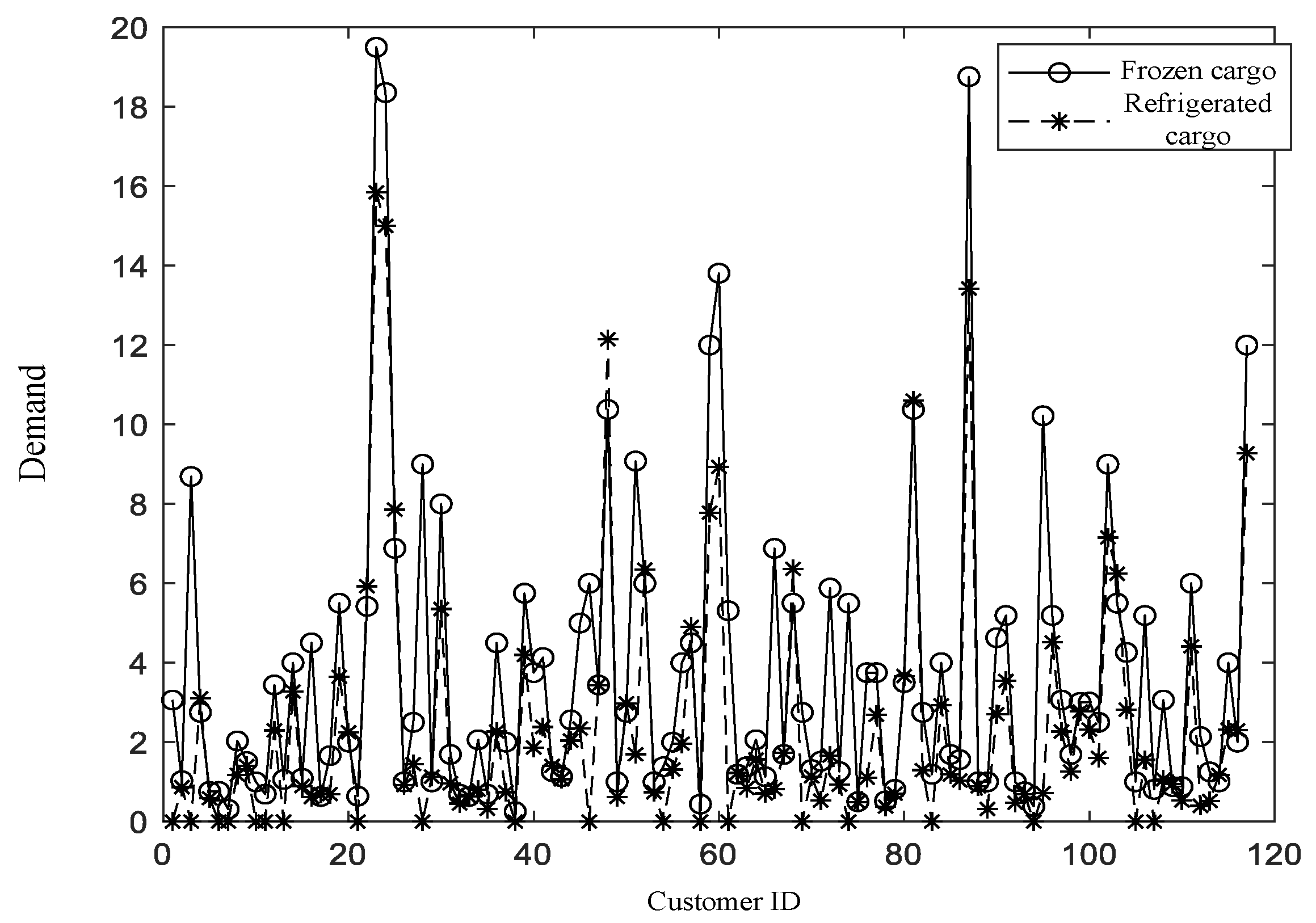
To validate the correctness of the proposed MIP model and the developed algorithm, we conducted a case study using actual delivery data from a cold-chain company in Shanghai. The case represents the real-world distribution scenario of the cold-chain logistics company in Shanghai. The distribution starts from a location in Jiading District, Shanghai, and covers the entire city, including a total of 117 customer points. The goods requested by customers are categorized as refrigerated and frozen, with demand quantities known in advance. The demand distribution across customer points is illustrated in Figure 7.

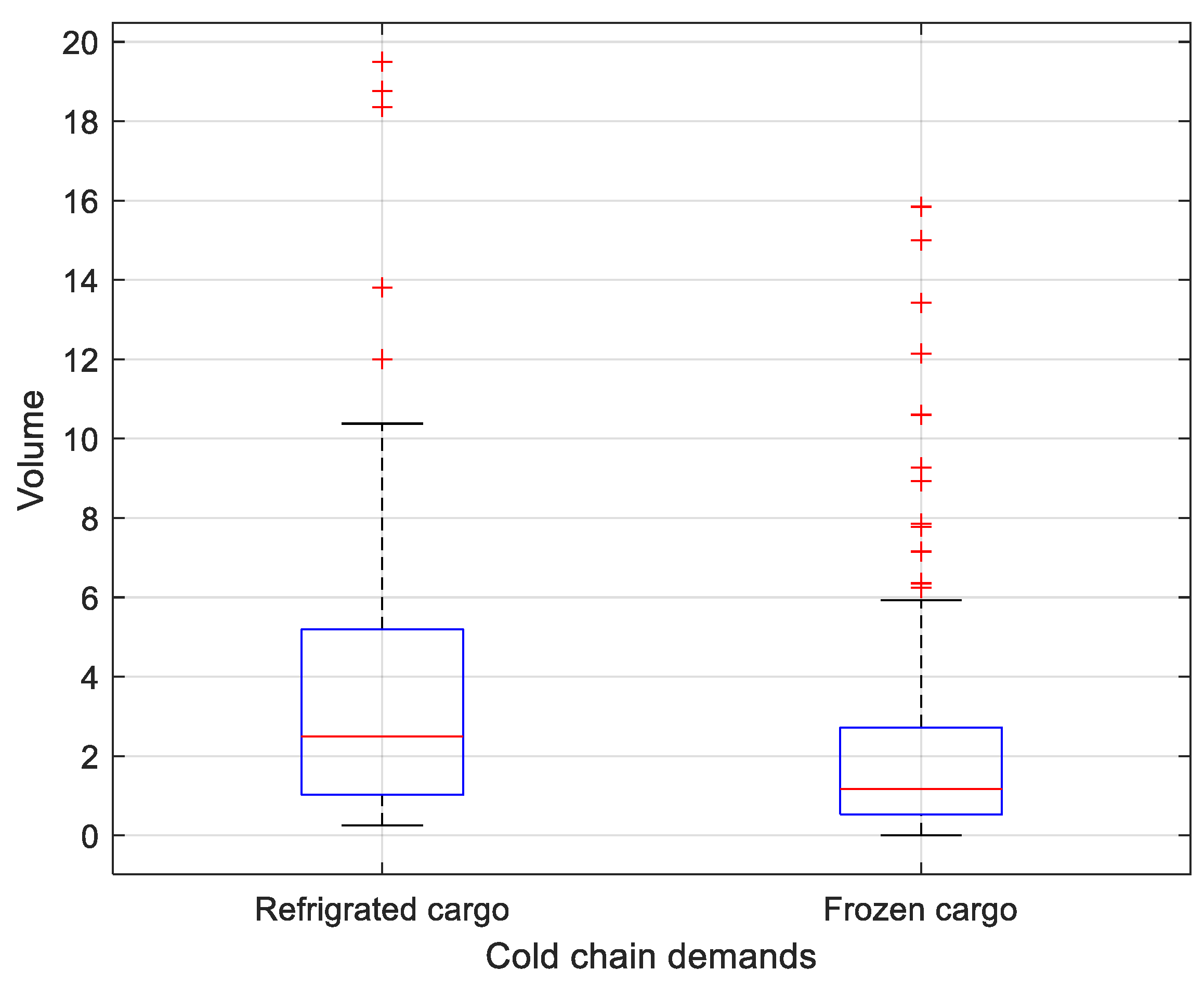
To better contrast the differences in the distribution of refrigerated cargo versus frozen cargo, we constructed box plots for analysis, as Figure 8 shows. Compared to refrigerated cargo, the demand for frozen cargo exhibited more dispersed data points, indicating an uneven demand pattern that necessitates careful distribution planning.

The locations of charging stations in Shanghai were obtained from the Baidu Map API. The simulation was performed on a computer with a Win10 64-bit operating system, 16 GB of RAM, and a CPU frequency of 2.6 GHz.

5.2. Parameter Settings

This experiment was conducted using Matlab 2017b, with the genetic algorithm parameters set as follows: population size of 50, 500 generations, crossover probability of 0.9, and mutation probability of 0.05. To validate the effectiveness of the proposed method, real business data from a major cold-chain company in Shanghai were utilized. The distribution data were categorized by range, as detailed in

Table 1. Distribution case.

Case Name	Distribution Area	Number of Customers	Number of Charging Stations
$R_1$	Jiading District, Baoshan District, Hongkou District, Jingan District	28	25
$R_2$	Jiading District, Baoshan District, Hongkou District, Jingan District, Huangpu District, Xuhui District	49	33
$R_3$	All regions of Shanghai	117	78

, and three cold-chain distribution scenarios were constructed: small scale (R1), medium scale (R2), and large scale (R3). Additional experimental parameters are provided in

Table 2. Parameter settings.

Parameter	Value	Unit
Capacity of refrigerated compartment	30	box
Capacity of frozen compartment	20	box
Electricity capacity	40	kWh
Driving electricity consumption	0.3	kWh/km
Refrigerated system power	2.5	kW
Unloading time	20	min
Charging time	60	min

.

5.3. Case Study Results

The experiment in this paper was divided into two parts. (1) We compared the distribution of two-compartment cold-chain electric vehicles with that of single-compartment cold-chain electric vehicles. By analyzing relevant distribution indicators, the advantages and disadvantages were compared. (2) We compared the genetic algorithm with the rollback strategy and the genetic algorithm based on the traditional penalty strategy, using the distribution data of the entire city of Shanghai ($R_3$ case) as input, to verify the merits and drawbacks of the improved algorithm.

A comparative analysis of the indicators across various vehicle models is detailed in

Table 3. Comparison of experimental results.

Case Name	Single-Temperature Cold-Chain EV			Multi-Temperature Cold-Chain EV
	Freshness Loss Value	Loss Rate/%	Charging Cycles	Freshness Loss Value	Loss Rate/%	Charge Cycles
$R_1$	19.36	10.86%	3	7.57	4.25%	1
$R_2$	38.24	13.26%	9	14.84	5.15%	2
$R_3$	186.35	26.55%	46	53.03	7.86%	22

, revealing the presented observations.

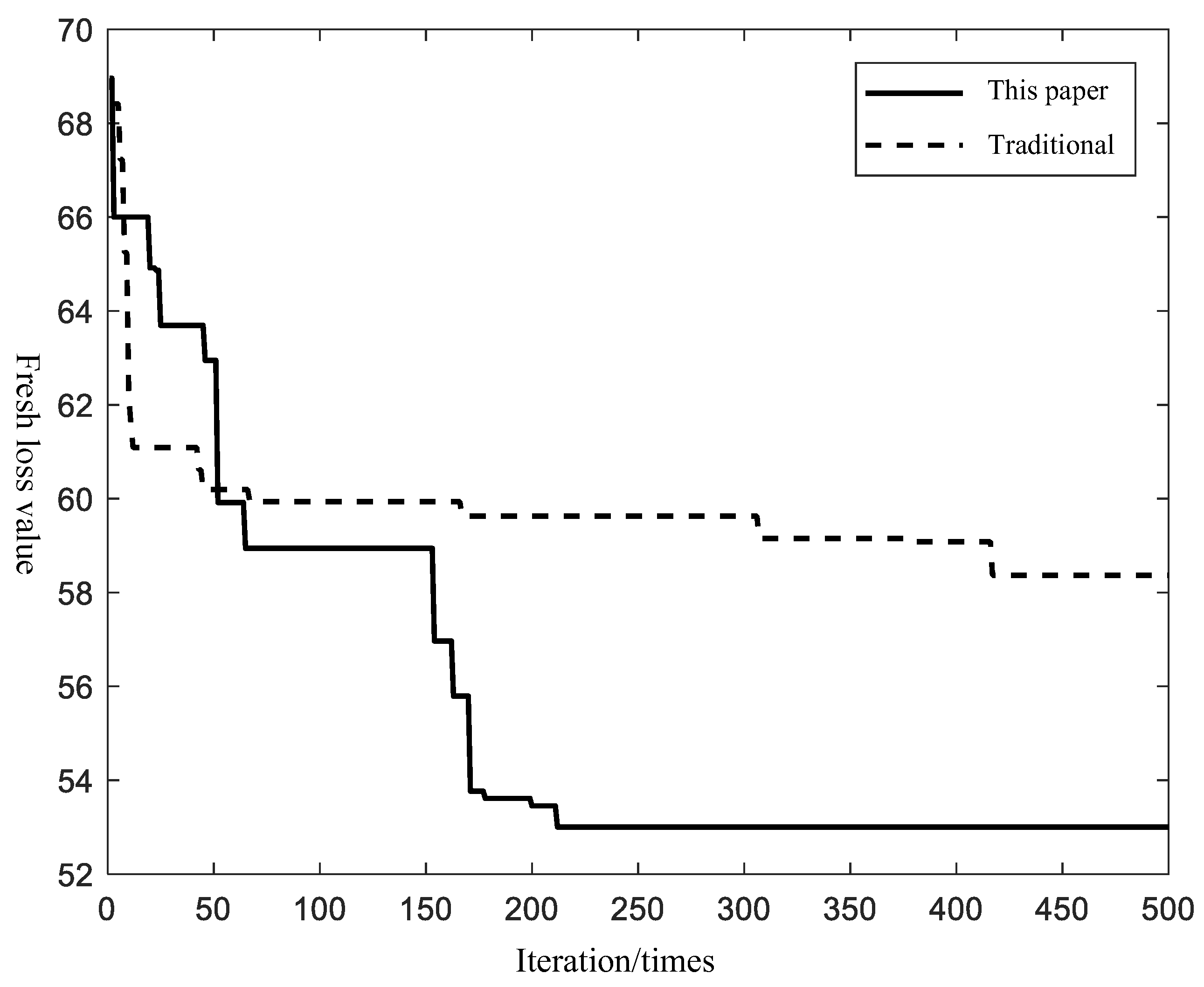
In terms of algorithm performance analysis, we evaluated the decoding process of genetic algorithms using both the rollback strategy and the traditional penalty operations. As shown in Figure 9, the implementation of the rollback strategy effectively identified better computational results, enhanced the efficiency of genetic algorithm operations, and improved the overall algorithm performance. The traditional genetic algorithm does not incorporate a rollback operation [42]. The primary reason for this improvement is that the rollback strategy enabled the transformation of a portion of chromosomes from infeasible solutions into feasible solutions, allowing them to be retained and proceed to the next iteration. In contrast, under the traditional penalty strategy, infeasible solutions are often unable to advance to the next iteration, leading to the loss of potentially valuable chromosomes. Consequently, compared to traditional penalty strategies, the rollback strategy offered greater flexibility in chromosome decoding and was well suited for solving NP-hard problems under complex constraints.

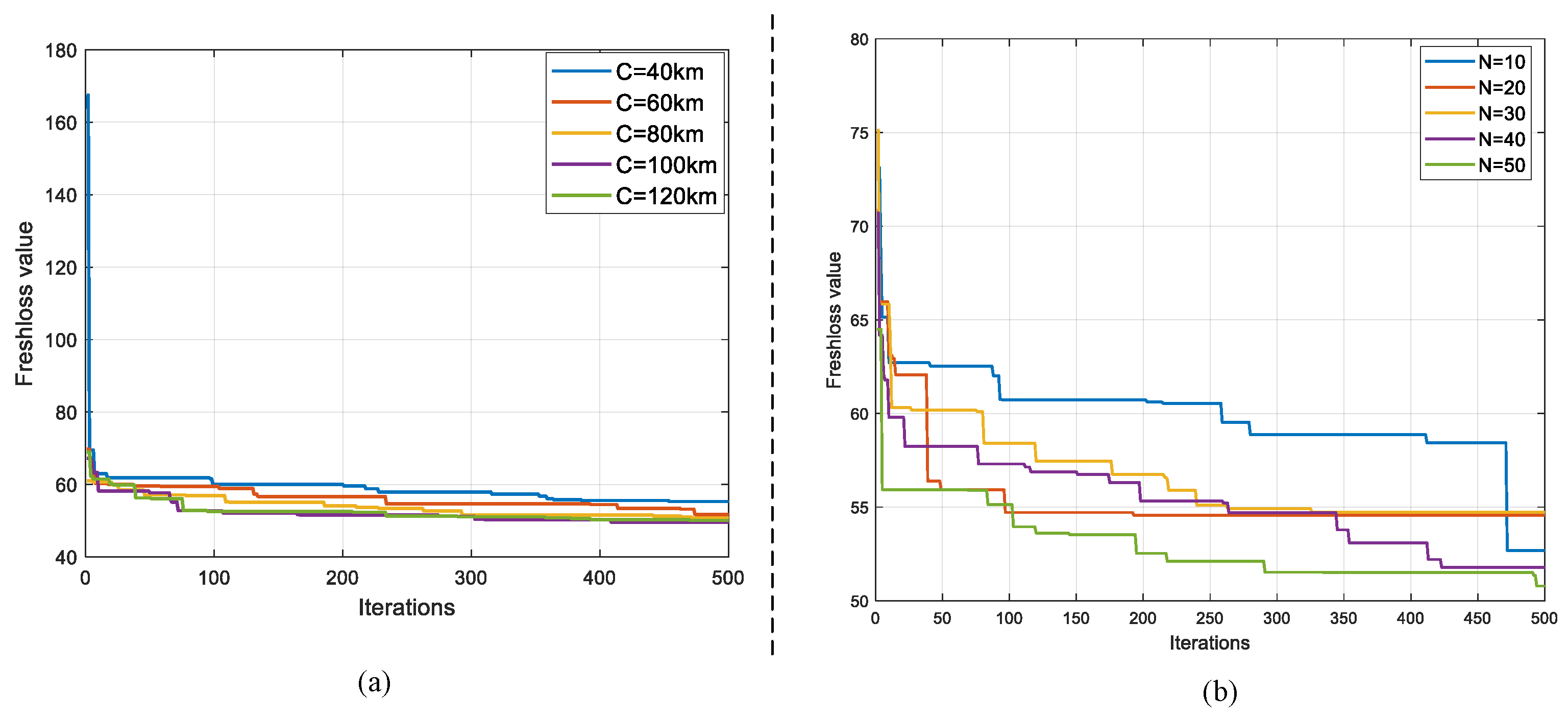
To test the robustness of the algorithm, we conducted sensitivity analysis experiments, focusing on the vehicle’s range and population size for the sensitivity tests, as Figure 10 shows. Figure 10a illustrates the impact of the vehicle’s range on the outcomes. As can be seen from the graph, the algorithm consistently yielded satisfactory charging and distribution methods across different ranges, optimizing the reduction in delivery freshness loss. Figure 10b demonstrates the influence of the algorithm’s population size on the results. The graph reveals that a larger population size can significantly enhance the algorithm’s convergence rate. Therefore, it is advisable to consider moderately increasing the population size during the algorithm parameter configuration process.

6. Managerial Insights

(1)

Adopting multi-compartment cold-chain EVs could reduce charging frequency and minimize cargo loss.

Under the same delivery scenario, the multi-compartment electric cold-chain vehicle demonstrated significant advantages in reducing the freshness loss of goods and lowering the loss rate. In terms of freshness loss, compared to single-compartment cold-chain vehicles, the two-compartment model achieved a notable reduction in freshness loss, which could save significant costs, thereby enhancing user satisfaction. Additionally, regarding charging performance, the two-compartment cold-chain vehicle not only saved a significant amount of total freshness loss but also reduced the charging cycles compared to its single-compartment counterpart.

(2)

The theoretical method proposed in this study applies to cold-chain logistics scenarios of various scales and could be adopted by multiple types of customers to support sustainable development.

Through analysis of different delivery scenarios, it can be seen that compared to delivery cases $R_1$ and $R_2$, there was a significant increase in both the loss of goods and the number of charges, especially in the case $R_3$. This is due to the delivery range of cases $R_1$ and $R_2$ being relatively close to the delivery starting point (Jiading District, Shanghai), and because the battery capacity of the vast majority of vehicles could run back to the starting point after a single delivery. The case $R_3$ involved distributions throughout the city, with a significant increase in the distribution radius. Some distribution routes span a considerable distance, extending from the northern part of Jiading District in Shanghai to the southern part of Pudong District, crossing the entire Shanghai urban area. Consequently, when formulating large-scale, long-distance local distribution plans, it is essential to incorporate reasonable optimization of vehicle charging strategies.

(3)

Logistics enterprises should actively embrace new-energy vehicles and emerging optimization technologies to reduce carbon emissions for the world.

Cold-chain logistics enterprises are characterized by high energy consumption and high carbon emissions. The introduction of multi-compartment new-energy cold-chain vehicles can help reduce corporate carbon emissions and enhance corporate social responsibility. Although the scheduling optimization of electric cold-chain vehicles is complex, requiring consideration of both charging and operational aspects, this case study demonstrated that by adopting reasonable and effective distribution optimization theories and models, it is possible to balance the charging and operational processes during the generation of scheduling plans. This approach not only reduces operational costs and improves customer satisfaction but also contributes to the global green transition.

7. Conclusions

Research on routing optimization for cold-chain vehicles has been a critical issue in the logistics field, but EV cold-chain logistics research is emerging in interdisciplinary research. The multi-temperature co-distribution of electric vehicle (EV) cold-chain systems not only addresses practical needs but also enriches the classical vehicle routing problem (VRP) theoretical model. This paper introduced the novel concept of “freshness loss” to quantify the value degradation of cold-chain products over the transit time and proposed the use of two-compartment cold-chain EVs for delivery operations, thereby optimizing the business processes of cold-chain logistics. In terms of model construction, this paper aimed to minimize the total freshness loss of all goods while comprehensively considering constraints, such as vehicle range and compartment capacity, ultimately formulating a mixed-integer programming model. For algorithm design, an improved genetic algorithm was employed to solve the model. During chromosome decoding, a rollback strategy was introduced, which significantly enhanced the algorithm’s performance compared to the traditional penalty strategy, yielding a more effective delivery decision scheme. Finally, the feasibility of the proposed method and algorithm was validated using real-world distribution data from cold-chain logistics companies.

However, there are still certain challenges in the model construction process. Among these, the availability of data is a significant challenge. The construction of the model requires detailed and reliable data for support. Additionally, it is necessary to consider whether the construction of charging infrastructure can meet the future charging needs of large-scale electric cold-chain vehicles. At the same time, corresponding legal regulations also need to be updated accordingly.

For future research, we recommend that researchers could integrate other realistic constraints, which may influence the EV charging process. These constraints may include congestion queues at charging stations during peak hours, nonlinear battery power consumption patterns, and the refrigeration performance on goods’ freshness. The introduction of these constraints will further enrich the mathematical model, facilitating better solutions to practical problems. Meanwhile, further studies could also explore innovative operational patterns and business models, particularly in the context of cold-chain logistics companies’ operation innovations in the business ecosystem aspect. Besides, the further development of artificial intelligence technologies, such as large language models like Deepseek and GPT, can also provide support for cold-chain customer transportation services, enhancing the intelligence and sustainability of cold-chain logistics services.

In summary, we hope that this study can expand the research content on new-energy vehicle management and inspire more scholars to contemplate how algorithms and soft technologies can serve the sustainable development of humanity.