Research on Energy Management Strategy Based on Adaptive Equivalent Fuel Consumption Minimum for Hydrogen Hybrid Energy Systems

Abstract

Hydrogen has attracted widespread attention due to its zero emissions and high energy density, and hydrogen-fueled power systems are gradually emerging. This paper combines the advantages of the high conversion efficiency of fuel cells and strong engine power to propose a hydrogen hybrid energy system architecture based on a mixture of fuel cells and engines in order to improve the conversion efficiency of the energy system and reduce its fuel consumption rate. Firstly, according to the topology of the hydrogen hybrid energy system and the circuit model of its core components, a state-space model of the hydrogen hybrid energy system is established using the Kirchhoff node current principle, laying the foundation for the control and management of hydrogen hybrid energy systems. Then, based on the state-space model of the hydrogen hybrid system and Pontryagin’s minimum principle, a hydrogen hybrid system management strategy based on adaptive equivalent fuel consumption minimum strategy (A-ECMS) is proposed. Finally, a hydrogen hybrid power system model is established using the AVL Cruise simulation platform and a control strategy is developed using matlab 2021b/Simulink to analyze the output power and fuel economy of the hybrid energy system. The results show that, compared with the equivalent fuel consumption minimum strategy (ECMS), the overall fuel economy of A-ECMS could improve by 10%. Meanwhile, the fuel consumption of the hydrogen hybrid energy system is less than half of that of traditional engines.

1. Introduction

Hydrogen energy has the characteristics of a high energy density and zero emissions, which have been widely recognized by researchers. Hybrid energy systems are widely used by car companies for their energy recovery, low fuel consumption, and long range. Based on the characteristics of hydrogen and hybrid energy systems, this paper studies hydrogen hybrid energy systems. The core of high conversion efficiency and low fuel consumption in hybrid power systems lies in the management and control strategy of the hybrid energy system. Hybrid energy systems typically have two energy management strategies [1,2,3,4], namely, a rule-based energy management strategy and an optimization-based energy management strategy.

The power management strategy based on deterministic rules is a management strategy based on professional knowledge or experience. Wahono et al. [5] used rule-based energy management strategies to simulate the dynamic behavior of an extended-range hybrid system under selected operating conditions, achieving improvements in performance and fuel consumption. Li Xuefang et al. [6] proposed a new rule-based control strategy, the torque-leveling threshold variation strategy (TTS), and its effectiveness was verified using benchmark testing. M. Cipek et al. [7] designed a rule-based controller for a dual-mode energy-split hybrid system and conducted simulations. Oumala Mechichi et al. [8] proposed the application of rule-based control strategies in parallel plug-in hybrid power systems and pointed out the influence of the initial battery state of charge (SOC) on the fuel economy of plug-in hybrid energy systems. Ravi Kant Yadav et al. [9] utilized a fuzzy logic PID gain-tuning method to optimize the performance of hybrid energy systems and improve their conversion efficiency. Swapnil Srivastava et al. [10] proposed a controller based on an adaptive neural fuzzy inference system (ANFIS) to ensure effective energy distribution between an internal combustion engine (ICE) and an electric motor (EM), providing fuel economy for hybrid energy systems. The above methods did not involve clear minimization or optimization objectives, making it difficult to achieve optimal fuel economy and efficiency in hybrid energy systems.

The optimization-based energy management strategy relies on the optimal control strategy calculated by a model. This strategy is based on various optimization theories, including multi-objective optimization, dynamic programming, etc., using techniques such as optimal control [11], genetic algorithms [12], and dynamic programming (DP) [13] to solve the energy management problem of hybrid energy systems. The most classic global optimal control strategy is the DP algorithm. Reference [14] proposed a hybrid energy system control based on a stochastic dynamic programming algorithm. However, the DP algorithm had problems such as excessive computational complexity. Reference [15] proposed a control strategy with minimum equivalent fuel consumption, which greatly improved the real-time performance of the system. The dynamic programming algorithm takes ten hours to complete, while ECMS only takes about thirty minutes. Therefore, the control strategy with minimum equivalent fuel consumption has become a research hotspot in hybrid energy control and management. Yu Zhang et al. [16] designed an online real-time ECMS energy management strategy and compared the results of NEDC and UDDS cycles with the global optimal results of offline DP. The results showed that the differences between the ECMS control strategy and the global optimal DP hydrogen consumption were only 0.59% and 2.10%, respectively. Tian Shaopeng et al. [17] proposed a whale optimization algorithm (WOA) to optimize the equivalent fuel consumption minimization strategy (ECMS) parameters. Under the premise of maintaining the stability of the state of charge (SOC), the comprehensive fuel consumption of WOA-ECMS in both NEDC and WLTC cycles was reduced. Jen Chou Guan et al. [18] used an adaptive fuzzy sliding mode control (AFSMC) to adaptively adjust the common state vector based on the SOC of the battery, converting electrical energy into equivalent fuel consumption. Zhen Shen et al. [19] proposed a two-level control strategy that combined adaptive ECMS and adaptive dynamic programming (ADP). Alessandro Picchirallo et al. [20] used the SERCA algorithm as a calibration tool to develop an A-ECMS controller for hybrid energy systems, aiming to achieve the approximate optimization of fuel economy and flexibly apply it to the size and optimization processes of hybrid energy systems.

The above literature focuses on the research of hybrid energy systems with lithium-ion batteries and engines. In this hybrid energy system, the energy density of lithium-ion batteries is lower, making it difficult to achieve a high power supply. Therefore, studying the hydrogen hybrid energy system of hydrogen fuel cells and engines, fully leveraging the advantages of the high conversion efficiency and high energy density of fuel cells and meeting the needs of high conversion efficiency, low fuel consumption, and high power supply in hybrid power systems. However, there have been no reports on hydrogen hybrid energy systems and their management strategies in the relevant literature. The paper conducts cutting-edge research on hydrogen hybrid energy systems, constructs the topological structure of hydrogen hybrid energy systems, establishes a digital model of hydrogen hybrid energy systems, and uses adaptive equivalent fuel consumption minimization strategies to manage and control hydrogen hybrid energy systems, laying the foundation for subsequent research on hydrogen hybrid energy systems.

The paper is organized as follows. We investigate the model of hydrogen hybrid energy systems in Section 2. In Section 3, a management strategy for a hydrogen hybrid energy system is designed. The simulation and analysis are shown in Section 4 and, finally, we present our conclusions about the work in Section 5.

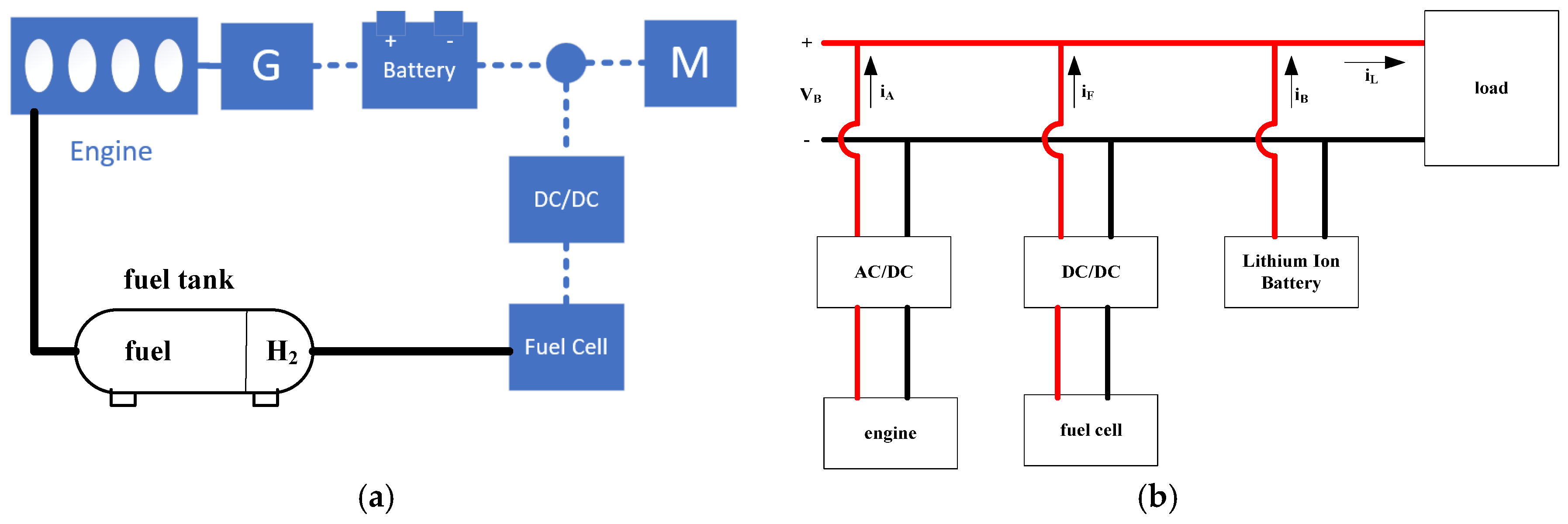
2. Model of Hydrogen Hybrid Energy Systems

In order to fully utilize the advantages of the high energy density of hydrogen and the high conversion efficiency of fuel cells, a hydrogen hybrid energy system structure can be constructed as shown in Figure 1a, which mainly consists of an engine, a fuel cell, and a lithium-ion battery. The engine adopts a gasoline piston engine and the fuel cell adopts a proton exchange membrane fuel cell (PEMFC). In Figure 1a, G represents a generator with AC/DC and M represents a DC motor. Its working principle is that the fuel tank stores fuel and hydrogen, and the mass ratio of fuel to hydrogen is 94:6, providing fuel for the engine and the fuel cell, respectively. The engine burns fuel to provide active power for the system, the fuel cell generates electricity for the system, and the lithium-ion battery regulates the energy balance of the system to improve the system conversion efficiency. The system has the characteristics of high conversion efficiency, low fuel consumption, and high power consumption, and can be used as the power system for vehicles, drones, and other vehicles, especially unmanned platforms, to enhance the endurance and load capacity of the unmanned platforms. An equivalent to the hydrogen hybrid energy system, a circuit model, is shown in Figure 1b; the fuel cell, engine, lithium-ion battery, and load share a voltage bus. The lithium-ion batteries are directly connected to the bus and are in a float charging state to balance the bus voltage. The engine generates electricity through AC/DC conversion to the DC connection to the bus, and the fuel cell is connected to the bus through a DC/DC boost.

According to the equivalent circuit diagram of the hydrogen hybrid energy system shown in Figure 1b, the current relationships of the engine, fuel cell, lithium battery, load, etc., are shown in Equation (1).

$${\mathrm{i}}_{\mathrm{B}}={\mathrm{i}}_{\mathrm{L}}-{\mathrm{i}}_{\mathrm{A}}-{\mathrm{i}}_{\mathrm{F}}$$

(1)

where ${\mathrm{i}}_{\mathrm{B}}$ is the lithium battery current, ${\mathrm{i}}_{\mathrm{L}}$ is the load current, ${\mathrm{i}}_{\mathrm{A}}$ is the engine AC/DC output current, and ${\mathrm{i}}_{\mathrm{F}}$ is the fuel cell DC/DC output current.

(1)

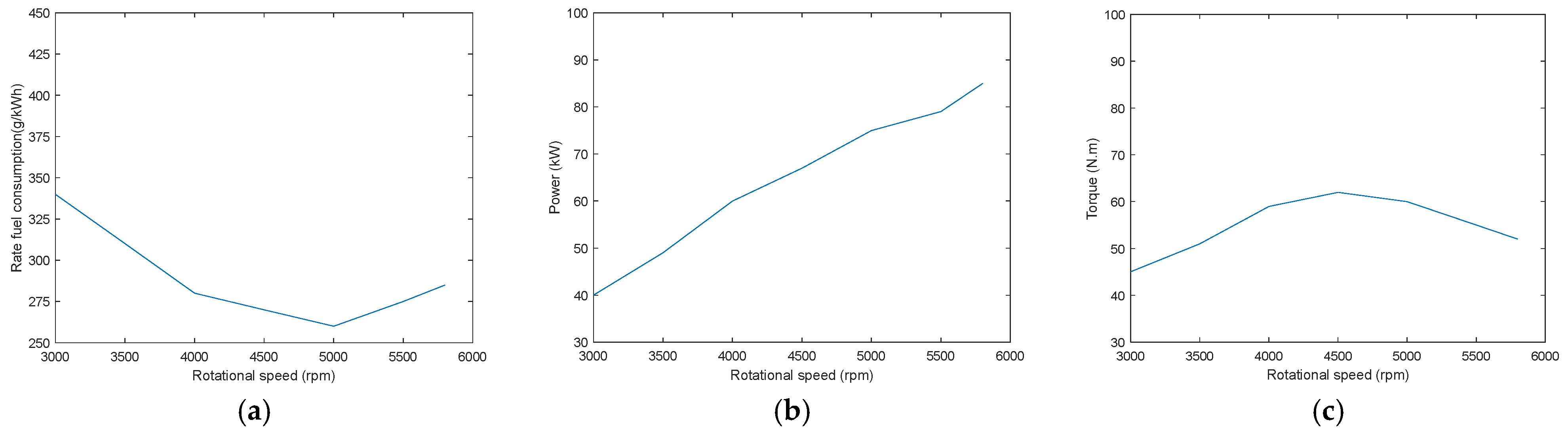
Engine model

The AC/DC output current of the engine is shown in Equation (2).

$${\mathrm{i}}_{\mathrm{A}}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{G}}}{{\mathrm{V}}_{\mathrm{B}}}}={\displaystyle \frac{{\mathsf{\eta }}_{\mathrm{E}}{\mathrm{P}}_{\mathrm{E}}}{{\mathrm{V}}_{\mathrm{B}}}}$$

(2)

where ${\mathrm{V}}_{\mathrm{B}}$ is the bus voltage, ${\mathrm{P}}_{\mathrm{G}}$ is the AC/DC output power, ${\mathrm{P}}_{\mathrm{E}}$ is the engine output power, and ${\mathsf{\eta }}_{\mathrm{E}}$ is the AC/DC conversion efficiency.

The relationship between engine fuel consumption and power [17] is shown in Equation (3).

$${\mathrm{Q}}_{\mathrm{E}}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{E}}{\mathrm{b}}_{\mathrm{E}}}{3600\mathsf{\rho }}}$$

(3)

where ${\mathrm{P}}_{\mathrm{E}}$ is the engine output power (kW), ${\mathrm{b}}_{\mathrm{E}}$ is the engine fuel consumption rate (g/kWh), $\mathsf{\rho }$ is the fuel density (kg/L), and ${\mathrm{Q}}_{\mathrm{E}}$ is the fuel flow rate (mL/s).

The fuel consumption rate of the engine can be expressed as a function of engine speed and torque [10], as shown in Equation (4). The function relationship curve is shown in Figure 2 for a certain model of engine. Figure 2a shows the fuel consumption curve, Figure 2b shows the power curve, and Figure 2c shows the torque curve,

$${\mathrm{b}}_{\mathrm{E}}=\mathrm{f}({\mathsf{\omega }}_{\mathrm{E}},{\mathrm{T}}_{\mathrm{E}})$$

(4)

where ${\mathrm{T}}_{\mathrm{E}}$ is the engine torque and ${\mathsf{\omega }}_{\mathrm{E}}$ is the engine speed.

Substituting Equation (3) into Equation (2) yields the relationship between the output current and fuel consumption, as shown in Equation (5).

$${\mathrm{i}}_{\mathrm{A}}={\displaystyle \frac{3600{\mathsf{\eta }}_{\mathrm{E}}\mathsf{\rho }{\mathrm{Q}}_{\mathrm{E}}}{{\mathrm{b}}_{\mathrm{E}}{\mathrm{V}}_{\mathrm{B}}}}$$

(5)

(2)

Fuel-cell model

According to the principle of fuel-cell power generation, each hydrogen molecule provides 2 electrons and the molar flow rate of hydrogen gas in the fuel cell [21] is shown in Equation (6).

$${\mathrm{Q}}_{\mathrm{H}\_\mathrm{m}\mathrm{o}\mathrm{l}}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{H}}}{2\mathrm{F}{\mathrm{V}}_{\mathrm{s}}}}$$

(6)

where ${\mathrm{Q}}_{\mathrm{H}\_\mathrm{m}\mathrm{o}\mathrm{l}}$ is the molar flow rate of hydrogen gas (mol/s), ${\mathrm{P}}_{\mathrm{H}}$ is the power of a single fuel cell (W), $\mathrm{F}$ is the Faraday constant, and ${\mathrm{V}}_{\mathrm{s}}$ is the voltage of a single fuel cell.

The fuel cell is composed of N single fuel cells connected in series. By modifying Equation (6), the expression for the mass flow rate of hydrogen gas in the fuel cell is shown in Equation (7).

$${\mathrm{Q}}_{\mathrm{H}}=2.02\times {10}^{-3}{\displaystyle \frac{\mathrm{N}{\mathrm{P}}_{\mathrm{H}}}{2\mathrm{F}{\mathrm{V}}_{\mathrm{s}}}}=2.02\times {10}^{-3}{\displaystyle \frac{\mathrm{N}{\mathrm{i}}_{\mathrm{f}\mathrm{c}}}{2\mathrm{F}}}$$

(7)

where ${\mathrm{Q}}_{\mathrm{H}}$ is the mass flow rate of hydrogen gas (kg/s), N is the number of fuel cells, and ${\mathrm{i}}_{\mathrm{f}\mathrm{c}}$ is the fuel-cell current.

By modifying Equation (7) and combining it with the DC/DC conversion efficiency, the expression for the fuel-cell DC/DC output current can be obtained, as shown in Equation (8).

$${\mathrm{i}}_{\mathrm{F}}={\mathsf{\eta }}_{\mathrm{F}}{\displaystyle \frac{1}{2.02\times {10}^{-3}}}{\displaystyle \frac{{2\mathrm{F}\mathrm{Q}}_{\mathrm{H}}}{\mathrm{N}}}{\displaystyle \frac{{\mathrm{V}}_{\mathrm{F}}}{{\mathrm{V}}_{\mathrm{B}}}}$$

(8)

where ${\mathsf{\eta }}_{\mathrm{F}}$ is the DC/DC and fuel-cell conversion efficiency and ${\mathrm{V}}_{\mathrm{F}}$ is the fuel-cell voltage.

(3)

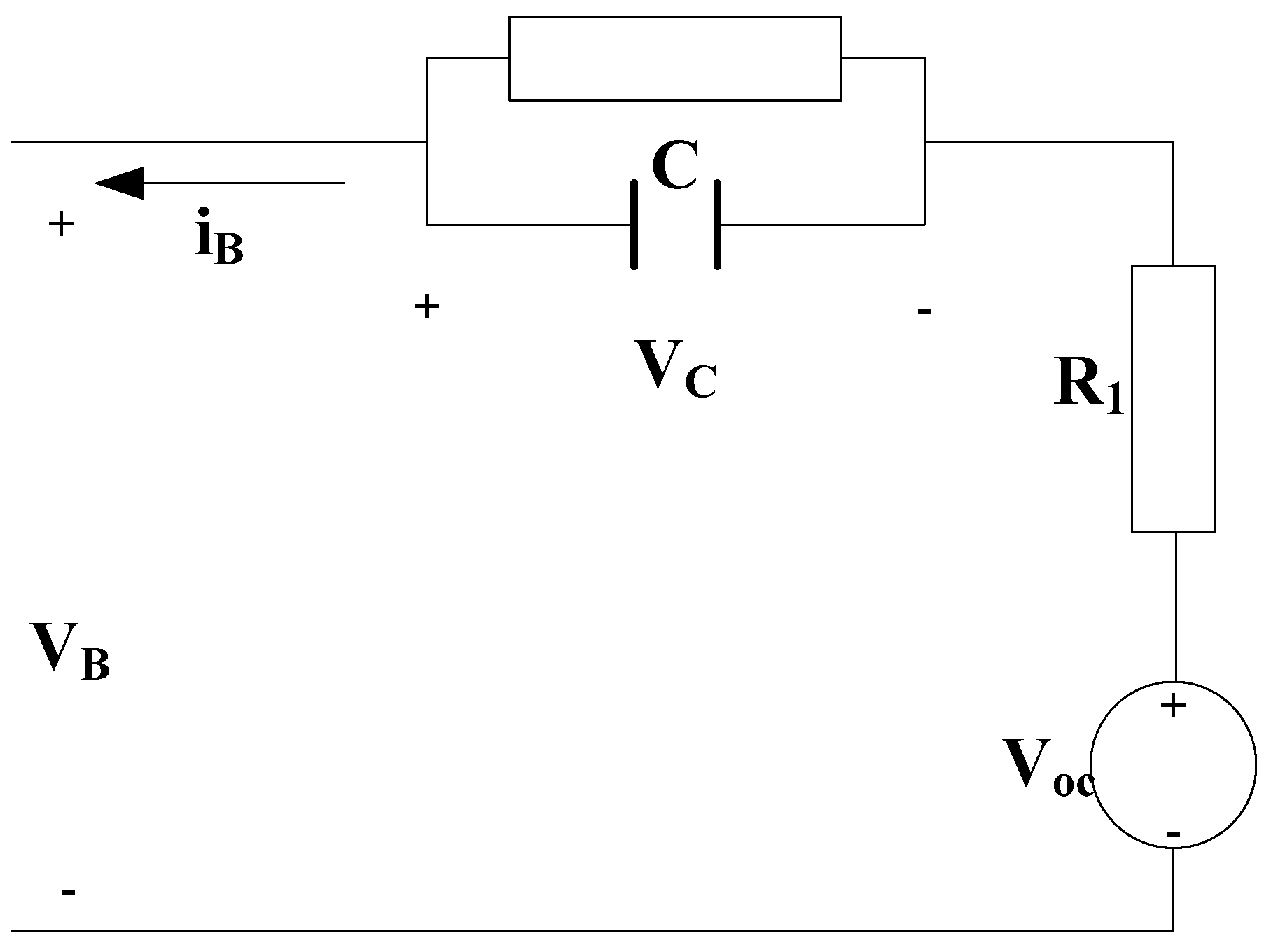
Lithium-ion battery model

A lithium-ion battery adopts the RC model [4], which is shown in Figure 3.

According to the lithium-ion battery model, the current expression of the lithium-ion battery is shown in Equations (9) and (10).

$$\mathrm{C}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}}{\mathrm{V}}_{\mathrm{c}}={\mathrm{i}}_{\mathrm{B}}-{\displaystyle \frac{{\mathrm{V}}_{\mathrm{c}}}{{\mathrm{R}}_2}}$$

(9)

$${\mathrm{V}}_{\mathrm{B}}={\mathrm{V}}_{\mathrm{o}\mathrm{c}}-{\mathrm{V}}_{\mathrm{c}}-{\mathrm{i}}_{\mathrm{B}}{\mathrm{R}}_1$$

(10)

where ${\mathrm{V}}_{\mathrm{o}\mathrm{c}}$ is the open circuit voltage, which has a nonlinear relationship with the battery SOC; $\mathrm{C}$ is the capacitance value; ${\mathrm{V}}_{\mathrm{c}}$ is the capacitance voltage; and ${\mathrm{R}}_1$ and ${\mathrm{R}}_2$ are the internal resistances, respectively.

(4)

Load model

The load is equivalent to the controllable current source model [22], and its current expression is shown in Equation (11).

$$\mathrm{L}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}}{\mathrm{i}}_{\mathrm{L}}=-{\mathrm{i}}_{\mathrm{L}}{\mathrm{R}}_{\mathrm{p}}+{\mathrm{V}}_{\mathrm{B}}$$

(11)

where ${\mathrm{R}}_{\mathrm{p}}$ is the internal resistance of the controllable current source.

(5)

Hydrogen hybrid energy system model

From Equations (1), (5), (8)–(11), the system state equation can be obtained, as shown in Equation (12).

$$\dot{\mathrm{x}}=\mathrm{A}\left(\mathrm{x}\right)\mathrm{x}+\mathrm{G}(\mathrm{x},\mathrm{u})$$

(12)

where,

The state variables are shown in Equation (13).

$$\mathrm{x}\left(\mathrm{t}\right)\triangleq {[{\mathrm{V}}_{\mathrm{c}}\hspace{1em}{\mathrm{i}}_{\mathrm{L}}]}^{\mathrm{T}}\in {\mathrm{R}}^2$$

(13)

The input quantity is shown in Equation (14).

$$\mathrm{u}\left(\mathrm{t}\right)\triangleq {\left[\begin{array}{cc}{\mathrm{i}}_{\mathrm{f}\mathrm{c}}& {\mathrm{i}}_{\mathrm{A}}\end{array}\right]}^{\mathrm{T}}\in {\mathrm{R}}^2$$

(14)

The matrices A($\mathrm{x}$) and G (x, u) are shown in Equations (15) and (16), respectively.

$$\mathrm{A}(\mathrm{x})\triangleq \left(\begin{array}{cc}-{\displaystyle \frac{1}{{\mathrm{R}}_2\mathrm{C}}}& {\displaystyle \frac{1}{\mathrm{C}}}\\ -{\displaystyle \frac{1}{\mathrm{L}}}& -{\displaystyle \frac{{\mathrm{R}}_{\mathrm{p}}{+\mathrm{R}}_1}{\mathrm{L}}}\end{array}\right)$$

(15)

$$\mathrm{G}(\mathrm{x},\mathrm{u})\triangleq \left(\begin{array}{c}-{\mathsf{\eta }}_{\mathrm{F}}{\displaystyle \frac{{\mathrm{V}}_{\mathrm{f}\mathrm{c}}}{\mathrm{C}{\mathrm{V}}_{\mathrm{B}}}}{\mathrm{i}}_{\mathrm{f}\mathrm{c}}-{\mathrm{i}}_{\mathrm{A}}\\ {\displaystyle \frac{{\mathrm{R}}_1{\mathrm{V}}_{\mathrm{f}\mathrm{c}}}{\mathrm{L}{\mathrm{V}}_{\mathrm{B}}}}{{\mathsf{\eta }}_{\mathrm{F}}\mathrm{i}}_{\mathrm{f}\mathrm{c}}+{\displaystyle \frac{{\mathrm{V}}_{\mathrm{o}\mathrm{c}}}{\mathrm{L}}}+{\displaystyle \frac{{\mathrm{R}}_1{\mathrm{i}}_{\mathrm{A}}}{\mathrm{L}}}\end{array}\right)$$

(16)

Transforming the expression of G (x, u), and the result is as follows::

$$\mathrm{G}(\mathrm{x},\mathrm{u})\triangleq \left(\begin{array}{c}-{\mathsf{\eta }}_{\mathrm{F}}{\displaystyle \frac{{\mathrm{V}}_{\mathrm{f}\mathrm{c}}}{\mathrm{C}{\mathrm{V}}_{\mathrm{B}}}}·{\displaystyle \frac{1}{2.02\times {10}^{-3}}}·{\displaystyle \frac{{2\mathrm{F}\mathrm{Q}}_{\mathrm{H}}}{\mathrm{N}}}-{\displaystyle \frac{3600{\mathsf{\eta }}_{\mathrm{E}}\mathsf{\rho }{\mathrm{Q}}_{\mathrm{E}}}{{\mathrm{b}}_{\mathrm{E}}{\mathrm{V}}_{\mathrm{B}}\mathrm{C}}}\\ {\displaystyle \frac{{\mathrm{R}}_1{\mathrm{V}}_{\mathrm{f}\mathrm{c}}}{\mathrm{L}{\mathrm{V}}_{\mathrm{B}}}}·{\mathsf{\eta }}_{\mathrm{F}}{\displaystyle \frac{1}{2.02\times {10}^{-3}}}·{\displaystyle \frac{{2\mathrm{F}\mathrm{Q}}_{\mathrm{H}}}{\mathrm{N}}}+{\displaystyle \frac{{\mathrm{V}}_{\mathrm{o}\mathrm{c}}}{\mathrm{L}}}+{\displaystyle \frac{{\mathrm{R}}_1}{\mathrm{L}}}·{\displaystyle \frac{3600{\mathsf{\eta }}_{\mathrm{E}}\mathsf{\rho }{\mathrm{Q}}_{\mathrm{E}}}{{\mathrm{b}}_{\mathrm{E}}{\mathrm{V}}_{\mathrm{B}}}}\end{array}\right)$$

(17)

The system state space is shown in Equation (18).

$$\left(\begin{array}{c}\dot{{\mathrm{V}}_{\mathrm{c}}}\\ \dot{{\mathrm{i}}_{\mathrm{L}}}\end{array}\right)=\left(\begin{array}{cc}-{\displaystyle \frac{1}{{\mathrm{R}}_2\mathrm{C}}}& {\displaystyle \frac{1}{\mathrm{C}}}\\ -{\displaystyle \frac{1}{\mathrm{L}}}& -{\displaystyle \frac{{\mathrm{R}}_{\mathrm{p}}{+\mathrm{R}}_1}{\mathrm{L}}}\end{array}\right)\left(\begin{array}{c}{\mathrm{V}}_{\mathrm{C}}\\ {\mathrm{i}}_{\mathrm{L}}\end{array}\right)+\left(\begin{array}{c}-{\mathsf{\eta }}_{\mathrm{F}}{\displaystyle \frac{{\mathrm{V}}_{\mathrm{f}\mathrm{c}}}{\mathrm{C}{\mathrm{V}}_{\mathrm{B}}}}·{\displaystyle \frac{1}{2.02\times {10}^{-3}}}·{\displaystyle \frac{{2\mathrm{F}\mathrm{Q}}_{\mathrm{H}}}{\mathrm{N}}}-{\displaystyle \frac{3600{\mathsf{\eta }}_{\mathrm{E}}\mathsf{\rho }{\mathrm{Q}}_{\mathrm{E}}}{{\mathrm{b}}_{\mathrm{E}}{\mathrm{V}}_{\mathrm{B}}\mathrm{C}}}\\ {\displaystyle \frac{{\mathrm{R}}_1{\mathrm{V}}_{\mathrm{f}\mathrm{c}}}{\mathrm{L}{\mathrm{V}}_{\mathrm{B}}}}·{\mathsf{\eta }}_{\mathrm{F}}{\displaystyle \frac{1}{2.02\times {10}^{-3}}}·{\displaystyle \frac{{2\mathrm{F}\mathrm{Q}}_{\mathrm{H}}}{\mathrm{N}}}+{\displaystyle \frac{{\mathrm{V}}_{\mathrm{o}\mathrm{c}}}{\mathrm{L}}}+{\displaystyle \frac{{\mathrm{R}}_1}{\mathrm{L}}}·{\displaystyle \frac{3600{\mathsf{\eta }}_{\mathrm{E}}\mathsf{\rho }{\mathrm{Q}}_{\mathrm{E}}}{{\mathrm{b}}_{\mathrm{E}}{\mathrm{V}}_{\mathrm{B}}}}\end{array}\right)$$

(18)

In summary, establishing a digital model for hydrogen hybrid energy systems lays the foundation for future research on management strategies for hydrogen hybrid energy systems.

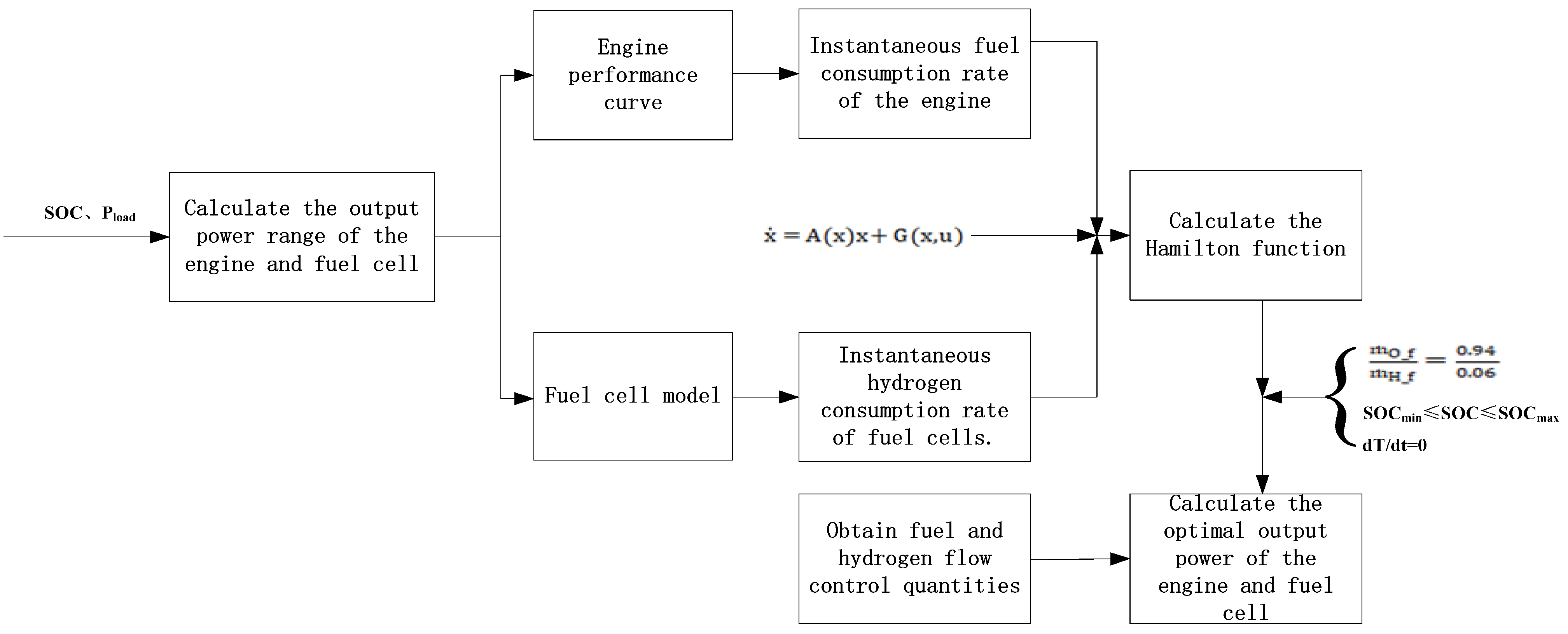
3. Energy Management Strategy

According to the hydrogen hybrid energy system model, the state equation of the hydrogen hybrid energy system is shown in Equation (19).

$$\dot{\mathrm{x}}=\mathrm{A}\left(\mathrm{x}\right)\mathrm{x}+\mathrm{G}(\mathrm{x},\mathrm{u})$$

(19)

According to the fuel conditions of the hydrogen hybrid energy system, the fuel constraint conditions are shown in Equation (20).

$${\displaystyle \frac{{\dot{\mathrm{m}}}_{\mathrm{O}\_\mathrm{f}}}{{\dot{\mathrm{m}}}_{\mathrm{H}\_\mathrm{f}}}}={\displaystyle \frac{0.94}{0.06}}$$

(20)

where ${\dot{\mathrm{m}}}_{\mathrm{O}\_\mathrm{f}}$ is the fuel consumption per unit time of the engine and ${\dot{\mathrm{m}}}_{\mathrm{H}\_\mathrm{f}}$ is the hydrogen consumption per unit time of the fuel cell.

The engine operates at its optimal operating point with minimal torque variation, and its constraint condition is shown in Equation (21).

$${\displaystyle \frac{\mathrm{d}}{\mathrm{d}\mathrm{t}}}\mathrm{T}=0$$

(21)

where T is the engine torque.

To prevent the overcharging and overdischarging of lithium-ion batteries, which may affect their lifespan and safety, the state of charge of lithium-ion batteries is constrained, as shown in Equation (22).

$${\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathrm{m}\mathrm{i}\mathrm{n}}\le \mathrm{S}\mathrm{O}\mathrm{C}\le {\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(22)

where ${\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ and ${\mathrm{S}\mathrm{O}\mathrm{C}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ are the minimum and maximum values of the charge state of lithium-ion batteries, respectively.

Taking the optimal energy consumption of the hydrogen hybrid energy system as the goal, its performance indicators are shown in Equation (23).

$$\mathrm{J}={\int }_{{\mathrm{t}}_0}^{{\mathrm{t}}_{\mathrm{f}}}{\dot{[\mathrm{m}}}_{{\mathrm{O}}_{\mathrm{f}}}\left(\mathrm{u}\left(\mathrm{t}\right),\mathrm{t}\right)+{\dot{\mathrm{m}}}_{{\mathrm{H}}_{\mathrm{f}}}\left(\mathrm{u}\left(\mathrm{t}\right),\mathrm{t}\right)]\mathrm{d}\mathrm{t}$$

(23)

The optimal energy consumption calculation converts the solution of the optimal value of the Hamilton function, and the definition of the Hamilton function for hydrogen hybrid energy systems is shown in Equation (24).

$$\mathrm{H}(\mathrm{x}(\mathrm{t}),\mathrm{u}(\mathrm{t}),\mathsf{\lambda }(\mathrm{t}),\mathrm{t})={\dot{[\mathrm{m}}}_{{\mathrm{O}}_{\mathrm{f}}}\left(\mathrm{u}\left(\mathrm{t}\right),\mathrm{t}\right)+{\dot{\mathrm{m}}}_{{\mathrm{H}}_{\mathrm{f}}}\left(\mathrm{u}\left(\mathrm{t}\right),\mathrm{t}\right)]+{\mathsf{\lambda }(\mathrm{t})}^{\mathrm{T}}[\mathrm{A}(\mathrm{x})\mathrm{x}+\mathrm{G}(\mathrm{x},\mathrm{u})]$$

(24)

where ${\mathsf{\lambda }\left(\mathrm{t}\right)}^{\mathrm{T}}$ is the co-state vector.

During the operation of the hydrogen hybrid energy system, the total power meets the operational requirements, as shown in Equation (25).

$${{\mathsf{\eta }}_{\mathrm{F}}\mathrm{P}}_{\mathrm{f}\mathrm{c}}\left(\mathrm{t}\right)+{\mathsf{\eta }}_{\mathrm{E}}{\mathrm{P}}_{\mathrm{E}}\left(\mathrm{t}\right)+{\mathrm{P}}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(\mathrm{t}\right)={\mathrm{P}}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\left(\mathrm{t}\right)$$

(25)

where ${\mathrm{P}}_{\mathrm{f}\mathrm{c}}\left(\mathrm{t}\right)$ is the output power of the fuel cell, ${\mathrm{P}}_{\mathrm{E}}\left(\mathrm{t}\right)$ is the output power of the engine, ${\mathrm{P}}_{\mathrm{B}\mathrm{a}\mathrm{t}}\left(\mathrm{t}\right)$ is the output power of the lithium-ion battery, and ${\mathrm{P}}_{\mathrm{l}\mathrm{o}\mathrm{a}\mathrm{d}}\left(\mathrm{t}\right)$ is the load power.

Based on the above analysis, this article adopted the ECMS, whose logical flow is shown in Figure 4 and main parameters are shown in

Table 1. ECMS main parameters.

Name	Symbol	Value	Unit
Maximum SOC	SOCmax	30	%
Minimum SOC	SOCmin	80	%
Torque resolution	T	0.01	N*m
Power resolution	P	0.01	Kw

. The ECMS algorithm process is as follows:

(1)

Calculate the output power range of the engine and fuel cell based on the overall power and SOC;

(2)

Calculate the transient fuel consumption rate of the engine and fuel cell using the engine characteristic curve and fuel-cell model;

(3)

Calculate the Hamilton function based on the transient fuel consumption rate of the engine and fuel cell as well as the state equation of the hydrogen hybrid energy system;

(4)

Calculate the optimal output power of the engine and fuel cell using the Hamilton function based on the constraint conditions;

(5)

Obtain fuel and hydrogen flow-control quantities based on the output power of the engine and fuel cell.

According to the performance function and Hamilton function, the co-state vector of ECMS is a fixed value, which is difficult to adapt to the changing working conditions. To improve the performance of ECMS, the co-state vector is adjusted in real time according to the working conditions; that is, the adaptive equivalent fuel consumption minimum strategy (A-ECMS). An adaptive co-state vector $\mathsf{\lambda }\left(\mathrm{t}\right)$ of A-ECMS can be designed in which $\mathsf{\lambda }\left(\mathrm{t}\right)$ is linearly adjusted through the output power of the fuel cell. That is, a function relationship can be constructed [23], as shown in Figure 5 and Formula (26), where ${\mathrm{Q}}_{{\mathrm{H}}_2\_\mathrm{l}\mathrm{h}\mathrm{v}}$ and ${\mathrm{Q}}_{\mathrm{o}\mathrm{i}\mathrm{l}\_\mathrm{l}\mathrm{h}\mathrm{v}}$ are the calorific value (J/g) of hydrogen and fuel, $\mathsf{\epsilon }={\dot{\mathrm{m}}}_{\mathrm{o}\mathrm{i}\mathrm{l}}/{\dot{\mathrm{m}}}_{{\mathrm{H}}_2}$ and ${\mathsf{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{*}}$ are the maximum co-state vector values under the lithium-ion battery driving mode, and ${\mathrm{P}}_{\mathrm{f}\mathrm{c}}^{\mathrm{m}\mathrm{a}\mathrm{x}}$ and ${\mathrm{P}}_{\mathrm{f}\mathrm{c}}^{\mathrm{m}\mathrm{i}\mathrm{n}}$ are the maximum and minimum output powers of the fuel cell during the operation of the hybrid energy system, respectively.

$$\mathsf{\lambda }(\mathrm{t})={\displaystyle \frac{1}{({\mathrm{Q}}_{{\mathrm{H}}_2\_\mathrm{l}\mathrm{h}\mathrm{v}}+{\mathrm{Q}}_{\mathrm{o}\mathrm{i}\mathrm{l}\_\mathrm{l}\mathrm{h}\mathrm{v}}\mathsf{\epsilon })}}({\mathsf{\lambda }}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{\mathrm{*}}-{\displaystyle \frac{1}{({\mathrm{Q}}_{{\mathrm{H}}_2\_\mathrm{l}\mathrm{h}\mathrm{v}}+{\mathrm{Q}}_{\mathrm{o}\mathrm{i}\mathrm{l}\_\mathrm{l}\mathrm{h}\mathrm{v}}\mathsf{\epsilon })}}){\displaystyle \frac{{\mathrm{P}}_{\mathrm{f}\mathrm{c}}^{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{P}}_{\mathrm{f}\mathrm{c}}(\mathrm{t})}{{\mathrm{P}}_{\mathrm{f}\mathrm{c}}^{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{P}}_{\mathrm{f}\mathrm{c}}^{\mathrm{m}\mathrm{i}\mathrm{n}}}}$$

(26)

4. Simulation and Analysis

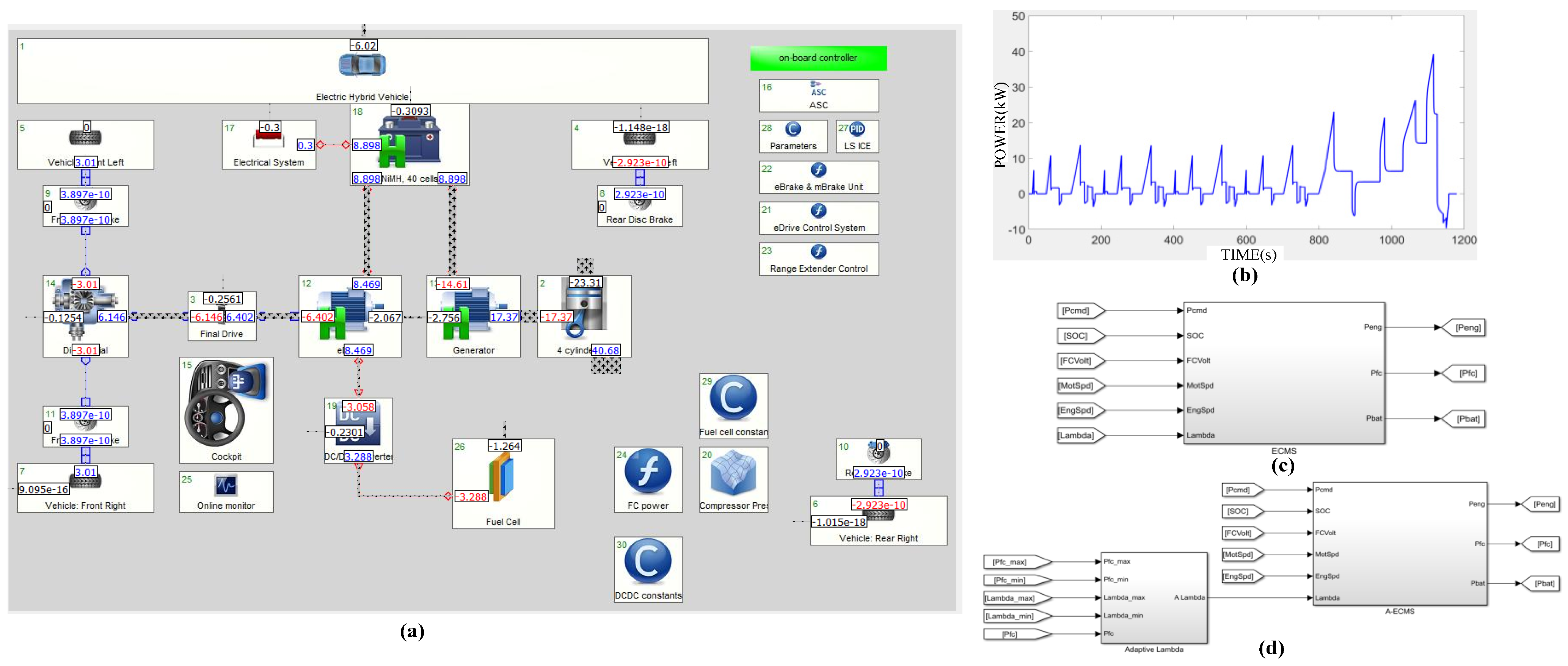
4.1. Simulation and Analysis Platform

The digital model of the hydrogen hybrid energy system constructed using AVL CRUISE is shown in Figure 6a. The system mainly consists of the following three energy sources: the engine, the fuel cell, and the lithium-ion battery. The engine serves as the main energy source, the fuel cell as the auxiliary power source, and the lithium-ion battery as the regulating source. The maximum power output of the engine is 90 kW, which is the main power source of the hydrogen hybrid energy system. The fuel cell consists of 150 fuel-cell units with a maximum power of 45 kW, which converts hydrogen into electrical energy as an auxiliary power source of the hydrogen hybrid energy system. Lithium-ion batteries are used as power regulation sources to feed back and regulate hybrid energy systems.

The NEDC operating condition is used as the simulation verification condition, and its operating condition curve is shown in Figure 6b. MATLAB/Simulink is used to build ECMS and A-ECMS, as shown in Figure 6c and Figure 6d, respectively, and to conduct the simulation analysis on ECMS and A-ECMS using the joint simulation of AVL Cruise and MATLAB/Simulink.

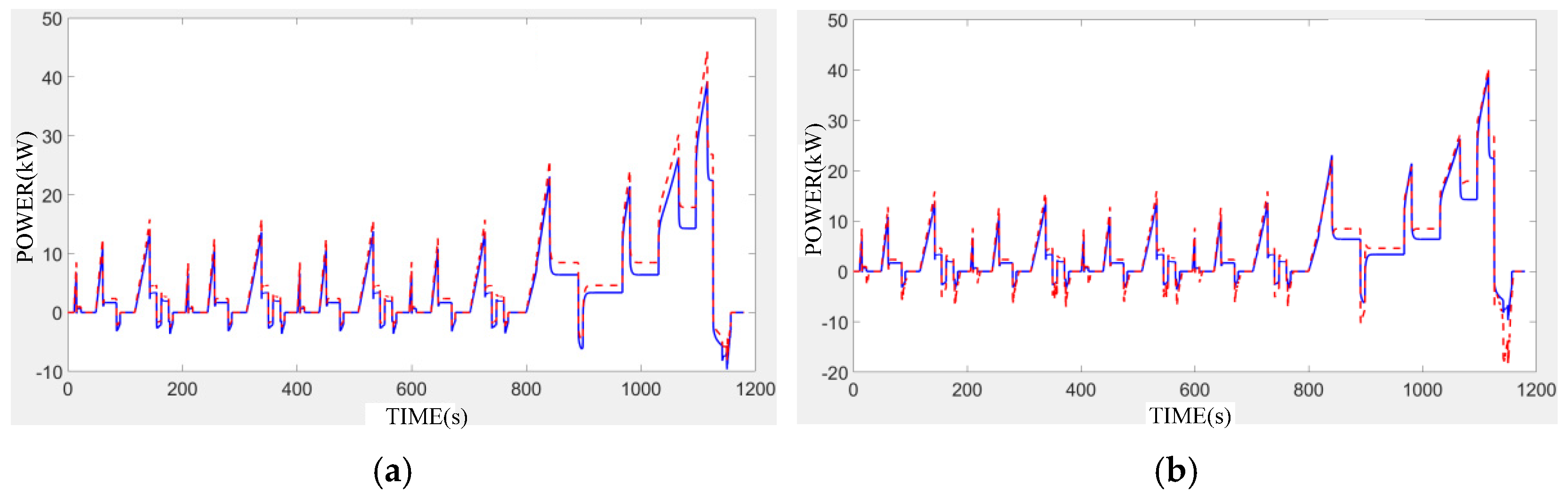
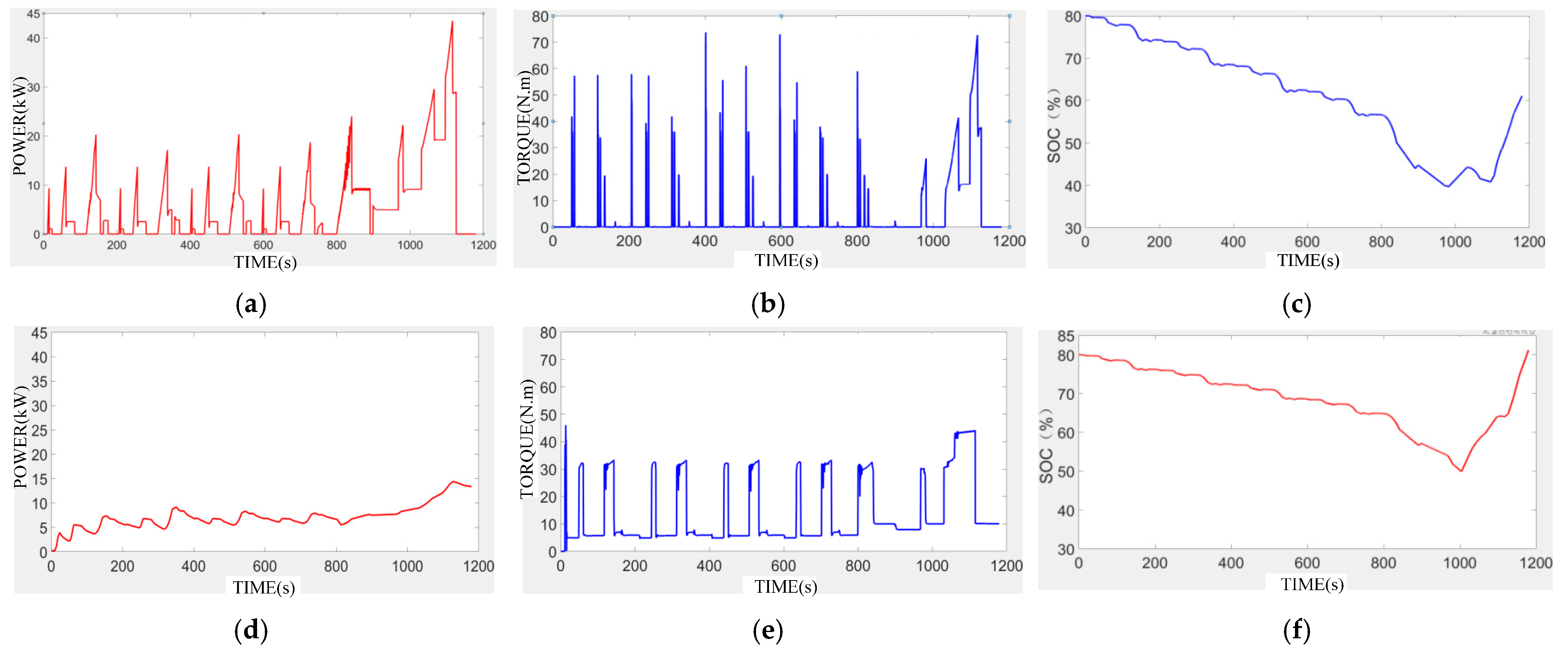
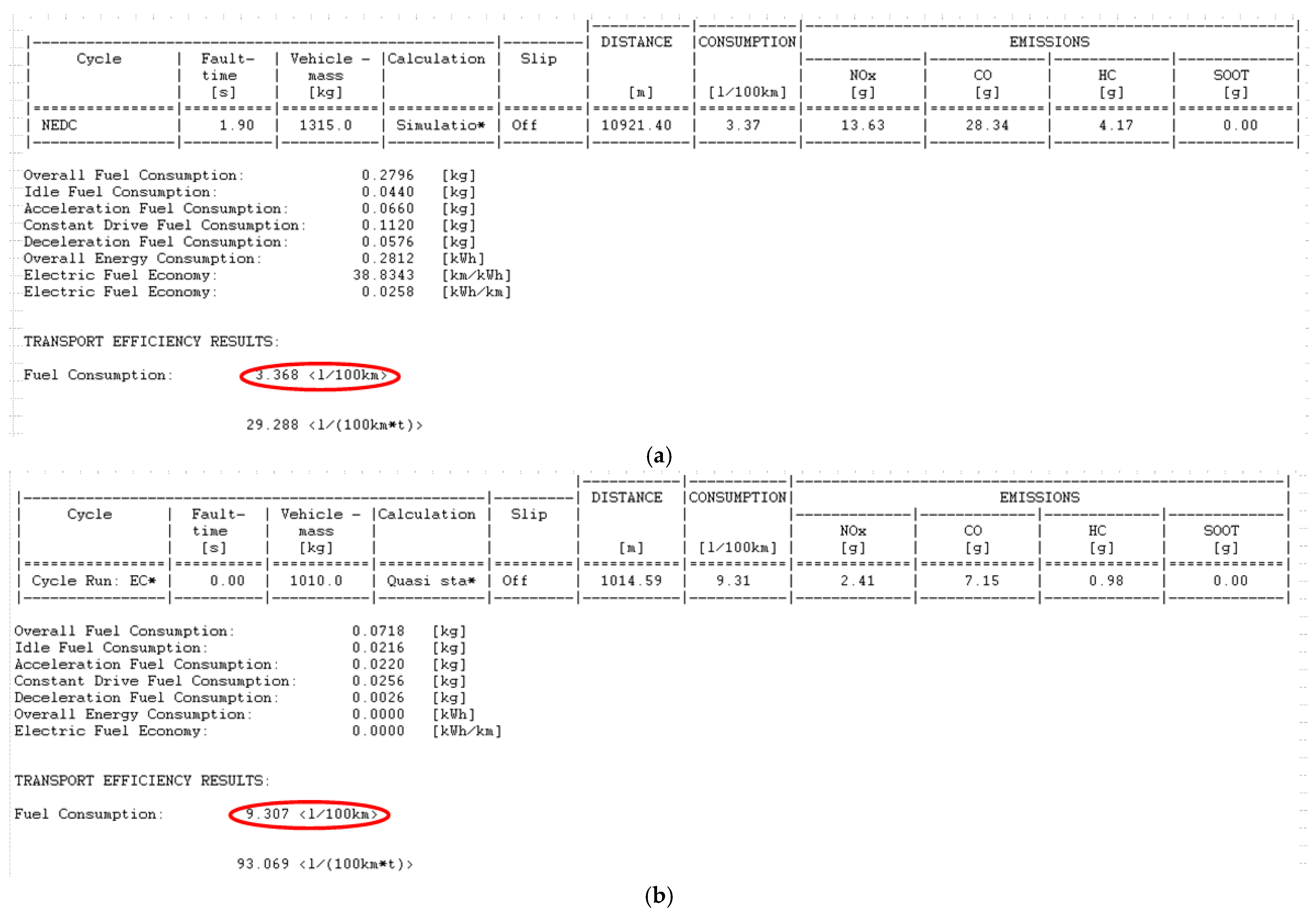
4.2. Simulation Analysis of Energy Management Strategy

According to the method described in Section 3, ECMS and A-ECMS are used to simulate the NEDC conditions. The simulation results are shown in Figure 7, where the “red line” represents the following power curve and the “blue line” represents the required power curve. From an analysis of Figure 7, it can be seen that both ECMS and A-ECMS can follow the operating conditions well. By using the mean error calculation, the errors of ECMS and A-ECMS can be obtained as 0.97 kw and 0.94 kw, respectively. A-ECMS has a smaller error. Therefore, A-ECMS is superior to ECMS in terms of condition tracking.

By using a simulation analysis platform, the SOC changes in the engine, fuel cell, and lithium-ion battery can be analyzed and compared when ECMS and A-ECMS are used to allocate and manage hybrid energy systems. The changes in fuel-cell output power, engine output torque, and lithium battery SOC are shown in Figure 8.

When analyzing Figure 8a,d, it can be seen that, under the same NEDC operating conditions, there are frequent and significant fluctuations in the output power of the fuel cell when ECMS is used for management and control. When using A-ECMS, the output power of the fuel cell is very smooth. However, frequent and significant fluctuations in the output of fuel cells will seriously affect their lifespan and conversion efficiency. Therefore, from the perspective of fuel cells, A-ECMS is superior to ECMS.

The engine output torque is shown in Figure 8b,e. When ECMS is used for management and control, the engine output torque frequently and greatly fluctuates, making it difficult to achieve the optimal operating point of the engine. However, in A-ECMS, the engine output torque is smoothly output, which can regulate the engine to operate at the optimal operating point. Therefore, the engine fuel consumption for ECMS is higher than A-ECMS.

The SOC changes in lithium-ion batteries under NEDC conditions are shown in Figure 8c,f. The SOC changes in lithium-ion batteries caused by A-ECMS and ECMS are both between 30 and 80%, meeting the requirements of lithium-ion battery control in hydrogen hybrid energy systems, and there are no overshoot or overdischarge phenomena.

Based on the above analysis, the control and management of the engine and fuel cell in A-ECMS are superior to ECMS. The reason for this is that the covariance vector of A-ECMS varies with power, which is beneficial for the regulation of lithium-ion battery stack hybrid energy systems.

Three different operating conditions, NEDC, FTP72, and WLTC, are used to simulate and analyze the management strategies of ECMS and A-ECMS.

The hydrogen consumption per 100 km is shown in Equation (27).

$${\mathrm{Q}}_{\mathrm{H}\_\mathrm{W}}={\displaystyle \frac{{\int }_0^{{\mathrm{T}}_{\mathrm{E}}}{\mathrm{P}}_{\mathrm{H}}\left(\mathrm{t}\right)/{\mathsf{\eta }}_{\mathrm{F}}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}}{{\mathrm{C}}_{\mathrm{H}}}}$$

(27)

where ${\mathrm{Q}}_{\mathrm{H}\_\mathrm{W}}$ is the hydrogen consumption per 100 km (kg), ${\mathrm{T}}_{\mathrm{E}}$ is the running time per 100 km (t), ${\mathrm{P}}_{\mathrm{H}}\left(\mathrm{t}\right)$ is the transient power output of fuel cells (kW), ${\mathsf{\eta }}_{\mathrm{F}}\left(\mathrm{t}\right)$ is the transient conversion efficiency of fuel cells (50%), and ${\mathrm{C}}_{\mathrm{H}}$ is is the calorific value of hydrogen gas (kWh/kg).

The fuel consumption per 100 km is shown in Equation (28).

$${\mathrm{Q}}_{\mathrm{E}\_\mathrm{W}}={\int }_0^{{\mathrm{T}}_{\mathrm{E}}}{\mathrm{P}}_{\mathrm{E}}\left(\mathrm{t}\right){\mathrm{b}}_{\mathrm{E}}\left(\mathrm{t}\right)\mathrm{d}\mathrm{t}$$

(28)

where ${\mathrm{Q}}_{\mathrm{E}\_\mathrm{W}}$ is the fuel consumption per 100 km (kg), ${\mathrm{T}}_{\mathrm{E}}$ is the running time per 100 km (t), ${\mathrm{P}}_{\mathrm{E}}\left(\mathrm{t}\right)$ is the transient power output of engine (kW), and ${\mathrm{b}}_{\mathrm{E}}\left(\mathrm{t}\right)$ is the transient fuel consumption rate of the engine (kg/kWh).

The operating results are shown in

Table 2. Results of three operating conditions.

	ECMS			A-ECMS
Cycle	NEDC	FTP75	EUDC	NEDC	FTP75	EUDC
H2 consumptions per 100 km (kg)	0.217	0.205	0.219	0.198	0.193	0.200
Fuel consumptions per 100 km (L)	4.49	4.31	4.60	4.04	3.88	4.09
Fuel consumptions per 100 km (kg)	3.233	3.101	3.312	2.910	2.794	2.945
Mass ratio of hydrogen to oil	0.067	0.066	0.066	0.068	0.069	0.068
Different from reference ratio	0.003	0.002	0.002	0.004	0.005	0.004

. Under the three cycle conditions, the fuel consumptions per 100 km using the standard ECMS were 4.49 L, 4.31 L, and 4.60 L, while A-ECMS’s were 4.04 L, 3.88 L, and 4.09 L. The overall fuel economy of A-ECMS improved by 10%, 10%, and 11% compared with ECMS. The hydrogen consumptions per 100 km of A-ECMS under the three cycle conditions were 0.198 kg, 0.0.193 kg, and 0.200 kg, which were better than ECMS’s, which were 0.217 kg, 0.205 kg, and 0.219 kg. The overall hydrogen economy improved by 10%, 10%, and 11%, respectively, increasing by 9%, 6%, and 9.5%, respectively. Therefore, compared with ECMS, A-ECMS effectively improved fuel and hydrogen economy.

In order to further analyze the economic characteristics of the hydrogen hybrid energy system, a comparative analysis was conducted between the hydrogen hybrid power system and a traditional engine system. The same engine (of the same model) as the hydrogen hybrid energy system was used as the power source, and the simulation results are shown in Figure 9. According to the analysis of Figure 9, the fuel consumption of the hydrogen hybrid energy system was 3.36 L/100 km, while the fuel consumption of the traditional engine was 9.03 L/100 km. Therefore, the fuel consumption of the hydrogen hybrid energy system was less than half of that of the traditional engine.

5. Conclusions

The paper prospectively proposes a hybrid energy system architecture comprising fuel cells and an engine, and equates it to the circuit model. Using Kirchhoff’s principle, we established a state-space model for hydrogen hybrid energy systems and digitized complex hydrogen hybrid energy systems, laying the foundation for subsequent research on hydrogen hybrid energy systems. A hydrogen hybrid energy system management strategy based on A-ECMS was proposed, according to the state-space model of the hydrogen hybrid power system. A joint simulation platform was constructed using AVL Cruise and MATLAB/Simulink. On this simulation platform, experimental verification was conducted on the hybrid energy systems and A-ECMS algorithm, and a comparative analysis was conducted between the A-ECMS algorithm and the ECMS algorithm. The results showed that the A-ECMS algorithm outperformed the ECMS algorithm in terms of the output characteristics of the fuel cell and engine as well as the economy of hydrogen hybrid energy systems.