Collaborative Game Theory Between Microgrid Operators and Distribution System Operator Considering Multi-Faceted Uncertainties

Abstract

In the vigorous development of the power system, to address the economic challenges of multi-microgrid systems, this paper proposes a Nash bargaining model for collaboration between microgrid operators (MGs) and a distribution system operator (DSO) under conditions of multiple uncertainties. Firstly, a model for energy transactions between multiple complementary microgrid systems and a distribution system is established. Secondly, the chance-constrained method and robust optimization method are applied to model the multiple uncertainties in renewable energy generation and electricity trading prices. Moreover, using Nash bargaining theory, a cooperative operation model between MGs and a DSO is established, which is then transformed into two subproblems: cost minimization in cooperation and revenue maximization from power trading. To protect the privacy of each participant, a distributed solution approach using the alternating direction method of multipliers (ADMM) is applied to solve these subproblems. Finally, the simulation results indicate that the benefit values of all entities have improved after cooperative operation through the proposed model. Specifically, the benefit value of MG 1 is CNY 919,974.3, MG 2 is CNY 1,420,363.2, MG 3 is CNY 790,288.3, and the DSO is CNY 26,257.2. These results demonstrate that the proposed model has favorable economic performance.

1. Introduction

With the continuous extraction and consumption of a large amount of traditional fossil fuels, resulting in energy shortages and a series of issues such as climate change, wind and solar power, as renewable and clean energy sources, are indispensable components of the new power system. Achieving sustainable, economical, and efficient utilization of renewable energy is a focal point of attention worldwide [1,2,3,4,5,6]. Integrated energy microgrid systems play a crucial role in the local integration of renewable energy and regional grid reliability. Therefore, constructing a multi-energy complementary microgrid system is imperative. However, since the formal definition of microgrids in 2002 [7], single-microgrid systems have faced challenges such as poor self-regulation capability and high economic costs. Multiple microgrid systems can operate in coordination, leveraging energy complementarity among microgrids to significantly enhance overall system economy and stability [8].

In the cooperative operation of multiple microgrids, the issue of fair benefit allocation among the microgrid operators (MGs) is a crucial aspect that must be addressed. Game theory offers significant advantages in studying multi-agent decision-making [9,10]. In the context of power systems, game theory is primarily categorized into non-cooperative games [11,12,13] and cooperative games [14,15,16,17,18,19,20,21]. Researchers both domestically and internationally have extensively explored the application of these game theory categories in the collaborative optimization of multi-microgrid systems. Reference [11] proposes a robust scheduling model for fair benefit allocation using non-cooperative game theory, ensuring the equitable distribution of benefits among MGs. Reference [12] explores the energy management problem between multiple microgrids and shared energy storage by establishing a non-cooperative game model, leveraging the flexible control capabilities of shared energy storage systems to optimize the economic performance of each microgrid system. Reference [13] proposes a leader–follower game model with the multi-microgrid system as the leader and power users as followers, effectively addressing the electricity trading price issue between microgrids and power users. However, because non-cooperative game theory emphasizes individual interests, it may lead to local optima and fails to ensure fairness at the system level.

Compared to non-cooperative games, cooperative games prioritize collective interests, enabling stable solutions and achieving Pareto optimality [14]. Reference [15] proposes a cross-regional cooperative game model involving a large power grid and small microgrids, resulting in profit improvement for each participant. References [16,17,18] incorporate pollution emission control in the multi-microgrid cooperation model, ensuring both low-carbon operation and economic viability of multiple microgrids. References [19,20] propose a multi-microgrid cooperative game model based on Nash bargaining theory, ensuring equitable benefit allocation and the economic efficiency of the system. Thus, it is clear that the aforementioned studies all prove that the cooperative game model is better suited for the cooperative operation of multi-microgrid systems from an economic perspective. However, it should be noted that the aforementioned studies fail to account for the effects of the uncertainties related to renewable energy output and electricity trading prices on the operation of multi-microgrid systems. Effectively managing these uncertainties will significantly improve the profits of individual microgrids and the overall system [21]. Existing studies have explored the variability in renewable energy output [22,23,24] and the fluctuations in electricity trading prices [25], but few have addressed the combined effects of these uncertainties on the cooperative operation of multi-microgrid systems. Most studies so far rely on probability density functions to generate probabilistic scenario sets to characterize these uncertainties. However, this approach struggles to accurately reflect the real-world uncertainties in system operations. Additionally, few studies explore the operation and trading of four or more energy entities within this framework. Therefore, it is crucial to conduct in-depth research on the uncertainties surrounding renewable energy output and electricity trading prices in the cooperative operation of multi-microgrid systems.

In summary, in response to the uncertainties in renewable energy output and electricity prices, as well as the issue of benefit distribution among microgrid participants in cooperative operation, the main contributions of this paper are as follows:

• Three microgrid models and one distribution system model are individually established, each of which includes different energy conversion devices and demand responses. Based on Nash bargaining theory, an energy trading model for the multi-microgrid system with multi-energy complementarity and the distribution system is developed.
• Chance constraints and robust optimization methods are incorporated into the model to mitigate the risks posed by various uncertainties, thereby enhancing the system’s security and stability.
• The alternating direction method of multipliers (ADMM) is employed to solve the Nash bargaining model for MGs and the distribution system operator (DSO), which safeguards the privacy of individuals involved in the transaction while enabling energy sharing among operators, thereby reducing operational costs.

The structure of the rest of this paper is as follows: Section 2 develops the energy trading model between MGs and the DSO; Section 3 presents the uncertainty model for MGs and the DSO; Section 4 develops the cooperative game model between multiple microgrids and the DSO using Nash bargaining theory, and solves it using the ADMM algorithm; Section 5 provides a case study; Section 6 presents a summary and outlook on the research findings.

2. MGs and DSO Electricity Trading Model

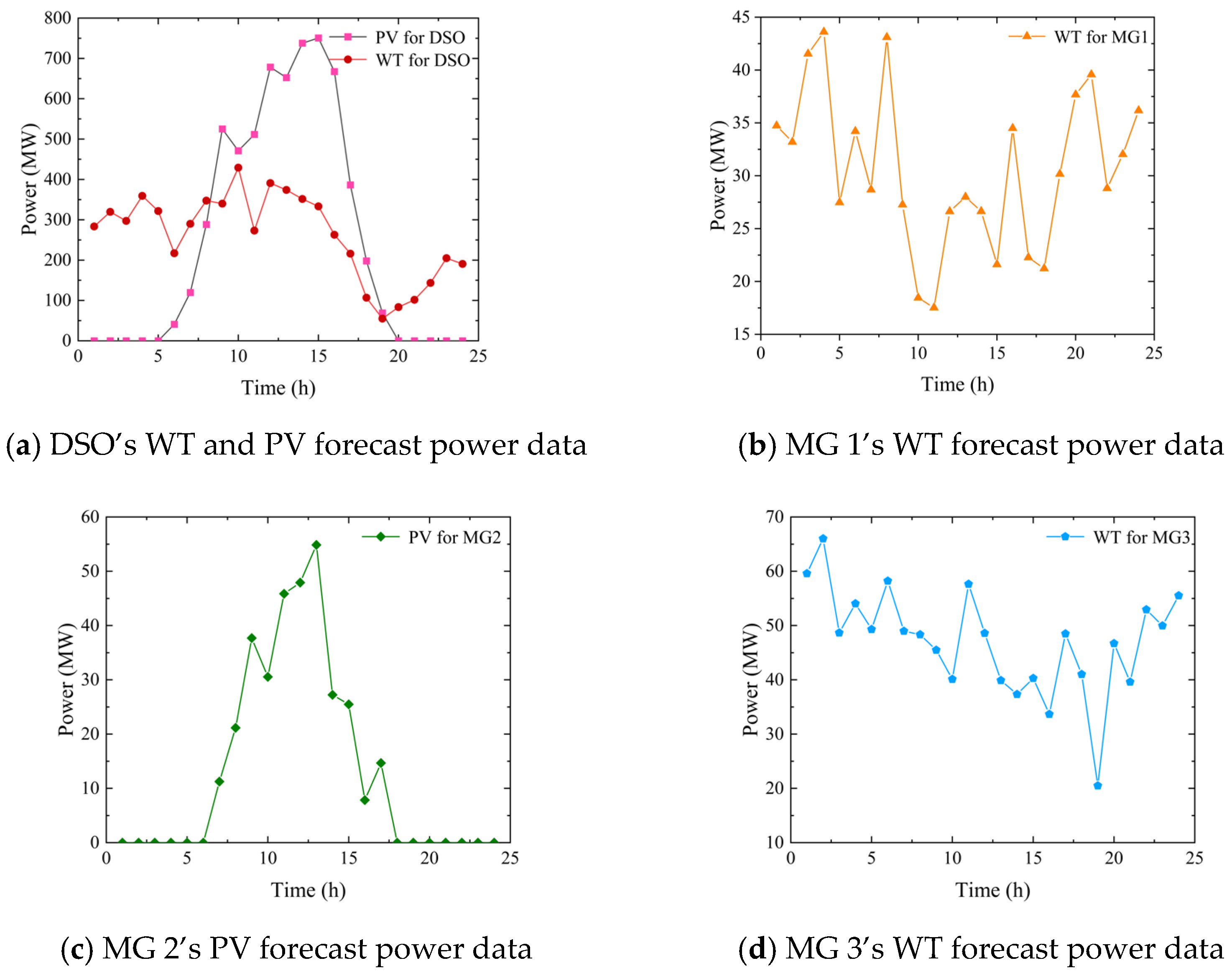
The multi-microgrid system constructed in this study comprises a DSO, a higher-level distribution network (interacting solely with the DSO for electrical energy exchange), and three MGs (MG1, MG2, MG3), as illustrated in Figure 1. It is assumed that each microgrid belongs to a different entity and independently engages in energy exchange with the DSO. Through this process, each entity satisfies its own electrical and thermal load demands. The integrated energy microgrid system involves numerous devices, with each microgrid containing different types of equipment including combined heat and power (CHP) units, wind turbines (WTs), photovoltaic (PV) arrays, thermal power (TP) units, gas boilers (GBs), and energy storage systems (ESSs). The collaborative interaction among multiple grids facilitates the efficient utilization of renewable energy and supports sustainable development.

The specific cooperation operation process is as follows: In the cooperative operation of the DSO and the three MGs, the parties are in a relationship of equality and cooperation to optimize the allocation of power resources. Each MG makes the decision to buy or sell electricity or energy storage based on the trading tariff set by the DSO and the availability of its own internal wind and light resources, equipment output status, and power demand, while the DSO adjusts the tariff and power scheduling strategy based on its own operation, the higher-level distribution grid time-of-day tariff, and the demand of each MG, striving to maximize the benefits of cooperation. Information is collected and exchanged in chronological order: The DSO and each MG collect relevant data, such as wind and light resource forecasts, load demand, storage status, and tariff information, at the beginning of each trading cycle (24-h cycle). The DSO and the MGs then jointly make decisions based on this information, with the DSO setting the trading tariff and adjusting the power flow based on feedback from the MGs (updating the trading tariff every hour), and the MGs choosing whether to buy, sell, or store power based on the tariffs, their own internal demand for electricity and heat loads, and their equipment’s operating conditions. In this process, both parties exchange information (including real-time data and historical data) and game decision-making to ensure the optimal operation of the power system and maximize the benefits of each party.

2.1. Formula Symbols in the Model

We now explain each of the formula symbols involved throughout the text. We use subscripts for indices and superscripts for descriptions. Also, the unit of each parameter and variable is given in parentheses after its definition.

Sets

$t\in T$	Set of all time periods (h), $1\le T\le 24$
$\Delta t$	Set of one-hour time periods
$i\in \left\{MG1,MG2,MG3\right\}$	Set of all operational costs, MG-exclusive equipment, and DSO operational transactions
$i\in \left\{MG1,MG2,MG3,DSO\right\}$	Set of all devices and demand responses jointly owned by MG and DSO
$n\in \left\{TP1,TP2\right\}$	Set of all TP units

Operational Parameters

$C_i$, $C^{dso}$	Total operating costs for MG i and DSO, respectively (CNY)
$C_i^{renew}$, $C_{}^{dso,renew}$	Renewable energy penalty costs for MG i and DSO, respectively (CNY)
$C_i^{chp}$, $C_i^{gb}$, $C_i^{es}$	Operating costs for CHP, GB, and ESS in MG i, respectively (CNY)
$C_i^{dr}$, $C_{}^{dso,dr}$	Demand response costs for MG i and DSO, respectively (CNY)
$C_i^{trad}$, $C_{}^{dso,trad}$	The MG i pays the cost of electricity to the DSO and the DSO pays the cost of electricity to the MG i, respectively (CNY)
$C_{}^{dso,grid}$	Costs for the DSO to interact with the higher-level grid electricity (CNY)
$C_{}^{dso,g}$, $C_{}^{dso,es}$	Operating costs for TP units and ESS in DSO, respectively (CNY)
$C_{}^{dso,penalty}$	Penalty costs for price deviations for DSO (CNY)
$C_i^{be}$, $C_i^{af}$	The operating costs of subject i before and after the cooperation, respectively (CNY)
$C_{}^{dso,0}$, $C_i^0$	Costs of DSO, MG i when operating independently, respectively, i.e., negotiation rupture point (CNY)
$C_{}^{dso,cooper}$, $C_i^{cooper}$	DSO cooperation costs and MG cooperation costs without electricity trading costs, respectively (CNY)
$C_i^{0,\ast }$, $C_{}^{dso,0,\ast }$	The operating costs of MGs before cooperation with DSO, respectively, solved by the solver (CNY)
$C_{}^{dso,cooper\ast }$, $C_i^{cooper\ast }$	The solved minimum cooperation costs for the distribution network operator and the multi-microgrid operator, respectively (CNY)
$P_{i,t}^{dso\sim mg\ast }$	Solved optimal power interactions between DSO and MG i (MW)
$P_{i,t}^{dso/mg\ast }$	Optimal electricity interaction prices between distribution grid operators and multi-microgrid operators (CNY/MWh)

Renewable energy parameters

${\theta }^{renew}$	Renewable energy penalty coefficient (CNY/MW)
$P_{i,t}^{wt,cur}$, $P_{i,t}^{pv,cur}$, $P_t^{dso,wt,cur}$, $P_t^{dso,pv,cur}$	WT and PV abandonment for MG i and DSO, respectively (MW)
$P_t^{wt}$, $P_t^{pv}$	The outputs of WT and PV in subject i at time t, respectively (MW)
$P_{}^{wt,max}$, $P_{}^{pv,max}$	The predicted output values of WT and PV in subject i at time t, respectively (MW)

CHP parameters

${\theta }_i^{chp}$	Unit loss costs of CHP in MG i (CNY/m3)
$V_{i,t}^{chp,gas}$	Gas intake of CHP in MG i at time t (m3)
$P_{i,t}^{chp,e}$, $P_{i,t}^{chp,h}$	The generation and heating power of the CHP in MG i at time t, respectively (MW)
$H^{gas}$	Calorific value of natural gas combustion (MW/m3)
$P_i^{chp,e,max}$, $P_i^{chp,h,max}$	The upper bounds on the power generation and heat generation of CHP in MG i, respectively (MW)

GB parameters

${\theta }_i^{gb}$	Unit loss costs of GB in MG i (CNY/m3)
$V_{i,t}^{gb,gas}$	Gas intake to the GB in MG i at time t (m3)
$P_{i,t}^{gb,h}$	Heat generation power of GB in MG i at time t (MW)
$P_i^{gb,h,max}$	Upper limit of heat generation power of GB in MG i (MW)

ESS parameters

${\theta }_i^{es},{\theta }_{}^{dso,es}$	Unit loss costs of ESS in MG i and DSO (CNY/MW)
$P_{i,t}^{es,char},P_{i,t}^{es,dis},P_t^{dso,es,char},P_t^{dso,es,dis}$	Charging and discharging power of ESS in MG i and DSO, respectively (MW)
$S_{i,t}^{es,cap}$	Capacity of storage device i at time t (MWh)
$S_i^{es,cap,max}, S_i^{es,cap,min}$	Upper and lower limits of the capacity of ESS i, respectively (MWh)
$P_i^{es,char,max},P_i^{es,dis,max}$	The maximum charging and discharging power of ESS i, respectively (MW)

TP unit parameters

${\theta }_n^{dso,g}$	Unit operating cost of the nth TP unit (CNY/MW)
$P_{n,t}^{dso,g}$	Output of the nth TP unit at time t (MW)
$P_n^{dso,g,max}$, $P_n^{dso,g,min}$	The upper and lower limits of the output electric power of TP unit n, respectively (MW)
$P_n^{dso,g,up}$, $P_n^{dso,g,down}$	The maximum upward climb and downward climb of TP unit n output electric power, respectively (MW)

Demand response parameters

${\theta }^{cut}$, ${\theta }^{tran}$	Unit penalty costs for curtailable load, transferable load, respectively (CNY/MW)
$P_{i,t}^{eload,cut}$, $P_{i,t}^{eload,tran}$, $P_{i,t}^{hload,cut}$, $P_{i,t}^{hload,tran}$	Curtailable electrical loads, transferable electrical loads, curtailable thermal loads, and transferable thermal loads in MG i, respectively (MW)
$P_t^{dso,eload,cut}$, $P_t^{dso,eload,tran}$	Curtailable electric loads, transferable electric loads in DSO, respectively (MW)
$P_{i,t}^{eload,pre}$, $P_{i,t}^{eload}$	The electrical loads of subject i before and after the demand response at moment t, respectively (MW)
$P_{i,t}^{hload,pre}$, $P_{i,t}^{hload}$	The heat loads of MG i before and after the demand response at moment t, respectively (MW)

Technology parameters

$\lambda$	Price deviation coefficient
$\nu$	Electricity price uncertainty adjustment parameters (constant)
$\epsilon$	confidence level (constant)
${\eta }^{char}$, ${\eta }^{dis}$	Charging and discharging efficiency of the storage device, respectively (constant)
${\eta }_{}^{chp,e}$, ${\eta }_{}^{chp,h}$	The power and heat generation efficiencies of CHP, respectively (constant)
${\eta }_{}^{gb,h}$	Heat generation efficiency of GB (constant)
${\gamma }_{}^{cut,e}$, ${\gamma }_{}^{tran,e}$	The proportions of the curtailable and transferable electric loads of subject i to the total electric load at moment t, respectively (constant)
${\gamma }_{}^{cut,h}$, ${\gamma }_{}^{tran,h}$	The ratios of curtailable and transferable heat loads of MG i to the total heat load at moment t, respectively (constant)
$\Omega$, $\mho$	Maximum number of iterations (constant)

Algorithmic parameters

${\varphi }_t^e$, ${\phi }_t^e$	Lagrange multiplier
${\omega }_{}^e$, ${\tau }_{}^e$	Penalty factor

Function name

$F$	Probability cumulative distribution function
${\psi }^{-1}\left(\epsilon \right)$, ${\Psi }^{-1}\left(\epsilon \right)$	Standard normal distribution inverse function
${\left({\delta }_{}^{wt}\right)}^2$, ${\left({\partial }_{}^{wt}\right)}^2$${\left({\delta }_{}^{pv}\right)}^2$, ${\left({\partial }_{}^{pv}\right)}^2$	The variance of WT and PV, respectively

Continuous variables

Electricity trading variables

$P_{i,t}^{mg}$, $P_{i,t}^{dso}$	The traded power of MG i and DSO at time t, respectively (MW)
$P_{i,t}^{mg,pri}$, $P_{i,t}^{dso,pri}$	The transaction tariffs of MG i and DSO at moment t, respectively (CNY/MWh)
$P_t^{dso,buy,pri}$, $P_t^{dso,sell,pri}$	The unit price of electricity purchased from the higher grid by the DSO at time t and the unit price of electricity sold, respectively (CNY/MWh)
$P_t^{dso,buy}$, $P_t^{dso,sell}$	The amount of electricity purchased and sold by the DSO to the higher grid at time t, respectively (MW)
$P_i^{mg,max}$, $P_i^{mg,min}$	The upper and lower bounds on the amount of electricity traded by MG i with the DSO at moment t, respectively (MW)
$P_i^{dso,max}$, $P_i^{dso,min}$	The upper and lower bounds on the amount of electricity traded between DSO and MG i at moment t, respectively (MW)
$P_{}^{dso,buy,max}$, $P_{}^{dso,sell,max}$	The upper limits of the power purchased and sold by the DSO to the higher grid at time t, respectively (MW)

Auxiliary Variables

$Y_t$	Variables for relaxation the problem
$\rho$	Variables used to linearize the robust problem
$P_{i,t}^{dso\sim mg}$, $P_{i,t}^{dso/mg}$	Variables that decouple the problem (MW)

Dual variables

$\alpha$, $\beta$

Uncertainty time variables

Binary and integer variables

Battery variables

$X_{i,t}^{es,char}$	A state of 1 for ESS i indicates charging at moment t, otherwise 0
$X_{i,t}^{es,dis}$	A state of 1 for ESS i indicates discharging at moment t, otherwise 0

Trading Variables

$X_t^{dso,buy}$	A status of 1 indicates that the DSO purchases power from the higher grid, otherwise 0
$X_t^{dso,sell}$	A status of 1 indicates that the DSO sells power to the higher grid, otherwise 0

2.2. MG Model

In addition to coordinating devices within their respective areas, each microgrid must engage in electricity trading with the DSO to meet its own electric and thermal load requirements. The specific model and constraints are detailed below.

$$\mathit{min}{C}_i=\mathit{min}\left(C_i^{renew}+C_i^{chp}+C_i^{gb}+C_i^{es}+C_i^{dr}+C_i^{trad}\right)$$

(1)

The specific model is as follows:

$$\left\{\begin{array}{l}{C}_i^{renew}={\theta }^{renew}{\displaystyle \sum _{t=1}^T}\left(P_{i,t}^{wt,cur}+P_{i,t}^{pv,cur}\right)\\ C_i^{chp}={\theta }_i^{chp}{\displaystyle \sum _{t=1}^T}{V}_{i,t}^{chp,gas}\\ C_i^{gb}={\theta }_i^{gb}{\displaystyle \sum _{t=1}^T}{V}_{i,t}^{gb,gas}\\ C_i^{es}={\theta }_i^{es}{\displaystyle \sum _{t=1}^T}\left(P_{i,t}^{es,char}+P_{i,t}^{es,dis}\right)\\ C_i^{dr}={\theta }^{cut}{\displaystyle \sum _{t=1}^T}\left(P_{i,t}^{eload,cut}+P_{i,t}^{hload,cut}\right)+{\theta }^{tran}{\displaystyle \sum _{t=1}^T}\left(\left|P_{i,t}^{eload,tran}\right|+\left|P_{i,t}^{hload,tran}\right|\right)\\ C_i^{trad}={\displaystyle \sum _{t=1}^T}\left(P_{i,t}^{mg}{P}_{i,t}^{mg,pri}\right)\mathrm{\Delta }t\end{array}\right.$$

(2)

2.3. DSO Model

$$\mathit{min}{C}^{dso}=\mathit{min}\left(C_{}^{dso,renew}+C_{}^{dso,grid}+C_{}^{dso,g}+C_{}^{dso,es}+C_{}^{dso,dr}+C_{}^{dso,trad}+C_{}^{dso,penalty}\right)$$

(3)

The specific model is as follows:

$$\left\{\begin{array}{l}{C}_{}^{dso,renew}={\theta }^{renew}{\displaystyle \sum _{t=1}^T}\left(P_t^{dso,wt,cur}+P_t^{dso,pv,cur}\right)\\ C_{}^{dso,grid}={\displaystyle \sum _{t=1}^T}\left(P_t^{dso,buy,pri}{P}_t^{dso,buy}-P_t^{dso,sell,pri}{P}_t^{dso,sell}\right) \mathrm{\Delta }t\\ C_{}^{dso,g}={\displaystyle \sum _{t=1}^T}{\displaystyle \underset{n\notin \varphi }{{\displaystyle \sum _{n=1}^N}}}{\theta }_n^{dso,g}{P}_{n,t}^{dso,g}\\ C_{}^{dso,es}={\theta }_{}^{dso,es}{\displaystyle \sum _{t=1}^T}\left(P_t^{dso,es,char}+P_t^{dso,es,dis}\right)\\ C_{}^{dso,dr}={\theta }^{cut}{\displaystyle \sum _{t=1}^T}{P}_t^{dso,eload,cut}+{\theta }^{tran}{\displaystyle \sum _{t=1}^T}\left|P_t^{dso,eload,tran}\right|\\ C_{}^{dso,trad}={\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^N}\left(P_{i,t}^{dso}{P}_{i,t}^{dso,pri}\right)\mathrm{\Delta }t\\ C_{}^{dso,penalty}=\mathit{max}{\displaystyle \sum _{t=1}^T}\lambda \left|P_t^{dso,buy}-P_t^{dso,sell}\right| \mathrm{\Delta }t\end{array}\right.$$

(4)

2.4. System Equipment Model

The system equipment maintains functions such as energy production and exchange for the microgrids within each campus. Different types of equipment serve distinct roles in this process. The following describes the models of the system equipment included in the microgrid:

2.4.1. Renewable Energy Unit

Renewable energy units are devices that utilize renewable resources for energy production, thereby promoting green and sustainable development.

$$\left\{\begin{array}{c}0\le P_t^{wt}\le P_{}^{wt,max}\\ 0\le P_t^{pv}\le P_{}^{pv,max}\end{array}\right.$$

(5)

2.4.2. ESS

ESSs are devices that store electrical energy when it is needed and release it when it is not, playing a crucial role in balancing energy supply and demand within systems.

$$\left\{\begin{array}{c}{S}_{i,t+1}^{es,cap}=S_{i,t}^{es,cap}+{\eta }^{char}{P}_{i,t}^{es,char}-{\displaystyle \frac{P_{i,t}^{es,dis}}{{\eta }^{dis}}}\\ \hspace{1em}S\hfill \\ i\\ es,cap,mi{n_{i,t}^{es,cap}}_i^{es,cap,max}\\ 0\le P_{i,t}^{es,char}\le X_{i,t}^{es,char}{P}_i^{es,char,max}\\ 0\le P_{i,t}^{es,dis}\le X_{i,t}^{es,dis}{P_i^{es,dis,max}}_{X_{i,t}^{es,char}+X_{i,t}^{es,dis}\le 1}^{S_{i,1}^{es,cap}=S_{i,24}^{es,cap}\{}\end{array}\right.$$

(6)

2.4.3. TP

TP units are devices that convert fossil fuels into electrical energy. They are characterized by their efficiency and stability in electricity generation.

$$\left\{\begin{array}{c}P\\ n_{dso,g,mi{n_{n,t}^{dso,g}}_n^{dso,g,max}}^{P_n^{dso,g,down}\le P_{n,t}^{dso,g}-P_{n,t-1}^{dso,g}\le P_n^{dso,g,up}}\end{array}\right.$$

(7)

2.4.4. CHP

CHP units refer to devices that utilize the heat energy from fuel to generate both electricity and heat in the form of hot water or steam, significantly enhancing energy efficiency.

$$\left\{\begin{array}{l}{P}_{i,t}^{chp,e}={\eta }_{}^{chp,e}{H}^{gas}{V}_{i,t}^{chp,gas}\\ P_{i,t}^{chp,h}={\eta }_{}^{chp,h}{H}^{gas}{V}_{i,t}^{chp,gas}\\ 0\le P_{i,t}^{chp,e}\le P_i^{chp,e,max}\\ 0\le P_{i,t}^{chp,h}\le P_i^{chp,h,max}\end{array}\right.$$

(8)

2.4.5. GB

GBs are devices that generate heat by burning natural gas as fuel, providing heating services.

$$\left\{\begin{array}{l}{P}_{i,t}^{gb,h}={\alpha }_{}^{gb,h}{H}^{gas}{V}_{i,t}^{gb,gas}\\ 0\le P_{i,t}^{gb,h}\le P_i^{gb,h,max}\end{array}\right.$$

(9)

2.5. Demand Response Model

Demand response models can achieve supply–demand balance by adjusting users’ energy consumption behaviors during different time periods. Flexible loads can be categorized into flexible electrical loads and flexible thermal loads, as detailed in the following models:

2.5.1. Flexible Electrical Load

Flexible electrical load refers to the capability to adjust power consumption flexibly according to the system’s electricity demand.

$$\left\{\begin{array}{l}{P}_{i,t}^{eload}=P_{i,t}^{eload,pre}-P_{i,t}^{eload,cut}+P_{i,t}^{eload,tran}\\ 0\le P_{i,t}^{eload,cut}\le {\gamma }_{}^{cut,e}{P}_{i,t}^{eload,pre}\\ -{\gamma }_{}^{tran,e}{P}_{i,t}^{eload,pre}\le P_{i,t}^{eload,tran}\le {\gamma }_{}^{tran,e}{P}_{i,t}^{eload,pre}\\ {\displaystyle \sum _{t=1}^T}{P}_{i,t}^{eload,tran}=0\end{array}\right.$$

(10)

2.5.2. Flexible Thermal Load

Flexible thermal load refers to the capability to adjust heat consumption flexibly according to the system’s thermal demand.

$$\left\{\begin{array}{l}{P}_{i,t}^{hload}=P_{i,t}^{hload,pre}-P_{i,t}^{hload,cut}+P_{i,t}^{hload,tran}\\ 0\le P_{i,t}^{hload,cut}\le {\gamma }_{}^{cut,h}{P}_{i,t}^{hload,pre}\\ -{\gamma }_{}^{tran,h}{P}_{i,t}^{hload,pre}\le P_{i,t}^{hload,tran}\le {\gamma }_{}^{tran,h}{P}_{i,t}^{hload,pre}\\ {\displaystyle \sum _{t=1}^T}{P}_{i,t}^{hload,tran}=0\end{array}\right.$$

(11)

3. Modeling Uncertainty for MGs and DSO

3.1. Electricity Market Price Uncertainty Model

In the context of transactions between the DSO and the electricity market, there are numerous sources of uncertainty, with electricity price volatility being a particularly significant issue. This price uncertainty directly affects the scheduling decisions and operational costs of the various stakeholders involved. To address this challenge, this study employs robust optimization techniques [26], which characterize uncertainty through the use of confidence intervals for the uncertain variables when the probability distribution functions are unknown. This approach enables the consideration of extreme market price scenarios during the trading process and seeks to derive an optimal solution.

To facilitate solving the Min–Max problem of the final term in Equation (3), an auxiliary variable $Y_t$ is introduced to relax the inner Max problem as follows:

$$\left\{\begin{array}{l}\mathit{max}{\displaystyle \sum _{t\in T}}\lambda \left|P_t^{dso,buy}-P_t^{dso,sell}\right|Y_t\\ \begin{array}{cc}s.t.& {\displaystyle \sum _{t\in T}}{Y}_t\le \nu \\ & 0\le Y_t\le 1\end{array}\end{array}\right.$$

(12)

Based on strong duality theory, the Min–Max problem can be converted into the following Min problem:

$$\left\{\begin{array}{l}\mathit{min}\left({\displaystyle \sum _{t=1}^T}\beta +\alpha \nu \right)\\ \begin{array}{cc}s.t.& \alpha \ge 0\\ & \beta \ge 0\\ & \rho \ge 0\\ & \alpha +\beta \ge \lambda \rho \\ & -\rho \le P_t^{dso,buy}-P_t^{dso,sell}\le \rho \end{array}\end{array}\right.$$

(13)

After transformation, the final objective function of Equation (3) is

$$\mathit{min}{C}^{dso}=\mathit{min}\left(C_{}^{dso,renew}+C_{}^{dso,grid}+C_{}^{dso,g}+C_{}^{dso,es}+C_{}^{dso,dr}+C_{}^{dso,trad}+{\displaystyle \sum _{t=1}^T}\beta +\alpha \nu \right)$$

(14)

3.2. Modeling Uncertainty in Renewable Energy Output

The integration of renewable energy not only helps the power grid reduce carbon emissions but also mitigates wind and solar curtailment, thereby promoting sustainable energy development. However, as new energy sources become extensively integrated into the power system, they can impact the operators’ ability to maintain the system’s power balance [27]. Moreover, the uncertainty in renewable energy output can directly affect the economic operation of the power grid, making it crucial to consider the impact of this uncertainty on microgrids. Based on this, this paper adopts the chance-constrained method to model the uncertainty in renewable energy output, represented by WT and PV, within the system. Taking the DSO as a case, it can be expressed as

$$\left.\mathit{Pr}\left\{\left(\begin{array}{c}{\displaystyle \sum _{n=1}^N}{P}_{n,t}^{dso,g}+P_t^{dso,buy}+P_t^{dso,es,dis}+P_t^{dso,wt}+P_t^{dso,pv}\hfill \\ +{\displaystyle \sum _{n=1}^N}{P}_{i,t}^{dso}-P_t^{dso,sell}-P_t^{dso,es,char}-P_t^{dso,eload}\hfill \end{array}\right)\right.\ge 0\right\}\ge \epsilon$$

(15)

Assuming the cumulative distribution function F of a random variable, Equation (15) can be further transformed into

$$\begin{gathered} {\displaystyle {\sum }_{n=1}^N}{P}_{n,t}^{dso,g}+P_t^{dso,buy}+P_t^{dso,es,dis}+P_t^{dso,wt}+P_t^{dso,pv}+{\displaystyle {\sum }_{n=1}^N}{P}_{i,t}^{dso}-P_t^{dso,sell}- \\ {P}_t^{dso,es,char}-P_t^{dso,eload}\ge F^{-1}\left(\epsilon \right) \end{gathered}$$

(16)

Based on the calculation method of F [28], the power balance constraint of the DSO mentioned above is transformed into

$$\begin{gathered} {\displaystyle \sum _{n=1}^N}{P}_{n,t}^{dso,g}+P_t^{dso,buy}+P_t^{dso,es,dis}+P_t^{dso,wt}+P_t^{dso,pv}+{\displaystyle \sum _{n=1}^N}{P}_{i,t}^{dso}-P_t^{dso,sell} \\ -P_t^{dso,es,char}-P_t^{dso,eload}\ge {\psi }^{-1}\left(\epsilon \right)\sqrt{{\left({\delta }_{}^{wt}\right)}^2+{\left({\delta }_{}^{pv}\right)}^2} \end{gathered}$$

(17)

Due to the similarity in the transformation method of the power balance constraints for each microgrid, which aligns closely with Equation (17), it is omitted here for brevity and can be expressed as:

$$P_{i,t}^{chp,e}+P_{i,t}^{es,dis}+P_{i,t}^{wt}+P_{i,t}^{pv}+P_{i,t}^{mg}-P_{i,t}^{es,char}-P_{i,t}^{eload}\ge {\Psi }^{-1}\left(\epsilon \right)\sqrt{{\left({\partial }_{}^{wt}\right)}^2+{\left({\partial }_{}^{pv}\right)}^2}$$

(18)

3.3. System Constraints

3.3.1. DSO and MG Electric Power Balance Constraints

The electric power balance constraints for DSOs and MGs are demonstrated in Equations (17) and (18), respectively.

3.3.2. MG Thermal Power Balance Constraint

$$P_{i,t}^{chp,h}+P_{i,t}^{gb,h}=P_{i,t}^{hload}$$

(19)

3.3.3. DSO and MG Electricity Interaction Constraint3

$$\left\{\begin{array}{c}P\\ i_{mg,mi{n_{i,t}^{mg}}_i^{mg,max}}^{P_i^{dso,mi{n_{i,t}^{dso}}_i^{dso,max}}}\end{array}\right.$$

(20)

3.3.4. DSO and Upper-Level Grid Power Interaction Constraint

$$\left\{\begin{array}{l}0\le P_t^{dso,sell}\le X_t^{dso,sell}{P}_{}^{dso,sell,max}\\ 0\le P_t^{dso,buy}\le X_t^{dso,buy}{P}_{}^{dso,buy,max}\\ X_t^{dso,sell}+X_t^{dso,buy}\le 1\end{array}\right.$$

(21)

4. Cooperative Game Model and Solution for MGs and DSO

4.1. Nash Bargaining Model

To reduce operational costs for each entity, cooperation in energy trading between MGs and the DSO is essential. The Nash bargaining model, a pivotal component of cooperative game theory, ensures that while enhancing individual interests, overall benefits are not compromised [29]. Therefore, this paper adopts Nash bargaining theory to settle the operational costs after cooperation between MGs and DSO, formulated as follows:

$$\left\{\begin{array}{l}\mathit{max}{\displaystyle \prod _{i=1}^N}\left(C_i^{be}-C_i^{af}\right)\\ s.t.\hspace{1em}{C}_i^{be}\ge C_i^{af}\end{array}\right.$$

(22)

4.2. Cooperative Game Model of MGs and DSO Based on Nash Bargaining Theory

Based on the mathematical model of Nash bargaining theory, the cooperative game model between MGs and DSO proposed in this paper can be formulated as follows:

$$\left\{\begin{array}{l}\mathit{max}\left(C_{}^{dso,0}-C^{dso}\right){\displaystyle \prod _{i=1}^N}\left(C_i^0-C_i\right)\\ s.t\hspace{1em}\begin{array}{l}{C}_{}^{dso,0}\ge C^{dso}\\ C_i^0\ge C_i\end{array}\end{array}\right.$$

(23)

Due to the presence of the product term between the variables of electricity trading volume and electricity trading price in Equation (23), it constitutes a non-convex and non-linear optimization problem, which complicates the direct derivation of the optimal solution. Consequently, it needs to be equivalently transformed into two convex optimization subproblems (subproblem 1: minimization of cooperation costs; subproblem 2: maximization of electricity trading revenues), tackled sequentially. The specific transformation process is detailed in reference [25].

4.2.1. Cooperation Cost Minimization Problem

When MGs engage in electricity trading with the DSO, the purchasing price for electricity by the buyer equals the selling price by the seller. Therefore, in cooperative operations, the costs of electricity trading cancel each other out when accumulated. According to the principle of inequalities, Equation (23) can be equivalently transformed as follows:

$$\left\{\begin{array}{l}\mathit{min}\left\{\left.C_{}^{dso,cooper}+{\displaystyle \sum _{i=1}^N}{C}_i^{cooper}\right\}\right.\\ C_{}^{dso,cooper}=C^{dso}-C_{}^{dso,trad}\\ C_i^{cooper}=C_i-C_i^{trad}\\ \begin{array}{cc}s.t.& \left(2\right)\left(4\right)-\left(11\right)\left(13\right)\left(17\right)-\left(21\right)\end{array}\end{array}\right.$$

(24)

4.2.2. Electricity Trading Profit Maximization Problem

For computational convenience, Equation (23) is equivalently transformed into the following equation:

$$\left\{\begin{array}{l}\mathit{min}\left\{\left.-\left[\mathit{ln}\left(C_{}^{dso,0,\ast }-C_{}^{dso,cooper\ast }-C_{}^{dso,trad}\right)+\mathit{ln}{\displaystyle \sum _{i=1}^N}\left(C_i^{0,\ast }-C_i^{cooper\ast }-C_i^{trad}\right)\right]\right\}\right.\\ \begin{array}{cc}s.t.& \begin{array}{c}{C}_{}^{dso,0,\ast }-C_{}^{dso,cooper\ast }-C_{}^{dso,trad}\ge 0\\ C_i^{0,\ast }-C_i^{cooper\ast }-C_i^{trad}\ge 0\\ \left(2\right)\left(4\right)-\left(11\right)\left(13\right)\left(17\right)-\left(21\right)\end{array}\end{array}\end{array}\right.$$

(25)

4.3. Solving Cooperative Game Models Between MGs and DSO Based on Nash Bargaining

Due to the convex nature of the objective functions and constraints in both the cost minimization and revenue maximization problems associated with cooperative cooperation, the ADMM distributed algorithm exhibits strong convergence and robustness, commonly applied to solve separable convex optimization problems [30]. Therefore, this paper employs the ADMM distributed algorithm for distributed solving, with the specific solution process illustrated in Figure 2.

4.3.1. ADMM-Based Solution of the Cooperation Cost Minimization Problem

Considering that Equation (24) contains coupled variables representing the power exchange between various entities, an auxiliary variable $P_{i,t}^{dso\sim mg}$ is introduced to decouple them. This can be expressed as follows:

$$P_{i,t}^{dso\sim mg}=P_{i,t}^{dso}=P_{i,t}^{mg}$$

(26)

On the basis of the above conditions, according to the ADMM distributed algorithm principle, the Lagrange multiplier ${\varphi }_t^e$ and penalty factor ${\omega }_{}^e$ are introduced, and the augmented Lagrange function for subproblem 1 is constructed. The distributed optimal operation model of DSO is as follows:

$$\left\{\begin{array}{l}\mathit{min}\left\{\left.C_{}^{dso,cooper}+{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^N}{\varphi }_t^e\left(P_{i,t}^{dso\sim mg}-P_{i,t}^{dso}\right)+{\displaystyle \sum _{t=1}^T}{\displaystyle \frac{{\omega }_{}^e}{2}}{‖P_{i,t}^{dso\sim mg}-P_{i,t}^{dso}‖}_2^2\right\}\right.\\ \begin{array}{cc}s.t.& \left(20\right)—\left(21\right)\end{array}\end{array}\right.$$

(27)

The distributed optimization operation model of MGs is as follows:

$$\left\{\begin{array}{l}\mathit{min}\left\{\left.C_i^{cooper}+{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^N}{\varphi }_t^e\left(P_{i,t}^{dso\sim mg}-P_{i,t}^{mg}\right)+{\displaystyle \sum _{t=1}^T}{\displaystyle \frac{{\omega }_{}^e}{2}}{‖P_{i,t}^{dso\sim mg}-P_{i,t}^{mg}‖}_2^2\right\}\right.\\ \begin{array}{cc}s.t.& \left(20\right)\end{array}\end{array}\right.$$

(28)

The above two distributed optimization operation models are solved by the ADMM distributed algorithm for subproblem 1, where the distributed iterative formulation is (29), and when Equation (30) is iterated to no more than the error $\Omega$, the minimum co-operation cost of the DSO’s $C_{}^{dso,cooper\ast }$ and the MGs’ $C_i^{cooper\ast }$ is solved, and the amount of power interaction $P_{i,t}^{dso\sim mg\ast }$ between the DSO and the MGs can be obtained.

$${\varphi }_{t+1}^e={\varphi }_t^e+{\omega }_{}^e\left(P_{i,t}^{dso\sim mg}-P_{i,t}^{mg}\right)$$

(29)

$$\mathit{max}\left\{{\displaystyle \sum _{t=1}^T}{‖P_{i,t}^{dso~mg}-P_{i,t}^{mg}‖}_2^2\right\}\le \Omega$$

(30)

4.3.2. ADMM-Based Solution of the Electricity Trading Profit Maximization Problem

Similar to the solution method for subproblem 1, the electricity trading prices between various entities are coupled variables, and the auxiliary variable $P_{i,t}^{dso/mg}$ needs to be introduced to decouple them, as shown in the following equation:

$$P_{i,t}^{dso/mg}=P_t^{dso,pri}=P_{i,t}^{mg,pri}$$

(31)

On this basis, based on the ADMM distributed algorithm principle, the Lagrange multiplier ${\phi }_t^e$ and penalty factor ${\tau }_{}^e$ are introduced, and the augmented Lagrange function for subproblem 2 is constructed. The distributed optimal operation model of DSO is as follows:

$$\left\{\begin{array}{l}\mathit{min}\left\{\left.-\left[\begin{array}{c}{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^N}{\phi }_t^e\left(P_{i,t}^{dso/mg}-P_{i,t}^{dso,pri}\right)+\mathit{ln}\left(C_{}^{dso,0,\ast }-C_{}^{dso,cooper\ast }-P_{i,t}^{dso,pri}{P}_{i,t}^{dso\sim mg\ast }\right)\\ +{\displaystyle \sum _{t=1}^T}{\displaystyle \frac{{\tau }_{}^e}{2}}{‖P_{i,t}^{dso/mg}-P_{i,t}^{dso,pri}‖}_2^2\hfill \end{array}\right]\right\}\right.\\ \begin{array}{cc}s.t.& C_{}^{dso,0,\ast }-C_{}^{dso,cooper\ast }-P_{i,t}^{dso,pri}{P}_{i,t}^{dso\sim mg\ast }\ge 0\end{array}\end{array}\right.$$

(32)

The distributed optimization operation model of MGs is as follows:

$$\left\{\begin{array}{l}\mathit{min}\left\{\left.-\left[\begin{array}{c}{\displaystyle \sum _{t=1}^T}{\displaystyle \sum _{i=1}^N}{\phi }_t^e\left(P_{i,t}^{dso/mg}-P_{i,t}^{mg,pri}\right)+\mathit{ln}\left(C_i^{0,\ast }-C_i^{cooper\ast }-P_{i,t}^{mg,pri}{P}_{i,t}^{dso\sim mg\ast }\right)\\ +{\displaystyle \sum _{t=1}^T}{\displaystyle \frac{{\tau }_{}^e}{2}}{‖P_{i,t}^{dso/mg}-P_{i,t}^{mg,pri}‖}_2^2\hfill \end{array}\right]\right\}\right.\\ \begin{array}{cc}s.t.& C_i^{0,\ast }-C_i^{cooper\ast }-P_{i,t}^{mg,pri}{P}_{i,t}^{dso\sim mg\ast }\ge 0\end{array}\end{array}\right.$$

(33)

The two distributed optimization models solve subproblem 2 based on the distributed iteration Formula (34). When Equation (35) converges to a value not greater than $\mho$, the electricity exchange price $P_{i,t}^{dso/mg\ast }$ between the distribution system operator and multi-microgrid operators is determined.

$${\phi }_{t+1}^e={\phi }_t^e+{\tau }_{}^e\left(P_{i,t}^{dso/mg}-P_{i,t}^{mg,pri}\right)$$

(34)

$$\mathit{max}\left\{{\displaystyle \sum _{t=1}^T}{‖P_{i,t}^{dso/mg}-P_{i,t}^{mg,pri}‖}_2^2\right\}\le \mho$$

(35)

5. Case Study

5.1. Case Setting

This paper examines the energy exchange between a DSO and three MGs as a research scenario to validate the proposed method. The DSO is equipped with WTs and PV arrays, MG1 is equipped with WTs, MG2 is equipped with PV arrays, and MG3 is equipped with WTs. The energy data used in this paper are all from historical data of a certain northern region. The WT and PV forecast power data for the DSO and each MG are provided in Appendix A. The confidence level for the uncertainty in renewable energy output is set to 0.80, and the initial parameters of the ADMM distributed algorithm, electricity price uncertainty parameters, and microgrid interaction pricing are referenced in [25]. In the MATLAB environment, subproblem 1 is solved using the CPLEX solver via the Yalmip toolbox, while subproblem 2 is solved using the Mosek solver via the Yalmip toolbox.

5.2. Analysis of Simulation Results

5.2.1. Algorithm Convergence Analysis

In this study, we employ the ADMM distributed algorithm to solve subproblems 1 and 2 in a distributed manner. The specific iteration convergence details are illustrated in Figure 3 to Figure 4.

Figure 3 illustrates the iterative convergence results of subproblem 1, where the ADMM distributed algorithm achieves convergence for both microgrids and the DSO after 30 iterations, taking 95 s. Figure 4 depicts the iterative convergence results of subproblem 2, with convergence achieved for all microgrids and the DSO after only nine iterations, taking 27 s using the ADMM distributed algorithm. These results demonstrate the effective convergence performance of the ADMM algorithm in solving the aforementioned problems, requiring only the exchange variables of electricity among microgrid entities, thereby significantly preserving their privacy during computation.

5.2.2. Algorithm Convergence Analysis Multi-Subject Operation Optimization Result Analysis

Figure 5 presents the results of electricity transactions between the DSO and MGs under consideration of multiple uncertainties. Figure 5a illustrates the results of power exchange between the distribution system and the multiple microgrids. Negative values indicate that MG i is purchasing electricity from the distribution system, suggesting that all three microgrids are operating as electricity-deficient systems. In MG 1, the electricity purchase is lowest between 17:00 and 22:00, as this period is characterized by lower load demand and higher WT generation. In MG 2, the electricity purchase is relatively uniform and high during most time periods, except between 20:00 and 21:00. This is because the energy consumption load in this microgrid significantly exceeds the output of each unit, and the PV arrays only generate power between 7:00 and 17:00. In MG 3, electricity purchase is lower during the periods from 1:00 to 4:00, 7:00 to 8:00, 11:00 to 14:00, and 17:00 to 23:00, due to high WT generation or low load demand during these times.

Figure 5b illustrates the electricity power transaction prices between the DSO and MGs under varying uncertainties. The results show that the electricity transaction prices of the microgrids are similar across different time periods and fall within the range of prices for buying and selling electricity from the main grid. Upon closer inspection of the enlarged portions in the figure, it is evident that the electricity transaction prices vary among different microgrids during each time period. The negotiation between multiple microgrids and the distribution network follows Nash bargaining, resulting in electricity transactions at prices slightly higher than those set by the main grid, thereby significantly enhancing the benefits for all involved entities.

The energy optimization results for the distribution network and multiple microgrids are presented in Figure 6 and Figure 7. Each MG participates in the cooperative energy optimization with the DSO, while ensuring its own energy optimization. The DSO determines the electricity trading price based on the renewable energy output and their electricity load for the day. Each MG follows the principle of “buying less when prices are high and more when prices are low” to maximize cost reduction and make optimal energy purchases. Taking MG 1 as an example, it mainly relies on WTs for electricity generation, GBs for heat, and CHP for both heating and electricity generation. When electricity prices are high, MG 1 reduces electricity purchases, ESSs discharge as needed, and the use of CHP is minimized, with heating primarily provided by GBs. When electricity prices are low, MGs increase electricity purchases, and ESSs charge as needed. Heating is mainly provided by CHP, or jointly by both CHP and GBs. The energy optimization patterns for other microgrids and the distribution system follow the same principles and will not be elaborated here.

From the costs and benefits of the DSO and MGs presented in

Table 1. Cost and benefits of DSO and MGs.

Cost Type	MG1/CNY	MG2/CNY	MG3/CNY	DSO/CNY	Alliance/CNY
Breakpoint cost	3,234,425.3	4,345,234.1	2,173,793.8	4,358,208.7	14,111,661.9
Cooperation cost	1,511,536.4	1,891,680.3	646,485.7	6,904,925.1	10,954,627.5
Payment cost	−802,914.6	−1,033,190.5	−737,019.8	2,572,973.6	−151.3
Negotiation termination cost	2,314,451.0	2,924,870.8	1,383,505.5	4,331,951.5	10,954,778.8
Benefit enhancement value	919,974.3	1,420,363.3	790,288.3	26,257.2	3,156,883.1

, it can be seen that under independent operation, the cost at the alliance breakup point is CNY 14,111,661.9, with MG 1 at CNY 3,234,425.3, MG 2 at CNY 4,345,234.1, MG 3 at CNY 2,173,793.8, and the DSO at CNY 4,358,208.7. In cooperative operation, the alliance cooperation cost is CNY 10,954,627.5, representing a cost reduction of CNY 3,157,034.4 compared to independent operation. Moreover, each microgrid, through cooperative operation, has significantly reduced its own operational costs. Although the cooperative operation cost for the DSO increases, the alliance benefit rises to CNY 3,156,883.1 after the redistribution of energy trading payment costs among the entities, as shown by the post-negotiation costs. Specifically, MG 1 has CNY 919,974.3, MG 2 has CNY 1,420,363.3, MG 3 has CNY 790,288.3, and the DSO has CNY 26,257.2. The results demonstrate that the proposed model successfully balances the benefits of the alliance and the individual entities.

5.2.3. Benefit Analysis of the Impact of Uncertainty on Subject Systems

To better explore the impact of uncertainty on the systems of each entity, this paper defines four scenarios under cooperative operation, each considering different uncertainty factors, as referenced in [21] and shown in

Table 2. Uncertainty scenario setting.

Scene Number	Uncertainty of Renewable Energy Output	Uncertainty of Electricity Price
Scene 1	×	×
Scene 2	×	√
Scene 3	√	×
Scene 4	√	√

.

From the impact of different scenarios on the operational costs of each entity in

Table 3. The impact of different scenarios on the operational costs of each entity.

Scene Number	MG1/CNY	MG2/CNY	MG3/CNY	DSO/CNY	Alliance/CNY
Scene 1	1,555,924.9	1,880,758.8	708,243.6	5,722,249.5	9,130,713.18
Scene 2	1,426,248.8	1,857,668.8	607,940.8	6,142,861.6	10,034,720.0
Scene 3	1,570,630.8	1,909,407.8	716,284.8	6,653,389.8	10,849,713.2
Scene 4	1,511,536.4	1,891,680.3	646,485.7	6,904,925.1	10,954,627.5

, it can be seen that the alliance cooperation cost in Scenario 1 is lower than in Scenarios 2, 3, and 4. This is because, in Scenario 1, each entity does not need to consider the economic losses caused by various uncertainty risks for the system. Moreover, by comparing the alliance cooperation costs in Scenarios 2, 3, and 4, it can be observed that the risk caused by uncertainty in renewable energy output is higher than that caused by uncertainty in electricity prices, and the risk is highest when both uncertainties are present.

In order to further explore the ability of the proposed method to cope with uncertainty risks in the system, this paper conducts research and verification on the impact of confidence levels in renewable energy uncertainty, the number of uncertainty periods in electricity price uncertainty, and electricity price deviation coefficients on the operating costs of each entity based on the proposed scenario (Scenario 4).

Renewable Energy Uncertainty Impact Analysis

From

Table 4. Impact of renewable energy uncertainty confidence levels on operating costs for each entity.

Confidence Level	MG1/CNY	MG2/CNY	MG3/CNY	DSO/CNY	Alliance/CNY
$\epsilon =0.80$	1,511,536.4	1,891,680.3	646,485.7	6,904,925.1	10,954,627.5
$\epsilon =0.85$	1,517,369.8	1,900,952.8	647,662.8	7,108,326.6	11,174,312.0
$\epsilon =0.90$	1,524,590.5	1,912,654.9	662,848.9	7,357,546.6	11,457,640.9

, it can be observed that as the confidence level of uncertainty in renewable energy increases from 0.80 to 0.90, the cooperative operating costs of each entity and its alliance gradually increase. The results indicate that when considering uncertainty in renewable energy, each alliance entity will make decisions at the cost of sacrificing a certain cooperative operating cost in exchange for the system’s ability to resist uncertainty risks.

Analysis of the Impact of Electricity Price Uncertainty

In order to better regulate the robustness of the system, this paper adopts electricity price uncertainty adjustment parameters for adjustment processing [31]. The value of this parameter indicates the number of tariff uncertainty periods in a cycle, which can be rationally adjusted to effectively reduce the operating costs of each entity.

Table 5. Impact of electricity price uncertainty periods on the operating costs of each entity.

Uncertainty Adjustment Parameter	MG1/CNY	MG2/CNY	MG3/CNY	DSO/CNY	Alliance/CNY
$\nu =0$	1,570,630.8	1,909,407.8	716,284.8	6,653,389.8	10,849,713.2
$\nu =5$	1,525,434.3	1,909,407.8	660,923.0	6,849,189.4	10,944,954.5
$\nu =10$	1,511,536.4	1,891,680.3	646,485.7	6,904,925.1	10,954,627.5

shows the impact of electricity price uncertainty periods on the operating costs of each entity, as shown below.

From Table 5, it can be seen that as the number of uncertain periods increases, the cost of alliance cooperation also continues to increase. This is because the system needs to sacrifice more operational economy to resist the impact of electricity price uncertainty on the system. But as the number of uncertain periods increases, the growth rate of alliance cooperation costs gradually slows down, indicating that the more uncertain periods of electricity prices, the more significant the economic effect of alliance cooperation.

From the impact of the electricity price deviation coefficient on the operating costs of each entity in

Table 6. Impact of electricity price deviation coefficient on the operating costs of each entity.

Electricity Price Deviation Coefficient	MG1/CNY	MG2/CNY	MG3/CNY	DSO/CNY	Alliance/CNY
$\lambda =0.05$	1,568,572.8	1,909,407.8	703,813.1	6,736,959.4	10,918,753.1
$\lambda =0.10$	1,511,536.4	1,891,680.3	646,485.7	6,904,925.1	10,954,627.5
$\lambda =0.15$	1,510,822.2	1,892,226.1	643,906.0	6,913,651.5	10,960,605.8

, it can be observed that as the electricity price deviation coefficient increases from 0.05 to 0.15, the cost of alliance cooperation also gradually increases. This is due to the increased punishment for electricity price fluctuations. And similar to the impact of electricity price uncertainty periods, the larger the electricity price deviation coefficient, the more significant the economic effect of alliance cooperation.

5.2.4. Discussion of Results

A cooperative game model of DSOs and MGs considers multiple uncertainties to enhance renewable energy consumption capacity and system flexibility through resource complementarity and synergistic optimization. Within the adjustable range of uncertainty, choosing a smaller confidence level (taking about 0.80), uncertainty adjustment parameter (taking the number of time slots less than five), and electricity price deviation coefficient (taking about 0.10) can make the system enhance robustness to intermittent power generation and market fluctuations, and realize multi-principal cost-sharing and benefit-sharing with the help of the cooperative game theory to reduce the operation risk. The model not only improves the reliability of the power supply, but also, through the joint scheduling of energy storage, demand response, and other measures, makes the benefits of the main body worth tens of thousands of dollars to millions of dollars from the enhancement, ultimately achieving win–win energy ecological synergistic development.

6. Conclusions

This paper focuses on a multi-microgrid and distribution network system under a multi-uncertainty environment and proposes a Nash bargaining model for MGs and the DSO considering multiple uncertainties. The model is equivalently transformed into problems of minimizing cooperative costs for the multi-microgrid system and maximizing electricity transaction revenues. To address the uncertainty issues, opportunity constraints and robust optimization methods are employed to significantly reduce the impact of uncertainties. Finally, the ADMM distributed algorithm is applied to solve the above subproblems in a distributed manner, and the following conclusions are drawn from the case simulation:

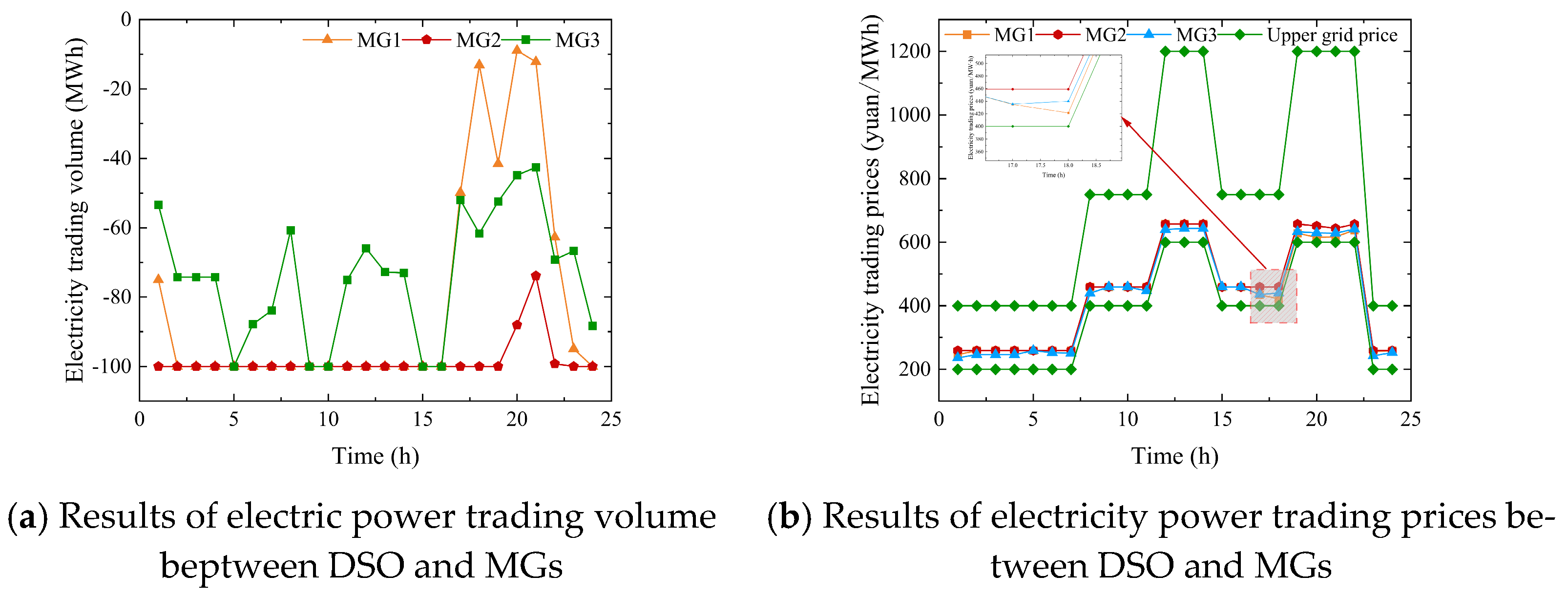
• By applying the ADMM distributed algorithm to sequentially solve the cooperative cost minimization and energy trading revenue maximization problems of the multi-microgrid system, it can be concluded that the algorithm demonstrates good convergence performance and ensures the confidentiality of each entity’s information.
• Considering the multiple uncertainties in renewable energy output and electricity prices, this approach allows operators to anticipate the risk levels posed by uncertainties to the microgrid system and make sufficient preparations, thereby enhancing the stability and safety of system operation.
• Compared to the independent operation model of the multi-microgrid and distribution network system, the operational costs of each entity are lower under the proposed cooperative operation model, which promotes the economic efficiency of the system. Additionally, as the confidence level of renewable energy output, the electricity price deviation coefficient, and the number of periods with electricity price uncertainty increase, the cooperative operation costs of the multi-microgrid and distribution network system also rise. Properly chosen uncertainty parameters can help protect the interests of each entity from excessive harm.
• To enhance the accuracy of renewable energy power forecasting, future work will involve using meteorological data as input to the forecasting model and selecting relevant features through correlation analysis, which will reduce the impact of redundant information on the model.

In real life, the proposed model can help optimize the power distribution and the energy production and consumption strategies of microgrids, ensuring that costs are minimized, efficiency is maximized, and system stability is maintained in an uncertain environment. This is of great significance for improving the economic viability of MGs, enhancing the stability of power supply in DSO, and reducing risks caused by fluctuations in wind and solar resources. Particularly in situations where electricity market volatility is high, the model can provide decision-makers with scientific power dispatch and price forecasting solutions.