A Novel Model for U-Tube Steam Generators for Pressurized Water Reactors
Abstract
1. Introduction
- A newly modified nodal form: A UTSG was separated into 14 different nodes and modeled using nonlinear differential equations developed from mass and energy basic conservation equations. In previous investigations, some structures of models utilizing fewer nodes showed lower granularity. In the developed model, the primary section has four nodes, the metal tube section has four nodes, and the secondary section has six (subcooled, boiling, downcomer, riser, separator and steam) nodes.
- Utilization of correct water feature data: Previous investigations in this field generally utilized linear extrapolation and interpolation for water features. As the terms of liquid and steam phases water alter throughout transients, a linear approach may not supply correct feature data. This research utilizes CoolProp features to correctly access the suitable values at each numerical analysis time step throughout the simulation of differential equations. CoolProp is a free C++ library that carries out Fast IAPWS-IF97 (Industrial Formulation) for water and steam along with many other fluids [37].
- Utilization of Julia programming language: Julia is a comparatively novel programming language made especially for high-performance calculation. It utilizes a nominal-level virtual machine to reach the performance of collected languages, while maintaining the flexibility and speed of improvement of interpreted languages. It can be regarded as a replacement for C or Fortran with a very rich ecosystem like Python (version 3.13.2) [38]. In addition, a fourth order of Runge–Kutta method was applied to solve the developed nonlinear differential equation system in the Julia environment. The model was closed as a loop by adding a three-element PI control system.
2. UTSG Model
2.1. Primary Section
2.2. Metal Tube Section
2.3. Secondary Section
2.4. Simulations
2.5. Three-Element PI Control
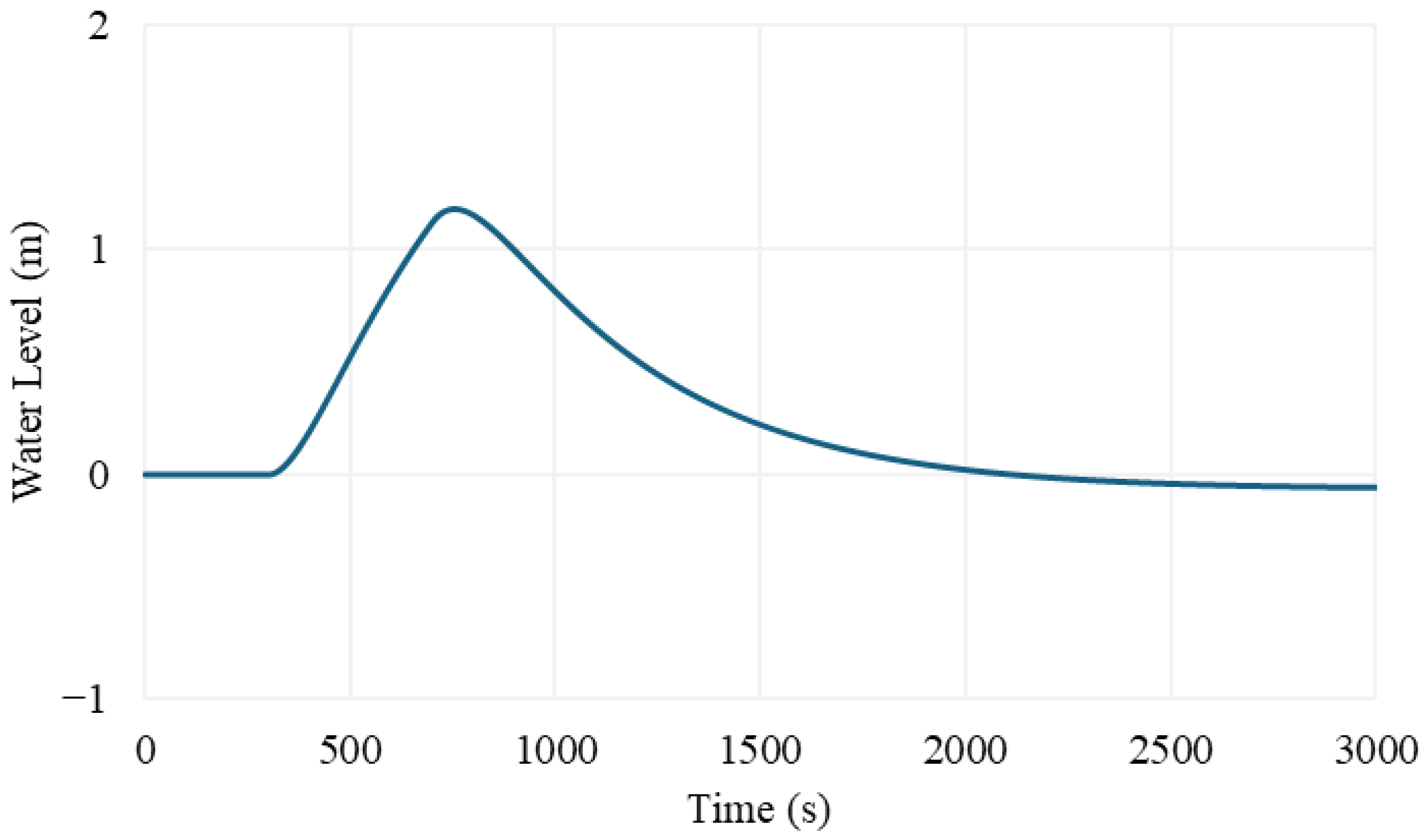
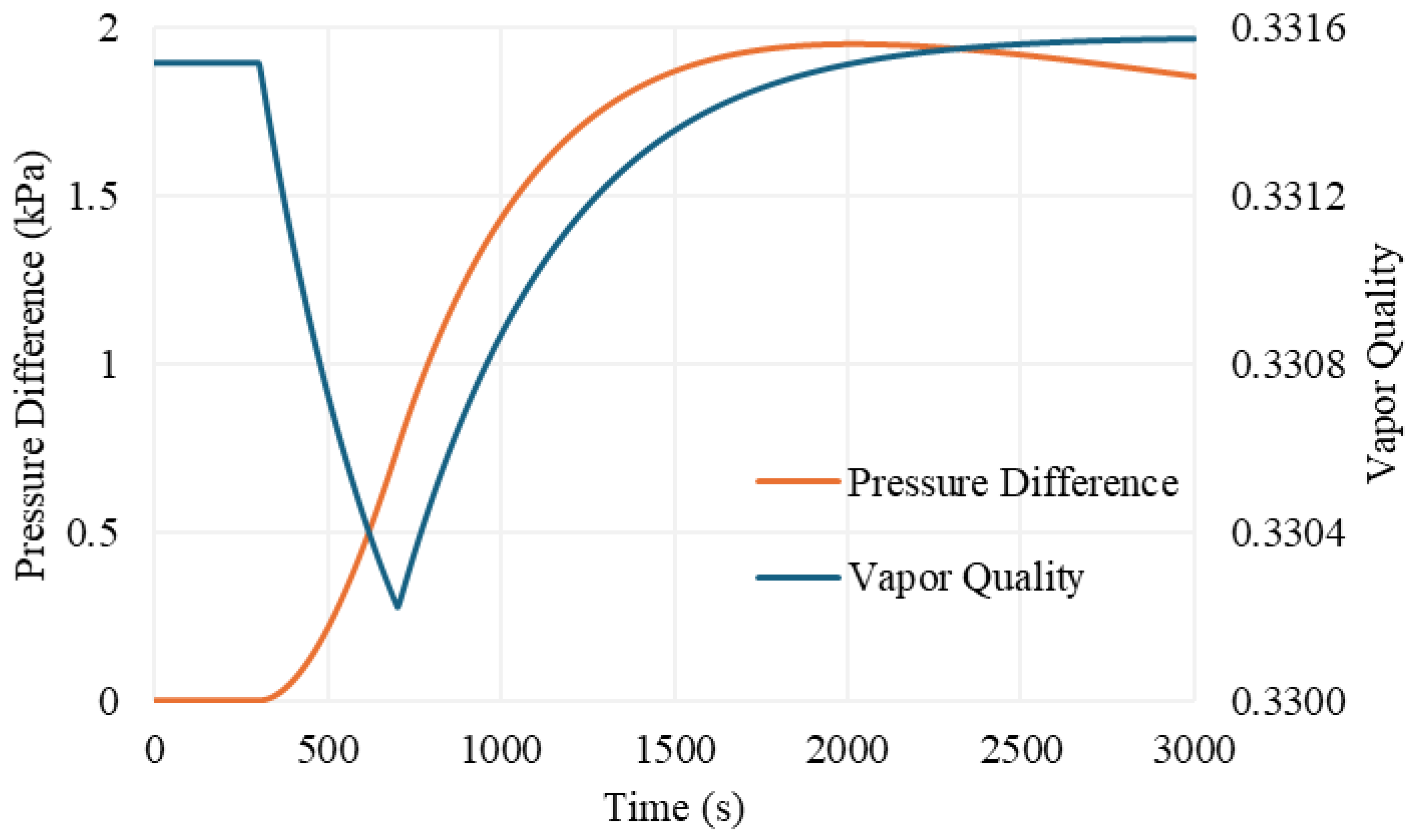
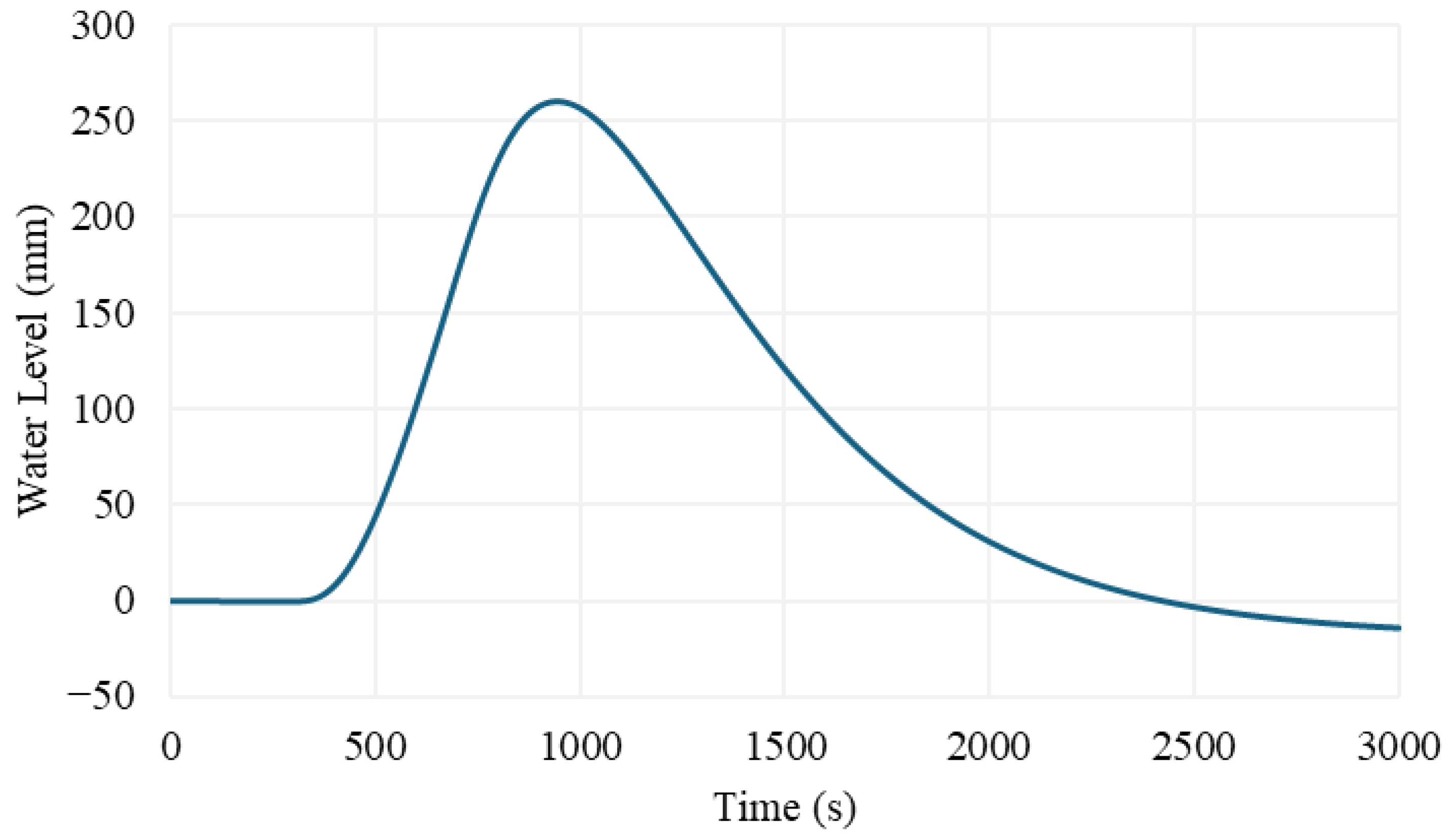
3. Results
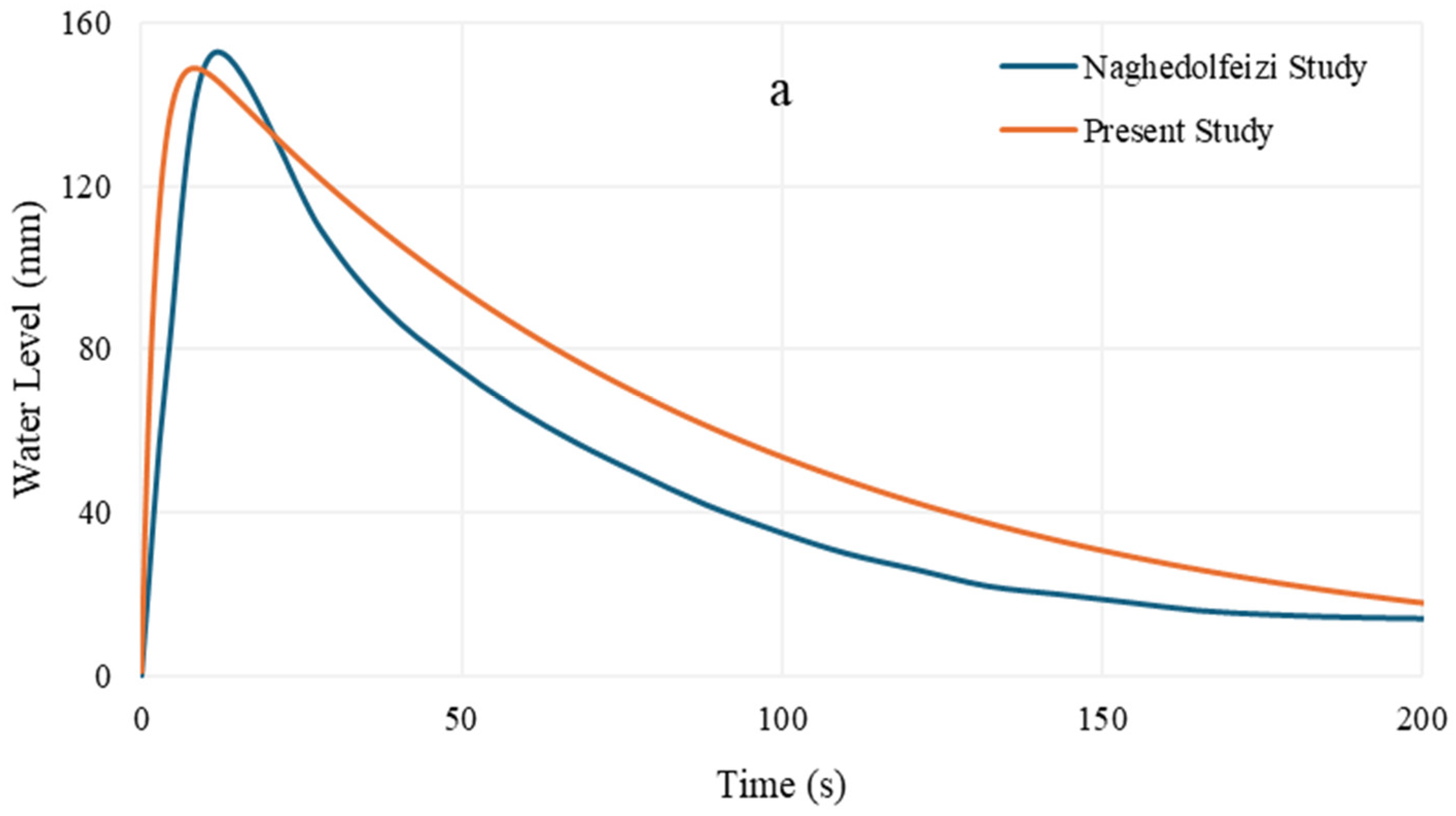
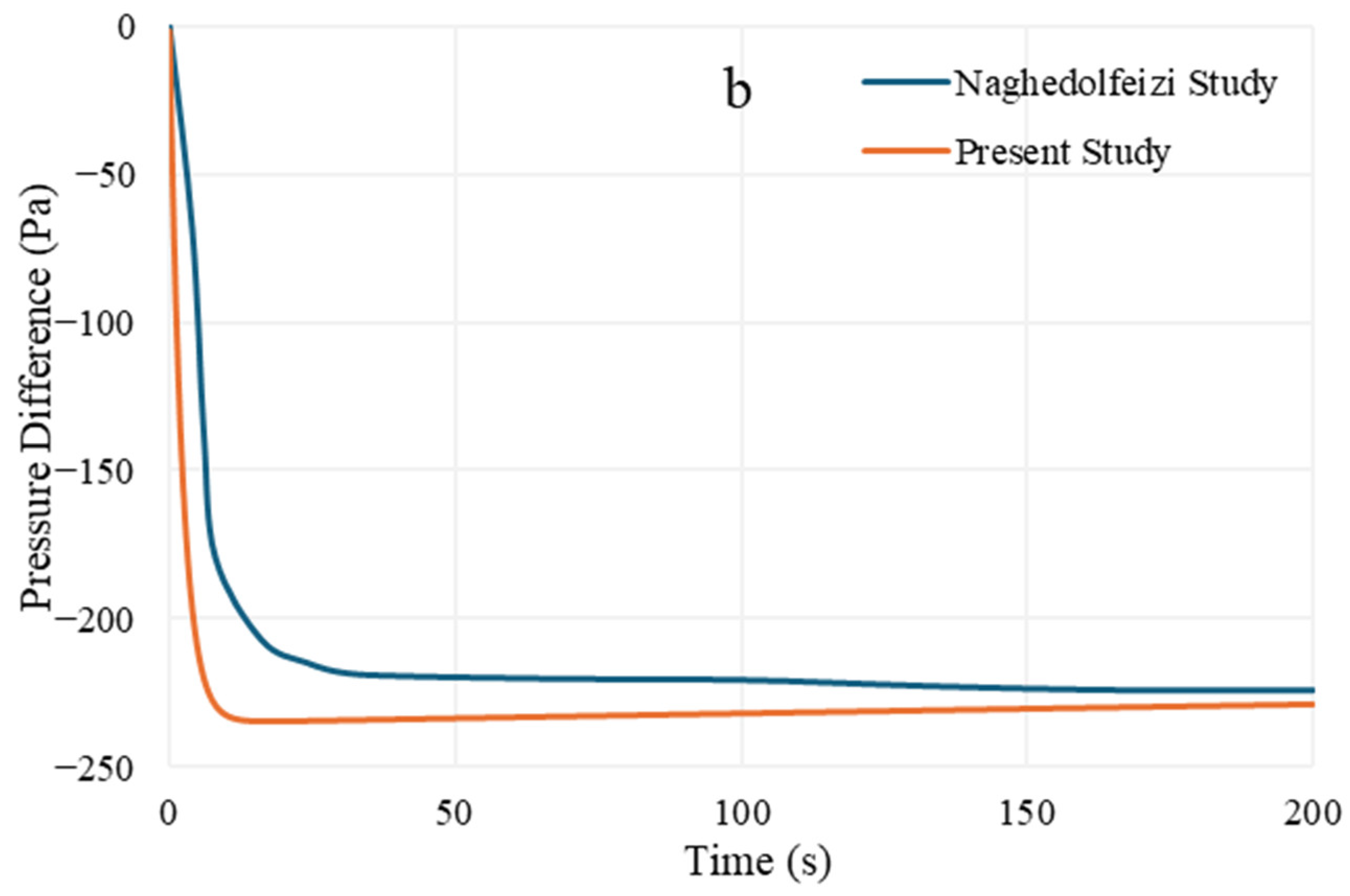
3.1. Validation of the Model
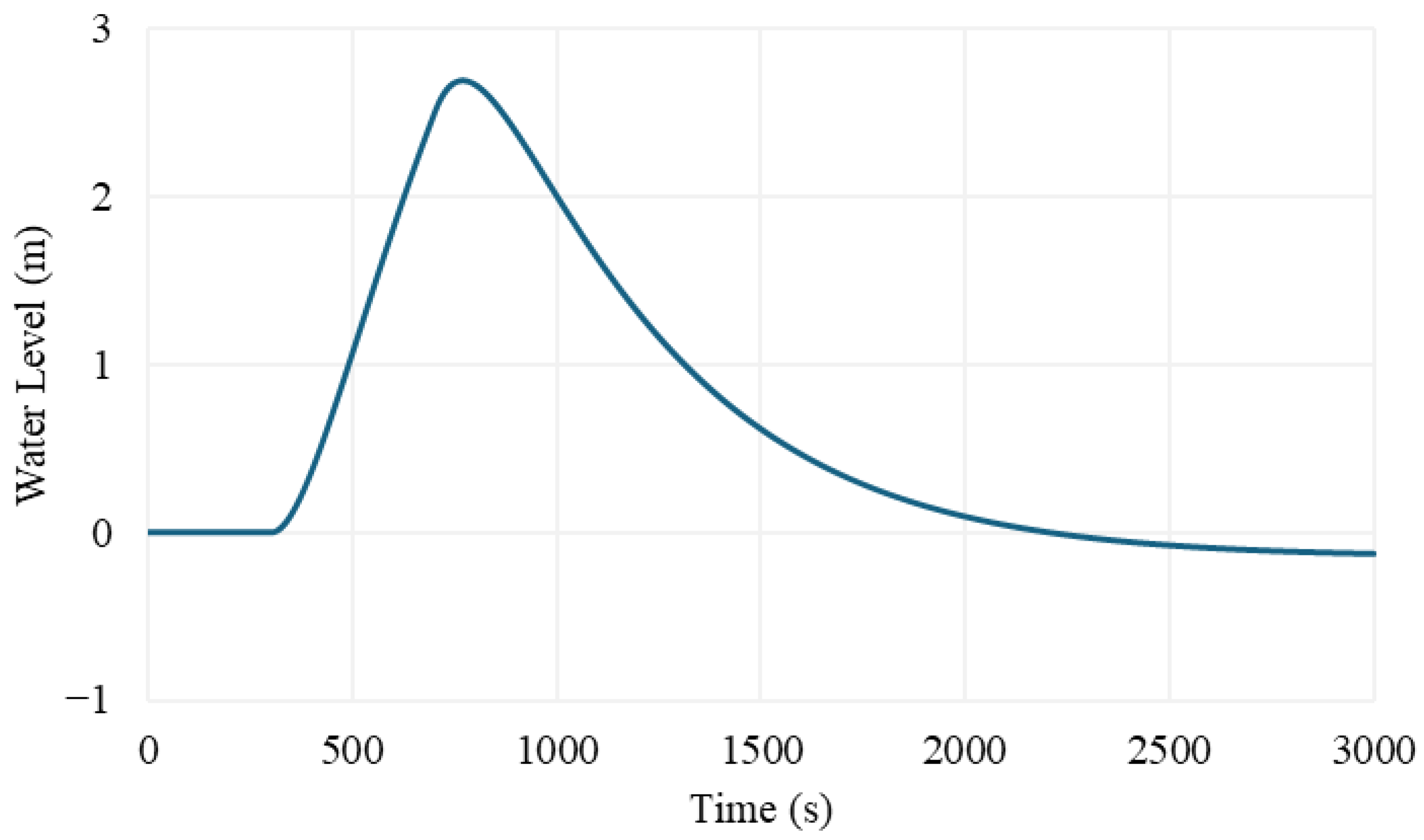
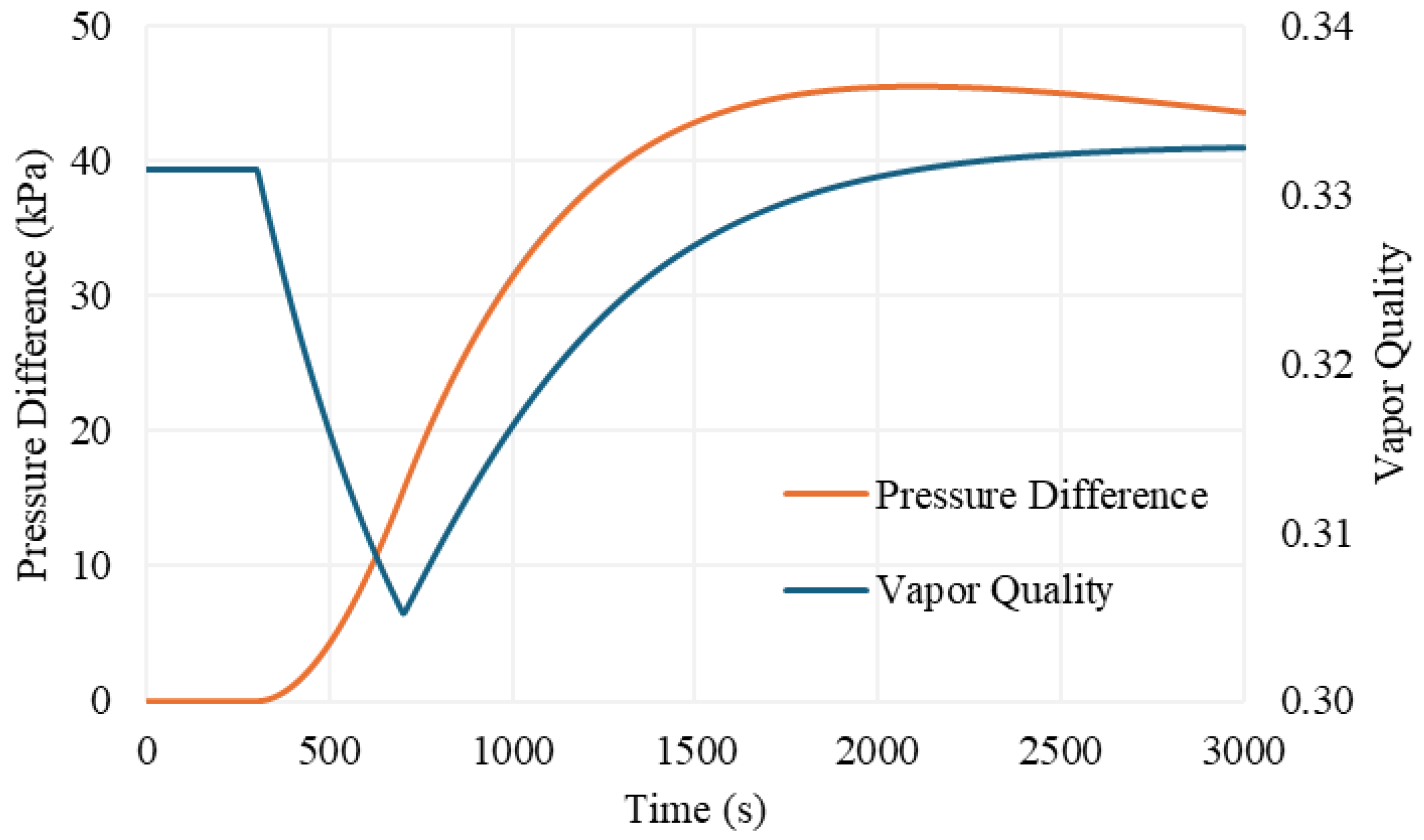
3.2. Results of Simulations
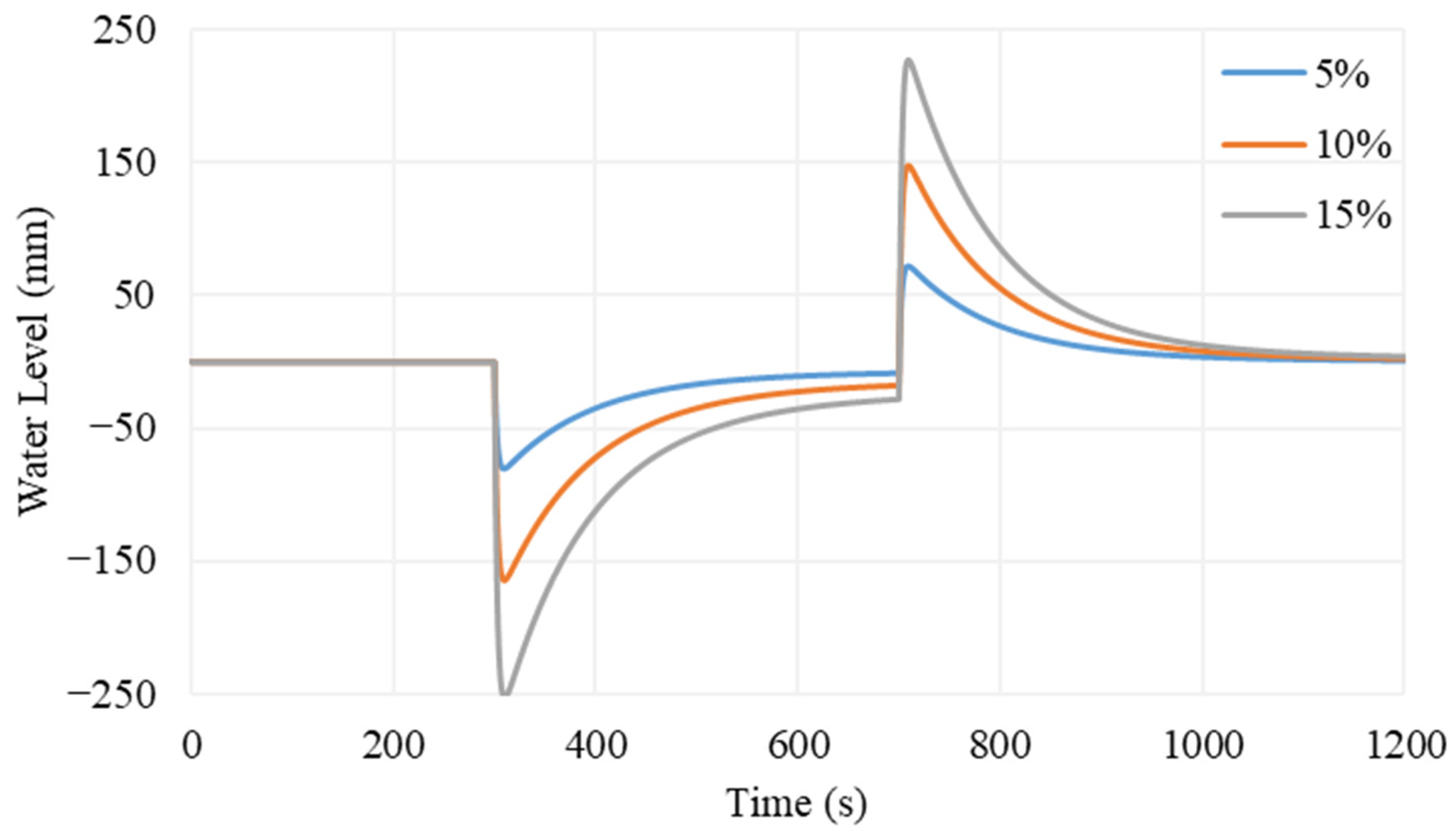


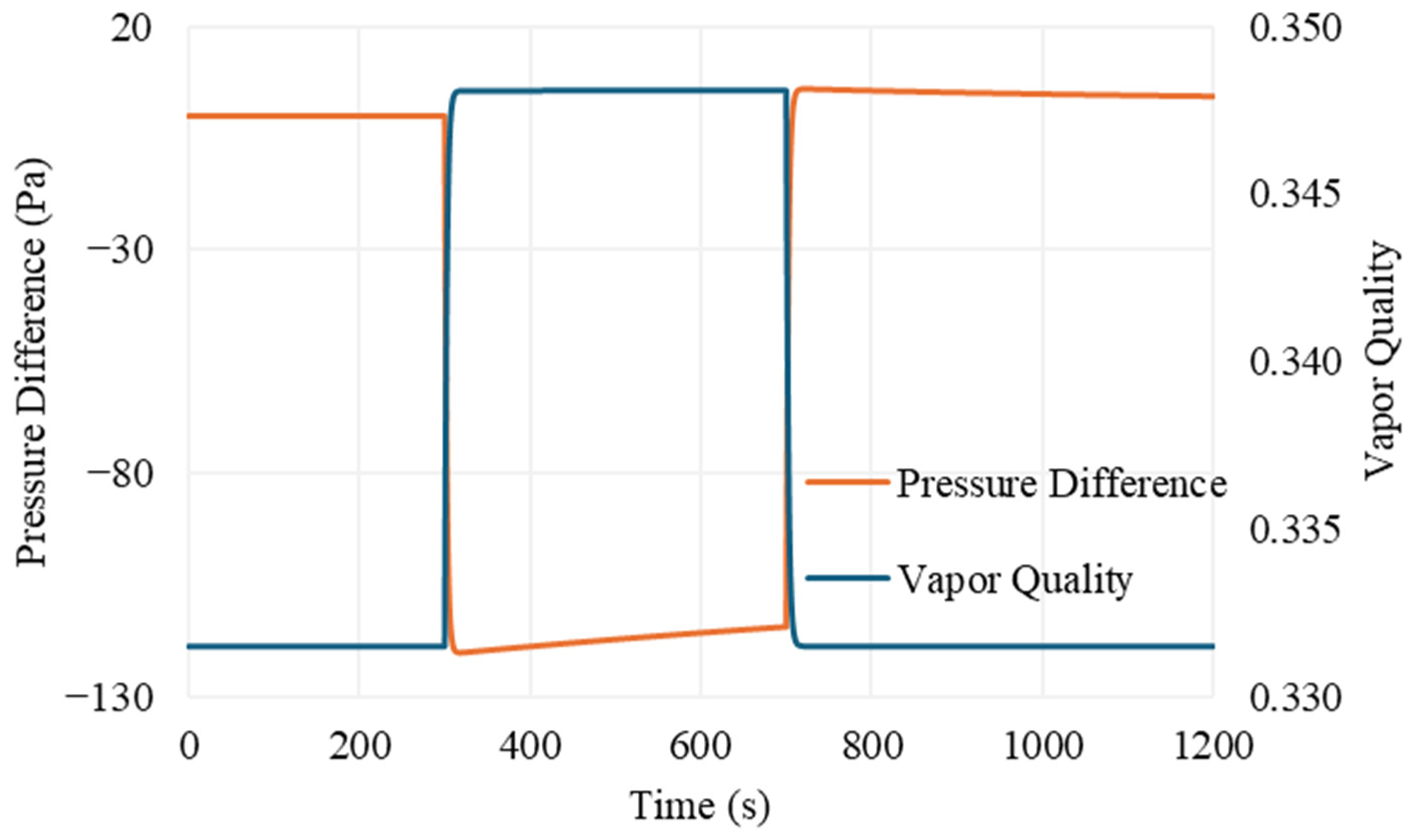
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Westinghouse Electric Corporation. The Westinghouse Pressurized Water Reactor Nuclear Power Plant; Westinghouse Electric Corporation: Pittsburgh, PA, USA, 1984. [Google Scholar]
- Kavaklioglu, K. Support vector regression model based predictive control of water level of U-tube steam generators. Nucl. Eng. Des. 2014, 278, 651–660. [Google Scholar] [CrossRef]
- Dong, W.; Doster, J.M.; Mayo, C.W. Steam Generator control in Nuclear Power Plants by water mass inventory. Nucl. Eng. Des. 2008, 238, 859–871. [Google Scholar] [CrossRef]
- Irving, E.; Miossec, C.; Tassart, J. Towards efficient full automatic operation of the PWR steam generator with water level adaptive control. In Proceedings of the 2nd International Conference on Boiler Dynamics and Control in Nuclear Power Stations, Bournemouth, UK, 23–25 October 1980; pp. 309–329. [Google Scholar]
- Ali, M.R.A. Lumped Parameter, State Variable Dynamic Models for U-tube Recirculation Type Nuclear Steam Generators. Ph.D. Thesis, University of Tennessee, Knoxville, TN, USA, 1976. Available online: https://trace.tennessee.edu/utk_graddiss (accessed on 15 January 2023).
- Naghedolfeizi, M. Dynamic Modeling of a Pressurized Water Reactor Plant for Diagnostics and Control. Master’s Thesis, University of Tennessee, Knoxville, TN, USA, 1990. Available online: https://trace.tennessee.edu/utk_gradthes/2667 (accessed on 15 January 2023).
- Guimarães, L.N.F.; da Silva Oliveira, N.; Borges, E.M. Derivation of a nine variable model of a U-tube steam generator coupled with a three-element controller. Appl. Math. Model. 2008, 32, 1027–1043. [Google Scholar] [CrossRef]
- Wan, J.; He, J.; Li, S.; Zhao, F. Dynamic modeling of AP1000 steam generator for control system design and simulation. Ann. Nucl. Energy 2017, 109, 648–657. [Google Scholar] [CrossRef]
- Qiu, L.; Sun, A.; Wang, H.; Zhang, R.; Jiang, G.; Sun, P.; Wei, X. Study on water level control system of natural circulation steam generator. Prog. Nucl. Energy 2022, 153, 104436. [Google Scholar] [CrossRef]
- Parlos, A.G.; Rais, O.T. Nonlinear control of U-tube steam generators via H∞ control. Control Eng. Pract. 2000, 8, 921–936. [Google Scholar] [CrossRef]
- Salehi, A.; Kazemi, M.H.; Safarzadeh, O. The μ–synthesis and analysis of water level control in steam generators. Nucl. Eng. Technol. 2019, 51, 163–169. [Google Scholar] [CrossRef]
- Ansarifar, G.R. Control of the nuclear steam generators using adaptive dynamic sliding mode method based on the nonlinear model. Ann. Nucl. Energy 2016, 88, 280–300. [Google Scholar] [CrossRef]
- Man Gyun Na Design of a steam generator water level controller via the estimation of the flow errors. Ann. Nucl. Energy 1995, 22, 367–376. [CrossRef]
- Tan, W. Water level control for a nuclear steam generator. Nucl. Eng. Des. 2011, 241, 1873–1880. [Google Scholar] [CrossRef]
- Dong, Z.; Huang, X.; Feng, J. Water-level control for the U-tube steam generator of nuclear power plants based on output feedback dissipation. IEEE Trans. Nucl. Sci. 2009, 56, 1600–1612. [Google Scholar] [CrossRef]
- Kothare, M.V.; Mettler, B.; Morari, M.; Bendotti, P.; Falinower, C.M. Level Control in the Steam Generator of a Nuclear Power Plant. 2000. Available online: http://www.edf.fr (accessed on 15 January 2023).
- Zhao, X.; Wang, M.; Wu, G.; Zhang, J.; Tian, W.; Qiu, S.; Su, G.H. The development of high fidelity Steam Generator three dimensional thermal hydraulic coupling code: STAF-CT. Nucl. Eng. Technol. 2021, 53, 763–775. [Google Scholar] [CrossRef]
- Li, M.; Chen, W.; Hao, J.; Li, W. Experimental and numerical investigations on effect of reverse flow on transient from forced circulation to natural circulation. Nucl. Eng. Technol. 2020, 52, 1955–1962. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Y.; Yang, Y.; Li, Y.; Sun, B. Dynamic heat transfer performance study of steam generator based on distributed parameter method. Ann. Nucl. Energy 2014, 63, 658–664. [Google Scholar] [CrossRef]
- Qiu, L.; Huo, Y.; Zhang, R.; Wang, H.; Jiang, G.; Sun, P.; Wei, X. Research on fuzzy weighted gain scheduling water level control system of U-tube steam generator. Ann. Nucl. Energy 2023, 187, 109812. [Google Scholar] [CrossRef]
- Chu, X.; Li, M.; Chen, W.; Hao, J. Investigation on reverse flow characteristics in U-tubes under two-phase natural circulation. Nucl. Eng. Technol. 2020, 52, 889–896. [Google Scholar] [CrossRef]
- Hui, J.; Ling, J.; Dong, H.; Wang, G.; Yuan, J. Distributed parameter modeling for the steam generator in the nuclear power plant. Ann. Nucl. Energy 2021, 152, 107945. [Google Scholar] [CrossRef]
- Chen, Y.; Xie, Y.; Li, Y.; Ling, J.; Zhou, X. Full-range steam generator’s water level model and analysis method based on cross-calculation. Prog. Nucl. Energy 2021, 133, 103635. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, D.; Lin, J.; Hao, J. Development of a computer code for thermal–hydraulic design and analysis of helically coiled tube once-through steam generator. Nucl. Eng. Technol. 2017, 49, 1388–1395. [Google Scholar] [CrossRef]
- Hui, J. Fixed-time fractional-order sliding mode controller with disturbance observer for U-tube steam generator. Renew. Sustain. Energy Rev. 2024, 205, 114829. [Google Scholar] [CrossRef]
- Li, X.; Yang, Z.; Yang, Y.; Kong, X.; Shi, C.; Shi, J. GK-SPSA-Based Model-Free Method for Performance Optimization of Steam Generator Level Control Systems. Energies 2023, 16, 8050. [Google Scholar] [CrossRef]
- Qi, B.; Liang, J.; Tong, J. Fault Diagnosis Techniques for Nuclear Power Plants: A Review from the Artificial Intelligence Perspective. Energies 2023, 16, 1850. [Google Scholar] [CrossRef]
- Xiao, K.; Li, Y.; Yang, P.; Zhang, Y.; Zhao, Y.; Pu, X. Study on IMC-PID Control of Once-Through Steam Generator for Small Fast Reactor. Energies 2022, 15, 7475. [Google Scholar] [CrossRef]
- Bolfo, L.; Devia, F.; Lomonaco, G. Nuclear Hydrogen Production: Modeling and Preliminary Optimization of a Helical Tube Heat Exchanger. Energies 2021, 14, 3113. [Google Scholar] [CrossRef]
- Li, Z.; Yan, Y.; Fan, G.; Zeng, X.; Hao, S.; Yan, C. Non-uniform boiling heat transfer characteristics and calculation evaluation in U-tube steam generator tube bundle. Energy 2024, 303, 131867. [Google Scholar] [CrossRef]
- Ma, Q.; Fan, Z.; Zhang, X.; Sun, P.; Wei, X. Water level control of U-tube steam generator based on model-based active disturbance rejection control method. Ann. Nucl. Energy 2024, 206, 110618. [Google Scholar] [CrossRef]
- Zhong, X.; Guo, P.; Zhang, X.; Saeed, M.; Ma, H.; Huang, J.; Yu, J. Development of a seven-region lumped parameter nonlinear dynamic model for U-tube recirculation nuclear steam generator. Ann. Nucl. Energy 2022, 174, 109190. [Google Scholar] [CrossRef]
- Sun, X.; Song, F.; Yuan, J. Transient analysis and dynamic modeling of the steam generator water level for nuclear power plants. Prog. Nucl. Energy 2024, 170, 105103. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Y.; Yin, S.; Lu, J.; Hu, Y. Enabling High-Degree-of-Freedom Thermal Engineering Calculations via Lightweight Machine Learning. Energies 2024, 17, 3916. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Methods for Ordinary Differential Equations, 3rd ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Julia Programming Language Julia. MIT. Available online: https://julialang.org/ (accessed on 1 January 2022).
- Bell, I.H.; Wronski, J.; Quoilin, S.; Lemort, V. Pure and Pseudo-Pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library Coolprop. Ind. Eng. Chem. Res. 2014, 53, 2498–2508. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Alramady, A.M.; Al-Sharif, S.; Nafee, S.S. Modeling of UTSG in the Pressurized Water Reactor Using Accurate Formulae of Thermodynamic Properties. J. Appl. Math. Phys. 2021, 9, 947–967. [Google Scholar] [CrossRef]
- Kerlin, T.W.; Upadhyaya, B.R. Dynamics and Control of Nuclear Reactors; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Dong, Z.; Huang, X.; Feng, J.; Zhang, L. Dynamic model for control system design and simulation of a low temperature nuclear reactor. Nucl. Eng. Des. 2009, 239, 2141–2151. [Google Scholar] [CrossRef]
- Westinghouse Westinghouse Technology Systems Manual. 2020. Available online: https://www.nrc.gov/docs/ML2116/ML21166A218.pdf (accessed on 15 January 2023).
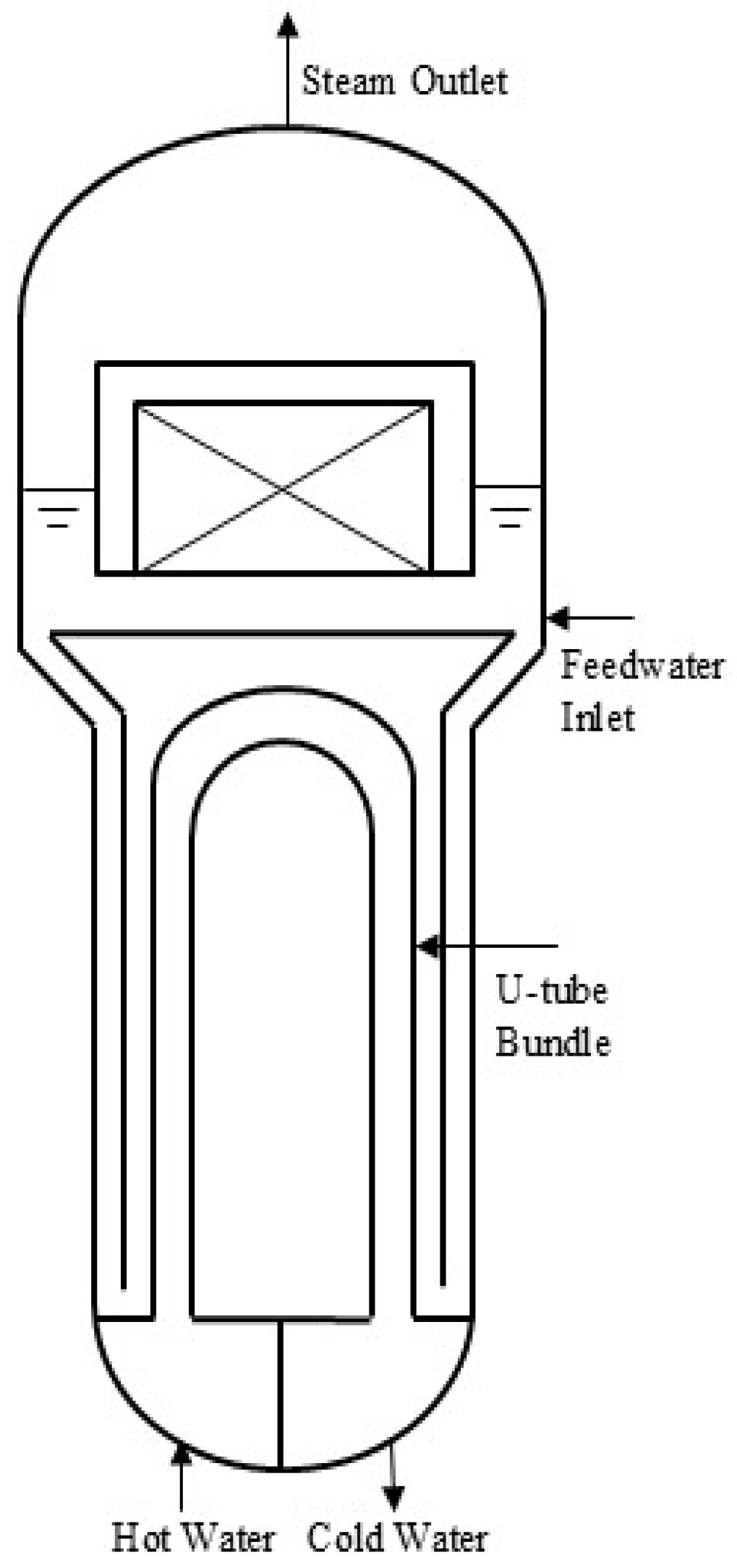

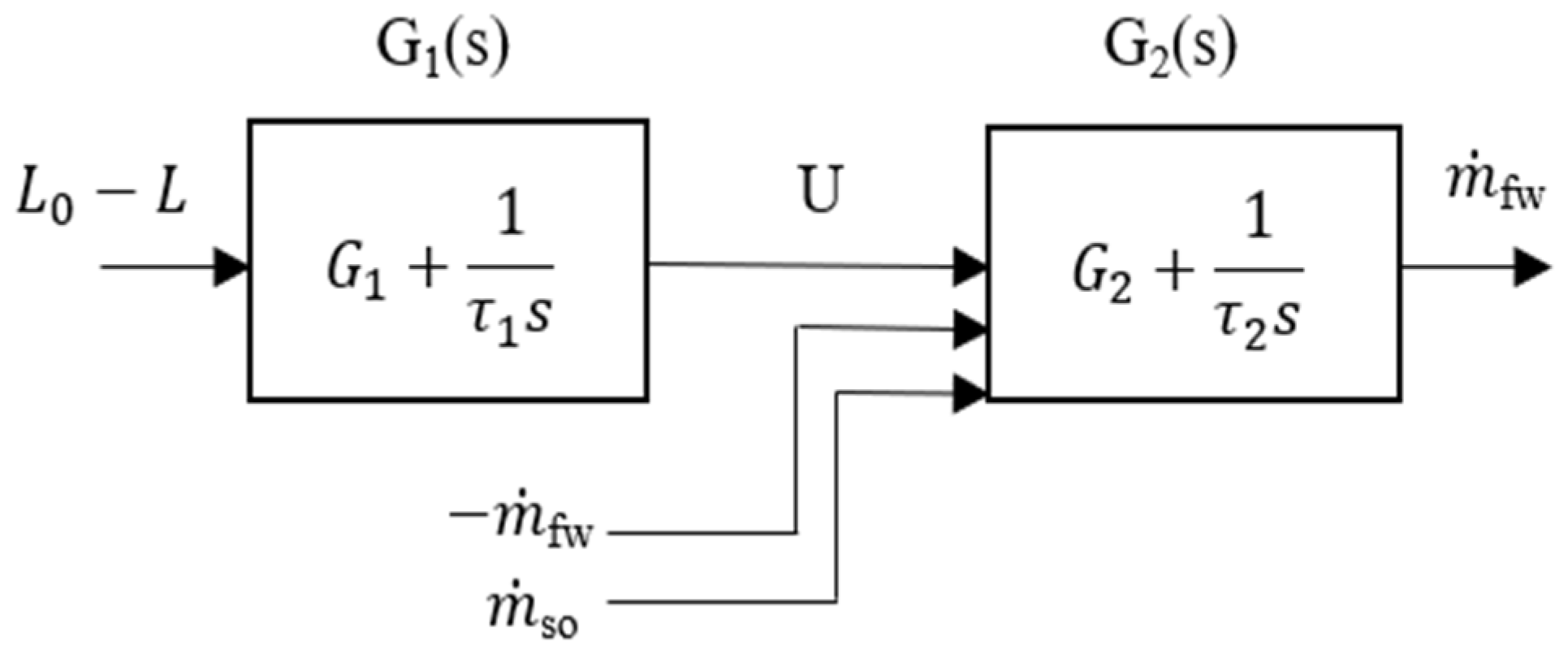

| Node Number | Symbol | Explanation |
|---|---|---|
| 1 | P1 | Primary fluid first node |
| 2 | P2 | Primary fluid second node |
| 3 | P3 | Primary fluid third node |
| 4 | P4 | Primary fluid fourth node |
| 5 | M1 | Metal tube first node |
| 6 | M2 | Metal tube second node |
| 7 | M3 | Metal tube third node |
| 8 | M4 | Metal tube fourth node |
| 9 | S1 | Subcooled region node |
| 10 | S2 | Boiling region node |
| 11 | R | Riser node |
| 12 | S | Separator-Dryer node |
| 13 | St | Steam node |
| 14 | D | Downcomer node |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahin, H.E.; Ozturk, H.K. A Novel Model for U-Tube Steam Generators for Pressurized Water Reactors. Energies 2025, 18, 1506. https://doi.org/10.3390/en18061506
Sahin HE, Ozturk HK. A Novel Model for U-Tube Steam Generators for Pressurized Water Reactors. Energies. 2025; 18(6):1506. https://doi.org/10.3390/en18061506
Chicago/Turabian StyleSahin, Huseyin Emre, and Harun Kemal Ozturk. 2025. "A Novel Model for U-Tube Steam Generators for Pressurized Water Reactors" Energies 18, no. 6: 1506. https://doi.org/10.3390/en18061506
APA StyleSahin, H. E., & Ozturk, H. K. (2025). A Novel Model for U-Tube Steam Generators for Pressurized Water Reactors. Energies, 18(6), 1506. https://doi.org/10.3390/en18061506








