Uniqueness of Optimal Power Management Strategies for Energy Storage Dynamic Models
Abstract
1. Introduction
2. Main Result
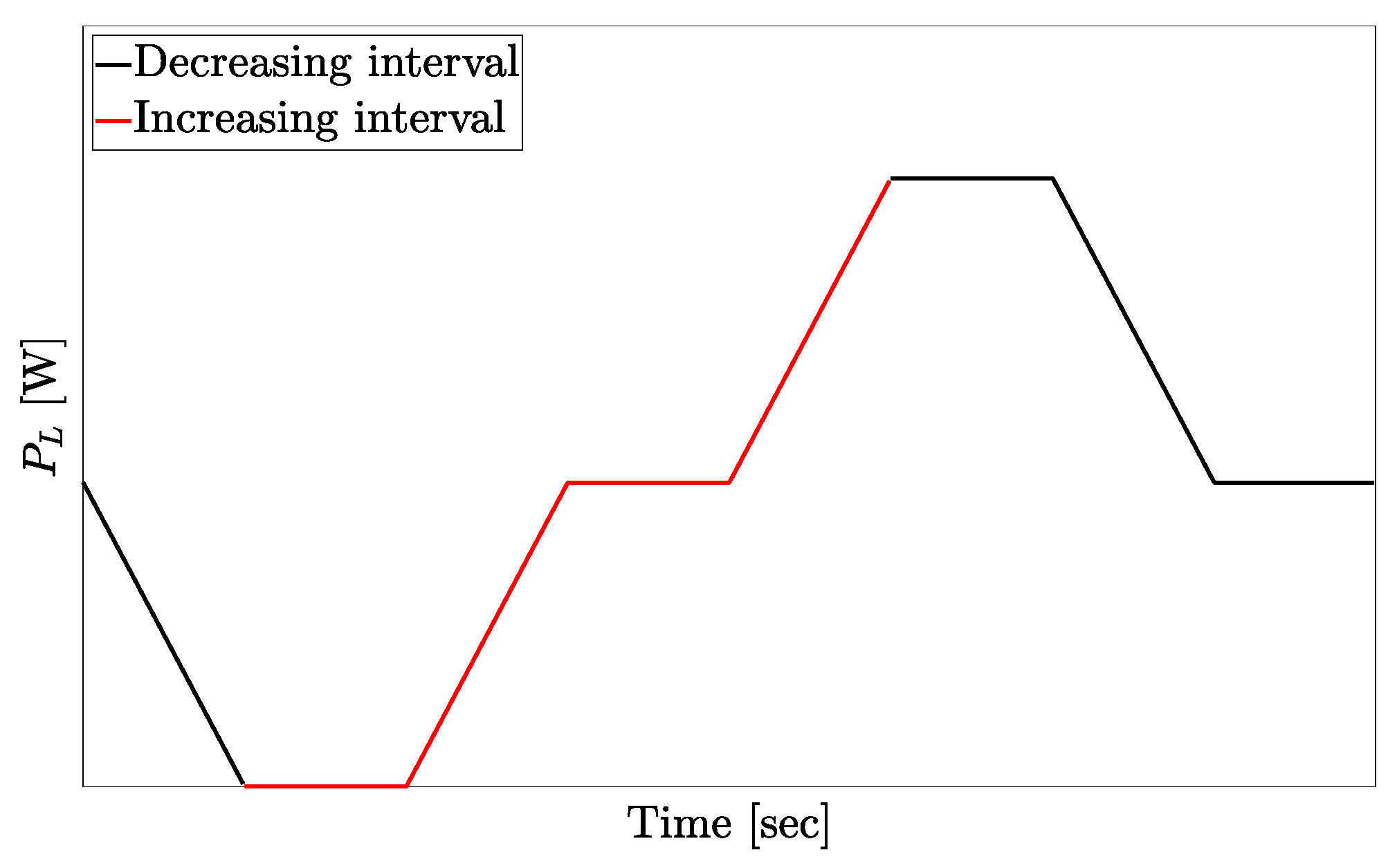
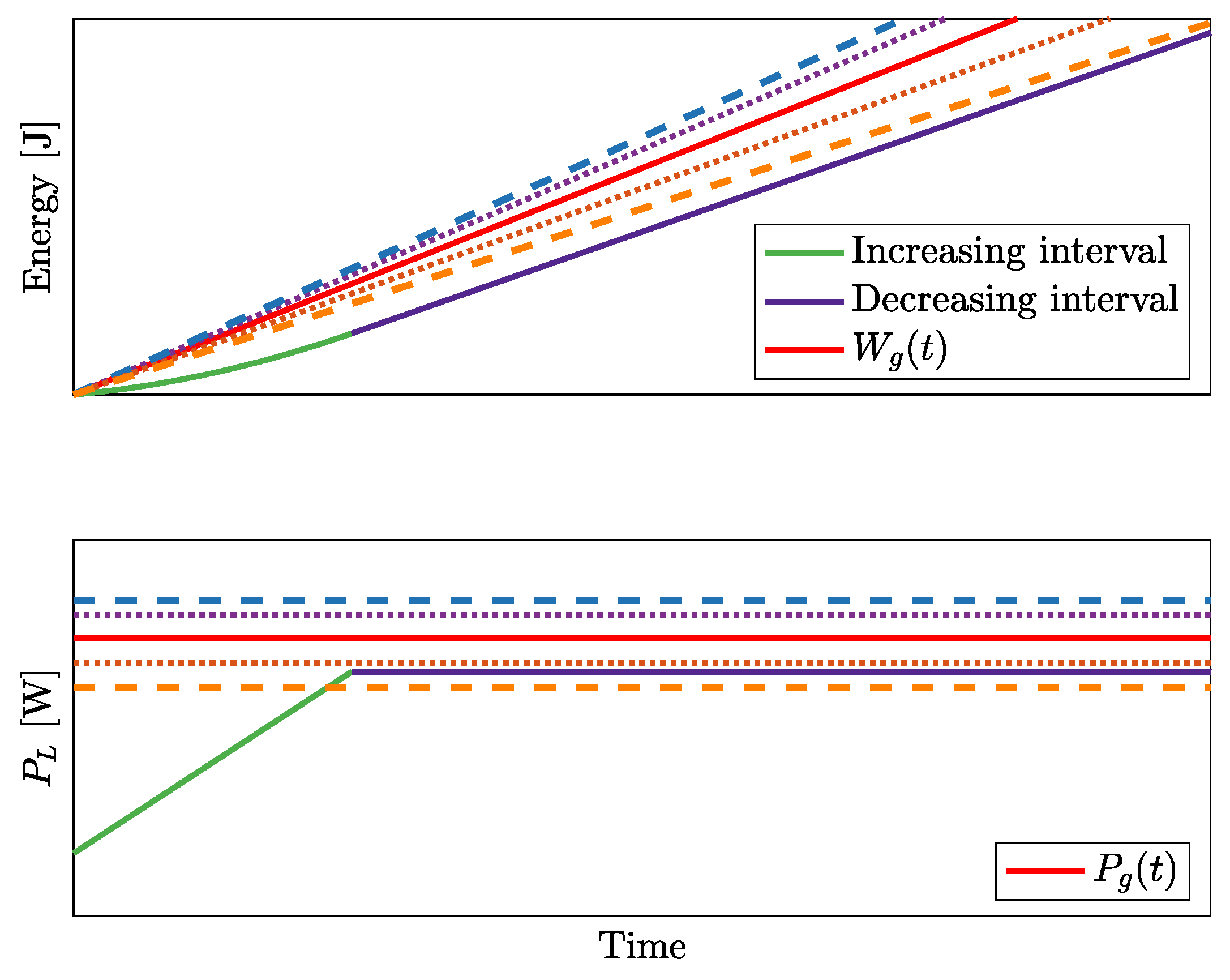
- When not bounded, the generated energy is a straight line.
- When bounded, the generated energy is tangent to the constraint.
- 1.
- The function is increasing in :.
- 2.
- If the point is not at the edge of the domain of definition of the function, then the function is decreasing on the interval [0,c):.
- 3.
- If the point is not at the edge of the domain of definition of the function, then the function is decreasing from some point inside the interval :.
- 1.
- The function is decreasing in :.
- 2.
- If the point is not at the edge of the domain of definition of the function, then the function is increasing on the interval [0,c):.
- 3.
- If the point is not at the edge of the domain of definition of the function, then the function is increasing from some point inside the interval :
- 1.
- ,
- 2.
- .
- 1.
- ,
- 2.
- .
2.1. The Third Lemma
- 1.
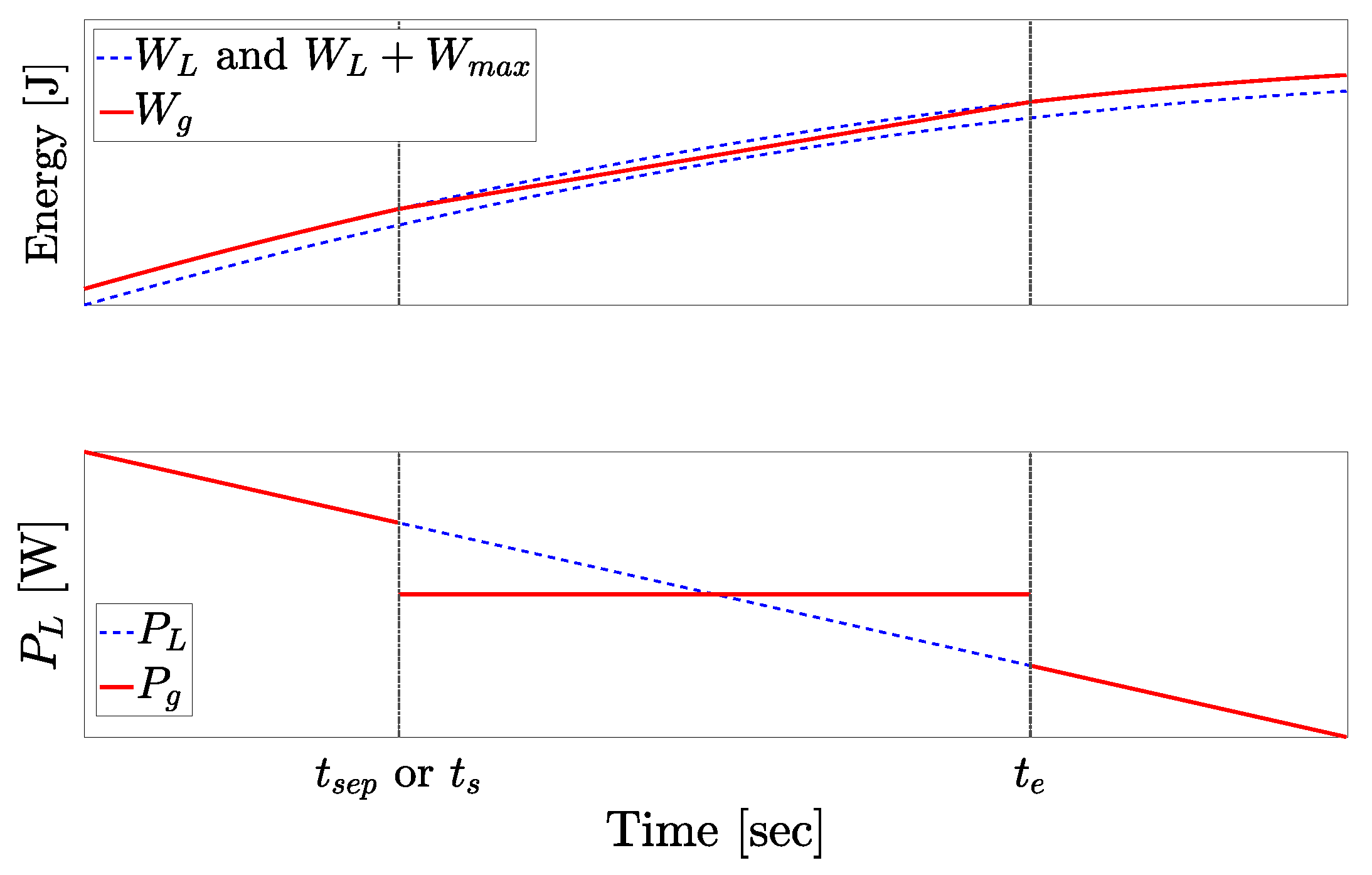
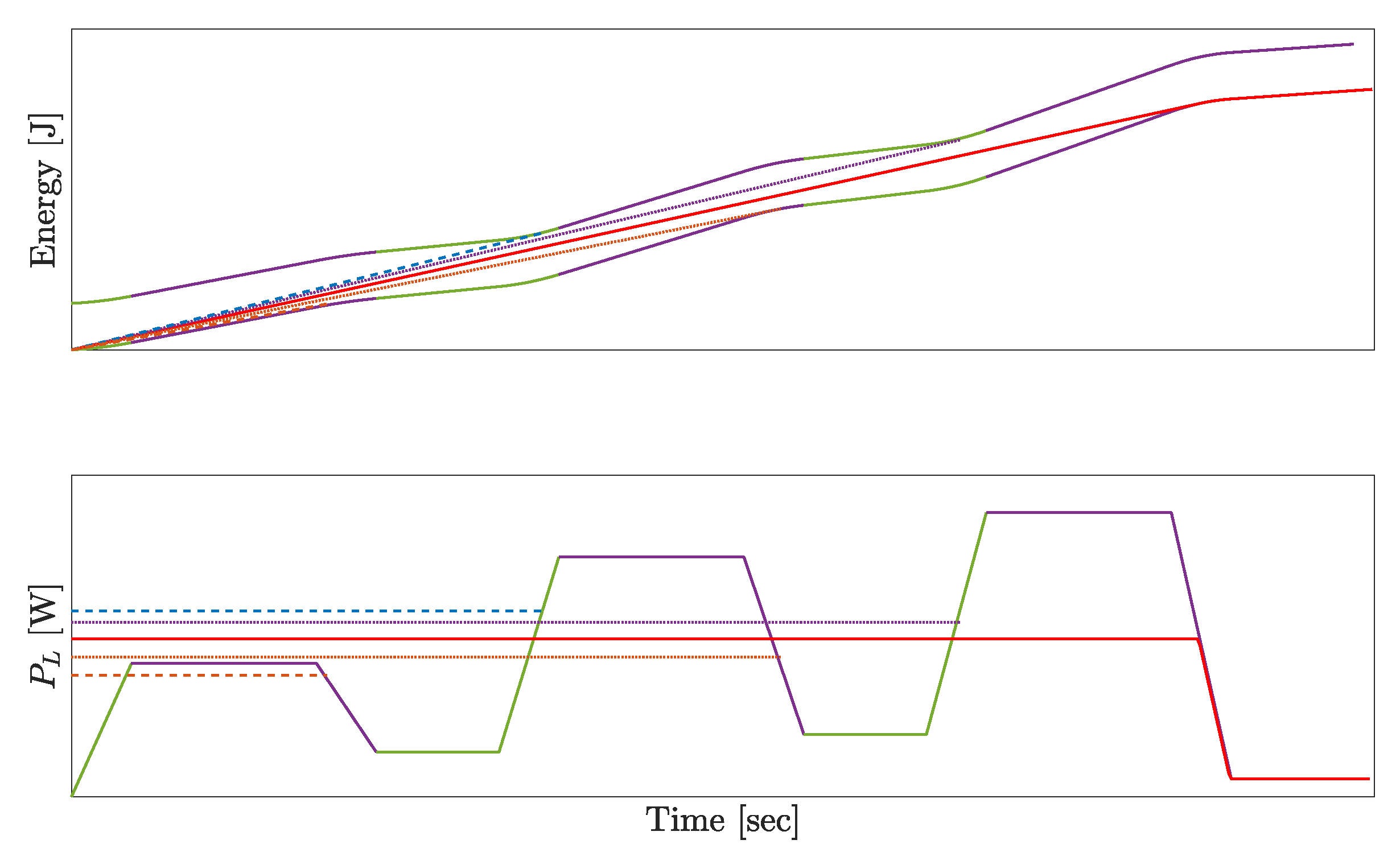
- If such that and is a union point of , since is in an increasing interval of , the following is produced:This contradicts TC lemma at . An illustration of this case can be seen in Figure 6.
- 2.
- Otherwise, such that and is a union point of . But then from SF lemma is constant for , and
2.2. The Fourth Lemma
- 1.
- ,
- 2.
- satisfies SF lemma on ,
- 3.
- satisfies TC lemma on .
- 1.
- such that is a COS on ,
- 2.
- such that is a separation point of and ,
- 3.
- such that is a union point of and ,
- 4.
- .
- 1.
- such that is a separation point of and ,
- 2.
- such that is a union point of and ,
- 3.
- with where .
- 1.
- such that ,
- 2.
- such that ,
- 3.
- ,
2.3. The Fifth Lemma
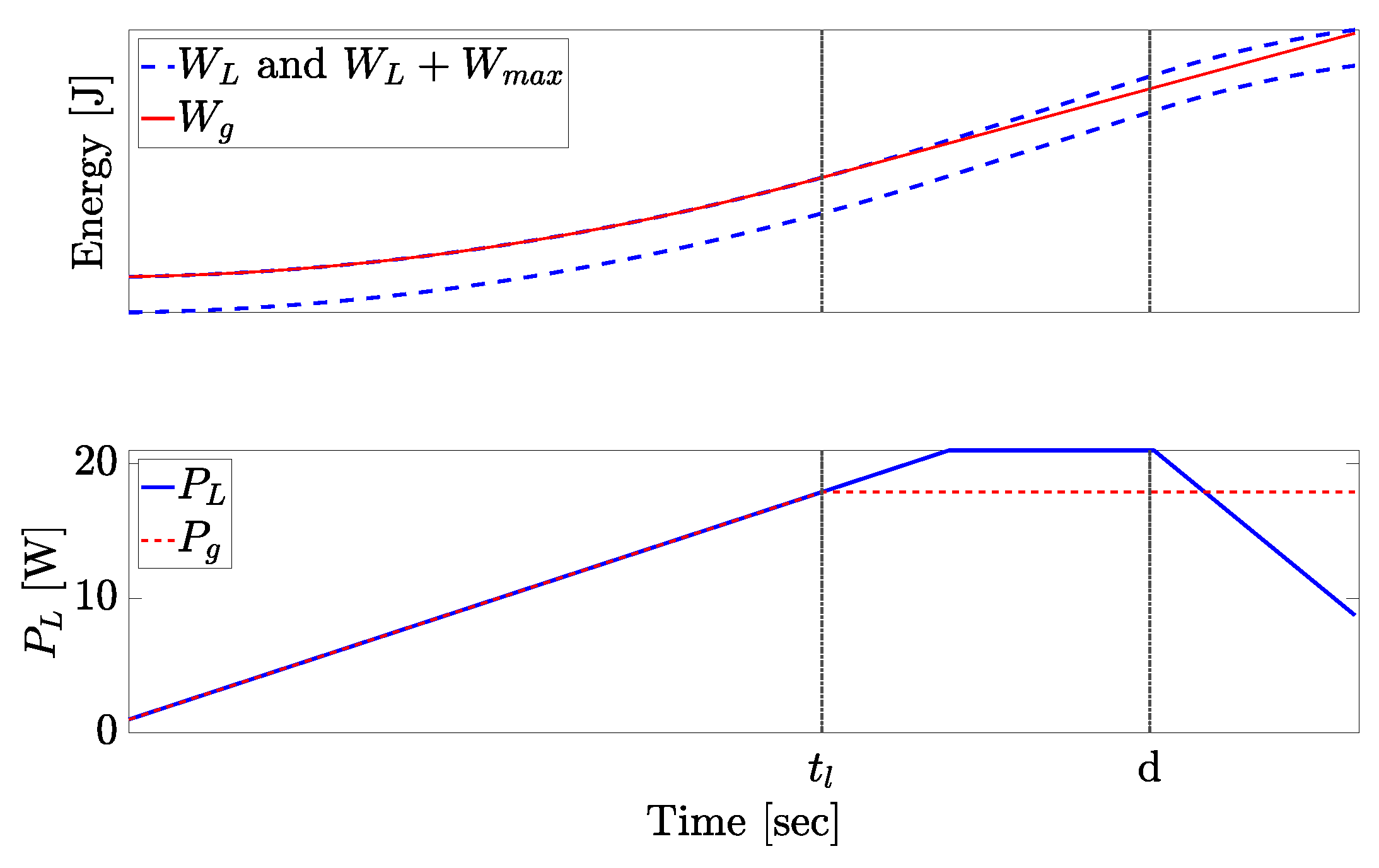
- 1.
- The first part formulates the connection between the slopes of generated energies routed between monotone intervals of and the distance between the different monotone intervals.
- 2.
- The second part utilizes the conclusion regarding those connections and proves that an optimal solution cannot be routed to a monotone interval which is not either the most distant reachable increasing interval of possible or the most distant reachable decreasing interval of possible.
- 3.
- The last part proves that only one of those monotone intervals is a valid solution.
- 1.
- if is an increasing interval, ;
- 2.
- if is a decreasing interval, .
- 1.
- If and are both increasing intervals, a COS on that is routed from to .
- 2.
- If and are both decreasing intervals, a COS on that is routed from to .
- 1.
- is increasing; hence, ;
- 2.
- Utilizing “Fan Behavior”, one may conclude that ;
- 3.
- is decreasing; thus, .
- 1.
- If , then we have a contradiction to the starting condition.
- 2.
- The case where is not possible because both and must be straight lines in the neighborhood of (SF lemma). Therefore, there must be such that , which contradicts the definition of .
- 3.
- If , then we know such that is a decreasing interval of . We now have a contradiction, because
- (a)
- If both are routed from to the same reachable monotone interval, we have a contradiction to UBMI lemma.
- (b)
- If and are routed from to different monotone intervals, we have a contradiction to MDRI lemma.
- 4.
- The case where is similar to the last one.
- 5.
- Lastly, if , we have a contradiction to the ending condition.
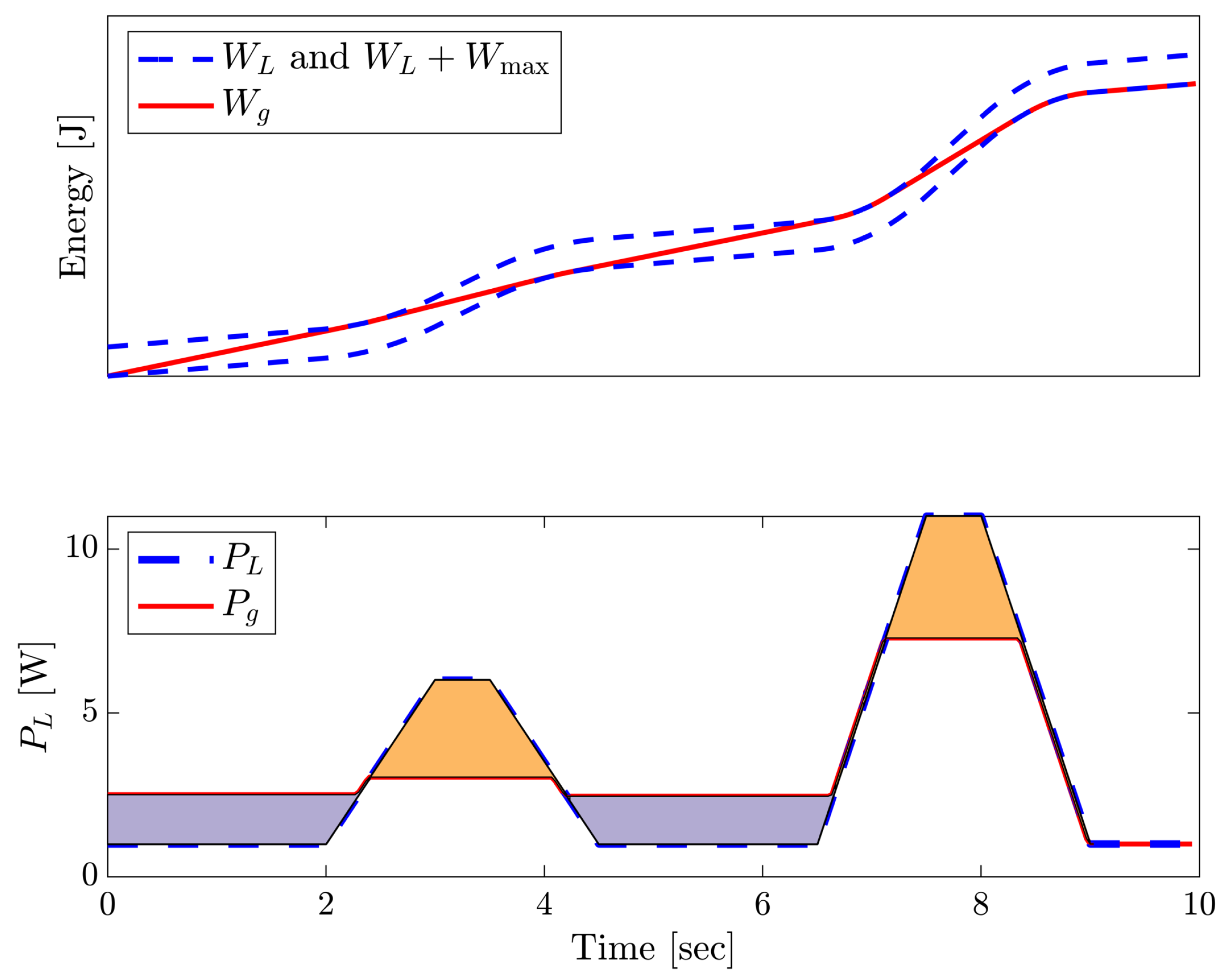
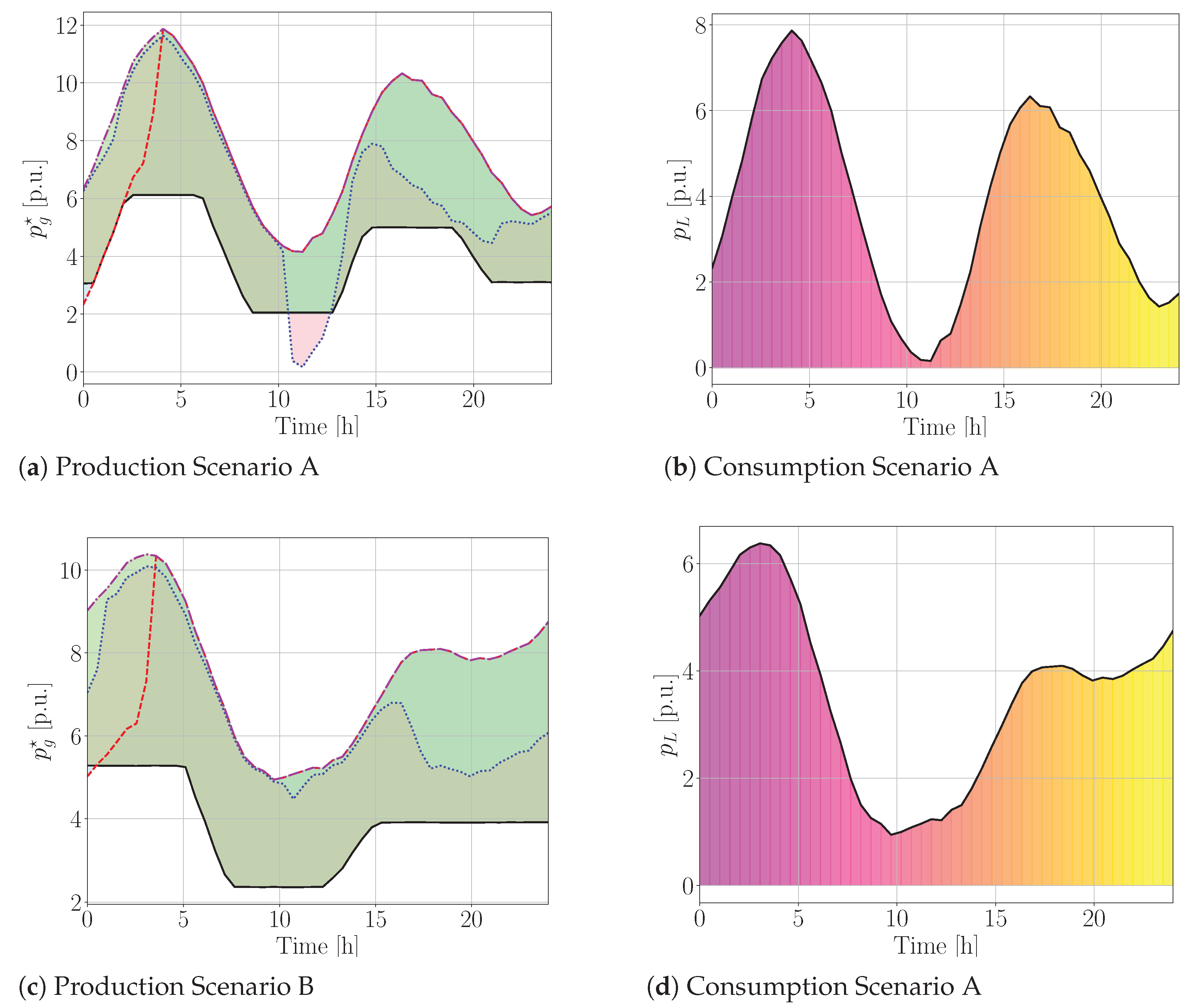
3. Comparative Analysis
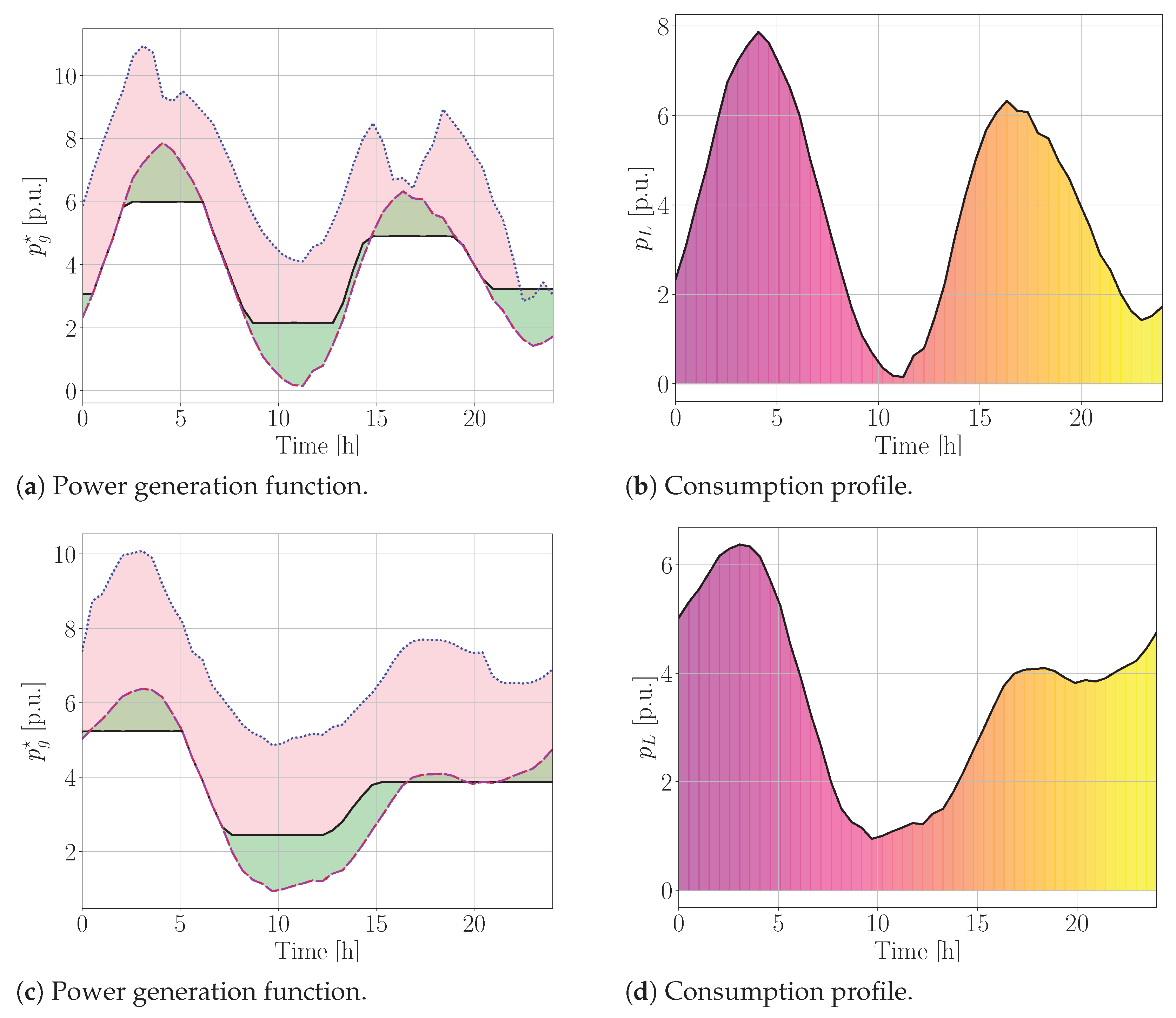
3.1. Energy Balancing with Transients
- 1.
- When examining consecutive days with similar demand and PV production patterns, policies tend to be similar due to the Cauchy-bounded nature of the value function.
- 2.
- The system dynamics remain consistent over time, ensuring stable relationships between storage, PV generation, grid interaction, and load.
- 3.
- The reward function exhibits convexity, preventing local minima.
- 4.
- The reward function exhibits symmetry concerning certain states and actions, guiding both algorithms toward similar policies. For example, we consider state , where high PV generation satisfies demand but additional charging ( p.u.) is necessary due to anticipated future demand, versus state , where low PV production requires purchasing 1 p.u. from the grid. Despite differing conditions, identical rewards may cause algorithms to converge to similar policies.
3.2. Hybrid Electrical Vehicle Simulation
4. Discussion
5. Conclusions
- The main contribution of this work is a rigorous proof of the central result provided in [19], which is one of the first papers in this group. This proof justifies the “shortest path” graphical design method, and assures that the optimal solution obtained is indeed unique, thus allowing to avoid possible conflicts between different competing optimal solutions.
- Most importantly, the uniqueness proof presented in this paper has practical implications, since a guarantee that the solution is unique allows for more confident decision-making in real-world applications, such as grid management, and energy dispatch. Furthermore, the analytical nature of the solution, in contrast to purely numerical approaches, offers potential advantages in terms of computational efficiency and interpretability. The graphical design procedure, coupled with a guarantee of a unique solution, facilitates a deeper understanding of the system’s behavior and can aid in the design and optimization of storage systems.
- The validation of the proposed solution through two distinct comparative studies further strengthens its credibility. The comparison with reinforcement learning algorithms on synthetic data highlights the potential advantages of the proposed method in terms of convergence speed and solution quality. The data analysis, using an electrical vehicle storage device, demonstrates the practical applicability and effectiveness of the proposed solution in a realistic scenario.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Integration interval | |
| Generated power | |
| Load power consumption | |
| Power that flows into the battery | |
| W | State of charge of the battery |
| Generated energy | |
| Energy demand of the load | |
| Energy capacity of the battery |
References
- Akinyele, D.; Rayudu, R. Review of energy storage technologies for sustainable power networks. Sustain. Energy Technol. Assessments 2014, 8, 74–91. [Google Scholar] [CrossRef]
- Khodadoost Arani, A.; Gharehpetian, G.B.; Abedi, M. Review on Energy Storage Systems Control Methods in Microgrids. Int. J. Electr. Power Energy Syst. 2019, 107, 745–757. [Google Scholar] [CrossRef]
- Machlev, R.; Zargari, N.; Chowdhury, N.; Belikov, J.; Levron, Y. A review of optimal control methods for energy storage systems–Energy trading, energy balancing and electric vehicles. J. Energy Storage 2020, 32, 101787. [Google Scholar] [CrossRef]
- Deng, K.; Sun, Y.; Li, S.; Lu, Y.; Brouwer, J.; Mehta, P.G.; Zhou, M.; Chakraborty, A. Model predictive control of central chiller plant with thermal energy storage via dynamic programming and mixed-integer linear programming. IEEE Trans. Autom. Sci. Eng. 2014, 12, 565–579. [Google Scholar] [CrossRef]
- Dolara, A.; Grimaccia, F.; Magistrati, G.; Marchegiani, G. Optimization Models for islanded micro-grids: A comparative analysis between linear programming and mixed integer programming. Energies 2017, 10, 241. [Google Scholar] [CrossRef]
- Harsha, P.; Dahleh, M. Optimal Management and Sizing of Energy Storage Under Dynamic Pricing for the Efficient Integration of Renewable Energy. IEEE Trans. Power Syst. 2015, 30, 1164–1181. [Google Scholar] [CrossRef]
- Yoon, Y.; Kim, Y.H. Effective scheduling of residential energy storage systems under dynamic pricing. Renew. Energy 2016, 87, 936–945. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, Y.; Zeeshan, M.; Han, F.; Song, K. Super-twisting sliding mode control of grid-side inverters for wind power generation systems with parameter perturbation. Int. J. Electr. Power Energy Syst. 2025, 165, 110501. [Google Scholar] [CrossRef]
- Asadi, Y.; Eskandari, M.; Mansouri, M.; Moradi, M.H.; Savkin, A.V. A universal model for power converters of battery energy storage systems utilizing the impedance-shaping concepts. Int. J. Electr. Power Energy Syst. 2023, 149, 109055. [Google Scholar] [CrossRef]
- Cirocco, L.R.; Belusko, M.; Bruno, F.; Boland, J.; Pudney, P. Controlling stored energy in a concentrating solar thermal power plant to maximise revenue. IET Renew. Power Gener. 2015, 9, 379–388. [Google Scholar] [CrossRef]
- Cirocco, L.; Pudney, P.; Boland, J.; Bruno, F.; Belusko, M. Maximising revenue via optimal control of a concentrating solar thermal power plant with limited storage capacity. IET Renew. Power Gener. 2016, 10, 729–734. [Google Scholar] [CrossRef]
- Lifshitz, D.; Weiss, G. Optimal Control of a Capacitor-Type Energy Storage System. IEEE Trans. Autom. Control 2015, 60, 216–220. [Google Scholar] [CrossRef]
- Nguyen, A.; Lauber, J.; Dambrine, M. Optimal control based algorithms for energy management of automotive power systems with battery/supercapacitor storage devices. Energy Convers. Manag. 2014, 87, 410–420. [Google Scholar] [CrossRef]
- Li, Q.; Huang, W.; Chen, W.; Yan, Y.; Shang, W.; Li, M. Regenerative braking energy recovery strategy based on Pontryagin’s minimum principle for fell cell/supercapacitor hybrid locomotive. Int. J. Hydrogen Energy 2019, 44, 5454–5461. [Google Scholar] [CrossRef]
- Cao, J.; Harrold, D.; Fan, Z.; Morstyn, T.; Healey, D.; Li, K. Deep reinforcement learning-based energy storage arbitrage with accurate lithium-ion battery degradation model. IEEE Trans. Smart Grid 2020, 11, 4513–4521. [Google Scholar] [CrossRef]
- Bui, V.H.; Hussain, A.; Kim, H.M. Double deep Q-learning-based distributed operation of battery energy storage system considering uncertainties. IEEE Trans. Smart Grid 2019, 11, 457–469. [Google Scholar] [CrossRef]
- Lee, H.; Song, C.; Kim, N.; Cha, S.W. Comparative analysis of energy management strategies for HEV: Dynamic Programming and Reinforcement Learning. IEEE Access 2020, 8, 67112–67123. [Google Scholar] [CrossRef]
- Jiang, D.R.; Pham, T.V.; Powell, W.B.; Salas, D.F.; Scott, W.R. A comparison of approximate dynamic programming techniques on benchmark energy storage problems: Does anything work? In Proceedings of the 2014 IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning (ADPRL), Orlando, FL, USA, 9–12 December 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Levron, Y.; Shmilovitz, D. Optimal power management in fueled systems with finite storage capacity. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 2221–2231. [Google Scholar] [CrossRef]
- Zivic Djurovic, M.; Milacic, A.; Krsulja, M. A simplified model of quadratic cost function for thermal generators. In Proceedings of the 23rd International DAAAM Symposium, Vienna, Austria, 24–25 October 2012; pp. 24–27. [Google Scholar]
- Chowdhury, N.R.; Ofir, R.; Zargari, N.; Baimel, D.; Belikov, J.; Levron, Y. Optimal control of lossy energy storage systems with nonlinear efficiency based on dynamic programming and Pontryagin’s Minimum Principle. IEEE Trans. Energy Convers. 2021, 36, 524–533. [Google Scholar] [CrossRef]
- Hobbs, B.F.; Drayton, G.; Bartholomew Fisher, E.; Lise, W. Improved transmission representations in oligopolistic market models: Quadratic losses, phase shifters, and DC lines. IEEE Trans. Power Syst. 2008, 23, 1018–1029. [Google Scholar] [CrossRef]






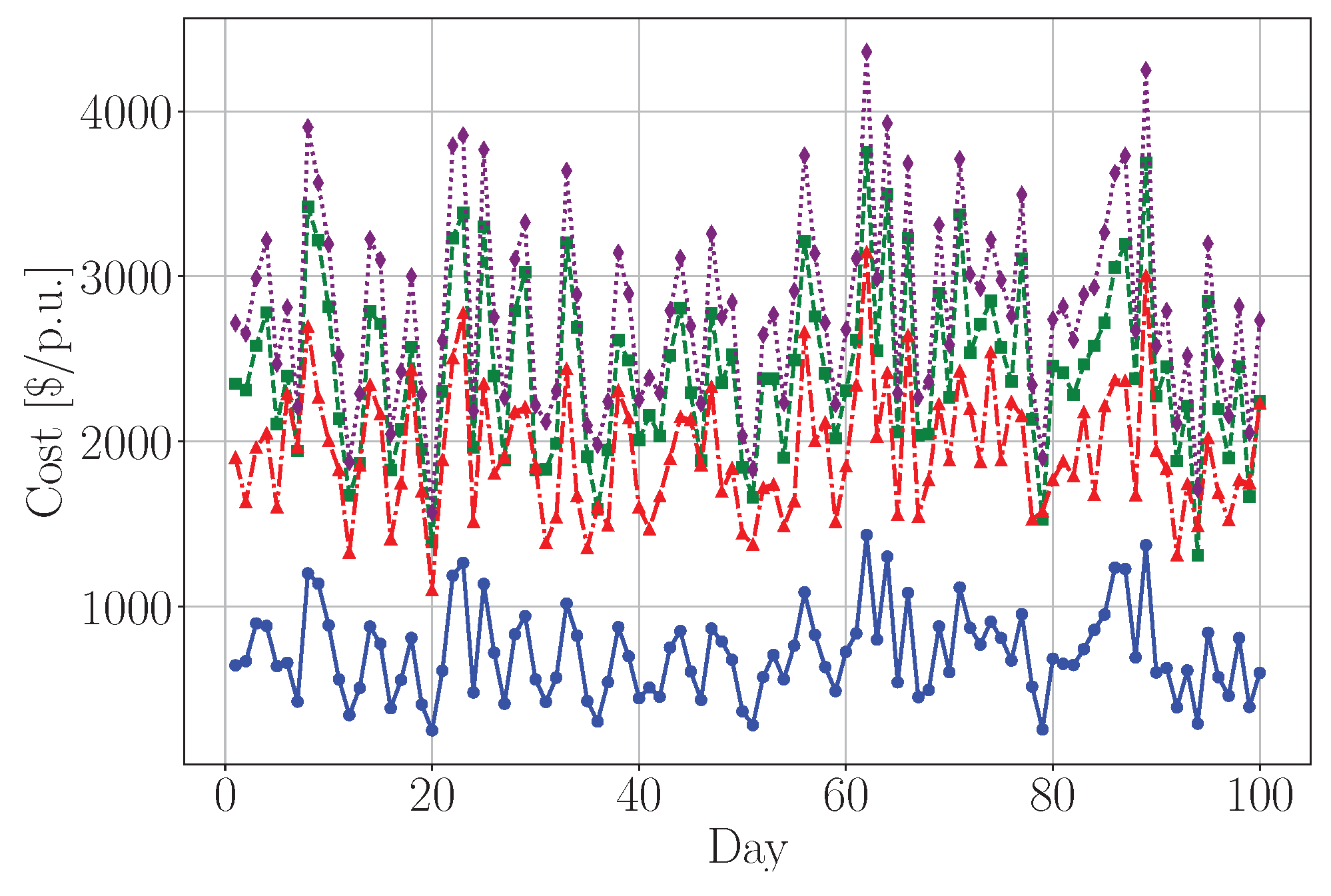
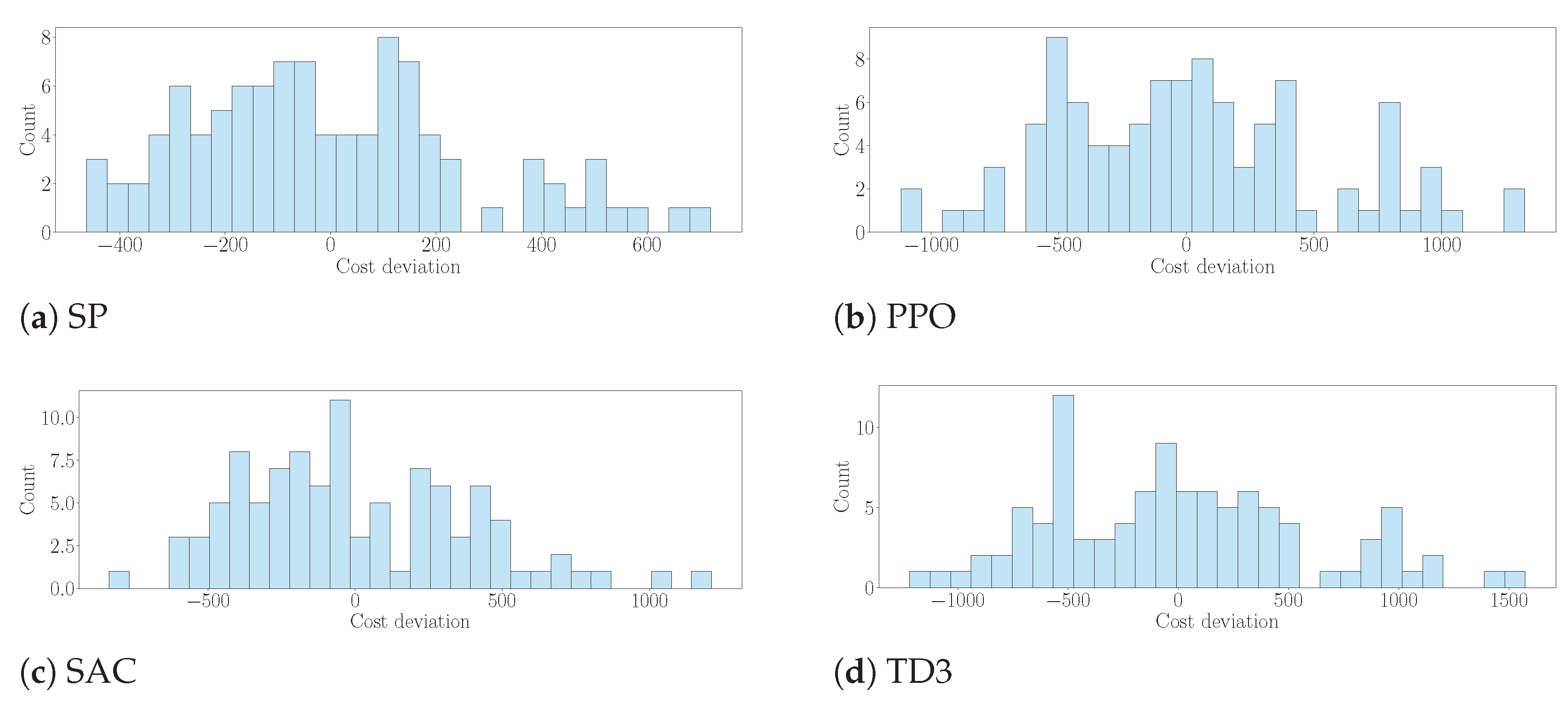


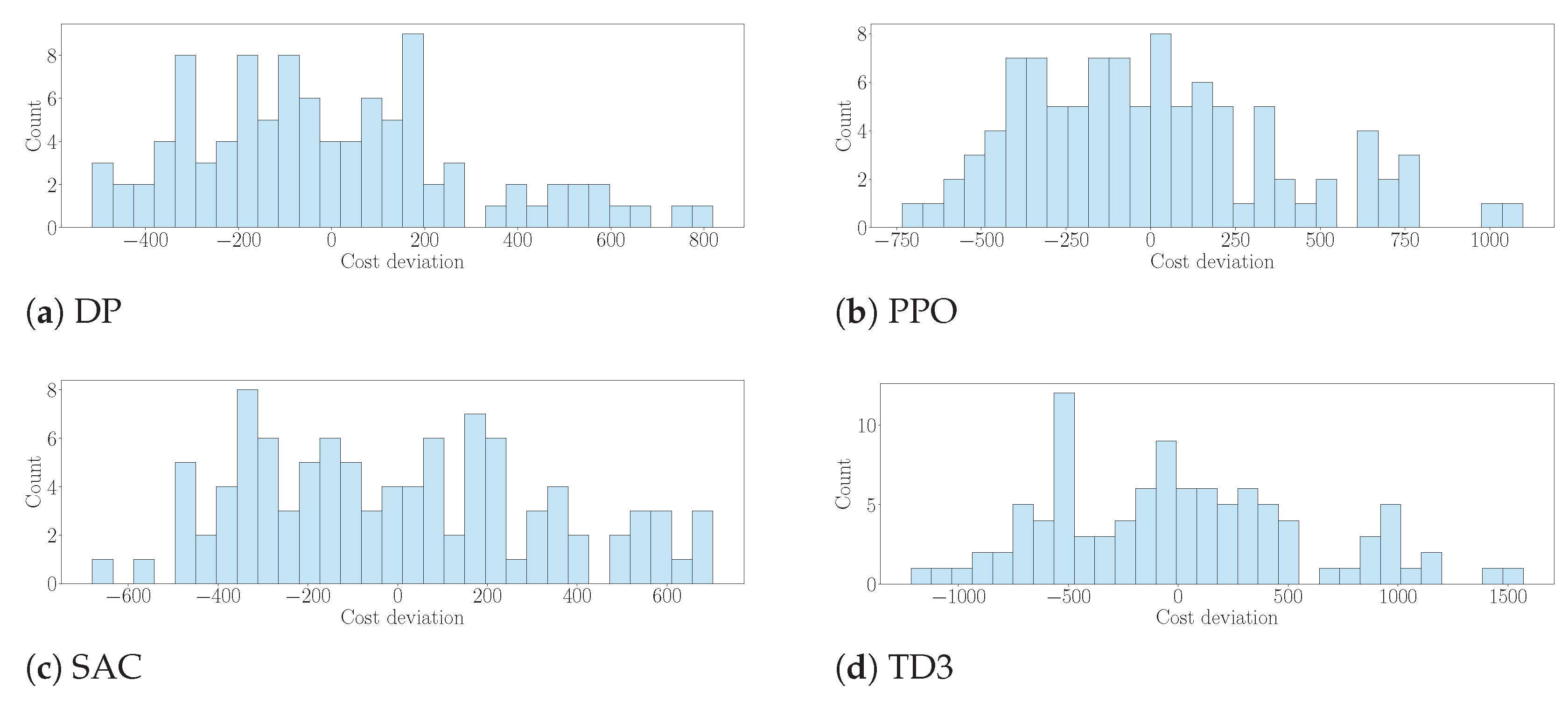
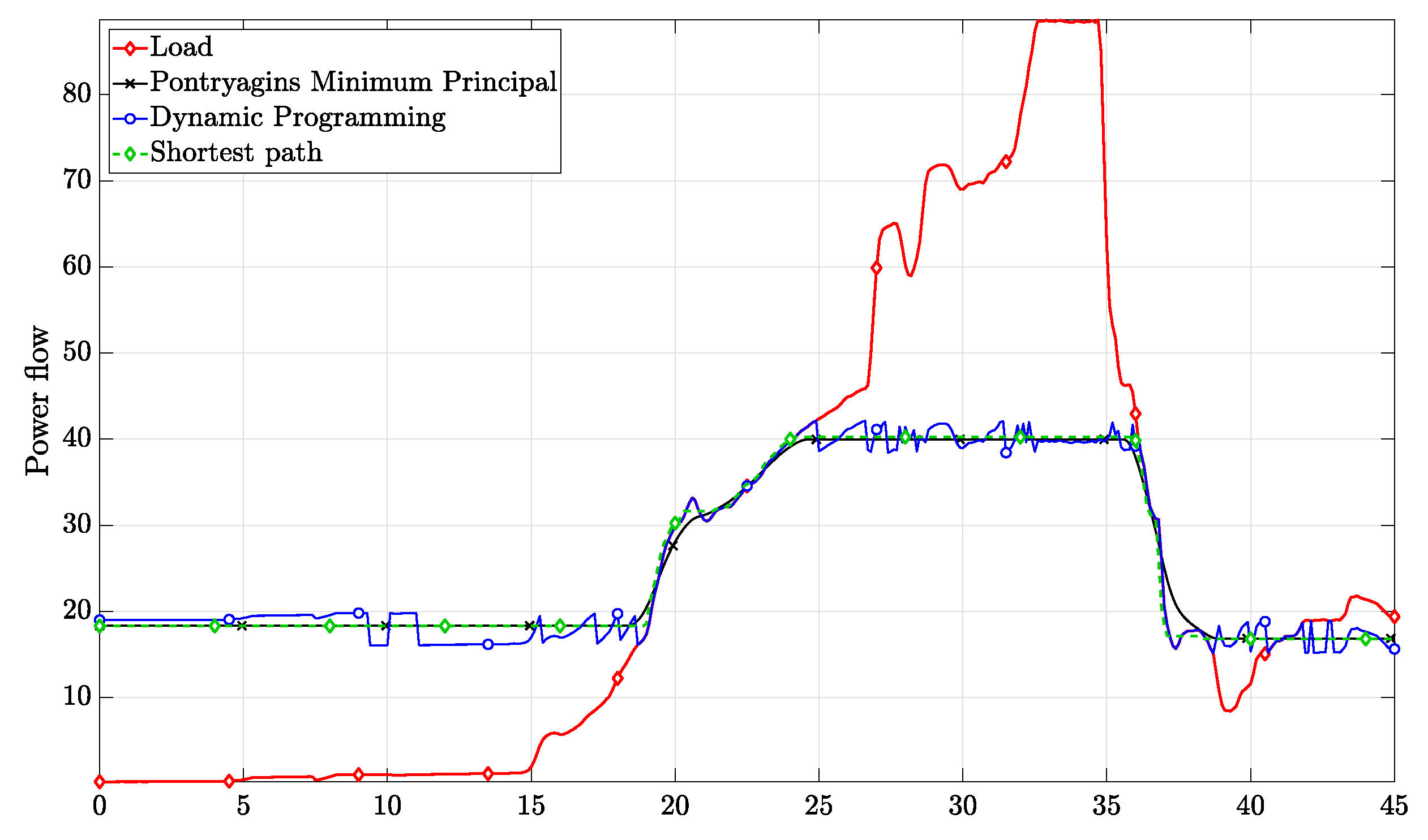
| Algorithm | Mean | Var |
|---|---|---|
| SP | 711.85 | 70,854.35 |
| PPO | 2428.24 | 271,321.64 |
| SAC | 1935.02 | 154,239.84 |
| TD3 | 2787.36 | 342,948.40 |
| Algorithm | Mean | Var |
|---|---|---|
| PMP | 705.82 | 69,024.48 |
| PPO | 748.17 | 88,234.85 |
| SAC | 2280.81 | 207,902.61 |
| TD3 | 748.17 | 88,234.85 |
| Algorithm | Mean | Var |
|---|---|---|
| DP | 773.10 | 89,220.93 |
| PPO | 1165.14 | 146,485.45 |
| SAC | 1293.96 | 109,379.59 |
| TD3 | 2779.89 | 342,000.82 |
| Model Name | Nominal | Shortes-Path | No |
|---|---|---|---|
| Mercedes-Benz | 13.1000 | 2.4811 | 79 |
| Nissan Leaf SV | 20.0757 | 3.0375 | 144 |
| Mitsubishi I-MiEV | 6.5887 | 1.1180 | 100 |
| Chevrolet Spark EV | 7.8028 | 1.9977 | 21 |
| Volkswagen e-Golf | 38.6643 | 19.2181 | 207 |
| Smart EV | 16.1382 | 8.9181 | 188 |
| BMW i3BEV | 21.7496 | 5.6388 | 1 |
| Ford Focus | 8.8122 | 1.7193 | 42 |
| Kia Soul | 82.2908 | 30.2048 | 64 |
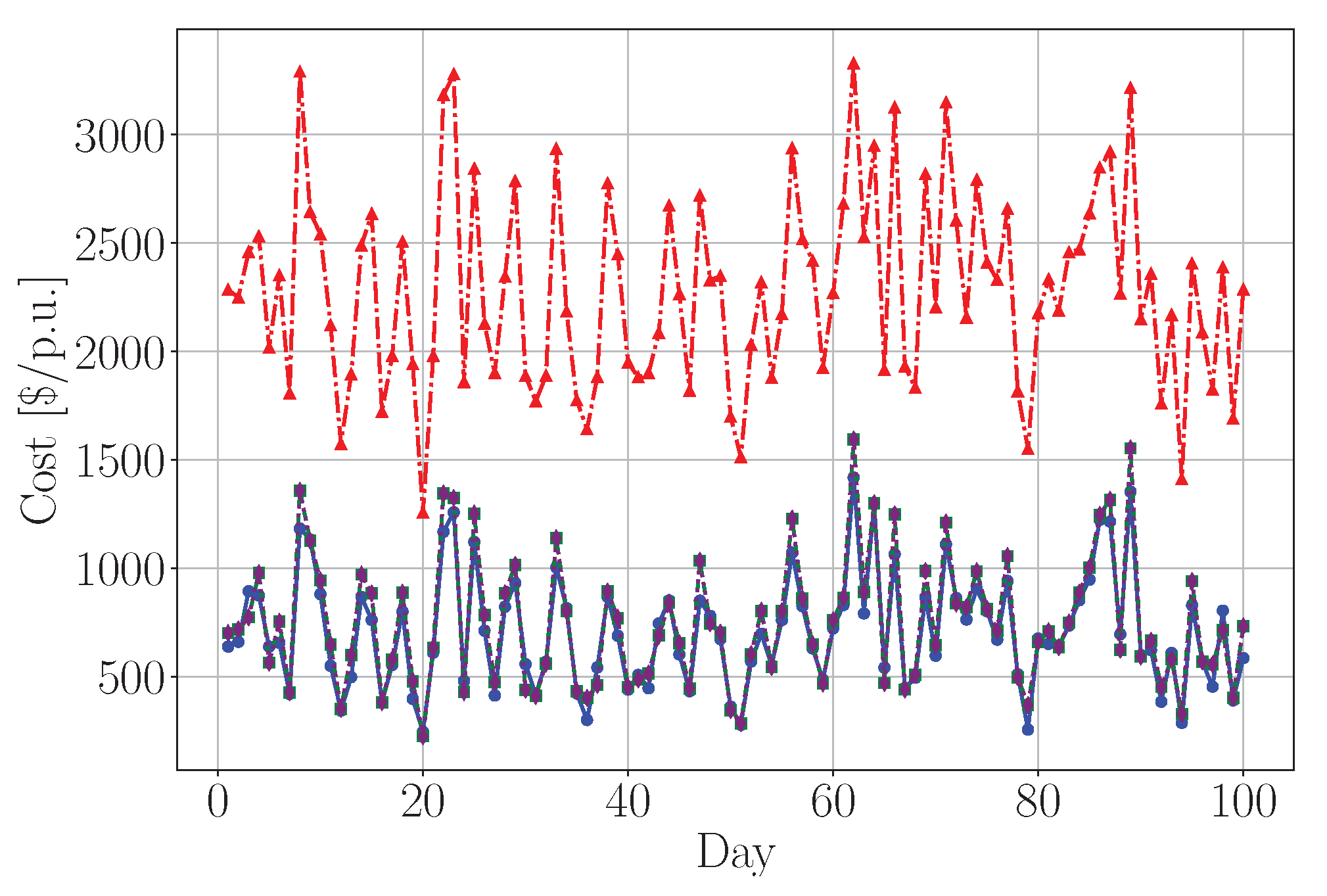
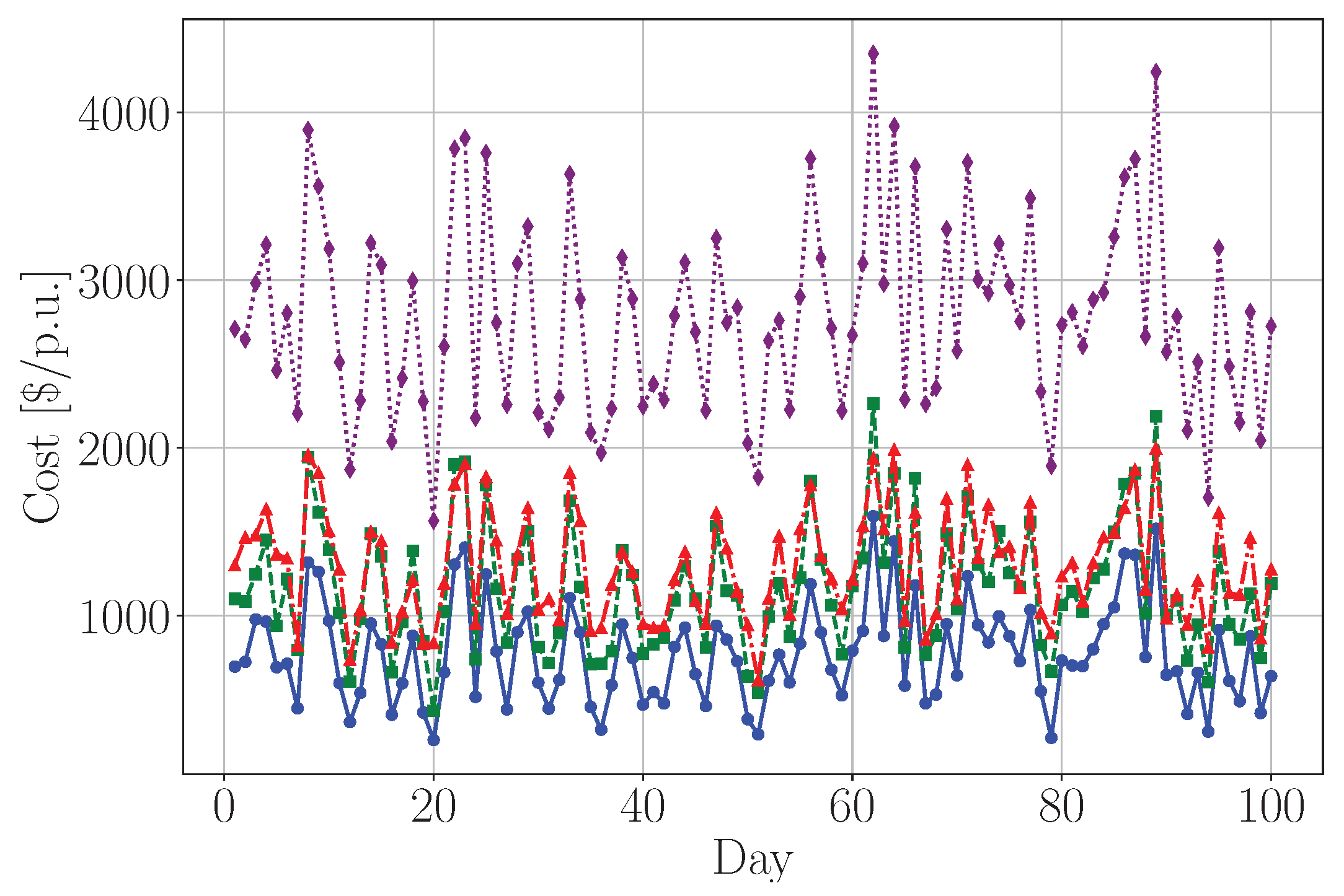
| Experiment | Key Observations | Role of SP as a Benchmarking Tool |
|---|---|---|
| Baseline Case | SP exhibits the lowest mean cost (711.85) and variance (70,854.35). RL algorithms perform significantly worse, with higher variance, indicating unstable policies. | SP serves as an interpretable reference, revealing structural properties of the optimal energy trajectory. It highlights RL inefficiencies in capturing the long-term dynamics of the system. |
| Lossy Storage Model | PMP achieves the lowest cost (705.82) and variance (69,024.48), demonstrating the effect of incorporating physical constraints explicitly. RL methods improve but still exhibit performance gaps. | SP provides a qualitative baseline for assessing the effect of adding realistic losses. By comparing RL outputs to SP and PMP, it is evident that RL struggles with long-term energy planning. |
| Lossy Transmission Line Model | DP achieves the lowest mean cost (773.10) and variance (89,220.93), outperforming RL methods. RL variance remains high, showing unstable learning behavior. | SP acts as an initial structural guide, allowing researchers to interpret whether more advanced algorithms are following expected energy trajectories. The graphical approach aids in evaluating solution smoothness and feasibility. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goldstein-Tweg, T.; Ginzburg-Ganz, E.; Belikov, J.; Levron, Y. Uniqueness of Optimal Power Management Strategies for Energy Storage Dynamic Models. Energies 2025, 18, 1483. https://doi.org/10.3390/en18061483
Goldstein-Tweg T, Ginzburg-Ganz E, Belikov J, Levron Y. Uniqueness of Optimal Power Management Strategies for Energy Storage Dynamic Models. Energies. 2025; 18(6):1483. https://doi.org/10.3390/en18061483
Chicago/Turabian StyleGoldstein-Tweg, Tom, Elinor Ginzburg-Ganz, Juri Belikov, and Yoash Levron. 2025. "Uniqueness of Optimal Power Management Strategies for Energy Storage Dynamic Models" Energies 18, no. 6: 1483. https://doi.org/10.3390/en18061483
APA StyleGoldstein-Tweg, T., Ginzburg-Ganz, E., Belikov, J., & Levron, Y. (2025). Uniqueness of Optimal Power Management Strategies for Energy Storage Dynamic Models. Energies, 18(6), 1483. https://doi.org/10.3390/en18061483







