Demonstration of a Practical Cooling Storage System for Lithium-Ion Batteries with Trimethylolethane (TME) Hydrate for EV
Abstract
1. Introduction
2. Estimation of Heat Generation in Lithium-Ion Batteries
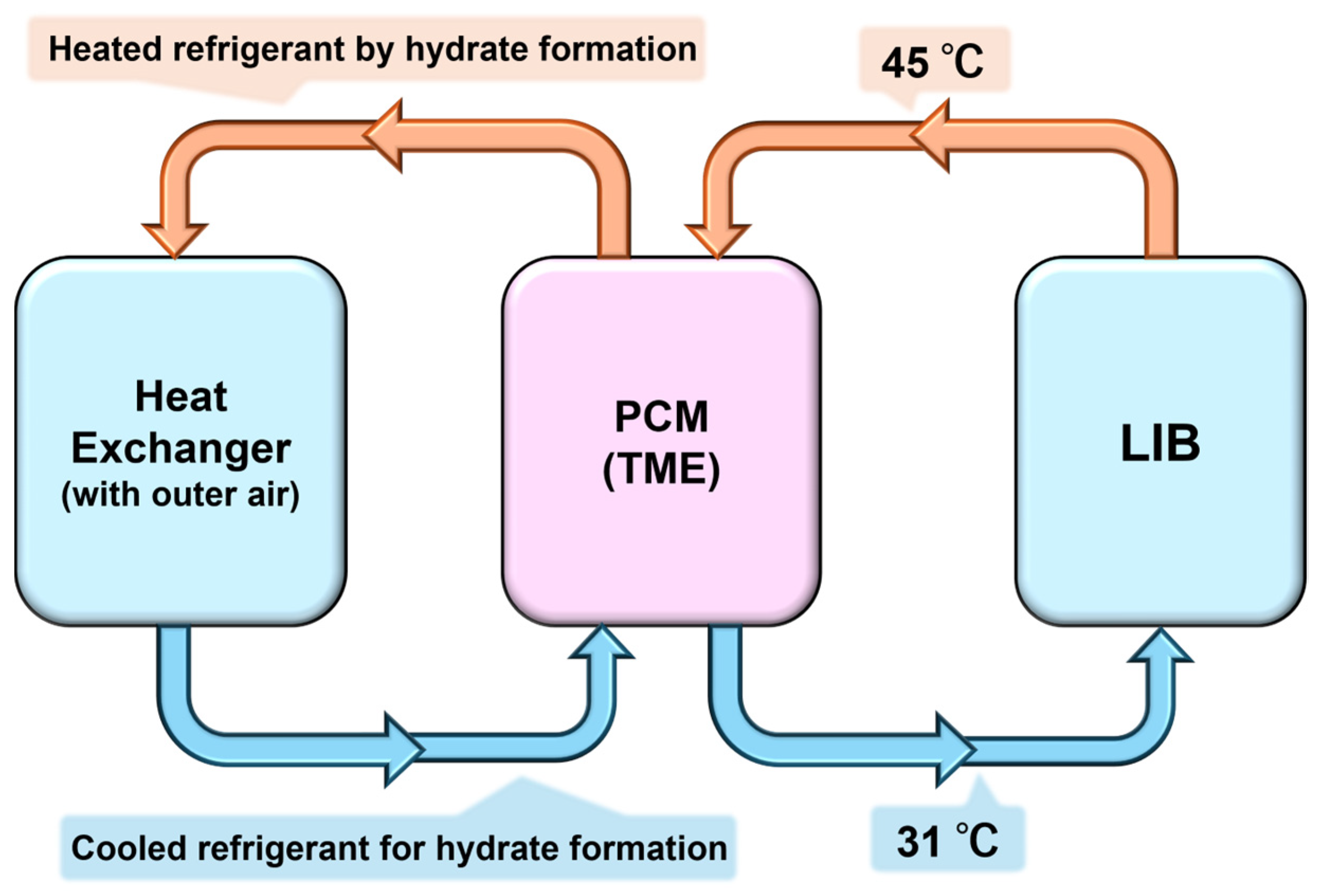
3. Heat Exchanger and Thermal Energy Tank with TME Hydrate
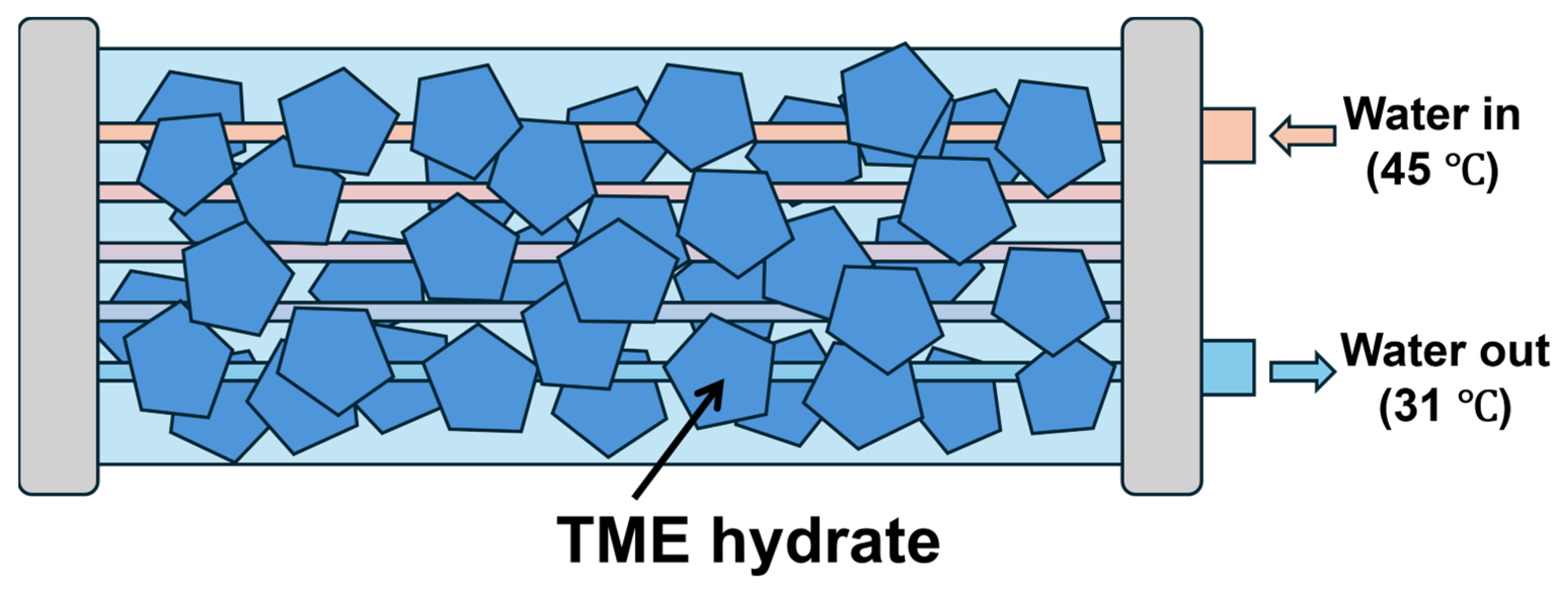
3.1. TME Hydrate Reservoir (PCM-Based Heat Exchanger)
3.2. Heat Transfer Coefficient on Waterside
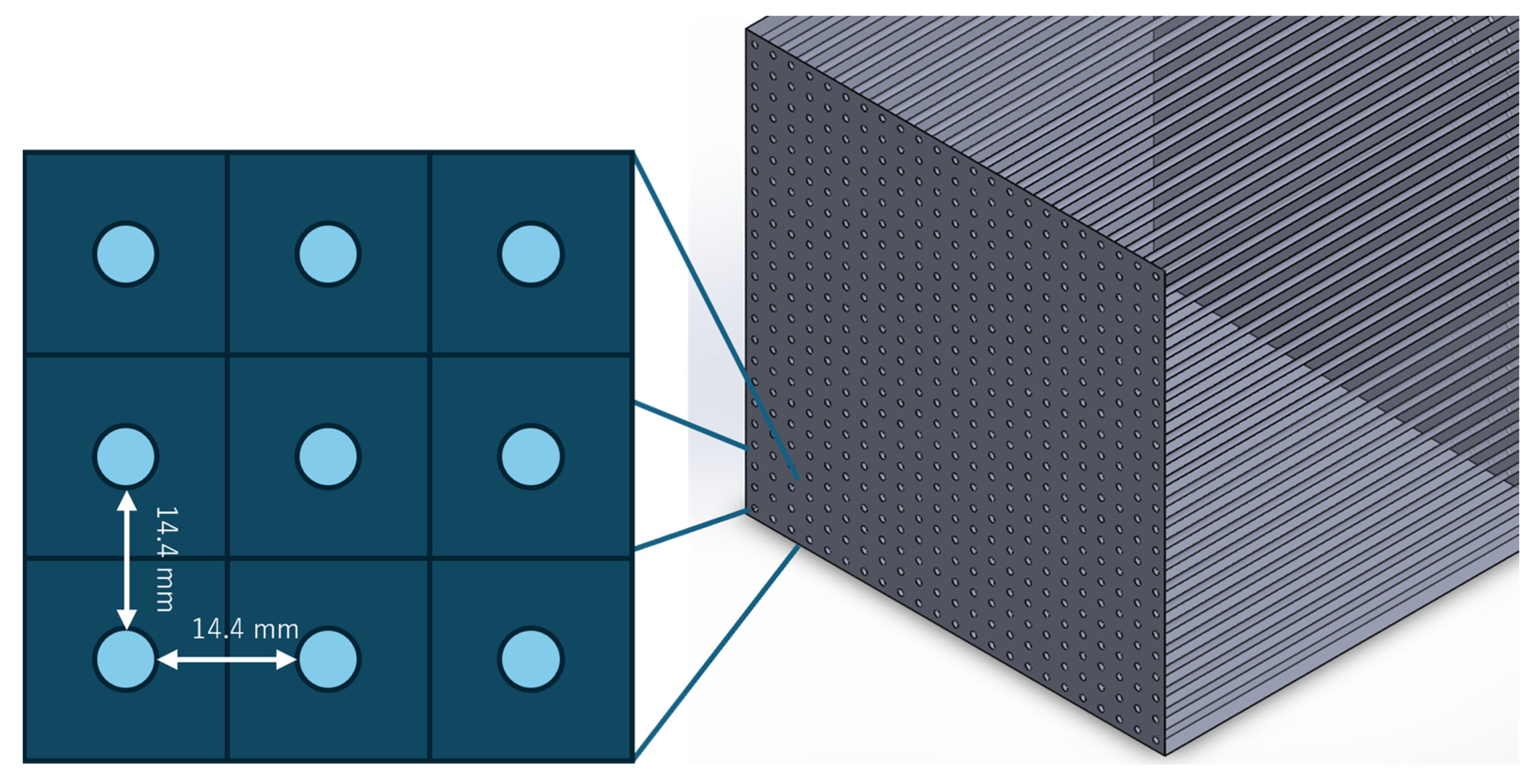
3.3. Detail Design of Pipe Configuration
3.4. The Heat Exchange with the Outer Air
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karimi, G.; Li, X. Thermal management of lithium-ion batteries for electric vehicles. Int. J. Energy Res. 2013, 37, 13–24. [Google Scholar] [CrossRef]
- Khateeb, S.A.; Farid, M.M.; Selman, J.R.; Al-Hallaj, S. Design and simulation of a lithium-ion battery with a phase change material thermal management system for an electric scooter. J. Power Sources 2004, 128, 292–307. [Google Scholar] [CrossRef]
- Rao, Z.; Wang, S. A review of power battery thermal energy management. Renew. Sustain. Energy Rev. 2011, 15, 4554–4571. [Google Scholar] [CrossRef]
- Wang, X.; Xie, Y.; Day, R.; Wu, H.; Hu, Z.; Zhu, J.; Wen, D. Performance analysis of a novel thermal management system with composite phase change material for a lithium-ion battery pack. Energy 2018, 156, 154–168. [Google Scholar] [CrossRef]
- Chen, G.; Shi, Y.; Yu, Y. A thermal management design using phase change material in embedded finned shells for lithium-ion batteries. Int. J. Heat Mass. Transf. 2024, 229, 125680. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Xin, Q.; Yang, T.; Zhang, H.; Yang, J.; Zeng, J.; Xiao, J. Experimental and numerical study of lithium-ion battery thermal management system using composite phase change material and liquid cooling. J. Energy Storage 2023, 71, 108003. [Google Scholar] [CrossRef]
- Chavan, S.; Venkateswarlu, B.; Salman, M.; Liu, J.; Pawar, P.; Joo, S.W.; Choi, G.S.; Kim, S.C. Thermal management strategies for lithium-ion batteries in electric vehicles: Fundamentals, recent advances, thermal models, and cooling techniques. Int. J. Heat Mass. Transf. 2024, 232, 125918. [Google Scholar] [CrossRef]
- Fan, L.; Khodadadi, J.M.; Pesaran, A.A. A parametric study on thermal management of an air-cooled lithium-ion battery module for plug-in hybrid electric vehicles. J. Power Sources 2013, 238, 301–312. [Google Scholar] [CrossRef]
- Wang, D.; Xie, J.; Wang, D.; Xie, J. Investigation of the Liquid Cooling and Heating of a Lithium-Ion Battery Package for an Electric Vehicle. World Electr. Veh. J. 2023, 14, 169. [Google Scholar] [CrossRef]
- Park, H. A design of air flow configuration for cooling lithium ion battery in hybrid electric vehicles. J. Power Sources 2013, 239, 30–36. [Google Scholar] [CrossRef]
- Wang, S.; Ma, Z. Supervisory and optimal control of building HVAC systems: A review. HVAC R Res. 2008, 14, 3–32. [Google Scholar] [CrossRef]
- Sanaye, S.; Shirazi, A. Thermo-economic optimization of an ice thermal energy storage system for air-conditioning applications. Energy Build. 2013, 60, 100–109. [Google Scholar] [CrossRef]
- MacPhee, D.; Dincer, I. Performance assessment of some ice TES systems. Int. J. Therm. Sci. 2009, 48, 2288–2299. [Google Scholar] [CrossRef]
- Oró, E.; de Gracia, A.; Castell, A.; Farid, M.M.; Cabeza, L.F. Review on phase change materials (PCMs) for cold thermal energy storage applications. Appl. Energy 2012, 99, 513–533. [Google Scholar] [CrossRef]
- da Cunha, J.P.; Eames, P. Thermal energy storage for low and medium temperature applications using phase change materials—A review. Appl. Energy 2016, 177, 227–238. [Google Scholar] [CrossRef]
- Tsai, W.T. An overview of environmental hazards and exposure risk of hydrofluorocarbons (HFCs). Chemosphere 2005, 61, 1539–1547. [Google Scholar] [CrossRef]
- Matsuura, R.; Maruyama, M.; Ohmura, R. Review of Ionic Semiclathrate Hydrates as Thermal Energy Storage Materials: Properties and Applications. ACS Appl. Eng. Mater. 2024, 2, 503–520. [Google Scholar] [CrossRef]
- Antunes, A.H.P.; Filho, E.P.B. Experimental investigation on the performance and global environmental impact of a refrigeration system retrofitted with alternative refrigerants. Int. J. Refrig. 2016, 70, 119–127. [Google Scholar] [CrossRef]
- Sanker, S.B.; Baby, R. Phase change material based thermal management of lithium ion batteries: A review on thermal performance of various thermal conductivity enhancers. J. Energy Storage 2022, 50, 104606. [Google Scholar] [CrossRef]
- Nakajima, M.; Ohinura, R.; Mori, Y.H. Clathrate hydrate formation from cyclopentane-in-water emulsions. Ind. Eng. Chem. Res. 2008, 47, 8933–8939. [Google Scholar] [CrossRef]
- Delroisse, H.; Plantier, F.; Marlin, L.; Dicharry, C.; Frouté, L.; André, R.; Torré, J.P. Determination of thermophysical properties of cyclopentane hydrate using a stirred calorimetric cell. J. Chem. Thermodyn. 2018, 125, 136–141. [Google Scholar] [CrossRef]
- Masahiro, N.; Atsushi, H. High-Efficient Thermal Energy Storage Technique with a Clathrate Hydrate. IHI Eng. Rev. 2009, 4, 210–218. [Google Scholar]
- Muromachi, S.; Udachin, K.A.; Alavi, S.; Ohmura, R.; Ripmeester, J.A. Selective occupancy of methane by cage symmetry in TBAB ionic clathrate hydrate. Chem. Commun. 2016, 52, 5621–5624. [Google Scholar] [CrossRef] [PubMed]
- Kiyokawa, H.; Kondo, Y.; Koyama, R.; Kurokawa, N.; Atsushi, H.; Alavi, S.; Ota, I.; Ohmura, R. Pinacol hydrate as a novel thermal energy storage medium for electric vehicles. J. Energy Storage 2022, 51, 104404. [Google Scholar] [CrossRef]
- Koyama, R.; Arai, Y.; Yamauchi, Y.; Takeya, S.; Endo, F.; Hotta, A.; Ohmura, R. Thermophysical properties of trimethylolethane (TME) hydrate as phase change material for cooling lithium-ion battery in electric vehicle. J. Power Sources 2019, 427, 70–76. [Google Scholar] [CrossRef]
- Kakiuchi, H.; Yabe, M.; Yamazaki, M. A Study of Trimethylolethane Hydrate as a Phase Change Material. J. Chem. Eng. Jpn. 2003, 36, 788–793. [Google Scholar] [CrossRef]
- Kiyokawa, H.; Tokutomi, H.; Ishida, S.; Nishi, H.; Ohmura, R. Thermal Energy Storage Performance of Tetrabutylammonium Acrylate Hydrate as Phase Change Materials. Appl. Sci. 2021, 11, 4848. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Shabani, B.; Biju, M. Theoretical modelling methods for thermal management of batteries. Energies 2015, 8, 10153–10177. [Google Scholar] [CrossRef]
- An, Z.; Jia, L.; Ding, Y.; Dang, C.; Li, X. A review on lithium-ion power battery thermal management technologies and thermal safety. J. Therm. Sci. 2017, 26, 391–412. [Google Scholar] [CrossRef]
- Dai, N.; Long, J. Research on fast-charging battery thermal management system based on refrigerant direct cooling. Sci. Rep. 2023, 13, 11707. [Google Scholar] [CrossRef] [PubMed]
- Abada, S.; Marlair, G.; Lecocq, A.; Petit, M.; Sauvant-Moynot, V.; Huet, F. Safety focused modeling of lithium-ion batteries: A review. J. Power Sources 2016, 306, 178–192. [Google Scholar] [CrossRef]
- Yamazaki, M.; Sasaki, C.; Kakiuchi, H.; Osano, Y.T.; Suga, H. Thermal and structural characterization of trimethylolethane trihydrate. Thermochim. Acta 2002, 387, 39–45. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Yang, K.; Chen, Z.; Zhang, P. Production and flow behaviors of CO2+TBAB hydrate slurry for cold storage and transport application. Energy 2025, 316, 134485. [Google Scholar] [CrossRef]
- Yang, K.; Guo, W.; Zhang, P. Cold energy transport and release characteristics of CO2+TBAB hydrate slurry flow with hydrate dissociation. Energy 2024, 294, 130620. [Google Scholar] [CrossRef]
- Christensen, K.G.; Kauffeld, M. Heat Transfer Measurements with Ice Slurry. In Proceedings of the IIR/IIF International Conference, Heat Transfer Issues in Natural Refrigerants, College Park, MD, USA, 6–7 November 1997. [Google Scholar]
- The Japan Society of Mechanical Engineers. Data Book Thermophysical Properties of Fluids; JSME: Fukuoka, Japan, 1983. [Google Scholar]
- Japan Society Mechanical Engineering. JSME Data Book: Heat Transfer; Japan Society Mechanical Engineering: Fukuoka, Japan, 2009; Volume 6, 332p. [Google Scholar]
- Iida, T.; Mori, H.; Mochizuki, T.; Mori, Y.H. Formation and dissociation of clathrate hydrate in stoichiometric tetrahydrofuran–water mixture subjected to one-dimensional cooling or heating. Chem. Eng. Sci. 2001, 56, 4747. [Google Scholar] [CrossRef]
- Kim, H.; Zheng, J.; Babu, P.; Kumar, S.; Tee, J.; Linga, P. Key factors influencing the kinetics of tetra-n-butylammonium bromide hydrate formation as a cold storage and transport material. Chem. Eng. J. 2022, 446, 136843. [Google Scholar] [CrossRef]
- Yamamoto, K.; Iwai, T.; Hiraga, K.; Miyamoto, T.; Hotta, A.; Ohmura, R. Synthesis and thermophysical properties of Tetrabutylammonium picolinate hydrate as an energy storage phase change material for cold chain. J. Energy Storage 2022, 55, 105812. [Google Scholar] [CrossRef]


| Parameters. | Value |
|---|---|
| 190.1 | |
| Dissociation temperature of TME hydrate (wTME = 0.60) Teq/°C | 29.6 |
| 5.84 | |
| The inlet temperature of coolant Tin/°C | 45.0 |
| Outlet temperature of coolant Tout/°C | 31.0 |
| /kW | 12.0 |
| Overall Heat Transfer: U/W m−2 K−1 | 500 | 1000 | 2500 |
|---|---|---|---|
| Tube length (1/4 inch): L/m | 206.0 | 103.0 | 41.2 |
| Tube length (1/8 inch): L/m | 412.1 | 206.0 | 82.4 |
| System volume; PCM = 0.05: V (1/4 inch)/m3 | 0.05652 | 0.05326 | 0.05065 |
| System volume; PCM = 0.1 m3: V (1/4 inch)/m3 | 0.1065 | 0.1032 | 0.1013 |
| Area density; A/V (PCM = 0.05 m3):/m2/m3 | 77.17 | 38.59 | 16.02 |
| Area density; A/V (PCM = 0.1 m3):/m2/m3 | 39.80 | 19.90 | 8.11 |
| Parameters | Value |
|---|---|
| Total system volume m3 | 0.100 |
| The volume of TME hydrate m3 | 0.0926 |
| Tube length (1/4 inch): L/m | 232.7 |
| 5.84 | |
| The inlet temperature of coolant Tin/°C | 45.0 |
| Outlet temperature of coolant Tout/°C | 31.0 |
| /kW | 12.0 |
| Assumed heat transfer coefficients | 500 |
| Heating face m2 | 4.65 |
| Area density m2/m3 | 46.5 |
| Thermal storage capacity kJ | 19,715 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamiya, L.; Koyama, R.; Arai, Y.; Ohmura, R. Demonstration of a Practical Cooling Storage System for Lithium-Ion Batteries with Trimethylolethane (TME) Hydrate for EV. Energies 2025, 18, 1457. https://doi.org/10.3390/en18061457
Kamiya L, Koyama R, Arai Y, Ohmura R. Demonstration of a Practical Cooling Storage System for Lithium-Ion Batteries with Trimethylolethane (TME) Hydrate for EV. Energies. 2025; 18(6):1457. https://doi.org/10.3390/en18061457
Chicago/Turabian StyleKamiya, Leo, Ryo Koyama, Yuta Arai, and Ryo Ohmura. 2025. "Demonstration of a Practical Cooling Storage System for Lithium-Ion Batteries with Trimethylolethane (TME) Hydrate for EV" Energies 18, no. 6: 1457. https://doi.org/10.3390/en18061457
APA StyleKamiya, L., Koyama, R., Arai, Y., & Ohmura, R. (2025). Demonstration of a Practical Cooling Storage System for Lithium-Ion Batteries with Trimethylolethane (TME) Hydrate for EV. Energies, 18(6), 1457. https://doi.org/10.3390/en18061457





