Research on Thermo-Mechanical Response of Solid-State Core Matrix in a Heat Pipe Cooled Reactor
Abstract
1. Introduction
2. Methodology and Validation
2.1. HPR Design
2.2. Material Property Models
2.2.1. Stainless Steel 316 [24]
2.2.2. UO2 Fuel [26]
2.3. Thermal and Mechanical Models
2.3.1. Thermal Models
2.3.2. Mechanical Models
2.4. Simulation Methodology with ABAQUS and Validation
3. Simulation Results and Discussion
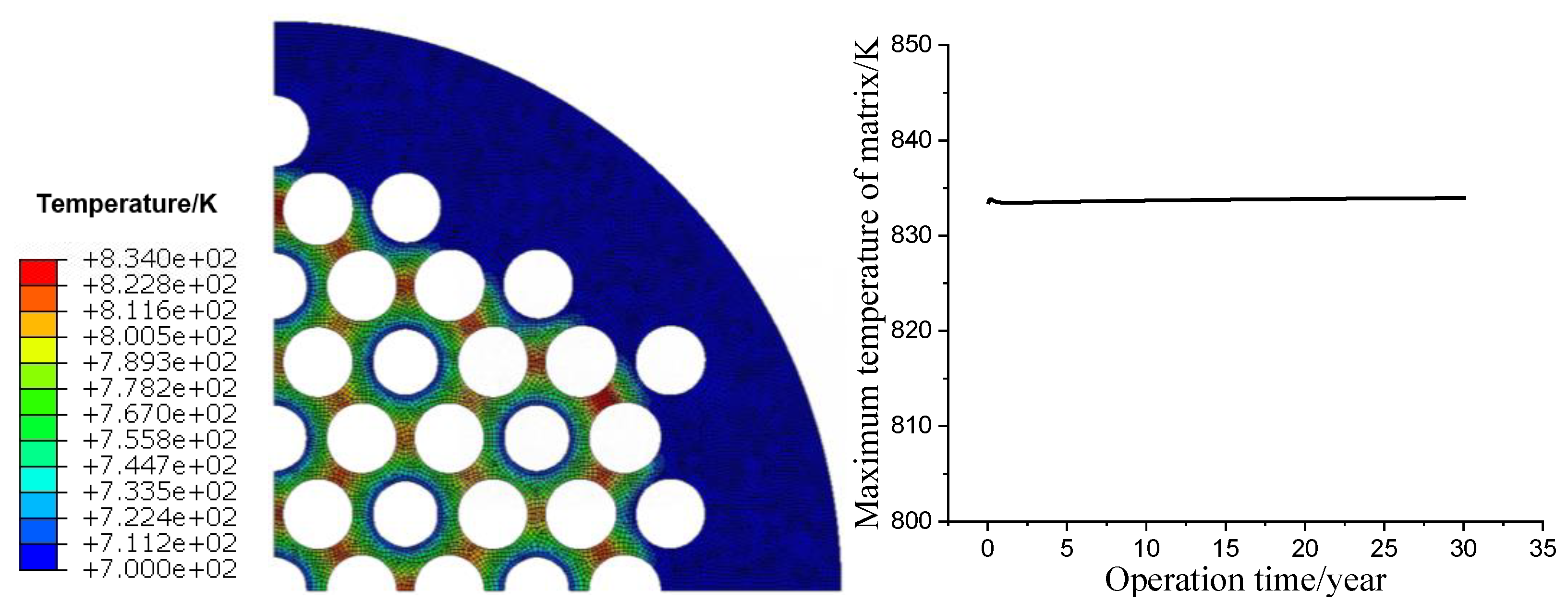
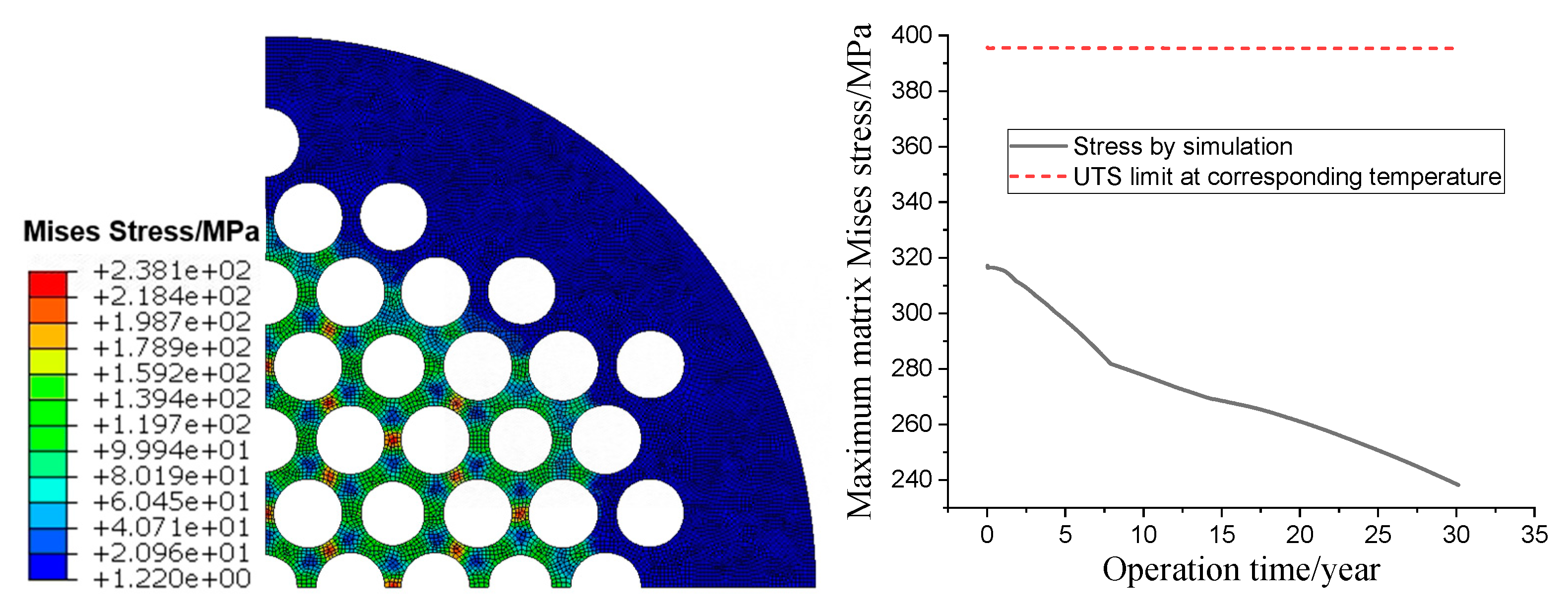
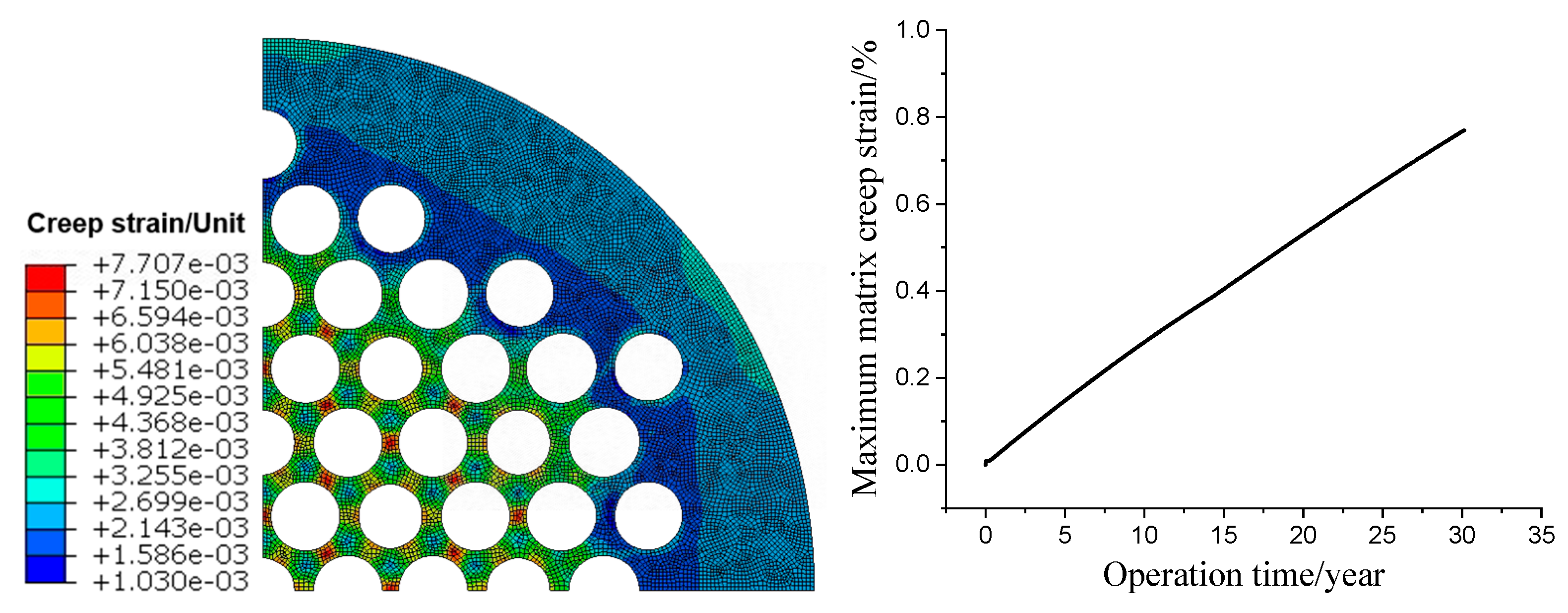
3.1. Long-Life Normal Operation
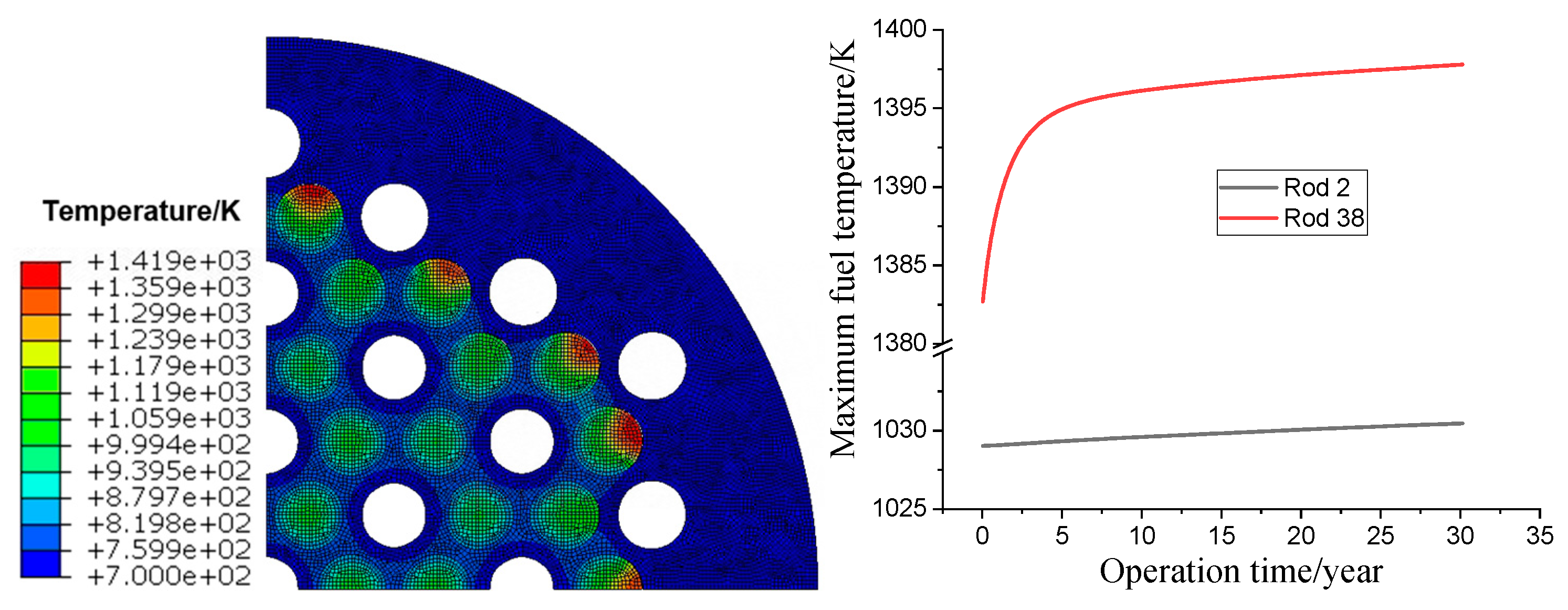
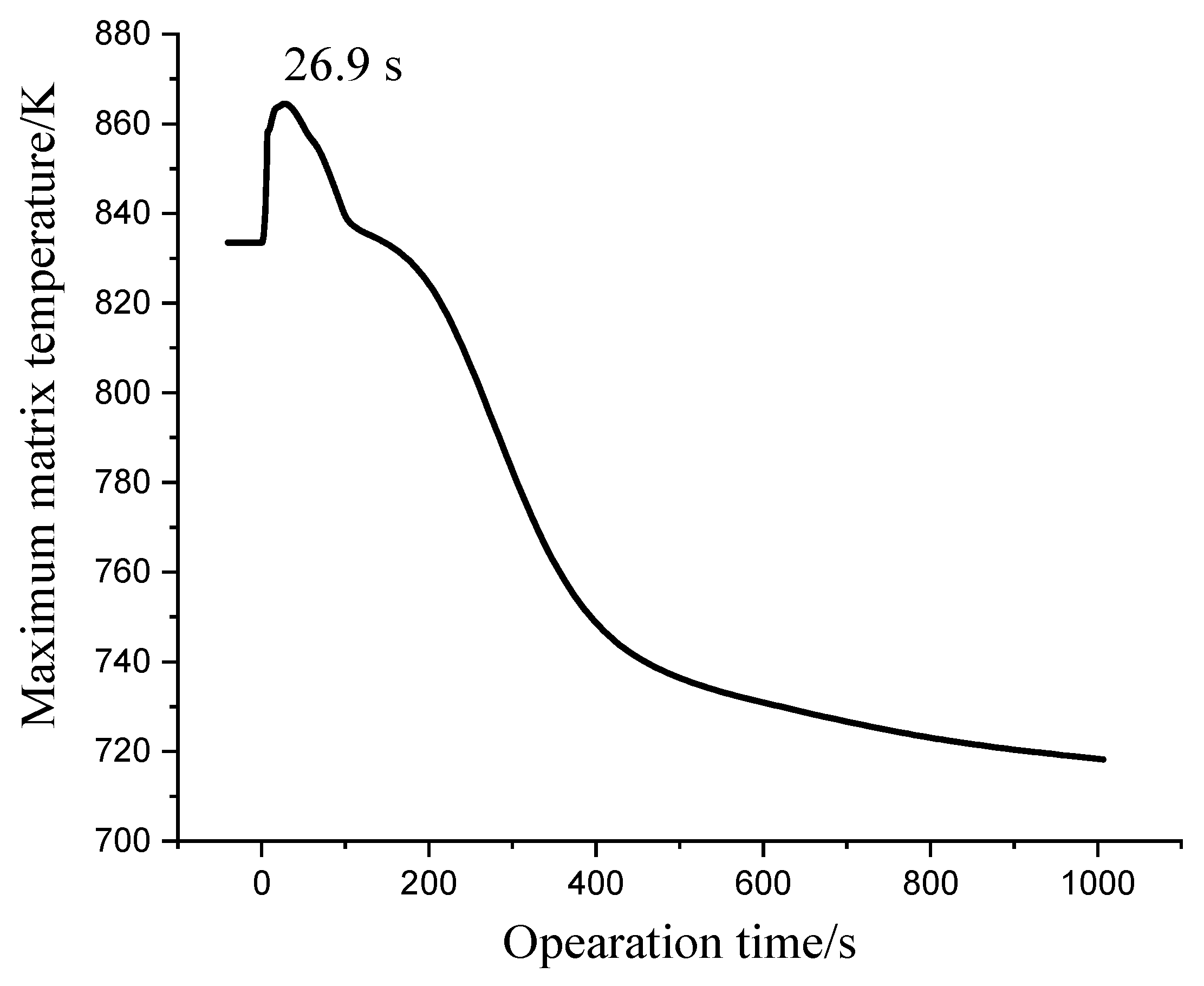
3.2. Operation Under Single Heat Pipe Failed Condition
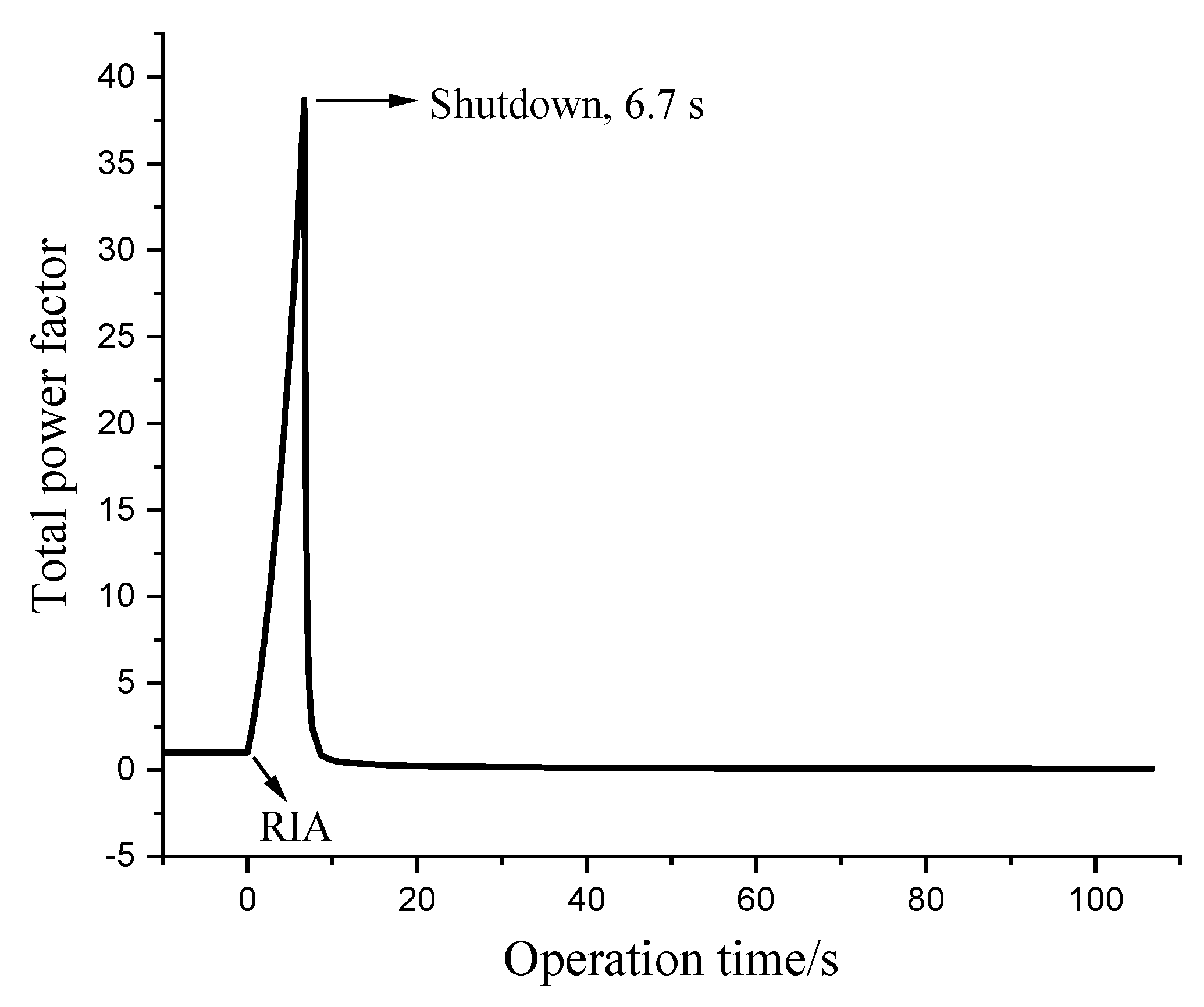
3.3. Operation Under RIA Condition
4. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sadekin, S.; Zaman, S.; Mahfuz, M.; Sarkar, R. Nuclear power as foundation of a clean energy future: A review. Energy Procedia 2019, 160, 513–518. [Google Scholar] [CrossRef]
- Bayraktar, M.; Pamik, M. Nuclear power utilization as a future alternative energy on icebreakers. Nucl. Eng. Technol. 2023, 55, 580–586. [Google Scholar] [CrossRef]
- Yan, B.H.; Wang, C.; Li, L.G. The technology of micro heat pipe cooled reactor: A review. Ann. Nucl. Energy 2020, 135, 106948. [Google Scholar] [CrossRef]
- Poston, D.I. The Heat pipe-Operated Mars Exploration Reactor (HOMER). AIP Conf. Proc. 2001, 552, 797–804. [Google Scholar]
- Poston, D.I.; Mcclure, P.R.; Dixon, D.D. Experimental demonstration of a heat pipe–stirling engine nuclear reactor. Nucl. Technol. 2014, 188, 229–237. [Google Scholar] [CrossRef]
- Bess, J.D. A Basic LEGO reactor design for the provision of lunar surface power. Report of Idaho National Laboratory. In Proceedings of the International Congress on Advances in Nuclear Power Plants (ICAPP ’08), Anaheim, CA, USA, 8–12 June 2008. [Google Scholar]
- Bushman, A.; Carpenter, D.M.; Ellis, T.S. The Martian Surface Reactor: An Advanced Nuclear Power Station for manned Extraterrestrial Exploration; Report of Massachusetts Institute of Technology. MIT-NSA-TR-003; Massachusetts Institute of Technology: Cambridge, MA, USA, 2004. [Google Scholar]
- Mcclure, P.R.; Reid, R.S.; Dixon, D.D. Advantages and applications of megawatt sized heat pipe reactors. Report of Los Alamos National Lab. In Proceedings of the International Congress on Advances in Nuclear Power Plants 2012 (ICAPP 2012), Chicago, IL, USA, 24–28 June 2012. [Google Scholar]
- Mcclure, P.R.; Poston, D.I.; Dixon, D.D. Final Results of Demonstration Using Flattop Fissions (DUFF) Experiment. 2012. Available online: https://www.osti.gov/servlets/purl/1052794 (accessed on 5 October 2012).
- Alawneh, L.M.; Vaghetto, R.; Hassan, Y.; White, H.G. Conceptual design of a 3 MWth yttrium hydride moderated heat pipe cooled micro reactor. Nucl. Eng. Des. 2022, 397, 111931. [Google Scholar] [CrossRef]
- Choi, S.H.; Lee, S.N.; Jo, C.K.; Kim, C.S. Conceptual core design and neutronics analysis for a space heat pipe reactor using a low enriched uranium fuel. Nucl. Eng. Des. 2022, 387, 111603. [Google Scholar] [CrossRef]
- Wang, C.L.; Sun, H.; Tang, S.M.; Tian, W.X.; Qiu, S.Z.; Su, G.H. Thermal-hydraulic analysis of a new conceptual heat pipe cooled small nuclear reactor system. Nucl. Eng. Technol. 2020, 52, 19–26. [Google Scholar] [CrossRef]
- Neubert, M.; Hauser, A.; Pourhossein, B.; Dillig, M.; Karl, J. Experimental evaluation of a heat pipe cooled structured reactor as part of a two-stage catalytic methanation process in power-to-gas applications. Appl. Energy 2018, 229, 289–298. [Google Scholar] [CrossRef]
- Deng, Y.B.; Qiu, B.W.; Yin, Y.; Wu, Y.W.; Su, G.H. Design and evaluation of a high power density and high energy efficiency fuel element for space nuclear reactors. Appl. Therm. Eng. 2021, 191, 116915. [Google Scholar] [CrossRef]
- Wang, D.Q.; Yan, B.H.; Chen, J.Y. The opportunities and challenges of micro heat piped cooled reactor system with high efficiency energy conversion units. Ann. Nucl. Energy 2020, 149, 107808. [Google Scholar] [CrossRef]
- Yin, L.; Liu, H.P.; Liu, W.Q. Capillary character and evaporation heat transfer in the wicks of high temperature liquid metal heat pipe. Appl. Therm. Eng. 2020, 175, 115284. [Google Scholar] [CrossRef]
- Panda, K.K.; Dulera, I.V.; Basak, A. Numerical simulation of high temperature sodium heat pipe for passive heat removal in nuclear reactors. Nucl. Eng. Des. 2017, 323, 376–385. [Google Scholar] [CrossRef]
- Ma, Y.G.; Chen, E.H.; Yu, H.X.; Zhong, R.C.; Deng, J.; Chai, X.M.; Huang, S.F.; Ding, S.H.; Zhang, Z.H. Heat pipe failure accident analysis in megawatt heat pipe cooled reactor. Ann. Nucl. Energy 2020, 149, 107755. [Google Scholar] [CrossRef]
- Ma, Y.G.; Tian, C.Q.; Yu, H.X.; Zhong, R.C.; Zhang, Z.H.; Huang, S.F.; Deng, J.; Chai, X.M.; Yang, Y.J. Transient heat pipe failure accident analysis of a megawatt heat pipe cooled reactor. Prog. Nucl. Energy 2021, 140, 103904. [Google Scholar] [CrossRef]
- Laubscher, R.; Dobson, R.T. Theoretical and experimental modelling of a heat pipe heat exchanger for high temperature nuclear reactor technology. Appl. Therm. Eng. 2013, 61, 259–267. [Google Scholar] [CrossRef]
- Chen, X.W.; Zou, Y.; Chen, Z.H.; Dai, Y. Effect of core configuration on natural convection and heat transfer in heat pipe cooled micro-MSRs. Nucl. Eng. Des. 2022, 395, 111839. [Google Scholar] [CrossRef]
- Li, T.; Xiong, J.B.; Zhang, T.F.; Chai, X.; Liu, X.J. Multi-physics coupled simulation on steady-state and transients of heat pipe cooled reactor system. Ann. Nucl. Energy 2023, 187, 109774. [Google Scholar] [CrossRef]
- Nie, J.Y.; Li, B.Q.; Wu, Y.W.; Zhang, J.; He, Y.N.; Zhang, G.L.; Ren, Q.S.; Su, G.H. Thermo-neutronics coupled simulation of a heat pipe reactor based on OPENMC/COMSOL. In Proceedings of the 2024 31st International Conference on Nuclear Engineering, 4, ICONE31, Prague, Czech Republic, 4–8 August 2024. [Google Scholar]
- Hales, J.D.; Williamson, R.L.; Novascone, S.R. The Equations Behind Nuclear Fuel Analysis, BISON Theory Manual; Idaho National Laboratory: Idaho Falls, ID, USA, 2018. [Google Scholar]
- William, C.; Artem, A.; David, H. Development of Additive Manufacturing at Westinghouse. In Proceedings of the Top Fuel, Seattle, WA, USA, 22–27 September 2019. [Google Scholar]
- Macdonald, P.E.; Thompson, L.B. MATPRO: A Handbook of Materials Properties for Use in the Analysis of Light Water Reactor Fuel Rod Behavior; Specific Nuclear Reactors & Associated Plants; AEROJET Nuclear Company: Rancho Cordova, CA, USA, 1976. [Google Scholar]
- Deng, Y.B.; Wu, Y.W.; Li, Y.M.; Zhang, D.L.; Tian, W.X.; Su, G.H.; Qiu, S.Z. Mechanism study and theoretical simulation on heat split phenomenon in dual-cooled annular fuel element. Ann. Nucl. Energy 2016, 94, 44–54. [Google Scholar] [CrossRef]
- Cox, B. Pellet-clad interaction (PCI) failures of zirconium alloy fuel cladding—A review. J. Nucl. Mater. 1990, 172, 249–292. [Google Scholar] [CrossRef]

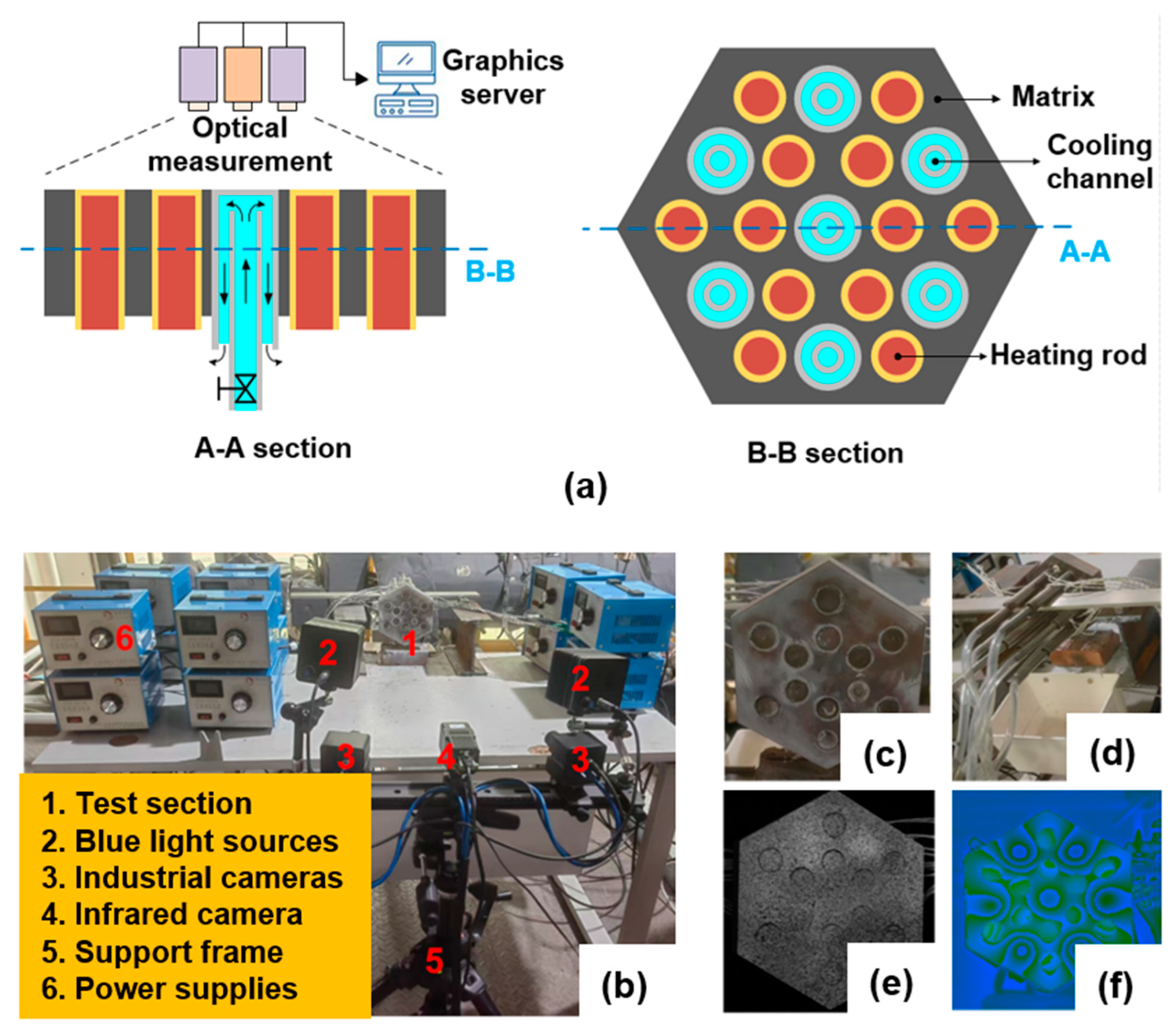
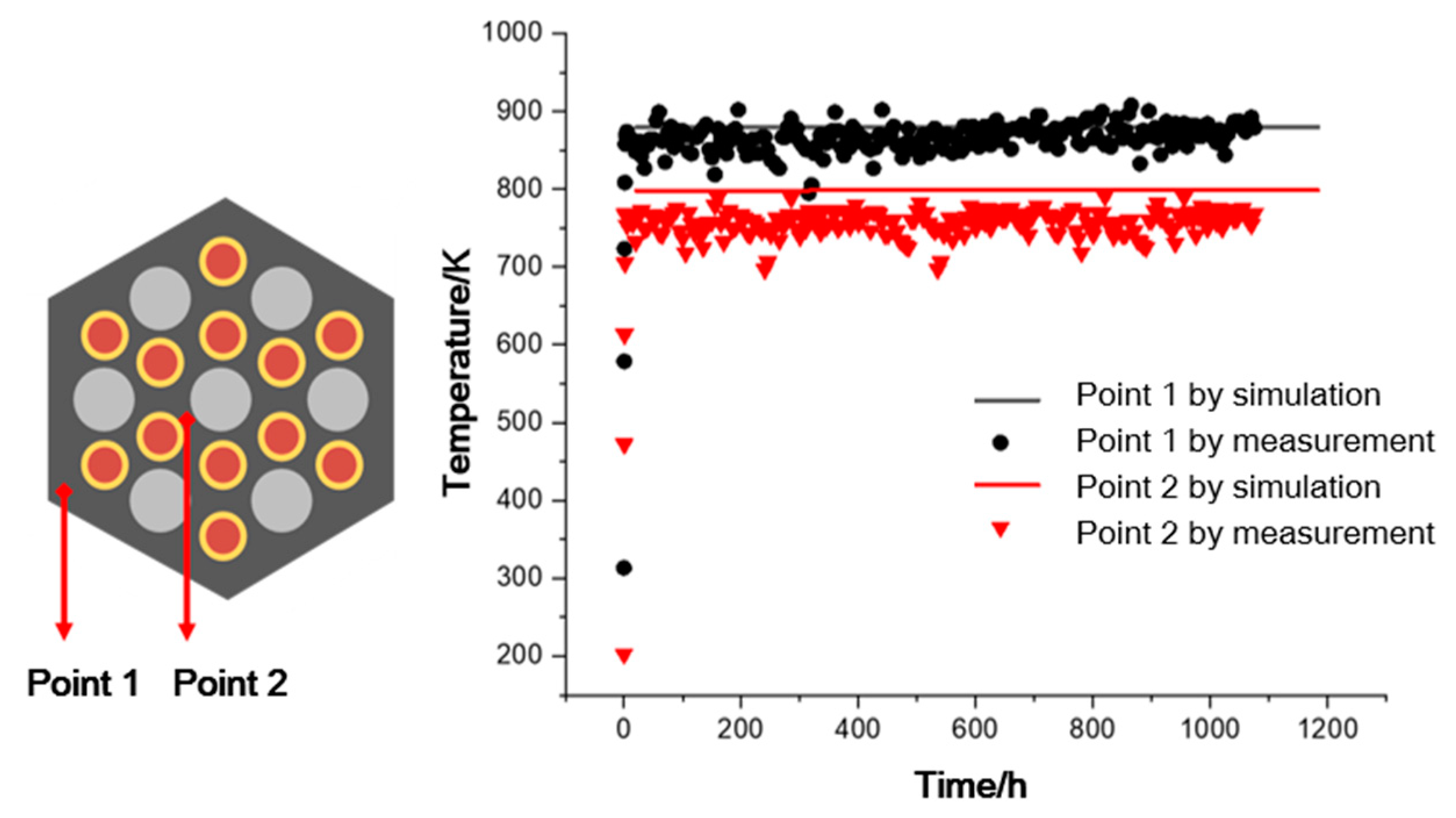









| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Total thermal power | 500 kW | Core diameter | 0.835 m |
| Core active length | 0.400 m | Side reflector diameter | 1.180 m |
| Bottom/top reflector length | 0.200 m | Rod/pipe pitch | 0.065 m |
| Control drum number | 6 | Control drum diameter | 0.070 m |
| Type 1 fuel rod number | 6 | Type 2 fuel rod number | 30 |
| Type 1 fuel rod diameter | 0.054 m | Type 2 fuel rod diameter | 0.054 m |
| Type 1 fuel/clad material | UO2/SS316 | Type 2 fuel/clad material | UO2/SS316 |
| Type 1 fuel enrichment | 14.75% | Type 2 fuel enrichment | 19.75% |
| Type 3 fuel rod number | 18 | Heat pipe number | 37 |
| Type 3 fuel rod diameter | 0.054 m | Heat pipe diameter | 0.052 m |
| Type 3 fuel/clad material | UO2/SS316 | Heat pipe length | 0.200 m |
| Type 3 fuel enrichment | 19.25% | Heat pipe material | SS316/Na |
| Rod NO | Power Factor | Rod NO | Power Factor | Rod NO | Power Factor |
|---|---|---|---|---|---|
| 1 | 1.172 | 19 | 1.076 | 37 | 0.902 |
| 2 | 1.146 | 20 | 0.921 | 38 | 0.866 |
| 3 | 1.144 | 21 | 1.168 | 39 | 0.885 |
| 4 | 1.153 | 22 | 1.167 | 40 | 0.868 |
| 5 | 1.122 | 23 | 0.907 | 41 | 0.911 |
| 6 | 1.142 | 24 | 1.072 | 42 | 0.863 |
| 7 | 0.926 | 25 | 1.124 | 43 | 0.880 |
| 8 | 0.921 | 26 | 0.948 | 44 | 0.885 |
| 9 | 0.940 | 27 | 1.069 | 45 | 0.860 |
| 10 | 1.090 | 28 | 1.174 | 46 | 0.893 |
| 11 | 1.085 | 29 | 1.175 | 47 | 0.882 |
| 12 | 0.958 | 30 | 1.119 | 48 | 0.895 |
| 13 | 1.082 | 31 | 0.919 | 49 | 0.867 |
| 14 | 1.165 | 32 | 1.08 | 50 | 0.875 |
| 15 | 1.166 | 33 | 1.083 | 51 | 0.892 |
| 16 | 1.065 | 34 | 0.946 | 52 | 0.901 |
| 17 | 0.925 | 35 | 0.913 | 53 | 0.903 |
| 18 | 1.097 | 36 | 0.926 | 54 | 0.877 |
| Case | Max Fuel Temperature/K | Max Matrix Temperature/K | Max Matrix Stress/MPa | Max Matrix Displacement/mm |
|---|---|---|---|---|
| No failure | 1419 | 834 | 237.7 | 3.68 |
| Pipe 1 failure | 1419 | 1096 | 237.6 | 3.68 |
| Pipe 2 failure | 1419 | 1093 | 238.0 | 3.68 |
| Pipe 3 failure | 1640 | 1111 | 238.1 | 3.94 |
| Pipe 4 failure | 1486 | 901 | 238.4 | 4.09 |
| Pipe 5 failure | 1555 | 1093 | 237.4 | 3.96 |
| Pipe 6 failure | 1561 | 946 | 238.2 | 4.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, X.; Liu, C.; Deng, Y.; Nie, J.; Wu, Y.; Su, G. Research on Thermo-Mechanical Response of Solid-State Core Matrix in a Heat Pipe Cooled Reactor. Energies 2025, 18, 1423. https://doi.org/10.3390/en18061423
Peng X, Liu C, Deng Y, Nie J, Wu Y, Su G. Research on Thermo-Mechanical Response of Solid-State Core Matrix in a Heat Pipe Cooled Reactor. Energies. 2025; 18(6):1423. https://doi.org/10.3390/en18061423
Chicago/Turabian StylePeng, Xintong, Cong Liu, Yangbin Deng, Jingyu Nie, Yingwei Wu, and Guanghui Su. 2025. "Research on Thermo-Mechanical Response of Solid-State Core Matrix in a Heat Pipe Cooled Reactor" Energies 18, no. 6: 1423. https://doi.org/10.3390/en18061423
APA StylePeng, X., Liu, C., Deng, Y., Nie, J., Wu, Y., & Su, G. (2025). Research on Thermo-Mechanical Response of Solid-State Core Matrix in a Heat Pipe Cooled Reactor. Energies, 18(6), 1423. https://doi.org/10.3390/en18061423






