Abstract
As a clean energy technology, air source heat pump (ASHP) technology has garnered increasing attention nowadays; however, the sharp decline in energy efficiency under low-temperature conditions remains a significant challenge impeding their widespread adoption. In this paper, in response to the demand under the Australian standard, mathematical modeling was carried out to explore the technical strategy for improving the performance of an ASHP; then, these strategies were evaluated by simulation calculation and experiment. The results show that, using frequency conversion, the coefficient of performance of the heat pump system (COP) reaches a maximum value of 2.48 when the frequency is 50 Hz, and the COP of the heat pump can reach a maximum value of 2.51 when the opening of the expansion valve is about 40%. Then, a new type of mixed refrigerant (R134a:R600a:R290) was proposed; the COP of the system reaches 2.502 when the mixture ratio is 1:6:3, which is an improvement of 6.61% compared to the use of only R134a. Finally, an analysis of the annual energy consumption under Australian weather conditions was conducted; the average COP is about 3.894, which is 6.3% higher than the result of using R134a. These results provide a theoretical basis for the development of a heat pump system that meets Australian standards.
1. Introduction
In recent years, driven by the global push for carbon neutrality and the growing complexity of the international energy landscape resulting from regional instability, countries have reached broad consensus on the urgent need to accelerate the transformation of energy structures. Within this framework, air source heat pump (ASHP) technology has emerged as a promising clean energy solution for large-scale application. Among the various ASHP technologies, air source heat pump water heater (ASHPWH) systems have become a focal point for development, with ongoing advancements in both their fundamental theory and engineering applications.
The efficiency of an ASHP is heavily influenced by fluctuations in ambient temperature. In colder environments, conventional systems often experience inadequate evaporation pressure, leading to a substantial rise in the compressor’s pressure ratio. This results in a marked decline in the compressor’s energy efficiency and elevated exhaust temperatures. At extremely low temperatures, such as −30 °C, traditional air source heat pumps struggle to achieve the desired water temperature [1]. Therefore, enhancing their stability and efficiency during winter remains a critical technical challenge for broader adoption. To address this, researchers have proposed numerous solutions for effective winter heating.
With regard to the optimization and enhancement of the structural design of ASHPWH systems, Bahman et al. [1] have emphasized that the precise regulation of the compressor discharge temperature is decisive for safeguarding the long-term reliability and operational efficiency of the system under low-temperature operating conditions. Studies have confirmed that this temperature control goal can be effectively achieved by using engineering and technical means, such as multiphase compression cycles, gradient cycle regulation strategies, and oil and gas separation devices. Zhang, D. [2] conducted empirical experimental studies under varying climatic conditions by establishing a multi-operating condition experimental platform for an enhanced steam-injection air source heat pump system. Notably, the coefficient of performance (COP) of this innovative system remained exceptionally high at 2.0, even under extreme operating conditions of −11.2 °C. These impressive data offer strong evidence that steam-injection technology significantly enhances the performance of heat pump systems under various operating conditions.
Bach, C. K. [3] investigated a multifunctional heat pump configuration capable of operating through three operational strategies: adjustable dual-stage air injection, flash gas bypass, and conventional single-stage compression. Under fixed compressor rotation conditions, the modified system exhibited a 28% enhancement in heating capacity at the 8.33 °C operating condition relative to conventional non-injected systems. Notably, when matching heating outputs through compressor speed regulation between standard and vapor-injection configurations, the system achieved up to a 6% improvement in COP under sub-zero conditions (−8.33 °C). Xu, Y. et al. [4] performed experimental research on a leaf-grid air source heat pump in the harsh −20 °C conditions of northern China, analyzing the effects of ambient temperature and operational modes on the system’s COP. The results revealed that the COP could consistently exceed 1.69. Recent studies suggest that dividing the refrigerant compression process into multiple stages is a common approach to improving air source heat pump performance in sub-zero temperatures. However, the implementation of the lobe-grid cycle is limited by the high initial costs, and multi-stage compressors often experience significant performance degradation under off-design conditions. In contrast, techniques such as variable frequency regulation of conventional compressors and the use of variable expansion valves are still considered more effective for optimizing the annual performance of air source heat pump systems.
Research into refrigerants reveals that air source heat pumps utilizing conventional refrigerants like pure R134a experience notable COP deterioration under lower ambient temperatures [5]. Luo, J. et al. [6] conducted comprehensive analytical and experimental investigations on an integrated single-stage air source heat pump employing a ternary refrigerant blend. The system’s operating parameters, such as pressure and concentration, were precisely controlled through the coordinated adjustment of multiple valves and reservoirs. By employing CO2/R134a/R600 as the refrigerant, the operating pressure and mixture concentration were effectively managed within an ambient temperature range of −30 °C to 0 °C. Additionally, the coefficient of performance (COP) rose from 1.834 to 2.546 when generating hot water at 75 °C.
Xiao, B. et al. [7] from the Green Energy Research Laboratory proposed a refrigerant blend composed of R290, R600a, and R13I1, which has a low global warming potential (GWP) and zero ozone depletion potential (ODP), as a substitute for R134a in an ASHPWH. They also evaluated the cycling performance of this proposed blend, a control blend, and R134a under various operating conditions. The analysis aimed to show that, compared to R134a, the blend offers advantages such as reduced condensing pressure, lower compression ratio, higher heat capacity, and an improved coefficient of performance (COP).
Current research highlights that pure CO2, R290, R600a, and refrigerant mixtures are viable options for low-temperature applications. However, pure CO2 is unsuitable for systems where the return water temperature surpasses its critical temperature limit [5,8]. Conversely, mixed refrigerants demonstrate superior performance in applications requiring substantial thermal gradients between heat exchangers and thermal sources, particularly in hydronic systems where supply/return water temperatures exceed ambient conditions.
Li, J. [9] conducted a performance evaluation of a hybrid heating system integrating a large-scale flat-plate solar collector (FPC) with an air source heat pump (ASHP). Through experimental and numerical investigations, the study revealed an average collector efficiency of 0.42 for the FPC system, with solar energy contributing 31.8% of seasonal heating demand and an average system COP of 3.08, demonstrating effective synergy between solar and ambient energy utilization. In subsequent research [10], Li further investigated an air source heat pump-assisted solar evacuated tube water heater (SETWH-ASHP) for winter heating, performing a comprehensive analysis of technical and economic viability across three operational configurations. The results indicated that, during the heating season, the solar water heat pump (SWHP) delivered 6300.3 kWh of thermal energy at an average COP of 3.5, while the auxiliary ASHP provided 7970.8 kWh with a COP of 2.9.
The advancement of single-stage air source heat pump systems employing eco-friendly refrigerant combinations for low-temperature water heating represents a critical research focus, balancing thermal performance optimization, system configuration complexity, capital expenditure requirements, and ecological sustainability considerations. However, the existing literature needs to be more robust with studies of region-specific design conditions, and studies of year-round system energy optimization are relatively scarce, especially in regard to compliance with Australian standards. The purpose of AS/NZS4234:2021 [11] is to provide methods to quantify the energy consumption of a heating liquid system and to calculate the energy savings relative to a reference heater. The reference heater system used to quantify energy savings relative to the previous version has been updated in accordance with the latest environmental protection and service requirements as well as the most recent weather records for a typical meteorological year. This regulatory evolution necessitates the accelerated development of standardized heat pump systems compliant with updated benchmarking criteria.
2. System Modelling
2.1. Principle of Heat Pump for Air Source Water Heater
The thermodynamic operational principles of an ASHPWH share fundamental parallels with vapor-compression refrigeration cycles. A minimal electrical input drives compressor operation, generating a high-enthalpy vapor state. This pressurized vapor undergoes phase transition in the condenser, transferring latent heat to elevate water temperature while condensing to high-pressure liquid. The refrigeration cycle is completed through isenthalpic expansion and subsequent ambient heat absorption in the evaporator via metered refrigerant flow control. During the condensation phase, a phase-change heat rejection process elevates stored water temperatures to the 50–65 °C operational range, sustaining cyclical heating as schematized in Figure 1. However, the operational efficacy of air source water heating systems exhibits strong thermal coupling with ambient conditions, accompanied by inherently transient thermodynamic characteristics. This interdependence necessitates the implementation of adaptive control frameworks integrating real-time compressor frequency modulation synchronized with dynamic thermal load fluctuations and coordinated electronic expansion valve orifice adjustments. Through such synergistic actuation strategies, precise superheat regulation and enhanced COP can be systematically maintained across variable operating regimes, thereby optimizing energy conversion efficiency while ensuring stable system operation under transient environmental conditions.
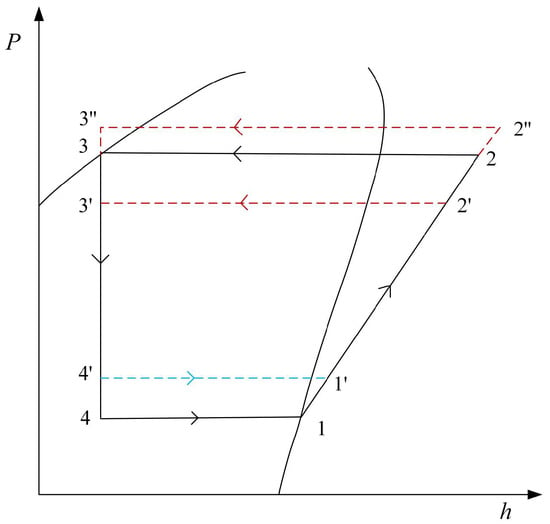
Figure 1.
Pressure–enthalpy diagram of the system.
In the operational cycle of an air source heat pump water heater (ASHPWH), the compressor elevates low-temperature, low-pressure refrigerant vapor from the evaporator outlet (State 1) to a high-enthalpy vapor state (State 2). While ideal compression follows an isentropic trajectory (Process 1–2), practical deviations (1–2′ to 1–2′′) arise from variable-speed modulation and non-ideal compression efficiency. The superheated vapor then undergoes phase transition in the water-cooled condenser (The ideal Process is 2–3, but in practice it is 2′–3′ or Process 2″–3″), rejecting latent heat to the hydronic loop and transitioning to a subcooled liquid state (State 3). Subsequent isenthalpic expansion through the electronically regulated metering device induces flash vaporization, yielding a low-quality two-phase mixture (State 4). Theoretically modeled as a constant-enthalpy process (3–4), actual throttling dynamics (3–4 to 3–4′) are governed by valve aperture modulation and transient pressure differentials. This biphasic refrigerant subsequently enters the air source evaporator, absorbing ambient thermal energy during isobaric evaporation (Process 4–1 or Process 4′–1′), thereby completing the thermodynamic cycle.
The operational parameters of a refrigeration cycle typically encompass a range of variables, including the condensing temperature, evaporating temperature, subcooling temperature, and superheat. The required parameters will be determined according to the climate characteristics of the area where the unit is applicable and according to relevant norms and experience. The mathematical model of an ASHPWH is based on the following assumptions [12,13]:
- (1)
- The pressure drop of the refrigerant in the exchanger and piping is assumed to be negligible.
- (2)
- Heat loss from the evaporator, condenser, compressor, electronic expansion valve, and piping to the surroundings needs to be addressed.
- (3)
- The compressor inlet superheat temperature is assumed to be 5 °C, with a subcooling of 5 °C at the condenser outlet temperature.
- (4)
- The throttling process in the throttle valve is isenthalpic.
- (5)
- The compression process of the compressor is adiabatic.
2.2. Compressor Modelling
The compressor represents the most critical component in an ASHP, exerting a direct influence on the operational characteristics of the unit. The rotational speed of the compressor can be determined through a calculation based on the compressor’s rotational frequency (), the rate of rotation (s), and the logarithm of the electrode. This calculation is presented in Equation (1):
The refrigerant mass flow rate through the compressor can be calculated using four key parameters: the compressor’s displacement volume (V), volumetric efficiency (), rotational speed (N), and the refrigerant’s inlet-specific volume. This relationship is mathematically represented in Equation (2), which provides the formula for determining the compressor’s mass flow rate:
The compressor’s volumetric efficiency () and isentropic efficiency () exhibit functional dependence on the pressure ratio (), with their mathematical correlation explicitly established in Equation (3) [14]:
The compressor’s shaft power can be determined through the thermodynamic relationship analytically defined in Equation (4):
Within the thermodynamic framework, denotes the refrigerant mass flow rate through the compressor, with h1 (state point 1) and h2 (state point 2) corresponding to the refrigerant’s specific enthalpy at the suction and discharge ports, respectively. The discharge enthalpy h2 is derived through the isentropic efficiency, a critical thermodynamic parameter formulated in Equation (5) that quantifies the deviation between actual and ideal compression processes:
Equation (5) above calculates the isentropic power. However, due to the existence of heat exchange loss, friction, and other factors in the compressor itself, the mechanical efficiency (), indicated efficiency (), and motor efficiency () also need to be taken into account in calculating the actual efficiency of the compressor. Therefore, the actual power of the compressor can be expressed in Equation (6) as follows:
2.3. Condenser Modelling
In ASHPWH systems, the condenser assembly integrates a tubular heat exchanger immersed within the insulated water storage vessel. The refrigerant-side thermal characteristics are governed by the phase-change heat transfer correlation expressed in Equation (7) [7]:
The heat exchanger performance on the refrigerant side can be obtained by the following Equation (8):
where Q, h, and represent the total thermal transport capacity, heat transfer coefficient, and logarithmic mean temperature differential, respectively, and A is the heat transfer area. The subscripts r and w represent the refrigerant side and the water side, respectively, and the subscripts i and 0 indicate the internal and external wall temperatures of the condensing coil. For single-phase flow on the refrigerant interfaces, the heat transfer coefficient can be calculated using the standard Dittus–Boelter model by the following Equations (9) [15] and (10):
where is the thermal conductivity, v is the refrigerant flow rate, is the refrigerant side of the heat transfer coefficient, is the viscosity coefficient, is the density of the refrigerant, and is the diameter of the refrigerant circulation pipe.
In this study, a one-dimensional condenser heat transfer model is proposed to describe the energy exchange process between refrigerant and hot water. According to this model, it can be deduced that the refrigerant can be approximated to maintain a relatively stable temperature distribution during the heat transfer process, which ensures that the overall heat exchange capacity of the condenser basically matches the actual working conditions. The modelling method has been validated in the literature [7] and proved to be suitable for the analytical calculation of one-dimensional steady-state heat transfer processes. For more accurate condenser model modelling, a three-dimensional heat transfer model is required.
2.4. Throttle Modelling
The throttling phenomenon occurring within the throttle valve is regarded as an isenthalpic process, wherein the specific enthalpy of the refrigerant exhibits invariance prior to and subsequent to the throttling event. Consequently, the mass flow rate traversing the throttle valve can be determined via the subsequent Equation (11):
where is the flow coefficient of the throttle valve. is the refrigerant density at point 3 of the valve inlet. and are the inlet pressure and outlet pressure of the valve, i.e., the pressure at state point 3 and state point 4, respectively. According to the opening of the throttle valve (φ) and nominal orifice (), the effective flow area of the throttle valve can be obtained as follows:
where the openness φ ranges from 0% to 100%.
2.5. Evaporators
The mass flow rate of the refrigerant in the evaporator corresponds to the compressor’s mass flow rate; consequently, the thermal energy transfer on the refrigerant side can be derived utilizing Equation (13):
where is the flow rate of refrigerant in the tube, is the enthalpy of refrigerant at 4 points and 1 point, respectively, is the heat transfer coefficient of the refrigerant side of the evaporator, A is the heat transfer area of the refrigerant side, and is the tube wall temperature and the average temperature of the refrigerant, respectively.
The heat exchange capacity on the air side can be obtained from the following Equations (14) and (15):
where is the flow rate of air in the tube, are the enthalpy of the air outlet and inlet, respectively, is the heat transfer coefficient of the evaporator air measurement, is the outer surface area of the evaporator tube, is the average temperature of the air, . is the coefficient of humidity precipitation, and is the specific heat of the air. For single-phase flow on the refrigerant side, the heat transfer coefficient is calculated using the Petukhov–Popov formula [16]:
where is the Prandtl number of the refrigerant, is the Rayleigh number, is the turbulent friction number, and is the thermal conductivity of the refrigerant.
2.6. Performance Analysis Modelling
The schematic configuration of the ASHPWH system is illustrated in Figure 2. The system incorporates four principal components: an evaporator unit, a condensation assembly, a reciprocating compressor, and an expansion device. The experimental setup employed a Panasonic H124C6REAAC2 compressor (Model: SC-51173999-FG-01, Panasonic Wanbao (Guangzhou) Compressor Co., Ltd., Guangzhou, China), featuring a rotational velocity of 2900 rpm and a displacement volume of 12.4 cm3. The thermal exchange subsystems consist of an air-side finned-tube heat exchanger for evaporative processes and a water-cooled shell-and-tube heat exchanger for condensation applications.

Figure 2.
Description of the principle of single-stage air source heat pumps.
To investigate the thermodynamic performance of aerothermal heat pump systems, Trnsys v18 simulation software was initially employed for assessing critical operational metrics, including energy expenditure and coefficient of performance (COP). However, this research entails dynamic modulation of multiple system variables—compressor frequency, electronic expansion valve aperture, and evaporative/condensing temperature thresholds—introducing parametric control limitations within the Trnsys environment. Consequently, an Aspen-based simulation framework was implemented, with the integrated system architecture presented in Figure 3. The Aspen platform enables methodical development of component-level models for the four principal subsystems of aerothermal pumps, facilitating system-level simulation through parameter optimization processes. Furthermore, composition modulation of novel refrigerant mixtures can be systematically executed via Aspen’s thermodynamic libraries. Through bidirectional data interfacing between Aspen and Trnsys, cross-platform parameter correlation was achieved. By transmitting Aspen’s simulation results to Trnsys, relevant data can be correlated. A transient model of a heat pump capable of analyzing the annual thermal performance of an ASHPWH was developed, and the Aspen and Trnsys joint simulation system was constructed, as shown in Figure 3.
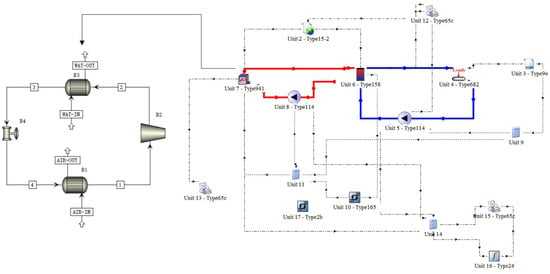
Figure 3.
Simulation model based on ASPEN and TRNSYS.
2.7. Performance Analysis at Different Air and Water Temperatures
2.7.1. Simulation Results
The variation in ambient temperature and outlet water temperature exerts a direct impact on the operational performance of air source heat pumps. Through simulation analysis of the model, this study derived the correlation between the COP of the air source heat pump unit and outlet water temperature variations under different ambient temperature conditions, as illustrated in Figure 4. The results demonstrate that, when the system’s initial water temperature was set at 20 °C, the maximum COP value of 10.79 was achieved under combined conditions of 35 °C ambient temperature and 35 °C hot water temperature. However, as the ambient temperature decreased and the outlet water temperature increased, the COP exhibited a gradual decline, showing particular sensitivity to ambient temperature fluctuations. Notably, under extreme operating conditions with ambient temperature dropping to −15 °C and outlet water temperature rising to 65 °C, the system’s COP diminished significantly to 1.283.
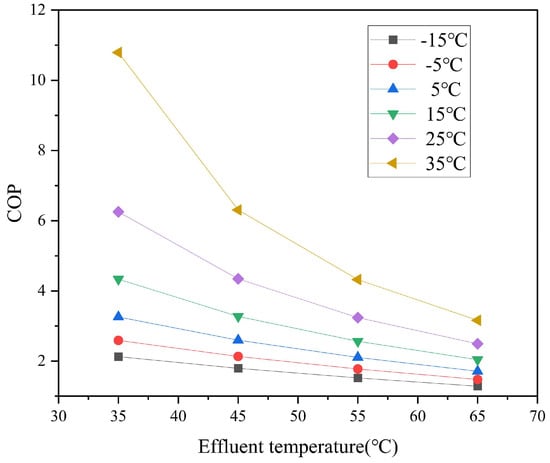
Figure 4.
System COP under different weather and water discharge temperatures.
2.7.2. Analysis of Causes
The reason for this change pattern is that, as the demand for hot water temperature increases, the heat exchange temperature difference of the condenser gradually decreases, and the compressor needs to increase power to meet the increase in heat exchange capacity, resulting in an increase in COP. Similarly, as the demand temperature decreases, the heat exchange temperature difference of the evaporator decreases, and the compressor also needs to increase power to improve the working fluid flow rate and outlet demand conditions, resulting in a decrease in the COP of the air heat pump system. As shown in the figure, when the ambient temperature is below 5 °C, the energy efficiency of the heat pump is only about 2.3, which is more than double that of 25 °C. Therefore, improving the energy efficiency of the system under low-temperature conditions is the primary issue faced by air source water heaters, and this deserves further discussion and analysis.
2.7.3. Experimental Result
In order to verify the accuracy of the simulation model, the environmental conditions of the simulation and experiment are detailed in Table 1, and several key temperature points in the heating process were simulated, specifically including the inlet water temperatures of 20 °C, 30 °C, 40 °C, and 50 °C, respectively. The leading test equipment is shown in Figure 5.

Table 1.
Experimental environmental conditions.

Figure 5.
Main system equipment.
As shown in Figure 6, by comparing the simulated data with the experimental results, we find that there is a certain error between the experimental power and the simulated power, and the maximum power error is 13.4%. As can be seen from the last two figures, this error is mainly due to the deviation between the inlet and discharge temperatures of the compressor in the simulation and experiment. It was found that the difference between the simulated and experimental results at low inlet temperatures, especially at the suction temperature shown in Figure 6, can be attributed to several potential factors. These factors are usually related to limitations of the model or experimental setup rather than measurement errors. The following are possible reasons for such differences. The simulation model may have made certain assumptions or simplifications that do not fully reflect the complex behaviors at lower inlet temperatures. For example, the model may not take into account certain non-linear or transient effects that become more pronounced at lower temperatures, leading to differences from actual behaviors. Heat transfer coefficients or thermodynamic properties may be simplified or assumed to be constants, whereas in reality, they may vary with temperature, especially at low temperatures, making the simulation model relatively accurate. Based on this model, research on energy consumption improvement schemes for heat pump systems can be carried out.
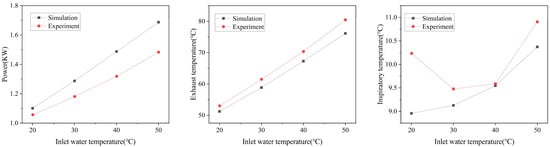
Figure 6.
The comparison between the simulation and experimental results.
3. Results of COP Improvement Strategies
3.1. Compressor Inverter
Unlike in Europe, the heat pumps used in Australia are capable of operating independently throughout the year without support from other heat sources. Therefore, compared to other energy control strategies, variable frequency compressor technology is the most widely used and effective technology available. Adjusting the compressor speed to achieve the basic idea of frequency converter energy control is to change the compressor speed so that the mass flow of refrigerant changes. The corresponding simulation conditions are shown in Table 2.

Table 2.
Simulation working conditions.
The variation in the coefficient of performance (COP) of the heat pump unit with compressor frequency is shown in Figure 7. The results of the analysis show that the COP of the heat pump unit shows an increasing and then decreasing trend as the compressor frequency increases. When the motor frequency is 25 Hz, the COP of the heating system is 2.25, and when the frequency is increased to 50 Hz, the COP reaches the simulated maximum value of 2.48 and then gradually decreases. The reason for this is that, as the compressor frequency increases, the work mass flow rate increases, while the specific enthalpy of the refrigerant at the compressor outlet (approximately equal to the specific enthalpy at the condenser inlet) remains basically unchanged, and the optimum heat exchange condition of the equipment in the condenser and evaporator is gradually reached, which is consistent with the design of the system at the rated frequency with the highest energy efficiency; however, as the compressor speed is further increased, the heat exchange is limited by the design of the condenser and evaporator, and the exchange rate is limited by the design of the condenser and evaporator. However, as the compressor speed continues to increase, due to the design of the condenser and evaporator and the limitations of the heat exchange rate, the heat exchanged becomes saturated, resulting in the increase in compressor power not being effectively utilized and the COP showing a decreasing trend.
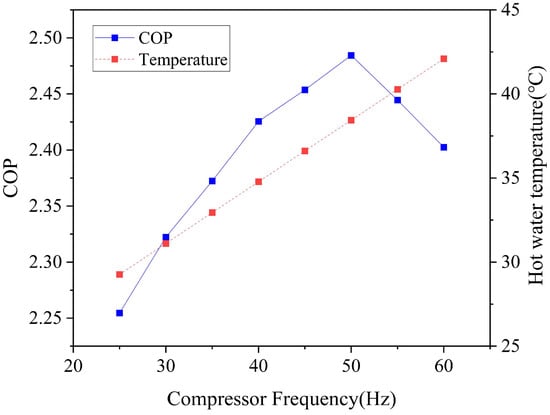
Figure 7.
System COP at different compressor frequencies.
The simulation results show that the heating system exhibits optimum values when the compressor frequency is between 45 and 55 Hz. Since the inlet water temperature is constant, the outlet water temperature increases almost linearly from 29.26 °C at the beginning to 42.09 °C at the end; the energy efficiency of the compressor has to be sacrificed in order to obtain the required hot water temperature.
3.2. Electronic Expansion Valve Regulation
Theoretical modeling shows that regulating the opening of the expansion valve also achieves regulation of the flow rate and state of the refrigerant, so the use of an electronic expansion valve is also an effective means of regulating the efficiency of the system as the temperature changes.
The relationship between the COP of the heat pump system and the opening of the electronic expansion valve at low temperatures is shown in Figure 8. Other things being equal, the COP shows a tendency to increase and then decrease as the opening of the electronic expansion valve increases. When the degree of opening is 0.1, the COP is 2.01; when the degree of opening is increased to 0.4, the COP reaches the maximum value of 2.51; then, with a further increase in the degree of opening, the COP gradually decreases, and the rate of decrease gradually slows down until the degree of opening reaches 1. At the same time, the temperature of the outlet water continues to increase from the initial value of 25 °C to the final value of 50 °C, although the rate of increase gradually slows down.
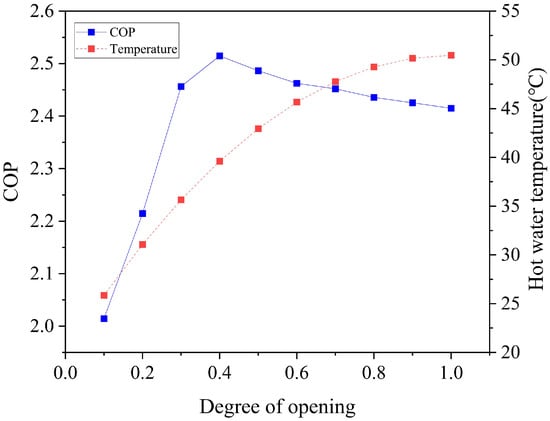
Figure 8.
COP of the system with different openings of the electronic expansion valve.
This is due to the fact that increasing the opening of the expansion valve causes a change in the refrigerant flow rate, which increases the heat absorption in the evaporator and the overall heat production, increasing the coefficient of performance (COP). However, the COP of heat pump systems is inherently constrained by evaporator heat exchanger design limitations, as these systems exhibit an optimal COP threshold. When operational demands exceed this design threshold, compressor capacity must be augmented to maintain prescribed condensation temperatures, resulting in a marginal COP degradation due to disproportionate energy input requirements. In addition, the electronic expansion valve opening is adjusted by controlling the percentage of the circle radius relative to the opening diameter (see Equation (12)). At smaller orifices, the change in flow area is significant and rapid, whereas at larger orifices, the change in flow area is relatively slow. Therefore, the rate of decrease in the COP of the heat pump system is slower. At the same time, the change in outlet water temperature shows a similar trend, which is mainly caused by the change in refrigerant flow rate. In the initial stage, the outlet water temperature increases rapidly with the rapid increase in the refrigerant flow; however, as the rate of change in the refrigerant flow decreases, the rate of increase in the outlet water temperature slows down.
3.3. New Refrigerant Mass Ratio
The rapid pressure escalation of R134a with rising temperatures, particularly under Australia’s relatively warm winter conditions, poses challenges to improving system energy efficiency. Consequently, optimizing more efficient and environmentally sustainable refrigerants is imperative to enhance the heating capacity of air source heat pump systems. Among various refrigerants, R290 and R600a are recognized for their low global warming potential (GWP) and zero ozone depletion potential (ODP), establishing them as eco-friendly alternatives. Systematic optimization of their blending ratios may yield a novel environmentally benign refrigerant mixture with enhanced thermodynamic cycle performance, thereby improving heat pump operational efficacy under extreme low-temperature conditions. Key parameters of R290, R600a, and R134a are summarized in Table 3.

Table 3.
Parameter performance table.
In Figure 9a, it can be seen that, at the same pressure, the condensation temperature of R600a is the highest at 0 °C, followed by R134a with a condensation temperature of −10 °C, and the condensation temperature of R290 is the lowest at −30 °C. Although the changes in the entropy of these three refrigerants as they change the state of matter are relatively close to each other, they are all around 20 cal/mol-K, and to ensure the effective heat production of the air source heat pump system in the low-temperature conditions of Australia, the ratio of these three refrigerants must be adjusted appropriately to optimize their heat absorption capacity.
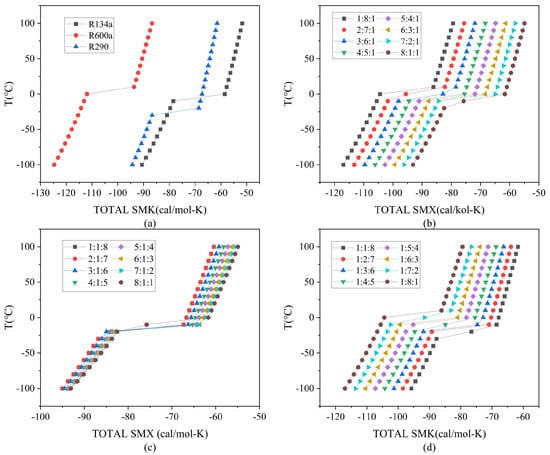
Figure 9.
Temperature–entropy diagram for different refrigerants. (a) Temperature–entropy diagram for RI34a, R600a, and R290 vaporization curves. (b–d) Temperature–entropy plots for mixed masses with different mass ratios (R134a:R600a:R290).
In order to ensure that the refrigerants can absorb more heat during the phase change process, the molar ratios of the R134a, R600a, and R290 blends in this study were set to 1:1:8, 1:2:7~1:8:1 alternately. The temperature–entropy variations under different mixing ratios are shown in Figure 9b–d.
In Figure 9b, it can be seen that, when the molar proportion of R290 in the mixed mass is kept constant, with the increase in the molar proportion of R134a in the mixed refrigerant, the bubble point temperature of the mixed mass substance decreases significantly from the initial 0 °C to −20 °C. At the same time, the entropy of the mixed mass substance decreases significantly from the initial 0 °C to −20 °C. At the same time, the entropy value during the change in substance morphology also experiences a significant change, decreasing from −104.4 cal/mol-K to −82.4 cal/mol-K.
In Figure 9c, it can be seen that, when the mole ratio of R600a in the mixed medium is kept constant, the bubble point temperature of the mixed medium is almost unchanged with the increase in the mole ratio of R134a, and it is always kept at about −25 °C. The entropy of the mixed medium changes only slightly from −87.7 cal/mol-K to −82.4 cal/mol-K. At the same time, the entropy of the working medium changes only slightly from −87.7 cal/mol-K to −82.4 cal/mol-K. It can be concluded that, if the molar ratio of R600a is kept constant, the heating capacity of the mixture would not change significantly, even if the ratios of R134a and R290 were changed significantly.
In Figure 9d, it can be seen that, when the molar fraction of R134a in the mixed mass is kept constant, the bubble point temperature of the mixed mass gradually increases as the R600a fraction increases, from an initial −30 °C to a final 0 °C. At the same time, the entropy at the change in state changes correspondingly from −87.7 cal/mol-K to −104.4 cal/mol-K. These changes lead to a decrease in the corresponding pressure at the same condensation temperature, which increases the work required to reach the same evaporation temperature.
Through the analysis of the temperature–entropy diagram, it can be seen that the molar ratio of the refrigerant has a significant influence on the thermodynamic performance of the mixed refrigerant, such as bubble point temperature, critical pressure, etc. In order to accurately determine the optimum mixing ratio of the mixed refrigerant under the environmental conditions in Australia, this study uses Aspen to simulate the performance of the air heat pump system model with different mixing ratios of the refrigerant. Under the same condensing and evaporating temperature conditions, the energy efficiency ratio (COP) of the air heat pumps with each proportion of mixed refrigerant was compared to identify the optimum mixing ratio. The simulation results are shown in Figure 10.
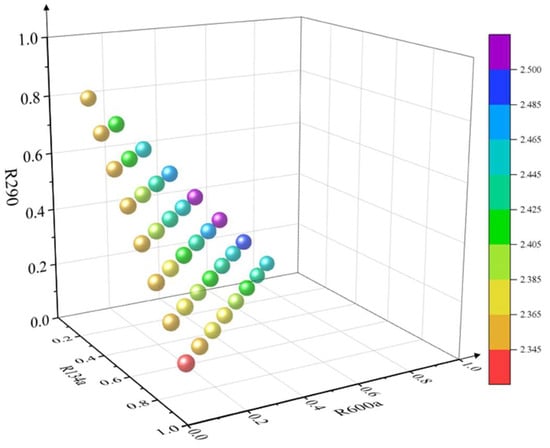
Figure 10.
COP of the system for different mixing ratios.
According to the simulation results, the COP of this heat pump simulation system reached a maximum value of 2.502 when the molar ratio of the mixed work mass was set to R134a:R600a:R290 = 0.1:0.6:0.3, which is 6.61% higher than when pure R134a was used under the same conditions (2.347). In addition, from a practical safety point of view, R600a and R290 have the potential to cause an explosion when exposed to open flames in the volume concentration ranges of 1.8% to 8.4% and 2.1% to 9.5%, respectively. However, the optimum mix ratio we have chosen is not within this hazardous range, and therefore, the safety of the mix ratio can be confirmed.
4. Calculation of Annual Energy Consumption Under Australian Standards
4.1. Annual Performance Analysis
In order to investigate the feasibility of refrigerant blends to replace R134a in low-temperature environments, this study analyzes the heating capacity of the refrigerant blends and their performance under standard Australian conditions using Trnsys software based on the simulation results in the previous section. Sydney was used as the study site, and its daily ambient maximum and minimum temperatures are shown in Figure 11. As Australia is located in the southern hemisphere, the maximum ambient temperature in Sydney usually occurs from November to January and reaches 37 °C, while the minimum ambient temperature occurs from June to August and drops to 5 °C.
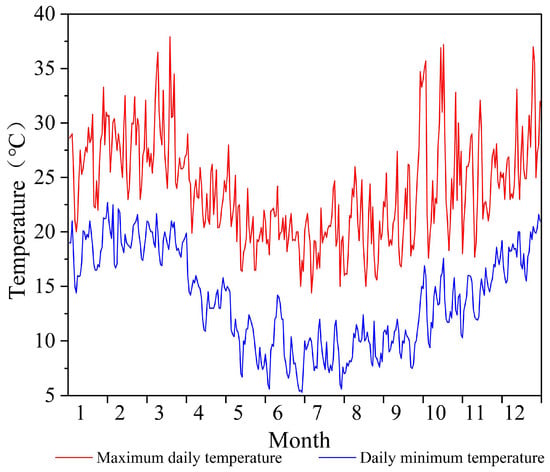
Figure 11.
Daily minimum and maximum temperatures in Sydney.
Figure 12 illustrates the hourly heating capacity variations in the heating system across annual operation. Under rated operating conditions, the heat pump system delivers a heating capacity of 2.5 kW. As demonstrated in the figure, the system’s heating output progressively intensifies with rising ambient temperatures. The system maintained heating capacity at or above the rated level for 6106 operating hours annually, accounting for approximately 69.70% of the total operational duration. At an ambient temperature of 5 °C, the minimum heating output was measured at 1.9306 kW, while the peak capacity reached 4.679 kW under elevated ambient conditions of 35.3 °C.
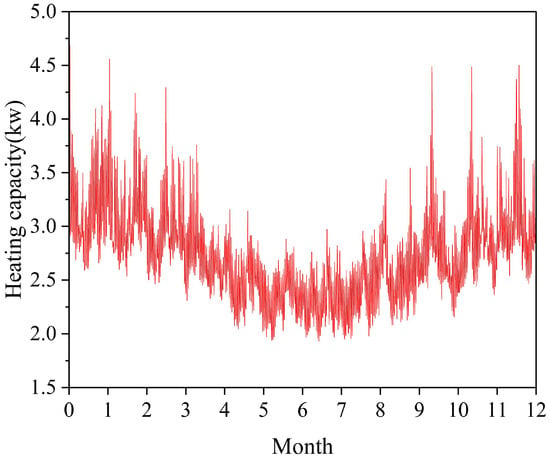
Figure 12.
System heating capacity per hour throughout the year.
4.2. Years of Thermal Performance
To evaluate the annual thermal performance of the air source heat pump employing the newly formulated refrigerant blend, the COP of this mixed refrigerant was systematically compared with that of R134a, as illustrated in Figure 13. The findings indicate a temperature-dependent COP enhancement, aligning with the previously established correlation between COP elevation and increased evaporating temperatures. Figure 13 reveals that the heat pump utilizing the blended refrigerant exhibited marginally superior COP values relative to the R134a-based system for the majority of operational hours annually. The novel refrigerant configuration achieved a maximum COP of 6.5, with an annual average COP of 3.894, surpassing the R134a-based system’s annual average COP (3.66) by 6.3%.
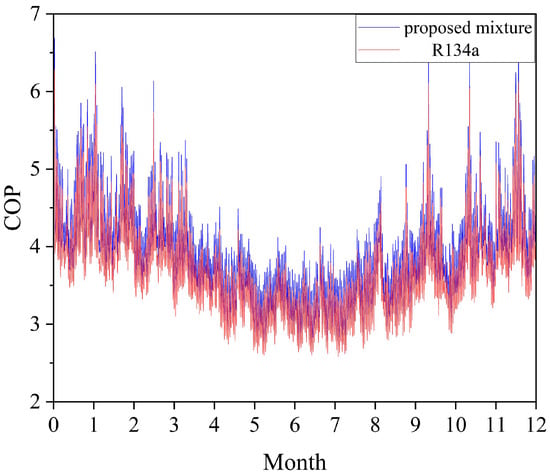
Figure 13.
Hourly COP of the system throughout the year.
5. Conclusions
To address the low thermal efficiency of an ASHPWH in low-temperature environments, this study simulated an ASHPWH system using Aspen and Trnsys software based on experimental validation of the simulation model. In addition, a detailed performance analysis was carried out under the climatic conditions of Sydney, Australia. The main research findings can be summarized as follows:
- (1)
- An innovative joint Aspen and Trnsys simulation model was developed for this study. The model combines the flexibility of Aspen v11 software in constructing models of the four main components of the heat pump and setting parameters and the advantages of Trnsys software in evaluating the energy consumption and the COP of the system to reflect the system behavior under different operating conditions accurately. Based on this common simulation platform, we were able to thoroughly study the effects of various improvement measures and ensure that the results obtained are highly reliable and practical.
- (2)
- In a low-temperature environment, when the compressor frequency is adjusted individually, the heating system shows the best performance in the frequency range of 45 to 55 Hz, with a coefficient of performance (COP) of 2.51. At the same time, the outlet water temperature continues to increase as the frequency increases.
- (3)
- In a low-temperature environment, the COP tends to increase and then decrease as the opening degree of the electronic expansion valve increases. When the degree of opening is 0.4, the coefficient of performance reaches a maximum value of 2.51; then, as the degree of opening continues to increase, the coefficient of performance gradually decreases. At the same time, the water temperature continues to rise, but the rate of increase has also slowed down.
- (4)
- A new hybrid refrigerant R290/R600a/R134a is proposed to replace the conventional R134a in the air source heat pump system, and the simulation results show that, when the molar ratio of the mixed work masses is set to R134a:R600a:R290 = 0. 1:0.6:0.3, the COP of the simulated heat pump system reaches a maximum value of 2.502, which is higher than that of R134a. Under the same conditions, the COP of R134a (2.347) is improved by 6.61%.
- (5)
- Based on the previous optimization conclusions, a full-year energy analysis for standard Australian weather conditions was carried out, which showed that the ASHPWH system with this refrigerant could operate up to 69.70% for one year. The minimum heating capacity is 1.9306 kW, and the maximum heating capacity can be up to 4.679 kW. The maximum COP is 6.5, and the average COP is approximately 3.894, which is a 6.3% improvement over the results using R134a.
All these results provide a theoretical basis for the development of a heat pump system that meets Australian standards.
Author Contributions
J.X.: Writing—review & editing/Conceptualization; C.L.: Writing—original draft); X.L.: Validation/Investigation; X.S.: Funding acquisition/Investigation; Y.L.: Resources/Formal analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Natural Science Foundation of China (Grant No. 52305062), Introduced Talents Science Start-up Foundation of Nanjing Institute of Technology (Grant No. YKJ201904).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
Author Xiaojun Liu was employed by the company Jiangsu Guangmang New Energy Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| Abbreviations | |
| COP | Coefficient of performance |
| ASHPWH | Air source heat pump water heater |
| COMP | Compressor |
| EVA | Evaporator |
| CON | Condenser |
| EXV | Expansion valve |
| ai | Input air |
| ao | Eliminate air |
| wi | Water inlet |
| wo | Water outlet |
| GWP | Global warming potential |
| ODP | Ozone depletion potential |
| English letters | |
| A | Area, m2 |
| Effective passage flow area of the valve, m2 | |
| Nominal orifice of the valve, m2 | |
| Discharge coefficient of the throttle valve | |
| Frequency, Hz | |
| h | Specific enthalpy, |
| m | Mass flow, kg/s |
| N | Rotational speed |
| p | Number of electrode pairs/Pressure, MPa |
| Q | Heating capacity, kW |
| T | Temperature, °C |
| V | Volume, m3 |
| Specific volume, | |
| Greek symbols | |
| Compression ratio | |
| Density, kg/m3 | |
| Volumetric efficiency | |
| Isentropic efficiency | |
| Mechanical efficiency | |
| Indicated efficiency | |
| Motor efficiency | |
| Opening degree of the valve | |
| Subscripts | |
| 1–4 | State point in Figure 1 |
| m | Average |
| i | Inner wall of condenser |
| 0 | Outer wall of condenser |
| r | Refrigerant |
| valve, in | Inlet of the valve |
| valve, out | Outlet of the valve |
| w | Water |
| wall | Wall |
References
- Bahman, A.M.; Parikhani, T.; Ziviani, D. Multi-objective optimization of a cold-climate two-stage economized heat pump for residential heating applications. J. Build. Eng. 2022, 46, 103799. [Google Scholar] [CrossRef]
- Zhang, D.; Li, J.; Liu, W.; Nan, J.; Wang, L. Evaluation and Prediction of Thermal Performance of Jet Enthalpy Air Source Heat Pump. J. Chem. Eng. 2014, 65, 5004–5009. [Google Scholar]
- Bach, C.K.; Vetsch, B.; Groll, E.A.; Horton, W.T.; Braun, J.E. Experimental investigation of vapor injected compression for cold climate heat pumps. In Proceedings of the 15th International Refrigeration and Air Conditioning Conference, West Lafayette, IN, USA, 14–17 July 2014. [Google Scholar]
- Xu, Y.; Huang, Y.; Jiang, N.; Song, M.; Xie, X.; Xu, X. Experimental and theoretical study on an air-source heat pump water heater for northern China in cold winter: Effects of environment temperature and switch of operating modes. Energy Build. 2019, 191, 164–173. [Google Scholar] [CrossRef]
- Yang, L.; Yuan, H.; Peng, J.-W.; Zhang, C.-L. Performance modeling of air cycle heat pump water heater in cold climate. Renew. Energy 2016, 87, 1067–1075. [Google Scholar] [CrossRef]
- Luo, J.; Yang, K.; Liu, Y.; Zhao, Z.; Chen, G.; Wang, Q. Experimental and theoretical assessments on the systematic performance of a single-stage air-source heat pump using ternary mixture in cold regions. Appl. Therm. Eng. 2023, 234, 121300. [Google Scholar] [CrossRef]
- Xiao, B.; Chang, H.; He, L.; Zhao, S.; Shu, S. Annual performance analysis of an air source heat pump water heater using a new eco-friendly refrigerant mixture as an alternative to R134a. Renew. Energy 2020, 147, 2013–2023. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, X.; Xu, M.; Xie, S. Hybrid model based on Preisach and support vector machine for novel dual-stack piezoelectric actuator. Mech. Syst. Signal Process. 2013, 34, 156–172. [Google Scholar] [CrossRef]
- Li, J.; Qu, C.; Li, C.; Liu, X.; Novakovic, V. Technical and economic performance analysis of large flat plate solar collector coupled air source heat pump heating system. Energy Build. 2022, 277, 112564. [Google Scholar] [CrossRef]
- Li, J.; Wei, S.; Dong, Y.; Liu, X.; Novakovic, V. Technical and economic performance study on winter heating system of air source heat pump assisted solar evacuated tube water heater. Appl. Therm. Eng. 2023, 221, 119851. [Google Scholar] [CrossRef]
- AS/NZS 4234:2021; Heated Water Systems—Calculation of Energy Consumption. Standards Australia: Sydney, Australia, 2021.
- Li, Y.; Yu, J. Theoretical analysis on optimal configurations of heat exchanger and compressor in a two-stage compression air source heat pump system. Appl. Therm. Eng. 2016, 96, 682–689. [Google Scholar] [CrossRef]
- Bertsch, S.S.; Groll, E.A. Two-stage air-source heat pump for residential heating and cooling applications in northern US climates. Int. J. Refrig. 2008, 31, 1282–1292. [Google Scholar] [CrossRef]
- Brunin, O.; Feidt, M.; Hivet, B. Comparison of the working domains of some compression heat pumps and a compression-absorption heat pump. Int. J. Refrig. 1997, 20, 308–318. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, X.; Deng, S. A simulation study on the operating performance of a solar–air source heat pump water heater. Appl. Therm. Eng. 2006, 26, 1257–1265. [Google Scholar] [CrossRef]
- Sleicher, C.; Rouse, M. A convenient correlation for heat transfer to constant and variable property fluids in turbulent pipe flow. Int. J. Heat Mass Transf. 1975, 18, 677–683. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).