Next Article in Journal
Analysis of the Mechanical Stability of Power Transformer Windings Considering the Influence of Temperature Field
Previous Article in Journal
Influence of Microwave Thermohydrolysis on Biomass Digestion
Previous Article in Special Issue
Wind Turbine SCADA Data Imbalance: A Review of Its Impact on Health Condition Analyses and Mitigation Strategies
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 18
Issue 6
10.3390/en18061372
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluation of the Sensitivity of PBL and SGS Treatments in Different Flow Fields Using the WRF-LES at Perdigão

by
Erkan Yılmaz
1,*,
Şükran Sibel Menteş
1 and
Gokhan Kirkil
2
1
Department of Climate Science and Meteorological Engineering, Faculty of Aeronautics and Astronautics, Istanbul Technical University, ITU Maslak Campus, Maslak, Istanbul 34469, Turkey
2
Faculty of Engineering and Natural Sciences, Kadir Has University, Cibali, Fatih, Istanbul 34083, Turkey
*
Author to whom correspondence should be addressed.
Energies 2025, 18(6), 1372; https://doi.org/10.3390/en18061372
Submission received: 24 January 2025 / Revised: 23 February 2025 / Accepted: 4 March 2025 / Published: 11 March 2025
(This article belongs to the Special Issue Computational and Experimental Fluid Dynamics for Wind Energy)
Browse Figures
Versions Notes

Abstract

:
This study investigates the effectiveness of the large eddy simulation version of the Weather Research and Forecasting model (WRF-LES) in reproducing the atmospheric conditions observed during a Perdigão field experiment. When comparing the results of the WRF-LES with observations, using LES settings can accurately represent both large-scale events and the specific characteristics of atmospheric circulation at a small scale. Six sensitivity experiments are performed to evaluate the impact of different planetary boundary layer (PBL) schemes, including the MYNN, YSU, and Shin and Hong (SH) PBL models, as well as large eddy simulation (LES) with Smagorinsky (SMAG), a 1.5-order turbulence kinetic energy closure (TKE) model, and nonlinear backscatter and anisotropy (NBA) subgrid-scale (SGS) stress models. Two case studies are selected to be representative of flow conditions. In the northeastern flow, the MYNN NBA simulation yields the best result at a height of 100 m with an underestimation of 3.4%, despite SH generally producing better results than PBL schemes. In the southwestern flow, the MYNN TKE simulation at station Mast 29 is the best result, with an underestimation of 1.2%. The choice of SGS models over complex terrain affects wind field features in the boundary layer more than above the boundary layer. The NBA model generally produces better results in complex terrain when compared to other SGS models. In general, the WRF-LES can model the observed flow with high-resolution topographic maps in complex terrain with different SGS models for both flow regimes.

1. Introduction

Wind farm siting in complex terrain conditions creates significant challenges and requires thorough validation of modeling methods. Meso–micro coupling is one of the most widely used techniques nowadays. A higher horizontal resolution enables accurate modeling of the boundary layer, resulting in a more accurate depiction of the temporal and spatial distribution of the atmosphere, boundary layer, and turbulence [1,2,3,4,5,6,7,8,9,10].
The motion of winds in complex terrain is affected by the characteristics of the surface features (land class/roughness length) and the specific elevation of the area, including hills, ridges, and mountains [11]. Modeling wind farms in complex terrain requires a more sophisticated approach than the typically employed linearized models like WAsP [12]. Computational fluid dynamics (CFD) methods are being used more and more to predict flows over complex terrain areas to consider these phenomena and offer more precise predictions of wind resources [13]. However, enhancing numerical modeling techniques for complex terrain necessitates considering several microscale processes, such as flow recirculation and the impact of the topography. Atmospheric models like the Weather Research and Forecasting model (WRF) allow for downscaling through grid nesting [14]. This means that the lateral boundary conditions for a smaller region in the model are determined by the outer grid simulations surrounding it.
To perform an accurate simulation of the turbulent flow field in the atmospheric boundary layer, it is required to conduct high-resolution simulations and account for the consequences of the large-scale features of the flow. A successful approach involves employing coupled mesoscale and microscale simulations, which accurately address different scales of atmospheric motion. The turbulence effects in traditional mesoscale grid cells, which have large horizontal footprints (with a horizontal grid spacing of approximately a couple of thousand meters), are parameterized only in the vertical direction. This is achieved using turbulence schemes such as the Mellor–Yamada–Nakanishi–Niino level 2.5 (MYNN) scheme or the Yonsei University (YSU) scheme [15,16]. An assumption of horizontal homogeneity is made by these schemes. On the other hand, when conducting turbulence-resolving simulations with a horizontal grid spacing of 100 m, turbulence models are required to parameterize the turbulence in all three orthogonal directions, such as by using the Smagorinsky approach or the Lilly method down to the inertial subrange scales [17,18,19].
Large eddy simulation (LES) is a method that involves resolving the energy-producing scales of three-dimensional atmospheric turbulence while filtering out the smaller-scale component of the turbulence spectrum from the flow field using a spatial filter [20,21]. By choosing a filter scale within the inertial subrange, the flow field might be divided into two parts: a resolved component that includes many scales responsible for turbulent transport and turbulence kinetic energy production, and a subfilter component that consists of scales within the turbulence cascade [22,23]. The subfilter component’s main role is to dissipate energy from the resolved scales. The effects of the unresolved scales are captured within the subfilter-scale (SFS) stress. SFS stresses and fluxes are typically represented using SGS models, which offer time- and space-dependent inputs for the explicitly resolved turbulent motion. These models aim to accurately replicate the statistical dissipation of energy in the turbulence cascade. The SGS can have a significant impact on the performance of LES. Additional information regarding the incorporation of large eddy simulation into the Weather Research and Forecasting model can be found in the works of Mirocha and Kirkil [24,25].
Over the past few decades, researchers have created and refined large eddy simulation models that effectively simulate turbulence in the atmospheric boundary layer. These models also account for the interaction between the atmosphere and the ground surface, as well as the formation of the boundary layer [26,27,28,29,30,31,32].
In addition, LES simulations conducted in the WRF can utilize a wide range of atmospheric physics parameterizations, including a developing collection of parameterizations that are sensitive to scale [33,34]. Although LES is ideal for studying turbulent flow in the atmosphere at the scale of the Weather Research and Forecasting model, the model’s use of terrain-following coordinates makes it challenging to operate LES over more complex terrain [35,36]. Terrain-following coordinates are effective for mesoscale simulation resolutions. However, when high resolutions are utilized to record steep terrain, numerical errors can occur, leading to a grid that is extremely skewed and has significant numerical inaccuracies [37,38,39,40,41].
Field observations are necessary to validate numerical models for complex terrain. One of the first field studies at Askervein Hill investigated an isolated hill [42]. The Bolund Hill campaign was another campaign that was carried out over an isolated hill in Denmark, as outlined by Bechmann [43]. Rodrigo conducted the Alaiz field campaign in Spain, which encompassed mountain valley topography [44]. The Perdigão field campaign was the selected test site for a study conducted in Portugal in 2017 [45]. The Perdigão experiment completed a comprehensive analysis of the airflow along two parallel ridges and yielded significant data for the characterization of flow in complex terrain [9,10,46,47,48,49].
Ensuring suitable treatment of the planetary boundary layer (PBL) in the “gray zone” is another crucial concern in multiscale simulations on complex terrain, in addition to the correct parameterization of turbulence. Within the resolution range of around 1.5 km to 100 m, known as the “gray zone” or “terra incognita”, models begin to explicitly resolve the bigger turbulent eddies [50,51,52,53,54,55]. Implementing a turbulence scheme may thus deteriorate the depiction of the bigger eddies, while still being essential to parameterize the smaller components of the turbulent spectrum [50,53,56,57].
Mesoscale turbulence parameterizations are not appropriate for the gray zone scales and are too large for an LES scheme to accurately represent turbulent eddies. When dealing with complex terrain, a substantial increase in the mesh refinement ratio might result in a notable discrepancy in topography at the boundaries between the mesoscale and the nested LES domains. Hence, it is crucial to examine the model’s performance at gray zone sizes in areas with complex topography.
The aim of this study is to facilitate the shift towards high-resolution atmospheric modeling by assessing the advantages and drawbacks of existing approaches. The WRF-LES is tested for its accuracy by modeling the flow pattern caused by the topography and comparing it with the measurement results from the Perdigão experimental field [45]. This study aims to demonstrate how combining mesoscale-to-microscale simulations can enhance wind characteristics in complex terrain. A study is conducted on how PBL and SGS schemes affect a single day in a complex terrain. We examine two specific case studies that serve as typical examples of varied atmospheric wind direction patterns: northern flow and southern flow. These patterns were frequently noticed throughout the field experiment. Six sensitivity simulations are performed using three distinct approaches: a conventional local PBL parameterization, Mellor–Yamada–Nakanishi–Niino level 2.5 (MYNN); a conventional, nonlocal PBL parameterization, Yonsei University (YSU); and a scale-aware PBL parameterization, Shin–Hong (SH), with three LES SGS stress models. Section 2 presents the chosen case study, outlines the model setup and optimization, and explains the technique used to assess the model’s performance. Section 3 provides an analysis of the spatial and temporal changes in the boundary layer across several model settings in the multinested configuration. Section 4 examines the outcomes, establishes connections with the findings of previous research, and summarizes the major results.

2. Materials and Methods

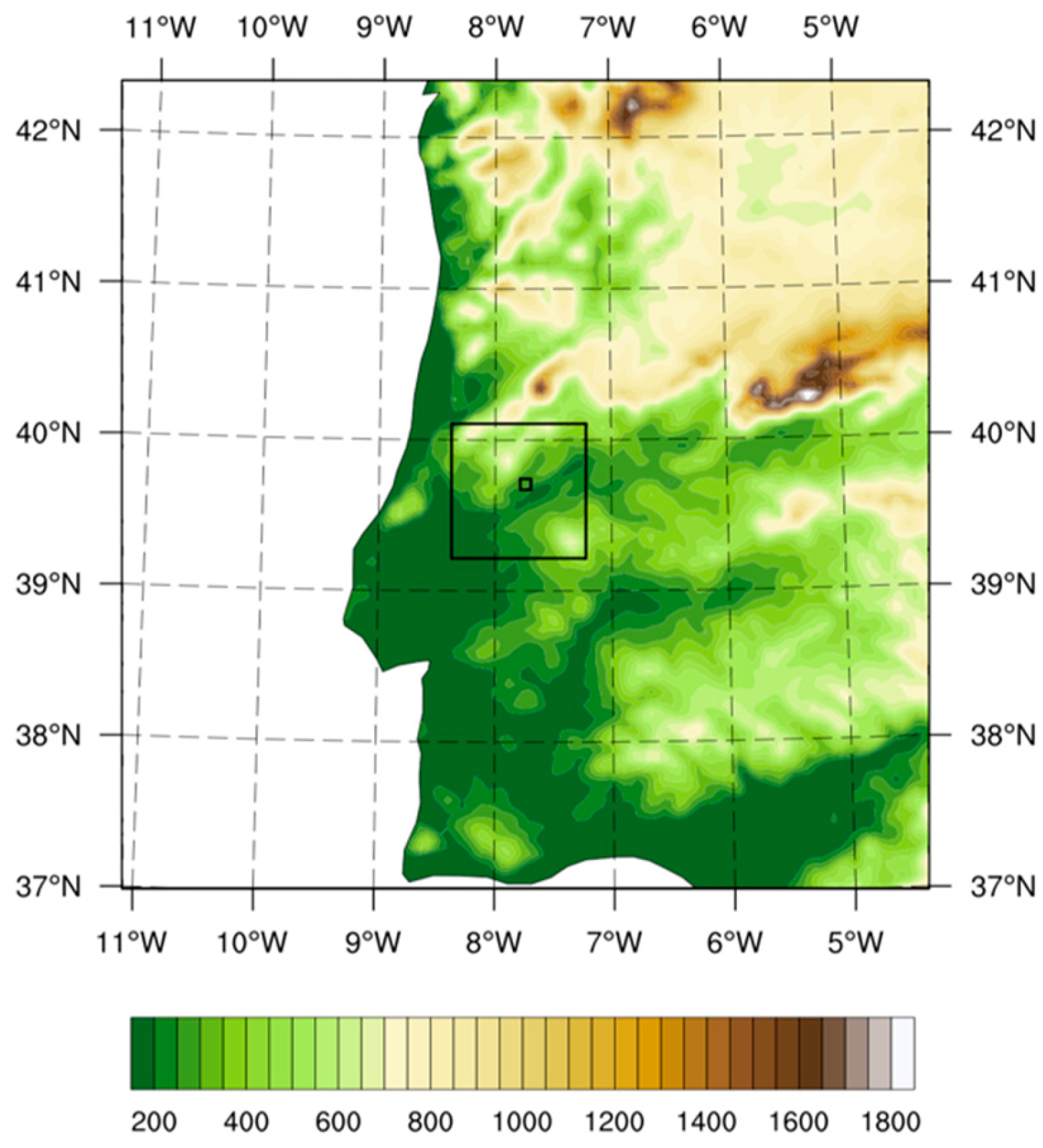
2.1. Perdigão

The Perdigão field campaign was a collaborative effort between the European Union and the United States, involving more than 70 scientists, engineers, and supporting people. This site was chosen because of the elongated valley that spans more than 2 km, indicating that the flow seen here may accurately mimic the characteristics of a simplified two-dimensional valley flow in the natural environment (Figure 1) [45]. A comprehensive and high-resolution dataset was obtained throughout the intensive operation time, which lasted from 1 May 2017 to 15 June 2017.
The data collection equipment consisted of 49 meteorological towers, ranging in height from 10 to 100 m, provided by UCAR/NCAR—Earth Observing Laboratory [58,59]. Additionally, there were over 180 sonic anemometers, 21 scanning wind lidars, 7 profiling wind lidars, 3 microwave radiometers (MWRs), a radio acoustic sounding system (RASS) wind profiler, and radiosonde launches conducted every 6 h [9]. This study utilized tower measurements from towers Mast 20 (also known as tower 20 or TSE04, 7°44′37.37″ W 39°42′21.47″ N), Mast 25 (also known as tower 25 or TSE09, 7°44′5.40″ W 39°42′40.36″ N), and Mast 29 (also known as tower 29 or TSE13, 7°43′49.38″ W 39°42′48.97″ N). The predominant wind directions in Perdigão are from the northeast (NE) and southwest (SW). So, this study specifically examines the wind flow that is perpendicular (cross-valley) to the double ridge.
Three 100 m meteorological towers were positioned in a transect that was approximately at a right angle to the ridges. The location of Mast 20, situated around 150 m southeast of the wind turbine along the ridgeline, accurately represents the inflow circumstances. Mast 25 is situated in the valley, whereas Mast 20 is positioned on the northeastern ridge.

2.2. Case Selection

In May and June 2017, a series of intensive operational periods (IOPs) were carried out to specifically study the wind patterns in mountain valley areas and the boundary layer. The objective of the project was to assess and enhance the efficiency of numerical models with high-resolution (10 m–100 m) grids [45].
Our study focuses on two specific cases: one on 19–20 May 2017 for northeastern flow and another on 13–14 June 2017 for southwestern flow. These cases were chosen for three reasons: Firstly, these were time periods when a wide variety of measurements were observed simultaneously. Secondly, there was no precipitation, allowing us to avoid the complexities associated with wet processes. Lastly, these cases represent a typical weather scenario of spring days with higher and moderate winds.

2.3. Multiscale Simulation Setup

In order to capture scales ranging from synoptic to turbulent eddies, the WRF-LES (version 3.8.1) system was set up with a three-domain, one-way online nesting configuration (Table 1). The online method helps the model maintain a realistic connection to the real atmosphere at the edges of the nested simulation grids. Online processing is more efficient than offline processing due to the simultaneous operation of all domains [33].
Initial experiments within the 100 m domain during simulation preparation revealed that the performance of the WRF-LES is highly dependent on the model configuration. Sensitivity studies were conducted and qualitatively evaluated to identify the model configuration that resulted in the most accurate flow development within the innermost 100 m domain. The criteria included the domain size, the number of vertical levels, and a determination of whether the WRF-LES mode or a PBL parameterization is more effective in the 100 m domain. The outer domain (D01) had a horizontal resolution of 5000 m and was made up of a 121 × 121 grid (Figure 2). The coarser horizontal resolution for d01-d02 had the advantage of reducing the computational time and costs. Additionally, two nested domains with a horizontal resolution of 1000 m and 100 m were incorporated to achieve a gradual refinement towards the desired endpoint of 100 m. The two larger domains employed mesoscale simulations with a planetary boundary layer (PBL) technique, whilst the smallest domain utilized a microscale LES turbulence closure.
The parent grid ratio from d02 to d03 was deliberately set at 10, which is relatively large. This decision was made to navigate the gray zone where turbulence is only substantially addressed [50,55,60].
It is important to mention that the WRF does not have a built-in mechanism to create turbulence at the sides of the LES domain. This means that it does not have a method like the one described in Muñoz-Esparza [8]. To implement these strategies effectively, it is necessary to use grid resolutions of approximately 50 m for convective conditions and 10 m for stably stratified conditions [8,61]. Consequently, this study did not aim to recreate genuine turbulence over the double ridge. Instead, its concentration was on replicating the meso–microscale flow over complex terrain.
To ensure numerical instability, it is recommended to adopt an aspect ratio Dz/Dx of less than 1 in the innermost domain. Research conducted by Muñoz-Esparza determined that precise vertical grid spacing is essential for PBL systems to prevent the overestimation of the observed low-level jet height and the excessive diffusion of the jet structure [8]. The model incorporated 28 vertical levels that were positioned below 1 km above ground level (a.g.l.). The altitude of the first model vertical level, denoted by z, was approximately 10 m a.g.l.
The entire WRF was utilized for a spin-up simulation in the outer domain to address the issue of soil equilibrium in cold start simulations [62]. The ECMWF provided the initial and boundary conditions. We utilized ERA5 (synoptic) data with a horizontal resolution of around 31 km and a temporal resolution of 1 h as input for the Weather Research and Forecasting model (WRF), which operates at a mesoscale level. We conducted nudging simulations at Perdigão while evaluating the WRF PBL scheme that generated wind simulations with the most minor errors.
The initial 12 h of the simulation was dedicated to model spin-up and was not included in the analysis. The model configuration used in this study is presented in Table 1. The selected relevant physical parameterizations included the Noah land surface model, the Rapid Radiative Transfer Model for longwave radiation, and the Dudhia shortwave radiation model [63,64,65].
Three topographic datasets of varying resolution were utilized to examine the impact of terrain on surface wind. Two of these are available in the WRF: the traditional Global 30 Arc-Second Elevation (GTOPO30) digital elevation model with a resolution of 900 m, and the high-resolution Shuttle Radar Topography Mission (SRTM) dataset with a resolution of 30 m [66]. Additionally, there is a military dataset from the Portuguese Army with a horizontal resolution of 10 m, specifically for the area around Perdigão [67]. The land cover classification used in this study was obtained from the CORINE Land Cover (CLC) 2012 dataset [68]. It was then adjusted to match the classification system used by the United States Geological Survey (USGS), as described in reference [69].
The resulting classification was integrated into the Weather Research and Forecasting model, together with the land-use lookup table from the New European Wind Atlas (NEWA) [70]. Despite the availability of the latest CORINE database, CLC 2018, it was not utilized in this study due to its susceptibility to the significant fire incident that took place in the region after the Perdigão measuring campaign.
It is important to mention that the initial boundary conditions (IBCs) of the microscale large eddy simulation (LES) domain, derived from a smooth mesoscale inflow, do not encompass all the atmospheric motions that can be resolved by the microscale mesh. Consequently, for the turbulence related to the absence of scales to form within the smaller-scale domain, a considerable distance needs to be covered [60]. Various techniques have been examined to initiate turbulence along the inflow, including the generalized cell perturbation method [71]. This method involves introducing finite-amplitude perturbations to the potential temperature field along the boundaries of the microscale domain inflow. However, the approach of initializing turbulence was not utilized in this work. In the sensitivity experiments discussed in Section 4, the simulation results from the inner microscale domains were compared and analyzed using various IBCs obtained from the parent domain d02.
The output interval for domain d3 in the WRF was adjusted to 5 min to facilitate a more accurate comparison with tower measurements that were averaged over the same 5 min period.

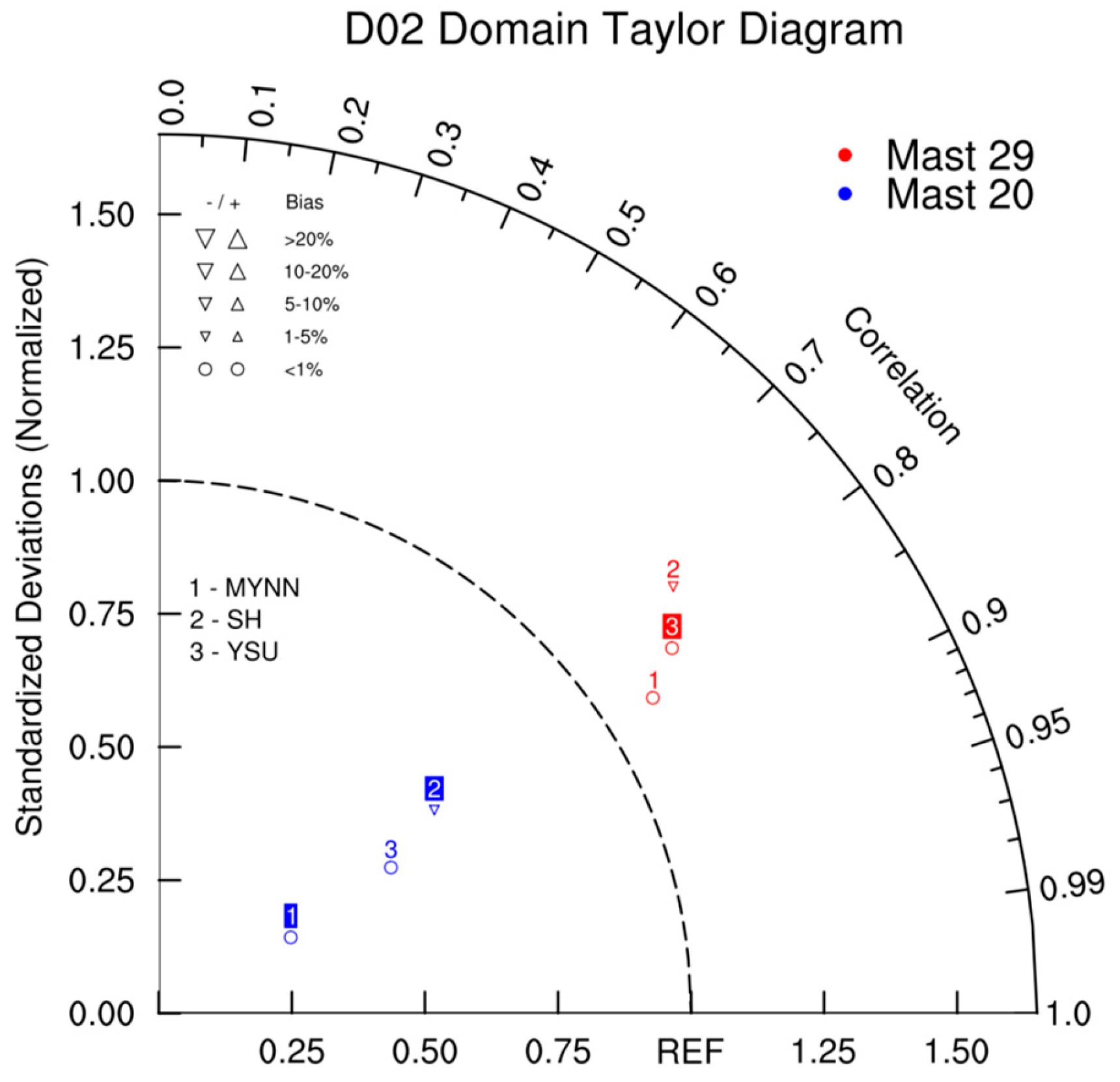
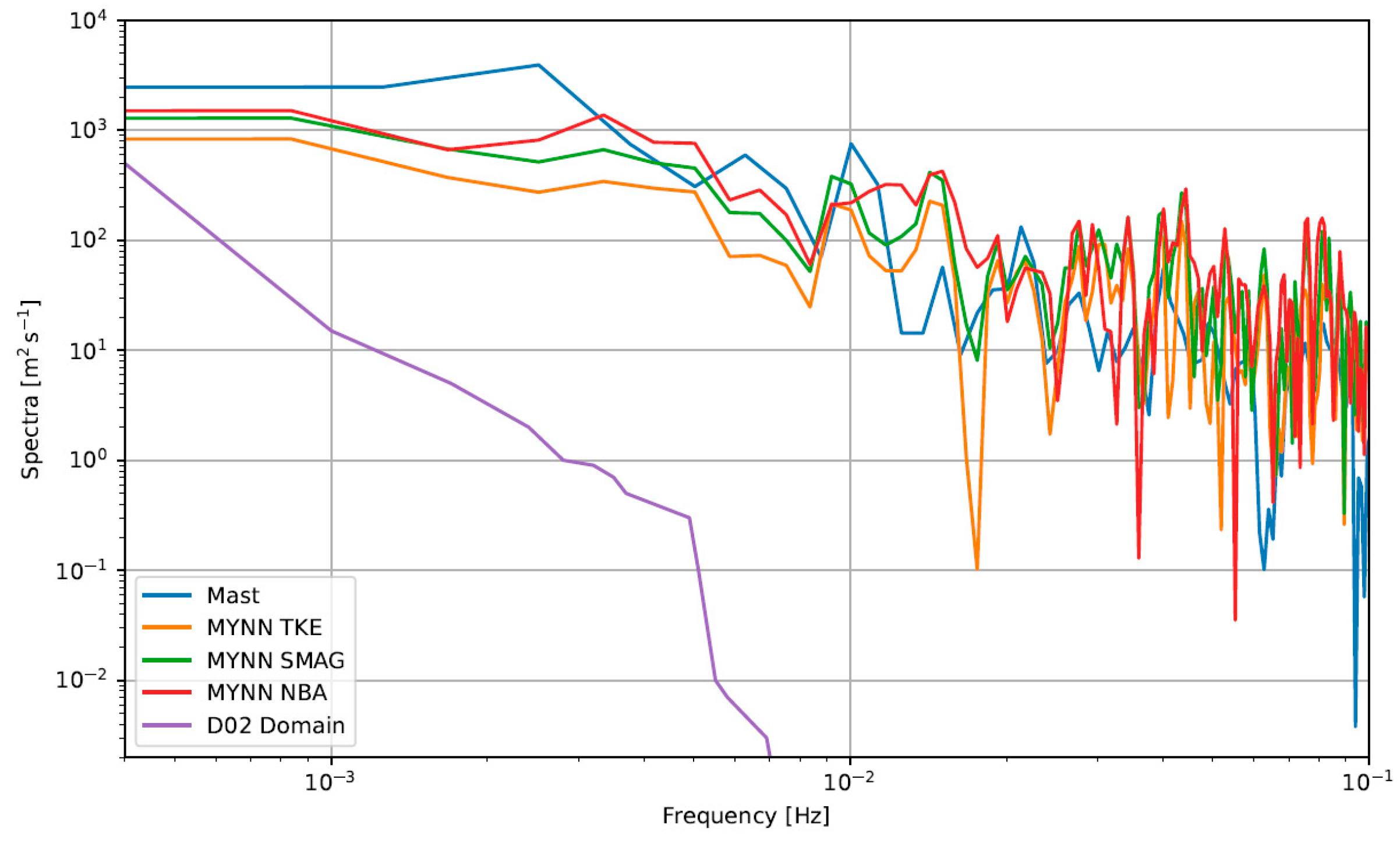
3. Results and Discussion

3.1. Description of Sensitivity Experiments

The averaged results of the simulations were examined to assess the effectiveness of the high-resolution WRF-LES in simulating wind patterns in the Perdigão area. It was observed in the statistical analysis that higher-resolution topography datasets produced better outcomes. A high model resolution and SRTM data help partially relieve the problem of underestimating wind speed at the mountaintop and overestimating it in the valley [7,72,73,74]. The assessment indicates that accurately representing the terrain is more crucial than the selection of PBL treatment for achieving a realistic simulation of wind speed.
The variability of several treatments (three PBL schemes and three SGS stress models of LES) was examined. The PBL schemes used in the present study were MYNN, YSU, and its scale-aware version, SH [75]. The three SGS models utilized in this study were the SMAG linear eddy viscosity model, the 1.5TKE model (Lilly 1966), and the NBA model based on SMAG [17,18,24,76].
Table 2 lists the details of nine sensitivity experiments; the YSU, MYNN, and SH PBL schemes were each used in three different experiments over d01 and d02, whose inner domain, d03, used LES models. By comparing the results, we intended to find the differences between simulations of PBL and LES in the boundary layer and the importance of scale-aware PBL treatment. We aimed to assess the impact of the SGS stress model of LES in d03.
Due to diurnal variation, the gray zone is not fixed and is not clearly defined in the real world. In qualitative terms, the gray zone scale range is approximately the size of the dominant eddy motion [56]. The scales of flow structures also play a role in complex terrain [77].
Zhou selected 400 m as the minimum gray zone scale in multiple previous gray zone studies, whereas Shin and Hong (2015) used 250 m [56,75]. Moreover, many real case studies of LES use a 100 m resolution as their LES resolution scale [73,78,79].
In the present study, 1000 m was utilized as a reasonable resolution for gray zone analysis. The following refers to d02 as the “gray zone domain” and d03 as the “microscale domains”.

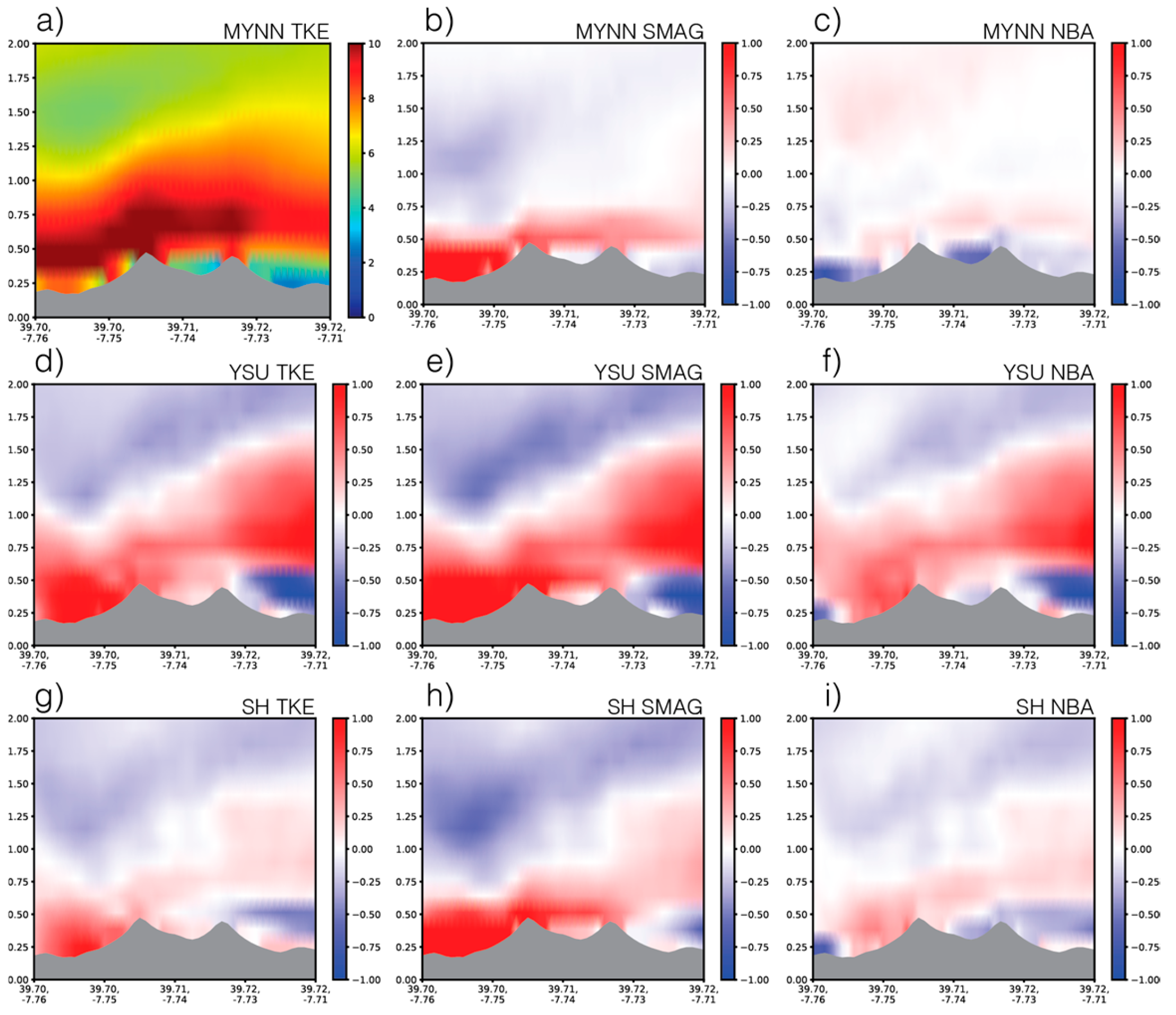
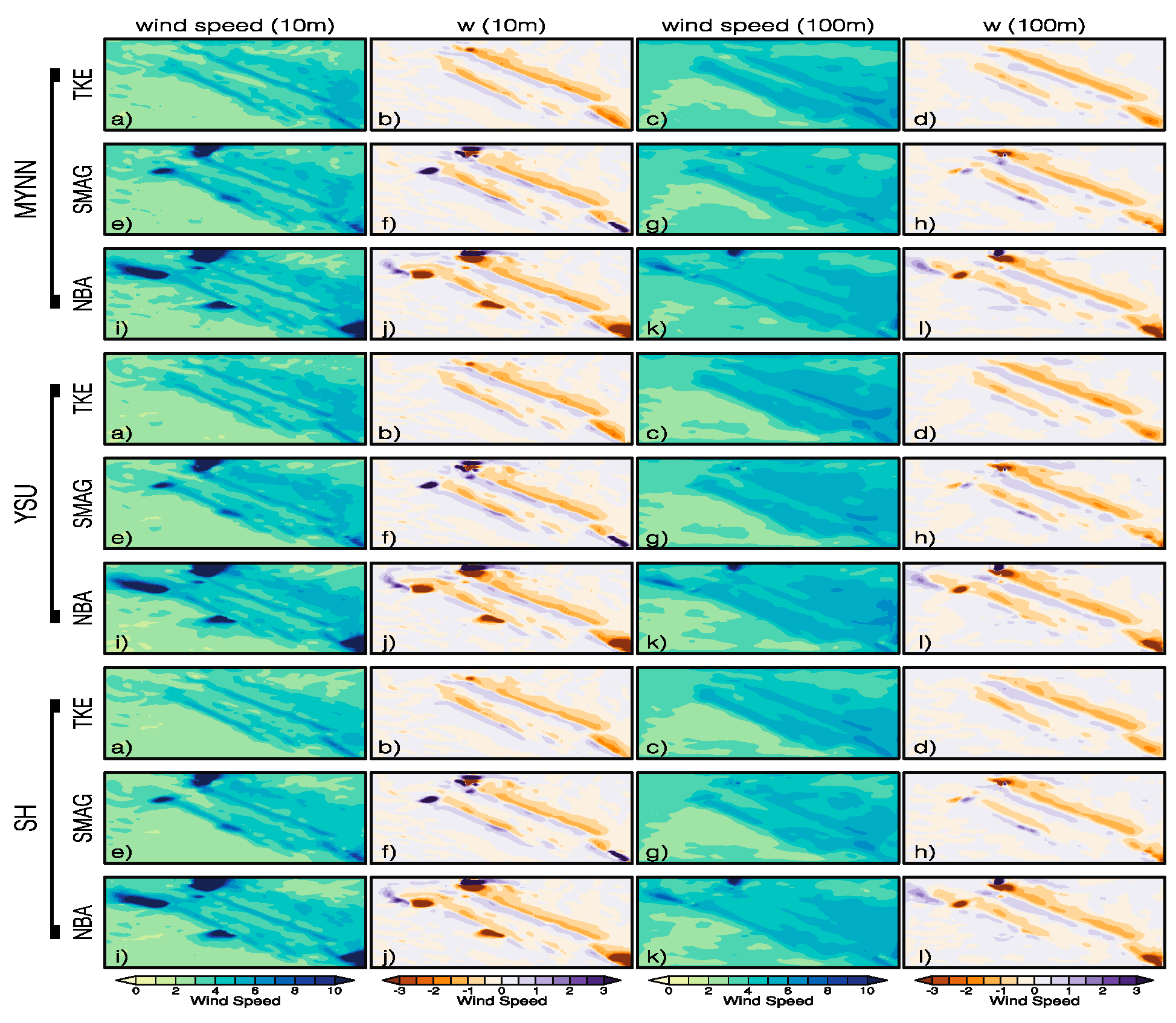
3.2. Northeastern Flow

The averaged results of the simulations were examined to assess the performance of the high-resolution WRF-LES in simulating wind patterns over the Perdigão area. Statistical evaluations of the model results are shown in Figure 3, which gives a Taylor diagram of a 100 m wind speed comparison with three different PBL schemes. It was detected that the normalized standardized deviation (a measure of how the standard deviation of the model output compares to the observed) between the simulated and observed wind speeds increased at the second hill (Mast 29) with increasing complexity, and the correlation coefficient showed higher values at the first hill (Mast 20). In contrast, all the PBL schemes showed higher precision at the second hill (Mast 29) than at Mast 20. The MYNN scheme better modeled wind speeds at both measurement locations compared to the other two PBL schemes.
The horizontal wind speeds and vertical wind speed component were compared at two different heights, 100 m and 10 m, and the transects of wind speed over the d03 area were compared with observations. Since the flow was divided into northeastern and southwestern regions, the variations in the simulated wind direction at different scales were not as big as the variations in simulated wind speeds. Therefore, this study should conclude with verifying wind speeds.
Figure 4 shows the average wind speed values and average vertical wind component values at 10 m and 100 m. The differences between the nine setups are summarized in Table 2. The first three graphs in the working chart show the images for MYNN, the next three graphs are for YSU, and the last three graphs show the visuals for SH. Higher wind speed values were observed in simulations using the SMAG parameterization when the area change in wind speed at 10 m was examined on the windward side. When the wind speed values at 100 m were examined, the distribution at the second hill was seen in a wider area. In the northeastern flow, the mountain wave also formed a strong wind area on the leeward side. When the speed of both the 10 m and 100 m low winds was examined, it was found that the flow from the second hill spread to a wider area. The upward winds on the windy sides of the hills were more clearly observed at both 10 m and 100 m, while strong descending low winds were observed on the leeward side.
PBL and LES parameters generally yielded similar results, with small differences in fields. The mountain area is mainly controlled by typical large-scale synoptic northwesterly flow. Wind speeds at the mountaintop are significantly higher than those in the valley.
The selection of each of the three PBL parameters as the meso model starting condition did not add any difference to the results in general. But different parameter selections in the LES model created differences in the flow in the experimental field. Especially in the flow area within the valley, the selection of different turbulence parameters showed small differences in the results at both 10 m and 100 m. The change in wind strength in the NBA model was more limited in the TKE and SMAG models, while the change in the strength of the wind was broader in the area. In each of the three models, the mountain wave on the downward side was modeled and the increase in wind strength was captured. The increase in wind strength at both peak points, and the decrease in wind strength behind the peak, was observed in all model results at both 10 m and 100 m heights. Increases in wind strength and downward currents were also modeled on the leeward side. Increasing the vertical resolution improved the accuracy of vertical transports, and when a large eddy simulation (LES) domain was used, resolved turbulence affected the inner domain.
In Figure 5, we present the difference from the MYNN TKE scheme for all model results regarding the daily average wind speed values. Figure 5a shows the result of the MYNN TKE model simulation of the transects of average wind speed for the northeastern flow. In the first column, we show the differential results for the TKE parameter; in the second column, the areal differentials for the SMAG parameter; and in the third column, those for the NBA model.
The first line shows PBL schemes for the MYNN parameter, the second line shows the YSU parameter, and the third line shows the area differences for the SH parameter from the MYNN TKE parameter. When the transect differences for different PBL schemes of the TKE model from the LES parameters were examined (Figure 5d), the YSU and SH parameters on the windward side showed higher wind speed values, as shown in the graph, whereas the MYNN parameter in the valley and on the leeward side had higher wind speed values. The YSU parameter results showed more changes in the positive and negative sides of the field.
When the transect results of the MYNN parameterization for different LES parameters (Figure 5b,c) were examined, they showed higher wind speed values on the windward side and in the valley compared to the SMAG and NBA parameterizations. The MYNN TKE parameterization on the leeward side of the second hill showed higher wind speed values. The MYNN TKE parameterization indicated higher wind speeds at both peaks in the northeastern flow but lower wind speed values inside the valley. The MYNN parameterization contributed more to the flow on the leeward side in different SGS models. In the northeastern flow, the change in wind speed at the second hill was stronger than that at the first hill.
When the YSU parameterization was examined, a strong flow on the windward side was observed in all SGS models. In the YSU SMAG parameterization, the wind speed on the windward side was stronger than that in the other two SGS models. When the results of SH parameterization (Figure 5g–i) were examined, MYNN generally showed results more like the PBL parameter than the YSU parameter. The change in wind speed in the SMAG parameterization was stronger, while the change in the NBA model was more limited. The microscale model successfully reproduced several key characteristics of the flow dynamics at the study site, including wave-like patterns associated with nocturnal low-level jets (LLJs), such as the standing wave observed on the lee side of the ridge during specific wind conditions. The LLJs’ fine details were not fully captured, probably due to the mesoscale tendencies’ resolution ability.
The most important difference was seen in the valley. In the NBA model, the change in wind speed showed higher wind speed values, while in the SMAG model, it showed lower wind speed values than in the TKE model. When we examined the flow at the second peak, the SMAG model showed the lowest change in wind speed. In general, the contribution of both PBL schemes and LES parameterization to the change was identical when we examined the results. A strong descending flow was generated on the second hill and the leeward side by the MYNN TKE parameterization.
The wind speed is also compared with meteorological tower measurements in Figure 6. The modeled wind speed typically followed the observations at 100 m, but there was a larger range of variation in the valley than on top of the two ridges.
Figure 7 displays errors quantified in terms of bias. The statistical details are shared in Appendix A. The wind speed errors at 100 m and along the two ridges range between −1.5 m/s and 3.5 m/s. While the bias errors show negative values at lower parts of the boundary at both hills, all models show overprediction on the top of measurements. Within the valley, the wind speed errors are on the order of 4 m/s and 1.2 m/s. While the errors show overprediction at 10 m, the error rate decreases moving away from the surface. The model captured the wind speed fluctuations more effectively in the valley than on the ridges, considering the wind speeds present on the second hill. The presence of this contradiction indicates that Mast 25 is located below the mountain wave and in a region of more well-mixed and coherent turbulence.

3.3. Southwestern Flow

WRF runs were used to test the ability of the model to reproduce the flow situation over complex terrain. Three different PBL schemes are compared with 100 m wind speed using Taylor diagrams in Figure 8. It can be observed that the normalized standardized deviation and correlation coefficient have more errors and low correlations for both hills with decreasing average wind speeds. The correlations of all the PBL schemes at the second hill (Mast 29) are higher than those at Mast 20. The MYNN scheme modeled wind speeds at both measurement locations better than the other two PBL schemes, as seen in the northeastern flow pattern results.
Figure 9 shows averaged flows of cross-valley wind speed simulations of domain D3. All models accurately replicated the flow pattern approaching the double ridge from the southwest. The simulated and observed single-point findings show a high level of agreement. The configuration of the airflow, particularly the atmospheric layers near the surface, exhibits notable disparities when simulations employing distinct parameterization techniques are compared. The flow fails to adequately detach from the surface, resulting in weak or non-existent recirculation zones. The inconsistencies can be partially attributed to incorrect and diminished surface friction.
Figure 9 shows the average wind speed values and average vertical wind component values at 10 m and 100 m. The average speed of the southwest wind flow was lower than that of the northeast wind, and the average wind speed at 100 m was less pronounced in all models. Topographical effects were lesser, especially in the entire flow area at 100 m. For the northeast flow, the wind speed on the hill behind the flow spread to a wider area. The results at 10 m show a strong wind field on the windward side of the Mast 20 measurement point in both the SMAG and the NBA models. This strong wind field creates a limited flow area due to the inadequate resolution of the model topography. There is no such flow area in the 100 m altitude results.
We looked at the differences (Figure 10) from the MYNN TKE parameterization for all model results of the average wind speed values. Figure 8 shows the result of the MYNN TKE model simulation of the transects of average wind speed for the southwestern flow. When the field difference results for different PBL schemes of the TKE model from the LES parameters were examined (Figure 10d), the change in the YSU and SH parameterization varied area by area, as shown in the graph. In the YSU parameterization, YSU showed higher wind speeds in the valley and on the leeward side, while in the SH parameterization, higher valley wind speed values were observed. When the areal results of the MYNN parameter for different LES parameters (Figure 10b,c) were examined, they showed lower wind speed values over windward and leeward sides and in the valley compared to the SMAG and NBA parameterizations, while MYNN TKE parameterization on both hills showed higher wind speed values. In the southwestern flow, the change in wind speed at the second hill was more severe than that at the first hill.
When the results for YSU parameterization were examined, strong flow on the windward side was observed in the TKE and SMAG models, while lower wind speed values were observed in the SMAG model. In the YSU and SMAG parameterizations, the changes in wind speed on the windward side and in the valley were stronger in the YSU parameterization.
The results of the SH parameterization were examined (Figure 10g–i) and generally showed more similar results to the YSU parameter. The change in the wind showed lower wind speed values in the TKE and SMAG parameters compared to the MYNN TKE model, while the change in wind speed in the NBA model showed higher wind speed values. When we looked at the flow on both hills, it showed the lowest change in wind speed in all SGS models. When we looked at the results in general, the contribution of both the PBL parameters and the LES parameters to the change was similar.
The wind speed is also compared with meteorological tower measurements in Figure 11. The modeled wind speed generally follows the observations at 100 m, with greater variability and fluctuations in the valley and on top of the two ridges. All the models captured the general flow pattern all day, except at midday, when all models fluctuated much more. Figure 12 displays errors quantified in terms of bias for the southeastern flow. At 100 m and along the two ridges, the wind speed errors range between −0.75 m/s and 1 m/s. The wind speed errors in the valley are around 3 m/s and 1.5 m/s. While the model overpredicts at 10 m, the error rate decreases moving away from the surface. Only the second hill has negative errors at the lower part of the boundary layer, while it shows overprediction at the upper part of the boundary layer.
Figure 13 shows the 100 m boxplot results of nine different simulations at three different observation stations. In this boxplot study, we tried to see the differences in more detail by dividing the one-day simulation into a diurnal cycle. For the daily cycle in the southwestern flow, all model simulations yielded closer results, while in the northeast flow, the contradiction was greater at the measurement station on the southeast hill. Again, the station in the valley exhibited significantly more inconsistencies when compared to the observations.
Based on the resolution of both the terrain and land-use data, as well as the capability to resolve turbulent flow structures, nested WRF–LES simulations produce progressively more comprehensive flow predictions. The power spectral density of the 100 m wind speed signals in Figure 14 can be used to detect higher-frequency turbulence as the grid resolution increases thorough analysis. The spectra of d03 exhibit an inertial subrange and possess energy contents congruent with the data.
The wind speed spectra in d02 exhibit a drop-off, which is characteristic of models that use finite-difference discretization methods. Table 3 shows the error metrics at Mast 20 and Mast 25. The consistency of the bias and RMSE values between the two domains suggests that there is no substantial decrease in errors at the Mast 20 position when nesting to a higher grid resolution. The inaccuracies mostly arise from the steady background flow, which remains rather constant across the domains. Although the recirculation zone is clearly defined on d03, the less steep resolved slopes on d02 do not cause recirculation in the same areas. The enhanced grid resolution and terrain resolution have a direct impact on d03, resulting in a more precise depiction of the observed flow characteristics at Mast 25’s position.
In general, LES results show better outcomes in unstable conditions, while in stable conditions, they have not demonstrated a very good approach to solving turbulent flow.

4. Conclusions

This study used a comprehensive WRF-LES to replicate a 36 h real weather scenario in the Perdigão region on 19–20 May 2017 and 13–14 June 2017. The averaged meteorological aspects and statistical properties of the flow were strongly correlated during IOP verifications.
Creating a high-performance microscale atmospheric simulation requires the use of high-quality topographical data. The efficiency of high-resolution modeling is increased by using high-resolution topographical data. The WRF-LES exhibits the capability to accurately depict diverse surface fluxes and small-scale circulations within relevant areas, such as the mountainous Perdigão region.
The present work also aimed to examine the uncertainty of various planetary boundary layer (PBL) treatments at gray zone scales. To do this, sensitivity tests using large eddy simulation (LES), Mellor–Yamada–Nakanishi–Niino (MYNN), Yonsei University (YSU), and Simulated Heating (SH) were conducted, and the findings were compared. Different PBL schemes offer various advantages under different geographical conditions. The YSU scheme performs better in larger areas with less complex topographical structures, particularly in convective movements. On the other hand, the MYNN scheme demonstrates better performance in more complex topographies (such as mountains areas and valleys) and turbulent flows. Although the SH scheme yields better results in turbulent flows within mountainous and complex terrains, it requires a high resolution and high computational capacity to achieve this. When we examined the results of our study, despite showing comparable outcomes, the MYNN scheme achieved higher performance due to an insufficient resolution for SH modeling in our simulations. To obtain more effective results, it is necessary for MYNN to have a greater capacity for both nonlocal and local heat transport.
Three distinct SFS models, including basic to advanced methodologies in complex terrain, were employed to analyze the effects of horizontal mesh refinement. The two most basic models are linear, constant-coefficient eddy viscosity models, where the eddy viscosity coefficient is determined using either the strain rate (SMAG) or a 1.5-order prognostic equation for subgrid-scale (SFS) turbulence kinetic energy [17,18]. The nonlinear backscatter and anisotropy (NBA) model, developed by Kosovic in 1997 and further studied by Kosovic and Curry in 2000, was also investigated [76,80]. This model incorporates a nonlinear constitutive connection.
Generally, large eddy simulation (LES) models are more effective than planetary boundary layer (PBL) parameterization techniques when simulating real flow over complex terrain at the gray zone scale. The difference in day-to-night emissions at the Mast 20 measurement station in NE flow is greater than that in SW flow. At station Mast 20, in the northeastern flow, the difference between night and day is most noticeable. The results for low wind speeds under southwesterly flow show similarities with the observations.
Research on the combined performance of large eddy simulation and the planetary boundary layer has significantly increased in recent times. We observed that similar approaches to this subject have been simultaneously presented, with large eddy simulations being preferred to planetary boundary layer models for better addressing the gray zone [7,81,82,83,84]. The characteristics of the wind field in the lower atmosphere over complex terrain are highly influenced by the choice of planetary boundary layer treatments.
To assess the level of uncertainty in the SGS stress model at the microscale, we evaluated three regularly employed SGS stress models in the LES: 1.5TKE, SMAG, and NBA. On the gray zone scale, each SGS model has a reduced impact on both the simulated average values and statistical measures. On a smaller scale, the impact becomes more pronounced. The stress models developed by SGS have a greater influence compared to the IBCs built using various PBL treatments in the parent gray zone domain.
Out of these models, the NBA model demonstrated the highest level of performance, which aligns with the results of simulations conducted by Kirkil, Mirocha, and Zhou and Chow [24,25,85,86,87].
Recently, there has been tremendous progress in the study of the planetary boundary layer (PBL) through measurement campaigns and modeling efforts. A significant amount of effort has been devoted to improving the parameterizations of the PBL in complex terrain [88,89,90,91]. Nevertheless, PBL parameterization is not yet a reliable method for navigating complex terrain. However, despite the positive findings from idealized studies suggesting that LES is highly effective in simulating boundary layer winds (Kosovic’ & Curry 2000; Mirocha et al. 2010), it is not a flawless solution for complex terrain [24,80].
Additional research should prioritize enhancing the capabilities of the LES model to accurately represent vertical momentum structures in different atmospheric conditions. This study showcases the capabilities of the WRF-LES as a valuable instrument for acquiring fresh knowledge about PBL processes in areas with complex topography. The WRF-LES has great potential for accurately simulating the flow field in complex terrain. Nonlinear models solve the effects in the boundary layer better than linear models.
The results of this study are promising and suggest that it could be useful in complex terrain, too. The microscale model records the weather patterns that change slowly, which are fed to it by mesoscale tendencies while also including local orographic and surface effects. Although mesoscale models appear to provide the correct large-scale force, validating their use for coupling is not an easy task, particularly in complex terrain.
In the Perdigão field campaign, the setup of boundary conditions in WRF-LES simulations was critical for accurately capturing the complex terrain effects and turbulence dynamics. The turbulence generated by orographic effects at the boundary layer and near inflow regions in WRF-LES simulations plays a critical role in accurately capturing complex flow structures, such as wake effects, flow separation, and recirculation, which are essential for understanding wind patterns and atmospheric dynamics in mountainous regions.
It is important to highlight that the findings of this paper are based on a limited number of individual cases of two different flows. Therefore, it is necessary to assess these results using a wider range of case situations and validate them against further observations. Additional research conducted at the Perdigão site may potentially involve analyzing and contrasting observed turbulence measurements. This study specifically examined the impact of large-scale synoptic flow on the topography. Additional improvements in modeling, such as the development of parameterization for the gray zone that considers different scales and the implementation of adaptive subgrid-scale stress (SGS) models at higher resolutions, are anticipated to significantly improve the capabilities of multiscale modeling. The incorporation of turbulence, such as through cell perturbation, together with the utilization of more accurate land-use datasets that include improved roughness and forest maps, as well as enhanced soil moisture data, is expected to improve the simulation of the small-scale valley flows in Perdigão in a more realistic manner.

Author Contributions

Conceptualization, E.Y., Ş.S.M. and G.K.; methodology, E.Y.; software, E.Y.; writing—original draft preparation, E.Y.; writing—review and editing, Ş.S.M.; writing—review and editing, G.K.; visualization, E.Y. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the ITU Coordination Unit for Scientific Research Projects (ITU-BAP) (grant nos. MDK—2018-41233) and part of the Special Issue “Meso-Micro Model Coupling with WRF-LES and High Resolution Wind Filed Determination” (ITU-BAP).

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).

Acknowledgments

The Perdigão field campaign was primarily funded by the US National Science Foundation, European Commission’s ERANET+, Danish Energy Agency, German Federal Ministry of Economy and Energy, Portugal Foundation for Science and Technology, US Army Research Laboratory, and Israel Binational Science Foundation. This study used the Advanced Research WRF-ARW model and the WRF Preprocessing System (WPS) version 3.8.1 (Boulder, CO, USA). The WRF-ARW and WPS are publicly available at http://www2.mmm.ucar.edu/wrf/users/ (accessed on 1 November 2021). Initial and boundary condition data were provided by the ERA-5 dataset with 0.3° from https://cds.climate.copernicus.eu/ (accessed on 1 November 2021). Land cover and elevation datasets at 30 s resolutions were used and provided by http://www2.mmm.ucar.edu/wrf/src/wps_files/ (accessed on 1 November 2021). The computing resources used in this work were provided by the National Center for High Performance Computing of Turkey (UHeM) under grant number 1016072023. Acknowledgment is due to Fahri Mert Sayınta for his support throughout this study.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
a.g.l.Above ground level
CFDComputational fluid dynamics
CLCCorine Land Cover
CORINECoordination of Information on the Environment
ECMWFEuropean Centre for Medium-range Weather Forecast
ERA5ECMWF reanalysis 5th generation
GTOPO30Global topography at 30 arcsec
IBCInitial boundary condition
IOPIntensive operational period
LESLLJLarge eddy simulationLow-level jet
MYNNMellor–Yamada–Nakanishi–Niino level 2.5
MWRMicrowave radiometer
NBANonlinear backscatter and anisotropy
NCARNational Center for Atmospheric Research
NENortheast
NEWANew European Wind Atlas
PBLPlanetary boundary layer
RASSRadio acoustic sounding system
SFSSubfilter scale
SGSSubgrid scale
SHShin–Hong
SMAGSmagorinsky
SRTMShuttle Radar Topography Mission
SWSouthwest
TKE1.5-order turbulence kinetic energy closure
UCARUniversity Corporation for Atmospheric Research
USGSUnited States Geological Survey
YSUYonsei University
WAsPWind Atlas Analysis and Application Program
WRFWeather Research and Forecasting model
WRF-LESWeather Research and Forecasting model and large eddy simulation

Appendix A

Table A1 presents the statistical RMSE values of the results calculated at three measurement stations and at four different altitudes; the best result for 100 m was 1.37 m/s for the station on the northeast hill (Mast 29) using the MYNN NBA model simulation for northeastern flow. For the measuring station inside the valley, the best result was calculated with SH TKE simulation. Simulations on both hills showed higher wind speeds than the observed wind speed values, while lower values were observed in the valley. More statistical evaluations of the model results are shown in Table A1, which gives the 10 min 10 m, 30 m, 60 m, and 100 m wind speed comparisons from all simulations.
Table A1. RMSE results of comparisons of WRF–LES (simulations) and meteorological tower measurements (observed data) for northeastern and southwestern flow case studies of wind speed.
Table A1. RMSE results of comparisons of WRF–LES (simulations) and meteorological tower measurements (observed data) for northeastern and southwestern flow case studies of wind speed.
PBLSGSz [m a.g.l.]Mast 20Mast 25Mast 29
NESWNESWNESW
MYNNTKE1003.692.014.423.141.511.86
603.451.953.782.872.561.85
303.221.862.562.493.051.84
103.131.771.632.073.851.82
SMAG1003.512.004.273.541.432.20
603.351.893.083.252.072.17
303.021.822.432.982.922.13
102.881.681.802.733.992.11
NBA1003.481.944.833.071.352.21
603.341.893.982.921.892.08
303.131.823.052.782.671.99
102.971.702.032.633.791.90
SHTKE1003.612.074.363.541.791.96
603.352.063.693.172.161.90
303.012.052.312.952.951.82
102.722.051.342.273.721.76
SMAG1003.391.973.943.631.372.06
603.041.892.733.302.012.03
302.911.852.003.003.022.00
102.481.801.422.743.791.98
NBA1003.371.904.643.271.462.10
603.081.883.653.041.902.01
302.961.842.132.922.451.95
102.581.821.712.723.661.84
YSUTKE1004.002.064.233.802.362.18
603.481.943.583.482.952.09
303.011.822.822.973.271.99
102.921.731.372.603.821.86
SMAG1003.961.964.143.782.272.06
603.651.903.563.352.792.00
303.191.822.353.063.061.95
102.821.741.522.833.941.89
NBA1003.941.994.433.372.172.09
603.331.883.453.022.862.01
303.061.762.162.903.061.94
102.871.681.652.723.551.82

References

  1. Bauer, H.; Weusthoff, T.; Dorninger, M.; Wulfmeyer, V.; Schwitalla, T.; Gorgas, T.; Arpagaus, M.; Warrach-Sagi, K. Predictive skill of a subset of models participating in D-PHASE in the COPS region. Q. J. R. Meteorol. Soc. 2011, 137, 287–305. [Google Scholar] [CrossRef]
  2. Schwitalla, T.; Bauer, H.; Wulfmeyer, V.; Aoshima, F. High-resolution simulation over central Europe: Assimilation experiments during COPS IOP 9c. Q. J. R. Meteorol. Soc. 2011, 137, 156–175. [Google Scholar] [CrossRef]
  3. Zittis, G.; Bruggeman, A.; Camera, C.; Hadjinicolaou, P.; Lelieveld, J. The added value of convection permitting simulations of extreme precipitation events over the eastern Mediterranean. Atmos. Res. 2017, 191, 20–33. [Google Scholar] [CrossRef]
  4. Feng, Z.; Leung, L.R.; Houze, R.A.; Hagos, S.; Hardin, J.; Yang, Q.; Han, B.; Fan, J. Structure and Evolution of Mesoscale Convective Systems: Sensitivity to Cloud Microphysics in Convection-Permitting Simulations Over the United States. J. Adv. Model. Earth Syst. 2018, 10, 1470–1494. [Google Scholar] [CrossRef]
  5. Martínez, R.I.; Chaboureau, J.P. Precipitation and Mesoscale Convective Systems: Explicit versus Parameterized Convection over Northern Africa. Mon. Weather Rev. 2018, 146, 797–812. [Google Scholar] [CrossRef]
  6. Woodhams, B.J.; Birch, C.E.; Marsham, J.H.; Bain, C.L.; Roberts, N.M.; Boyd, D.F. What Is the Added Value of a Convection-Permitting Model for Forecasting Extreme Rainfall over Tropical East Africa? Mon. Weather Rev. 2018, 146, 2757–2780. [Google Scholar] [CrossRef]
  7. Wagner, J.; Gerz, T.; Wildmann, N.; Gramitzky, K. Long-term simulation of the boundary layer flow over the double-ridge site during the Perdigão 2017 field campaign. Atmos. Chem. Phys. 2019, 19, 1129–1146. [Google Scholar] [CrossRef]
  8. Muñoz-Esparza, D.; Lundquist, J.K.; Sauer, J.A.; Kosović, B.; Linn, R.R. Coupled mesoscale-LES modelling of a diurnal cycle during the CWEX-13 field campaign: From weather to boundary-layer eddies. J. Adv. Model. Earth Syst. 2017, 9, 1572–1594. [Google Scholar] [CrossRef]
  9. Wildmann, N.; Kigle, S.; Gerz, T. Coplanar lidar measurement of a single wind energy converter wake in distinct atmospheric stability regimes at the Perdigão 2017 experiment. J. Phys. Conf. Ser. 2018, 1037, 052006. [Google Scholar] [CrossRef]
  10. Wildmann, N.; Bodini, N.; Lundquist, J.K.; Bariteau, L.; Wagner, J. Estimation of turbulence dissipation rate from Doppler wind lidars and in situ instrumentation for the Perdigão 2017 campaign. Atmos. Meas. Tech. 2019, 12, 6401–6423. [Google Scholar] [CrossRef]
  11. Emeis, S. Wind Energy Meteorology, vol. 2 of Atmospheric Physics for Wind Power Generation; Springer International Publishing: Twente, Belgium, 2013; ISBN 978-3-642-30523-8. [Google Scholar] [CrossRef]
  12. Jørgensen, H.; Nielsen, M.; Barthelmie, R.; Mortensen, N. Modelling offshore wind resources and wind conditions. In Proceedings of the (CD-ROM) Copenhagen Offshore Wind, Roskilde, Denmark, 26–28 October 2005. Available online: https://backend.orbit.dtu.dk/ws/portalfiles/portal/107919793/Modelling_offshore_wind_resources_and_wind_conditions.pdf (accessed on 10 January 2023).
  13. Blocken, B. 50 years of Computational Wind Engineering: Past present and future. J. Wind Eng. Ind. Aerod. 2014, 129, 69–102. [Google Scholar] [CrossRef]
  14. Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A description of the advanced research WRF version 3. NCAR Tech. Note 2008, 475, 10–5065. [Google Scholar]
  15. Nakanishi, M.; Niino, H. An Improved Mellor–Yamada Level-3 Model: Its Numerical Stability and Application to a Regional Prediction of Advection Fog. Bound. Layer Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
  16. Hong, S.Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
  17. Smagorınsky, J. General Cırculatıon Experıments with the Prımıtıve Equatıons. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
  18. Lilly, D.K. On the application of the eddy viscosity concept in the inertial sub-range of turbulence. NCAR Manuscr. 1966, 123, 19. [Google Scholar] [CrossRef]
  19. Lilly, D.K. The representation of small-scale turbulence in numerical experiment. In Proceedings of the IBM Scientific Computing Symposium on Environmental Sciences, White Plains, NY, USA, 14–16 November 1967; pp. 195–210. [Google Scholar]
  20. Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
  21. Stoll, R.; Gibbs, J.A.; Salesky, S.T.; Anderson, W.; Calaf, M. Large-Eddy Simulation of the Atmospheric Boundary Layer. Bound. Layer Meteorol. 2020, 177, 541–581. [Google Scholar] [CrossRef]
  22. Shaw, R.H.; Schumann, U. Large-eddy simulation of turbulent flow above and within a forest. Bound. Layer Meteorol. 1992, 61, 47–64. [Google Scholar] [CrossRef]
  23. Quimbayo-Duarte, J.; Wagner, J.; Wildmann, N.; Gerz, T.; Schmidli, J. Evaluation of a forest parameterization to improve boundary layer flow simulations over complex terrain. A case study using WRF-LES V4.0.1. Geosci. Model Dev. 2022, 15, 5195–5209. [Google Scholar] [CrossRef]
  24. Mirocha, J.D.; Lundquist, J.K.; Kosović, B. Implementation of a Nonlinear Subfilter Turbulence Stress Model for Large-Eddy Simulation in the Advanced Research WRF Model. Mon. Weather Rev. 2010, 138, 4212–4228. [Google Scholar] [CrossRef]
  25. Kirkil, G.; Mirocha, J.; Bou-Zeid, E.; Chow, F.K.; Kosović, B. Implementation and Evaluation of Dynamic Subfilter-Scale Stress Models for Large-Eddy Simulation Using WRF*. Mon. Weather Rev. 2012, 140, 266–284. [Google Scholar] [CrossRef]
  26. Deardorff, J.W. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
  27. Deardorff, J.W. Numerical Investigation of Neutral and Unstable Planetary Boundary Layers. J. Atmos. Sci. 1972, 29, 91–115. [Google Scholar] [CrossRef]
  28. Deardorff, J.W. Stratocumulus-capped mixed layers derived from a three-dimensional model. Bound. Layer Meteorol. 1980, 18, 495–527. [Google Scholar] [CrossRef]
  29. Moeng, C.H. A Large-Eddy-Simulation Model for the Study of Planetary Boundary-Layer Turbulence. J. Atmos. Sci. 1984, 41, 2052–2062. [Google Scholar] [CrossRef]
  30. Chlond, A.; Wolkau, A. Large-Eddy Simulation Of A Nocturnal Stratocumulus-Topped Marine Atmospheric Boundary Layer: An Uncertainty Analysis. Bound. Layer Meteorol. 2000, 95, 31–55. [Google Scholar] [CrossRef]
  31. Raasch, S.; Schröter, M. PALM—A large-eddy simulation model performing on massively parallel computers. Meteorol. Z. 2001, 10, 363–372. [Google Scholar] [CrossRef]
  32. Heinze, R.; Dipankar, A.; Henken, C.C.; Moseley, C.; Sourdeval, O.; Trömel, S.; Xie, X.; Adamidis, P.; Ament, F.; Baars, H.; et al. Large-eddy simulations over Germany using ICON: A comprehensive evaluation. Q. J. R. Meteorol. Soc. 2017, 143, 69–100. [Google Scholar] [CrossRef]
  33. Talbot, C.; Bou-Zeid, E.; Smith, J. Nested Mesoscale Large-Eddy Simulations with WRF: Performance in Real Test Cases. J. Hydrometeorol. 2012, 13, 1421–1441. [Google Scholar] [CrossRef]
  34. Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The Weather Research and Forecasting Model: Overview, system efforts, and future directions. Bull. Amer. Meteor. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
  35. Catalano, F.; Moeng, C.H. Large-Eddy Simulation of the Daytime Boundary Layer in an Idealized Valley Using the Weather Research and Forecasting Numerical Model. Bound. Layer Meteorol. 2010, 137, 49–75. [Google Scholar] [CrossRef]
  36. Taylor, D.M.; Chow, F.K.; Delkash, M.; Imhoff, P.T. Numerical simulations to assess the tracer dilution method for measurement of landfill methane emissions. Waste Manag. 2016, 56, 298–309. [Google Scholar] [CrossRef]
  37. Klemp, J.B.; Skamarock, W.C.; Fuhrer, O. Numerical Consistency of Metric Terms in Terrain-Following Coordinates. Mon. Weather Rev. 2003, 131, 1229–1239. [Google Scholar] [CrossRef]
  38. Mahrer, Y. An Improved Numerical Approximation of the Horizontal Gradients in a Terrain-Following Coordinate System. Mon. Weather Rev. 1984, 112, 918–922. [Google Scholar] [CrossRef]
  39. Schär, C.; Leuenberger, D.; Fuhrer, O.; Lüthi, D.; Girard, C. A New Terrain-Following Vertical Coordinate Formulation for Atmospheric Prediction Models. Mon. Weather Rev. 2002, 130, 2459–2480. [Google Scholar] [CrossRef]
  40. Zängl, G. An Improved Method for Computing Horizontal Diffusion in a Sigma-Coordinate Model and Its Application to Simulations over Mountainous Topography. Mon. Weather Rev. 2002, 130, 1423–1432. [Google Scholar] [CrossRef]
  41. Zängl, G.; Gantner, L.; Hartjenstein, G.; Noppel, H. Numerical errors above steep topography: A model intercomparison. Meteorol. Z. 2004, 13, 69–76. [Google Scholar] [CrossRef]
  42. Salmon, J.; Bowen, A.; Hoff, A.; Johnson, R.; Mickle, R.; Taylor, P.; Tetzlaff, G.; Walmsley, J. The Askervein Hill Project: Mean wind variations at fixed heights above ground. Bound. Layer Meteorol. 1988, 43, 247–271. [Google Scholar] [CrossRef]
  43. Bechmann, A.; Berg, J.; Courtney, M.; Jørgensen, H.; Mann, J.; Sørensen, N. The Bolund Experiment: Blind Comparison of Models for Wind in Complex Terrain (Invited), American Geo-physical Union (AGU) Fall Meeting Abstracts. Available online: https://ui.adsabs.harvard.edu/abs/2009AGUFM.A33H..08B/abstract (accessed on 10 January 2023).
  44. Rodrigo, J.; Santos, P.; Chavez, R.; Avila, M.; Cavar, D.; Lehmkuhl, O.; Owen, H.; Li, R.; Tromeur, E. The ALEX17 diurnal cycles in complex terrain benchmark. J. Phys. Conf. Ser. 1934, 1934, 012002. [Google Scholar] [CrossRef]
  45. Fernando HJ, S.; Mann, J.; Palma JM, L.M.; Lundquist, J.K.; Barthelmie, R.J.; Belo-Pereira, M.; Brown WO, J.; Chow, F.K.; Gerz, T.; Hocut, C.M.; et al. The Perdigão: Peering into Microscale Details of Mountain Winds. Bull. Am. Meteorol. Soc. 2019, 100, 799–819. [Google Scholar] [CrossRef]
  46. Menke, R.; Vasiljević, N.; Hansen, K.S.; Hahmann, A.N.; Mann, J. Does the wind turbine wake follow the topography? A multi-lidar study in complex terrain. Wind. Energy Sci. 2018, 3, 681–691. [Google Scholar] [CrossRef]
  47. Menke, R.; Vasiljević, N.; Mann, J.; Lundquist, J.K. Characterization of flow recirculation zones at the Perdigão site using multi-lidar measurements. Atmos. Chem. Phys. 2019, 19, 2713–2723. [Google Scholar] [CrossRef]
  48. Menke, R.; Vasiljević, N.; Wagner, J.; Oncley, S.P.; Mann, J. Multi-lidar wind resource mapping in complex terrain. Wind. Energy Sci. 2020, 5, 1059–1073. [Google Scholar] [CrossRef]
  49. Barthelmie, R.J.; Pryor, S.C. Automated wind turbine wake characterization in complex terrain. Atmos. Meas. Tech. 2019, 12, 3463–3484. [Google Scholar] [CrossRef]
  50. Wyngaard, J.C. Toward Numerical Modelling in the “Terra Incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
  51. Honnert, R.; Masson, V.; Couvreux, F. A Diagnostic for Evaluating the Representation of Turbulence in Atmospheric Models at the Kilometric Scale. J. Atmos. Sci. 2011, 68, 3112–3131. [Google Scholar] [CrossRef]
  52. Boutle, I.A.; Eyre, J.E.J.; Lock, A.P. Seamless Stratocumulus Simulation across the Turbulent Gray Zone. Mon. Weather Rev. 2014, 142, 1655–1668. [Google Scholar] [CrossRef]
  53. Efstathiou, G.A.; Beare, R.J.; Osborne, S.; Lock, A.P. Grey zone simulations of the morning convective boundary layer development. J. Geophys. Res. Atmos. 2016, 121, 4769–4782. [Google Scholar] [CrossRef]
  54. Honnert, R. Representation of the grey zone of turbulence in the atmospheric boundary layer. Adv. Sci. Res. 2016, 13, 63–67. [Google Scholar] [CrossRef]
  55. Chow, F.; Schär, C.; Ban, N.; Lundquist, K.; Schlemmer, L.; Shi, X. Crossing Multiple Gray Zones in the Transition from Mesoscale to Microscale Simulation over Complex Terrain. Atmosphere 2019, 10, 274. [Google Scholar] [CrossRef]
  56. Zhou, B.; Simon, J.S.; Chow, F.K. The Convective Boundary Layer in the Terra Incognita. J. Atmos. Sci. 2014, 71, 2545–2563. [Google Scholar] [CrossRef]
  57. Zhou, B.; Xue, M.; Zhu, K. A Grid-Refinement-Based Approach for Modelling the Convective Boundary Layer in the Gray Zone: A Pilot Study. J. Atmos. Sci. 2017, 74, 3497–3513. [Google Scholar] [CrossRef]
  58. UCAR/NCAR—Earth Observing Laboratory. NCAR/EOL Quality Controlled High-Rate ISFS Surface Flux Data, Geographic Coordi- Nate, Tilt Corrected, Version 1.1; UCAR/NCAR—Earth Observing Laboratory: Boulder, CO, USA, 2019. [Google Scholar] [CrossRef]
  59. UCAR/NCAR—Earth Observing Laboratory. NCAR/EOL Quality Controlled 5-Minute ISFS Surface Flux Data, Geographic Coordi- Nate, Tilt Corrected, Version 1.1; UCAR/NCAR—Earth Observing Laboratory: Boulder, CO, USA, 2019. [Google Scholar] [CrossRef]
  60. Haupt, S.E.; Kosovic, B.; Shaw, W.; Berg, L.K.; Churchfield, M.; Cline, J.; Draxl, C.; Ennis, B.; Koo, E.; Kotamarthi, R.; et al. On Bridging A Modelling Scale Gap: Mesoscale to Microscale Coupling for Wind Energy. Bull. Am. Meteorol. Soc. 2019, 100, 2533–2550. [Google Scholar] [CrossRef]
  61. Muñoz-Esparza, D.; Kosović, B. Generation of Inflow Turbulence in Large-Eddy Simulations of Nonneutral Atmospheric Boundary Layers with the Cell Perturbation Method. Mon. Weather Rev. 2018, 146, 1889–1909. [Google Scholar] [CrossRef]
  62. Cai, X.; Yang, Z.; Xia, Y.; Huang, M.; Wei, H.; Leung, L.R.; Ek, M.B. Assessment of simulated water balance from Noah, Noah-MP, CLM, and VIC over CONUS using the NLDAS test bed. J. Geophys. Res. Atmos. 2014, 119, 13–751. [Google Scholar] [CrossRef]
  63. Chen, F.; Dudhia, J. Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modelling System. Part I: Model Implementation and Sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
  64. Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
  65. Dudhia, J. Numerical Study of Convection Observed during the Winter Monsoon Experiment Using a Mesoscale Two-Dimensional Model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
  66. Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
  67. Palma, J.M.L.M.; Silva, C.A.M.; Gomes, V.C.; Silva Lopes, A.; Simões, T.; Costa, P.; Batista, V.T.P. The digital terrain model in the computational modelling of the flow over the Perdigão site: The appropriate grid size. Wind Energ. Sci. 2020, 5, 1469–1485. [Google Scholar] [CrossRef]
  68. Copernicus Land Monitoring Service: CORINE Land Cover. Available online: https://land.copernicus.eu/pan-european/corine-land-cover (accessed on 15 April 2019).
  69. Pineda, N.; Jorba, O.; Jorge, J.; Baldasano, J.M. Using NOAA AVHRR and SPOT VGT data to estimate surface parameters: Application to a mesoscale meteorological model. Int. J. Remote Sens. 2004, 25, 129–143. [Google Scholar] [CrossRef]
  70. Hahmann, A.N.; Sīle, T.; Witha, B.; Davis, N.N.; Dörenkämper, M.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Navarro, J.; Olsen, B.T.; et al. The making of the New European Wind Atlas—Part 1: Model sensitivity. Geosci. Model Dev. 2020, 13, 5053–5078. [Google Scholar] [CrossRef]
  71. Muñoz-Esparza, D.; Kosović, B.; García-Sánchez, C.; van Beeck, J. Nesting Turbulence in an Offshore Convective Boundary Layer Using Large-Eddy Simulations. Bound. Layer Meteorol. 2014, 151, 453–478. [Google Scholar] [CrossRef]
  72. Jiménez, P.A.; Dudhia, J. Improving the Representation of Resolved and Unresolved Topographic Effects on Surface Wind in the WRF Model. J. Appl. Meteorol. Climatol. 2012, 51, 300–316. [Google Scholar] [CrossRef]
  73. Liu, Y.; Warner, T.; Liu, Y.; Vincent, C.; Wu, W.; Mahoney, B.; Swerdlin, S.; Parks, K.; Boehnert, J. Simultaneous nested modelling from the synoptic scale to the LES scale for wind energy applications. J. Wind. Eng. Ind. Aerodyn. 2011, 99, 308–319. [Google Scholar] [CrossRef]
  74. Draxl, C.; Worsnop, R.P.; Xia, G.; Pichugina, Y.; Chand, D.; Lundquist, J.K.; Sharp, J.; Wedam, G.; Wilczak, J.M.; Berg, L.K. Mountain waves can impact wind power generation. Wind Energ. Sci. 2021, 6, 45–60. [Google Scholar] [CrossRef]
  75. Shin, H.H.; Hong, S.Y. Representation of the Subgrid-Scale Turbulent Transport in Convective Boundary Layers at Gray zone Resolutions. Mon. Weather Rev. 2015, 143, 250–271. [Google Scholar] [CrossRef]
  76. Kosovic, B. Subgrid-scale modelling for the large-eddy simulation of high-Reynolds-number boundary layers. J. Fluid Mech. 1997, 336, 151–182. [Google Scholar] [CrossRef]
  77. Cuxart, J. When Can a High-Resolution Simulation Over Complex Terrain be Called LES? Front. Earth Sci. 2015, 3, 87. [Google Scholar] [CrossRef]
  78. Xue, L.; Chu, X.; Rasmussen, R.; Breed, D.; Geerts, B. A Case Study of Radar Observations and WRF LES Simulations of the Impact of Ground-Based Glaciogenic Seeding on Orographic Clouds and Precipitation. Part II: AgI Dispersion and Seeding Signals Simulated by WRF. J. Appl. Meteorol. Climatol. 2016, 55, 445–464. [Google Scholar] [CrossRef]
  79. Doubrawa, P.; Montornès, A.; Barthelmie, R.J.; Pryor, S.C.; Giroux, G.; Casso, P. Effect of Wind Turbine Wakes on the Performance of a Real Case WRF-LES Simulation. J. Phys. Conf. Ser. 2017, 854, 012010. [Google Scholar] [CrossRef]
  80. Kosović, B.; Curry, J.A. A Large Eddy Simulation Study of a Quasi-Steady, Stably Stratified Atmospheric Boundary Layer. J. Atmos. Sci. 2000, 57, 1052–1068. [Google Scholar] [CrossRef]
  81. Ching, J.; Rotunno, R.; LeMone, M.; Martilli, A.; Kosovic, B.; Jimenez, P.A.; Dudhia, J. Convectively Induced Secondary Circulations in Fine-Grid Mesoscale Numerical Weather Prediction Models. Mon. Weather Rev. 2014, 142, 3284–3302. [Google Scholar] [CrossRef]
  82. Rai, R.K.; Berg, L.K.; Kosović, B.; Haupt, S.E.; Mirocha, J.D.; Ennis, B.L.; Draxl, C. Evaluation of the Impact of Horizontal Grid Spacing in Terra Incognita on Coupled Mesoscale–Microscale Simulations Using the WRF Framework. Mon. Weather Rev. 2019, 147, 1007–1027. [Google Scholar] [CrossRef]
  83. Johnson, A.; Wang, X. Multicase Assessment of the Impacts of Horizontal and Vertical Grid Spacing, and Turbulence Closure Model, on Subkilometer-Scale Simulations of Atmospheric Bores during PECAN. Mon. Weather Rev. 2019, 147, 1533–1555. [Google Scholar] [CrossRef]
  84. Wise, A.S.; Neher, J.M.T.; Arthur, R.S.; Mirocha, J.D.; Lundquist, J.K.; Chow, F.K. Meso- to microscale modelling of atmospheric stability effects on wind turbine wake behavior in complex terrain. Wind. Energy Sci. 2022, 7, 367–386. [Google Scholar] [CrossRef]
  85. Zhou, B.; Chow, F.K. Turbulence Modelling for the Stable Atmospheric Boundary Layer and Implications for Wind Energy. Flow Turbul. Combust. 2011, 88, 255–277. [Google Scholar] [CrossRef]
  86. Mirocha, J.; Kosović, B.; Kirkil, G. Resolved Turbulence Characteristics in Large-Eddy Simulations Nested within Mesoscale Simulations Using the Weather Research and Forecasting Model. Mon. Weather Rev. 2014, 142, 806–831. [Google Scholar] [CrossRef]
  87. Mirocha, J.D.; Kosovic, B.; Aitken, M.L.; Lundquist, J.K. Implementation of a generalized actuator disk wind turbine model into the weather research and forecasting model for large-eddy simulation applications. J. Renew. Sustain. Energy 2014, 6, 013104. [Google Scholar] [CrossRef]
  88. De Wekker, S.F.J.; Kossmann, M. Convective Boundary Layer Heights Over Mountainous Terrain—A Review of Concepts. Front. Earth Sci. 2015, 3, 77. [Google Scholar] [CrossRef]
  89. Lehner, M.; Rotach, M. Current Challenges in Understanding and Predicting Transport and Exchange in the Atmosphere over Mountainous Terrain. Atmosphere 2018, 9, 276. [Google Scholar] [CrossRef]
  90. Goger, B.; Rotach, M.W.; Gohm, A.; Fuhrer, O.; Stiperski, I.; Holtslag, A.A.M. The Impact of Three-Dimensional Effects on the Simulation of Turbulence Kinetic Energy in a Major Alpine Valley. Bound. Layer Meteorol. 2018, 168, 1–27. [Google Scholar] [CrossRef] [PubMed]
  91. Liu, Y.; Liu, Y.; Muñoz-Esparza, D.; Hu, F.; Yan, C.; Miao, S. Simulation of Flow Fields in Complex Terrain with WRF-LES: Sensitivity Assessment of Different PBL Treatments. J. Appl. Meteorol. Climatol. 2020, 59, 1481–1501. [Google Scholar] [CrossRef]
Energies 18 01372 g001
Figure 1. Perdigão terrain.
Figure 1. Perdigão terrain.
Energies 18 01372 g001
Energies 18 01372 g002
Figure 2. Topography of domains used in the multiscale simulation. The three domains had resolutions of 5000 m as d01 (the coarsest corresponding to the entire domain), d02 and d03 (the finest), 1000 m, and 100 m.
Figure 2. Topography of domains used in the multiscale simulation. The three domains had resolutions of 5000 m as d01 (the coarsest corresponding to the entire domain), d02 and d03 (the finest), 1000 m, and 100 m.
Energies 18 01372 g002
Energies 18 01372 g003
Figure 3. Taylor diagram of 100 m northeastern flow wind speeds at Mast 20 (blue dot) and Mast 29 (red dot), comparing observations with simulation results for 3 different PBL parameters in (I) MYNN PBL scheme, (II) SH PBL scheme, and (III) YSU PBL scheme for D02 domain.
Figure 3. Taylor diagram of 100 m northeastern flow wind speeds at Mast 20 (blue dot) and Mast 29 (red dot), comparing observations with simulation results for 3 different PBL parameters in (I) MYNN PBL scheme, (II) SH PBL scheme, and (III) YSU PBL scheme for D02 domain.
Energies 18 01372 g003
Energies 18 01372 g004
Figure 4. Average horizontal wind velocity and vertical wind component for 3 different PBL parameters and 3 different LES schemes of northeast flow: (I) MYNN PBL scheme, (II) YSU PBL scheme, and (III) SH PBL scheme for D03 domain. First column is horizontal wind velocity at 10 m, second column is vertical wind component at 10 m, third column is horizontal wind velocity at 100 m, and fourth column is vertical wind component at 100 m for d03 domain area. First lines of each PBL parameterization are TKE model results, second lines are SMAG model results, and third lines are NBA model results.
Figure 4. Average horizontal wind velocity and vertical wind component for 3 different PBL parameters and 3 different LES schemes of northeast flow: (I) MYNN PBL scheme, (II) YSU PBL scheme, and (III) SH PBL scheme for D03 domain. First column is horizontal wind velocity at 10 m, second column is vertical wind component at 10 m, third column is horizontal wind velocity at 100 m, and fourth column is vertical wind component at 100 m for d03 domain area. First lines of each PBL parameterization are TKE model results, second lines are SMAG model results, and third lines are NBA model results.
Energies 18 01372 g004
Energies 18 01372 g005
Figure 5. Transect of one-day time-averaged along-transect velocity differences from MYNN TKE model results for (a) MYNN TKE model, (b) MYNN SMAG model, (c) MYNN NBA model, (d) YSU TKE model, (e) YSU SMAG model, (f) YSU NBA model, (g) SH TKE model, (h) SH SMAG model, and (i) SH NBA model for northeastern flow.
Figure 5. Transect of one-day time-averaged along-transect velocity differences from MYNN TKE model results for (a) MYNN TKE model, (b) MYNN SMAG model, (c) MYNN NBA model, (d) YSU TKE model, (e) YSU SMAG model, (f) YSU NBA model, (g) SH TKE model, (h) SH SMAG model, and (i) SH NBA model for northeastern flow.
Energies 18 01372 g005
Energies 18 01372 g006
Figure 6. Time series graphs and comparisons of simulated and observed wind speeds at 100 m for northeastern flow. First column shows MYNN results, second column shows YSU results, and third column shows SH results. First row is Mast 20, second row is Mast 25, and third row is Mast 29 results. Black lines represent measurements, green lines TKE simulations, blue lines SMAG simulations, and red lines NBA simulations.
Figure 6. Time series graphs and comparisons of simulated and observed wind speeds at 100 m for northeastern flow. First column shows MYNN results, second column shows YSU results, and third column shows SH results. First row is Mast 20, second row is Mast 25, and third row is Mast 29 results. Black lines represent measurements, green lines TKE simulations, blue lines SMAG simulations, and red lines NBA simulations.
Energies 18 01372 g006
Energies 18 01372 g007
Figure 7. Wind speed bias results of comparisons of simulated and observed data vertical profiles for northeastern flow at (a) Mast 20, (b) Mast 25, and (c) Mast 29.
Figure 7. Wind speed bias results of comparisons of simulated and observed data vertical profiles for northeastern flow at (a) Mast 20, (b) Mast 25, and (c) Mast 29.
Energies 18 01372 g007
Energies 18 01372 g008
Figure 8. Taylor diagram of 100 m southwestern flow wind speeds at Mast 20 (blue dot) and Mast 29 (red dot), comparing observations with simulation results for 3 different PBL parameters in (I) MYNN PBL scheme, (II) SH PBL scheme, and (III) YSU PBL scheme for D02 domain.
Figure 8. Taylor diagram of 100 m southwestern flow wind speeds at Mast 20 (blue dot) and Mast 29 (red dot), comparing observations with simulation results for 3 different PBL parameters in (I) MYNN PBL scheme, (II) SH PBL scheme, and (III) YSU PBL scheme for D02 domain.
Energies 18 01372 g008
Energies 18 01372 g009
Figure 9. Average horizontal wind velocity and vertical wind component for 3 different PBL parameters and 3 different LES schemes of southwestern flow: (I) MYNN PBL scheme, (II) YSU PBL scheme, and (III) SH PBL scheme. First columns are horizontal wind velocity at 10 m, second columns are vertical wind component at 10 m, third columns are horizontal wind velocity at 100 m, and fourth columns are vertical wind component at 100 m for d03 domain area. First line is TKE model results, second line is SMAG model results, and third line is NBA model results.
Figure 9. Average horizontal wind velocity and vertical wind component for 3 different PBL parameters and 3 different LES schemes of southwestern flow: (I) MYNN PBL scheme, (II) YSU PBL scheme, and (III) SH PBL scheme. First columns are horizontal wind velocity at 10 m, second columns are vertical wind component at 10 m, third columns are horizontal wind velocity at 100 m, and fourth columns are vertical wind component at 100 m for d03 domain area. First line is TKE model results, second line is SMAG model results, and third line is NBA model results.
Energies 18 01372 g009
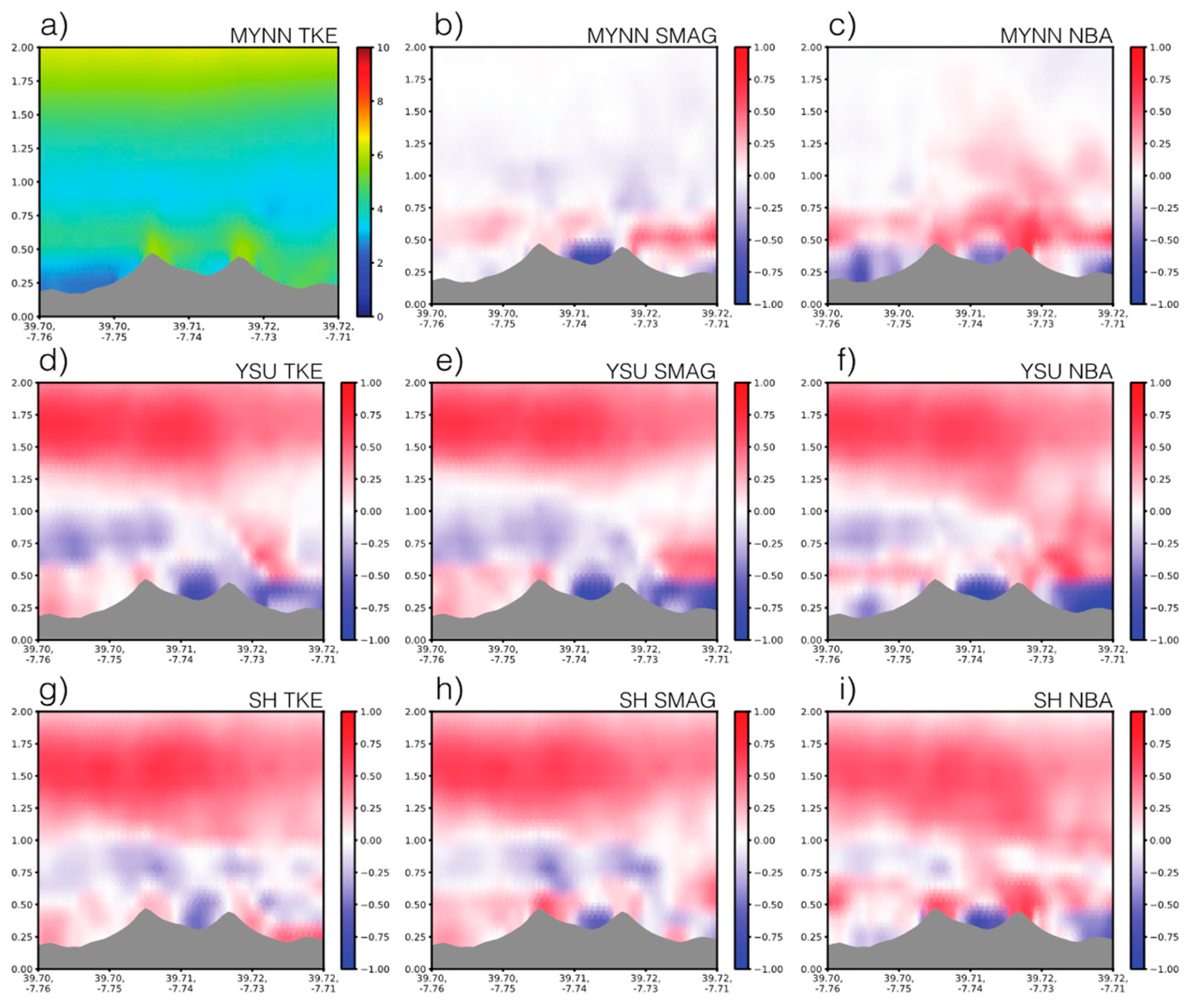
Energies 18 01372 g010
Figure 10. Transect of one-day time-averaged along-transect velocity difference from MYNN TKE model results (a) MYNN TKE model, (b) MYNN SMAG model, (c) MYNN NBA model, (d) YSU TKE model, (e) YSU SMAG model, (f) YSU NBA model, (g) SH TKE model, (h) SH SMAG model, and (i) SH NBA model for southwestern flow.
Figure 10. Transect of one-day time-averaged along-transect velocity difference from MYNN TKE model results (a) MYNN TKE model, (b) MYNN SMAG model, (c) MYNN NBA model, (d) YSU TKE model, (e) YSU SMAG model, (f) YSU NBA model, (g) SH TKE model, (h) SH SMAG model, and (i) SH NBA model for southwestern flow.
Energies 18 01372 g010
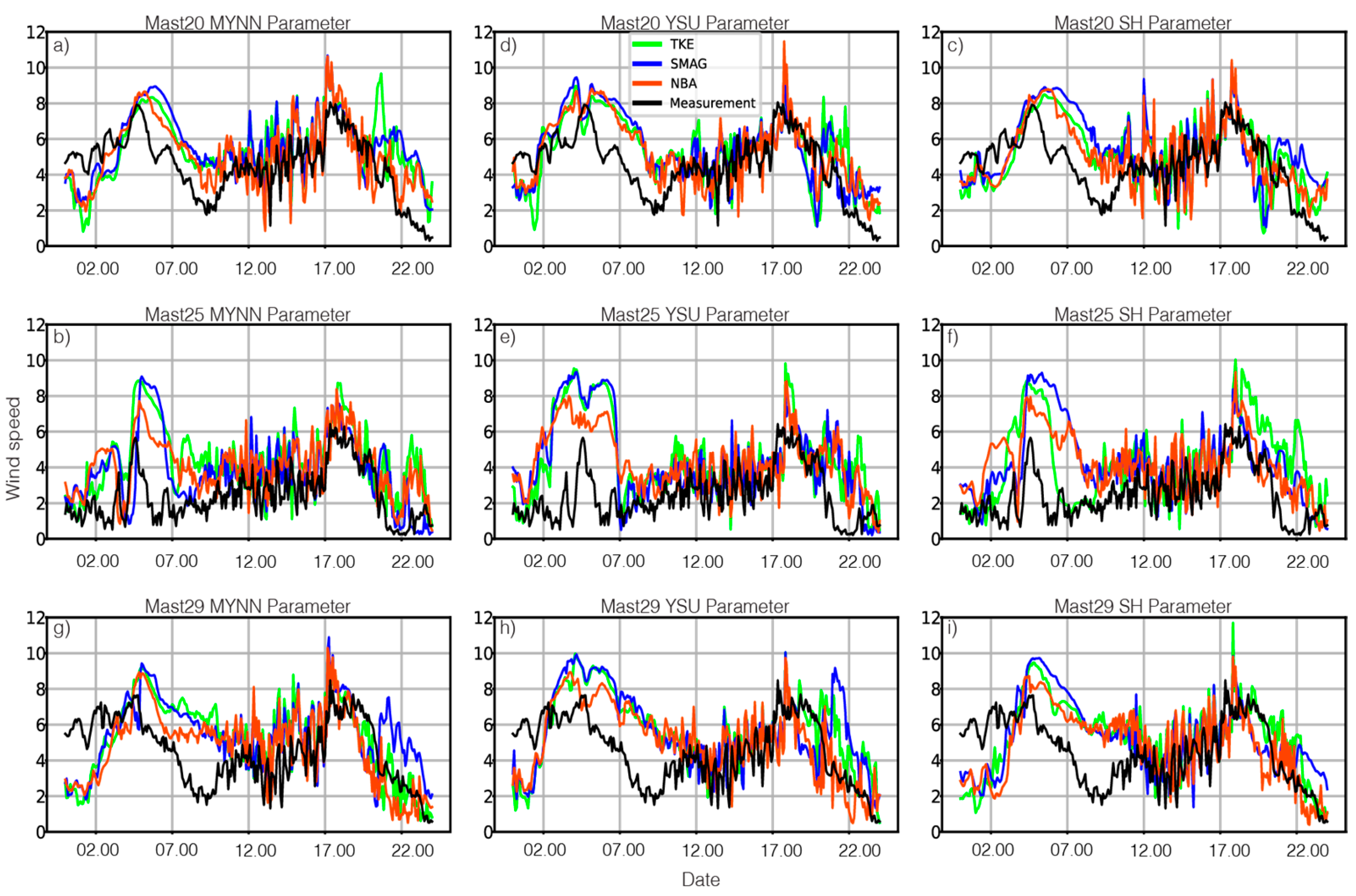
Energies 18 01372 g011
Figure 11. Time series graphs and comparisons of simulated and observed wind speeds at 100 m for southwestern flow. First column shows MYNN results, second column shows YSU results, and third column shows SH results. First row is Mast 20, second row is Mast 25, and third row is Mast 29 results. Black lines represent measurements, green lines TKE simulations, blue lines SMAG simulations, and red lines NBA simulations.
Figure 11. Time series graphs and comparisons of simulated and observed wind speeds at 100 m for southwestern flow. First column shows MYNN results, second column shows YSU results, and third column shows SH results. First row is Mast 20, second row is Mast 25, and third row is Mast 29 results. Black lines represent measurements, green lines TKE simulations, blue lines SMAG simulations, and red lines NBA simulations.
Energies 18 01372 g011
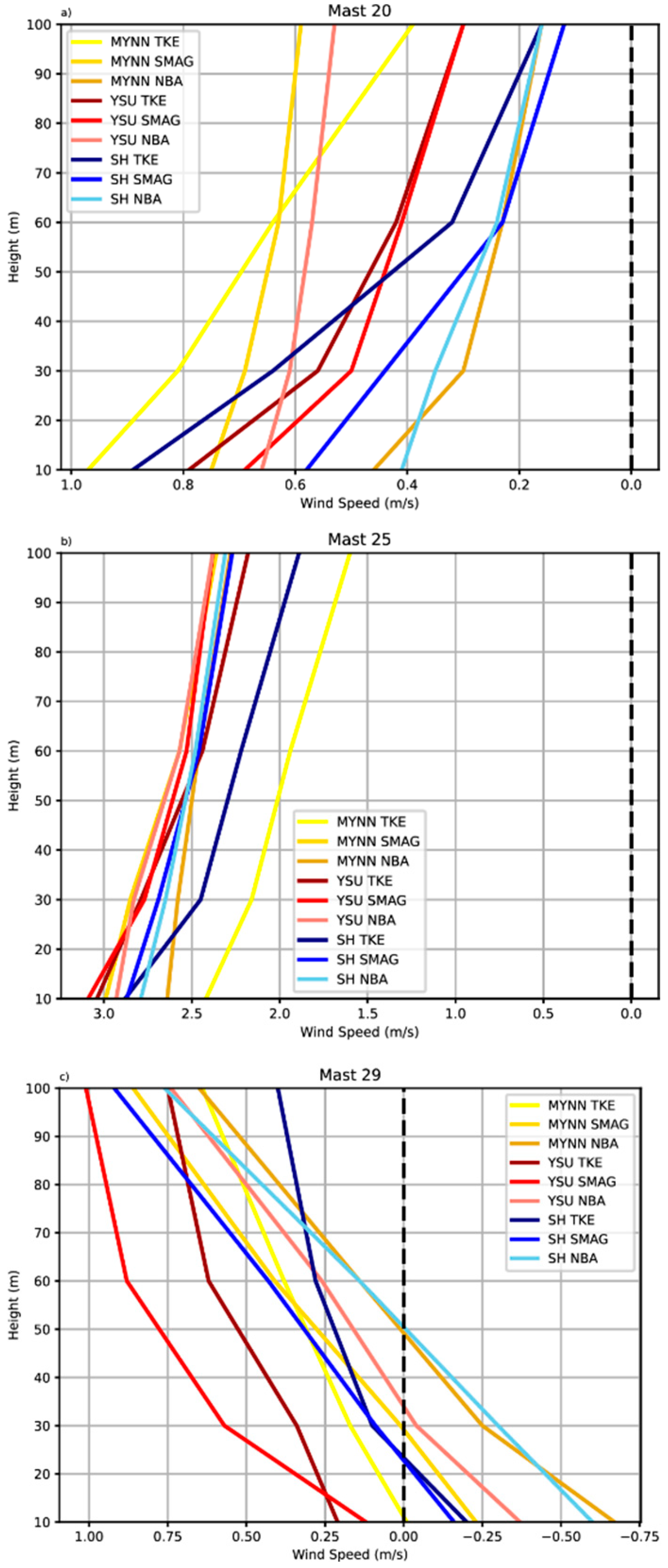
Energies 18 01372 g012
Figure 12. Wind speed bias results of comparisons of simulated and observed data vertical profiles for southwestern flow at (a) Mast 20, (b) Mast 25, and (c) Mast 29.
Figure 12. Wind speed bias results of comparisons of simulated and observed data vertical profiles for southwestern flow at (a) Mast 20, (b) Mast 25, and (c) Mast 29.
Energies 18 01372 g012
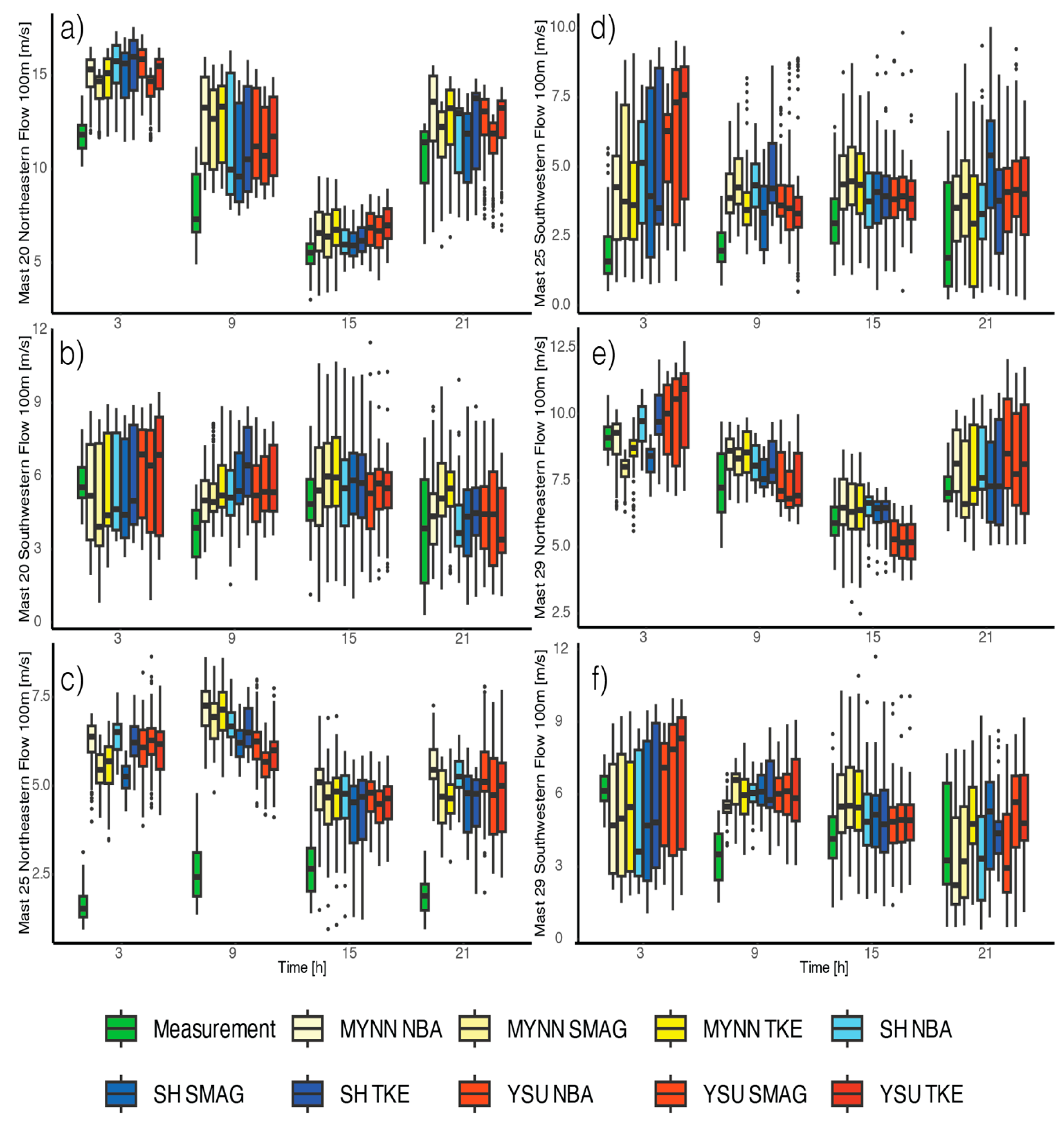
Energies 18 01372 g013
Figure 13. Daily diurnal wind speeds at 100 m of (a) northeastern flow at Mast 20, (b) southwestern flow at Mast 20, (c) northeastern flow at Mast 25, (d) southwestern flow at Mast 25, (e) northeastern flow at Mast 29, and (f) southwestern flow at Mast 29. Box plots include entire time period of study.
Figure 13. Daily diurnal wind speeds at 100 m of (a) northeastern flow at Mast 20, (b) southwestern flow at Mast 20, (c) northeastern flow at Mast 25, (d) southwestern flow at Mast 25, (e) northeastern flow at Mast 29, and (f) southwestern flow at Mast 29. Box plots include entire time period of study.
Energies 18 01372 g013
Energies 18 01372 g014
Figure 14. Comparison of spectra between Mast 20 and WRF-LES d03 domain (Δx = 100 m) results for MYNN parameter and d02 domain (Δx = 1000 m).
Figure 14. Comparison of spectra between Mast 20 and WRF-LES d03 domain (Δx = 100 m) results for MYNN parameter and d02 domain (Δx = 1000 m).
Energies 18 01372 g014
Table 1. Information on nested simulation domains.
Table 1. Information on nested simulation domains.
DomainDelta X [m]Nest RatioDelta Z [m]Nx × Ny Delta t [s]
d015000-50121 × 121 5
d021000550101 × 101 1
d03100101081 × 81 0.2
Table 2. Design of 9 experiments with different PBL and SGS modeling approaches.
Table 2. Design of 9 experiments with different PBL and SGS modeling approaches.
NameMesoscale (d01)
5 km		Mesoscale (d02) 1 kmMicroscale (d03) 100 m
MYNN–TKEMYNNMYNNLES (1.5 TKE)
MYNN–SMAGMYNNMYNNLES (SMAG)
MYNN–NBAMYNNMYNNLES (NBA)
SH–TKESHSHLES (1.5 TKE)
SH–SMAGSHSHLES (SMAG)
SH–NBASHSHLES (NBA)
YSU–TKEYSUYSULES (1.5 TKE)
YSU–SMAGYSUYSULES (SMAG)
YSU–NBAYSUYSULES (NBA)
Table 3. RMSE and bias results for WRF–LES (simulations) and meteorological towers at 100 m.
Table 3. RMSE and bias results for WRF–LES (simulations) and meteorological towers at 100 m.
DomainMast 20Mast 25
RMSEBiasRMSEBias
WRF d03 (Δx = 100 m)
WRF d02 (Δx = 1000 m)		1.940.463.072.64
1.960.525.474.95
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Yılmaz, E.; Menteş, Ş.S.; Kirkil, G. Evaluation of the Sensitivity of PBL and SGS Treatments in Different Flow Fields Using the WRF-LES at Perdigão. Energies 2025, 18, 1372. https://doi.org/10.3390/en18061372

AMA Style

Yılmaz E, Menteş ŞS, Kirkil G. Evaluation of the Sensitivity of PBL and SGS Treatments in Different Flow Fields Using the WRF-LES at Perdigão. Energies. 2025; 18(6):1372. https://doi.org/10.3390/en18061372

Chicago/Turabian Style

Yılmaz, Erkan, Şükran Sibel Menteş, and Gokhan Kirkil. 2025. "Evaluation of the Sensitivity of PBL and SGS Treatments in Different Flow Fields Using the WRF-LES at Perdigão" Energies 18, no. 6: 1372. https://doi.org/10.3390/en18061372

APA Style

Yılmaz, E., Menteş, Ş. S., & Kirkil, G. (2025). Evaluation of the Sensitivity of PBL and SGS Treatments in Different Flow Fields Using the WRF-LES at Perdigão. Energies, 18(6), 1372. https://doi.org/10.3390/en18061372

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop