Voltage Control Nonlinearity in QZSDMC Fed PMSM Drive System with Grid Filtering
Abstract
1. Introduction
2. PMSM
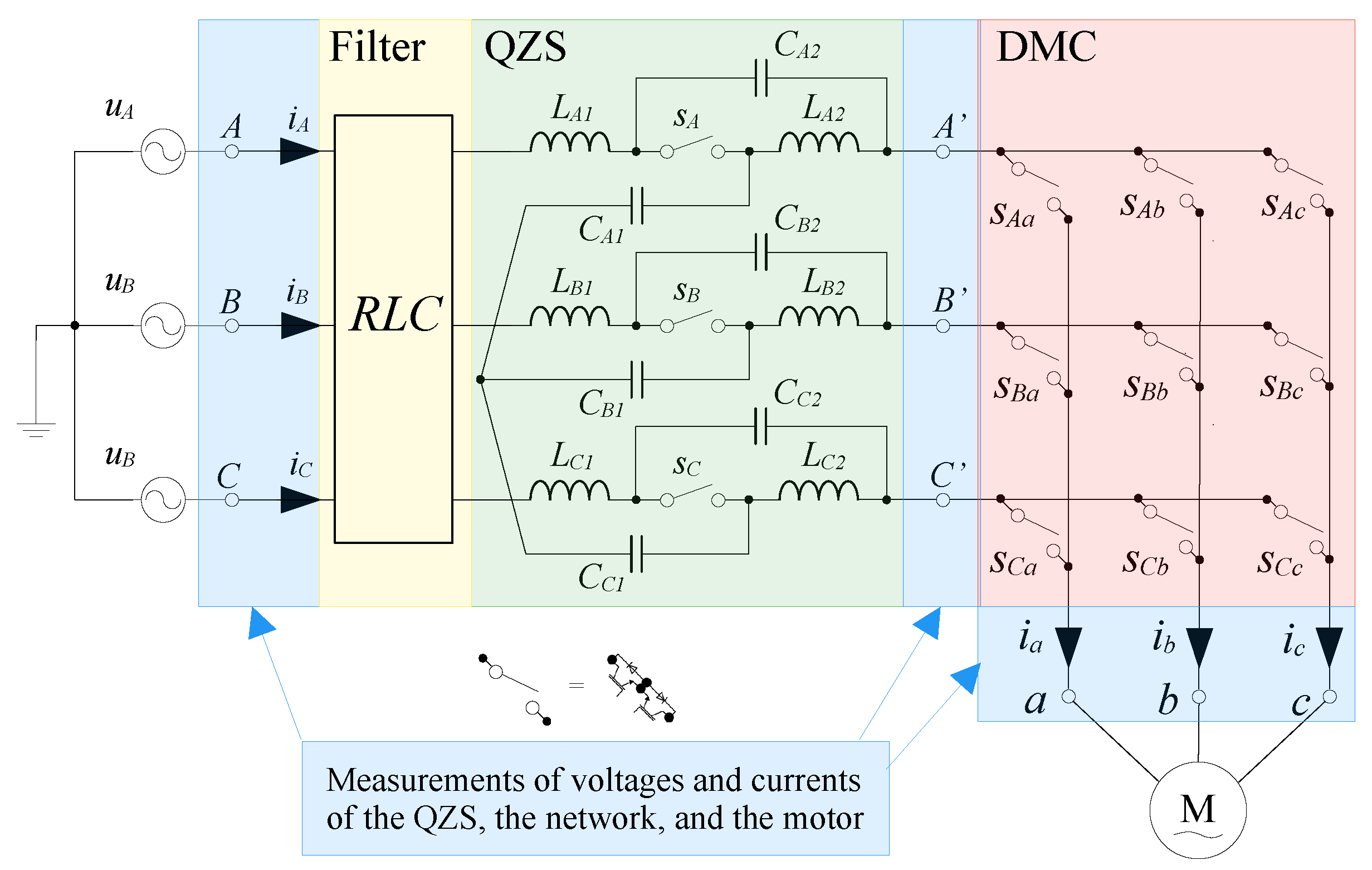
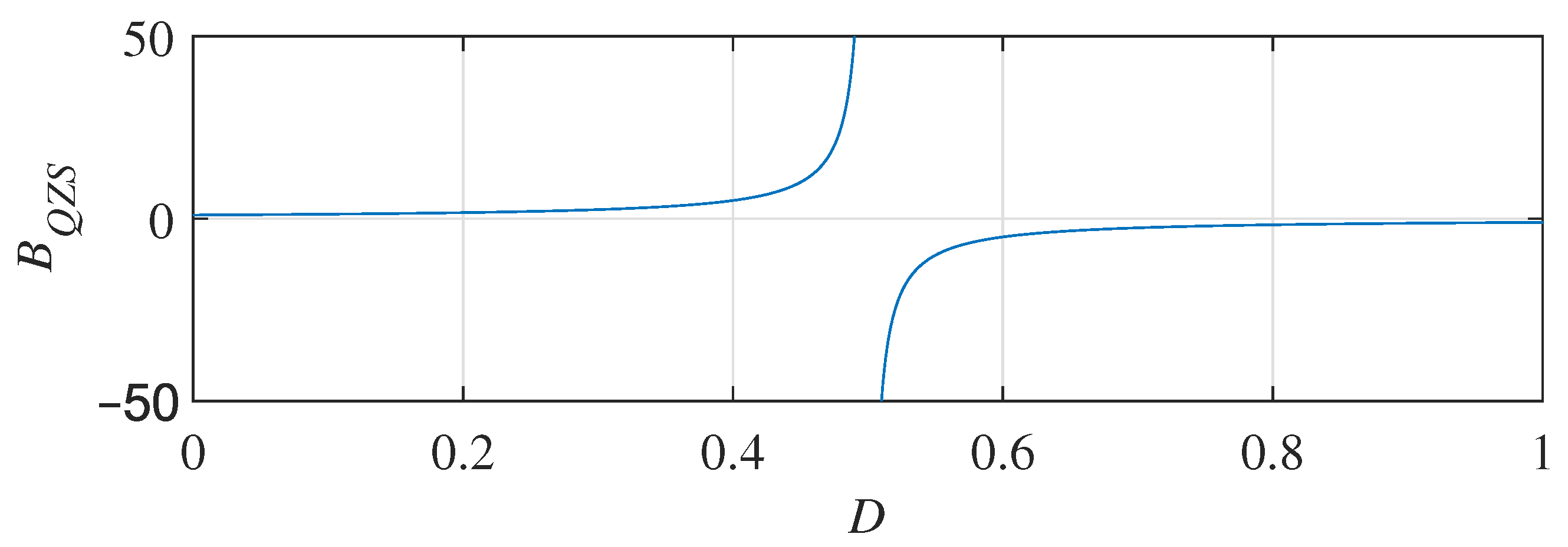
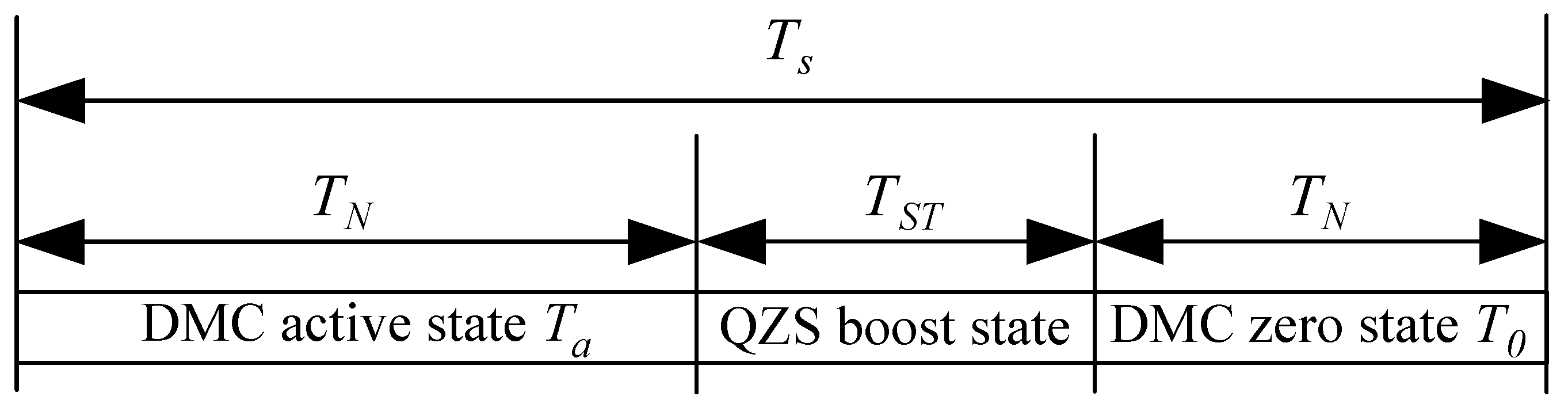
3. Quasi-Z-Source Direct Matrix Converter
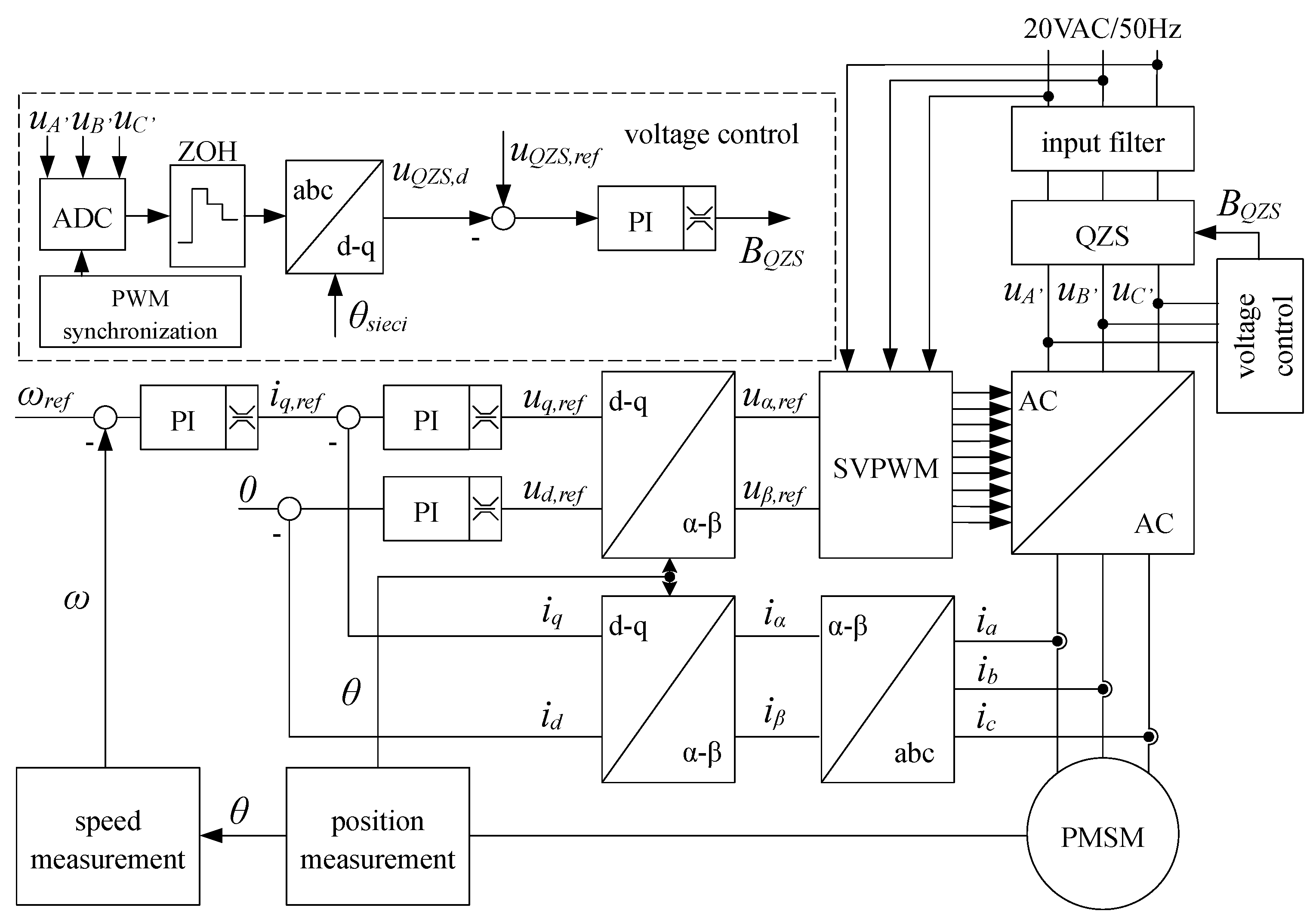
4. Control System
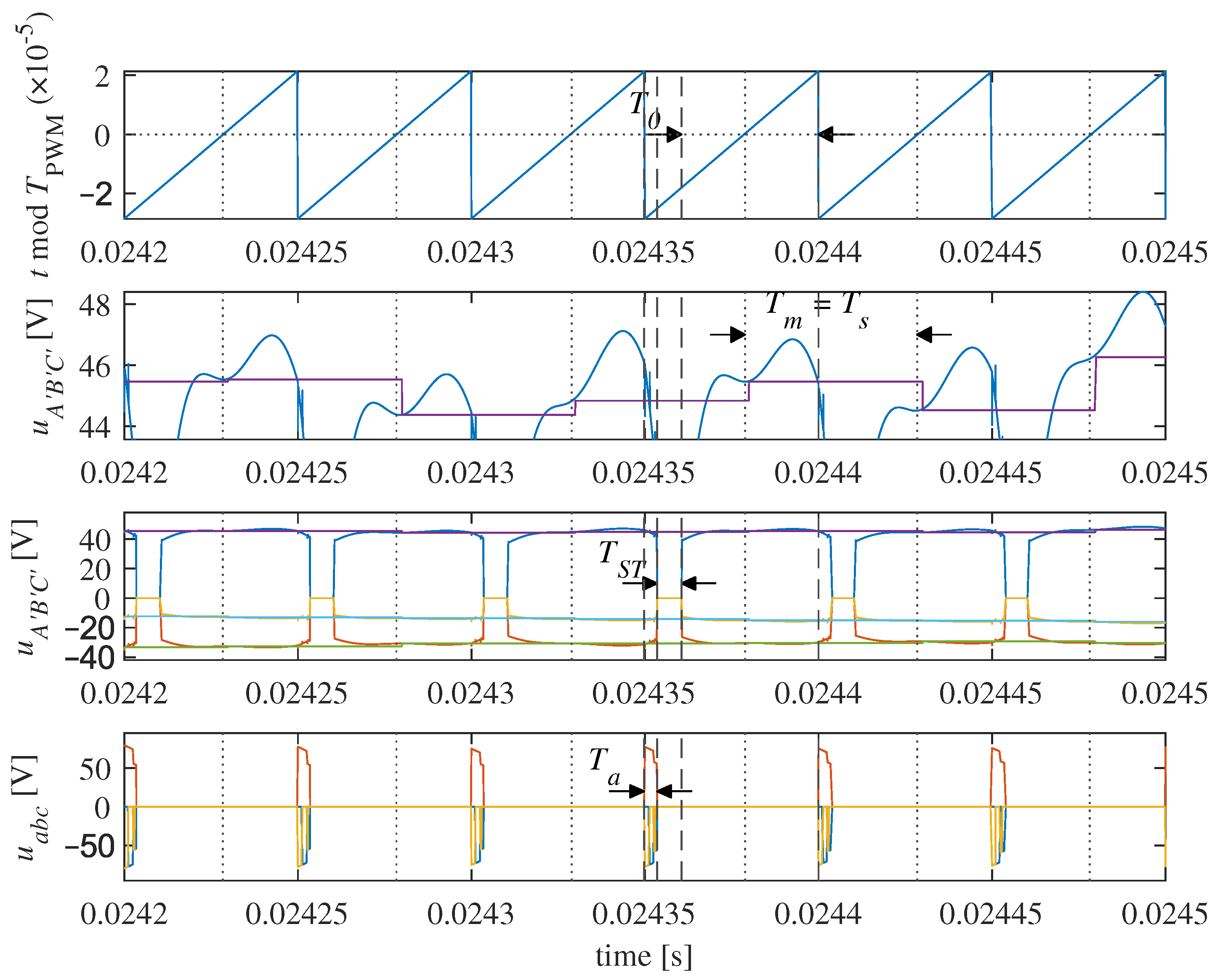
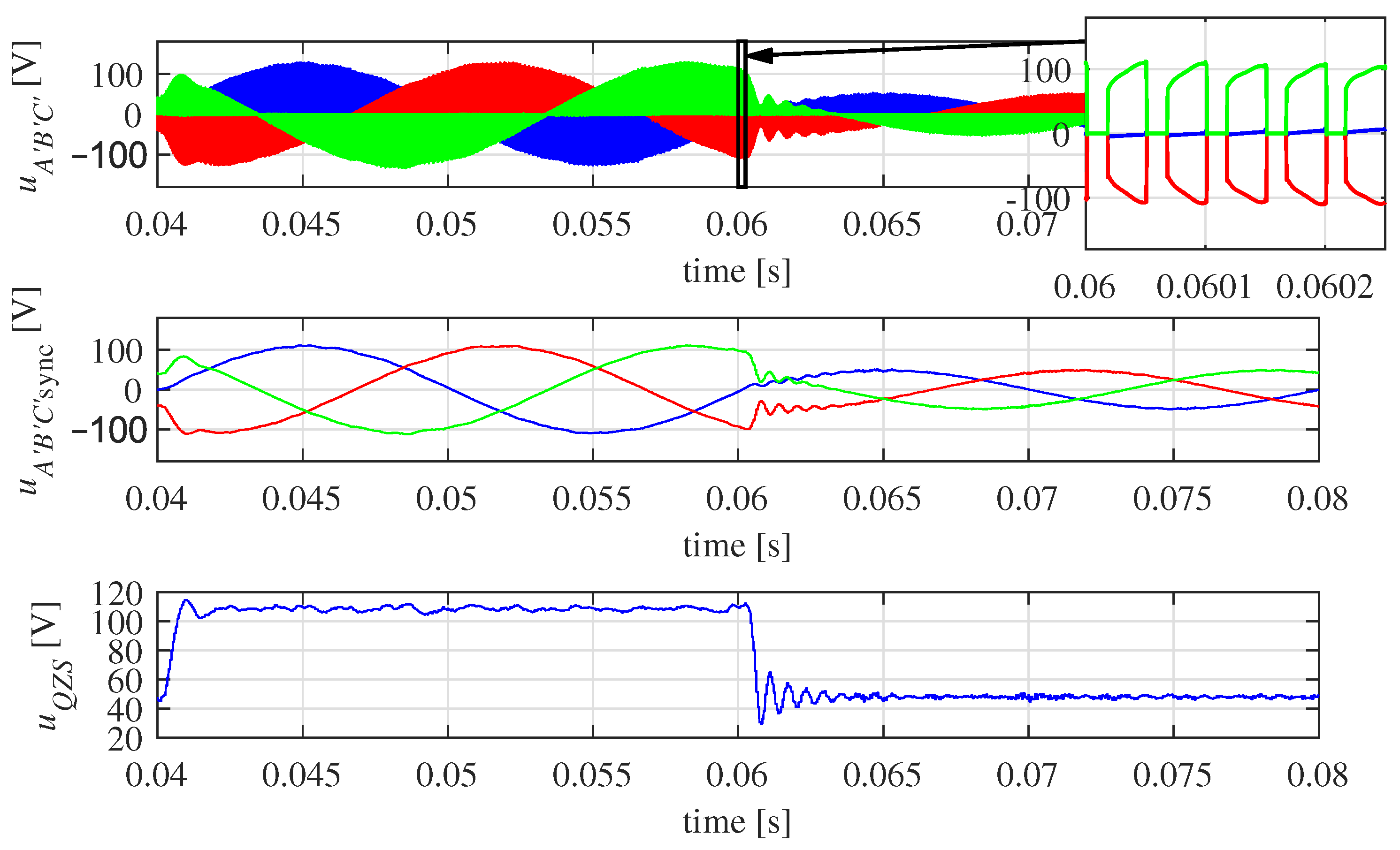
5. Simulation Research
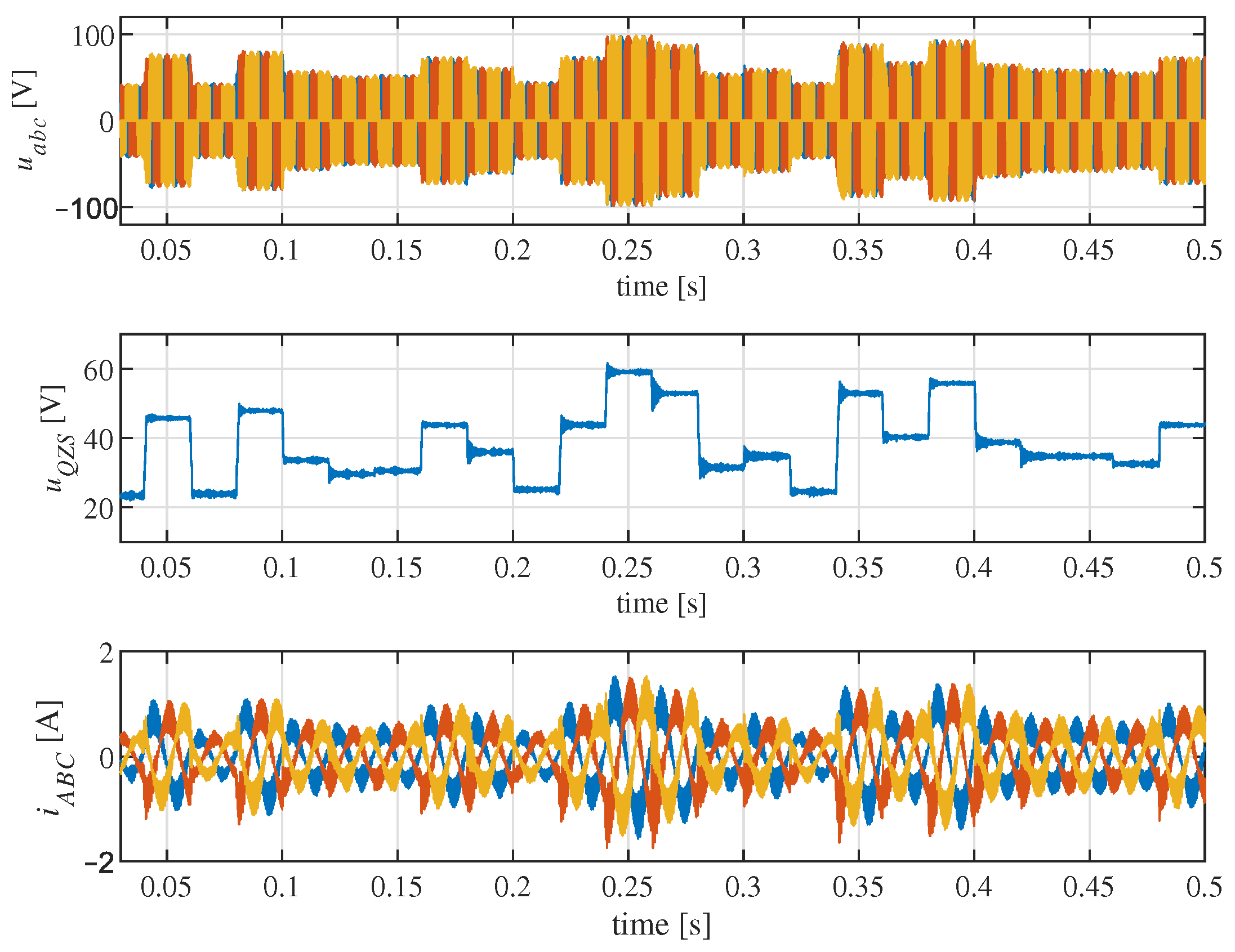
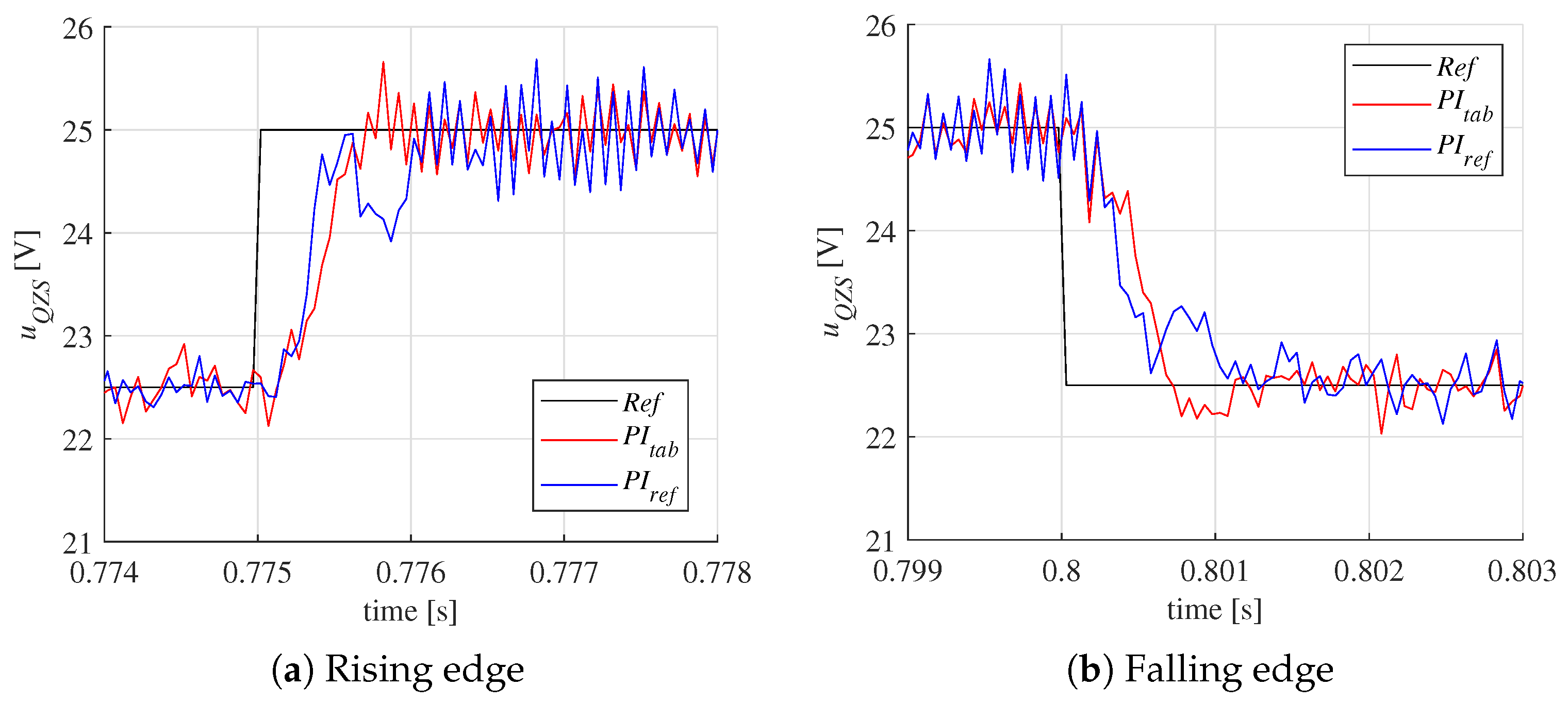
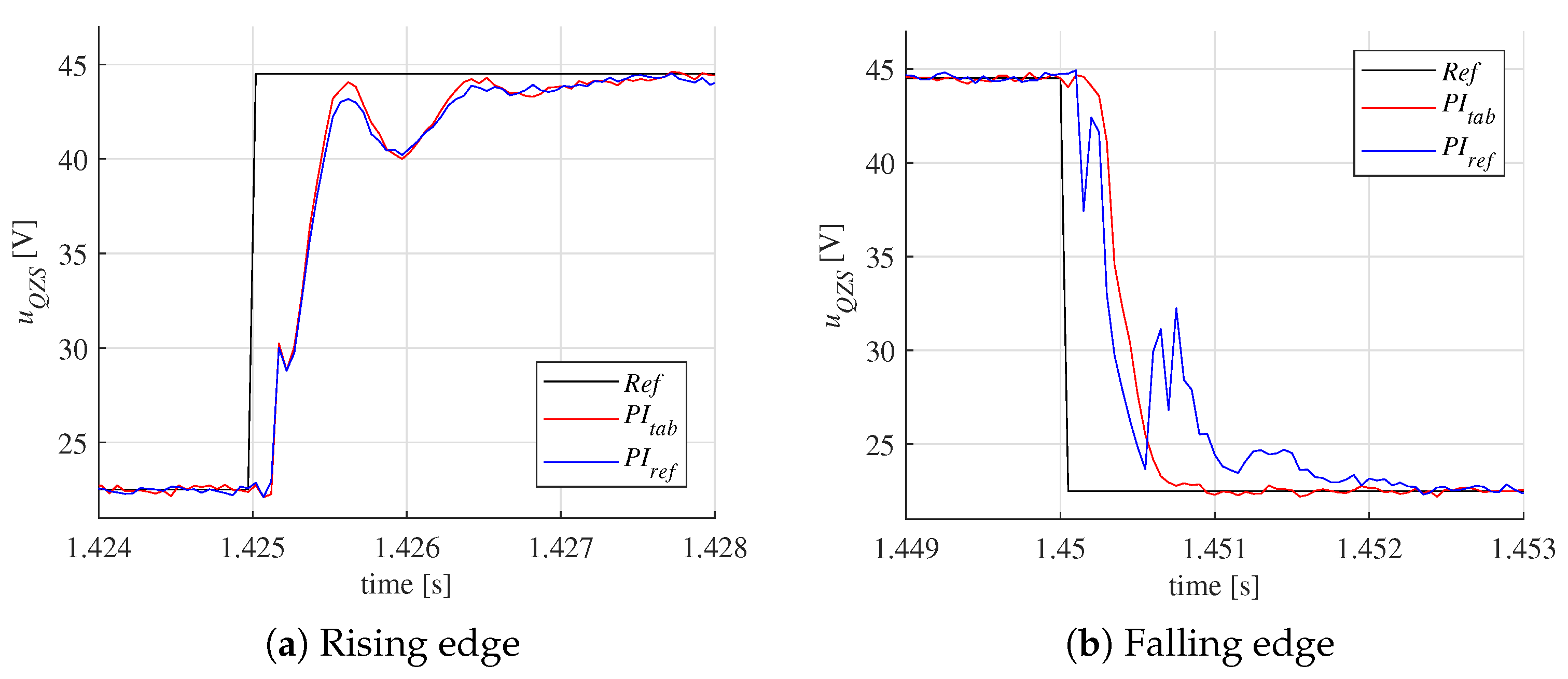
6. Experimental Research
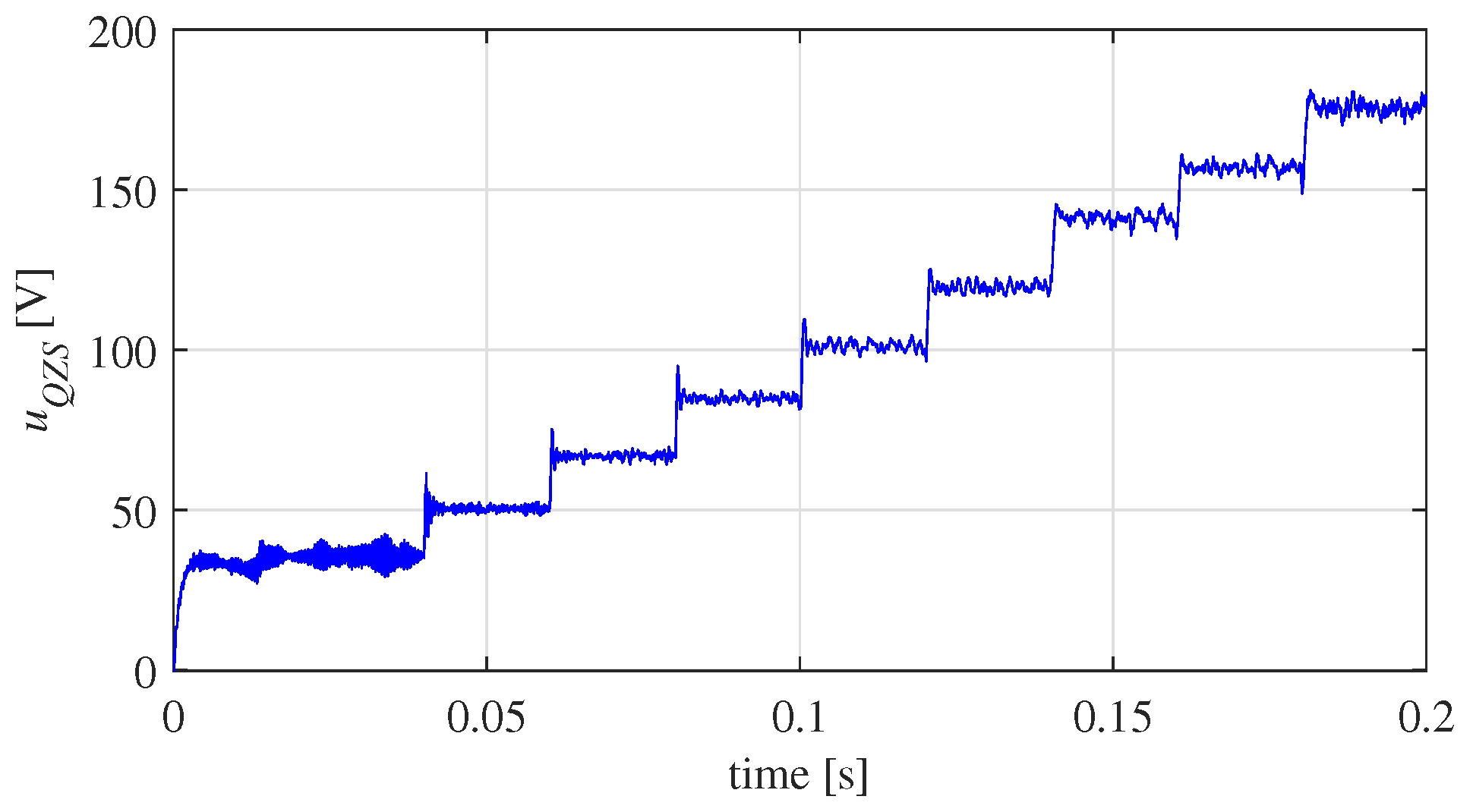
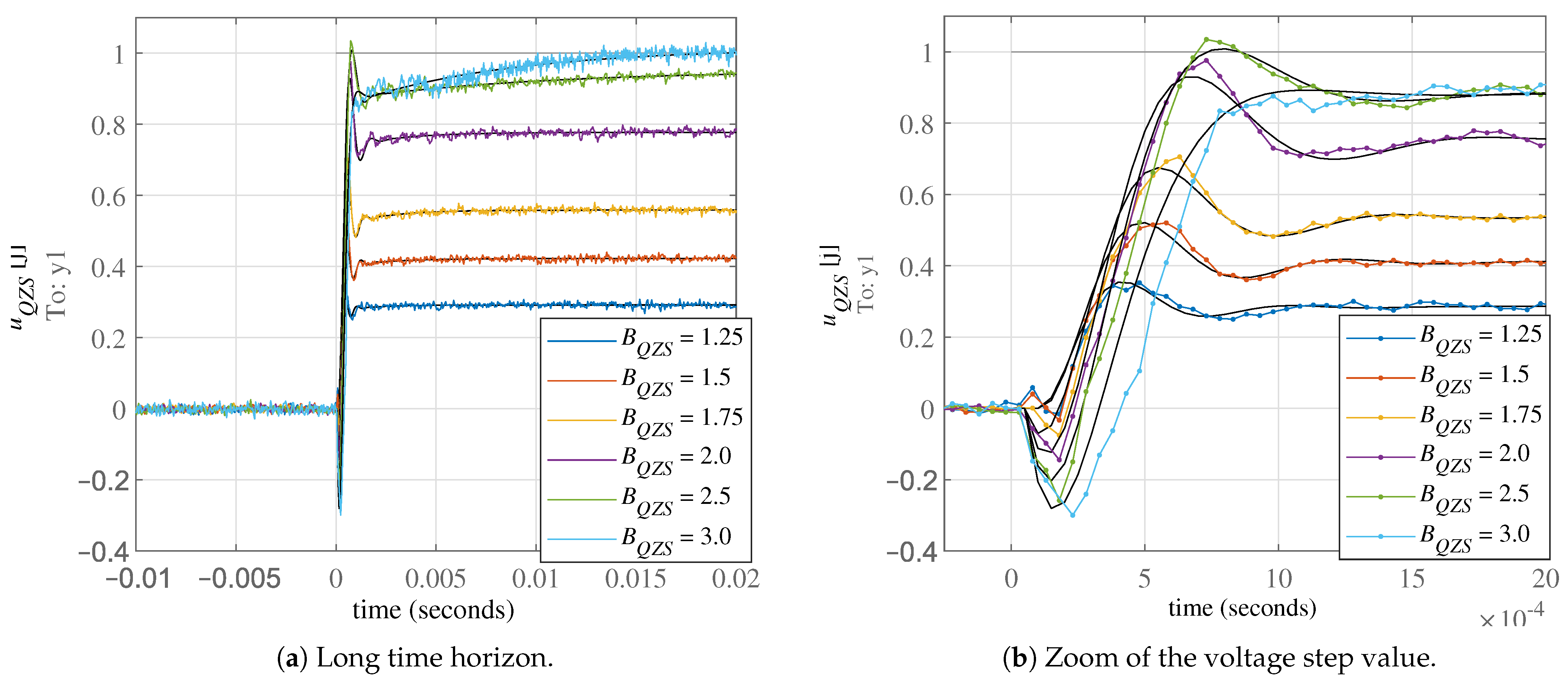
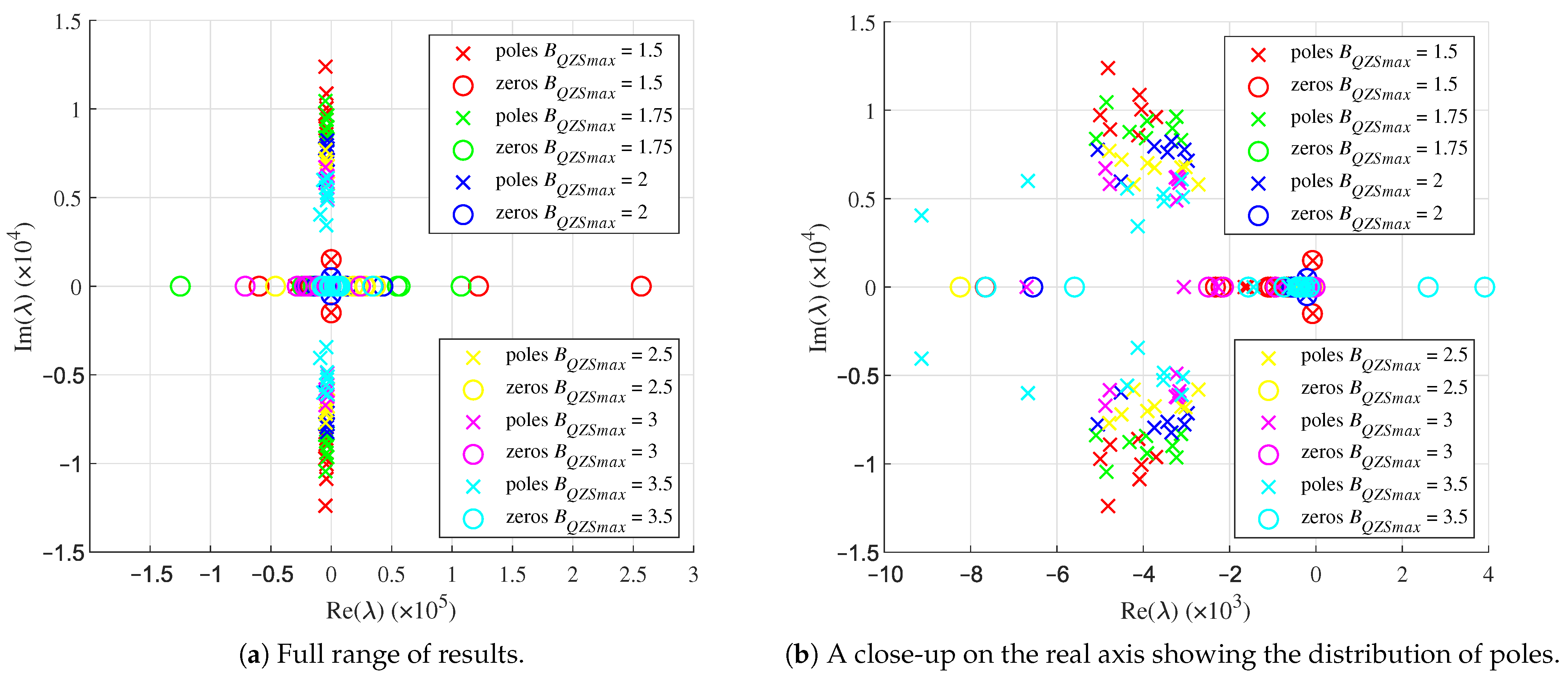
6.1. System Identification
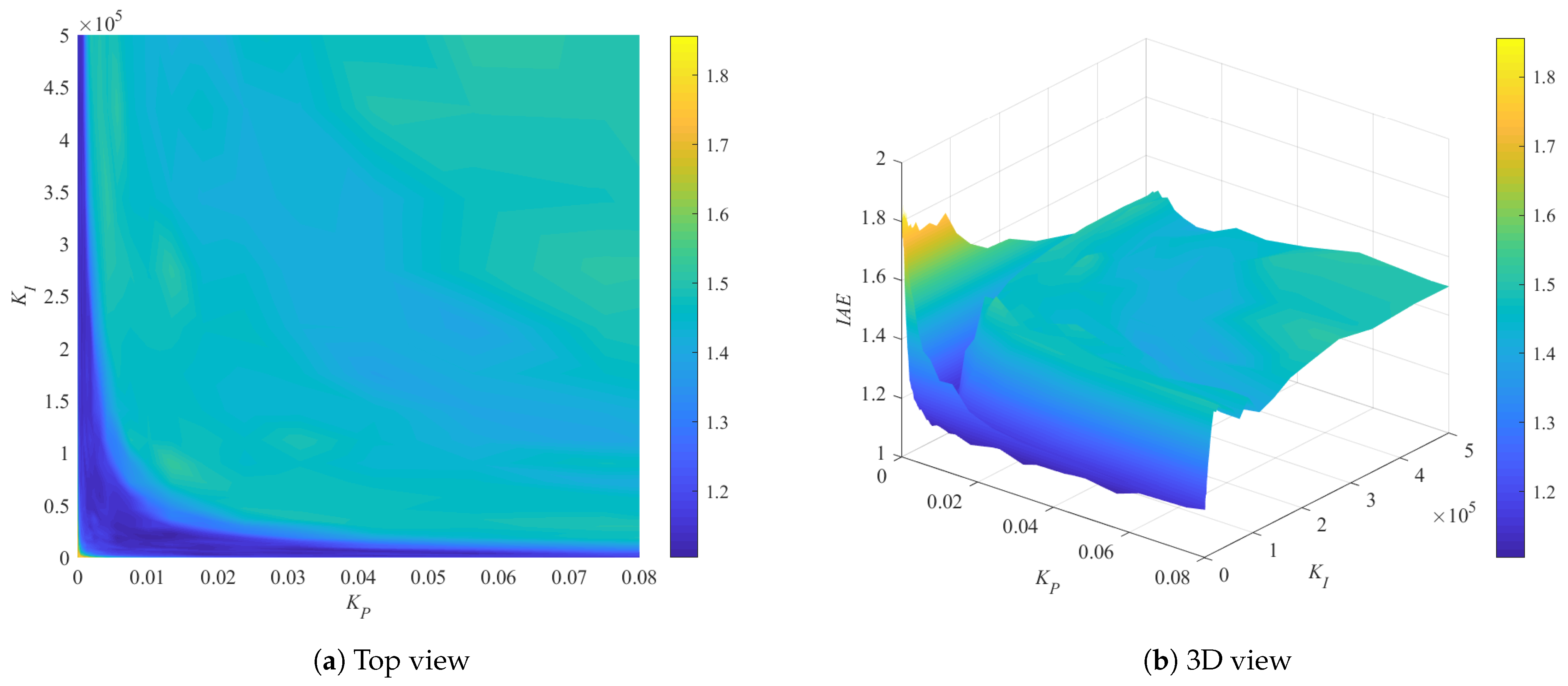
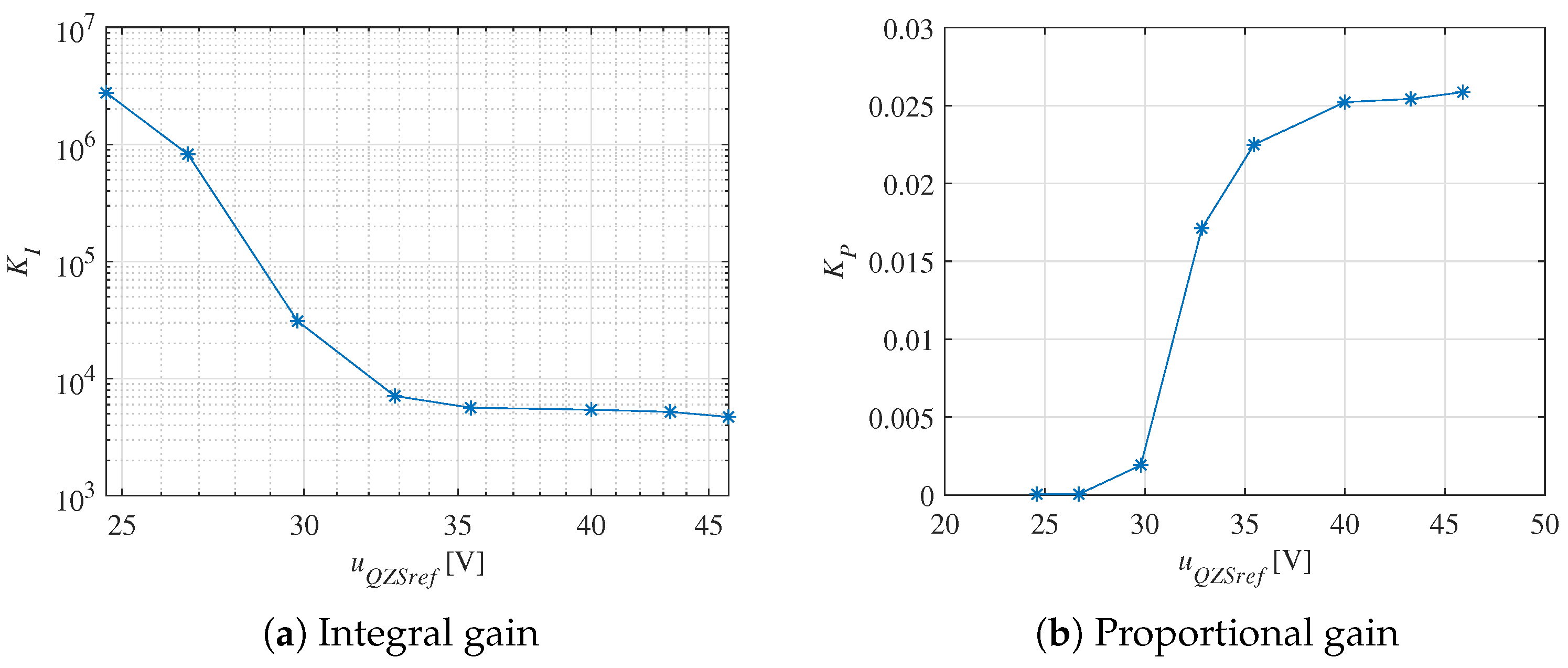
6.2. Controller Design
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Peng, F.Z. Z-source inverter. IEEE Trans. Ind. Appl. 2003, 39, 504–510. [Google Scholar] [CrossRef]
- Anderson, J.; Peng, F. Four quasi-Z-Source inverters. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 2743–2749. [Google Scholar] [CrossRef]
- Nguyen, M.K.; Jung, Y.G.; Lim, Y.C. Single-Phase Z-Source Buck-Boost Matrix Converter. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 846–850. [Google Scholar] [CrossRef]
- Ge, B.; Lei, Q.; Qian, W.; Peng, F.Z. A Family of Z-Source Matrix Converters. IEEE Trans. Ind. Electron. 2012, 59, 35–46. [Google Scholar] [CrossRef]
- Liu, S.; Ge, B.; Abu-Rub, H.; Jiang, X.; Peng, F.Z. A novel indirect quasi-Z-source matrix converter applied to induction motor drives. In Proceedings of the 2013 IEEE Energy Conversion Congress and Exposition, Denver, CO, USA, 15–19 September 2013; pp. 2440–2444. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H.; Baoming, G. Field oriented control of an induction motor fed by a quasi-Z-source direct matrix converter. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 4850–4855. [Google Scholar] [CrossRef]
- Li, M.; Liu, Y.; Abu-Rub, H. Optimizing control strategy of quasi-Z source indirect matrix converter for induction motor drives. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; pp. 1663–1668. [Google Scholar] [CrossRef]
- Liu, S.; Ge, B.; Abu-Rub, H.; Peng, F.Z.; Liu, Y. Quasi-Z-source matrix converter based induction motor drives. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 5303–5307. [Google Scholar] [CrossRef]
- Ellabban, O.; Abu-Rub, H.; Ge, B. A Quasi-Z-Source Direct Matrix Converter Feeding a Vector Controlled Induction Motor Drive. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 339–348. [Google Scholar] [CrossRef]
- Guo, M.; Liu, Y.; Liu, S.; Nie, N. High efficiency operation control of quasi-Z-source based permanent magnetic synchronous motor drive. In Proceedings of the 2018 IEEE 12th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG 2018), Doha, Qatar, 10–12 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Sri Vidhya, D.; Venkatesan, T. Quasi-Z-Source Indirect Matrix Converter Fed Induction Motor Drive for Flow Control of Dye in Paper Mill. IEEE Trans. Power Electron. 2018, 33, 1476–1486. [Google Scholar] [CrossRef]
- Guo, M.; Liu, Y.; Ge, B.; Li, X.; de Almeida, A.T.; Ferreira, F.J.T.E. Dual, Three-Level, Quasi-Z-Source, Indirect Matrix Converter for Motors With Open-Ended Windings. IEEE Trans. Energy Convers. 2023, 38, 64–74. [Google Scholar] [CrossRef]
- Maheswari, K.; Bharanikumar, R.; Manivannan, S. Comparative evaluation of Z source / quasi Z-source direct and indirect matrix converters for PMG based WECS. Results Eng. 2024, 22, 102219. [Google Scholar] [CrossRef]
- Manivannan, S.; Saravanakumar, N.; Vijeyakumar, K.N. Dual space vector PWM technique for a three-phase to five-phase quasi Z-source direct matrix converter. Automatika 2022, 63, 756–778. [Google Scholar] [CrossRef]
- Maheswari, K.T.; Kumar, C.; Balachandran, P.K.; Senjyu, T. Modeling and analysis of the LC filter-integrated quasi Z-source indirect matrix converter for the wind energy conversion system. Front. Energy Res. 2023, 11, 1230641. [Google Scholar] [CrossRef]
- Guo, Y.; Dai, F. Current predictive control of Quasi-Z source three-phase four-leg direct matrix converter. IET Conf. Proc. 2022, 2022, 994–1001. [Google Scholar] [CrossRef]
- Fang, F.; Li, Y.; Zhang, R.; Liu, Y. An nonlinear control strategy for single-phase Quasi-Z-source grid-connected inverter. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; pp. 7685–7690. [Google Scholar] [CrossRef]
- Liu, C.; Liu, P.; Luo, H.; Huang, S.; Xu, J. A New Model Predictive Control Strategy for Quasi-Z-Source Inverters. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Bakeer, A.; Ismeil, M.A.; Kouzou, A.; Orabi, M. Development of MPC algorithm for quasi Z-source inverter (qZSI). In Proceedings of the 2015 3rd International Conference on Control, Engineering & Information Technology (CEIT), Tlemcen, Algeria, 25–27 May 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, P.; Tong, L.; Liu, C.; Huang, S. Model Predictive Control for Quasi-Z-Source Inverter without Weighting Factors. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020; pp. 3045–3050. [Google Scholar] [CrossRef]
- Ayad, A.; Karamanakos, P.; Kennel, R. Direct model predictive voltage control of quasi-Z-source inverters with LC filters. In Proceedings of the 2016 18th European Conference on Power Electronics and Applications (EPE’16 ECCE Europe), Karlsruhe, Germany, 5–9 September 2016; pp. 1–10. [Google Scholar] [CrossRef]
- Mo, W.; Loh, P.C.; Blaabjerg, F. Model predictive control for Z-source power converter. In Proceedings of the 8th International Conference on Power Electronics—ECCE Asia, Jeju, Republic of Korea, 30 May–3 June 2011; pp. 3022–3028. [Google Scholar] [CrossRef]
- Saavedra, J.L.; Baier, C.R.; Marciel, E.I.; Rivera, M.; Carreno, A.; Hernandez, J.C.; Melín, P.E. Comparison of FCS-MPC Strategies in a Grid-Connected Single-Phase Quasi-Z Source Inverter. Electronics 2023, 12, 2052. [Google Scholar] [CrossRef]
- Diaz-Bustos, M.; Baier, C.R.; Torres, M.A.; Melin, P.E.; Acuna, P. Application of a Control Scheme Based on Predictive and Linear Strategy for Improved Transient State and Steady-State Performance in a Single-Phase Quasi-Z-Source Inverter. Sensors 2022, 22, 2458. [Google Scholar] [CrossRef] [PubMed]
- Abid, A.; Bakeer, A.; Zellouma, L.; Bouzidi, M.; Lashab, A.; Rabhi, B. Low Computational Burden Predictive Direct Power Control of Quasi Z-Source Inverter for Grid-Tied PV Applications. Sustainability 2023, 15, 4153. [Google Scholar] [CrossRef]
- Horrillo-Quintero, P.; García-Triviño, P.; Sarrias-Mena, R.; García-Vázquez, C.A.; Fernández-Ramírez, L.M. Model predictive control of a microgrid with energy-stored quasi-Z-source cascaded H-bridge multilevel inverter and PV systems. Appl. Energy 2023, 346, 121390. [Google Scholar] [CrossRef]
- Zandi, O.; Poshtan, J. Voltage Control of a Quasi Z-Source Converter Under Constant Power Load Condition Using Reinforcement Learning. Control Eng. Pract. 2023, 135, 105499. [Google Scholar] [CrossRef]
- Rostami, H.; Khaburi, D.A. Neural networks controlling for both the DC boost and AC output voltage of Z-source inverter. In Proceedings of the 2010 1st Power Electronic & Drive Systems & Technologies Conference (PEDSTC), Tehran, Iran, 17–18 February 2010; pp. 135–140. [Google Scholar] [CrossRef]
- Guo, Y.; Wu, M.; Peng, S.; Liu, F. Fault-tolerant Control of PMSM Based on Double Quasi-Z-Source Four-Leg Indirect Matrix Converter. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 1807–1812. [Google Scholar] [CrossRef]
- Morawiec, M. The Adaptive Backstepping Control of Permanent Magnet Synchronous Motor Supplied by Current Source Inverter. IEEE Trans. Ind. Inform. 2013, 9, 1047–1055. [Google Scholar] [CrossRef]
- Urbanski, K.; Janiszewski, D. Improving the Dynamics of an Electrical Drive Using a Modified Controller Structure Accompanied by Delayed Inputs. Appl. Sci. 2024, 14, 10126. [Google Scholar] [CrossRef]
- Liu, H.; Li, S. Speed Control for PMSM Servo System Using Predictive Functional Control and Extended State Observer. IEEE Trans. Ind. Electron. 2012, 59, 1171–1183. [Google Scholar] [CrossRef]
- Qu, K.; Pang, P.; Hua, W. High-Precision Rotor Position Fitting Method of Permanent Magnet Synchronous Machine Based on Hall-Effect Sensors. Energies 2024, 17, 5625. [Google Scholar] [CrossRef]
- Aguilar-Mejia, O.; Valderrabano-Gonzalez, A.; Hernández-Romero, N.; Seck-Tuoh-Mora, J.C.; Hernandez-Ochoa, J.C.; Minor-Popocatl, H. A Neuroadaptive Position-Sensorless Robust Control for Permanent Magnet Synchronous Motor Drive System with Uncertain Disturbance. Energies 2024, 17, 5477. [Google Scholar] [CrossRef]
- Akrami, M.; Jamshidpour, E.; Baghli, L.; Frick, V. Application of Low-Resolution Hall Position Sensor in Control and Position Estimation of PMSM—A Review. Energies 2024, 17, 4216. [Google Scholar] [CrossRef]
- Yu, F.; Liu, J. Switching Current Predictive Control of a Permanent Magnet Synchronous Motor Based on the Exponential Moving Average Algorithm. Energies 2024, 17, 3577. [Google Scholar] [CrossRef]
- Kovács, K.; Rácz, I. Transiente Vorgänge in Wechselstrommaschinen; Number t. 1; Verlag der Ungarischen Akademie der Wissenschaften: Budapest, Hungary, 1959. [Google Scholar]
- Pillay, P.; Krishnan, R. Modeling, simulation, and analysis of permanent-magnet motor drives. I. The permanent-magnet synchronous motor drive. IEEE Trans. Ind. Appl. 1989, 25, 265–273. [Google Scholar] [CrossRef]
- Casadei, D.; Grandi, G.; Serra, G.; Tani, A. Space vector control of matrix converters with unity input power factor and sinusoidal input/output waveforms. In Proceedings of the 1993 Fifth European Conference on Power Electronics and Applications, Brighton, UK, 13–16 September 1993; Volume 7, pp. 170–175. [Google Scholar]
- Siwek, P.; Urbański, K. Quasi Z-source direct matrix converter for enhanced resilience to power grid faults in permanent magnet synchronous motor applications. Bull. Pol. Acad. Sci. Tech. Sci. 2024, 72, e150201. [Google Scholar] [CrossRef]
- Huber, L.; Borojevic, D. Space vector modulated three-phase to three-phase matrix converter with input power factor correction. IEEE Trans. Ind. Appl. 1995, 31, 1234–1246. [Google Scholar] [CrossRef]
- Rodriguez, J.; Rivera, M.; Kolar, J.W.; Wheeler, P.W. A Review of Control and Modulation Methods for Matrix Converters. IEEE Trans. Ind. Electron. 2012, 59, 58–70. [Google Scholar] [CrossRef]
- Majchrzak, D.; Siwek, P. Comparison of FOC and DTC methods for a Matrix Converter-fed permanent magnet synchronous motor. In Proceedings of the 2017 22nd International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 28–31 August 2017; pp. 525–530. [Google Scholar] [CrossRef]
- Toledo, S.; Caballero, D.; Maqueda, E.; Cáceres, J.J.; Rivera, M.; Gregor, R.; Wheeler, P. Predictive Control Applied to Matrix Converters: A Systematic Literature Review. Energies 2022, 15, 7801. [Google Scholar] [CrossRef]
- von Jouanne, A.; Agamloh, E.; Yokochi, A. A Review of Matrix Converters in Motor Drive Applications. Energies 2025, 18, 164. [Google Scholar] [CrossRef]
- Liu, S.; Ge, B.; Liu, Y.; Abu-Rub, H.; Balog, R.S.; Sun, H. Modeling, Analysis, and Parameters Design of LC-Filter-Integrated Quasi-Z -Source Indirect Matrix Converter. IEEE Trans. Power Electron. 2016, 31, 7544–7555. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Fang, R. Virtual Inertia Implemented by Quasi-Z-Source Power Converter for Distributed Power System. Energies 2023, 16, 6667. [Google Scholar] [CrossRef]
- Cao, Y.; Xiao, S.; Lin, Z. A Flying Restart Strategy for Position Sensorless PMSM Driven by Quasi-Z-Source Inverter. Energies 2022, 15, 3469. [Google Scholar] [CrossRef]
- Strzelecki, R.; Vinnikov, D. Modele przekształtników typu qZ. Przegląd Elektrotechniczny 2010, 86, 80–84. [Google Scholar]
- Bauer, J.; Fligl, S.; Steimel, A. Design and Dimensioning of Essential Passive Components for the Matrix Converter Prototype. Automatika 2012, 53, 134. [Google Scholar] [CrossRef]
- Permanent Magnet Synchronous Motor with Sinusoidal Flux Distribution. Available online: https://www.mathworks.com/help/sps/ref/pmsm.html (accessed on 8 May 2024).
- System Identification Toolbox. Available online: https://www.mathworks.com/help/ident/ (accessed on 10 April 2024).
- Orelind, G.; Wozniak, L.; Medanic, J.; Whittemore, T. Optimal PID gain schedule for hydrogenerators-design and application. IEEE Trans. Energy Convers. 1989, 4, 300–307. [Google Scholar] [CrossRef]
- Shao, P.; Zhou, Z.; Ma, S.; Bin, L. Structural robust gain-scheduled PID control and application on a morphing wing UAV. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; pp. 3236–3241. [Google Scholar] [CrossRef]
- Veselý, V.; Ilka, A. PID robust gain-scheduled controller design. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 2756–2761. [Google Scholar] [CrossRef]
- Moser, I. Hooke-Jeeves revisited. In Proceedings of the 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, 18–21 May 2009; pp. 2670–2676. [Google Scholar] [CrossRef]
- Hooke, R.; Jeeves, T.A. “Direct Search” Solution of Numerical and Statistical Problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]



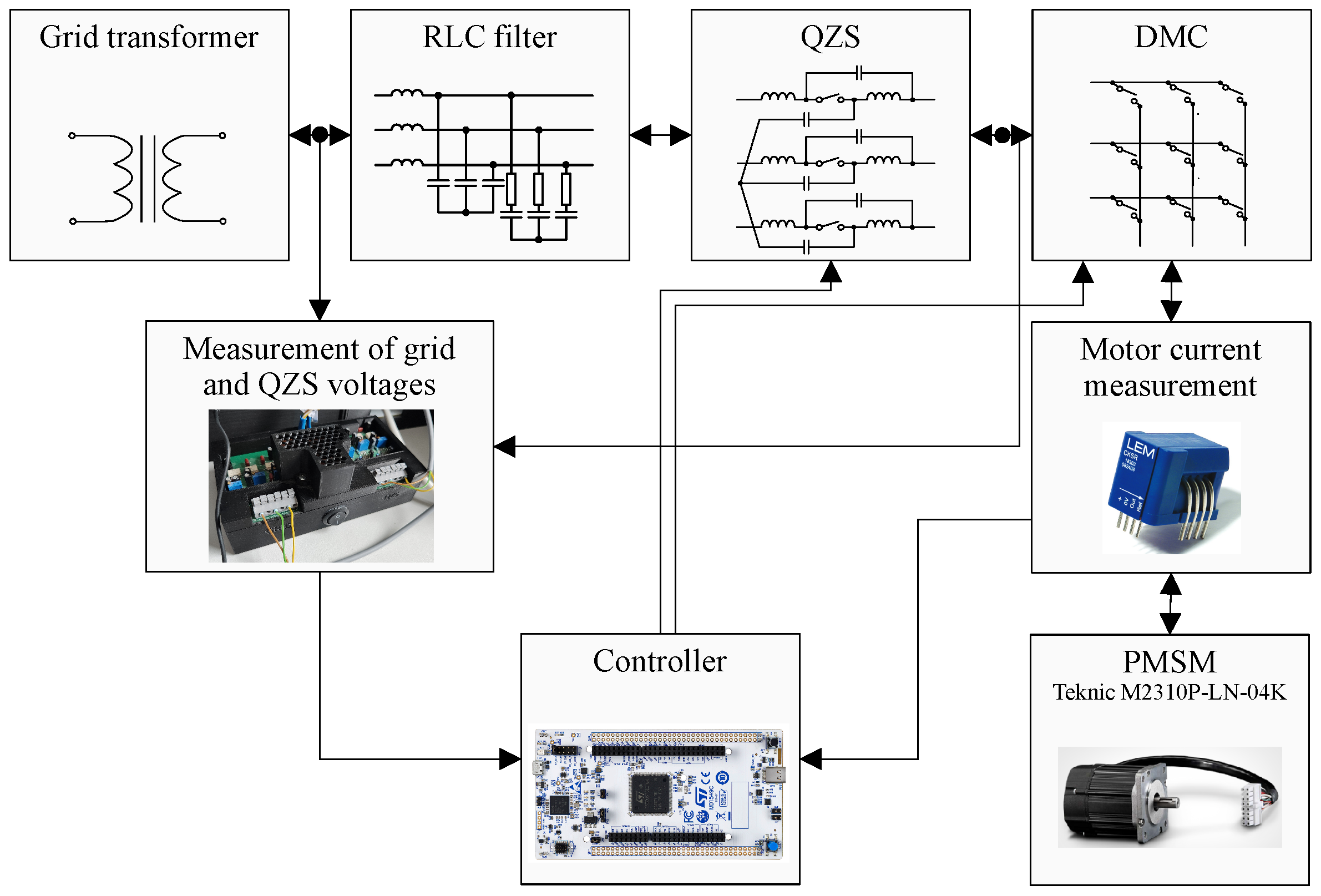


| Parameter | Symbol | Value |
|---|---|---|
| Maximum voltage | 40 V | |
| Rated voltage | 24 V | |
| Rated current | A | |
| Electromagnetic torque | ||
| Rated speed | ||
| Number of pole pairs | p | 3 |
| Stator resistance | ||
| Inductance in the d-axis | 336 | |
| Inductance in the q-axis | 336 |
| Parameter | Symbol | Value |
|---|---|---|
| Filter inductance | 375 | |
| Filter capacitance | ||
| Damping capacitance | ||
| Damping resistance | 35 |
| Parameter | Symbol | Value |
|---|---|---|
| QZS inductance | 30 | |
| QZS capacitance | 10 |
| System Transfer Function | |
|---|---|
| 1.25 | model order too low |
| 1.5 | |
| 1.75 | |
| 2 | |
| 2.5 | |
| 3 | |
| 3.5 |
| [V] | ||
|---|---|---|
| 7120 | ||
| 5640 | ||
| 5430 | 40 | |
| 5210 | ||
| 4710 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siwek, P.; Urbanski, K. Voltage Control Nonlinearity in QZSDMC Fed PMSM Drive System with Grid Filtering. Energies 2025, 18, 1334. https://doi.org/10.3390/en18061334
Siwek P, Urbanski K. Voltage Control Nonlinearity in QZSDMC Fed PMSM Drive System with Grid Filtering. Energies. 2025; 18(6):1334. https://doi.org/10.3390/en18061334
Chicago/Turabian StyleSiwek, Przemysław, and Konrad Urbanski. 2025. "Voltage Control Nonlinearity in QZSDMC Fed PMSM Drive System with Grid Filtering" Energies 18, no. 6: 1334. https://doi.org/10.3390/en18061334
APA StyleSiwek, P., & Urbanski, K. (2025). Voltage Control Nonlinearity in QZSDMC Fed PMSM Drive System with Grid Filtering. Energies, 18(6), 1334. https://doi.org/10.3390/en18061334






