Evaluating Combustion Ignition, Burnout, Stability, and Intensity of Coal–Biomass Blends Within a Drop Tube Furnace Through Modelling
Abstract
1. Introduction
2. Experimental Methods
2.1. Fuel Blend Characterisation
2.2. Drop Tube Furnace Experimental Setup
3. Numerical Methods
- ρ: represents the density;
- φ: variable (mass, specific enthalpy, or species mass fraction);
- Ui: velocity (u, v, w);
- Γ: variable diffusion coefficient;
- Sφ: variable source or sink.
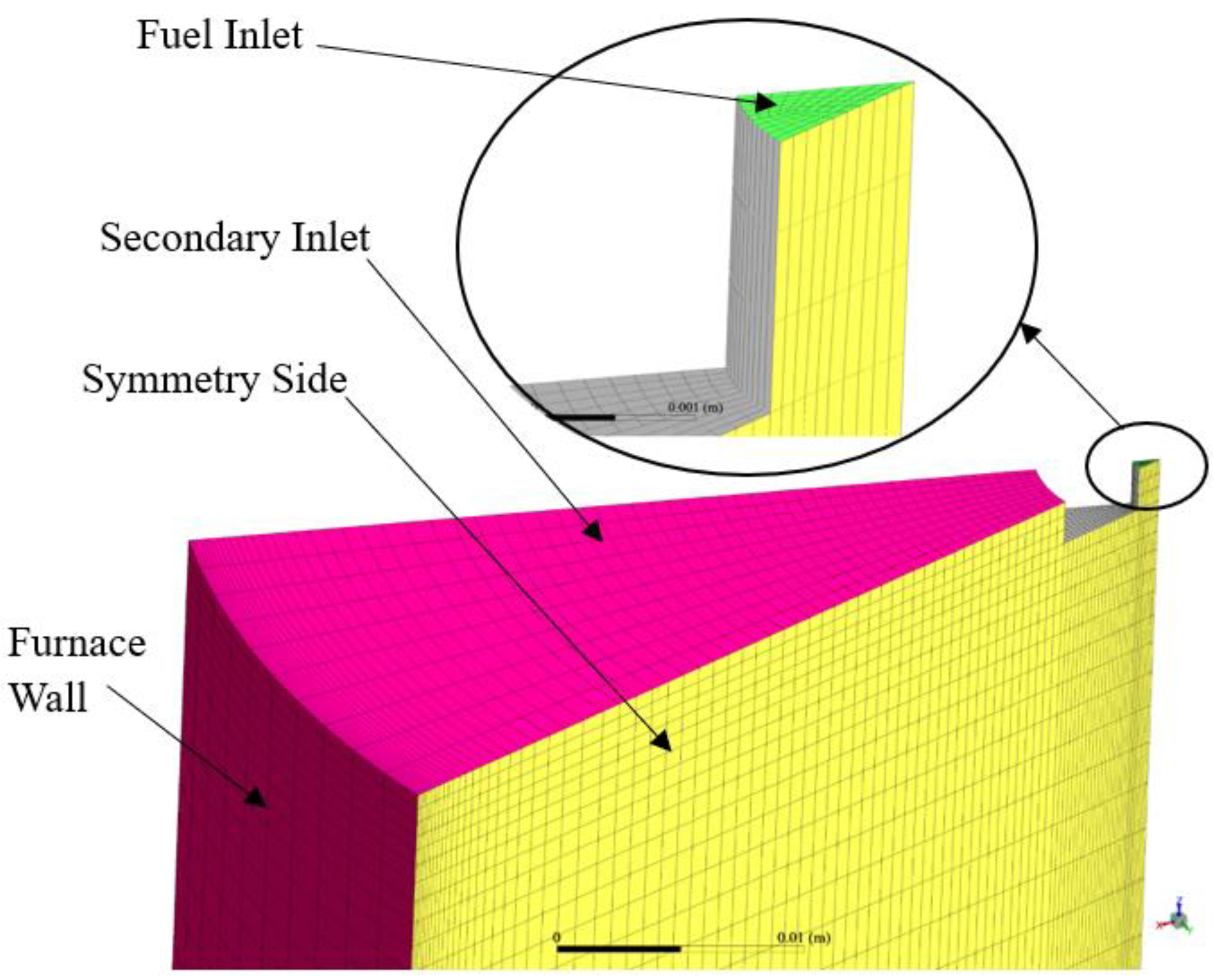
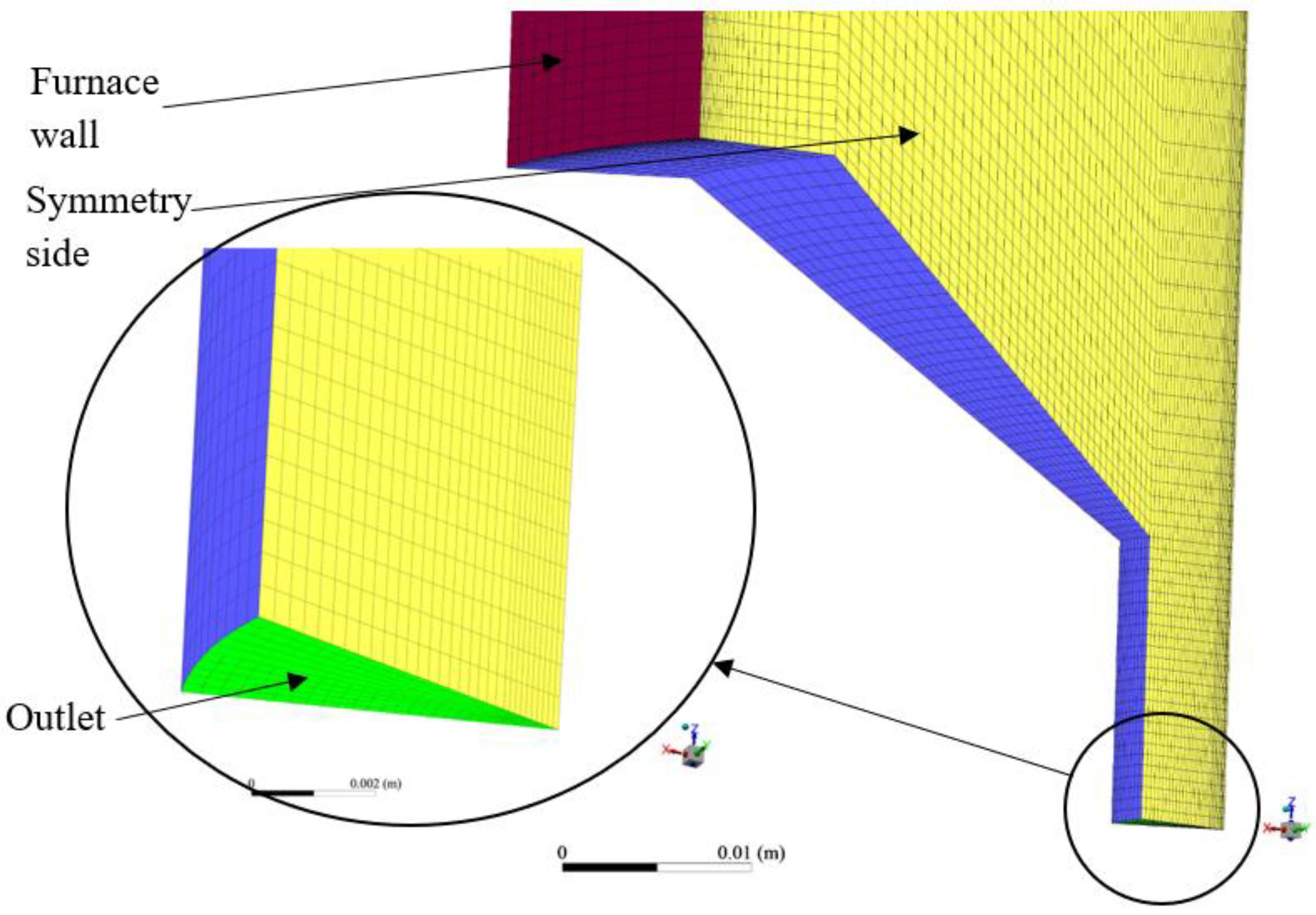
3.1. Furnace Geometry and Meshing
- There was a need to reduce the computational power required to run the setup;
- The geometry was cylindrical about the furnace axis;
- A 3D analysis would be able to capture the axial and radial variation in parameters with more precision as compared to a 2D analysis;
- The inlets (fuel inlet and secondary carrier gas inlet) and outlet boundaries were all normal to the symmetrical planes that were defined;
- The expected flow was going to be repeated periodically about the axis since the fuel and secondary carrier gas inlet flows were distributed evenly and normal to their corresponding boundaries.
3.2. Cocombustion Model Setup
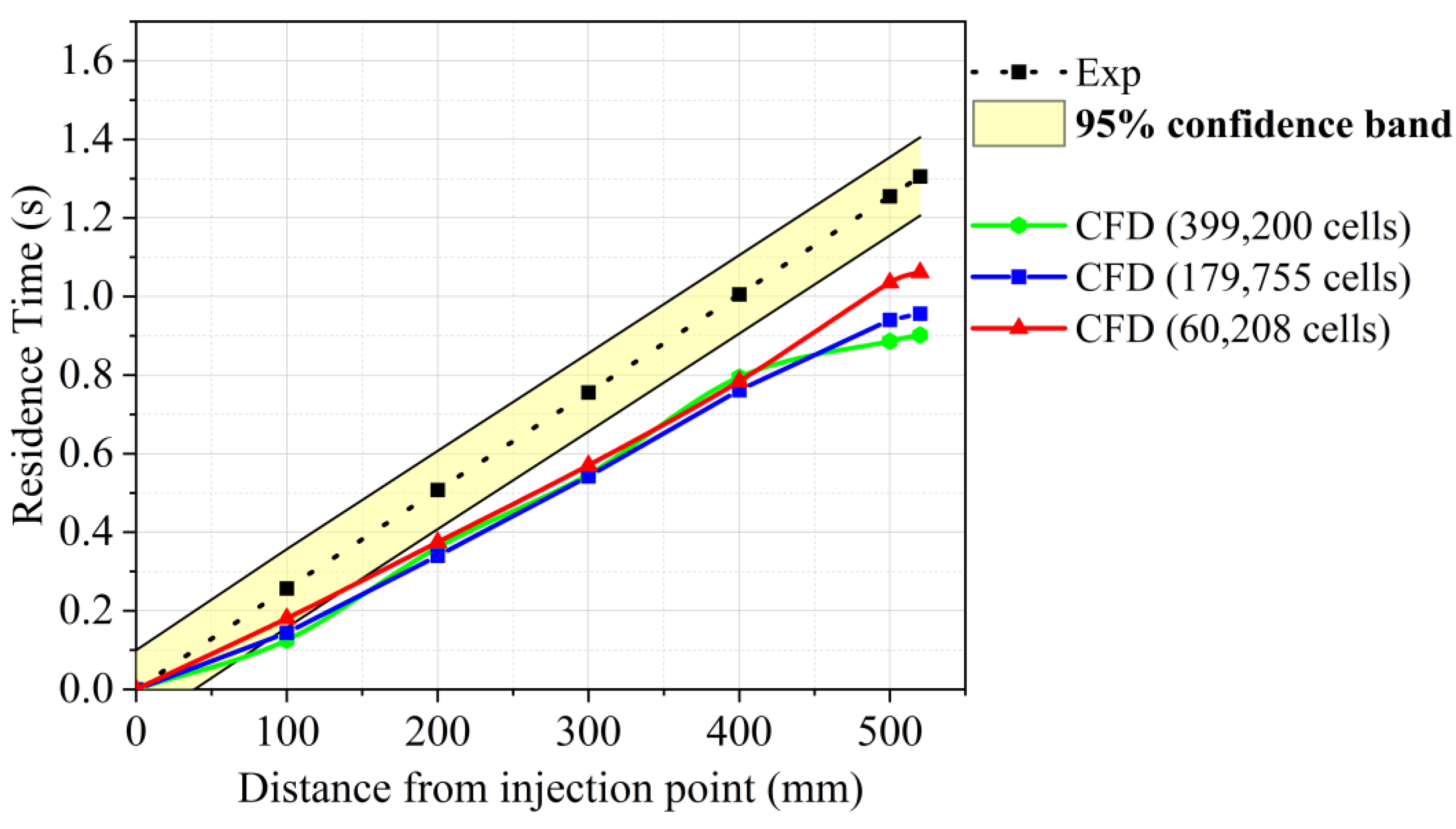
3.3. Drop Tube Furnace Model Sensitivity Analysis
- p: order of convergence;
- f: performance parameter;
- r: refinement ratio = 2.576;
- GCI: grid convergence index;
- Fs: factor of safety (in this case, 2 levels of refinement = 1.25).
| Mesh Cells | Mesh Label | Performance Parameter | p | GCI1 | GCI2 | Asymptotic Range Value |
|---|---|---|---|---|---|---|
| [Particle residence time (s)] | ||||||
| 399,200 | 1 | 1.2991 | 0.4986 | 0.0932 | 0.1565 | 1.0471 |
| 159,755 | 2 | 1.2407 | ||||
| 60,208 | 3 | 1.3343 | ||||
| [Particle peak temperature (K)] | ||||||
| 399,200 | 1 | 1006.14 | 1.1840 | 0.0137 | 0.0413 | 0.9778 |
| 159,755 | 2 | 1029.03 | ||||
| 60,208 | 3 | 958.85 |
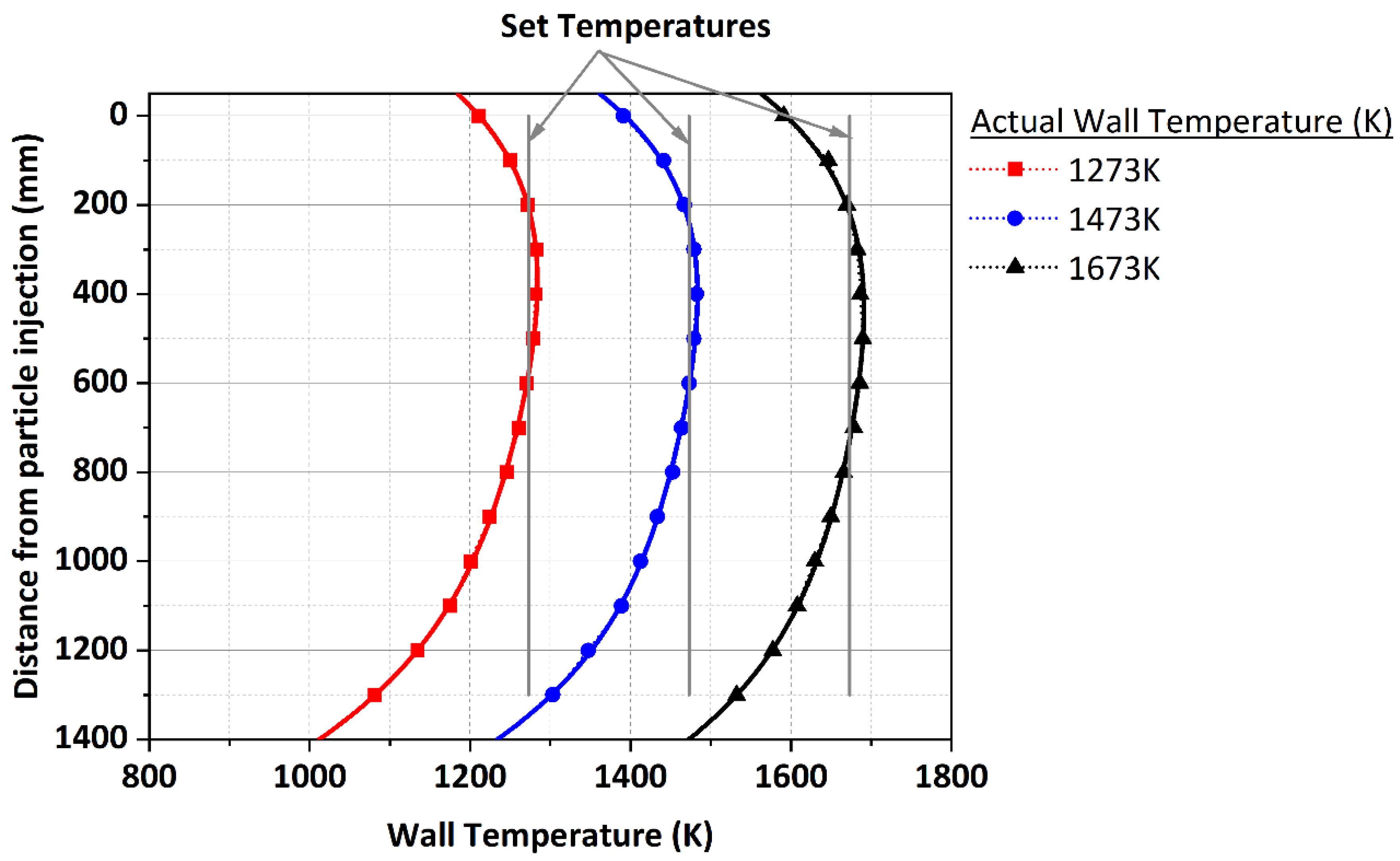
3.4. Cocombustion Model Validation
4. Results and Discussion
5. Conclusions
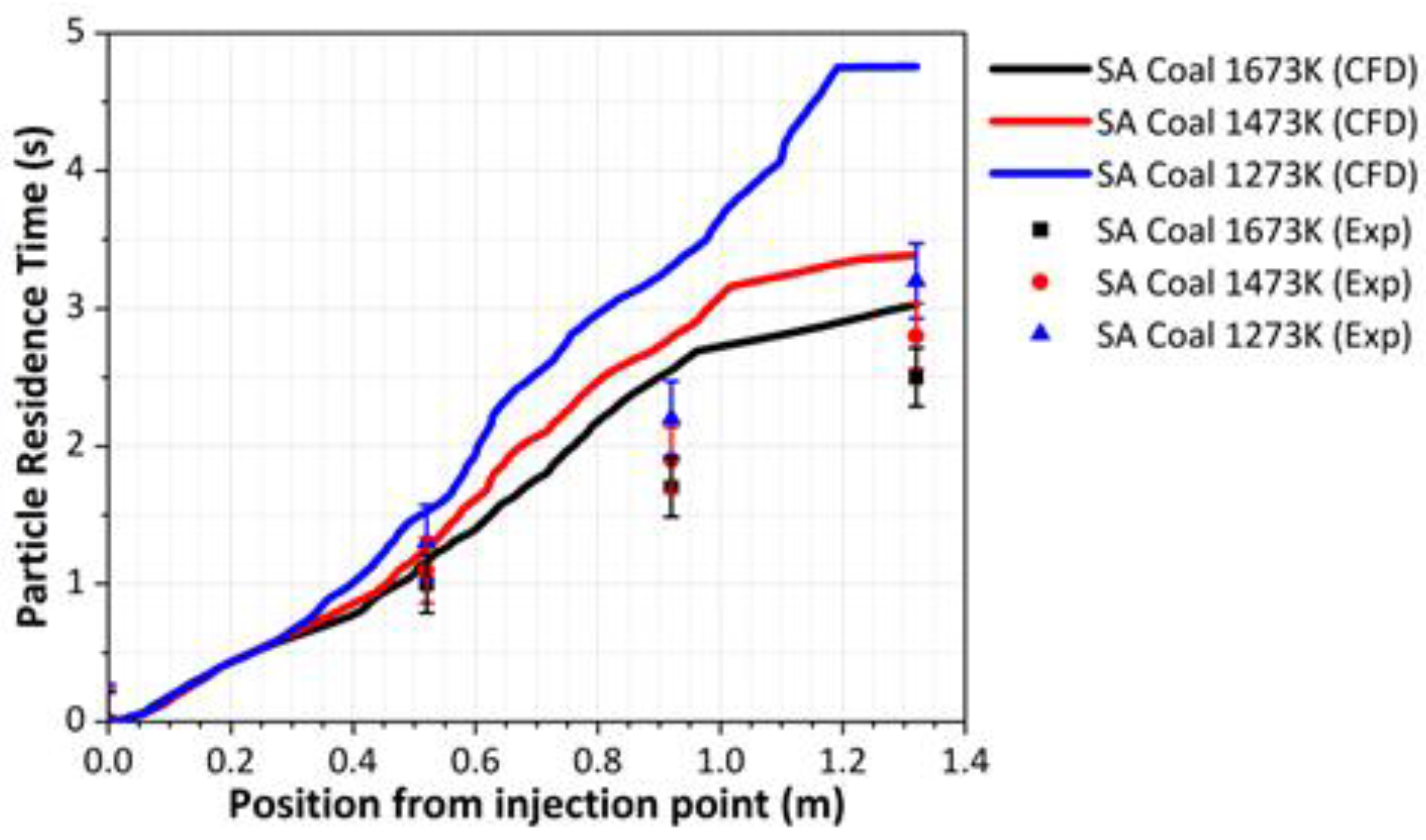
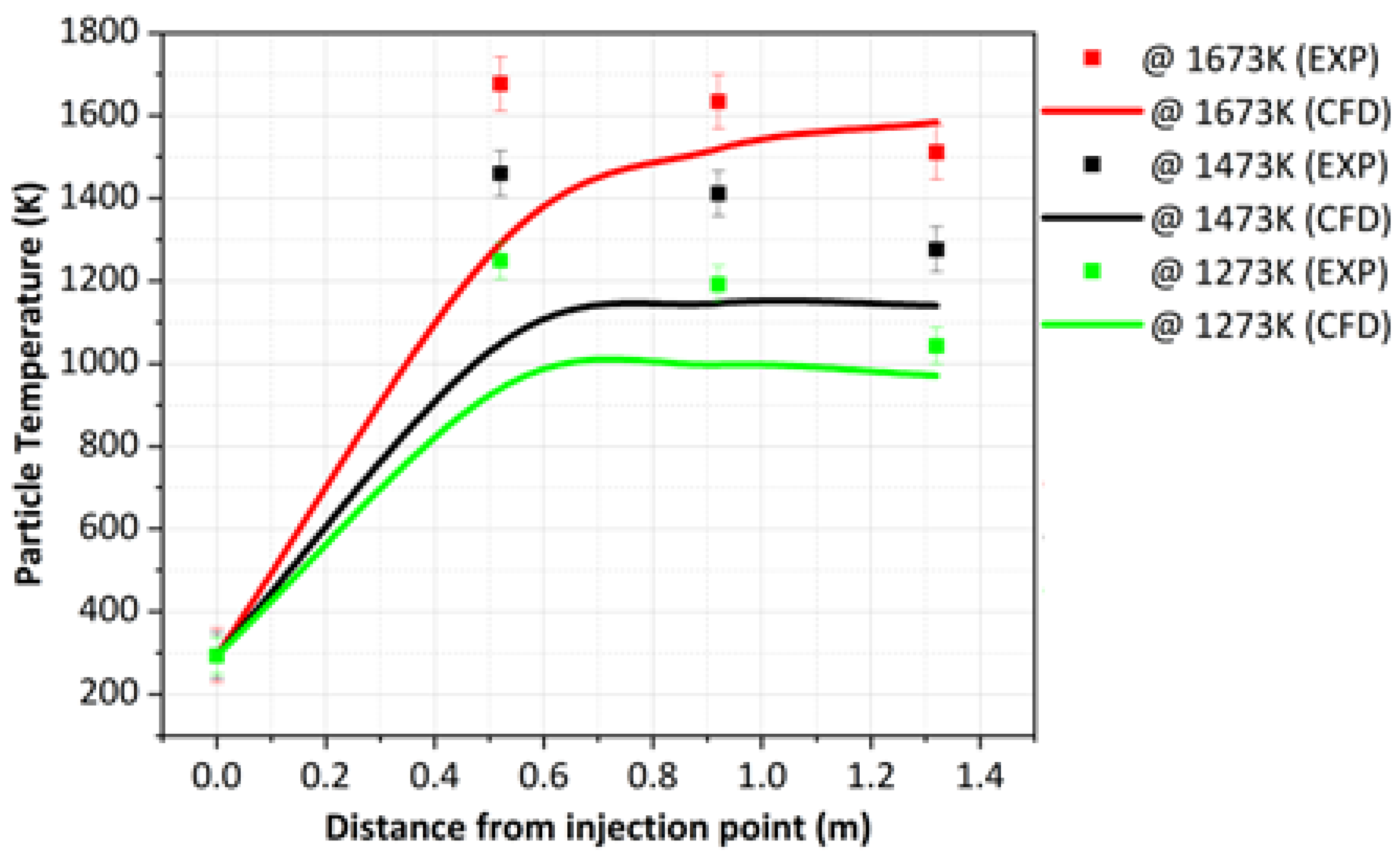
- The variation in the particle residence time and temperature within the DTF was used to validate the cocombustion model. The predicted values produced a similar trend as compared to experimental values, though an overprediction was experienced with an average root mean square error (RMSE) of 1.117 at a 1273 K DTF wall temperature and 0.557 at a 1673 K DTF wall temperature. This overprediction was attributed to various factors related to the experimental procedure; hence, further research with regard to the characterisation of the char and volatiles produced by devolatilisation was suggested.
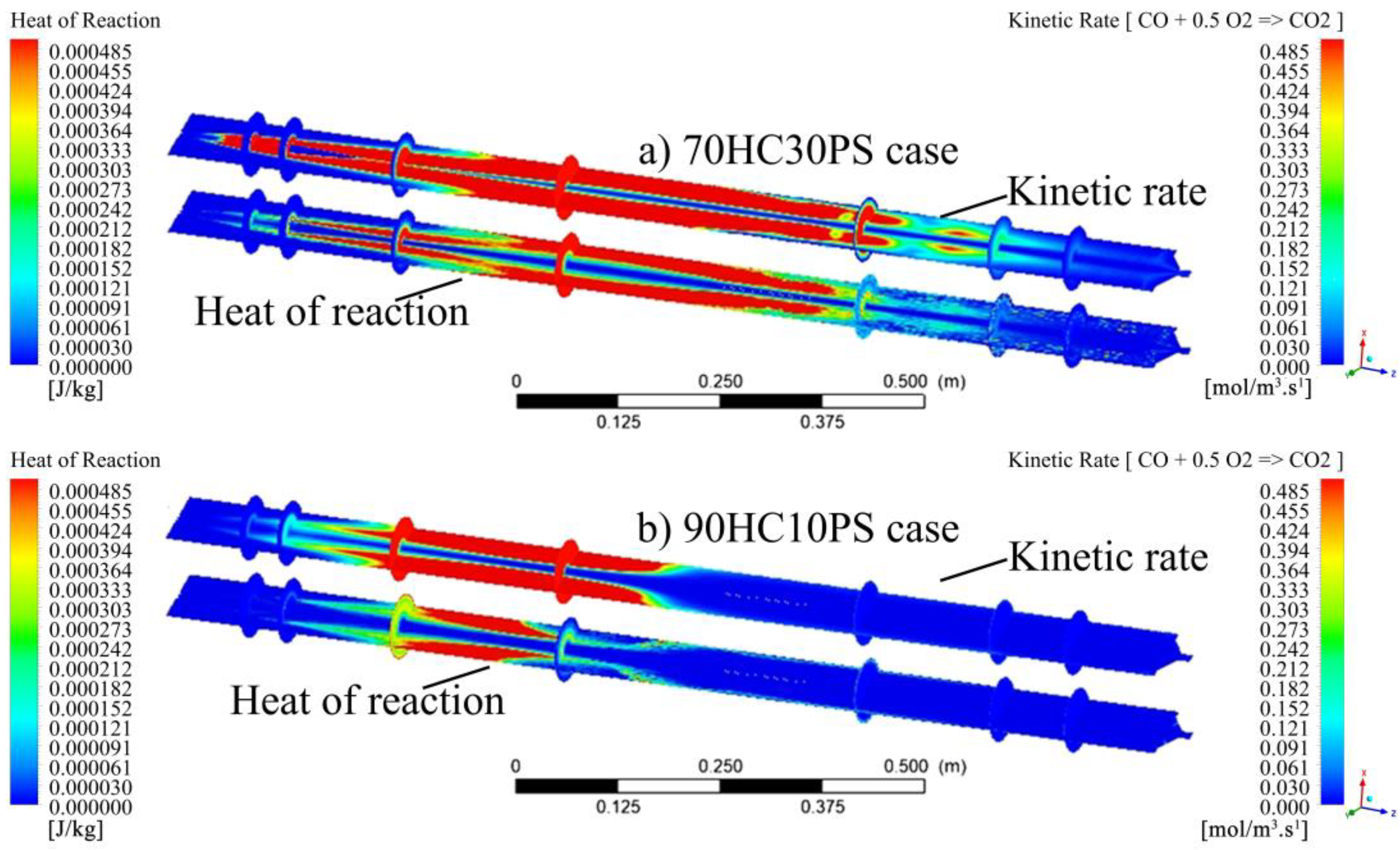
- Increasing the Pinus sawdust blending ratio resulted in more volatiles being released, as mirrored by the proximate composition of the fuel blends. As such, the volatile composition on the fuel blends showed that the molar ratio of carbon increased with blending (0% to 30% sawdust) from 0.292 up to 0.579. The hydrogen and oxygen molar ratios also increased with Pinus sawdust blending, though to a lesser magnitude. The nitrogen molar ratio decreased from 0.086 to 0.052 as blending with Pinus sawdust increased, whilst the sulphur molar ratio decreased marginally.
- The cocombustion model was able to bring synergy between various submodels of interest which tend to be overlooked in certain instances. The eddy dissipation concept submodel captured the combustion mechanisms successfully; the weighted sum of grey gases model captured the radiation from the combustion products successfully.
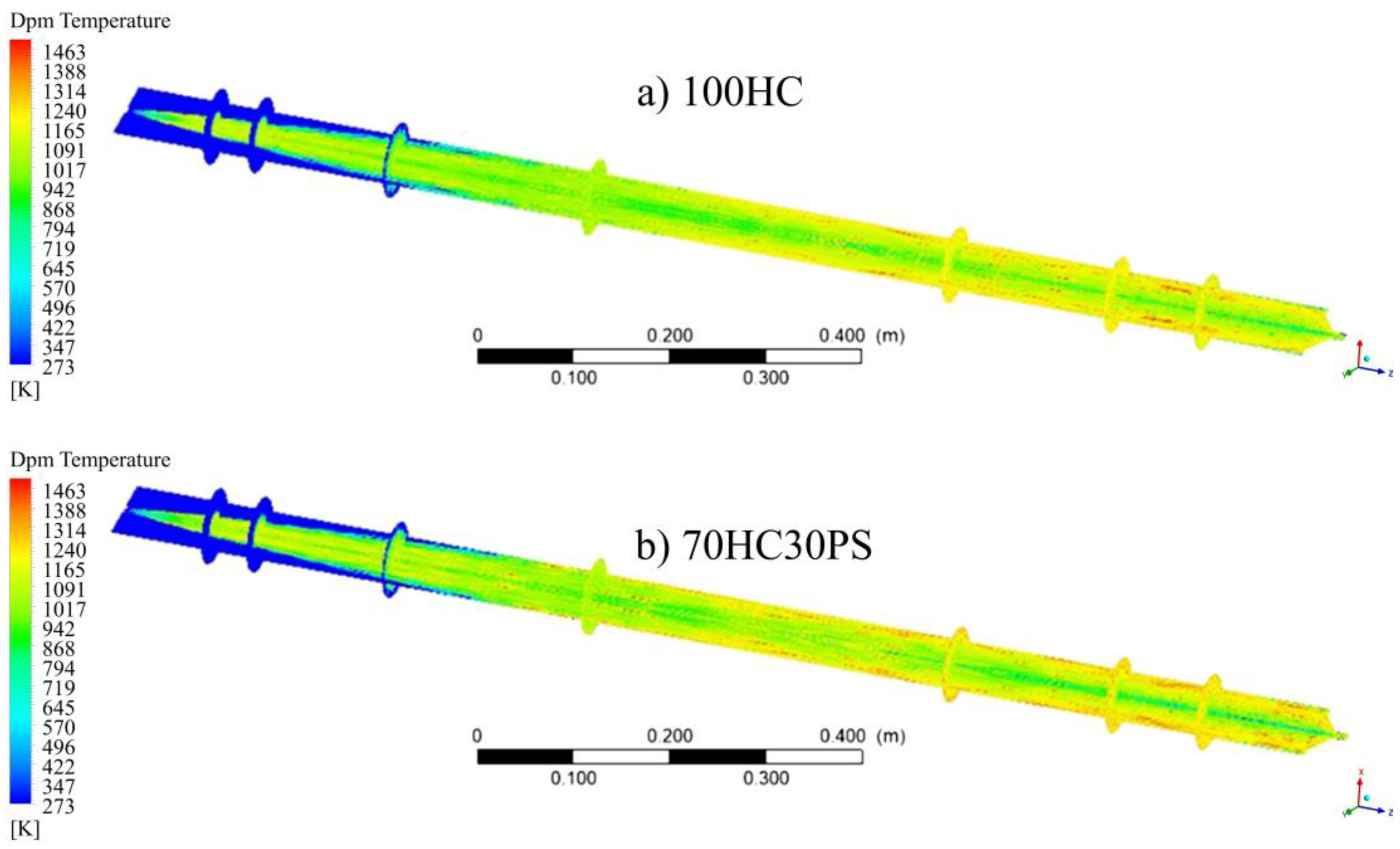
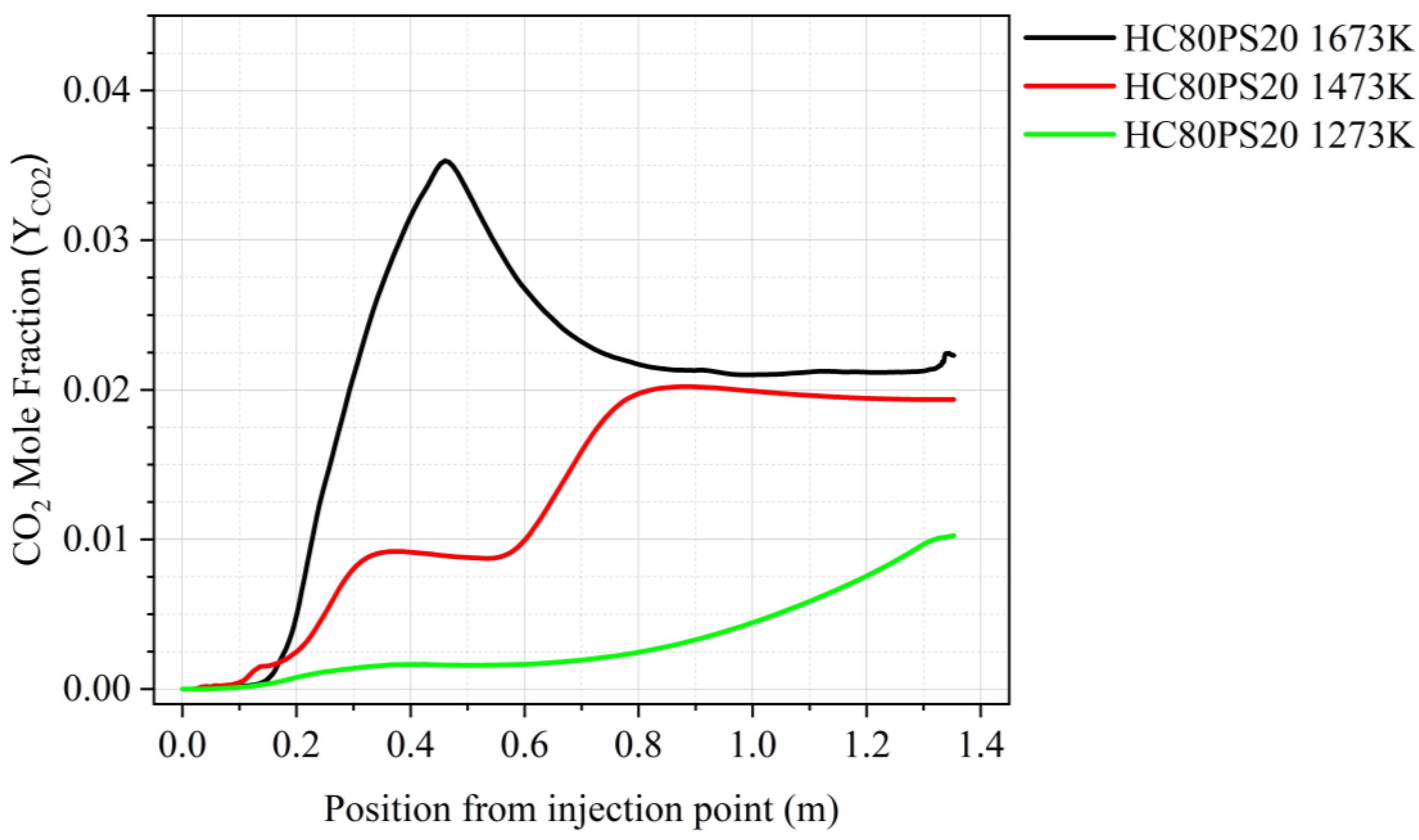
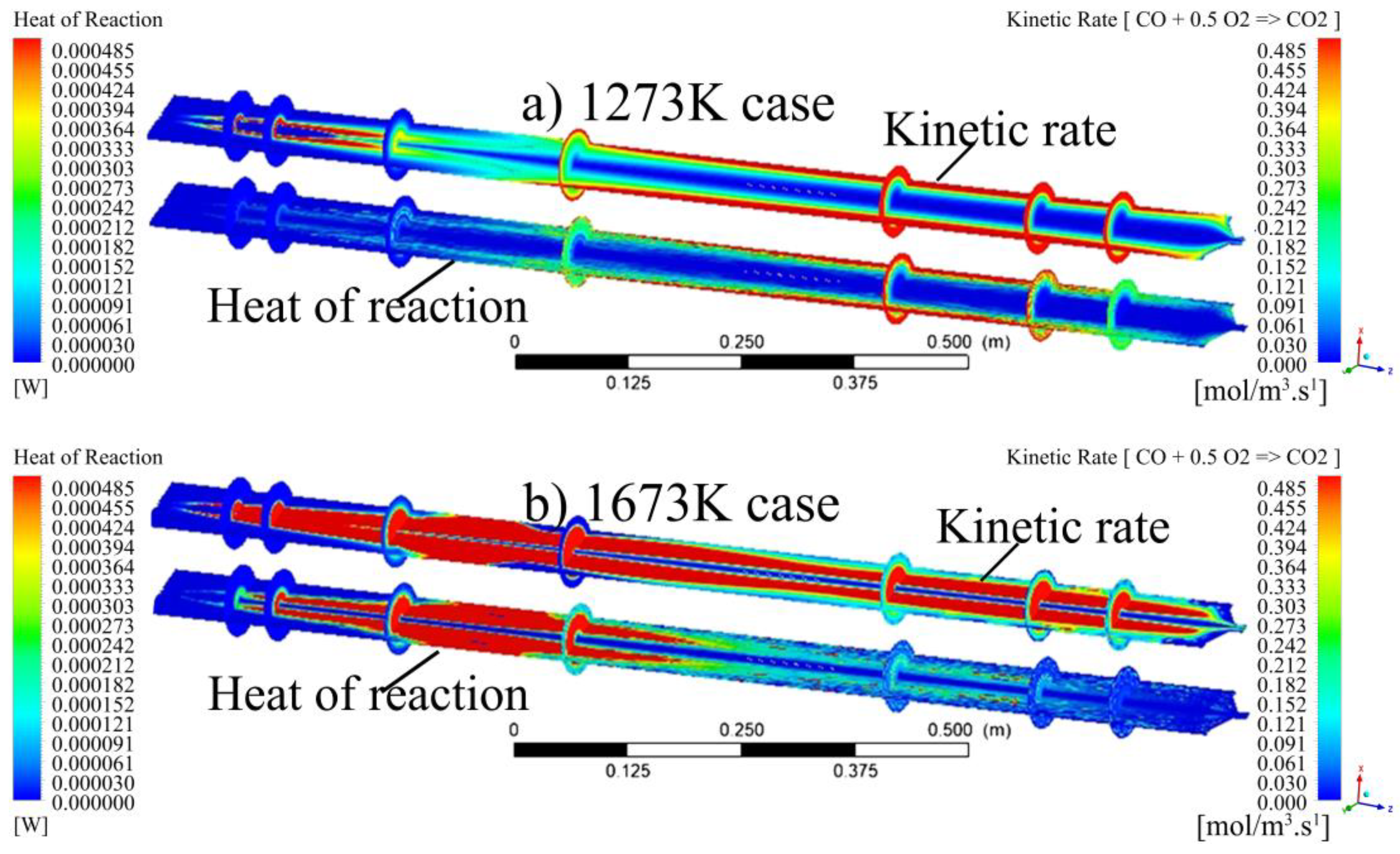
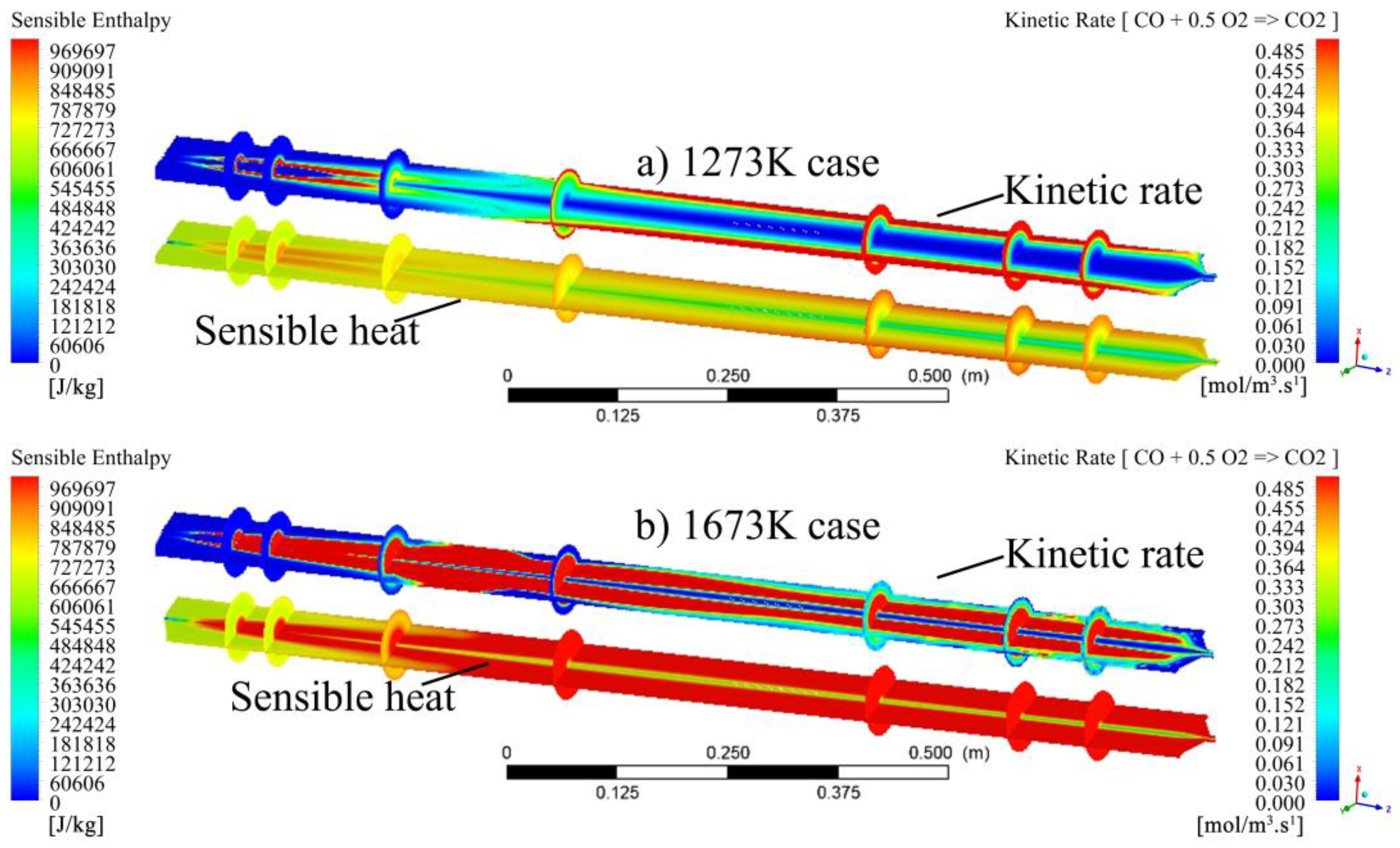
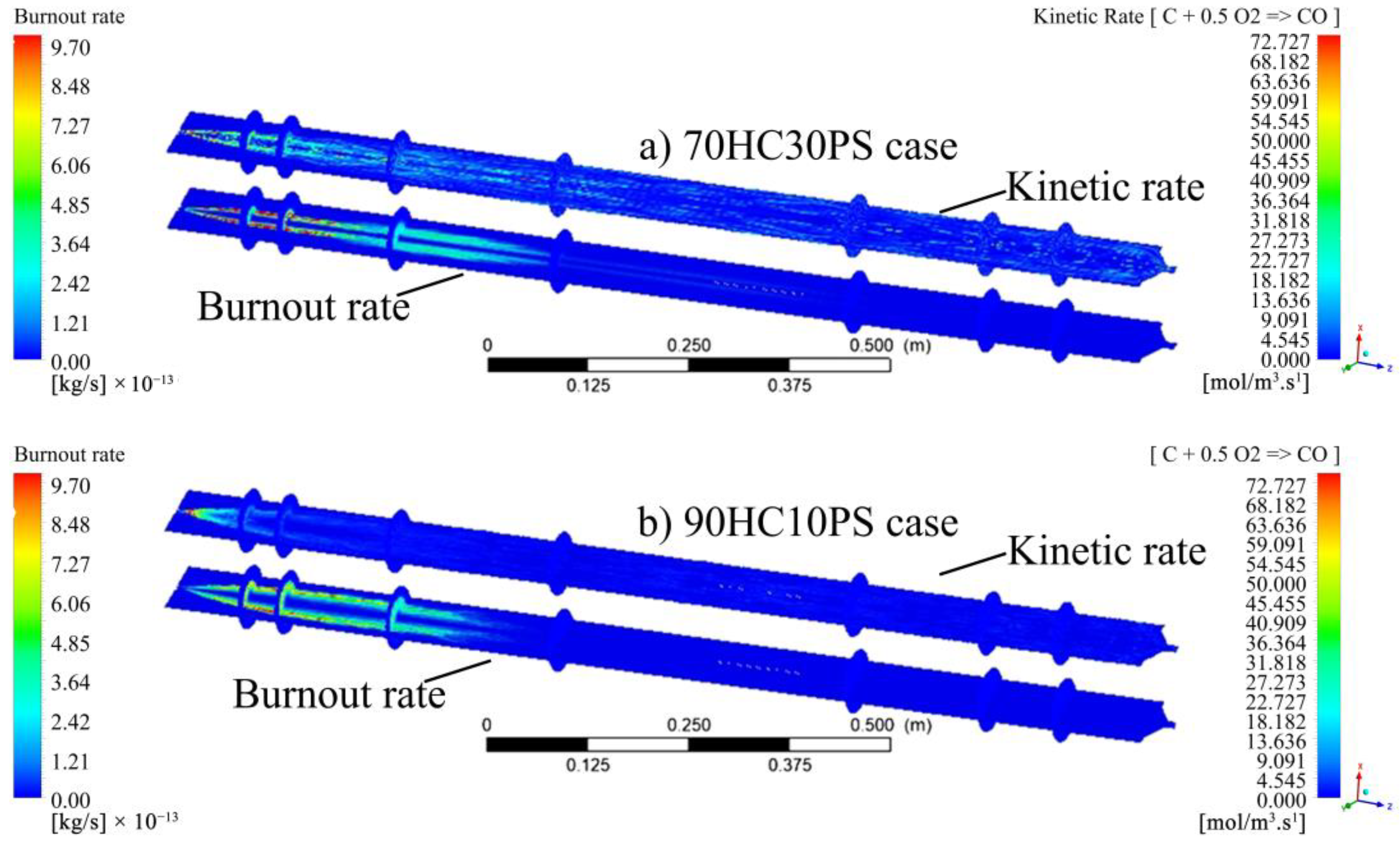
- The visualisation of various profiles highlighted the co-dependency of certain combustion parameters on others. The discrete-phase particle burnout profiles were shown to be dependent on the oxidation of CO to form CO2 kinetic rate of reaction. It was also made evident that low DTF wall temperatures hindered the oxidation of CO to form CO2, thus delaying the reaction zone to an average location of 0.8 m from the injection point as compared to the initial 0.4 m obtained at high DTF wall temperatures.
- Blending affected the heat of the reaction by promoting the onset of the reaction zone as well as increasing the combustion intensity within the reaction zone. The gradual release of heat was shown to be directly linked to the gradual burnout of the char particle. In conclusion, the reaction zone was modelled successfully to highlight the important combustion parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Units | |
| Ea | Activation energy (kJ/mol) |
| T | Static temperature (K) |
| A | Pre-exponential factor (s−1) |
| Ui | Velocity (m/s) |
| Greek Symbols | |
| ρ | Density |
| φ | Variable (mass, specific enthalpy, or species mass fraction) |
| Γ | Variable diffusion coefficient |
| Sφ | Variable source or sink |
| Abbreviations | |
| HC | Bituminous coal |
| PS | Pinus sawdust |
| TGA | Thermogravimetric analysis |
| CFD | Computational fluid dynamics |
| FC | Fixed carbon |
| VM | Volatile matter |
| DTF | Drop tube furnace |
| EDC | Eddy dissipation concept |
| HHV | Higher heat value |
| GCI | Grid convergence index |
| Subscripts | |
| daf | Dry ash free |
| vol | Volatile |
References
- Zhou, C.; Gao, F.; Yu, Y.; Zhang, W.; Liu, G. Effects of Gaseous Agents on Trace Element Emission Behavior during Co-Combustion of Coal with Biomass. Energy Fuels 2020, 34, 3843–3849. [Google Scholar] [CrossRef]
- Benim, A.C.; Deniz Canal, C.; Boke, Y.E. Computational Investigation of Oxy-Combustion of Pulverized Coal and Biomass in a Swirl Burner. Energy 2022, 238, 121852. [Google Scholar] [CrossRef]
- Cardoso, J.S.; Silva, V.; Chavando, J.A.M.; Eusébio, D.; Hall, M.J. Numerical Modelling of the Coal Phase-out through Ammonia and Biomass Co-Firing in a Pilot-Scale Fluidized Bed Reactor. Fuel Commun. 2022, 10, 100055. [Google Scholar] [CrossRef]
- Wei, D.; An, D.; Wang, T.; Zhang, H.; Guo, Y.; Sun, B. Influence of Fuel Distribution on Co-Combustion of Sludge and Coal in a 660 MW Tangentially Fired Boiler. Appl. Therm. Eng. 2023, 227, 120344. [Google Scholar] [CrossRef]
- Lyu, Q.; Wang, R.; Du, Y.; Liu, Y. Numerical Study on Coal/Ammonia Co-Firing in a 600 MW Utility Boiler. Int. J. Hydrogen Energy 2023, 48, 17293–17310. [Google Scholar] [CrossRef]
- Marangwanda, G.T.; Madyira, D.M.; Ndungu, P.G.; Chihobo, C.H. Combustion Characterisation of Bituminous Coal and Pinus Sawdust Blends by Use of Thermo-Gravimetric Analysis. Energies 2021, 14, 7547. [Google Scholar] [CrossRef]
- Jin, W.; Si, F.; Kheirkhah, S.; Yu, C.; Li, H.; Wang, Y. Numerical Study on the Effects of Primary Air Ratio on Ultra-Low-Load Combustion Characteristics of a 1050 MW Coal-Fired Boiler Considering High-Temperature Corrosion. Appl. Therm. Eng. 2023, 221, 119811. [Google Scholar] [CrossRef]
- Gao, H.; Runstedtler, A.; Majeski, A.; Boisvert, P.; Campbell, D. Optimizing a Woodchip and Coal Co-Firing Retrofit for a Power Utility Boiler Using CFD. Biomass Bioenergy 2016, 88, 35–42. [Google Scholar] [CrossRef]
- Gu, T.; Ma, W.; Guo, Z.; Berning, T.; Yin, C. Stable and Clean Co-Combustion of Municipal Sewage Sludge with Solid Wastes in a Grate Boiler: A Modeling-Based Feasibility Study. Fuel 2022, 328, 125237. [Google Scholar] [CrossRef]
- Chen, B.; Liu, B.; Shi, Z. Combustion Characteristics and Combustion Kinetics of Dry Distillation Coal and Pine Tar. Int. J. Aerosp. Eng. 2020, 2020, 8888556. [Google Scholar] [CrossRef]
- Choi, C.R.; Kim, C.N. Numerical Investigation on the Flow, Combustion and NOx Emission Characteristics in a 500 MWe Tangentially Fired Pulverized-Coal Boiler. Fuel 2009, 88, 1720–1731. [Google Scholar] [CrossRef]
- Mohanna, H. Combustion of Pulverized Biomass: Impact of Fuel Preparation and Flow Conditions. Ph.D. Thesis, Normandie Université, Montpellier, France, 2021. [Google Scholar]
- Ma, W.; Zhou, H.; Zhang, J.; Zhang, K.; Liu, D.; Zhou, C.; Cen, K. Behavior of Slagging Deposits during Coal and Biomass Co-Combustion in a 300 KW Down-Fired Furnace. Energy Fuels 2018, 32, 4399–4409. [Google Scholar] [CrossRef]
- Fang, Y.; Qiao, L.; Wang, C.; Luo, X.; Xiong, T.; Tian, R.; Tang, Z.; Sun, H. Study on the Influence of the Activation Energy on the Simulation of Char Combustion. IOP Conf. Ser. Earth Environ. Sci. 2019, 300, 042062. [Google Scholar] [CrossRef]
- Xinjie, L.; Shihong, Z.; Xincheng, W.; Jinai, S.; Xiong, Z.; Xianhua, W.; Haiping, Y.; Hanping, C. Co-Combustion of Wheat Straw and Camphor Wood with Coal Slime: Thermal Behaviour, Kinetics, and Gaseous Pollutant Emission Characteristics. Energy 2021, 234, 121292. [Google Scholar] [CrossRef]
- Wang, G.; Guiberti, T.F.; Cardona, S.; Jimenez, C.A.; Roberts, W.L. Effects of Residence Time on the NOx Emissions of Premixed Ammonia-Methane-Air Swirling Flames at Elevated Pressure. Proc. Combust. Inst. 2022, 39, 4277–4288. [Google Scholar] [CrossRef]
- Sarroza, A.C.; Bennet, T.D.; Eastwick, C.; Liu, H. Characterising Pulverised Fuel Ignition in a Visual Drop Tube Furnace by Use of a High-Speed Imaging Technique. Fuel Process. Technol. 2017, 157, 1–11. [Google Scholar] [CrossRef]
- Yin, C.; Rosendahl, L.A.; Kær, S.K. Towards a Better Understanding of Biomass Suspension Co-Firing Impacts via Investigating a Coal Flame and a Biomass Flame in a Swirl-Stabilized Burner Flow Reactor under Same Conditions. Fuel Process. Technol. 2012, 98, 65–73. [Google Scholar] [CrossRef]
- Demirbaş, A. Biomass Co-Firing for Boilers Associated with Environmental Impacts. Energy Sources 2005, 27, 1385–1396. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, J.; Tang, C.; Pan, W. Research and Application of Online Monitoring of Coal and Biomass Co-Combustion and Biomass Combustion Characteristics Based on Combustion Flame. J. Energy Inst. 2023, 108, 101191. [Google Scholar] [CrossRef]
- Kuznetsov, V.A.; Minakov, A.V.; Bozheeva, D.M.; Dekterev, A.A. International Journal of Greenhouse Gas Control Oxy-Fuel Combustion of Pulverized Coal in an Industrial Boiler with a Tangentially Fired Furnace. Int. J. Greenh. Gas Control 2023, 124, 103861. [Google Scholar] [CrossRef]
- Marangwanda, G.T.; Madyira, D.M.; Chihobo, C.H. Determination of Cocombustion Kinetic Parameters for Bituminous Coal and Pinus Sawdust Blends. ACS Omega 2022, 7, 32108–32118. [Google Scholar] [CrossRef] [PubMed]
- ANSYS. ANSYS FLUENT User’s Guide; ANSYS: Canonsburg, PA, USA, 2021; pp. 1–170. [Google Scholar]
- Yin, C.; Rosendahl, L.A.; Condra, T.J.; Kær, S.K. Use of Numerical Modeling in Design for Co-Firing Biomass in Wall-Fired Burners. Chem. Eng. Sci. 2004, 59, 3281–3292. [Google Scholar] [CrossRef]
- Al-Abbas, A.H.; Naser, J. Effect of Chemical Reaction Mechanisms and NOx Modeling on Air-Fired and Oxy-Fuel Combustion of Lignite in a 100-KW Furnace. Energy Fuels 2012, 26, 3329–3348. [Google Scholar] [CrossRef]
- Marangwanda, G.T.; Madyira, D.M.; Babarinde, T.O. Coal Combustion Models: An Overview. J. Phys. Conf. Ser. 2019, 1378, 032070. [Google Scholar] [CrossRef]
- Maisyarah, A.; Shiun, J.; Nasir, F.; Hashim, H. Ultimate and Proximate Analysis of Malaysia Pineapple Biomass from MD2 Cultivar for Biofuel Application. Chem. Eng. Trans. 2018, 63, 127–132. [Google Scholar] [CrossRef]
- Marangwanda, G.T.; Madyira, D.M. Experimental Investigation on the Effect of Blending Bituminous Coal with Pinus Sawdust on Combustion Performance Parameters. Heliyon 2024, 10, e27287. [Google Scholar] [CrossRef]
- Zou, C.; Cai, L.; Wu, D.; Liu, Y.; Liu, S.; Zheng, C. Ignition Behaviors of Pulverized Coal Particles in O2/N2 and O2/H2O Mixtures in a Drop Tube Furnace Using Flame Monitoring Techniques. Proc. Combust. Inst. 2015, 35, 3629–3636. [Google Scholar] [CrossRef]
- Liu, M.; Han, B.; Bai, J.; Ru, J.; Wang, X.; Xing, L.; Li, H.; Lv, S.; Gao, A.; Wang, Y.; et al. Investigation on the Synergistic Effects and Thermokinetic Analyses during Co-Combustion of Corn Stalk and Polyethylene Plastic: Effect of Heating Rate and Placement Method. Fuel 2025, 385, 134032. [Google Scholar] [CrossRef]
- Czajka, K.M.; Modliński, N.; Kisiela-Czajka, A.M.; Naidoo, R.; Peta, S.; Nyangwa, B. Volatile Matter Release from Coal at Different Heating Rates –Experimental Study and Kinetic Modelling. J. Anal. Appl. Pyrolysis 2019, 139, 282–290. [Google Scholar] [CrossRef]
- Mularski, J.; Lue, L.; Li, J. Development of a Numerical Method for the Rapid Prediction of Ignition Performance of Biomass Particles. Fuel 2023, 348, 128520. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method Approach; Prentice Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- de Souza-Santos, M.L. Solid Fuels Combustion and Gasification; CRC Press: Boca Raton, FL, USA, 2010; ISBN 9781420047509. [Google Scholar]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Potgieter, M.S.W.; Bester, C.R.; Bhamjee, M. Experimental and CFD Investigation of a Hybrid Solar Air Heater. Sol. Energy 2020, 195, 413–428. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag Coefficient and Terminal Velocity of Spherical and Nonspherical Particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, L.; Guo, L.; Qian, B.; Wang, Z.; Cen, K. Computational Modeling of Oxy-Coal Combustion with Intrinsic Heterogeneous Char Reaction Models. Fuel Process. Technol. 2017, 161, 169–181. [Google Scholar] [CrossRef]
- Graeser, P.; Schiemann, M. Investigations on the Emissivity of Burning Coal Char Particles: Influence of Particle Temperature and Composition of Reaction Atmosphere. Fuel 2020, 263, 116714. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, S.; Chen, C.; Wang, X.; ur Rahman, Z.; Tan, H. Kinetic Model Study on Biomass Pyrolysis and CFD Application by Using Pseudo-Bio-CPD Model. Fuel 2021, 293, 120266. [Google Scholar] [CrossRef]
- Mandø, M.; Rosendahl, L.A.; Yin, C.; Sørensen, H. Pulverized Straw Combustion in a Low-NOx Multifuel Burner: Modeling the Transition from Coal to Straw. Fuel 2010, 89, 3051–3062. [Google Scholar] [CrossRef]
- Turns, S. An Introduction to Combustion: Concepts and Applications, 2nd ed.; McGraw-Hill Series in Mechanical Engineering; McGraw-Hill: New York, NY, USA, 1996; ISBN 9780077418946. [Google Scholar]
- Tang, L.; Xiao, J.; Mao, Q.; Zhang, Z.; Yao, Z.; Zhu, X.; Ye, S.; Zhong, Q. Thermogravimetric Analysis of the Combustion Characteristics and Combustion Kinetics of Coals Subjected to Different Chemical Demineralization Processes. ACS Omega 2022, 7, 13998–14008. [Google Scholar] [CrossRef]
- Di Blasi, C. Modeling Chemical and Physical Processes of Wood and Biomass Pyrolysis. Prog. Energy Combust. Sci. 2008, 34, 47–90. [Google Scholar] [CrossRef]
- Sadhukhan, A.K.; Gupta, P.; Saha, R.K. Modeling and Experimental Investigations on the Pyrolysis of Large Coal Particles. Energy Fuels 2011, 25, 5573–5583. [Google Scholar] [CrossRef]
- Vyas, A.; Chellappa, T.; Goldfarb, J.L. Porosity Development and Reactivity Changes of Coal–Biomass Blends during Co-Pyrolysis at Various Temperatures. J. Anal. Appl. Pyrolysis 2017, 124, 79–88. [Google Scholar] [CrossRef]


| Description | Fuels | Method of Reporting on | |||
|---|---|---|---|---|---|
| Ignition | Burnout | Intensity | Stability | ||
| Combustion in a 150 kW reactor [18] | Coal and wheat straw | Temperatures | Char percentage | - | - |
| Lab-scale bubbling fluidised bed combustor [19] | Coal, lignite, spruce wood, wheat straw, and hazelnut shell | - | Unburnt carbon | - | - |
| Cocombustion in a 660 MW tangentially fired boiler [4] | Coal and sewage sludge | - | - | Heat flux | - |
| Experimental study on combustion with nitrogen [20] | Coal, poplar wood, and corn stalks | Temperature Radiation spectrum | - | - | Image processing |
| Cocombustion in a 500 MW boiler [21] | Coal slurry | Temperature | Species molar fractions | - | - |
| Constituent | %Weight | %Mol |
|---|---|---|
| C | ||
| H | ||
| O | ||
| N | ||
| S |
| Fuel Blend | Proximate Analysis on a Dry Basis | Volatile Molar Composition | Volatile Molar Mass | Enthalpy of Formation for Volatile (Hf,vol) |
|---|---|---|---|---|
| 100HC | 53.97FC, 23.10VM, 22.93Ash | C0.292H2.200O0.618N0.086S0.014 | 17.24 | −5.904 × 107 |
| 90HC10PS | 48.21FC, 29.91VM, 21.88Ash | C0.535H2.102O0.556N0.0646S0.0111 | 18.68 | −7.862 × 107 |
| 80HC20PS | 46.35FC, 31.82VM, 21.83Ash | C0.559H2.36O0.618N0.0585S0.011 | 20.11 | −9.819 × 107 |
| 70HC30PS | 46,02FC, 33.74VM, 20.24Ash | C0.579H2.615O0.683N0.052S0.011 | 21.55 | −1.178 × 108 |
| 100PS | 15.62FC, 80.68VM, 3.70Ash | C1.107H2.37O0.99N0.01 | 31.63 | −2.548 × 108 |
| Fuel Blend | Stage | Ea (kJ/mol) | A (s−1) |
|---|---|---|---|
| 100HC | Volatile combustion | 92.98 | 5.84 × 105 |
| Char combustion | 52.90 | 1.16 × 103 | |
| 90HC10PS | Volatile combustion | 107.89 | 5.05 × 106 |
| Char combustion | 68.99 | 2.78 × 104 | |
| 80HC20PS | Volatile combustion | 104.95 | 2.94 × 108 |
| Char combustion | 90.52 | 9.53 × 105 | |
| 70HC30PS | Volatile combustion | 106.05 | 2.72 × 109 |
| Char combustion | 103.85 | 6.12 × 107 |
| Physics | Model |
|---|---|
| Turbulence | RNG k-epsilon, scalable wall function |
| Radiation | Discrete ordinate model, P1 model weighted sum of grey gases model (WSGGM) |
| Particle distribution | 40 continuous-phase iterations per DPM iteration Rosin–Rammler diameter distribution |
| Inlets | Fuel velocity inlet as 1.85 m/s For a 30° modelled section, total fuel mass flow rate translated to 2.08 × 10−6 kg/s, primary carrier gas mass flow rate was 4.85 × 10−7 kg/s, and secondary carrier gas was 2.43 × 10−5 kg/s |
| Chemical rection | Species transport option, eddy dissipation concept |
| Ash | VM | FC | MC | C | H | N | S | Carbonates | O | HHV (MJ/kg) |
|---|---|---|---|---|---|---|---|---|---|---|
| 28.9 | 20.4 | 47.9 | 2.8 | 54.75 | 2.41 | 1.30 | 1.47 | 3.96 | 4.41 | 21.00 |
| Position | Designation | Residence Time at Various Furnace Wall Temperatures (s) | ||
|---|---|---|---|---|
| 1273 K | 1473 K | 1673 K | ||
| 520 mm | SA coal (Exp) | 1.3000 | 1.1000 | 1.0000 |
| SA coal (CFD) | 1.5217 | 1.2755 | 1.0826 | |
| 920 mm | SA coal (Exp) | 2.2000 | 1.9000 | 1.7000 |
| SA coal (CFD) | 3.3290 | 2.9557 | 2.5335 | |
| 1320 mm | SA coal (Exp) | 3.2000 | 2.8000 | 2.5000 |
| SA coal (CFD) | 4.7551 | 3.3035 | 2.9774 | |
| RSME | 1.1168 | 0.6828 | 0.5566 | |
| Position | Designation | Particle Temperature (K) | ||
|---|---|---|---|---|
| 1273 K | 1473 K | 1673 K | ||
| 520 mm | SA coal (Exp) | 1248.00 | 1459.82 | 1676.80 |
| SA coal (CFD) | 939.61 | 1048.27 | 1289.18 | |
| 920 mm | SA coal (Exp) | 1191.80 | 1411.48 | 1633.88 |
| SA coal (CFD) | 997.21 | 1145.57 | 1519.20 | |
| 1320 mm | SA coal (Exp) | 1042.74 | 1276.33 | 1511.19 |
| SA coal (CFD) | 970.60 | 1140.55 | 1583.59 | |
| RSME | 0.1759 | 0.2052 | 0.1422 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marangwanda, G.T.; Madyira, D.M. Evaluating Combustion Ignition, Burnout, Stability, and Intensity of Coal–Biomass Blends Within a Drop Tube Furnace Through Modelling. Energies 2025, 18, 1322. https://doi.org/10.3390/en18061322
Marangwanda GT, Madyira DM. Evaluating Combustion Ignition, Burnout, Stability, and Intensity of Coal–Biomass Blends Within a Drop Tube Furnace Through Modelling. Energies. 2025; 18(6):1322. https://doi.org/10.3390/en18061322
Chicago/Turabian StyleMarangwanda, Garikai T., and Daniel M. Madyira. 2025. "Evaluating Combustion Ignition, Burnout, Stability, and Intensity of Coal–Biomass Blends Within a Drop Tube Furnace Through Modelling" Energies 18, no. 6: 1322. https://doi.org/10.3390/en18061322
APA StyleMarangwanda, G. T., & Madyira, D. M. (2025). Evaluating Combustion Ignition, Burnout, Stability, and Intensity of Coal–Biomass Blends Within a Drop Tube Furnace Through Modelling. Energies, 18(6), 1322. https://doi.org/10.3390/en18061322






