Advances in Numerical Modeling for Heat Transfer and Thermal Management: A Review of Computational Approaches and Environmental Impacts
Abstract
1. Introduction
2. Overview of Numerical Modeling Techniques in Heat Transfer
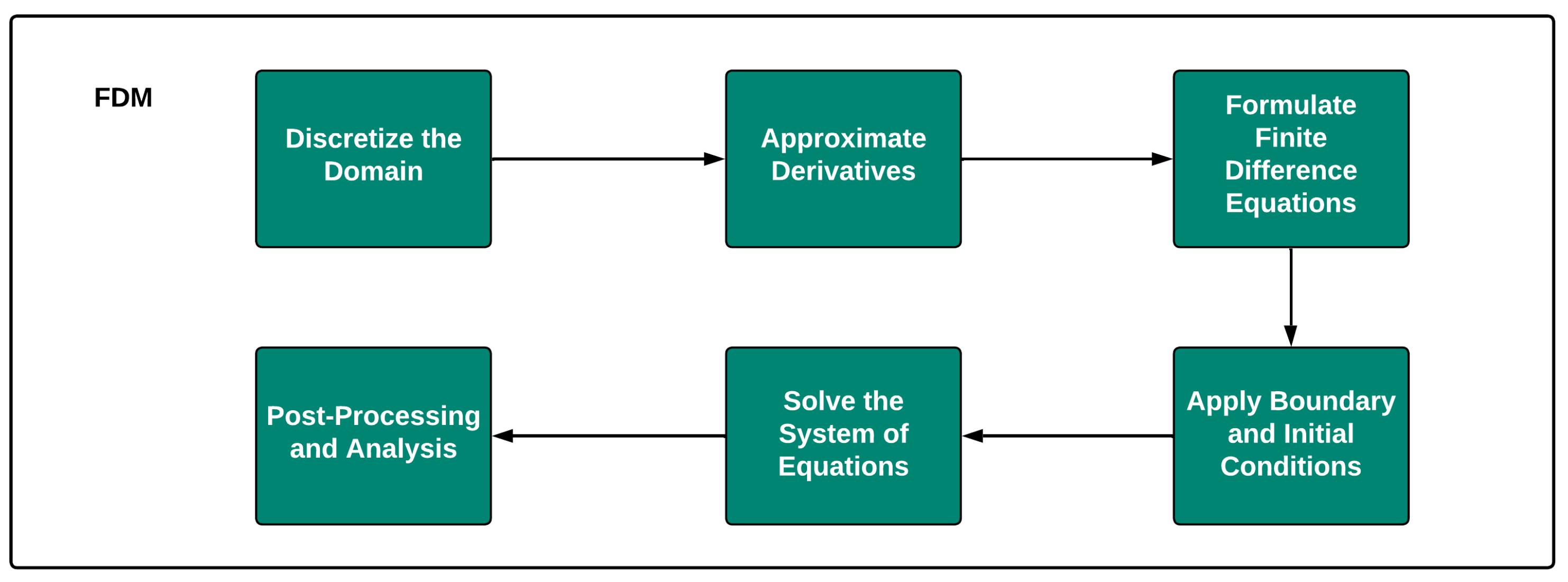
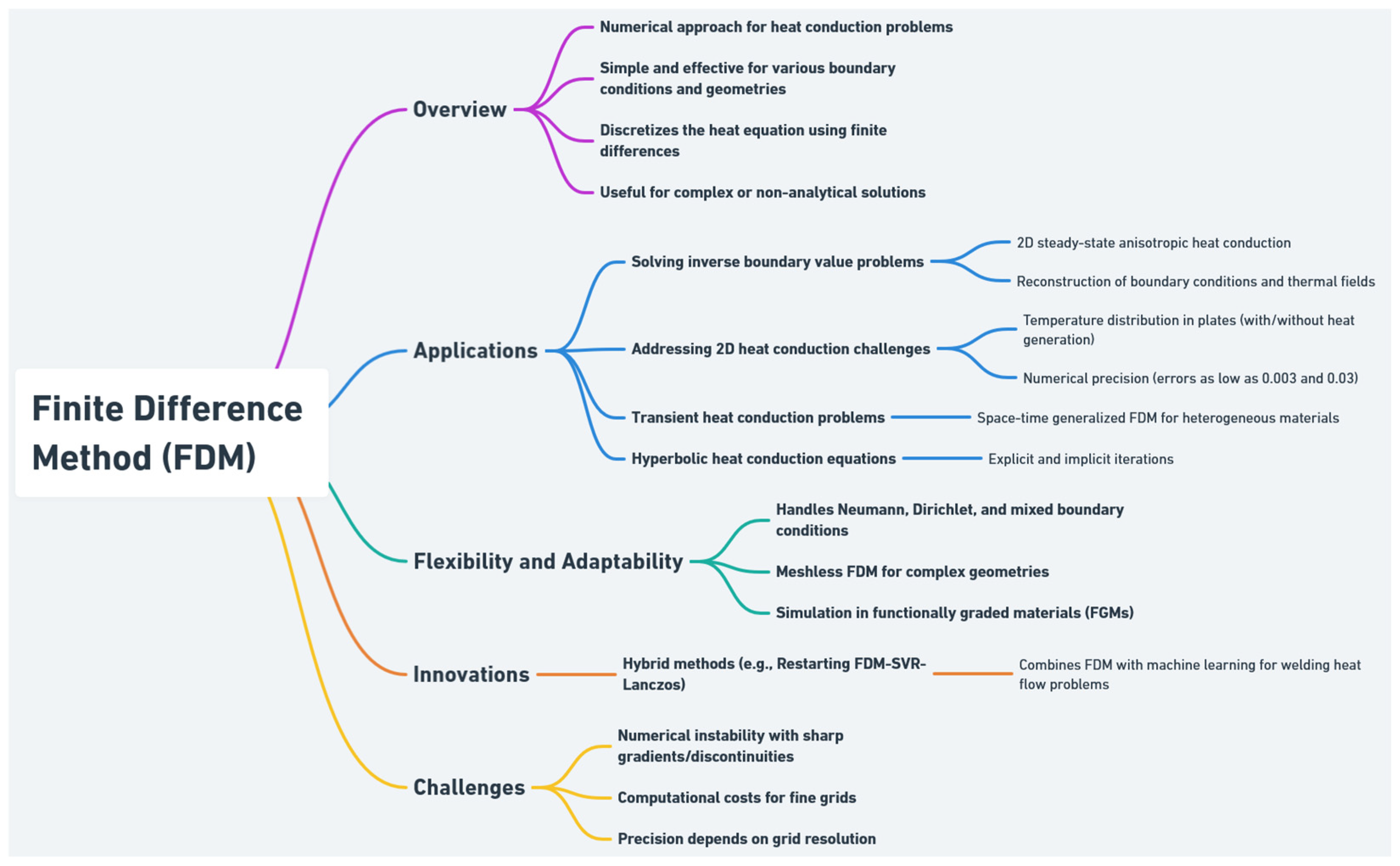
2.1. Finite-Difference Method (FDM)
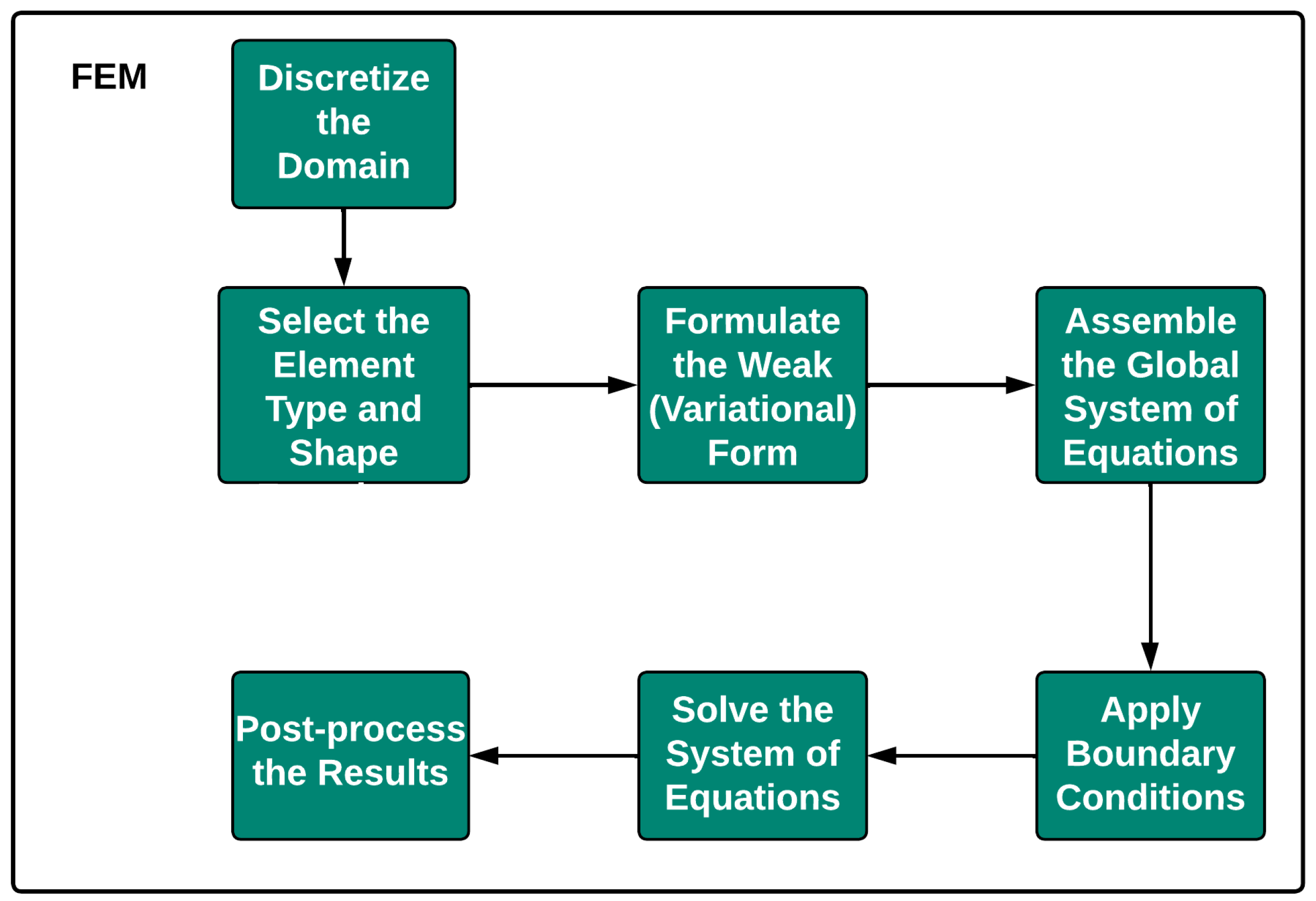
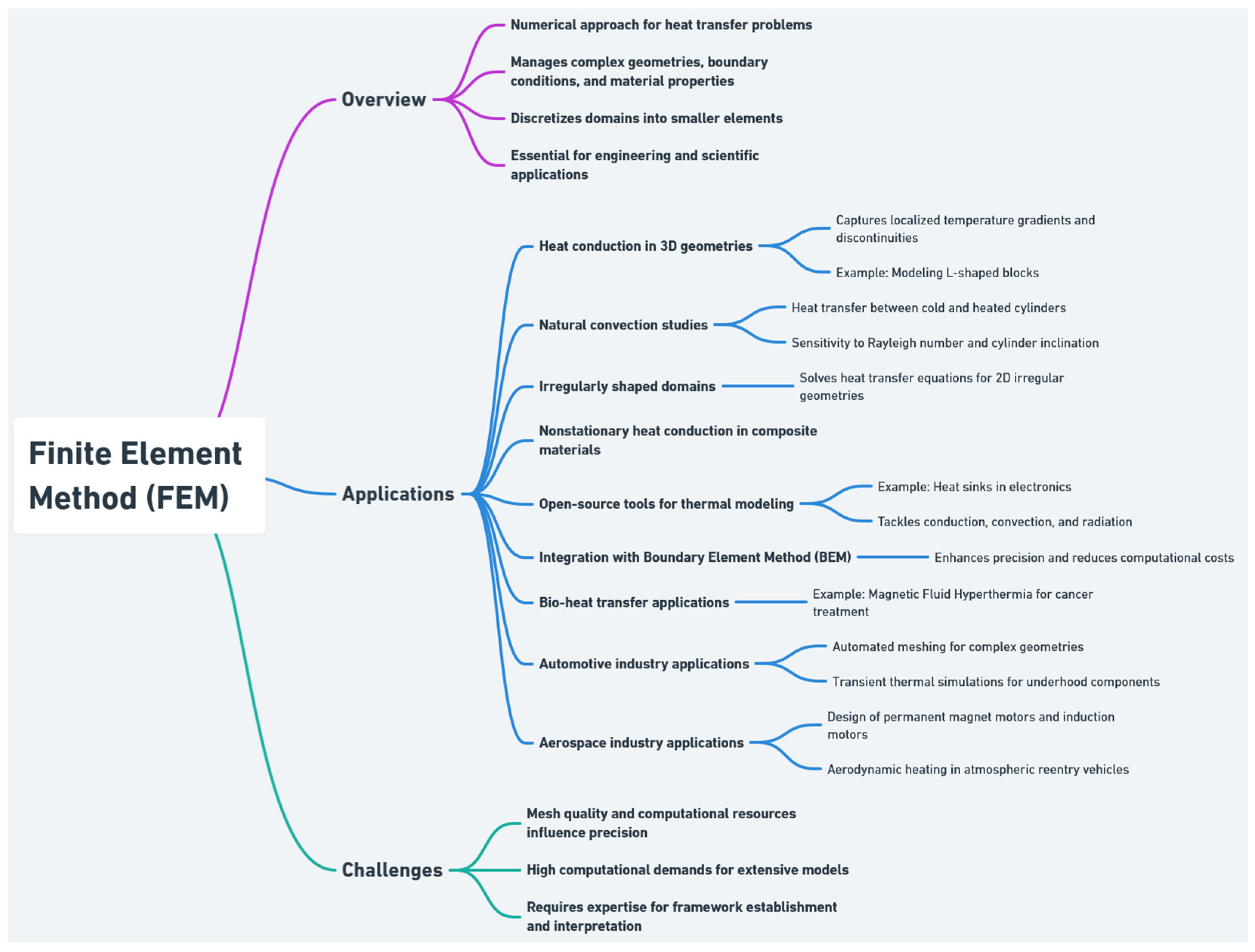
2.2. Finite Element Method (FEM)
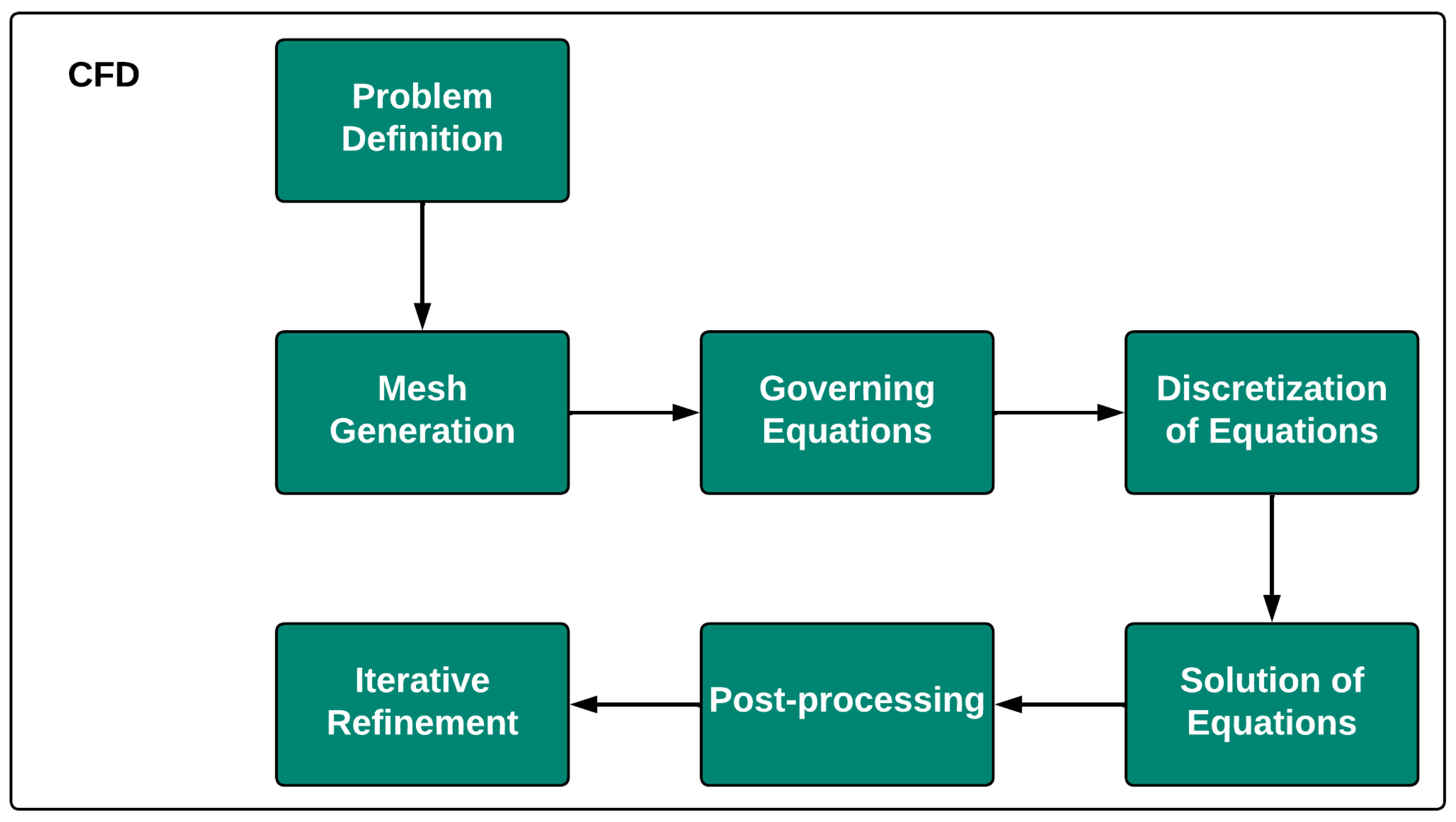
2.3. Computational Fluid Dynamics (CFD)
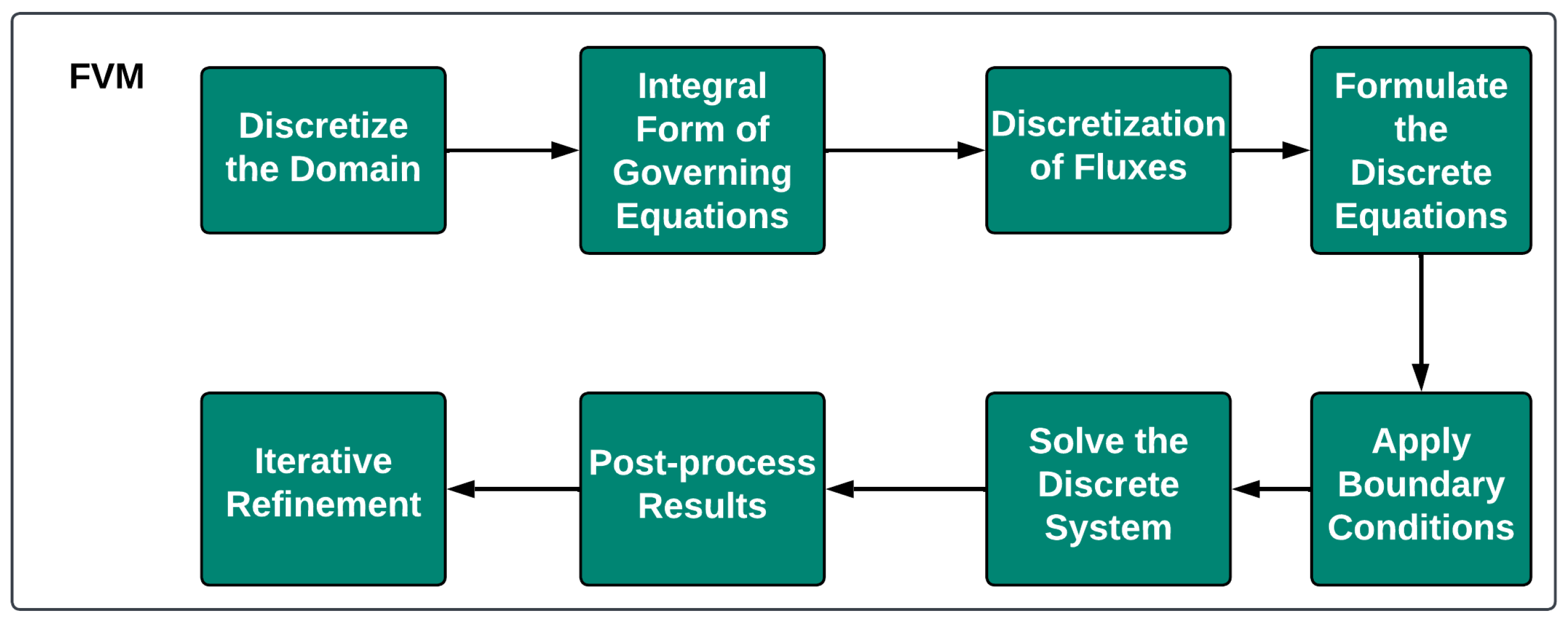
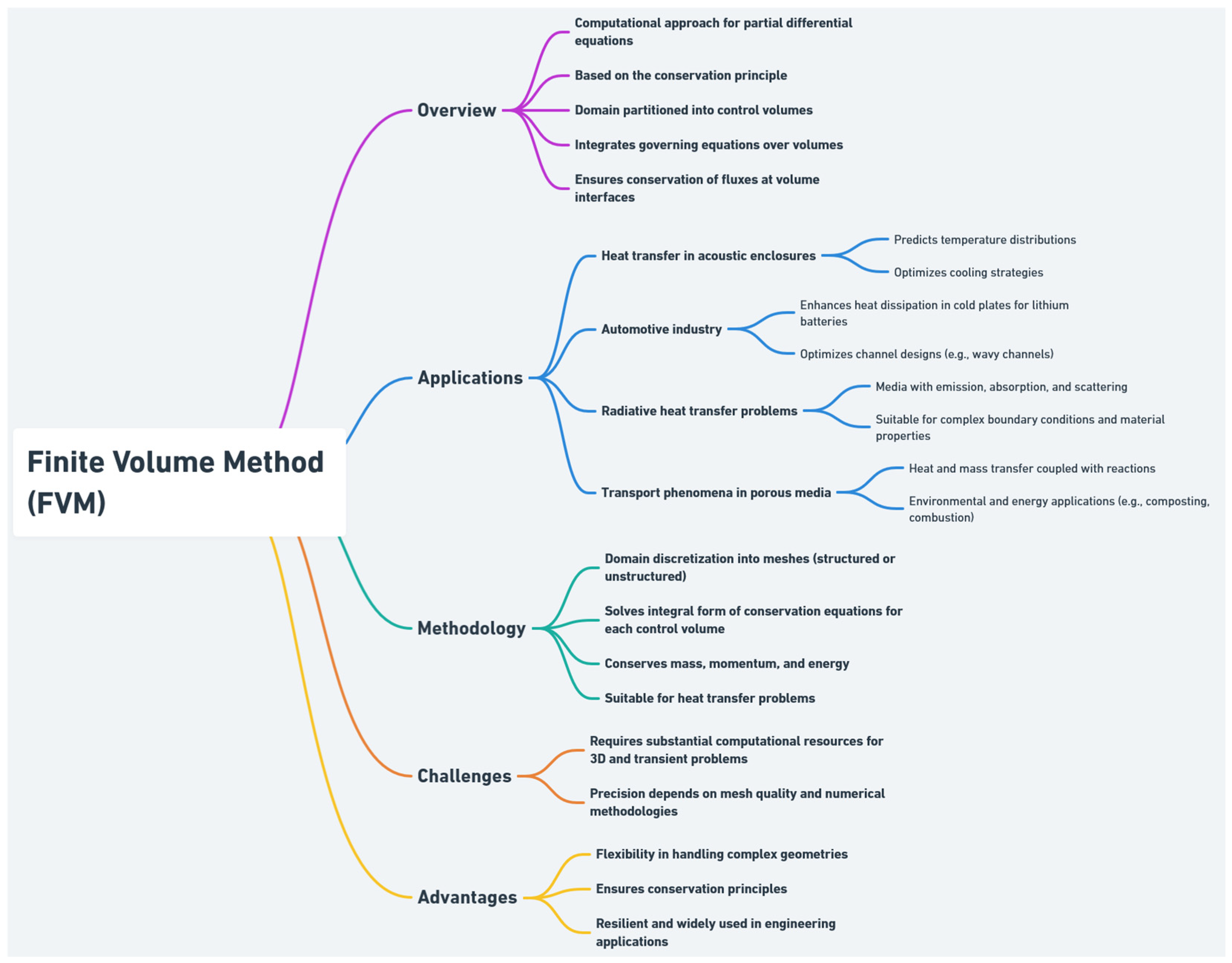
2.4. Finite Volume Method (FVM)
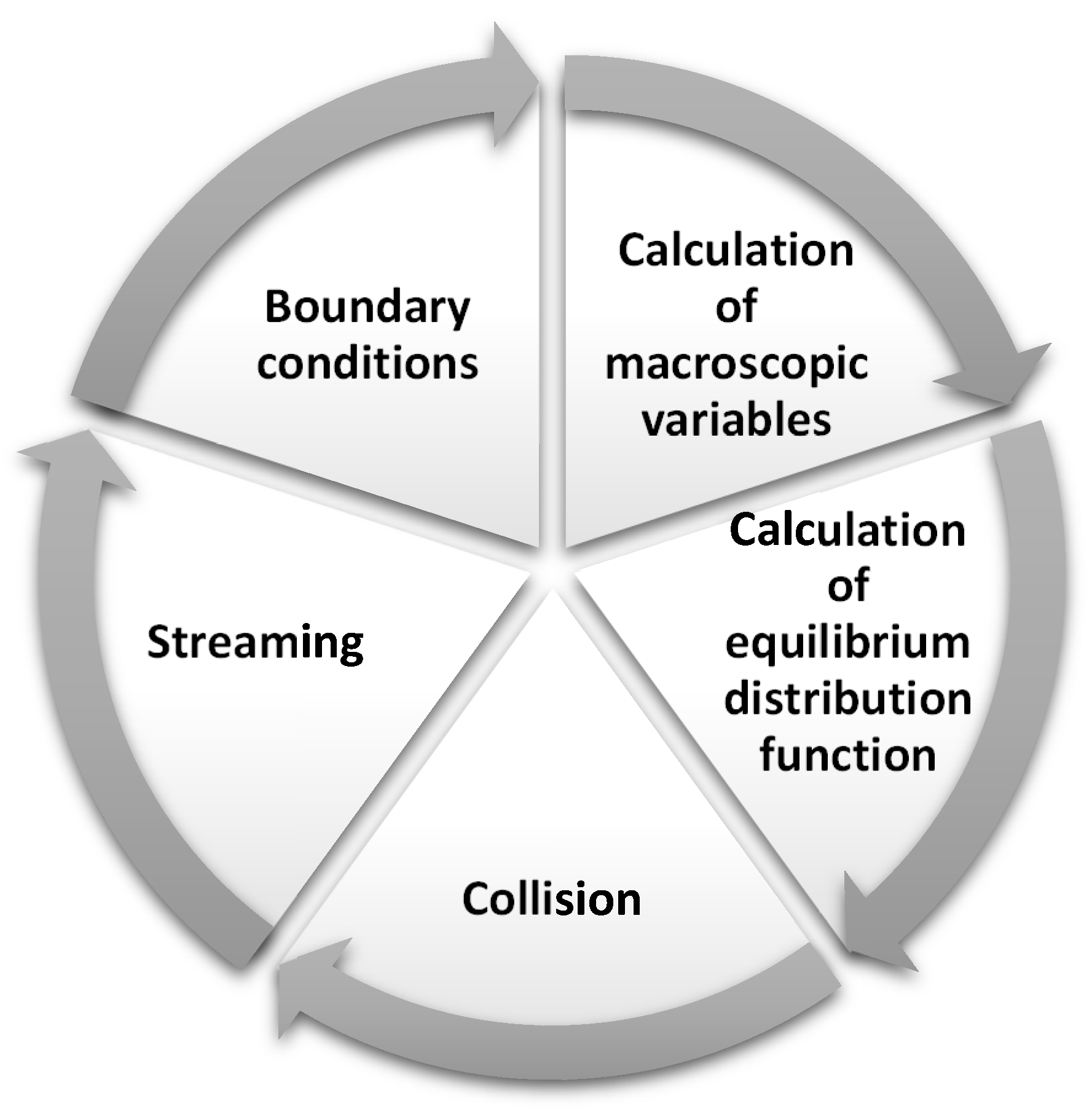
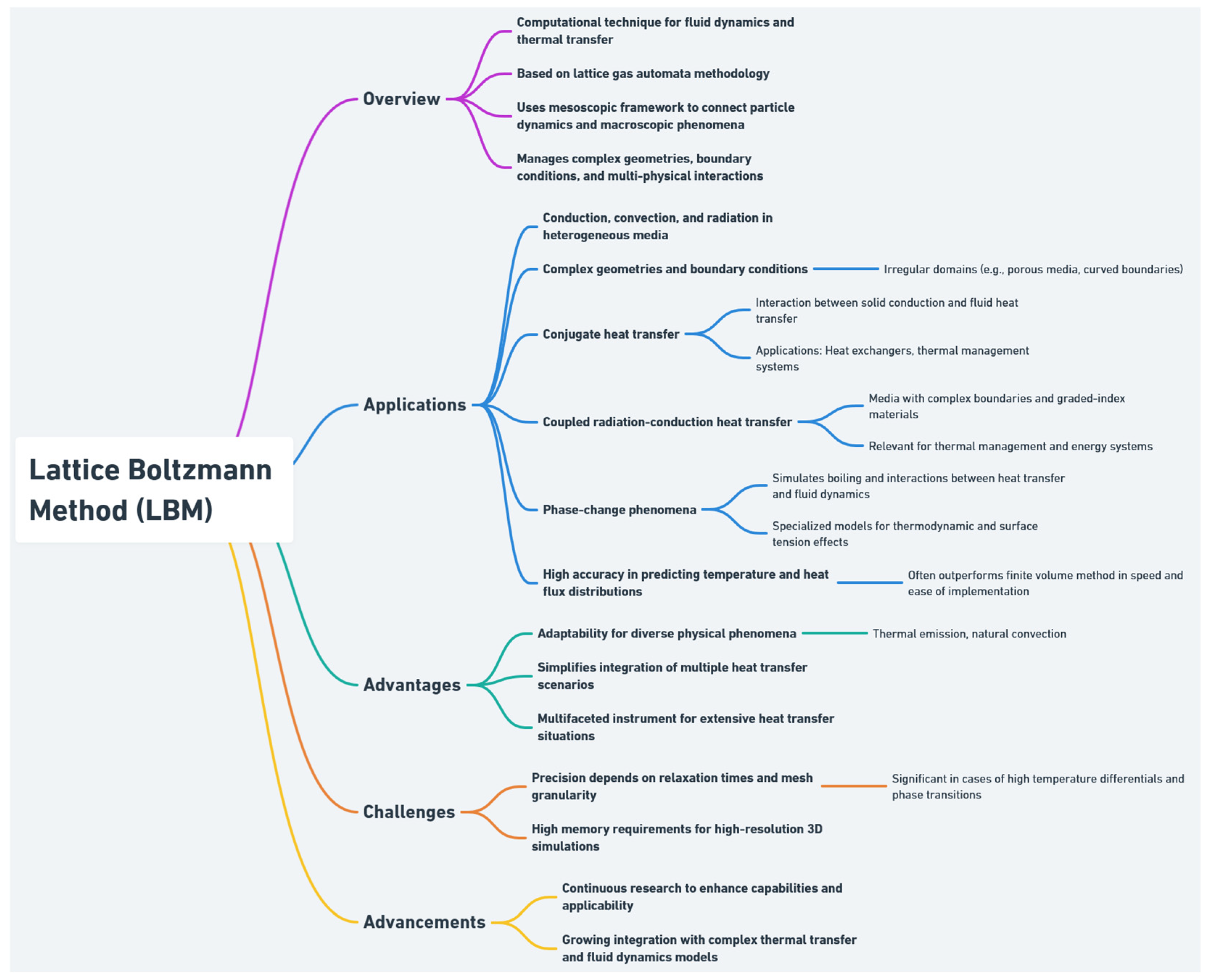
2.5. Lattice Boltzmann Method (LBM)
- Calculation of macroscopic variables such as density (ρ), velocity (u), temperature (T), concentration (C), and others.
- Evaluation of the equilibrium distribution function feq for the modeled variables.
- Collision operation, which involves the determination of the output distribution function fout.
- Streaming operation, which transfers the distribution function to the appropriate cells, sites, or nodes.
- Application of boundary conditions.
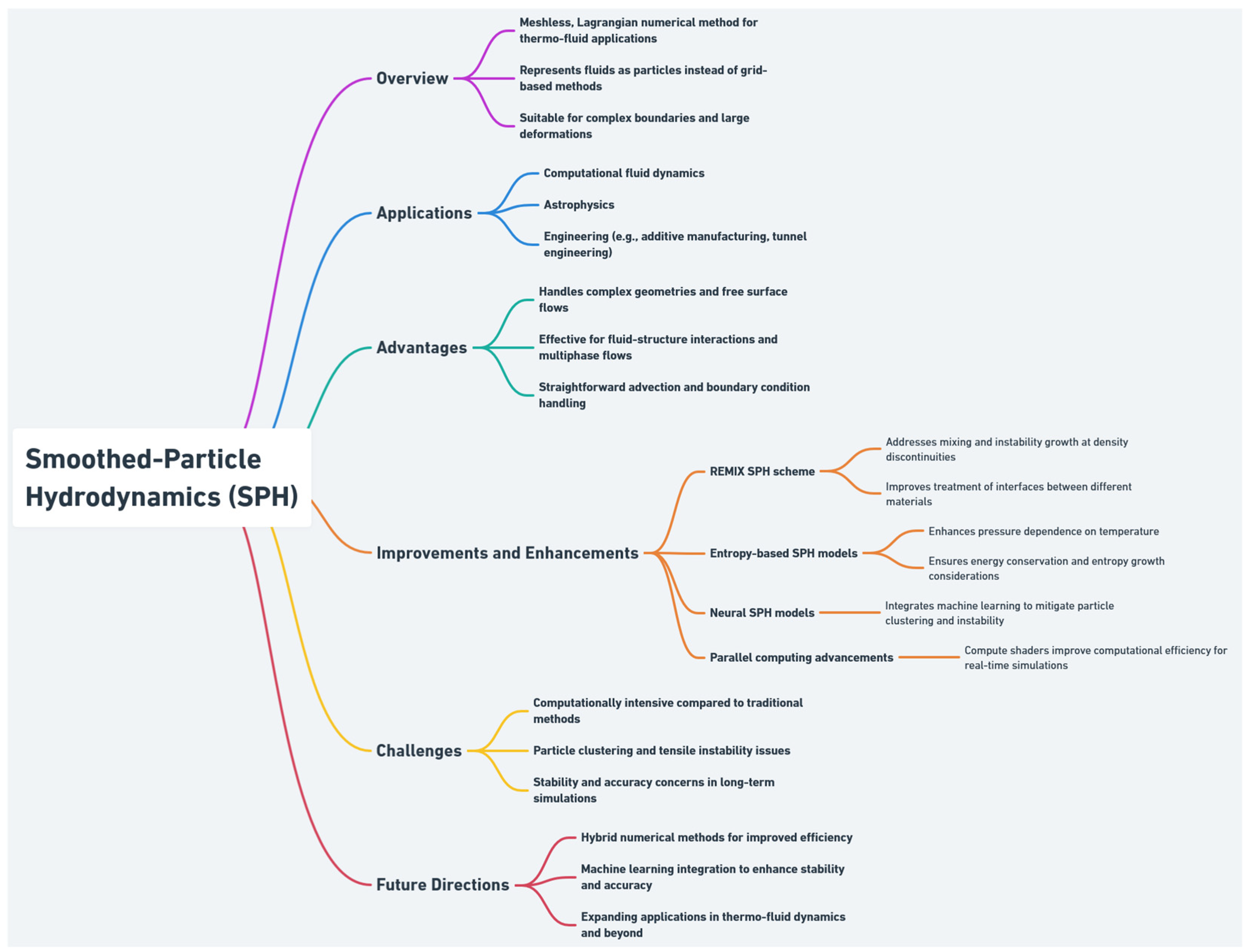
2.6. Smoothed-Particle Hydrodynamics (SPH)
3. Recent Advances in Computational Approaches for Heat Transfer
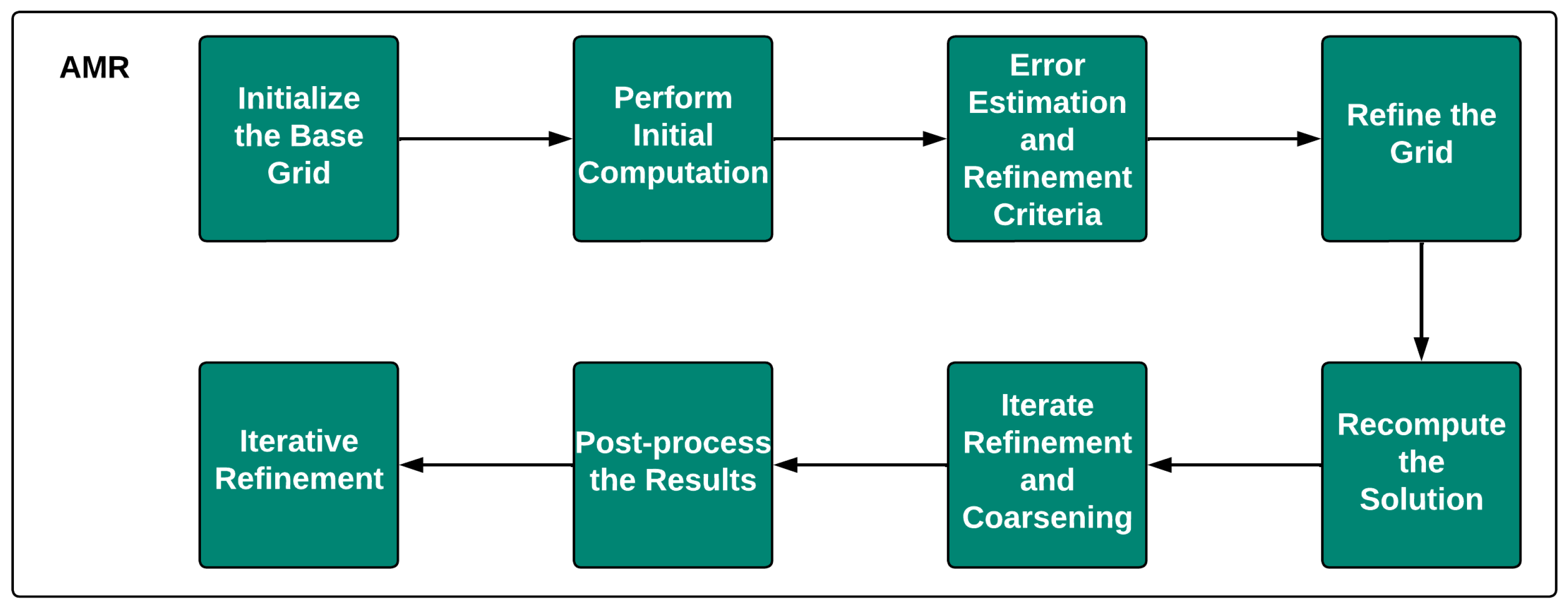
3.1. Adaptive Mesh Refinement (AMR)
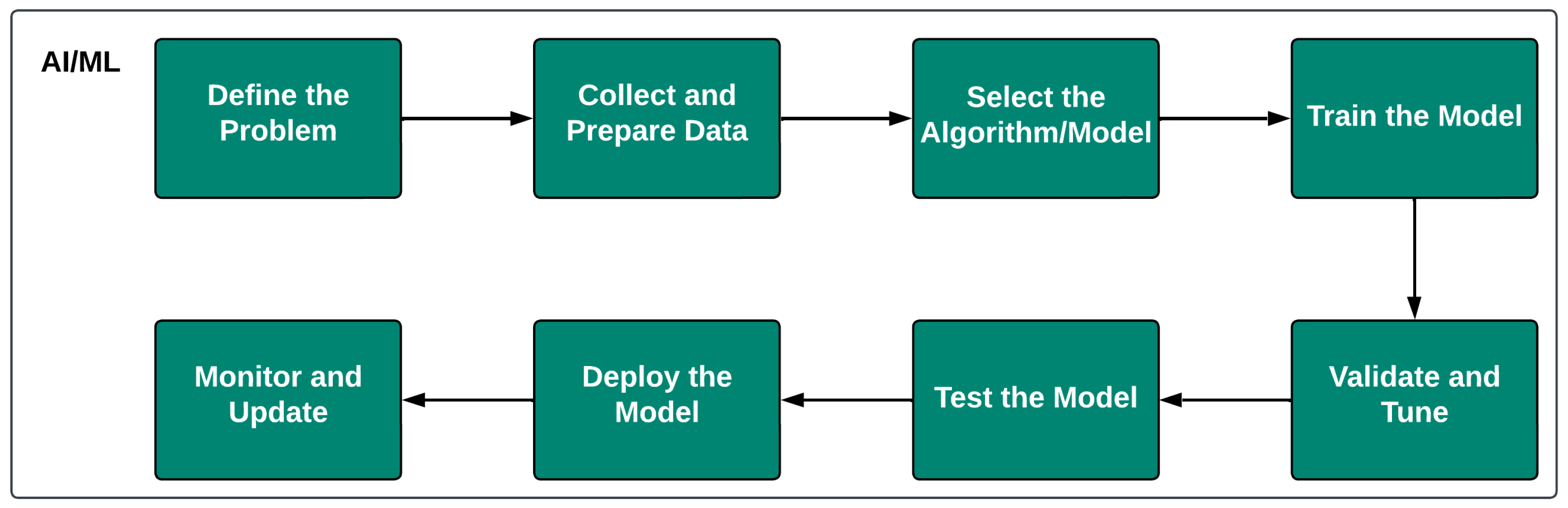
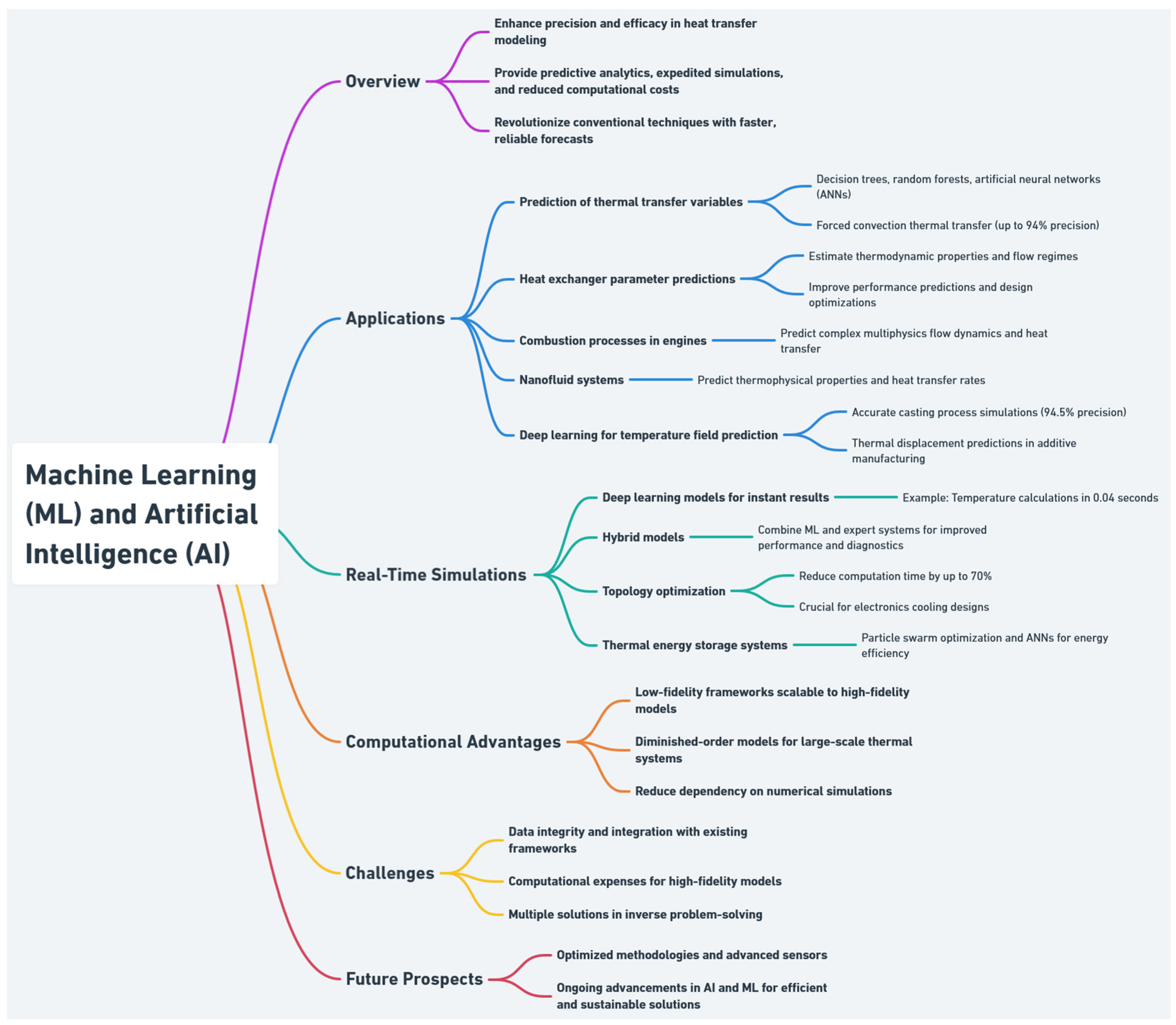
3.2. Artificial Intelligence and Machine Learning (AI/ML)
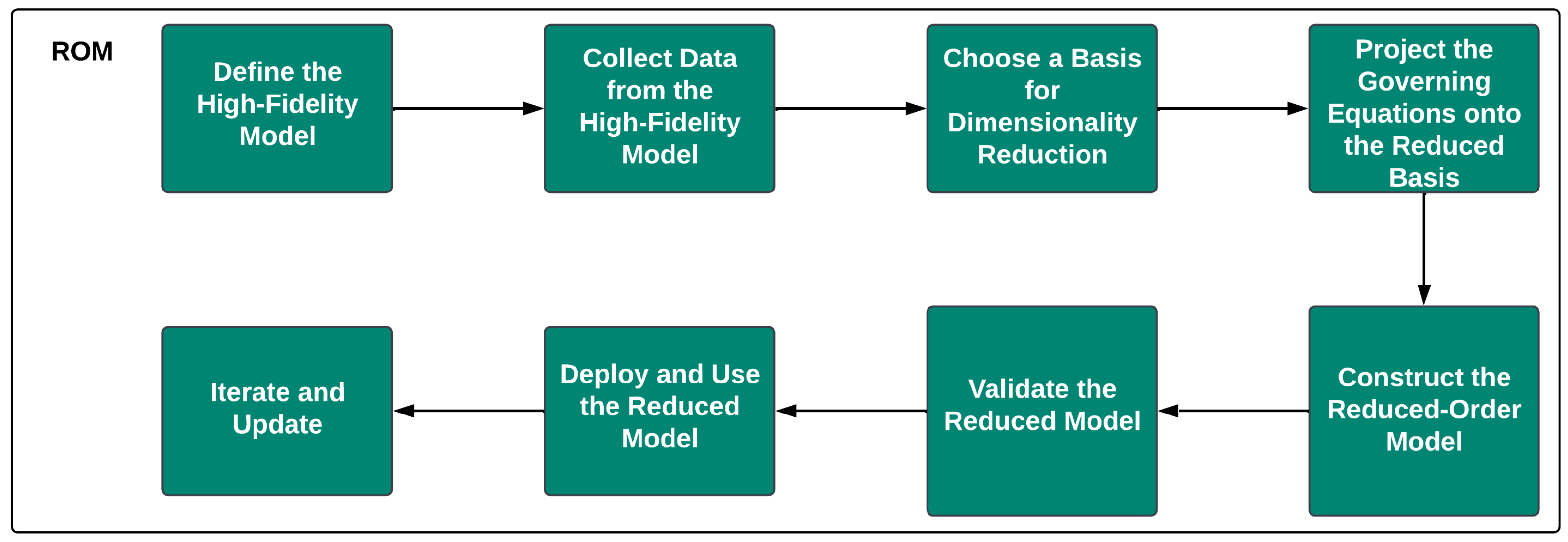
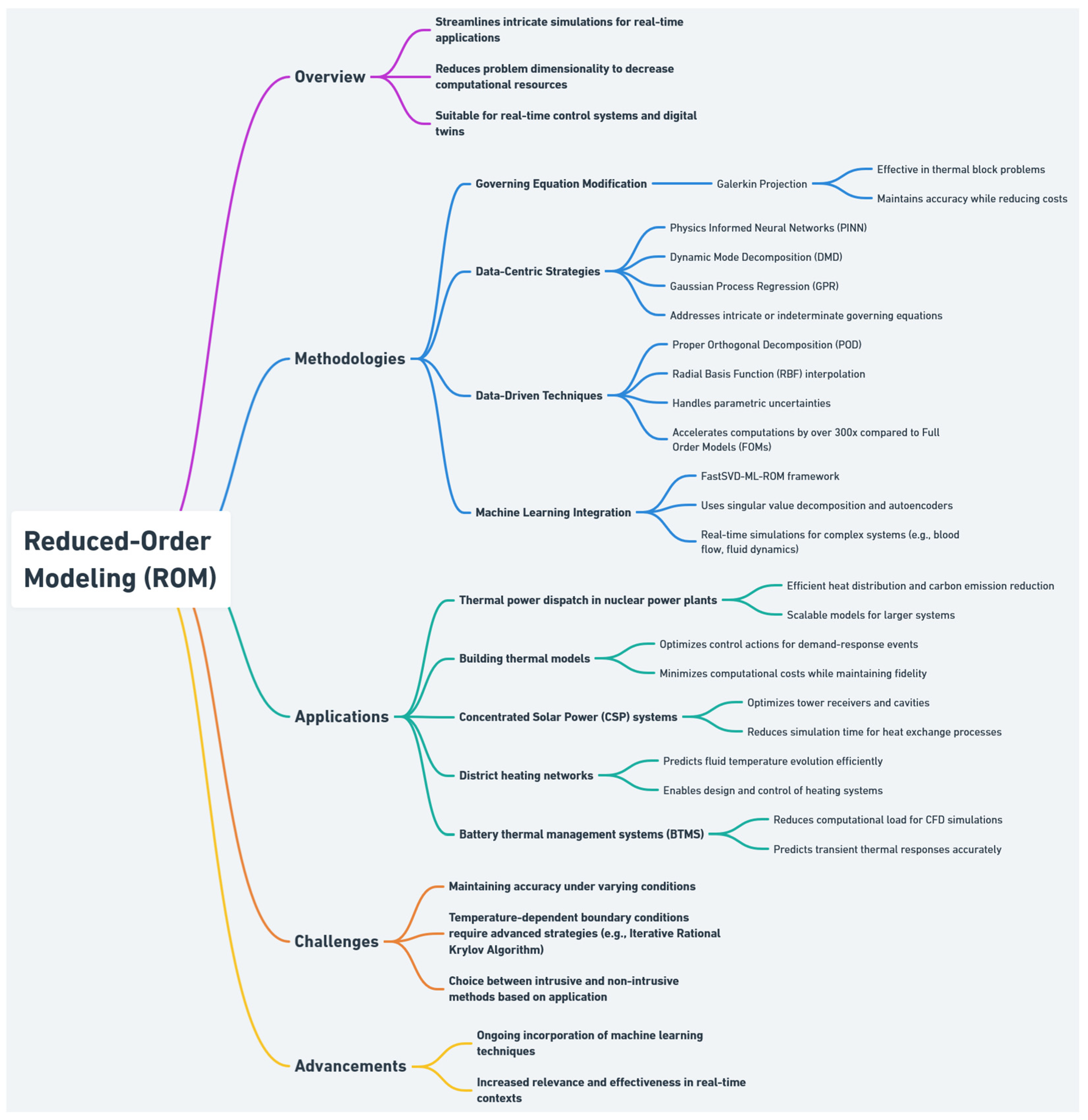
3.3. Reduced-Order Modeling (ROM)
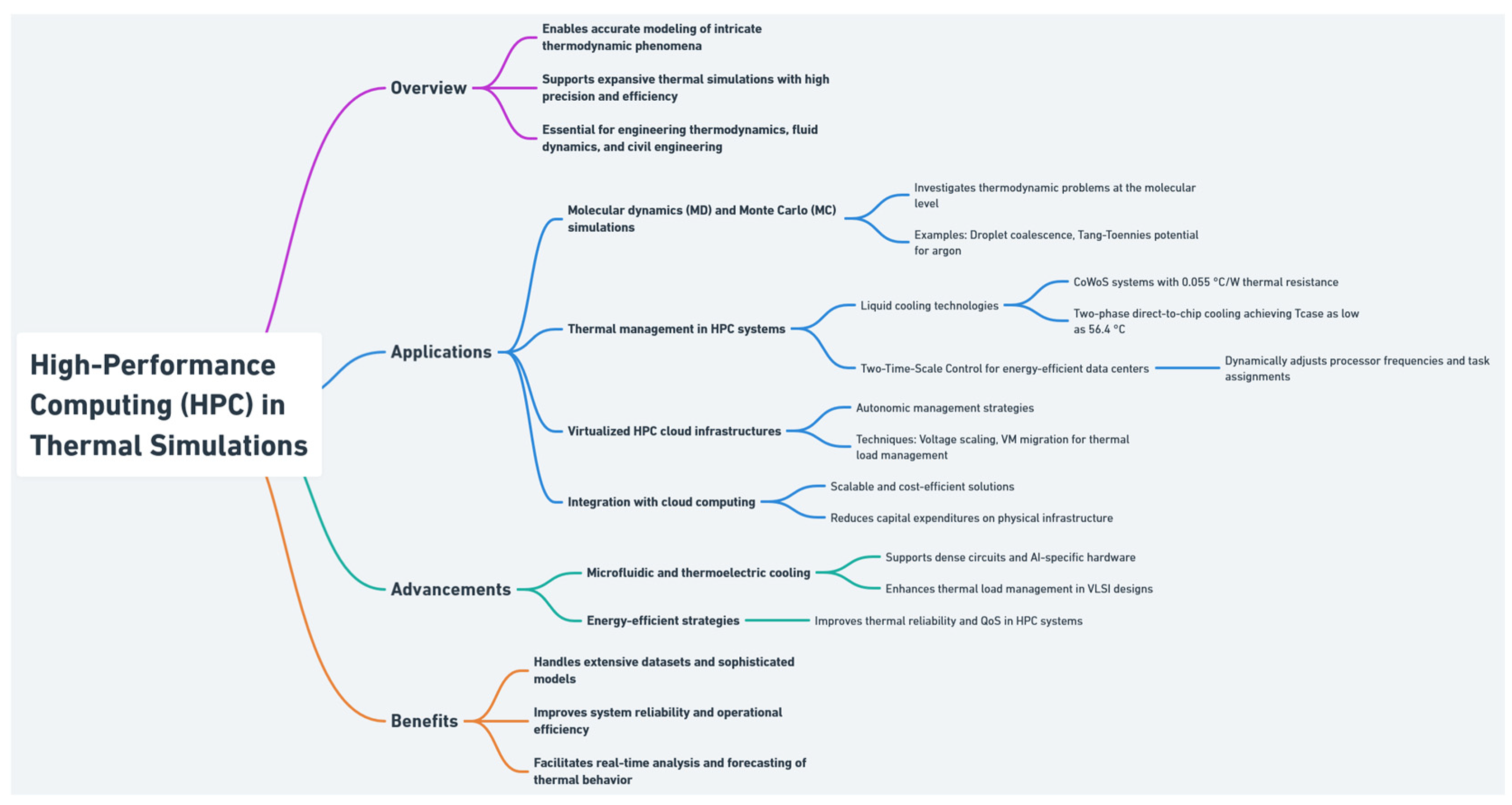
3.4. High-Performance Computing (HPC)
4. Applications of Numerical Modeling in Thermal Management
4.1. Electronics Cooling
4.2. Energy Systems
4.3. Automotive and Aerospace
4.4. Industrial Processes
4.5. Healthcare and Biomedical Applications
5. Environmental Impacts of Computational Modeling for Heat Transfer
5.1. Energy and Resource Demands
5.2. Environmental Benefits Through Optimization
5.3. Sustainability and Lifecycle Assessment
5.4. Challenges and Future Needs in Green Computing
6. Challenges in Numerical Modeling for Heat Transfer
- -
- Partitioned (or loosely coupled) approaches: These solve the fluid and structural equations separately, iteratively exchanging boundary conditions. Although offering flexibility, they require robust interpolation schemes to transfer data such as pressure, displacement, and thermal loads between solvers [262].
- -
- Monolithic (or strongly coupled) approaches: These solve fluid and structural equations simultaneously within a unified framework, enhancing stability but increasing computational complexity [263].
- -
- Sharp-interface methods: Techniques such as Front Tracking and Level-Set Methods explicitly track phase boundaries, providing precise interface representation but often requiring fine spatial resolution, which increases computational demands [266].
- -
- Diffuse-interface methods: Approaches such as the Volume of Fluid (VOF) and Phase-Field Models represent interfaces over a finite thickness, allowing for more robust simulations on coarser grids but potentially introducing numerical diffusion [267].
7. Future Directions and Emerging Trends
7.1. Quantum Computing for Thermal Simulations
7.2. Real-Time Adaptive Models
7.3. Green Computing and Sustainable Numerical Modeling
7.4. Open-Source and Collaborative Platforms
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sidebotham, G. Heat Transfer Modes: Conduction, Convection, and Radiation. In Heat Transfer Modeling; Springer: Cham, Switzerland, 2015; pp. 61–93. ISBN 978-3-319-14514-3. [Google Scholar]
- Jaluria, Y. Challenges in the accurate numerical simulation of practical thermal processes and systems. Int. J. Numer. Methods Heat Fluid Flow 2013, 23, 158–175. [Google Scholar] [CrossRef]
- Chharia, A.; Mehta, N.; Gupta, S.; Prajapati, S. Recent Trends in Artificial Intelligence-Inspired Electronic Thermal management—A Review. In Recent Advances in Thermal Sciences and Engineering; Springer: Singapore, 2023; pp. 165–175. ISBN 978-981-19-7214-0. [Google Scholar]
- Potgieter, J.; Lombaard, L.; Hannay, J.; Moghimi, M.A.; Valluri, P.; Meyer, J.P. Adaptive mesh refinement method for the reduction of computational costs while simulating slug flow. Int. Commun. Heat Mass Transf. 2021, 129, 105702. [Google Scholar] [CrossRef]
- Ren, Y. Optimizing Predictive Maintenance With Machine Learning for Reliability Improvement, ASME. ASME J. Risk Uncertain. Part B 2021, 7, 030801. [Google Scholar] [CrossRef]
- Aguado, J.V.; Huerta, A.; Chinesta, F.; Cueto, E. Real-time monitoring of thermal processes by reduced-order modeling. Int. J. Numer. Methods Eng. 2015, 102, 991–1017. [Google Scholar] [CrossRef]
- Bode, M.; Göbbert, J.H. Acceleration of complex high-performance computing ensemble simulations with super-resolution-based subfilter models. Comput. Fluids 2024, 271, 106150. [Google Scholar] [CrossRef]
- Ni, K.; Hu, Y.; Ye, X.; AlZubi, H.S.; Goddard, P.; Alkahtani, M. Carbon Footprint Modeling of a Clinical Lab. Energies 2018, 11, 3105. [Google Scholar] [CrossRef]
- Jain, A.; Patel, H.; Nagalapatti, L.; Gupta, N.; Mehta, S.; Guttula, S.; Mujumdar, S.; Afzal, S.; Sharma Mittal, R.; Munigala, V. Overview and Importance of Data Quality for Machine Learning Tasks. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Association for Computing Machinery, Virtual, 6–10 July 2020; pp. 3561–3562. [Google Scholar]
- Paudel, H.P.; Syamlal, M.; Crawford, S.E.; Lee, Y.-L.; Shugayev, R.A.; Lu, P.; Ohodnicki, P.R.; Mollot, D.; Duan, Y. Quantum Computing and Simulations for Energy Applications: Review and Perspective. ACS Eng. Au 2022, 2, 151–196. [Google Scholar] [CrossRef]
- Jaksch, D.; Givi, P.; Daley, A.J.; Rung, T. Variational Quantum Algorithms for Computational Fluid Dynamics. AIAA J. 2023, 61, 1885–1894. [Google Scholar] [CrossRef]
- Paul, S.G.; Saha, A.; Arefin, M.S.; Bhuiyan, T.; Biswas, A.A.; Reza, A.W.; Alotaibi, N.M.; Alyami, S.A.; Moni, M.A. A Comprehensive Review of Green Computing: Past, Present, and Future Research. IEEE Access 2023, 11, 87445–87494. [Google Scholar] [CrossRef]
- Abidin, M.N.Z.; Misro, M.Y. Numerical Simulation of Heat Transfer using Finite Element Method. J. Adv. Res. Fluid Mech. Therm. Sci. 2022, 92, 104–115. [Google Scholar] [CrossRef]
- Sharma, R.; Jadon, V.K.; Singh, B. A Review on the Finite Element Methods for Heat Conduction in Functionally Graded Materials. J. Inst. Eng. Ser. C 2015, 96, 73–81. [Google Scholar] [CrossRef]
- Padagannavar, P. Computational Engineering of Finite Element Modelling for Automotive Application Using Abaqus. Int. J. Adv. Res. Eng. Technol. 2016, 7, 30–52. [Google Scholar]
- Nurhaniza, M.; Ariffin, M.; Ali, A.; Mustapha, F.; Noraini, A.W. Finite element analysis of composites materials for aerospace applications. IOP Conf. Ser. Mater. Sci. Eng. 2010, 11, 012010. [Google Scholar] [CrossRef]
- Loustau, J. Numerical Differential Equations: Theory and Technique, ODE Methods, Finite Differences, Finite Elements and Collocation; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2016; ISBN 9789814719506. [Google Scholar]
- Mazumder, S. Numerical Methods for Partial Differential Equations: Finite Difference and Finite Volume Methods; Elsevier: Amsterdam, The Netherlands, 2015; ISBN 9780128498941. [Google Scholar]
- Necati Özişik, M.; Orlande, H.R.B.; Colaço, M.J.; Cotta, R.M. Finite Difference Methods in Heat Transfer, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781482243468. [Google Scholar]
- Bucataru, M.; Marin, L. FDM-based alternating iterative algorithms for inverse BVPs in 2D steady-state anisotropic heat conduction with heat sources. J. Comput. Appl. Math. 2024, 451, 116051. [Google Scholar] [CrossRef]
- de Brito dos Santos, V.G.; dos Anjos, P.T.G. Finite Difference Method Applied in Two-Dimensional Heat Conduction Problem in the Permanent Regime in Rectangular Coordinates. Adv. Pure Math. 2022, 12, 505–518. [Google Scholar] [CrossRef]
- Lei, J.; Wang, Q.; Liu, X.; Gu, Y.; Fan, C.M. A novel space-time generalized FDM for transient heat conduction problems. Eng. Anal. Bound. Elem. 2020, 119, 1–12. [Google Scholar] [CrossRef]
- Majchrzak, E.; Mendakiewicz, J. Application of FDM for numerical solution of hyperbolic heat conduction equation. Pr. Nauk. Inst. Mat. Inform. Politech. Częstochowskiej 2006, 5, 134–139. [Google Scholar]
- Varanasi, C.; Murthy, J.Y.; Mathur, S. A meshless finite difference method for conjugate heat conduction problems. J. Heat Transfer 2010, 132, 081303. [Google Scholar] [CrossRef]
- Azis, M.I.; Toaha, S.; Hamzah, S.; Solekhudin, I. A numerical investigation of 2D transient heat conduction problems in anisotropic FGMs with time-dependent conductivity. J. Comput. Sci. 2023, 73, 102122. [Google Scholar] [CrossRef]
- Szlachetka, O.; Giorgio, I. Heat conduction in multi-component step-wise FGMs. Contin. Mech. Thermodyn. 2024, 36, 1393–1411. [Google Scholar] [CrossRef]
- Bensafi, M.; Draoui, B.; Menni, Y.; Ameur, H. A Thermal Conduction Comparative Study Between the FDM and SPH Methods with A Proposed C++ Home Code. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 78, 137–145. [Google Scholar] [CrossRef]
- Thalib, R.; Bakar, M.A. Simulation of heat flow in welding using hybrid restarting FDM-SVR-Lanczos. In Proceedings of the AIP Conference Proceedings, Kuala Terengganu, Malaysia, 21 June 2021; American Institute of Physics Inc.: College Park, MD, USA, 2023; Volume 2484. [Google Scholar]
- Kovács, E. A class of new stable, explicit methods to solve the non-stationary heat equation. Numer. Methods Partial Differ. Equ. 2021, 37, 2469–2489. [Google Scholar] [CrossRef]
- Nagy, Á.; Bodnár, I.; Kovács, E. Simulation of the Thermal Behavior of a Photovoltaic Solar Panel Using Recent Explicit Numerical Methods. Adv. Theory Simul. 2024, 7, 2400089. [Google Scholar] [CrossRef]
- Jalghaf, H.K.; Omle, I.; Kovács, E. A Comparative Study of Explicit and Stable Time Integration Schemes for Heat Conduction in an Insulated Wall. Buildings 2022, 12, 824. [Google Scholar] [CrossRef]
- Rao, S.S. The Finite Element Method in Engineering, 5th ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2010; ISBN 9781856176613. [Google Scholar]
- Pepper, D.W.; Heinrich, J.C. The Finite Element Method: Basic Concepts and Applications with MATLAB®, MAPLE, and COMSOL; Taylor and Francis: Abingdon, UK, 2017; ISBN 9781315395098. [Google Scholar]
- Wen, Q. Finite element solution of heat conduction in complex 3D geometries. Appl. Comput. Eng. 2024, 78, 115–122. [Google Scholar] [CrossRef]
- Daiz, A.; Hidki, R.; Fares, R.; Charqui, Z. Finite element method (FEM) analysis of heat transfer by natural convection in a circular cavity containing a corrugated hollow cylinder. Int. J. Numer. Methods Heat Fluid Flow 2024, 34, 4159–4178. [Google Scholar] [CrossRef]
- Ikramov, A.; Polatov, A.; Pulatov, S.; Zhumaniyozov, S. Computer Simulation of Two-Dimensional Nonstationary Problems of Heat Conduction for Composite Materials Using the FEM. In Proceedings of the AIP Conference Proceedings, Samarkand, Uzbekistan, 27–29 October 2021; American Institute of Physics Inc.: College Park, MD, USA, 2022; Volume 2637. [Google Scholar]
- Gil, F.J.R.; Delgado-Mejía, Á.; Foronda-Obando, E.; Olmos-Villalba, L.C. Thermal finite element analysis of complex heat sinks using open source tools and high-performance computing. Rev. Fac. Ing. 2022, 106, 124–133. [Google Scholar] [CrossRef]
- Qin, F.; He, Q.; Gong, Y.; An, T.; Chen, P.; Dai, Y. The application of FEM-BEM coupling method for steady 2D heat transfer problems with multi-scale structure. Eng. Anal. Bound. Elem. 2022, 137, 78–90. [Google Scholar] [CrossRef]
- Irawati, F.D.; Kartono, A. Numerical FEM Models of Bio-heat Transfer for Magnetic Fluid Hyperthermia Treatments. J. Multidiscip. Acad. 2021, 5, 41–47. [Google Scholar]
- Dawes, W.N.; Kellar, W.; Harvey, S.; Eccles, N. Automated Meshing for Aero-Thermal Analysis of Complex Automotive Geometries. In Proceedings of the SAE 2011 World Congress and Exhibition, Detroit, MI, USA, 12–14 April 2011. [Google Scholar]
- Wu, Y.H.; Patterson, S.; Srinivasan, K.; Bot, E. Transient Thermal Analysis for the Automotive Underhood and Underbody Components. In Proceedings of the ASME 2013 Heat Transfer Summer Conference Collocated with the ASME 2013 7th International Conference on Energy Sustainability and the ASME 2013 11th International Conference on Fuel Cell Science, Engineering and Technology, HT 2013, Minneapolis, MN, USA, 14–19 July 2013; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2013; Volume 4. [Google Scholar]
- Kefalas, T.D.; Kladas, A.G. Finite element transient thermal analysis of PMSM for aerospace applications. In Proceedings of the 20th International Conference on Electrical Machines, ICEM 2012, Marseille, France, 2–5 September 2012; pp. 2566–2572. [Google Scholar]
- Kefalas, T.D.; Kladas, A.G. 3–D FEM and lumped–parameter network transient thermal analysis of induction and permanent magnet motors for aerospace applications. Mater. Sci. Forum 2016, 856, 245–250. [Google Scholar] [CrossRef]
- Kamimura, Y.; Nakamura, T.; Igawa, H.; Morino, Y. Transient inverse heat conduction analysis of atmospheric reentry vehicle using FEM. AIP Conf. Proc. 2012, 1493, 511–517. [Google Scholar] [CrossRef]
- Cebo-Rudnicka, A.; Malinowski, Z.; Buczek, A. The influence of selected parameters of spray cooling and thermal conductivity on heat transfer coefficient. Int. J. Therm. Sci. 2016, 110, 52–64. [Google Scholar] [CrossRef]
- Hadała, B.; Malinowski, Z.; Szajding, A. Solution strategy for the inverse determination of the specially varying heat transfer coefficient. Int. J. Heat Mass Transf. 2017, 104, 993–1007. [Google Scholar] [CrossRef]
- Malinowski, Z.; Hadała, B.; Cebo-Rudnicka, A. Inverse solutions to a vertical plate cooling in air–a comparative study. Int. J. Heat Mass Transf. 2022, 188, 122636. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Perić, M.; Street, R.L. Computational Methods for Fluid Dynamics, 4th ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; ISBN 9783319996936. [Google Scholar]
- Tu, J.; Yeoh, G.H.; Liu, C. Computational Fluid Dynamics: A Practical Approach; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780081011270. [Google Scholar]
- Lü, X.; Lu, T.; Yang, T.; Salonen, H.; Dai, Z.; Droege, P.; Chen, H. Improving the Energy Efficiency of Buildings Based on Fluid Dynamics Models: A Critical Review. Energies 2021, 14, 5384. [Google Scholar] [CrossRef]
- Khoshbakhtnejad, E.; Golezani, F.B.; Mohammadian, B.; Yassine, A.H.A.; Sojoudi, H. Trajectory and impact dynamics of snowflakes: Fundamentals and applications. Powder Technol. 2024, 448, 120298. [Google Scholar] [CrossRef]
- Saiyad, A.; Fulpagare, Y.; Bhargav, A. Comparison of detached eddy simulation and standard k—ε RANS model for rack-level airflow analysis inside a data center. Build. Simul. 2022, 15, 1595–1610. [Google Scholar] [CrossRef]
- Zhai, Z.J.; Zhang, Z.; Zhang, W.; Chen, Q.Y. Evaluation of Various Turbulence Models in Predicting Airflow and Turbulence in Enclosed Environments by CFD: Part 1—Summary of Prevalent Turbulence Models. HVAC&R Res. 2007, 13, 853–870. [Google Scholar] [CrossRef]
- Morozova, N.; Trias, F.X.; Capdevila, R.; Pérez-Segarra, C.D.; Oliva, A. On the feasibility of affordable high-fidelity CFD simulations for indoor environment design and control. Build. Environ. 2020, 184, 107144. [Google Scholar] [CrossRef]
- Domingo, P.; Vervisch, L. Recent developments in DNS of turbulent combustion. Proc. Combust. Inst. 2023, 39, 2055–2076. [Google Scholar] [CrossRef]
- Peksen, M. Multiphysics Modelling: Materials, Components, and Systems; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780128118245. [Google Scholar]
- Pinto, G.; Silva, F.; Porteiro, J.; Míguez, J.; Baptista, A. Numerical Simulation Applied to PVD Reactors: An Overview. Coatings 2018, 8, 410. [Google Scholar] [CrossRef]
- Messa, G.V.; Yang, Q.; Adedeji, O.E.; Chára, Z.; Duarte, C.A.R.; Matoušek, V.; Rasteiro, M.G.; Sean Sanders, R.; Silva, R.C.; Souza, F.J. De Computational Fluid Dynamics Modelling of Liquid–Solid Slurry Flows in Pipelines: State-of-the-Art and Future Perspectives. Processes 2021, 9, 1566. [Google Scholar] [CrossRef]
- Zhang, S.; Hess, S.; Marschall, H.; Reimer, U.; Beale, S.; Lehnert, W. openFuelCell2: A new computational tool for fuel cells, electrolyzers, and other electrochemical devices and processes. Comput. Phys. Commun. 2024, 298, 109092. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Ngo, S.I.; Lim, Y. Il Multiscale Eulerian CFD of Chemical Processes: A Review. Chem. Eng. 2020, 4, 23. [Google Scholar] [CrossRef]
- Spyropoulos, N.; Papadakis, G.; Prospathopoulos, J.M.; Riziotis, V.A. Assessment of a Hybrid Eulerian–Lagrangian CFD Solver for Wind Turbine Applications and Comparison with the New MEXICO Experiment. Fluids 2022, 7, 296. [Google Scholar] [CrossRef]
- Ryan, E.M.; Mukherjee, P.P. Mesoscale modeling in electrochemical devices—A critical perspective. Prog. Energy Combust. Sci. 2019, 71, 118–142. [Google Scholar] [CrossRef]
- Zhang, D.; Bertei, A.; Tariq, F.; Brandon, N.; Cai, Q. Progress in 3D electrode microstructure modelling for fuel cells and batteries: Transport and electrochemical performance. Prog. Energy 2019, 1, 012003. [Google Scholar] [CrossRef]
- Lamotte-Dawaghreh, J.; Herring, J.; Gupta, G.; Agonafer, D.; Madril, J.; Ouradnik, T.; Winfield, I.; Matthews, M. CFD Study of Electrochemical Additive Manufacturing Based Cold Plate Designs for Enhanced Electronics Cooling. In Proceedings of the Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, Aurora, CO, USA, 28–31 May 2024; IEEE Computer Society: Washington, DC, USA, 2024. [Google Scholar]
- Kulkarni, V.; Dotihal, B. CFD and conjugate heat transfer analysis of heat sinks with different fin geometries subjected to forced convection used in electronics cooling. Int. J. Res. Eng. Technol. 2015, 4, 158–163. [Google Scholar] [CrossRef]
- Parry, J. The changing role of CFD in electronics thermal design. In Proceedings of the EuroSime 2007: International Conference on Thermal, Mechanical and Multi-Physics Simulation Experiments in Microelectronics and Micro-Systems, London, UK, 16–18 April 2007. [Google Scholar]
- Carello, M.; Bovio, M.; Ricci, F.; Dall’acqua, S.; Strano, D.I.; Rizzello, A. CFD Simulation and Modelling of a Battery Thermal Management System: Comparison between Indirect and Immersion Cooling. SAE Int. J. Adv. Curr. Pract. Mobil. 2023, 6, 545–558. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, R.; Wang, S.; Huang, D. Heat transfer characteristics and influencing factors of immersion coupled direct cooling for battery thermal management. J. Energy Storage 2023, 62, 106821. [Google Scholar] [CrossRef]
- Li, R.; Yang, Y.; Liang, F.; Liu, J.; Chen, X. Investigation on Battery Thermal Management Based on Enhanced Heat Transfer Disturbance Structure within Mini-Channel Liquid Cooling Plate. Electronics 2023, 12, 832. [Google Scholar] [CrossRef]
- Szpicer, A.; Bińkowska, W.; Wojtasik-Kalinowska, I.; Salih, S.M.; Półtorak, A. Application of computational fluid dynamics simulations in food industry. Eur. Food Res. Technol. 2023, 249, 1411–1430. [Google Scholar] [CrossRef]
- Chekifi, T.; Boukraa, M. CFD applications for sensible heat storage: A comprehensive review of numerical studies. J. Energy Storage 2023, 68, 107893. [Google Scholar] [CrossRef]
- Höhne, T. CFD simulation of a heat pipe using the homogeneous model. Int. J. Thermofluids 2022, 15, 100163. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, Y.; Zhang, J. Application of New Finite Volume Method (FVM) on Transient Heat Transferring. In Proceedings of the Communications in Computer and Information Science, Tangshan, China, 15–18 October 2010; Springer: Berlin/Heidelberg, Germany, 2010; Volume 105 CCIS, pp. 109–116. [Google Scholar]
- Gazdallah, M.; Feldheim, V.; Claramunt, K.; Hirsch, C. Finite volume method for radiative heat transfer in an unstructured flow solver for emitting, absorbing and scattering media. In Proceedings of the Eurotherm Conference No. 95: Computational Thermal Radiation in Participating Media IV, Nancy, France, 18–20 April 2012; IOP Publishing: Bristol, UK, 2012; Volume 369, p. 012020. [Google Scholar]
- Reddy, J.N.; Anand, N.K.; Roy, P. Finite Element and Finite Volume Methods for Heat Transfer and Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2022; ISBN 9781009275484. [Google Scholar]
- Wróbel, J.; Warzynska, U. Finite Volume Method Modeling of Heat Transfer in Acoustic Enclosure for Machinery. Materials 2022, 15, 1562. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Liu, Y.; Yan, W.; Zhang, J.; Wang, J.; Lan, W.; Sang, T.; Yu, T. Heat transfer enhancement in cold plate based on FVM method and field synergy theory. J. Mech. Sci. Technol. 2021, 35, 2035–2047. [Google Scholar] [CrossRef]
- Lygidakis, G.N.; Nikolos, I.K. Using a Parallel Spatial/Angular Agglomeration Multigrid Scheme to Accelerate the FVM Radiative Heat Transfer Computation—Part I: Methodology. Numer. Heat Transf. Part B Fundam. 2014, 66, 471–497. [Google Scholar] [CrossRef]
- Moraga, N.O.; Zambra, C.E.; Moraga, N.O.; Zambra, C.E. On FVM Transport Phenomena Prediction in Porous Media with Chemical/Biological Reactions or Solid-Liquid Phase Change. In Finite Volume Method–Powerful Means of Engineering Design; IntechOpen: London, UK, 2012; ISBN 978-953-51-0445-2. [Google Scholar]
- Mohamad, A.A. Lattice Boltzmann Method Fundamentals and Engineering Applications with Computer Codes; Springer: London, UK, 2011; ISBN 978-0-85729-454-8. [Google Scholar]
- Delavar, M.A.; Wang, J. Lattice Boltzmann method and its applications. In Handbook of HydroInformatics: Classic Soft-Computing Techniques; Elsevier: Amsterdam, The Netherlands, 2023; Volume 1, pp. 289–319. ISBN 9780128212851. [Google Scholar]
- Sharifi, M.; Siavashi, M.; Hosseini, M. Investigation of the lattice Boltzmann method to resolve combined radiation-conduction heat transfer in participating media with curved boundaries. Int. J. Numer. Methods Heat Fluid Flow 2024, 34, 1351–1379. [Google Scholar] [CrossRef]
- Tolia, K.; Anupindi, K. Conjugate Heat Transfer Simulations Using Characteristic-Based Off-Lattice Boltzmann Method. In Proceedings of the Lecture Notes in Mechanical Engineering (LNME), Virtual, 17 January 2024; Springer: Singapore, 2024; pp. 67–80. [Google Scholar]
- Wei, Y.; Wu, S.; Liu, X.; Zhu, K.; Huang, Y. Lattice Boltzmann method for coupled radiation-conduction heat transfer in participating medium with graded-index. J. Quant. Spectrosc. Radiat. Transf. 2024, 313, 108844. [Google Scholar] [CrossRef]
- Jaramillo, A.; Pessoa Mapelli, V.; Cabezas-Gómez, L. Pseudopotential Lattice Boltzmann Method for boiling heat transfer: A mesh refinement procedure. Appl. Therm. Eng. 2022, 213, 118705. [Google Scholar] [CrossRef]
- Łach, Ł.; Svyetlichnyy, D.; Straka, R. Heat flow model based on lattice Boltzmann method for modeling of heat transfer during phase transformation. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 2255–2271. [Google Scholar] [CrossRef]
- Łach, Ł.; Svyetlichnyy, D. 3D Model of Heat Flow during Diffusional Phase Transformations. Materials 2023, 16, 4865. [Google Scholar] [CrossRef] [PubMed]
- Landl, M.; Prieler, R.; Monaco, E.; Hochenauer, C. Numerical Investigation of Conjugate Heat Transfer and Natural Convection Using the Lattice-Boltzmann Method for Realistic Thermophysical Properties. Fluids 2023, 8, 144. [Google Scholar] [CrossRef]
- Chaabane, R.; Jemni, A.; Aloui, F. An Efficient Lattice Boltzmann Model for 3D Transient Flows. In Green Energy and Technology (GREEN); Springer: Singapore, 2023; pp. 415–430. ISBN 978-981-16-8274-2. [Google Scholar]
- Sharma, K.V.; Straka, R.; Tavares, F.W. Current status of Lattice Boltzmann Methods applied to aerodynamic, aeroacoustic, and thermal flows. Prog. Aerosp. Sci. 2020, 115, 100616. [Google Scholar] [CrossRef]
- Sharma, K.V.; Straka, R.; Tavares, F.W. Natural convection heat transfer modeling by the cascaded thermal lattice Boltzmann method. Int. J. Therm. Sci. 2018, 134, 552–564. [Google Scholar] [CrossRef]
- Dutra Fraga Filho, C.A. Smoothed Particle Hydrodynamics; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Pozorski, J.; Olejnik, M. Smoothed particle hydrodynamics modelling of multiphase flows: An overview. Acta Mech. 2024, 235, 1685–1714. [Google Scholar] [CrossRef]
- Fan, R.; Chen, T.; Li, M.; Wang, S. Applications and Prospects of Smooth Particle Hydrodynamics in Tunnel and Underground Engineering. Appl. Sci. 2024, 14, 8552. [Google Scholar] [CrossRef]
- Islam, M.R.I. SPH-based framework for modelling fluid–structure interaction problems with finite deformation and fracturing. Ocean Eng. 2024, 294, 116722. [Google Scholar] [CrossRef]
- Venâncio Pains Soares Pamplona, A.J.; Silva, K.F.; Bucar Filho, C.; Vasco, J. Numerical Solution using SPH Method: An Application to Transient Heat Conduction. In Proceedings of the 25th International Congress of Mechanical Engineering, Dallas, TX, USA, 11–14 August 2025; Associacao Brasileira de Engenharia e Ciencias Mecanicas—ABCM: Rio de Janeiro, Brazil, 2019. [Google Scholar]
- Ng, K.C.; Ng, Y.L.; Sheu, T.W.H.; Alexiadis, A. Assessment of Smoothed Particle Hydrodynamics (SPH) models for predicting wall heat transfer rate at complex boundary. Eng. Anal. Bound. Elem. 2020, 111, 195–205. [Google Scholar] [CrossRef]
- Lüthi, C.; Afrasiabi, M.; Bambach, M. An adaptive smoothed particle hydrodynamics (SPH) scheme for efficient melt pool simulations in additive manufacturing. Comput. Math. Appl. 2023, 139, 7–27. [Google Scholar] [CrossRef]
- Sandnes, T.D.; Eke, V.R.; Kegerreis, J.A.; Massey, R.J.; Ruiz-Bonilla, S.; Schaller, M.; Teodoro, L.F.A. REMIX SPH–improving mixing in smoothed particle hydrodynamics simulations using a generalised, material-independent approach. arXiv 2024, arXiv:2407.18587. [Google Scholar]
- Pavelka, M.; Klika, V.; Kincl, O. Approaches to conservative Smoothed Particle Hydrodynamics with entropy. arXiv 2024, arXiv:2406.14229. [Google Scholar]
- Toshev, A.P.; Erbesdobler, J.A.; Adams, N.A.; Brandstetter, J. Neural SPH: Improved Neural Modeling of Lagrangian Fluid Dynamics. arXiv 2024, arXiv:2402.06275. [Google Scholar]
- Hrytsyshyn, O.; Venherskyi, P.; Trushevskyi, V.; Terletskyi, O. Smoothed Particle Hydrodynamics Implementation Using Compute Shaders. In Proceedings of the 2023 IEEE 13th International Conference on Electronics and Information Technologies, ELIT 2023-Proceedings, Lviv, Ukraine, 26–28 September 2023; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2023; pp. 127–131. [Google Scholar]
- Hornung, R.D.; Wissink, A.M.; Kohn, S.R. Managing complex data and geometry in parallel structured AMR applications. Eng. with Comput. 2006, 22, 181–195. [Google Scholar] [CrossRef]
- van der Holst, B.; Keppens, R. Hybrid block-AMR in cartesian and curvilinear coordinates: MHD applications. J. Comput. Phys. 2007, 226, 925–946. [Google Scholar] [CrossRef]
- Burstedde, C.; Ghattas, O.; Gurnis, M.; Isaac, T.; Stadler, G.; Warburton, T.; Wilcox, L.C. Extreme-scale AMR. In Proceedings of the 2010 ACM/IEEE International Conference for High Performance Computing, Networking, Storage and Analysis, SC 2010, New Orleans, LA, USA, 13–19 November 2010. [Google Scholar]
- Zuzio, D.; Estivalezes, J.L. An efficient block parallel AMR method for two phase interfacial flow simulations. Comput. Fluids 2011, 44, 339–357. [Google Scholar] [CrossRef]
- Anderson, R.W.; Elliott, N.S.; Pember, R.B. An arbitrary Lagrangian–Eulerian method with adaptive mesh refinement for the solution of the Euler equations. J. Comput. Phys. 2004, 199, 598–617. [Google Scholar] [CrossRef]
- Huang, X.; Chen, J.; Zhang, J.; Wang, L.; Wang, Y. An Adaptive Mesh Refinement–Rotated Lattice Boltzmann Flux Solver for Numerical Simulation of Two and Three-Dimensional Compressible Flows with Complex Shock Structures. Symmetry 2023, 15, 1909. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, B.; Liang, C.; Rong, Y. A high-order flux reconstruction method with adaptive mesh refinement and artificial diffusivity on unstructured moving/deforming mesh for shock capturing. Comput. Fluids 2016, 139, 17–35. [Google Scholar] [CrossRef]
- Luitjens, J.; Worthen, B.; Berzins, M.; Hen, T.C. Scalable Parallel AMR for the Uintah Multi-Physics Code. In Petascale Computing; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007; pp. 121–136. ISBN 9780429143496. [Google Scholar]
- Watanabe, S.; Aoki, T. Large-scale flow simulations using lattice Boltzmann method with AMR following free-surface on multiple GPUs. Comput. Phys. Commun. 2021, 264, 107871. [Google Scholar] [CrossRef]
- Cant, R.S.; Ahmed, U.; Fang, J.; Chakarborty, N.; Nivarti, G.; Moulinec, C.; Emerson, D.R. An unstructured adaptive mesh refinement approach for computational fluid dynamics of reacting flows. J. Comput. Phys. 2022, 468, 111480. [Google Scholar] [CrossRef]
- Wang, Y.D.; Zhan, Q.; Liang, Y.Z.; Yin, W.Y. Adaptive Mesh Refinement for Heat Transfer Problems in Electronic Devices. In Proceedings of the 2023 International Applied Computational Electromagnetics Society Symposium, Hangzhou, China, 15–18 August 2023; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2023. [Google Scholar]
- Gallorini, E.; Hèlie, J.; Piscaglia, F. An adjoint-based solver with adaptive mesh refinement for efficient design of coupled thermal-fluid systems. Int. J. Numer. Methods Fluids 2023, 95, 1090–1116. [Google Scholar] [CrossRef]
- McManus, L.; Karalus, M.; Munktell, E.; Rogerson, J. Investigation of Adaptive Mesh Refinement on an Industrial Gas Turbine Combustor. J. Eng. Gas Turbines Power 2023, 145, 031022. [Google Scholar] [CrossRef]
- Duan, Y.; Edwards, J.S.; Dwivedi, Y.K. Artificial intelligence for decision making in the era of Big Data–evolution, challenges and research agenda. Int. J. Inf. Manag. 2019, 48, 63–71. [Google Scholar] [CrossRef]
- Janiesch, C.; Zschech, P.; Heinrich, K. Machine learning and deep learning. Electron. Mark. 2021, 31, 685–695. [Google Scholar] [CrossRef]
- Brnabic, A.; Hess, L.M. Systematic literature review of machine learning methods used in the analysis of real-world data for patient-provider decision making. BMC Med. Inform. Decis. Mak. 2021, 21, 54. [Google Scholar] [CrossRef]
- Jiang, H. Machine Learning Fundamentals: A Concise Introduction; Cambridge University Press: Cambridge, UK, 2021; ISBN 9781108940023. [Google Scholar]
- Zhao, X.; Sun, Y.; Li, Y.; Jia, N.; Xu, J. Applications of machine learning in real-time control systems: A review. Meas. Sci. Technol. 2024, 36, 012003. [Google Scholar] [CrossRef]
- Ardabili, S.; Mosavi, A.; Felde, I. Machine Learning in Heat Transfer: Taxonomy, Review and Evaluation. In Proceedings of the SACI 2023-IEEE 17th International Symposium on Applied Computational Intelligence and Informatics, Timisoara, Romania, 23–26 May 2023; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2023; pp. 433–441. [Google Scholar]
- Godasiaei, S.H.; Chamkha, A.J. Advancing heat transfer modeling through machine learning: A focus on forced convection with nanoparticles. Numer. Heat Transf. Part A Appl. 2023, 1–23. [Google Scholar] [CrossRef]
- Zou, J.; Hirokawa, T.; An, J.; Huang, L.; Camm, J. Recent advances in the applications of machine learning methods for heat exchanger modeling—A review. Front. Energy Res. 2023, 11, 1294531. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Majumdar, P. Artificial Intelligence-Machine Learning Algorithms for the Simulation of Combustion Thermal Analysis. Heat Transf. Eng. 2024, 45, 176–193. [Google Scholar] [CrossRef]
- Patel, H.; Kumar Singh, D.; Prakash Verma, O.; Kadian, S. Machine Learning Approach for Thermal Characteristics and Improvement of Heat Transfer of Nanofluids—A Review. In Proceedings of the Lecture Notes in Networks and Systems, Virtual, 13 January 2024; Springer: Singapore, 2024; Volume 831, pp. 227–233. [Google Scholar]
- Kang, J.; Wang, J.; Han, X.; Zhao, Q. Deep learning based heat transfer simulation of the casting process. Sci. Rep. 2024, 14, 29068. [Google Scholar] [CrossRef] [PubMed]
- Ball, A.K.; Basak, A. AI modeling for high-fidelity heat transfer and thermal distortion forecast in metal additive manufacturing. Int. J. Adv. Manuf. Technol. 2023, 128, 2995–3010. [Google Scholar] [CrossRef]
- Abdoh, D.A. Using Neural Networks for Thermal Analysis of Heat Conduction. J. Therm. Sci. Eng. Appl. 2023, 16, 021009. [Google Scholar] [CrossRef]
- Lodhi, S.K.; Hussain, H.K.; Hussain, I. Using AI to Increase Heat Exchanger Efficiency: An Extensive Analysis of Innovations and Uses. Int. J. Multidiscip. Sci. Arts 2024, 3, 1–14. [Google Scholar] [CrossRef]
- Hua, Y.; Luo, L.; Corre, S.L.; Fan, Y. Machine-learning topology optimization with stochastic gradient descent optimizer for heat conduction problems. Int. J. Heat Mass Transf. 2024, 223, 125226. [Google Scholar] [CrossRef]
- Olabi, A.G.; Abdelghafar, A.A.; Maghrabie, H.M.; Sayed, E.T.; Rezk, H.; Radi, M.A.; Obaideen, K.; Abdelkareem, M.A. Application of artificial intelligence for prediction, optimization, and control of thermal energy storage systems. Therm. Sci. Eng. Prog. 2023, 39, 101730. [Google Scholar] [CrossRef]
- Hughes, M.T.; Kini, G.; Garimella, S. Status, Challenges, and Potential for Machine Learning in Understanding and Applying Heat Transfer Phenomena. J. Heat Transf. 2021, 143, 120802. [Google Scholar] [CrossRef]
- Hamid, T.J.; Chakshu, N.K.; Thomas, H.; Nithiarasu, P. Deep Learning in Heat Transfer. Annu. Rev. Heat Transf. 2022, 24, 271–301. [Google Scholar] [CrossRef]
- Kumar, R.; Ezhilarasi, D. A state-of-the-art survey of model order reduction techniques for large-scale coupled dynamical systems. Int. J. Dyn. Control 2022, 11, 900–916. [Google Scholar] [CrossRef]
- Vega, J.M.; Clainche, S. Le Higher Order Dynamic Mode Decomposition and Its Applications; Elsevier: Amsterdam, The Netherlands, 2020; ISBN 9780128197431. [Google Scholar]
- Peters, N.J.; Wissink, A.; Ekaterinaris, J. On the construction of a mode based reduced order model for a moving store. Aerosp. Sci. Technol. 2022, 123, 107484. [Google Scholar] [CrossRef]
- Espinoza-Contreras, N.; Bayona-Roa, C.; Castillo, E.; Gándara, T.; Moraga, N.O. Hyperreduced-order modeling of thermally coupled flows. Appl. Math. Model. 2024, 125, 59–81. [Google Scholar] [CrossRef]
- Siena, P.; Africa, P.C.; Girfoglio, M.; Rozza, G. On the accuracy and efficiency of reduced order models: Towards real-world applications. arXiv 2024, arXiv:2407.03325. [Google Scholar]
- Hua, J.; Sørheim, E.A. Nonintrusive reduced-order modeling approach for parametrized unsteady flow and heat transfer problems. Int. J. Numer. Methods Fluids 2022, 94, 976–1000. [Google Scholar] [CrossRef]
- Padula, G.; Girfoglio, M.; Rozza, G. A brief review of reduced order models using intrusive and non-intrusive techniques. PAMM 2024, 24, e202400210. [Google Scholar] [CrossRef]
- German, P.; Tano, M.E.; Fiorina, C.; Ragusa, J.C. Data-Driven Reduced-Order Modeling of Convective Heat Transfer in Porous Media. Fluids 2021, 6, 266. [Google Scholar] [CrossRef]
- Drakoulas, G.I.; Gortsas, T.V.; Bourantas, G.C.; Burganos, V.N.; Polyzos, D. FastSVD-ML–ROM: A reduced-order modeling framework based on machine learning for real-time applications. Comput. Methods Appl. Mech. Eng. 2023, 414, 116155. [Google Scholar] [CrossRef]
- Zeipel, H.; Frank, T.; Wielitzka, M.; Ortmaier, T. Comparative Study of Model Order Reduction for Linear Parameter-Variant Thermal Systems. In Proceedings of the 2020 IEEE International Conference on Mechatronics and Automation, ICMA 2020, Beijing, China, 13–16 October 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020; pp. 990–995. [Google Scholar]
- Svietlichnyj, D.; Pietrzyk, M. On-line model of thermal roll profile during hot rolling. Metall. Foundry Eng. 2001, 27, 73–95. [Google Scholar]
- Lew, R.; Poudel, B.; Wallace, J.; Westover, T.L. A Reduced-Order Model of a Nuclear Power Plant with Thermal Power Dispatch. Energies 2024, 17, 4298. [Google Scholar] [CrossRef]
- Chen, Q.; Li, N. Study on key factors affecting the high-order building model order reduction for model predictive control application. Energy Build. 2023, 296, 113392. [Google Scholar] [CrossRef]
- Valverde, J.; Galan-Vioque, J.; Herruzo, J.C.; Rubino, S.; Chacón, T.; Nuñez Fernandez, C. Reduced Order Modelling for the Optimization of CSP Tower Receivers and Their Cavities for High Temperature Applications. In Proceedings of the SolarPACES Conference Proceedings, Albuquerque, NM, USA, 27–30 September 2022; TIB Open Publishing: Hanover, Germany, 2023; Volume 1. [Google Scholar]
- Jiang, M.; Speetjens, M.; Rindt, C.; Smeulders, D. A data-based reduced-order model for dynamic simulation and control of district-heating networks. Appl. Energy 2023, 340, 121038. [Google Scholar] [CrossRef]
- Xiang, L.; Lee, C.W.; Zikanov, O.; Hsu, C.C. Efficient reduced order model for heat transfer in a battery pack of an electric vehicle. Appl. Therm. Eng. 2022, 201, 117641. [Google Scholar] [CrossRef]
- Homes, S.; Antolović, I.; Fingerhut, R.; Guevara-Carrion, G.; Heinen, M.; Nitzke, I.; Saric, D.; Vrabec, J. High-Performance Computing as a Key to New Insights into Thermodynamics. In Proceedings of the High Performance Computing in Science and Engineering’22, Virtual, 3 April 2024; Springer: Cham, Germany, 2024; pp. 399–413. [Google Scholar]
- Hung, J.N.; Li, H.C.; Lin, P.F.; Ku, T.; Yu, C.H.; Yee, K.C.; Yu, D.C.H. Advanced System Integration for High Performance Computing with Liquid Cooling. In Proceedings of the Proceedings-Electronic Components and Technology Conference, San Diego, CA, USA, 1 June–4 July 2021; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2021; Volume 2021, pp. 105–111. [Google Scholar]
- Heydari, A.; Al-Zu’Bi, O.; Manaserh, Y.; Gharaibeh, A.R.; Tipton, R.; Mehrabikermani, M.; Rodriguez, J.; Sammakia, B. Advancing in Data Centers Thermal Management: Experimental Assessment of Two-Phase Liquid Cooling Technology. In Proceedings of the ASME 2024 International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems, InterPACK 2024, San Jose, CA, USA, 8–10 October 2024; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2024. [Google Scholar]
- Fang, Q.; Wang, J.; Gong, Q.; Song, M. Thermal-Aware Energy Management of an HPC Data Center via Two-Time-Scale Control. IEEE Trans. Ind. Inform. 2017, 13, 2260–2269. [Google Scholar] [CrossRef]
- Rodero, I.; Viswanathan, H.; Lee, E.K.; Gamell, M.; Pompili, D.; Parashar, M. Energy-Efficient Thermal-Aware Autonomic Management of Virtualized HPC Cloud Infrastructure. J. Grid Comput. 2012, 10, 447–473. [Google Scholar] [CrossRef]
- Kumar, M. Combination of Cloud Computing and High Performance Computing. Int. J. Eng. Comput. Sci. 2016, 5, 5. [Google Scholar] [CrossRef]
- Sathish, K.; Sathya, A.; Pattunnarajam, P.; Rao, A.S.; Lakshmisridevi, S.; Pushpa Priya, C. Innovative Approaches in Advanced VLSI Design for High-Performance Computing Applications. In Proceedings of the 2nd International Conference on Intelligent Cyber Physical Systems and Internet of Things, ICoICI 2024, Coimbatore, India, 28–30 August 2024; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2024; pp. 643–648. [Google Scholar]
- Pavlidis, V.F.; Savidis, I.; Friedman, E.G. Thermal Modeling and Analysis. In Three-Dimensional Integrated Circuit Design, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 295–331. [Google Scholar] [CrossRef]
- Persoons, T.; Codecasa, L. Guest Editorial Special Section on Advances in Modeling and Characterization for Electronics Cooling. IEEE Trans. Compon. Packag. Manuf. Technol. 2023, 13, 1085–1087. [Google Scholar] [CrossRef]
- Mathew, J.; Krishnan, S. A Review on Transient Thermal Management of Electronic Devices. J. Electron. Packag. 2022, 144, 010801. [Google Scholar] [CrossRef]
- Terraneo, F.; Leva, A.; Fornaciari, W.; Atienza, D. Modeling and Simulation Challenges and Solutions in Cooling Systems for Nanoscale Integrated Circuits [Feature]. IEEE Circuits Syst. Mag. 2023, 23, 36–56. [Google Scholar] [CrossRef]
- Yeh, L.-T.; Chu, R.C.; Janna, W.S. Thermal Management of Microelectronic Equipment: Heat Transfer Theory, Analysis Methods, and Design Practices; ASME Press Book Series on Electronic Packaging; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2003; Volume 56, ISBN 3540434941. [Google Scholar]
- Yuan, Z.; Coskun, A.K. Neural network-based cooling design for high-performance processors. iScience 2022, 25, 103582. [Google Scholar] [CrossRef]
- Lombardi, A.; Zampieri, L.; Agrawal, M.; Singhal, M.; Tschammer, T.V.; Lombardi, A.; Zampieri, L.; Agrawal, M.; Singhal, M.; Tschammer, T. Von Optimization of Power Module Cooling Plate: An Application of Deep Learning for Thermal Management Devices; SAE Technical Paper 2024-01-2583; SAE: Warrendale, PA, USA, 2024. [Google Scholar] [CrossRef]
- Gammaidoni, T.; Zembi, J.; Battistoni, M.; Biscontini, G.; Mariani, A. CFD Analysis of an Electric Motor’s Cooling System: Model Validation and Solutions for Optimization. Case Stud. Therm. Eng. 2023, 49, 103349. [Google Scholar] [CrossRef]
- Kim, S.; Ki, S.; Bang, S.; Han, S.; Seo, J.; Ahn, C.; Maeng, S.; Lee, B.J.; Nam, Y. Optimizing Energy-Efficient jet impingement cooling using an artificial neural network (ANN) surrogate model for high heat flux Semiconductors. Appl. Therm. Eng. 2024, 239, 122101. [Google Scholar] [CrossRef]
- Cai, F.; Zhou, H.; Chen, F.; Yao, M.; Ren, Z. Deep learning-aided active subspace exploration of free-stream effects for fan-shaped film cooling. Phys. Fluids 2024, 36, 095136. [Google Scholar] [CrossRef]
- Herring, J.; Smith, P.; Lamotte-Dawaghreh, J.; Bansode, P.; Saini, S.; Bhandari, R.; Agonafer, D. Machine Learning-Based Heat Sink Optimization Model for Single-Phase Immersion Cooling. In Proceedings of the ASME 2022 International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems, InterPACK 2022, Garden Grove, CA, USA, 25–27 October 2022; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2022. [Google Scholar]
- Fatunmbi, E.O.; Obalalu, A.M.; Khan, U.; Hussain, S.M.; Muhammad, T. Model development and heat transfer characteristics in renewable energy systems conveying hybrid nanofluids subject to nonlinear thermal radiation. Multidiscip. Model. Mater. Struct. 2024, 20, 1328–1342. [Google Scholar] [CrossRef]
- Maseer, M.M.; Ismail, F.B.; Kazem, H.A.; Wai, L.C.; Hadi Al-Gburi, K.A. Optimal evaluation of photovoltaic-thermal solar collectors cooling using a half-tube of different diameters and lengths. Sol. Energy 2024, 267, 112193. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Desideri, U. Heat transfer performance enhancement and mechanism analysis of thermal energy storage unit designed by using a modified transient topology optimization model. J. Clean. Prod. 2024, 434, 140281. [Google Scholar] [CrossRef]
- Khosravi, K.; Mohammed, H.I.; Mahdi, J.M.; Silakhori, M.; Ebrahimnataj Tiji, M.; Kazemian, A.; Ma, T.; Talebizadehsardari, P. Optimizing performance of water-cooled photovoltaic-thermal modules: A 3D numerical approach. Sol. Energy 2023, 264, 112025. [Google Scholar] [CrossRef]
- Shboul, B.; Zayed, M.E.; Al-Tawalbeh, N.; Usman, M.; Irshad, K.; Odat, A.S.; Alam, M.A.; Rehman, S. Dynamic numerical modeling and performance optimization of solar and wind assisted combined heat and power system coupled with battery storage and sophisticated control framework. Results Eng. 2024, 22, 102198. [Google Scholar] [CrossRef]
- Dezhdar, A.; Assareh, E.; Agarwal, N.; Baheri, A.; Ahmadinejad, M.; Zadsar, N.; Fard, G.Y.; Ali bedakhanian; Aghajari, M.; Ghodrat, M.; et al. Modeling, optimization, and economic analysis of a comprehensive CCHP system with fuel cells, reverse osmosis, batteries, and hydrogen storage subsystems Powered by renewable energy sources. Renew. Energy 2024, 220, 119695. [Google Scholar] [CrossRef]
- Rudakov, D.; Inkin, O. Evaluation of vertical closed loop system performance by modeling heat transfer in geothermal probes. Geothermics 2022, 106, 102567. [Google Scholar] [CrossRef]
- Rana, M.; Nuhash, M.M.; Bhuiyan, A.A. A CFD modelling for optimizing geometry parameters for improved performance using clean energy geothermal ground-to-air tunnel heat exchangers. Case Stud. Therm. Eng. 2024, 53, 103867. [Google Scholar] [CrossRef]
- Egidi, N.; Giacomini, J.; Maponi, P. Inverse heat conduction to model and optimise a geothermal field. J. Comput. Appl. Math. 2023, 423, 114957. [Google Scholar] [CrossRef]
- Assareh, E.; Hoseinzadeh, S.; Agarwal, N.; Delpisheh, M.; Dezhdar, A.; Feyzi, M.; Wang, Q.; Garcia, D.A.; Gholamian, E.; Hosseinzadeh, M.; et al. A transient simulation for a novel solar-geothermal cogeneration system with a selection of heat transfer fluids using thermodynamics analysis and ANN intelligent (AI) modeling. Appl. Therm. Eng. 2023, 231, 120698. [Google Scholar] [CrossRef]
- Fu, D.; Hu, G.; Agrawal, M.K.; Peng, F.; Alotaibi, B.; Abuhussain, M.; Alsenani, T.R. Multi-criteria optimization of a renewable combined heat and power system using response surface methodology. Process Saf. Environ. Prot. 2023, 176, 898–917. [Google Scholar] [CrossRef]
- Patel, J.; Patel, R.; Saxena, R.; Nair, A. Thermal analysis of high specific energy NCM-21700 Li-ion battery cell under hybrid battery thermal management system for EV applications. J. Energy Storage 2024, 88, 111567. [Google Scholar] [CrossRef]
- Sevinc, S.; Dagdevir, T. Research Progress of Battery Thermal Management Systems with Minichannels. Energy Environ. Storage 2024, 4, 109–115. [Google Scholar] [CrossRef]
- Abadie, P.T.; Docimo, D.J. An Investigation into the Viability of Cell-Level Temperature Control in Lithium-Ion Battery Packs. ASME Lett. Dyn. Syst. Control 2025, 5, 011005. [Google Scholar] [CrossRef]
- Yang, L.; Nik-Ghazali, N.N.; Ali, M.A.H.; Chong, W.T.; Yang, Z.; Liu, H. A review on thermal management in proton exchange membrane fuel cells: Temperature distribution and control. Renew. Sustain. Energy Rev. 2023, 187, 113737. [Google Scholar] [CrossRef]
- Philip, N.; Ghosh, P.C. Optimal sizing of electrical and thermal energy storage systems for application in fuel cell based electric vehicles. J. Energy Storage 2024, 83, 110753. [Google Scholar] [CrossRef]
- Di Giorgio, P.; Di Ilio, G.; Jannelli, E.; Conte, F.V. Innovative battery thermal management system based on hydrogen storage in metal hydrides for fuel cell hybrid electric vehicles. Appl. Energy 2022, 315, 118935. [Google Scholar] [CrossRef]
- Li, A.; Weng, J.; Yuen, A.C.Y.; Wang, W.; Liu, H.; Lee, E.W.M.; Wang, J.; Kook, S.; Yeoh, G.H. Machine learning assisted advanced battery thermal management system: A state-of-the-art review. J. Energy Storage 2023, 60, 106688. [Google Scholar] [CrossRef]
- Gao, W.; Drake, J.; Brushett, F.R. Towards Efficient Thermal Management within Intercalation Batteries through Electrolyte Convection. In ECS Meeting Abstracts; IOP Publishing: Bristol, UK, 2022; Volume MA2022-02, p. 557. [Google Scholar]
- Thaler, S.M.; Zwatz, J.; Zettel, D.; Hauser, R.; Lackner, R. Development of a Temperature Management System for Battery Packs Using Phase Change Materials and Additive Manufacturing Options. Appl. Sci. 2023, 13, 8585. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, X.; Wang, X.; Duan, Y.; Shangguan, W. Bin Modeling and Control Strategy for Engine Thermal Management System; SAE Technical Paper 2024-01-2234; SAE: Warrendale, PA, USA, 2024. [Google Scholar] [CrossRef]
- Zhang, S.; Tang, K.; Zheng, X. Modelling and optimal control of energy-saving-oriented automotive engine thermal management system. Therm. Sci. 2021, 25, 2897–2904. [Google Scholar] [CrossRef]
- Park, C.-S.; Lee, B.-S.; KIM, D.-K.; CHAE, D.-S. Vehicle Thermal Management System Applying an Integrated Thermal Management Valve and a Cooling Circuit Control Method Thereof 2020. U.S. Patent 11,022,024, 1 June 2021. [Google Scholar]
- Lokur, P.; Nicklasson, K.; Verde, L.; Larsson, M.; Murgovski, N. Modeling of the Thermal Energy Management System for Battery Electric Vehicles. In Proceedings of the 2022 IEEE Vehicle Power and Propulsion Conference, VPPC 2022-Proceedings, Merced, CA, USA, 1–4 November 2022; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2022. [Google Scholar]
- Bayraktar, I. Computational simulation methods for vehicle thermal management. Appl. Therm. Eng. 2012, 36, 325–329. [Google Scholar] [CrossRef]
- Palaniswamy, H.; Ngaile, G.; Altan, T. Finite element simulation of magnesium alloy sheet forming at elevated temperatures. J. Mater. Process. Technol. 2004, 146, 52–60. [Google Scholar] [CrossRef]
- Holub, P.; Gulan, L.; Korec, A.; Chovančíková, V.; Nagy, M.; Nagy, M. Application of Advanced Design Methods of “Design for Additive Manufacturing” (DfAM) to the Process of Development of Components for Mobile Machines. Appl. Sci. 2023, 13, 12532. [Google Scholar] [CrossRef]
- Ren, C.; Guo, X. The lightweight design for the frame structure of FSEC. J. Phys. Conf. Ser. 2022, 2390, 012041. [Google Scholar] [CrossRef]
- Al-Samman, T. Material and Process Design for Lightweight Structures. Metals 2019, 9, 415. [Google Scholar] [CrossRef]
- Anibal, J.L.; Martins, J.R.R.A. CFD-based shape optimization of a plate-fin heat exchanger. In Proceedings of the AIAA AVIATION 2022 Forum, Chicago, IL, USA, 27 June–1 July 2022; American Institute of Aeronautics and Astronautics Inc., AIAA: Reston, VA, USA, 2022. [Google Scholar]
- Khosravian, E. Numerical Investigation and Machine Learning Predictions for Enhanced Thermal Management in Pulsating Heat Pipes: Modeling Turbulent Flow and Heat Transfer Characteristics in Nuclear Applications. Int. J. Numer. Methods Fluids 2025, 97, 446–461. [Google Scholar] [CrossRef]
- Mohamed, M.A.E.M.; Meana-Fernández, A.; González-Caballín, J.M.; Bowman, A.; Gutiérrez-Trashorras, A.J. Numerical Study of a Heat Exchanger with a Rotating Tube Using Nanofluids under Transitional Flow. Processes 2024, 12, 222. [Google Scholar] [CrossRef]
- Patel, R.; Bhartiya, S.; Gudi, R. Optimal temperature trajectory for tubular reactor using physics informed neural networks. J. Process Control 2023, 128, 103003. [Google Scholar] [CrossRef]
- Al Ruhaili, E.; Walke, S.; Lakkimsetty, N.R.; Joy, V.M. Modeling and optimization of heat exchanger using artificial neural network and genetic algorithm. AIP Conf. Proc. 2023, 2690, 020028. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, B.; Yu, H.; Ren, J.; Pan, M.; He, C.; Chen, Q. Accelerating heat exchanger design by combining physics-informed deep learning and transfer learning. Chem. Eng. Sci. 2023, 282, 119285. [Google Scholar] [CrossRef]
- Rahman, M.W.; Chowdhury, M.S.; Abedin, M.Z. CFD Analysis of Coolant Flow Characteristics in Reactor Pressure Vessel: A Comprehensive Review. Am. J. Sci. Eng. Technol. 2024, 9, 42–49. [Google Scholar] [CrossRef]
- Behrens, C.; Ostermann, N.; Sehrt, J.T.; Ploshikhin, V. Temperature control by simulated adaptive layer times in powder bed fusion processes. Prog. Addit. Manuf. 2024, 9, 705–713. [Google Scholar] [CrossRef]
- Liao, S.; Xue, T.; Jeong, J.; Webster, S.; Ehmann, K.; Cao, J. Hybrid thermal modeling of additive manufacturing processes using physics-informed neural networks for temperature prediction and parameter identification. Comput. Mech. 2023, 72, 499–512. [Google Scholar] [CrossRef]
- Soni, H.; Gor, M.; Rajput, G.S.; Sahlot, P. Thermal Modeling of Laser Powder-Based Additive Manufacturing Process. Adv. Intell. Syst. Comput. 2021, 1287, 401–409. [Google Scholar] [CrossRef]
- Svyetlichnyy, D. Lattice Boltzmann Modeling of Additive Manufacturing of Functionally Graded Materials. Entropy 2024, 27, 20. [Google Scholar] [CrossRef]
- Svyetlichnyy, D. Simulation of the selective laser sintering/melting process of bioactive glass 45S5. Simul. Model. Pract. Theory 2024, 136, 103009. [Google Scholar] [CrossRef]
- Svyetlichnyy, D. Model of the Selective Laser Melting Process-Powder Deposition Models in Multistage Multi-Material Simulations. Appl. Sci. 2023, 13, 6196. [Google Scholar] [CrossRef]
- Svyetlichnyy, D.S. Development of the Platform for Three-Dimensional Simulation of Additive Layer Manufacturing Processes Characterized by Changes in State of Matter: Melting-Solidification. Materials 2022, 15, 1030. [Google Scholar] [CrossRef] [PubMed]
- Łach, Ł.; Svyetlichnyy, D. New Platforms Based on Frontal Cellular Automata and Lattice Boltzmann Method for Modeling the Forming and Additive Manufacturing. Materials 2022, 15, 7844. [Google Scholar] [CrossRef] [PubMed]
- Łach, Ł.; Svyetlichnyy, D. Recent Progress in Heat and Mass Transfer Modeling for Chemical Vapor Deposition Processes. Energies 2024, 17, 3267. [Google Scholar] [CrossRef]
- Bai, J.; Rui, W.; Chen, H. Numerical Simulation of Low-Temperature Thermal Management of Lithium-Ion Batteries Based on Composite Phase Change Material. J. Energy Eng. 2024, 150, 04024012. [Google Scholar] [CrossRef]
- Broumand, M.; Yun, S.; Hong, Z. A novel phase change material-based thermal management of electric machine windings enabled by additive manufacturing. Appl. Therm. Eng. 2024, 244, 122802. [Google Scholar] [CrossRef]
- Favero, G.; Bonesso, M.; Rebesan, P.; Dima, R.; Pepato, A.; Mancin, S. Additive manufacturing for thermal management applications: From experimental results to numerical modeling. Int. J. Thermofluids 2021, 10, 100091. [Google Scholar] [CrossRef]
- Saha, A.; Basu, A.; Banerjee, S. Enhancing thermal management systems: A machine learning and metaheuristic approach for predicting thermophysical properties of nanofluids. Eng. Res. Express 2024, 6, 045537. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Dinh, T.; McGordon, A. Numerical modelling and control of electric two-wheeler battery thermal management system with thermoelectric coolers. In Proceedings of the 2024 IEEE Transportation Electrification Conference and Expo, ITEC 2024, Chicago, IL, USA, 19–21 June 2024; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2024. [Google Scholar]
- Zhoghuo, Y.; Alex, K.H. Innovations in Thermal Management Techniques for Enhanced Performance and Reliability in Engineering Applications. J. Eng. Res. Rep. 2024, 26, 69–81. [Google Scholar] [CrossRef]
- Verdad, S.M.R.; Lucido, R.J.R.; Carcabuso, C.L.C.; Tenorio, R.J.C.; Castillo, S.B.G.; Arcillas, F.L.L.; Pamplona, C.M.M.; Lara, J.D.M.; Salvador, A.L.; Magon, S.A. Modeling and Simulation of Central Processing Unit Cooling Modes for Thermal Management. In Proceedings of the 2024 ASU International Conference in Emerging Technologies for Sustainability and Intelligent Systems, ICETSIS 2024, Manama, Bahrain, 28–29 January 2024; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2024; pp. 852–855. [Google Scholar]
- Yang, X.; Zhang, W.; Abkar, M.; Anderson, W. Computational fluid dynamics: Its carbon footprint and role in carbon reduction. J. Renew. Sustain. Energy 2024, 16, 055906. [Google Scholar] [CrossRef]
- Li, B.; Samsi, S.; Gadepally, V.; Tiwari, D. Sustainable HPC: Modeling, Characterization, and Implications of Carbon Footprint in Modern HPC Systems. arXiv 2023, arXiv:2306.13177. [Google Scholar] [CrossRef]
- Akimoto, H.; Okamoto, T.; Kagami, T.; Seki, K.; Sakai, K.; Imade, H.; Shinohara, M.; Sumimoto, S. File System and Power Management Enhanced for Supercomputer Fugaku. Fujitsu Tech. Rev. 2020, 3, 1–9. [Google Scholar]
- Gupta, U.; Kim, Y.G.; Lee, S.; Tse, J.; Lee, H.H.S.; Wei, G.Y.; Brooks, D.; Wu, C.J. Chasing Carbon: The Elusive Environmental Footprint of Computing. IEEE Micro 2022, 42, 37–47. [Google Scholar] [CrossRef]
- Patterson, D.; Gonzalez, J.; Le, Q.; Liang, C.; Munguia, L.-M.; Rothchild, D.; So, D.; Texier, M.; Dean, J. Carbon Emissions and Large Neural Network Training. arXiv 2021, arXiv:2104.10350. [Google Scholar]
- Li, B.; Roy, R.B.; Wang, D.; Samsi, S.; Gadepally, V.; Tiwari, D. Toward Sustainable HPC: Carbon Footprint Estimation and Environmental Implications of HPC Systems. In Proceedings of the SC’23: International Conference for High Performance Computing, Networking, Storage and Analysis, Denver, CO, USA, 12–17 November 2023; IEEE Computer Society: Washington, DC, USA, 2023. [Google Scholar]
- Mathrani, R. Challenges and Innovations in Achieving Sustainable Computing: A Comprehensive Analysis. Int. J. Sci. Res. 2023, 12, 203–209. [Google Scholar] [CrossRef]
- Haghshenas, K.; Setz, B.; Bloch, Y.; Aiello, M. Enough Hot Air: The Role of Immersion Cooling. Energy Inform. 2022, 6, 14. [Google Scholar] [CrossRef]
- Souza, A.; Jasoria, S.; Chakrabarty, B.; Irwin, D.; Shenoy, P.; Bridgwater, A.; Lundberg, A.; Skogh, F.; Ali-Eldin, A. CASPER: Carbon-Aware Scheduling and Provisioning for Distributed Web Services. In Proceedings of the IGSC ’23: Proceedings of the 14th International Green and Sustainable Computing Conference, Toronto, ON, Canada, 28–29 October 2023; Association for Computing Machinery: New York, NY, USA, 2023; pp. 67–73. [Google Scholar]
- Lannelongue, L.; Aronson, H.E.G.; Bateman, A.; Birney, E.; Caplan, T.; Juckes, M.; McEntyre, J.; Morris, A.D.; Reilly, G.; Inouye, M. GREENER principles for environmentally sustainable computational science. Nat. Comput. Sci. 2023, 3, 514–521. [Google Scholar] [CrossRef] [PubMed]
- Lannelongue, L.; Grealey, J.; Inouye, M. Green Algorithms: Quantifying the Carbon Footprint of Computation. Adv. Sci. 2021, 8, 2100707. [Google Scholar] [CrossRef]
- Portegies Zwart, S. The ecological impact of high-performance computing in astrophysics. Nat. Astron. 2020, 4, 819–822. [Google Scholar] [CrossRef]
- Cho, J.; Nam, S.; Yang, H.; Yun, S.-B.; Hong, Y.; Park, E. Separable Physics-Informed Neural Networks. In Proceedings of the 37th Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Sui, Z.; Wu, W. AI-assisted maldistribution minimization of membrane-based heat/mass exchangers for compact absorption cooling. Energy 2023, 263, 125922. [Google Scholar] [CrossRef]
- Jaluria, Y. Optimization of Thermal Systems to Reduce Energy Consumption and Environmental Effect. Tech. Ital. J. Eng. Sci. 2019, 63, 1–12. [Google Scholar] [CrossRef]
- Wang, Y.; Krolick, W.C.; Kaminsky, A.L.; Tison, N.; Ruan, Y.; Korivi, V.; Pant, K. A hybrid reduced order modeling approach for rapid transient thermal simulation and signature analysis. In Proceedings of the 2021 NDIA Ground Vehicle Systems Engineering And Technology Symposium, Novi, MI, USA, 10–12 August 2024. [Google Scholar]
- Gaspar, P.D.; Da Silva, P.D.; Gonçalves, J.P.M.; Carneiro, R. Computational modelling and simulation to assist the improvement of thermal performance and energy efficiency in industrial engineering systems: Application to cold stores. In Handbook of Research on Computational Simulation and Modeling in Engineering; IGI Global: Hershey, PA, USA, 2015; pp. 1–67. ISBN 9781466688247. [Google Scholar]
- Gul, E.; Wang, J.; Zhang, G. Simulation and Optimization Model for Energy Efficient Building and Environmental Assessment. In Proceedings of the 2nd IEEE Conference on Energy Internet and Energy System Integration, EI2 2018, Beijing, China, 20–22 October 2018; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2018. [Google Scholar]
- Jin, Z.L.; Chen, X.T.; Wang, Y.Q.; Liu, M.S. Heat exchanger network synthesis based on environmental impact minimization. Clean Technol. Environ. Policy 2014, 16, 183–187. [Google Scholar] [CrossRef]
- Gabor, T.; Dan, V.; Tiuc, A.E.; Sur, I.M.; Bădilă, I.N. Modelling and simulation of heat transfer processes for heat exchangers used in wastewater treatment. Environ. Eng. Manag. J. 2016, 15, 1027–1033. [Google Scholar] [CrossRef]
- Eze, V.H.U.; Tamball, J.S. Advanced Modeling Approaches for Latent Heat Thermal Energy Storage Systems. IAA J. Appl. Sci. 2024, 11, 49–56. [Google Scholar] [CrossRef]
- Nguyen, G.; Šipková, V.; Dlugolinsky, S.; Nguyen, B.M.; Tran, V.; Hluchý, L. A comparative study of operational engineering for environmental and compute-intensive applications. Array 2021, 12, 100096. [Google Scholar] [CrossRef]
- Reveron Baecker, B.; Hamacher, T.; Slednev, V.; Müller, G.; Sehn, V.; Winkler, J.; Bailey, I.; Gardian, H.; Gils, H.C.; Muschner, C.; et al. Comprehensive and open model structure for the design of future energy systems with sector coupling. Renew. Sustain. Energy Transit. 2025, 6, 100094. [Google Scholar] [CrossRef]
- Acun, B.; Usa, M.; Lee, B.; Kazhamiaka, F.; Maeng, K.; Gupta, U.; Chakkaravarthy, M.; Brooks, D.; Wu, C.-J. Carbon Explorer: A Holistic Framework for Designing Carbon Aware Datacenters. In Proceedings of the 28th ACM International Conference on Architectural Support for Programming Languages and Operating Systems, Vancouver, BC, Canada, 25–29 March 2023; Volume 1. [Google Scholar]
- Mahmud, M.A.P.; Huda, N.; Farjana, S.H.; Lang, C. Environmental Impacts of Solar-Photovoltaic and Solar-Thermal Systems with Life-Cycle Assessment. Energies 2018, 11, 2346. [Google Scholar] [CrossRef]
- Struhala, K.; Stránská, Z.; Pěnčík, J.; Matějka, L. Environmental assessment of thermal insulation composite material. Int. J. Life Cycle Assess. 2014, 19, 1908–1918. [Google Scholar] [CrossRef]
- Zhukov, A.D.; Zhuk, P.M.; Stepina, I.V. Assessment of the environmental impact on the life cycle of polystyrene thermal insulation materials. J. Phys. Conf. Ser. 2022, 2388, 012101. [Google Scholar] [CrossRef]
- Salaudeen, S.A. Investigation on the performance and environmental impact of a latent heat thermal energy storage system. J. King Saud Univ. Eng. Sci. 2019, 31, 368–374. [Google Scholar] [CrossRef]
- Balli, L.; Hlimi, M.; Achenani, Y.; Atifi, A.; Hamri, B. Experimental study and numerical modeling of the thermal behavior of an industrial prototype ceramic furnace: Energy and environmental optimization. Energy Built Environ. 2024, 5, 244–254. [Google Scholar] [CrossRef]
- Struhala, K.; Ostrý, M. Life-Cycle Assessment of phase-change materials in buildings: A review. J. Clean. Prod. 2022, 336, 130359. [Google Scholar] [CrossRef]
- Bernal, D.C.; Muñoz, E.; Manente, G.; Sciacovelli, A.; Ameli, H.; Gallego-Schmid, A. Environmental assessment of latent heat thermal energy storage technology system with phase change material for domestic heating applications. Sustainability 2021, 13, 11265. [Google Scholar] [CrossRef]
- Sharma, P.; Pegus, P.; Irwin, D.; Shenoy, P.; Goodhue, J.; Culbert, J. Design and Operational Analysis of a Green Data Center. IEEE Internet Comput. 2017, 21, 16–24. [Google Scholar] [CrossRef]
- Chien, A.A. Owning computing’s environmental impact. Commun. ACM 2019, 62, 5. [Google Scholar] [CrossRef]
- Murino, T.; Monaco, R.; Nielsen, P.S.; Liu, X.; Esposito, G.; Scognamiglio, C. Sustainable Energy Data Centres: A Holistic Conceptual Framework for Design and Operations. Energies 2023, 16, 5764. [Google Scholar] [CrossRef]
- Naug, A.; Guillen, A.; Luna, R.; Gundecha, V.; Rengarajan, D.; Ghorbanpour, S.; Mousavi, S.; Babu, A.R.; Markovikj, D.; Kashyap, L.D.; et al. SustainDC: Benchmarking for Sustainable Data Center Control. arXiv 2024, arXiv:2408.07841. [Google Scholar]
- Khaleel, T.; Kareem, J. A Review of Issues and Challenges to Address the Problem of Implementing Green Computing for Sustainability. Al-Rafidain Eng. J. 2023, 28, 300–311. [Google Scholar] [CrossRef]
- Hoheisel, A.; Betterman, B.; Dunham, I.; O’Leary, H.; Mahmoud, M. Green Computing from a Holistic Perspective. In Proceedings of the 2022 International Conference on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, 14–16 December 2022; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2022; pp. 1299–1302. [Google Scholar]
- Pazienza, A.; Baselli, G.; Vinci, D.C.; Trussoni, M.V. A holistic approach to environmentally sustainable computing. Innov. Syst. Softw. Eng. 2024, 20, 347–371. [Google Scholar] [CrossRef]
- Dombrovsky, L.A.; Li, X. Editorial: Editor’s challenge in heat transfer mechanisms and applications: 2022. Front. Therm. Eng. 2023, 3, 1203906. [Google Scholar] [CrossRef]
- Danilushkin, I.; Diligenskaya, A.; Kolpashchikov, S. Dynamic Models of Heat Exchangers under Restrictions of Computational Resources. In Proceedings of the 2020 International Multi-Conference on Industrial Engineering and Modern Technologies, FarEastCon 2020, Vladivostok, Russia, 6–9 October 2020; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2020. [Google Scholar]
- Menin, B.M. Accuracy limits of modelling predictions of multivariable heat and mass transfer processes. Int. J. Math. Model. Numer. Optim. 2015, 6, 321–336. [Google Scholar] [CrossRef]
- Degroote, J. Partitioned Simulation of Fluid-Structure Interaction. Arch. Comput. Methods Eng. 2013, 20, 185–238. [Google Scholar] [CrossRef]
- Robinson-Mosher, A.; Schroeder, C.; Fedkiw, R. A symmetric positive definite formulation for monolithic fluid structure interaction. J. Comput. Phys. 2011, 230, 1547–1566. [Google Scholar] [CrossRef]
- Boustani, J.; Barad, M.F.; Kiris, C.C.; Brehm, C. An immersed boundary fluid–structure interaction method for thin, highly compliant shell structures. J. Comput. Phys. 2021, 438, 110369. [Google Scholar] [CrossRef]
- Basting, S.; Quaini, A.; Čanić, S.; Glowinski, R. Extended ALE Method for fluid–structure interaction problems with large structural displacements. J. Comput. Phys. 2017, 331, 312–336. [Google Scholar] [CrossRef]
- Saye, R.I.; Sethian, J.A. A review of level set methods to model interfaces moving under complex physics: Recent challenges and advances. In Handbook of Numerical Analysis; Elsevier: Amsterdam, The Netherlands, 2020; Volume 21, pp. 509–554. ISBN 9780444640031. [Google Scholar]
- Mirjalili, S.; Ivey, C.B.; Mani, A. Comparison between the diffuse interface and volume of fluid methods for simulating two-phase flows. Int. J. Multiph. Flow 2019, 116, 221–238. [Google Scholar] [CrossRef]
- Lakehal, D.; Caviezel, D. Large-Eddy Simulation of convective wall-boiling flow along an idealized PWR rod bundle. Nucl. Eng. Des. 2017, 321, 104–117. [Google Scholar] [CrossRef]
- Owoeye, E.J.; Schubring, D.W. CFD analysis of bubble microlayer and growth in subcooled flow boiling. Nucl. Eng. Des. 2016, 304, 151–165. [Google Scholar] [CrossRef]
- Shafi, J.; Ghalambaz, M.; Fteiti, M.; Ismael, M.; Ghalambaz, M. Computational Modeling of Latent Heat Thermal Energy Storage in a Shell-Tube Unit: Using Neural Networks and Anisotropic Metal Foam. Mathematics 2022, 10, 4774. [Google Scholar] [CrossRef]
- Belhamadia, Y.; Fortin, A.; Briffard, T. A two-dimensional adaptive remeshing method for solving melting and solidification problems with convection. Numer. Heat Transf. Part A Appl. 2019, 76, 179–197. [Google Scholar] [CrossRef]
- Bazgir, A.; Zhang, Y. Harnessing Deep Learning to Solve Inverse Transient Heat Transfer with Periodic Boundary Condition. J. Therm. Sci. Eng. Appl. 2024, 16, 121001. [Google Scholar] [CrossRef]
- Mei, T.; Zhao, J.; Liu, Z.; Peng, X.; Chen, Z.; Bobaru, F. The Role of Boundary Conditions on Convergence Properties of Peridynamic Model for Transient Heat Transfer. J. Sci. Comput. 2021, 87, 50. [Google Scholar] [CrossRef]
- Ren, J.; Xu, K.; Ren, H.; Jiang, T.; Yuan, J. Numerical Study of the 3D Variable Coefficient Heat Transfer Problem by Using the Finite Pointset Method. Arab. J. Sci. Eng. 2021, 46, 3483–3502. [Google Scholar] [CrossRef]
- Li, X.X.; Wang, L.; Li, C.Y.; Wan, Y.Y.; Qian, Y.C. Semianalytical Solution of Transient Heat Transfer for Laminated Structures under Time-Varying Boundary Conditions. Math. Probl. Eng. 2021, 2021, 5545566. [Google Scholar] [CrossRef]
- Gondipalli, S.; Ibrahim, M.; Bhopte, S.; Sammakia, B.; Murray, B.; Ghose, K.; Iyengar, M.K.; Schmidt, R. Numerical modeling of data center with transient boundary conditions. In Proceedings of the 2010 12th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, ITherm 2010, Las Vegas, NV, USA, 2–5 June 2010. [Google Scholar]
- Bindick, S.; Ahrenholz, B.; Krafczyk, M. Efficient Simulation of Transient Heat Transfer Problems in Civil Engineering. In Heat Transfer-Mathematical Modelling, Numerical Methods and Information Technology; InTech: London, UK, 2011. [Google Scholar]
- Loyola-Fuentes, J.; Nazemzadeh, N.; Diaz-Bejarano, E.; Mancin, S.; Coletti, F. A framework for data regression of heat transfer data using machine learning. Appl. Therm. Eng. 2024, 248, 123043. [Google Scholar] [CrossRef]
- Soibam, J.; Aslanidou, I.; Kyprianidis, K.; Fdhila, R.B. Inverse flow prediction using ensemble PINNs and uncertainty quantification. Int. J. Heat Mass Transf. 2024, 226, 125480. [Google Scholar] [CrossRef]
- Helleso, S.M.; Eberg, E. Simplified Model for Heat Transport for Cables in Pipes. IEEE Trans. Power Deliv. 2022, 37, 3813–3822. [Google Scholar] [CrossRef]
- Dey, S.; Joshi, Y. Recent Progress and Challenges in Microscale Urban Heat Modeling and Measurement for Urban Engineering Applications. J. Therm. Sci. Eng. Appl. 2023, 15, 010801. [Google Scholar] [CrossRef]
- Regnier, G.; Salinas, P.; Jacquemyn, C.; Jackson, M.D. Numerical simulation of aquifer thermal energy storage using surface-based geologic modelling and dynamic mesh optimisation. Hydrogeol. J. 2022, 30, 1179–1198. [Google Scholar] [CrossRef]
- Kaewbumrung, M.; Charoenloedmongkhon, A. Numerical Simulation of Turbulent Flow in Eccentric Co-Rotating Heat Transfer. Fluids 2022, 7, 131. [Google Scholar] [CrossRef]
- Dmytro, S.; Szymon, B.; Michal, K. An extended laser beam heating model for a numerical platform to simulate multi-material selective laser melting. Int. J. Adv. Manuf. Technol. 2023, 128, 3451–3470. [Google Scholar] [CrossRef]
- Pal, S.; Bhattacharya, M.; Dash, S.; Lee, S.S.; Chakraborty, C. Future Potential of Quantum Computing and Simulations in Biological Science. Mol. Biotechnol. 2023, 66, 2201–2218. [Google Scholar] [CrossRef]
- Singh, N.B. From Schrodinger’s Equation to Deep Learning: A Quantum Approach; AdmitHub Reference Service Press: Noida, India, 2023; ISBN 9798850817046. Available online: https://www.harvard.com/book/9798850817046 (accessed on 23 February 2025).
- Leong, F.Y.; Ewe, W.B.; Koh, D.E. Variational quantum evolution equation solver. Sci. Rep. 2022, 12, 10817. [Google Scholar] [CrossRef] [PubMed]
- Daribayev, B.; Mukhanbet, A.; Azatbekuly, N.; Imankulov, T. A Quantum Approach for Exploring the Numerical Results of the Heat Equation. Algorithms 2024, 17, 327. [Google Scholar] [CrossRef]
- Qian, W.; Wu, B. Quantum computation in fermionic thermal field theories. J. High Energy Phys. 2024, 2024, 166. [Google Scholar] [CrossRef]
- Araz, J.Y.; Spannowsky, M.; Wingate, M. Exploring thermal equilibria of the Fermi-Hubbard model with variational quantum algorithms. Phys. Rev. A 2024, 109, 062422. [Google Scholar] [CrossRef]
- Mueller, N.; Wang, T.; Katz, O.; Davoudi, Z.; Cetina, M. Quantum Computing Universal Thermalization Dynamics in a (2+1) D Lattice Gauge Theory. arXiv 2024, arXiv:2408.00069. [Google Scholar]
- Ye, C.C.; An, N.B.; Ma, T.Y.; Dou, M.H.; Bai, W.; Sun, D.J.; Chen, Z.Y.; Guo, G.P. A hybrid quantum-classical framework for computational fluid dynamics. Phys. Fluids 2024, 36, 127111. [Google Scholar] [CrossRef]
- Koska, O.; Baboulin, M.; Gazda, A. A mixed-precision quantum-classical algorithm for solving linear systems. arXiv 2025, arXiv:2502.02212. [Google Scholar]
- Oz, F.; San, O.; Kara, K. An efficient quantum partial differential equation solver with chebyshev points. Sci. Rep. 2023, 13, 7767. [Google Scholar] [CrossRef]
- Lokare, Y.M.; Wei, D.; Chan, L.; Rubenstein, B.M.; Marston, J.B. Steady-State Statistics of Classical Nonlinear Dynamical Systems from Noisy Intermediate-Scale Quantum Devices. arXiv 2024, arXiv:2409.06036. [Google Scholar]
- Guo, X.-Y.; Li, S.-S.; Xiao, X.; Xiang, Z.-C.; Ge, Z.-Y.; Li, H.-K.; Song, P.-T.; Peng, Y.; Wang, Z.; Xu, K.; et al. Variational quantum simulation of thermal statistical states on a superconducting quantum processer. Chin. Phys. B 2023, 32, 010307. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, D.; Wang, C.; Xi, H. An innovative end-to-end PINN-based solution for rapidly simulating homogeneous heat flow problems: An adaptive universal physics-guided auto-solver. Case Stud. Therm. Eng. 2024, 56, 104277. [Google Scholar] [CrossRef]
- Liu, G.; Li, R.; Zhou, X.; Sun, T.; Zhang, Y. Reconstruction and fast prediction of 3D heat and mass transfer based on a variational autoencoder. Int. Commun. Heat Mass Transf. 2023, 149, 107112. [Google Scholar] [CrossRef]
- Jia, Y.; Saadlaoui, Y.; Feulvarch, E.; Bergheau, J.M. An efficient local moving thermal-fluid framework for accelerating heat and mass transfer simulation during welding and additive manufacturing processes. Comput. Methods Appl. Mech. Eng. 2024, 419, 116673. [Google Scholar] [CrossRef]
- Belhamadia, Y.; Seaid, M. Computing enhancement of the nonlinear SPN approximations of radiative heat transfer in participating material. J. Comput. Appl. Math. 2023, 434, 115342. [Google Scholar] [CrossRef]
- Ghadikolaei, S.S.; Siahchehrehghadikolaei, S.; Gholinia, M.; Rahimi, M. A CFD modeling of heat transfer between CGNPs/H2O Eco-friendly nanofluid and the novel nature-based designs heat sink: Hybrid passive techniques for CPU cooling. Therm. Sci. Eng. Prog. 2023, 37, 101604. [Google Scholar] [CrossRef]
- Aljehani, A.; Nitsche, L.C.; Al-Hallaj, S. Numerical modeling of transient heat transfer in a phase change composite thermal energy storage (PCC-TES) system for air conditioning applications. Appl. Therm. Eng. 2020, 164, 114522. [Google Scholar] [CrossRef]
- Adrian, Ł.; Szufa, S.; Piersa, P.; Mikołajczyk, F. Numerical Model of Heat Pipes as an Optimization Method of Heat Exchangers. Energies 2021, 14, 7647. [Google Scholar] [CrossRef]
- Ruiz, M.; Masson, V.; Bonhomme, M.; Ginestet, S. Numerical method for solving coupled heat and mass transfer through walls for future integration into an urban climate model. Build. Environ. 2023, 231, 110028. [Google Scholar] [CrossRef]
- Terraneo, F.; Leva, A.; Fornaciari, W. An Open-Hardware Platform for MPSoC Thermal Modeling. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Samos, Greece, 7–11 July 2019; Springer: Cham, Germany, 2019; Volume 11733 LNCS, pp. 184–196. [Google Scholar]
- Gunnell, L.G.; Nicholson, B.; Hedengren, J.D. Equation-based and data-driven modeling: Open-source software current state and future directions. Comput. Chem. Eng. 2024, 181, 108521. [Google Scholar] [CrossRef]
- Bayat, S.; Shahmansouri, N.; Peddada, S.R.; Tessier, A.; Butscher, A.; Allison, J.T. Advancing Fluid-Based Thermal Management Systems Design: Leveraging Graph Neural Networks for Graph Regression and Efficient Enumeration Reduction. In Proceedings of the ASME 2024 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 25–28 August 2024. [Google Scholar]
- Han, X.; Tian, W.; VanGilder, J.; Zuo, W.; Faulkner, C. An open source fast fluid dynamics model for data center thermal management. Energy Build. 2021, 230, 110599. [Google Scholar] [CrossRef]



| Method | Scope of Application | Computational Cost | Accuracy | Advantages | Disadvantages |
|---|---|---|---|---|---|
| FDM | Heat conduction, simple geometries | Low to moderate | Moderate | Easy to implement, sufficiently efficient for structured grids | Limited to structured grids, less flexible for complex geometries |
| FEM | Structural-thermal interactions, complex geometries | Moderate to high | High | High accuracy, sufficiently flexible for complex geometries | Computationally expensive, requires meshing |
| FVM | Fluid and thermal simulations, CFD applications | Moderate | High | Conservative properties, suitable for control volume approach | Requires complex discretization for accuracy |
| CFD | General fluid flow and thermal interactions | Moderate to high | High | Sufficiently versatile for fluid dynamics problems | Computationally intensive for transient simulations |
| LBM | Micro-scale and porous media flow, multiphysics applications | High | Moderate to high | Suitable for parallel computing, captures complex boundaries | Requires large computational resources, limited industrial adoption |
| SPH | Free-surface flows, highly deformable materials | Moderate to high | Moderate | Mesh-free, sufficiently efficient for complex interfaces | High computational cost, lower accuracy in some cases |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łach, Ł.; Svyetlichnyy, D. Advances in Numerical Modeling for Heat Transfer and Thermal Management: A Review of Computational Approaches and Environmental Impacts. Energies 2025, 18, 1302. https://doi.org/10.3390/en18051302
Łach Ł, Svyetlichnyy D. Advances in Numerical Modeling for Heat Transfer and Thermal Management: A Review of Computational Approaches and Environmental Impacts. Energies. 2025; 18(5):1302. https://doi.org/10.3390/en18051302
Chicago/Turabian StyleŁach, Łukasz, and Dmytro Svyetlichnyy. 2025. "Advances in Numerical Modeling for Heat Transfer and Thermal Management: A Review of Computational Approaches and Environmental Impacts" Energies 18, no. 5: 1302. https://doi.org/10.3390/en18051302
APA StyleŁach, Ł., & Svyetlichnyy, D. (2025). Advances in Numerical Modeling for Heat Transfer and Thermal Management: A Review of Computational Approaches and Environmental Impacts. Energies, 18(5), 1302. https://doi.org/10.3390/en18051302







