Study on the Deflagration Characteristics of Methane–Air Premixed Gas in Sudden Expansion Pipelines
Abstract
1. Introduction
2. Experimental Setup and Methods
2.1. Experimental Setup
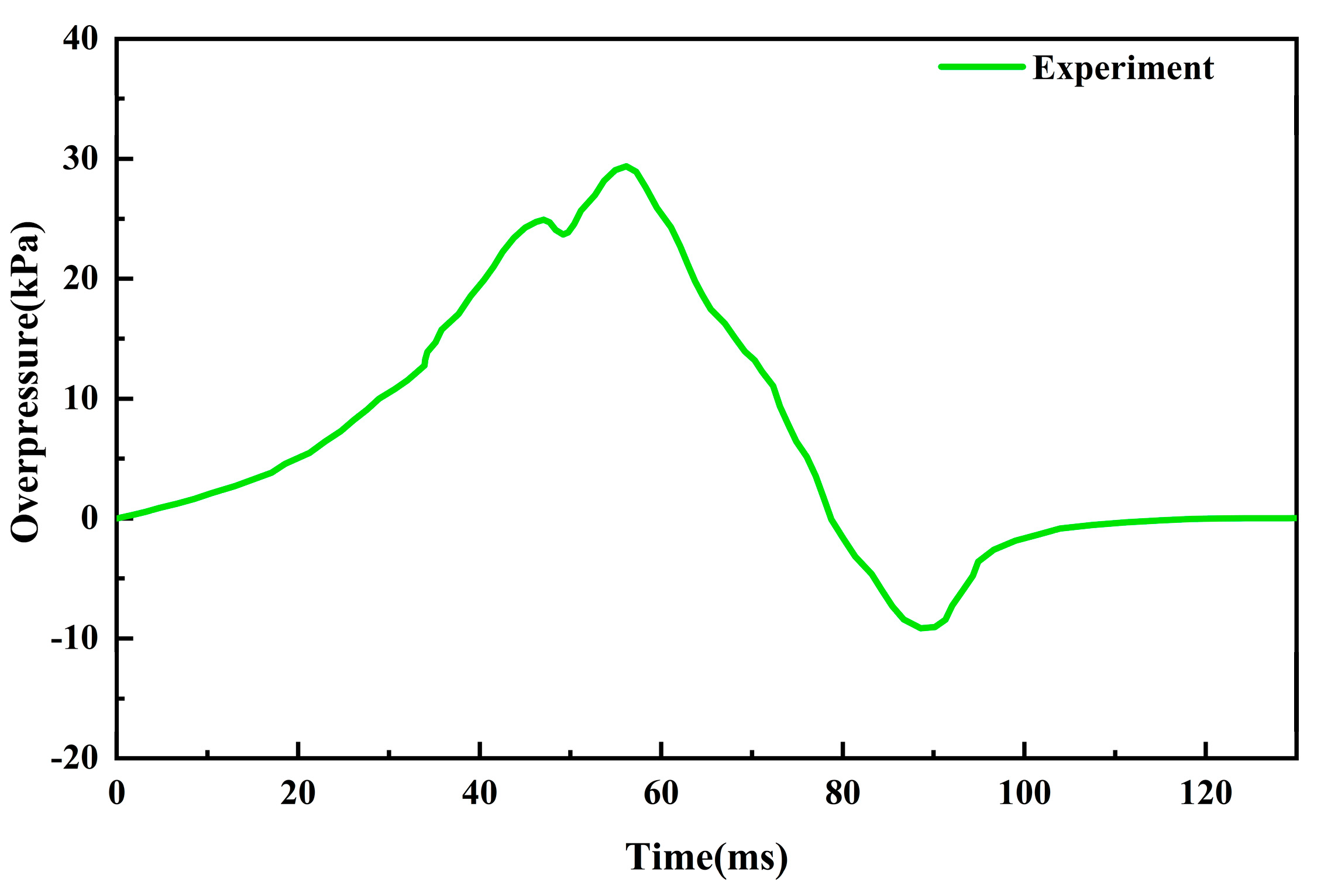
2.2. Experimental Methods
3. Numerical Models and Details
3.1. Governing Equations
3.2. Geometric Models and Numerical Details
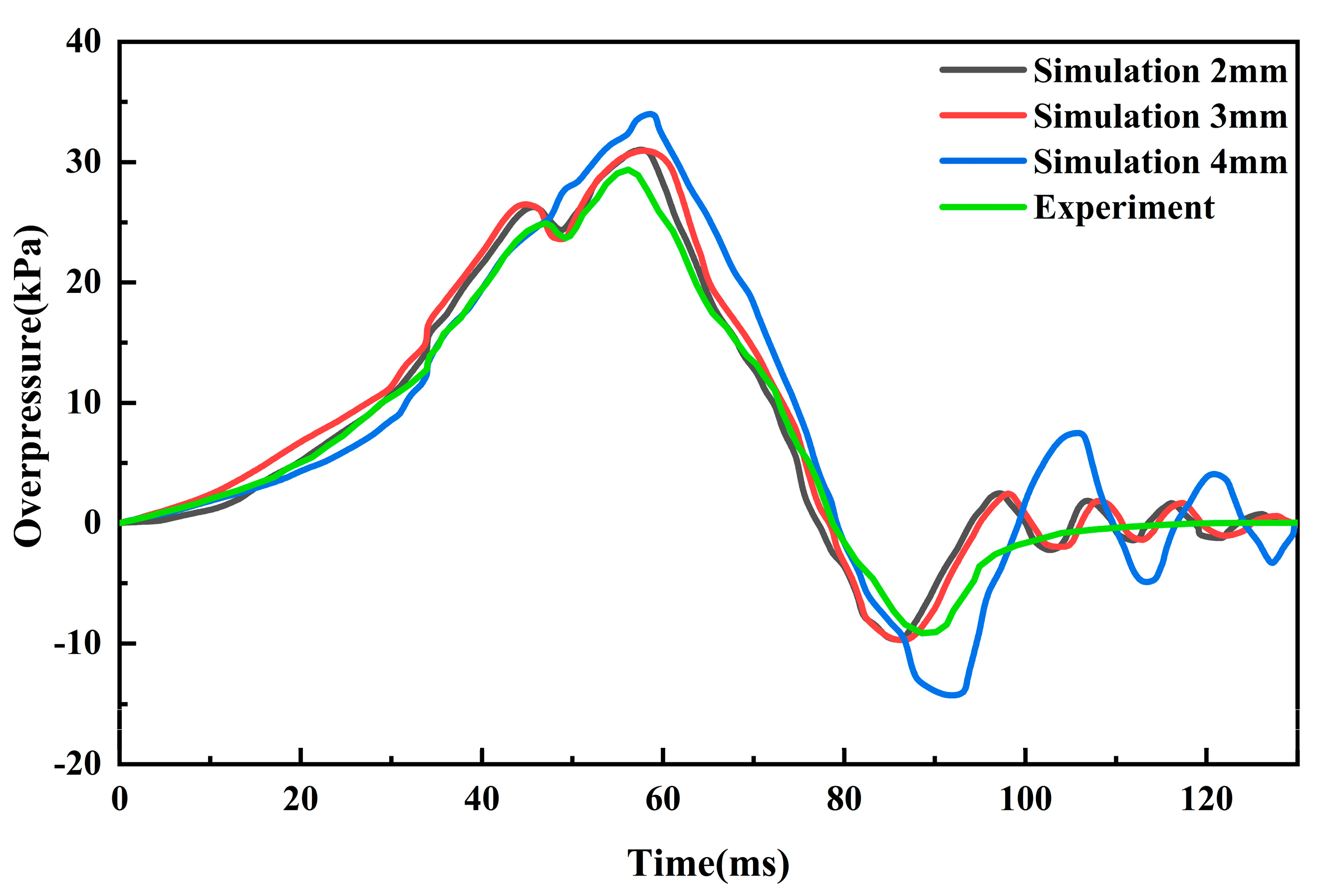
3.3. Model Validation
4. Results and Discussion
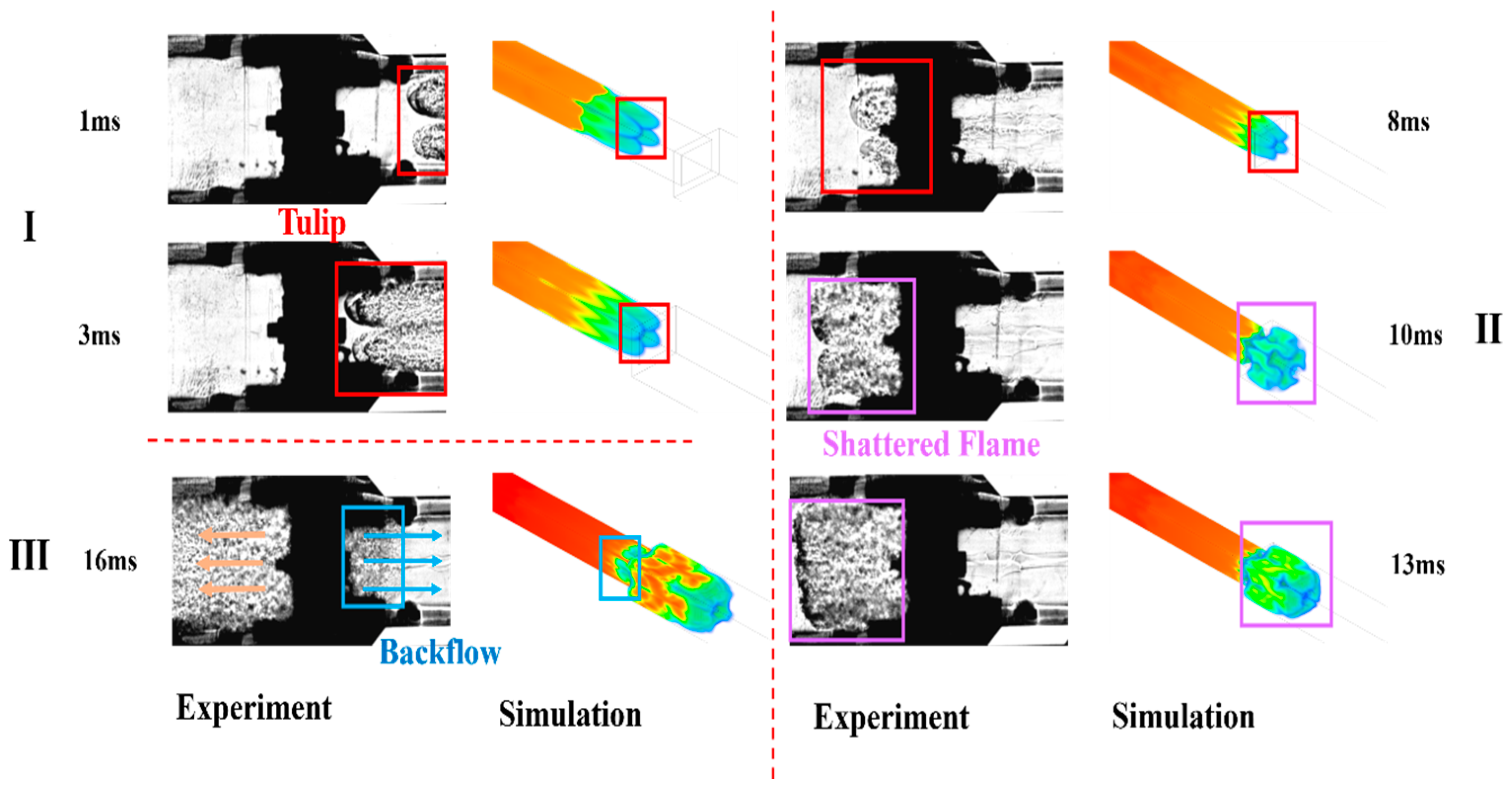
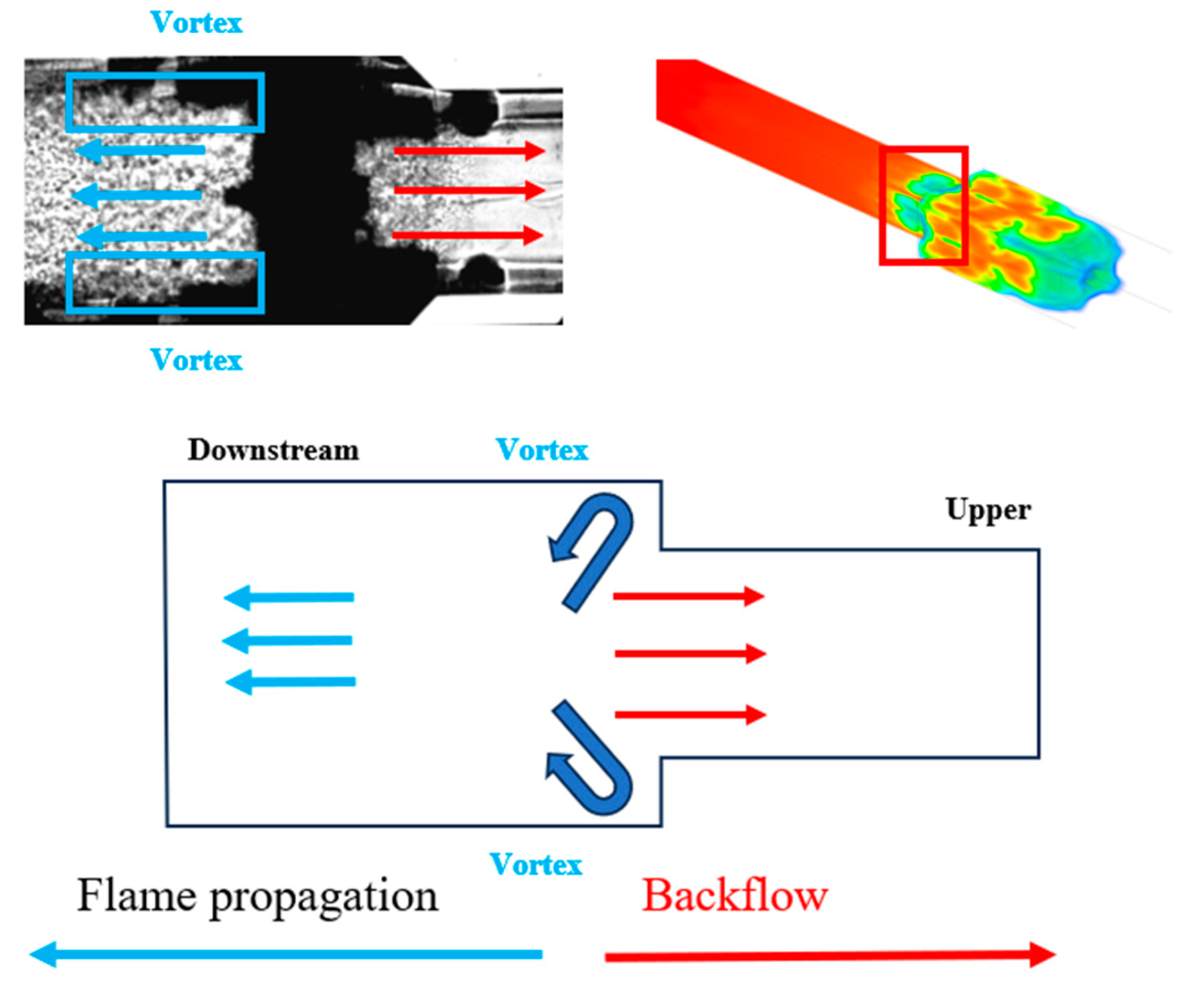
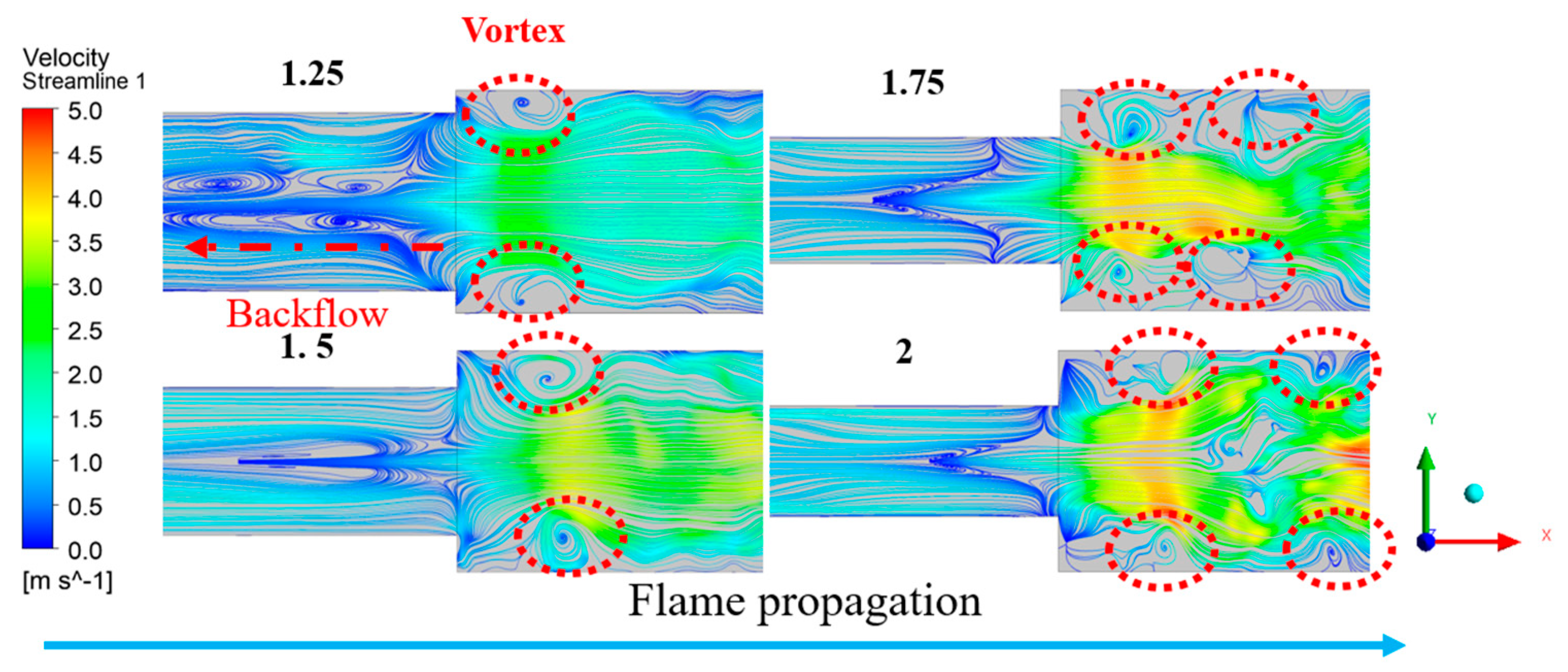
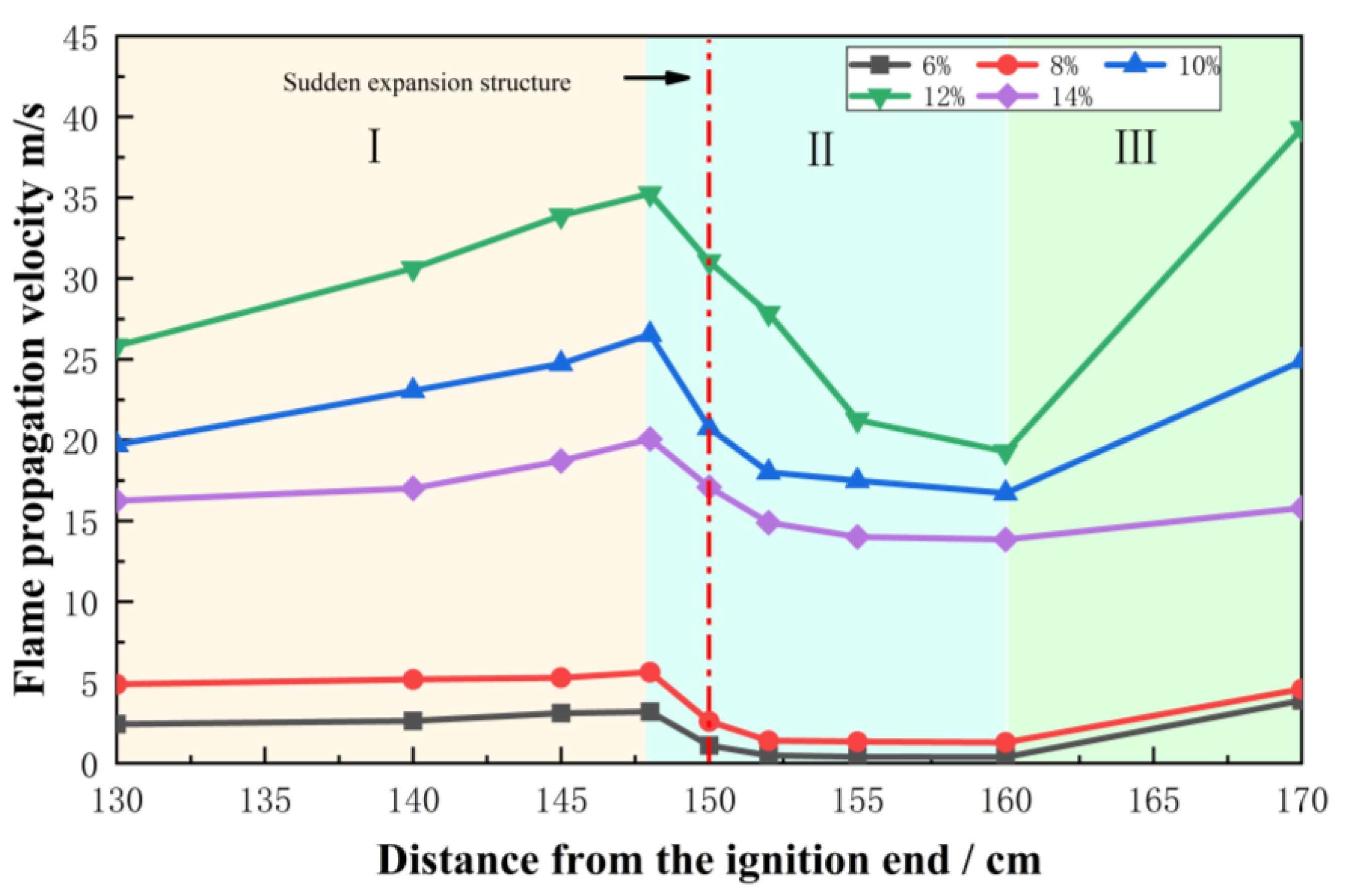
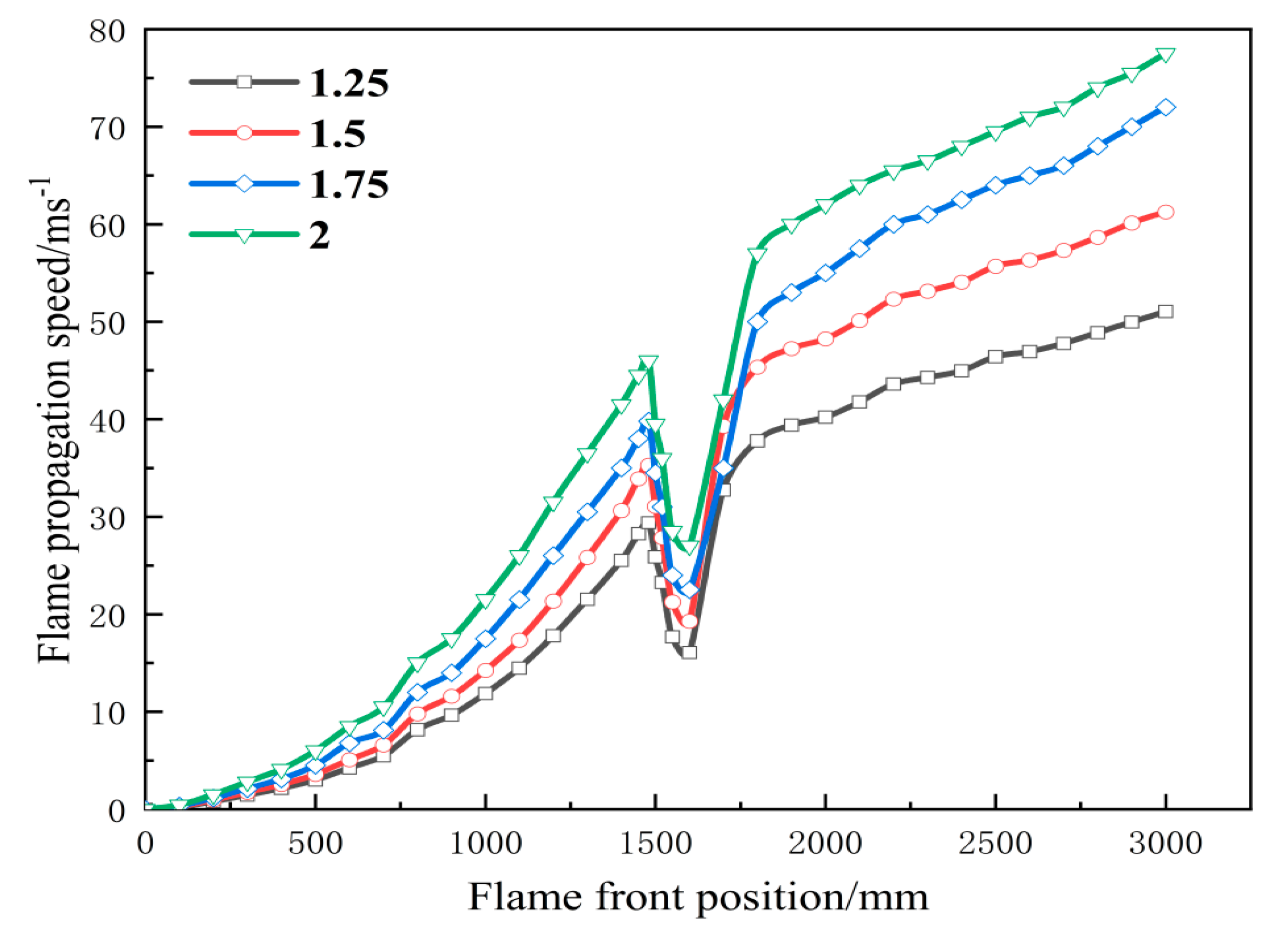
4.1. Impact of Sudden Pipeline Expansion on Flame Propagation Dynamics
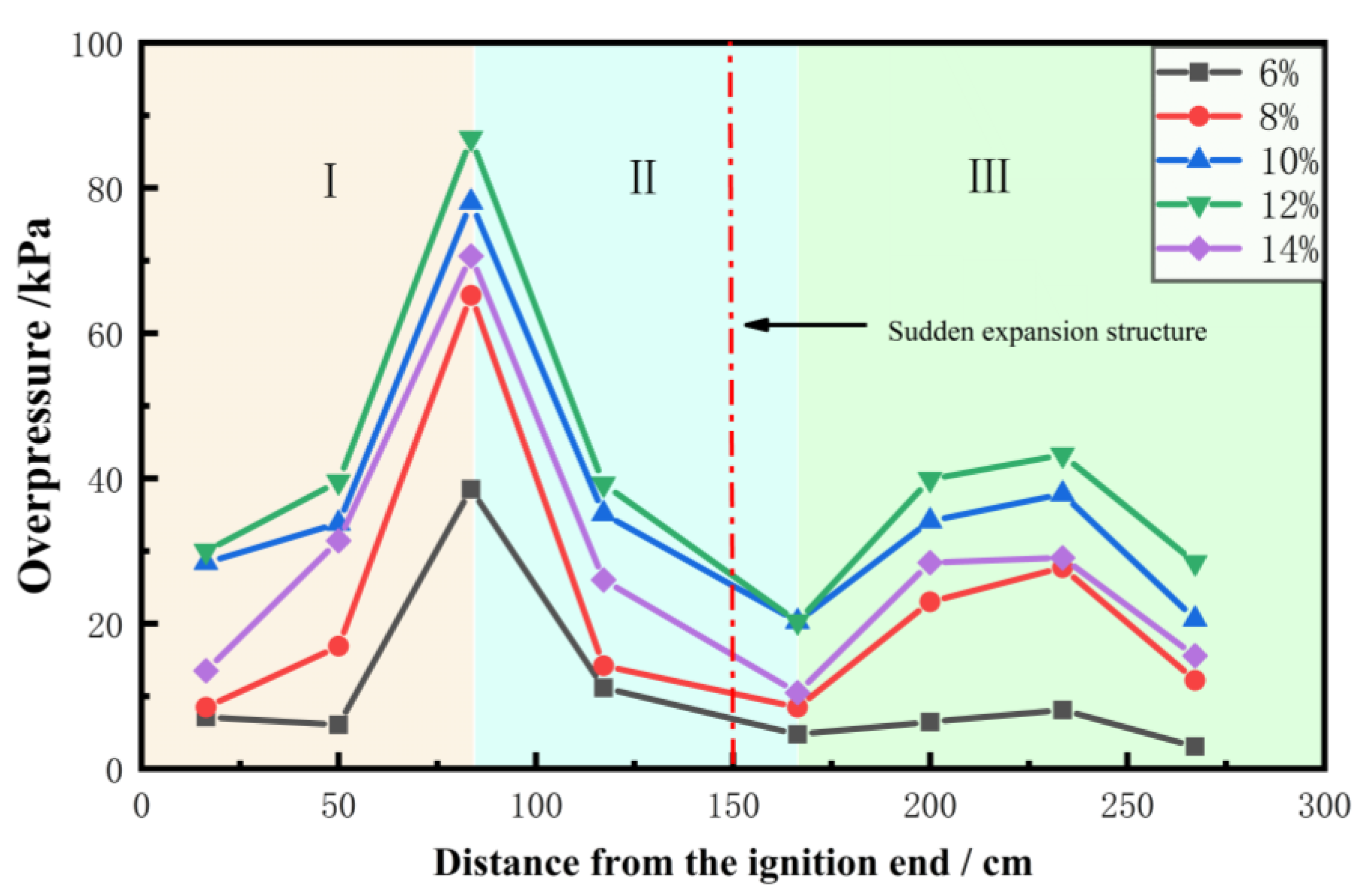
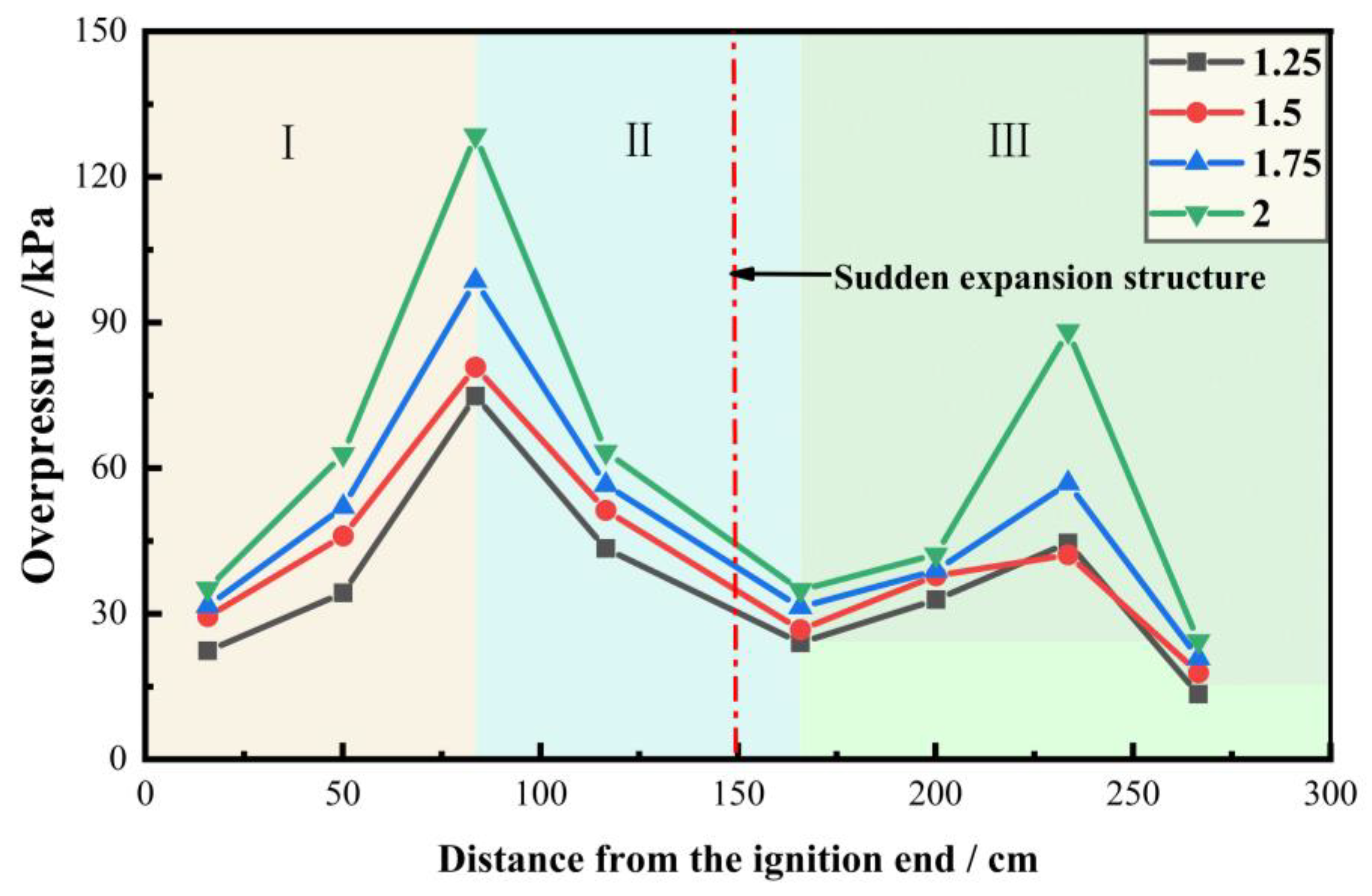
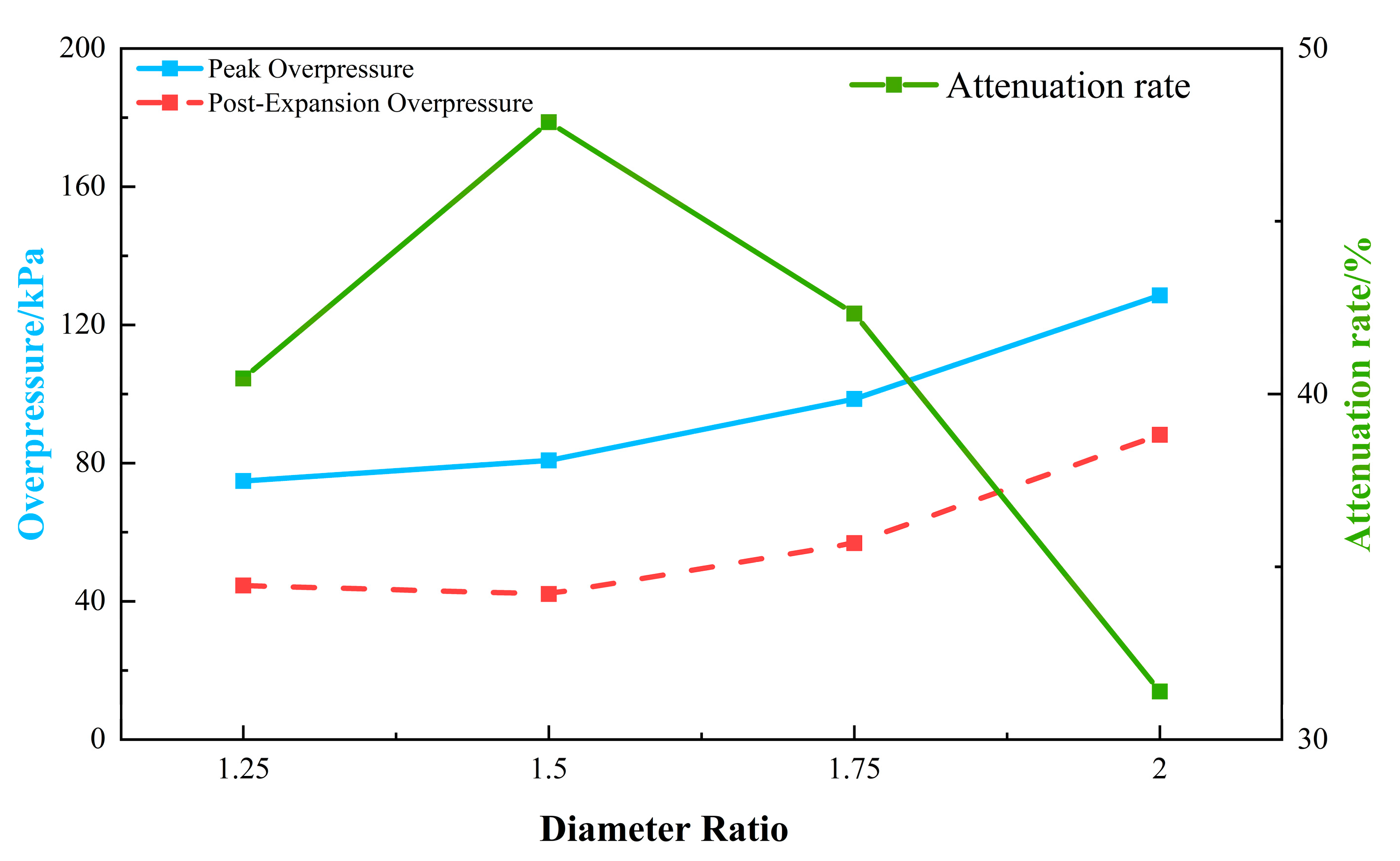
4.2. Impact of Sudden Pipeline Expansion on Explosion Overpressure Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| D1, D2 | Diameter of the pipeline at the initial and expanded sections |
| ∆D | Diameter difference between the two sections of the pipeline |
| L | Length of the pipeline |
| P | Pressure |
| ΔP | Pressure difference |
| Pmax | Maximum overpressure |
| Pmin | Minimum overpressure |
| T | Kelvin |
| Vf | Flame propagation velocity |
| Φ | Equivalence ratio of the methane–air mixture |
| ρ | Density of the gas mixture |
| u’ | Subgrid turbulent fluctuation velocity |
| v | Viscosity of the gas mixture |
| ReT | Turbulent Reynolds number |
| α | Thermal diffusivity |
| λ | Turbulent characteristic length scale |
| λL | Laminar burning velocity |
| Cp | Specific heat at constant pressure |
| β | Flame stretch factor |
| Keff | Effective turbulent kinetic energy |
| E | Energy |
| Dr | Diameter ratio of the sudden expansion |
References
- Vo, D.H.; Vo, A.T.; Ho, C.M.; Nguyen, H.M. The role of renewable energy, alternative and nuclear energy in mitigating carbon emissions in the CPTPP countries. Renew. Energy 2020, 161, 278–292. [Google Scholar] [CrossRef]
- Li, L. National Gas Accident Analysis Report (2024, First Half Report)—Gas Safety Situation Continues to Improve. China Energy News 2024. Available online: http://paper.people.com.cn/zgnyb/pc/attachement/202410/14/8437e99a-3c63-43c8-9a5a-9a7b4924c136.pdf (accessed on 14 February 2025).
- Tang, C.; Zhang, S.; Si, Z.; Huang, Z.; Zhang, K.; Jin, Z. High methane natural gas/air explosion characteristics in confined vessel. J. Hazard. Mater. 2014, 278, 520–528. [Google Scholar] [CrossRef] [PubMed]
- Kundu, S.; Zanganeh, J.; Moghtaderi, B. A review on understanding explosions from methane–air mixture. J. Loss Prev. Process Ind. 2016, 40, 507–523. [Google Scholar] [CrossRef]
- Kuznetsov, M.S.; Alekseev, V.I.; Yankin, Y.G.; Dorofeev, S.B. Flame acceleration in a tube with variable cross-section. J. Phys. IV 2002, 12, 317–324. [Google Scholar] [CrossRef]
- Fan, H.Y.; Lu, F.K. Numerical simulation of detonation processes in a variable cross-section chamber. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2008, 222, 673–686. [Google Scholar] [CrossRef]
- Zheng, Y.-S.; Wang, C. Numerical simulation for the influence of variable cross-section tube on explosion characteristics of methane. Trans. Beijing Inst. Technol. 2009, 11, 947–949. [Google Scholar]
- Liu, J.; Yao, L.; Zhang, Y.; Chen, J. Study on the Calculation Method of Local Pressure Drop for Variable Cross-Section Structure of Circular Pipe. J. Mech. Des. Manuf. 2016, 83–87. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Y.; Zheng, L.; Yu, M.; Pan, R.; Shan, W. Study on the propagation characteristics of hydrogen/methane/air premixed flames in variable cross-section ducts. Process Saf. Environ. Prot. 2020, 135, 135–143. [Google Scholar] [CrossRef]
- Zhou, N.; Dai, Y.; Chen, B.; Li, X.; Zhao, H.; Huang, W. Research on the Propagation of Explosion in Gas Cloud in Variable Cross-Section Pipeline. J. Saf. Environ. 2021, 21, 599–606. [Google Scholar]
- Du, Q.; Zhu, Y.; Liu, P.; Liu, Z.; Liu, W. Thermo-hydraulic characteristic investigation of a circular tube inserted with constructal bifurcation semi-pipes by numerical simulation and PIV experiments. Int. J. Heat Mass Transf. 2024, 221, 125059. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, Z.; Ma, C.; Cao, X.; Guo, P.; Guo, W.; Lu, Y. Experimental study on the domino effect in explosions caused by vertically distributed methane/air vapor clouds. Fuel 2021, 290, 120014. [Google Scholar] [CrossRef]
- Kanoshima, R.; Hayakawa, A.; Kudo, T.; Okafor, E.C.; Colson, S.; Ichikawa, A.; Kudo, T.; Kobayashi, H. Effects of initial mixture temperature and pressure on laminar burning velocity and Markstein length of ammonia/air premixed laminar flames. Fuel 2022, 310, 122149. [Google Scholar]
- Mao, R.; Wang, J.; Lin, W.; Han, W.; Zhang, W.; Huang, Z. Effects of flow–flame interactions on the stabilization of ultra-lean swirling CH4/H2/air flames. Fuel 2022, 319, 123619. [Google Scholar] [CrossRef]
- Li, G.; Gao, W.; Jiang, H.; Wang, W.; Zhao, F.; Huang, Z.; Si, R.; Wen, G. On the lower explosion limit of ventilation air methane under high temperatures. Int. J. Hydrogen Energy 2024, 77, 1457–1466. [Google Scholar] [CrossRef]
- Yang, K.; Liu, G.; Ji, H.; Xing, Z.; Jiang, J.; Yin, Y. The effects of different equivalence ratios and initial pressures on the explosion of methane/air premixed gas in closed space. Energy 2024, 297, 131213. [Google Scholar] [CrossRef]
- Faghih, M.; Gou, X.; Chen, Z. The explosion characteristics of methane, hydrogen and their mixtures: A computational study. J. Loss Prev. Process Ind. 2016, 40, 131–138. [Google Scholar]
- Figueroa-Labastida, M.; Zheng, L.; Streicher, J.W.; Hanson, R.K. Effect of elevated temperatures (550–860 K) on the laminar flame speeds of methane/hydrogen blends. Fuel 2024, 372, 132219. [Google Scholar] [CrossRef]
- Cui, G.; Li, Z.; Yang, C. Experimental study of flammability limits of methane/air mixtures at low temperatures and elevated pressures. Fuel 2016, 181, 1074–1080. [Google Scholar] [CrossRef]
- Li, Y.; Bi, M.; Li, B.; Zhou, Y.; Gao, W. Effects of hydrogen and initial pressure on flame characteristics and explosion pressure of methane/hydrogen fuels. Fuel 2018, 233, 269–282. [Google Scholar] [CrossRef]
- Clanet, C.; Searby, G. On the “tulip flame” phenomenon. Combust. Flame 1996, 105, 225–238. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, Q.; Shen, X.; Guo, S.; Sun, J. An experimental study of distorted tulip flame formation in a closed duct. Combust. Flame 2013, 160, 1725–1728. [Google Scholar] [CrossRef]
- Markstein, G.H. A shock-tube study of flame front-pressure wave interaction. Symp. (Int.) Combust. 1957, 6, 387–398. [Google Scholar] [CrossRef]
- Dunn-Rankin, D.; Barr, P.K.; Sawyer, R.F. Numerical and experimental study of “tulip” flame formation in a closed vessel. Symp. (Int.) Combust. 1988, 21, 1291–1301. [Google Scholar] [CrossRef]
- Gonzalez, M.; Borghi, R.; Saouab, A. Interaction of a flame front with its self-generated flow in an enclosure: The “tulip flame” phenomenon. Combust. Flame 1992, 88, 201–220. [Google Scholar] [CrossRef]
- Bychkov, V.; Akkerman, V.y.; Fru, G.; Petchenko, A.; Eriksson, L.-E. Flame acceleration in the early stages of burning in tubes. Combust. Flame 2007, 150, 263–276. [Google Scholar] [CrossRef]
- Ponizy, B.; Claverie, A.; Veyssière, B. Tulip flame—The mechanism of flame front inversion. Combust. Flame 2014, 161, 3051–3062. [Google Scholar] [CrossRef]
- Zhou, N.; Xu, Y.; Chen, B.; Li, X.; Qiao, S.; Yuan, X.; Liu, J.; Huang, W.; Zhao, H. Numerical Simulation of the Influence of Venting Conditions on the Combustion Characteristics of Premixed H2/Air Explosions. Chem. Eng. Prog. 2021, 40, 3656–3663. [Google Scholar]
- Tricco, T.S. The Kelvin–Helmholtz instability and smoothed particle hydrodynamics. Mon. Not. R. Astron. Soc. 2019, 488, 5210–5224. [Google Scholar] [CrossRef]
- Zhao, H.; Yuan, C.; Li, G.; Tian, F. The Propagation Characteristics of Turbulent Expanding Flames of Methane/Hydrogen Blending Gas. Energies 2024, 17, 5997. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, Q.; He, X.; Sun, J.; Shen, X. Experimental study on the behaviors and shape changes of premixed hydrogen–air flames propagating in horizontal duct. Int. J. Hydrogen Energy 2011, 36, 6325–6336. [Google Scholar] [CrossRef]
- Duva, B.C.; Chance, L.E.; Toulson, E. Dilution effect of different combustion residuals on laminar burning velocities and burned gas Markstein lengths of premixed methane/air mixtures at elevated temperature. Fuel 2020, 267, 117153. [Google Scholar] [CrossRef]
- Sabelnikov, V.A.; Lipatnikov, A.N.; Nishiki, S.; Dave, H.L.; Hernández Pérez, F.E.; Song, W.; Im, H.G. Dissipation and dilatation rates in premixed turbulent flames. Phys. Fluids 2021, 33. [Google Scholar] [CrossRef]
- Kagan, L.; Gordon, P.V.; Sivashinsky, G. A reduced model for a self-accelerating expanding flame subjected to the Darrieus-Landau and Rayleigh-Taylor instabilities: Transition to detonation. Combust. Flame 2022, 245, 112333. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, Z.; Dou, Z.; Zhang, C. Premixed CO/air combustion in a closed duct with inhibition. Energy 2021, 230, 120782. [Google Scholar] [CrossRef]
- Klopov, B.A.; Meshkov, E.E. Behavior of a perturbed rarefaction wave. Combust. Explos. Shock. Waves 1982, 18, 472–475. [Google Scholar] [CrossRef]
- Liu, F.; Huang, C.-Y.; Xin, K.; Gao, Y.-H.; Yan, M.-H.; Zhang, Y.-Y.; Zhou, L.-Q. Study on the Propagation Law of Explosion Shock Waves in Closed Variable-Section Tube Under High-Pressure Environment. J. Vib. Eng. Technol. 2023, 12, 7249–7264. [Google Scholar] [CrossRef]

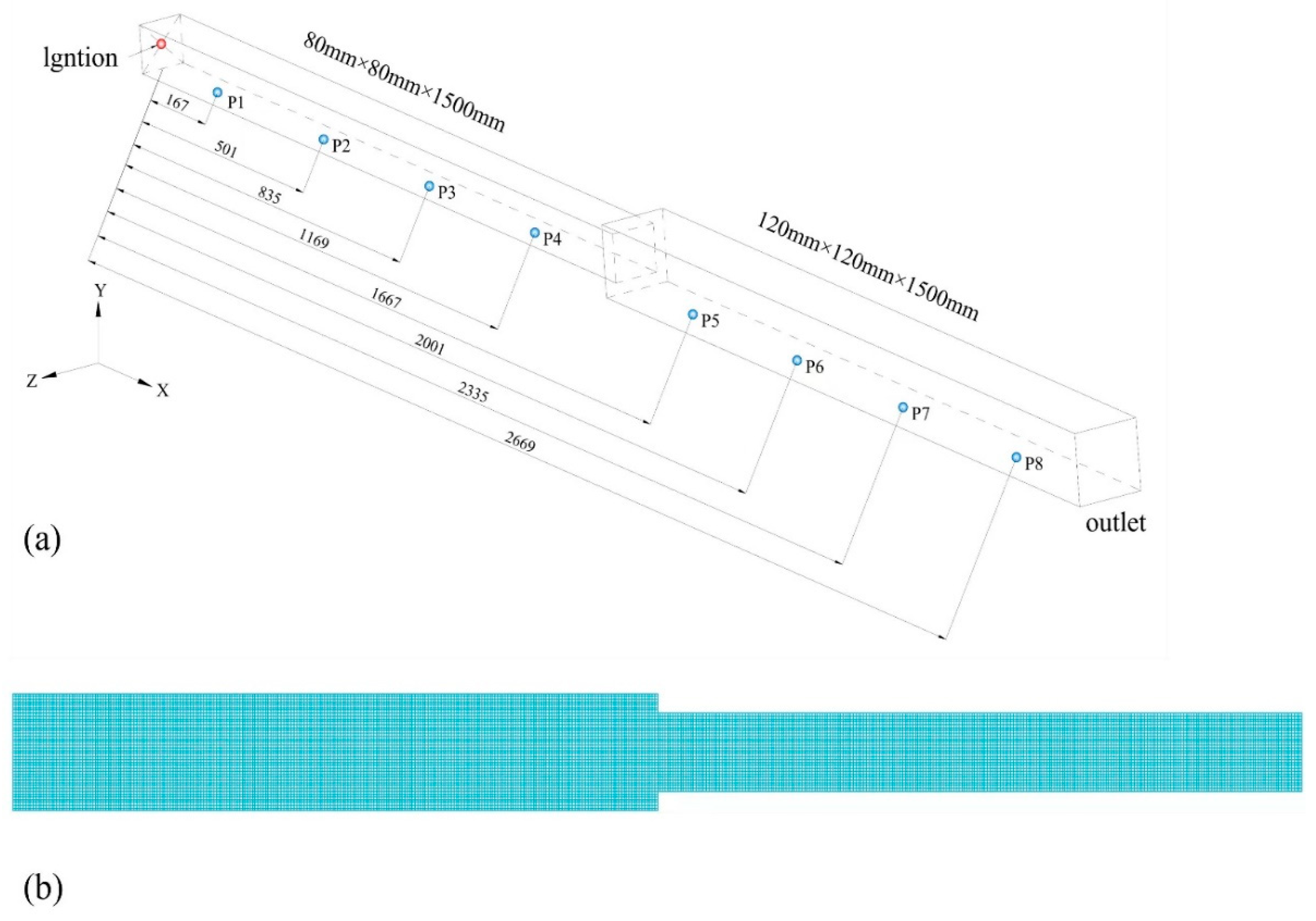



| Numbering | Distance From the Ignition End/cm | Numbering | Distance From the Ignition End/cm |
|---|---|---|---|
| P1 | 16.7 | P5 | 166.7 |
| P2 | 50.1 | P6 | 200.1 |
| P3 | 83.5 | P7 | 233.5 |
| P4 | 116.9 | P8 | 266.9 |
| Diameter Ratio | Dimensions |
|---|---|
| 1.25 | 80 mm × 80 mm × 1500 mm–100 mm × 100 mm × 1500 mm |
| 1.5 | 80 mm × 80 mm × 1500 mm–120 mm × 120 mm × 1500 mm |
| 1.75 | 80 mm × 80 mm × 1500 mm–140 mm × 140 mm × 1500 mm |
| 2.0 | 80 mm × 80 mm × 1500 mm–160 mm × 160 mm × 1500 mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, N.; Shi, Z.; Li, X.; Chen, B.; Liang, Y.; Li, Z.; Yang, C.; Liu, X.; Huang, W.; Yuan, X. Study on the Deflagration Characteristics of Methane–Air Premixed Gas in Sudden Expansion Pipelines. Energies 2025, 18, 1301. https://doi.org/10.3390/en18051301
Zhou N, Shi Z, Li X, Chen B, Liang Y, Li Z, Yang C, Liu X, Huang W, Yuan X. Study on the Deflagration Characteristics of Methane–Air Premixed Gas in Sudden Expansion Pipelines. Energies. 2025; 18(5):1301. https://doi.org/10.3390/en18051301
Chicago/Turabian StyleZhou, Ning, Zhuohan Shi, Xue Li, Bing Chen, Yiting Liang, Zhaoyu Li, Chunhai Yang, Xuanya Liu, Weiqiu Huang, and Xiongjun Yuan. 2025. "Study on the Deflagration Characteristics of Methane–Air Premixed Gas in Sudden Expansion Pipelines" Energies 18, no. 5: 1301. https://doi.org/10.3390/en18051301
APA StyleZhou, N., Shi, Z., Li, X., Chen, B., Liang, Y., Li, Z., Yang, C., Liu, X., Huang, W., & Yuan, X. (2025). Study on the Deflagration Characteristics of Methane–Air Premixed Gas in Sudden Expansion Pipelines. Energies, 18(5), 1301. https://doi.org/10.3390/en18051301






