Abstract
The porous solar receiver (PSR) is a promising technology in advanced high-temperature applications. However, the non-uniform distribution of concentrated solar flux (CSF) and the dense pore structure lead to localized overheating and significant thermal losses for the PSR. This review focuses on the optimization strategies to enhance the thermal performance of the PSR, including porosity parameters, spectral selectivity, geometric configurations, and optical windows. Furthermore, mitigation strategies for addressing localized high temperatures in the PSR were thoroughly discussed, including methods for homogenizing CSF and improving the velocity of heat transfer fluid (HTF). Additionally, a numerical simulation and experimental measurements were introduced and evaluated. Additionally, the paper emphasizes the need to optimize the macroscopic geometry of OPSRs to improve their flow and heat transfer performance, thereby enhancing their practical value. It also suggests designing PPSRs that integrate adjustments for HTF mass velocity, CSF, optical window load, and reflection losses. Consequently, future studies should focus on developing efficient simulation and validation methods to advance the practical application of PSRs.
1. Introduction
Solar energy, as a rich, clean, and renewable resource, represents an essential approach to addressing the energy crisis and advancing energy efficiency and emission reductions [1,2,3]. Solar receivers are extensively employed as essential devices for transforming concentrated solar energy into thermal energy. Based on the absorption method, solar receivers can be classified as surface solar receivers (SSRs) and volumetric solar receivers (VSRs) [4]. SSRs comprise coiled tubes and heat transfer fluid (HTF), where concentrated solar flux (CSF) heats the tube walls and transfers heat to the HTF via conduction and convection. The low thermal efficiency of SSRs results from large infrared radiation losses at the aperture and significant convective heat losses to the environment [5,6].
VSRs with a porous core, referred to as porous solar receivers (PSRs), capture incoming CSF and transfer heat to the HTF, completing the thermal conversion. Porous cores from metal mesh, silicon carbide, and zirconia feature interconnected 3D networks that provide a large surface area, efficient convective heat transfer, and strong thermal shock resistance [7,8]. The tortuous internal channels of the porous core enhance convective heat transfer between the HTF and the porous skeleton while reducing infrared radiation losses, thereby improving the system’s thermal efficiency [9]. Research indicates that compared to the SSR, the PSR achieves a higher thermal conversion efficiency, greater heat absorption intensity, and better stability [10].
Due to these advantages, PSRs hold significant promise for high-temperature solar thermal applications, including solar-driven power generation [11,12], thermochemical fuel production, and industrial process heat. Their ability to efficiently absorb and transfer solar energy makes them particularly suitable for concentrated solar power (CSP) systems [13,14], where maximizing thermal efficiency is crucial. Additionally, the high thermal stability and durability of porous structures enable their integration into next-generation solar reactors for hydrogen production, solar metallurgy, and waste heat recovery.
However, the unevenly concentrated solar flux and the complex pathways of porous media create several challenges. On the one hand, for open porous solar receivers (OPSRs), Gaussian-distributed CSF directly strikes the surface of the porous foam, causing local overheating and significant infrared radiation losses [15]. On the other hand, pressured porous solar receivers (PPSRs) with optical windows reduce infrared radiation losses from the porous skeleton. Nevertheless, the presence of the optical window increases optical losses and suffers considerable thermal loads, requiring effective cooling strategies [16]. Furthermore, the mismatch between the HTF and the intensity of the CSF exacerbates thermal stress on the porous skeleton. Therefore, significant efforts have been devoted to enhancing porous solar receivers’ flow and heat transfer performance.
The optimization strategies for enhancing the flow and heat transfer performance of the PSR can be classified into three primary approaches, each focusing on different aspects of the receiver’s thermal and optical behavior. The first strategy is to adjust the porosity parameters (pore size or porosity) of the porous medium to strengthen its volumetric effect, which plays a crucial role in improving the receiver’s ability to absorb and transfer heat.
The second strategy is to alter the optical properties of the PSR, such as the absorption coefficient of the porous medium and the transmittance of the optical window, to reduce infrared emission losses. The third strategy is to modify the geometric configuration of the PSR, which leads to a more uniform heat distribution, reduced thermal gradients, and improved convective heat transfer between the porous medium and the HTF.
The optimization strategies to reduce the peak solid temperature in a PSR can be implemented through two primary strategies: homogenizing the concentrated energy flux and enhancing the mass flow of the HTF. Homogenizing the concentrated energy flux aims to distribute the absorbed solar energy more uniformly across the porous medium, thereby mitigating localized overheating and reducing temperature gradients. Enhancing the mass flow of the HTF can significantly improve convective heat transfer, thereby reducing peak solid temperatures and enhancing the overall thermal efficiency.
This review focuses on the structural optimization of PSRs, categorizing flow and heat transfer enhancement strategies into three key aspects: porosity parameters, spectral properties, and geometric configurations. It also examines methods for mitigating localized overheating by homogenizing CSF and enhancing HTF velocity. Additionally, this work provides an in-depth comparison of numerical simulation methods, including direct pore-scale modeling and volume-averaging modeling, highlighting their applicability and accuracy across different PSR configurations. By synthesizing recent advancements, the study offers new insights into the comprehensive optimization of PSRs and outlines potential future research directions in high-temperature solar energy applications.
2. Optimization of Porous Solar Receivers
2.1. Open Porous Solar Receivers
Open porous solar receivers (OPSRs) suffer from significant infrared radiation losses due to the direct exposure of the solid skeleton to the external environment [11]. Reducing infrared radiation losses is essential to increase the working temperature and thermal efficiency. Recent optimization studies have focused on three aspects of porous media: pore parameters, spectral selectivity, and geometric design.
2.1.1. Optimization of Pore Parameters
Pore parameters, such as the pore diameter and porosity, are crucial geometric factors in the design of porous solar receivers. Table 1 presents the optimization approaches of the pore parameters.
The first effective optimization strategy is the construction of axially graded porous receivers, where the porosity decreases and pore diameter increases along the axial direction. This configuration enhances the penetration depth of solar radiation while strengthening the convective heat transfer between the fluid and the solid matrix, decreasing the inlet solid temperature.
Fend et al. [17] was the first to propose a double-layer porous volumetric receiver with graded porosity, as shown in Figure 1a. In this design, the first layer uses a high-porosity material to facilitate the transmission of solar radiation, while the second layer employs a low-porosity material to improve effective thermal conductivity. The experimental results demonstrated that the double-layer configuration achieves significantly higher heat transfer efficiency than single-layer receivers with uniform porosity.
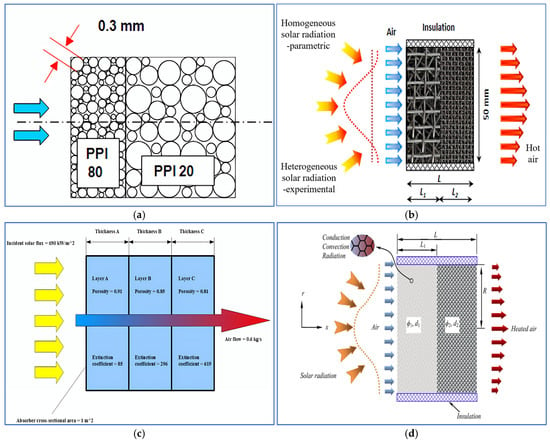
Figure 1.
Axial gradient design of the pore parameters of OPSRs. (a) Fend [17]; (b) Avila-Marin [18,19,20]; (c) Zaversky [21]; (d) Chen [22].
Avila-Marin et al. [18,19,20] utilized a local thermal non-equilibrium (LTNE) model and the P1 approximation model to calculate the temperature distribution in a graded-porosity metal mesh absorber, as shown in Figure 1b. The accuracy of the numerical model was validated through comparisons with small-scale solar receiver tests. The findings indicated that graded-porosity absorbers substantially enhanced receiver performance. However, a three-layer configuration did not outperform the optimal double-layer design. In the double-layer configuration, the combination of high porosity and a low extinction coefficient in the first layer with moderate porosity and a large specific surface area in the second layer achieved the best results. These conclusions were corroborated by Zaversky et al. [21].
Chen et al. [22] (2015) investigated the thermal performance of a double-layer ceramic foam volumetric solar receiver. By employing the LTNE model to solve the energy equations and using a modified P1 approximation to address radiative transfer within the foam, the study demonstrated that an axially decreasing porosity configuration enables higher air outlet temperatures and lower solid inlet temperatures. Additionally, a design with an increasing pore diameter was shown to enhance effective convective heat transfer while minimizing pressure losses.

Table 1.
Optimization of the pore parameters in OPSRs.
Table 1.
Optimization of the pore parameters in OPSRs.
| Reference | Year | Method | Material | Direction | Configuration | Pore Parameters |
|---|---|---|---|---|---|---|
| Fend et al. [17] | 2004 | Experiment | Sic | Axial | Double-layer | Porosity |
| Avila-Marin et al. [20] | 2014 | Experiment | Wire meshes | Double-layer | Porosity | |
| Avila-Marin et al. [18] | 2019 | Simulation | Wire meshes | Multi-layer | Porosity | |
| Avila-Marin et al. [19] | 2022 | Experiment Simulation | Wire meshes | Double-layer | Porosity | |
| Zaversky et al. [21] | 2017 | Experiment Simulation | Ceramic foam | Multi-layer | Porosity, PPI | |
| Chen et al. [22] | 2015 | Simulation | Ceramic foam | Double-layer | Cell size, porosity | |
| Chen et al. [23] | 2017 | Simulation | Ceramic foam | Radial | Composite | Cell size, porosity |
| Chen et al. [24] | 2019 | Simulation | Metal foams | Double-layer | Porosity, PPI | |
| M. Pelanconi et al. [25] | 2019 | Experiment Simulation | Al2O3 | Composite | Cell size | |
| Du et al. [26] | 2020 | Experiment Simulation | Inconel 718 | Multi-layer | Porosity, PPI | |
| Li et al. [27] | 2021 | Simulation | Porous material | Bidirectional | Multi-layer | Pore diameter, porosity |
| Sonika Sharma et al. [28] | 2022 | Simulation | Porous material | Multi-layer | Pore diameter, porosity | |
| Sonika Sharma et al. [29] | 2024 | Simulation | Porous material | Multi-layer | Pore diameter, porosity |
The second strategy is modifying the pore parameters along the radial direction of the PSR, attempting to enhance convective heat transfer at the center of the porous medium’s front surface. The optimal design radially decreases the porosity and pore diameter as it minimizes resistance in the central region, directs more air into the high-temperature zones, and generates a uniform temperature distribution of the porous structure. Chen et al. [23,24] studied the performance of a porous solar absorber with a composite structure, where different pore parameters were configured at the inlet region. The results indicated that placing low-porosity and small-pore foam near the wall can significantly reduce the solid temperature gradient and increase the average fluid outlet temperature.
M. Pelanconi et al. [25] explored the heat transfer performance of three radial distributions (uniform, increasing, and decreasing) in ceramic structures and validated the designs through experiments and simulations, as shown in Figure 2a. Figure 2b shows that an alumina tubular heat exchanger (dia. 20 mm, length 500 mm) with cellular architectures was realized and tested inflowing air at 773, 873, and 973 K. The RDCS lattice design (large cells outside and small cells inside) allows a higher fraction of thermal radiation to reach the central struts, thereby improving heat transfer effectiveness. The RICS lattice design produced the lowest pressure drop.
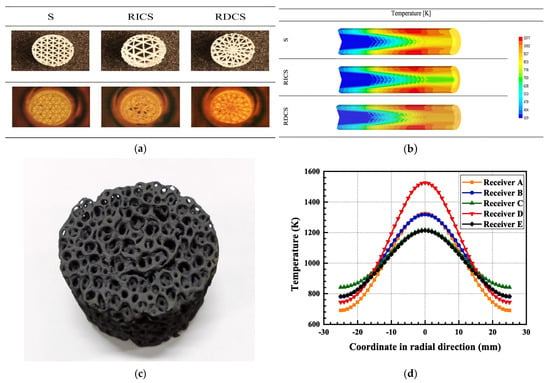
Figure 2.
Radial gradient design and results of pore parameters of OPSRs. (a) M. Pelanconi model [25]; (b) M. Pelanconi result [25]; (c) Du model [26]; (d) Du result [26].
Du et al. [26] fabricated a radially graded porous volumetric solar receiver via X-ray tomography and 3D printing and optimized the pore size distribution with a genetic algorithm, as seen in Figure 2c. Radiation heat transfer was calculated using the Rosseland approximation. Figure 2d shows that a radially graded pore diameter configuration effectively adjusts the mass flow distribution, aligns with non-uniform solar radiation, and mitigates local overheating.
The third strategy is the bidirectional configuration, where the pore parameters vary synchronously along the radial and axial directions. Therefore, the comprehensive flow and heat transfer performance could be enhanced more thoroughly than the one-direction method.
Li et al. [27] optimized the porosity and pore diameters of three types of porous solar receivers (radial variation, axial variation, and bidirectional variation) using a genetic algorithm, regulating the distribution of concentrated solar flux and heat transfer fluid to enhance flow and heat transfer performance, as shown in Figure 3. The results indicated that the bidirectional variation configuration exhibited a higher PEC (performance evaluation criterion balancing thermal efficiency and flow resistance) than unidirectional variations. The radial porosity reduction configuration also showed a 6.14% higher thermal efficiency than the optimal uniform porosity configuration. The configuration with decreasing axial pore diameter (2 mm to 1.49 mm) demonstrated the highest PEC value of 1.25.
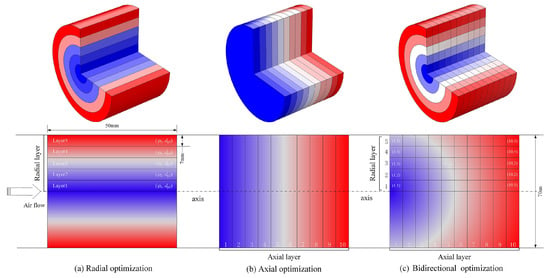
Figure 3.
Bidirectional gradient design of pore parameters [27].
Sonika Sharma et al. [28,29] investigated the flow and heat transfer performance of graded porous absorbers. The volume-averaging method and the LTNE model simulated the internal temperature distribution. The results indicated that a bidirectional configuration with radially decreasing porosity and axially increasing pore diameter achieved the optimal performance, increasing the air outlet temperature by 8.96% and reducing the pressure drop by 4%. This advantage persisted across airflow velocities ranging from 0.4 to 2.4 m/s. Additionally, axial grading had a more significant impact on thermal performance, while radial grading had a more significant influence on the pressure drop.
2.1.2. Optimization of Optical Properties
The infrared radiation losses at the PSR’s front surface significantly impact their thermal efficiency. Using spectral selective absorption can effectively mitigate this gap by lowering the reflective losses of concentrated sunlight and reducing infrared emissions from the absorber’s high-temperature core. Until now, several studies have modified the spectral selectivity of materials to create multi-layered structures that optimize sunlight absorption and minimize infrared emissions; Table 2 presents the optimization approaches for the optical properties.

Table 2.
Optimization of the optical properties of OPSRs.
Meni-gault et al. [30] developed a two-layer selective volumetric receiver, incorporating a silica honeycomb front layer and a rear layer of SiC particles. The purpose of these layers was to recycle infrared emissions and improve the absorption of solar radiation. When compared to a pure SiC porous receiver, the thermal efficiency of the two-slab design was enhanced by 5%.
Zhu and Xuan [31] carried out a numerical simulation on a multi-layer porous volumetric solar receiver with MoSi2-Si3N4 coatings or an ideal coating with a cutoff wavelength of 2 μm. These coatings were found to increase the thermal efficiency by 1.2% and 2.9%, respectively, when compared to traditional PSRs.
Ali et al. [32] introduced a honeycomb solar receiver design with varying absorption rates, as shown in Figure 4. The first segment coats a high-reflection layer (absorption rate of 0.2), and the second coats a high-absorption layer (absorption rate of 0.95). The energy flux distribution was calculated using Monte Carlo ray tracing and then converted into a volumetric heat source for the numerical model. The results indicate that surface coatings controlling the absorption of radiative flux inside the honeycomb receiver can achieve positive volumetric effects and high thermal efficiency.
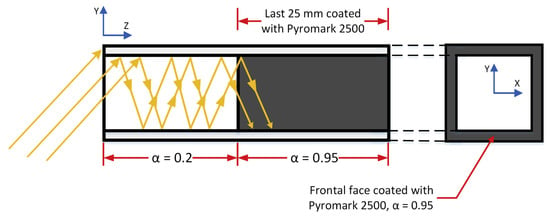
Figure 4.
Honeycomb solar receiver with different absorptions [32].
Dai et al. [33] developed a glass-porous media double-layer absorber core and used Monte Carlo and P1 approximation methods to analyze its multi-spectral thermal radiation transfer characteristics quantitatively. The findings suggest that the double-layer absorber effectively reduces high-temperature infrared radiation losses from the porous media compared to a single-layer absorber. Furthermore, when the operating temperature exceeds 1000 K, the double-layer absorber’s radiative efficiency improves by about 30%.
Chen et al. [34] employed pore-scale direct 3D modeling to calculate the energy conversion efficiency of silicon carbide and alumina ceramic foam solar absorbers. Figure 5 compares the thermal efficiency of various porous materials with different optical properties, such as gradient surface absorption, spectral selectivity, and the combination of opaque porous structures with transparent front-end layers. The results show that spectrally selective coatings are superior designs for enhancing the solar-to-thermal energy conversion efficiency.
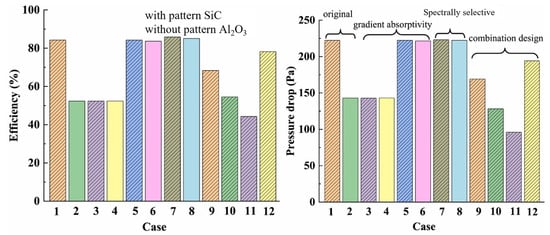
Figure 5.
Different optical property control strategies [34].
At present, spectrally selective absorption is confined to the porous receiver and incorporates the optical properties of the heat transfer fluid. Many studies have investigated replacing the heat transfer fluid with a molten salt to recover radiation heat losses in the absorber.
Du et al. [35] proposed a porous volumetric solar receiver utilizing a molten salt as the heat transfer medium. Pore-scale numerical simulations were performed to evaluate its flow and thermal performance in comparison to air-based receivers. As shown in Figure 6a, employing Hitec molten salt increases the thermal efficiency by 9.6% over conventional air-based receivers. Additionally, the molten salt system demonstrates reduced pressure losses at an outlet temperature of 1000 K.
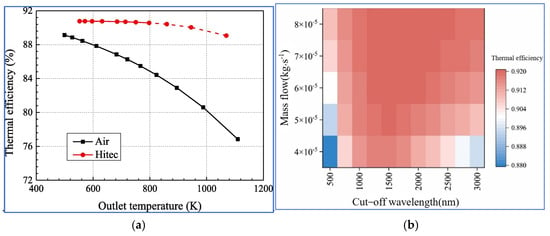
Figure 6.
Optimization results for the spectrally selective absorption of the HTF. (a) Different porous receivers [35]; (b) different cut-off wavelengths and mass flow rates [36].
He et al. [36] conducted pore-scale simulations to analyze how spectral selectivity affects the thermal performance of porous volumetric solar receivers. They optimized the cut-off wavelength to achieve a balance between energy losses in the porous structure and the fluid. The findings indicate that the heat transfer fluid’s cut-off wavelength plays a crucial role in thermal efficiency. At a mass flow rate of 4 × 10−5 kg/s, altering the wavelength from 500 nm to 2500 nm leads to a 3.8% variation in efficiency. However, considering the fluid’s optical properties results in a 2.77% reduction in thermal efficiency, as illustrated in Figure 6b.
2.1.3. Optimization of the Configuration Shape
Optimizing the geometry of porous solar receivers can increase the CSF’s absorption area and enhance convective heat transfer in the central region by incorporating specialized shapes [14]. Luque et al. [37] designed fractal-like, hierarchically layered porous volumetric solar receivers with additive manufacturing techniques. The results showed that the volumetric effect could be achieved, but the solar–thermal efficiency was relatively low, mainly due to the high emissivity of the stainless steel material. Capuano et al. [38] employed additive manufacturing techniques to create porous media with a pin zone and gradually changed structures. Compared with HiTRec-II, which uses a uniform honeycomb structure, the thermal efficiency was improved by 12%, and the volumetric effect was achieved.
Avila-Marin et al. [39] investigated the impact of three geometric parameters—the chamfer height, angle, and the height of the straight protruding side—on the thermal efficiency of standard cup volumetric absorbers, as illustrated in Figure 7. In their study, 126 different geometric configurations were analyzed using a two-dimensional CFD model combined with an LTNE model and the Rosseland approximation for the volumetric absorber. The results showed that increasing the chamfer height led to a decrease in the air temperature at the outlet. Additionally, the effect of the protruding absorber parameter was influenced by two possible boundary conditions—the inlet fluid velocity and the wall temperature—with the latter producing a higher air outlet temperature.

Figure 7.
Standard cup volumetric absorber [39].
2.2. Optimization of Pressured Solar Porous Receivers
The open porous solar receiver becomes a closed system called a pressured porous solar receiver (PPSR) by adding an optical window. The porous core is isolated from the environment in this configuration, resulting in a homogenized incident energy flux and decreased infrared radiation losses from the porous skeleton [37].
However, the optical window increases optical losses and suffers significant thermal loads from the porous medium [40]. In PPSRs, higher and uneven temperature levels of the porous medium are the challenges [41]. There are three optimization approaches to tackle these challenges.
2.2.1. Optimization of Pore Parameters
Many scholars have conducted the optimization of the pore parameters, including Villafán-Vidales et al. [42], Wang et al. [43], Chen et al. [44] Zhang et al. [45], and Ali et al. [46], as shown in Table 3. The pore parameter optimization results for OPSRs can be directly applied to PPSRs. The ideal pore parameter gradient configuration involves decreasing porosity and increasing the pore diameter along the flow direction while both parameters decrease radially. This design not only enhances the penetration depth of the incident energy flux but also strengthens convective heat transfer, thereby improving the thermal efficiency of the closed system.

Table 3.
Optimization of the pore parameters in PPSRs.
Chen et al. [44] analyzed the effects of different axial and radial gradient foam structure parameters (porosity and cell size) on the reforming process in solar reactors using the P1 approximation and an LTNE model, as shown in Figure 8. The results indicated that reactors with non-uniform pore parameters performed better than those with uniform parameters. Additionally, designs with decreasing structural parameters in the axial or radial direction performed better than those with increasing parameters.
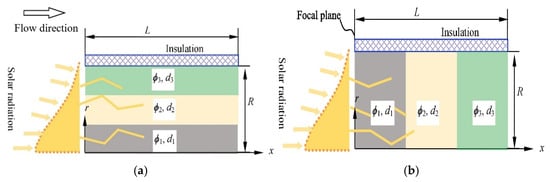
Figure 8.
Schematic of the thermochemical reactor heated by concentrated solar radiation [44]. (a) Gradual design in the radial direction; (b) gradual design in the axial direction.
2.2.2. Optimization of Optical Properties
Compared to OPSR systems, optimizing the spectral characteristics of PPSRs typically focuses on the optical window. Special coatings on the optical window surface can reduce reflection losses of concentrated sunlight or improve the transmittance of solar flux, thereby enhancing the optical efficiency of the absorber.
By adjusting the optical properties of the compound parabolic concentrator (CPC) and the porous catalytic absorber (PCA), Yao et al. [47] achieved targeted control of the spectral response characteristics within the reactor. The study showed that CO2 conversion increased by 68.52%, CH4 conversion increased by 54.48%, and solar fuel efficiency improved to 6.16%. The results indicate that the selectivity of different spectral bands across the entire spectrum can significantly affect reactor performance, as shown in Figure 9a.
Gema San Vicente et al. [48] prepared an anti-reflective coating on quartz glass by depositing a silica porous layer formed in a polymeric solution on both sides of the glass. The experimental findings revealed that as the temperature increased, the coating’s thickness and/or porosity decreased, enhancing its wear resistance and surface activity. After the coating treatment, the solar transmittance improved from 0.931 to 0.975.
Roger et al. [49] introduced a rugate filter coating on the inner surface of fused silica windows, which was designed to reflect part of the thermal spectrum (λ > 2.5 μm) while maintaining solar transmittance. Compared with uncoated windows, the average window temperature dropped by 175 K, and the receiver loss decreased by 11%.
Jin et al. [50] employed the Monte Carlo method (MCM) and finite element methods (FEMs) to investigate the effect of the cut-off wavelength on solar reactors. The results demonstrated that cut-off wavelength coatings and CPC effectively reduced radiation losses by 80%, increasing thermal efficiency to 76.02%. At the same time, CPC and RPC structures could also improve the uniformity of solar distribution within the catalyst, with maximum temperatures of 850 °C and 800 °C, respectively, minimizing the temperature gradient and thermal stress in the reactor, as shown in Figure 9b.
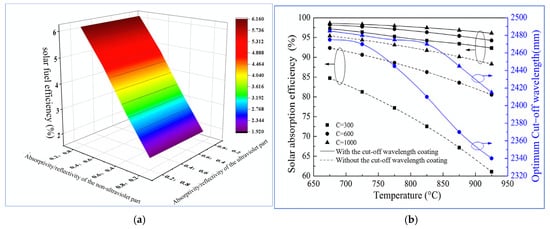
Figure 9.
Optimization results for spectrally selective absorption on PPSRs. (a) Yao et al. [47]; (b) Jin et al. [50].
2.2.3. Optimization of the Configuration Shape
The porous core absorbs concentrated energy flux and heats the heat transfer fluid. Proper shape optimization can effectively homogenize the heat flow and increase the flow velocity of the heat transfer fluid.
Shuai et al. [51] introduced a spherical cavity absorber with a flat–convex optical window, considering the directional characteristics of the focal spot and the impact of quartz optical windows on the heat flux density distribution. The MCM method was used to calculate and predict the coupled optical properties, offering a design with a more uniform heat flux density distribution and higher efficiency. Qiu [11] designed and optimized a cavity reactor featuring a hemispherical porous absorber and a secondary concentrator, as shown in Figure 10. The results indicated that the peak flux occurred at the center of the window, reaching 672.9 kW/m−2, and gradually decreased from the center toward the edge. The temperature dropped sharply radially along the hemispherical absorber.
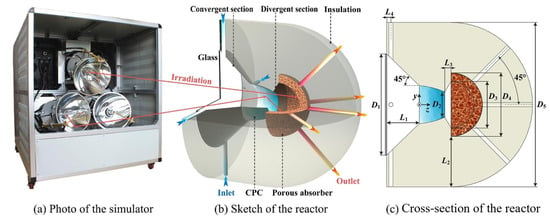
Figure 10.
The designed reactor irradiated by a high-flux solar simulator [11].
Meng [52] designed a closed cup-shaped porous volumetric absorber, as shown in Figure 11a. The energy flux distribution between the optical window and absorber core was modeled using MCM. The temperature field of the absorber was solved using an LTNE model and the Rosseland approximation. In Figure 11b, the results indicated that although the optical window increased the reflection losses of concentrated sunlight, the peak temperature of the porous skeleton rose by 213 K, reducing infrared radiation losses. Furthermore, accounting for internal radiation transfer within the cavity reduced the temperature difference of the solid to 700 K, leading to a more uniform temperature distribution.
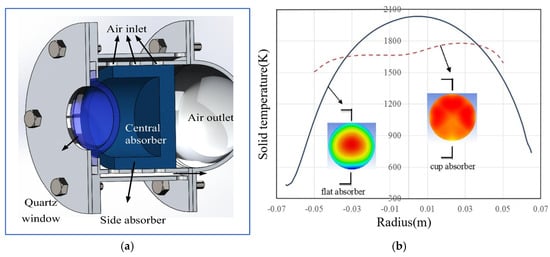
Figure 11.
Cup-shaped Al2O3 porous absorber model and result [52]. (a) Cup-shaped Al2O3 porous absorber; (b) temperature profiles of cup-shaped and flat absorbers.
Li et al. [53] investigated six types of PSRs (hexagonal prism type, octagonal type, drum type, composite circular platform type, frustum type, and scaled cone type) to analyze how the structural shape affects the outlet temperature and pressure drop of the heat transfer fluid (HTF), as shown in Figure 12. The local non-thermal equilibrium model and P1 approximation method were applied to describe the heat transfer process. The findings indicate that the drum-type structure demonstrates the highest thermal efficiency among the six structures.
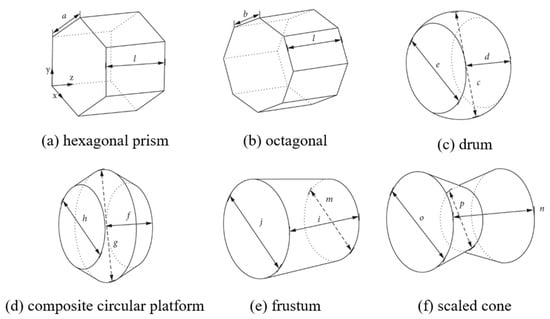
Figure 12.
Six different structures of the PSR [53].
The optical window plays a crucial sealing role. It is an indispensable component in the closed volumetric solar high-temperature absorber, significantly contributing to its thermal conversion efficiency at high temperatures. Currently, optimizing the optical window focuses on increasing transmittance and reducing temperature. Some researchers have optimized the optical window shape and materials, as shown in Table 4.
Karni et al. [40] developed a novel frustum-like high-pressure fused silica window for volumetric receiver applications. Their analysis and testing show that the window meets the receiver’s requirements, with a peak operating pressure and absorber temperature of 30 bar and 1973 K, respectively.
In Figure 13, Dai et al. [54] designed an ellipsoidal curved optical window and developed an integrated model combining the concentrator and window. Monte Carlo ray tracing predicted the window’s transmittance under concentrated sunlight. Their results showed that enhancing concentrator performance increased window transmittance, and the window’s geometry had less of an impact on transmittance.
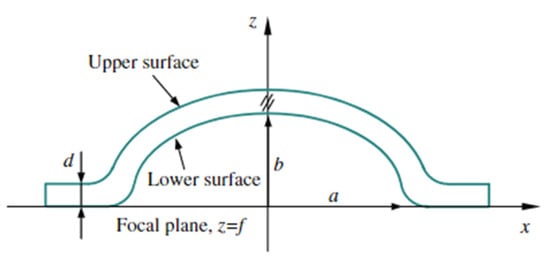
Figure 13.
Ellipsoidal curved optical window [54].
Maag and Steinfeld et al. [55] adopted the spectrum band approximation method to simulate radiation transfer between the optical window and the high-temperature solar absorber. They compared sapphire and quartz materials, finding that sapphire requires more incident solar energy than quartz to achieve the same absorber temperature and energy absorption rate.
Nie [56] designed four types of concave quartz windows (conical, spherical, sinusoidal, and hyperbolic tangent shapes), as shown in Figure 14a. This study used the Monte Carlo ray to simulate their impacts on heat flux uniformity. The results showed that the local concentration ratio of four optimal structure schemes and their non-uniformity coefficients decreased to 0.31, 0.35, 0.36, and 0.39, and the peak concentration values were reduced to 806.82, 841.31, 853.23, and 875.89, respectively.
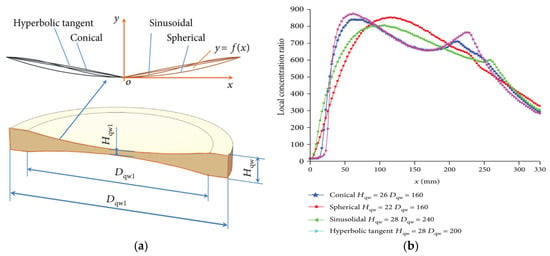
Figure 14.
Concave quartz window model and results [56] (a) Structures of the quartz windows; (b) local concentration ratios.

Table 4.
Optimization of the optical window shape in PPSRs.
Table 4.
Optimization of the optical window shape in PPSRs.
| Reference | Year | Material | Optical Window Shape |
|---|---|---|---|
| Karni et al. [40] | 1998 | quartz glass | Frustum of a circular cone window |
| Maag and Steinfeld et al. [55] | 2011 | quartz glass; sapphire | Flat window |
| Dai et al. [54] | 2014 | quartz glass; sapphire | Ellipsoidal curved optical window |
| Li et al. [57] | 2019 | quartz glass | Dual window |
| Nie et al. [56] | 2020 | quartz glass | Four types of concave quartz windows (conical, spherical, sinusoidal, and hyperbolic tangent shapes) |
Furthermore, Li [57] designed a dual-window pressurized volumetric receiver, as shown in Figure 15. A numerical model was developed by the MCM and finite volume method (FVM), incorporating a gray-band approximation to account for the spectral properties of the windows. The results indicated that increasing the cavity size, inner window thickness, the emissivity of inner surfaces, and the distance between the windows can significantly improve the total efficiency.
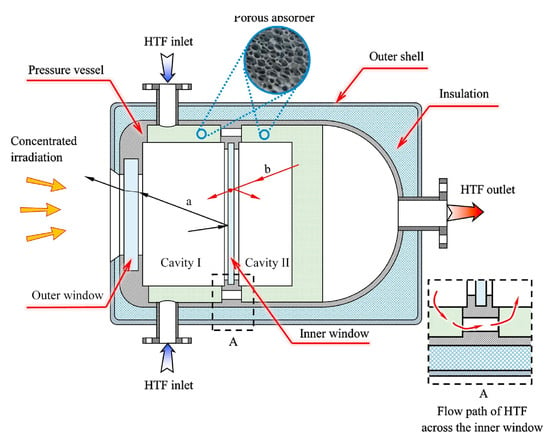
Figure 15.
Drawing of the dual-window pressurized volumetric receiver [57]. a–reflection path; b–re-radiation path.
3. Reducing the Peak Solid Temperature
Due to the uneven distribution of incident CSF [58], the PSRs (including both open and pressured types) face the issue of excessively high peak solid temperatures and uneven temperature distribution [15]. This issue poses significant challenges to the system’s safety and solar–thermal conversion efficiency, as it can cause excessive thermal stress in porous materials [59,60,61,62], carbon ablation, and result in an excessive thermal load on the optical window of the PPSR, potentially causing cracking [63]. Moreover, local overheating can increase the viscosity of the heat transfer fluid and reduce the heat transfer capacity.
He [64] systematically expounds on solutions to overcome local overheating in solar receivers. He emphasizes that the key approach to these issues is aligning the velocity of the heat transfer fluid with the distribution of incident energy flux density. The first approach is to homogenize the incident energy flux, known as an active solution, and the second is to enhance the heat transfer fluid velocity in the central region, known as a passive solution.
3.1. Homogenizing the Concentrated Energy Flux
Several approaches exist to homogenize the concentrated energy flux, such as installing a homogenizer [58,65,66], adding an optical window [55,67,68,69], or a multi-point [70,71,72,73] aiming strategy and optimizing the absorber core [74,75,76] (e.g., pore parameters and geometry) to lower the peak heat flux.
Mey-Cloutier and Caliot et al. [66] placed a homogenizer at the absorber’s front to create spatially uniform flux conditions. As illustrated in Figure 16a, multiple reflections inside the homogenizer were used to homogenize the incident Gaussian heat flux distribution. The infrared image demonstrated that the front surface temperature of the porous absorber was relatively uniform, validating the effectiveness of the homogenizer. Yan et al. [65] proposed a discrete solar dish concentrator (DSDC) to enhance flux uniformity within cavity receivers. The DSDC was created by dividing an ideal parabolic curve into several segments and rotating each segment around one of its ends. As shown in Figure 16b, the DSDC enhances flux uniformity and reduces peak flux, with a marginal reduction in collector optical efficiency by a few percentage points.
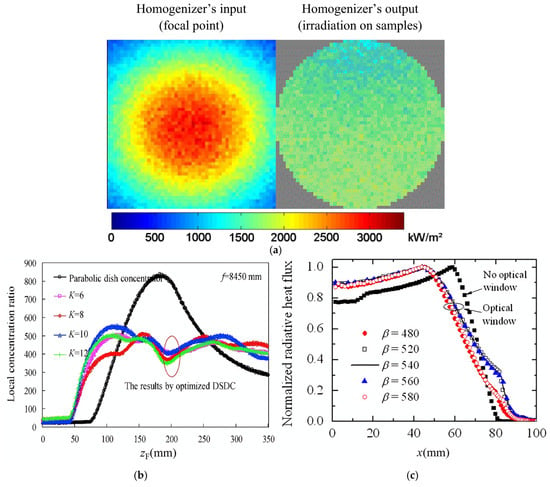
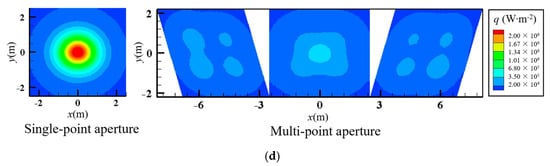
Figure 16.
Results of homogenizing the concentrated energy flux. (a) Mey-Cloutier and Caliot et al. [66]; (b) Yan et al. [65]; (c) Shuai et al. [68]; (d) Du et al. [71].
M. Faizan et al. [67], Shuai et al. [68], and Wang et al. [69] applied optical windows to the front of the absorber core to mitigate peak solar irradiance. Shuai et al. [68] developed a plano-convex quartz window, which was later applied by Wang to porous media absorbers to mitigate heat flux gradients. MCM was employed to model radiative heat transfer in solar collectors featuring quartz windows. As illustrated in Figure 16c, a plano-convex quartz window effectively decreases the peak heat flux at the porous receiver’s leading edge, enlarges the image radius, and maintains energy balance.
Besarati et al. [70], Du et al. [71], Wang et al. [72] and Yu et al. [73] suggested adopting multi-point focusing instead of single-point focusing, which proved to be an effective solution. Du et al. [71] constructed a comprehensive numerical model for closed porous solar receivers, integrating MCRT, FVM, and FEM approaches. As demonstrated in Figure 16d, under single-point solar focusing, the closed absorber model experienced a peak flux intensity of 1 × 109 W/m2, resulting in excessively high central temperatures and silicon carbide ablation. In the multi-point focusing model, the peak heat flux dropped to 1.1 × 108 W/m2, significantly dropping the peak flux level and avoiding local overheating. The peak temperature of the quartz glass window was lowered to 456 K, which was far below its melting point, preventing material degradation.
Optimizing the absorber’s pore parameters can also enhance the uniformity of solar flux distribution. Significant contributions in this field have been proposed by Wang et al. [74] Du and He [75] Roldán et al. [76] and Chen et al. [44] Roldán et al. [76] numerically investigated porous structures with graded porosity in both the axial and radial directions using a local thermal equilibrium model. The typical results revealed that reducing axial porosity increases the solar radiation penetration depth and improves flux uniformity.
3.2. Enhancing the Mass Flow of the HTF
Strengthening convective heat transfer between the fluid and the porous skeleton is an effective way to reduce temperature non-uniformity in solar receivers and its associated negative impacts.
For OPSRs, Nimvari et al. [77] introduced a theoretical method involving a non-uniform airflow velocity at the inlet to mitigate the maximum solid temperature and reduce temperature gradients in internal materials. The findings confirmed that this method significantly reduced the maximum solid temperature inside the receiver. Ahlbrink et al. [78] introduced a method based on dynamic programming to optimize the irradiance distribution on the receiver’s surface, employing orifices and air flaps. This method involves selecting fixed orifice sizes and adjusting air flaps to control the air mass flow and distribution. Du et al. [79]. extended this concept by designing a volumetric solar receiver with an axially graded porosity structure to align with the incident energy flux intensity. The results indicated that a radially decreasing structure effectively directed more heat transfer fluid into high heat flux regions, facilitating forced convection with the porous medium and significantly reducing the peak solid temperature.
For PPSRs, Li [80,81] developed a closed porous absorber featuring a double-layer optical window with an internal annular window, as shown in Figure 17a,b. The volume-averaging and Monte Carlo methods were employed to model concentrated flux and wall radiation transfer. In Figure 17c, the annular window design increased the heat transfer fluid velocity, significantly enhancing thermal efficiency by up to 7.18%. However, additional reflections from the internal window caused increased optical losses. Furthermore, the heat transfer fluid moved into high heat flux areas, which shifted the localized high-temperature zone to the edges and led to higher thermal losses.
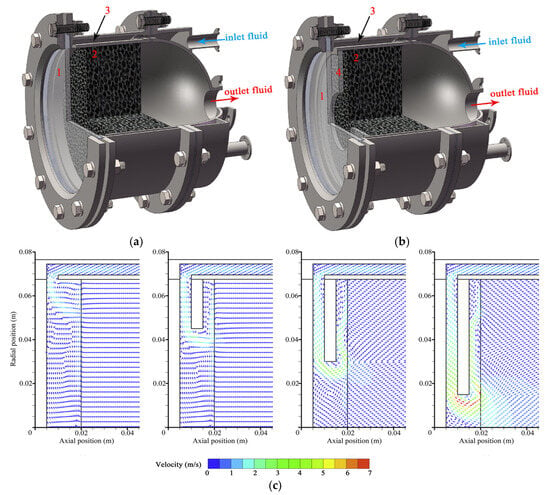
Figure 17.
Double-window volumetric solar receiver [80,81] (a) Conventional configuration; (b) double-windowed configuration; (c) normalized velocity vector counters. 1—outer window; 2—cylindrical porous absorber; 3—annular passage; 4—inner window.
Besides reducing the peak temperature of the porous absorber core, it is also crucial to lower the optical window’s temperature. Roger et al. [82] developed a novel multi-jet cooling technique for the windows of high-temperature pressurized volumetric receivers. Through asymmetric cooling designs and pulsed air flow, they maintained a window temperature below 800 °C while achieving an air outlet temperature above 1000 °C, enhancing thermal efficiency.
Liu [83] investigated non-uniform solar radiation in PPSRs by proposing three inlet models and incorporating non-uniform pore parameter effects. Temperature and gas distributions were calculated using a volume-averaged model.
In Figure 18, the findings indicated that aligning the fluid flow direction opposite to the incident solar radiation can significantly enhance the performance of the solar reactor. Reactions were most vigorous in areas with smaller pore diameters, and a layered porous structure achieved a methane conversion rate of 58.96%, outperforming reactors with uniform pore diameters. Similarly, Lovegrove and Luzzi [84] employed a method to cool the window by directing the inlet working fluid toward it.
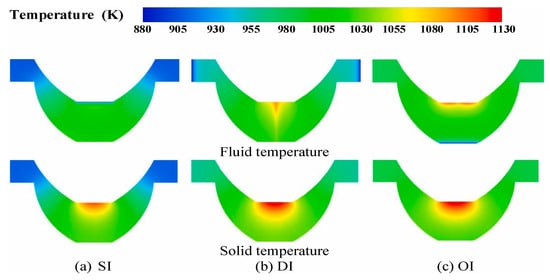
Figure 18.
Temperature distribution in different flow modes [83].
4. Heat Transfer Model
The numerical simulation methods for coupled heat transfer in porous solar receivers can be categorized into continuum-scale and pore-scale approaches [85,86]. In the continuum-scale method, the actual morphology of the porous skeleton is neglected, and the heat transfer between the fluid phase and the solid phase is computed using empirical parameters derived from the volume-averaging approach. In the pore-scale method, the actual complex structure of porous materials is considered, with its main task being to construct the microstructure of porous foam materials. Solar radiation and coupled heat transfer are solved directly in the fluid and solid phases. In general, pore-scale simulations yield accurate results but require substantial computational resources. The volume-averaging method offers high computational efficiency, but its accuracy depends on empirical parameters.
4.1. Convection Heat Transfer
- (1)
- Volume-Averaging Method
In applying the volume-averaging method (VAM), Darcy’s law is commonly used in the momentum equation to account for fluid resistance. At the same time, the Darcy–Forchheimer term is employed to describe the inertial forces induced by increasing flow velocity [87] The energy equation treats the porous region as solid and fluid phases. Depending on the heat exchange assumption between the porous solid and the HTF, two models are used: the local thermal equilibrium (LTE) model and the local thermal non-equilibrium (LTNE) model [88].
The LTE model assumes no temperature difference between the fluid and the solid skeleton, allowing the temperature of both phases to be represented by a single value at any given location. Vafai K et al. [89] found that the LTE model is not suitable for situations where the thermal properties of the fluid and solid phases differ significantly. The LTNE model accounts for the sizeable thermal conductivity disparity between the HTF and skeleton, assumes a heat transfer temperature difference, and is now widely utilized [90,91]. Effective convective parameters and source terms are applied to solve the energy conservation equation.
The VAM model generally assumes that the heat transfer fluid is incompressible. Additionally, the porosity parameters of the foam-based porous medium are considered to be uniformly distributed. Furthermore, the porous foam medium is treated as a gray body, where radiative properties such as absorptivity and emissivity are assumed to be isotropic.
The continuity equation is
The momentum equation is
The energy equations are as follows
Fluid phase
Solid phase
where denotes the fluid density and U is the superficial velocity, ϕ represents the porosity, p is the pressure of the HTF, and μf is the dynamic viscosity. Ts and Tf are the solid and fluid temperatures, respectively. kse and kfe are the effective thermal conductivity of the solid and fluid. hv represents the volumetric convective heat transfer coefficient between the solid and the fluid. Sr is the energy source term, which is the combination of solar radiation and the radiative emission from porous media. Solar radiation models are usually categorized into surface absorption models and volumetric absorption models.
- (2)
- Pore-scale model
In applying the pore-scale method (PSM), the key to solving porous media absorbers’ flow and heat transfer process is the reconstruction of foam structures using software such as Rhino-Grasshopper, EDEM, Voro++, or a custom-developed code. Typical foam-based porous media reconstruction models include periodic types (L-K and W-P), random types (VT), and scan-based types (SEM, μ-CT, and MRI), as shown in Figure 19.
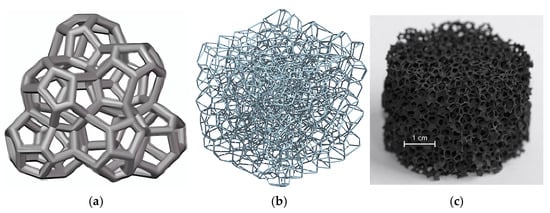
Figure 19.
Common foam-based porous media reconstruction models. (a) Periodic types [34]; (b) random types [92]; (c) scan-based types [93].
For example, the reconstruction process of Laguerre–Voronoi Tessellation (LVT) modeling is performed by creating a packed bed model in EDEM, exporting sphere center coordinates and radii, applying the Laguerre–Voronoi subdivision in Grasshopper, and reconstructing the LV foam in SpaceClaim using Python scripts. Finally, the solutions are obtained via ANSYS Fluent or COMSOL Multiphysics.
The governing equations are as follows:
where p is the static pressure, u is the velocity, ρ is the density, cp is specific heat, and λf and λs are thermal conductivity of fluid and solid, respectively.
4.2. Radiation Heat Transfer
Internal radiation transfer significantly affects the PSR’s total heat transfer rate, which varies as the fourth power of the temperature. However, the radiation transfer equation (RTE) is complex and difficult to solve since it is a nonlinear integrodifferential equation. The RTE is often transformed into a pure differential equation by simplification and transformation to combine a solution with N-S equations. Common methods for the RTE include the P1 approximation, Rosseland approximation, Monte Carlo Method (MCM), and discrete ordinates method (DOM) [94].
The Rosseland (Ro) approximation treats radiative heat transfer as conduction, providing a simplified representation of radiative processes. It applies to optically thick media and assumes a near-isotropic radiative intensity. Despite its lower accuracy at boundaries, the Ro approximation is recommended for its low computational cost. In porous media, the short transmission distance of radiation limits its interaction with adjacent locations. The Ro approximation simplifies radiative transfer as thermal diffusion, as expressed by Equation (9):
where σ is the Stefan–Boltzmann constant; n is the refractive index of the porous material, typically taken as 1.0; and β is the attenuation coefficient associated with the porosity ϕ and the pore parameter dp [95].
The P1 approximation is derived from spherical harmonics, expanding the radiative intensity using orthogonal spherical harmonic functions to transform the radiative transfer equation into a more straightforward partial differential equation. It represents the first-order expansion of the Pn model. The P1 approximation can handle different scattering phase functions, with isotropic scattering as the common assumption expressed in Equation (12):
where G represents projected radiation. a and σs are the absorption and scattering coefficients, respectively. For typical foam media, the absorption and scattering coefficients can be estimated as
where is the reflectivity of the skeleton of the porous foam.
Wang et al. [96] compared the Rosseland approximation with the modified P1 model for porous volumetric solar receivers. The results showed that the maximum temperature difference between the two models was 4.97%.
In the DOM, the radiative transfer equation is converted into multiple partial differential equations by discretizing the radiative intensity concerning the direction. Du et al. [97] Xuan er al. [98,99], Cheng et al. [100], and others used DOM to compute the energy equation.
where is unit vector in the direction of scattering, is unit vector in the direction of the incident radiation, is the total radiation intensity in each direction, and is the isotropic phase function.
Moreover, Mey et al. [101] compared the thermal performance of porous volumetric solar receivers using the Rosseland approximation, the P1 model, and the two-flux approximation. In the Rosseland approximation, solar flux was treated as a heat flux boundary condition and included in the energy equation. In contrast, the P1 model considered solar flux as a heat flux boundary condition within the radiative transfer equation. Zaversky et al. [21] compared the results obtained using the Rosseland approximation and the DOM, where solar energy was treated as the source term in the energy conservation equation. These comparisons highlight that both the handling of solar energy and the choice of radiation models significantly affect the accuracy of radiation heat transfer calculations.
The MCM solves radiative transfer through probabilistic models. The MCM transforms radiative transfer into a series of independent sub-processes, including emission, transmission, reflection, absorption, and scattering. Each cell emits a certain number of light rays, whose paths are traced to determine the radiative energy distribution in the cell. The introduction of the radiative transfer factor RDi-j decouples spatial positions, geometry, and radiative properties (absorption, attenuation, and scattering coefficients) from temperature, effectively simplifying the physical model and improving the computational accuracy, as expressed in Equation (16):
The MCM is feasible for complex systems, which can treat the internal radiation transfer in porous media and PPSR. The MCM is the most precise calculation method when the number of light rays is enough. However, it demands a considerable amount of computing resources. Overcoming the trade-off between accuracy and the computational cost requires significant practice. The accuracy of the MCM is inherently dependent on the number of sampled rays, as a higher ray count leads to reduced statistical variance and more reliable results. However, this increased accuracy comes at the expense of exponentially growing computational costs, as a larger number of rays require greater processing power and memory allocation. The stochastic nature of the MCM introduces a trade-off between accuracy and computational efficiency, where an insufficient number of rays may result in high statistical noise, whereas excessive ray tracing significantly prolongs the computation time. Addressing this challenge requires implementing variance reduction techniques, parallel computing strategies, or hybrid numerical models to enhance computational efficiency while maintaining an acceptable level of accuracy.
4.3. Optimization Method
Coupling the VAM with optimization algorithms provides an efficient way to improve porous solar receiver performance. Standard optimization algorithms include exhaustive search, response surfaces, and neural networks. Exhaustive search is the most commonly employed method to identify the optimal thermal efficiency and flow resistance within localized porous parameters of solar receivers. Neural networks have been utilized by Du [26,79], Li [27], and others to optimize the porosity parameter distribution of porous media, thereby enhancing the flow and heat transfer performance of solar receivers. Response surface methods have been applied by Zaversky [21], Ali [46], and others to identify critical factors affecting solar receivers, establish relationships between influencing factors and optimization objectives, and predict the thermal performance of porous media receivers.
4.4. Experimental Measurement
An efficient measurement of the solid temperature in porous solar receivers is essential for ensuring their safe and effective operation. Owing to the complex structure of porous media, among the existing temperature measurement methods, both thermocouple techniques and infrared thermal imaging have been proven suitable for monitoring temperatures within porous structures. Researchers such as Dietrich et al. [102], Wu et al. [103], Chen et al. [104], and George et al. [105] have embedded thermocouples within the porous skeleton to measure various solid temperatures and the outlet temperature; however, this method only provides discrete temperature data and cannot capture the complete temperature field on the receiver’s surface.
Infrared thermal imaging, on the other hand, can capture images of the temperature field at the receiver’s inlet surface, thereby monitoring the operational status of the porous medium, as shown in Figure 20. Albanakis et al. [106] employed an SC100 device to measure the surface temperature of receiver samples, while thermocouples were simultaneously used to record the air outlet temperature for stability monitoring. In Figure 20a, Mey-Cloutier et al. [66] utilized an infrared imager to obtain surface temperature maps of various samples, which enabled the evaluation of foam thermal emission losses under different configurations. Wang et al. [107] measured the non-uniformity of the front surface temperature of foams with varying porosities using infrared radiation, as shown in Figure 20b. The results, as depicted in the figure, indicate that the extinction coefficient of the porous medium increases with decreasing pore size, and a higher extinction coefficient leads to a steeper gradient in the radiative heat flux at the irradiated surface, resulting in a non-uniform temperature distribution.
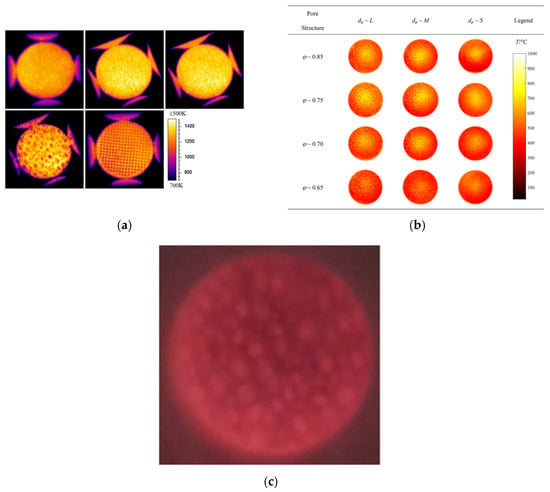
Figure 20.
Infrared temperature images of PSRs. (a) Mey-Cloutier [66]; (b) Wang [107]; (c) Shuai [108].
Shuai [108] used an infrared camera to measure the temperature field of the porous medium inside a closed solar receiver. The measurement image, shown in Figure 20c, has low accuracy and is blurred, making it unable to accurately reflect the temperature field of the porous solid. The study suggests that the addition of an optical window blocks the infrared radiation energy from the porous absorber core, preventing it from reaching conventional infrared thermography instruments.
5. Outlook and Conclusions
Porous solar receivers have gained increasing attention due to their high operating temperatures and low heat losses. An uneven CSF intensity and dense porous structures result in temperature non-uniformity, which causes multiple problems. In OPSRs, the non-uniform temperature distribution leads to high infrared radiation losses and a reduced efficiency. In PPSRs, the main challenges are the excessive thermal load on the optical window and increased reflection losses. Now, the non-uniform temperature distribution and localized high temperatures significantly impair the heat transfer performance of PSRs. Therefore, mitigating these issues and improving heat transfer performance is crucial.
Figure 21 illustrates the methods for enhancing heat transfer performance. OPSRs are widely applied in concentrated solar power systems and industrial heating processes, where efficient heat transfer and high thermal stability are critical. For OPSRs, performance enhancement has focused on the pore parameters, spectral selectivity, and geometric design optimization. The optimization of pore parameters has evolved from a single-directional (axial or radial) configuration to bidirectional (axial and radial) configuration. The concept of spectral selectivity has evolved from porous materials to heat transfer fluids (molten salts replacing air). Geometric optimization still mainly involves using materials with varying porosities. Only a few studies have proposed novel structures, such as cup-shaped honeycomb absorbers. Due to the high cost and limited feasibility of pore and spectral parameter optimization, geometric design optimization is essential to create cost-effective, efficient, and safe OPSRs.
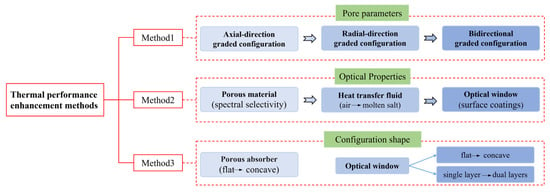
Figure 21.
The methods for enhancing heat transfer performance.
PPSRs are particularly suited for high-efficiency concentrated solar power plants and the solar-driven dry reforming of methane, where maintaining optimal thermal performance under high flux conditions is critical. For PPSRs, performance enhancement involves an additional focus on optimizing the optical window compared to open receivers. This aspect focuses on the optical window’s shape and spectral selectivity. Optical window designs have transitioned from flat to concave due to their higher compressive strength and better transmittance. Spectral selectivity optimization for optical windows typically involves adding surface coatings. Furthermore, the findings on pore parameters and spectral parameter optimization for OPSRs also apply to PPSRs. Although these methods have demonstrated excellent heat transfer performance in simulations, long-term testing is still needed to verify their feasibility.
Figure 22 illustrates the methods for reducing the peak solid temperature. The key to mitigating excessive peak solid temperature in PSRs is aligning the CSF with the HTF mass flow rate. Research on homogenizing the CSF is relatively advanced, but methods to enhance local heat transfer between the HTF and the porous medium are still lacking. Additionally, for PPSRs, cooling the optical window is essential to maintain the absorber’s stability and safety. Currently, cooling optical windows requires additional components, increasing system complexity. Hence, designing PPSRs that integrate mass flow rate control, solar flux density regulation, and window thermal load management is critical.
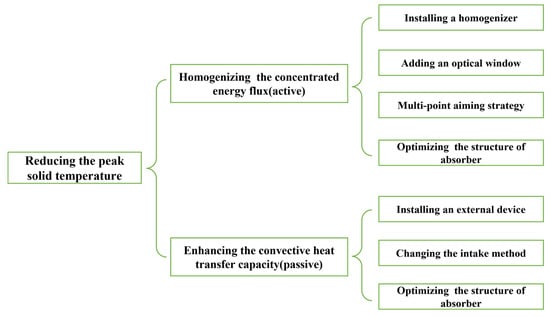
Figure 22.
The methods for reducing the peak solid temperature.
Experimental measurements have demonstrated that while thermocouples effectively capture the internal temperature of porous media, their measurements are limited to discrete points, thereby restricting the ability to obtain a continuous thermal profile. In contrast, infrared thermography offers a direct and non-invasive method for mapping the temperature field in OPSRs. However, in PPSRs equipped with optical windows, the direct measurement of the internal temperature field is hindered by the window’s interference, necessitating the use of measurement inversion techniques to accurately reconstruct the thermal distribution.
Currently, there are two main methods for coupling heat transfer theory in PSRs: the VAM and the PSM. The VAM can be quickly coupled with optimization techniques (such as response surface methodology, genetic algorithms, and exhaustive search) to evaluate receiver performance. However, this method relies on selecting empirical parameters (volumetric convective heat transfer coefficient). The PSM can reconstruct the actual internal structure of porous media, accurately revealing the flow and heat transfer processes within the receiver. However, this method requires extensive computational resources and time, and full-scale modeling remains challenging. Consequently, developing more effective optimization strategies for the VAM that account for factors affecting porous solar receivers is essential to improve the overall performance. For the PSM, developing full-scale models to study the effects of the porous skeleton structure on flow and heat transfer performance is essential. Integrating the VAM and PSM offers the potential for enhancing the porous receiver design by achieving a balance between computational efficiency and accuracy. Future research should focus on developing efficient numerical simulation methods and experimental validation techniques to advance the practical application of porous solar receivers.
Author Contributions
Conceptualization, G.D. and Y.L.; formal analysis, G.D., Y.L. and X.C.; data curation, G.D, Y.L. and X.C.; writing—original draft, Y.L., G.D. and X.C.; writing—review and editing, G.D. and T.Z.; visualization, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant Nos. 52176181 and 52476044), the Natural Science Foundation of Fujian Province, China (Grant No. 2024J01828), and the Open-End Foundation of the Scientific Research Platform of Fujian University of Technology (Grant No. KF-09-23006).
Acknowledgments
The support from the National Natural Science Foundation of China is deeply appreciated. The authors would also like to thank the engineers who provided and debugged the experimental devices.
Conflicts of Interest
The authors declare no conflicts of interest.
Acronyms
| CPC | compound parabolic concentrator |
| CSF | concentrated solar flux |
| DOM | discrete ordinates method |
| DSDC | discrete solar dish concentrator |
| FEM | finite element method |
| FVM | finite volume method |
| HTF | heat transfer fluid |
| LTE | local thermal equilibrium |
| LTNE | local thermal non-equilibrium |
| MCM | Monte Carlo method |
| OPSR | open porous solar receivers |
| PCA | porous catalytic absorber |
| PEC | performance evaluation criterion |
| PSR | porous solar receivers |
| PSM | pore scale method |
| PPSR | pressured porous solar receivers |
| Ro | Rosseland |
| RTE | radiation transfer equation |
| SSR | surface solar receivers |
| VAM | volume-averaging method |
| VSR | volumetric solar receivers |
| Greek Symbols | |
| a | absorption coefficient |
| cp | specific heat |
| dp | pore parameter (m) |
| G | projected radiation |
| hv | volumetric convective heat transfer coefficient (W/(m2·K)) |
| total radiation intensity in each direction | |
| k | conductivity |
| n | refractive index |
| p | pressure (Pa) |
| RDi-j | radiative transfer factor |
| Sr | energy source term (W/m3) |
| unit vector in the direction of scattering | |
| unit vector in the direction of the incident radiation | |
| T | temperature (K) |
| U | superficial velocity (m/s) |
| u | velocity (m/s) |
| β | attenuation coefficient |
| ϕ | porosity |
| isotropic phase function | |
| λ | thermal conductivity (W/(m·K)) |
| μf | dynamic viscosity (Pa·s) |
| fluid density (kg/m3) | |
| reflectivity of the skeleton of the porous foam | |
| σ | Stefan–Boltzmann constant |
| σs | scattering coefficient |
| Subscripts | |
| eff | effective value |
| f | fluid |
| s | solid |
References
- He, Y.-L.; Du, S.; Shen, S. Advances in porous volumetric solar receivers and enhancement of volumetric absorption. Energy Rev. 2023, 2, 100035. [Google Scholar] [CrossRef]
- Avila-Marin, A.L.; Fernandez-Reche, J.; Martinez-Tarifa, A. Modelling strategies for porous structures as solar receivers in central receiver systems: A review. Renew. Sustain. Energy Rev. 2019, 111, 15–33. [Google Scholar] [CrossRef]
- Capuano, R.; Fend, T.; Schwarzbözl, P.; Smirnova, O.; Stadler, H.; Hoffschmidt, B.; Pitz-Paal, R. Numerical models of advanced ceramic absorbers for volumetric solar receivers. Renew. Sustain. Energy Rev. 2016, 58, 656–665. [Google Scholar] [CrossRef]
- Ávila-Marín, A.L. Volumetric receivers in Solar Thermal Power Plants with Central Receiver System technology: A review. Sol. Energy 2011, 85, 891–910. [Google Scholar] [CrossRef]
- Ho, C.K.; Iverson, B.D. Review of high-temperature central receiver designs for concentrating solar power. Renew. Sustain. Energy Rev. 2014, 29, 835–846. [Google Scholar] [CrossRef]
- Hachicha, A.A.; Yousef, B.A.; Said, Z.; Rodríguez, I. A review study on the modeling of high-temperature solar thermal collector systems. Renew. Sustain. Energy Rev. 2019, 112, 280–298. [Google Scholar] [CrossRef]
- Fend, T.; Hoffschmidt, B.; Pitz-Paal, R.; Reutter, O.; Rietbrock, P. Porous materials as open volumetric solar receivers: Experimental determination of thermophysical and heat transfer properties. Energy 2004, 29, 823–833. [Google Scholar] [CrossRef]
- Dai, G.; Huangfu, J.; Wang, X.; Du, S.; Zhao, T. A Review of Radiative Heat Transfer in Fixed-Bed Particle Solar Receivers. Sustainability 2023, 15, 9918. [Google Scholar] [CrossRef]
- Sedighi, M.; Padilla, R.V.; Lake, M.; Rose, A.; Lim, Y.Y.; Novak, J.P.; Taylor, R.A. Design of high-temperature atmospheric and pressurised gas-phase solar receivers: A comprehensive review on numerical modeling and performance parameters. Sol. Energy 2020, 201, 701–723. [Google Scholar] [CrossRef]
- Kribus, A.; Gray, Y.; Grijnevich, M.; Mittelman, G.; Mey-Cloutier, S.; Caliot, C. The promise and challenge of solar volumetric absorbers. Sol. Energy 2014, 110, 463–481. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Q.; Qiu, Y. Design and optimization of a solar-driven methane dry reforming reactor by developing an optical-thermal-chemical model. Chem. Eng. J. 2024, 483, 149094. [Google Scholar] [CrossRef]
- Ma, T.; Fu, M.; Cong, J.; Zhang, X.; Zhang, Q.; Sayfieva, K.F.; Chang, Z.; Li, X. Analysis of heat and mass transfer in a porous solar thermochemical reactor. Energy 2024, 294, 130842. [Google Scholar] [CrossRef]
- Lougou, B.G.; Wu, L.; Ma, D.; Geng, B.; Jiang, B.; Han, D.; Zhang, H.; Łapka, P.; Shuai, Y. Efficient conversion of solar energy through a macroporous ceramic receiver coupling heat transfer and thermochemical reactions. Energy 2023, 271, 126989. [Google Scholar] [CrossRef]
- Li, M.J.; Tao, W.Q. Review of methodologies and polices for evaluation of energy efficiency in high energy-consuming industry. Appl. Energy 2017, 187, 203–215. [Google Scholar] [CrossRef]
- Wang, F.; Shuai, Y.; Tan, H.; Yu, C. Thermal performance analysis of porous media receiver with concentrated solar irradiation. Int. J. Heat Mass Transf. 2013, 62, 247–254. [Google Scholar] [CrossRef]
- Huang, H.; Lin, M. Optimization of solar receivers for high-temperature solar conversion processes: Direct vs. Indirect illumination designs. Appl. Energy 2021, 304, 117675. [Google Scholar] [CrossRef]
- Fend, T.; Pitz-Paal, R.; Reutter, O.; Hoffschmidt, B. Two novel high-porosity materials as volumetric receivers for concentrated solar radiation. Sol. Energy Mater. Sol. Cells 2004, 84, 291–304. [Google Scholar] [CrossRef]
- Avila-Marin, A.L.; Fernandez-Reche, J.; Caliot, C.; Martinez-Tarifa, A.; de Lara, M.A. CFD numerical model for open volumetric receivers with graded porosity dense wire meshes and experimental validation. AIP Conf. Proc. 2019, 2126, 030005. [Google Scholar]
- Avila-Marin, A.L.; Alvarez-Lara, M.; Fernandez-Reche, J. Experimental Results of Gradual Porosity Wire Mesh Absorber for Volumetric Receivers. Energy Procedia 2014, 49, 275–283. [Google Scholar] [CrossRef]
- Avila-Marin, A.L. CFD parametric analysis of wire meshes open volumetric receivers with axial-varied porosity and comparison with small-scale solar receiver tests. Renew. Energy 2022, 193, 1094–1105. [Google Scholar] [CrossRef]
- Zaversky, F.; Aldaz, L.; Sánchez, M.; Ávila-Marín, A.L.; Roldán, M.I.; Fernández-Reche, J.; Füssel, A.; Beckert, W.; Adler, J. Numerical and experimental evaluation and optimization of ceramic foam as solar absorber—Single-layer vs. multi-layer configurations. Appl. Energy 2018, 210, 351–375. [Google Scholar] [CrossRef]
- Chen, X.; Xia, X.L.; Meng, X.L.; Dong, X.H. Thermal performance analysis on a volumetric solar receiver with double-layer ceramic foam. Energy Convers. Manag. 2015, 97, 282–289. [Google Scholar] [CrossRef]
- Chen, X.; Xia, X.L.; Yan, X.W.; Sun, C. Heat transfer analysis of a volumetric solar receiver with composite porous structure. Energy Convers. Manag. 2017, 136, 262–269. [Google Scholar] [CrossRef]
- Chen, X.; Xia, X.; Sun, C.; Wang, F.; Liu, R. Performance evaluation of a double-pipe heat exchanger with uniform and graded metal foams. Heat Mass Transf. 2020, 56, 291–302. [Google Scholar] [CrossRef]
- Pelanconi, M.; Barbato, M.; Zavattoni, S.; Vignoles, G.L.; Ortona, A. Thermal design, optimization and additive manufacturing of ceramic regular structures to maximize the radiative heat transfer. Mater. Des. 2019, 163, 107539. [Google Scholar] [CrossRef]
- Du, S.; Xia, T.; He, Y.L.; Li, Z.Y.; Li, D.; Xie, X.Q. Experiment and optimization study on the radial graded porous volumetric solar receiver matching non-uniform solar flux distribution. Appl. Energy 2020, 275, 115343. [Google Scholar] [CrossRef]
- Li, J.B.; Wang, P.; Liu, D.Y. Optimization on the gradually varied pore structure distribution for the irradiated absorber. Energy 2022, 240, 122787. [Google Scholar] [CrossRef]
- Sharma, S.; Talukdar, P. Thermo-mechanical analysis of a porous volumetric solar receiver subjected to concentrated solar radiation. Sol. Energy 2022, 247, 41–54. [Google Scholar] [CrossRef]
- Sharma, S.; Talukdar, P. Thermo-mechanical performance enhancement of volumetric solar receivers using graded porous absorbers. Energy 2024, 304, 132070. [Google Scholar] [CrossRef]
- Menigault, T.; Flamant, G.; Rivoire, B. Advanced high-temperature two-slab selective volumetric receiver. Sol. Energy Mater. 1991, 24, 192–203. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, Y. Improving the performance of volumetric solar receivers with a spectrally selective gradual structure and swirling characteristics. Energy 2019, 172, 467–476. [Google Scholar] [CrossRef]
- Ali, M.; Rady, M.; Attia, M.A.; Ewais, E.M. Consistent coupled optical and thermal analysis of volumetric solar receivers with honeycomb absorbers. Renew. Energy 2020, 145, 1849–1861. [Google Scholar] [CrossRef]
- Dai, G.; Chen, X.; Zhuang, Y. Thermal radiation performances of solar volumetric absorbers made up of multiple tubes and porous. Acta Energiae Solaris Sin. 2022, 43, 186–190. [Google Scholar]
- Chen, X.; Lyu, J.; Sun, C.; Xia, X.; Wang, F. Pore-scale evaluation on a volumetric solar receiver with different optical property control strategies. Energy 2023, 278, 128006. [Google Scholar] [CrossRef]
- Du, S.; Li, M.J.; He, Y.L.; Shen, S. Conceptual design of porous volumetric solar receiver using molten salt as heat transfer fluid. Appl. Energy 2021, 301, 117400. [Google Scholar] [CrossRef]
- Du, S.; He, Y.L. Investigation and optimization on spectrally selective absorption for enhanced thermal performance in porous volumetric solar receivers. Sol. Energy Mater. Sol. Cells 2024, 277, 113135. [Google Scholar] [CrossRef]
- Luque, S.; Menéndez, G.; Roccabruna, M.; González-Aguilar, J.; Crema, L.; Romero, M. Exploiting volumetric effects in novel additively manufactured open solar receivers. Sol. Energy 2018, 174, 342–351. [Google Scholar] [CrossRef]
- Capuano, R.; Fend, T.; Stadler, H.; Hoffschmidt, B.; Pitz-Paal, R. Optimized volumetric solar receiver: Thermal performance prediction and experimental validation. Renew. Energy 2017, 114, 556–566. [Google Scholar] [CrossRef]
- Avila-Marin, A.L.; Fernandez-Reche, J.; Carballo, J.A.; Carra, M.E.; Gianella, S.; Ferrari, L.; Sanchez-Señoran, D. CFD analysis of the performance impact of geometrical shape on volumetric absorbers in a standard cup. Renew. Energy 2022, 201, 256–272. [Google Scholar] [CrossRef]
- Karni, J.; Kribus, A.; Ostraich, B.; Kochavi, E. A High-Pressure Window for Volumetric Solar Receivers. J. Sol. Energy Eng. 1998, 120, 101–107. [Google Scholar] [CrossRef]
- Wang, P.; Li, J.B.; Bai, F.W.; Liu, D.Y.; Xu, C.; Zhao, L.; Wang, Z.F. Experimental and theoretical evaluation on the thermal performance of a windowed volumetric solar receiver. Energy 2017, 119, 652–661. [Google Scholar] [CrossRef]
- Villafán-Vidales, H.; Abanades, S.; Caliot, C.; Romero-Paredes, H. Heat transfer simulation in a thermochemical solar reactor based on a volumetric porous receiver. Appl. Therm. Eng. 2011, 31, 3377–3386. [Google Scholar] [CrossRef]
- Wang, F.; Shi, X.; Zhang, C.; Cheng, Z.; Chen, X. Effects of non-uniform porosity on thermochemical performance of solar driven methane reforming. Energy 2020, 191, 116575. [Google Scholar] [CrossRef]
- Chen, X.; Wang, F.; Yan, X.; Han, Y.; Cheng, Z.; Jie, Z. Thermochemical performance of solar driven CO2 reforming of methane in volumetric reactor with gradual foam structure. Energy 2018, 151, 545–555. [Google Scholar] [CrossRef]
- Zhang, H.; Shuai, Y.; Lougou, B.G.; Jiang, B.; Yang, D.; Pan, Q.; Wang, F.; Huang, X. Effects of foam structure on thermochemical characteristics of porous-filled solar reactor. Energy 2022, 239, 122219. [Google Scholar] [CrossRef]
- Godini, A.; Kheradmand, S. Optimization of volumetric solar receiver geometry and porous media specifications. Renew. Energy 2021, 172, 574–581. [Google Scholar] [CrossRef]
- Yao, J.L.; Zhang, Z.Y.; Xu, B.Y.; Li, T.; Xie, T. Spectral properties regulation for the performance improvement of solar-driven methane dry reforming reactor based on the photothermal synergistic catalysis. Fuel 2025, 380, 133228. [Google Scholar] [CrossRef]
- Vicente, G.S.; Germán, N.; Farchado, M.; Morales, A. Antireflective coatings on quartz glass for high temperature solar receivers. AIP Conf. Proc. 2018, 2033, 220006. [Google Scholar]
- Röger, M.; Rickers, C.; Uhlig, R.; Neumann, F.; Polenzky, C. Infrared-Reflective Coating on Fused Silica for a Solar High-Temperature Receiver. J. Sol. Energy Eng. 2009, 131, 021004. [Google Scholar] [CrossRef]
- Jin, J.; Wei, X.; Liu, M.; Yu, Y.; Li, W.; Kong, H.; Hao, Y. A solar methane reforming reactor design with enhanced efficiency. Appl. Energy 2018, 226, 797–807. [Google Scholar] [CrossRef]
- Shuai, Y.; Xia, X.L.; Tan, H.P. Radiation performance of dish solar concentrator/cavity receiver systems. Sol. Energy 2008, 82, 13–21. [Google Scholar] [CrossRef]
- Meng, X.L.; Xia, X.L.; Sellami, N.; Mallick, T. Coupled heat transfer performance of a high temperature cup shaped porous absorber. Energy Convers. Manag. 2016, 110, 327–337. [Google Scholar] [CrossRef]
- Li, T.; Xie, L.; Zhao, B.; Shen, W.; Liu, Y. Analysis on the Effects of Different Receiver Structures and Porous Parameters on the Volumetric Effects and Heat Transfer Performance of Porous Volumetric Solar Receiver. Int. J. Energy Res. 2023, 2023, 3289428. [Google Scholar] [CrossRef]
- Dai, G.L.; Xia, X.L.; Hou, G.F. Transmission performances of solar windows exposed to concentrated sunlight. Sol. Energy 2014, 103, 125–133. [Google Scholar] [CrossRef]
- Maag, G.; Falter, C.; Steinfeld, A. Temperature of a Quartz/Sapphire Window in a Solar Cavity-Receiver. J. Sol. Energy Eng. 2011, 133, 014501. [Google Scholar] [CrossRef]
- Nie, D.Z.; Peng, Y.D.; Yan, J.; Mi, C.J.; Liu, Y.X.; Tian, Y. Improvement in the Flux Uniformity of the Solar Dish Concentrator System through a Concave Quartz Window. Int. J. Photoenergy 2020, 2020, 2421391. [Google Scholar] [CrossRef]
- Li, X.L.; Xia, X.L.; Li, Z.H.; Chen, X. Effects of double windows on optical and thermal performance of solar receivers under concentrated irradiation. Sol. Energy 2019, 184, 331–344. [Google Scholar] [CrossRef]
- Barreto, G.; Canhoto, P.; Collares-Pereira, M. Three-dimensional modelling and analysis of solar radiation absorption in porous volumetric receivers. Appl. Energy 2018, 215, 602–614. [Google Scholar] [CrossRef]
- Khanna, S.; Kedare, S.B.; Singh, S. Deflection and stresses in absorber tube of solar parabolic trough due to circumferential and axial flux variations on absorber tube supported at multiple points. Sol. Energy 2014, 99, 134–151. [Google Scholar] [CrossRef]
- Gray, V.; Truong-Ba, H.; Picotti, G.; Cholette, M.E. Using statistical analysis to understand creep modelling error and the ramifications for Solar Tower receivers. Sol. Energy Mater. Sol. Cells 2023, 257, 112408. [Google Scholar] [CrossRef]
- Walczak, M.; Pineda, F.; Fernández, Á.G.; Mata-Torres, C.; Escobar, R.A. Materials corrosion for thermal energy storage systems in concentrated solar power plants. Renew. Sustain. Energy Rev. 2018, 86, 22–44. [Google Scholar] [CrossRef]
- Perrero, M.; Papurello, D. Solar Disc Concentrator: Material Selection for the Receiver. Energies 2023, 16, 6870. [Google Scholar] [CrossRef]
- Salem, J.A.; Quinn, G.D. Failure Analysis of Sapphire Refractive Secondary Concentrators; NASA: Washington, DC, USA, 2009.
- He, Y.L.; Wang, K.; Qiu, Y.; Du, B.C.; Liang, Q.; Du, S. Review of the solar flux distribution in concentrated solar power: Non-uniform features, challenges, and solutions. Appl. Therm. Eng. 2019, 149, 448–474. [Google Scholar] [CrossRef]
- Yan, J.; Peng, Y.D.; Cheng, Z.R. Optimization of a discrete dish concentrator for uniform flux distribution on the cavity receiver of solar concentrator system. Renew. Energy 2018, 129, 431–445. [Google Scholar] [CrossRef]
- Mey-Cloutier, S.; Caliot, C.; Kribus, A.; Gray, Y.; Flamant, G. Experimental study of ceramic foams used as high temperature volumetric solar absorber. Sol. Energy 2016, 136, 226–235. [Google Scholar] [CrossRef]
- Faizan, M.; Almerbati, A.; Yilbas, B. A novel approach for volumetric solar receiver performance assessments. Appl. Therm. Eng. 2022, 211, 118487. [Google Scholar] [CrossRef]
- Shuai, Y.; Wang, F.-Q.; Xia, X.-L.; Tan, H.-P.; Liang, Y.-C. Radiative properties of a solar cavity receiver/reactor with quartz window. Int. J. Hydrogen Energy 2011, 36, 12148–12158. [Google Scholar]
- Wang, F.; Tan, J.; Ma, L.; Shuai, Y.; Tan, H.; Leng, Y. Thermal performance analysis of porous medium solar receiver with quartz window to minimize heat flux gradient. Sol. Energy 2014, 108, 348–359. [Google Scholar]
- Besarati, S.M.; Goswami, D.Y.; Stefanakos, E.K. Optimal heliostat aiming strategy for uniform distribution of heat flux on the receiver of a solar power tower plant. Energy Convers. Manag. 2014, 84, 234–243. [Google Scholar] [CrossRef]
- Du, B.C.; Qiu, Y.; He, Y.L.; Xue, X.D. Study on heat transfer and stress characteristics of the pressurized volumetric receiver in solar power tower system. Appl. Therm. Eng. 2018, 133, 341–350. [Google Scholar] [CrossRef]
- Wang, K.; He, Y.L.; Xue, X.D.; Du, B.C. Multi-objective optimization of the aiming strategy for the solar power tower with a cavity receiver by using the non-dominated sorting genetic algorithm. Appl. Energy 2017, 205, 399–416. [Google Scholar] [CrossRef]
- Yu, Q.; Wang, Z.; Xu, E. Analysis and improvement of solar flux distribution inside a cavity receiver based on multi-focal points of heliostat field. Appl. Energy 2014, 136, 417–430. [Google Scholar] [CrossRef]
- Wang, P.; Li, J.; Zhou, L.; Liu, D. Acceptance-Rejection Sampling Based Monte Carlo Ray Tracing in Anisotropic Porous Media. Energy 2020, 199, 117455. [Google Scholar] [CrossRef]
- Du, S.; Ren, Q.; He, Y.-L. Optical and radiative properties analysis and optimization study of the gradually-varied volumetric solar receiver. Appl. Energy 2017, 207, 27–35. [Google Scholar] [CrossRef]
- Roldán, M.; Smirnova, O.; Fend, T.; Casas, J.; Zarza, E. Thermal analysis and design of a volumetric solar absorber depending on the porosity. Renew. Energy 2014, 62, 116–128. [Google Scholar] [CrossRef]
- Nimvari, M.E.; Jouybari, N.F.; Esmaili, Q. A new approach to mitigate intense temperature gradients in ceramic foam solar receivers. Renew. Energy 2018, 122, 206–215. [Google Scholar] [CrossRef]
- Ahlbrink, N.; Andersson, J.; Diehl, M.; Pitz-Paal, R. Optimization of the Mass Flow Rate Distribution of an Open Volumetric Air Receiver. J. Sol. Energy Eng. 2013, 135, 041003. [Google Scholar] [CrossRef]
- Du, S.; Li, Z.; He, Y.; Li, D.; Xie, X.; Gao, Y. Experimental and numerical analysis of the hydraulic and thermal performances of the gradually-varied porous volumetric solar receiver. Sci. China Technol. Sci. 2020, 63, 1224–1234. [Google Scholar] [CrossRef]
- Li, X.L.; Xia, X.L.; Sun, C.; Chen, Z.H. Performance analysis on a volumetric solar receiver with an annular inner window. Renew. Energy 2021, 170, 487–499. [Google Scholar] [CrossRef]
- Li, X.L.; Sun, C.; Xia, X.L.; Li, Z.H.; Li, Y. Modeling of coupled heat transfer in a windowed volumetric solar receiver. Sol. Energy 2020, 201, 195–208. [Google Scholar] [CrossRef]
- Röger, M.; Pfänder, M.; Buck, R. Multiple Air-Jet Window Cooling for High-Temperature Pressurized Volumetric Receivers: Testing, Evaluation, and Modeling. J. Sol. Energy Eng. 2006, 128, 265–274. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, L.T.; Shen, W.R.; Xu, C.; Zhao, B.Y. Relative flow direction modes and gradual porous parameters for radiation transport and interactions with thermochemical reaction in porous volumetric solar reactor. Renew. Energy 2023, 203, 612–621. [Google Scholar] [CrossRef]
- Lovegrove, K.; Luzzi, A. Endothermic reactors for an ammonia based thermochemical solar energy storage and transport system. Sol. Energy 1996, 56, 361–371. [Google Scholar] [CrossRef]
- Yuan, J.; Sundén, B. On continuum models for heat transfer in micro/nano-scale porous structures relevant for fuel cells. Int. J. Heat Mass Transf. 2013, 58, 441–456. [Google Scholar] [CrossRef]
- Krishnan, S.; Murthy, J.Y.; Garimella, S.V. Direct Simulation of Transport in Open-Cell Metal Foam. J. Heat Transf. 2006, 128, 793–799. [Google Scholar] [CrossRef]
- Jiang, P.X.; Ren, Z.P. Numerical investigation of forced convection heat transfer in porous media using a thermal non-equilibrium model. Int. J. Heat Fluid Flow 2001, 22, 102–110. [Google Scholar] [CrossRef]
- Vafai, K. Handbook of Porous Media; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Yang, K.; Vafai, K. Transient Aspects of Heat Flux Bifurcation in Porous Media: An Exact Solution. J. Heat Transf. 2011, 133, 052602. [Google Scholar] [CrossRef]
- Coutinho, J.A.; Lemos, M.S. Laminar flow with combustion in inert porous media. Int. Commun. Heat Mass Transf. 2012, 39, 896–903. [Google Scholar] [CrossRef]
- Nimvari, M.; Maerefat, M.; Jouybari, N.; El-Hossaini, M. Numerical simulation of turbulent reacting flow in porous media using two macroscopic turbulence models. Comput. Fluids 2013, 88, 232–240. [Google Scholar] [CrossRef]
- Nie, Z.; Lin, Y.; Tong, Q. Modeling structures of open cell foams. Comput. Mater. Sci. 2017, 131, 160–169. [Google Scholar] [CrossRef]
- Petrasch, J.; Meier, F.; Friess, H.; Steinfeld, A. Tomography based determination of permeability, Dupuit–Forchheimer coefficient, and interfacial heat transfer coefficient in reticulate porous ceramics. Int. J. Heat Fluid Flow 2008, 29, 315–326. [Google Scholar] [CrossRef]
- Cuevas, J.; García-Vidal, F.J. Radiative Heat Transfer. ACS Photonics 2018, 5, 3896–3915. [Google Scholar] [CrossRef]
- Cunsolo, S.; Coquard, R.; Baillis, D.; Chiu, W.K.; Bianco, N. Radiative properties of irregular open cell solid foams. Int. J. Therm. Sci. 2017, 117, 77–89. [Google Scholar] [CrossRef]
- Wang, F.; Tan, J.; Yong, S.; Tan, H.; Chu, S. Thermal performance analyses of porous media solar receiver with different irradiative transfer models. Int. J. Heat Mass Transf. 2014, 78, 7–16. [Google Scholar] [CrossRef]
- Du, S.; Li, M.-J.; Ren, Q.; Liang, Q.; He, Y.-L. Pore-scale numerical simulation of fully coupled heat transfer process in porous volumetric solar receiver. Energy 2017, 140, 1267–1275. [Google Scholar] [CrossRef]
- Zhu, Q.; Xuan, Y. Performance analysis of a volumetric receiver composed of packed shaped particles with spectrally dependent emissivity. Int. J. Heat Mass Transf. 2018, 122, 421–431. [Google Scholar] [CrossRef]
- Liu, D.; Li, Q.; Xuan, Y. Reticulated porous volumetric solar receiver designs guided by normal absorptance and hemispherical volumetric emittance investigations. Int. J. Heat Mass Transf. 2017, 114, 1067–1071. [Google Scholar] [CrossRef]
- Cheng, Z.D.; He, Y.L.; Cui, F.Q. Numerical investigations on coupled heat transfer and synthetical performance of a pressurized volumetric receiver with MCRT–FVM method. Appl. Therm. Eng. 2013, 50, 1044–1054. [Google Scholar] [CrossRef]
- Mey, S.; Caliot, C.; Flamant, G.; Kribus, A.; Gray, Y. Optimization of High Temperature SiC Volumetric Solar Absorber. Energy Procedia 2014, 49, 478–487. [Google Scholar] [CrossRef]
- Dietrich, B. Heat transfer coefficients for solid ceramic sponges—Experimental results and correlation. Int. J. Heat Mass Transf. 2013, 61, 627–637. [Google Scholar] [CrossRef]
- Wu, Z.; Caliot, C.; Flamant, G.; Wang, Z. Numerical simulation of convective heat transfer between air flow and ceramic foams to optimise volumetric solar air receiver performances. Int. J. Heat Mass Transf. 2011, 54, 1527–1537. [Google Scholar] [CrossRef]
- Xia, X.L.; Chen, X.; Sun, C.; Li, Z.H.; Liu, B. Experiment on the convective heat transfer from airflow to skeleton in open-cell porous foams. Int. J. Heat Mass Transf. 2017, 106, 83–90. [Google Scholar] [CrossRef]
- George, G.R.; Bockelmann, M.; Schmalhorst, L.; Beton, D.; Gerstle, A.; Lindermeir, A.; Wehinger, G.D. Radial heat transport in a fixed-bed reactor made of metallic foam pellets: Experiment and particle-resolved computational fluid dynamics. Int. J. Heat Mass Transf. 2022, 197, 123376. [Google Scholar] [CrossRef]
- Albanakis, C.; Missirlis, D.; Michailidis, N.; Yakinthos, K.; Goulas, A.; Omar, H.; Tsipas, D.; Granier, B. Experimental analysis of the pressure drop and heat transfer through metal foams used as volumetric receivers under concentrated solar radiation. Exp. Therm. Fluid Sci. 2009, 33, 246–252. [Google Scholar] [CrossRef]
- Wang, P.; Li, J.; Zhou, L.; Vafai, K. Experimental characterization on pore parameter and the irradiation absorption efficiency of a series SiC foam specimens. Energy Convers. Manag. 2020, 212, 112795. [Google Scholar] [CrossRef]
- Lougou, B.G.; Shuai, Y.; Pan, R.; Chaffa, G.; Tan, H. Heat transfer and fluid flow analysis of porous medium solar thermochemical reactor with quartz glass cover. Int. J. Heat Mass Transf. 2018, 127, 61–74. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).