Abstract
As global climate change accelerates and fossil fuel reserves dwindle, renewable energy sources, especially wind energy, are progressively emerging as the primary means for electricity generation. Yet, wind energy’s inherent stochasticity and uncertainty present significant challenges, impeding its wider application. Consequently, precise prediction of wind turbine power generation becomes crucial. This paper introduces a novel wind power prediction model, the Wind-Mambaformer, which leverages the Transformer framework, with unique modifications to overcome the adaptability limitations faced by traditional wind power prediction models. It embeds Flow-Attention with Mamba to effectively address issues related to high computational complexity, weak time-series prediction, and poor model adaptation in ultra-short-term wind power prediction tasks. This can help to greatly optimize the operation and dispatch of power systems. The Wind-Mambaformer model not only boosts the model’s capability to extract temporal features but also minimizes computational demands. Experimental results highlight the exceptional performance of the Wind-Mambaformer across a variety of wind farms. Compared to the standard Transformer model, our model achieves a remarkable reduction in mean absolute error (MAE) by approximately 30% and mean square error (MSE) by nearly 60% across all datasets. Moreover, a series of ablation experiments further confirm the soundness of the model design.
1. Introduction
As the global climate change problem becomes increasingly serious, all countries and enterprises are promoting the transformation of their energy structure. China’s “double carbon” goal strives to achieve a carbon peak before 2030 and to achieve carbon neutrality before 2060. The development and utilization of new energy, as a shared objective among nations globally, is driven by the goal of achieving an energy structure transformation. Wind energy, recognized for its importance, stands out among the diverse renewable energy sources, attracting broad interest and focus. The instability inherent in wind speed gives rise to a profound uncertainty in wind turbine power generation, subsequently posing significant challenges to the scheduling and operation of the power system [1]. This uncertainty, being a direct consequence of unpredictable wind patterns, is a critical factor to consider. In the event that wind power is integrated directly into the power grid, its fluctuations have the potential to severely disrupt grid stability. The precise forecasting of wind power is thus of utmost importance, as it offers valuable reference data for the management and planning of the power system. Additionally, it mitigates the effects of wind power fluctuations on the power grid’s stability [2].
Three primary categories encompass traditional wind power forecasting methods: statistical models, machine learning models, and deep learning models. Widely employed in wind power forecasting, statistical models, such as linear regression and time-series analysis, rely on historical data to establish a linear relationship between input and output variables [3]. The nonlinear relationship between meteorological variables and wind output may not be fully captured by traditional statistical models. Consequently, machine learning models, specifically, support vector regression (SVR) [4], have been employed in wind power forecasting to surpass these limitations. Additionally, a hybrid methodology, which integrates Extreme Learning Machine (ELM) and error correction modeling, has emerged for short-term forecasts [5]. Furthermore, a wavelet-based neural network (WNN) prediction model has been explored [6]. These sophisticated models excel in grasping the intricate nonlinear connections between input and output variables in wind power prediction. Nevertheless, the intricacies of power system dynamics and the environment pose challenges, resulting in less than satisfactory prediction outcomes.
Recently, deep learning in computer vision and natural language processing [7], among many other areas, has demonstrated impressive nonlinear fitting capabilities. Exploration has been conducted on the application of deep learning methods in wind power prediction automation. Particularly, both recurrent neural networks (RNNs) [8] and long short-term memory (LSTM) [9] have demonstrated their efficacy in distilling crucial features and grasping sequential patterns from vast datasets of power output. Nevertheless, a significant drawback arises in RNN-centered methods, which is their inadequacy in offering a holistic global modeling viewpoint when confronted with extended input sequences. For inputs with long time spans in wind power prediction, this may affect the accuracy of the model.
The Transformer model solves the global modeling problem and makes major breakthroughs in natural language processing tasks [10,11,12]. Transformer has been rapidly expanding into various domains, including image processing [13,14,15]. A Spatio-Temporal Attention Network (STAN)-based wind power prediction model considers correlations between wind farms through a spatial self-attention mechanism and captures temporal dependencies through a Seq2Seq model [16]. The Spatial-Temporal Graph Transformer Network (STGTN) is composed of two modules: one for temporal feature extraction and another for spatial feature extraction [17]. This model architecture facilitates the capture of both temporal and spatial correlations amongst wind turbine nodes, providing a comprehensive framework for wind power prediction that overcomes the limitations of traditional RNN-based methods. Despite its proven effectiveness in multiple tasks, the Transformer model encounters difficulties in power prediction applications. These challenges arise from the model’s substantial computational requirements and its susceptibility to extraneous temporal noise present in time-series data. Addressing these concerns is imperative to guarantee the model’s validity and dependability.
This paper presents Wind-Mambaformer, a novel framework based on Transformer, to address the previously mentioned challenges in ultra-short-term wind power prediction. The framework introduces Flow-Attention, which is designed to reduce computational costs. Additionally, the Mamba structure, an innovative replacement for the traditional decoder, is employed to minimize the accumulation of errors. Experimental results based on cases from five distinct wind farms, each distinguished by their unique geographic and topographic traits, validate the effectiveness of the proposed method compared with the CNN [18], LSTM [9], Transformer [10], and Mamba models [19].
The primary advancements presented in this paper can be summarized as follows.
- (1)
- A novel network architecture termed Wind-Mambaformer is introduced in this paper, offering superior time-series processing capabilities compared to current models, thereby advancing wind power prediction.
- (2)
- A structure embedding Flow-Attention with Mamba is proposed to solve the problems of high computational complexity, weak time-series prediction, and weak model adaptation in the task of wind power prediction.
- (3)
- The multi-head flow-attention mechanism is introduced in the proposed Wind-Mambaformer model. The multi-variable correlations between variables related to wind power can be extracted by this mechanism to effectively improve the feature extraction capacity.
2. Related Work
In the realm of time-series forecasting, autoregression (AR) [20] stands as a prominent tool among traditional statistical models, framing the forecast as a straightforward linear correlation of historical data points, ideally suited for univariate datasets devoid of trends or seasonal variations. The Moving Average (MA) [21] approach, on the other hand, constructs its predictions based on a linear relationship with past residuals derived from the averaging process, utilizing data akin to that employed in AR. The Autoregressive Moving Average (ARMA) [22] method amalgamates the strengths of AR and MA, formulating the upcoming forecast as a linear outcome of both past observations and residuals. For univariate time series exhibiting a trend but lacking a seasonal element, the Autoregressive Integrated Moving Average (ARIMA) [23] proves invaluable, as it models wind power prediction series through a linear lens that considers variable past observations and residuals. Ultimately, the Seasonal Autoregressive Integrated Moving Average (SARIMA) [23] takes a comprehensive view, treating the subsequent forecast as a linear combination of historical data, errors, seasonal observations, and seasonal discrepancies. Although these techniques aspire to grasp the unpredictable fluctuations inherent in time-series data, they frequently necessitate substantial feature engineering efforts and may not always deliver exceptionally accurate forecasting outcomes.
In time-series forecasting, a crucial step involves transforming time-series data into a suitable format for supervised learning, a process that often relies on the application of machine learning techniques [24].
The methods commonly in use include SVR [4], Light Gradient Enhancement Machine (LightGBM) [25], and Extreme Gradient Boost (XGBoost) [26]. Regression problems with linear models can be aptly handled by SVR. As for LightGBM, it employs a decision tree-based learning algorithm as a gradient enhancement framework. And XGBoost stands as an enhancement algorithm implementation.
Several deep learning models, thanks to technological advancements, have found their application in the field of time-series forecasting. Prominent among these are models such as RNNs [8], renowned for their recursive process and memory capability, LSTM [9], which stands out in managing long-term dependencies and extracting key features from time-series data, and GRU [27], a streamlined version of LSTM that enhances computational efficiency while simplifying the model structure. Furthermore, 1D-CNN [28] has demonstrated its effectiveness in capturing short-term local dependencies and spatial information. Transformer models, although proficient in modeling distant dependencies and interactions within time-series forecasting, face challenges in extracting temporal features. Nevertheless, since their emergence in 2017 [10], Transformer models have made significant strides in natural language processing tasks. Their versatility has facilitated a rapid expansion into various fields, including image processing, document retrieval, and time-series prediction [29]. Additionally, specifically tailored for time-series forecasting, a plethora of Transformer variants have emerged, such as Longformer [30], which introduces a more efficient attention mechanism with a sliding window approach, enabling it to handle long sequences while reducing memory and computational complexity. Reformer [31] optimizes the attention mechanism by using locality-sensitive hashing, allowing it to process very long sequences more efficiently while maintaining high performance. Informer [32] leverages a self-attention mechanism that focuses on learning long-range dependencies, incorporating a probabilistic selection mechanism to improve the efficiency of the attention process in time-series forecasting. Flowformer [33] combines the strengths of Flow-based models and the Transformer architecture, providing a more flexible and scalable approach to time-series forecasting by enhancing the model’s ability to learn from both short-term and long-term dependencies.
The utilization of techniques in the wind farm sector is continuously expanding. Among these, the Quaternionic Convolutional Long Short-Term Memory Neural Models stand out, leveraging Adaptive Decomposition Methods for predicting wind speeds in the North Aegean Islands [34]. Wind speed prediction has also benefited from the integration of Sentinel family satellite images and machine learning techniques [35], as well as the implementation of deep learning models at the Lillgrund offshore wind farm [36]. Wave energy prediction has seen advancements through the use of an efficient decomposition-based convolutional bi-directional model paired with a balanced Nelder–Mead optimizer [37]. Moreover, a hybrid neuroevolutionary approach has emerged as a viable method for predicting wind turbine output power [38]. In the optimization of power system currents, efficient metaheuristic algorithms have proven their effectiveness [39]. A short-term wind power prediction method based on NWP wind speed trend correction is proposed to address the prediction errors caused by the limitations of NWP accuracy [40]. A multi-layer neural network is used to classify precipitation zones based on weather station data, identifying adverse meteorological phenomena for wind farms [41]. Overall, these methodologies have demonstrated outstanding results. However, some of the above methods may be specific to a particular geographic region or climatic conditions and have limited applicability in other regions and lack generalizability. The prediction accuracy and reliability of the model are directly influenced by the adequacy of high-quality data, which holds a central significance. Unlike the previously mentioned methods, the Wind-Mambaformer model, introduced in this study, showcases its methodological framework through Figure 1.
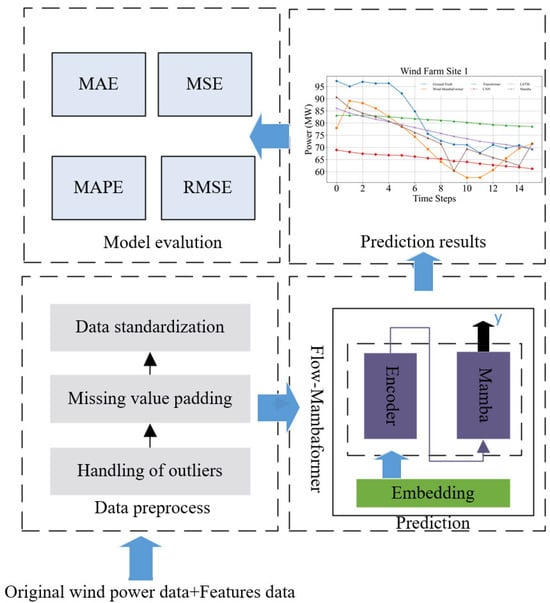
Figure 1.
Wind-Mambaformer model prediction flowchart.
3. Methodology
This study presents the Wind-Mambaformer, a refined Transformer model specifically designed for ultra-short-term wind power prediction. The model’s main objective is to tackle the issues related to computational cost and error accumulation, which are the primary challenges it aims to overcome. Compared with the common Transformer, Wind-Mambaformer has made the following updates: (1) Adopting Flow-Attention to alleviate the heavy computational cost. (2) To address the issue of dynamic decoding error transfer and enhance prediction accuracy, the Mamba structure is incorporated. The model’s architecture, as illustrated in Figure 2, demonstrates the integration of this structure; the input WT historical data are first processed through the embedding layer, which maps the original data into a high-dimensional space and adds positional encoding (Positional Embedding) to include the temporal information of the sequence. After this part of the processing is completed, the output is fed to the encoder. The encoder consists of multiple encoder layers, each including Multi-Head Flow-Attention, Feed-Forward Network, and Add & Norm layers. The encoder output is further processed by the Mamba block, which consists of several components to enhance the model’s ability to model long time series. Finally, the features processed by the Mamba block are fed into the Fully Connected Layer (fc), where the output dimensions are aligned with the prediction target dimensions. The final output is used as the prediction result of the model.
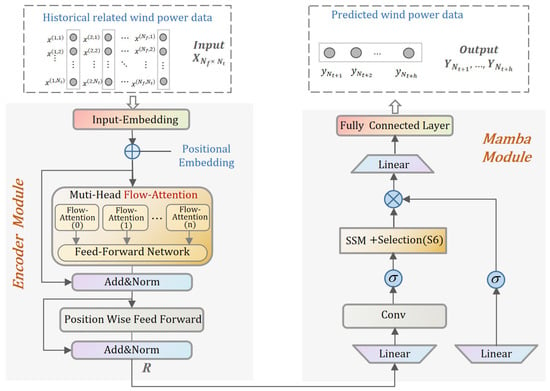
Figure 2.
Structure of the proposed Wind-Mambaformer model.
3.1. Problem Formulation
Denoted as , the input processed by the Wind-Mambaformer model involves components and , signifying the time step and feature dimension, respectively. Notably, , which includes past power values, forms . For instance, if wind data at a given moment contains details like temperature, wind direction, wind speed, humidity, and power, then the value of is 5. Designated as , the model’s output predicts the power value for the future time frame. Additionally, reflects the number of future time steps that the model anticipates from the current time.
3.2. Flow-Attention
- (1)
- During the processing of input sequences, the Transformer model can focus on different information locations due to its attention mechanism, which serves as a core component. This capability provides the Transformer with a significant advantage over traditional RNN or CNN models. In these latter models, computational complexity is frequently represented as , where N stands for the length of the sequence, unlike Transformer’s approach. For Transformer, although the attention mechanism greatly improves the performance of processing long sequences, there still exists a secondary computational complexity problem in its model. It is mainly manifested in the following three points: (1) The computational formula for Self-attention, presented in Equation (1), describes the self-attention mechanism, which is based on the idea of adjusting the representation of each element by calculating its similarity to all other elements in the input sequence. In this mechanism, the similarity between the query (Q) and key (K) is first measured by computing their dot product, followed by scaling and softmax normalization of the results to obtain the weighted importance of each element with respect to others. Finally, these weights are applied to the values (V) for weighted summation, generating a new representation for each element. This formula underscores the dependency of each position’s output on the entire set of positions within the input sequences in the Transformer’s Self-attention layer. This reliance gives rise to a computational complexity denoted as , which is a function of N, representing the length of the sequence. This means that as the length of the sequence increases, the computation of the Self-attention layer will grow quadratically.
- (2)
- The processing of long sequences by Transformer models gives rise to a notable need for extensive memory and computational resources, a requirement that stems from the quadratic computational complexity deeply rooted in the Self-attention mechanism. When the sequence length is very long, the model often exceeds the available memory limit or computational resource limit, resulting in training or inference becoming difficult or even infeasible.
- (3)
- The accuracy of long-range prediction needs to be further improved: when the sequence is very long, each element needs to take into account the information of many other elements associated with it. This may result in important information being diluted in the attention distribution, especially when the attention mechanism needs to select information from a large number of inputs. Information dilution poses a challenge for the model in capturing crucial long-distance dependencies, thereby influencing the accuracy of predictions. Additionally, an increase in sequence length results in a greater number of elements competing for limited “attention” resources during the computation of attention weights using the Softmax function. This competition has the potential to cause a more even spread of most weights. This averaged distribution of attention may make it difficult for the model to highlight the truly important parts of the sequence, thus reducing the ability to capture long-distance dependencies.
The widespread use of matrix multiplication, particularly in computing multiple attention mechanisms at every time step, is the primary reason for the high computational complexity that Transformer models encounter in time-series forecasting tasks. The computational cost grows exponentially as the time step increases.
The Wind-Mambaformer model, inspired by the Flowformer model [33], utilizes Flow-Attention as a means of reducing the significant computational burden.
Equation (1) shows the formula of Attention mechanism; it can be seen that the quadratic complexity mainly comes from in Softmax, so related researchers propose the method of kernel function to avoid direct calculation, as shown in Equation (2). In this formula, and are the query and key vectors, and is the mapping function for the query and key. The represents the dot product between the vectors. Through this method, the Flow-attention mechanism can adjust the representation of each position and prevent the occurrence of “trivial attention”, thus reducing the complexity to linear.
At the same time, the Softmax function plays a key role in the attention mechanism to avoid ‘trivial attention’, which refers to a situation in the attention mechanism where attention is either too concentrated or unreasonably distributed, causing the model to be unable to learn and infer effectively, thereby reducing its performance across a variety of tasks. In Flowformer, a new attention mechanism, Flow-Attention, is proposed based on the network flow theory, which considers the input node and the output node as the source and sink in the network flow theory. In network flows, the flow of information between nodes is finite, meaning that the amount of information that sinks into and out of each node is conserved. Flowformer utilizes this concept to achieve competition by controlling the amount of information that flows into and out of a node. This competition mechanism ensures a rational allocation in generating the attention weights, thus effectively directing the model’s attention. In this way, Flowformer is able to focus its attention on the information that is most important to the task at hand, without paying too much attention to secondary or irrelevant information.
Compared to traditional Softmax functions, Flow-Attention is able to reduce the complexity to linear while maintaining the same advantages of the attention mechanism. This means that Flowformer is able to compute more efficiently and keep the computational cost low when dealing with complex long sequence data. Moreover, due to its design based on network flow theory, Flowformer shows exceptional performance when processing various types of sequence data.
Figure 3 shows the Flow-Attention schematic diagram. , , and are first dimensionally transformed through the linear layer, and, then, and are transformed into and through nonlinear mapping by the method of kernel function, and is a nonnegative function because the flow capacity in the network flow must be positive [33]. Here, the exchange law of matrix operation can also be applied to calculate first, thus reducing the computational complexity.
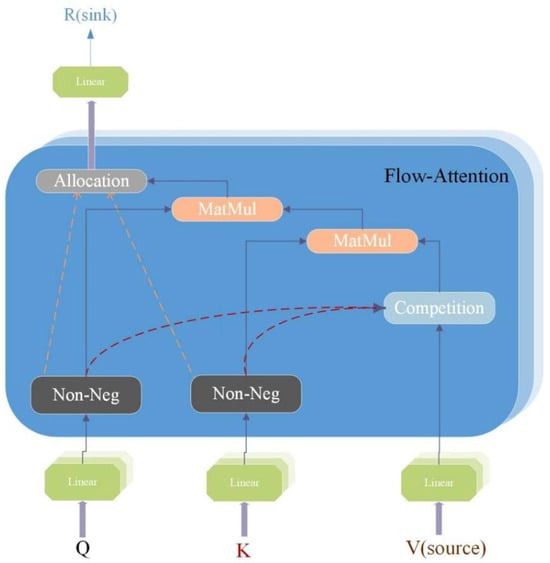
Figure 3.
Flow-Attention schematic diagram.
3.3. Mamba Module
The basic components of the Mamba module include linear projections, convolutions, activation functions, Structured State Space Model (SSM) custom S6 modules, and residual connectivity, as shown in Figure 4 [19]. The S6 module is a complex component of the Mamba architecture responsible for processing the input sequence through a series of linear transformations and discretization processes. It plays a key role in capturing the temporal dynamics of the sequence, which is a critical aspect of the sequence modeling task. Included here are tensor operations and custom discretization methods to handle the complex demands of sequence data. Mamba utilizes selective state spaces to support more efficient and effective capture of relevant information across long sequences.
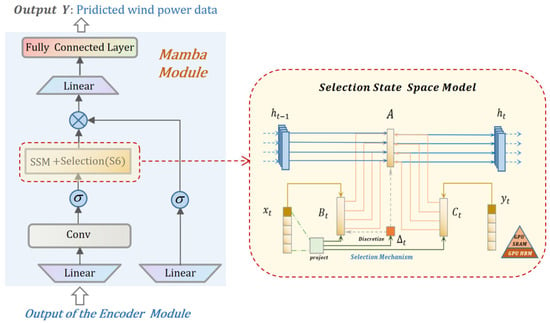
Figure 4.
Structure of Mamba module.
Mamba’s operation boasts a linear time complexity with respect to sequence length, a notable difference from Transformer, which fails to demonstrate such linearity. This property makes it particularly suitable for tasks involving very long sequences, where traditional models would struggle.
Improving SSMs with Selection by adding an input-dependent selection mechanism to the structured state space model (SSM). The following are its detailed steps:
In this study, the number of input samples is 128, representing the batch size, denoted as B. The input tensor, known as the sequence x, possesses a shape of (B, L, D), where L and D represent other dimensions of the tensor. L is the length of the sequence, that is, the number of time steps contained in each input sample, which is 48. D is the feature dimensions, which is 12. Parameters that need to be initialized include A, a matrix of shape (D, N) representing the structure of the matrix. This is one of the core matrices in the system, controlling the dynamics of the state. The parameter N represents the “state dimension” of the Selective Structured State Space Model (SSM). The dimension N determines the hidden state space size in the SSM, significantly affecting the model’s ability to retain time-related information. Generally, a larger N value boosts the model’s skill in identifying and keeping track of long-term dependencies in the input data, thereby improving the efficiency of storing and managing contextual data, particularly for longer sequences. Specifically, in our research, N is assigned a value of 32. Moreover, the algorithm adjusts parameters B, C, and Δ dynamically based on the input sequence x. The core strength of the model lies in its capacity to identify and maintain long-term dependencies within the input, with a value of 32 utilized in this study.
A central part of the algorithm is the generation of the dynamic parameters B, C, and Δ from the input sequence x: the matrix linked to the input x is represented by the tensor B, which is shaped as (B, L, N) and produced through a process involving . This matrix comes into existence through the transformation of the input x into an N-dimensional space, alternatively described as the projection of x onto this multi-dimensional plane. Similarly, tensor C, with dimensions (B, L, N) matching those of B, is generated via a comparable mapping process that projects the input x into the N-dimensional space through .
It is used to control how the state affects the output. Δ is a tensor of shape (B, L, D), computed from the parameters and via the function, which controls the choice of time step. The input’s information can be selectively remembered or ignored by the model, thanks to the activation function known as .
Once the input-dependent parameters B, C, and Δ have been generated, parameter discretization is needed next to convert these continuous parameters into discrete time steps: A, B, and Δ are discretized using Equations (7) and (8) to obtain the new A, B, and to adapt them to the time-recursive model. This operation treats A and B into shapes suitable for scanning operations (B, L, D, N).
The formula for discretization is as follows:
The recursive computation is executed step by step on the sequence according to the generated discretized parameters. This step is at the heart of executing the state space model: recursive operations using the discretized A, B, and C parameters perform the SSM model computations on the sequence x in a time-step recursive manner (scan). Because these parameters are generated based on the input x, the dynamics of the entire model changes over time steps, rather than a fixed time-invariant model as in conventional models. Finally, the output sequence y is computed by recursive computation of the state space model with the shape (B, L, D). This is the final output sequence obtained after selective filtering and information memorization.
The Improving SSMs with Selection model enables the SSM to handle time-varying sequential tasks by integrating an input-dependent selection mechanism into the SSM that selectively remembers or ignores specific input information in the state space. Due to the integration of the selection mechanism, the dissemination and retention of information can be dynamically adjusted by the model according to the particular content of inputs. This allows for the selective filtering of unimportant details and the retention of vital contextual information. Compared to traditional time-invariant models (e.g., convolutional models or fixed recursive models), this algorithm is more content-aware and therefore more suitable for handling long sequences and complex tasks.
The model’s adaptability to diverse temporal variations is facilitated by the discretization operation, which enables dynamic modifications of the state transfer matrix A and the input influence matrix B. Additionally, this operation regulates the time step through Δ. This makes the model not only time-aware but also content-aware and able to filter irrelevant information.
3.4. Implementation Details of the Model
When the model loads data through DataLoader, it divides the data into distinct sets for training, validation, and testing purposes. Additionally, the features of these data undergo a normalization process to ensure a consistent scale across all datasets. Within each training cycle, known as an epoch, the input data progress through several key components: the embedding layer, encoder, Mamba block module, and, finally, the fully connected layer. This sequential processing enables the completion of forward propagation. Following the acquisition of prediction results, loss of the MSE is utilized to calculate the difference between the predicted values and the actual values, as demonstrated in the corresponding Equation (9), and the model parameters are updated by backpropagation. During the training process, the MSE of the validation set is observed to evaluate the model’s progress. If no improvement in loss is noticed over ten consecutive epochs, the training process is terminated. This helps to save training time and improve generalization. During inference, the trained model is recovered using the saved model weights file to ensure that the parameters during inference are consistent with training.
The input data are transformed into high dimensional features by data embedding to add location and feature information. After multiple layers of the Encoder, the attention mechanism helps to extract time-step to time-step dependencies in the sequence. The model’s capability to capture long-term characteristics within the time series is enhanced by Mamba block. Subsequently, the extracted features undergo mapping onto the target dimensions through a fully connected layer, ultimately yielding the comprehensive predicted sequence. The model finally generates forecasts by calling the forecast function through the forward function and extracts the predicted values for the last h time steps. In this way, we obtain the final forecast result.
4. Experiments and Results
This section presents a comprehensive account of the experiment’s specifics.
4.1. Dataset
In this investigation, the assessment of the introduced approach was conducted through the utilization of five authentic datasets. Sourced and provided by the State Grid of China, a third-party entity, these datasets offer comprehensive coverage. They specifically include wind farm locations in China’s northern, central, and northwestern regions. Additionally, the datasets provide detailed descriptions of terrains, which comprise deserts, mountains, and plains.
The dataset, which encompasses 12 distinct input features detailed in Table 1, underwent a collection process spanning approximately two years. This comprehensive data gathering initiated on 1 January 2019, at the stroke of midnight, and came to a close on 31 December 2020, at 11:45 p.m. Notably, each data point within this extensive dataset is separated by a 15-min interval.

Table 1.
Characteristics of the dataset.
In this study, the sliding window method was utilized for efficient data sample processing. The prediction of power for the next 16 points relied on the previous 48 data points, specifically using historical data from the past 12 h to anticipate power for the subsequent 4 h. Furthermore, the dataset was divided into training, validation, and test sets, with respective allocation ratios of 0.9, 0.05, and 0.05. To ensure the effectiveness of the model, we chose a longer time period for training, resulting in a larger proportion of training data. Although the validation set only uses 5% of the data (approximately 36 days), it contains 3508 sampling points. To ensure the representativeness of the validation set, its selection was random and covered various conditions within the dataset, including wind speed variations and seasonal fluctuations. These diverse conditions allow the validation set to effectively reflect the model’s performance under different scenarios, thereby ensuring the reliability and generalizability of the validation results.
4.2. Data Preprocessing
The outlier situation of data from the five wind farms is shown in Table 2. There are several methods for outlier detection. The bottom accumulated points are identified based on power values, while the middle accumulated points and outliers are detected using algorithms. The outliers are removed using the quantile method. The middle accumulated points are removed using the K-means clustering method. This paper uses an attention-based imputation model (Self-Attention Imputation for Time Series, SAITS) for missing value imputation. The model input includes the time series with missing values, which is stacked with a mask vector and passed through an embedding layer. After encoding and decoding, the reconstructed complete time series is output. Both the input features and the target values are normalized using StandardScaler(), with the goal of setting their mean to 0 and standard deviation to 1. This ensures that each feature contributes equally to the model during training.

Table 2.
The situation of outliers of the dataset.
4.3. Baselines
The comparison conducted in this study encompasses several state-of-the-art models: CNN, Long Short-Term Memory (LSTM), Mamba, and Transformer. Additionally, the subsequent section presents a concise overview of each of these models.
Extensively applied in computer vision tasks such as image classification and target detection, the Convolutional Neural Network (CNN) is a deep learning architecture specifically designed for processing image data. Moreover, its usefulness also reaches into the field of time-series prediction. The main advantage of CNNs in time series is their efficient local feature extraction capability, which is able to capture patterns in the time series, such as short-term trends and cyclical fluctuations. CNNs can extract features on different time scales by using convolutional kernels of different sizes. Smaller convolutional kernels excel at capturing short-term variations, while larger convolutional kernels can capture patterns over longer periods of time. This is very effective in dealing with time-series data that has a multilevel structure.
LSTM: Due to their unique ability to selectively retain or discard information, LSTM (Long Short-Term Memory) networks, a type of recurrent neural networks, stand out in time-series prediction. The utilization of gate control mechanisms such as input gates, forgetting gates, and output gates by the LSTM model is the reason behind this advantage. By effectively filtering information, these gates establish LSTM as a powerful tool for time-series forecasting. Additionally, LSTM networks exhibit a capability to automatically learn features during the forecasting process, thereby improving their adaptability to a wide range of time-series data types.
In processing long sequences, Transformer, an attention-based deep learning model, demonstrates excellence. Through the utilization of the self-attention mechanism, it skillfully acquires knowledge of the dependencies present within sequences, thus effectively grasping long-term connections inherent in time-series data.
Mamba: The most recent results from 2024 show that Mamba achieves performance comparable to Transformer in language modeling with linear time complexity. On the performance side, Mamba introduces a selective mechanism to remember relevant information and filter out irrelevant information indefinitely. On the computational side, Mamba implements a hardware-aware parallel training algorithm similar to CNNs, which can be viewed as an RNN for linear time inference. The two aforementioned advantages of Mamba have led to its high regard, primarily because of its proficiency in handling remote time-series data. The datasets mentioned undergo a uniform assessment procedure applicable to all methods, with Wind-Mambaformer being included. This involves utilizing the training set to educate a particular model and identifying the best model through its results on the validation set. Afterward, the test set documents reveal the capabilities of the chosen model.
4.4. Metrics
This study incorporates four key evaluation metrics, namely MSE (mean square error), MAE (mean absolute error), RMSE (root mean square error), and MAPE (mean absolute percentage error), which are extensively used in electricity forecasting. Detailed formulas and explanations of these metrics are subsequently presented.
MSE denotes the expected value of the squared difference between the predicted and actual parameter values [42].
A more precise depiction of the real forecast value error is offered by the Mean Absolute Error, commonly referred to as MAE.
The sample standard deviation of the differences between predicted and actual values is represented by the root mean square error, or RMSE, as it is commonly known. This comprehensive measure provides an accurate reflection of the variations in forecast errors.
MAPE is the mean absolute percentage error. Theoretically, the smaller the MAPE value, the better the fit of the predictive model and the higher the accuracy [43], where is the total number of data, is the true value, and is the predicted value.
4.5. Results
A comparative analysis of prediction outcomes for the forthcoming four-hour period on a specified date across five wind farms is showcased in Figure 5. Ground Truth refers to the actual power values. After making the predictions, we performed inverse normalization on the normalized data in order to plot a graph that reflects the prediction accuracy, showing the comparison between the actual power values and the predicted power values. The Flow-Mamba former model’s performance is clearly superior to all other models, as evidenced by the results. Furthermore, the model’s excellence is confirmed through four distinct evaluation criteria, highlighting Wind-Mambaformer’s efficacy in addressing the complexities of wind power forecasting.
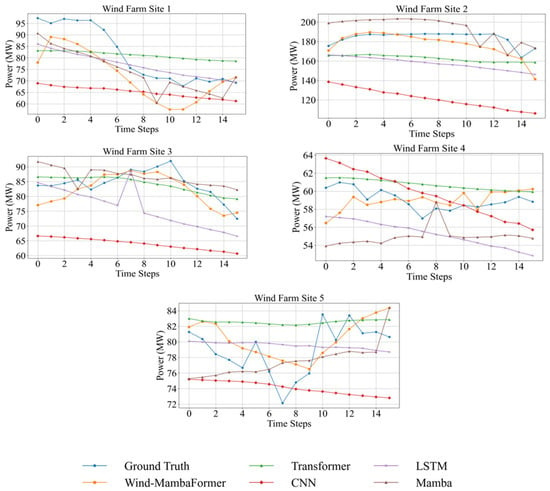
Figure 5.
Comparison of predicted results for the next 4 h on a given date in five wind farms.
The Wind-Mambaformer model and the LSTM model in Wind Farm 1 are the best in capturing the fluctuations and changes of the real values, and the prediction results are closer to the real values, while the Transformer, Mamba, and CNN models are poorer in prediction, especially the CNN model, which hardly reflects the fluctuations of the real values, and the prediction results are too smooth.
The Wind-Mambaformer model performs better overall in Wind Farm 2, fitting the trend of the real values better. The Mamba model fluctuates in the late prediction and is not stable enough. The Transformer and LSTM models’ prediction curves are too smooth, failing to reflect the fluctuations in the real data. The CNN model performs the worst, consistently underestimating the power, and could not capture the trend changes in the real values.
In Wind Farm 3, the prediction curve of the Wind-Mambaformer model in wind farm 3 shows a closer match to the actual value, specifically in the first 12 time steps; although there is a minor underestimation, the general pattern remains consistent. Nevertheless, after step 12, there is a clear increase in the speed of decrease for the predicted values when compared to the real values. On the other hand, while the Transformer model’s forecasts seem more even, they display a notable difference from the actual values, particularly from time steps 7 to 10, where a significant rise in actual values occurs, a change that the model’s predictions are unable to capture adequately. The Mamba model shows large fluctuations in the first few time steps, and the gap with the true values is large. Although the model predicts a trend close to the true value after time step 8, the fluctuations still fail to accurately reflect the true situation. The LSTM model’s prediction curve deviates significantly from the fluctuations in the true value, especially at time step 8, when the true value rises sharply, the LSTM prediction dips, showing a clear trend of error. The CNN model’s prediction curve has an almost linear downtrend, failing to capture any fluctuations in the true values. The model predictions are consistently lower than the true values, which is a poor performance.
In Wind Farm 4, the Wind-Mambaformer model predicts curves that are close to those of the true values, but there are significant deviations in a few time steps, especially the fluctuations after step 9 that are not accurately predicted. Transformer model: the predicted curves are smoother, and do not capture the fluctuations in the curve of the true values, especially the downward trend in the segment of time steps 10–15 that is not accurately reflected. Mamba model: The model predicts large deviations, especially around time steps 8 and 9, predicting an anomalous fluctuation that is much higher than the true value. The LSTM model, especially after time step 13, predicts a steeper downward trend than the true value. The CNN model: again, there is a tendency to smoothing, and it fails to capture the fluctuations in the true value well, especially in the downward trend from time steps 4 to 8 where there is a large deviation.
In Wind Farm 5, the Wind-Mambaformer model predicts curves that match the true values in the early stage but start to deviate from time steps 8 to 16. Transformer model: the predicted curve is almost a flat line, failing to capture the trend of power fluctuations, especially the drop and subsequent rise in time steps 5 to 10. Mamba model: the curve is basically smooth in the first half of the curve, not following the fluctuations of the true values, while there is a significant rise after time step 14, much higher than the true value, but, after time step 14, there is a significant increase, much higher than the true value. LSTM model: the fluctuation trend with the true value has a low degree of agreement, and the model’s prediction curve shows an overall downward trend, which cannot accurately reflect the ups and downs of the real data. CNN model: The prediction curve displays a marginal upward trajectory; nevertheless, a significant divergence is observed between its variations and the actual value. This divergence becomes especially apparent within the time steps spanning from 5 to 10, as the curve is unable to precisely reflect the fluctuations in power.
Overall, it seems that the Wind-Mambaformer model has the best predictive performance and is able to follow the fluctuations of the true values better. Regarding the issue of CNN model predictions decreasing with increasing time steps, CNNs were originally designed for processing image data, primarily focusing on local feature extraction in two-dimensional spaces (e.g., image pixels). Their core advantages are (1) the ability to identify local patterns (such as image edges and textures) and (2) improved parameter efficiency through weight sharing.
However, time-series data have temporal dependencies, meaning that the significance of each data point depends not only on its value but also on its position within the sequence and its contextual relationships. This temporal dependency is difficult to capture with CNNs’ convolutional kernels. Time-series data often require capturing long-range dependencies, such as how trends from a week ago can impact current predictions. CNNs’ convolutional kernels can only extract features within local windows, making them ineffective for handling long-span data.
Combining the above five wind farms’ prediction effect comparison chart and error result comparison, that is, Figure 6, we can see that the Wind-Mambaformer model is the most effective, with the smallest error, which can capture the trend of power change as much as possible and realize the higher accuracy of power prediction.
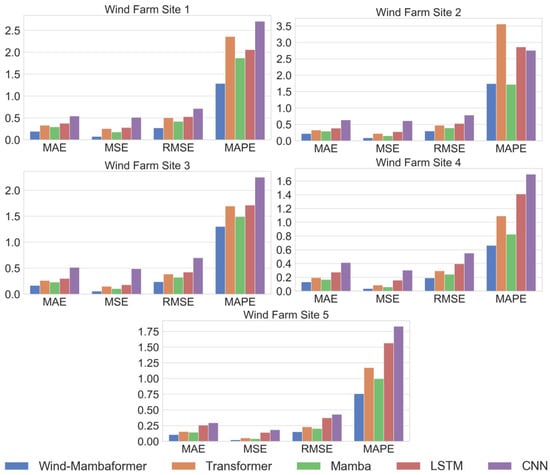
Figure 6.
Comparison of prediction errors of different models for the next 4 h for five wind.
As can be seen from Table 3, the model makes predictions at different time steps (4, 8, 12, 16). Overall, the error remains stable with increasing time steps and even performs better in some cases (e.g., Wind Farm 5), indicating that the model has good robustness in long time prediction. It can be concluded that the Wind-Mambaformer model shows robust performance in multi-step prediction tasks.

Table 3.
Comparison of multi-step prediction performance.
4.6. Ablation Studies
A series of ablation experiments were carried out to assess the efficacy of the unique elements presented by Wind-Mambaformer, in which one module was modified while keeping all other conditions consistent.
The outcomes of the ablation study assessment are showcased in Table 4, whereas a visualization of the findings is provided in Figure 7 below. Specifically, WindMambaformer-FlowAttention is used to represent WindMambaformer without the aforementioned Flow-Attention module to verify the effect of adding Flow-Attention. Similarly, WindMambaformer without the Mamba module is referred to as WindMambaformer-Mamba to validate the effect of adding Mamba. WindMambaformer with both modules removed is referred to as WindMambaformer-WindMambaformer-Mamba. These variants were trained and evaluated using the same settings and datasets. The observations clearly indicate that the original Wind-Mambaformer model exhibits the weakest prediction performance across the five datasets specifically when deprived of both FlowAttention and Mamba. Nevertheless, the model’s performance undergoes improvement with the incorporation of either the FlowAttention or Mamba component. Wind-Mambaformer achieves the best regression performance when these two components are combined. These ablation findings emphasize the validity of the key contributions in this study.

Table 4.
Comparison table of ablation experiments.
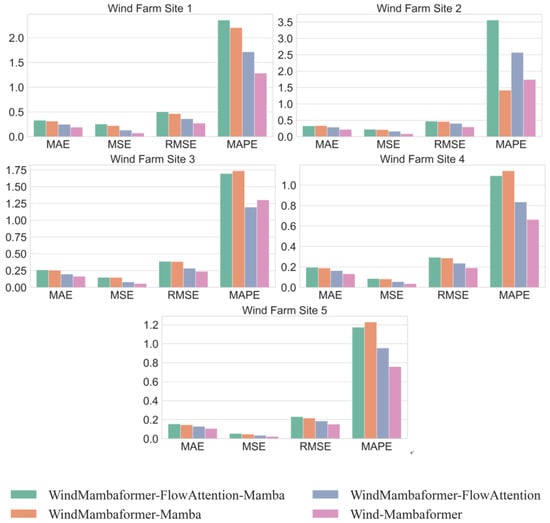
Figure 7.
Comparative visualization of ablation experiment results.
5. Discussion
Despite Wind-Mambaformer’s excellent performance in wind power prediction, there is still room for further optimization: compared to onshore wind farms, offshore wind farms operate under more complex conditions, are more affected by weather and equipment conditions, and require more timely and accurate predictions. The Wind-Mambaformer model has the potential to be further integrated, presented by the intricate correlation between variables in the SCADA system of offshore wind farms. These farms are commonly outfitted with a multitude of sensors for monitoring equipment operating conditions. Through this integration, the model can be adapted to accommodate the distinctive environmental requirements of offshore wind power, capitalizing on the complex relationships amidst these variables.
Future research will continue to optimize the Wind-Mambaformer model structure and explore its potential in other application areas. By combining more datasets and forecasting tasks, its performance under different environmental conditions will be further evaluated with the aim of providing smarter and more efficient forecasting solutions in wind power and other energy sectors.
6. Conclusions
This paper introduces Wind-Mambaformer, a wind power prediction model that reduces computational complexity and excels in data-dependent tasks requiring strong model adaptation. The model’s efficiency and superior prediction performance are validated through experiments on various datasets. The key advantages include the following:
- (1)
- Improved prediction accuracy with Mamba: Wind-Mambaformer incorporates the Mamba module to capture long-term wind power dependencies, significantly reducing MAE by 30% and MSE by 60% compared to the standard Transformer model.
- (2)
- Reduced computational complexity with Flow-Attention: the Flow-Attention mechanism lowers the computational burden while maintaining high efficiency, providing an edge in large-scale power prediction tasks.
- (3)
- Enhanced adaptability and generalization: the model performs well across diverse wind farm datasets, showing strong adaptability and accuracy in handling variable wind conditions and power changes.
Author Contributions
Conceptualization and Methodology, Z.D.; Conceptualization and Writing—Original Draft, Y.Z.; Software, Validation, and Supervision, A.W.; Writing—Review and Editing, M.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by National Key R&D Program of China under Grant 2023YFC3306401, in part by the Yuxiu Innovation Project of NCUT (No.2024NCUTYXCX205), and in part by the Yuxiu Innovation Project of NCUT (No. 2024NCUTYXCX107).
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xue, Y.; Lei, X.; Xue, F.; Yu, C.; Dong, Z.; Wen, F.; Ju, P. A review on the impact of wind power uncertainty on power systems. Chin. J. Electr. Eng. 2014, 34, 5029–5040. [Google Scholar]
- Qian, Z.; Pei, Y.; Zareipour, H.; Chen, N. A review of wind power prediction methods. High Volt. Technol. 2016, 42, 1047–1060. [Google Scholar]
- Stathopoulos, C.; Kaperoni, A.; Galanis, G.; Kallos, G. Windpower prediction based on numerical and statistical models. J. Wind Eng. Ind. Aerodyn. 2013, 112, 25–38. [Google Scholar] [CrossRef]
- Awad, M.; Khanna, R.; Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Springer: Berlin/Heidelberg, Germany, 2015; pp. 67–80. [Google Scholar]
- Li, Z.; Ye, L.; Zhao, Y.; Song, X.; Teng, J.; Jin, J. Short-Term Wind Power Prediction Based on Extreme Learning Machine with Error Correction. Prot. Control. Mod. Power Syst. 2016, 1, 1–8. [Google Scholar] [CrossRef]
- Abhinav, R.; Pindoriya, N.M.; Wu, J.; Long, C. Short-term wind power forecasting using wavelet-based neural network. Energy Procedia 2017, 142, 455–460. [Google Scholar] [CrossRef]
- Voulodimos, A.; Doulamis, N.; Doulamis, A.; Protopapadakis, E. Deep learning for computer vision: A brief review. Comput. Intell. Neurosci. 2018, 2018, 7068349. [Google Scholar] [CrossRef]
- Medsker, L.R.; Jain, L. Recurrent neural networks. Des. Appl. 2001, 5, 64–67. [Google Scholar]
- Graves, A. Long short-term memory. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 37–45. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wang, A.; Pei, Y.; Qian, Z.; Zareipour, H.; Jing, B.; An, J. A two-stage anomaly decomposition scheme based on multi-variable correlation extraction for wind turbine fault detection and identification. Appl. Energy 2022, 321, 119373. [Google Scholar] [CrossRef]
- Wang, A.; Pei, Y.; Zhu, Y.; Qian, Z. Wind turbine fault detection and identification through self-attention-based mechanism embedded with a multivariable query pattern. Renew. Energy 2023, 211, 918–937. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.; Guo, T.; Xu, C.; Deng, Y.; Liu, Z.; Ma, S.; Xu, C.; Xu, C.; Gao, W. Pre-trained image processing transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 12299–12310. [Google Scholar]
- Hofstätter, S.; Zamani, H.; Mitra, B.; Craswell, N.; Hanbury, A. Local self-attention over long text for efficient document retrieval. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval, Virtual Event, China, 25–30 July 2020; p. 2021. [Google Scholar]
- Wu, N.; Green, B.; Ben, X.; O’Banion, S. Deep transformer models for time series forecasting: The influenza prevalence case. arXiv 2020, arXiv:2001.08317. [Google Scholar]
- Putz, D.; Gumhalter, M.; Auer, H. A novel approach to multi-horizon wind power forecasting based on deep neural architecture. Renew. Energy 2021, 178, 494–505. [Google Scholar] [CrossRef]
- Pan, X.; Wang, L.; Wang, Z.; Huang, C. Short-term wind speed forecasting based on spatial-temporal graph transformer networks. Energy 2022, 253, 124095. [Google Scholar] [CrossRef]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Gu, A.; Dao, T. Mamba: Linear-time sequence modeling with selective state spaces. arXiv 2023, arXiv:2312.00752. [Google Scholar]
- Hannan, E.J.; Kavalieris, L. Regression, autoregression models. J. Time Ser. Anal. 1986, 7, 27–49. [Google Scholar] [CrossRef]
- Hansun, S. A new approach of moving average method in time series analysis. In Proceedings of the 2013 Conference on New Media Studies (CoNMedia), Tangerang, Indonesia, 27–28 November 2013; IEEE: New York, NY, USA, 2013; pp. 1–4. [Google Scholar]
- Benjamin, M.A.; Rigby, R.A.; Stasinopoulos, D.M. Generalized autoregressive moving average models. J. Am. Stat. Assoc. 2003, 98, 214–223. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, Y.; Lu, H. Seasonal autoregressive integrated moving average and support vector machine models: Prediction of short-term traffic flow on freeways. Transp. Res. Rec. 2011, 2215, 85–92. [Google Scholar] [CrossRef]
- Shen, X.; Liu, X.; Hu, X.; Zhang, D.; Song, S. Contrastive learning of subject-invariant EEG representations for cross-subject emotion recognition. IEEE Trans. Affect. Comput. 2022, 14, 2496–2511. [Google Scholar] [CrossRef]
- Fan, J.; Ma, X.; Wu, L.; Zhang, F.; Yu, X.; Zeng, W. Light gradient boosting machine: An efficient soft computing model for estimating daily reference evapotranspiration with local and external meteorological data. Agricult. Water Manag. 2019, 225, 105758. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. xgboost: Extreme gradient boosting. R Package Version 0.4-2 2015, 1, 1–4. [Google Scholar]
- Dey, R.; Salem, F.M. Gate-variants of gated recurrent unit (GRU) neural networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS), Boston, MA, USA, 6–9 August 2017; IEEE: New York, NY, USA, 2017; pp. 1597–1600. [Google Scholar]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Signal Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Bommidi, B.S.; Teeparthi, K.; Kosana, V. Hybrid wind speed forecasting using ICEEMDAN and transformer model with novel loss function. Energy 2023, 265, 126383. [Google Scholar] [CrossRef]
- Beltagy, I.; Peters, M.E.; Cohan, A. Longformer: The long-documenttransformer. arXiv 2020, arXiv:2004.05150. [Google Scholar]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. Proc. AAAI Conf. Artif. Intell. 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- Wu, H.; Wu, J.; Xu, J.; Wang, J.; Long, M. Flowformer: Linearizing Transformers with Conservation Flows. arXiv 2022, arXiv:2202.06258. [Google Scholar] [CrossRef]
- Neshat, M.; Nezhad, M.M.; Mirjalili, S.; Piras, G.; Garcia, D.A. Quaternion convolutional long short- term memory neural model with an adaptive decomposition method for wind speed forecasting: North aegean islands case studies. Energy Convers. Manag. 2022, 259, 115590. [Google Scholar] [CrossRef]
- Nezhad, M.M.; Heydari, A.; Pirshayan, E.; Groppi, D.; Garcia, D.A. A novel forecasting model for wind speed assessment using sentinel family satellites images and machine learning method. Renew. Energy 2021, 179, 2198–2211. [Google Scholar] [CrossRef]
- Neshat, M.; Nezhad, M.M.; Abbasnejad, E.; Mirjalili, S.; Tjernberg, L.B.; Garcia, D.A.; Alexander, B.; Wagner, M. A deep learning-based evolutionary model for short-term wind speed forecasting: A case study of the lillgrund offshore wind farm. Energy Convers. Manag. 2021, 236, 114002. [Google Scholar] [CrossRef]
- Neshat, M.; Nezhad, M.M.; Sergiienko, N.Y.; Mirjalili, S.; Piras, G.; Garcia, D.A. Wave power forecasting using an effective decomposition-based convolutional Bi-directional model with equilibrium Nelder-Mead optimiser. Energy 2022, 256, 124623. [Google Scholar] [CrossRef]
- Neshat, M.; Nezhad, M.M.; Abbasnejad, E.; Mirjalili, S.; Groppi, D.; Heydari, A.; Tjernberg, L.B.; Garcia, D.A.; Alexander, B.; Shi, Q.; et al. Wind turbine power output prediction using a new hybrid neuro-evolutionary method. Energy 2021, 229, 120617. [Google Scholar] [CrossRef]
- Le, T.M.C.; Le, X.C.; Huynh, N.N.P.; Doan, A.T.; Dinh, T.V.; Duong, M.Q. Optimal power flow solutions to power systems with wind energy using a highly effective meta-heuristic algorithm. Int. J. Renew. Energy Dev. 2023, 12, 467–477. [Google Scholar] [CrossRef]
- Yang, M.; Jiang, Y.; Che, J.; Han, Z.; Lv, Q. Short-Term Forecasting of Wind Power Based on Error Traceability and Numerical Weather Prediction Wind Speed Correction. Electronics 2024, 13, 1559. [Google Scholar] [CrossRef]
- Kovalnogov, V.N.; Fedorov, R.V.; Chukalin, A.V.; Klyachkin, V.N.; Tabakov, V.P.; Demidov, D.A. Applied Machine Learning to Study the Movement of Air Masses in the Wind Farm Area. Energies 2024, 17, 3961. [Google Scholar] [CrossRef]
- Allen, D.M. Mean square error of prediction as a criterion for selectingvariables. Technometrics 1971, 13, 469–475. [Google Scholar] [CrossRef]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Meanabsolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).