Comparative Analysis of Offshore Wind Resources and Optimal Wind Speed Distribution Models in China and Europe
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Resources and Quality Assessment
2.2. Wind Resource Characteristics Analysis
2.2.1. Data Preprocessing for Offshore Wind Resource Analysis
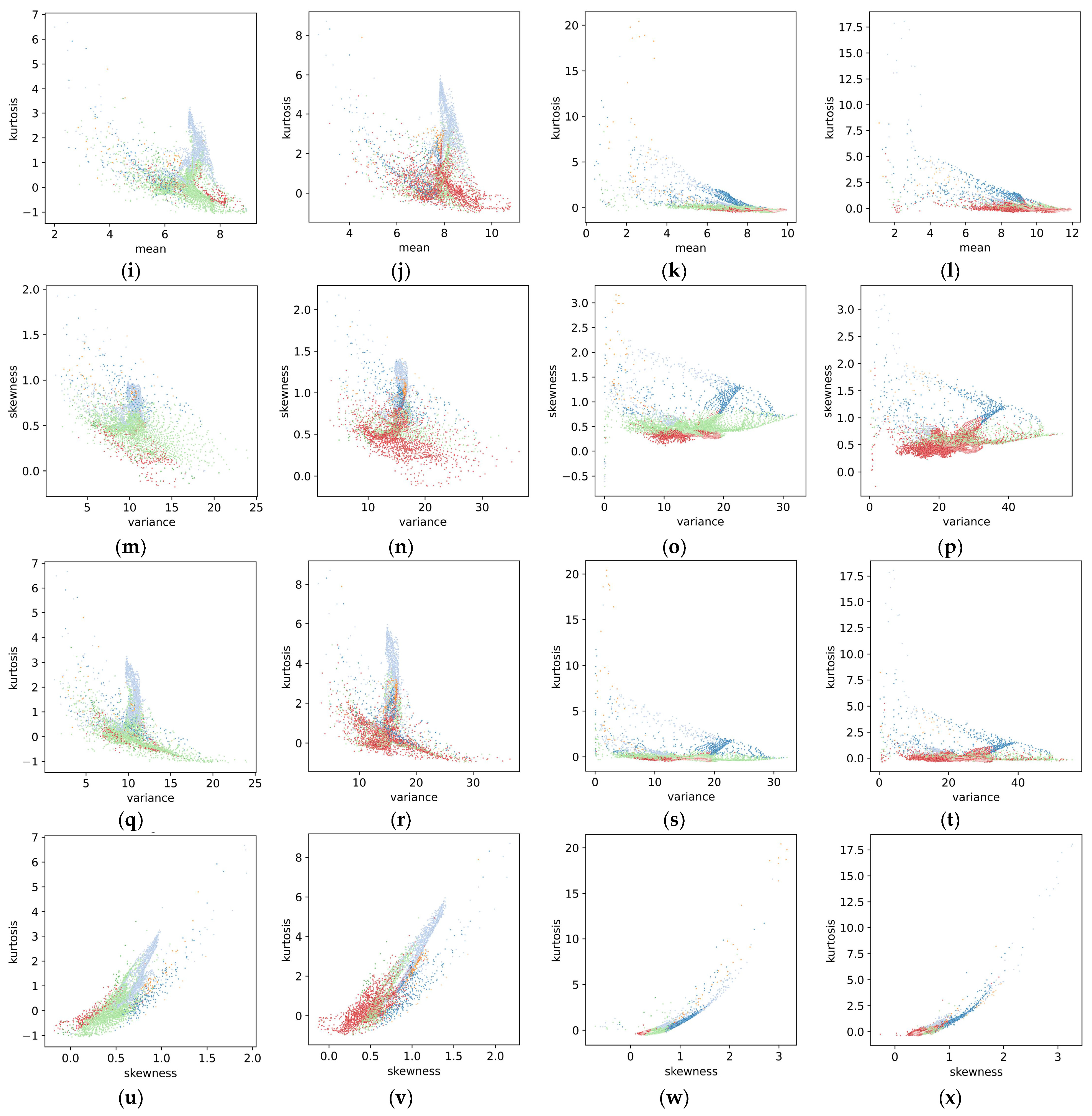
2.2.2. Statistical Characteristics of Wind Speed
2.2.3. Theoretical Potential of Wind Resources
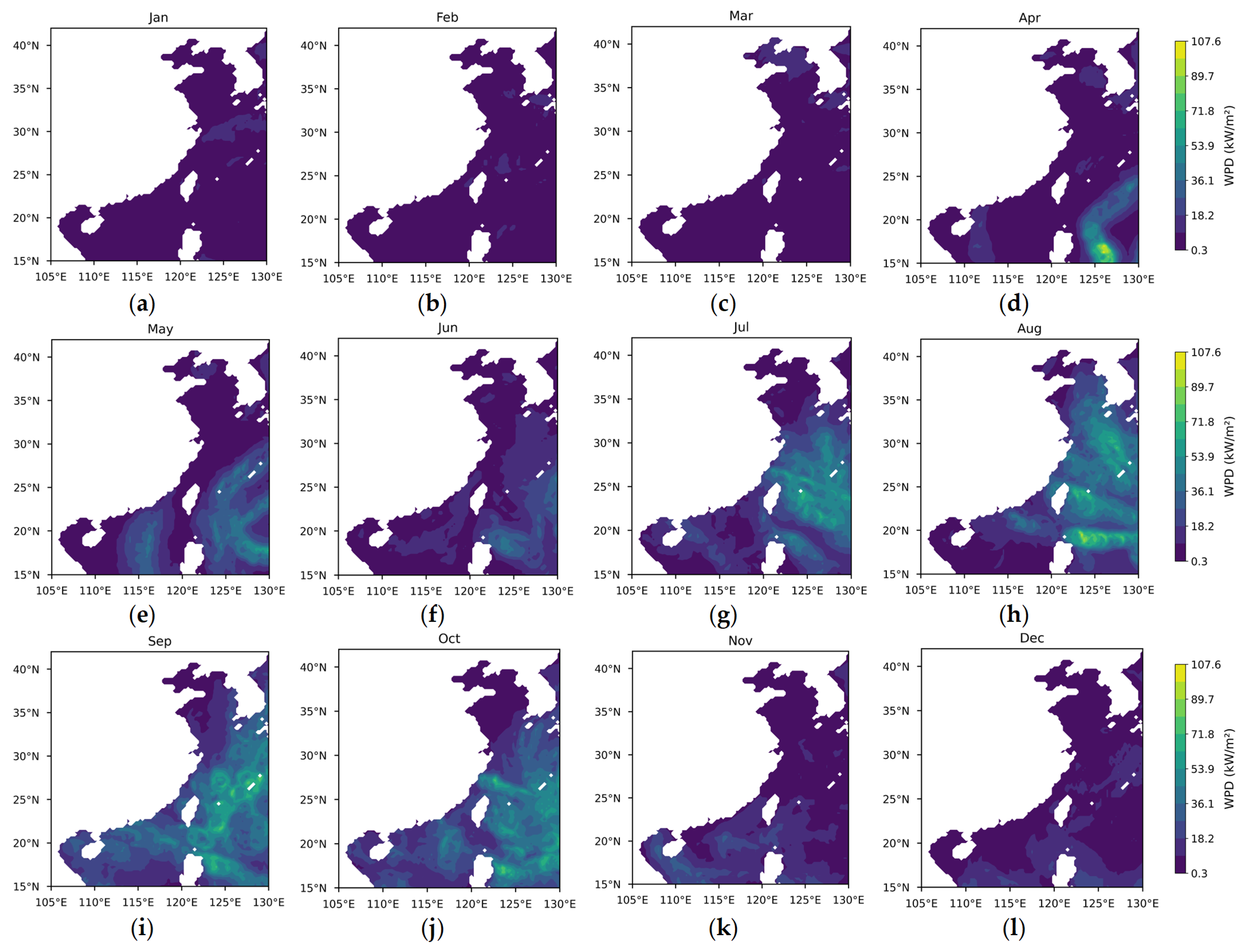
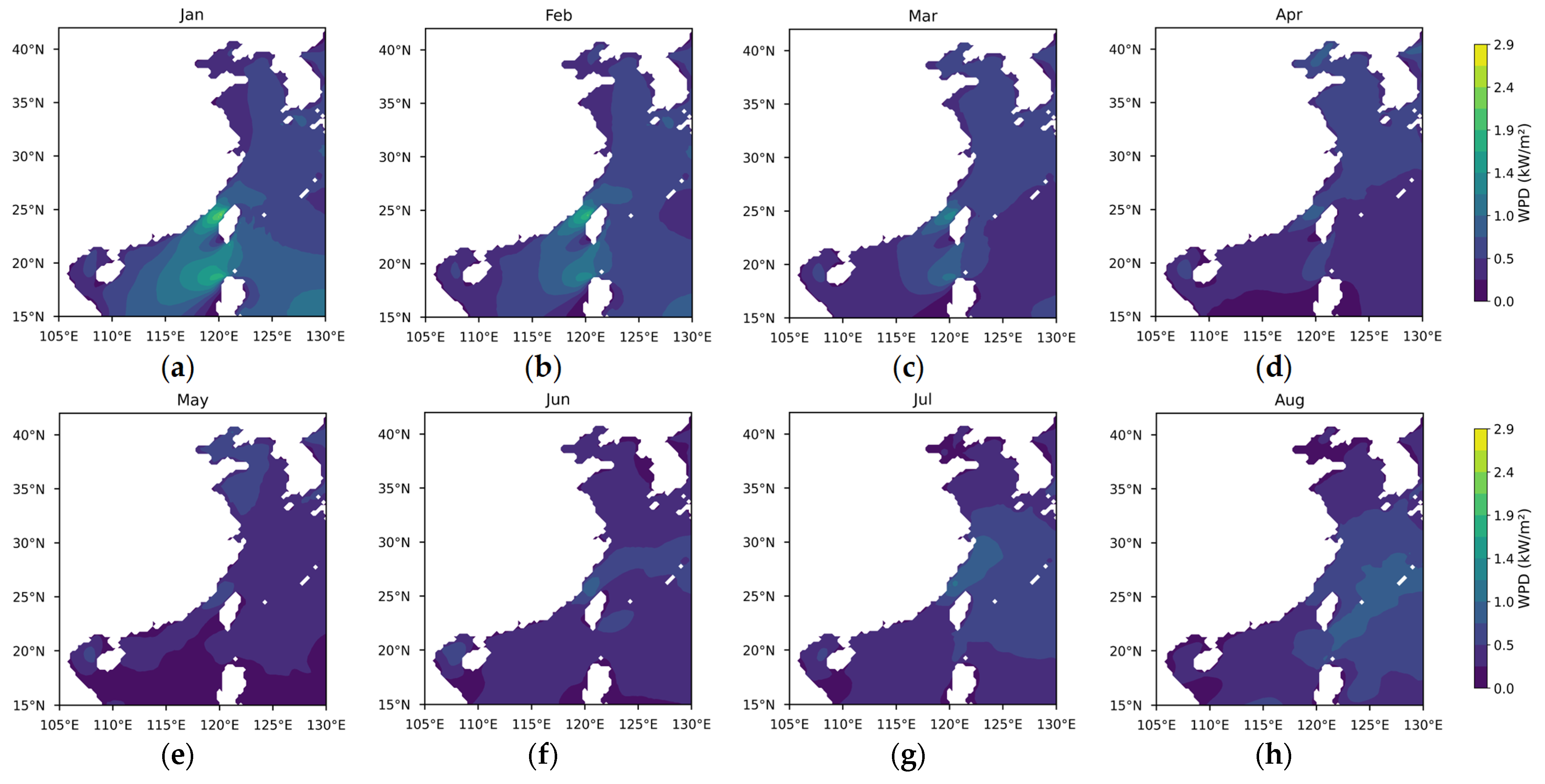
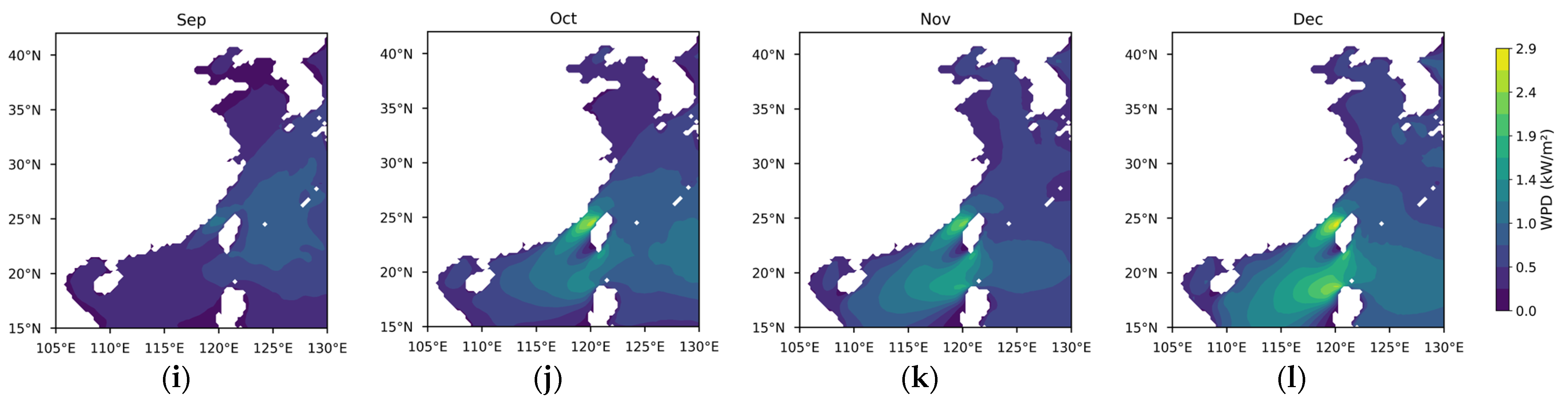
- Wind power density (WPD).
- 2.
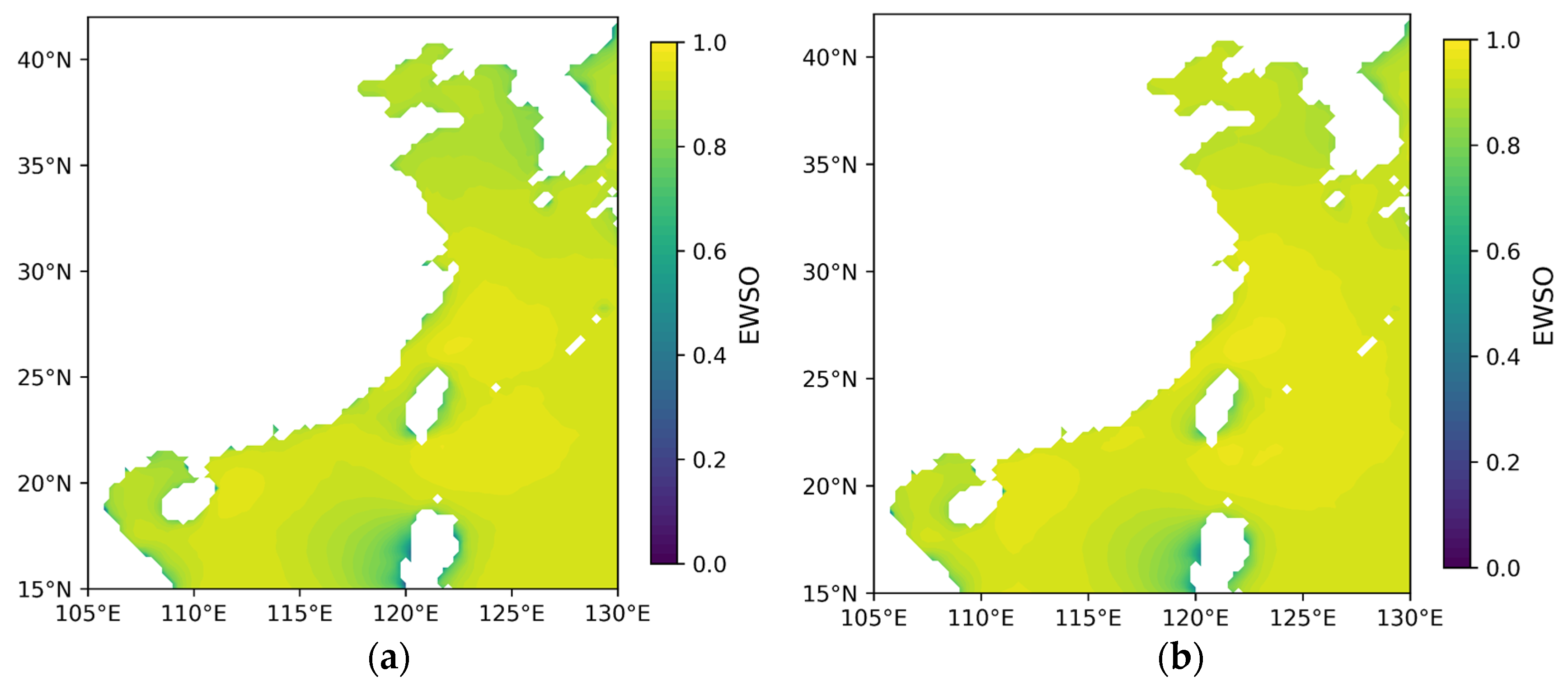
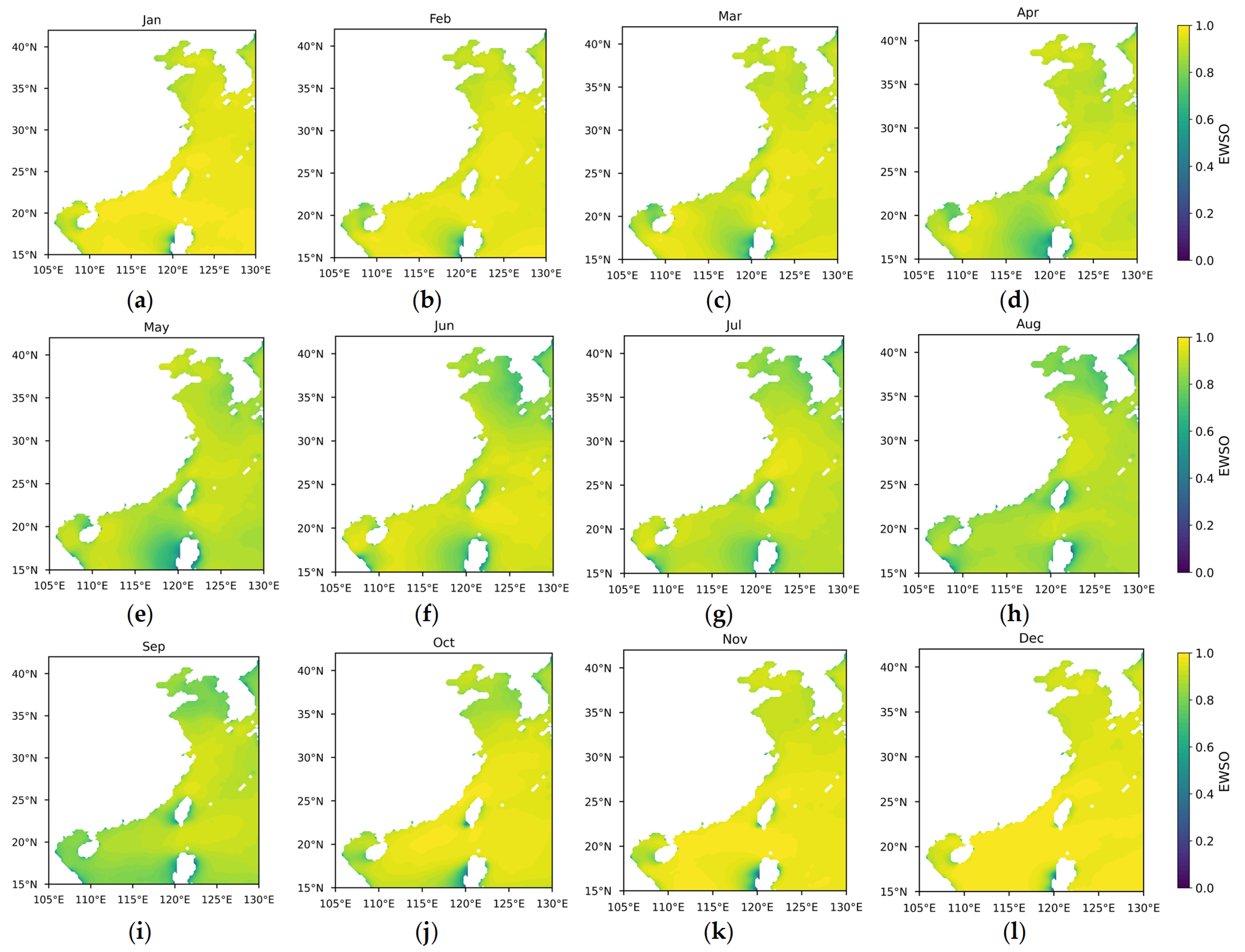
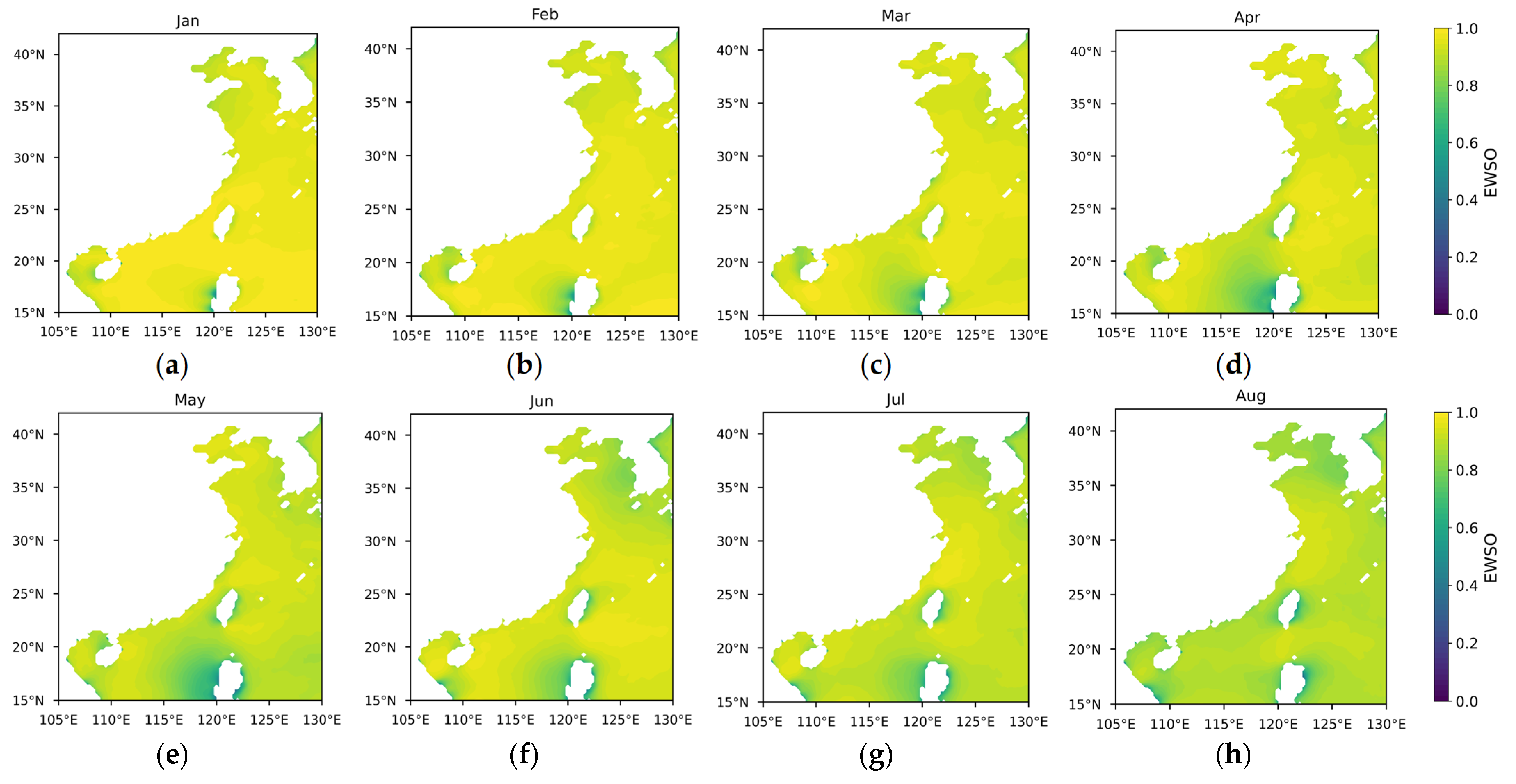
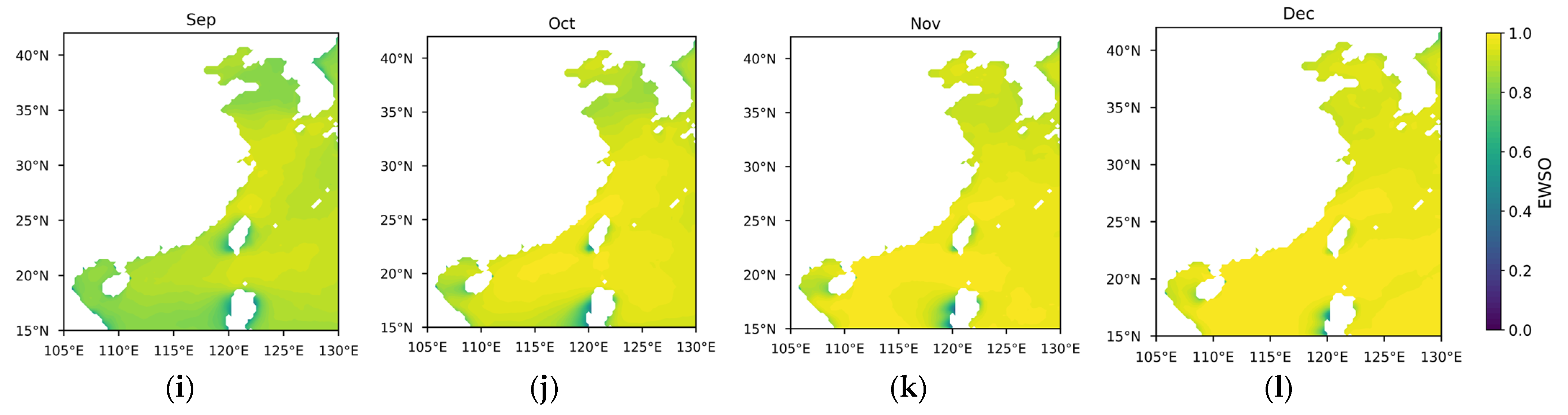
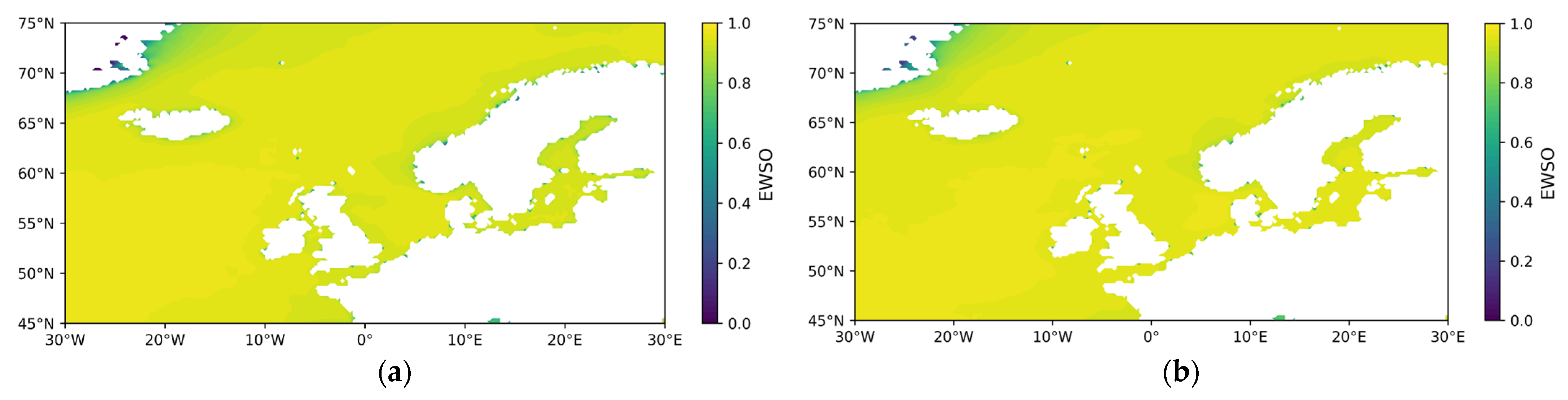
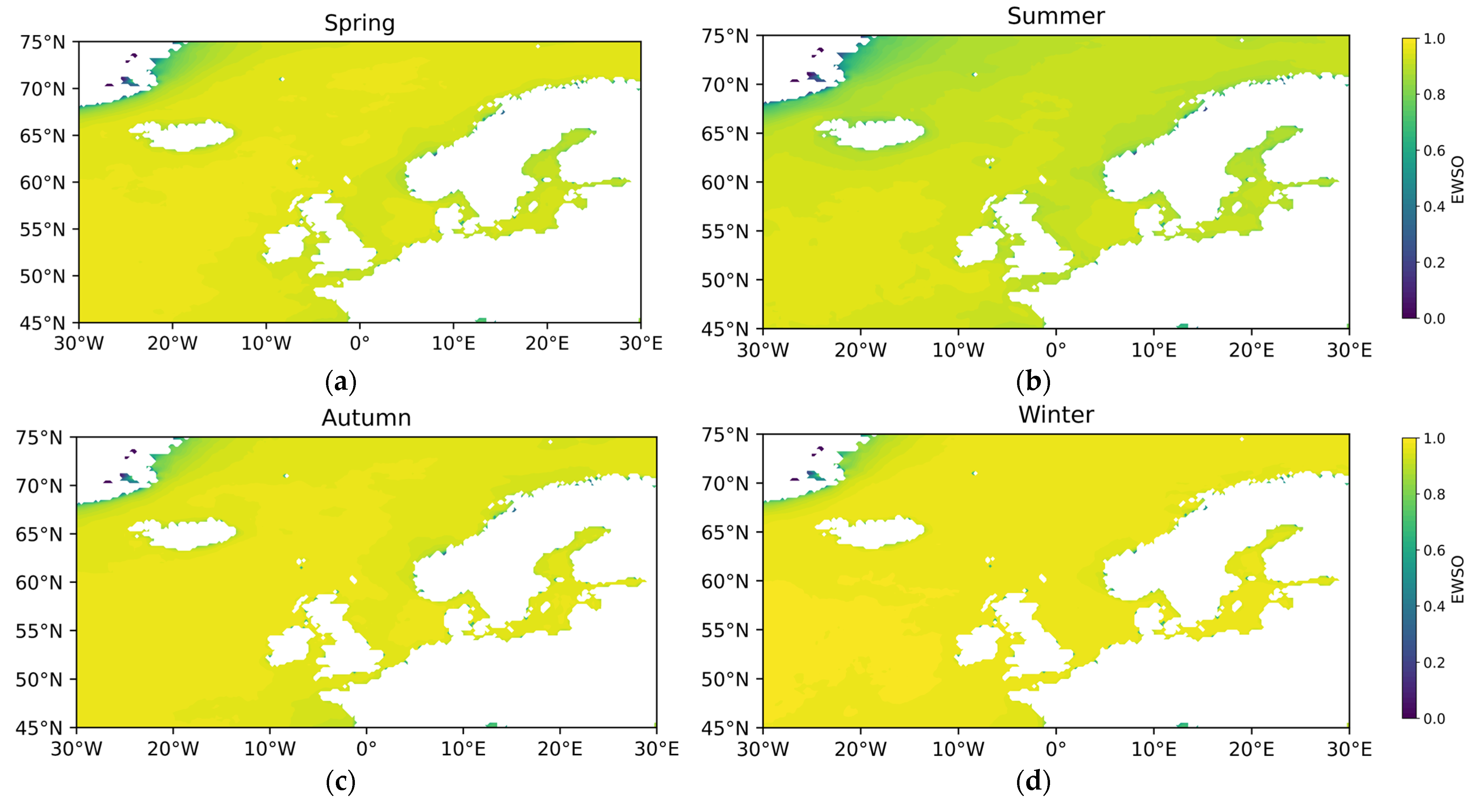
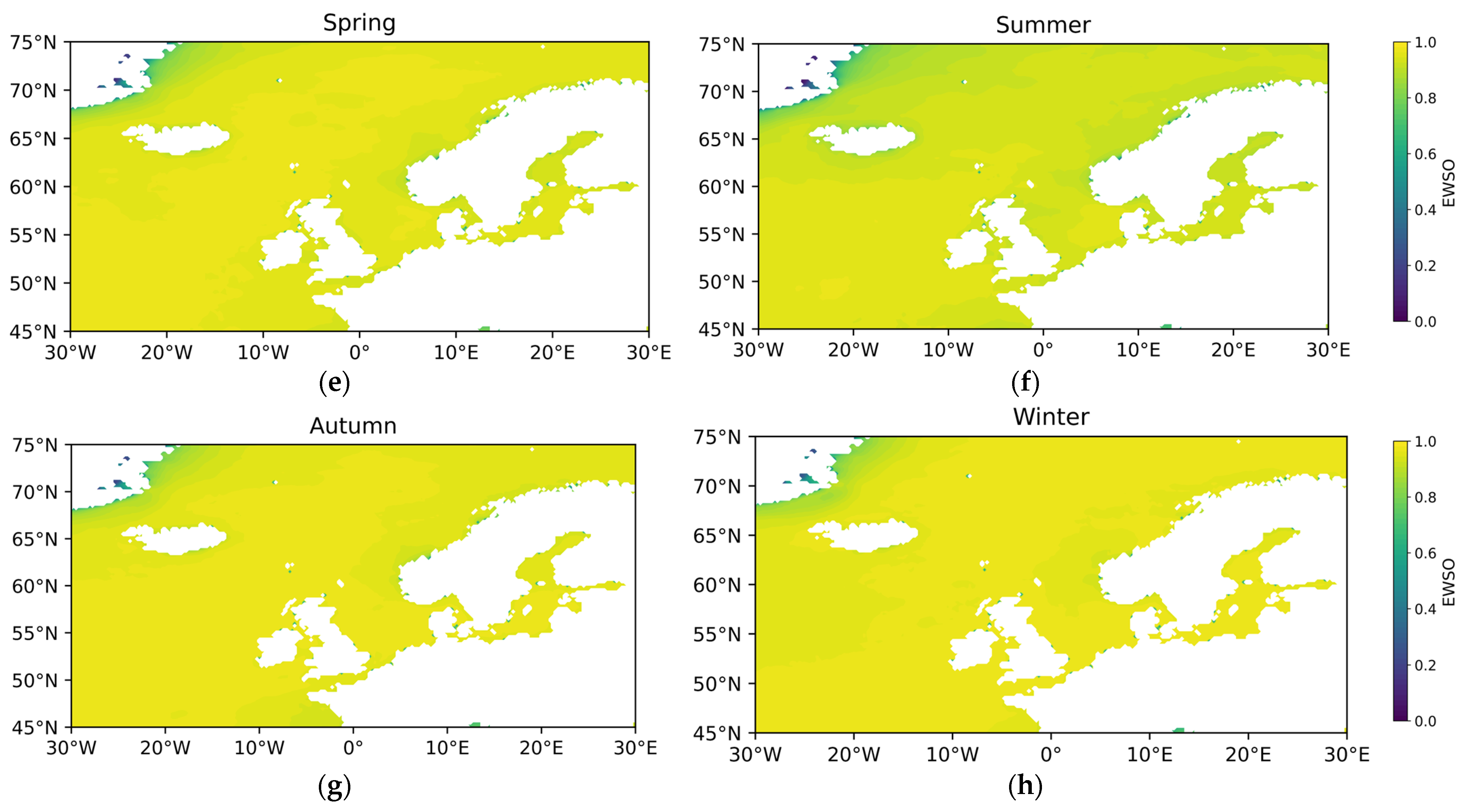
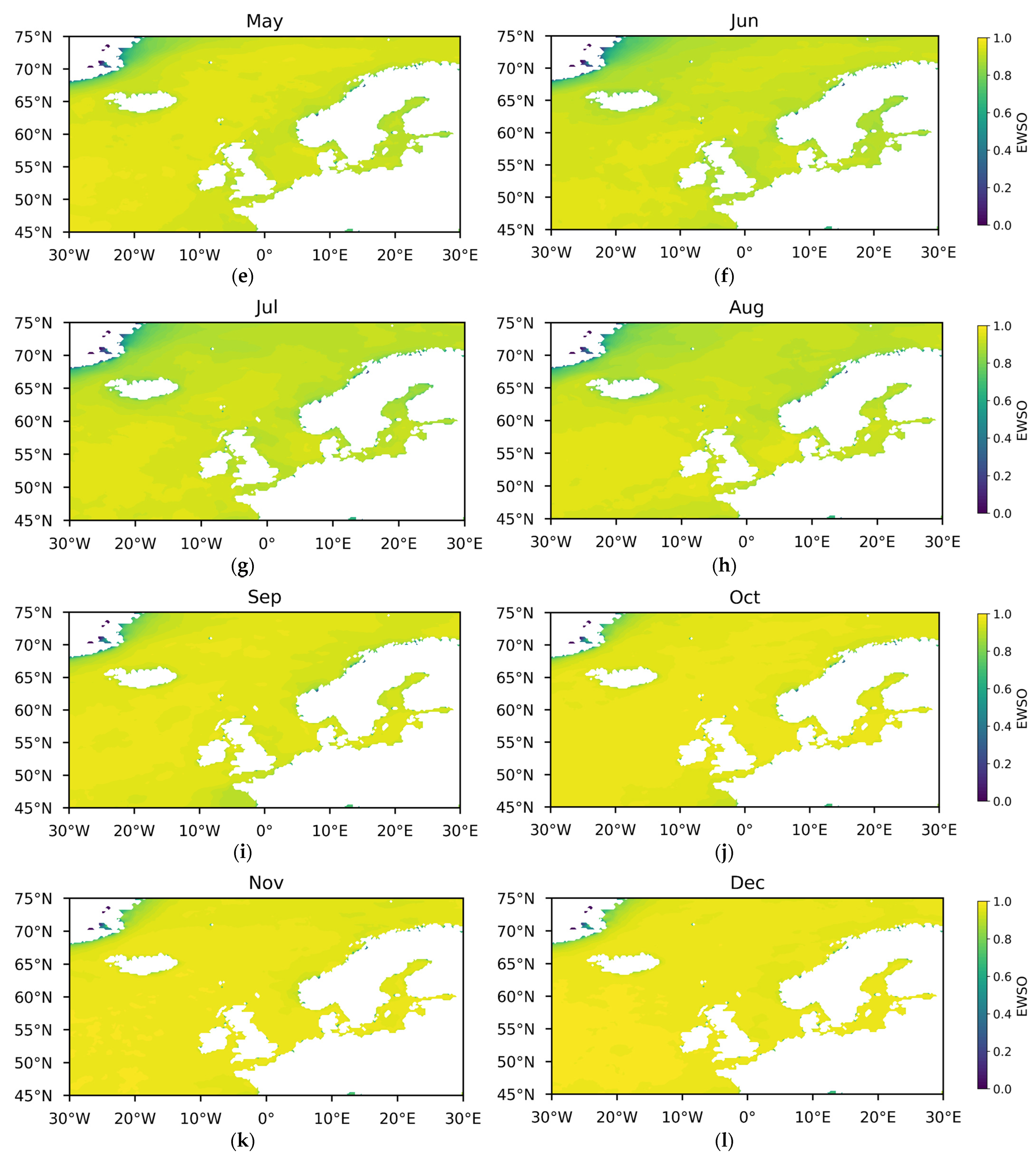
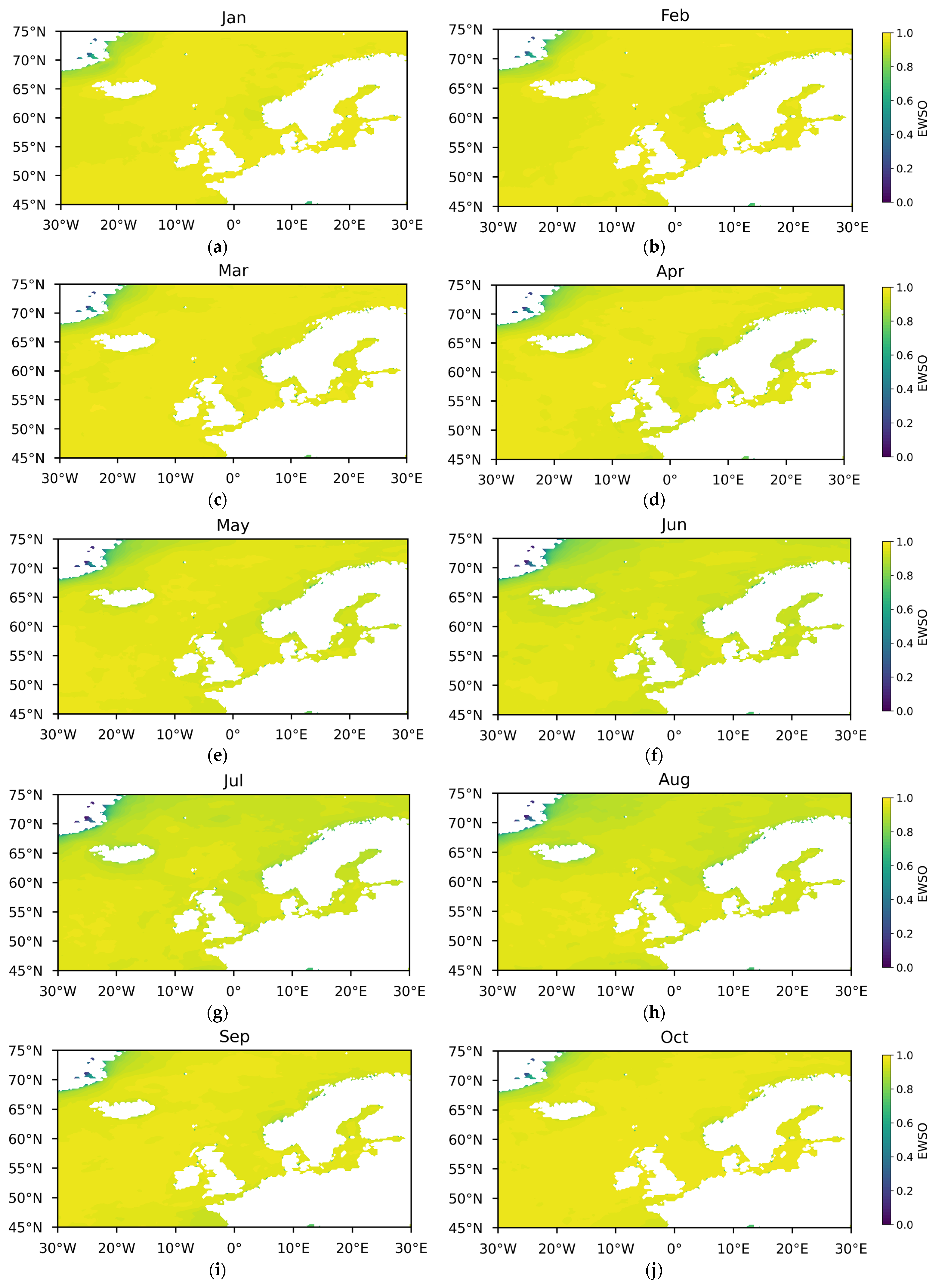
- Effective wind speed occurrence (EWSO).
2.2.4. Stability Assessment of Wind Resources
- Coefficient of variation (CV).
- 2.
- Monthly variability index (MVI).
- 3.
- Seasonal variability index (SVI).
2.3. WSPD-Based Wind Speed Modeling
2.3.1. Selection of WSPD Models
2.3.2. Evaluation of Goodness-of-Fit Metrics
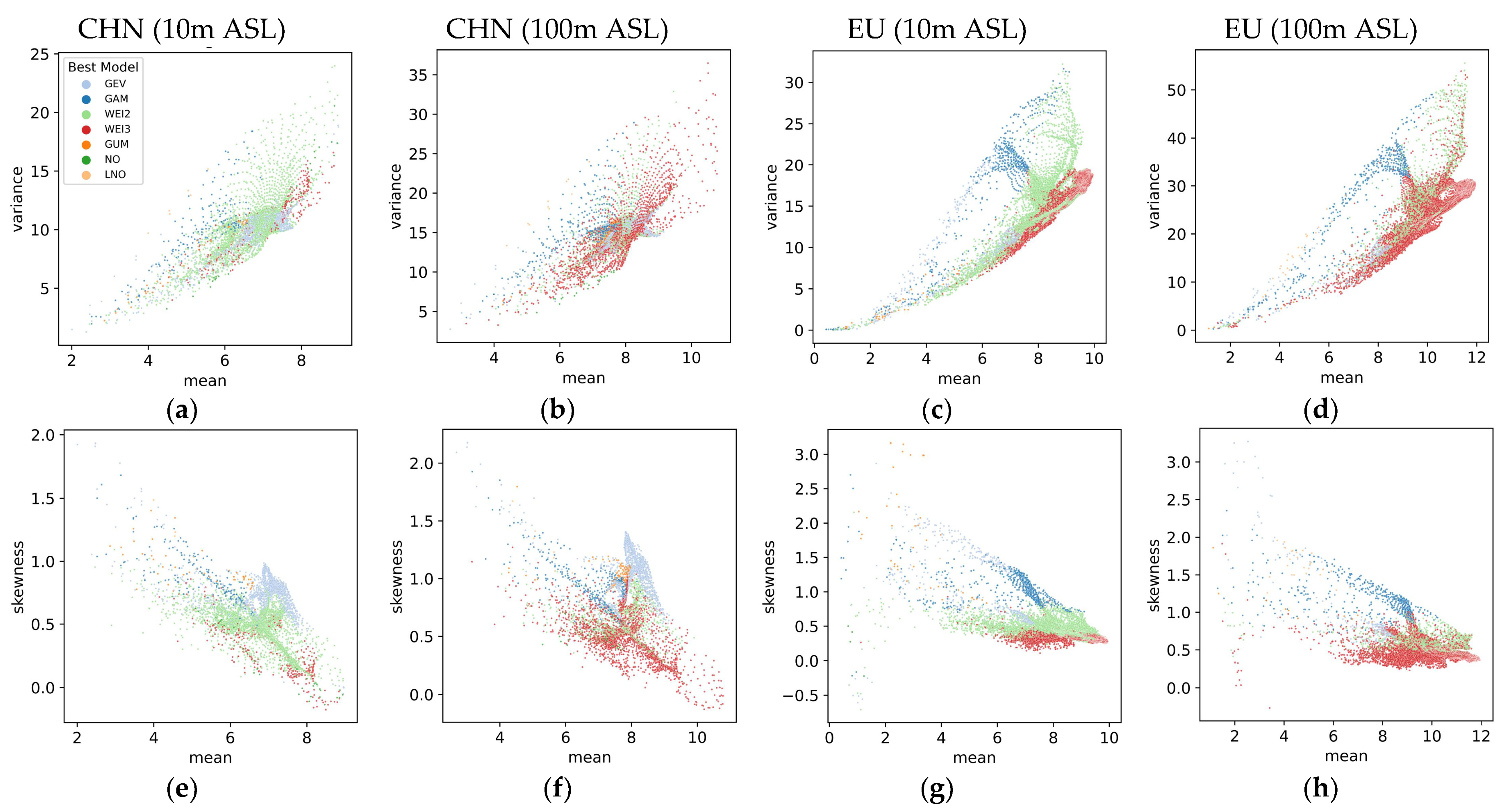
2.3.3. Machine Learning Methods for Feature Importance Ranking
- Random Forest (RF) method.
- Bootstrap sampling: RF generates multiple decision trees by sampling the dataset with replacement. Each tree is trained on a different subset of the original data.
- Feature selection at each node: At each node, a random subset of features is considered for splitting. This ensures diversity across the trees and reduces overfitting.
- Prediction aggregation: Each decision tree makes an independent prediction. The final model output is obtained by averaging (for regression tasks) or majority voting (for classification tasks) across all trees.
- 2.
- XGBoost method.
- 3.
- Permutation Feature Importance (PFI) method.
- Random permutation: The values of each feature are independently shuffled while keeping other features unchanged.
- Performance evaluation: The model’s performance (e.g., accuracy, MSE) is re-evaluated using the permuted data.
- Importance determination: The importance of a feature is quantified based on the extent to which its permutation affects model performance. A significant drop in performance indicates higher feature importance.
3. Results and Discussion
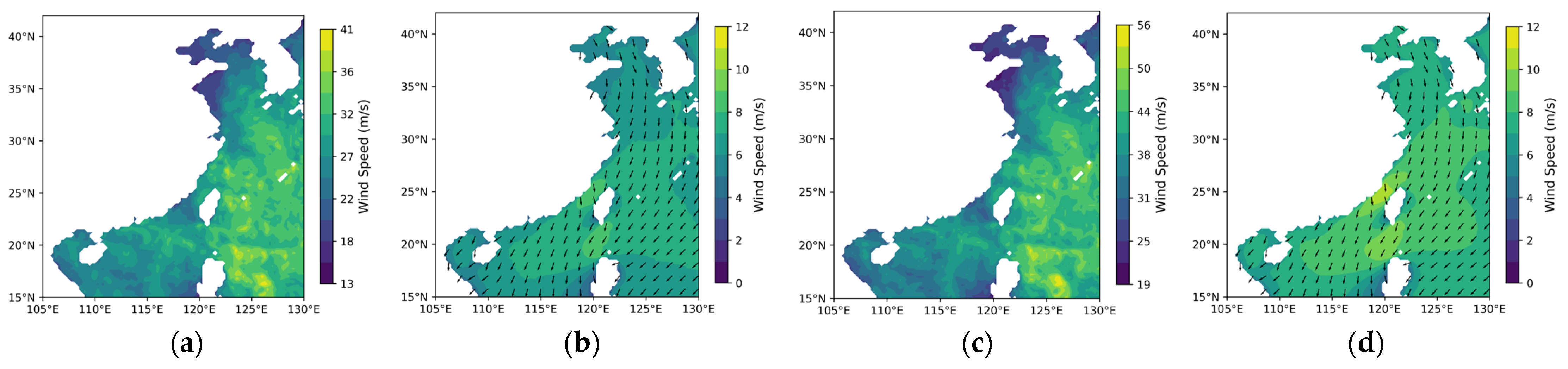
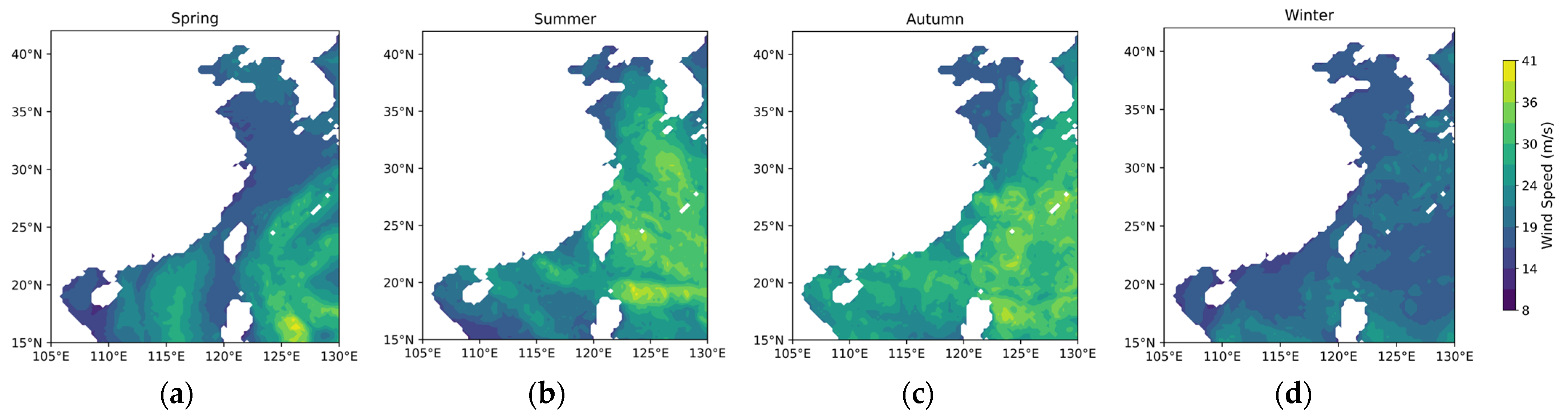
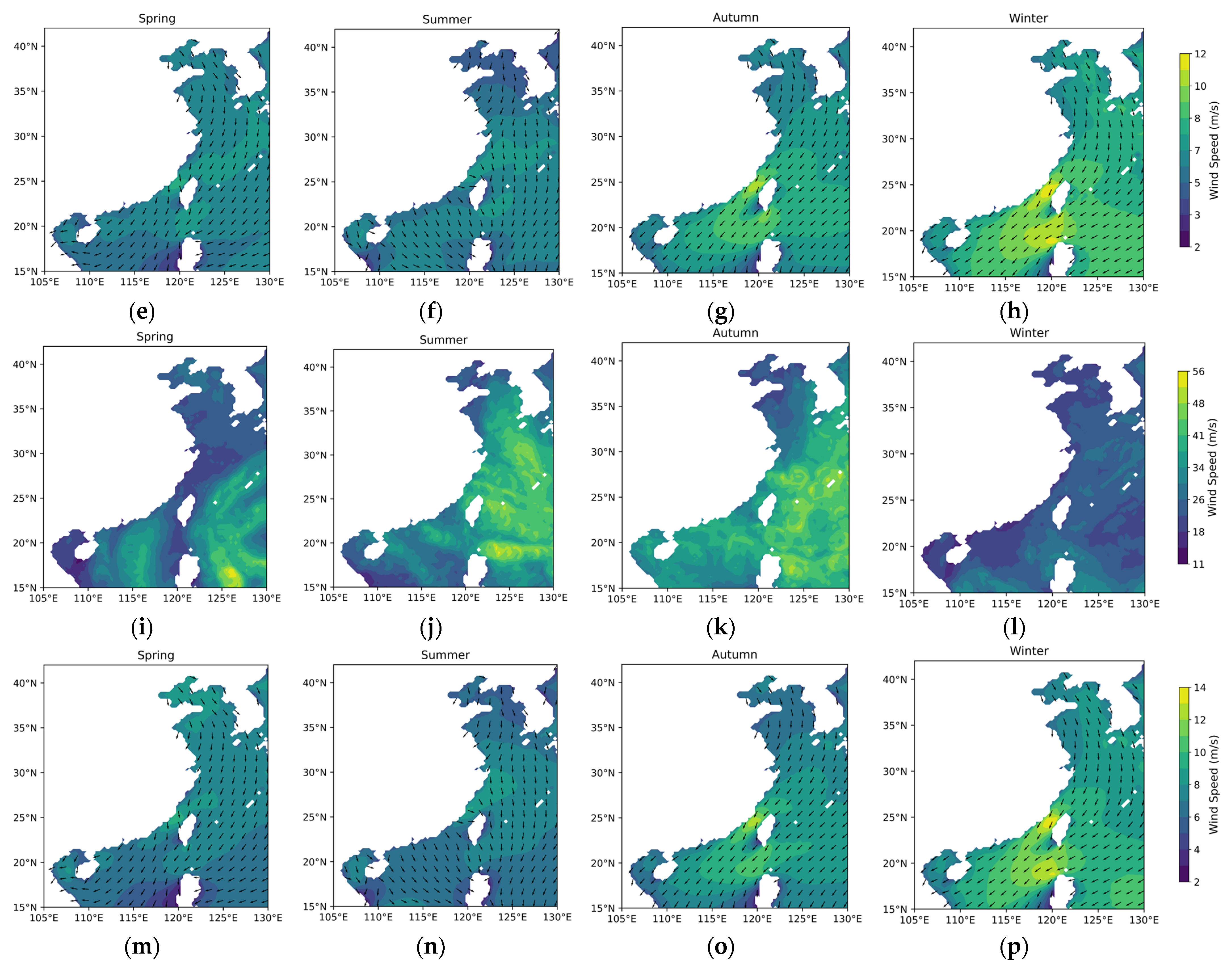
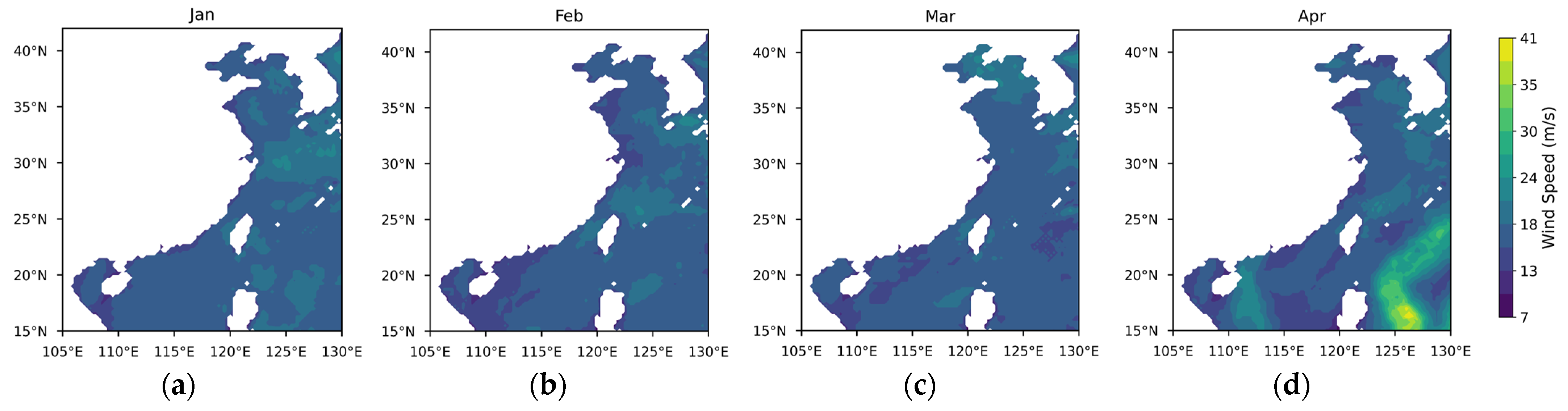
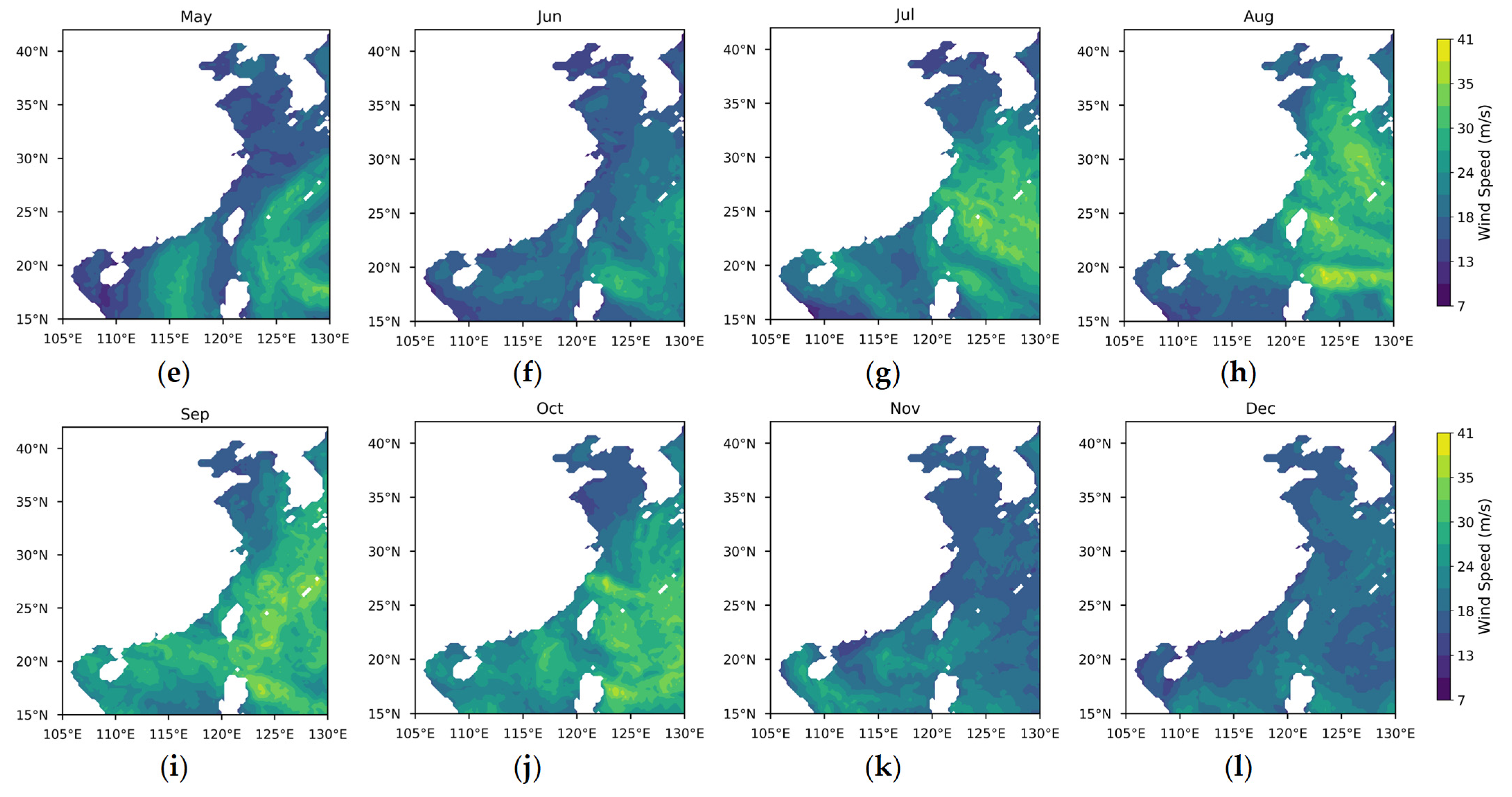
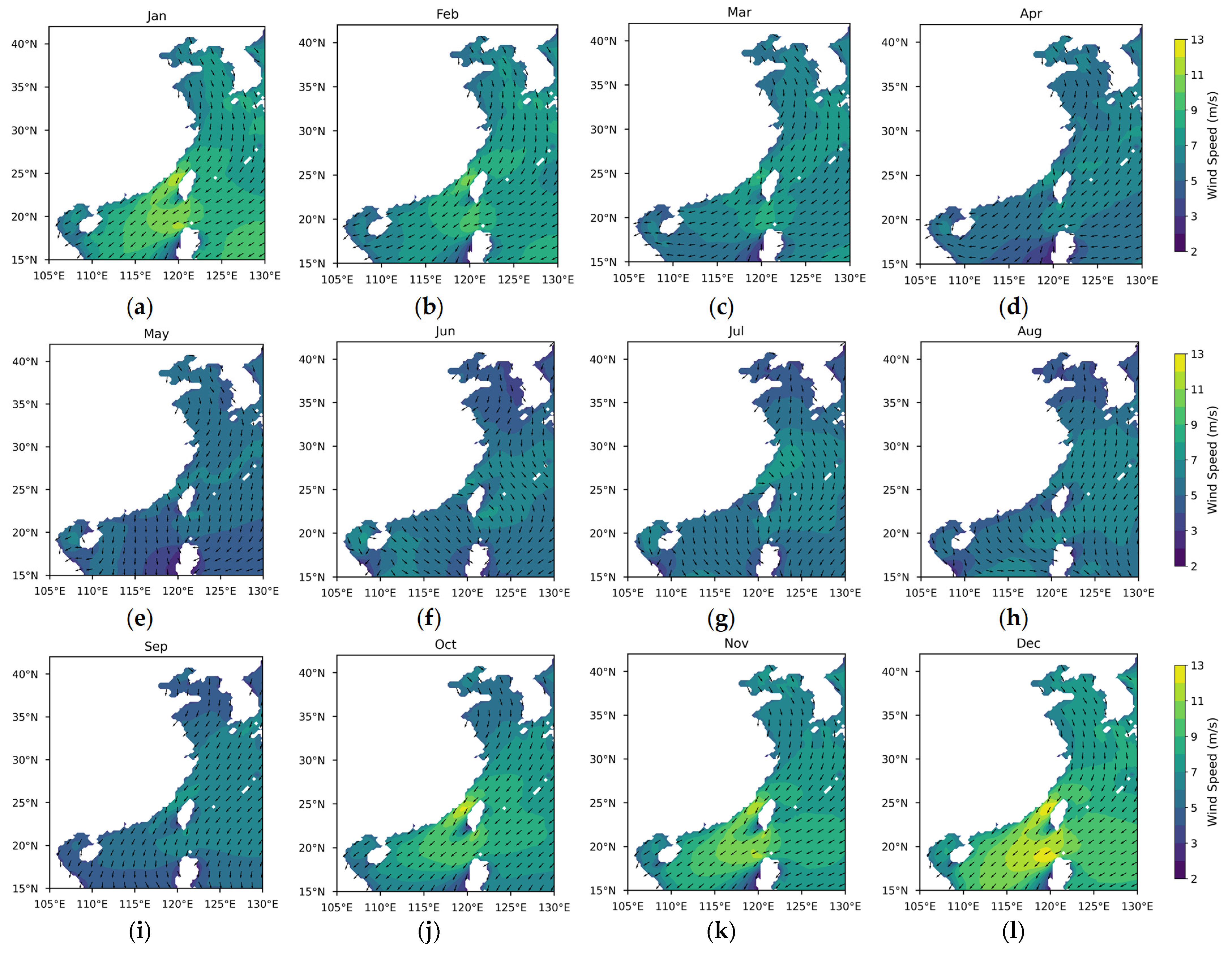
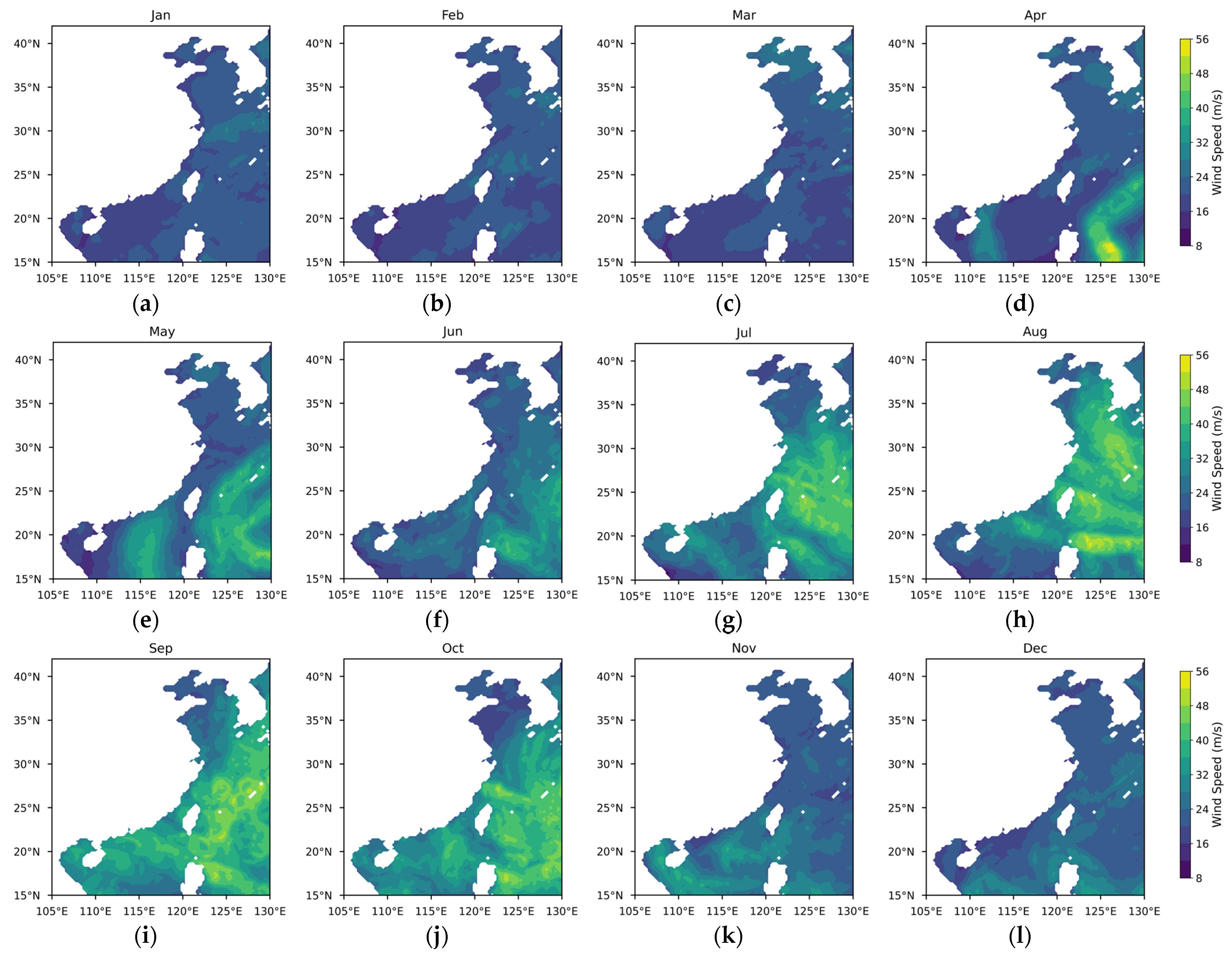
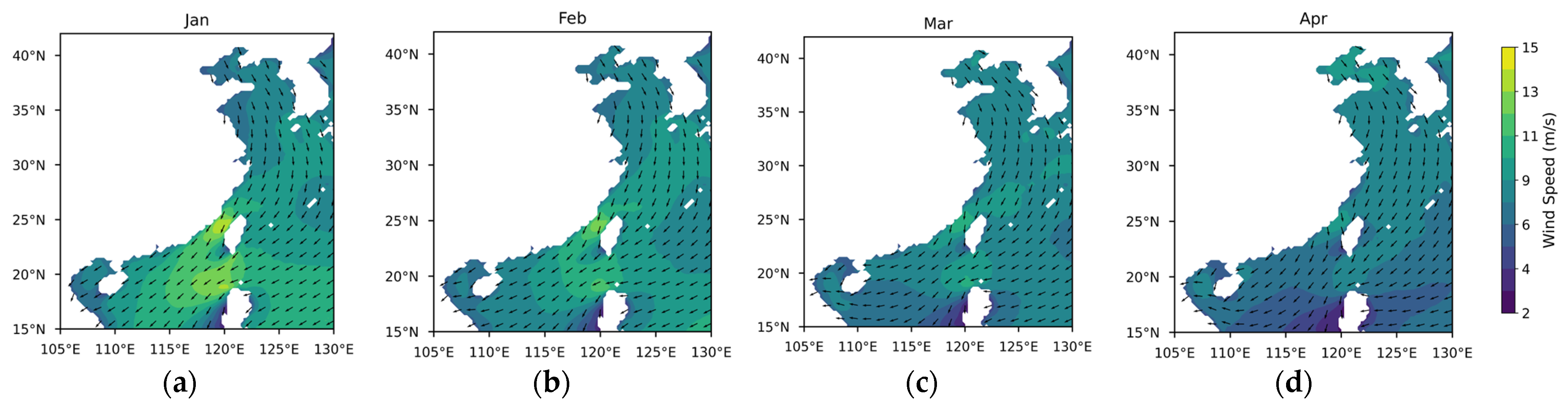
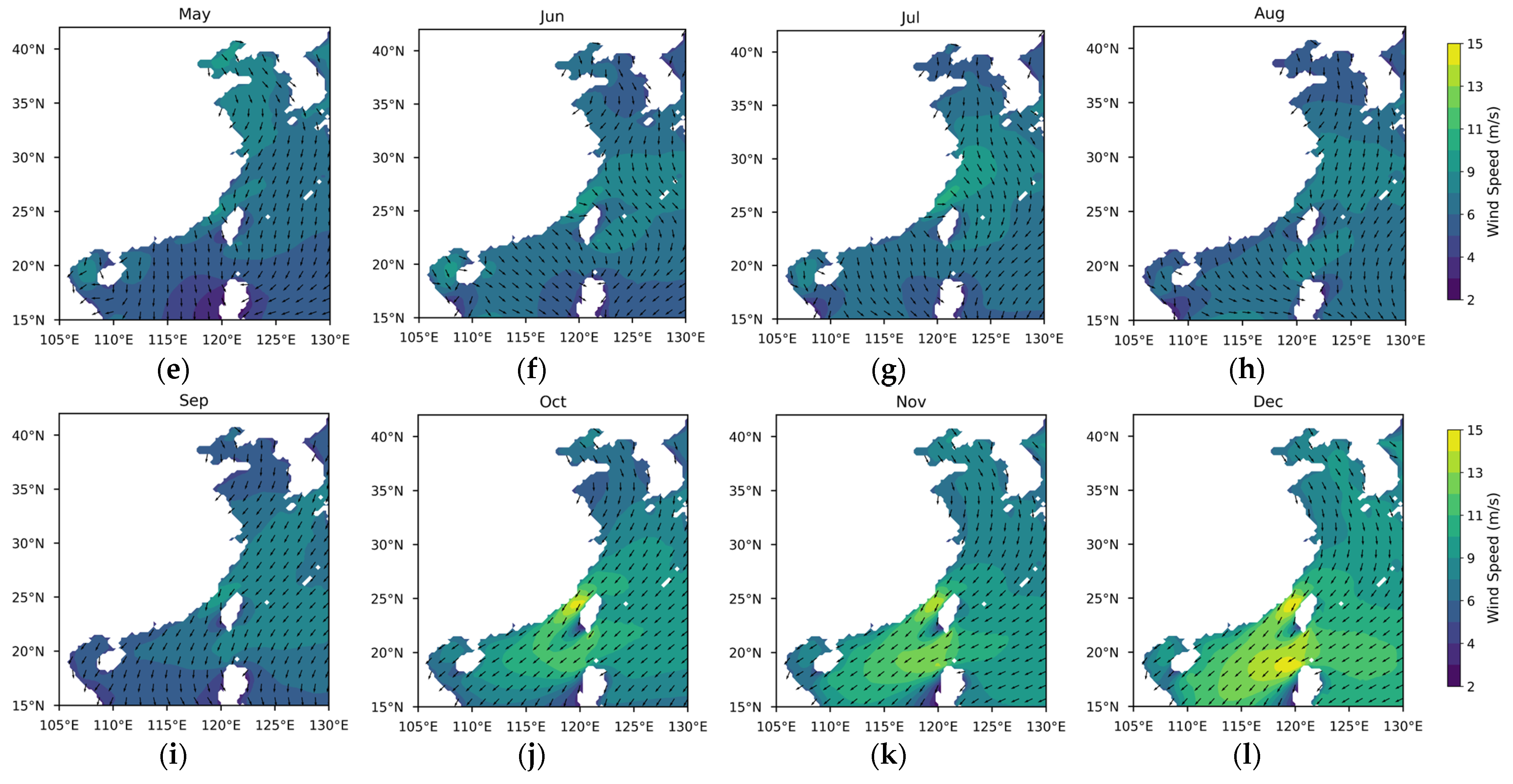
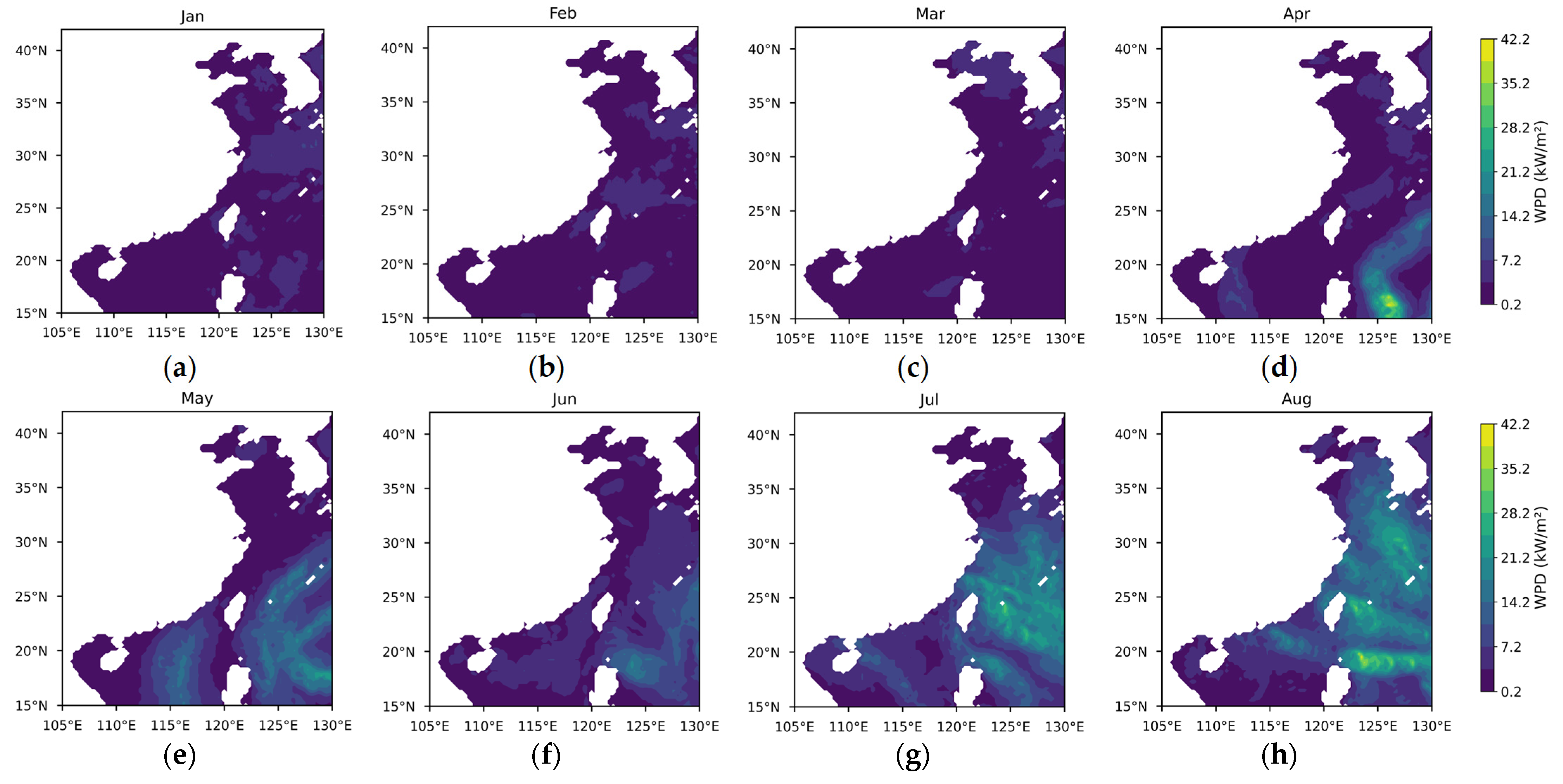
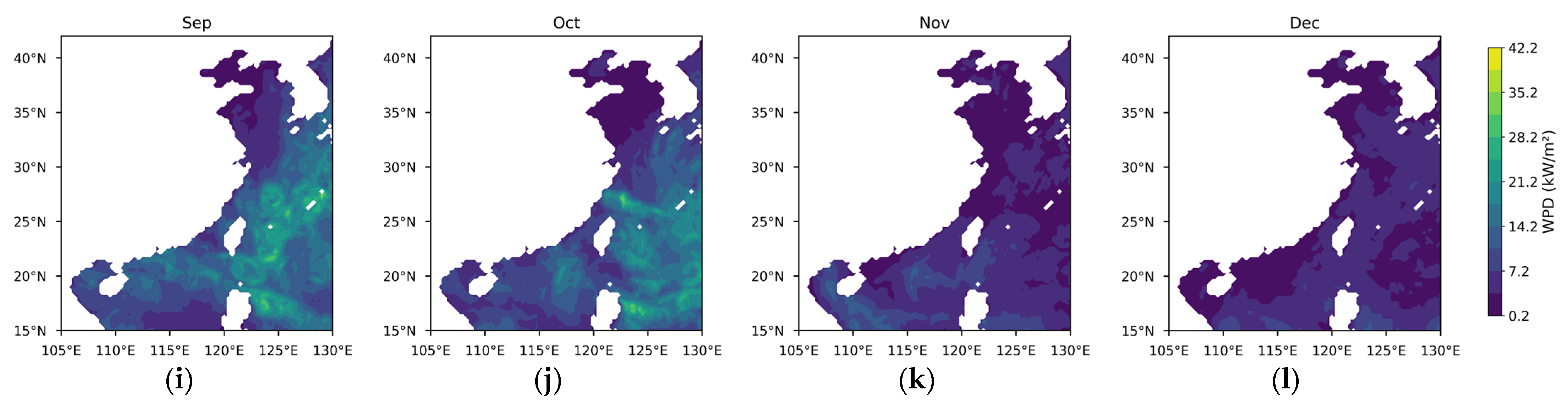
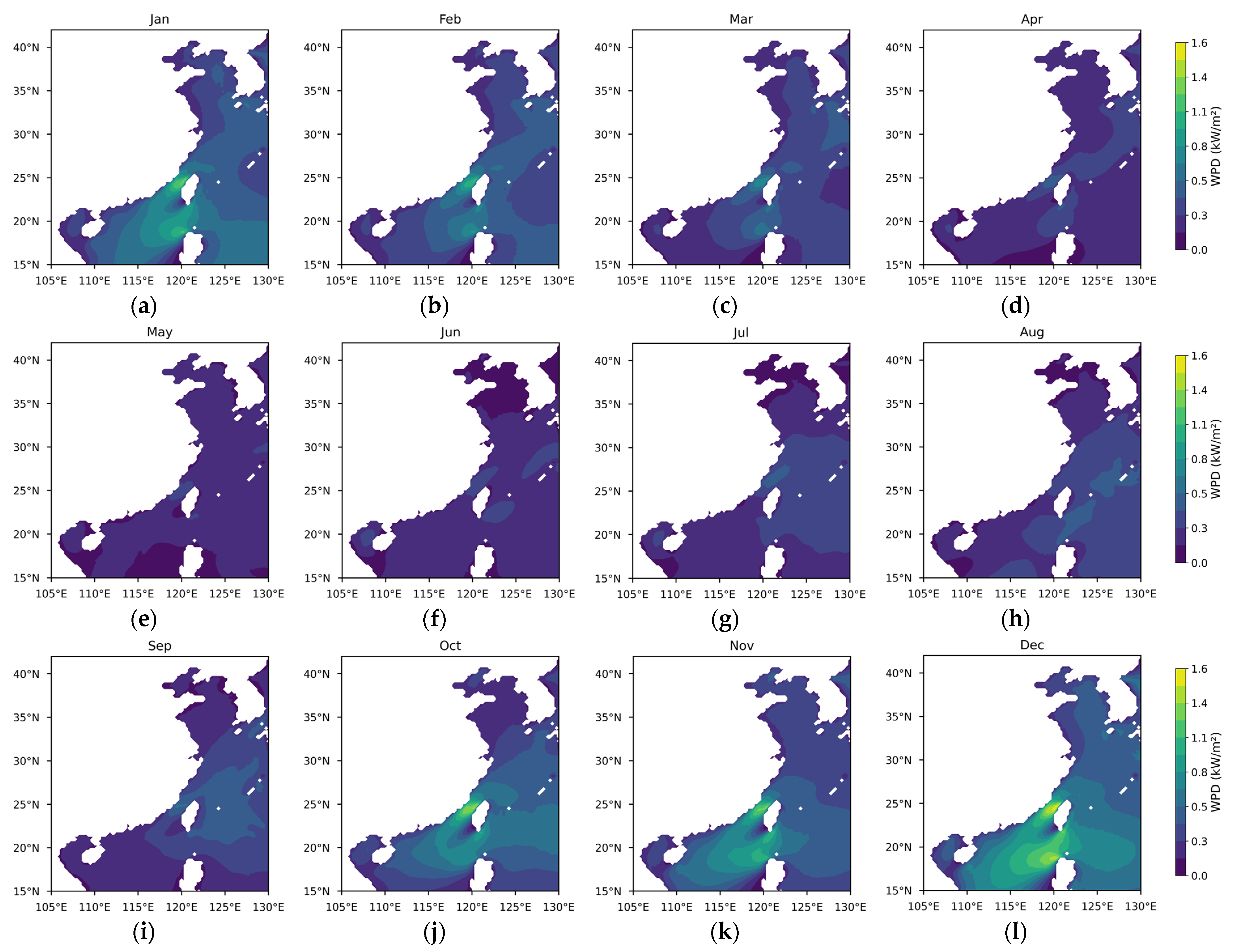
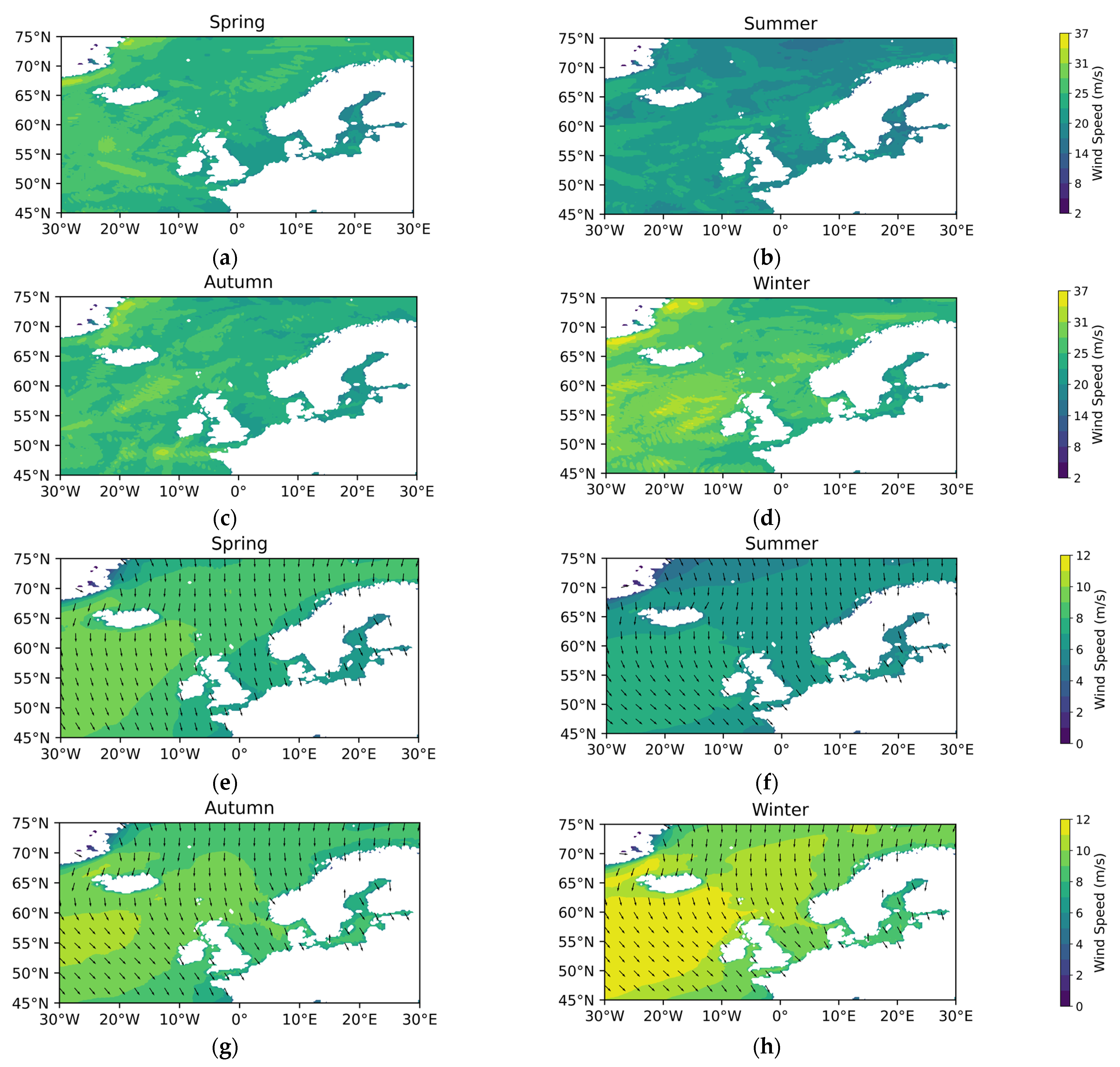
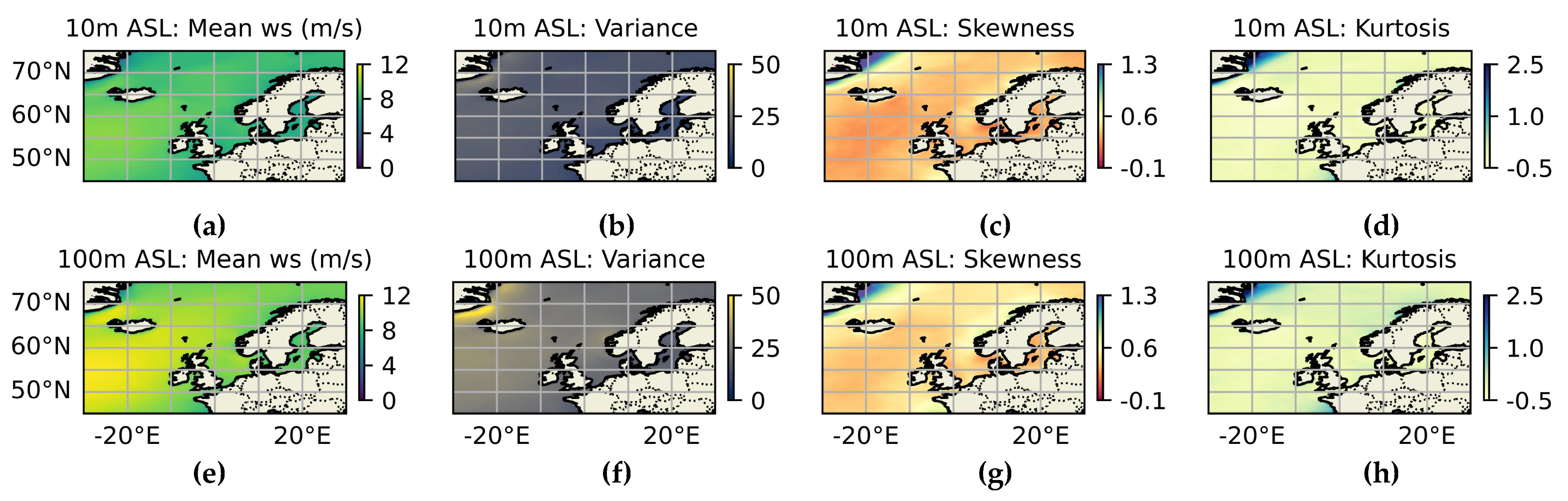
3.1. Differences in Offshore Wind Resources Between China and Europe
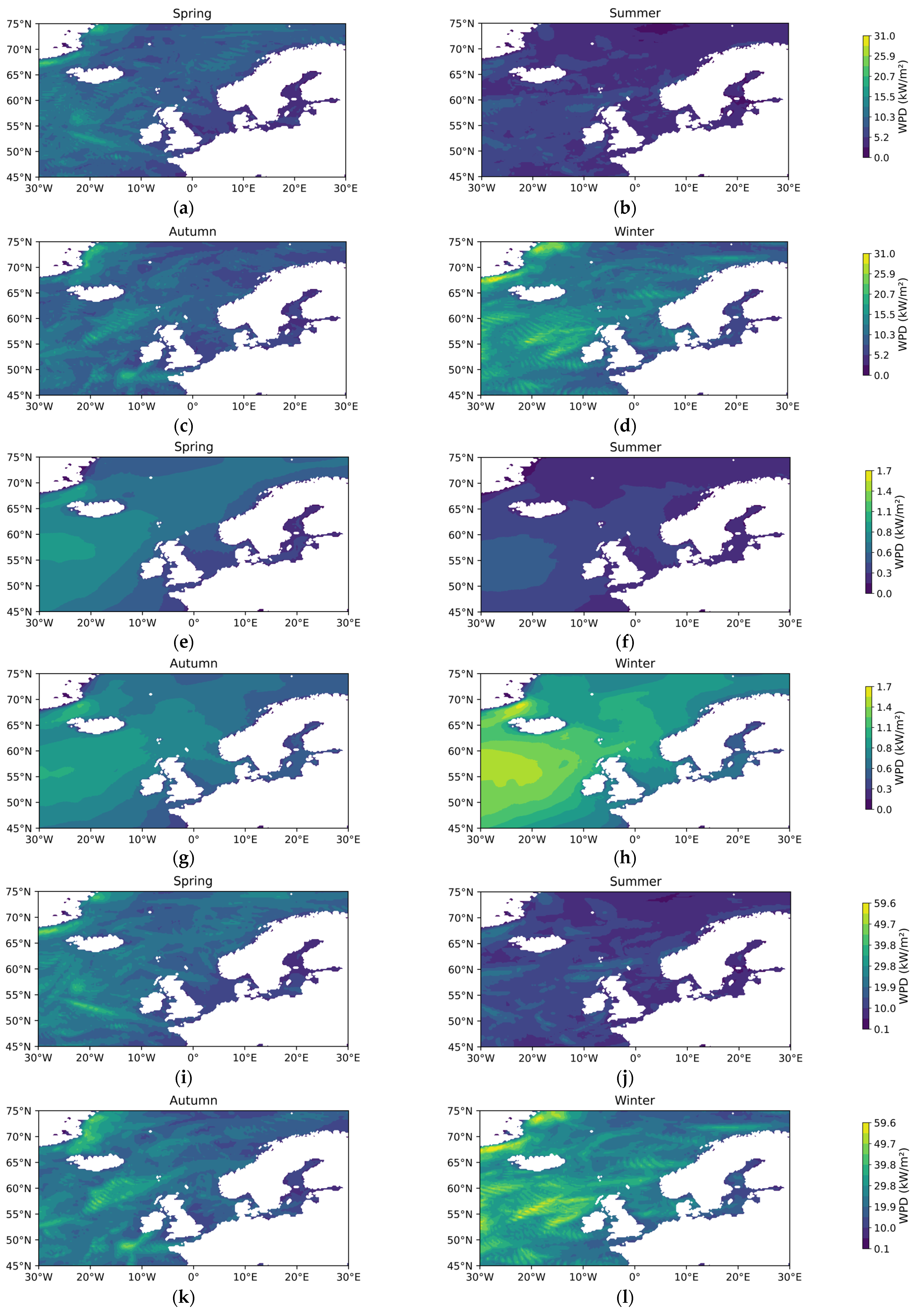
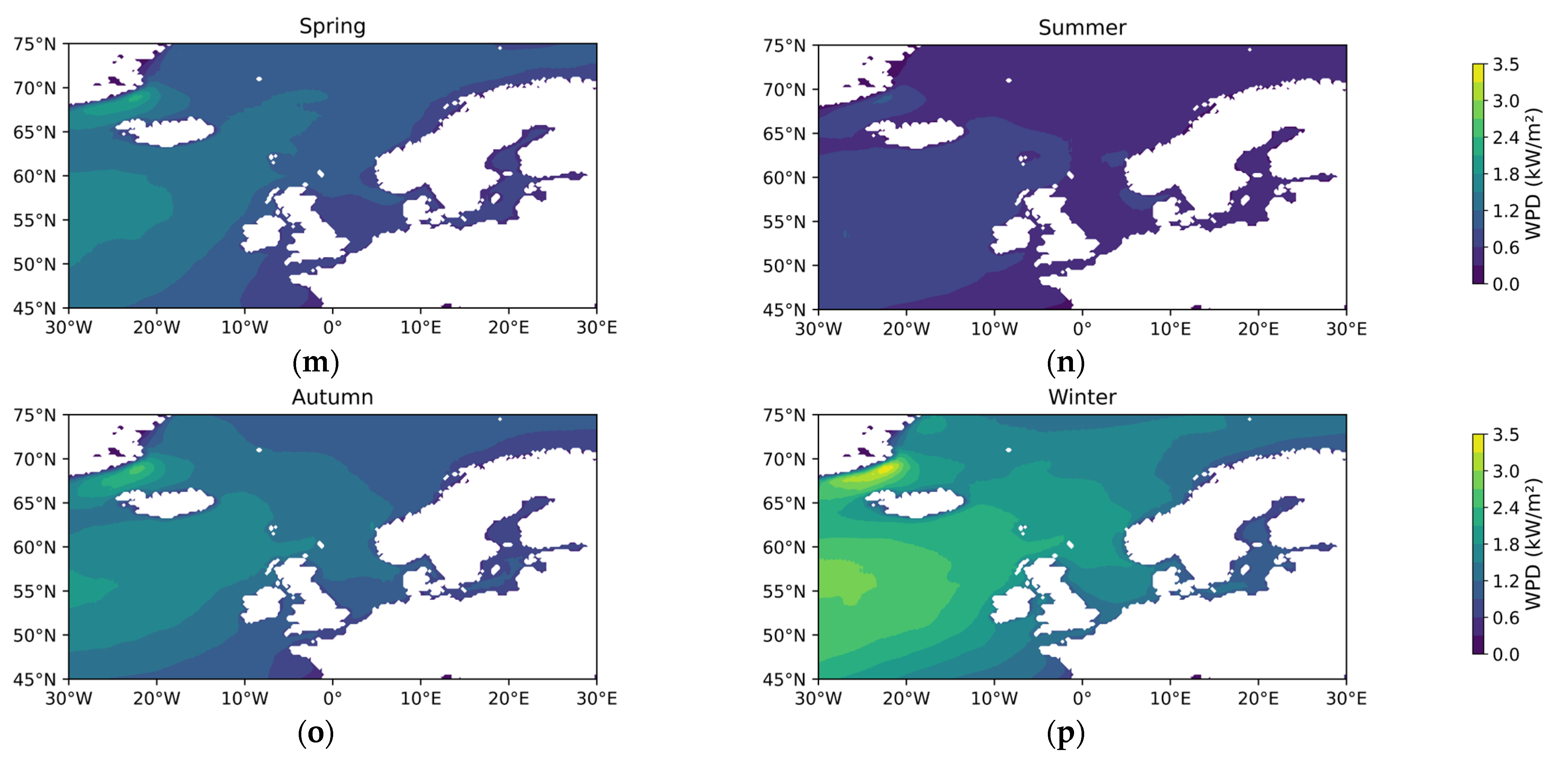
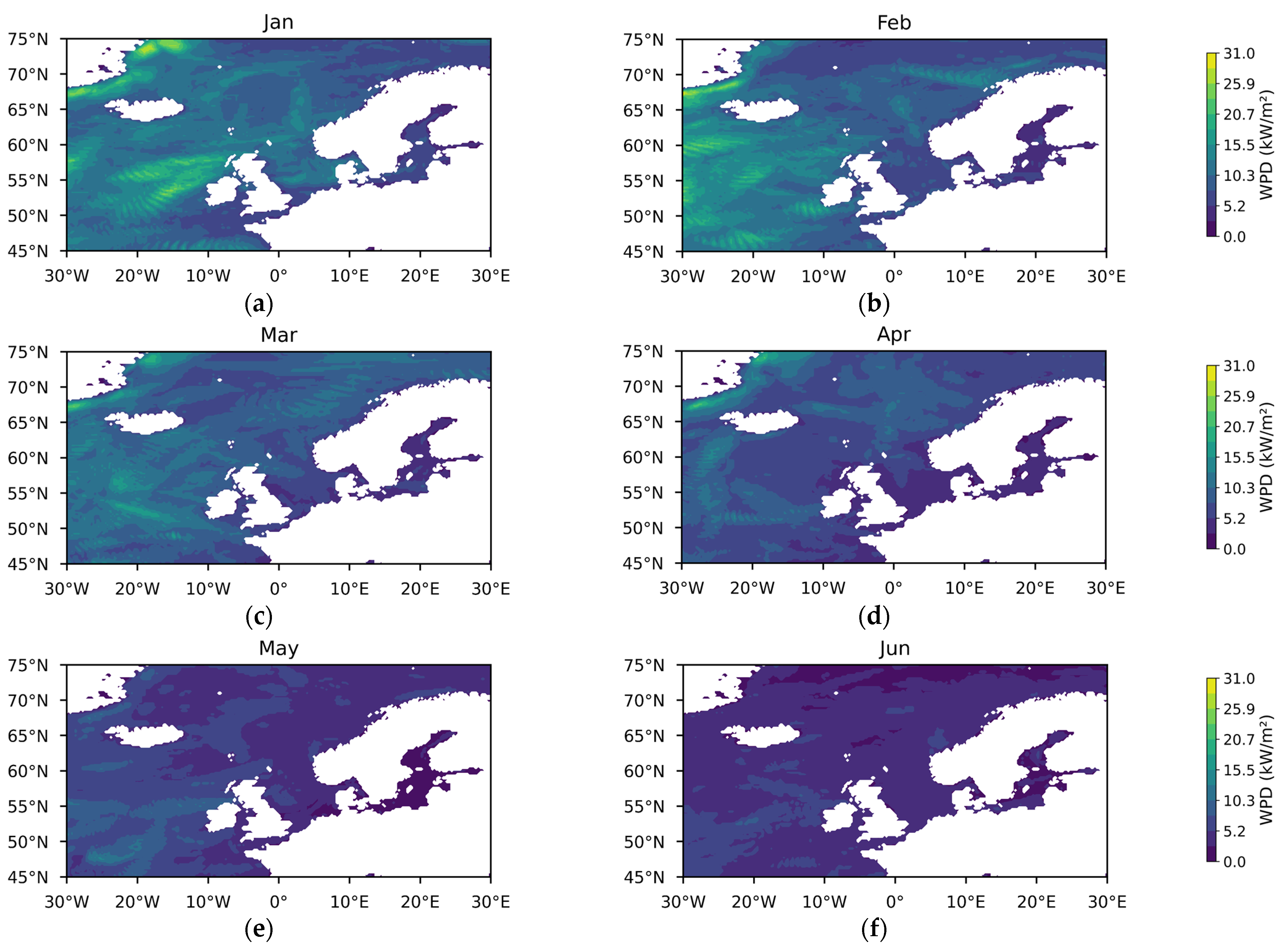
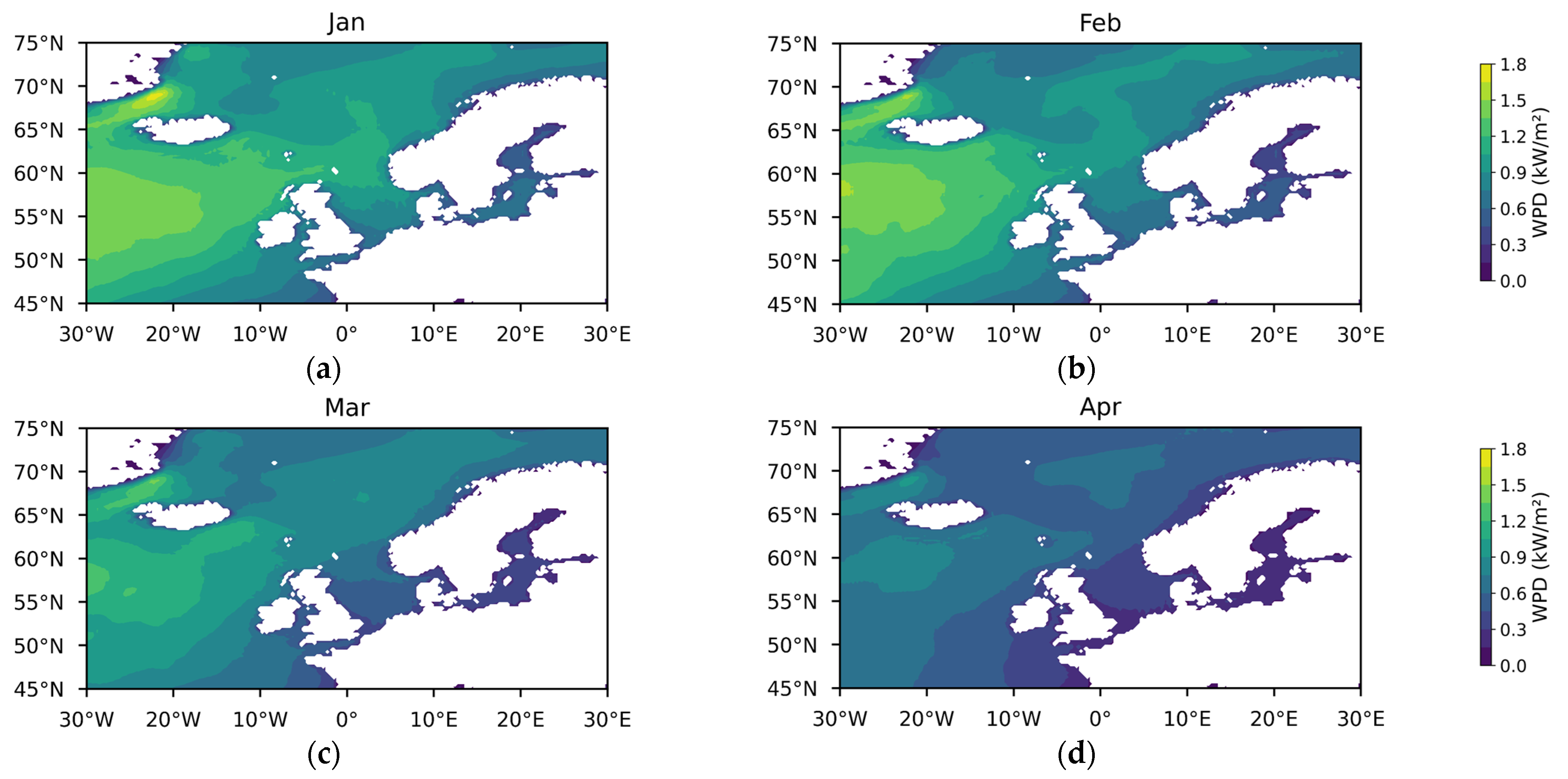
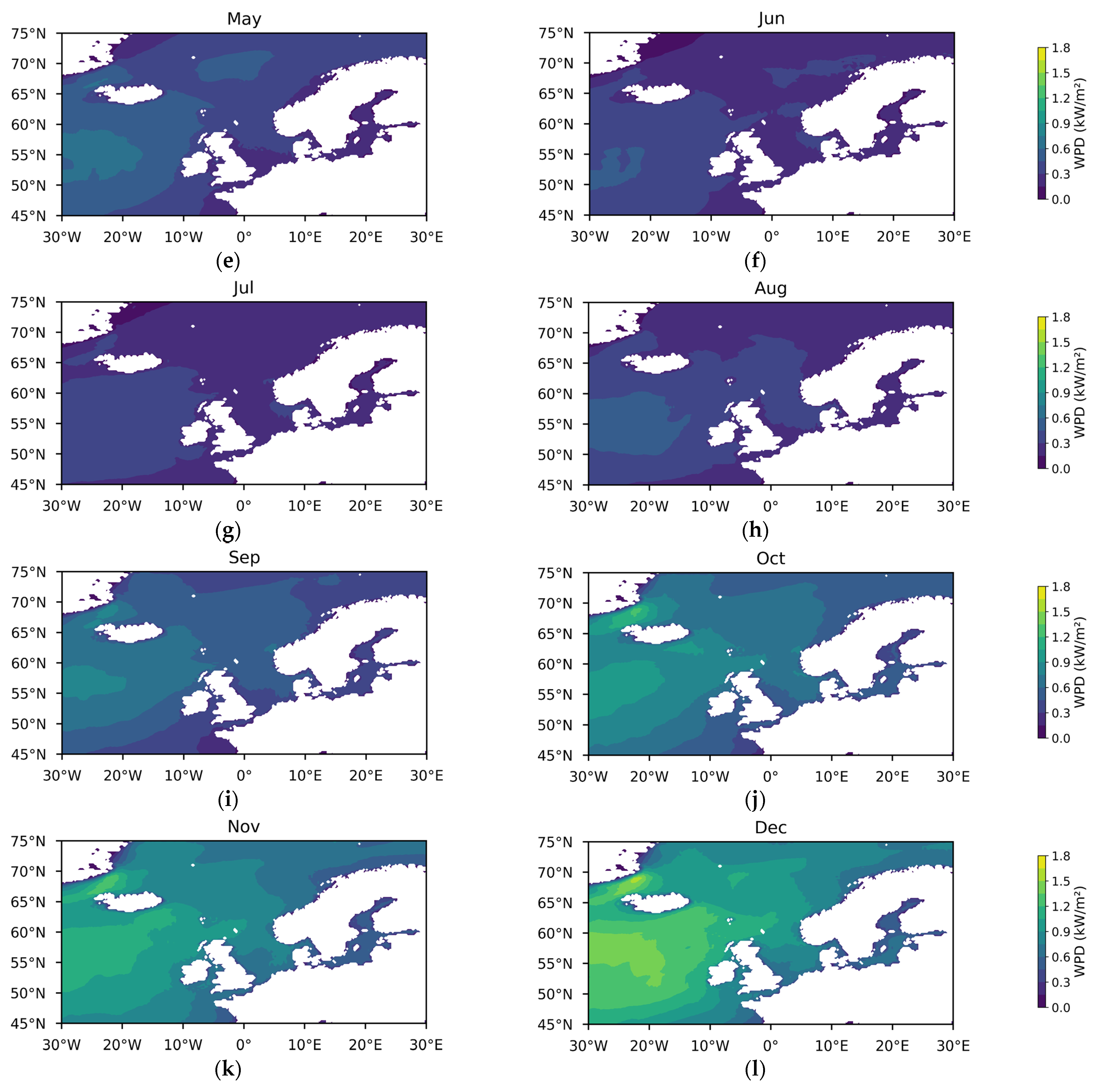
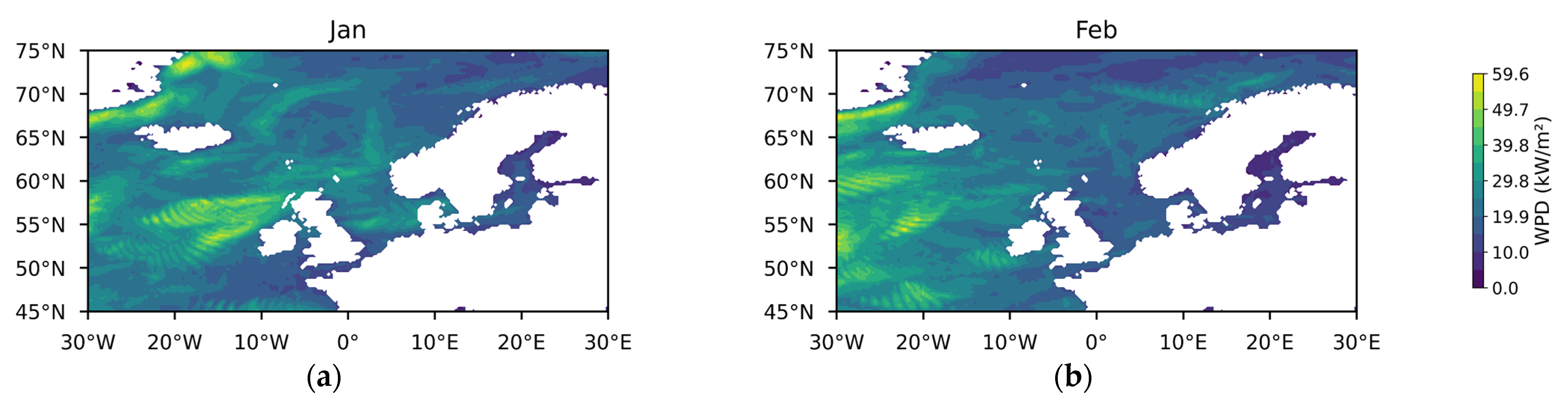
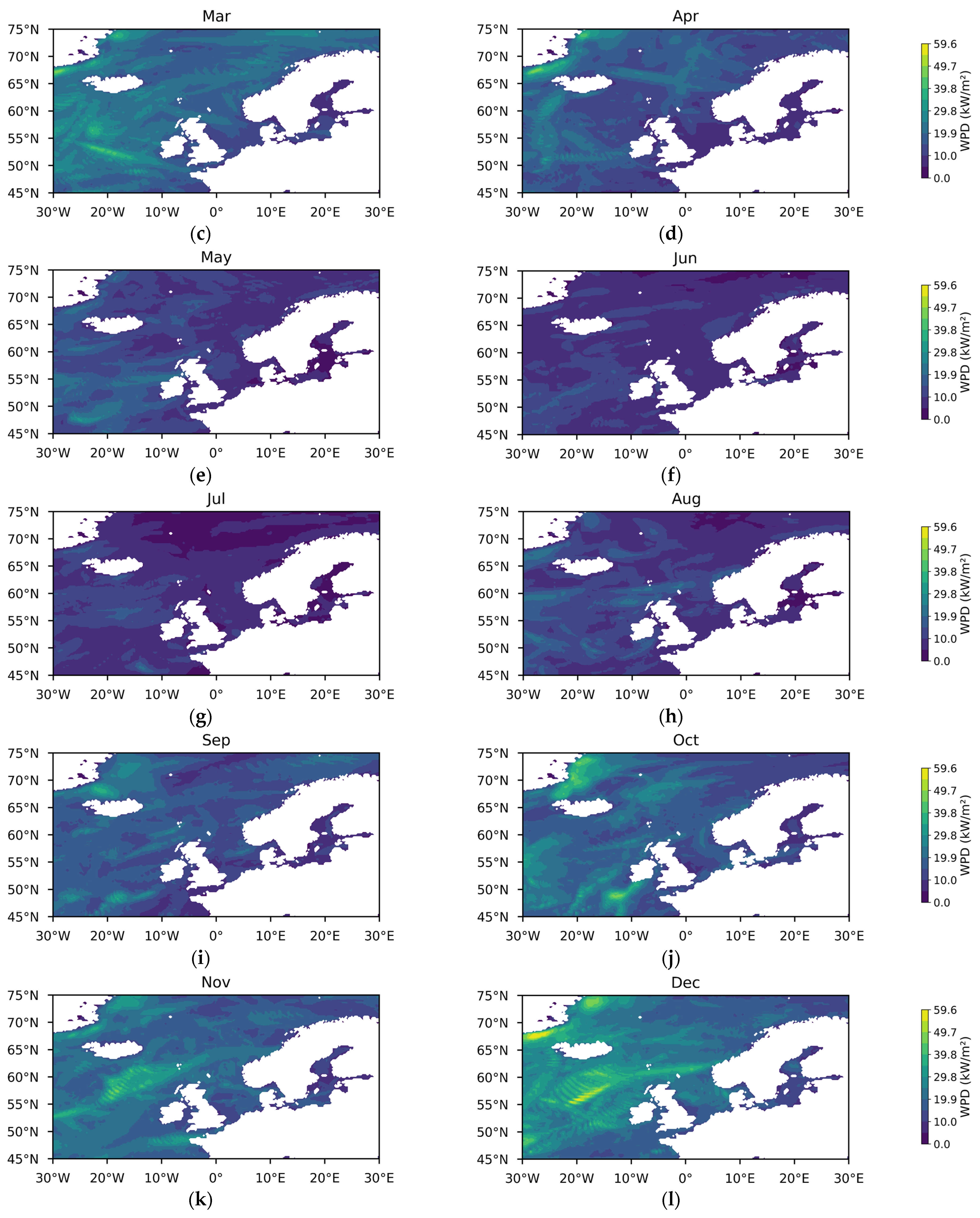
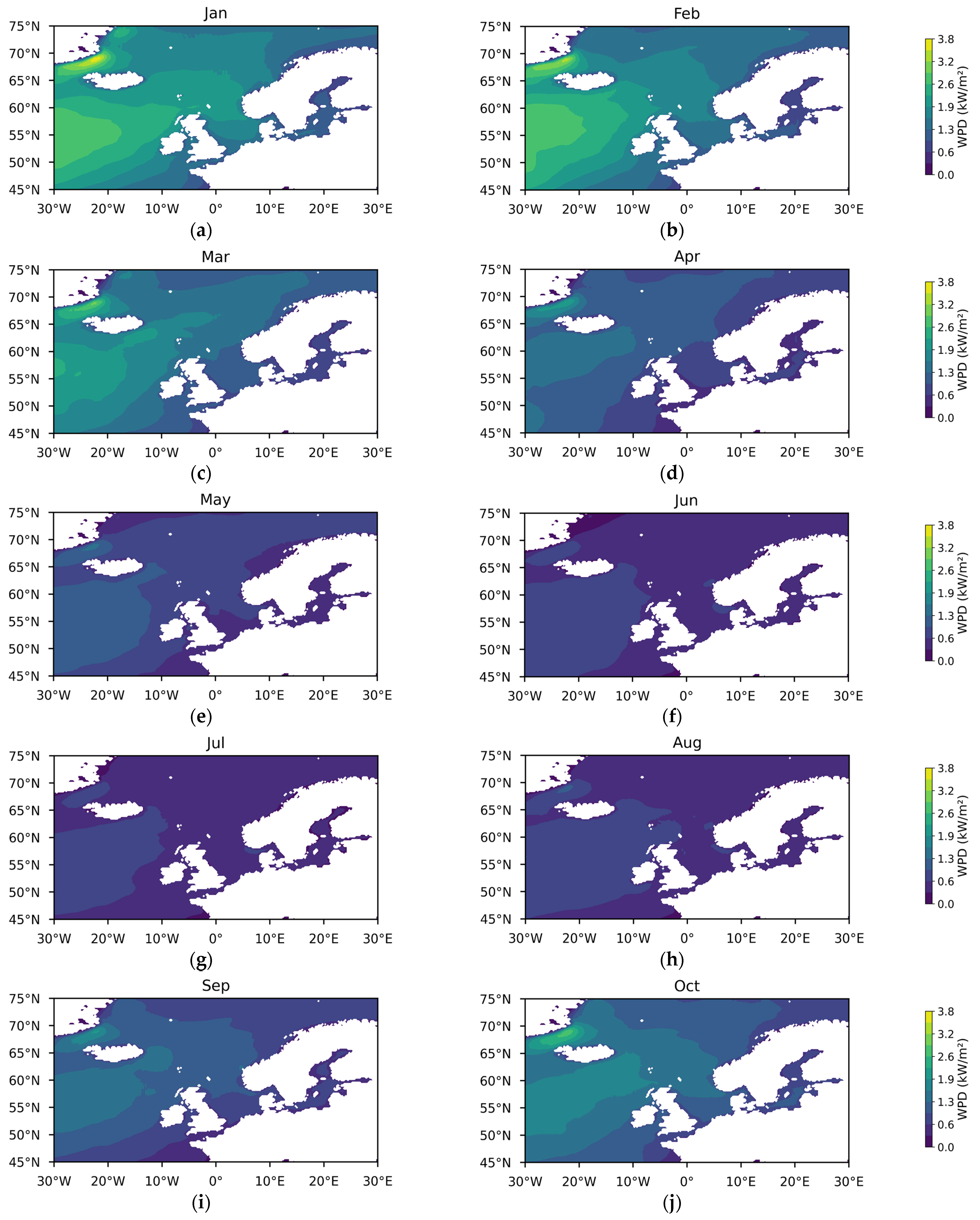
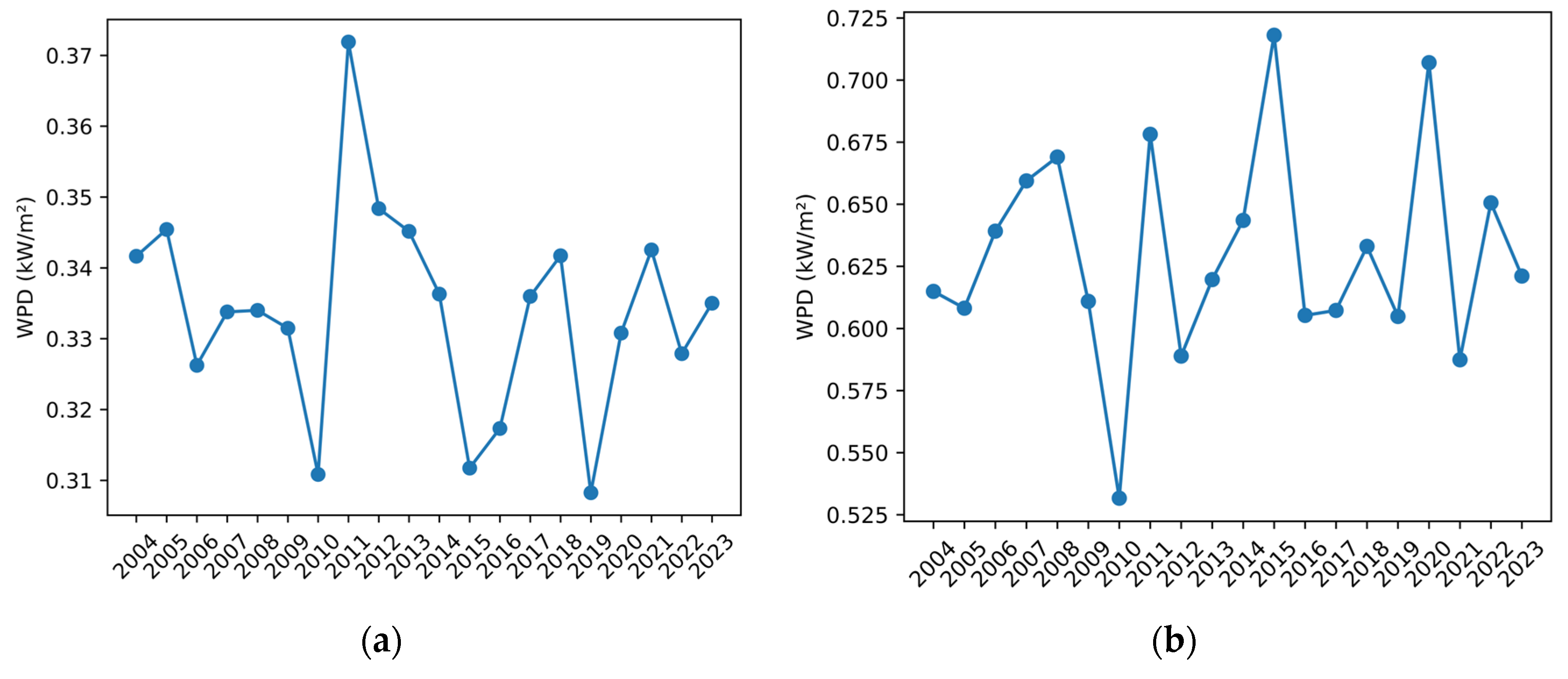
3.1.1. Theoretical Potential of Wind Energy
3.1.2. Temporal and Spatial Variability in Wind Energy Stability
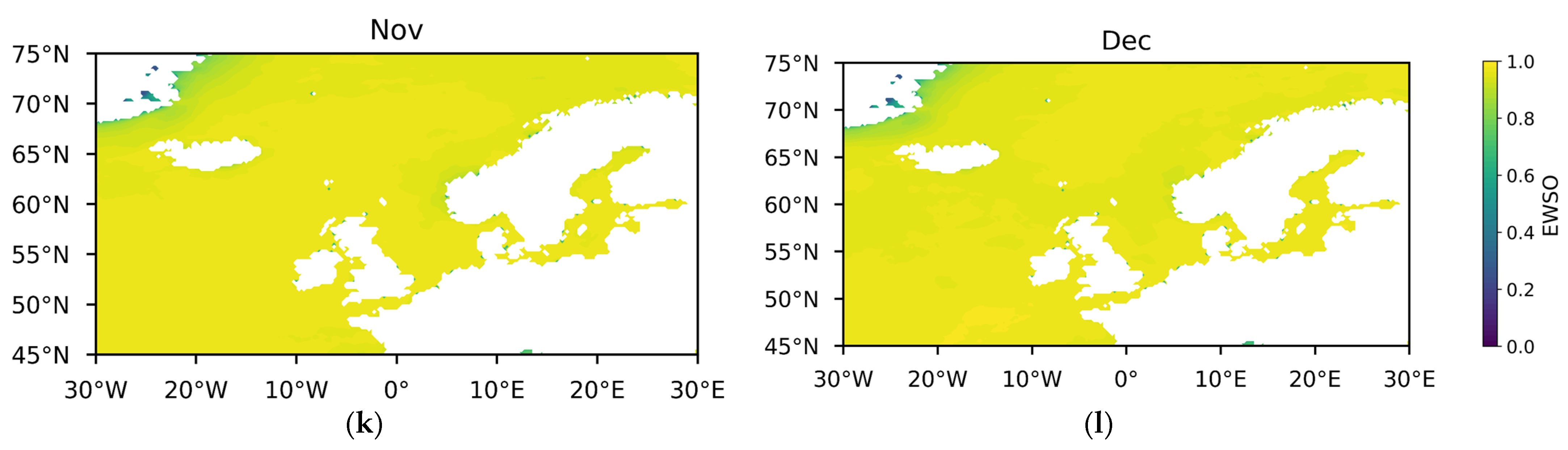
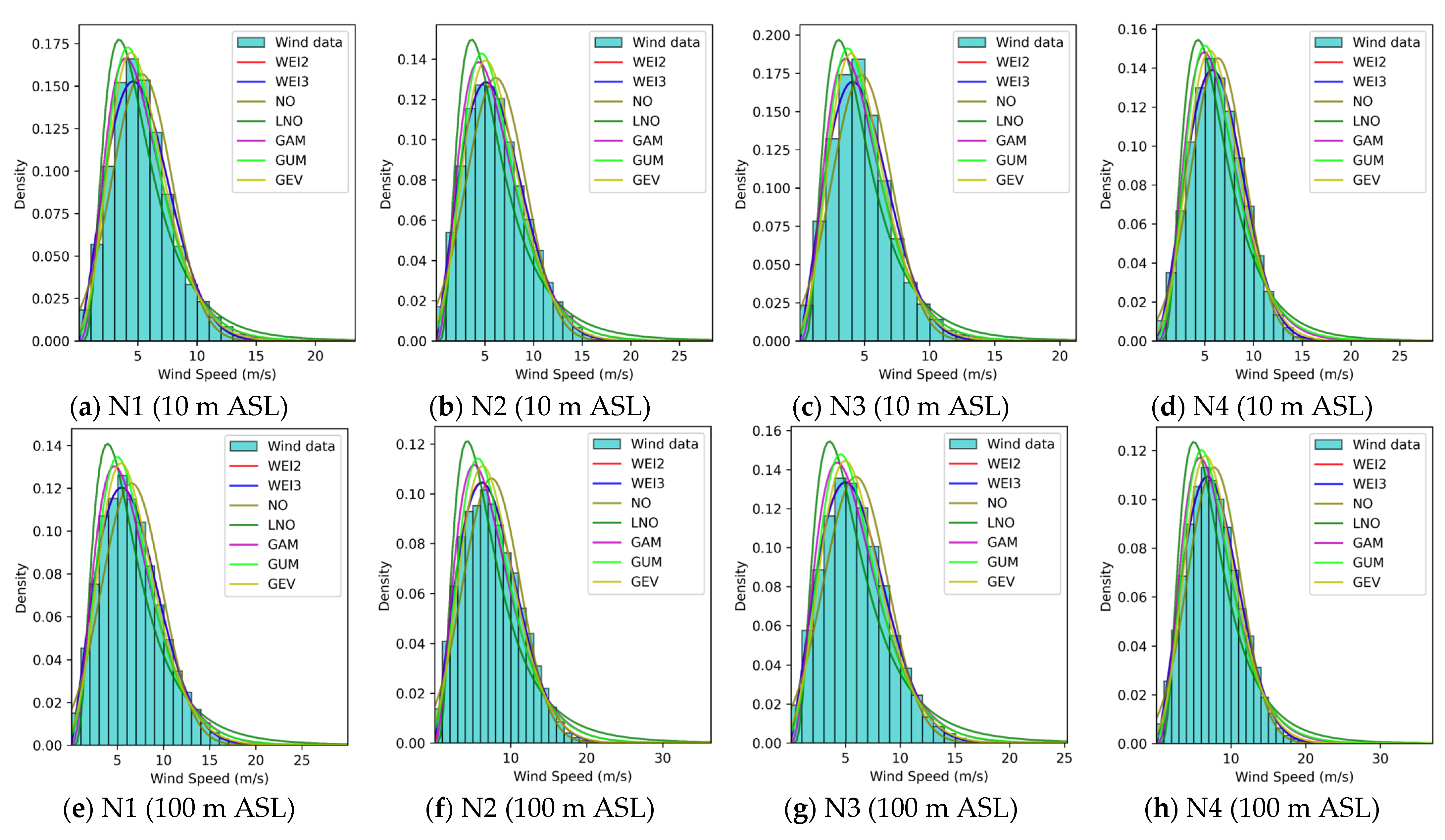
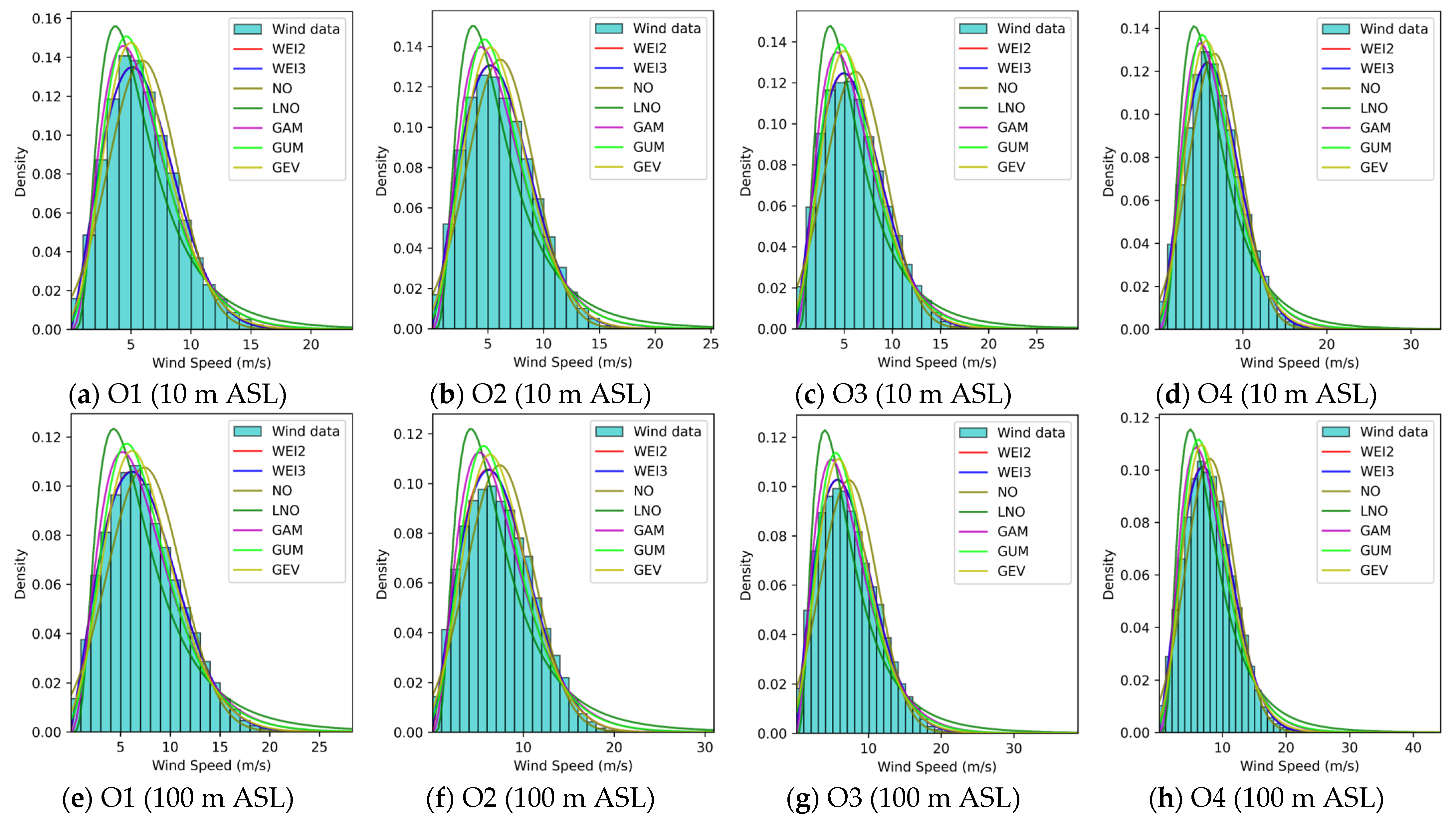
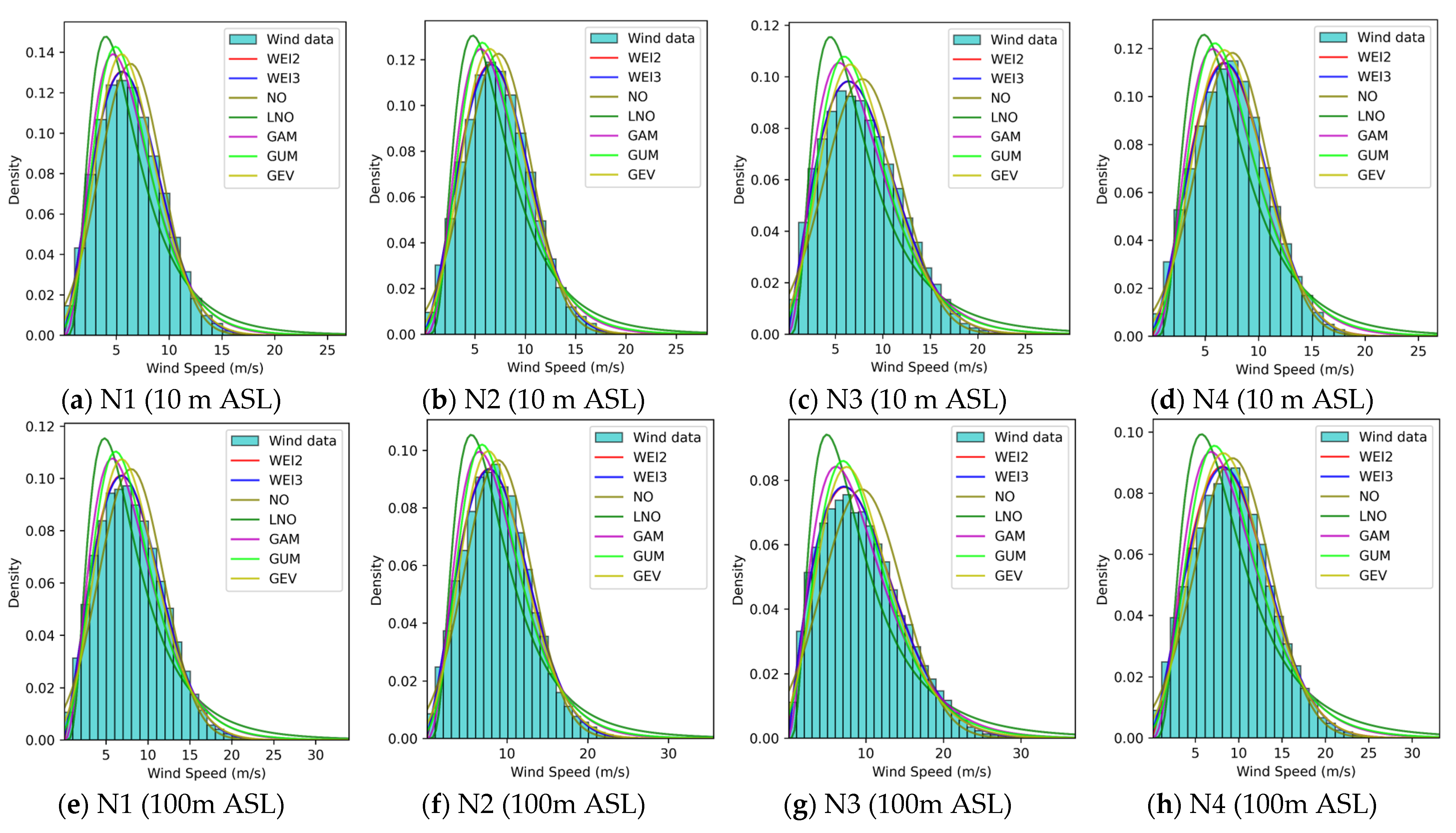
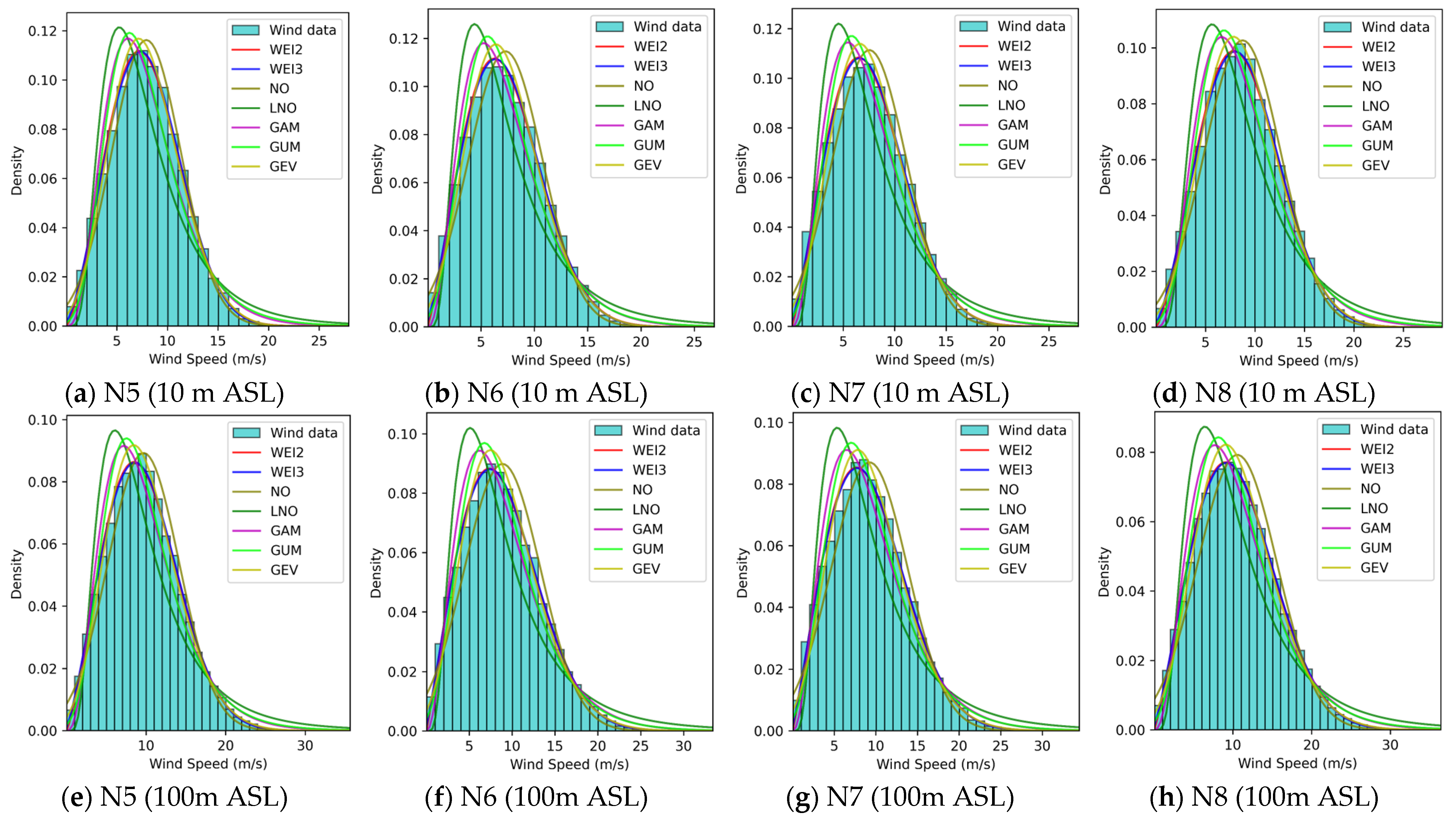
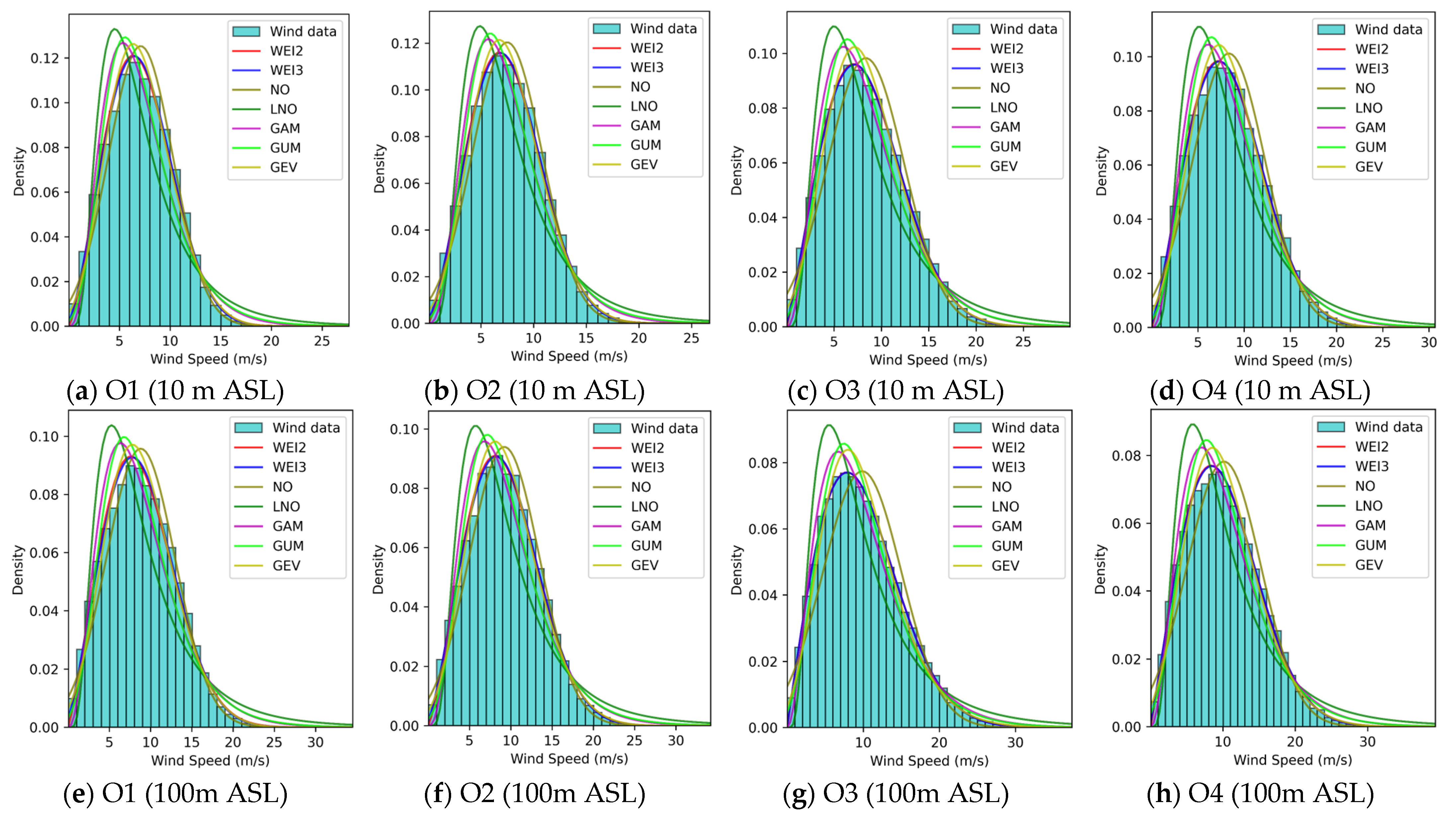
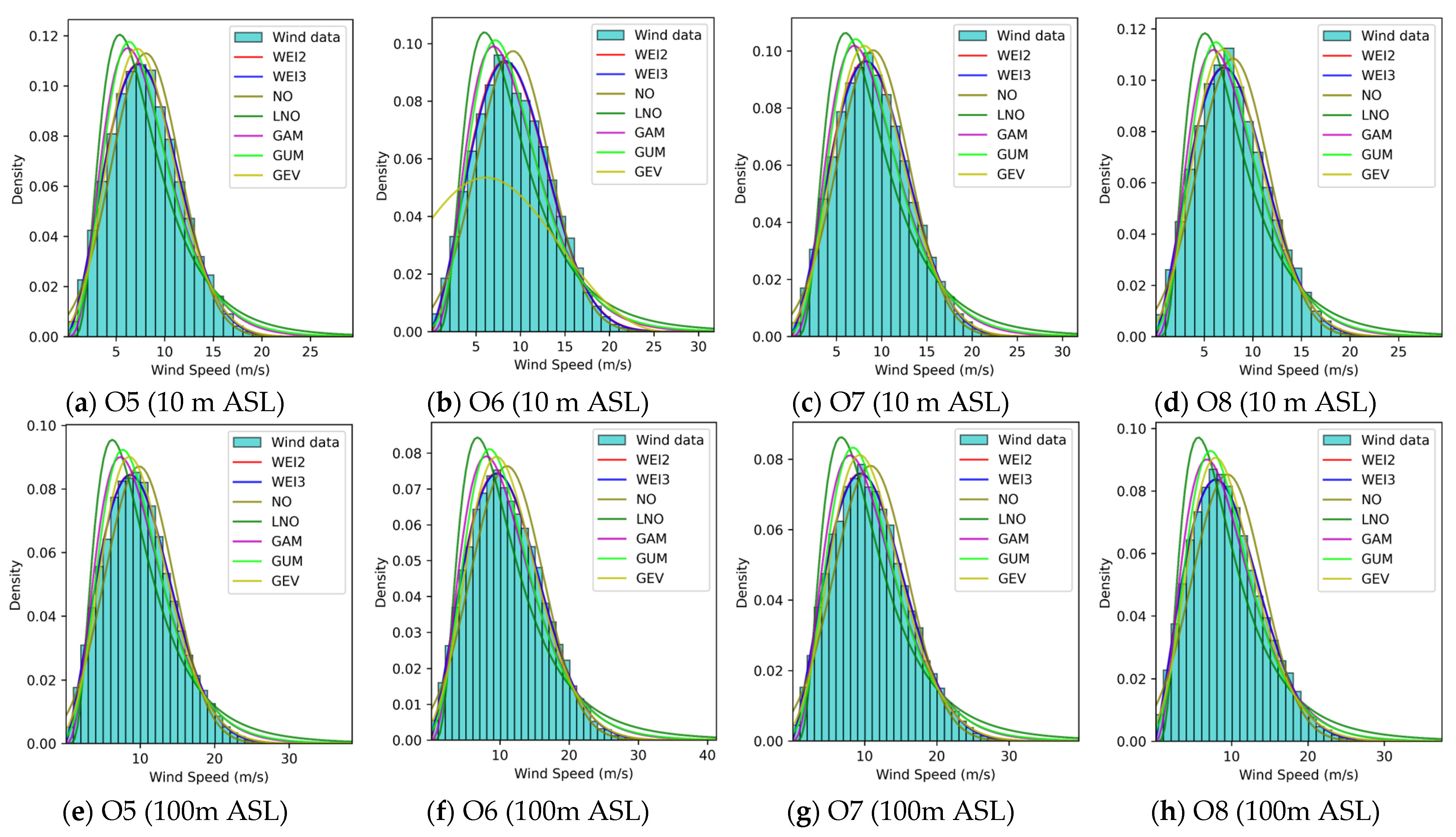
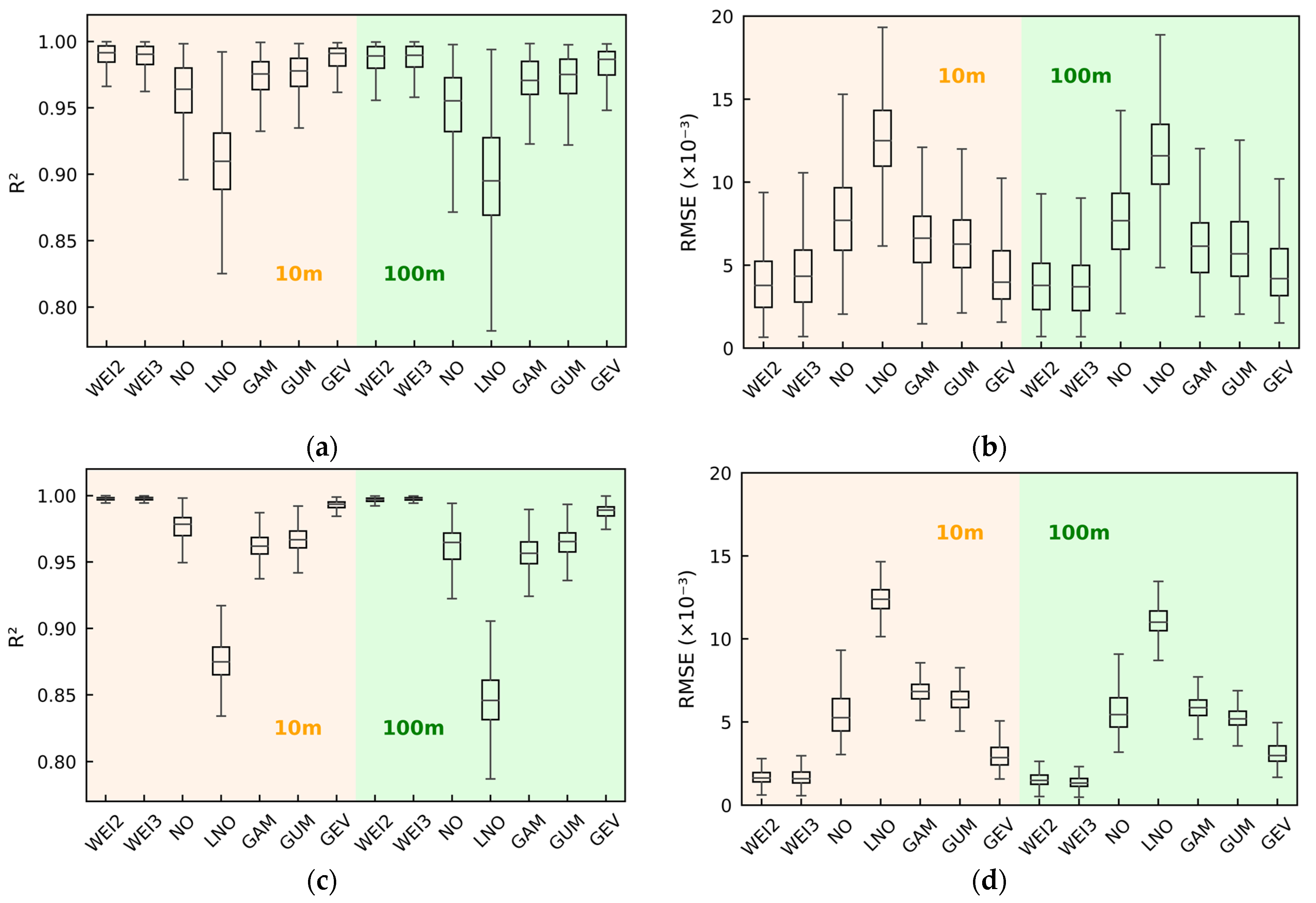
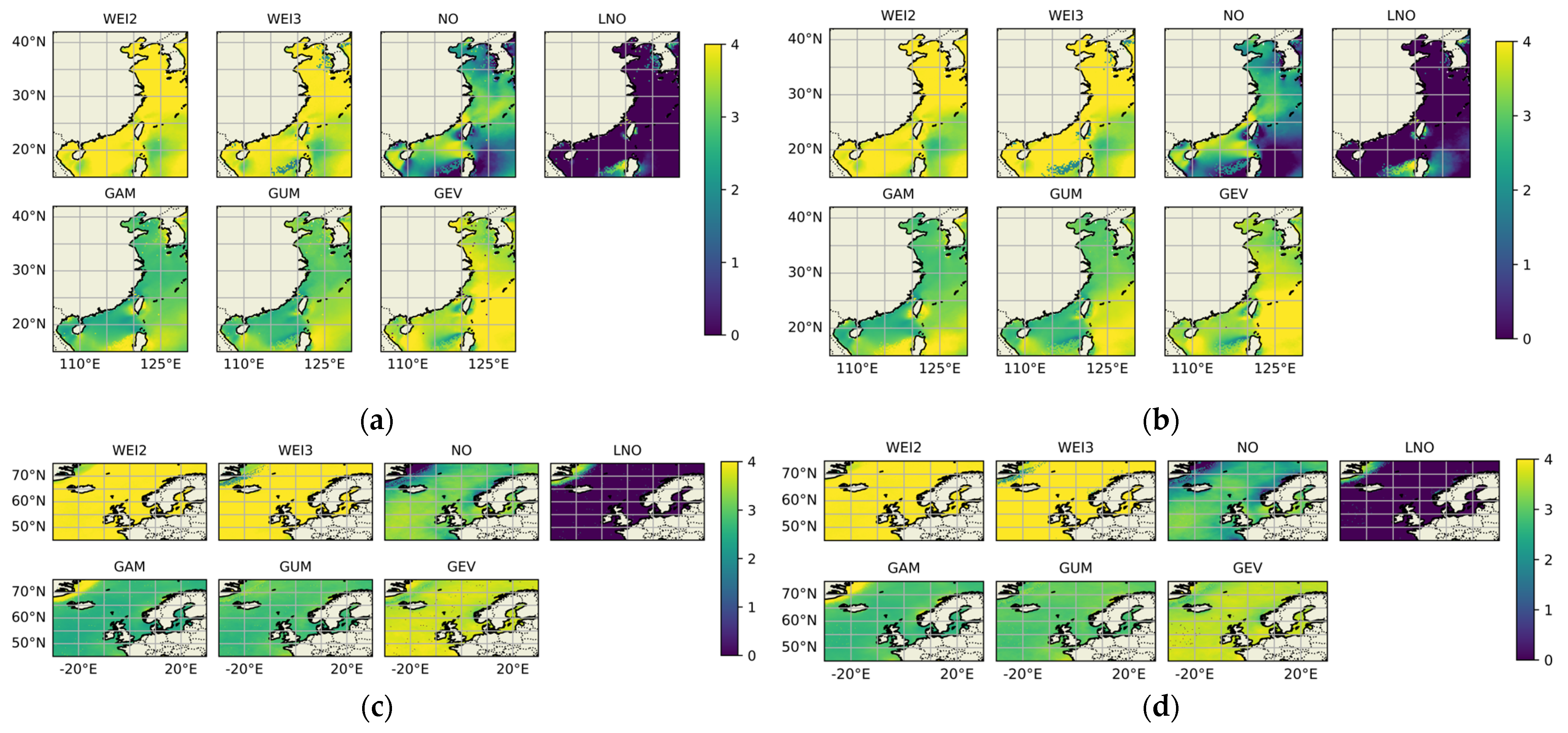
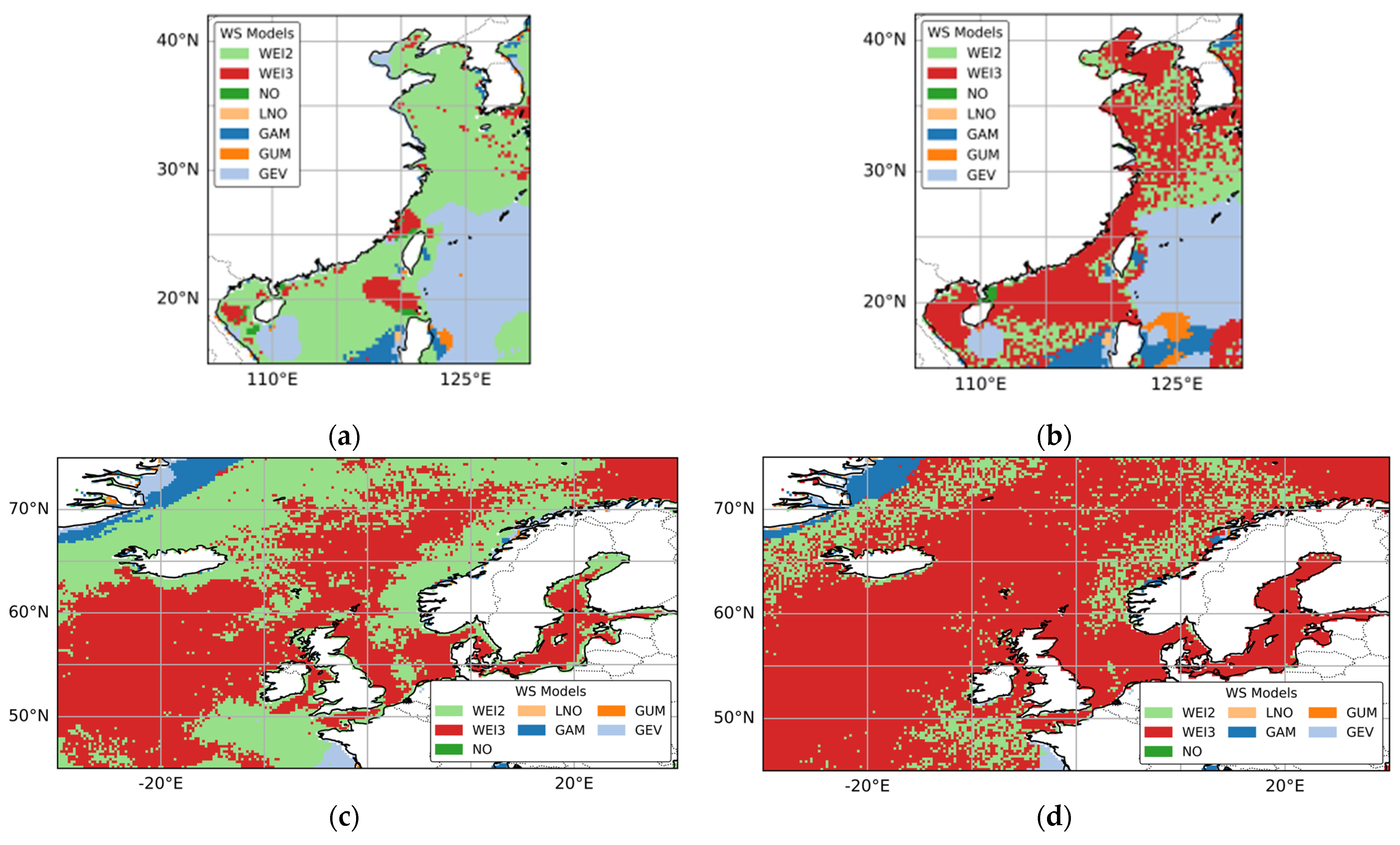
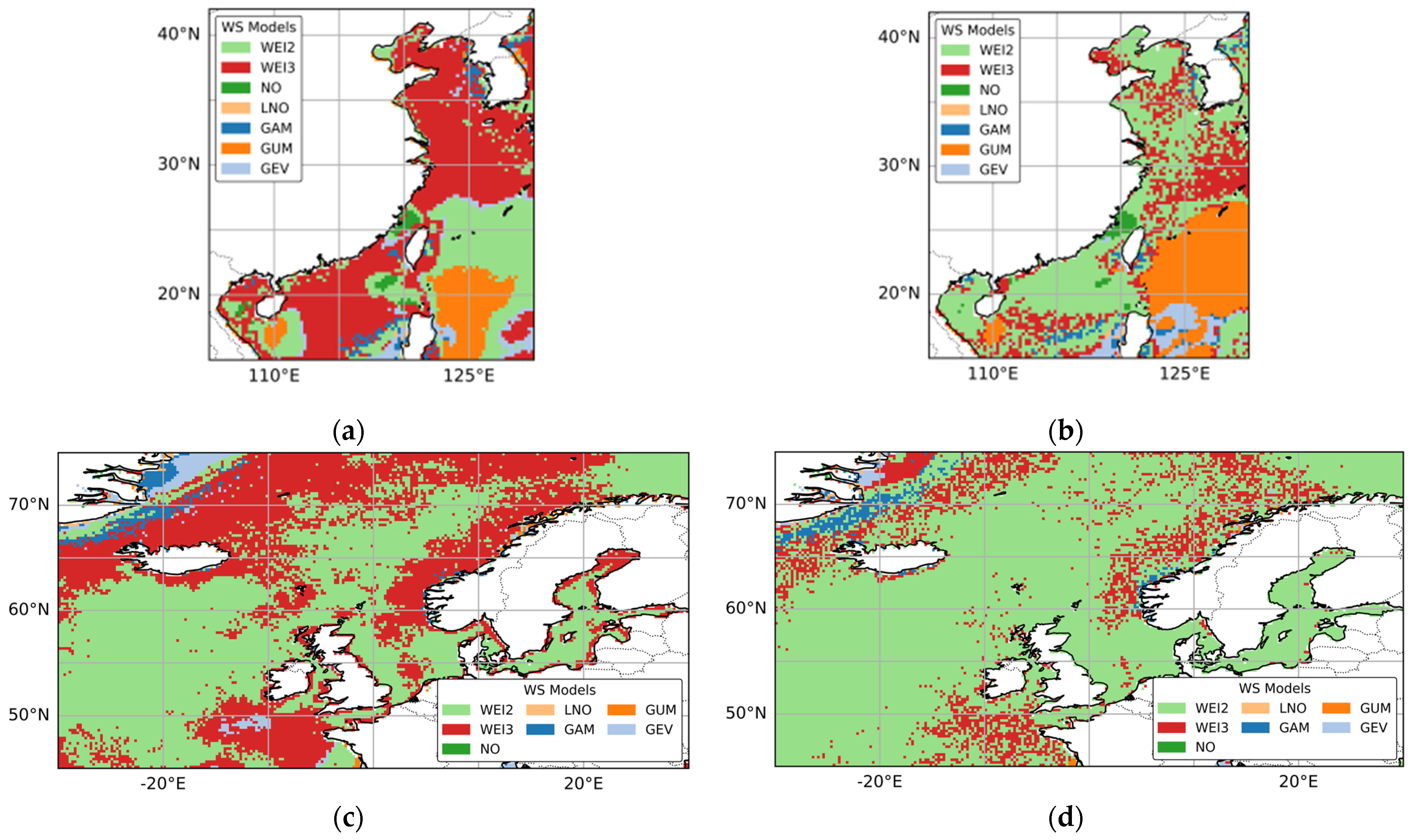
3.2. Comprehensive Performances of WSPD Models
- Wind speed patterns in China seas.
- 2.
- Wind speed patterns in European seas.
- 3.
- Summary.
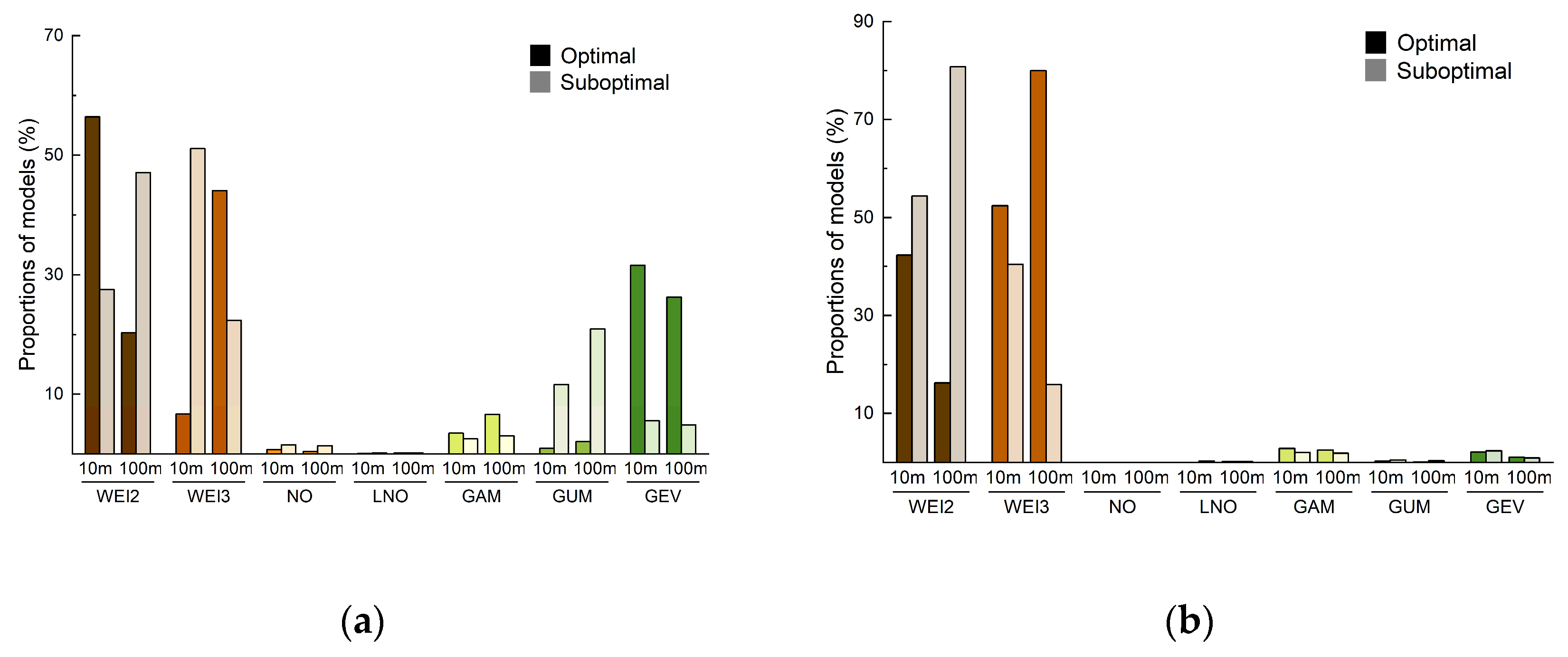
3.3. Distributions of Optimal and Suboptimal WSPD Models
3.4. Guidelines for Selecting the Optimal WSPD Model
3.5. Recommendations
- Model selection based on wind speed characteristics.
- 2.
- Consideration of altitude in model application.
- 3.
- Importance of skewness and kurtosis.
- 4.
- Regional variability and model flexibility.
- 5.
- Future research directions.
4. Conclusions
- Original research contributions.
- 2.
- Positive aspects.
- 3.
- Observed deficiencies and suggestions for improvement.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A








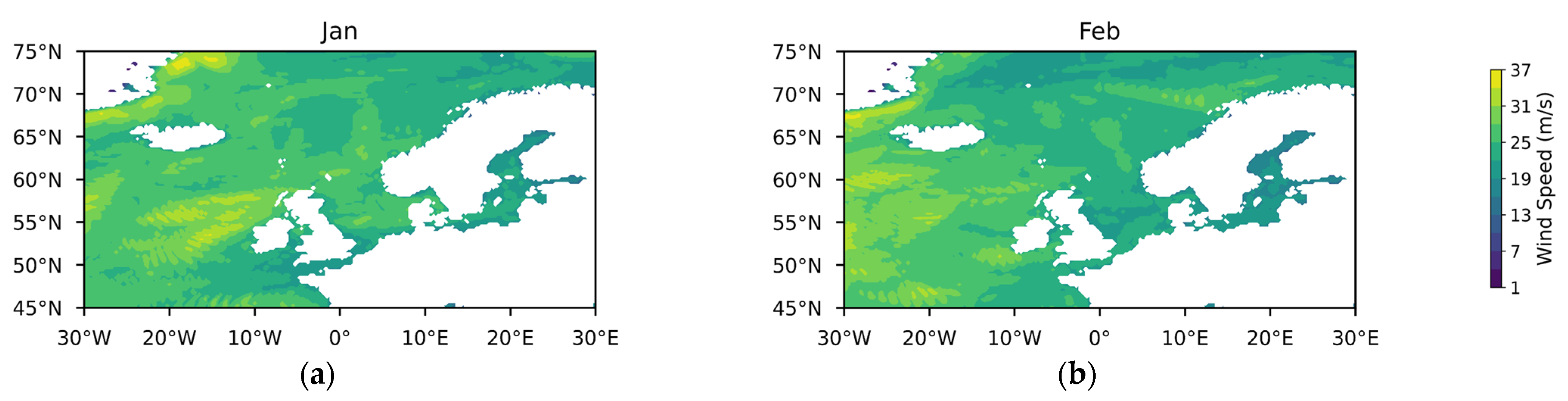
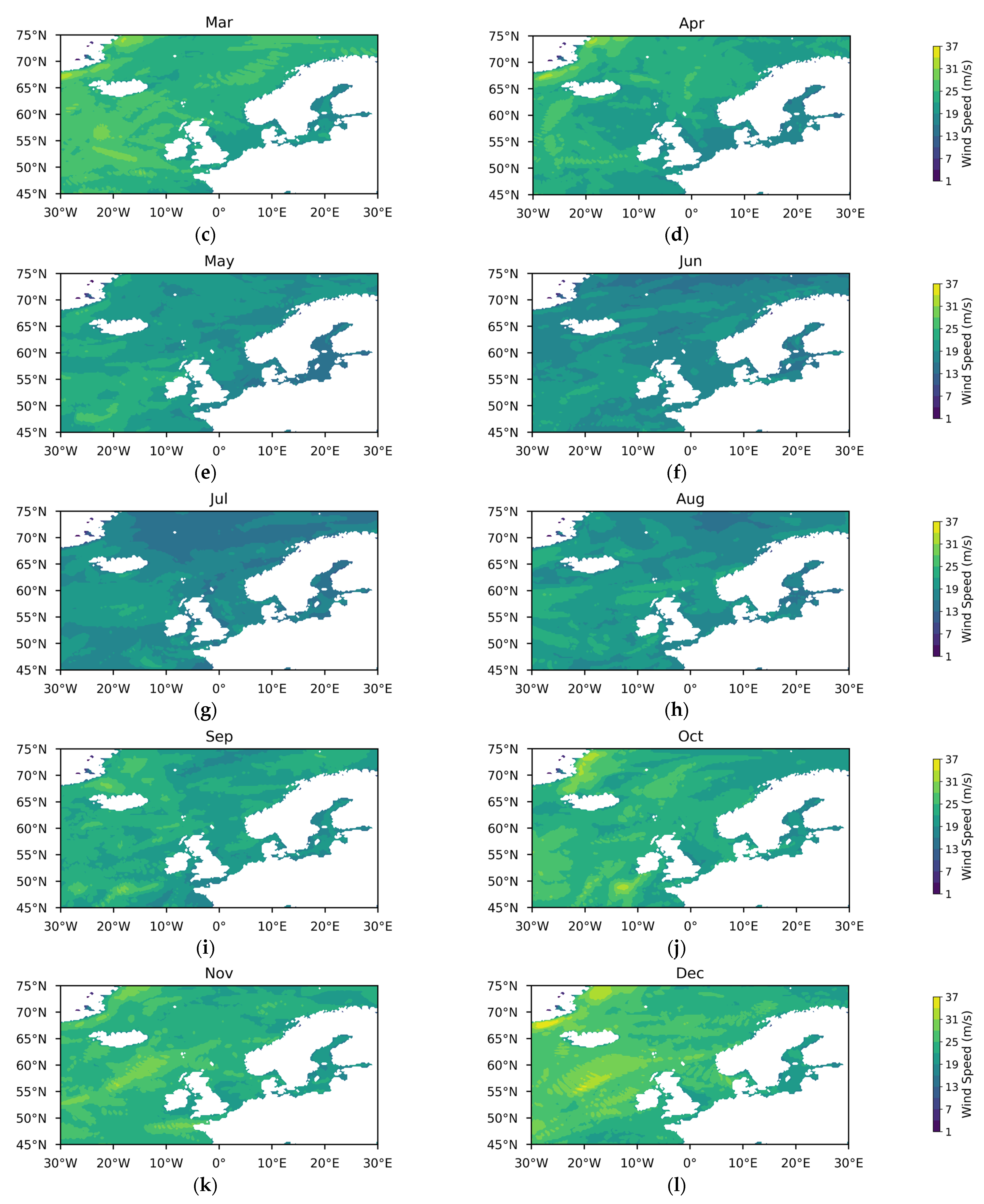
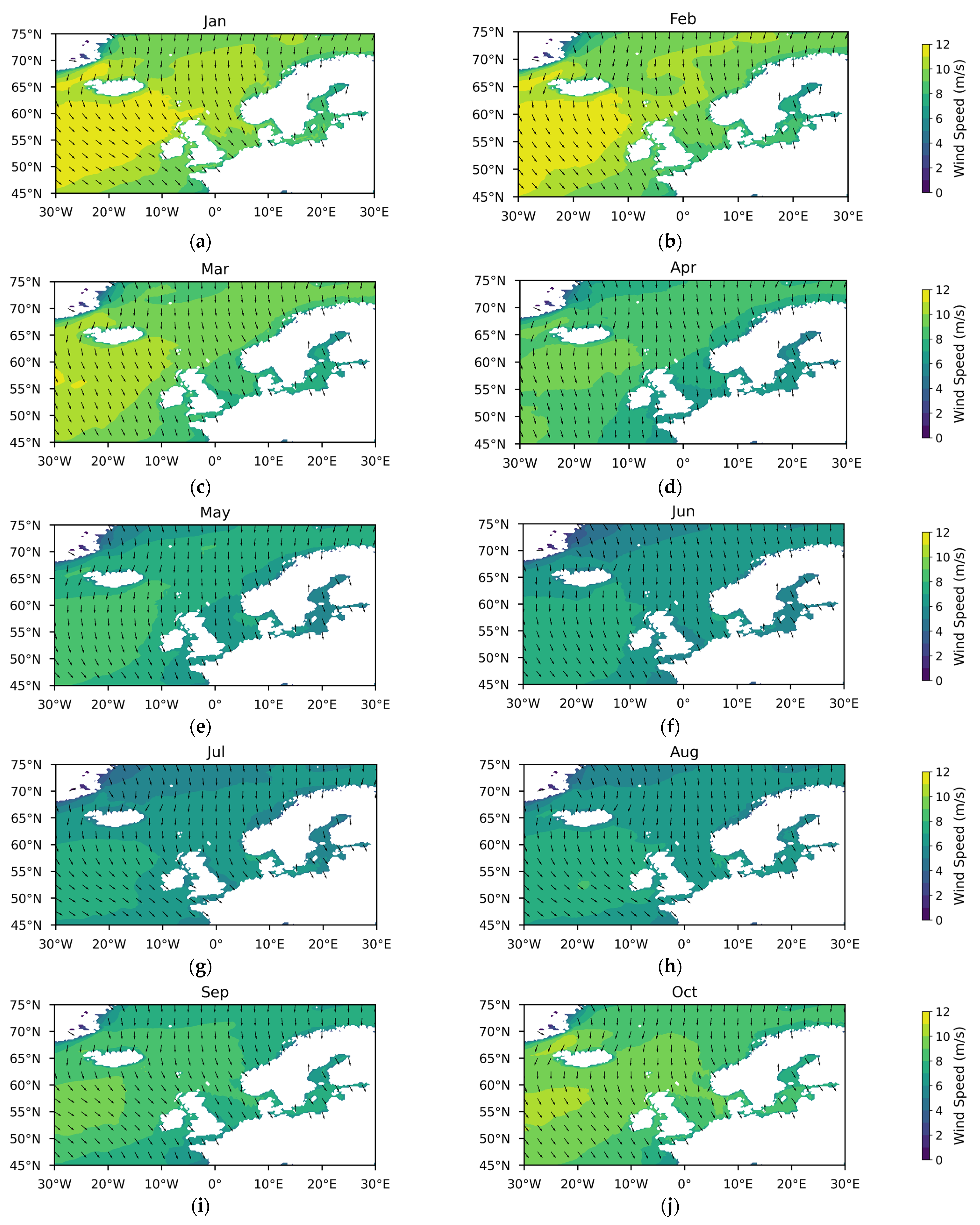
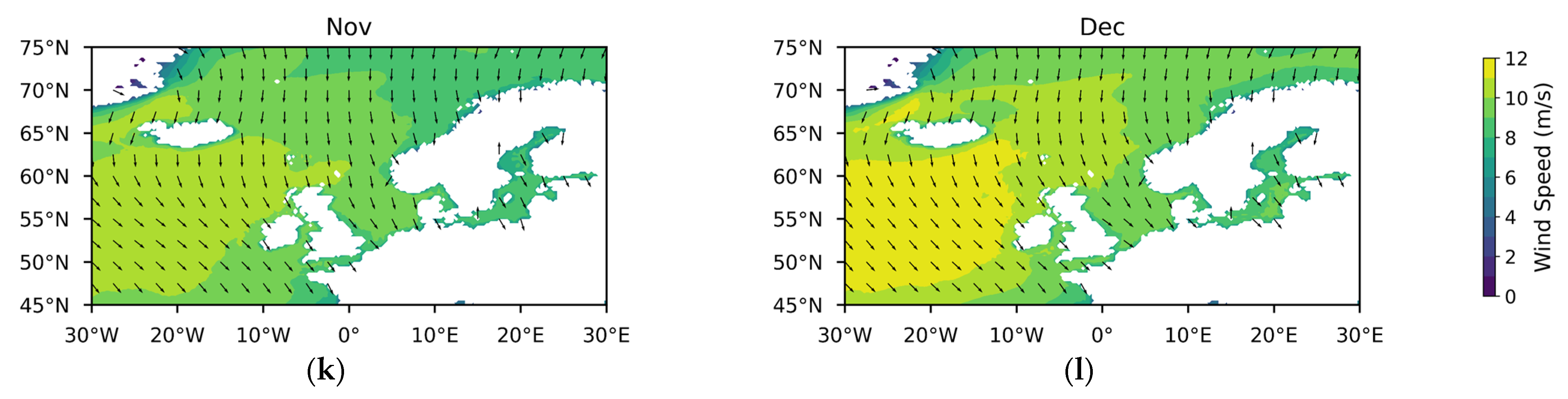
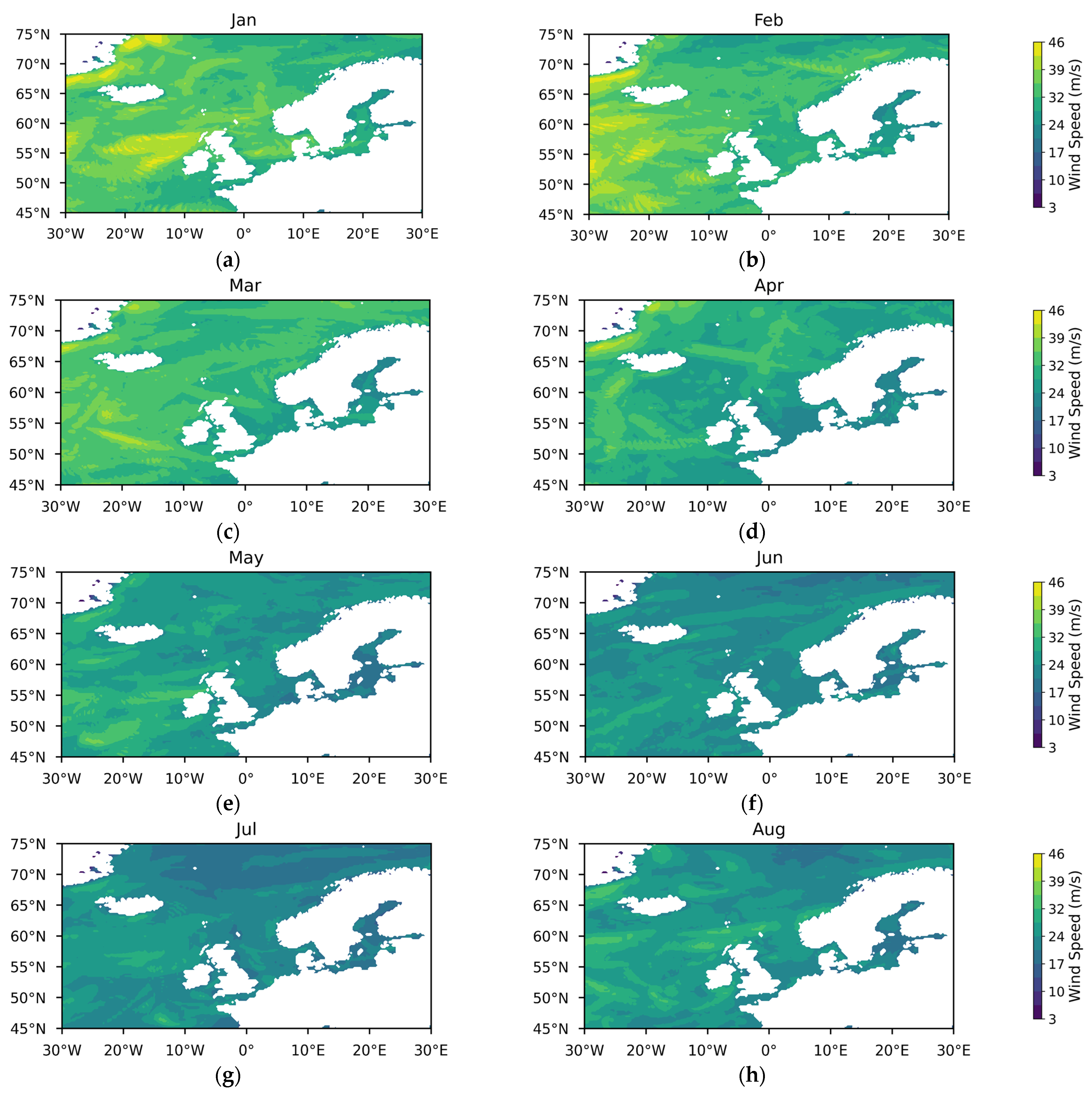
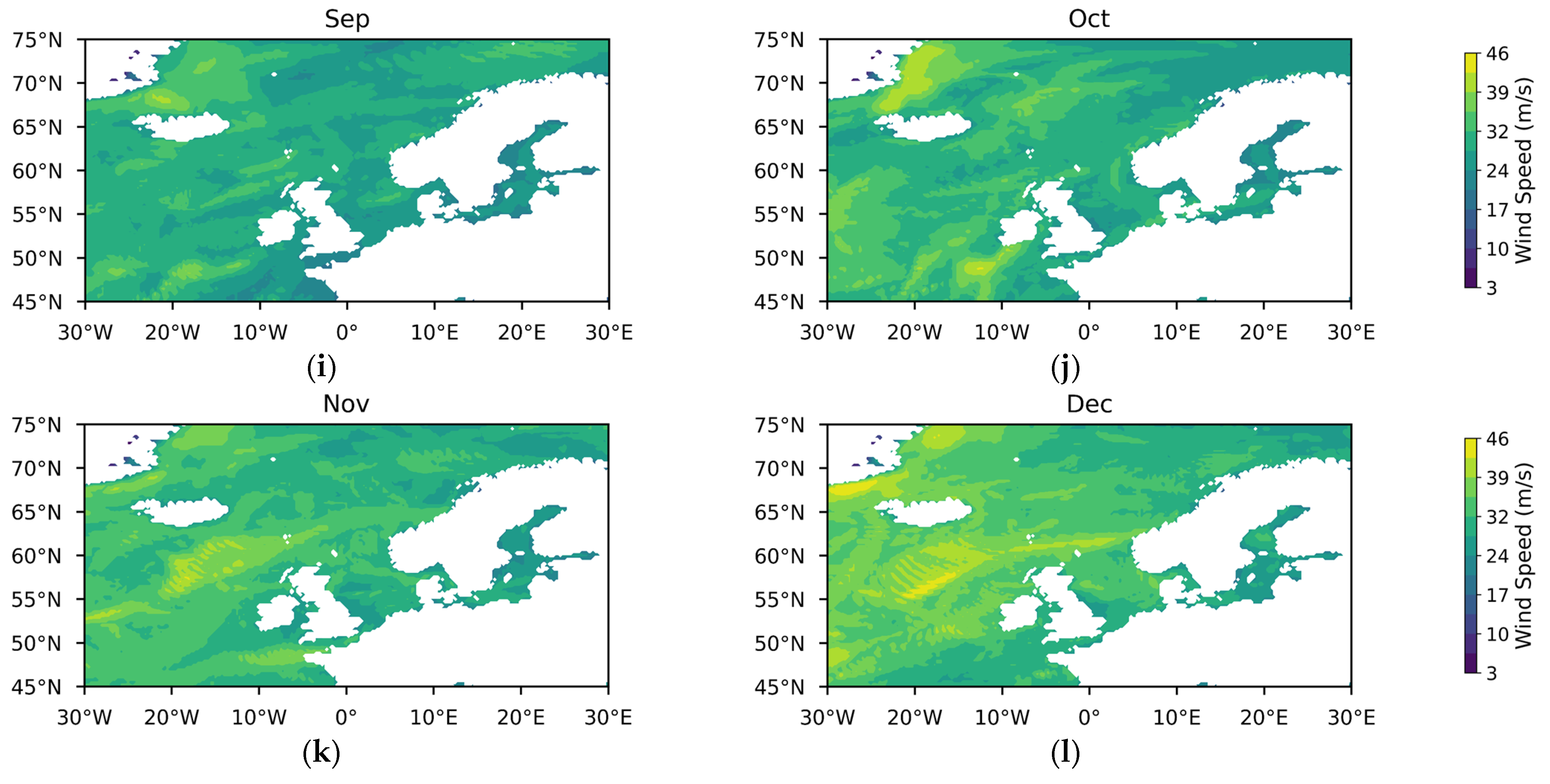
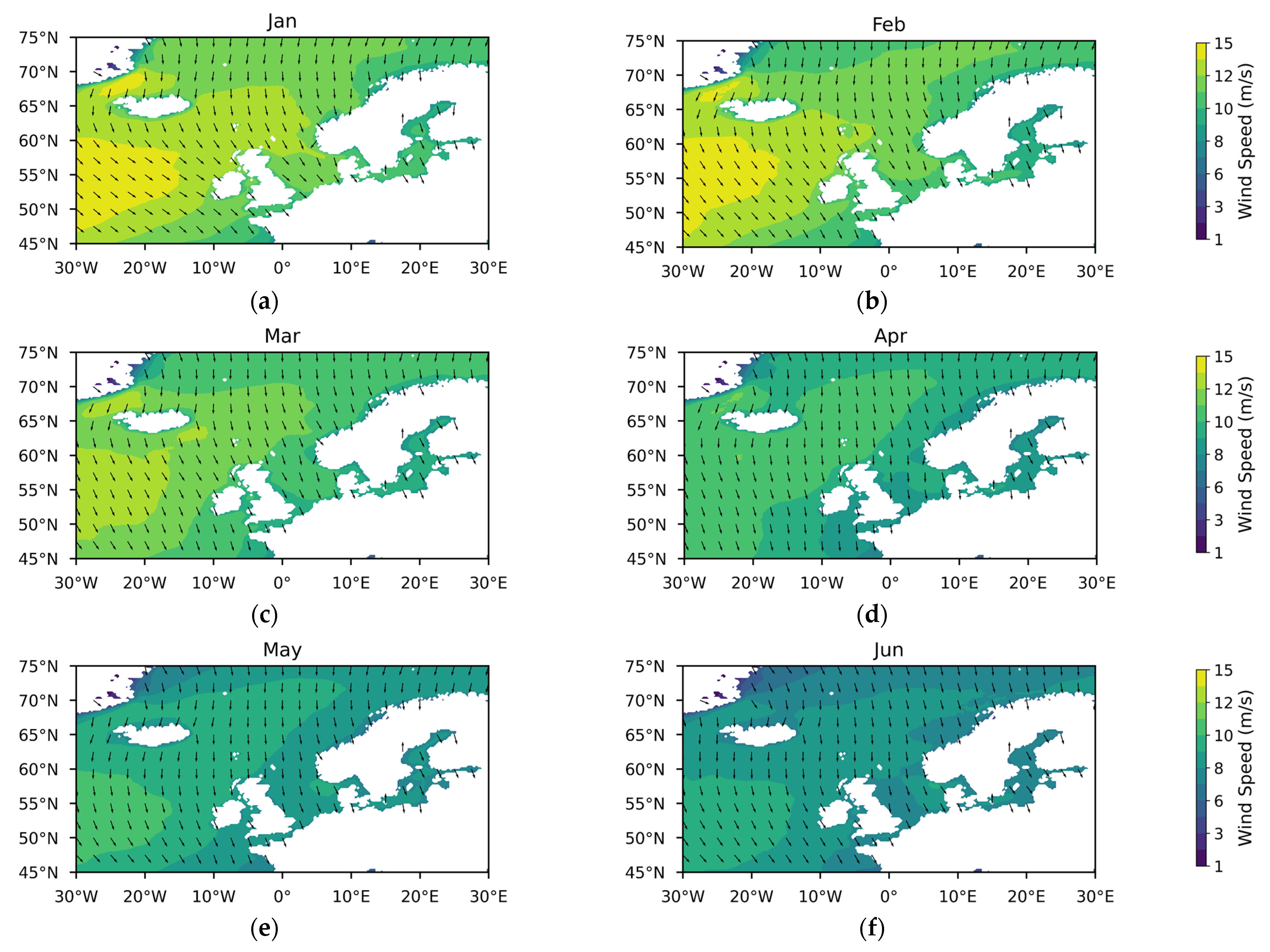
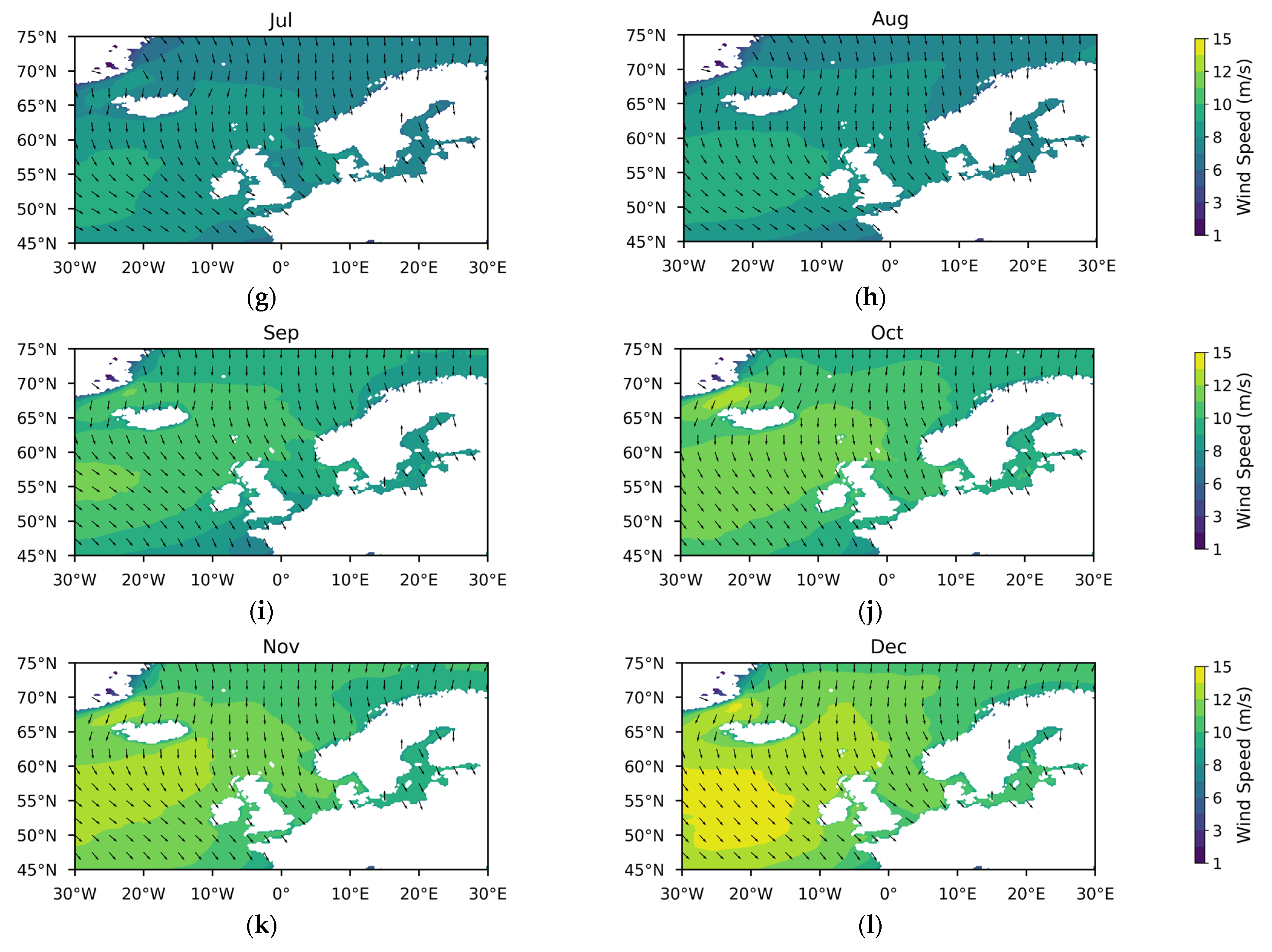







References
- Jung, C.; Sander, L.; Schindler, D. Future global offshore wind energy under climate change and advanced wind turbine technology. Energy Convers. Manag. 2024, 321, 119075. [Google Scholar] [CrossRef]
- Meng, D.; Yang, H.; Yang, S.; Zhang, Y.; De Jesus, A.M.P.; Correia, J.; Fazeres-Ferradosa, T.; Macek, W.; Branco, R.; Zhu, S.-P. Kriging-assisted hybrid reliability design and optimization of offshore wind turbine support structure based on a portfolio allocation strategy. Ocean Eng. 2024, 295, 116842. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; Yang, H.; De Jesus, A.M.P.; Correia, J.; Zhu, S.-P. Intelligent-inspired framework for fatigue reliability evaluation of offshore wind turbine support structures under hybrid uncertainty. Ocean Eng. 2024, 307, 118213. [Google Scholar] [CrossRef]
- Meng, D.; Yang, S.; De Jesus, A.M.P.; Fazeres-Ferradosa, T.; Zhu, S.-P. A novel hybrid adaptive Kriging and water cycle algorithm for reliability-based design and optimization strategy: Application in offshore wind turbine monopile. Comput. Methods Appl. Mech. Eng. 2023, 412, 116083. [Google Scholar] [CrossRef]
- Akhtar, N.; Geyer, B.; Schrum, C. Larger wind turbines as a solution to reduce environmental impacts. Sci. Rep. 2024, 14, 6608. [Google Scholar] [CrossRef]
- Sherman, P.; Chen, X.; McElroy, M. Offshore wind: An opportunity for cost-competitive decarbonization of China’s energy economy. Sci. Adv. 2020, 6, eaax9571. [Google Scholar] [CrossRef]
- Guo, X.; Chen, X.; Chen, X.; Sherman, P.; Wen, J.; McElroy, M. Grid integration feasibility and investment planning of offshore wind power under carbon-neutral transition in China. Nat. Commun. 2023, 14, 2447. [Google Scholar] [CrossRef]
- Beiter, P.; Mai, T.; Mowers, M.; Bistline, J. Expanded modelling scenarios to understand the role of offshore wind in decarbonizing the United States. Nat. Energy 2023, 8, 1240–1249. [Google Scholar] [CrossRef]
- Ning, Y.; Wang, L.; Yu, X.; Li, J. Recent development in the decarbonization of marine and offshore engineering systems. Ocean Eng. 2023, 280, 114883. [Google Scholar] [CrossRef]
- von Krauland, A.K.; Long, Q.; Enevoldsen, P.; Jacobson, M.Z. United States offshore wind energy atlas: Availability, potential, and economic insights based on wind speeds at different altitudes and thresholds and policy-informed exclusions. Energy Convers. Manag. X 2023, 20, 100410. [Google Scholar] [CrossRef]
- Costoya, X.; deCastro, M.; Carvalho, D.; Feng, Z.; Gómez-Gesteira, M. Climate change impacts on the future offshore wind energy resource in China. Renew. Energy 2021, 175, 731–747. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, D.; Li, S.; Chan, P.W. Discerning the spatial variations in offshore wind resources along the coast of China via dynamic downscaling. Energy 2018, 160, 582–596. [Google Scholar] [CrossRef]
- Hasager, C.B.; Hahmann, A.N.; Ahsbahs, T.; Karagali, I.; Sile, T.; Badger, M.; Mann, J. Europe’s offshore winds assessed with synthetic aperture radar, ASCAT and WRF. Wind Energy Sci. 2020, 5, 375–390. [Google Scholar] [CrossRef]
- Cheynet, E.; Li, L.; Jiang, Z. Metocean conditions at two Norwegian sites for development of offshore wind farms. Renew. Energy 2024, 224, 120184. [Google Scholar] [CrossRef]
- Gualtieri, G. Analysing the uncertainties of reanalysis data used for wind resource assessment: A critical review. Renew. Sustain. Energy Rev. 2022, 167, 112741. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Santos, C.S. Offshore wind energy resource simulation forced by different reanalyses: Comparisn with observed data in the Iberian Peninsula. Appl. Energy 2014, 134, 57–64. [Google Scholar] [CrossRef]
- West, C.G.; Smith, R.B. Global patterns of offshore wind variability. Wind Energy 2021, 24, 1466–1481. [Google Scholar] [CrossRef]
- Shi, H.; Dong, Z.; Xiao, N.; Huang, Q. Wind speed distributions used in wind energy assessment: A review. Front. Energy Res. 2021, 9, 769920. [Google Scholar] [CrossRef]
- Morales, J.M.; Mínguez, R.; Conejo, A.J. A methodology to generate statistically dependent wind speed scenarios. Appl. Energy 2010, 87, 843–855. [Google Scholar] [CrossRef]
- Katikas, L.; Dimitriadis, P.; Koutsoyiannis, D.; Kontos, T.; Kyriakidis, P. A stochastic simulation scheme for the long-term persistence, heavytailed and double periodic behavior of observational and reanalysis wind time-series. Appl. Energy 2021, 295, 116873. [Google Scholar] [CrossRef]
- Carta, J.A.; Ramírez, P.; Bueno, C. A joint probability density function of wind speed and direction for wind energy analysis. Energy Convers. Manag. 2008, 49, 1309–1320. [Google Scholar] [CrossRef]
- Huang, G.; Jiang, Y.; Peng, L.; Solari, G.; Liao, H.; Li, M. Characteristics of intense winds in mountain area based on field measurement: Focusing on thunderstorm winds. J. Wind. Eng. Ind. Aerodyn. 2019, 190, 166–182. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, T.; Gou, H.; Pu, Q.; Bao, Y. Joint distribution of wind speed and direction over complex terrains based on nonparametric copula models. J. Wind. Eng. Ind. Aerodyn. 2023, 241, 105509. [Google Scholar] [CrossRef]
- Huang, S.; Li, Q.; Shu, Z.; Chan, P.W. Copula-based joint distribution analysis of wind speed and wind direction: Wind energy development for Hong Kong. Wind Energy 2023, 26, 900–922. [Google Scholar] [CrossRef]
- Weibull, W. A statistical distribution function of wide applicability. J. Appl. Mech. 1951, 18, 293–297. [Google Scholar] [CrossRef]
- Torrielli, A.; Repetto, M.P.; Solari, G. Extreme wind speeds from long-term synthetic records. J. Wind. Eng. Ind. Aerodyn. 2013, 115, 22–38. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Global comparison of the goodness-of-fit of wind speed distributions. Energy Convers. Manag. 2017, 133, 216–234. [Google Scholar] [CrossRef]
- Hossain, J.; Sharma, S.; Kishore, V.V.N. Multi-peak Gaussian fit applicability to wind speed distribution. Renew. Sust. Energy Rev. 2014, 34, 483–490. [Google Scholar] [CrossRef]
- Parzen, E. On estimation of a probability density function and mode. Ann. Math. Stat. 1962, 33, 1065–1076. [Google Scholar] [CrossRef]
- Han, Q.; Ma, S.; Wang, T.; Chu, F. Kernel density estimation model for wind speed probability distribution with applicability to wind energy assessment in China. Renew. Sustain. Energy Rev. 2019, 115, 109387. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, Y.-J.; Liu, Z.-Y. Study on the Maximum Entropy Principle applied to the annual wind speed probability distribution: A case study for observations of intertidal zone anemometer towers of Rudong in East China Sea. Appl. Energy 2014, 114, 931–938. [Google Scholar] [CrossRef]
- Wais, P. A review of Weibull functions in wind sector. Renew. Sustain. Energy Rev. 2017, 70, 1099–1107. [Google Scholar] [CrossRef]
- IEC 61400-1:2019; Wind Energy Generation Systems—Part 1: Design Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2019.
- Tenreiro, C. Fourier series-based direct plug-in bandwidth selectors for Kernel Density Estimation. J. Nonparametr. Stat. 2011, 23, 533–545. [Google Scholar] [CrossRef]
- Kantar, Y.M.; Usta, I. Analysis of the upper-truncated Weibull distribution for wind speed. Energy Convers. Manag. 2015, 96, 81–88. [Google Scholar] [CrossRef]
- Wais, P. Two and three-parameter Weibull distribution in available wind power analysis. Renew. Energy 2017, 103, 15–29. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Olauson, J. ERA5: The new champion of wind power modelling? Renew. Energy 2018, 126, 322–331. [Google Scholar] [CrossRef]
- Gualtieri, G. Reliability of ERA5 reanalysis data for wind resource assessment: A comparison against tall towers. Energies 2021, 14, 4169. [Google Scholar] [CrossRef]
- Soares, P.M.M.; Lima, D.C.A.; Nogueira, M. Global offshore wind energy resources using the new ERA-5 reanalysis. Environ. Res. Lett. 2020, 15, 1040a2. [Google Scholar] [CrossRef]
- Wu, L.; Su, H.; Zeng, X.; Posselt, D.J.; Wong, S.; Chen, S.; Stoffelen, A. Uncertainty of atmospheric winds in three widely used global reanalysis datasets. J. Appl. Meteorol. Clim. 2024, 63, 165–180. [Google Scholar] [CrossRef]
- Jiang, B.; Hou, E.; Gao, Z.; Ding, J.; Fang, Y.; Khan, S.S.; Wu, G.; Wang, Q.; Meng, F.; Li, Y.; et al. Resource assessment for combined offshore wind and wave energy in China. Sci. China Technol. Sci. 2023, 66, 2530–2548. [Google Scholar] [CrossRef]
- Zheng, C.; Li, X.; Azorin-Molina, C.; Li, C.; Wang, Q.; Xiao, Z.; Yang, S.; Chen, X.; Zhan, C. Global trends in oceanic wind speed, wind-sea, swell, and mixed wave heights. Appl. Energy 2022, 321, 119327. [Google Scholar] [CrossRef]
- Feng, X.; Chen, X. Feasibility of ERA5 reanalysis wind dataset on wave simulation for the western inner-shelf of Yellow Sea. Ocean Eng. 2021, 236, 109413. [Google Scholar] [CrossRef]
- Hayes, L.; Stocks, M.; Blakers, A. Accurate long-term power generation model for offshore wind farms in Europe using ERA5 reanalysis. Energy 2021, 229, 120603. [Google Scholar] [CrossRef]
- Molina, M.O.; Gutiérrez, C.; Sánchez, E. Comparison of ERA5 surface wind speed climatologies over Europe with observations from the HadISD dataset. Int. J. Climatol. 2021, 41, 4864–4878. [Google Scholar] [CrossRef]
- MathWorks. atan2d, MATLAB R2024a. Available online: https://www.mathworks.com/help/matlab/ref/atan2d.html (accessed on 21 January 2025).
- Karin, T. Global Land Mask, Version 1.0.0. PyPI. Available online: https://pypi.org/project/global-land-mask/ (accessed on 21 January 2025).
- National Centers for Environmental Information (NCEI), NOAA ETOPO1 Data Set, National Oceanic and Atmospheric Administration. Available online: https://www.ngdc.noaa.gov/mgg/global/global.html (accessed on 21 January 2025).
- Huang, W.; Zhu, X.; Xia, H.; Wu, K. Offshore Wind Energy Assessment with a clustering approach to mixture model parameter estimation. J. Mar. Sci. Eng. 2023, 11, 2060. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J.; Ma, K. Wind speed probability distribution estimation and wind energy assessment. Renew. Sustain. Energy Rev. 2016, 60, 881–899. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0 Contributors. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Gunturu, U.B.; Schlosser, C.A. Characterization of wind power resource in the United States. Atmos. Chem. Phys. 2012, 12, 9687–9702. [Google Scholar] [CrossRef]
- Zheng, C. Temporal-spatial characteristics dataset of offshore wind energy resource for the 21st Century Maritime Silk Road. China Sci. Data 2020, 5, 102–115. [Google Scholar] [CrossRef]
- Ren, G.; Wan, J.; Liu, J.; Yu, D. Characterization of wind resource in China from a new perspective. Energy 2019, 167, 994–1010. [Google Scholar] [CrossRef]
- Wen, Y.; Kamranzad, B.; Lin, P. Assessment of long-term offshore wind energy potential in the south and southeast coasts of China based on a 55-year dataset. Energy 2021, 224, 120225. [Google Scholar] [CrossRef]
- Zheng, C.; Pan, J.; Li, J. Assessing the China Sea wind energy and wave energy resources from 1988 to 2009. Ocean Eng. 2013, 65, 39–48. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Elsevier: Oxford, UK, 2011; pp. 125–128. [Google Scholar]
- Masseran, N.; Razali, A.M.; Ibrahim, K. An analysis of wind power density derived from several wind speed density functions: The regional assessment on wind power in Malaysia. Renew. Sustain. Energy Rev. 2012, 16, 6476–6487. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Krzywinski, M.; Altman, N. Classification and regression trees. Nat. Methods 2017, 14, 757–758. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Fisher, A.; Rudin, C.; Dominici, F. All Models are Wrong, but Many are Useful: Learning a Variable’s Importance by Studying an Entire Class of Prediction Models Simultaneously. J. Mach. Learn. Res. 2019, 20, 177. [Google Scholar]
- Hughes, M.; Cassano, J.J. The climatological distribution of extreme Arctic winds and implications for ocean and sea ice processes. J. Geophys. Res. Atmos. 2015, 120, 7358–7377. [Google Scholar] [CrossRef]
- Gorter, W.; van Angelen, J.H.; Lenaerts, J.T.M.; van den Broeke, M.R. Present and future near-surface wind climate of Greenland from high resolution regional climate modelling. Clim. Dyn. 2014, 42, 1595–1611. [Google Scholar] [CrossRef]
- Laurila, T.K.; Sinclair, V.A.; Gregow, H. Climatology, variability, and trends in near-surface wind speeds over the North Atlantic and Europe during 1979–2018 based on ERA5. Int. J. Climatol. 2021, 41, 2253–2278. [Google Scholar] [CrossRef]
- Ngo, T.; Letchford, C. A comparison of topographic effects on gust wind speed. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 2273–2293. [Google Scholar] [CrossRef]
- Pei, C.; Zhang, X.; Cheng, X.; Yang, X.; Ma, C. Impact of different terrains on the distribution of wind pressure on airport terminal roofs in mountainous areas. Structures 2024, 69, 107265. [Google Scholar] [CrossRef]


| Name (Symbol) | Np | Probability Distribution Function | Key Features | Chosen Reasons |
|---|---|---|---|---|
| Weibull (WEI2) | 2 | Suitable for most wind speed distributions with moderate skewness and kurtosis | Simple, high flexibility, and computational efficient; widely applied in wind speed modeling | |
| Weibull (WEI3) | 3 | Adds a location parameter (μ) based on the two-parameter model | More suitable for complex wind speed distributions, especially for wind speed data with considerable null wind probability | |
| Normal (NO) | 2 | A symmetric distribution applicable to regions with minor wind speed variations and an approximately normal distribution | Suitable for modeling stable wind patterns characteristic | |
| Log-normal (LNO) | 2 | Suitable for wind speed data that exhibit log-normal distribution characteristics | Fits right-skewed wind speed data well | |
| Gamma (GAM) | 2 | Suitable for skewed distributions | Effective for modeling extreme wind speed events | |
| Gumbel (GUM) | 2 | Known for its heavy right tail | Provides more precise estimates of extreme wind speeds than the Weibull | |
| Generalized extreme value | 3 | A comprehensive model integrating various extreme value distributions | Suitable for complex wind speed characteristics and extreme wind events |
| Index | Coordinates (CHN) | Coordinates (EU) | |
|---|---|---|---|
| nearshore points | N1 | (38.75° N, 118.00° E) | (63.00° N, 19.00° E) |
| N2 | (37.50° N, 122.75° E) | (55.00° N, 19.00° E) | |
| N3 | (35.00° N, 119.50° E) | (60.00° N, 4.00° E) | |
| N4 | (31.00° N, 122.25° E) | (55.00° N, 0.50° W) | |
| N5 | (24.25° N, 118.50° E) | (54.00° N, 6.00° E) | |
| N6 | (23.50° N, 121.75° E) | (50.50° N, 1.00° E) | |
| N7 | (20.25° N, 110.00° E) | (53.00° N, 5.50° W) | |
| N8 | (21.25° N, 109.00° E) | (53.00° N, 11.00° W) | |
| offshore points | O1 | (38.50° N, 120.00° E) | (61.00° N, 19.50° E) |
| O2 | (38.50° N, 123.00° E) | (56.00° N, 19.00° E) | |
| O3 | (35.50° N, 123.75° E) | (65.00° N, 5.00° E) | |
| O4 | (31.50° N, 125.00° E) | (58.50° N, 1.00° E) | |
| O5 | (27.00° N, 124.00° E) | (55.00° N, 4.00° E) | |
| O6 | (21.00° N, 119.00° E) | (60.00° N, 8.00° W) | |
| O7 | (19.00° N, 113.00° E) | (52.00° N, 13.00° W) | |
| O8 | (18.00° N, 117.00° E) | (47.50° N, 8.00° W) |
| 10 m ASL | 100 m ASL | |||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Variance | Skewness | Kurtosis | Mean | Variance | Skewness | Kurtosis | |
| N1 | 5.3491 | 6.4417 | 0.6847 | 0.5447 | 6.5539 | 10.6193 | 0.6024 | 0.1909 |
| N2 | 6.1297 | 9.3071 | 0.5427 | −0.0209 | 7.4772 | 14.0968 | 0.4441 | −0.2053 |
| N3 | 4.7815 | 5.2563 | 0.6847 | 0.5574 | 5.9377 | 8.5579 | 0.5544 | 0.1820 |
| N4 | 6.3413 | 7.5491 | 0.4591 | 0.3367 | 7.7209 | 12.4279 | 0.5177 | 0.4294 |
| N5 | 7.9714 | 15.3298 | 0.1333 | −0.8964 | 9.5660 | 20.8942 | 0.0883 | −0.7274 |
| N6 | 5.9744 | 14.8770 | 0.6734 | −0.2009 | 6.7701 | 21.0287 | 0.8165 | 0.3160 |
| N7 | 4.2126 | 3.5845 | 0.5293 | 1.3325 | 5.8562 | 6.5856 | 0.4555 | 1.6242 |
| N8 | 5.3760 | 7.7344 | 0.5790 | 0.2541 | 6.3135 | 10.6380 | 0.6457 | 0.6886 |
| O1 | 5.9781 | 8.3171 | 0.5838 | 0.1921 | 7.3904 | 13.7411 | 0.5252 | −0.0700 |
| O2 | 6.1286 | 8.9178 | 0.4454 | −0.2449 | 7.4041 | 13.7975 | 0.4146 | −0.2954 |
| O3 | 6.1595 | 10.1012 | 0.5701 | −0.0145 | 7.3104 | 15.1018 | 0.5735 | 0.0684 |
| O4 | 6.6838 | 9.6816 | 0.5265 | 0.3435 | 8.0290 | 14.6057 | 0.5748 | 0.7700 |
| O5 | 7.5259 | 10.1073 | 0.5856 | 1.1038 | 8.6803 | 14.6588 | 0.8267 | 2.6348 |
| O6 | 7.5523 | 10.9725 | 0.0840 | −0.2759 | 8.5766 | 15.4635 | 0.2303 | 0.2020 |
| O7 | 7.1267 | 9.9827 | 0.3753 | −0.0736 | 8.1351 | 14.1181 | 0.4574 | 0.3078 |
| O8 | 7.2561 | 15.1524 | 0.3185 | −0.6642 | 8.3505 | 22.4485 | 0.4089 | −0.5066 |
| 10 m ASL | 100 m ASL | |||||||
|---|---|---|---|---|---|---|---|---|
| Mean | Variance | Skewness | Kurtosis | Mean | Variance | Skewness | Kurtosis | |
| N1 | 6.3564 | 8.8171 | 0.4301 | −0.1323 | 7.9894 | 14.8194 | 0.4246 | −0.1486 |
| N2 | 7.3191 | 10.5888 | 0.3808 | −0.0385 | 8.8885 | 17.0481 | 0.4691 | 0.1899 |
| N3 | 7.8580 | 16.2005 | 0.4742 | −0.2504 | 9.4819 | 26.7340 | 0.5759 | −0.0844 |
| N4 | 7.5491 | 11.3857 | 0.3259 | −0.2143 | 9.3209 | 19.0244 | 0.3669 | −0.1564 |
| N5 | 7.9163 | 11.7771 | 0.3091 | −0.1802 | 9.6757 | 19.9670 | 0.4314 | −0.0037 |
| N6 | 7.2980 | 12.0184 | 0.3809 | −0.2507 | 8.8808 | 19.7093 | 0.5096 | 0.0307 |
| N7 | 7.5376 | 12.8315 | 0.3741 | −0.2251 | 9.2352 | 20.9977 | 0.4971 | 0.05357 |
| N8 | 8.7466 | 15.0919 | 0.3507 | −0.1499 | 10.5704 | 25.3312 | 0.4538 | −0.0624 |
| O1 | 7.0874 | 10.1322 | 0.3007 | −0.2524 | 8.8142 | 17.3472 | 0.3258 | −0.2795 |
| O2 | 7.4992 | 10.9823 | 0.3215 | −0.1980 | 9.2120 | 18.0297 | 0.3815 | −0.0617 |
| O3 | 8.3569 | 16.4719 | 0.4483 | −0.1678 | 9.8636 | 26.5421 | 0.5962 | 0.07529 |
| O4 | 8.3489 | 15.5360 | 0.4102 | −0.1952 | 10.1472 | 26.0047 | 0.4874 | −0.0892 |
| O5 | 8.0455 | 12.4473 | 0.3551 | −0.1971 | 9.8697 | 20.9753 | 0.4486 | −0.0284 |
| O6 | 9.1660 | 16.7673 | 0.3310 | −0.2690 | 10.9947 | 27.2762 | 0.4267 | −0.1320 |
| O7 | 9.0514 | 15.8313 | 0.3587 | −0.1687 | 10.8327 | 26.0596 | 0.4573 | −0.0669 |
| O8 | 7.9743 | 13.5199 | 0.4336 | −0.1075 | 9.4651 | 21.8541 | 0.5491 | 0.0691 |
| Feature | CHN (10 m ASL) | CHN (100 m ASL) | EU (10 m ASL) | EU (100 m ASL) | |
|---|---|---|---|---|---|
| Random Forest (RF) | Skewness | 0.44066 | 0.39655 | 0.45416 | 0.46330 |
| Kurtosis | 0.25798 | 0.26433 | 0.21886 | 0.24658 | |
| Mean | 0.18139 | 0.18924 | 0.18248 | 0.16349 | |
| Variance | 0.11997 | 0.14988 | 0.14450 | 0.12664 | |
| XGBoost | Skewness | 0.37448 | 0.43004 | 0.41520 | 0.42654 |
| Kurtosis | 0.26499 | 0.23955 | 0.28166 | 0.27186 | |
| Mean | 0.21244 | 0.18550 | 0.16850 | 0.16732 | |
| Variance | 0.14810 | 0.14491 | 0.13464 | 0.13428 | |
| Permutation Feature Importance (PFI) | Skewness | 0.41945 | 0.42630 | 0.43559 | 0.19974 |
| Kurtosis | 0.16647 | 0.18260 | 0.10132 | 0.04506 | |
| Mean | 0.14203 | 0.12004 | 0.09438 | 0.03612 | |
| Variance | 0.05386 | 0.06911 | 0.08663 | 0.01616 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhao, M.; Liu, Z.; Ma, J.; Yang, L. Comparative Analysis of Offshore Wind Resources and Optimal Wind Speed Distribution Models in China and Europe. Energies 2025, 18, 1108. https://doi.org/10.3390/en18051108
Chen Y, Zhao M, Liu Z, Ma J, Yang L. Comparative Analysis of Offshore Wind Resources and Optimal Wind Speed Distribution Models in China and Europe. Energies. 2025; 18(5):1108. https://doi.org/10.3390/en18051108
Chicago/Turabian StyleChen, Yanan, Ming Zhao, Zhengxian Liu, Jianlong Ma, and Lei Yang. 2025. "Comparative Analysis of Offshore Wind Resources and Optimal Wind Speed Distribution Models in China and Europe" Energies 18, no. 5: 1108. https://doi.org/10.3390/en18051108
APA StyleChen, Y., Zhao, M., Liu, Z., Ma, J., & Yang, L. (2025). Comparative Analysis of Offshore Wind Resources and Optimal Wind Speed Distribution Models in China and Europe. Energies, 18(5), 1108. https://doi.org/10.3390/en18051108






