Deep-Fuzzy Logic Control for Optimal Energy Management: A Predictive and Adaptive Framework for Grid-Connected Microgrids
Abstract
1. Introduction
- To design and implement a novel Deep-FLC framework that integrates predictive LSTM models with fuzzy logic to optimise battery energy management.
- To evaluate and compare the performance of three systems—conventional, FLC, and Deep-FLC—using key performance metrics, including total cost, battery efficiency, State of Health (SOH), and Depth of Discharge (DoD).
- To minimise energy costs and reduce reliance on grid power by dynamically adjusting charging and discharging priorities based on real-time battery conditions and predicted energy demands.
- To enhance battery lifespan by reducing DoD and ensuring stable State of Charge (SOC) levels, thus minimising stress on the battery system and lowering degradation rates.
1.1. Purpose
1.2. Research Gaps in Energy Management for MGs
- Static control in conventional systems:Traditional energy management approaches are often based on fixed thresholds for battery charging and discharging. These static methods lack the flexibility to adapt to highly dynamic energy demand; uncertain renewable energy generation, irrespective of whether PV systems or wind turbines (WT) are used; and battery conditions, leading to inefficiencies.
- Limitations of existing FLC systems: Whilst providing adaptability to certain conditions, FLC does not incorporate predictive capabilities. As a result, these systems struggle to respond proactively to sudden changes in load demand, renewable energy availability, or grid constraints.
- Neglect of battery degradation and long-term sustainability: Current EMSs often fail to adequately account for key factors such as SOH and DoD, both of which are essential for extending the battery lifespan and ensuring long-term system efficiency.
2. Literature Review
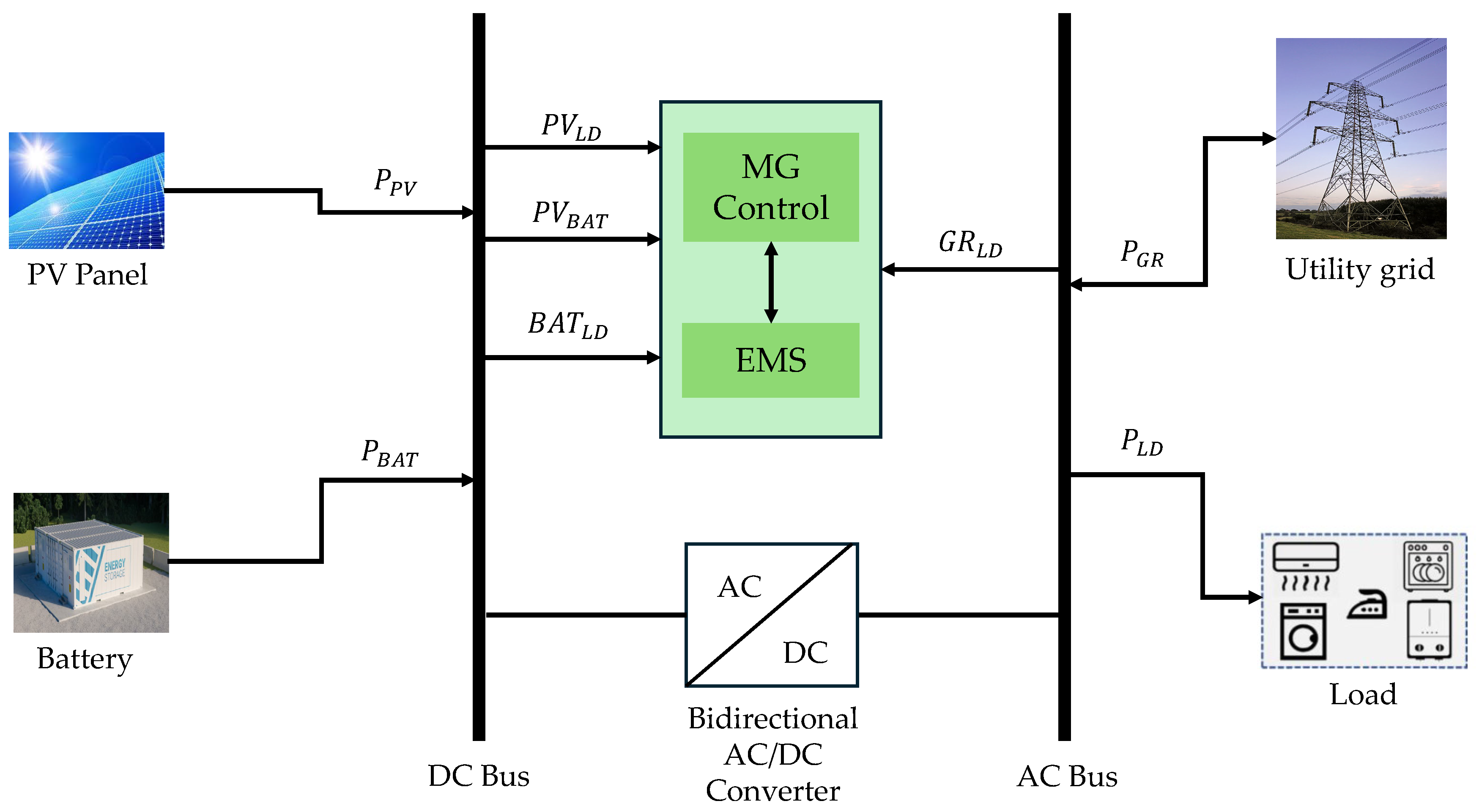
3. Proposed Framework and Methodology for Deep-FLC Implementation
3.1. Design Assumptions for a Grid-Connected MG with Battery Storage
- Battery parameters: The battery capacity, , is set to 4500 mAh, equivalent to as follows:
- SOC: The initial SOC is , and its range is constrained to to prevent overcharging or deep discharge.
- SOH: The initial SOH is , with degradation calculated dynamically.
- Efficiency: The charging efficiency is 95%, and the discharging efficiency is 90%.
- Cost dynamics: The baseline electricity cost is 0.20 $/kWh. Peak-hour costs are doubled, and off-peak hours incur a discount factor of , as follows:
- Battery temperature: Ambient temperature is °C, and the critical temperature is °C.
3.2. Baseline Simulation of a Conventional EMS
3.2.1. Grid Power and Cost Calculation
3.2.2. SOC and Temperature Updates
3.3. Real-Time EMS Using FLC
3.3.1. Fuzzy Membership Function Design for SOC and SOH
- Charging priority (): Determines battery charging preference.
- Grid priority (): Determines reliance on grid power.
3.3.2. Fuzzy Rules and Decision-Making for Charging and Grid Reliance
- Rule 1: If SOC is “low” and load is “high”, then = “high” and = “high”.
- Rule 2: If SOC is “high” and temperature is “high”, then = “low”.
3.3.3. Optimisation for Energy Allocation
System Constraints
- Load demand balance (Equation (11)): At each time step k, the total load demand is supplied through three sources, such as direct PV power to load (), import power from the grid (), and battery discharge power ().
- PV power distribution (Equation (12)): The total PV power is split into power directly supplied to the load () and power used to charge the battery ().
- SOH constraints (Equation (14)): The SOH of the battery must also be maintained within an acceptable range, to , ensuring the battery’s longevity and reliability. The acceptable range for the SOH is generally determined based on the specific application, battery type, and operational requirements and ensures the battery’s longevity and reliability while preventing excessive degradation.
3.4. Deep-FLC: Integrating Prediction and Adaptation
3.4.1. LSTM-Based Forecasting of SOC, SOH, and Load Demand
3.4.2. Fuzzy Inputs from Predictions
3.4.3. Dynamic Control
3.5. Performance Metrics for Comparing Energy Management Strategies
- Total cost: Computed using Equation (5).
- SOC stability: Range and variability of SOC over time.
- Battery efficiency: Ratio of energy used to total energy input.
- SOH degradation: Updated iteratively, as follows:where is the depth of discharge, as follows:
3.5.1. Depth of Discharge (DoD)
3.5.2. Battery Efficiency
3.5.3. Cost Analysis
3.5.4. SOH Degradation
3.6. Evaluation of Deep-FLC Model Performance
3.6.1. Mean Absolute Percentage Error (MAPE)
3.6.2. Root Mean Square Error (RMSE)
3.7. Implementation Steps for the Deep-FLC Framework
| Algorithm 1 Energy management using Deep-FLC | |
| 1: | Input: , , Battery (), and Cost Parameters, N |
| 2: | Output: Optimal Grid Power , Battery Usage , and PV Distribution |
| 3: | Step 1: Initialisation and preprocessing |
| 4: | Load dataset and preprocess , , , |
| 5: | Set constraints: , , , , and |
| 6: | Step 2: Conventional system simulation |
| 7: | for do |
| 8: | |
| 9: | |
| 10: | Clamp within |
| 11: | |
| 12: | end for |
| 13: | Step 3: FLC simulation |
| 14: | Define fuzzy inputs: SOC, SOH, Load, Temperature |
| 15: | Define fuzzy outputs: Charging Priority and Grid Priority |
| 16: | Construct fuzzy membership functions and rules |
| 17: | for do |
| 18: | Compute fuzzy outputs: Charging Priority, Grid Priority |
| 19: | Solve |
| 20: | Update and |
| 21: | end for |
| 22: | Step 4: Deep-FLC simulation |
| 23: | Train LSTM model on historical data: SOC, SOH, and |
| 24: | for do |
| 25: | Predict using LSTM |
| 26: | Compute fuzzy logic outputs with predicted values |
| 27: | Solve |
| 28: | Update and |
| 29: | end for |
| 30: | Step 5: Evaluate systems |
| 31: | Calculate metrics: Total cost, Battery efficiency, Average DoD, Final SOC and SOH |
| 32: | Compare conventional, FLC, and Deep-FLC systems |
| 33: | return Results |
4. Results
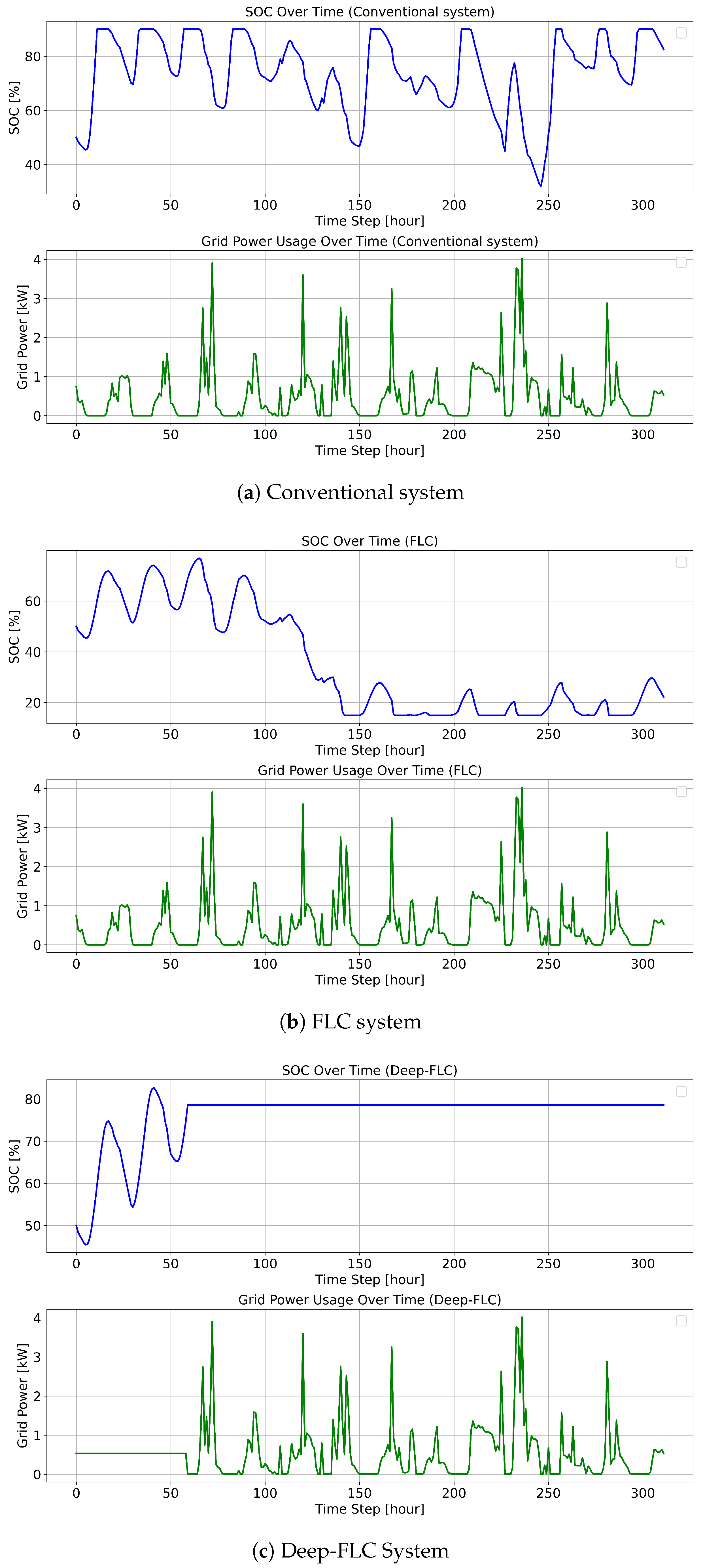
4.1. Improved SOC Stability with Deep-FLC Compared to Baselines
- Conventional system: The SOC fluctuates significantly, varying between 40% and 90%, with frequent falls below 50%, as illustrated in Figure 4a. These fluctuations highlight inefficiencies in charging and discharging, leading to suboptimal battery usage.
- FLC system: SOC variability is reduced compared to the conventional system, generally ranging between 40% and 60%, see Figure 4b. However, SOC occasionally falls below 40%, which could lead to increased battery stress and a reduced lifespan.
- Deep-FLC system: After the initial increase during the first 50 time steps, the SOC is maintained with exceptional stability at around 80%, as shown in Figure 4c. This consistency indicates that Deep-FLC manages energy flow more effectively, ensuring the battery operates within its optimal charge range.
4.1.1. Clarification of the Optimisation Function
- represents the degree to which grid power is prioritised.
- dictates battery charging preferences based on the SOC, SOH, and anticipated load demand.
4.1.2. Simulation Validation and Robustness
- Benchmarking against established methods: The Deep-FLC framework was compared with both conventional rule-based and fuzzy logic control systems under identical operational conditions. This comparative approach highlights improved grid independence, cost efficiency, and battery longevity.
- Sensitivity analysis: Parameter sensitivity analysis was performed to examine how variations in SOC thresholds, load demand fluctuations, and renewable generation uncertainty affect system performance. Results indicate that Deep-FLC consistently maintains stable SOC levels and reduces battery stress.
- Error metrics for predictive accuracy: The predictive modelling component, implemented using LSTM networks, was evaluated using MAPE and RMSE. The MAPE value of 0.68 and RMSE value of 0.74 demonstrate a strong forecasting capability, supporting the proactive energy management approach.
- SOC stability: Unlike the conventional and FLC systems, which exhibit significant fluctuations in SOC levels, the Deep-FLC framework maintains SOC stability within an optimal operational range. This ensures improved battery health and extends lifespan.
- Grid dependency reduction: The Deep-FLC system demonstrates a smoother and more controlled reliance on grid power, particularly during peak demand periods, due to its predictive capability and adaptive control strategy.
- Charging and discharging cycles: The optimised fuzzy control mechanism, in conjunction with the LSTM-based predictions, allows the system to proactively schedule battery operations, thereby reducing unnecessary deep discharges and minimising energy losses.
4.2. Reduction in Grid Dependency Through Optimised Battery Use
- Conventional system: Grid power use is highly variable, with frequent spikes exceeding 3.5 kW, see Figure 4a. The heavy reliance on the grid during peak hours is evident and reflects inefficiencies in energy management and a lack of proactive storage utilisation.
- FLC system: Figure 4b demonstrates reduced peaks in grid power use compared to the conventional system, although occasional spikes still reach 3.5 kW. However, variability remains, indicating there is room for improvement in balancing grid dependency.
- Deep-FLC system: Figure 4c shows that grid power use is significantly smoother, with peaks rarely exceeding 4.0 kW. The reliance on the grid is minimised during high-demand periods, illustrating the system’s ability to maximise renewable energy utilisation and battery storage.
4.3. Minimisation of DoD to Extend Battery Lifespan
- Conventional system: DoD fluctuates significantly, with spikes often exceeding 10% per time step, for example, at steps 0, 0, 55, and 50, contributing to high battery stress.
- FLC system: DoD is reduced to below 4% per time step, but occasional larger discharges above 5% still occur, such as at steps 5, 20, and 70. Interestingly, the spikes occur at different steps compared to the conventional system.
- Deep-FLC system: DoD consistently remains below 4% per time step; throughout the monitored period and beyond 50 steps, the DoD is close to 0%. As a result, the battery street is minimised, enhancing longevity.
4.4. Superior SOH Preservation Under Deep-FLC
- Conventional system: SOH falls from 100% with systematically increasing slope to below 97% over 300 simulation steps due to frequent deep discharges and large SOC fluctuations.
- FLC system: Whilst initially moderate degradation due to occasional deep discharges, SOH retention improves, reaching approximately 99.3% after 300 steps.
- Deep-FLC system: SOH performed statistically in a similar manner to the FLC up to about 60 simulation steps; however, beyond that, SOH remained above 99.8%, reflecting minimal degradation due to stable SOC management and reduced DoD.
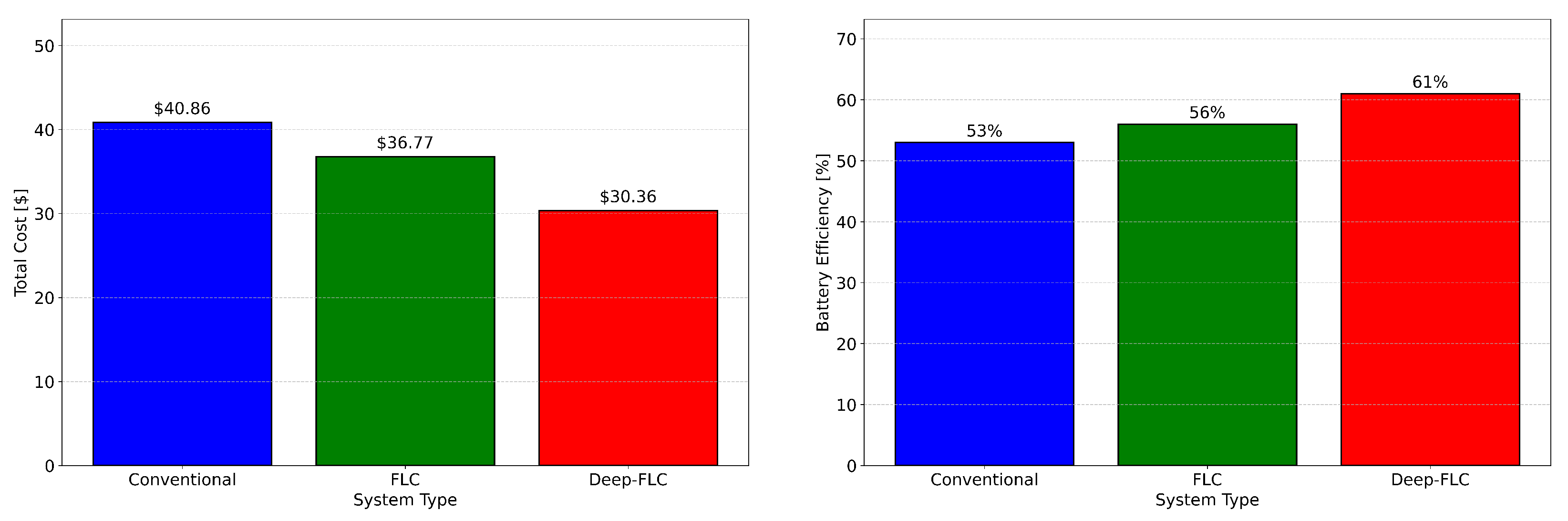
4.5. Cost and Energy Efficiency Improvements in Deep-FLC
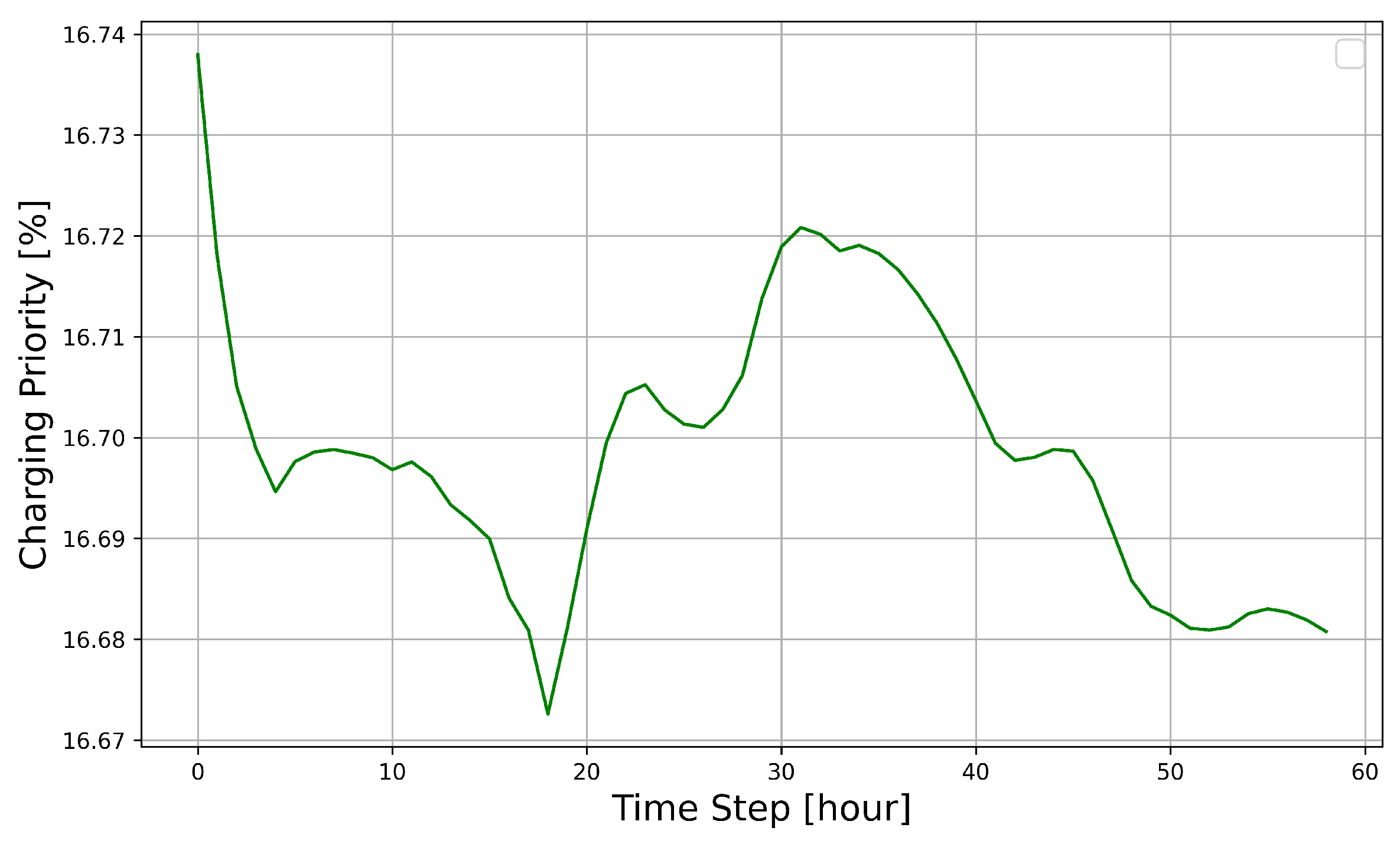
4.6. Dynamic Charging Priority Adjustments for Real-Time Optimisation
5. Discussion
5.1. Cost Reduction Achieved Through Predictive Energy Control
5.2. Enhancing SOC Stability and Maximising Battery Efficiency in EMSs
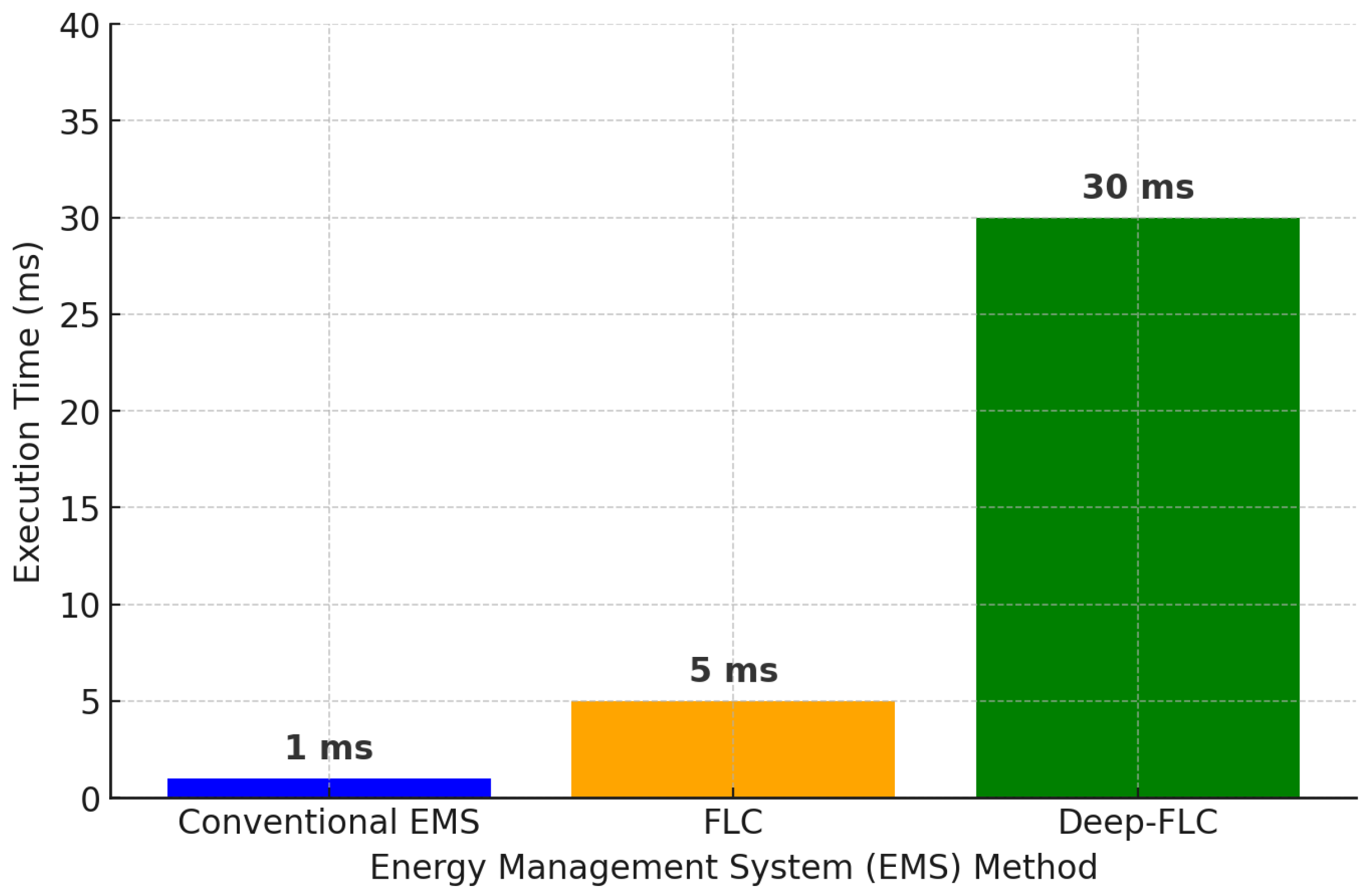
5.3. The Computational Time Comparison of EMS Methods
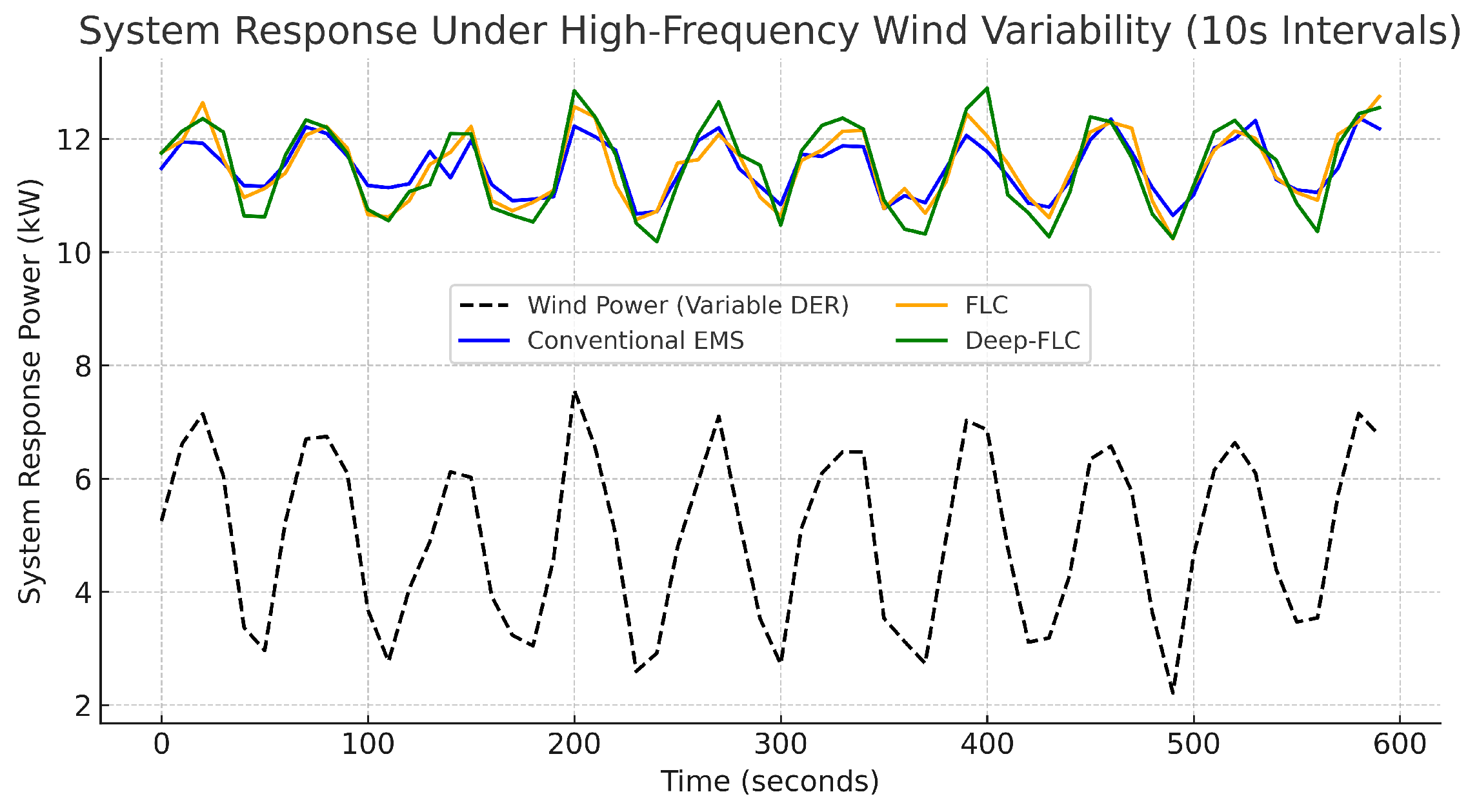
5.4. System Response Under High-Frequency Wind Variability
5.5. Optimising Battery Efficiency Through Adaptive Charging and Discharging Cycles
How Deep-FLC Achieves Higher Efficiency
- SOC stability: The Deep-FLC system leverages predictive modelling (via LSTM) to forecast energy demand and renewable energy availability. This foresight enables the system to pre-emptively adjust battery charging and discharging operations, maintaining the SOC within its optimal range (e.g., 40–90%). This approach reduces energy losses associated with overcharging and deep discharges, which are more prevalent in the conventional and FLC systems due to their reactive strategies.
- Minimised Depth of Discharge (DoD): By keeping DoD consistently below 2%, Deep-FLC reduces the cumulative stress on the battery during discharging cycles. Research shows that lower DoD values lead to higher energy utilisation efficiency and slower degradation of battery capacity [25]. In contrast, larger DoD fluctuations in the conventional and FLC systems result in greater energy losses during charge/discharge cycles.
5.6. Minimising DoD and Preserving Battery SOH Through Proactive Energy Management
5.7. Adaptive Charging Priority Adjustments Using LSTM Predictions for Enhanced Energy Flow Management
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Ocłoń, P.; Klemeš, J.J.; Michorczyk, P.; Pielichowska, K.; Pielichowski, K. Renewable energy systems for building heating, cooling and electricity production with thermal energy storage. Renew. Sustain. Energy Rev. 2022, 165, 112560. [Google Scholar] [CrossRef]
- Chowdhury, N.R.; Belikov, J.; Beck, Y.; Levron, Y.; Baimel, D. The role of storage degradation in energy management problems: An optimal control perspective. J. Energy Storage 2023, 67, 107412. [Google Scholar] [CrossRef]
- Ali, M.; Prakash, K.; Hossain, M.A.; Pota, H.R. Intelligent energy management: Evolving developments, current challenges, and research directions for sustainable future. J. Clean. Prod. 2021, 314, 127904. [Google Scholar] [CrossRef]
- Abdalla, A.N.; Nazir, M.S.; Tao, H.; Cao, S.; Ji, R.; Jiang, M.; Yao, L. Integration of energy storage system and renewable energy sources based on artificial intelligence: An overview. J. Energy Storage 2021, 40, 102811. [Google Scholar] [CrossRef]
- Cavus, M.; Allahham, A.; Adhikari, K.; Zangiabadi, M.; Giaouris, D. Energy management of grid-connected microgrids using an optimal systems approach. IEEE Access 2023, 11, 9907–9919. [Google Scholar] [CrossRef]
- Bird, L.; Milligan, M.; Lew, D. Integrating Variable Renewable Energy: Challenges and Solutions; National Renewable Energy Lab (NREL): Golden, CO, USA, 2013. [Google Scholar]
- Song, H.; Liu, C.; Amani, A.M.; Gu, M.; Jalili, M.; Meegahapola, L.; Yu, X.; Dickeson, G. Smart optimization in battery energy storage systems: An overview. Energy AI 2024, 17, 100378. [Google Scholar] [CrossRef]
- Klausmann, F.; Klingler, A.-L. Adaptive control strategy for stationary electric battery storage systems with reliable peak load limitation at maximum self-consumption of locally generated energy. Energies 2023, 16, 3964. [Google Scholar] [CrossRef]
- Suganthi, L.; Iniyan, S.; Samuel, A.A. Applications of fuzzy logic in renewable energy systems–a review. Renew. Sustain. Energy Rev. 2015, 48, 585–607. [Google Scholar] [CrossRef]
- Ibrahim, O.; Bakare, M.S.; Amosa, T.I.; Otuoze, A.O.; Owonikoko, W.O.; Ali, E.M.; Adesina, L.M.; Ogunbiyi, O. Development of fuzzy logic-based demand-side energy management system for hybrid energy sources. Energy Convers. Manag. X 2023, 18, 100354. [Google Scholar] [CrossRef]
- El Zerk, A.; Ouassaid, M. Real-time fuzzy logic-based energy management system for microgrid using hardware in the loop. Energies 2023, 16, 2244. [Google Scholar] [CrossRef]
- Emrani, A.; Achour, Y.; Sanjari, M.J.; Berrada, A. Adaptive energy management strategy for optimal integration of wind/PV system with hybrid gravity/battery energy storage using forecast models. J. Energy Storage 2024, 96, 112613. [Google Scholar] [CrossRef]
- Harrou, F.; Kadri, F.; Sun, Y. Forecasting of photovoltaic solar power production using LSTM approach. Adv. Stat. Model. Forecast. Fault Detect. Renew. Energy Syst. 2020, 3, 1–16. [Google Scholar]
- Wen, X.; Liao, J.; Niu, Q.; Shen, N.; Bao, Y. Deep learning-driven hybrid model for short-term load forecasting and smart grid information management. Sci. Rep. 2024, 14, 13720. [Google Scholar] [CrossRef]
- Pushpavalli, M.; Dhanya, D.; Kulkarni, M.; Rajitha Jasmine, R.; Umarani, B.; RamprasadReddy, M.; Garapati, D.P.; Yadav, A.S.; Rajaram, A. Enhancing electrical power demand prediction using LSTM-based deep learning models for local energy communities. Electr. Power Components Syst. 2024, 1–18. [Google Scholar] [CrossRef]
- Alzoubi, A. Machine learning for intelligent energy consumption in smart homes. Int. J. Comput. Inf. Manuf. 2022, 2, 62–75. [Google Scholar] [CrossRef]
- Cavus, M.; Allahham, A. Enhanced microgrid control through genetic predictive control: Integrating genetic algorithms with model predictive control for improved non-linearity and non-convexity handling. Energies 2024, 17, 4458. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Mamun, A.A.; Ansari, S.; Miah, M.S.; Hasan, K.; Meraj, S.T.; Abdolrasol, M.G.M.; Rahman, T.; Maruf, M.H.; Sarker, M.R. Battery management, key technologies, methods, issues, and future trends of electric vehicles: A pathway toward achieving sustainable development goals. Batteries 2022, 8, 119. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Z.; Hou, X.; Cheng, Y.; Guo, T.; Xiao, H.; Ren, J.; Mansor, M.R.A. Fuzzy logic optimized threshold-based energy management strategy for fuel cell hybrid E-bike. Int. J. Hydrog. Energy 2024, 63, 123–132. [Google Scholar] [CrossRef]
- DeSando, M. Universal Programmable Battery Charger with Optional Battery Management System. Master’s Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2015. Available online: https://digitalcommons.calpoly.edu/theses/1409/ (accessed on 13 January 2025).
- Fan, C.; Lu, M.; Sun, Y.; Liang, D. A novel linear programming-based predictive control method for building battery operations with reduced cost and enhanced computational efficiency. Renew. Energy 2024, 237, 121847. [Google Scholar] [CrossRef]
- Cavus, M.; Allahham, A.; Adhikari, K.; Giaouris, D. A hybrid method based on logic predictive controller for flexible hybrid microgrid with plug-and-play capabilities. Appl. Energy 2024, 359, 122752. [Google Scholar] [CrossRef]
- Impram, S.; Nese, S.V.; Oral, B. Challenges of renewable energy penetration on power system flexibility: A survey. Energy Strategy Rev. 2020, 31, 100539. [Google Scholar] [CrossRef]
- Brandi, S.; Gallo, A.; Capozzoli, A. A predictive and adaptive control strategy to optimize the management of integrated energy systems in buildings. Energy Rep. 2022, 8, 1550–1567. [Google Scholar] [CrossRef]
- Shamarova, N.; Suslov, K.; Ilyushin, P.; Shushpanov, I. Review of battery energy storage systems modeling in microgrids with renewables considering battery degradation. Energies 2022, 15, 6967. [Google Scholar] [CrossRef]
- Singh, B.; Mishra, A.K. Fuzzy logic control system and its applications. Int. Res. J. Eng. Technol. 2015, 2, 742–746. [Google Scholar]
- Arcos-Aviles, D.; Pascual, J.; Marroyo, L.; Sanchis, P.; Guinjoan, F. Fuzzy logic-based energy management system design for residential grid-connected microgrids. IEEE Trans. Smart Grid 2016, 9, 530–543. [Google Scholar] [CrossRef]
- Assem, H.; Azib, T.; Bouchafaa, F.; Laarouci, C.; Belhaouas, N.; Hadj Arab, A. Adaptive Fuzzy Logic-Based Control and Management of Photovoltaic Systems with Battery Storage. Int. Trans. Electr. Energy Syst. 2023, 2023, 9065061. [Google Scholar] [CrossRef]
- Whig, P.; Bhatia, B.; Bhatia, A.B.; Sharma, P. Renewable energy optimization system using fuzzy logic. In Machine Learning and Metaheuristics: Methods and Analysis; Springer: Singapore, 2023; pp. 177–198. [Google Scholar]
- Liu, W.; Xu, Y.; Feng, X.; Wang, Y. Optimal fuzzy logic control of energy storage systems for V/f support in distribution networks considering battery degradation. Int. J. Electr. Power Energy Syst. 2022, 139, 107867. [Google Scholar] [CrossRef]
- Shirinda, K.; Kusakana, K.; Ostraszewski, M. Combinatorial optimization of a fuzzy logic-controlled grid connected photovoltaic with hybrid energy storage systems using time of use tariff. J. Energy Storage 2024, 99, 113251. [Google Scholar] [CrossRef]
- Hochreiter, S. Long Short-term memory. In Neural Computation; MIT-Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for solar power forecasting—An approach using AutoEncoder and LSTM Neural Networks. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 2858–2865. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28, 1–9. [Google Scholar]
- Cavus, M.; Ugurluoglu, Y.F.; Ayan, H.; Allahham, A.; Adhikari, K.; Giaouris, D. Switched Auto-Regressive Neural Control (S-ANC) for Energy Management of Hybrid Microgrids. Appl. Sci. 2023, 13, 11744. [Google Scholar] [CrossRef]
- Pang, Z.; Niu, F.; O’Neill, Z. Solar radiation prediction using recurrent neural network and artificial neural network: A case study with comparisons. Renew. Energy 2020, 156, 279–289. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, C.; Zhang, Z.; Li, X. Electric load forecasting in smart grids using long-short-term-memory based recurrent neural network. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017; pp. 1–6. [Google Scholar]
- Alabi, T.M.; Aghimien, E.I.; Agbajor, F.D.; Yang, Z.; Lu, L.; Adeoye, A.R.; Gopaluni, B. A review on the integrated optimization techniques and machine learning approaches for modeling, prediction, and decision making on integrated energy systems. Renew. Energy 2022, 194, 822–849. [Google Scholar] [CrossRef]
- Arrar, S.; Xioaning, L. Energy management in hybrid microgrid using artificial neural network, PID, and fuzzy logic controllers. Eur. J. Electr. Eng. Comput. Sci. 2022, 6, 38–47. [Google Scholar] [CrossRef]
- Aslam, S.; Herodotou, H.; Mohsin, S.M.; Javaid, N.; Ashraf, N.; Aslam, S. A survey on deep learning methods for power load and renewable energy forecasting in smart microgrids. Renew. Sustain. Energy Rev. 2021, 144, 110992. [Google Scholar] [CrossRef]
- Han, D.; Kwon, S.; Kim, J.; Yoo, K.; Lee, S.-E. Integration of long-short term memory network and fuzzy logic for high-safety in a FR-ESS with degradation and failure. Sustain. Energy Technol. Assess. 2022, 49, 101790. [Google Scholar] [CrossRef]
- Li, D.; Xu, P.; Gu, J.; Zhu, Y. A Review of Reliability Research in Regional Integrated Energy System: Indicator, Modeling, and Assessment Methods. Buildings 2024, 14, 3428. [Google Scholar] [CrossRef]
- Amine, H.M.; Aissa, B.; Rezk, H.; Messaoud, H.; Othmane, A.; Saad, M.; Abdelkareem, M.A. Enhancing hybrid energy storage systems with advanced low-pass filtration and frequency decoupling for optimal power allocation and reliability of cluster of DC-microgrids. Energy 2023, 282, 128310. [Google Scholar] [CrossRef]




| Parameter | Symbol/Variable | Value | Description |
|---|---|---|---|
| Battery Capacity | (mAh) | 4500 | Total capacity of the battery system in milliamp-hours (mAh). |
| (kWh) | 16.2 | Converted capacity of the battery system in kilowatt-hours (kWh). | |
| Initial SOC | SOCinit | 50% | Percentage of battery charge at the start of the simulation. |
| Initial Battery Temperature | (°C) | 25 | Battery temperature at the start of the simulation. |
| SOH | SOHinit (%) | 100 | Initial SOH of the battery. |
| Critical Battery Temperature | (°C) | 60 | Maximum allowable temperature for battery operation. |
| Charging Efficiency | 0.95 | Efficiency of battery charging processes. | |
| Discharging Efficiency | 0.90 | Efficiency of battery discharging processes. | |
| Electricity Cost | ($/kWh) | 0.20 | Cost of electricity per kilowatt-hour during off-peak hours. |
| Peak Hour Multiplier | 2 | Cost multiplier for electricity during peak hours (5–9 p.m.). | |
| Ambient Temperature | (°C) | 25 | Default ambient temperature used in thermal analysis. |
| DoD Degradation Factor | 0.0015 | Degradation rate of battery due to DoD. | |
| Temperature Degradation Factor | 0.001 | Degradation rate of battery due to high temperatures exceeding ambient. |
| Metric | Conventional System | FLC System | Deep-FLC System |
|---|---|---|---|
| Total Cost ($) | $40.86 | $36.77 | $30.36 |
| Battery Efficiency (%) | 53% | 56% | 61% |
| Average DoD | 14.1% | 12.3% | 11.4% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cavus, M.; Dissanayake, D.; Bell, M. Deep-Fuzzy Logic Control for Optimal Energy Management: A Predictive and Adaptive Framework for Grid-Connected Microgrids. Energies 2025, 18, 995. https://doi.org/10.3390/en18040995
Cavus M, Dissanayake D, Bell M. Deep-Fuzzy Logic Control for Optimal Energy Management: A Predictive and Adaptive Framework for Grid-Connected Microgrids. Energies. 2025; 18(4):995. https://doi.org/10.3390/en18040995
Chicago/Turabian StyleCavus, Muhammed, Dilum Dissanayake, and Margaret Bell. 2025. "Deep-Fuzzy Logic Control for Optimal Energy Management: A Predictive and Adaptive Framework for Grid-Connected Microgrids" Energies 18, no. 4: 995. https://doi.org/10.3390/en18040995
APA StyleCavus, M., Dissanayake, D., & Bell, M. (2025). Deep-Fuzzy Logic Control for Optimal Energy Management: A Predictive and Adaptive Framework for Grid-Connected Microgrids. Energies, 18(4), 995. https://doi.org/10.3390/en18040995









