Two-Stage Dual-Level Dispatch Optimization Model for Multiple Virtual Power Plants with Electric Vehicles and Demand Response Based on a Stackelberg Game
Abstract
1. Introduction
- (1)
- A two-layer, two-stage multi-objective optimization scheduling model based on Stackelberg game theory has been proposed.
- (2)
- Based on the UI of each EV, the corresponding charging mode is selected, and the optimization is carried out with comprehensive satisfaction, better meeting EV users’ needs and increasing their enthusiasm for participating in VPP scheduling.
- (3)
- Based on the day-ahead stage, a Stackelberg game equilibrium algorithm based on a Kriging metamodel is proposed; this algorithm not only achieves the purpose of protecting the privacy of the VPP but also meets the different needs of multiple stakeholders.
2. VPP Multi-Time-Scale Optimization Scheduling Framework
3. The Day-Ahead Optimization Model for Virtual Power Plants
3.1. EV Layer
3.1.1. Charging Mode Selection
3.1.2. Objective Function
- (1)
- The cost satisfaction of the i-th EV
- (2)
- The travel satisfaction of the i-th EV
3.1.3. Constraints
- (1)
- The constraints for the fast-charging mode are as follows:
- (2)
- The constraints for the slow-charging mode are as follows:
3.2. VPP Layer
3.2.1. Objective Function
- (1)
- Minimum VPP Operating Cost
- (2)
- Minimization of Interactive Power
3.2.2. Constraints
- (1)
- Gas Turbine Constraints
- (2)
- Energy Storage Constraints
- (3)
- Demand Response Constraints
- (4)
- Interactive Power Constraints
- (5)
- Power Balance Constraints
4. Intraday Optimization Model for Virtual Power Plants
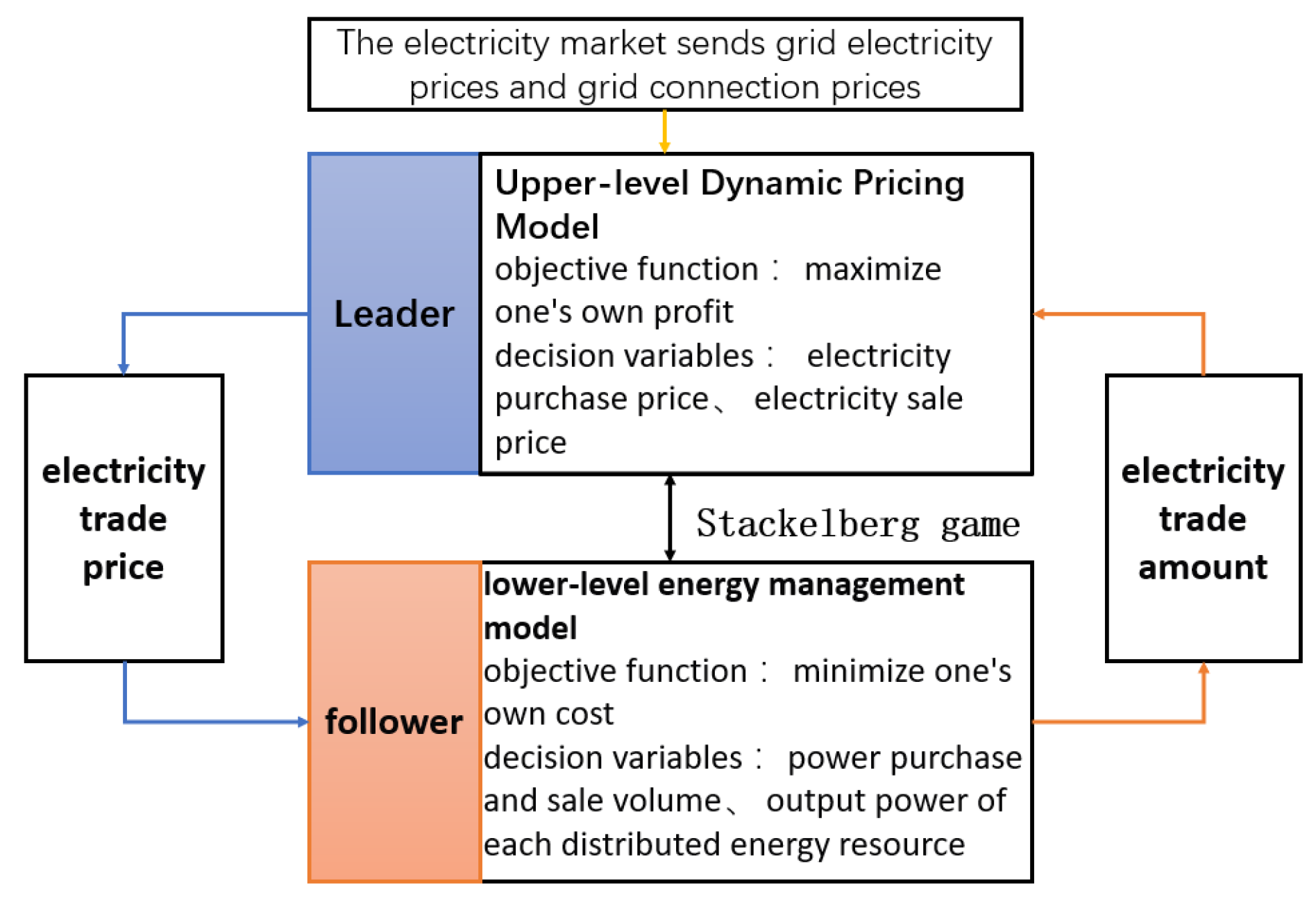
4.1. Leader (DNO) Dynamic Pricing Utility Model
Charging Mode Selection
4.2. The Utility Model for Energy Scheduling of the Follower VPPs
4.2.1. VPP Utility Function
4.2.2. Constraints
4.3. Stackelberg Game Model
5. Case Study Discussion
5.1. Model Parameters
5.2. Results and Analysis
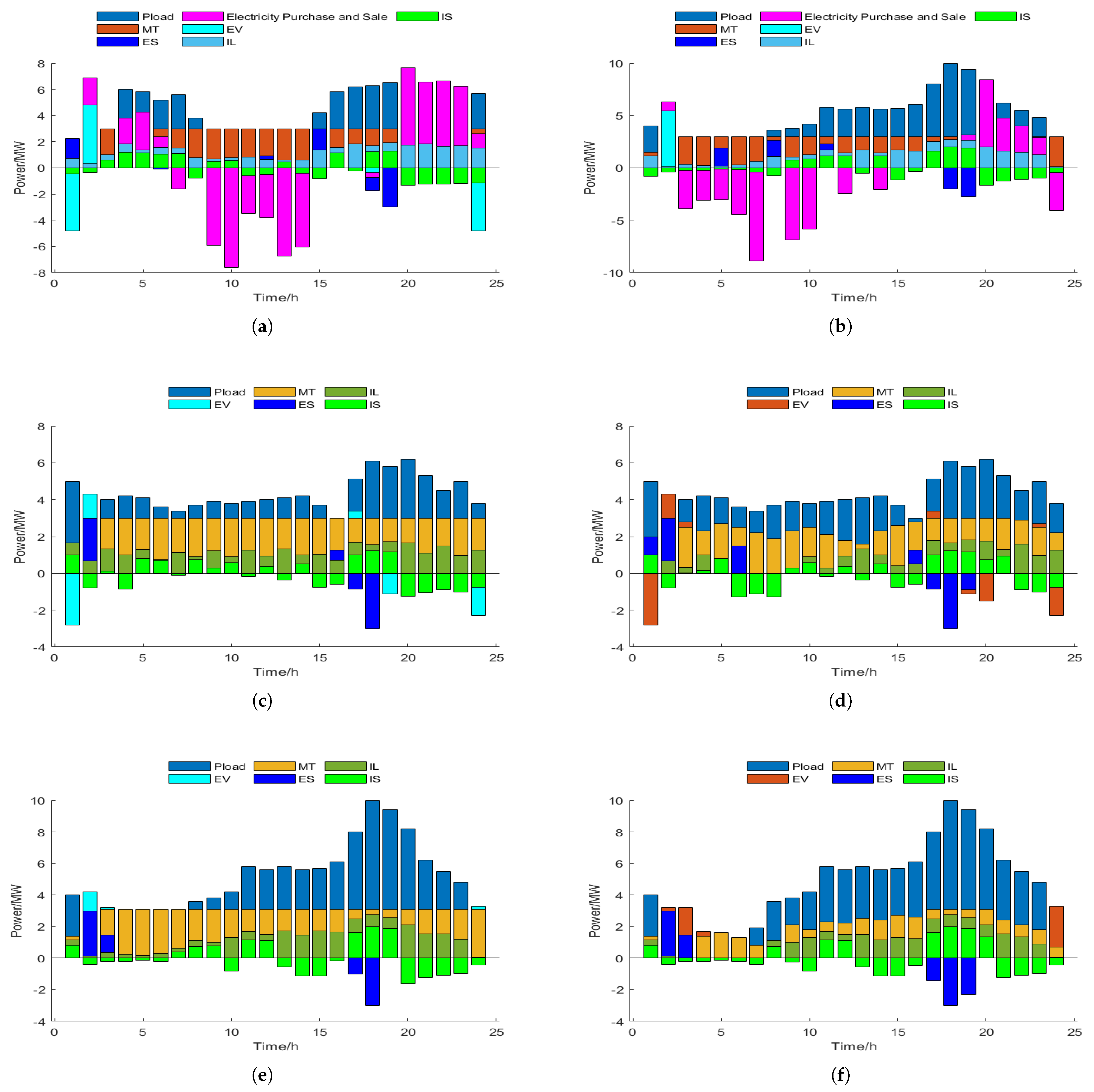
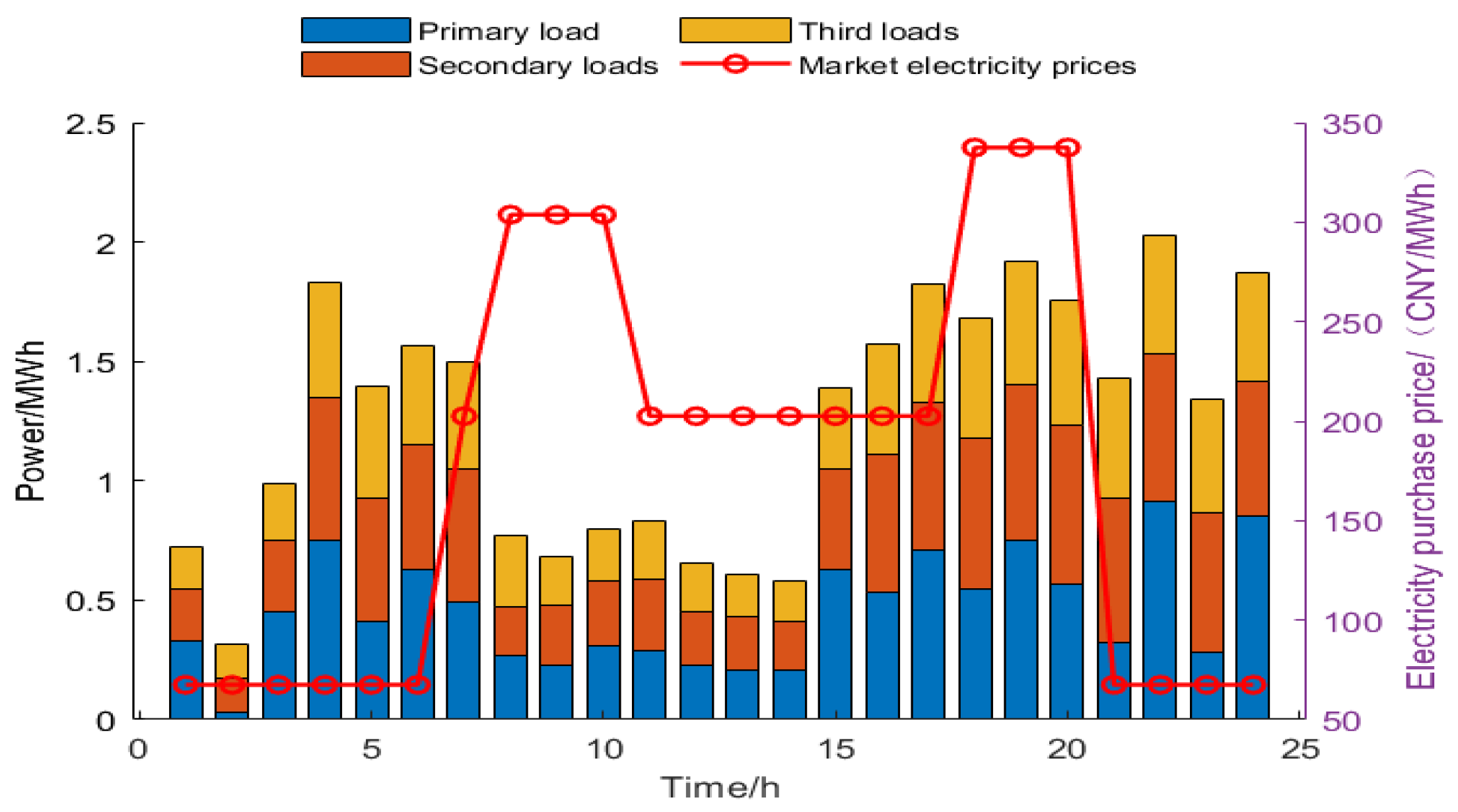
5.2.1. Day-Ahead Optimization Results of the Electric Vehicle Layer
5.2.2. Day-Ahead VPP Layer Optimization Results
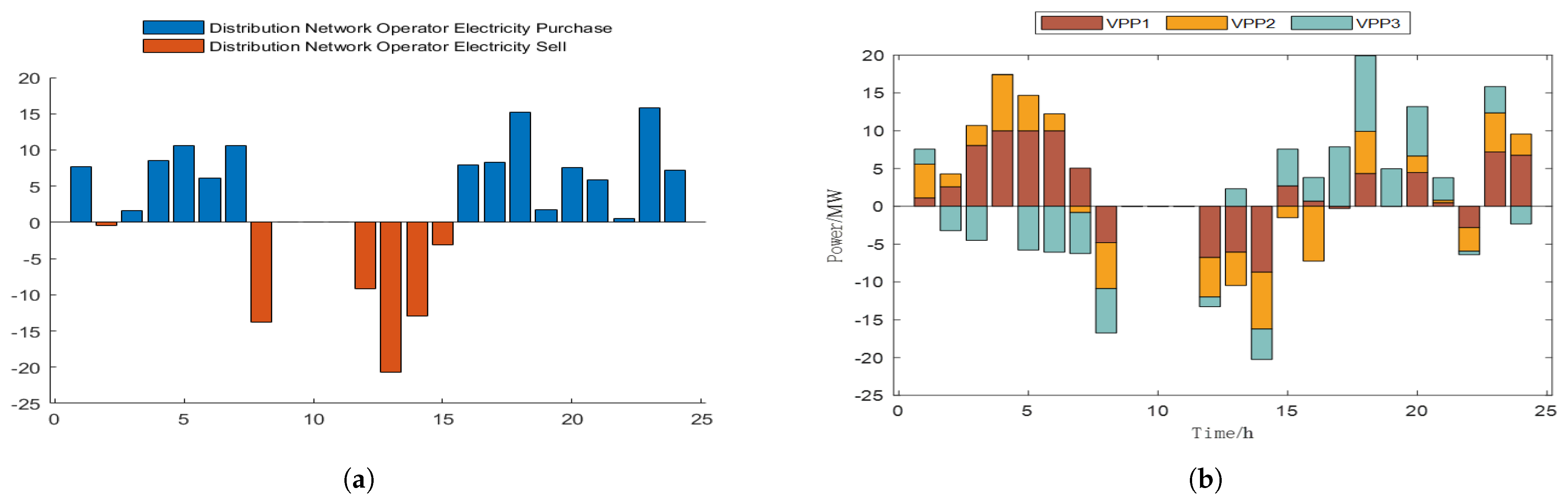
5.2.3. Intraday Optimization Scheduling Results
6. Conclusions
- (1)
- The proposed comprehensive satisfaction model makes the charging and discharging of EVs more rational, effectively reducing the peak-to-valley difference of the load curve.
- (2)
- In the day-ahead scheduling stage, both the economic aspect of the VPPs and the demand for interactive power are considered, which can reduce the interaction with the distribution network and further reduce the operating cost of the VPPs while ensuring economical and low-carbon operation.
- (3)
- In the established Stackelberg game model, the DNO maximizes its own interests by optimizing the purchase and sale electricity prices to promote electricity sharing between VPPs. Each VPP aims to minimize operating costs, and the optimized transaction electricity will affect the operator’s electricity price setting. The operator can guide the VPP to reasonably purchase and sell electricity through dynamic pricing, and there is a game of interests between the two.
- (4)
- The two-stage, two-layer optimization scheduling model proposed in this paper optimizes multi-objective day-ahead scheduling to determine the output of each distributed energy resource. In the intraday scheduling stage, taking the day-ahead scheduling results as a reference, the model further optimizes the electricity prices and the output of distributed energy resources, thereby effectively achieving a win–win situation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| weight coefficients for , | |
| a, b | cost coefficients |
| maximum and minimum expense that EV owners can afford | |
| battery replacement cost | |
| distance traveled by the EV during time period t | |
| battery capacity of the EV | |
| energy demand of the EV | |
| maximum charging and discharging capacity of the EV | |
| G | maximum amount of electricity that the VPP can buy or sell in the DNO |
| , | power output of the w-th wind turbine and v-th photovoltaic unit |
| output of the s-th gas turbine during time period t | |
| charging amount of the energy storage system during time period t | |
| discharging amount of the energy storage system during time period t | |
| maximum and minimum power outputs of the s-th gas turbine | |
| maximum charging and discharging rates of the energy storage system |
| fixed cost of the s-th gas turbine | |
| amount of interrupted load at level m during time period t | |
| upper limit of the load interruption amount for the m-th level | |
| amount of load interrupted for the m-th level during time period t | |
| maximum amount of load that can be interrupted | |
| amount of shifted load after transfer during time period t | |
| amount of load that can be shifted during time period t | |
| upper limit of the shifted load during time period t | |
| , | total load and fixed load during time period t |
| numbers of EVs, GTs, interruption levels, wind turbines, and PV units | |
| , | slow-charging and fast-charging power of the EV |
| slow-discharging power of the EV | |
| maximum and minimum power of the EV for travel satisfaction | |
| maximum fast-charging power of the i-th EV at time t | |
| , | maximum charging and discharging rates of the i-th EV |
| , | amounts of electricity set by the VPP one day ahead for purchase and sale |
| average transaction power during the dispatch cycle | |
| , | volumes of electricity purchased and sold by the DNO from/to the grid |
| , | volumes of electricity purchased and sold by the VPP from/to the DNO |
| , | upward and downward ramp rates of the s-th gas turbine |
| , | lower and upper bounds of the SOC at which the EV stops charging |
| state of the SOC of the i-th EV when it connects to the VPP | |
| , | amounts of energy stored by the i-th EV in fast- and slow-charging modes |
| energy stored at time t | |
| maximum and minimum values of energy storage | |
| , | arrival time and departure time of the EV |
| , | binary variables indicating whether the EV is charging or discharging |
| whether the i-th EV is connected to the grid during time period t | |
| , , | GT is operating, starting, or stopping during time period t |
| charging and discharging states of the energy storage at time t | |
| state of the VPP—buying or selling electricity | |
| slow- and fast-charging efficiency of the EV | |
| slow-discharging efficiency of the EV | |
| electricity purchase and sale prices set by the DNO in the day-ahead stage | |
| , | grid-connected electricity price and grid electricity price |
| , | start-up and shut-down costs of the gas turbine |
| compensation price for the m-th level of interrupted load | |
| , | electricity purchase and sale prices set for the VPP by the DNO |
Appendix A
| Subject | VPP1 | VPP2 | VPP3 |
|---|---|---|---|
| Maximum/Minimum Output Power | 3/1.3 | 3/1.5 | 3.1/1.2 |
| Upward/Downward Ramp Rate Power | 1.5/1.5 | 1.5/1.5 | 1.4/1.4 |
| Start/Stop Cost | 10 | 10 | 10 |
| Fixed Cost | 100 | 150 | 150 |

| Subject | VPP1 | VPP2 | VPP3 |
|---|---|---|---|
| Battery Replacement Cost | 19,380 | 8160 | 11,900 |
| Maximum Charging/Discharging Capacity | 1,000,000 | 900,000 | 700,000 |
| Initial/Final Stored Energy | 8.42/10.75 | 4.68/5.68 | 5.58/25.22 |
| Travel Period | 9/15 | 8/17 | 7/9 |
| Driving Distance | 22 | 11 | 20 |
References
- Mnatsakanyan, A.; Kennedy, S.W. A novel demand response model with an application for a virtual power plant. IEEE Trans. Smart Grid 2014, 6, 230–237. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, G.; Huang, W.; Xu, Z.; Wei, Z.; Zhang, H.; Chu, Y. Strategic bidding model for virtual power plant in different electricity markets considering electric vehicles and demand response. Power Syst. Technol. 2017, 41, 1759–1767. [Google Scholar]
- Cao, W.; Yu, J.; Xu, M. Optimization Scheduling of Virtual Power Plants Considering Source-Load Coordinated Operation and Wind–Solar Uncertainty. Processes 2023, 12, 11. [Google Scholar] [CrossRef]
- Javad Kasaei, M.; Gandomkar, M.; Nikoukar, J. Optimal operational scheduling of renewable energy sources using teaching–learning based optimization algorithm by virtual power plant. J. Energy Resour. Technol. 2017, 139, 062003. [Google Scholar] [CrossRef]
- Liu, J.; Zhuge, C.; Tang, J.H.C.G.; Meng, M.; Zhang, J. A spatial agent-based joint model of electric vehicle and vehicle-to-grid adoption: A case of Beijing. Appl. Energy 2022, 310, 118581. [Google Scholar] [CrossRef]
- Das, R.; Wang, Y.; Busawon, K.; Putrus, G.; Neaimeh, M. Real-time multi-objective optimisation for electric vehicle charging management. J. Clean. Prod. 2021, 292, 126066. [Google Scholar] [CrossRef]
- Yao, E.; Liu, T.; Lu, T.; Yang, Y. Optimization of electric vehicle scheduling with multiple vehicle types in public transport. Sustain. Cities Soc. 2020, 52, 101862. [Google Scholar] [CrossRef]
- Tu, R.; Gai, Y.J.; Farooq, B.; Posen, D.; Hatzopoulou, M. Electric vehicle charging optimization to minimize marginal greenhouse gas emissions from power generation. Appl. Energy 2020, 277, 115517. [Google Scholar] [CrossRef]
- Sun, B. A multi-objective optimization model for fast electric vehicle charging stations with wind, PV power and energy storage. J. Clean. Prod. 2021, 288, 125564. [Google Scholar] [CrossRef]
- Rezaei, N.; Khazali, A.; Mazidi, M.; Ahmadi, A. Economic energy and reserve management of renewable-based microgrids in the presence of electric vehicle aggregators: A robust optimization approach. Energy 2020, 201, 117629. [Google Scholar] [CrossRef]
- Hu, J.; Zhou, H.; Li, Y. Real-time dispatching strategy for aggregated electric vehicles to smooth power fluctuation of photovoltaics. Power Syst. Technol. 2019, 43, 2552–2560. [Google Scholar]
- Correia, A.F.; Moura, P.; de Almeida, A.T. Technical and economic assessment of battery storage and vehicle-to-grid systems in building microgrids. Energies 2022, 15, 8905. [Google Scholar] [CrossRef]
- Chen, H.; Gao, L.; Zhang, Z. Multi-objective optimal scheduling of a microgrid with uncertainties of renewable power generation considering user satisfaction. Int. J. Electr. Power Energy Syst. 2021, 131, 107142. [Google Scholar] [CrossRef]
- Wang, X.; Sun, C.; Wang, R.; Wei, T. Two-stage optimal scheduling strategy for large-scale electric vehicles. IEEE Access 2020, 8, 13821–13832. [Google Scholar] [CrossRef]
- Tang, W.; Gao, F. Optimal operation of household microgrid day-ahead energy considering user satisfaction. High Volt. Eng. 2017, 43, 140–148. [Google Scholar]
- Li, T.; Jin, S.; Li, G.; Zhou, B.; Wang, Y.; Hu, S. Double-Layer Optimal Scheduling Strategy for Charging and Discharging of Electric Vehicles Considering Cluster Schedulability. In Proceedings of the 2022 First International Conference on Cyber-Energy Systems and Intelligent Energy (ICCSIE), Shenyang, China, 14–15 January 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–6. [Google Scholar]
- Liu, C.; Zhang, H.; Shahidehpour, M.; Zhou, Q.; Ding, T. A two-layer model for microgrid real-time scheduling using approximate future cost function. IEEE Trans. Power Syst. 2021, 37, 1264–1273. [Google Scholar] [CrossRef]
- Pandey, A.K.; Jadoun, V.K.; Sabhahit, J.N. Real-time peak valley pricing based multi-objective optimal scheduling of a virtual power plant considering renewable resources. Energies 2022, 15, 5970. [Google Scholar] [CrossRef]
- Wang, Y.; Ai, X.; Tan, Z.; Yan, L.; Liu, S. Interactive dispatch modes and bidding strategy of multiple virtual power plants based on demand response and game theory. IEEE Trans. Smart Grid 2015, 7, 510–519. [Google Scholar] [CrossRef]
- Yin, S.; Ai, Q.; Li, Z.; Zhang, Y.; Lu, T. Energy management for aggregate prosumers in a virtual power plant: A robust Stackelberg game approach. Int. J. Electr. Power Energy Syst. 2020, 117, 105605. [Google Scholar] [CrossRef]
- Erol, Ö.; Filik, Ü.B. A Stackelberg game approach for energy sharing management of a microgrid providing flexibility to entities. Appl. Energy 2022, 316, 118944. [Google Scholar] [CrossRef]
- Fu, B.; Chen, M.; Fei, Z.; Wu, J.; Xu, X.; Gao, Z.; Wu, Z.; Yang, Y. Research on the stackelberg game method of building micro-grid with electric vehicles. J. Electr. Eng. Technol. 2021, 16, 1637–1649. [Google Scholar] [CrossRef]
- Cao, J.; Yang, D.; Dehghanian, P. Co-optimization of multiple virtual power plants considering electricity-heat-carbon trading: A Stackelberg game strategy. Int. J. Electr. Power Energy Syst. 2023, 153, 109294. [Google Scholar] [CrossRef]
- Lin, H.; Dang, J.; Zheng, H.; Yao, L.; Yan, Q.; Yang, S.; Guo, H.; Anvari-Moghaddam, A. Two-stage electric vehicle charging optimization model considering dynamic virtual price-based demand response and a hierarchical non-cooperative game. Sustain. Cities Soc. 2023, 97, 104715. [Google Scholar] [CrossRef]
- Azarhooshang, A.; Sedighizadeh, D.; Sedighizadeh, M. Two-stage stochastic operation considering day-ahead and real-time scheduling of microgrids with high renewable energy sources and electric vehicles based on multi-layer energy management system. Electr. Power Syst. Res. 2021, 201, 107527. [Google Scholar] [CrossRef]
- Wang, Z.; Jochem, P.; Fichtner, W. A scenario-based stochastic optimization model for charging scheduling of electric vehicles under uncertainties of vehicle availability and charging demand. J. Clean. Prod. 2020, 254, 119886. [Google Scholar] [CrossRef]
- Yin, W.; Ming, Z.; Wen, T. Scheduling strategy of electric vehicle charging considering different requirements of grid and users. Energy 2021, 232, 121118. [Google Scholar] [CrossRef]
- Liu, L.; Zhou, K. Electric vehicle charging scheduling considering urgent demand under different charging modes. Energy 2022, 249, 123714. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, F.; Liu, H.; Ding, J.; Gao, C. Interruptible load scheduling model based on an improved chicken swarm optimization algorithm. CSEE J. Power Energy Syst. 2020, 7, 232–240. [Google Scholar]
- Yang, H.; Zhang, S.; Zeng, J.; Tang, S.; Xiong, S. Future of sustainable renewable-based energy systems in smart city industry: Interruptible load scheduling perspective. Sol. Energy 2023, 263, 111866. [Google Scholar] [CrossRef]
- Yang, M.; Sun, L.; Wang, J. Multi-objective optimization scheduling considering the operation performance of islanded microgrid. IEEE Access 2020, 8, 83405–83413. [Google Scholar] [CrossRef]
- Khalili, T.; Nojavan, S.; Zare, K. Optimal performance of microgrid in the presence of demand response exchange: A stochastic multi-objective model. Comput. Electr. Eng. 2019, 74, 429–450. [Google Scholar] [CrossRef]
- Jani, A.; Karimi, H.; Jadid, S. Multi-time scale energy management of multi-microgrid systems considering energy storage systems: A multi-objective two-stage optimization framework. J. Energy Storage 2022, 51, 104554. [Google Scholar] [CrossRef]
- Dong, X.; Li, X.; Cheng, S. Energy management optimization of microgrid cluster based on multi-agent-system and hierarchical Stackelberg game theory. IEEE Access 2020, 8, 206183–206197. [Google Scholar] [CrossRef]
- Li, B.; Zhao, R.; Lu, J.; Xin, K.; Huang, J.; Lin, G.; Chen, J.; Pang, X. Energy management method for microgrids based on improved Stackelberg game real-time pricing model. Energy Rep. 2023, 9, 1247–1257. [Google Scholar] [CrossRef]
- Liang, N.; He, X.; Tan, J.; Pan, Z.; Zheng, F. Stackelberg game-based optimal scheduling for multi-community integrated energy systems considering energy interaction and carbon trading. Int. J. Electr. Power Energy Syst. 2023, 153, 109360. [Google Scholar] [CrossRef]
- Tang, J.; Wang, D.; Jia, H.; Zhang, Y.; Xiong, J. Optimal economic operation of active distribution networks based on hybrid algorithm of surrogate model and particle swarm optimization. Autom. Electr. Power Syst. 2018, 42, 95–103. [Google Scholar]









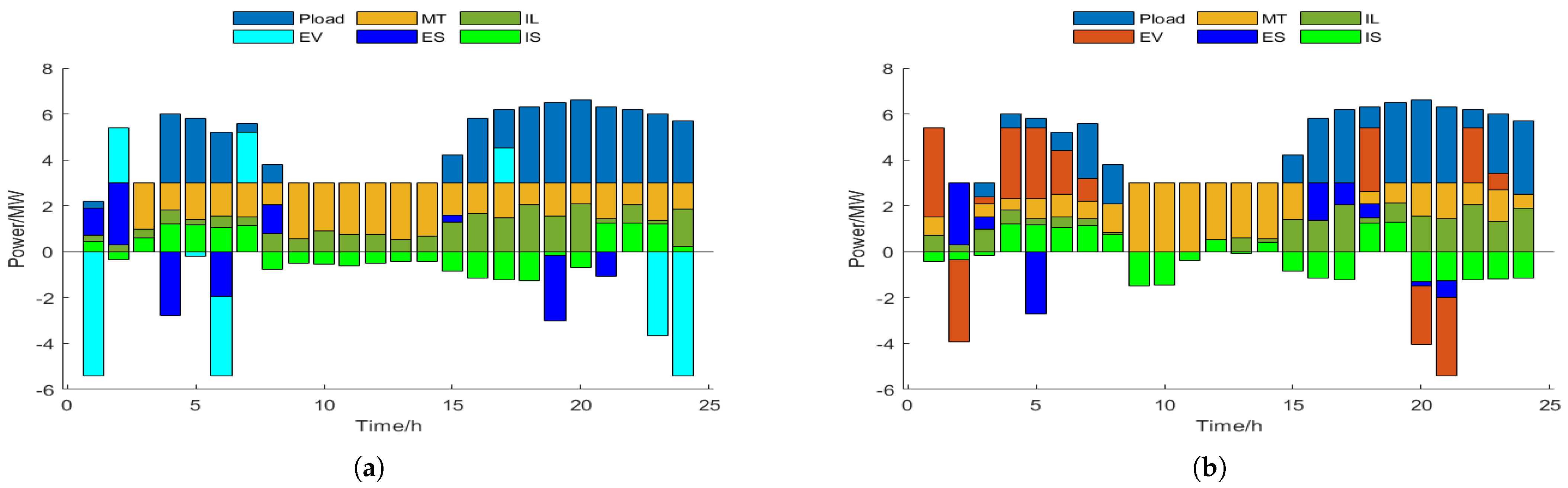
| Strategy | EV1 | EV2 | EV3 |
|---|---|---|---|
| Total Cost/CNY 10,000 | 496.8 | 204.6 | 256.6 |
| Load Peak-to-Valley Difference/MW | 6.3 | 5.6 | 4.6 |
| Comprehensive Satisfaction | 0.325 | 0.477 | 0.658 |
| Subject | Framework 1 | Framework 2 |
|---|---|---|
| VPP1 | 37.005 | 32.056 |
| VPP2 | 43.347 | 42.611 |
| VPP3 | 41.911 | 40.155 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Li, X. Two-Stage Dual-Level Dispatch Optimization Model for Multiple Virtual Power Plants with Electric Vehicles and Demand Response Based on a Stackelberg Game. Energies 2025, 18, 896. https://doi.org/10.3390/en18040896
Tang J, Li X. Two-Stage Dual-Level Dispatch Optimization Model for Multiple Virtual Power Plants with Electric Vehicles and Demand Response Based on a Stackelberg Game. Energies. 2025; 18(4):896. https://doi.org/10.3390/en18040896
Chicago/Turabian StyleTang, Jincheng, and Xiaolan Li. 2025. "Two-Stage Dual-Level Dispatch Optimization Model for Multiple Virtual Power Plants with Electric Vehicles and Demand Response Based on a Stackelberg Game" Energies 18, no. 4: 896. https://doi.org/10.3390/en18040896
APA StyleTang, J., & Li, X. (2025). Two-Stage Dual-Level Dispatch Optimization Model for Multiple Virtual Power Plants with Electric Vehicles and Demand Response Based on a Stackelberg Game. Energies, 18(4), 896. https://doi.org/10.3390/en18040896





