Software Package for Optimization of Burner Devices on Dispersed Working Fluids
Abstract
1. Introduction
- -
- The first goal is to show how CFD modeling can be extremely useful in experimental testing. It allows for a detailed understanding of the relationship between key burner performance characteristics and, therefore, the selection of optimal combustion process parameters.
- -
- The second goal is to show the possibility of developing and using an automated information system that automatically launches and collects the necessary data during mathematical modeling based on CFD.
- -
- The third goal is to present and share the results of an optimization method based on ANNs as a universal approximator of a complex nonlinear function able improve the parameters of existing power equipment and bring it to modern environmental requirements.
2. Description of Models
2.1. Modeling of Fuel–Air Mixture Combustion
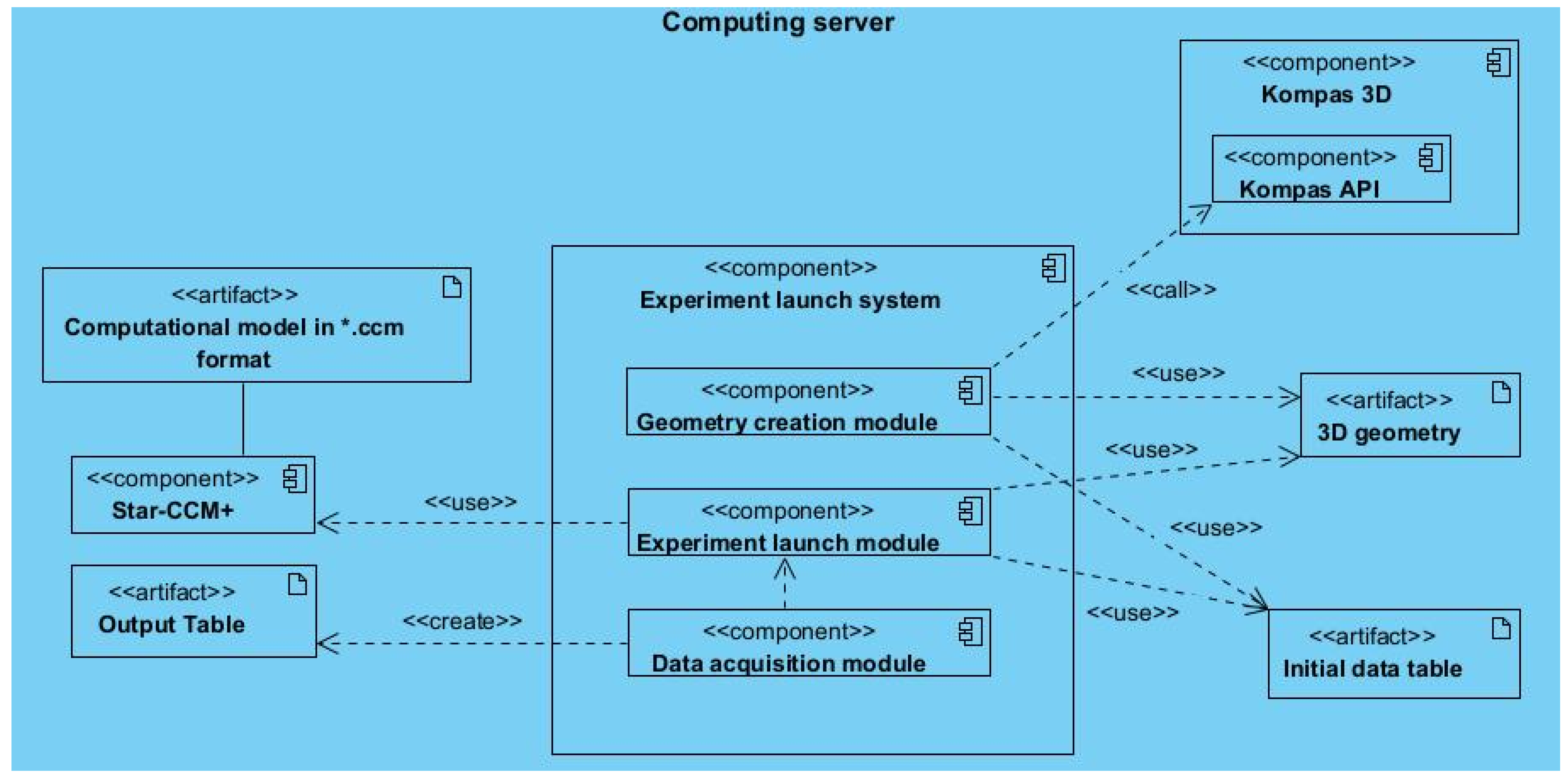
2.2. Automation System for Numerical Simulation of the Burner Operation
3. Application of Machine Learning Methods
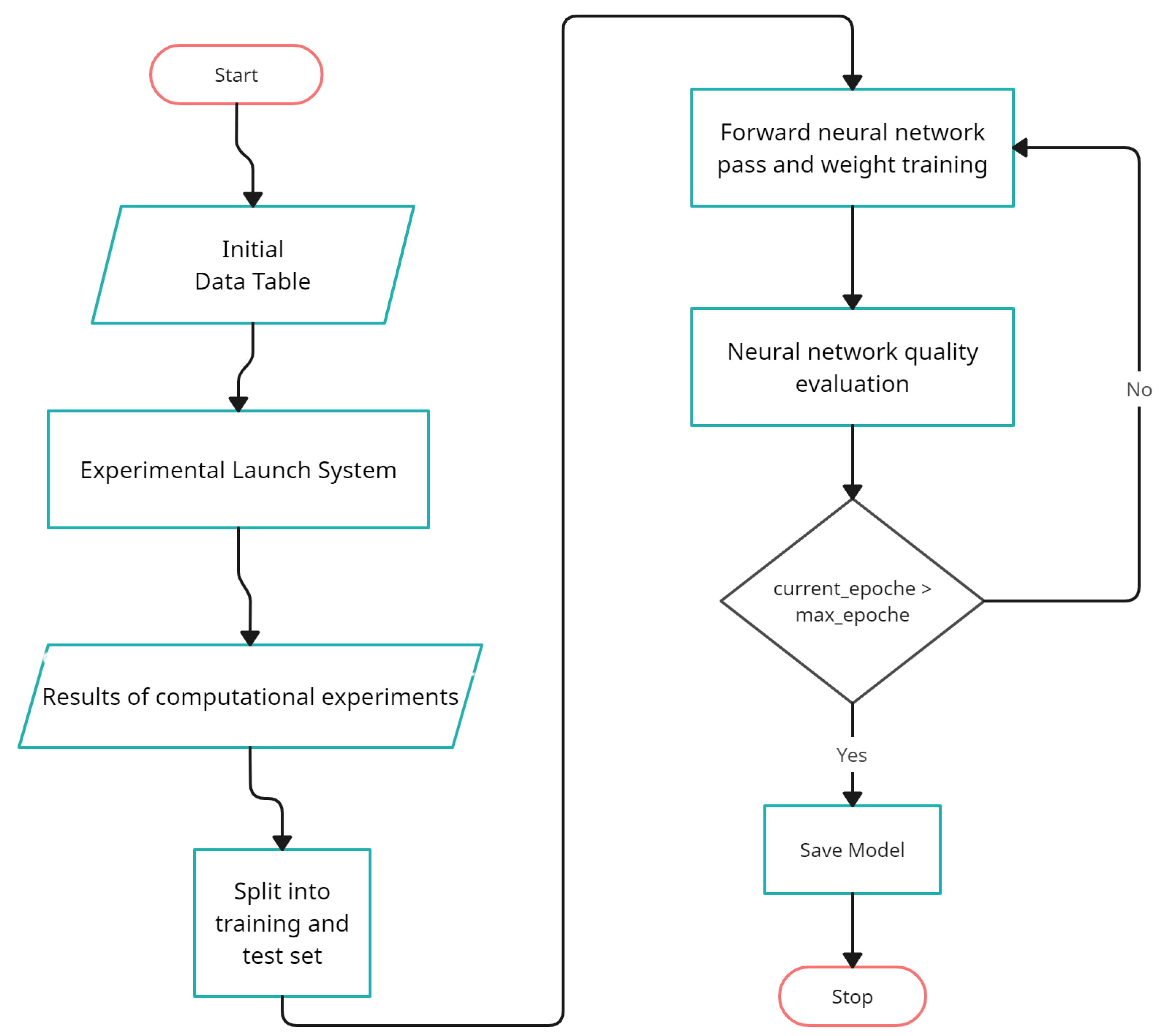
3.1. Deep Learning Problem Statement
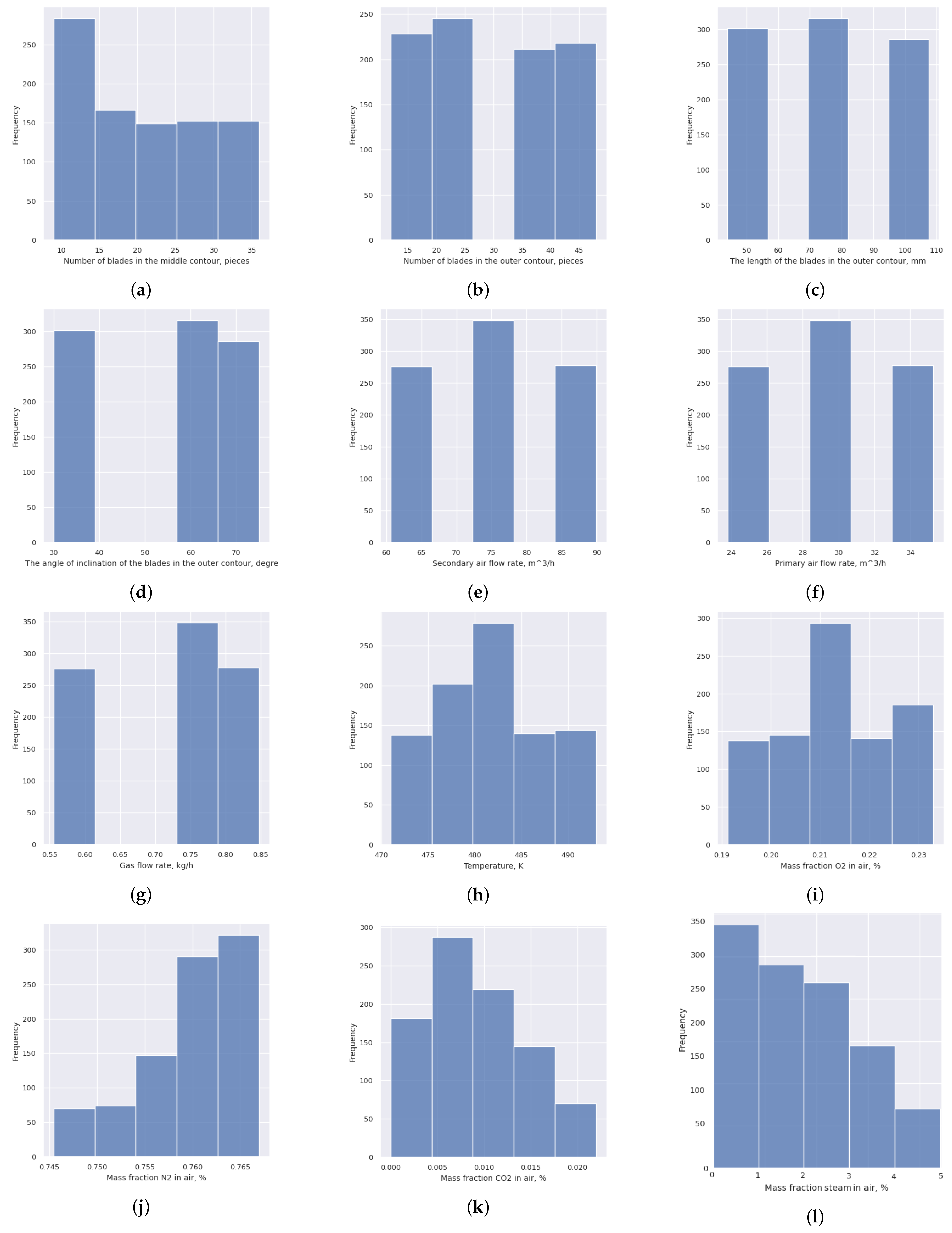
3.2. Dataset
3.3. Data Pre-Processing
3.4. Artificial Neural Networks
3.5. Model Comparison
- Training set: 928 samples (80% data);
- Test set: 232 samples (20% data);
- Optimizer: Pytorch Adam;
- Loss function: Pytorch MSE;
- Learning rate: 0.01;
- Epochs: 1500.
- Flame core position;
- Flame core temperature;
- Maximum distribution function;
- Maximum mass fraction of .
4. Results and Discussion of Parameter Optimization Using a Trained ANN
- Primary air quantity—60.63 m/s;
- Mass flow rate of fuel (methane)—0.556 kg/s;
- Number of blades in the middle contour—18;
- Number of blades in the outer contour—24;
- The length of the blades in the outer contour—70 mm;
- The angle of inclination of the blades in the outer contour—60 degrees.
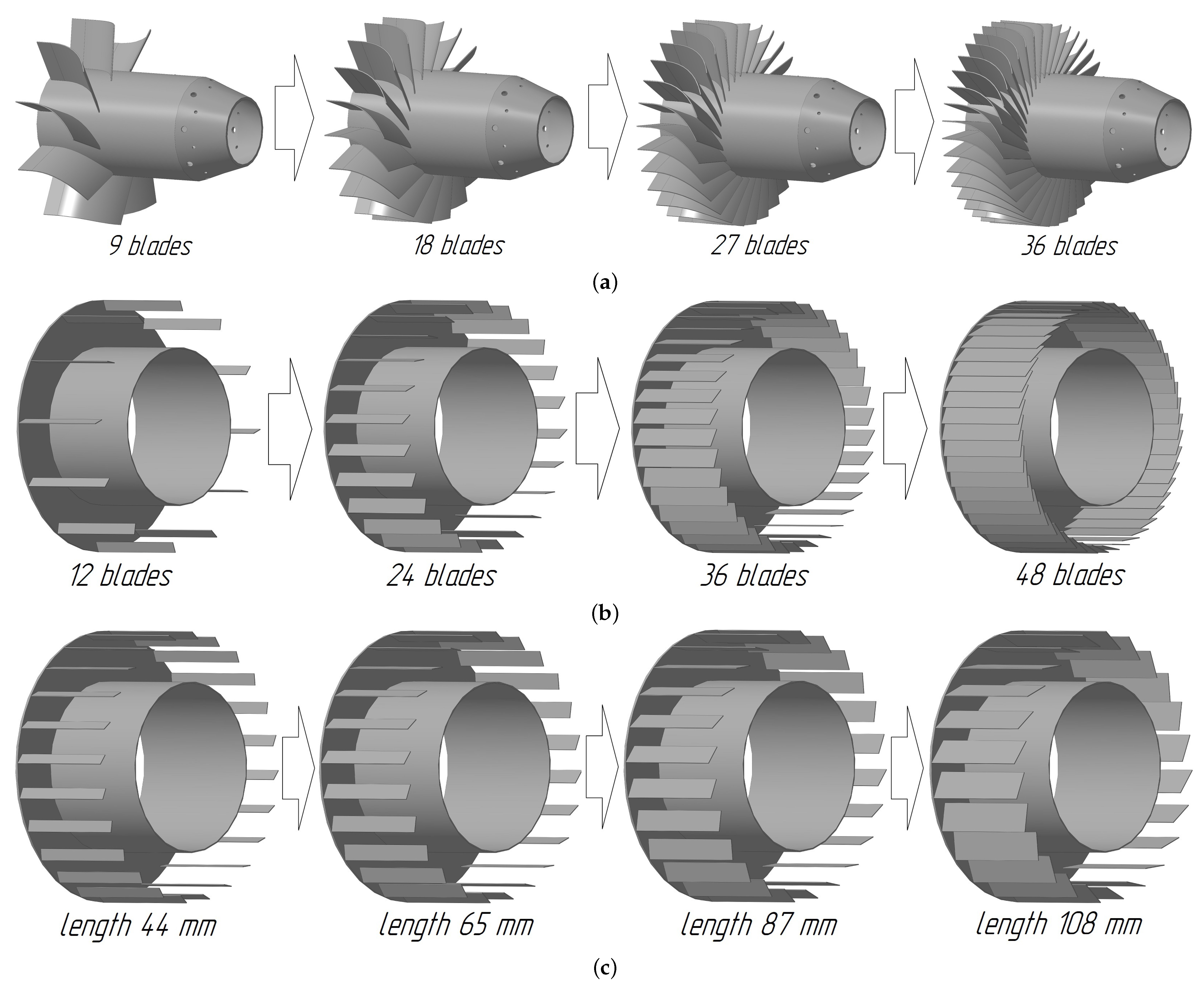
- Number of blades in the middle contour: from 9 to 36;
- Number of blades in the outer contour: from 12 to 48;
- The length of the blades in the outer contour: from 44 to 108 mm;
- The angle of inclination of the blades in the outer contour: from 30 to 75 degrees.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| CAD | Computer-Aided Design |
| CFD | Computational Fluid Dynamics |
| CHP | Combined Heat and Power Plants |
| E-500-13.8-560GMN | The another name TGME-464, Taganrog oil and gas natural circulation boiler, Russia steam capacity 139 kg/s, steam parameters 13.8 MPa, 833 K |
| FGM | Flamelet Generated Manifold |
| FGR | Flue Gas Recirculation |
| FIR | Fuel-Induced Recirculation |
| FO | Frequency of Occurrence |
| GMU-45 | Unified oil and gas burner, installed heat output 52.335 MW |
| MAE | Mean Absolute Error |
| MLP | Multilayer Perceptron |
| MSE | Mean Square Error |
| RF | Random Forest |
| SVR | Support Vector Regression |
References
- Senyuk, M.D.; Dmitrieva, A.A. Development of the method for dynamic stability assessment of power systems based on the application of the artificial intelligence theory taking into account the topological connectivity of the network. Electrotech. Syst. Complexes 2022, 4, 12–19. [Google Scholar] [CrossRef]
- Sartor, K.; Sylvain, Q.; Pierre, D. Simulation and optimization of a CHP biomass plant and district heating network. Appl. Energy 2014, 130, 474–483. [Google Scholar] [CrossRef]
- Xu, B.; Wang, J.; Wang, X.; Liang, Z.; Cui, L.; Liu, X.; Ku, A.Y. A case study of digital-twin-modelling analysis on power-plant-performance optimizations. Clean Energy 2019, 3.3, 227–234. [Google Scholar] [CrossRef]
- Baukal, C.E., Jr. Oxygen-Enhanced Combustion; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Shaw, S.; Van Heyst, B. An Evaluation of Risk Ratios on Physical and Mental Health Correlations due to Increases in Ambient Nitrogen Oxide (NOX) Concentrations. Atmosphere 2022, 13, 967. [Google Scholar] [CrossRef]
- Varaksin, A.Y.; Ryzhkov, S.V. Particle-laden and droplet-laden two-phase flows past bodies (a review). Symmetry 2023, 15, 388. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Effect of the Shape of Pulses on Heat Transfer at the Stagnation Point of a Nonstationary Axisymmetric Impact Gas–Droplet Jet. J. Eng. Phys. Thermophys. 2022, 95, 985–990. [Google Scholar] [CrossRef]
- Hibiki, T.; Tsukamoto, N. Drift-flux model for upward dispersed two-phase flows in vertical medium-to-large round tubes. Prog. Nucl. Energy 2023, 158, 104611. [Google Scholar] [CrossRef]
- Guo, Q.; Liu, H.L.; Xie, G.; Guo, C.; Xu, Z.; Shao, X.D. Investigation on the two-phase flow and heat transfer behaviors in a new central uniform dispersion-type heat exchanger. Int. Commun. Heat Mass Transf. 2022, 137, 106283. [Google Scholar] [CrossRef]
- Bamidele, O.E.; Ahmed, W.H.; Hassan, M. Characterizing two-phase flow-induced vibration in piping structures with U-bends. Int. J. Multiph. Flow 2022, 151, 104042. [Google Scholar] [CrossRef]
- Hundshagen, M.; Rave, K.; Nguyen, B.D.; Popp, S.; Hasse, C.; Mansour, M.; Thévenin, D.; Skoda, R. Two-phase flow simulations of liquid/gas transport in radial centrifugal pumps with special emphasis on the transition from bubbles to adherent gas accumulations. J. Fluids Eng. 2022, 144, 101202. [Google Scholar] [CrossRef]
- Zhang, J.; Lou, W.; Shao, P.; Zhu, M. Mathematical simulation of impact cavity and gas–liquid two-phase flow in top–bottom blown converter with Eulerian-multifluid VOF model. Metall. Mater. Trans. B 2022, 53, 3585–3601. [Google Scholar] [CrossRef]
- Tas, S. A comprehensive review of numerical and experimental research on the thermal-hydraulics of two-phase flows in vertical rod bundles. Int. J. Heat Mass Transf. 2024, 221, 125053. [Google Scholar] [CrossRef]
- Yao, Y.; Hrnjak, P. Developing adiabatic two-phase flow after an expansion valve: Flow development in an 8 mm tube. Int. J. Refrig. 2023, 149, 83–93. [Google Scholar] [CrossRef]
- Kocar, C.; Sokmen, C.N. A CFD model of two-phase flow in BWRs with results of sensitivity and uncertainty analysis. Nucl. Eng. Des. 2009, 239, 1839–1846. [Google Scholar] [CrossRef]
- Askarova, A.S.; Bolegenova, S.A.; Maximov, V. 3D visualization of the results of using modern OFA technology on the example of real boiler. WSEAS Trans. Fluid Mech. 2021, 16, 232–238. [Google Scholar] [CrossRef]
- Aversano, G.; Marco, F.; Parente, A. Digital twin of a combustion furnace operating in flameless conditions: Reduced-order model development from CFD simulations. Proc. Combust. Inst. 2021, 38, 5373–5381. [Google Scholar] [CrossRef]
- Chernov, A.A.; Maryandyshev, P.A.; Pankratov, E.V.; Lubov, V.K. CFD simulation of the combustion process of the low-emission vortex boiler. J. Phys. Conf. Ser. 2017, 891, 012216. [Google Scholar] [CrossRef]
- Karim, M.; Arafat, A.; Naser, J. CFD simulation of biomass thermal conversion under air/oxy-fuel conditions in a reciprocating grate boiler. Renew. Energy 2020, 146, 1416–1428. [Google Scholar] [CrossRef]
- Slotnick, J.P.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D.J. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences. 2014. No. NF1676L-18332. Available online: https://ntrs.nasa.gov/citations/20140003093 (accessed on 26 January 2025).
- Chen, S.; Xing, Y.; Li, A. CFD investigation on Low-NOX strategy of folded flame pattern based on fuel-staging natural gas burner. Appl. Therm. Eng. 2017, 112, 1487–1496. [Google Scholar] [CrossRef]
- Rossiello, G.; Uzair, M.A.; Ahmadpanah, S.B.; Morandi, L.; Ferrara, M.; Rago, G.D.; Torresi, M. Design and testing of a Multi-Fuel industrial burner suitable for syn-gases, flare gas and pure hydrogen. Therm. Sci. Eng. Prog. 2023, 42, 101845. [Google Scholar] [CrossRef]
- Chapela, S.; Porteiro, J.; Gómez, M.A.; Patiño, D.; Míguez, J.L. Comprehensive CFD modeling of the ash deposition in a biomass packed bed burner. Fuel 2018, 234, 1099–1122. [Google Scholar] [CrossRef]
- Garcia, A.M.; Rendon, M.A.; Amell, A.A. Combustion model evaluation in a CFD simulation of a radiant-tube burner. Fuel 2020, 276, 118013. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, W. A novel decision optimization for thermal power unit based on condition-based predictive maintenance and equilibrium optimizer. Phys. Commun. 2024, 65, 102372. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, M.; Yan, H.; Zhao, Y.; Yan, J. Improving flexibility of thermal power plant through control strategy optimization based on orderly utilization of energy storage. Appl. Therm. Eng. 2024, 240, 122231. [Google Scholar] [CrossRef]
- Kůdela, J.; Suja, J.; Šomplák, R.; Pluskal, J.; Hrabec, D. Optimal control of combined heat and power station operation. Optim. Eng. 2024, 25, 121–145. [Google Scholar] [CrossRef]
- Wang, Q.; Leng, Z.; Tan, H.; Mohamed, M.A.; Jin, T. Optimal scheduling of virtual power plants with reversible solid oxide cells in the electricity market. Renew. Energy 2024, 237, 121759. [Google Scholar] [CrossRef]
- Wu, S.; Wang, Y.; Liu, L.; Yang, Z.; Cao, Q.; He, H.; Cao, Y. Two-stage distributionally robust optimal operation of rural virtual power plants considering multi correlated uncertainties. Int. J. Electr. Power Energy Syst. 2024, 161, 110173. [Google Scholar] [CrossRef]
- Deon, B.; Cotta, K.P.; Silva, R.F.V.; Batista, C.B.; Justino, G.T.; Freitas, G.C.; Padoin, N. Digital twin and machine learning for decision support in thermal power plant with combustion engines. Knowl.-Based Syst. 2022, 253, 109578. [Google Scholar] [CrossRef]
- Ahmed, I.; Rehan, M.; Basit, A.; Hong, K.S. Greenhouse gases emission reduction for electric power generation sector by efficient dispatching of thermal plants integrated with renewable systems. Sci. Rep. 2022, 12, 12380. [Google Scholar] [CrossRef]
- Mahdavipour, P.; Wiel, C.; Spliethoff, H. Optimal control of combined-cycle power plants: A data-enabled predictive control perspective. IFAC-PapersOnLine 2022, 55, 91–96. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Klyachkin, V.N.; Kuvayskova, J.E.; Zhukov, D.A. Aggregated classifiers for state diagnostics of the technical object. In Proceedings of the International Multi-Conference on Industrial Engineering and Modern Technologies (FarEastCon), Vladivostok, Russia, 1–4 October 2019. [Google Scholar]
- Breiman, L. Classification and Regression Trees, 1st ed.; Routledge: London, UK, 2017. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16). Association for Computing Machinery, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Alshboul, O.; Shehadeh, A.; Mamlook, R.E.A.; Almasabha, G.; Almuflih, A.S.; Alghamdi, S.Y. Prediction Liquidated Damages via Ensemble Machine Learning Model: Towards Sustainable Highway Construction Projects. Sustainability 2021, 14, 9303. [Google Scholar] [CrossRef]
- Shehadeh, A.; Alshboul, O.; Al Mamlook, R.E.; Hamedat, O. Machine learning models for predicting the residual value of heavy construction equipment: An evaluation of modified decision tree, LightGBM, and XGBoost regression. Autom. Constr. 2021, 129, 103827. [Google Scholar] [CrossRef]
- Abdul Jameel, A.G.; Al-Muslem, A.; Ahmad, N.; Alquaity, A.B.S.; Zahid, U.; Ahmed, U. Predicting Enthalpy of Combustion Using Machine Learning. Processes 2022, 10, 2384. [Google Scholar] [CrossRef]
- Krayden, A.; Schohet, M.; Shmueli, O.; Shlenkevitch, D.; Blank, T.; Stolyarova, S.; Nemirovsky, Y. CMOS-MEMS Gas Sensor Dubbed GMOS for SelectiveAnalysis of Gases with Tiny Edge Machine Learning. Eng. Proc. 2022, 27, 81. [Google Scholar] [CrossRef]
- Brusa, A.; Giovannardi, E.; Barichello, M.; Cavina, N. Comparative Evaluation of Data-Driven Approaches to Develop an Engine Surrogate Model for NOX Engine-Out Emissions under Steady-State and Transient Conditions. Energies 2022, 15, 8088. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, H.; Xie, F.; Ma, T.; Qian, X. Combustion Regime Identification in Turbulent Non-Premixed Flames with Principal Component Analysis, Clustering and Back-Propagation Neural Network. Processes 2022, 10, 1653. [Google Scholar] [CrossRef]
- Yang, R.; Xie, T.; Liu, Z. The Application of Machine Learning Methods to Predict the Power Output of Internal Combustion Engines. Energies 2022, 15, 3242. [Google Scholar] [CrossRef]
- Yang, R.; Yan, Y.; Sun, X.; Wang, Q.; Zhang, Y.; Fu, J.; Liu, Z. An Artificial Neural Network Model to Predict Efficiency and Emissions of a Gasoline Engine. Processes 2022, 10, 204. [Google Scholar] [CrossRef]
- Bai, M.; Liu, J.; Ma, Y.; Zhao, X.; Long, Z.; Yu, D. Long Short-Term Memory Network-Based Normal Pattern Group for Fault Detection of Three-Shaft Marine Gas Turbine. Energies 2021, 14, 13. [Google Scholar] [CrossRef]
- Kuzhagaliyeva, N.; Horváth, S.; Williams, J.; Nicolle, A.; Sarathy, S.M. Artificial intelligence-driven design of fuel mixtures. Commun. Chem. 2022, 5, 111. [Google Scholar] [CrossRef] [PubMed]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics informed deep learning (part i): Data-driven solutions of nonlinear partial differential equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Thummar, D. Active Flow Control in Simulations of Fluid Flows Based on Deep Reinforcement Learning. Available online: https://zenodo.org/records/4897961 (accessed on 26 January 2025).
- Star CMM+. Available online: https://plm.sw.siemens.com/en-US/simcenter/fluids-thermal-simulation/star-ccm/ (accessed on 25 November 2024).
- Fedorov, R.V.; Generalov, D.A.; Sherkunov, V.V.; Sapunov, V.V.; Busygin, S.V. Improving the Efficiency of Fuel Combustion with the Use of Various Designs of Embrasures. Energies 2023, 16, 4452. [Google Scholar] [CrossRef]
- Fedorov, R.V.; Shepelev, I.I.; Maleshina, M.A.; Karpov, D.A.; Seleznev, K.A. Mathematical modeling and study of dispersed working fluid for a low-emission burner. Eurasian J. Math. Comput. Appl. 2025; accepted. [Google Scholar]
- Technical Report on the Results of Experiments to Revise the Energy Characteristics of the Boiler TGME-464 st. no. 3, Installed at the Cheboksary CHP-2; LLC “YugEnergoInzhiniring”: Krasnodar, Russia, 2017; 76p. (In Russian)
- KOMPAS-3D for Developers. Available online: https://kompas.ru/solutions/developers/ (accessed on 26 January 2025).
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: New York, NY, USA, 2009; pp. 1–758. [Google Scholar]
- Scikit-Learn Homepage. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html (accessed on 26 January 2025).
- Omiotek, Z.; Kotyra, A. Flame Image Processing and Classification Using a Pre-Trained VGG16 Model in Combustion Diagnosis. Sensors 2021, 21, 500. [Google Scholar] [CrossRef]
- Abdurakipov, S.S.; Gobyzov, O.A.; Tokarev, M.P.; Dulin, V.M. Combustion regime monitoring by flame imaging and machine learning. Optoelectron. Instrum. Data Process. 2018, 54, 513–519. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, Z.; Jiang, G.; He, Q.; Xie, P. Detecting Wind Turbine Blade Icing with a Multiscale Long Short-Term Memory Network. Energies 2022, 15, 2864. [Google Scholar] [CrossRef]
- Sun, Z.; Sun, H. Health status assessment for wind turbine with recurrent neural networks. Math. Probl. Eng. 2018, 2018, 1–16. [Google Scholar] [CrossRef]
- Zhou, H.; Ying, Y.; Li, J.; Jin, Y. Long-short term memory and gas path analysis based gas turbine fault diagnosis and prognosis. Adv. Mech. Eng. 2021, 13, 16878140211037767. [Google Scholar] [CrossRef]
- Losi, E.; Venturini, M.; Manservigi, L.; Bechini, G. Detection of the Onset of Trip Symptoms Embedded in Gas Turbine Operating Data. J. Eng. Gas Turbines Power 2018, 145, 031023. [Google Scholar] [CrossRef]
- Liu, Z.; Iftekhar, A.K. Gas turbine performance prediction via machine learning. Energy 2020, 192, 116627. [Google Scholar] [CrossRef]
- Aurelien, G. Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow. In Concepts, Tools, and Techniques to Build Intelligent Systems, 2nd ed.; O’Reilly Media, Inc.: Newton, MA, USA, 2019. [Google Scholar]
- Mehmood, F.; Ahmad, S.; Whangbo, T.K. An Efficient Optimization Technique for Training Deep Neural Networks. Mathematics 2023, 11, 1360. [Google Scholar] [CrossRef]
- Open Library PyTorch. Available online: https://github.com/pytorch/pytorch (accessed on 26 January 2025).
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Academic Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Brownlee, J. Better Deep Learning: Train Faster, Reduce Overfitting, and Make Better Predictions. Available online: https://www.google.com/books/edition/Better_Deep_Learning/T1-nDwAAQBAJ (accessed on 26 January 2025).
- CatBoost Homepage. Available online: https://catboost.ai/ (accessed on 26 January 2025).







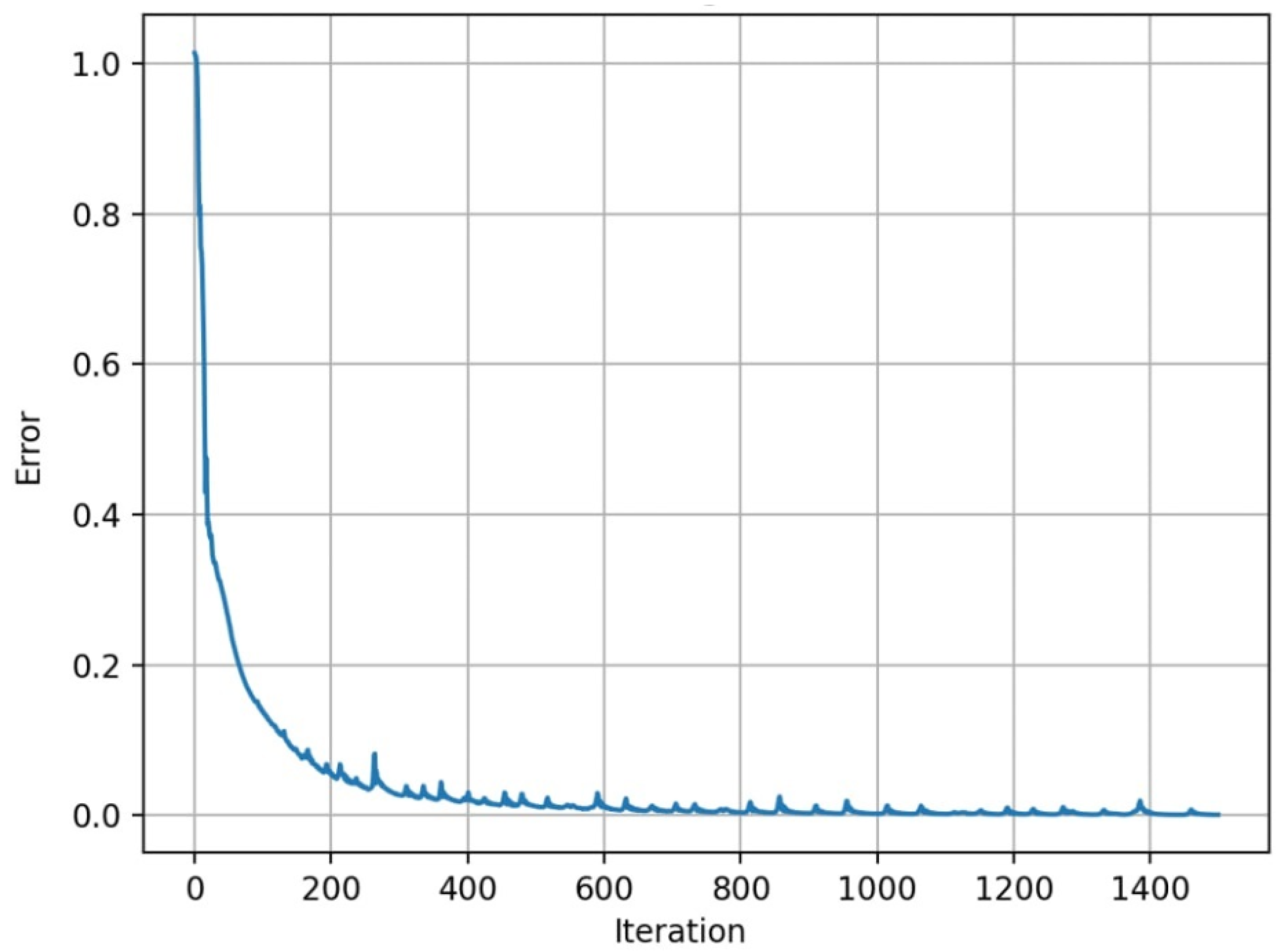

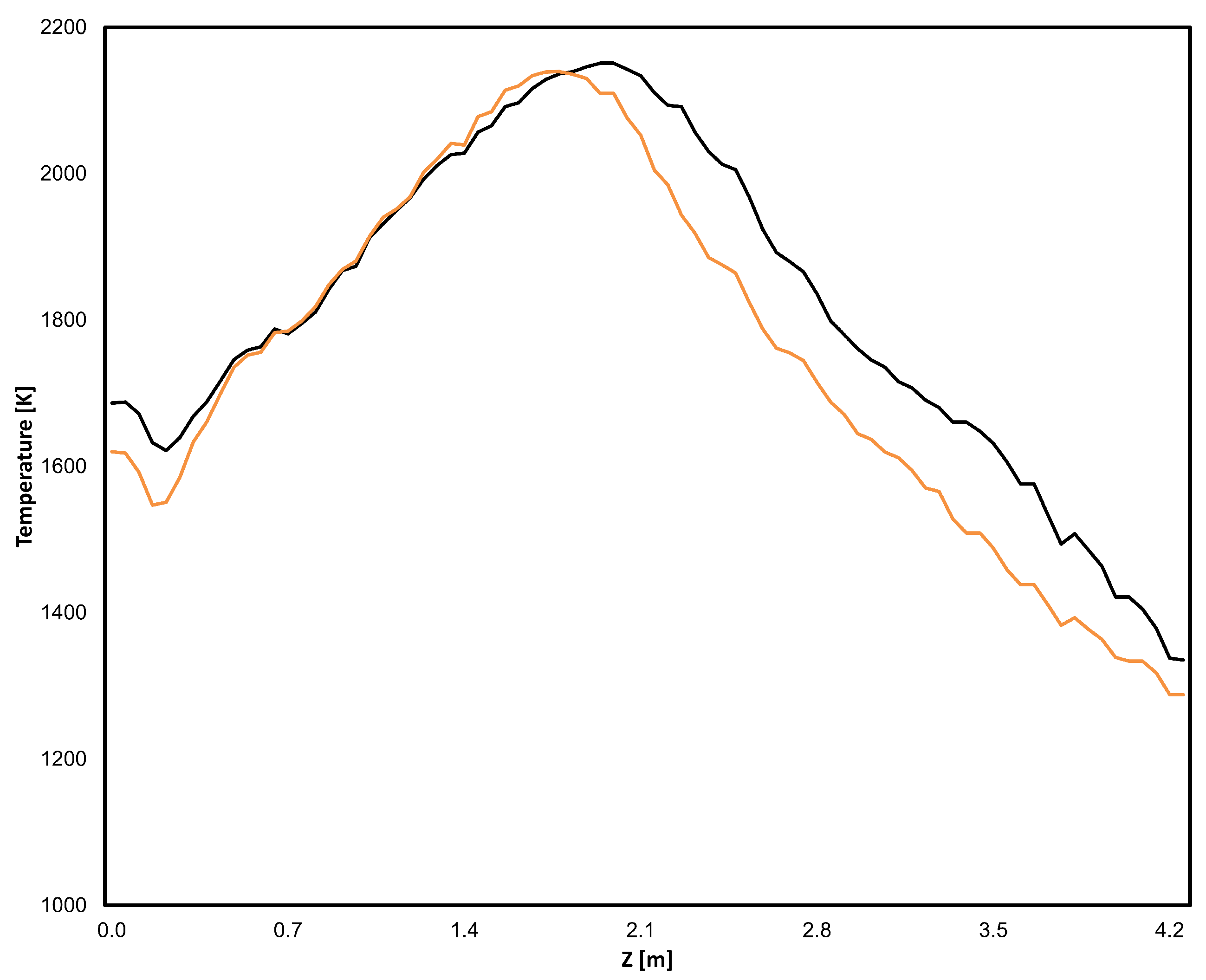
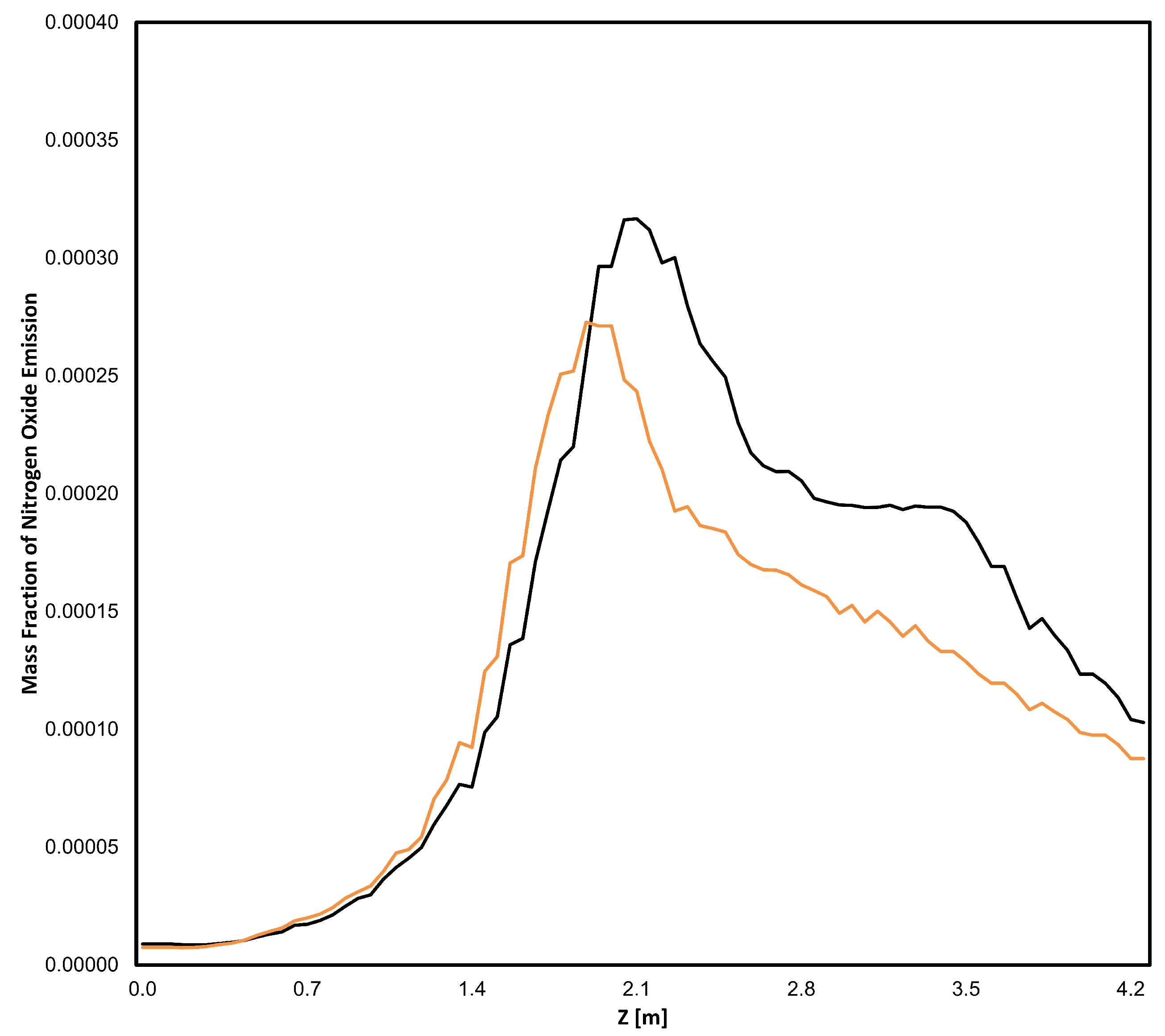

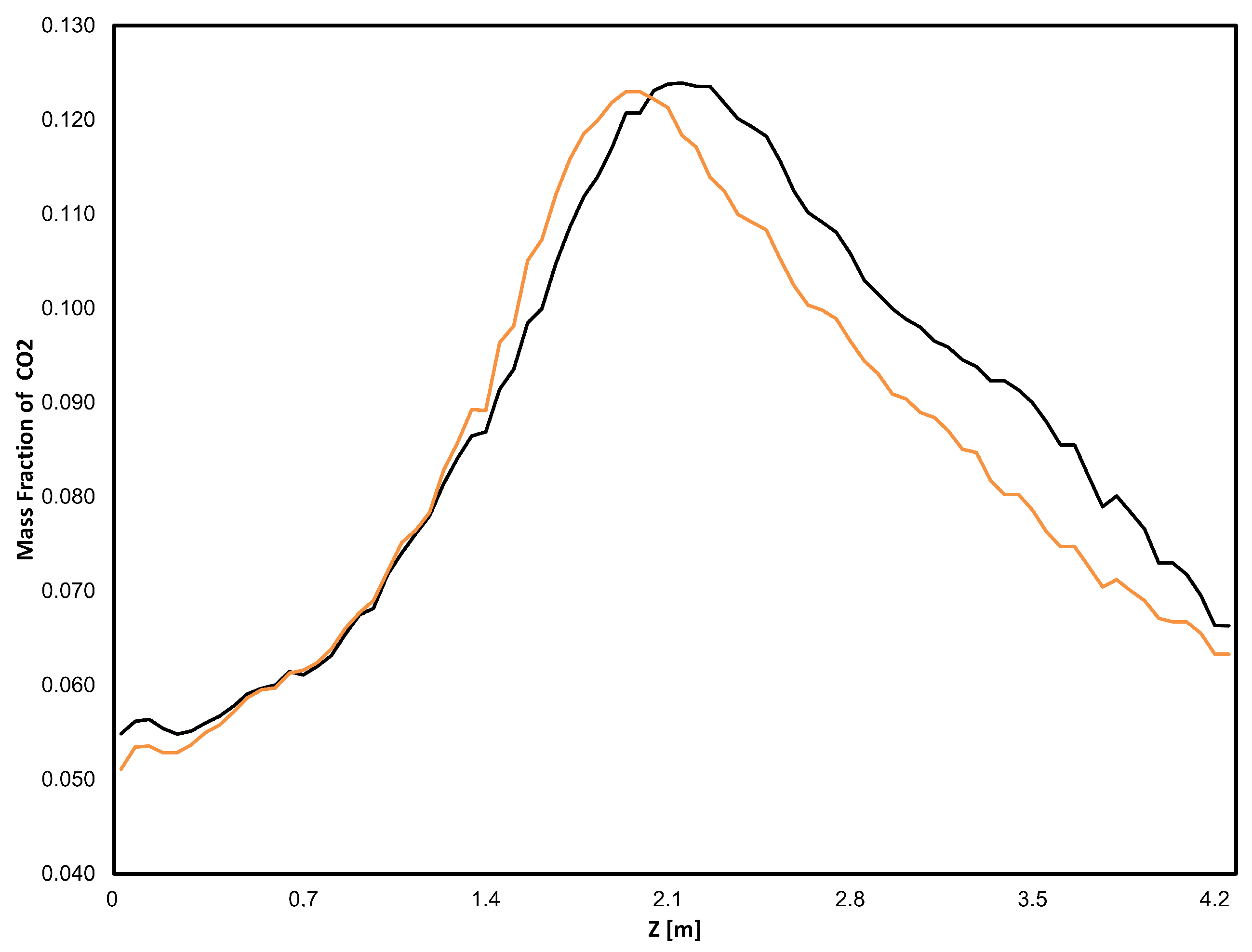
| Symbol | Name | Unit of Measure | Minimum | Maximum |
|---|---|---|---|---|
| X1 | Number of blades in the middle contour | pieces | 9 | 36 |
| X2 | Number of blades in the outer contour | pieces | 12 | 48 |
| X3 | The length of the blades in the outer contour | mm | 44 | 108 |
| X4 | The angle of inclination of the blades in the outer contour | degree | 30 | 75 |
| X5 | Primary air flow rate | m3/h | 60.63 | 89.89 |
| X6 | Secondary air flow rate | m3/h | 23.8 | 35.29 |
| X7 | Gas flow rate | kg/s | 0.556 | 0.848 |
| X8 | Temperature | K | 471 | 493 |
| X9 | Mass fraction in air | – | 0.191 | 0.233 |
| X10 | Mass fraction in air | – | 0.745 | 0.767 |
| X11 | Mass fraction in air | – | 0 | 0.022 |
| X12 | Amount of injected steam | % | 0 | 5 |
| Symbol | Name | Unit of Measure | Minimum | Maximum |
|---|---|---|---|---|
| Y1 | The position of the maximum temperature along the length of the combustion chamber | m | 1.2 | 4.118 |
| Y2 | The maximum temperature of the combustion chamber | K | 1901.728 | 2250.652 |
| Y3 | Distribution along the length of the combustion chamber of the maximum | m | 1.271 | 4.617 |
| Y4 | Maximum mass fraction of in the combustion chamber | % | 0.000004 | 0.000383 |
| Y5 | Distribution along the length of the combustion chamber of the maximum | m | 0.061 | 1.912 |
| Y6 | Maximum mass fraction of in the combustion chamber | % | 0.107 | 0.160 |
| Y7 | Distribution along the length of the combustion chamber of the maximum | m | 1.414 | 4.332 |
| Y8 | Maximum mass fraction of in the combustion chamber | % | 0.108 | 0.125 |
| Parameter | MAE | MSE | RMSE |
|---|---|---|---|
| Flame core position | 0.155 | 0.049 | 0.220 |
| Flame core temperature | 14.931 | 472.134 | 21.729 |
| Maximum distribution function | 0.214 | 0.094 | 0.306 |
| Maximum mass fraction of | |||
| Maximum distribution function | 0.207 | 0.079 | 0.281 |
| Maximum mass fraction of | 0.005 | 0.007 | |
| Maximum distribution function | 0.179 | 0.054 | 0.233 |
| Maximum mass fraction of | 0.002 | 0.003 |
| Parameter | ANN | CatBoost | SVR | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | MAE | MSE | RMSE | MAE | MSE | RMSE | |
| Flame core position | 0.155 | 0.049 | 0.220 | 0.161 | 0.056 | 0.237 | 0.167 | 0.061 | 0.247 |
| Flame core temperature | 14.931 | 472.134 | 21.729 | 14.631 | 470.871 | 21.7 | 16.129 | 474.237 | 21.78 |
| Maximum distribution function | 0.214 | 0.094 | 0.306 | 0.221 | 0.099 | 0.315 | 0.224 | 0.103 | 0.321 |
| Maximum mass fraction of | |||||||||
| Primary Air Flow Rate | Gas Flow Rate | Number of Blades in the Middle Contour | Number of Blades in the Outer Contour | The Length of the Blades in the Outer Contour | The Angle of Inclination of the Blades in the Outer Contour | Steam Content in the Air |
|---|---|---|---|---|---|---|
| 65.73 | 0.584 | 16 | 28 | 44 | 63 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedorov, R.V.; Shepelev, I.I.; Malyoshina, M.A.; Generalov, D.A.; Sherkunov, V.V.; Sapunov, V.V. Software Package for Optimization of Burner Devices on Dispersed Working Fluids. Energies 2025, 18, 806. https://doi.org/10.3390/en18040806
Fedorov RV, Shepelev II, Malyoshina MA, Generalov DA, Sherkunov VV, Sapunov VV. Software Package for Optimization of Burner Devices on Dispersed Working Fluids. Energies. 2025; 18(4):806. https://doi.org/10.3390/en18040806
Chicago/Turabian StyleFedorov, Ruslan V., Igor I. Shepelev, Mariia A. Malyoshina, Dmitry A. Generalov, Vyacheslav V. Sherkunov, and Valeriy V. Sapunov. 2025. "Software Package for Optimization of Burner Devices on Dispersed Working Fluids" Energies 18, no. 4: 806. https://doi.org/10.3390/en18040806
APA StyleFedorov, R. V., Shepelev, I. I., Malyoshina, M. A., Generalov, D. A., Sherkunov, V. V., & Sapunov, V. V. (2025). Software Package for Optimization of Burner Devices on Dispersed Working Fluids. Energies, 18(4), 806. https://doi.org/10.3390/en18040806







