Distributed Parameter Identification Framework Based on Intelligent Algorithms for Permanent Magnet Synchronous Wind Generator
Abstract
1. Introduction
2. Mathematical Model
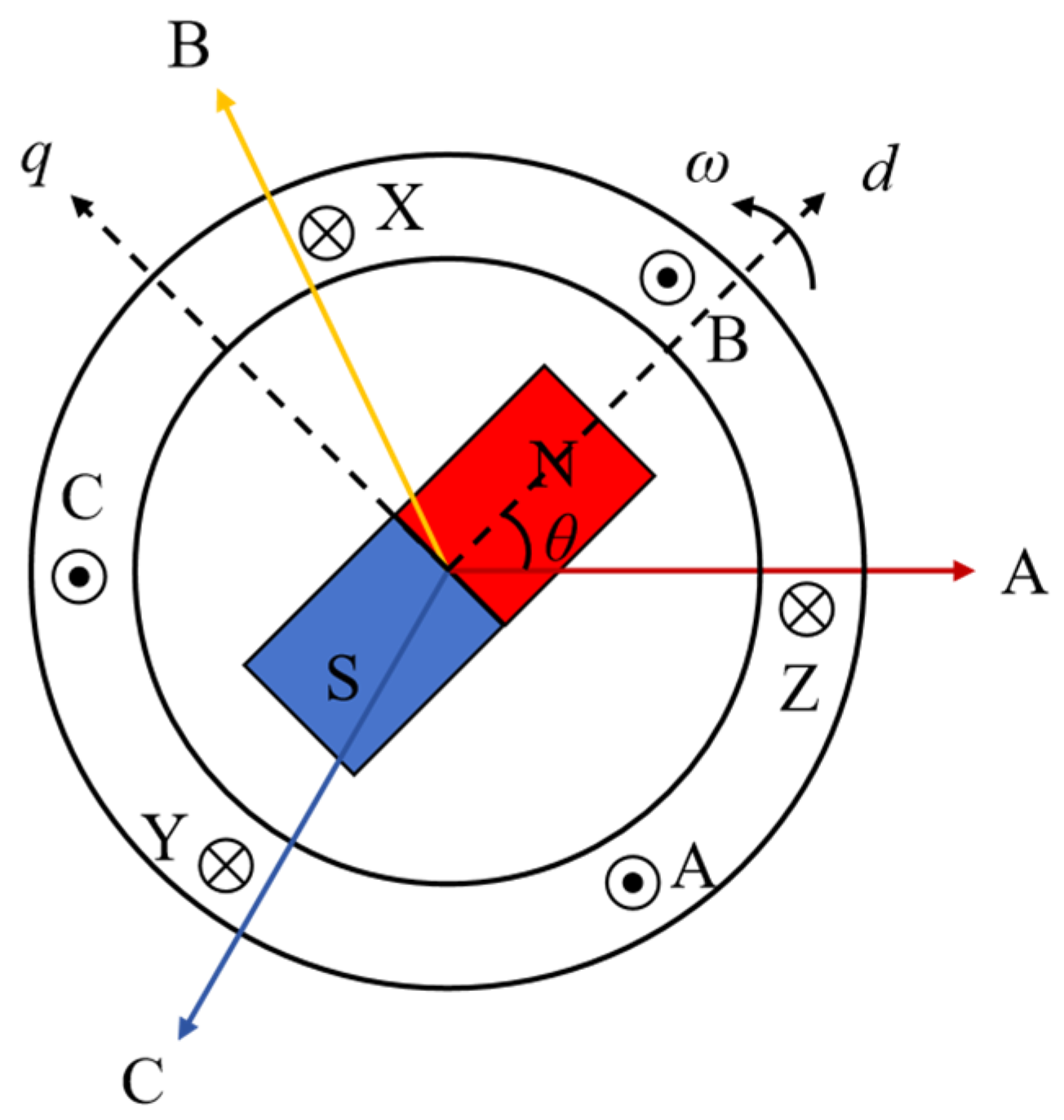
2.1. PMSWG Model
2.2. Parameter Identification Model
3. Methodology
3.1. Sparrow Search Algorithm
3.2. Particle Swarm Optimization Algorithm
3.3. Dung Beetle Optimization Algorithm
4. Distributed Parameter Identification Framework
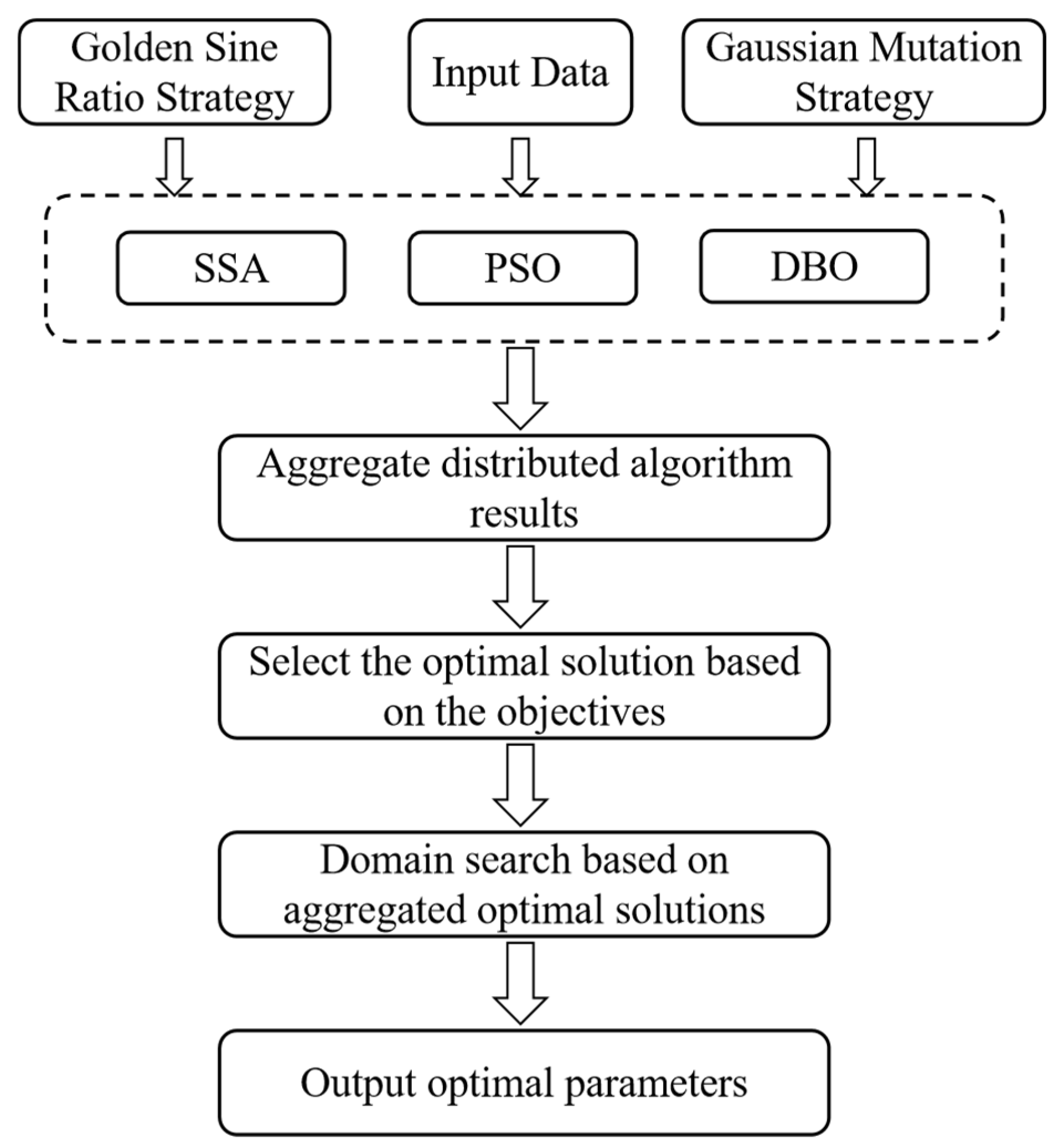
4.1. Distributed Framework
4.2. Improvement Strategy
4.3. Parameter Identification Process
5. Simulation
5.1. Parameter Settings
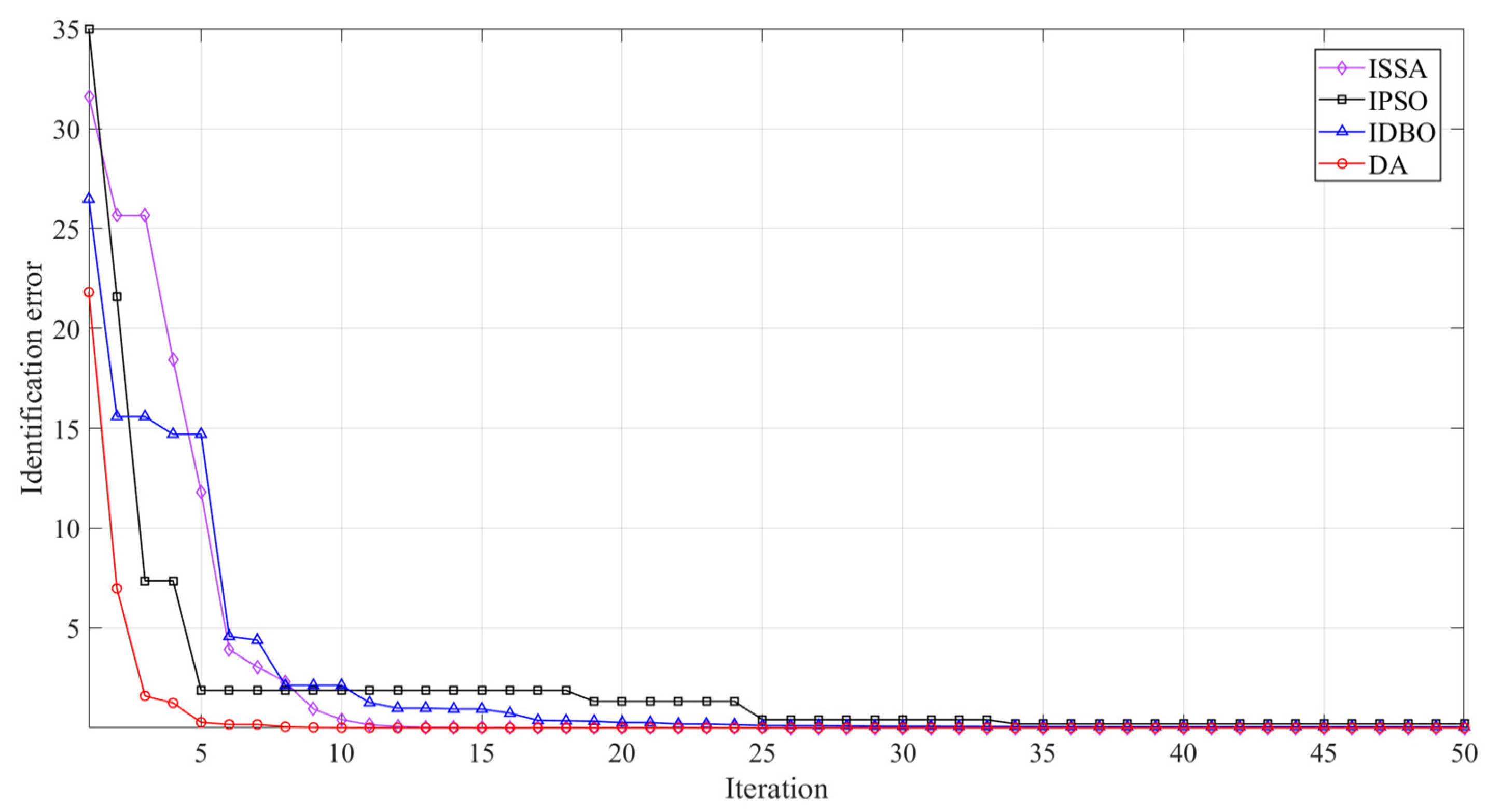
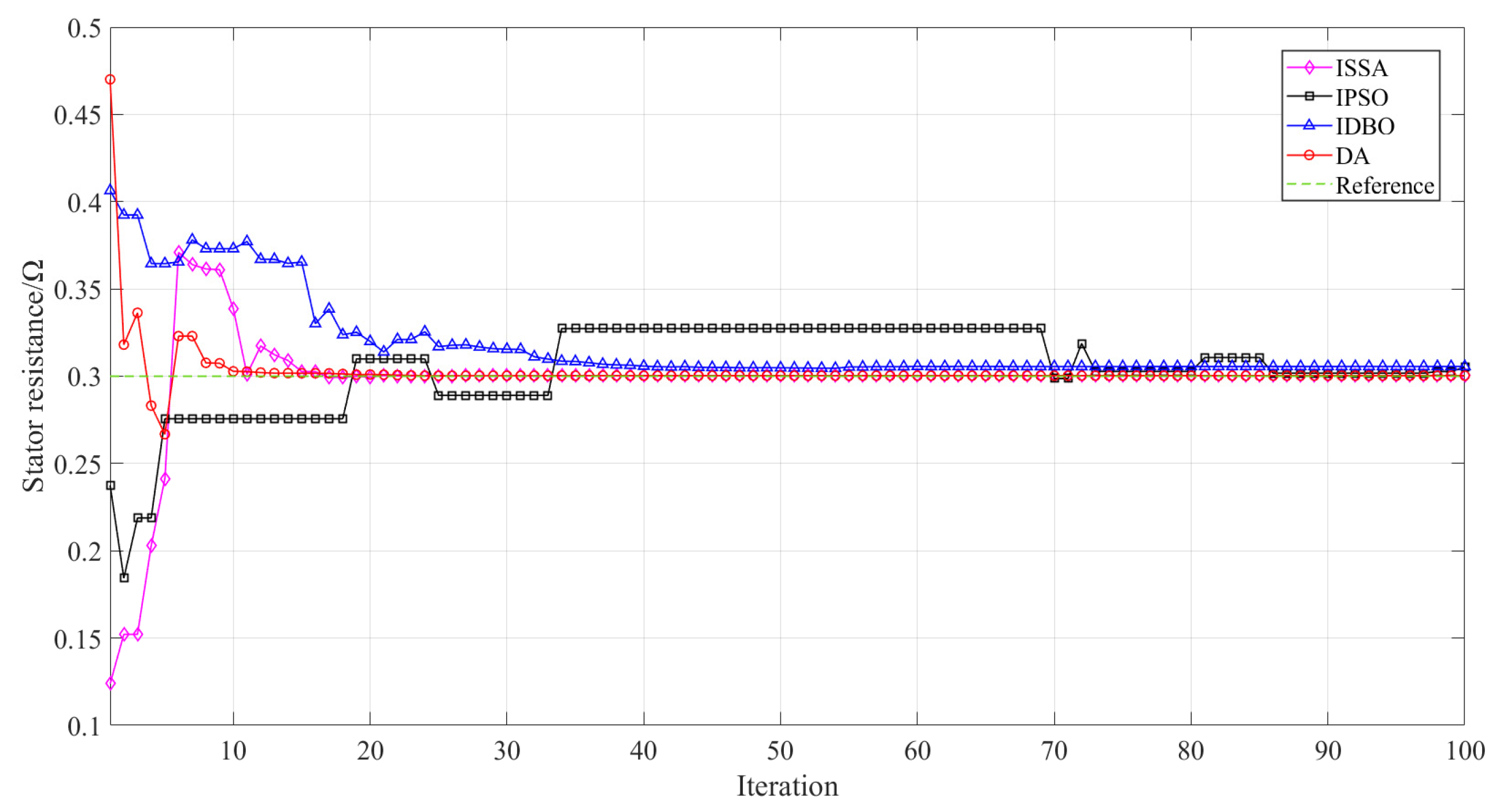
5.2. Parameter Identification of PMSWG
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Functions | Optimal Solution | SSA | ISSA | ||||
| Average | Min | Max | Average | Min | Max | ||
| F1 | 0 | 1.0363 × 10−48 | 2.5583 × 10−172 | 1.0363 × 10−47 | 1.2514 × 10−180 | 0 | 1.2514 × 10−179 |
| F2 | 0 | 1.0273 × 10−36 | 3.6493 × 10−72 | 1.0261 × 10−35 | 4.5307 × 10−100 | 0 | 4.5307 × 10−99 |
| F3 | 0 | 4.7411 × 10−44 | 7.8473 × 10−139 | 4.7411 × 10−43 | 1.3926 × 10−95 | 0 | 1.3926 × 10−94 |
| F4 | 0 | 1.4683 × 10−34 | 5.5768 × 10−87 | 1.4683 × 10−33 | 1.4238 × 10−107 | 0 | 1.4238 × 10−106 |
| F5 | 0 | 0.0375 | 0.0016 | 0.0492 | 0.0219 | 9.8284 × 10−8 | 0.2098 |
| F6 | 0 | 9.5303 × 10−4 | 2.8226 × 10−5 | 0.0031 | 1.0437 × 10−11 | 1.8436 × 10−13 | 6.7055 × 10−11 |
| F7 | 0 | 6.3157 × 10−4 | 1.8271 × 10−4 | 0.0018 | 5.609 × 10−4 | 9.8754 × 10−6 | 0.0015 |
| Functions | Optimal Solution | PSO | IPSO | ||||
| Average | Min | Max | Average | Min | Max | ||
| F1 | 0 | 20.3213 | 12.1001 | 36.8192 | 2.2757 × 10−11 | 2.1823 × 10−14 | 1.0732 × 10−10 |
| F2 | 0 | 2.123 | 1.3048 | 3.7498 | 1.5549 × 10−7 | 4.4196 × 10−9 | 4.0485 × 10−7 |
| F3 | 0 | 3.5626 × 103 | 1.4264 × 103 | 7.7483 × 103 | 2.3716 × 10−8 | 4.7847 × 10−11 | 1.8194 × 10−7 |
| F4 | 0 | 9.7574 | 6.0264 | 12.9101 | 9.1390 × 10−6 | 2.0707 × 10−7 | 3.1485 × 10−5 |
| F5 | 0 | 1.1113 × 103 | 466.5971 | 5.0207 × 103 | 10.85 | 2.7773 | 25.0989 |
| F6 | 0 | 27.6905 | 6.646 | 91.746 | 0.0627 | 0.0305 | 0.0801 |
| F7 | 0 | 0.0973 | 0.0302 | 0.1758 | 8.4526 × 10−4 | 8.9681 × 10−5 | 0.0019 |
| Functions | Optimal Solution | EEFO | DE | ||||
| Average | Min | Max | Average | Min | Max | ||
| F1 | 0 | 2.4232 × 10−58 | 7.7170 × 10−62 | 1.4618 × 10−57 | 1.2426 × 103 | 861.1411 | 1.5190 × 103 |
| F2 | 0 | 2.4304 × 10−29 | 9.1030 × 10−32 | 1.3928 × 10−28 | 12.4449 | 8.8694 | 13.9141 |
| F3 | 0 | 1.6754 × 10−42 | 1.9439 × 10−53 | 1.5714 × 10−41 | 3.7715 × 104 | 2.7594 × 104 | 4.6790 × 104 |
| F4 | 0 | 1.7331 × 10−27 | 6.0418 × 10−31 | 1.5569 × 10−26 | 56.4434 | 53.4479 | 60.5783 |
| F5 | 0 | 13.7247 | 0.0027 | 27.7519 | 3.1962 × 105 | 1.9743 × 105 | 4.1580 × 105 |
| F6 | 0 | 3.1607 × 10−4 | 1.7478 × 10−5 | 6.7358 × 10−4 | 1.1385 × 103 | 859.0187 | 1.3270 × 103 |
| F7 | 0 | 8.0498 × 10−4 | 8.5697 × 10−5 | 0.0016 | 0.615 | 0.4541 | 0.8051 |
| Functions | Optimal Solution | DBO | IDBO | ||||
| Average | Min | Max | Average | Min | Max | ||
| F1 | 0 | 1.6824 × 10−19 | 8.3194 × 10−35 | 1.5648 × 10−18 | 2.6363 × 10−97 | 2.3169 × 10−117 | 2.1760 × 10−96 |
| F2 | 0 | 3.3376 × 10−11 | 5.7735 × 10−17 | 2.1738 × 10−10 | 1.6603 × 10−52 | 1.6293 × 10−63 | 1.3468 × 10−51 |
| F3 | 0 | 1.3893 × 10−39 | 5.6477 × 10−22 | 0.0218 | 5.3475 × 10−87 | 6.3963 × 10−115 | 5.3475 × 10−86 |
| F4 | 0 | 5.2026 × 10−10 | 1.9791 × 10−16 | 4.5722 × 10−9 | 1.9451 × 10−45 | 3.4528 × 10−64 | 1.8713 × 10−44 |
| F5 | 0 | 13.9444 | 0.1079 | 28.4522 | 2.8843 | 4.0424 × 10−6 | 16.6363 |
| F6 | 0 | 0.0058 | 0.0018 | 0.0148 | 1.1313 × 10−10 | 4.7148 × 10−12 | 4.0828 × 10−10 |
| F7 | 0 | 7.1659 × 10−4 | 1.2192 × 10−4 | 0.0019 | 2.1818 × 10−4 | 4.5315 × 10−5 | 4.8412 × 10−4 |
| N | Mean | Std. Deviation | Std. Error | 95% Confidence Interval for Mean | Minimum | Maximum | |||
|---|---|---|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | ||||||||
| Stator resistance | ISSA | 10 | 0.300423440710562 | 0.000288979263111 | 0.000091383266799 | 0.300216717399013 | 0.300630164022110 | 0.299986076413453 | 0.300762617504750 |
| IDBO | 10 | 0.300421530771123 | 0.000224530386397 | 0.000071002742493 | 0.300260911408613 | 0.300582150133632 | 0.300085623440284 | 0.300677915578056 | |
| IPSO | 10 | 0.305813040160193 | 0.000975193204637 | 0.000308383168537 | 0.305115428966601 | 0.306510651353786 | 0.303797223722081 | 0.307106209098570 | |
| DA | 10 | 0.300116574828165 | 0.000055528268598 | 0.000017559580329 | 0.300076852297747 | 0.300156297358583 | 0.300011052007805 | 0.300182459740048 | |
| Total | 40 | 0.301693646617511 | 0.002463449095322 | 0.000389505502055 | 0.300905797375200 | 0.302481495859821 | 0.299986076413453 | 0.307106209098570 | |
| D-axis inductance | ISSA | 10 | 0.008644786120334 | 0.000435127481982 | 0.000137599391560 | 0.008333514671121 | 0.008956057569547 | 0.008109993900543 | 0.009573861272539 |
| IDBO | 10 | 0.008617441701002 | 0.000192549573261 | 0.000060889521400 | 0.008479700034028 | 0.008755183367976 | 0.008382695949475 | 0.008948504395077 | |
| IPSO | 10 | 0.008922628467097 | 0.000584948710451 | 0.000184977023940 | 0.008504181367437 | 0.009341075566757 | 0.008302308024616 | 0.009929230084906 | |
| DA | 10 | 0.008539879182029 | 0.000062823365874 | 0.000019866492644 | 0.008494938053395 | 0.008584820310663 | 0.008453441810402 | 0.008648643972847 | |
| Total | 40 | 0.008681183867616 | 0.000391879461519 | 0.000061961583332 | 0.008555854735619 | 0.008806512999612 | 0.008109993900543 | 0.009929230084906 | |
| Q-axis inductance | ISSA | 10 | 0.008400022931924 | 0.000290625990687 | 0.000091904007781 | 0.008192121622431 | 0.008607924241417 | 0.007944931050183 | 0.008886586250273 |
| IDBO | 10 | 0.007985058189605 | 0.000271303856848 | 0.000085793812563 | 0.007790979101993 | 0.008179137277218 | 0.007605788662789 | 0.008328551250747 | |
| IPSO | 10 | 0.008208999307511 | 0.000522997522789 | 0.000165386338264 | 0.007834869417778 | 0.008583129197244 | 0.007633019527008 | 0.009265446549331 | |
| DA | 10 | 0.008506377497732 | 0.000068992217225 | 0.000021817254726 | 0.008457023438681 | 0.008555731556782 | 0.008379900486660 | 0.008598657504943 | |
| Total | 40 | 0.008275114481693 | 0.000375639146959 | 0.000059393764136 | 0.008154979254269 | 0.008395249709117 | 0.007605788662789 | 0.009265446549331 | |
| Flux | ISSA | 10 | 8.000984969812112 | 0.000040695179946 | 0.000012868945842 | 8.000955858234098 | 8.001014081390126 | 8.000913617665820 | 8.001036797002600 |
| IDBO | 10 | 8.001014783809277 | 0.000537542286559 | 0.000169985796418 | 8.000630249222336 | 8.001399318396217 | 8.000175893233270 | 8.001798141507340 | |
| IPSO | 10 | 8.001923403443100 | 0.000920844954829 | 0.000291196742914 | 8.001264670645336 | 8.002582136240866 | 8.000754698455000 | 8.003365992410840 | |
| DA | 10 | 8.004792865605145 | 0.000368771669698 | 0.000116615841279 | 8.004529062244501 | 8.005056668965790 | 8.004283632150550 | 8.005524761185520 | |
| Total | 40 | 8.002179005667410 | 0.001666089436014 | 0.000263431870167 | 8.001646164415574 | 8.002711846919246 | 8.000175893233270 | 8.005524761185520 | |
| Levine Statistics | df1 | df2 | Sig. | ||
|---|---|---|---|---|---|
| Stator resistance | Based on mean | 9.284 | 3 | 36 | 0.000 |
| Based on median | 4.959 | 3 | 36 | 0.006 | |
| Based on median and with adjusted df | 4.959 | 3 | 10.294 | 0.022 | |
| Based on trimmed mean | 8.215 | 3 | 36 | 0.000 | |
| D-axis inductance | Based on mean | 10.601 | 3 | 36 | 0.000 |
| Based on median | 7.337 | 3 | 36 | 0.001 | |
| Based on median and with adjusted df | 7.337 | 3 | 18.534 | 0.002 | |
| Based on trimmed mean | 10.028 | 3 | 36 | 0.000 | |
| Q-axis inductance | Based on mean | 5.699 | 3 | 36 | 0.003 |
| Based on median | 4.360 | 3 | 36 | 0.010 | |
| Based on median and with adjusted df | 4.360 | 3 | 17.532 | 0.018 | |
| Based on trimmed mean | 5.309 | 3 | 36 | 0.004 | |
| Flux | Based on mean | 8.882 | 3 | 36 | 0.000 |
| Based on median | 6.879 | 3 | 36 | 0.001 | |
| Based on median and with adjusted df | 6.879 | 3 | 18.774 | 0.003 | |
| Based on trimmed mean | 8.711 | 3 | 36 | 0.000 |
| Sum of Squares | df | Mean Square | F | Sig. | ||
|---|---|---|---|---|---|---|
| Stator resistance | Between groups | 0.000227 | 3 | 0.000 | 278.04 | 0.000 |
| Within groups | 0.00001 | 36 | 0.000 | |||
| Total | 0.000237 | 39 | ||||
| D-axis inductance | Between groups | 8.365 × 10−7 | 3 | 0.000 | 1.948 | 0.139 |
| Within groups | 0.000005 | 36 | 0.000 | |||
| Total | 0.000006 | 39 | ||||
| Q-axis inductance | Between groups | 0.000002 | 3 | 0.000 | 4.815 | 0.006 |
| Within groups | 0.000004 | 36 | 0.000 | |||
| Total | 0.000006 | 39 | ||||
| Flux | Between groups | 0.000097 | 3 | 0.000 | 101.251 | 0.000 |
| Within groups | 0.000011 | 36 | 0.000 | |||
| Total | 0.000108 | 39 |
| Dependent Variable | (I) Algorithm | (J) Algorithm | Mean Difference (I-J) | Std. Error | Sig. | 95% Confidence Interval for Mean | |
|---|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | ||||||
| Stator resistance | ISSA | IDBO | 0.000001909939439 | 0.000115725065964 | 1.000 | −0.000327117490616 | 0.000330937369494 |
| IPSO | −0.005389599449632 * | 0.000321638119768 | 0.000 | −0.006364081165425 | −0.004415117733838 | ||
| DA | 0.000306865882397 * | 0.000093055039155 | 0.036 | 0.000020374999416 | 0.000593356765378 | ||
| IDBO | ISSA | −0.000001909939439 | 0.000115725065964 | 1.000 | −0.000330937369494 | 0.000327117490616 | |
| IPSO | −0.005391509389071 * | 0.000316451525638 | 0.000 | −0.006360501782974 | −0.004422516995167 | ||
| DA | 0.000304955942958 * | 0.000073141836885 | 0.009 | 0.000081577202017 | 0.000528334683899 | ||
| IPSO | ISSA | 0.005389599449632 * | 0.000321638119768 | 0.000 | 0.004415117733838 | 0.006364081165425 | |
| IDBO | 0.005391509389071 * | 0.000316451525638 | 0.000 | 0.004422516995167 | 0.006360501782974 | ||
| DA | 0.005696465332029 * | 0.000308882692131 | 0.000 | 0.004733454715957 | 0.006659475948101 | ||
| DA | ISSA | −0.000306865882397 * | 0.000093055039155 | 0.036 | −0.000593356765378 | −0.000020374999416 | |
| IDBO | −0.000304955942958 * | 0.000073141836885 | 0.009 | −0.000528334683899 | −0.000081577202017 | ||
| IPSO | −0.005696465332029 * | 0.000308882692131 | 0.000 | −0.006659475948101 | −0.004733454715957 | ||
| D-axis inductance | ISSA | IDBO | 0.000027344419332 | 0.000150469685897 | 0.998 | −0.000417270885739 | 0.000471959724404 |
| IPSO | −0.000277842346763 | 0.000230543037074 | 0.632 | −0.000934704283640 | 0.000379019590114 | ||
| DA | 0.000104906938305 | 0.000139026148934 | 0.873 | −0.000325602576440 | 0.000535416453050 | ||
| IDBO | ISSA | −0.000027344419332 | 0.000150469685897 | 0.998 | −0.000471959724404 | 0.000417270885739 | |
| IPSO | −0.000305186766095 | 0.000194740938691 | 0.434 | −0.000891903338154 | 0.000281529805963 | ||
| DA | 0.000077562518973 | 0.000064048507760 | 0.633 | −0.000115499747512 | 0.000270624785458 | ||
| IPSO | ISSA | 0.000277842346763 | 0.000230543037074 | 0.632 | −0.000379019590114 | 0.000934704283640 | |
| IDBO | 0.000305186766095 | 0.000194740938691 | 0.434 | −0.000281529805963 | 0.000891903338154 | ||
| DA | 0.000382749285068 | 0.000186040793687 | 0.236 | −0.000195384974764 | 0.000960883544901 | ||
| DA | ISSA | −0.000104906938305 | 0.000139026148934 | 0.873 | −0.000535416453050 | 0.000325602576440 | |
| IDBO | −0.000077562518973 | 0.000064048507760 | 0.633 | −0.000270624785458 | 0.000115499747512 | ||
| IPSO | −0.000382749285068 | 0.000186040793687 | 0.236 | −0.000960883544901 | 0.000195384974764 | ||
| Q-axis inductance | ISSA | IDBO | 0.000414964742319* | 0.000125725593736 | 0.019 | 0.000059464303477 | 0.000770465181161 |
| IPAO | 0.000191023624413 | 0.000189206203732 | 0.747 | −0.000358548348926 | 0.000740595597752 | ||
| DA | −0.000106354565808 | 0.000094458134907 | 0.683 | −0.000395277157652 | 0.000182568026036 | ||
| IDBO | ISSA | −0.000414964742319 * | 0.000125725593736 | 0.019 | −0.000770465181161 | −0.000059464303477 | |
| IPAO | −0.000223941117906 | 0.000186314838804 | 0.636 | −0.000767940068268 | 0.000320057832456 | ||
| DA | −0.000521319308126 * | 0.000088524408373 | 0.001 | −0.000791379832180 | −0.000251258784072 | ||
| IPSO | ISSA | −0.000191023624413 | 0.000189206203732 | 0.747 | −0.000740595597752 | 0.000358548348926 | |
| IDBO | 0.000223941117906 | 0.000186314838804 | 0.636 | −0.000320057832456 | 0.000767940068268 | ||
| DA | −0.000297378190220 | 0.000166819164031 | 0.339 | −0.000814618986611 | 0.000219862606171 | ||
| DA | ISSA | 0.000106354565808 | 0.000094458134907 | 0.683 | −0.000182568026036 | 0.000395277157652 | |
| IDBO | 0.000521319308126 * | 0.000088524408373 | 0.001 | 0.000251258784072 | 0.000791379832180 | ||
| IPSO | 0.000297378190220 | 0.000166819164031 | 0.339 | −0.000219862606171 | 0.000814618986611 | ||
| Flux | IDBO | −0.000029813997164 | 0.000170472228680 | 0.998 | −0.000560772632632 | 0.000501144638303 | |
| IPSO | −0.000938433630989 * | 0.000291480964817 | 0.043 | −0.001847660780322 | −0.000029206481656 | ||
| DA | −0.003807895793033 * | 0.000117323758055 | 0.000 | −0.004172396693937 | −0.003443394892128 | ||
| ISSA | 0.000029813997164 | 0.000170472228680 | 0.998 | −0.000501144638303 | 0.000560772632632 | ||
| IPSO | −0.000908619633824 | 0.000337180536312 | 0.072 | −0.001884422843920 | 0.000067183576271 | ||
| DA | −0.003778081795868 * | 0.000206141760498 | 0.000 | −0.004368121264954 | −0.003188042326783 | ||
| ISSA | 0.000938433630989 * | 0.000291480964817 | 0.043 | 0.000029206481656 | 0.001847660780322 | ||
| IDBO | 0.000908619633824 | 0.000337180536312 | 0.072 | −0.000067183576271 | 0.001884422843920 | ||
| DA | −0.002869462162044 * | 0.000313679450268 | 0.000 | −0.003802931466222 | −0.001935992857866 | ||
| ISSA | 0.00380789579303 3 * | 0.000117323758055 | 0.000 | 0.003443394892128 | 0.004172396693937 | ||
| IDBO | 0.003778081795868 * | 0.000206141760498 | 0.000 | 0.003188042326783 | 0.004368121264954 | ||
| IPSO | 0.002869462162044 * | 0.000313679450268 | 0.000 | 0.001935992857866 | 0.003802931466222 | ||
References
- Fisch, L.B.K.; Heldwein, M.L. Modeling, Control and Operation of a 10 MW Direct-Drive Wind Energy Conversion System. In Proceedings of the 2021 Brazilian Power Electronics Conference (COBEP), João Pessoa, Brazil, 7–10 November 2021; pp. 1–8. [Google Scholar]
- Dong, W.; Li, Z.; Sun, H.; Zhang, J. Modeling and Analysis of a Deflection Type Permanent Magnet Synchronous Wind Generator System. Energies 2020, 13, 1524. [Google Scholar] [CrossRef]
- Htet, T.Z.; Zhao, Z.; Gu, Q. Design analysis of direct-driven PMSG in wind turbine application. In Proceedings of the 2016 International Conference on System Reliability and Science (ICSRS), Paris, France, 15–18 November 2016; pp. 7–11. [Google Scholar]
- Tian, D.; Wu, X.; Meng, H.; Su, Y. A Two-Stage Multi-Objective Design Optimization Model for a 6 MW Direct-Drive Permanent Magnet Synchronous Generator. Energies 2024, 17, 4147. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Z.; Yan, Q.; Huang, N.; Du, G. An Improved Model-Free Current Predictive Control of Permanent Magnet Synchronous Motor Based on High-Gain Disturbance Observer. Energies 2023, 16, 141. [Google Scholar] [CrossRef]
- Pulvirenti, M.; Scarcella, G.; Scelba, G.; Testa, A.; Harbaugh, M.M. On-Line Stator Resistance and Permanent Magnet Flux Linkage Identification on Open-End Winding PMSM Drives. IEEE Trans. Ind. Appl. 2019, 55, 504–515. [Google Scholar] [CrossRef]
- Rafaq, M.S.; Jung, J. A comprehensive review of state-of-the-art parameter estimation techniques for permanent magnet synchronous motors in wide speed range. IEEE Trans. Ind. Informat. 2020, 16, 4747–4758. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Liang, D.; Liu, K. Online Parameter Estimation for Permanent Magnet Synchronous Machines: An Overview. IEEE Access 2021, 9, 59059–59084. [Google Scholar] [CrossRef]
- Takahashi, K.; Matayoshi, H.; Senjyu, T.; Takahashi, H.; Howlader, A.M. Online Parameter identification of PMSG Wind turbine for Output Power control. In Proceedings of the TENCON 2019–2019 IEEE Region 10 Conference (TENCON), Kochi, India, 17–20 October 2019; pp. 604–607. [Google Scholar]
- Wang, Y.; Xu, S.; Huang, H.; Guo, Y.; Jin, H. A coupled recursive total least squares-based online parameter estimation for PMSM. J. Electr. Eng. Technol. 2018, 13, 2344–2353. [Google Scholar]
- Li, X.; Wang, T.; Fan, W. Adaptive parameter identification based on dead-time compensation for Permanent Magnet Synchronous Machines for the 2011 11th international conference on control, automation and systems (ICCAS 2011). In Proceedings of the 2011 11th International Conference on Control, Automation and Systems, Gyeonggi-do, Republic of Korea, 26–29 October 2011; pp. 1570–1575. [Google Scholar]
- Vesely, I.; Vesely, L.; Bradac, Z. MRAS identification of permanent magnet synchronous motor parameters. IFAC-PapersOnLine. 2018, 51, 250–255. [Google Scholar] [CrossRef]
- Qi, X.; Sheng, C.; Guo, Y.; Su, T.; Wang, H. Parameter Identification of a Permanent Magnet Synchronous Motor Based on the Model Reference Adaptive System with Improved Active Disturbance Rejection Control Adaptive Law. Appl. Sci. 2023, 13, 12076. [Google Scholar] [CrossRef]
- Shi, Y.; Sun, K.; Huang, L.; Li, Y. Online Identification of Permanent Magnet Flux Based on Extended Kalman Filter for IPMSM Drive With Position Sensorless Control. IEEE Trans. Ind. Electron. 2012, 59, 4169–4178. [Google Scholar] [CrossRef]
- Yuan, T.; Wang, T.; Bai, J.; Fan, J. Parameter Identification of Maritime Vessel Rudder PMSM Based on Extended Kalman Particle Filter Algorithm. J. Mar. Sci. Eng. 2024, 12, 1095. [Google Scholar] [CrossRef]
- Udomsuk, S.; Areerak, K.; Areerak, T.; Areerak, K. Online Estimation of Three-Phase Induction Motor Parameters Using an Extended Kalman Filter for Energy Saving. Energies 2024, 17, 2115. [Google Scholar] [CrossRef]
- Avdeev, A.; Osipov, O. PMSM Identification Using Genetic Algorithm. In Proceedings of the 2019 26th International Workshop on Electric Drives: Improvement in Efficiency of Electric Drives (IWED), Moscow, Russia, 30 January–2 February 2019; pp. 1–4. [Google Scholar]
- Bui, M.X.; Dutta, R.; Rahman, F. Application of Deep Learning in Parameter Estimation of Permanent Magnet Synchronous Machines. IEEE Access 2024, 12, 40710–40721. [Google Scholar] [CrossRef]
- Zhai, B.; Ou, K.; Wang, Y.; Cao, T.; Dai, H.; Zheng, Z. Parameter Identification of PMSG-Based Wind Turbine Based on Sensitivity Analysis and Improved Gray Wolf Optimization. Energies 2024, 17, 4361. [Google Scholar] [CrossRef]
- Jiang, J.; Zhang, Z. Multi-parameter identification of permanent magnet synchronous motor based on improved grey wolf optimization algorithm. In Proceedings of the 2021 IEEE 4th Student Conference on Electric Machines and Systems (SCEMS), Huzhou, China, 1–3 December 2021; pp. 1–7. [Google Scholar]
- Gao, S.; Yan, W.; Li, L.; Sai, X.; Zhang, Z.; Shang, R. Parameter Identification of Permanent-Magnetic Synchronous Generator-Wind Turbine based on Particle Swarm Optimization. In Proceedings of the 2024 3rd International Conference on Energy, Power and Electrical Technology (ICEPET), Chengdu, China, 17–19 May 2024; pp. 1558–1561. [Google Scholar]
- Zhou, S.; Wang, D.; Li, Y. Parameter identification of permanent magnet synchronous motor based on modified-fuzzy particle swarm optimization. Energy Rep. 2023, 9, 873–879. [Google Scholar] [CrossRef]
- Su, G.; Wang, P.; Guo, Y.; Cheng, G.; Wang, S.; Zhao, D. Multiparameter Identification of Permanent Magnet Synchronous Motor Based on Model Reference Adaptive System-Simulated Annealing Particle Swarm Optimization Algorithm. Electronics 2022, 11, 159. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An Overview of Variants and Advancements of PSO Algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Tanyildizi, E.; Demir, G. Golden sine algorithm: A novel math-inspired algorithm. Golden sine algorithm: A novel math-inspired algorithm. Adv. Electr. Comput. Eng. 2017, 17, 71–78. [Google Scholar] [CrossRef]
- Yu, X.; Duan, Y.; Cai, Z. Sub-population improved grey wolf optimizer with Gaussian mutation and Lévy flight for parameters identification of photovoltaic models. Expert Syst. Appl. 2023, 232, 120827. [Google Scholar] [CrossRef]


| Parameter | Range |
|---|---|
| Rated power/kW | 6000 |
| Stator resistance/Ω | 0.3 |
| D-axis inductance/H | 0.0085 |
| Q-axis inductance/H | 0.0085 |
| Flux/Wb | 8 |
| Number of pole pairs | 60 |
| Rated line voltage/V | 720 |
| Parameter | ISSA | IDBO | IPSO | DA | ||||
|---|---|---|---|---|---|---|---|---|
| Value | Error (%) | Value | Error (%) | Value | Error (%) | Value | Error (%) | |
| Stator resistance/Ω | 0.3003 | 0.1 | 0.3003 | 0.1 | 0.3056 | 1.8667 | 0.3001 | 0.0333 |
| D-axis inductance/H | 0.0087 | 2.3529 | 0.0086 | 1.1765 | 0.0089 | 4.7059 | 0.00851 | 0.1176 |
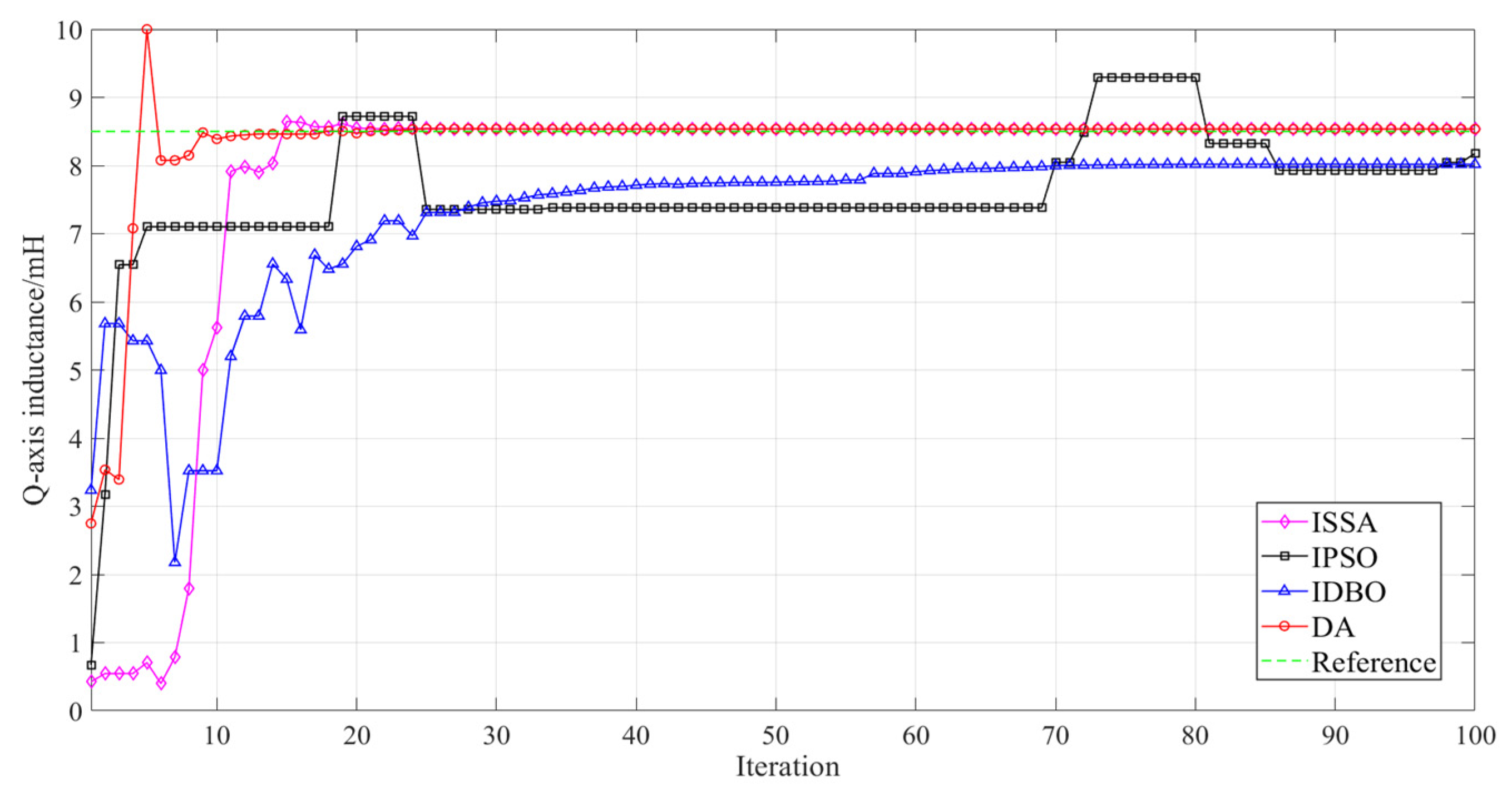
| Q-axis inductance/H | 0.00851 | 0.1176 | 0.0080 | 5.8824 | 0.0082 | 3.5294 | 0.00851 | 0.1176 |
| Flux/Wb | 8.005 | 0.0625 | 8.001 | 0.0125 | 8.002 | 0.025 | 8.001 | 0.0125 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, X.; Tian, D.; Meng, H.; Su, Y. Distributed Parameter Identification Framework Based on Intelligent Algorithms for Permanent Magnet Synchronous Wind Generator. Energies 2025, 18, 683. https://doi.org/10.3390/en18030683
Wu X, Tian D, Meng H, Su Y. Distributed Parameter Identification Framework Based on Intelligent Algorithms for Permanent Magnet Synchronous Wind Generator. Energies. 2025; 18(3):683. https://doi.org/10.3390/en18030683
Chicago/Turabian StyleWu, Xiaoxuan, De Tian, Huiwen Meng, and Yi Su. 2025. "Distributed Parameter Identification Framework Based on Intelligent Algorithms for Permanent Magnet Synchronous Wind Generator" Energies 18, no. 3: 683. https://doi.org/10.3390/en18030683
APA StyleWu, X., Tian, D., Meng, H., & Su, Y. (2025). Distributed Parameter Identification Framework Based on Intelligent Algorithms for Permanent Magnet Synchronous Wind Generator. Energies, 18(3), 683. https://doi.org/10.3390/en18030683




