Renewable Energy from Solid Waste: A Spherical Fuzzy Multi-Criteria Decision-Making Model Addressing Solid Waste and Energy Challenges

Abstract

With rapid urbanization and industrialization, Vietnam is facing many challenges in solid waste management and increasing energy demand. In this context, the development of renewable energy from solid waste not only solves the problem of environmental pollution but also makes an important contribution to energy security and sustainable economic development. Solid waste to energy is a system of solid waste reatment by thermal methods, in which the heat generated from this treatment process is recovered and utilized to produce energy. Site selection is one of the biggest challenges for renewable energy projects. In addition to technical factors, this decision must also consider environmental impacts, including protecting ecosystems, minimizing noise, and limiting impacts on public health. To solve this problem, multi-criteria decision making (MCDM) methods combined with fuzzy numbers are often used. These methods allow planners to evaluate and balance competing factors, thereby determining the most optimal location for the project. In this study, the authors proposed a Spherical Fuzzy Multi-Criteria Decision-making Model (SFMCDM) for site selection in solid waste-to-energy projects. In the first stage, all criteria affecting the decision-making process are defined based on literature review, experts and triple bottom line model (social, environmental, and economic), and analytic hierarchy process (AHP), and fuzzy theory is applied for calculating the weights in the second stage. The weighted aggregated sum product assessment (WASPAS) method is utilized for ranking four potential locations in the final stage. The contribution of the proposed process is its structured, systematic, and innovative approach to solving the location selection problem for renewable energy projects. Choosing the right location not only ensures the success of the project but also contributes to the sustainable development of renewable energy.

1. Introduction

Renewable energy is becoming a prominent field in the global energy system, playing a crucial role in sustainable development worldwide. It meets the demands of economic growth while utilizing clean and safe energy sources. Renewable energy is projected to grow at an annual rate of 7.1% over the next 2 decades, eventually surpassing coal to become the world’s leading energy source by 2040 [1]. In this context, Vietnam must effectively leverage its potential and strengths in renewable energy to achieve the goal of net-zero carbon emissions by 2050, fostering rapid and sustainable development while enhancing its economic competitiveness [2].

Renewable energy sources such as solar, wind, biomass, small hydropower, and solid waste energy all have great potential for development in Vietnam. Vietnam is currently facing an increasing amount of domestic and industrial waste, putting great pressure on the waste treatment system. Converting solid waste into energy not only helps solve the problem of environmental pollution and reduces the burden on landfills but also creates a sustainable energy source for economic development. Waste-to-energy incineration technology is a modern solution that Vietnam can apply to turn challenges into opportunities, while contributing to the implementation of national sustainable development goals.

However, the development of renewable energy projects often faces many challenges such as feasibility assessment, selection of appropriate technology, cost optimization, and risk management. To address these challenges, managers need to consider various factors, ranging from investment costs, technical performance, and environmental impacts to community acceptance. In this context, multi-criteria decision-making (MCDM) models have been applied to provide a systematic and transparent approach to identifying and selecting optimal solutions. The Multi-Criteria Decision-Making Model (MCDM) emerged in the early 1970s as an important research area in the field of decision science, helping to solve complex decision-making problems when considering many different criteria. MCDM has been widely applied in fields such as supply chain management, environmental and energy management, finance, healthcare, etc [3]. Nowadays, with the development of new methods and the integration of advanced techniques such as fuzzy set theory, MCDM models are becoming increasingly important and can be widely applied in many different fields. Fuzzy set theory combined with MCDM models helps to handle ambiguity and uncertainty in the decision-making process. Through fuzzy set theory, subjective and unclear assessments are presented flexibly, increasing the accuracy of the decision-making model and supporting better decision-making. From here, MCDM models are improved in adaptability and can be widely applied in many fields, from supply chain management to choosing the optimal solution in renewable energy development projects, thanks to the ability to integrate information from many different sources [4].

This research proposes a spherical fuzzy multi-criteria decision-making model (SFMCDM) for selecting solid waste energy plant locations. Combining the Spherical Fuzzy Analytic Hierarchy Process (SFAHP) and Weighted Aggregated Sum Product Assessment (WASPAS), the model uses Spherical Fuzzy Numbers (SFNs) to enhance uncertainty representation. This integration provides detailed analysis, improving efficiency and addressing the limitations of traditional MCDM models. At the same time, SFMCDM models support decision-makers in weighing both quantitative and qualitative factors.

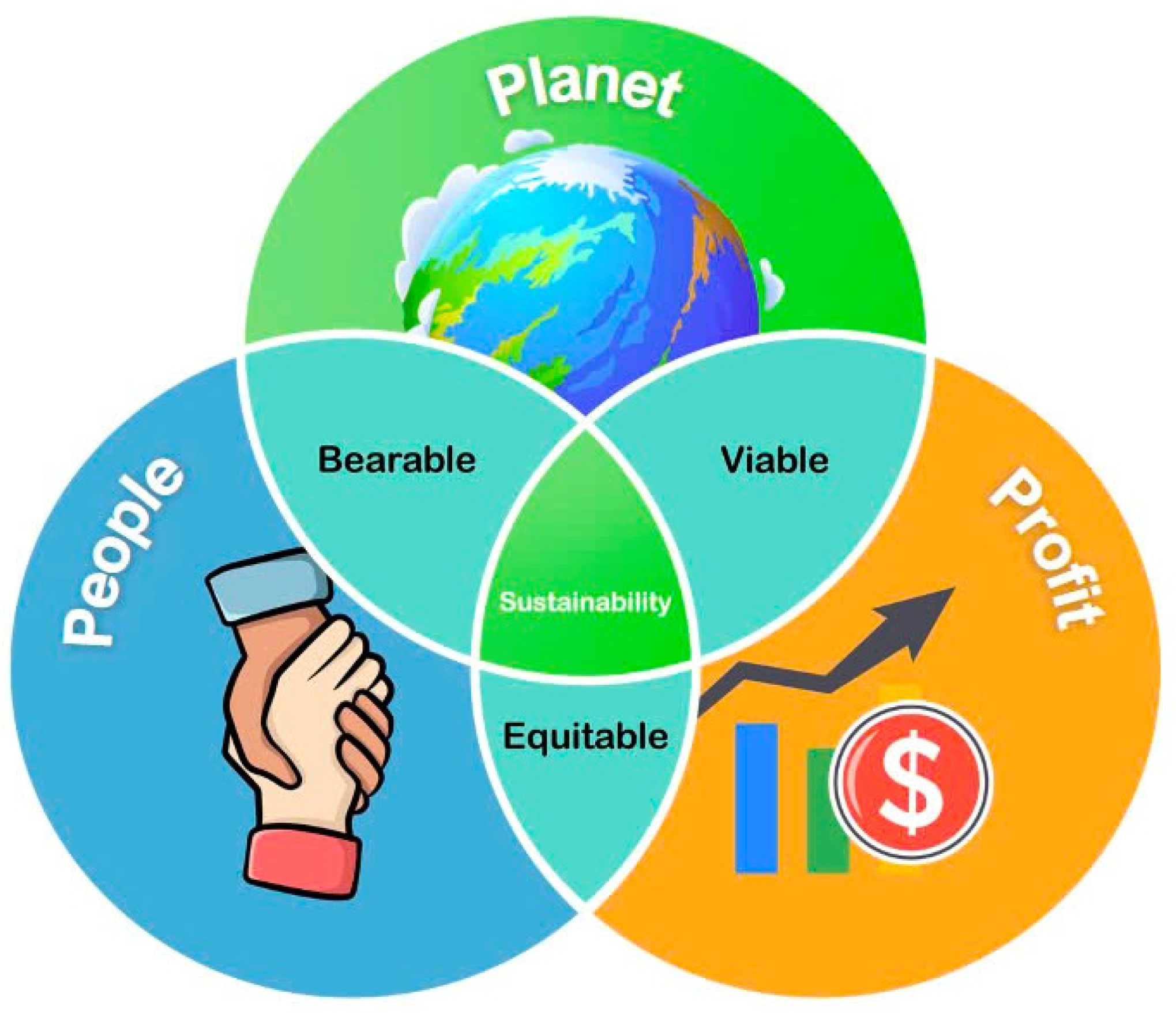
In this study, the authors identify the criteria that influence the decision-making process based on the Triple Bottom Line (TBL) model. The Triple Bottom Line (TBL) model is a framework for evaluating the performance of an organization or projects, focusing on three main aspects: economic (profit), social (people), and environmental (planet). Developed by John Elkington in 1994, the model encourages businesses to expand their goals beyond financial profit to consider social and environmental impact [5]. This approach helps to comprehensively evaluate options, balancing financial benefits with environmental protection requirements and social consensus. In addition, clearly defining criteria helps to increase transparency, minimize conflicts of interest, and improve the acceptability of stakeholders. This is especially important in long-term projects, such as renewable energy, where sustainability criteria play a decisive role in the overall success of the project. A structure of the Triple Bottom Line (TBL) model is shown in Figure 1 [6,7].

The main objective of this study is to develop a decision support model to assist in the assessment and selection of optimal locations for solid waste-to-energy plants, ensuring comprehensive consideration of economic, environmental, and social factors in a complex and uncertain context. The study not only provides a scientific and systematic approach to solving the problem of site selection in waste-to-energy projects, but also contributes to promoting sustainable development, reducing negative impacts on the environment, and optimizing the use of resources.

The structure of this paper is divided into five parts including Section 1 Introduction: presents the research context, the problem to be solved, and the objectives and significance of the research; Section 2 Literature review: provides an overview of previous studies related to the selection of renewable energy plant locations and MCDM methods, especially Spherical Fuzzy AHP and WASPAS; Section 3 Research method: describes in detail the process of building the SFMCDM model, including how to calculate the criteria weights using SFAHP and evaluate the options using WASPAS; Section 4 and Section 5 Case study and Discussion: applies the model to the problem of selecting the location of a solid waste-to-energy plant in a specific locality, including actual data, and analysis of results and discussion; Finally, Section 6 Conclusions: summarizes the results achieved, clearly states the contributions of the research and limitations and suggests future development directions.

2. Literature Review

MCDM models are regarded by researchers as one of the most popular approaches to complex decision-making problems in existing pieces of literature. The term MCDM refers to the process of picking the best choice from a group of possibilities. Different models have been developed to handle this decision process, some of which are based on MCDM methods, which have been employed alone or in conjunction with other MCDM methods and/or other strategies [8,9].

There has been much research on the application of MCDM models in the field of sustainable energy development. Most of these revolve around decision-making problems such as supplier evaluation and selection, location selection, project evaluation, technology evaluation and selection, etc. Qingpeng Cao et al. [10] proposed a three-stage MCDM model including the Stepwise Weight Assessment Ratio Analysis (SWARA), Full Consistency Method (FUCOM), and Evaluation based on Distance from Average Solution (EDAS) methods for evaluation of contractors for the installation of solar panels. Tien-Chin Wang et al. [11] introduced a hybrid MCDM model for evaluation and selection of solar panel supplier for a photovoltaic system design. In this study, the authors combined several MCDM model as FAHP and Data Envelopment Analysis (DEA) model. The result of this study lies in the evolution of a new model that is flexible and practical to the decision-maker in renewable energy sector. Pablo Aragonés Beltrán et al. [12] introduced a decision-making model based on the AHP and the Analytic Network Process (ANP) model. There are three phases in their decision approach. This research analyzed the factors that should be considered before accepting or rejecting proposals for investment in solar thermal power plants. Wang et al. [13] presented a MCDM model for risk ranking of energy performance contracting project under fuzzy environment. In this work, the authors applied Multi-Attributive Border approximation Area Comparison (MABAC) method with fuzzy theory for ranking the risks and identifying the priority of risks by reflecting the decision-maker’s bounded rationality and behavior psychology.

Over the years, many studies have investigated the application of MCDM techniques in solving location evaluation and selection problems of renewable energy projects (

Table 1. Overview of studies of MCDM and renewable energy plant location selection problem.

No.	Authors	Project Type	MCDM Techniques	Location	Main Findings
1	Lijian Sun et al. [14]	Solar energy	AHP	China	Utilized a combination of AHP and Geographic Information System (GIS). Considered quantitative factors only (Climate, Orography, Water availability, and Location). Case study results are validated via sensitivity analysis.
2	Seda Ozdemira and Gokhan Sahin [15]	Solar energy	AHP	Turkey	Utilized a combination of AHP and Photovoltaic Geographic Information System (GIS). Considered quantitative and qualitative factors (Potential energy production, Environmental criteria, Safety, Distance to existing transmission line, and Topographical properties).
3	Majid Vafaeipour et al. [16]	Solar energy	SWARA, WASPAS	Iran	Considered 14 qualitative and quantitative criteria, divided into Economical, Environmental, Social, and Risk factors. Economic factors are considered as the most important.
4	Younes Noorollahi et al. [17]	Solar energy	Fuzzy AHP	Iran	Utilized a combination of Fuzzy AHP and Photovoltaic Geographic Information System (PVGIS). Considered qualitative factors (Climatic, Economic, Orography, and Environment).
5	Meryem Tahri et al. [18]	Solar energy	AHP	Morocco	Utilized a combination of Fuzzy AHP and GIS. Considered qualitative factors (Climate, Location, Orography, and Land use). The most important factors are Climate factors, specifically, potential solar radiation and land surface temperature.
6	Olayinka S. Ohunakin and Burak Omer Saracoglu [19]	Solar energy	AHP, CDPC, DEX, ELECTRE III and IV	Nigeria	A comparative study where multiple MCDM techniques were applied. Considered Technological, Environmental, Legal, Political, and Social factors. While there is some inconsistency between the results of different techniques, the overall result can be used as the basis for further study.
7	Graciele Rediske et al. [20]	Solar energy	AHP, TOPSIS	Brazil	Utilized the combination of AHP and TOPSIS techniques with GIS. Considered qualitative factors: Environmental, Location, Climate, and Orographic. The most important factors are Location factors, followed by Environmental factors. The case study results were verified using sensitivity analysis.
8	Wang et al. [21]	Wind energy	Fuzzy AHP, TOPSIS	Vietnam	The authors considered qualitative and quantitative factors (Environmental, Economic, Social, and Technological). The most important factors are Economic factors.
9	Wang et al. [22]	Solar energy	Fuzzy AHP, TOPSIS, DEA	Vietnam	The authors considered qualitative and quantitative factors (Environmental, Economic, Social, Technological, and Site characteristics). The most important factors in this case are Environmental factors (Sunshine hours and Temperature).
10	Wang et al. [23]	Solid waste power	Fuzzy ANP, TOPSIS	Vietnam	The authors considered qualitative and quantitative factors (Environmental, Economic, Social, and Technological). The most important factors in this case are Economic factors.
11	García et al. [24]	Wind energy	Fuzzy AHP, TOPSIS	USA	Fuzzy AHP-TOPSIS models are applied in combination with GIS. The use of GIS allows a more graphical solution in comparison with traditional MCDM models.

). Most of these studies considered multiple evaluation factors and criteria. In some cases where qualitative criteria are considered, fuzzy logic is often used to convey the ambiguity of a human’s decision-making process. Lijian Sun et al. [14] combined the MCDM model and Geographic Information System (GIS) for the site selection of large-scale solar plants. In this study, the weight of all factors is calculated by the AHP model. A proposed model is illustrated by China. As a result, their model can be used for the selection of the potential location for solar power plant installation. Seda Ozdemira and Gokhan Sahin [15] used the AHP model for electricity production locations; the authors took into consideration both quantitative and qualitative characteristics that play an effective role in electricity production. Majid Vafaeipour et al. [16] proposed a hybrid MCDM model for ranking 25 scattered cities all around the country with the goal of constructing solar power plants. The SWARA and the Weighted Aggregated Sum Product Assessment (WASPAS) models are used in this research. Eventually, by considering the ranked cities, a comprehensive GIS map of their country was also presented.

Younes Noorollahi et al. [17] applied fuzzy Boolean logic, AHP model, and GIS to select the optimal location for constructing solar power plants. The authors considered both qualitative and quantitative factors. Meryem Tahri et al. [18] combined a hybrid MCDM model including GIS tools and the AHP method to assess the suitability of a certain set of locations. As a result, the most suitable sites are those where the ground is flat and oriented towards the south. Olayinka S. Ohunakin and Burak Omer Saracoglu [19] used several MCDM approaches including the AHP model, Consistency-Driven Pairwise Comparisons (CDPC) model, Decision EXpert (DEX), ELECTRE III and IV for location selection of very large concentrated solar power plants. Graciele Rediske et al. [20] combined AHP and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) methods with GIS for evaluation and classification of the best locations for the implantation of solar photovoltaic power plants. Wang et al. [21] developed a hybrid FAHP-TOPSIS model to support the location selection process of wind power plant development projects in Vietnam. A real-world case study was performed to validate the feasibility of the proposed model where seven alternatives were evaluated based on 12 criteria. Wang et al. [22] proposed an integrated methodology of Fuzzy AHP, Data Envelopment Analysis (DEA), and Fuzzy TOPSIS for evaluating and selecting optimal locations for building a solar power plant. The authors considered both quantitative and qualitative criteria including social, environmental, technological, economic, and site characteristics factors. Wang et al. [23] introduced a FANP-TOPSIS model to solve the solid waste power plant location selection problem. In the associated case study, the authors evaluated eight potential locations across 13 quantitative and qualitative criteria. Gil-García et al. [24] utilized a hybrid fuzzy AHP-TOPSIS in combination with GIS for optimal off-shore wind location evaluation process.

In recent years, there have been several MCDM models developed to support location selection problems in wave energy projects (Table 2). Many of these pieces of literature employed fuzzy theory in combination with classical and novel MCDM techniques. Wang et al. [25] presented a FAHP-WAPAS-based approach to the wave energy plant location selection project. A case study was performed where 10 potential locations were evaluated across 15 criteria. Le et al. [26] developed an AHP-TOPSIS model in combination with GIS to identify optimal wave energy locations around the coast of Tasmania, Australia. Eda Bolturk and Cengiz Kahraman [27] developed an Intuitionistic Fuzzy Combinative Distance-based Assessment (CODAS) model to evaluate the potential location of a wave energy farm in Turkey. Abaei et al. [28] introduced a novel Bayesian Network and Influence Diagram-based MCDM model to identify optimal wave energy converter locations in Tasmania. Wang et al. [29] combined Fuzzy Best-Worst Method (BWM) and Fuzzy TODIM to develop a comprehensive approach to the wave energy location evaluation problem.

The aim of this research is to develop a comprehensive and applicable SFMCDM model to support the solid waste-to-energy power plant location selection under a fuzzy decision-making environment. To avoid omitting expert opinion, spherical fuzzy logic is applied in conjunction with classical MCDM methods.

The primary contributions of this research include advancing the theoretical framework for addressing complex site selection challenges in renewable energy projects by integrating economic, environmental, and social criteria. The study introduces an innovative Spherical Fuzzy Multi-Criteria Decision-Making (SFMCDM) model, offering enhanced decision-making capabilities under uncertainty and ambiguity, with more detailed analysis than traditional fuzzy methods. Additionally, it provides a structured and systematic approach to support stakeholders in identifying optimal locations for solid waste-to-energy plants, thereby improving project feasibility, and promoting sustainability.

3. Methodology

3.1. Research Process

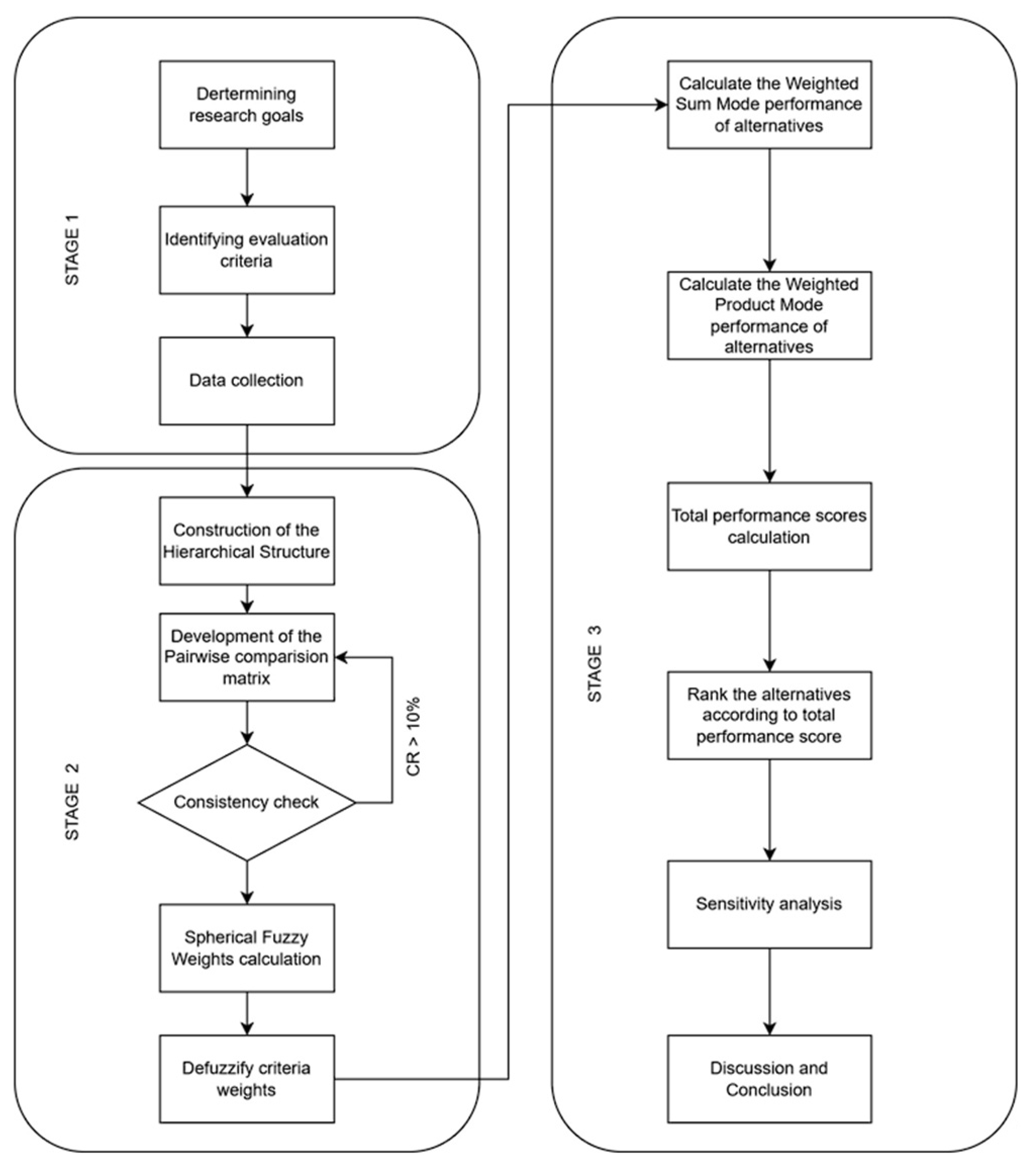
This study introduces a Spherical Fuzzy MCDM framework to determine the optimal site for constructing a renewable energy plant powered by solid waste. The research process is divided into three main stages, as illustrated in Figure 2.

Stage 1: Identifying Evaluation Criteria and Potential Locations

In this phase, key evaluation criteria are established based on insights from the literature, the Triple Bottom Line (TBL) framework, and expert opinions. These criteria encompass economic, environmental, and social dimensions. Concurrently, potential locations are selected to undergo assessment.

Stage 2: Determining Criteria Weights with the Spherical Fuzzy AHP Method

Next, the relative importance of each criterion is quantified using the Spherical Fuzzy AHP method. This approach incorporates expert judgment and accounts for uncertainty, employing a fuzzy data set to objectively and flexibly prioritize the criteria.

Stage 3: Evaluating and Ranking Locations using the WASPAS Method

With criteria weights established, the WASPAS method is then applied to evaluate the potential locations. This step calculates an overall efficiency score for each location, integrating all criteria to produce a final ranking. The outcome identifies the most suitable site for constructing the renewable energy plant.

The key difference between SF-AHP and FAHP lies in the distinction between Spherical Fuzzy Numbers (SFNs) and Triangular Fuzzy Numbers (TFNs). Theoretically, SFNs are superior to TFNs in capturing the vagueness of human decision-making, as TFNs are part of the Type-1 Fuzzy Sets family with two-dimensional membership functions, while SFNs belong to the Hesitant Type-2 Fuzzy Sets family with three-dimensional membership functions.

TFN-based decision-making models often emphasize the lower bound, upper bound, and median values while overlooking membership and possibility degrees. In contrast, SFNs account for these aspects, offering a more comprehensive representation of decision-makers’ opinions in MCDM models [30]. Consequently, the application of the SF-AHP model presents theoretical advantages over the conventional FAHP approach.

3.1.1. Spherical Fuzzy Sets Theory

Spherical fuzzy set theory was recently introduced by Gundogdu et al. [31] as a conceptual fusion of Pythagorean fuzzy sets [32] and Neutrosophic sets [33]. The core idea behind this theory is that a decision maker’s hesitancy can be represented independently from both membership and non-membership degrees. By defining a membership function on a spherical surface, spherical fuzzy sets provide a framework to generalize other extensions of fuzzy sets, thereby offering greater flexibility in handling uncertain and imprecise information.

Spherical fuzzy sets ${\tilde{\mathrm{A}}}_{\mathrm{S}}$ defined over the universe ${\mathrm{U}}_1$ can be represented as

$${\tilde{A}}_S=\left\{x, ({\mu }_{{\tilde{A}}_S}\left(x\right), v_{{\tilde{A}}_S}\left(x\right), {\pi }_{{\tilde{A}}_S}\left(x\right))\left|xϵU_1\right.\right\}$$

(1)

where:

$$\begin{array}{c}{\mu }_{{\tilde{A}}_S}\left(x\right) : U_1\to \left[\mathrm{0,1}\right], v_{{\tilde{A}}_S}\left(x\right) :U_1\to \left[\mathrm{0,1}\right], and {\pi }_{{\tilde{A}}_S}\left(x\right) :U_1\to \left[\mathrm{0,1}\right]\\ \mathrm{and} 0\le {\mu }_{{\tilde{A}}_S}^2\left(x\right)+v_{{\tilde{A}}_S}^2\left(x\right)+{\pi }_{{\tilde{A}}_S}^2(x)\le 1\mathrm{with} \forall x\in U_1\end{array}$$

(2)

${\mu }_{{\tilde{A}}_S}\left(x\right)$ is the degree of membership, $v_{{\tilde{A}}_S}\left(x\right)$ is the degree of non-membership, and ${\pi }_{{\tilde{A}}_S}\left(x\right)$ is the hesitancy of $x$ to ${\tilde{A}}_S$.

Gundogdu and Kahraman [33] established and illustrated the fundamental arithmetic operations for spherical fuzzy sets in their work.

3.1.2. Spherical Fuzzy Analytic Hierarchy Process (SF-AHP) Model

The Spherical Fuzzy AHP (SF-AHP) method, introduced by Gundogdu and Kahraman [34], extends the traditional AHP approach using spherical fuzzy sets. In this study, SF-AHP is applied to determine the weights of the DC selection criteria. Gundogdu and Kahraman’s SF-AHP methodology consists of seven steps:

Step 1: Constructing the Hierarchical Structure: Begin by developing a hierarchical model comprising at least three levels. At the top (Level 1) is the overarching goal, represented by a score index. Level 2 enumerates the nnn criteria influencing the score index. Finally, Level 3 identifies a set of m alternatives A, where $\mathrm{m}\ge 2$, to be evaluated against these criteria.

Step 2: Develop pairwise comparison matrices for the criteria using spherical fuzzy judgments. These judgments rely on the linguistic terms proposed by Gundogdu and Kahraman [34,35]:

Table 2. Linguistic measures of importance [34].

	$(\mathit{\mu },\mathit{v},\mathit{\pi })$	Score Index
Absolutely more importance (AM)	(0.9, 0.1, 0.0)	9
Very high importance (VH)	(0.8, 0.2, 0.1)	7
High importance (HI)	(0.7, 0.3, 0.2)	5
Slightly more importance (SM)	(0.6, 0.4, 0.3)	3
Equally importance (EI)	(0.5, 0.4, 0.4)	1
Slightly lower importance (SL)	(0.4, 0.6, 0.3)	1/3
Low importance (LI)	(0.3, 0.7, 0.2)	1/5
Very low importance (VL)	(0.2, 0.8, 0.1)	1/7
Absolutely low importance (AL)	(0.1, 0.9, 0.0)	1/9

Table 2. Linguistic measures of importance [34].

	$(\mathit{\mu },\mathit{v},\mathit{\pi })$	Score Index
Absolutely more importance (AM)	(0.9, 0.1, 0.0)	9
Very high importance (VH)	(0.8, 0.2, 0.1)	7
High importance (HI)	(0.7, 0.3, 0.2)	5
Slightly more importance (SM)	(0.6, 0.4, 0.3)	3
Equally importance (EI)	(0.5, 0.4, 0.4)	1
Slightly lower importance (SL)	(0.4, 0.6, 0.3)	1/3
Low importance (LI)	(0.3, 0.7, 0.2)	1/5
Very low importance (VL)	(0.2, 0.8, 0.1)	1/7
Absolutely low importance (AL)	(0.1, 0.9, 0.0)	1/9

Equations (3) and (4) are then used to determine the score indices (SI) for each alternative.

$$SI=\sqrt{\left|100\ast \left[{\left({\mu }_{{\tilde{A}}_s}-{\pi }_{{\tilde{A}}_s}\right)}^2-{\left(v_{{\tilde{A}}_s}-{\pi }_{{\tilde{A}}_s}\right)}^2\right]\right|}$$

(3)

For AM, VH, HI, SM, and EI.

$${\displaystyle \frac{1}{SI}}={\displaystyle \frac{1}{\sqrt{\left|100*\left[{\left({\mu }_{{\tilde{A}}_s}-{\pi }_{{\tilde{A}}_s}\right)}^2-{\left(v_{{\tilde{A}}_s}-{\pi }_{{\tilde{A}}_s}\right)}^2\right]\right|}}}$$

(4)

For SL, LI, VL, and AL.

Step 3: Convert the linguistic terms in each pairwise comparison matrix into their corresponding score indices. After this conversion, conduct a traditional consistency check. Ensure that the Consistency Ratio (CR) value does not exceed the 10% threshold:

$$CR={\displaystyle \frac{CI}{RI}}$$

(5)

Here, the Consistency Index (CI) is computed as:

$$CI={\displaystyle \frac{{\lambda }_{max}-n}{n-1}}$$

(6)

where ${\lambda }_{max}$ is the largest eigenvalue of the comparison matrix and nnn is the number of criteria. The Random Index (RI) is selected based on the number of criteria, following Gundogdu and Kahraman [34].

Step 4: Determine the spherical fuzzy weights for both the criteria and the alternatives.

The weight of each alternative relative to each criterion is calculated using the following equation:

$$\begin{array}{ll}{SWM}_w\left(A_{S1}, \dots , A_{Sn}\right)& =w_1{A}_{S1}+\dots +w_n{A}_{Sn}\\ & =〈{\left[1-{\prod }_{i=1}^n{\left(1-{\mu }_{A_{Si}}^2\right)}^{w_i}\right]}^{1/2}, {\prod }_{i=1}^n{V}_{A_{Si}}^{w_i}, {\left[{\prod }_{i=1}^n{\left(1-{\mu }_{A_{Si}}^2\right)}^{w_i}-{\prod }_{i=1}^n{\left(1-{\mu }_{A_{Si}}^2-{\pi }_{A_{Si}}^2\right)}^{w_i}\right]}^{1/2}〉\end{array}$$

(7)

where $w=1/n$.

Step 5: Determine the global weights through hierarchical layer sequencing.

The final ranking of the alternatives is determined by aggregating the spherical weights across all levels of the hierarchical structure. This can be achieved using one of two methods: The first method involves employing the score function in Equation (8) to defuzzify the criteria weights.

$$S\left({\tilde{w}}_j^S\right)=\sqrt{\left|100\times \left[{\left(3{\mu }_{{\tilde{A}}_s}-{\displaystyle \frac{{\pi }_{{\tilde{A}}_s}}{2}}\right)}^2-{\left({\displaystyle \frac{v_{{\tilde{A}}_s}}{2}}-{\pi }_{{\tilde{A}}_s}\right)}^2\right]\right|}$$

(8)

Next, the criteria weights are normalized using Equation (9), followed by the application of spherical fuzzy multiplication as outlined in Equation (10):

$${\overline{w}}_j^s={\displaystyle \frac{S\left({\tilde{w}}_j^s\right)}{{\sum }_{j=1}^{n}S\left({\tilde{w}}_j^s\right)}}$$

(9)

$${\tilde{A}}_{S_{ij}}={\overline{w}}_j^s\times {\tilde{A}}_{S_i}=〈{\left(1-{\left(1-{\mu }_{{\tilde{A}}_S}^2\right)}^{{\overline{w}}_j^s}\right)}^{1/2}, v_{{\tilde{A}}_S}^{{\overline{w}}_j^s}, {\left({\left(1-{\mu }_{{\tilde{A}}_S}^2\right)}^{{\overline{w}}_j^s}-{\left(1-{\mu }_{{\tilde{A}}_S}^2-{\pi }_{{\tilde{A}}_S}^2\right)}^{{\overline{w}}_j^s}\right)}^{1/2}〉$$

(10)

With $\forall i$.

The final ranking score ($\tilde{\mathrm{F}}$) for each alternative ${\mathrm{A}}_{\mathrm{i}}$ is computed using Equation (11):

$$\tilde{F}={\sum }_{j=1}^n{\tilde{A}}_{S_{ij}}={\tilde{A}}_{S_{i1}}+{\tilde{A}}_{S_{i2}}+\dots +{\tilde{A}}_{S_{in}}$$

(11)

With $\forall i$.

The second approach involves proceeding with the calculation without defuzzifying the criteria weights. In this method, the spherical fuzzy global weights are determined as follows:

$${\prod }_{j=1}^n{\tilde{A}}_{S_{ij}}={\tilde{A}}_{S_{i1}}\times {\tilde{A}}_{S_{i2}}\times \dots \times {\tilde{A}}_{S_{in}}$$

(12)

Subsequently, the final ranking score ($\tilde{F}$) for each alternative is computed using Equation (11).

3.1.3. Weighted Sum Method of Evaluation for Products

The Weighted Sum Model (WSM) is a widely used and effective multicriteria decision-making method for evaluating multiple alternatives across various criteria. Initially, $s$ alternatives and $c$ criteria are considered. The importance of each criterion, $x_{sc}$, is represented by $w_c$, while the performance level of alternative $s$ with respect to criterion $c$ is assessed. Ultimately, the relative significance of an alternative, $y$, is calculated using $L_y^{\left(1\right)}$ [36]:

$$L_y^{\left(1\right)}=\sum _{c=1}^n{\overline{x}}_{sc}{w}_c$$

(13)

For each initial criterion value, linear normalization is performed as follows:

$${\overline{x}}_{sc}={\displaystyle \frac{x_{sc}}{{max}_s{x}_{sc}}}$$

(14)

when ${max}_s{x}_{sc}$ indicates that cost is prioritized over value, or:

$${\overline{x}}_{sc}={\displaystyle \frac{{min}_s{x}_{sc}}{x_{sc}}}$$

(15)

when ${min}_{sc}{x}_{sc}$ signifies that minimizing cost is prioritized over maximizing value.

The Weighted Product Model (WPM) is another commonly used approach for evaluating multiple alternatives $y$ based on their overall relative value, $L_y^{\left(2\right)}$:

$$L_y^{\left(2\right)}={\prod }_{c=1}^n{\left({\overline{x}}_{sc}\right)}^{w_c}$$

(16)

The weights representing the overall relative importance are evenly distributed between the WSM and WPM values to calculate the total score. This approach integrates both methodologies for a comprehensive analysis of the evaluation of the alternatives:

$$L_y=0.5L_y^{\left(1\right)}+0.5L_y^{\left(2\right)}$$

(17)

The outcomes from the WSM and WPM models can be further analyzed and adjusted to align with the specific environmental requirements identified in the research. This process aims to enhance the accuracy and effectiveness of decision-making. Such modifications are encapsulated in the Weighted Aggregate Sum Product Assessment (WASPAS) model, which was utilized in this study to rank the alternatives. If the decision-maker has no specific preference, $\lambda$ is set to 0.5:

$$L_y=\lambda \sum _{c=1}^n{\overline{x}}_{sc}{w}_c+\left(1-\lambda \right){\prod }_{j=1}^n{\left({\overline{x}}_{sc}\right)}^{w_c}$$

(18)

3.2. The Subject of Analysis

Vietnam is currently among the top 20 countries generating the largest amounts of waste worldwide. On average, each Vietnamese person produces about 1.2 kg of waste per day, amounting to nearly 70,000 tons nationwide. Of this, more than 70% is buried, while only 13% is incinerated for energy recovery. In the context of increasingly scarce land resources, power plants utilizing waste as a resource are considered an effective solution to harmonize environmental preservation with economic development. Here is a revised version with improved grammar and clarity.

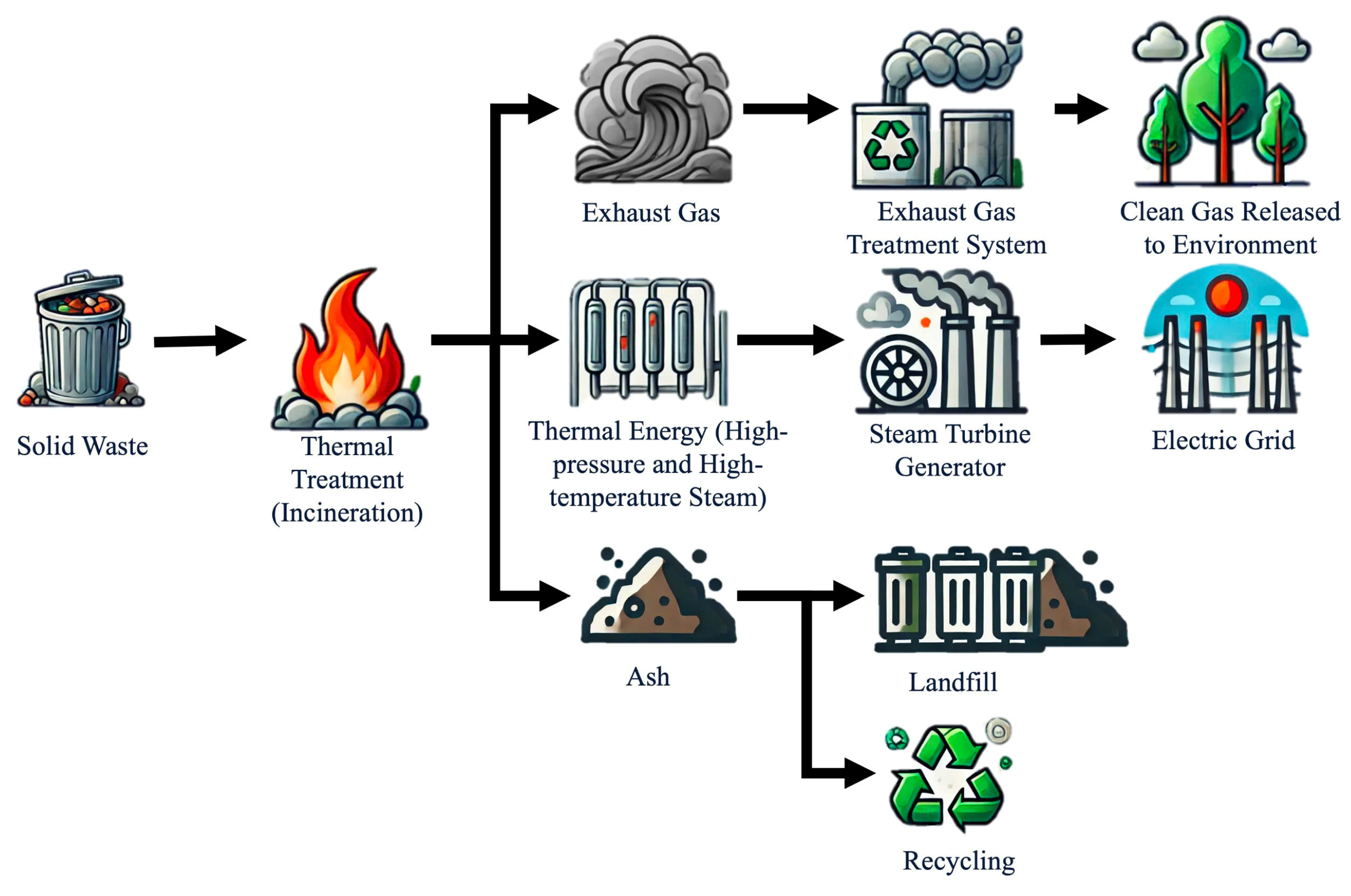
The thermal energy generated during the waste incineration process is recovered by the boiler system inside the incinerator. This system converts the heat into high-temperature and high-pressure steam, which is then transformed into electricity using a water turbine generator. The ash produced after the incineration process is collected and stabilized before being disposed of in landfills.

Additionally, this ash can be recycled to recover metals, produce construction materials, and more. By applying this technology, the volume of waste is significantly reduced (by approximately 90%) compared to its original volume. The closed treatment process effectively prevents odors, water leakage, and other environmental impacts. Furthermore, the treatment process generates electricity to support the plant’s operations and allows surplus electricity to be connected to and sold on the grid. The process of solid waste-to-energy technology is illustrated in Figure 3.

Choosing the location of a solid waste-to-energy plant is a strategic decision that directly affects economic efficiency, environmental impact, and social acceptance. This is a complex decision that requires comprehensive consideration of many related aspects, from the ability to provide stable raw materials and technical feasibility, to the long-term impact on the environment and surrounding community. Moreover, the construction of a solid waste-to-energy plant not only solves the problem of waste treatment but also contributes to promoting sustainable development through the production of renewable energy. Therefore, this decision is not simply a technical problem, but also a complex challenge that requires coordination among stakeholders, and a scientific and transparent assessment process. In this study, the authors develop a decision support model to assist in the assessment and selection of optimal locations for solid waste-to-energy plants, ensuring comprehensive consideration of economic, environmental, and social factors in a complex and uncertain context. A list of criteria affecting the decision-making process is shown in

Table 3. List of criteria.

Criteria	Subcriteria	Symbol
Economic factors	Initial investment cost	THAI01
	Operating and maintenance costs	THAI02
	Potential access to the energy market	THAI03
Social	Job creation	THAI04
	Impact on local communities	THAI05
	Community acceptance	THAI06
Environmental factors	Impact on ecosystems	THAI07
	Ability to manage and reduce pollution	THAI08
	Proximity to sensitive areas	THAI09

.

4. Case Study

The proposed method is applied to a case study where four potential locations are considered for building a solid waste-to-energy plant in Ho Chi Minh City, the economic center of Vietnam.

The spherical fuzzy AHP model offers a flexible approach for calculating weights under uncertainty, aiding decision-makers in making accurate choices. Data is gathered through expert surveys, where criteria are evaluated via pairwise comparisons expressed as spherical fuzzy numbers. These are aggregated into a consistent matrix, and weights are calculated, accounting for uncertainty in judgments. In this case, input for the SF-AHP model was gathered from four industry experts and four academic experts, all possessing extensive experience in renewable energy development. The weights of the nine criteria are shown in

Table 4. Initial Comparison Matrices.

Criteria	Left Criteria Is Greater				Equally Importance	Right Criteria Is Greater				Criteria	Number of Experts
	AMI	VHI	HI	SMI	EI	SLI	LI	VLI	ALI
A				4	3	1				B	8
A			3	2	2	1				C	8
A				4	3		1			D	8
A					5	2		1		E	8
A					4	2	1	1		F	8
A					3	3	1	1		G	8
A					5	1	1	1		H	8
A				2	3	1	1	1		I	8
B					2	4	2			C	8
B					4	1	3			D	8
B					4	3	1			E	8
B						5	2	1		F	8
B					2	2	3	1		G	8
B					2	2	3	1		H	8
B					4	3	1			I	8
C				2	2	2	2			D	8
C					5	2	1			E	8
C					1	3	3	1		F	8
C					2	3	2	1		G	8
C					3	2	2	1		H	8
C						3	4	1		I	8
D						1	3	4		E	8
D					3	4	1			F	8
D				2	3	1	2			G	8
D						3	3	1	1	H	8
D					3	4	1			I	8
E				5		3				F	8
E					4	4				G	8
E				2	3	1	2			H	8
E					4	2	1	1		I	8
F					4	2	1	1		G	8
F					5	2		1		H	8
F			2	3	1	2				I	8
G					3	4		1		H	8
G			2	2	2	1		1		I	8
H				1	2	3	1	1		I	8

.

The pairwise comparison evaluation matrix of experts is summarized in Table 4.

The geometric mean of experts’ evaluations is calculated to check the consistency of the data (Consistency Ratio—CR) as shown in

Table 5. Geometric mean of all experts.

Criteria	THAI01	THAI02	THAI03	THAI04	THAI05	THAI06	THAI07	THAI08	THAI09
THAI01	1.000	1.510	2.098	1.416	0.596	0.487	0.425	0.559	0.736
THAI02	0.662	1.000	0.386	0.477	0.542	0.264	0.326	0.326	0.542
THAI03	0.477	2.590	1.000	0.669	0.621	0.284	0.347	0.398	0.232
THAI04	0.706	2.098	1.495	1.000	0.180	0.472	0.767	0.216	0.472
THAI05	1.678	1.846	1.609	5.550	1.000	1.316	0.577	0.767	0.487
THAI06	2.053	3.789	3.521	2.118	0.760	1.000	0.487	0.596	1.715
THAI07	2.355	3.069	2.879	1.303	1.732	2.053	1.000	0.453	1.345
THAI08	1.789	3.069	2.510	4.634	1.303	1.678	2.209	1.000	0.487
THAI09	1.359	1.846	4.306	2.118	2.053	0.583	0.743	2.053	1.000

:

Normalized matrix of Table 5 as shown in

Table 6. Normalized matrix.

Criteria	THAI01	THAI02	THAI03	THAI04	THAI05	THAI06	THAI07	THAI08	THAI09	MEAN
THAI01	0.083	0.073	0.106	0.073	0.068	0.060	0.062	0.088	0.105	0.0796
THAI02	0.055	0.048	0.019	0.025	0.062	0.032	0.047	0.051	0.077	0.0463
THAI03	0.039	0.124	0.050	0.035	0.071	0.035	0.050	0.063	0.033	0.0556
THAI04	0.058	0.101	0.076	0.052	0.021	0.058	0.111	0.034	0.067	0.0642
THAI05	0.139	0.089	0.081	0.288	0.114	0.162	0.084	0.120	0.069	0.1273
THAI06	0.170	0.182	0.178	0.110	0.086	0.123	0.071	0.094	0.244	0.1398
THAI07	0.195	0.147	0.145	0.068	0.197	0.252	0.145	0.071	0.192	0.1570
THAI08	0.148	0.147	0.127	0.240	0.148	0.206	0.321	0.157	0.069	0.1739
THAI09	0.113	0.089	0.217	0.110	0.234	0.072	0.108	0.322	0.143	0.1563

.

The matrix weights are normalized as shown in

Table 7. Normalized weighted matrix.

Criteria	WSV	CV
THAI01	0.7800	9.7948
THAI02	0.4494	9.7034
THAI03	0.5354	9.6217
THAI04	0.6215	9.6807
THAI05	1.2764	10.0239
THAI06	1.3555	9.6995
THAI07	1.5269	9.7266
THAI08	1.7191	9.8883
THAI09	1.5420	9.8662

.

$$\mathrm{Lamda} \max ={\displaystyle \frac{9.7948+9.7034+9.6217+9.96807+10.0239+9.6995+9.7266+9.8883+9.8662}{9}}=9.7783$$

Using Formulas (5) and (6), CI and CR are calculated as follows:

$$\mathrm{CI}={\displaystyle \frac{9.7783-9}{9-1}}=0.0973$$

Since the problem involves a total of nine criteria, n = 9. According to Saaty, RI = 1.45

$$\mathrm{CR}={\displaystyle \frac{0.0973}{1.45}}=0.0671 \mathrm{satisfies} \mathrm{the} \mathrm{condition} \mathrm{CR}\le 0.1$$

Since the condition CR is satisfied, the spherical fuzzy weights are determined by using the conversion scale in Table 2 to transform the pairwise comparison matrix in Table 4 and calculate the geometric mean weights in spherical fuzzy numbers as shown in

Table 8. Geometric mean in spherical fuzzy.

	THAI01			THAI02			THAI03			THAI04			THAI05			THAI06			THAI07			THAI08			THAI09
THAI01	0.500	0.400	0.400	0.533	0.812	0.695	0.577	0.837	0.744	0.514	0.789	0.682	0.422	0.706	0.593	0.396	0.663	0.567	0.385	0.641	0.552	0.407	0.686	0.582	0.426	0.686	0.596
THAI02	0.421	0.703	0.587	0.500	0.400	0.400	0.394	0.647	0.558	0.401	0.673	0.577	0.431	0.713	0.600	0.341	0.563	0.500	0.348	0.585	0.517	0.348	0.585	0.517	0.431	0.713	0.600
THAI03	0.378	0.633	0.549	0.563	0.833	0.733	0.500	0.400	0.400	0.436	0.693	0.603	0.444	0.737	0.616	0.339	0.566	0.503	0.361	0.602	0.527	0.371	0.623	0.541	0.318	0.532	0.481
THAI04	0.429	0.710	0.598	0.519	0.818	0.703	0.509	0.778	0.678	0.500	0.400	0.400	0.254	0.441	0.414	0.420	0.689	0.584	0.448	0.717	0.619	0.277	0.470	0.429	0.420	0.689	0.584
THAI05	0.483	0.796	0.665	0.499	0.802	0.678	0.475	0.790	0.658	0.734	0.925	0.892	0.500	0.400	0.400	0.515	0.759	0.668	0.447	0.733	0.612	0.448	0.717	0.619	0.396	0.663	0.567
THAI06	0.518	0.815	0.698	0.646	0.871	0.802	0.626	0.868	0.793	0.525	0.813	0.698	0.466	0.709	0.618	0.500	0.400	0.400	0.396	0.663	0.567	0.422	0.706	0.593	0.551	0.801	0.712
THAI07	0.545	0.827	0.719	0.595	0.856	0.769	0.584	0.847	0.755	0.484	0.767	0.658	0.490	0.794	0.665	0.518	0.815	0.698	0.500	0.400	0.400	0.399	0.660	0.563	0.494	0.745	0.664
THAI08	0.492	0.804	0.677	0.595	0.856	0.769	0.555	0.835	0.733	0.693	0.898	0.846	0.484	0.767	0.658	0.483	0.796	0.665	0.534	0.819	0.706	0.500	0.400	0.400	0.394	0.641	0.559
THAI09	0.492	0.772	0.666	0.499	0.802	0.678	0.672	0.889	0.832	0.525	0.813	0.698	0.518	0.815	0.698	0.412	0.660	0.576	0.427	0.685	0.599	0.545	0.811	0.713	0.500	0.400	0.400

and

Table 9. Intergrated Spherical Fuzzy Comparison matrix.

	THAI01			THAI02			THAI03			THAI04			THAI05			THAI06			THAI07			THAI08			THAI09
THAI01	0.500	0.400	0.400	0.533	0.434	0.341	0.577	0.404	0.304	0.514	0.459	0.328	0.422	0.542	0.335	0.396	0.580	0.311	0.385	0.599	0.299	0.407	0.560	0.323	0.426	0.560	0.300
THAI02	0.421	0.545	0.340	0.500	0.400	0.400	0.394	0.594	0.299	0.401	0.572	0.311	0.431	0.536	0.336	0.341	0.661	0.251	0.348	0.644	0.262	0.348	0.644	0.262	0.431	0.536	0.336
THAI03	0.378	0.606	0.290	0.563	0.409	0.316	0.500	0.400	0.400	0.436	0.554	0.300	0.444	0.513	0.349	0.339	0.659	0.250	0.361	0.631	0.274	0.371	0.614	0.286	0.318	0.684	0.226
THAI04	0.429	0.539	0.334	0.519	0.427	0.339	0.509	0.471	0.316	0.500	0.400	0.400	0.254	0.748	0.165	0.420	0.558	0.324	0.448	0.532	0.313	0.277	0.728	0.202	0.420	0.558	0.324
THAI05	0.483	0.452	0.362	0.499	0.445	0.352	0.475	0.458	0.364	0.734	0.273	0.182	0.500	0.400	0.400	0.515	0.491	0.302	0.447	0.517	0.349	0.448	0.532	0.313	0.396	0.580	0.311
THAI06	0.518	0.430	0.342	0.646	0.359	0.264	0.626	0.364	0.274	0.525	0.432	0.339	0.466	0.540	0.301	0.500	0.400	0.400	0.396	0.580	0.311	0.422	0.542	0.335	0.551	0.446	0.299
THAI07	0.545	0.416	0.328	0.595	0.380	0.294	0.584	0.391	0.303	0.484	0.482	0.330	0.490	0.454	0.358	0.518	0.430	0.342	0.500	0.400	0.400	0.399	0.584	0.311	0.494	0.505	0.284
THAI08	0.492	0.443	0.355	0.595	0.380	0.294	0.555	0.406	0.320	0.693	0.319	0.230	0.484	0.482	0.330	0.483	0.452	0.362	0.534	0.426	0.336	0.500	0.400	0.400	0.394	0.599	0.287
THAI09	0.492	0.477	0.327	0.499	0.445	0.352	0.672	0.333	0.239	0.525	0.432	0.339	0.518	0.430	0.342	0.412	0.583	0.289	0.427	0.561	0.293	0.545	0.435	0.312	0.500	0.400	0.400

.

Determine the spherical fuzzy weight using Formula (7) as shown in

Table 10. Calculations to obtain spherical fuzzy weights.

	THAI01			THAI02			THAI03			THAI04			THAI05			THAI06			THAI07			THAI08			THAI09
THAI01	0.750	0.400	0.590	0.716	0.434	0.600	0.667	0.404	0.574	0.736	0.459	0.629	0.822	0.542	0.710	0.843	0.580	0.747	0.852	0.599	0.763	0.835	0.560	0.730	0.819	0.560	0.729
THAI02	0.823	0.545	0.707	0.750	0.400	0.590	0.845	0.594	0.755	0.839	0.572	0.742	0.814	0.536	0.701	0.883	0.661	0.821	0.879	0.644	0.810	0.879	0.644	0.810	0.814	0.536	0.701
THAI03	0.857	0.606	0.773	0.683	0.409	0.583	0.750	0.400	0.590	0.810	0.554	0.720	0.803	0.513	0.682	0.885	0.659	0.823	0.870	0.631	0.794	0.862	0.614	0.780	0.899	0.684	0.848
THAI04	0.816	0.539	0.704	0.731	0.427	0.616	0.741	0.471	0.641	0.750	0.400	0.590	0.936	0.748	0.908	0.824	0.558	0.719	0.799	0.532	0.701	0.923	0.728	0.882	0.824	0.558	0.719
THAI05	0.767	0.452	0.636	0.751	0.445	0.627	0.775	0.458	0.642	0.461	0.273	0.428	0.750	0.400	0.590	0.734	0.491	0.643	0.800	0.517	0.678	0.799	0.532	0.701	0.843	0.580	0.747
THAI06	0.732	0.430	0.615	0.582	0.359	0.512	0.608	0.364	0.532	0.724	0.432	0.609	0.783	0.540	0.692	0.750	0.400	0.590	0.843	0.580	0.747	0.822	0.542	0.710	0.697	0.446	0.608
THAI07	0.703	0.416	0.596	0.645	0.380	0.559	0.659	0.391	0.567	0.766	0.482	0.657	0.760	0.454	0.631	0.732	0.430	0.615	0.750	0.400	0.590	0.841	0.584	0.744	0.756	0.505	0.675
THAI08	0.758	0.443	0.631	0.645	0.380	0.559	0.692	0.406	0.589	0.519	0.319	0.467	0.766	0.482	0.657	0.767	0.452	0.636	0.715	0.426	0.602	0.750	0.400	0.590	0.845	0.599	0.763
THAI09	0.758	0.477	0.651	0.751	0.445	0.627	0.549	0.333	0.492	0.724	0.432	0.609	0.732	0.430	0.615	0.830	0.583	0.747	0.818	0.561	0.732	0.703	0.435	0.606	0.750	0.400	0.590

and

Table 11. Spherical Weighted Fuzzy Mean (SWM).

Criteria	SWM
THAI01	0.469	0.499	0.330
THAI02	0.406	0.565	0.318
THAI03	0.422	0.554	0.308
THAI04	0.432	0.540	0.316
THAI05	0.517	0.452	0.327
THAI06	0.527	0.449	0.320
THAI07	0.517	0.445	0.330
THAI08	0.537	0.428	0.325
THAI09	0.519	0.450	0.324

.

Defuzzify the criteria weights (calculate the crisp weights) using Formula (8) as presented in

Table 12. Crisp Weights.

Criteria	Calculations to Obtain Crisp Weights			Crisp Weights
THAI01	1.546	0.006	12.408	0.107
THAI02	1.121	0.001	10.583	0.091
THAI03	1.239	0.001	11.127	0.096
THAI04	1.297	0.002	11.381	0.098
THAI05	1.923	0.010	13.829	0.120
THAI06	2.023	0.009	14.191	0.123
THAI07	1.922	0.012	13.822	0.119
THAI08	2.099	0.012	14.444	0.125
THAI09	1.947	0.010	13.919	0.120

.

The final priority weights among the criteria are presented in

Table 13. Weight of criteria.

Criteria	Symbol	Weight
Initial investment cost	THAI01	0.1072
Operating and maintenance costs	THAI02	0.0915
Potential access to the energy market	THAI03	0.0962
Job creation	THAI04	0.0984
Impact on local communities	THAI05	0.1195
Community acceptance	THAI06	0.1227
Impact on ecosystems	THAI07	0.1195
Ability to manage and reduce pollution	THAI08	0.1248
Proximity to sensitive areas	THAI09	0.1203

.

In the next stage, the weighted aggregated sum product assessment (WASPAS) method is applied to rank four potential locations. The greatest option is the one that has the highest relative weights among the alternatives. The results of the WASPAS model are shown in

Table 14. Results of WASPAS model.

Alternatives	Li1	Li2	Li
WATHAI01	0.9569	1.0000	0.9784
WATHAI02	0.9123	0.9875	0.9499
WATHAI03	0.7852	0.9734	0.8793
WATHAI04	0.8045	0.9575	0.8810

.

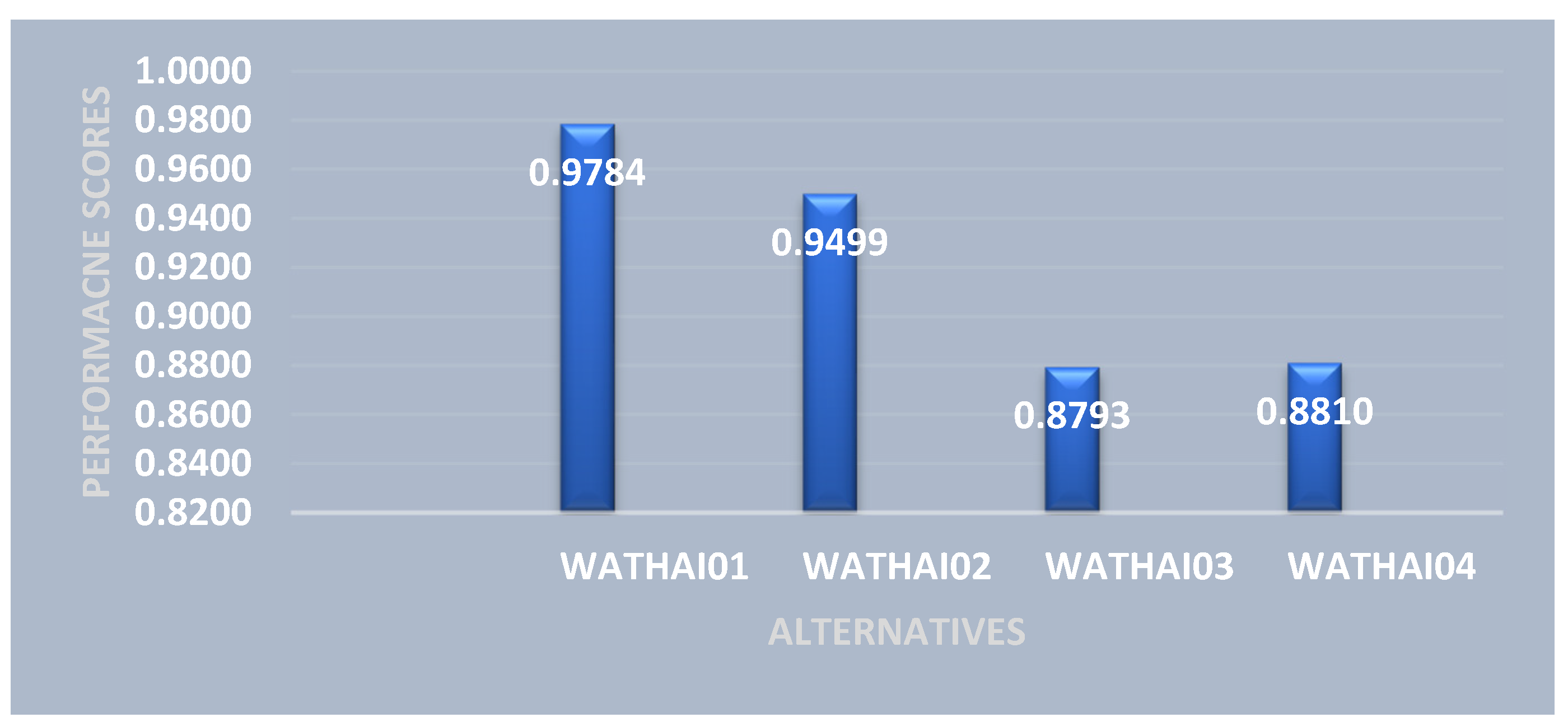
Based on the WASPAS model in

Table 15. Alternatives’ performance scores with changing λ value.

Alternatives	Performance Scores
	λ = 0.0	λ = 0.1	λ = 0.2	λ = 0.3	λ = 0.4	λ = 0.5	λ = 0.6	λ = 0.7	λ = 0.8	λ = 0.9	λ = 1.0
A1	1.0000	0.9957	0.9914	0.9871	0.9827	0.9784	0.9741	0.9698	0.9655	0.9612	0.9569
A2	0.9875	0.9799	0.9724	0.9649	0.9574	0.9499	0.9424	0.9349	0.9274	0.9198	0.9123
A3	0.9734	0.9546	0.9358	0.9169	0.8981	0.8793	0.8605	0.8416	0.8228	0.8040	0.7852
A4	0.9575	0.9422	0.9269	0.9116	0.8963	0.8810	0.8657	0.8504	0.8351	0.8198	0.8045

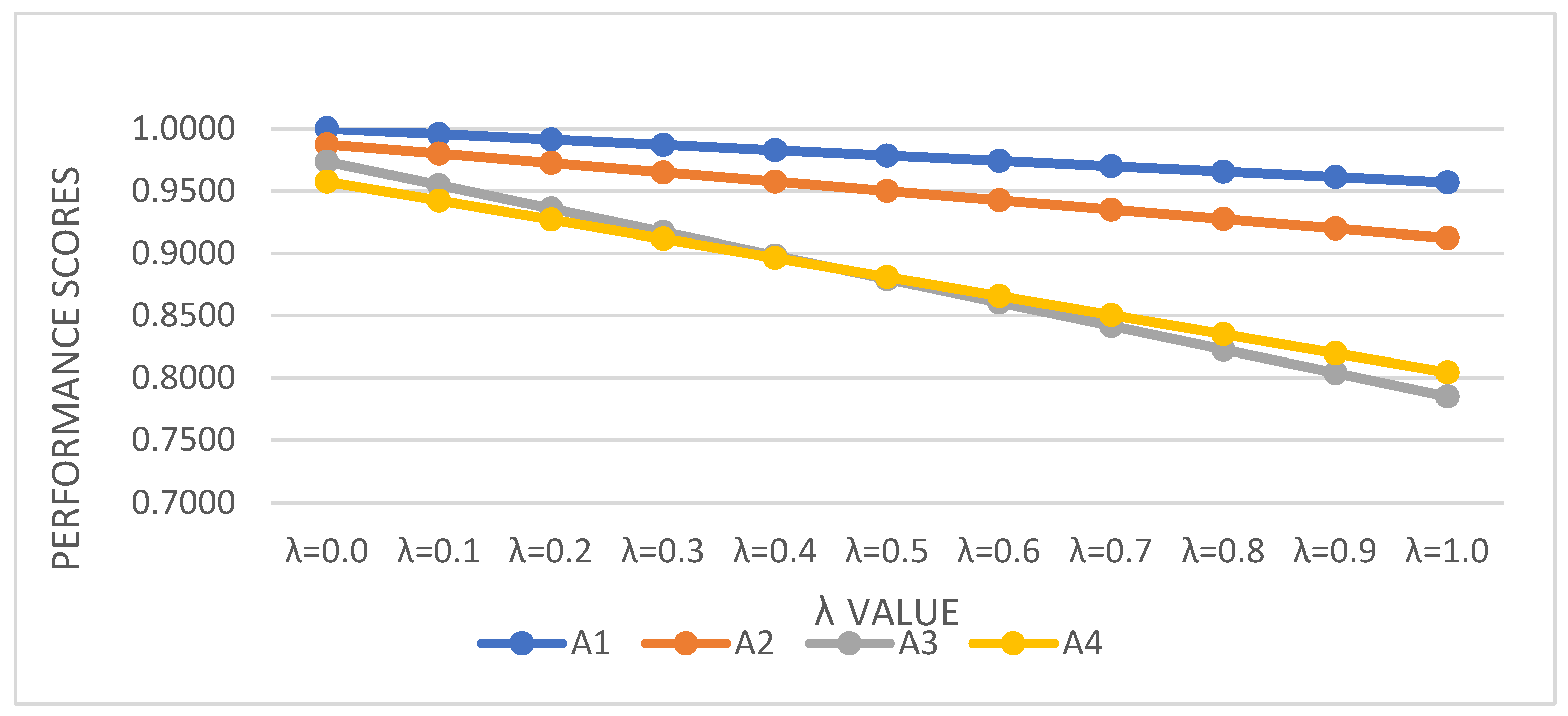
and Figure 4, four locations were ranked, and the potential location with the symbol WATHAI01 was found to be the most appropriate. The WASPAS model considers several factors and rates each location according to how well it meets these requirements. Although WATHAI01 performed the best overall in this instance, the model acknowledges that other providers might also be a good choice in some circumstances. To evaluate the robustness of the results of the proposed process, a sensitivity analysis is conducted. Various approaches can be used for robustness testing and sensitivity analysis. In this study, the rankings of alternatives are assessed under different values of λ, which represents the level of compromise between the WSM and WPM methods. Since λ can take any value between 0 and 1 based on the decision-makers’ preferences, the process is repeated using 10 different λ values. The performance scores of the alternatives corresponding to each λ value are presented in Table 15 and Figure 5.

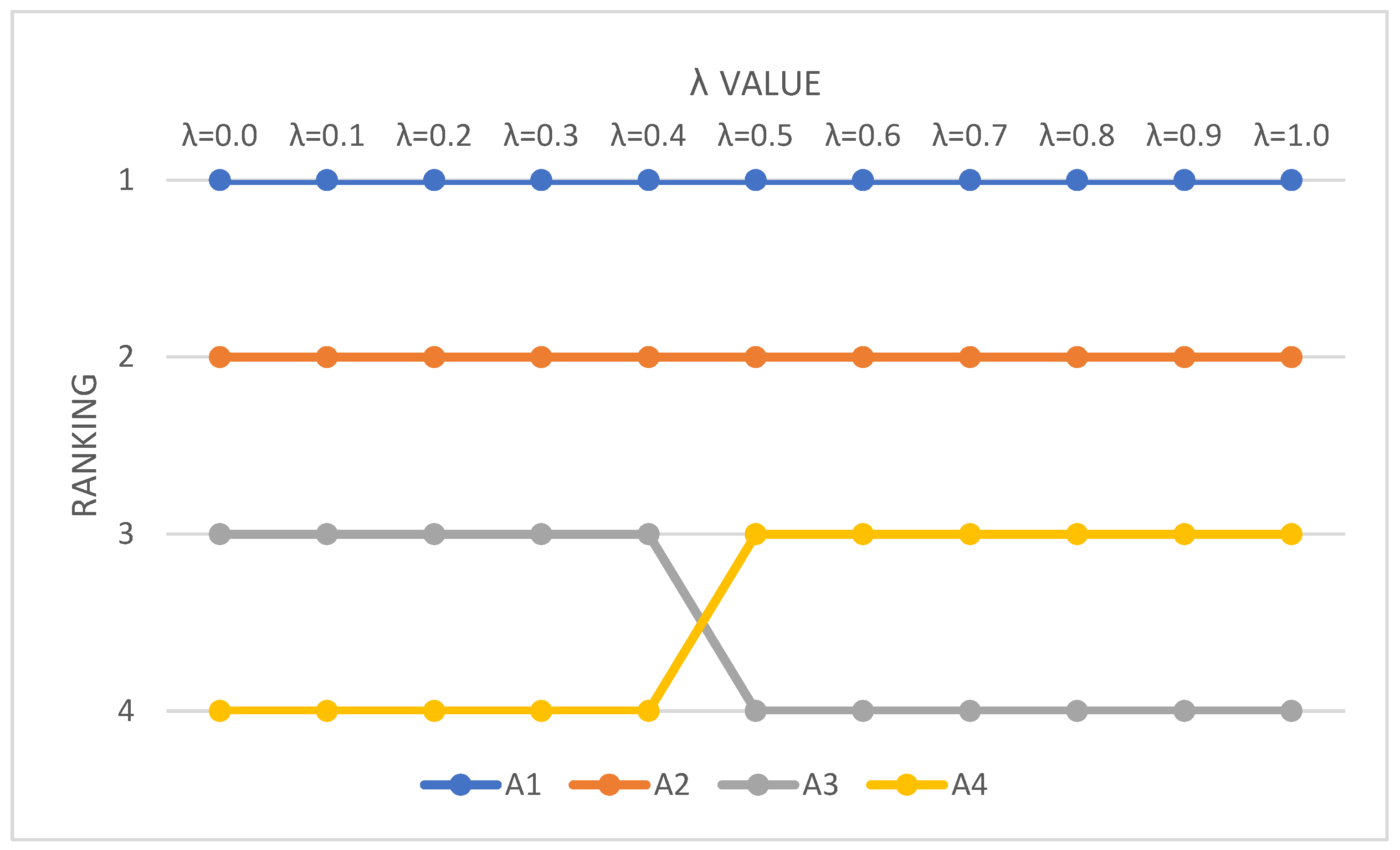
Consequently, the rankings of the alternatives are as shown in

Table 16. Alternatives’ rankings with changing λ value.

Alternatives	Ranking
	λ = 0.0	λ = 0.1	λ = 0.2	λ = 0.3	λ = 0.4	λ = 0.5	λ = 0.6	λ = 0.7	λ = 0.8	λ = 0.9	λ = 1.0
A1	1	1	1	1	1	1	1	1	1	1	1
A2	2	2	2	2	2	2	2	2	2	2	2
A3	3	3	3	3	3	4	4	4	4	4	4
A4	4	4	4	4	4	3	3	3	3	3	3

.

From Table 16 and Figure 6, The rankings of alternatives WATHAI01 and WATHAI02 remain unchanged regardless of the value of λ. This suggests that these alternatives perform consistently well under both the WSM and WPM methods, implying a strong overall performance across all criteria.

The rankings of WATHAI03 and WATHAI04 are reversed when λ reaches 0.5 or higher. This is likely due to the following inherent differences between the WSM and WPM methods:

• WSM aggregates criteria in a linear manner, emphasizing additive contributions of criteria weights and scores. Alternatives that perform moderately well across most criteria tend to be favored in WSM, as such, WATHAI03 with consistent performance across criteria leads to a higher rank.
• WPM is multiplicative, making it more sensitive to variation across criteria. It penalizes alternatives with low scores in any criterion but rewards those with high scores in specific criteria. A4’s higher performance in specific criteria (THAI05 and THAI09) outweighs its weaker performance in others, causing it to surpass A3.

The consistent rankings of WATHAI01 and WATHAI02 suggest robustness in their performance, making them reliable choices regardless of decision-maker preferences.

5. Discussion

The results of the study highlight the effectiveness of the proposed SFMCDM model in identifying optimal locations for solid waste-to-energy plants. Among the evaluated alternatives, WATHAI01 consistently ranked as the most suitable location, demonstrating superior performance across key economic, environmental, and social criteria. This outcome underscores the importance of considering a balanced set of criteria in location selection to achieve sustainable development objectives. The sensitivity analysis further validates the robustness of the proposed model. Regardless of the value of λ, WATHAI01 and WATHAI02 maintained their rankings, indicating their strong performance across different decision-maker preferences. The reversal in rankings between WATHAI03 and WATHAI04 at higher λ values highlights the model’s adaptability to prioritize criteria differently under changing conditions. This flexibility ensures the reliability of the results, supporting informed decision-making tailored to varying stakeholder priorities.

This study underscores the importance of a structured and systematic approach in addressing the complexities of selecting suitable locations for solid waste-to-energy plants. The integration of the Spherical Fuzzy Multi-Criteria Decision-Making (SFMCDM) model enhances the ability to accommodate uncertainty and ambiguity, offering a comprehensive evaluation framework that balances economic, environmental, and social factors. The application of the Spherical Fuzzy Analytic Hierarchy Process (SFAHP) to calculate criteria weights, combined with the Weighted Aggregated Sum Product Assessment (WASPAS) method for ranking alternatives, demonstrates the effectiveness of this approach in decision-making. Key criteria, such as community acceptance, pollution management, and proximity to sensitive areas, were identified as critical to the selection process. The robustness of the model was validated through sensitivity analysis, ensuring the reliability of the results under varying decision-maker preferences.

6. Conclusions

Rapid urbanization, industrialization, and lifestyle changes have led to the generation of large amounts of waste in urban and industrial areas worldwide. To address the issue of domestic waste, countries have implemented various technologies, notably waste-to-energy technology, which enables waste to be treated and recycled before disposal. This study presents a novel Spherical Fuzzy Multi-Criteria Decision-Making (SFMCDM) framework to support the selection of optimal locations for solid waste-to-energy plants, addressing the pressing challenges of renewable energy development in a complex and uncertain environment. By integrating the Spherical Fuzzy Analytic Hierarchy Process (SFAHP) and Weighted Aggregated Sum Product Assessment (WASPAS) methods, the proposed framework effectively balances economic, environmental, and social criteria, providing a comprehensive and systematic solution to the site selection problem.

The key contributions of this research include advancing the theoretical application of spherical fuzzy sets in MCDM and demonstrating its robustness through a sensitivity analysis that validates the consistency of results across various decision-maker preferences. The study also highlights critical insights into the role of criteria such as community acceptance, pollution management, and proximity to sensitive areas in determining optimal locations, contributing valuable knowledge to the field of renewable energy project planning. The impact of this research extends beyond its immediate application, offering policymakers, businesses, and stakeholders a transparent and adaptable tool to support strategic decision-making in renewable energy projects. By promoting sustainable development and efficient resource utilization, the framework aligns with global efforts to address environmental challenges and energy security.

Future research should explore potential enhancements to the SFMCDM framework, such as incorporating additional models specialized in handling quantitative data to further enhance the model’s precision. Additionally, expanding the framework’s application to other renewable energy technologies or diverse geographical contexts could further validate its versatility and practical relevance. By bridging theoretical advancements with practical implementation, this study lays a foundation for informed decision-making in renewable energy projects, contributing to sustainable energy transitions and fostering environmental resilience.