Research on Short-Term Load Forecasting of LSTM Regional Power Grid Based on Multi-Source Parameter Coupling
Abstract
1. Introduction
- (1)
- Multi-source data are used to improve the accuracy of load forecasting. The main data sources include historical load data, meteorological data, and date type information. The time interval of historical load data is 15 min, and 96 sampling points are collected every day. Meteorological data include daily maximum temperature, minimum temperature, rainfall, air humidity, etc. These data are collected in real time through dense sensing technology to ensure the timeliness and accuracy of the data.
- (2)
- To reflect different influencing factors of power load, this paper conducts an in-depth analysis of the historical load characteristics of a region in North China based on different time dimensions. The load in North China has obvious annual, weekly, daily, and holiday characteristics.
- (3)
- To facilitate the training of the model network, the multi-source coupling data such as historical load and characteristic weather are normalized, and the date type is quantified by One-Hot encoding. Considering that the mixing of abnormal power load data will seriously affect the accuracy of the load-forecasting model, a similar day-identification method based on grey correlation degree analysis is proposed to identify the close historical load data, and the linear interpolation method is adopted to correct the data, fill in the missing data, and ensure the continuity and consistency of the data. Most of the existing studies directly eliminate the abnormal load data. and will not be corrected.
- (4)
- Considering that it is difficult to determine parameters such as iteration times and neurons of the LSTM neural network, a load-forecasting modeling method for optimizing LSTM hyperparameters with IPSO is proposed. Linear differential decreasing inertia weights are used to improve the parameter-optimization performance of the basic PSO algorithm and optimize the parameter part of the LSTM neural network. The input data of the model take into account the influence of characteristic weather, date, and historical load data and are compared with the prediction results of other models through case analysis so as to confirm the effectiveness of the proposed model.
2. Load Characteristics Analysis Based on Different Time Dimensions
3. Multi-Source Parameter Coupling Data Processing
3.1. Data Normalization
3.2. Date Type Quantization
3.3. Abnormal Load Handling
4. Regional Power Grid Load-Forecasting Model Based on IPSO-LSTM
4.1. IPSO-LSTM Load-Forecasting Model
- Step 1: Multi-source data such as characteristic meteorological data and historical load are normalized, and date types are encoded by One-Hot technology to get a reasonable input between 0–1.
- Step 2: The grey relational analysis method is used to calculate similar days, and the linear interpolation method is used to correct abnormal historical load data.
- Step 3: Split the sample data into a training set and a testing set.
- Step 4: Initialization of model parameters: set the evolution number N_gen, population size sizepop, acceleration factors c1 and c2, limits of particle velocity and position values Vmin, Vmax, popmin, popmax, and maximum and minimum values of inertia weights wmax and wmin.
- Step 5: Randomly generate the initial particle population pop0(h, ε), where h corresponds to the number of neurons in the hidden layer and ε corresponds to the learning rate; randomly generate the initial velocity V0 of the particles, which corresponds to the velocities of the two important hyperparameters.
- Step 6: Select the evaluation function of the particles. The particles obtained in Step 5 are assigned to the hyperparameters of the LSTM network correspondingly. Input training samples for LSTM training, training to the maximum number of iterations of the LSTM when the termination of training, to obtain the output value of the training samples; in this paper, the mean square error MSE is selected as the evaluation function of the fitness.
- Step 7: Calculate the fitness value of each particle, take the particle value corresponding to the historical best fitness of each particle as the individual best particle pbest for each particle, and instead of the current particle position, select the particle with the smallest fitness as the group best particle gbest iteration.
- Step 8: After starting the next iteration, update the inertia weights and learning factors, and update the position and velocity of each particle. At this time, to avoid the particle swarm algorithm falling into the local optimum, a single particle random variation is added. Update the fitness of the population and repeat Step 7.
- Step 9: After reaching the maximum number of evolutions of the particle swarm, N_gen, or the value of the fitness, reaches stability, the particle updating iteration is stopped, and the optimal training result of the final gbest is obtained.
- Step 10: Assign the values of the gbest particles correspondingly to the LSTM, import the inputs from the training set into the IPSO-LSTM prediction model for iterative model optimization, and choose the Adam optimization method for the network training method.
- Step 11: The inputs of the test set are imported into the trained prediction model in Step 10 to calculate the predicted outputs, the predicted output loads are inverted normalized to obtain the predicted load truth values, and the expected outputs of the test set are used to calculate the model evaluation indexes and complete the load prediction.
4.2. IPSO Performance Verification
4.3. Model Evaluation Criteria
5. Calculus Analysis
5.1. Data Preprocessing
5.2. LSTM Parameter Determination and IPSO Optimization
6. Conclusions
- (1)
- The model prediction framework established in this paper is reasonable. Considering more comprehensive multi-source influencing factors as model input, using One-Hot coding to represent the date type with 6-bit register bits, expanding the data feature dimension, and calculating similar days by grey relational analysis can well correct the abnormal load, laying a foundation for the accuracy of the prediction model.
- (2)
- After preprocessing the multi-source parameter data of dense sensor coupling, the IPSO algorithm is used to optimize and solve the important parameters in the LSTM model. Tests are carried out on six commonly used standard test functions, and it is verified that the PSO algorithm with linear differential decreasing inertia weight has good convergence and optimization ability. The problem of selecting the initial parameters of standard LSTM is solved effectively.
- (3)
- The IPSO-optimized LSTM neural network model established in this paper can keep the relative error of more than 90% of the sampling points below 2%, and the short-term power load prediction results at different times are close to the actual load. Meanwhile, compared with other models in power load prediction, it has higher accuracy and stability and lower error, and it has certain practical application potential.
- (4)
- In practical applications, the power grid load is affected by a variety of complex factors, and the load characteristics in different scenarios may be quite different. Whether the IPSO-optimized LSTM neural network model established in this paper can adapt to these differences and maintain good prediction performance needs to be further tested and verified on a wider dataset. In the future, load data from different regions and different types of power grids can be collected and integrated to build more comprehensive and diverse data sets. By training and validating the model on these datasets, the generalization ability of the model can be improved, so that it can better adapt to the requirements of load forecasting in various complex scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lisardo, P.G.; Anna, F.; Juan, M.G.B.; Angela, P.; Antonio, d.A.S. A Survey on Energy Efficiency in Smart Homes and Smart Grids. Energies 2021, 14, 7273. [Google Scholar] [CrossRef]
- Chen, J.; Liu, L.; Guo, K.; Liu, S.; He, D. Short-Term Electricity Load Forecasting Based on Improved Data Decomposition and Hybrid Deep-Learning Models. Appl. Sci. 2024, 17, 5966. [Google Scholar] [CrossRef]
- Liao, Y.; Weng, Y.; Tan, C.W.; Rajagopal, R. Quick Line Outage Identification in Urban Distribution Grids via Smart Meters. CSEE J. Power Energy Syst. 2022, 8, 1074–1086. [Google Scholar]
- Alhamrouni, I.; Kahar, H.A.; Salem, M.; Swadi, M.; Zahroui, Y.; Kadhim, D.J.; Mohamed, F.A.; Nazari, M.A. A Comprehensive Review on the Role of Artificial Intelligence in Power System Stability, Control, and Protection: Insights and Future Directions. Appl. Sci. 2024, 14, 6214. [Google Scholar] [CrossRef]
- Liu, Y.; Du, W.; Xiao, L.; Wang, H.; Bu, S.; Cao, J. Sizing a Hybrid Energy Storage System for Maintaining Power Balance of an Isolated System With High Penetration of Wind Generation. IEEE Trans. Power Syst. 2016, 31, 3267–3275. [Google Scholar] [CrossRef]
- Li, X. Study on Correlation Between Load and Meteorological Information of Liaoning Power Grid; North China Electric Power University: Beijing, China, 2014. [Google Scholar]
- Xu, Y.; Zhang, J.; Ji, X.; Wang, B.; Deng, Z. Research on short-term load forecasting method based on multi-model fusion neuralnetwork. Control Eng. 2019, 4, 619–624. [Google Scholar]
- Zhang, L.; Zhang, T.; Wang, F.; Qi, X. Ultra-short-term forecasting method based on response characteristics of flexible load. Power Syst. Prot. Control 2019, 9, 27–34. [Google Scholar]
- Shi, J.; Zhang, J. Load forecasting based on multi model by Stacking ensemble learning. Proc. CSEE 2019, 14, 4032–4042. [Google Scholar]
- Chen, H.; Wang, S.; Wang, S.; Wang, D. Aggregated load forecasting method based on gated recurrent unit networks and model fusion. Autom. Electr. Power Syst. 2019, 43, 65–74. [Google Scholar]
- Liu, X.; Lin, Z.; Feng, Z. Short-term offshore wind speed forecast by seasonal ARIMA-A comparison against GRU and LSTM. Energy 2021, 227, 120492. [Google Scholar] [CrossRef]
- Chen, H.; Yang, Y.; Zhang, R. Study on Electric Power Steering System Based on ADAMS. Procedia Eng. 2011, 15, 474–478. [Google Scholar] [CrossRef]
- Fan, C.; Guo, Y. Design of the Auto Electric Power Steering System Controller. Procedia Eng. 2012, 29, 3200–3206. [Google Scholar]
- Paparoditis, E.; Sapatinas, T. Short-Term Load Forecasting: The Similar Shape Functional Time Series Predictor. IEEE Trans. Power Syst. 2013, 28, 3818–3825. [Google Scholar] [CrossRef]
- Lei, S.; Sun, X.; Zhou, Q.; Zhang, X. Research on multivariate time series linear regression forecasting method for short-term load of electricity. Proc. CSEE 2006, 1, 27–31. [Google Scholar]
- Song, K.; Ha, S.; Park, J.W. Hybrid load forecasting method with analysis of temperature sensitivities. IEEE Trans. Power Syst. 2006, 21, 869–876. [Google Scholar] [CrossRef]
- Rafiei, M.; Niknam, T.; Aghaei, J. Probabilistic Load Forecasting using an Improved Wavelet Neural Network Trained by Generalized Extreme Learning Machine. IEEE Trans. Smart Grid 2018, 9, 6961–6971. [Google Scholar] [CrossRef]
- Ko, C.; Lee, C. Short-term load forecasting using SVR (support vector regression)-based radial basis function neural network with dual extended Kalman filter. Energy 2013, 49, 413–422. [Google Scholar] [CrossRef]
- Reddy, S.S.; Jung, C.M. Short-term load forecasting using artificial neural networks and wavelet transform. Int. J. Appl. Eng. Res. 2016, 11, 9831–9836. [Google Scholar]
- Din, G.M.U.; Marnerides, A.K. Short term power load forecasting using Deep Neural Networks. In Proceedings of the 2017 International Conference on Computing, Networking and Communications (ICNC), Silicon Valley, CA, USA, 26–29 January 2017; pp. 594–598. [Google Scholar]
- Liang, Y.; Niu, D.; Hong, W. Short term load forecasting based on feature extraction and improved general regression neural network model. Energy 2019, 166, 653–663. [Google Scholar] [CrossRef]
- Zhao, Z.; Huang, W.; Wei, Y. A medium and long-term power load forecasting method based on wavelet analysis and Elman dynamic neural network. Shanxi Electr. Power 2013, 1, 1–5. [Google Scholar]
- Zhou, H.; Dou, Z.; Zhang, B.; Zhu, Y.; Liao, Q.; Sun, K. Short-term load forecasting based on boosted wavelets and improved PSO-Elman neural network. Electr. Meas. Instrum. 2020, 57, 119–125. [Google Scholar]
- Kong, W.; Dong, Z.; Jia, Y.; David, J.H.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Tan, M.; Yuan, S.; Li, S.; Su, Y.; Li, H.; He, F. Ultra-Short-Term Industrial Power Demand Forecasting Using LSTM Based Hybrid Ensemble Learning. IEEE Trans. Power Syst. 2020, 35, 2937–2948. [Google Scholar] [CrossRef]
- Stefan, U.; Vasile, T.; Andrei, C.C. Analysis for Non-Residential Short-Term Load Forecasting Using Machine Learning and Statistical Methods with Financial Impact on the Power Market. Energies 2021, 14, 6966. [Google Scholar] [CrossRef]
- Wei, T.; Pan, T. Short-term power load forecasting based on improved PSO optimized LSTM network. J. Syst. Simul. 2021, 4, 1–8. [Google Scholar]
- Ge, Z.; Liu, Y. Analytic Hierarchy Process Based Fuzzy Decision Fusion System for Model Prioritization and Process Monitoring Application. IEEE Trans. Ind. Inform. 2019, 15, 357–365. [Google Scholar] [CrossRef]
- Huang, T.D.; Shao, Z.D. An evidential network approach to reliability assessment by aggregating system-level imprecise knowledge. Qual. Reliab. Eng. Int. 2023, 39, 1863–1877. [Google Scholar] [CrossRef]
- Masood, Z.; Gantassi, R.; Choi, Y. Enhancing Short-Term Electric Load Forecasting for Households Using Quantile LSTM and Clustering-Based Probabilistic Approach. IEEE Access 2024, 12, 77257–77268. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, Z.; Li, X. Enhancing Short-Term Power Load Forecasting for Industrial and Commercial Buildings: A Hybrid Approach Using TimeGAN, CNN, and LSTM. IEEE Open J. Ind. Electron. Soc. 2023, 4, 451–462. [Google Scholar] [CrossRef]
- Kwang, H.K.; Byunghoon, C.; Kyu, C.H. Deep Learning Based Short-Term Electric Load Forecasting Models using One-Hot Encoding. J. IKEEE 2019, 23, 852–857. [Google Scholar]
- Wang, C.; Han, D.; Liu, Q.; Luo, S. A Deep Learning Approach for Credit Scoring of Peer-to-Peer Lending Using Attention Mechanism LSTM. IEEE Access 2019, 7, 2161–2168. [Google Scholar] [CrossRef]
- Ma, J.; Liu, H.; Peng, C.; Qiu, T. Unauthorized Broadcasting Identification: A Deep LSTM Recurrent Learning Approach. IEEE Trans. Instrum. Meas. 2020, 69, 5981–5983. [Google Scholar] [CrossRef]
- Xie, T.; Zhang, Y.; Zhang, G.; Zhang, K.; Li, H.; He, X. Research on electric vehicle load forecasting considering regional special event characteristics. Front. Energy Res. 2024, 12, 1341246. [Google Scholar] [CrossRef]
- Yan, H. A Novel Cloud-IPSO-DBN Algorithm for Evaluating Digital Smart City Construction. IEEE Syst. J. 2023, 17, 5109–5117. [Google Scholar] [CrossRef]
- Wang, S.; Liu, Y. A nonlinear dynamic adaptive inertia weight PSO algorithm. Comput. Simul. 2021, 38, 249–253. [Google Scholar]
- Li, M.; Cheng, H.; Yang, Z.; Han, X.; Yang, J. Using fractal interpolation prediction method of typical daily load curve of improvement. Proc. CSU-EPSA 2015, 27, 36–41. [Google Scholar]
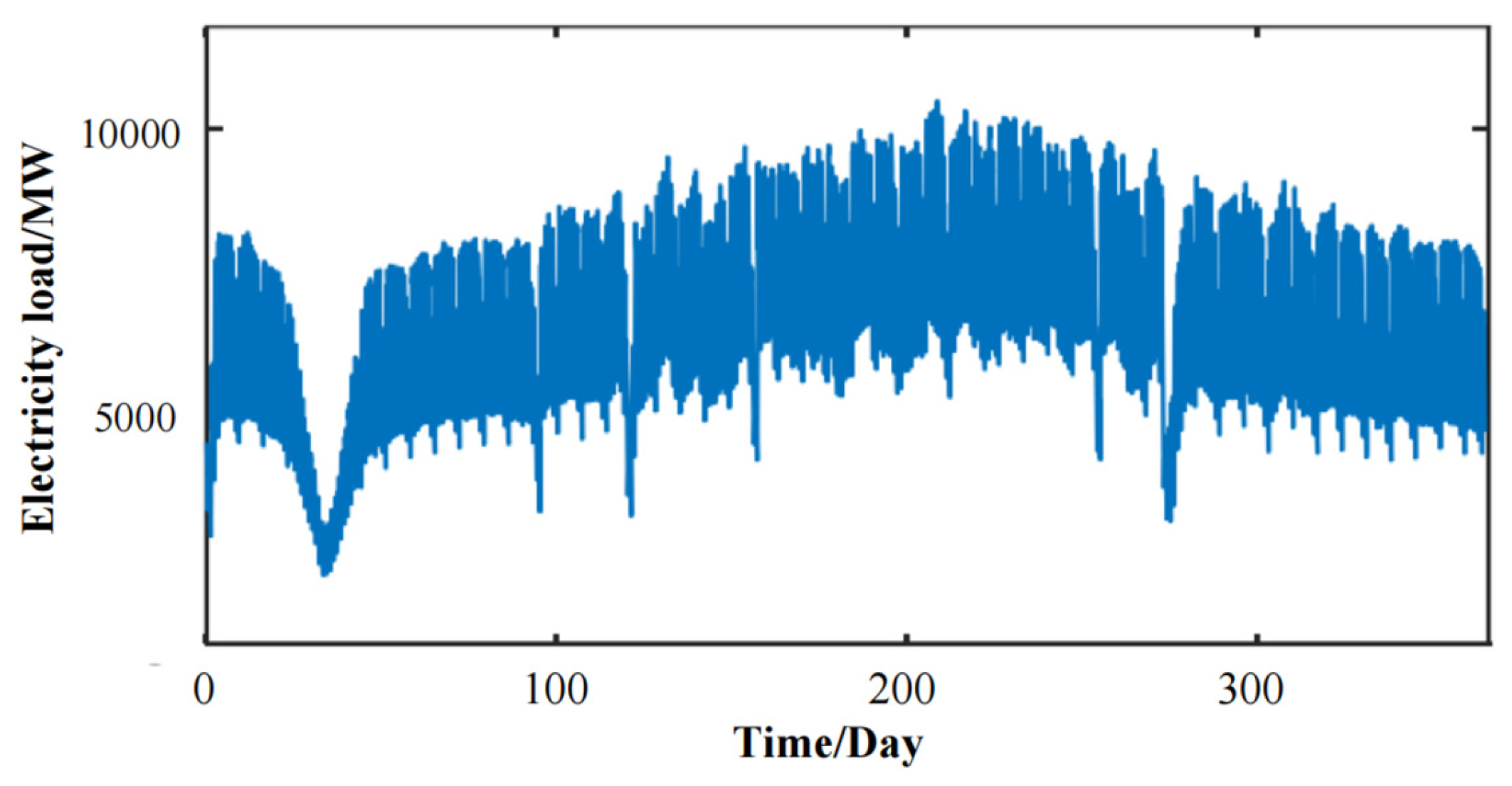
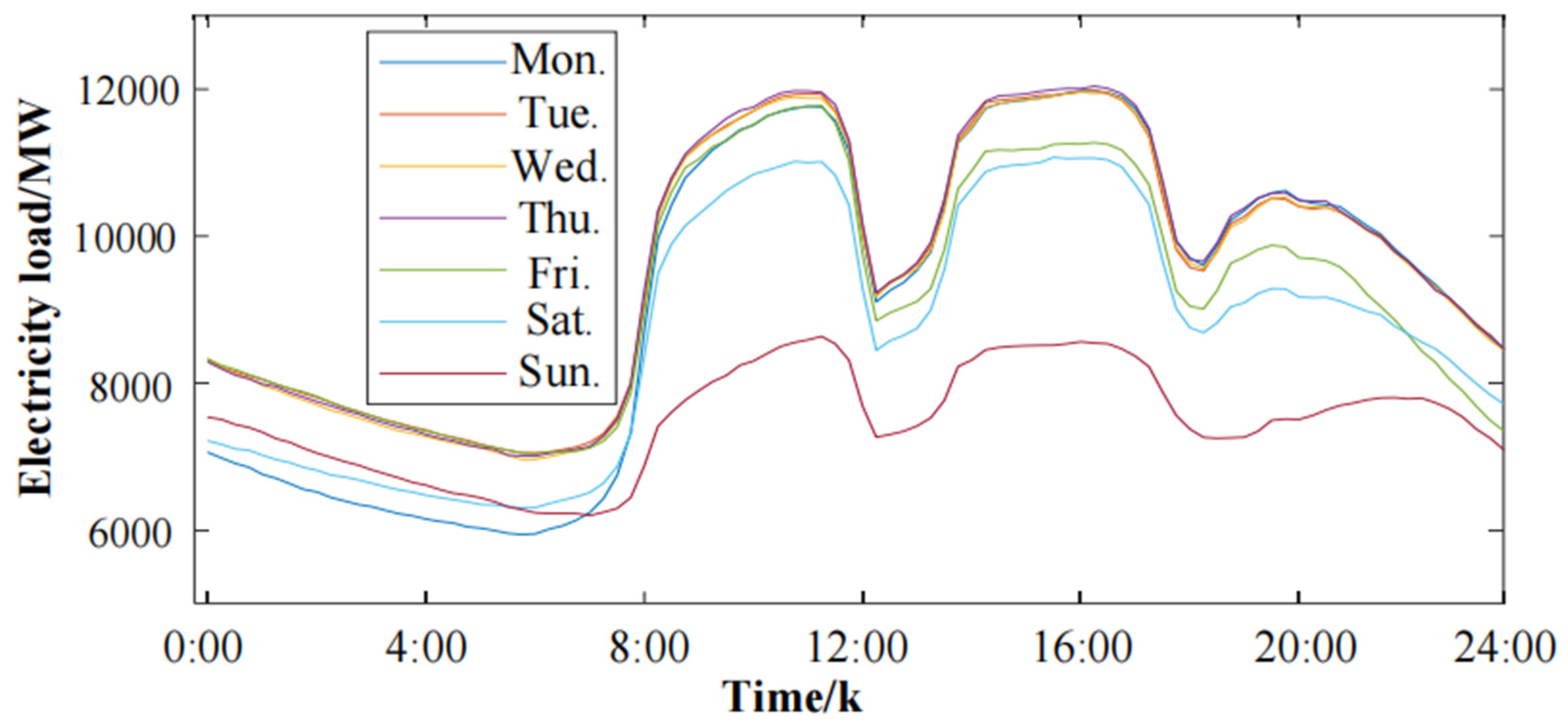









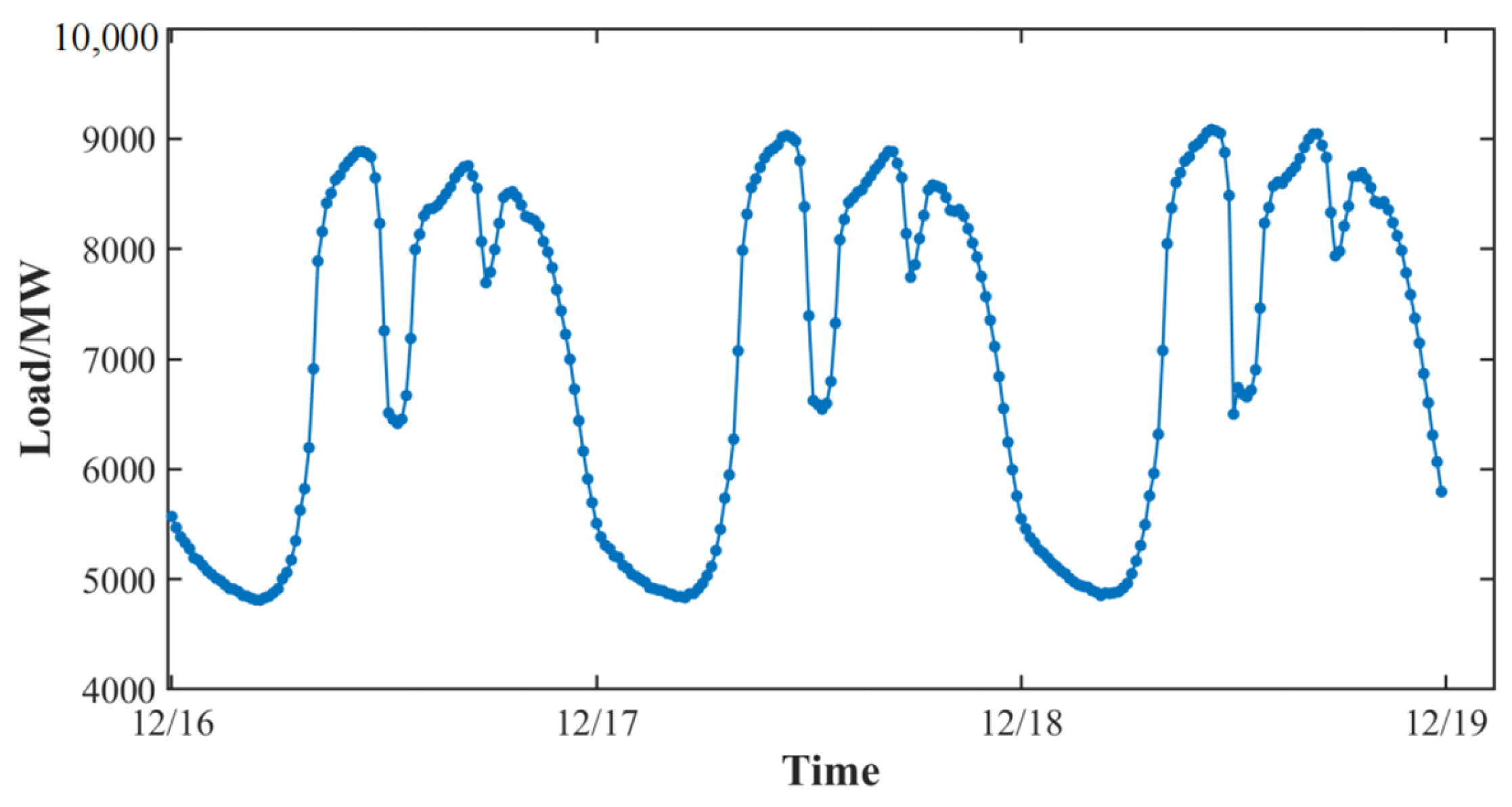





| Time Dimension | Peak Load (MW) | Minimum Load (MW) | Load Fluctuation Percentage (%) |
|---|---|---|---|
| year | 10,000 | 4000 | 150 |
| week | 12,000 | 7000 | 71.43 |
| day | 8500 | 4500 | 88.89 |
| Holidays and festivals | 8000 | 2200 | 263.64 |
| Date Type | Encoding | |
|---|---|---|
| Non-holiday | Monday | 000001 |
| Tuesday to Thursday | 000010 | |
| Friday | 000100 | |
| Saturday | 001000 | |
| Sunday | 010000 | |
| Holidays and festivals | 100000 | |
| Function Name | Optimal Value |
|---|---|
| Ackley function | (0, 0) |
| Griewank function | (0, 0, 0) |
| Rastrigin function | (0, 0) |
| Schaffer function | Multiple locally optimal solutions |
| Sphere function | (0, 0) |
| Rosenbrock function | (1, 1, 0) |
| Date | Raw Data | Normalized Data After Processing | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| DMAXT | DMINT | DMT | DR | AH | DMAXT | DMINT | DMT | DR | AH | |
| 12.8 | 19.6 | 11.9 | 14.9 | 81 | 3.2 | 0.65 | 0.51 | 0.46 | 0.79 | 0.29 |
| 12.9 | 22.7 | 15.4 | 18.2 | 64 | 0 | 0.96 | 0.91 | 0.86 | 0.56 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 12.18 | 14.5 | 7.9 | 11.2 | 35 | 0 | 0.14 | 0.045 | 0.023 | 0.15 | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| 12.27 | 16 | 13.2 | 14.3 | 96 | 11 | 0.29 | 0.66 | 0.39 | 1 | 1 |
| 12.28 | 14.5 | 11 | 12.6 | 87 | 4.8 | 0.14 | 0.40 | 0.19 | 0.87 | 0.43 |
| Time | Raw Data (MW) | Normalized Data After Processing | ||||
|---|---|---|---|---|---|---|
| 12.16 | 12.17 | 12.18 | 12.16 | 12.17 | 12.18 | |
| 0:00 | 5570 | 5506 | 5549 | 0.177 | 0.163 | 0.173 |
| 0:15 | 5469 | 5388 | 5459 | 0.153 | 0.138 | 0.152 |
| 0:30 | 5384 | 5308 | 5379 | 0.134 | 0.116 | 0.132 |
| … | … | … | … | … | … | … |
| 23:45 | 5910 | 5995 | 6066 | 0.257 | 0.277 | 0.294 |
| 24:00 | 5697 | 5756 | 5795 | 0.207 | 0.221 | 0.230 |
| MAPE/% | RMSE | MAE | |
|---|---|---|---|
| IPSO-BP | 2.6549 | 234.2583 | 192.7381 |
| IPSO-Elman | 1.2139 | 115.6638 | 86.1528 |
| IPSO-LSTM | 0.8840 | 80.1699 | 62.0612 |
| MAPE/% | RMSE | MAE | |
|---|---|---|---|
| Multivariate Linear Regression | 3.21 | 280.34 | 220.12 |
| Support Vector Regression | 2.98 | 256.78 | 201.34 |
| IPSO-LSTM | 0.8840 | 80.1699 | 62.0612 |
| Typical Day | MAPE/% | RMSE | MAE | Percentage of Error < 2% |
|---|---|---|---|---|
| 10 March | 0.87 | 83.9343 | 58.7613 | 90.63 |
| 18 June | 0.95 | 74.6874 | 89.7552 | 90.63 |
| 6 October | 0.71 | 86.4276 | 55.4041 | 93.75 |
| 3 December | 0.78 | 64.2497 | 55.0478 | 92.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Liao, Y.; Liu, S.; Liu, C.; Wu, Z. Research on Short-Term Load Forecasting of LSTM Regional Power Grid Based on Multi-Source Parameter Coupling. Energies 2025, 18, 516. https://doi.org/10.3390/en18030516
Li B, Liao Y, Liu S, Liu C, Wu Z. Research on Short-Term Load Forecasting of LSTM Regional Power Grid Based on Multi-Source Parameter Coupling. Energies. 2025; 18(3):516. https://doi.org/10.3390/en18030516
Chicago/Turabian StyleLi, Bo, Yaohua Liao, Siyang Liu, Chao Liu, and Zhensheng Wu. 2025. "Research on Short-Term Load Forecasting of LSTM Regional Power Grid Based on Multi-Source Parameter Coupling" Energies 18, no. 3: 516. https://doi.org/10.3390/en18030516
APA StyleLi, B., Liao, Y., Liu, S., Liu, C., & Wu, Z. (2025). Research on Short-Term Load Forecasting of LSTM Regional Power Grid Based on Multi-Source Parameter Coupling. Energies, 18(3), 516. https://doi.org/10.3390/en18030516






