Identification of Important Lines in Power Grids Based on Improved ProfitLeader Algorithm

Abstract

Rapid and accurate identification of important lines in power grids is crucial for enhancing grid reliability and preventing large-scale blackouts. This paper proposes a method for identifying important lines in power systems using an improved ProfitLeader (IPL) algorithm. First, a correlation network integrating power flow dynamics and topological structure is constructed. Then, by incorporating line weights and directionality, the method overcomes the limitation of traditional ProfitLeader algorithms that only consider node out-degree. Finally, the constructed correlation network and improved algorithm are applied to identify important lines. Comparative studies with other common identification methods on the IEEE 39-bus system show that after attacking the top seven important lines identified by the proposed algorithm, the number of electrical islands in the system increases significantly, and the remaining load rate drops to 43.7%. These results verify the accuracy and effectiveness of the proposed method.

1. Introduction

In recent years, the frequent occurrence of large-scale power outages worldwide has not only exerted profound societal impacts but also highlighted the vulnerability of power systems when confronting contingencies [1,2]. These blackouts are typically initiated by the failure of a specific power line, which subsequently triggers broader cascading effects through grid interconnections, leading to cascading failures or even collapse of the power system [3]. With the rapid integration of renewable energy and increasing complexity of grid structures, the risk of such large-scale blackouts may further escalate in the future [4]. Therefore, the accurate identification and assessment of critical lines within the power system is of paramount importance. This not only mitigates the severe consequences of cascading failures but also holds profound significance for enhancing overall grid stability and reliability [5]. At present, with the continued expansion of power networks, simulation-based methods for identifying critical lines are hindered by their high computational complexity and struggle to meet the demands for online analysis in large-scale systems. How to construct an evaluation model that balances accuracy and efficiency under limited computational resources has become a critical challenge requiring urgent breakthrough in this field of research.

Researchers have proposed various methods to identify critical lines in power systems, which can be broadly categorized into two approaches: large-scale power system simulation and complex network theory analysis. Simulation-based methods primarily focus on dynamic operational characteristics of the grid, employing deterministic or probabilistic analysis to describe the development process of cascading failures. For instance, the OPA (ORNL-PSERC-Alaska) cascading failure model based on self-organized criticality theory represents this category. Ref. [6] enhanced the OPA model by incorporating line outage probabilities in inner loops and grid line upgrades in outer loops to better align with actual grid operating conditions. Ref. [7] utilized cascading failure data to establish a social network describing failure propagation, identifying critical lines by quantifying line influence. Ref. [8] developed a power system splitting simulator based on DC power flow, effectively generating failure chains using stochastic chemical methods and achieving hierarchical clustering of these chains through edit distance to reveal critical lines during failure evolution. Ref. [9] identified critical lines by establishing a DC hidden failure model and employing Monte Carlo simulations for extensive computational analysis. Although these simulation methods demonstrate excellent accuracy, their high computational complexity makes them increasingly challenging to meet the timeliness requirements for online assessment of large-scale power grids. In contrast, scholar Geng proposed an algorithm called the Transmission Line–Stochastic Approach for Link Structure Analysis, which combines Internet-inspired thinking with the physical characteristics of power systems. By constructing an extended adjacency matrix and a Markov probability transition model, it achieves rapid screening of critical transmission lines [10]. Furthermore, scholar Li proposed an Electrical PageRank algorithm based on a dual grid model, enabling the efficient identification of critical lines from the dual dimensions of power transmission and cascading failures [11].

Complex network theory-based methods focus on analyzing system topology and network characteristics to identify critical lines, using parameters such as betweenness and node degree to measure line importance. A purely topological approach cannot capture the electrical characteristics of a power grid. Ref. [12] proposes an extended betweenness centrality method for identifying critical components in power grids by incorporating electrical characteristics such as power transfer distribution and node classification. Ref. [13] introduces a complex-network centrality metric based on maximum flow theory, which identifies critical lines by evaluating the maximum power transfer capacity from generator nodes to load nodes in the grid. Ref. [14] systematically compares the effectiveness of topology-based importance metrics in identifying critical N-k contingency scenarios by quantifying factors including load fluctuations and parameter inaccuracies. However, refs. [12,13,14] failed to account for interactions between lines. Given certain similarities between power grids and the Internet, various Internet evaluation algorithms have been successfully applied to power systems to identify critical components by integrating physical characteristics and system contexts. For example, ref. [15] ranked critical nodes based on node voltage, topology, and power transfer characteristics, refining node types and constructing a non-equiprobable transmission model. Ref. [16] identified lines potentially leading to cascading failures by combining a directed weighted model and line disconnection distribution factors, though the PageRank (PR) algorithm used therein failed to comprehensively evaluate line importance due to neglecting node out-degree. In correlation networks, node out-degree represents the influence of a node on others after its failure, while in-degree reflects the impact of other nodes’ failures on the node itself. In this context, comprehensive consideration of both in-degree and out-degree becomes particularly important.

To enhance the accuracy and comprehensiveness of identifying critical lines in power grids, this paper constructs a correlation network for power systems to quantify influence relationships between lines and incorporates line weights and directional features into the ProfitLeader algorithm. By combining in-degree and out-degree calculations, the comprehensive profit capability of each line is determined to identify critical lines. Finally, simulation results on the IEEE 39-bus system demonstrate the effectiveness and accuracy of the proposed method in identifying critical power grid lines.

2. Original ProfitLeader Algorithm

The ProfitLeader algorithm identifies and ranks important nodes in networks from a novel perspective, with experiments demonstrating its significant advantages in both efficiency and accuracy for node significance evaluation [17].

The ProfitLeader algorithm represents a node importance assessment methodology grounded in the concept of profit capacity. This algorithm treats each network node as an independent entity and determines its significance by computing the economic benefits it can deliver to surrounding nodes. The core premise posits that a node is deemed more important if it can generate substantial benefits for other nodes. The algorithm primarily considers two factors: the intrinsic resource capacity of the node itself, and the probability of resource sharing with other nodes. Consequently, the ProfitLeader algorithm identifies nodes possessing abundant resources and demonstrating willingness to share them as occupying crucial positions within the network.

The available resources of a node are quantified by its degree, which indicates the amount of benefit it can provide to other nodes in the network. Consider an undirected graph G(V,E), where V denotes the set of n nodes and E represents the set of m edges the available resource that node u provides to node v is defined as follows:

$$a_{\left(u\to v\right)}={\displaystyle \sum _{k\in E\left(u,v\right)}\left[d\left(k\right)+d\left(u\right)\right]}$$

(1)

where E(u,v) denotes the set of mutually exclusive neighboring nodes of nodes u and v, defined as E(u,v) = {x∣x ∈ Ω(u) − Ω(v)}, where Ω(u) and Ω(v) represent the sets of adjacent nodes of u and v, respectively; k is an element in E(u,v), such that k ∈ E(u,v); and d(k) and d(u) indicate the degrees of nodes k and u, respectively.

Within the framework of resource sharing between nodes, the proximity of two nodes influences the likelihood of resource sharing between them. In an undirected graph G(V,E), the sharing probability between nodes u and v is defined as follows:

$$s_{\left(u\to v\right)}=s_{\left(v\to u\right)}={\displaystyle \frac{\left|\mathrm{\Omega }\left(u\right)\cap \mathrm{\Omega }\left(v\right)\right|}{\left|\mathrm{\Omega }\left(u\right)\cup \mathrm{\Omega }\left(v\right)\right|}}$$

(2)

In summary, by integrating a node’s available resources and sharing probability, the importance of each node within the network can be quantified. The profit capacity of node u is defined as the sum of the products of its available resources a_(u→v) and sharing probabilities s_(u→v) for all adjacent nodes, as follows:

$$p\left(u\right)={\displaystyle \sum _{v\in \mathrm{\Omega }\left(u\right)}{a}_{\left(u\to v\right)}}{s}_{\left(u\to v\right)}$$

(3)

where Ω(u) denotes the set of neighboring nodes of node u.

In practical applications, most network structures exhibit weighted characteristics where edge weights represent variations in connection strength, and different weight values distinctly influence network stability. Under such circumstances, applying the conventional ProfitLeader algorithm to identify critical lines in power networks without adequately considering the physical characteristics of power systems may encounter several challenges:

• The ProfitLeader algorithm was originally designed for identifying key nodes in social networks. As this study focuses on identifying critical lines in power systems, it is necessary to transform the power network into a line correlation network before applying the algorithm, thereby adapting it to the specific requirements of line analysis.
• The ProfitLeader algorithm primarily analyzes direct connections between nodes but does not adequately account for variations in connection strength. Given the significant differences in connection strength between nodes, the weights of connections should be emphasized when screening for critical lines.
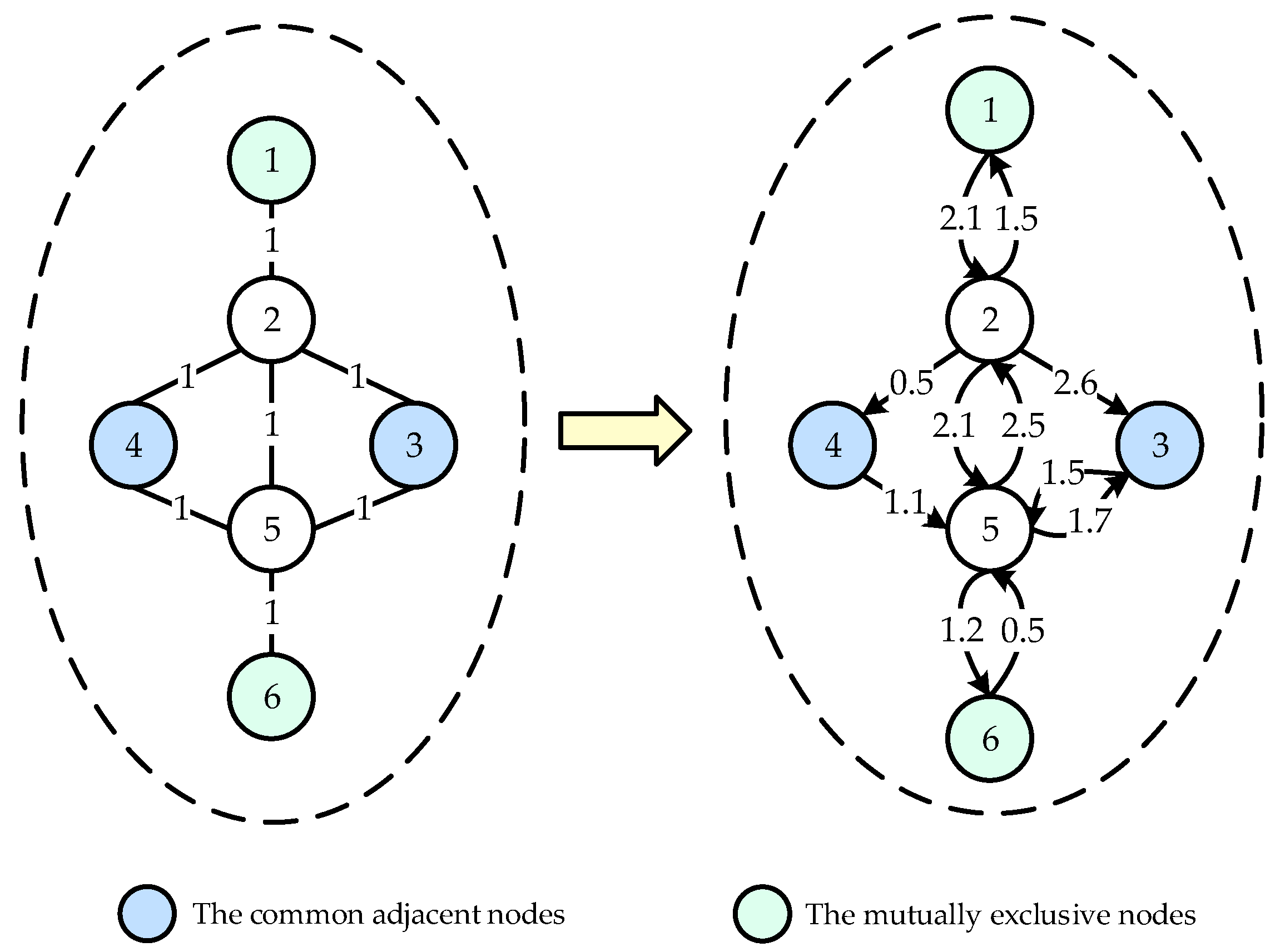
• In the network model constructed by the traditional ProfitLeader algorithm, the relationships between nodes are typically assumed to be symmetric and undirected. However, in the actual fault propagation process of power systems, the electrical coupling and power flow transfer between lines exhibit significant asymmetry and directionality. Consequently, to more accurately assess the importance of nodes in fault propagation, it is necessary to distinguish between the out-degree and in-degree of nodes in the model to reflect their differential influences in different propagation directions.

3. Improved ProfitLeader Algorithm

3.1. Comparison Between Social Network Evaluation and Power Grid Transmission Line Assessment

In the analysis of critical lines in power systems, conventional methods primarily focus on the operational status of individual lines or their topological positions within the grid, often neglecting the interactions between different lines. In practice, the failure of a single transmission line may lead to overloading conditions in other lines, potentially pushing the entire power grid toward a critical state and increasing the risk of cascading failures. To address this challenge, this chapter constructs a comprehensive correlation network that integrates both power flow characteristics and topological structure. While the N-1 criterion can assess system operating conditions under single failures, it struggles to accurately characterize fault propagation characteristics during large-scale cascading blackouts. To address this, this paper focuses on secondary failure scenarios following N-1 contingencies, thereby more precisely revealing interdependencies among transmission lines at the power transfer level.

To clearly illustrate the construction process of the line correlation network, this chapter utilizes the IEEE 9-bus power system for correlation mapping analysis. The corresponding relationships among social networks, power networks, and power system correlation networks are summarized in

Table 1. Mapping relationships among social networks, power networks and power system related networks.

Social Network	Power Network	Power System-Related Network
Entity	Transmission Line	Node
Inter-entity Connection	Inter-line linkage	Line

. The specific procedural steps are as follows:

• Calculate and record the power flow magnitude through each transmission line under normal operating conditions.
• Perform sequential branch outages by disconnecting each line individually, then compute and document the resulting power flow variations in all other lines.
• If no line exceeds its thermal stability limit, proceed to Step 4. Otherwise, disconnect the overloaded line, recalculate the power flow, and record the new system state.
• Normalize the power flow variation in each line by dividing it by the corresponding thermal stability limit, thereby obtaining the correlation matrix of the power system.

Schematic diagram of the directed weighted correlation network of lines is depicted in Figure 1. In the power network, red nodes represent buses, while red edges between nodes correspond to power transmission lines. Within the related network, power transmission lines are treated as blue nodes, where the mutual influences between lines serve as edge weights, thereby achieving the visualization of power flow direction and magnitude.

3.2. Construction of the Line Correlation Matrix

In power systems, a fault on one transmission line may cause significant power flow fluctuations in other lines. According to the operational characteristics of power systems, the power fluctuation magnitude on line j caused by a fault on line i is defined as follows:

$$\mathrm{\Delta }{P}_{i,j}=\left\{\begin{array}{ccc}\left|P_{i,j}-P_j\right|\hfill & \hfill ,\hfill & \hfill other\hfill \\ 0\hfill & \hfill ,\hfill & \hfill P_{i,j}{P}_j>0 and \left|P_{i,j}\right|<\left|P_j\right|\end{array}\right.$$

(4)

where P_i,j represents the power flow on line j after the fault of line i; P_j represents the normal operating power flow on line j before the fault of line i.

Since faults on critical lines can trigger large-scale power flow redistribution, the evaluation of ΔP_i,j should consider both magnitude and direction of power flow. Power flow variations are assessed as follows:

• If the power flow direction on the line remains unchanged before and after the fault, and the absolute value of the post-fault power flow is less than its initial absolute value, then ΔP_i,j is set to 0.
• If the power flow direction remains unchanged before and after the fault and the absolute value of the post-fault power flow is not less than the initial value, or if the power flow direction reverses after the fault, then ΔP_i,j is assigned the absolute value of the difference between the pre-fault and post-fault power flows on the line.

In power systems, the impact of a line fault on other lines depends not only on direct power variations but also requires comprehensive consideration of line safety margins to accurately reflect actual operational conditions. For lines experiencing identical power variations, those with lower safety margins demonstrate more significant impacts, while lines with higher safety margins exhibit relatively smaller influences. The impact magnitude of line i’s fault on line j is defined as follows:

$$\mathrm{\Delta }{w}_{i,j}=\left\{\begin{array}{cc}\mathrm{\Delta }{P}_{i,j}/M_j,\hfill & \hfill i\ne j\\ 0,\hfill & \hfill i=j\end{array}\right.$$

(5)

where M_j represents the thermal stability limit of line j.

Finally, through Equations (4) and (5), the mutual influences between lines are quantified, yielding the power system’s correlation matrix ΔW as follows:

$$\mathrm{\Delta }W=\left[\begin{array}{ccccc}0& \mathrm{\Delta }{w}_{1,2}& \mathrm{\Delta }{w}_{1,3}& \dots & \mathrm{\Delta }{w}_{1,n}\\ \mathrm{\Delta }{w}_{2,1}& 0& \mathrm{\Delta }{w}_{2,3}& \dots & \mathrm{\Delta }{w}_{2,n}\\ \mathrm{\Delta }{w}_{3,1}& \mathrm{\Delta }{w}_{3,2}& 0& \dots & \mathrm{\Delta }{w}_{3,n}\\ ⋮& ⋮& ⋮& & ⋮\\ \mathrm{\Delta }{w}_{n,1}& \mathrm{\Delta }{w}_{n,2}& \mathrm{\Delta }{w}_{n,3}& \dots & 0\end{array}\right]$$

(6)

3.3. Important Transmission Lines

The conventional ProfitLeader algorithm fails to adequately consider network weighting characteristics, which limits its accuracy and effectiveness in identifying critical lines. From the perspective of complex network analysis, while the traditional ProfitLeader algorithm can effectively compute profit capacity of nodes in unidirectional unweighted networks, its calculations for node profit capacity in directed weighted networks often yield relatively coarse results. This limitation may affect the algorithm’s accuracy in identifying critical nodes or important lines within networks.

To address this limitation, this chapter proposes an IPL algorithm that comprehensively considers both adjacent nodes and edge weight information when calculating node influence. The method reflects the importance of connections and their contribution to other nodes through edge weights and directionality. The available resources of a node are redefined as follows:

$$A_{\left(u\to v\right)}={\displaystyle \sum _{k\in \underset{¯}{EN}\left(u,v\right)}\left[\underset{¯}{e}\left(k\right)+\underset{¯}{e}\left(u\right)\right]}$$

(7)

where $\underset{¯}{EN}\left(u,v\right)$ represents the set of common neighboring nodes in the out-degree of nodes u and v; and $\underset{¯}{e}\left(u\right)={\displaystyle \sum _{v\in \mathrm{\Omega }\left(u\right)}{w}_{u,v}}$ denotes the weighted sum of node u’s out-degree, with w_u,v being the connection weight between nodes u and v.

Taking into account both the in-degree and out-degree of nodes comprehensively, the sharing probability between nodes is redefined as follows:

$$S_{\left(u\to v\right)}={\displaystyle \frac{{\displaystyle \sum _{j\in \left|\underset{¯}{\mathrm{\Omega }}\left(u\right)\cap \overline{\mathrm{\Omega }}\left(v\right)\right|}{w}_{u,j}}+{\displaystyle \sum _{i\in \left|\underset{¯}{\mathrm{\Omega }}\left(u\right)\cap \overline{\mathrm{\Omega }}\left(v\right)\right|}{w}_{i,v}+2\cdot w_{u,v}}}{\underset{¯}{e}\left(u\right)+\overline{e}\left(v\right)}}$$

(8)

where $\left|\underset{¯}{\mathrm{\Omega }}\left(u\right)\cap \overline{\mathrm{\Omega }}\left(v\right)\right|$ represents the set of common neighboring nodes between the out-degree of node u and the in-degree of node v. $\overline{e}\left(v\right)={\displaystyle \sum _{u\in \mathrm{\Omega }\left(v\right)}{w}_{u,v}}$ indicates the weighted sum of node v’s in-degree.

The profit capacity is redefined as follows:

$$P\left(u\right)={\displaystyle \sum _{v\in \mathrm{\Omega }\left(u\right)}{A}_{\left(u\to v\right)}}{S}_{\left(u\to v\right)}$$

(9)

Schematic diagram of a directed weighted network is shown in Figure 2. The network is transformed from an undirected unweighted form into a directed weighted network. The blue nodes 3 and 4 represent the common adjacent nodes of nodes 2 and 5, while the green nodes 1 and 6 denote the mutually exclusive nodes of nodes 2 and 5.

3.4. ProfitLeader Algorithm Calculation Process

The identification process of critical transmission lines in power systems based on the IPL Algorithm is illustrated in Figure 3.

The identification procedure is as follows:

• Load the power grid data, calculate the power flow distribution of each transmission line under the initial operating state, and record the thermal stability margin of each line.
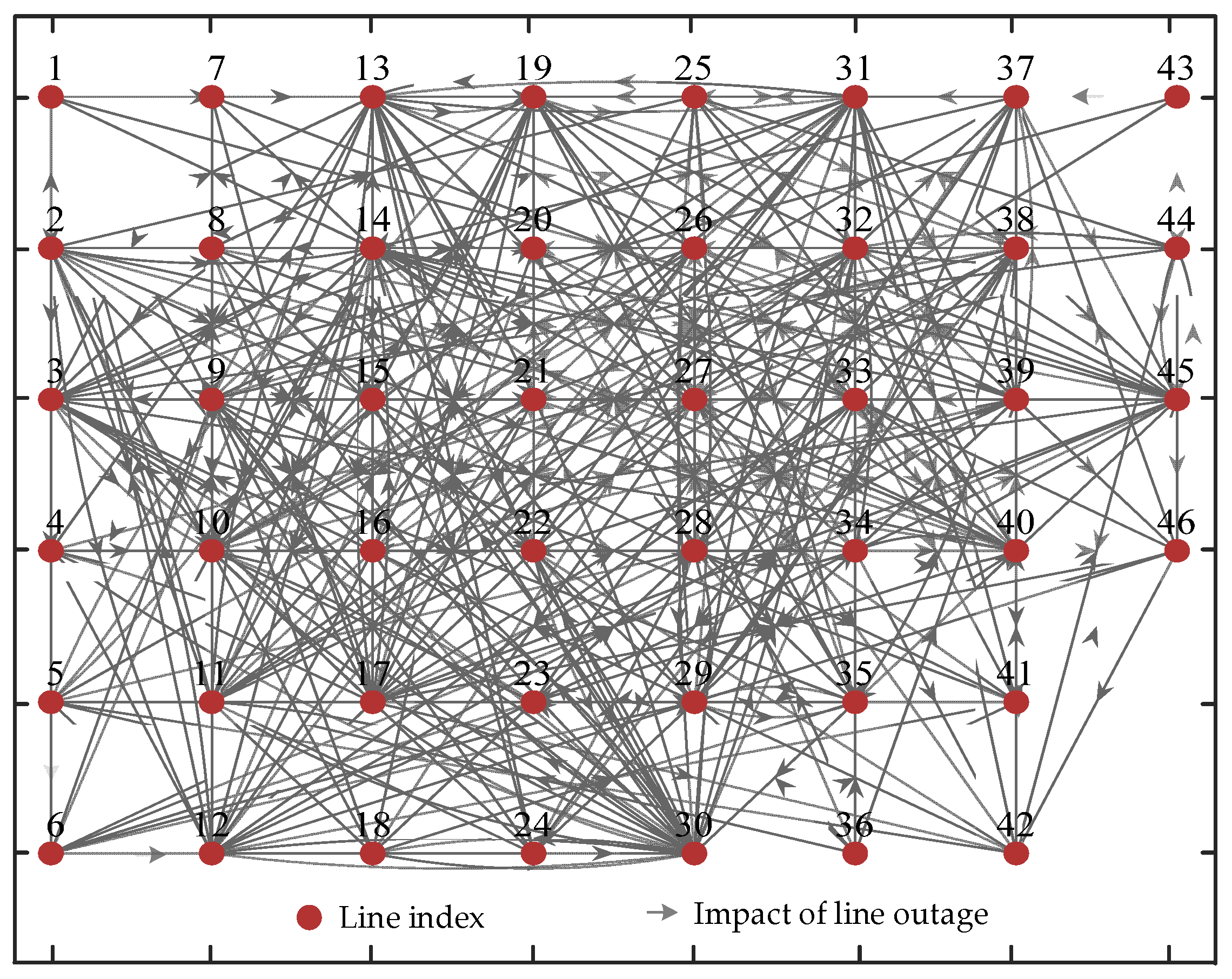
• Considering the subsequent overload failures under the N−1 security criterion, compute the correlation matrix according to Equations (4) and (5), and construct a correlation network that reflects the interdependencies among transmission lines. This transforms the line identification problem into a node evaluation problem.
• Based on Equations (7) and (8), calculate, respectively, the available resources each line can provide to neighboring lines and the probability of resource sharing.
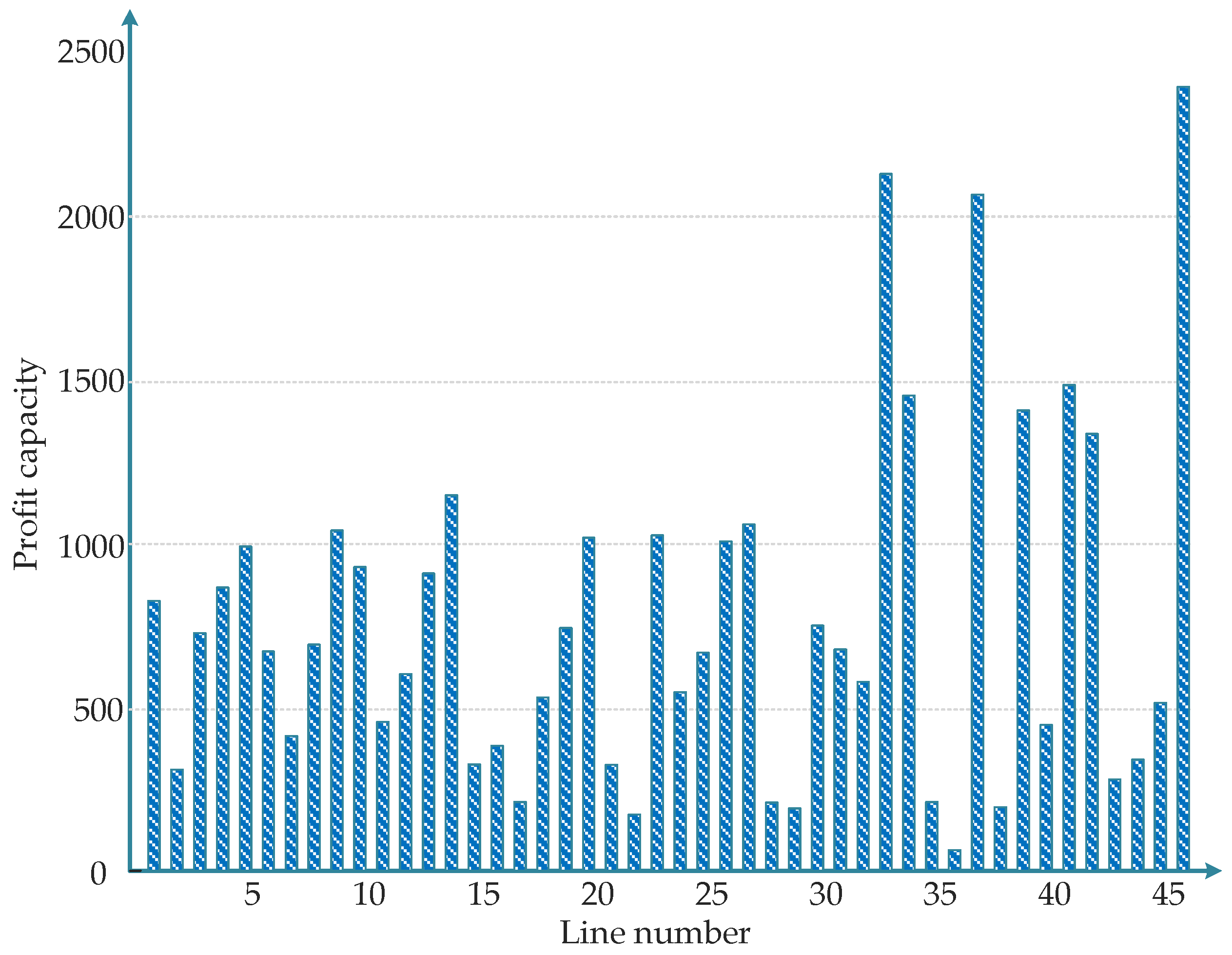
• Determine the profit capacity value of each transmission line using Equation (9).
• Rank the transmission lines in descending order of their profit capacity. Lines with higher profit capacity exert greater influence on surrounding lines when they fail, and thus possess higher importance.

4. Case Study

To validate the feasibility of the proposed IPL algorithm in power systems, this study conducts comparative analyses with the PR algorithm [11], Electric Betweenness (EB) [12], Maximum Flow (MF) method [13], and Catastrophic Expectation Index (CEI) [14] on the IEEE 39-bus test system. All simulations were implemented in MATLAB 2023b environment, where DC power flow analyses were performed using the MATPOWER 8.1 toolbox.

4.1. Indicator Verification

In the field of power system security assessment, transmission line criticality analysis is a fundamental task. Conventional methods quantify the structural and operational importance of target lines by simulating their disconnection and performing a comparative analysis of changes in key performance indicators before and after the fault. Commonly used evaluation metrics primarily include network connectivity, which reflects topological integrity, and system load loss rate, which reflects functional integrity [18]. A fast dynamic simulation method based on the DC-OPA (Direct ORNL-PSERC-Alaska) cascading failure model is employed, with the OPA model process illustrated in Figure 4.

4.1.1. System Connectivity Metric

In power systems, faults in critical lines may lead to generator disconnection and trigger cascading failures, thereby affecting grid connectivity. This chapter utilizes this metric to quantify the impact of critical lines on the integrity of the grid’s topological structure.

4.1.2. System Load Loss Metric

To quantify the impact of critical line failures on power supply reliability, the number of simulations is set to N. After disconnecting each line, the average load loss of the system is calculated as follows:

$$P_{\mathrm{lose}}\left(i\right)={\displaystyle \frac{{\displaystyle \sum _{j=1}^N{P}_{\mathrm{lose}}\left(j\right)}}{N}}$$

(10)

where P_lose(i) represents the average load loss following the fault of branch i, and P_lose(j) denotes the system load loss after the fault of branch j.

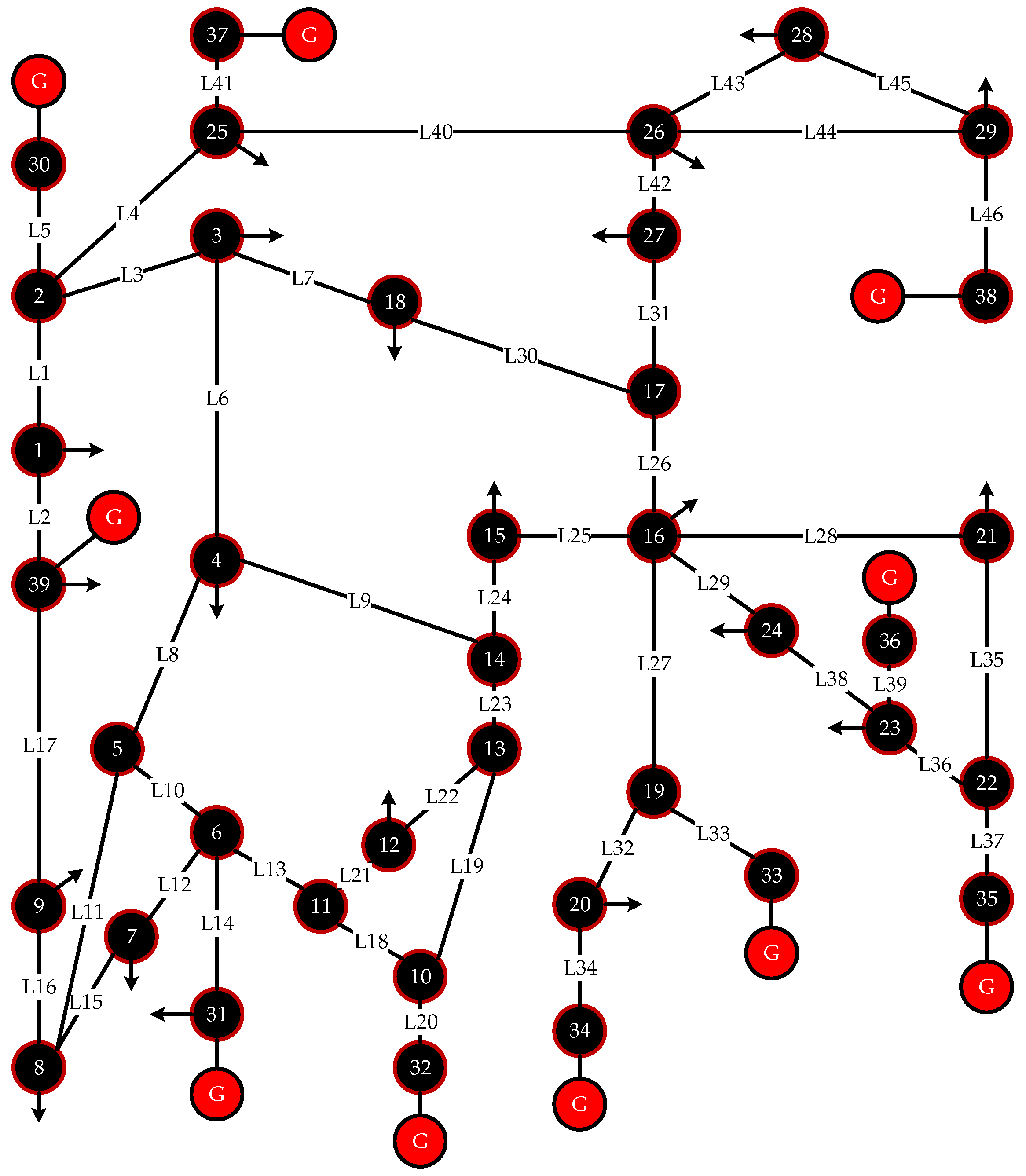
4.2. IEEE 39-Bus Electrical Power System

The topology of the IEEE 39-bus system is illustrated in Figure 5, comprising 39 buses (including 10 generator buses and 21 load buses) and 46 transmission lines.

As shown in Figure 6 (where blue labels indicate node numbers in the correlation network, corresponding to line numbers in the power network), Equations (4)–(6) were applied to construct the correlation network topology for the IEEE 39-bus system. This transforms the line identification problem into a node evaluation problem. Following the line identification process illustrated in Figure 3, simulation analysis was conducted to evaluate the profit capacity of the 46 transmission lines. The profit capacity of these 46 transmission lines in the IEEE 39-bus system are presented in Figure 7. Among them, Line 46 demonstrates the highest profit capacity, indicating its significant influence within the system. A fault occurring on Line 46 would substantially impact other lines, potentially causing major system disturbances or cascading failures, thus confirming its relatively high criticality.

Table 2. Comparison of important line identification results under different methods.

Ranking	IPL	PR	CEI	MF	EB
1	46	46	35	26	24
2	33	14	14	37	25
3	37	37	23	30	26
4	14	20	20	33	3
5	41	35	37	29	8
6	34	33	33	38	9
7	39	10	13	27	27
8	42	39	19	7	6
9	27	41	38	36	23
10	9	34	39	20	31

presents a comparison of critical line identification results obtained using different methodologies. Based on the proposed method, the top 10 critical lines screened by the Profit Capacity indicator show overlaps of 7, 4, 3, and 2 lines with the PR, CEI, MF, and EB methods, respectively. Specifically, the proposed method shares lines L46, L14, L37, L33, L34, L39, and L41 with the PR method, indicating a high degree of consistency. This alignment primarily stems from the fact that both methods construct secondary failure scenarios following N-1 contingencies, thereby enabling a more accurate capture of cascading failure propagation paths. In contrast, the proposed method overlaps with the EB method only on lines L9 and L27, revealing a notable discrepancy. This divergence can be attributed to the EB method’s reliance on network topology for evaluating line criticality, without sufficiently accounting for the influence of actual system operating conditions and power redistribution processes on line importance. These comparative results demonstrate that the proposed method achieves higher accuracy and effectiveness in identifying critical lines in power grids.

The line criticality ranking obtained through our method identifies Lines 46, 33, and 37 as crucial system components. These lines serve as transmission corridors for generators and carry significant generator power transmission tasks. Taking Line 46 as an example, this line connects Generator Bus 38 and normally transmits 824.7 MW of power. If Line 46 fails and is disconnected, it would trigger large-scale power flow redistribution, causing the transmission power on Lines 14, 19, 23, and 26 to approach their thermal stability limits, thereby increasing the risk of cascading failures. The outage of these lines would result in substantial load loss, confirming their high criticality. Meanwhile, Lines 42, 27, and 9 are identified as important power flow transmission paths and key topological positions. For instance, the disconnection of Line 27 would cause system separation into two islands, leading to the isolation of Generators 33 and 34 from the main grid and resulting in power-load imbalance within the islands. The failure of these lines would significantly alter the topological structure of the power system, thereby demonstrating their high criticality.

Figure 8 shows the changes in the system remaining load rate after deliberate attacks on the top seven important lines identified by different methods. As the number of attacks increases, the disconnection of lines identified by the IPL method proposed in this paper leads to a continuous decline in the system remaining load rate. Particularly after the seventh attack, the remaining load rate obtained by the IPL method drops to 43.7%. In comparison, the remaining load rates corresponding to the PR, CEI, MF, and EB methods are 58.5%, 66.9%, 87.1%, and 94.9%, respectively. Notably, after sequentially disconnecting the seven lines, the system remaining load rate obtained by the IPL method is 51.2% lower than that of the EB method. This difference mainly stems from the fact that the IPL method not only considers the topological structure of the lines but also further incorporates the dynamic propagation process of cascading failures, thereby more realistically reflecting the cumulative impact of multiple failures on the system. Such significant load loss will cause the system to deviate from its normal operating state and may trigger widespread power supply interruptions and shortages. This demonstrates that attacks targeting the important lines identified by the proposed method are more likely to cause large-scale load fluctuations and severe load loss in the power system.

Furthermore, to evaluate the importance of critical lines identified by different methods, this paper also examines the changes in the number of electrical islands in the system after sequentially applying deliberate attacks to the top seven critical lines. The results are shown in Figure 9. As the number of attacks increases, the disconnection of lines identified by the proposed IPL method leads to a continuous rise in the number of system islands. After the seventh attack, the system is divided into eight islands, which is the highest among all methods. In comparison, the PR and CEI methods result in six islands, while the MF and EB methods result in five and four islands, respectively. The increase in the number of islands severely disrupts the original topological structure of the system, reduces network connectivity, and directly weakens operational stability and power supply reliability. This result further confirms the effectiveness of the proposed IPL method in identifying critical lines in power systems.

5. Conclusions

Addressing the challenge of identifying critical lines in power systems, this paper introduces an identification method based on an IPL algorithm, inspired by its social network counterpart. Through simulation analysis on the IEEE 39-bus system using metrics of system remaining load ratio and number of electrical islands, the IPL algorithm is compared with other methods, leading to the following conclusions:

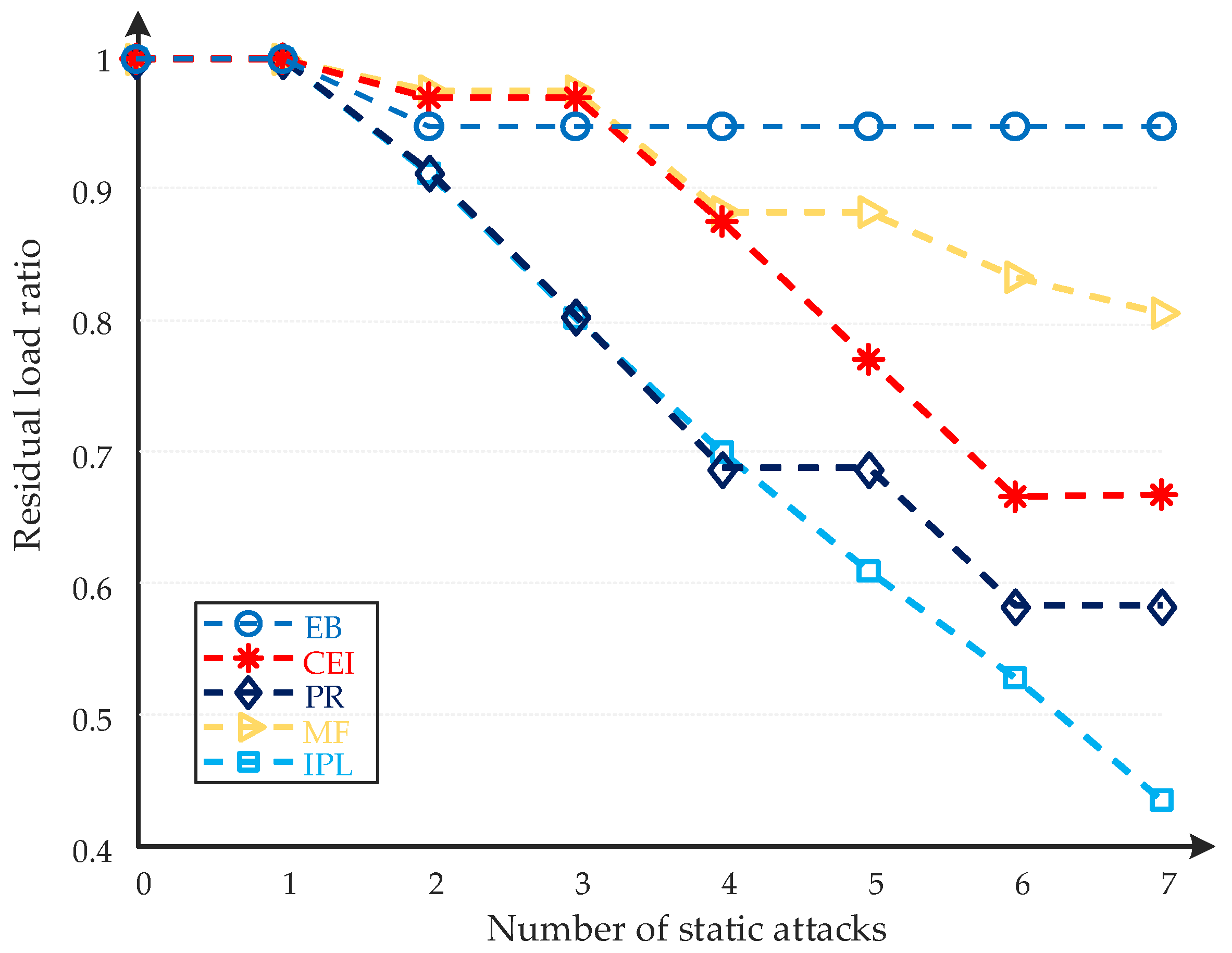
• The study constructs a directed weighted correlation network for power system lines, transforming the problem of line criticality identification into one of node importance evaluation in networks. This approach quantifies mutual influences between lines and, unlike MF and EB methods that primarily focus on topological impacts, comprehensively considers both power flow dynamics and topological structural effects on line identification.
• The IPL algorithm demonstrates superior performance over PR, CEI, MF, and EB methods in terms of both system remaining load ratio and number of electrical islands. When the top seven critical lines identified by the improved algorithm were subjected to static attacks, the system’s remaining load ratio decreased to 43.7% while the number of electrical islands increased to eight. These results confirm that the proposed method can more accurately identify critical lines in power systems.