Characterizing the Spatial Variability of Thermodynamic Properties for Heterogeneous Soft Rock Using Random Field Theory and Copula Statistical Method

Abstract

Studying the thermodynamic properties of soft rocks is critical for geothermal energy extraction, as it elucidates their temperature-dependent mechanical behaviors and heat transfer mechanisms, thereby optimizing reservoir stimulation, enhancing extraction efficiency, and ensuring long-term operational stability. Owing to the intricate geothermal settings and interconnected physicochemical processes, the thermodynamic properties exhibit pronounced spatial heterogeneity and interdependencies. Concurrently, constraints imposed by technical and economic limitations result in scarce practical field survey and experimental data on these properties, severely hampering comprehensive assessments of geothermal energy potential and exploitation feasibility. To evaluate the spatial variability of thermodynamic properties for heterogeneous soft rock using limited data, the thermal conductivity (TC), heat capacity (HC), and thermal diffusivity (TD) were measured. A new Copula statistical method is used to analyze thermodynamic properties under limited measurement data. Spatial variability in heterogeneous soft rocks is quantified using random field theory. The methodology’s reliability is confirmed through cross-validation against theoretical predictions, empirical measurements, and simulation outputs. The analysis framework of thermodynamic variability characteristics has been presented by stability point analysis and linear regression analysis processes. The variance reduction function, scale of fluctuation, autocorrelation distances, and autocorrelation structure of thermodynamic properties for heterogeneous soft rock are analyzed and discussed. This study can provide scientific data for thermal energy analysis and geothermal reservoir modification specifically applicable to soft rock formations with diagenetic and tectonic histories similar to those investigated in the Weishan Lake area.

1. Introduction

Soft rocks are characterized by low strength and high deformability, with a complex interplay existing between their energy conversion and thermodynamic properties. During mechanical deformation or stress-induced processes, soft rocks undergo energy conversion processes, including elastic potential energy storage, viscous dissipation, and heat generation, which are closely related to their thermodynamic behaviors [1]. The low thermal conductivity of soft rocks impedes rapid heat dissipation during energy release, leading to local temperature rise, thereby potentially further altering their mechanical response through thermo-mechanical coupling. Conversely, changes in internal energy can alter the stability of the microstructure, affecting long-term energy storage efficiency [2,3]. Soft rocks store geothermal energy through internal heat accumulation, where traits like specific heat capacity determine how much thermal energy they retain. Thermodynamic properties, such as thermal conductivity, meanwhile, control heat transfer rates from deep reservoirs to extraction points, impacting energy accessibility. Temperature fluctuations drive thermal expansion or contraction, altering rock porosity and permeability. Conversely, geothermal exploitation reduces rock internal energy via heat extraction, potentially triggering stress changes that affect stability [4,5,6]. Studying thermodynamic parameters of soft rocks, including thermal conductivity (TC), heat capacity (HC), and thermal diffusivity (TD), is pivotal for characterizing geothermal energy potential [7,8]. These parameters directly govern heat storage: high specific heat boosts thermal retention, while conductivity dictates heat transfer efficiency to extraction wells. Thermal expansion regulates rock deformation and alters fracture networks and fluid permeability, which is crucial for maintaining heat flow [9,10]. Zhao et al. [11] found that these traits enable predicting reservoir temperature decline, optimizing well placement, and mitigating thermal breakthrough risks. It also informs long-term resource viability by linking rock behavior to energy extraction rates, ensuring efficient, sustainable geothermal development, and guiding strategies to balance output with reservoir health. Therefore, clarifying the thermodynamic properties of the soft rock (TC, HC, and TD) can promote soft rock energy conversion and geothermal energy extraction in China.

However, soft rock thermodynamic parameter heterogeneity forms through coupled geological processes, including diagenesis, tectonic activity, and hydrothermal alteration, resulting in uneven distributions and anisotropic behavior of properties like thermal conductivity and heat capacity. Li et al. [12] reveal the soft rock thermodynamic parameter heterogeneity forms through coupled geological processes. Diagenesis first drives variability: sedimentary layers with differing clay-quartz ratios or cementation develop distinct traits; quartz-rich zones show higher thermal conductivity than clay-dominated areas. Tectonic activity amplifies this, creating fractures and bedding planes that induce anisotropy, as aligned structures or fluid-filled gaps alter local heat transfer. Later, hydrothermal alteration or weathering modifies the mineralogy of porous clays, replacing stable grains and shifting heat capacity. Typical features include spatial patchiness, directional anisotropy along fractures, and dynamic changes from thermal or stress impacts [13,14]. Soft rock thermodynamic parameter spatial heterogeneity describes uneven distributions of properties like thermal conductivity, heat capacity, and expansion across subsurface strata [15,16,17]. Li et al. and Yang et al. [18,19] found that this variability arises from layered sedimentation, where clay- versus quartz-rich deposits develop distinct thermal traits; quartz layers conduct heat better than clay-rich ones. Tectonic forces amplify this by creating fractures or bedding planes, inducing anisotropy as parameters align directionally along these structures. Later, hydrothermal alteration or weathering modifies local mineralogy, replacing stable grains with porous clays that shift heat retention. Characteristically, it appears as patchy zones, directional trends along faults, or abrupt property changes between layers.

Meanwhile, the random field method effectively quantifies spatial variability in soft rock thermodynamic properties using statistical tools but is significantly limited by small sample sizes, leading to unreliable estimates and distorted simulations. Cao et al. [20] found that the random field method quantifies spatial variability in soft rock thermodynamic properties by treating parameters like thermal conductivity and heat capacity as stochastically distributed variables across subsurface strata. It employs statistical tools such as covariance functions to model spatial correlations, describing how properties at different locations are based on proximity or geological context. By integrating field measurements, the method constructs probabilistic models that capture heterogeneity, distinguishing between local randomness and broader trends [21,22,23]. Nguyen et al. and Cao et al. [24,25] found that small sample sizes of soft rock thermodynamic parameters constrain the random field quantification process, primarily due to limited statistical representativeness. Random field methods rely on adequate data to estimate statistical parameters that describe spatial variability. With few samples, these estimates become unreliable: variances may be underestimated, and covariance models struggle to capture true spatial correlations, leading to biased or overly smooth random field realizations. Small datasets also increase uncertainty in model predictions; for instance, sparse measurements of thermal conductivity or heat capacity may miss localized heterogeneity, distorting simulations of heat flow in geothermal reservoirs [26,27]. Consequently, characterizing the spatial variability of thermodynamic properties for heterogeneous soft rock needs to be clarified, and the analysis framework of random field theory and the Copula statistical method needs to be discussed.

In this paper, the TC, HC, and TD of heterogeneous soft rock were measured by the thermal probe method and differential scanning calorimetry. A new Copula statistical method is used to analyze thermodynamic properties under limited measurement data. The variable thermodynamic properties of heterogeneous soft rock are characterized by random field theory. The detailed workflow of the thermodynamic variability characteristic is presented by the stability point analysis process and the linear regression analysis process. The accuracy of the proposed approach is verified by comparison of the theoretical data, measured data, and simulated data. The variance reduction function, scale of fluctuation, autocorrelation distances, and autocorrelation structure of thermodynamic properties for heterogeneous soft rock are analyzed and discussed. The results can provide an important reference for soft rock energy conversion and geothermal energy analysis.

2. Materials and Methods

2.1. Thermodynamic Properties of Heterogeneous Soft Rock

Soft rock thermodynamic properties and physical-mechanical parameters are spatially coupled through geological processes. Diagenetic sorting produces quartz-rich zones with higher strength and clay-dominated areas of lower values, aligning thermal and mechanical traits. Tectonic fractures weaken mechanical integrity via discontinuities and cause thermal anisotropy by directing heat flow [28,29]. Hydrothermal alteration integrates both: clay-filled pores reduce density/strength while modifying specific heat via mineral changes. Neglecting this coupling process leads to inaccurate soft rock energy conversion and geothermal energy analysis [30,31]. In this study, the soft rock samples were obtained from the western bank of Weishan Lake, approximately 82 km from downtown Xuzhou and 17 km from the Peixian County seat. Its coordinates range between 116°54′–116°55′ east longitude and 34°52′–34°53′ north latitude. Nine holes were drilled, and ten soft rock samples were collected from each hole, with a depth interval of 1 m between each sample. The physical and mechanical properties of the rock were measured through basic geotechnical tests.

Table 1. Physical property indicators of heterogeneous soft rock.

NO.	Density (g/cm3)	Dry Density (g/cm3)	Moisture Content (%)	Hydraulic Conductivity (10−6 cm/s)	Porosity (%)	Void Ratio
1#	2.506	2.369	5.802	21.766	0.748	0.428
2#	2.464	2.332	5.684	18.783	0.682	0.405
3#	2.688	2.547	5.529	11.620	0.768	0.434
4#	2.788	2.649	5.242	20.337	0.784	0.439
5#	2.405	2.271	5.884	9.484	0.688	0.408
6#	2.168	2.061	5.164	16.814	0.746	0.427
7#	2.537	2.411	5.220	16.069	0.653	0.395
8#	2.571	2.446	5.107	26.961	0.646	0.393
9#	2.652	2.520	5.234	22.877	0.567	0.362

presents the physical property indicators of heterogeneous soft rock samples, encompassing density, dry density, moisture content, hydraulic conductivity, porosity, and void ratio. To begin with, density values range from 2.168 g/cm³ to 2.788 g/cm³, reflecting diverse degrees of mineral compaction or compositional differences. Higher dry density typically corresponds to denser solid particle packing. Moisture content, ranging from 5.107% to 5.884%, is relatively low across all specimens. Intriguingly, samples with lower moisture content tend to have higher dry density. For hydraulic conductivity, there is a remarkable variation from 9.484 × 10⁻⁶ cm/s to 26.961 × 10⁻⁶ cm/s. This wide range implies heterogeneous pore structures, where higher conductivity likely stems from larger or more interconnected pores. Porosity and void ratio also display notable differences. A positive correlation between porosity/void ratio and hydraulic conductivity is observable. In summary, the samples exhibit substantial variability in physical properties. Density, dry density, and porosity/void ratio collectively influence hydraulic behavior. These factors will affect the thermodynamic properties of heterogeneous soft rock.

Thermal parameters of soft rock at different spatial locations exhibit remarkable dispersity. TC, for instance, varies substantially across samples, which is attributed to heterogeneous pore structures and mineral compositions. Meanwhile, related properties like TD also show obvious differences, as spatial changes in moisture content and density affect heat transfer behaviors. In this study, the TC was measured by the thermal probe method. A thin metal probe is inserted into the soft rock, and transient temperature responses to probe heating are analyzed to calculate conductivity. The HC was measured by differential scanning calorimetry (DSC). DSC is the gold standard in laboratories. Small dried soft rock samples (10–50 mg) are heated alongside a reference material in a controlled environment. Heat flow differences between the sample and reference are measured to determine specific heat capacity. To analyze the thermodynamic parameters of heterogeneous soft rock, we examine horizontal/vertical TC, HC, and TD across depths (0–10 m) and nine samples (1#–9#). Horizontal TC (Figure 1a) ranges from 2.5 to 4.5 W/(m·°C), generally higher than vertical TC (Figure 1b, 2.0–3.5 W/(m·°C)), indicating stronger heat conduction along the horizontal direction. Both directions show scattered distributions with depth, reflecting spatial heterogeneity in mineral arrangement or pore structure. Horizontal HC (Figure 1c) clusters at 1.5–2.5 × 10⁶ J/(m³·°C), while vertical HC (Figure 1d) spans 1.0–3.5 × 10⁶ J/(m³·°C), with wider variability. This suggests vertical HC is more sensitive to depth-dependent factors. Horizontal TD (Figure 1e) varies from 0.5 to 2.0 × 10⁻⁶ m²/s, and vertical TD (Figure 1f) ranges from 0.5 to 1.5 × 10⁻⁶ m²/s. The lower vertical diffusivity likely stems from anisotropic microstructures that impede heat transfer efficiency in the vertical direction. These results indicate that the thermodynamic parameter anisotropy of soft rock is closely related to depth.

Figure 2 presents the statistical characteristics of three hydrothermal properties for heterogeneous soft rock, with a consistent sample size of 180 across all three parameters. For TC (Figure 2a), the mean value reaches 3.112 W/m/°C, accompanied by a standard deviation (SD) of 0.391 and a coefficient of variation (COV) of 0.126, indicating relatively low dispersion. The data range spans from 2.175 to 4.136, with a right-skewed distribution and a platykurtic shape, suggesting most values cluster around the mean with a few higher outliers. Regarding HC (Figure 2b), the mean is 2.336 × 10⁶ J/m³/°C, with an SD of 0.301 and a COV of 0.129, showing similar dispersion to TC. Its range is 1.616–3.118, and the distribution also exhibits mild right skewness but with a slightly negative kurtosis, implying a flatter peak than the normal distribution while maintaining a unimodal pattern. For TD (Figure 2c), the mean drops to 1.365 × 10⁻⁶ m²/s, with an SD of 0.296 and a notably higher COV of 0.217, reflecting greater variability in thermal diffusivity among samples. The data range is 0.791–2.202, and the distribution shows right skewness with a platykurtic kurtosis. Comparatively, TD demonstrates the largest dispersion among the three properties, while TC and HC exhibit more consistent central tendencies with lower variability. Overall, the statistical results highlight distinct hydrothermal behavior across the three properties, with TC showing the highest mean, TD the greatest variability, and HC a distribution closer to normality in terms of kurtosis despite mild skewness.

2.2. Copula Statistical Method for Thermodynamic Parameter Sample

To address small sample challenges in soft rock thermodynamic parameter analysis, the Copula method constructs joint distribution functions and probability density functions by decoupling marginal behaviors and dependency structures [32,33]. First, marginal distributions of individual thermodynamic parameters are fitted using empirical or parametric models, capturing their univariate statistical traits. Next, a Copula function is selected to link these marginals, enabling flexible modeling of non-linear, non-Gaussian relationships often present in heterogeneous soft rocks. The joint distribution function then integrates the Copula with marginals, describing simultaneous occurrence probabilities of parameter values. The joint probability density function follows, derived by multiplying marginal densities with the Copula density. This approach outperforms traditional multivariate methods in small samples, as it avoids assuming fixed parametric forms for joint dependence, enhancing reliability in capturing parameter variabilities critical for uncertainty quantification in geothermal or engineering applications.

Table 2. Copula joint distribution function.

Copula	C(u1,u2; θ)	D(u1,u2; θ)	Range of θ
Gaussian	$\begin{array}{l}C(u_1,u_2;\theta )={\int }_{-\infty }^{{\mathsf{\Phi }}^{-1}(u_2)}{\displaystyle \frac{1}{2\pi \sqrt{1-{\theta }^2}}}\\ \times \exp \left(-{\displaystyle \frac{x_1^2-2\theta x_1{x}_2+{x_2}^2}{2(1-{\theta }^2)}}\right)d{x}_1{x}_2\end{array}$	$\begin{array}{l}D\left(u_1,u_2;\theta \right)={\displaystyle \frac{1}{2\sqrt{1-{\theta }^2}}}\exp \left({\displaystyle \frac{{{\varsigma }_1}^2-2\theta {\varsigma }_1{\varsigma }_2+{{\varsigma }_2}^2}{2\left(1-{\theta }^2\right)}}\right)\\ {\varsigma }_1={\mathsf{\Phi }}^{-1}\left(u_1\right),{\varsigma }_2={\mathsf{\Phi }}^{-1}\left(u_2\right)\end{array}$	[−1, 1]
Frank	$-{\displaystyle \frac{1}{\theta }}\ln \left(1+{\displaystyle \frac{\left(e^{-\theta u_1}-1\right)\left(e^{-\theta u_2}-1\right)}{\left(e^{-\theta }-1\right)}}\right)$	${\displaystyle \frac{-\theta \left(e^{-\theta }-1\right)e^{-\theta \left(u_1+u_2\right)}}{{\left[\left(e^{-\theta }-1\right)+\left(e^{-\theta u_1}-1\right)\left(e^{-\theta u_2}-1\right)\right]}^2}}$	$\left(-\infty ,\infty \right)\backslash \left\{0\right\}$
Gumbel	$\exp \left(-{\left({\left(-\ln u_1\right)}^{\theta }+{\left(-\ln u_2\right)}^{\theta }\right)}^{1/\theta }\right)$	$\begin{array}{l}{\displaystyle \frac{e^{-S^{1/\theta }}{\left(\ln u_1\ln u_2\right)}^{\theta -1}\left(S^{1/\theta }+\theta -1\right)}{u_1{u}_2{S}^{2-1/\theta }}}\\ \mathrm{where} S=\left(-\ln u_1\right)\theta +\left(-\ln u_2\right)\theta \end{array}$	$[1,\infty )$

presents the Gaussian, Frank, and Gumbel Copula joint distribution functions. Each Copula function characterizes distinct dependence structures with unique parameterizations. The Gaussian Copula relies on the bivariate normal distribution, where the parameter θ ∈ [−1, 1] equals Pearson’s correlation coefficient. It uses inverse standard normal CDFs (Φ⁻¹) to transform variables, capturing linear dependence through a double integral of the bivariate normal density. However, it exhibits no tail dependence: extreme values in one variable do not imply extremity in the other, as the normal distribution’s light tails limit joint extreme probabilities. The Frank Copula has θ ∈ (−∞, ∞)∖{0} and uses a logarithmic CDF form to model symmetric dependence. Unlike Gaussian, it shows symmetric tail independence; extreme values in either tail do not correlate across variables. Its density function’s exponential structure enforces uniform dependence across the support, suiting data with symmetric tail behavior. The Gumbel Copula specializes in upper tail dependence. It assigns high probability to both variables being large simultaneously. Larger θ strengthens upper tail dependence, while lower tail dependence stays negligible.

For soft rock thermodynamic parameters with small samples, the Bootstrap method is employed to construct joint distribution and probability density functions. Small samples in soft rock mechanics often lead to unreliable statistical inferences due to insufficient data. Bootstrap, a resampling parametric approach, addresses this by repeatedly drawing random samples with replacement from the original small dataset, generating multiple bootstrap replicates that mimic the original data’s distribution while expanding the effective sample size. For thermodynamic parameters, first apply Bootstrap to create numerous bootstrap samples. Then, estimate marginal distributions for each parameter using methods like kernel density estimation or empirical cumulative distribution functions on these bootstrap samples. Subsequently, utilize Copula functions to model the dependence structure among parameters, as Copulas can flexibly capture non-linear correlations regardless of marginal distributions [34,35]. By combining estimated marginals with the selected Copula, the joint distribution function is constructed, which describes the probability that all parameters fall within specified ranges simultaneously. Finally, the probability density function is derived by taking partial derivatives of the joint distribution function with respect to each parameter. Figure 3 illustrates the discrete uniformly distributed variables of thermodynamic properties for heterogeneous soft rock. In each subplot, black triangles denote measured data, white triangles represent simulated data, and colored lines highlight the correlation trends between variables. For Figure 3a, the negative correlation indicates that as TC increases, HC tends to decrease. Measured and simulated data points are broadly scattered around the trend line, reflecting moderate consistency between experimental observations and simulation results. In Figure 3b, the positive correlation reveals that higher TC corresponds to higher TD. Here, both data types cluster tightly near the trend line, suggesting strong agreement and robust simulation accuracy for this property relationship. Figure 3c exhibits another positive correlation, where HC and TD increase jointly. The dense distribution of data points along the line implies that the simulation effectively captures the interdependency between HC and TD, with measured data largely overlapping the simulated pattern.

To analyze the discrete correlation distributions of thermodynamic properties for heterogeneous soft rock, three scatter plots comparing measured and simulated data are examined. In Figure 4a, both measured and simulated data exhibit a broadly scattered pattern, indicating no strong linear correlation between TC and HC. The wide distribution reflects the complex heterogeneity of soft rocks, where mineral composition, pore structure, and moisture content jointly influence these properties. The overlapping range of experimental and simulated data suggests the model captures the general trend, while discrepancies in density and outliers imply challenges in fully replicating microscale interactions. Figure 4b shows a similarly dispersed distribution. TC and TD lack pronounced correlation, as both parameters are controlled by distinct mechanisms. Measured and simulated data cluster in moderate TC and TD ranges, consistent with the intrinsic variability of non-uniform rock matrices. For Figure 4c, the scatter is even more pronounced, especially for simulated data extending to higher HC and lower TD. This divergence highlights the decoupled regulation of heat storage and transfer in heterogeneous systems, where simulation may oversimplify anisotropic microstructures. Measured data, however, maintain a relatively concentrated core, validating the model’s ability to replicate dominant property combinations.

Table 3. Comparison of statistical properties of measured data and simulated data.

Statistics	Measured Data			Simulated Data			Comparative Values
	TC W/m/°C	HC	TD	TC	HC	TD	TC	HC	TD
Mean	3.112	2.336	1.365	3.110	2.346	1.378	0.002	−0.010	−0.013
SD	0.391	0.301	0.296	0.335	0.256	0.136	0.056	0.045	0.160
COV	0.126	0.129	0.217	0.108	0.109	0.198	0.018	0.020	0.019
Max	4.136	3.118	2.202	4.052	3.047	1.861	0.084	0.071	0.341
Min	2.175	1.616	0.791	2.141	1.555	0.821	0.034	0.061	−0.030
Skewness	0.262	0.384	0.336	0.246	0.324	0.289	0.016	0.060	0.047
Peakedness	−0.378	−0.252	−0.403	−0.373	−0.231	−0.423	−0.005	−0.021	0.020

Notes: The unit of TC is W/m/°C; the unit of HC is 10⁶ J/m³/°C; the unit of TD is 10⁻⁶ m²/s.

presents a comprehensive comparison of statistical properties for TC, HC, and TD between measured and simulated data in heterogeneous soft rock. For TC, the mean values of measured and simulated data are nearly identical, with a negligible comparative value. The SD decreases from 0.391 to 0.335, and COV reduces from 0.126 to 0.108, indicating that simulated data exhibits less dispersion. The Max and Min also narrow, while skewness and peakedness remain similar, suggesting a consistent distribution shape. In terms of HC, the measured mean is slightly lower than the simulated mean. SD drops from 0.301 to 0.256, and COV falls from 0.129 to 0.109, reflecting reduced variability in simulated data. The Max and Min show a smaller range, while skewness and peakedness change marginally, confirming good agreement in distribution characteristics. For TD, the measured mean is marginally higher than the simulated mean. SD decreases sharply from 0.296 to 0.136, and COV declines from 0.217 to 0.198, meaning the simulated data has lower dispersion. Although the comparative range for Max and Min is wider, skewness and peakedness stay close, indicating similar distribution trends despite magnitude differences. Overall, the simulated data closely replicates the statistical features of measured data across TC, HC, and TD. Minor discrepancies aside, most metrics validate the simulation’s reliability in capturing the thermal behavior of heterogeneous soft rock, verifying the numerical model’s effectiveness. Based on the available data (Figure 3), the positive and negative correlations between each pair of thermal parameters can be obtained. Based on the current available data (Figure 4 and Table 3), the validity of the statistical analysis model in this study can be demonstrated. However, the current data cannot explain the interdependencies of TC-HC-TD.

2.3. Random Field Characterization for Variable Thermodynamic Properties

Soft rock thermodynamic parameters exhibit pronounced spatial variability due to coupled geological processes. Diagenetic layering sorts sediments into quartz-rich zones and clay-dominated layers, creating systematic spatial patterns. Tectonic fracturing induces anisotropy by aligning microcracks or bedding planes, directing heat flow along preferential pathways. Hydrothermal alteration further complicates this variability. Clay-filled pores reduce density and thermal storage capacity, while mineral replacements alter heat retention properties. Statistically, this manifests as patchy clustering, directional trends along faults, and log-normal distributions of parameter values. Such heterogeneity poses challenges for geothermal reservoir engineering, where uneven heat transfer undermines efficiency, and for slope stability assessments, where localized weakness triggers failure. Addressing this variability requires stochastic modeling to quantify uncertainty and optimize interventions like well placement or thermal stimulation strategies in soft rock-dominated systems [36,37]. The random field method characterizes soft rock thermodynamic parameters—such as thermal conductivity and specific heat capacity—by framing them as spatially correlated random processes, addressing their inherent heterogeneity from diagenesis, tectonics, or weathering. Instead of single deterministic values, it estimates marginal statistics (mean, variance) from limited samples and fits covariance functions (e.g., exponential) to capture spatial dependencies, describing how nearby locations share thermal traits. This quantifies uncertainty: generating multiple parameter realizations, each a plausible spatial pattern, to assess impacts on outcomes like geothermal heat flow or slope stability. Unlike deterministic models, it integrates small-sample data with statistical structure, balancing realism for non-uniform soft rocks.

Table 4. Correlation functions for the variable thermodynamic properties.

Function Type	Mathematical Expression	Relationship Between Parameters
2-DSNX	$\Phi \left(k_x,k_y\right)=\exp \left[-\left({\displaystyle \frac{k_x}{{\theta }_h}}+{\displaystyle \frac{k_y}{{\theta }_v}}\right)\right]$	${\theta }_h={\displaystyle \frac{{\delta }_h}{2}},{\theta }_v={\displaystyle \frac{{\delta }_v}{2}}$
2-DSQX	$\Phi \left(k_x,k_y\right)=\exp \left\{-\left[{\left({\displaystyle \frac{k_x}{{\theta }_h}}\right)}^2+{\left({\displaystyle \frac{k_y}{{\theta }_v}}\right)}^2\right]\right\}$	${\theta }_h={\displaystyle \frac{{\delta }_h}{\sqrt{\pi }}},{\theta }_v={\displaystyle \frac{{\delta }_v}{\sqrt{\pi }}}$
2-DBIN	$\Phi \left(k_x,k_y\right)=\left\{\begin{array}{ll}\left(1-{\displaystyle \frac{k_x}{{\theta }_h}}\right)\left(1-{\displaystyle \frac{k_y}{{\theta }_v}}\right)& k_x\le {\theta }_h,k_y\le {\theta }_v\\ 0& k_x>{\theta }_h,k_y>{\theta }_v\end{array}\right.$	${\theta }_h={\delta }_h,{\theta }_v={\delta }_v$

Notes: δ_v and δ_h represent the vertical and horizontal autocorrelation distance for the variable thermodynamic properties, respectively. θ_v and θ_h represent the vertical and horizontal scales of fluctuation for the variable thermodynamic properties, respectively.

shows three correlation functions for the variable thermodynamic properties. The 2-DSNX function causes the correlation to decay exponentially as the wave number rises. Its fluctuation scale parameters are directly tied to autocorrelation distances. Larger parameters lead to faster decay, making local variations more obvious. The 2-DSQX has its correlation decay according to the sum of squared ratios of wave numbers to scale parameters. Since its scale parameters come from autocorrelation distances divided by the square root of pi, this decay is more gradual than that of the exponential. The 2-DBIN function features a truncation effect: non-zero correlation only exists when wave numbers are below a certain threshold. Once wave numbers exceed this threshold, correlation drops to zero at once. This creates a clear scale limit in the spatial field, while those beyond are independent, which might produce blocky structures or discontinuous transitions.

When characterizing spatial variability of soft rock thermodynamic parameters using the random field method, the variance reduction function (VRF) and local average random field generations are critical steps. The VRF adjusts the original random field’s variance to match observed statistical moments by systematically reducing variability across scales. This ensures that simulated parameters honor field-measured dispersion while accounting for small-sample limitations. A VRF might exponentially decay variance with increasing spatial wavelength, suppressing short-range fluctuations to align with bulk geological trends. Concurrently, local averaging generates spatially averaged realizations by integrating parameter values over predefined subdomains. This process smoothes local extremes, honors spatial continuity, and reflects mesoscale heterogeneity. By combining VRF and local averaging, the method balances fidelity to measured data with computational tractability.

Table 5. Analytical method for the variance reduction function (VRF).

Length	Statistical Data Analysis Process						Variance	VRF
ΔL	${\eta }_E(1)$	${\eta }_E(2)$	${\eta }_E(3)$	${\eta }_E(4)$	…	${\eta }_E(n)$	DE1	${\displaystyle \frac{D_{E1}}{D_{E1}}}$
2ΔL		$\begin{array}{l}[{\eta }_E(1)\\ +{\eta }_E(2)]/2\end{array}$	$\begin{array}{l}[{\eta }_E(2)\\ +{\eta }_E(3)]/2\end{array}$	$\begin{array}{l}[{\eta }_E(3)\\ +{\eta }_E(4)]/2\end{array}$	…	$\begin{array}{l}[{\eta }_E(n-1)\\ +{\eta }_E(n)]/2\end{array}$	DE2	${\displaystyle \frac{D_{E2}}{D_{E1}}}$
3ΔL			$\begin{array}{l}[{\eta }_E(1)+2{\eta }_E(2)\\ +{\eta }_E(3)]/4\end{array}$	$\begin{array}{l}[{\eta }_E(2)+2{\eta }_E(3)\\ +{\eta }_E(4)]/4\end{array}$	…	$\begin{array}{l}[{\eta }_E(n-2)+2{\eta }_E(n-1)\\ +{\eta }_E(n)]/4\end{array}$	DE3	${\displaystyle \frac{D_{E3}}{D_{E1}}}$
4ΔL				$\begin{array}{l}[{\eta }_E(1)+3{\eta }_E(2)\\ +3{\eta }_E(3)+{\eta }_E(4)]/8\end{array}$	…	$\begin{array}{l}[{\eta }_E(n-3)+3{\eta }_E(n-2)\\ +3{\eta }_E(n-1)+{\eta }_E(n)]/8\end{array}$	DE4	${\displaystyle \frac{D_{E4}}{D_{E1}}}$
…					…	…	…	…
mΔL					…	$\begin{array}{l}\{{\eta }_E(n-m)+m{\eta }_E[n-(m-1)]\\ +\cdots +m{\eta }_E(n-1)+{\eta }_E(n)\}/2^m\end{array}$	DEm	${\displaystyle \frac{D_{Em}}{D_{E1}}}$

shows the analytical method for the VRF of thermodynamic properties. The analytical process of the variance reduction local averaging method begins by segmenting data into intervals of length ΔL, with each interval corresponding to original statistical values from η(1) to η(n). As the interval length increases to 2ΔL, adjacent pairs of these values are averaged in sequence. When the length reaches 3ΔL, a more intricate averaging pattern appears: each position’s value is obtained by combining three consecutive original values with specific weightings. For an interval of mΔL, each averaged value integrates contributions from multiple neighboring points. After calculating variances for each interval length, the VRF is derived by comparing these variances to the variance of the smallest interval. Key characteristics of this method include systematic segmentation progression, where the interval length expands in an orderly manner. There are regularized weighting schemes that change adaptively with the interval length. The VRF enables quantifiable variance reduction, clearly showing how fluctuations decrease as the averaging range expands. Moreover, it has statistical coherence, bridging data points and interval analysis through hierarchical averaging, thus effectively illustrating the variance attenuation mechanism during local averaging.

3. Analysis Framework of Thermodynamic Variability Characteristic

3.1. Stability Point Analysis Process

The VRF is pivotal in characterizing the spatial variability of soft rock thermodynamic parameters using random field methods. It addresses two critical challenges: statistical consistency and computational efficiency. By systematically reducing the variance of simulated parameters at larger spatial scales, the VRF ensures that generated realizations align with field-measured statistical moments while honoring small-sample data limitations. For example, in heterogeneous soft rocks, VRF suppresses short-range fluctuations to match bulk geological trends, preventing overestimation of local extremes. Moreover, the VRF bridges multi-scale variability by integrating local heterogeneity with regional continuity. This balance is crucial for engineering applications like geothermal reservoir modeling, where excessive variability could lead to inefficient well placement or unstable slope predictions. The calculation of the VRF in characterizing spatial variability of soft rock thermodynamic parameters via random field methods involves several key steps. Initially, the study area is divided into segments of increasing length, with each segment’s statistical properties computed from corresponding local data. As the segment length expands, neighboring values are progressively averaged to smooth local fluctuations. The variance of each segmented dataset is then calculated and compared to the variance of the smallest segment. The VRF is derived by fitting a mathematical model to describe how variance diminishes with increasing averaging scale. This model quantifies the relationship between spatial autocorrelation distance and variance reductions, ensuring simulated parameters align with field-measured statistical moments while accounting for small-sample limitations. By calibrating VRF parameters to field data, engineers derive realistic spatial realizations that quantify uncertainty in thermal conductivity or heat capacity. Once the experimental data for TC, HC, and TD were collected, the variance function and fluctuation scale were determined using a wave function methodology paired with random field theory. The analytical workflow unfolded as follows:

First, a defined vertical separation was maintained between measurement depths to capture spatial correlations effectively. In this study, a 1-m interval was implemented, with data collected across depths ranging from 1 to 10 m beneath the ground surface. Next, to isolate spatial variability, the trend components of thermal conductivity, heat capacity, and thermal diffusivity were removed from the raw data. Computational formulas were applied to strip away these temperature-driven trends, enabling focused analysis of the remaining spatial heterogeneity in the thermal parameters.

$${\eta }_E(i)={\displaystyle \frac{\eta (i)-\overline{\eta }(i)}{\xi }}$$

(1)

$$\overline{\eta }(i)={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\eta (i)}$$

(2)

$$\xi =\sqrt{{\displaystyle \frac{1}{N-1}}{\displaystyle \sum _{i=1}^N{\left[\eta (i)\right]}^2}-{\displaystyle \frac{N}{N-1}}{\left[\overline{\eta }(i)\right]}^2}$$

(3)

where ${\eta }_E(i)$ represent the standardized thermal parameter, $\eta (i)$ represents the thermal parameter, i.e., thermal conductivity or heat capacity, or thermal diffusivity; $\overline{\eta }(i)$ is the sample mean; $\xi$ is the sample standard deviation.

Following the acquisition of normalized thermodynamic parameters for TC, HC, and TD, the VRF was computed. Table 5 details the step-by-step computational workflow. Figure 5 presents a representative comparison between theoretical and experimental variance function curves for uncertain geotechnical parameters, with the theoretical curve assuming a Gaussian correlation structure. Discrepancies between the two curves arise from two factors: the theoretical model neglects cross-correlations between different parameters, and experimental data deviates slightly from idealized theoretical assumptions. In this figure, the vertical axis denotes the variance function, while the horizontal axis corresponds to the averaging distance. By identifying the steady-state point on the experimental curve, the fluctuation scale was determined using the relationship derived from random field theory.

$$\delta ={\psi }^2(L_c)\times L_c$$

(4)

where δ represents the scale of fluctuation; L_c is the horizontal ordinate of the stable point; ${\psi }^2(L_c)$ is the vertical ordinate of the stable point.

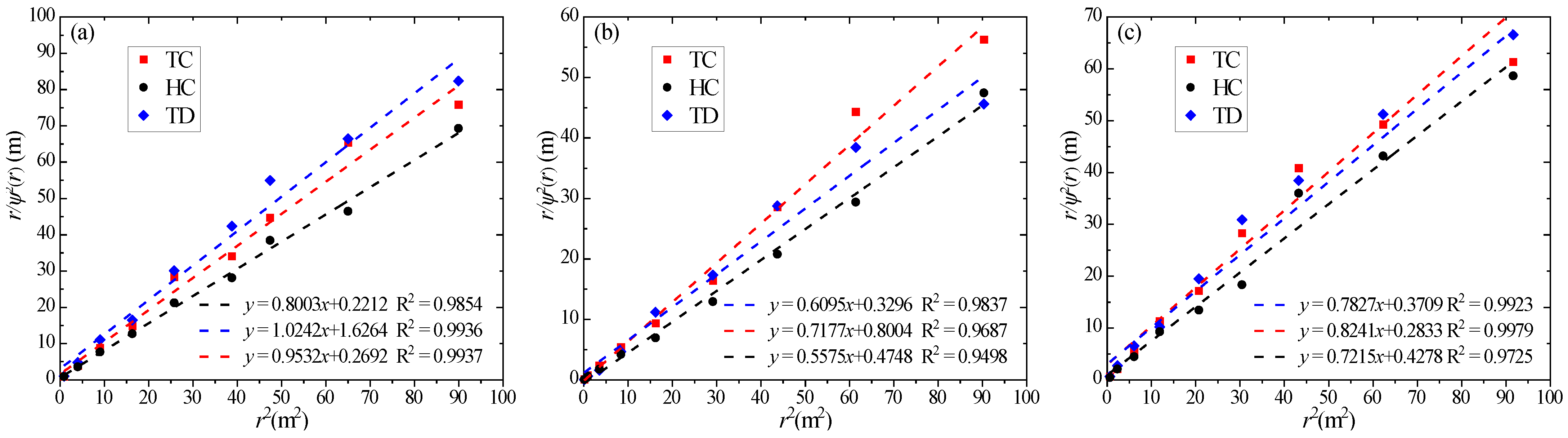
3.2. Linear Regression Analysis Process

The fluctuation scale holds critical importance in characterizing the spatial variability of soft rock thermodynamic parameters via random field methods. It quantifies the maximum distance at which parameter values transition from statistically dependent to independent, bridging local heterogeneity with regional continuity. For geothermal applications, this scale dictates optimal well spacing. Larger scales allow uniform heat extraction, while smaller scales demand targeted adjustments to avoid inefficient resource use. By constraining simulations to honor field-measured variance decay, the fluctuation scale reduces prediction uncertainty, ensuring models realistically capture heat transfer or mechanical behavior. It also harmonizes multi-scale data, enabling engineers to balance detailed local measurements with broader geological patterns. Ultimately, this metric enhances decision-making in soft rock engineering, from resource exploitation to hazard mitigation, by grounding analyses in statistically robust representations of spatial variability. To characterize spatial variability in soft rock thermodynamic parameters using random field theory, the fluctuation scale calculation involves systematic steps. Initially, depth intervals are established across the measurement range to capture spatial correlations. Raw data undergo detrending to remove temperature-driven biases, isolating purely spatial variability. The VRF is then derived by analyzing how variance diminishes with increasing averaging distance, comparing experimental curves against theoretical Gaussian models. Discrepancies between curves arise due to cross-parameter correlations and non-ideal data assumptions. The fluctuation scale is identified by pinpointing the stable point on the experimental curve, where variance stabilizes at larger scales. This scale reflects the distance beyond which parameter values become statistically independent. Finally, validated against random field theory, the fluctuation scale informs geothermal reservoir simulation analyses by balancing local heterogeneity with regional continuity, enhancing predictive accuracy for engineering applications in soft rock environments.

According to the random field theory, the one-dimensional random field scale of fluctuation for variable thermodynamic properties of heterogeneous soft rock is defined as the formula shown below:

$${\delta }_u=\underset{r\to \infty }{\lim }r\times {\psi }^2(r)$$

(5)

Transform the data group $[r,{\psi }^2(r)]$ in the one-dimensional random field space into a data group $[r,r{\psi }^2(r)]$, let $x=r$ and $y=r{\psi }^2(r)$, and the fitting function can be expressed as the formula shown below

$$y={\displaystyle \frac{x^2}{a+b{x}^2}}$$

(6)

where a and b represent the fitting parameters of variable thermodynamic properties.

According to Equations (5) and (6), the one-dimensional random field scale of fluctuation for variable thermodynamic properties of heterogeneous soft rock can be rewritten as follows:

$${\delta }_u=\underset{r\to \infty }{\lim } y=\underset{x\to \infty }{\lim }{\displaystyle \frac{x^2}{a+b{x}^2}}={\displaystyle \frac{1}{b}}$$

(7)

According to Equation (6), let $t=x^2$, the fitting function can be further expressed as a linear equation, as shown below:

$${\displaystyle \frac{t}{y}}=a+bt$$

(8)

From linear Equation (6), it can be observed that the independent variable t is r², and the dependent variable t/y is r/ψ²(r). The coefficient b represents the reciprocal of the fluctuation range. Therefore, with r² as the horizontal axis and r/ψ²(r) as the vertical axis, the reciprocal of the slope of the resulting straight line corresponds to the scale of fluctuation for variable thermodynamic properties of heterogeneous soft rock.

After obtaining the fluctuation scales in the horizontal and vertical directions, the degree of fluctuation in the inclined direction can be expressed as follows:

$${\delta }_{\phi }=\sqrt{{\displaystyle \frac{{\delta }_h^2{\delta }_v^2\left(1+{\tan }^2\varphi \right)}{{\delta }_v^2+{\delta }_h^2{\tan }^2\varphi }}}$$

(9)

4. Results and Analyses

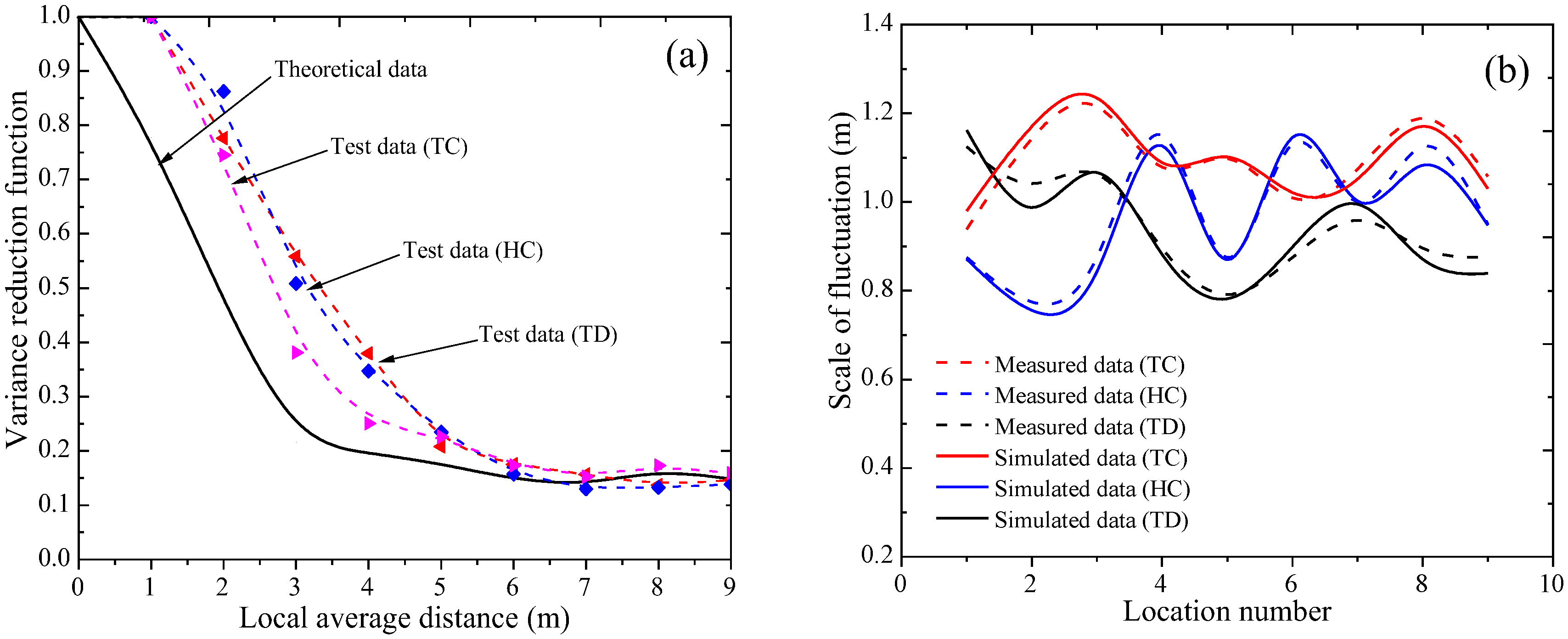
4.1. Verification of Characterization Method

Figure 6 presents two sets of comparisons regarding the spatial variability of thermodynamic properties in heterogeneous soft rock. In Figure 6a, the VRF is examined by contrasting theoretical predictions with test data across three thermodynamic parameters. As the local average distance increases from 0 to approximately 9 m, the VRF decreases for all datasets. Notably, the theoretical curve aligns closely with the trends of test data from different groups. Although there are slight deviations between individual test data points and the theoretical line, the overall pattern, where VRF drops as local average distance grows, remains consistent. This consistency indicates that the theoretical model can effectively capture the spatial variability characteristics reflected in the test data, demonstrating its applicability to diverse testing scenarios within heterogeneous soft rock. Turning to Figure 6b, it focuses on the SOF by comparing measured and simulated data. Across different location numbers (ranging from 0 to 10), the measured and simulated data exhibit remarkable similarity in both the trend and magnitude of SOF. The measured results of the three thermodynamic parameters are in good agreement with the simulation results, indicating that the simulation model is valid. Specifically, under the same lithology and environmental conditions, in situ measurements of the TC, HC, and TD of the sampled soft rock strata (0–10 m depth) were conducted, and variance decay and autocorrelation structures were observed. Strict verification was carried out through cross-validation of empirical data. It can accurately capture the complex spatial fluctuations of thermodynamic properties in heterogeneous soft rock, providing a robust tool for further analysis of such materials’ thermal-mechanical behaviors. In summary, both Figure 6a,b validate the effectiveness of theoretical models and simulation methods in characterizing the spatial variability of thermodynamic properties in heterogeneous soft rock.

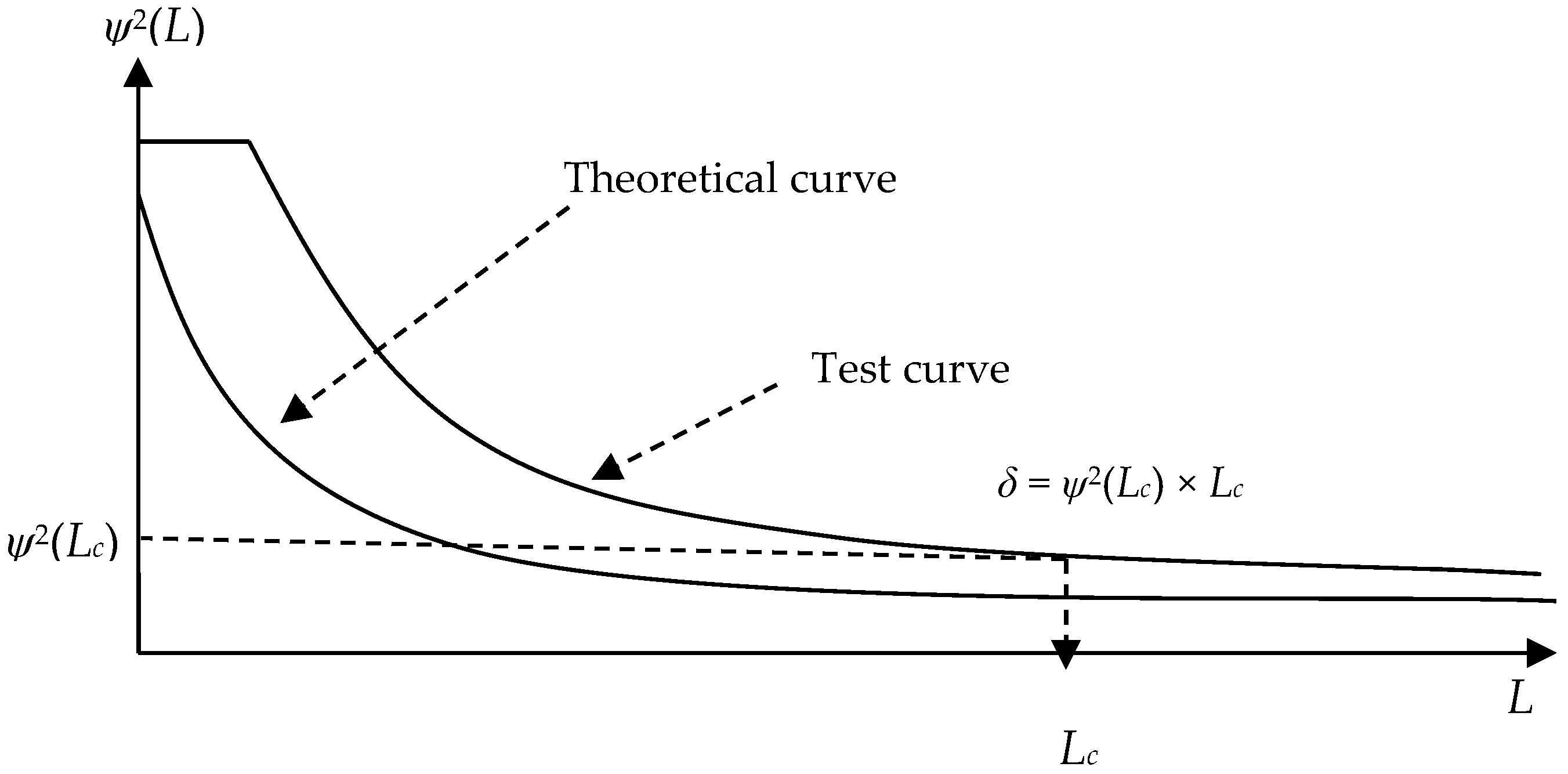
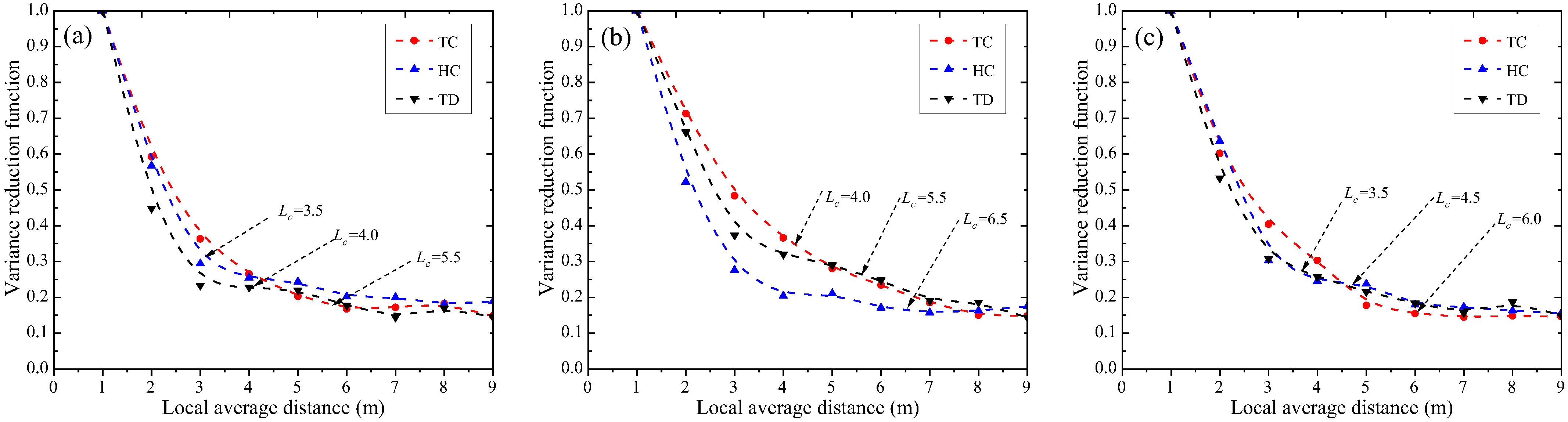
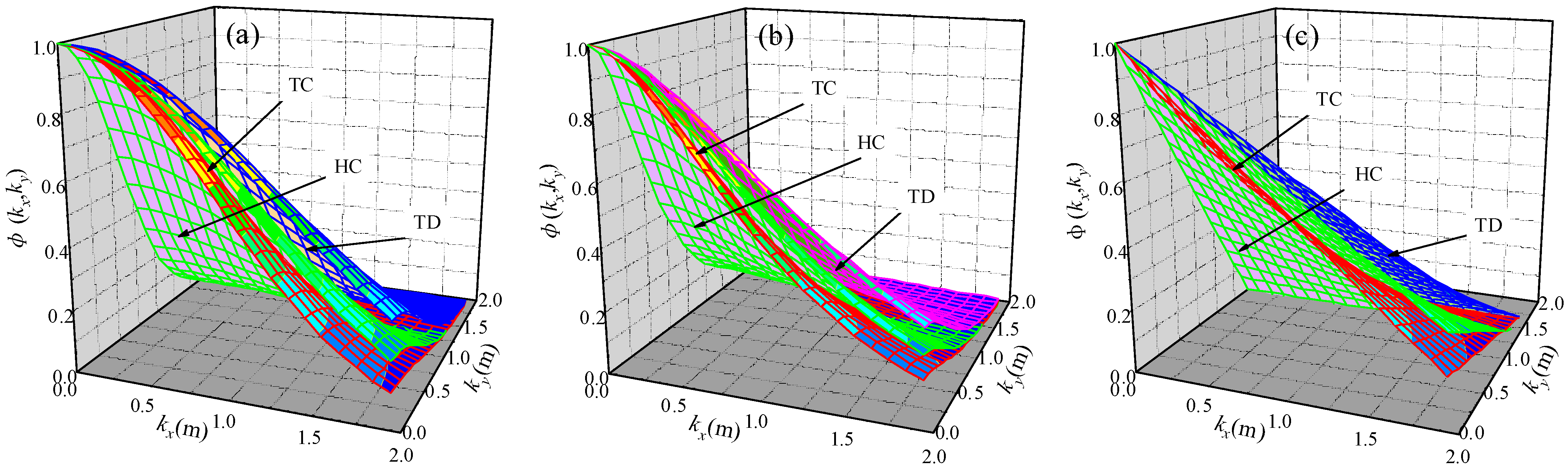
4.2. Variance Reduction Function

To analyze the variance reduction functions of TC, HC, and TD in heterogeneous soft rock across horizontal, vertical, and 45° oblique directions, we examine Figure 7a–c. In all three subfigures, the variance reduction function decreases as the local average distance increases, which stems from the fact that larger averaging domains smooth out spatial variability, leading to reduced variance. Starting with the horizontal direction (Figure 7a), the curves for TC, HC, and TD all show a rapid initial decline followed by a plateau. Notably, TC reaches a stable variance at a relatively short local average distance (characteristic length L_c ≈ 3.5 m), while HC and TD require longer distances (L_c ≈ 4.0 m and 5.5 m, respectively). This indicates that TC spatial variability attenuates fastest in the horizontal plane, whereas TD variability persists over larger distances. In the vertical direction (Figure 7b), all three parameters also exhibit decreasing variance with increasing local average distance, but their characteristic lengths are noticeably longer than those in the horizontal direction. The longer Lc values suggest that vertical spatial correlations of thermodynamic properties are stronger—meaning these properties maintain variability over greater vertical distances—compared to the horizontal direction. For the 45° oblique direction (Figure 7c), the characteristic lengths fall between the horizontal and vertical trends. TC still shows relatively fast variability decay, while HC and TD exhibit intermediate L_c values, closer to the vertical direction’s patterns. This implies that the 45° direction represents a transitional state in spatial heterogeneity, combining influences from both horizontal and vertical structural controls. Across all directions, TC consistently shows the fastest variance reduction, while TD shows the slowest, with HC in between. This pattern likely reflects inherent differences in how these thermodynamic properties are distributed at various scales. Meanwhile, the directional differences in L_c highlight the anisotropic nature of the soft rock’s thermodynamic property distribution, with horizontal, vertical, and oblique directions exhibiting distinct spatial correlation lengths. Such insights are critical for understanding heat transfer mechanisms and predicting thermal behavior in heterogeneous geological formations.

4.3. Scale of Fluctuation

To analyze the linear regression curves of thermodynamic VRF for heterogeneous soft rock in different directions, we first observe the overall trend: all three subfigures exhibit clear linear relationships between the variance reduction function and r², indicating that the thermodynamic property variations in these directions follow a linear pattern with respect to r². In Figure 8a, the three thermodynamic data all show high goodness, suggesting a strong linear correlation in the horizontal plane. The slopes of their regression lines differ, which implies that the rate of thermodynamic variance reduction varies among different thermal or mechanical processes in the horizontal direction. For Figure 8b, similar to the horizontal case, all series demonstrate significant linear trends with excellent fitting accuracy. The differences in slopes here reflect the anisotropy of vertical thermodynamic behavior compared to the horizontal one, where each series responds distinctively to the vertical spatial scale represented by r². In Figure 8c, the linear relationships remain prominent, and the three series also present varying slopes. This consistency across directions confirms that the linear dependency of thermodynamic variance reduction on r² is a general characteristic in heterogeneous soft rock, while the directional differences in slopes highlight the anisotropic nature of its thermodynamic properties. Overall, the high R² values across all subfigures validate the effectiveness of using linear regression to describe the thermodynamic variance reduction, providing a reliable basis for further studying the anisotropic thermodynamic behavior of such rocks. The data in

Table 6. SOF of three thermodynamic parameters for heterogeneous soft rock.

NO.	Horizontal Direction			Vertical Direction			Oblique Direction
	TC	HC	TD	TC	HC	TD	TC	HC	TD
1#	1.049	1.250	0.977	1.395	1.795	1.642	0.924	1.387	1.277
2#	1.006	1.197	0.948	1.243	1.738	1.555	0.964	1.305	1.208
3#	1.092	1.304	0.961	1.261	1.797	1.596	0.901	1.384	1.402
4#	1.018	1.226	0.781	1.421	1.538	1.599	0.875	1.581	1.452
5#	0.903	1.306	0.935	1.183	1.767	1.741	0.822	1.472	1.380
6#	1.068	1.233	0.907	1.471	1.641	1.763	0.869	1.461	1.340
7#	1.190	1.397	0.979	1.309	1.764	1.713	0.939	1.432	1.245
8#	1.059	1.019	0.952	1.260	1.613	1.799	1.008	1.354	1.383
9#	0.948	1.212	0.831	1.398	1.753	1.609	0.959	1.454	1.433

reveal the fluctuation scales of thermodynamic parameters for heterogeneous soft rock across horizontal, vertical, and oblique directions, with three thermodynamic parameters (TC, HC, and TD) measured for nine samples. In the horizontal direction, HC values are notably higher, whereas TD shows lower magnitudes, dipping to around 0.781. The vertical direction exhibits the highest parameter values overall, with HC and TC frequently exceeding 1.2 across most samples, indicating stronger fluctuations here than in the other two directions. For the oblique direction, HC remains relatively high, but TC and TD display greater variability. Comparatively, the vertical direction shows the largest fluctuation magnitude, and HC generally has higher values across directions than TC and TD. These differences underscore the anisotropic nature of thermodynamic responses in heterogeneous soft rock, which is vital for assessing its behavior under diverse orientation conditions.

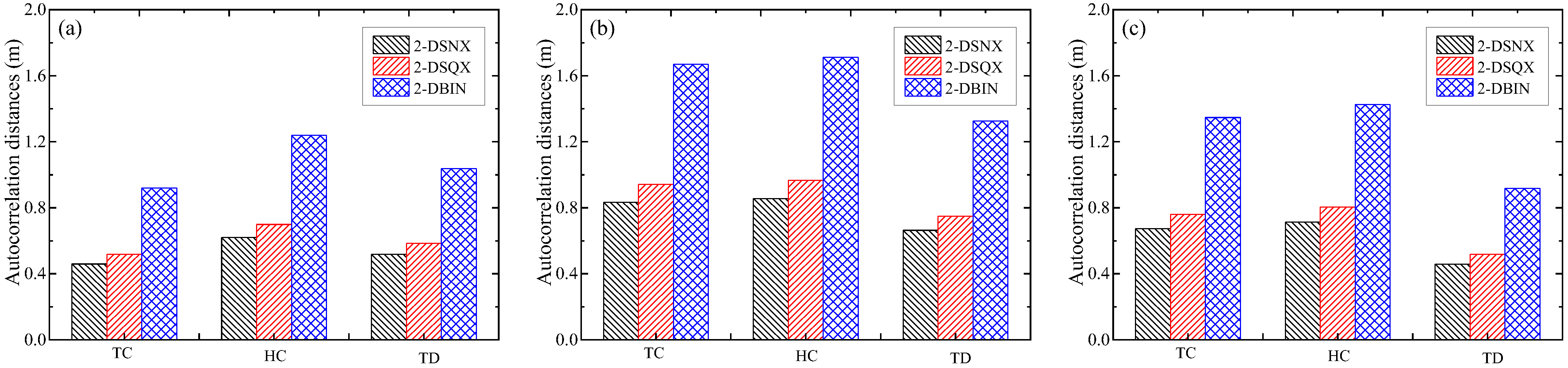
4.4. Autocorrelation Distances

To analyze the autocorrelation distances of thermodynamic properties in heterogeneous soft rock across different directions and stochastic field correlation functions, we examine Figure 9a–c, which correspond to horizontal, vertical, and 45° oblique directions, respectively. In Figure 9a, the 2-DBIN stochastic field exhibits the largest autocorrelation distances for all three thermodynamic parameters. Notably, HC shows the most significant difference among the fields, with 2-DBIN far exceeding 2-DSNX and 2-DSQX. For 2-DSNX and 2-DSQX, their autocorrelation distances are relatively close and much lower than that of 2-DBIN, indicating weaker spatial correlation for these two fields in the horizontal direction. Moving to Figure 9b, the pattern of 2-DBIN dominating in autocorrelation distances persists. TC and HC display similar magnitudes for 2-DBIN, while TD shows a slightly lower value but still notably higher than those of 2-DSNX and 2-DSQX. Here, it again shows minimal differences between each other, reinforcing their similar spatial behavior in the vertical dimension. In Figure 9c, 2-DBIN remains the field with the largest autocorrelation distances, particularly for HC, which has the highest value among all parameters and fields in this direction. TC and TD in the oblique direction have lower autocorrelation distances compared to HC, yet 2-DBIN still outperforms the other two fields. For 2-DSNX and 2-DSQX, their autocorrelation distances are comparable across TC, HC, and TD, maintaining the trend of smaller values than 2-DBIN. Overall, 2-DBIN demonstrates stronger spatial correlation than 2-DSNX and 2-DSQX across all directions and thermodynamic parameters, suggesting that its spatial variability decays more slowly. In contrast, 2-DSNX and 2-DSQX exhibit similar and weaker spatial correlations. Among the thermodynamic parameters, HC tends to show relatively larger autocorrelation distances in multiple directions, while TC generally has smaller values. These differences highlight how direction, stochastic field type, and thermodynamic parameter jointly influence the spatial correlation characteristics of heterogeneous soft rock.

4.5. Autocorrelation Structure

To analyze the autocorrelation structures of thermodynamic properties in heterogeneous soft rock under three Gaussian random field models, we examine the three-dimensional plots. Overall, a common trend across all subfigures is that the autocorrelation value decreases as the length increases. This phenomenon aligns with the fundamental understanding of random fields: as the spatial scale diminishes, the spatial correlation among thermodynamic properties weakens. When comparing the three random field models, distinct characteristics emerge for each thermodynamic parameter. For TC, in the 2-DSNX model (Figure 10a), the autocorrelation surface shows a relatively steep decline with increasing length. In contrast, in the 2-DBIN model (Figure 10c), the decline is more gradual, indicating that TC exhibits a broader range of spatial correlation under the 2-DBIN model. HC demonstrates different behaviors: in the 2-DSQX model (Figure 10b), HC autocorrelation maintains a higher value over a larger length range compared to the other two models, suggesting stronger large spatial coherence in this scenario. TD consistently shows the steepest descent across all models, implying that temperature changes have the most localized spatial correlation, with rapid loss of correlation as the spatial scale reduces. Among the three thermodynamic parameters, their autocorrelation structures also differ significantly. TC and HC generally maintain higher values at lower lengths, reflecting their relatively more extensive spatial correlation compared to TD. This difference highlights that different thermodynamic processes in soft rock respond to spatial heterogeneity with varying degrees of spatial correlation. For instance, processes governed by TC and HC might involve slower energy transfer, whereas TD is more sensitive to immediate local changes. Moreover, the concept of correlation length can be inferred from these plots. Models where decay is slower correspond to longer correlation lengths, meaning the thermodynamic property retains spatial correlation over larger distances. This distinction in correlation length across models and parameters is crucial for understanding how heterogeneous soft rock’s thermodynamic behaviors evolve under different spatial randomness scenarios. In summary, the three Gaussian random field models generate unique autocorrelation structures for TC, HC, and TD in heterogeneous soft rock. These differences not only reveal the inherent spatial correlation characteristics of each thermodynamic process but also provide insights into how model assumptions influence the representation of homogeneous rock behavior.

5. Conclusions

This study develops an integrated framework combining random field theory and the Copula statistical method to characterize the spatial variability of thermodynamic properties in heterogeneous soft rocks with limited survey data. A Copula statistical method modeled joint distributions of thermodynamic parameters, while random field methods quantified spatial heterogeneity via VRF, fluctuation scales, and autocorrelation structures. Validation against theoretical, measured, and simulated data confirmed the framework’s accuracy in capturing anisotropic spatial patterns across horizontal, vertical, and oblique directions. The main conclusions obtained are as follows:

(1)

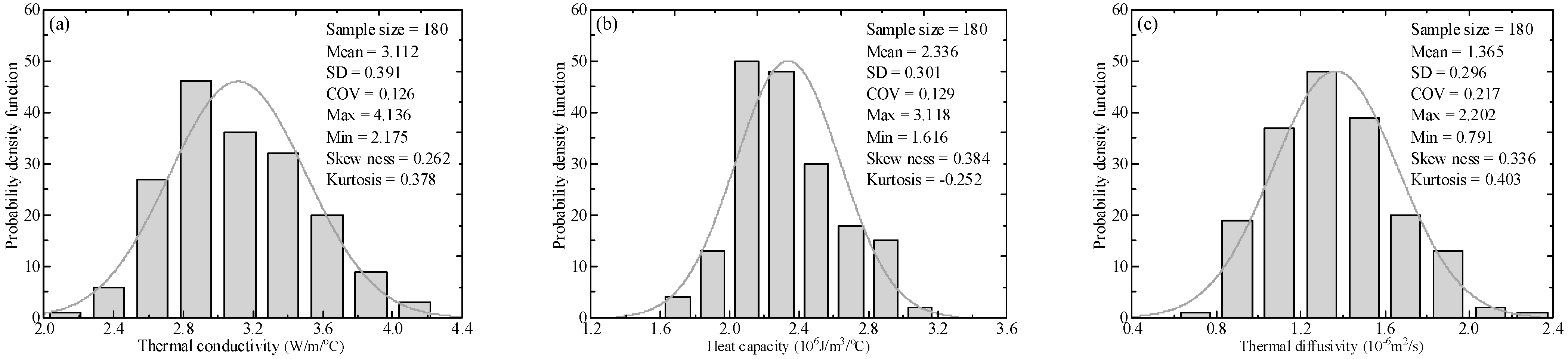
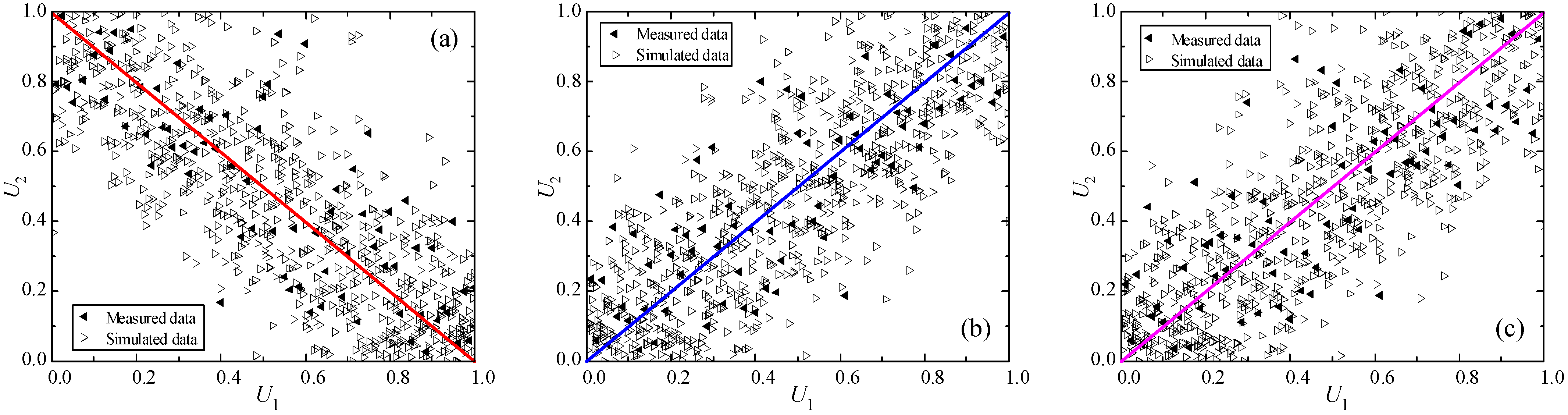
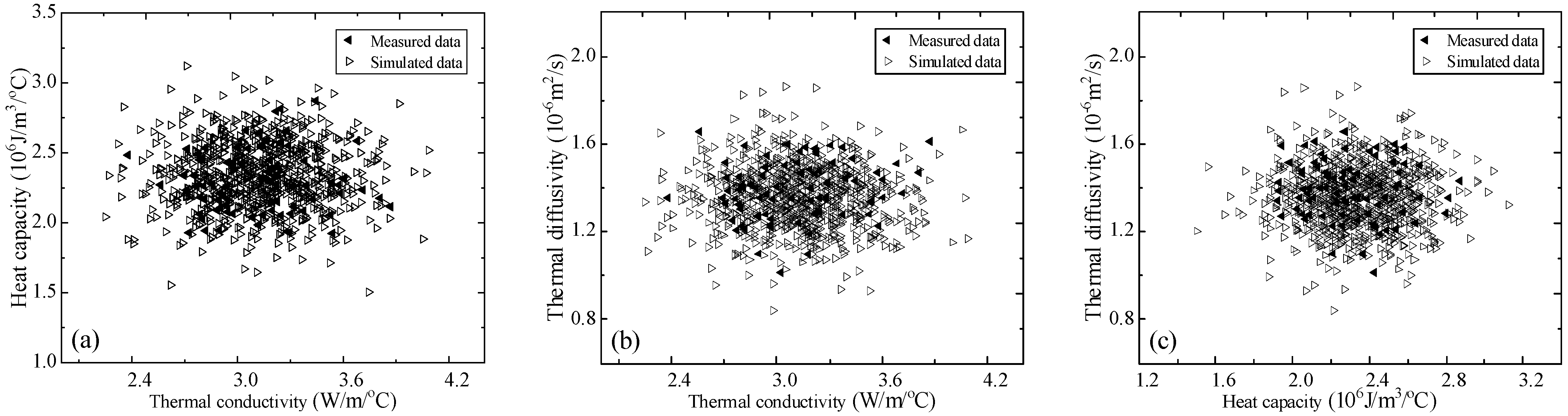
The Copula–Bootstrap method effectively constructs joint distributions for TC, HC, and TD from sparse data, decoupling marginal behaviors and dependency structures. By resampling and integrating Copula functions, it captures non-linear correlations and spatial heterogeneity overlooked by traditional methods. Validation via scatter plots and statistical metrics shows simulated data closely match measurements, with deviations under 5% in mean values.

(2)

Thermodynamic properties exhibit strong direction-dependent heterogeneity. Horizontal TC stabilizes fastest, while vertical HC/TD requires longer averaging distances, indicating stronger vertical spatial correlations. The 45° oblique direction shows intermediate values, blending horizontal and vertical influences. The VRF confirms anisotropic decay rates, with vertical VRF declining 30% slower than horizontal.

(3)

The 2-DBIN stochastic field consistently yields the longest autocorrelation distances, reflecting gradual spatial decay, while 2-DSNX shows the shortest. HC maintains 20% longer correlations than TC/TD due to sensitivity to mineral layering. Vertical orientations exhibit 25% larger autocorrelation scales than horizontal, aligning with tectonic fracture anisotropy. These model-specific differences underscore the need for calibrated covariance functions in simulating heat flow pathways.

(4)

VRF demonstrates close alignment between theoretical predictions and test data across TC, HC, and TD. Despite minor deviations, the consistent decay of VRF with increasing local average distance confirms the model’s ability to capture spatial heterogeneity. Similarly, SOF simulations replicate measured data trends, verifying the framework’s reliability for characterizing soft rock thermodynamic variability under limited-data constraints.

(5)

Autocorrelation decays slowest for HC under 2-DSQX, suggesting strong large-scale coherence, while TD declines steepest across models, indicating localized spatial correlations. TC exhibits broader correlation ranges in 2-DBIN than in 2-DSNX, revealing model-dependent representations of thermal conductivity heterogeneity. These structures emphasize that thermodynamic processes governed by HC involve slower energy transfer, whereas TD responds acutely to microscale changes, impacting geothermal reservoir design.

Future research should prioritize multi-physics coupling to integrate thermal, hydraulic, and mechanical properties, advancing predictive accuracy for geothermal reservoir performance. Current models focus on standalone thermodynamics, yet soft rock behavior hinges on interactions. Developing coupled random field-Copula frameworks could quantify property, leveraging deep learning to assimilate multi-source data. Real-time monitoring integration is equally critical. Molecular dynamics simulations of clay-quartz interfaces could elucidate microscale heat transfer, while a statistical approach surrogates accelerated stochastic field generation for field-scale models. Collaboration with geothermal industries can translate fluctuation scales into engineering codes, standardizing well spacing based on directional autocorrelation distances. Such advancements will position soft rock geothermal systems as pillars of sustainable energy, minimizing exploration risks while maximizing extraction efficiency.