Management of Zero-Sequence Parameters for Earth Faults on the Power Receiver’s Side in IT-Type Networks

Abstract

This study examines the behavior and control of zero-sequence parameters in IT-type electrical networks under conditions of capacitive insulation asymmetry and complex asymmetric faults on the power receiver side. Existing methods of zero-sequence analysis typically address either symmetrical network conditions or single-phase earth faults in isolation, and they often neglect the combined effects of conductor breakage, transient fault resistance, and capacitive unbalance. To overcome these limitations, this work develops an analytical model based on the general theory of electrical engineering and symmetrical components, enabling a unified description of zero-sequence voltages and currents that incorporates both insulation asymmetry and compound fault scenarios. The model establishes closed-form relationships linking zero-sequence quantities to network parameters, power receiver characteristics, and transient resistances at the fault point. The results demonstrate several previously unreported effects, including a 180° vector shift and nearly 50% reduction in zero-sequence voltage and current magnitudes during simultaneous conductor breakage and earth faults compared with conventional single-phase faults—phenomena that critically influence the correct setting of protection devices. The study further shows that capacitive insulation asymmetry alone may generate zero-sequence voltages sufficient to trigger earth-fault protection regardless of the neutral grounding mode. These findings reveal increased risks of fault escalation, misoperation of existing protection systems, and prolonged unsafe touch voltages. Overall, the derived dependencies provide a new analytical basis for improving the design and coordination of protection systems in IT-type networks.

1. Introduction

Reliable detection and management of earth faults in IT-type electrical networks remain a critical challenge for both industrial and utility power systems. Unlike TN or TT configurations, IT networks operate with an isolated or high impedance grounded neutral, which increases operational continuity but complicates fault localization and protection coordination [1]. The occurrence of capacitive asymmetry in network insulation, combined with complex asymmetrical damages on the power receiver’s side, can significantly alter the behavior of zero-sequence parameters [2]. This may cause traditional protections to fail, leading to longer fault duration, greater equipment damage, and safety risks for personnel [1,2,3].

Modern industrial processes, critical infrastructure, and high-reliability facilities increasingly rely on IT-type networks to maintain continuous operation [4]. Complex loads, distributed energy sources, and variable insulation conditions require more advanced diagnostic and management approaches [5]. Studying the regularities in zero-sequence voltage and current behavior is essential for understanding how electrical systems respond to fault conditions [6,7]. These patterns become particularly significant when capacitive asymmetry is present, as it can distort the expected signal characteristics [8]. By analyzing these variations across different fault scenarios, engineers gain deeper insights into system vulnerabilities and dynamic responses [9]. This also addresses gaps in standards, which often ignore the dynamic changes in vector positions and magnitudes under such conditions [3,8,9,10].

When a conductor of an overhead power line breaks and encounters the ground on the power supply side, a fault condition is immediately created [11]. This type of fault is characterized by a sudden and direct path for current to flow from the line to earth [12]. Its electrical behavior resembles a single-phase short circuit to ground [13]. Such incidents require prompt detection and isolation to prevent equipment damage and ensure system stability. This type of asymmetric fault has been extensively investigated in specialized literature, with well-established models and protective measures [11,12,13,14]. The electrical, thermal, and transient processes accompanying such events are generally predictable, allowing for effective detection and isolation by conventional relay protection systems.

However, when a conductor break occurs on the side of the power receiver and is accompanied by an earth fault, the nature of the damage is less well understood. In this case, the fault current flows through transformer primary windings or the stator windings of high-voltage motors [2,6,15]. This forms a different fault path than on the supply side, altering impedance and transient characteristics [16]. Thus, common assumptions about current magnitude, fault duration, and energy dissipation may not apply.

One major consequence is significant overvoltage that can spread through the entire network [17]. This may cause secondary insulation breakdown far from the fault, increasing system vulnerability [18]. The complexity of the electromagnetic processes involved, combined with the diversity of consumer-side equipment, makes this phenomenon difficult to model using traditional approaches.

Existing protection devices respond inconsistently to such consumer-side faults [17,18,19]. Depending on network topology, grounding, and insulation, relays may fail to trip, trip late, or operate incorrectly. The extended fault duration not only increases the risk of equipment damage but also deteriorates the electrical safety conditions for operational personnel and end users [18]. Delayed fault clearance can cause cascading failures and complicated recovery.

The practical importance of this research lies in its potential to reduce both the risk of cascading failures and the exposure time to dangerous touch voltages during earth faults. The developed models and parameter dependencies help optimize protection settings and ensure reliable operation across various configurations and fault types [17,18,20]. Ultimately, the results contribute to enhancing electrical safety, increasing the resilience of power supply systems, and aligning fault management practices with the operational realities of modern IT-type networks [1,4,21].

So, the general purpose of this study is to analyze the voltage and current parameters of the zero-sequence component during consumer-side earth faults and to establish their dependence on the insulation characteristics of the distribution network. To achieve this, it is necessary to develop a mathematical model that accurately represents the specific conditions of such faults. This model will support further research to improve protection selectivity and speed, enhance network stability, and reduce the risk of secondary insulation failures.

2. Reference Background in Management of Zero-Sequence Parameters for Earth Faults

The phenomenon of false positives in power system fault detection is frequently associated with capacitive asymmetry within network components. The physics-based model for hybrid asymmetric capacitors was validated using commercial lithium-ion capacitors. The results show that capacitive asymmetry can cause significant measurement errors and misinterpretations, affecting protection reliability [3,12,21]. These findings underscore the need for precise modeling of capacitive characteristics to avoid erroneous triggering of protective devices. Other studies show that geometric and manufacturing asymmetries generate noise and spurious signals during measurements, complicating fault detection [17,22]. These conditions may trigger unintended protection responses, underscoring the need to consider asymmetrical effects in diagnostic algorithms and relay settings.

Because fixed-parameter protection has inherent limitations, recent research focuses on adaptive protection methodologies [23]. Such approaches are designed to dynamically adjust protection settings in response to real-time changes in network operating conditions, thereby enhancing system resilience and reliability. Adaptive protection uses AI, rule-based logic, and optimization algorithms to maintain efficiency under variable loads and fault conditions [23,24]. These systems process large data volumes, detect evolving fault characteristics, and adjust their decisions in real time. Further studies [16,17,18,25] examine the functional and architectural requirements for implementing adaptive protection in networks with high DER penetration [26]. This research highlights the key role of automation and advanced decision-making algorithms in ensuring selective and fast fault clearance, especially under complex or non-standard conditions.

Accurate and timely monitoring of zero-sequence parameters is crucial for detecting asymmetric faults in electrical systems. These faults are especially challenging when they occur on the power-receiver side, where conventional detection may fail. Among various diagnostic techniques, zero-sequence voltage (ZSV) monitoring has demonstrated superior performance in identifying faults quickly and reliably [25]. Compared to motor current signature analysis using short-time Fourier transforms (MCSA-STFT), ZSV offers enhanced sensitivity and faster response times. This advantage is largely attributed to the use of Fortescue transforms combined with advanced signal processing methods, which enable real-time fault detection. As is highlighted, integrating ZSV monitoring into protection schemes can significantly improve the resilience and safety of induction motor systems [6,27].

Orthogonal distance regression has improved parameter estimation by addressing the challenges of mutual coupling and sparse synchrophasor data in modern transmission networks [28]. These methods allow for more accurate modeling of system parameters, thereby enhancing the reliability of network analysis and state estimation. In intelligent fault diagnosis, hybrid BiLSTM networks with attention improve both accuracy and interpretability, especially in complex industrial settings [29,30]. Combining wavelet transforms with fuzzy-logic controllers improves fault localization and classification in synchronous generators, offering real-time advantages [31]. These approaches improve reliability and support predictive maintenance that reduces downtime and operational costs [32]. Together, these developments show increasing synergy between advanced signal processing, machine learning, and control methods in power-system monitoring and protection [33]. Future research is expected to focus on further optimizing these hybrid approaches to handle increasingly complex network conditions and data uncertainties.

The theoretical foundation of zero-sequence analysis lies in the century-old symmetrical component theory developed by Fortescue. Practical guidance for applying symmetrical component theory within relay protection engineering reinforces its value for modeling asymmetric faults in modern power systems [34].

Despite many studies, there is still no systematic analysis of zero-sequence amplitude–phase characteristics under varying insulation parameters, transient resistances, and dynamic operating conditions. Existing methods mostly address steady-state capacitive behavior or use simplified equivalent circuits, but they do not offer a unified framework for both internal and external single-phase faults. Furthermore, many protection-setting approaches do not fully account for the coupled influence of insulation degradation, fault intermittency, and network capacitance on the resulting zero-sequence responses.

This study is oriented to investigate the behavior of voltage and current zero-sequence components during consumer-side earth faults in IT-type distribution networks, with particular emphasis on their dependence on insulation parameters. To support this analysis, a dedicated mathematical model will be developed to simulate the specific fault conditions accurately. This model will serve as a basis for advancing protection strategies by improving the selectivity and response time of protective devices, reinforcing overall network stability, and reducing the likelihood of cascading failures caused by secondary insulation breakdowns. The purpose of this study is to develop an analytical and simulation-based approach for evaluating zero-sequence amplitude and phase characteristics under various fault scenarios, and to determine how these dependencies can improve the sensitivity and selectivity of ground-fault protection in isolated-neutral and compensated mining networks.

3. Methods and Methodology for Management of Zero-Sequence Parameters for Earth Faults

The first step in the methodology involves the systematic selection of replacement schemes for managing earth faults in IT-type networks. Various configurations of grounding and isolation on the power receiver’s side are considered, with emphasis on minimizing false positives and ensuring network stability [1,4,15,21,35]. Comparative analysis using analytical models and simulations allows assessment of scheme effectiveness under different network topologies and load conditions [8,36]. The selection criteria prioritize safety, reliability, and the capacity to maintain continuous operation during single-phase-to-earth faults.

Because full-scale experiments on an operating open-pit mine network are not feasible, alternative approaches must be used. Full-scale testing would require intentional disturbances or controlled grounding faults, which involve significant organizational, technical, and safety challenges. In view of these limitations, we selected the most accessible and safe alternative—laboratory experiments on a physical model of the open-pit mine distribution network.

The laboratory model uses passive components that reproduce the equivalent parameters of the mining IT network. It also includes voltage and current transformers for galvanic isolation and measurement of zero-sequence components. This configuration enables controlled simulation of typical and extreme insulation conditions while maintaining operational safety. The resulting laboratory measurements, combined with the theoretical analysis, offer a practical and reliable means of validating the behavior of zero-sequence voltage and current under conditions representative of mining power supply systems.

Following scheme selection, the methodology addresses the measurement and analysis of zero-sequence voltage (ZSV). High-precision voltage sensors are deployed at strategic points in the network to capture the transient and steady-state components of ZSV during simulated fault conditions [15,17,18,19,37]. We apply Fourier analysis and filtering to distinguish genuine fault signals from noise caused by capacitive asymmetry or harmonics. This step ensures that the subsequent assessment of protection performance is based on accurate and reliable voltage measurements.

In parallel, the study examines zero-sequence currents (ZSCs) in the network, which are critical indicators of earth fault behavior in IT-type systems. Current transformers and differential measurement techniques are employed to monitor ZSC under normal and faulty conditions. The collected data helps identify current-flow patterns associated with various insulation failures, including asymmetrical and complex faults [16,17,20,38]. Advanced modeling tools MATLAB R2022b and PSCAD simulate network responses and validate the observed current behaviors against theory [39,40].

Also, it is necessary to note that in our research, the simplified assumptions used in developing the replacement schemes are consistent with the methodological approaches traditionally applied to calculating the parameters of mine electrical installation networks [33,35,41]. The active resistance of transformer windings is neglected because it is small and has little effect on calculations [29,38]. Likewise, line impedance is commonly simplified in analytical models of mining distribution networks to ensure computational tractability.

Finally, the methodology integrates the analysis of ZSV and ZSC to develop a comprehensive management strategy for zero-sequence parameters [38,42]. Combined voltage and current data are used to develop decision-making algorithms that optimize relay settings, improve detection sensitivity, and reduce false trips. Sensitivity and parametric analyses determine optimal ZSV and ZSC thresholds to ensure system robustness. Sensitivity studies and parametric analyses are conducted to determine the optimal thresholds for both ZSV and ZSC, ensuring the robustness of the proposed management framework. The methodology emphasizes iterative validation, where simulation results are continuously compared with experimental or field data to refine the protection approach.

4. Research Results and Its Discussion in Zero-Sequence Currents and Voltage

The reliable operation of distribution networks in open-pit mines is strongly affected by single-phase short circuits to ground. These faults are among the most common and hazardous in such environments. They typically occur when a conductor breaks at the insulator point and comes into direct contact with the ground. In such situations, zero-sequence voltage and current become key indicators for assessing protection system performance and power-receiver stability. In these cases, the zero-sequence voltage and current parameters play a decisive role in determining the performance of protection systems and the stability of power receivers. To ensure accurate assessment, it is necessary to develop equivalent replacement schemes that can reflect the physical conditions of the fault and capture the transient processes in the network.

In this study, a series of replacement schemes were designed to investigate zero-sequence voltages and currents for earth faults on the power receiver’s side. The models assume a symmetrical electromotive force. The distributed capacitances are replaced with concentrated parameters. Line and transformer impedances are considered negligible. These simplifications allow the analytical derivation of equations for fault currents and voltages. The resulting relations are validated using characteristic amplitude- and phase-variation curves. The obtained dependencies provide a theoretical foundation for evaluating the behavior of protective systems under different network insulation conditions and transient resistances.

4.1. Selection of the Replacement Schemes

A phase short to ground on the power-receiver side occurs when one of the overhead line conductors breaks. This situation is typical for distribution networks in open-pit mining operations. In most cases, the break occurs at the insulator—the mechanical fixing point. There, the conductor encounters a grounded, non-insulated surface [15,43,44]. As a result, the two undamaged phases at the fault location are connected to the ground through the impedances of the power receiver and the transient resistance.

To investigate the behavior of zero-sequence voltages and currents during earth faults on the power receiver (PR) side, replacement schemes were developed (Figure 1, Figure 2 and Figure 3). In these schemes, the insulation conductivity of the damaged line section behind the fault point is assumed to be zero. This modeling approach allows for the systematic study of fault conditions while simplifying the complex interactions in the network.

Several limitations and assumptions were introduced to make the analysis tractable [15,43]. These assumptions include the following. The electromotive force of the power supply is symmetrical and free of higher harmonics. The distributed capacitance and insulation resistance of the phases relative to ground are replaced by concentrated values. The resistance and reactance of the line conductors are considered negligible. The resistance and inductance of the transformer windings are also taken as zero.

The diagrams (Figure 2 and Figure 3) indicate: Y₁ and Y′—the conductivity of the phase insulation of the protected connection and the remainder of the distribution network, respectively; r₁ and r′—transient resistance at the point of damage in the protected connection and the remainder of the distribution network; X_H1 and X_H′—inductive reactance of the phase-to-phase winding of the power receivers.

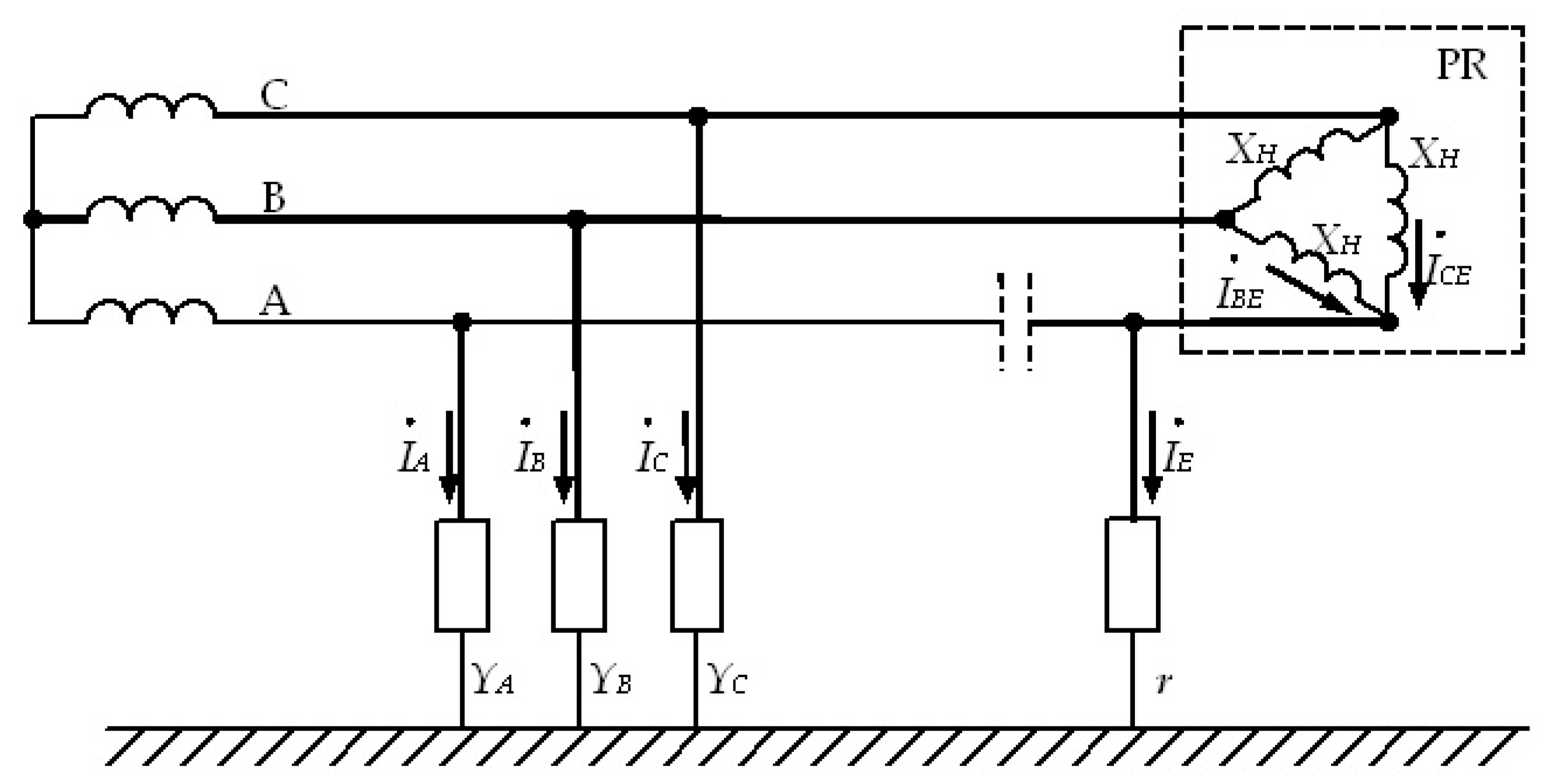
Figure 1. Distribution network replacement scheme for research zero-sequence voltages for earth faults on the side of the power receiver (PR): Y_A, Y_B, Y_C—conductivity of the insulation relative to the earth of the respective phases, r—transient resistance at the place of damage, X_H = ωL_H—inductive reactance of the phase-to-phase winding of the power receiver, I_BE, I_CE—ground-fault currents of phases B and C through load resistance and transient.

Figure 1. Distribution network replacement scheme for research zero-sequence voltages for earth faults on the side of the power receiver (PR): Y_A, Y_B, Y_C—conductivity of the insulation relative to the earth of the respective phases, r—transient resistance at the place of damage, X_H = ωL_H—inductive reactance of the phase-to-phase winding of the power receiver, I_BE, I_CE—ground-fault currents of phases B and C through load resistance and transient.

As shown in Figure 1, the equivalent circuit demonstrates the electrical behavior of the distribution network during an earth-fault event on the side of the power receiver. The insulation of each phase relative to ground is represented by the corresponding conductivities (Y_A, Y_B, Y_C), which determine how leakage currents may appear under fault conditions. The point of insulation breakdown is modeled by a transient resistance (r), reflecting the dynamic nature of the fault path as it forms and stabilizes. The inductive reactance of the phase-to-phase windings of the power receiver (X_H = ωL_H) influences the phase shift between voltage and current, thus affecting the overall fault current distribution. As the diagram illustrates, the ground-fault currents in phases B and C (I_BE and I_CE) flow through both the load resistance and the transient resistance, indicating a redistribution of current within the network. This provides a clearer understanding of how the system responds to insulation degradation and helps identify the critical parameters affecting zero-sequence voltage behavior during fault conditions.

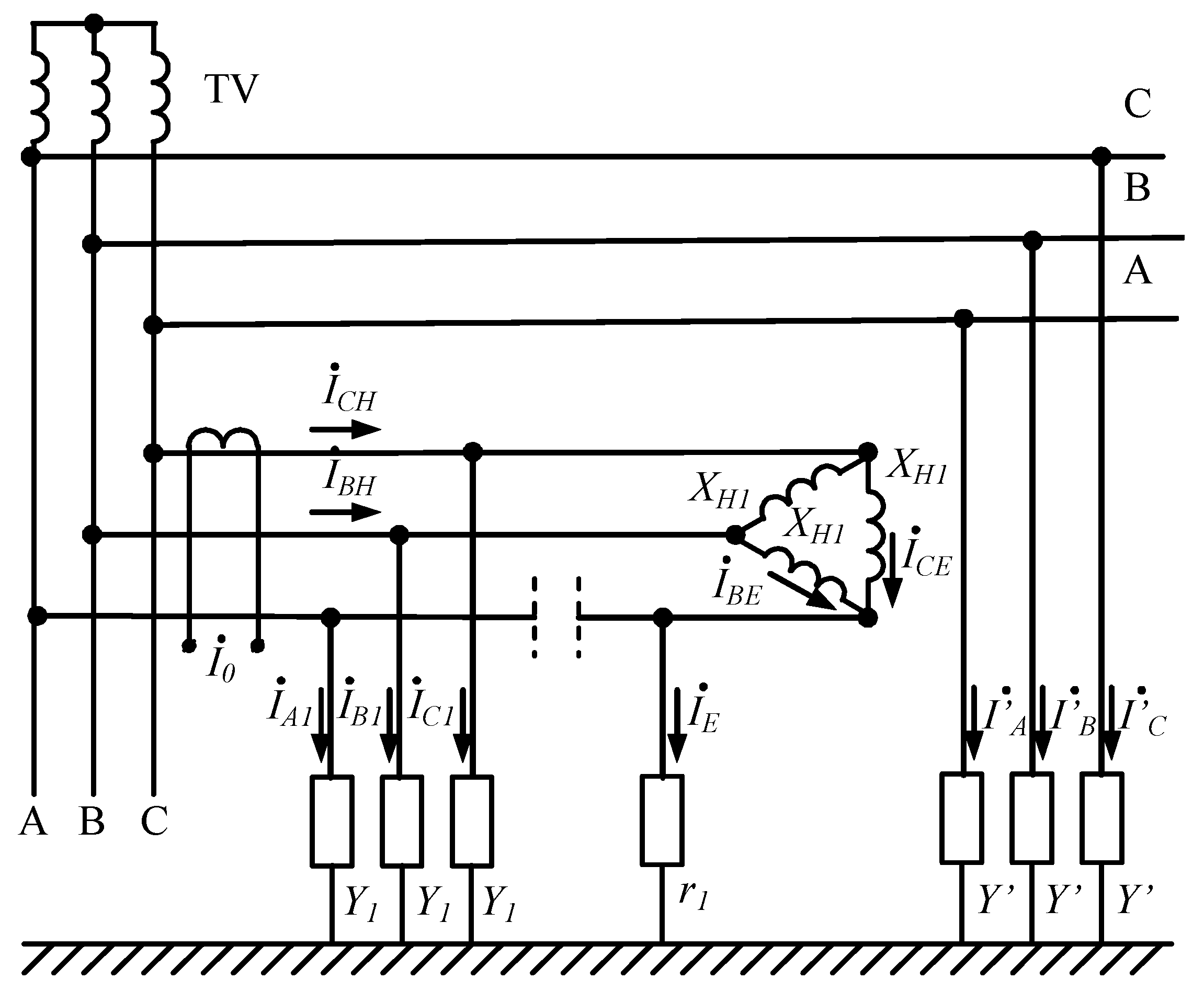
Figure 2. Network replacement scheme for investigation of the zero-sequence current for earth faults on the power receiver’s side.

Figure 2. Network replacement scheme for investigation of the zero-sequence current for earth faults on the power receiver’s side.

As shown in Figure 2, the equivalent circuit model is employed to analyze the behavior of zero-sequence currents that arise during earth faults on the side of the power receiver. In this configuration, the inductive reactance of each phase winding is taken to correspond to the typical parameters of standard distribution transformers (400 kVA, 6/0.4 kV). The active resistance of the windings is disregarded due to its relatively small value compared with the reactance, allowing the analysis to focus primarily on the magnetic coupling effects within the circuit. This simplification enables clearer interpretation of how zero-sequence components are generated and propagate through the network under unbalanced fault conditions. The model therefore serves as a practical tool for identifying the relationship between fault impedance, system asymmetry, and current redistribution among the affected phases.

Figure 3. Network replacement scheme for the investigation of the self-current protected line when closing in the external network.

Figure 3. Network replacement scheme for the investigation of the self-current protected line when closing in the external network.

Figure 3 presents the equivalent scheme developed to investigate the self-current characteristics of the protected line when the circuit is closed through the external network. In this model, the conductivities (Y₁ and Y′) represent the insulation of the protected connection and the remaining part of the network, respectively, while the transient resistances (r₁ and r′) correspond to the fault points within each section. The inductive reactance of the phase-to-phase windings (X_H1 and X_H′) determines the electromagnetic interaction between the protected and external circuits. The resulting analysis reveals how current redistribution occurs between the local and external parts of the system, emphasizing the influence of inductive coupling and insulation integrity on the network’s overall stability. Such an approach provides valuable insight into the protective behavior of the line and the potential for energy feedback during external network interactions.

The three equivalent circuit models (Figure 1, Figure 2 and Figure 3) provide a comprehensive representation of the distribution network’s behavior under earth-fault conditions. Figure 1 highlights the mechanisms of zero-sequence voltage formation due to insulation degradation and fault current redistribution. Figure 2 extends this analysis by examining the generation and flow of zero-sequence currents within the power receiver’s side, emphasizing the dominant role of inductive reactance in fault dynamics. Figure 3 integrates these findings into a broader system perspective, demonstrating how self-currents develop in the protected line coupled with an external network. Together, these models show how insulation parameters, transient resistance, and electromagnetic coupling interact. This provides a deeper understanding of the factors that determine fault response and network stability.

4.2. Zero-Sequence Voltage

In accordance with the replacement scheme shown in Figure 1 and considering the earth as the reference node of the circuit, the analysis of the system can be properly conducted. By applying the first Kirchhoff law to this configuration, one can derive the corresponding current relationships and equations [15,45]. This approach allows for a systematic investigation of the electrical behavior of the network under various operating conditions:

$${\dot{I}}_A+{\dot{I}}_B+{\dot{I}}_C+{\dot{I}}_{BE}+{\dot{I}}_{CE}=0 ,$$

where İ_BE and İ_CE—the earth fault currents of the phase B and C through the load resistance and transient resistance.

By replacing the currents with their values and the necessary substitutions, we obtain:

$$3{\dot{U}}_{0}Y+2{\dot{U}}_{0}y+({\dot{U}}_B+{\dot{U}}_C)y=0\hspace{0.17em},$$

where Y—conductivity of the insulation relative to the earth; y—the conductivity of phases B and C in the place of damage, taking into account the resistance of power receiver windings and transient resistance.

The expression for the voltage of the zero sequence at earth fault on the side of the power receiver is determined by the solution of the previous equation relative ${\dot{U}}_0$ and taking into account

$${\dot{U}}_B+{\dot{U}}_C=-{\dot{U}}_A$$

$${\dot{U}}_0={\displaystyle \frac{{\dot{U}}_A\cdot y}{3\cdot Y+2\cdot y}}$$

After substitution instead of conductivity their values, expressed through insulation parameters Y = 1/R + jωC, y = 1/(r + jωL_H) and performing the necessary transformations, we obtain:

$${\dot{U}}_0={\dot{U}}_A\cdot R\cdot {\displaystyle \frac{3r+2R-3{\omega }^{2}C{L}_{H}R-j3\omega \left(L_H+CRr\right)}{{\left(3r+2R-3{\omega }^{2}C{L}_{H}R\right)}^2+9{\omega }^2{\left(L_H+CRr\right)}^2}}$$

where R, C—active resistance and capacitance of insulation of one phase of the network relative to the ground; L_H—the inductive resistance of the phase-to-phase winding of the transformer; r—transient resistance at the place of damage.

The calculation formulas for the effective value of the zero-sequence voltage and the angle between its vector and the voltage vector of the damaged phase have the following form:

$$U_0={\displaystyle \frac{U_P\cdot R}{\sqrt{{\left(3r+2R-3{\omega }^{2}C{L}_{H}R\right)}^2+9{\omega }^2{\left(L_H+CRr\right)}^2}}}$$

where U_P—phase voltage.

$${\phi }_1=\mathrm{arctg}\left[{\displaystyle \frac{3\omega \left(L_H+CRr\right)}{3r+2R-3{\omega }^{2}C{L}_{H}R}}\right]$$

In Figure 4 and Figure 5 show the characteristic curves of the variation in the effective value of the voltage and the angle between the zero-sequence voltage and the damaged phase vectors for different values of the transient resistance at the point of damage and the network insulation parameters relative to the earth.

Figure 4 illustrates the variation in the zero-sequence voltage magnitude as a function of transient resistance r in the case of a fault on the power receiver side. The data indicates a clear inverse dependence between the transient resistance r and the zero-sequence voltage magnitude. At low resistance values (e.g., r = 0.02 kΩ), the voltage amplitude remains nearly constant across different insulation parameters, reflecting a strong capacitive coupling with the ground. As r increases beyond 1 kΩ, the voltage decreases sharply, especially for larger capacitances, confirming the dominant effect of capacitive current leakage on fault voltage formation.

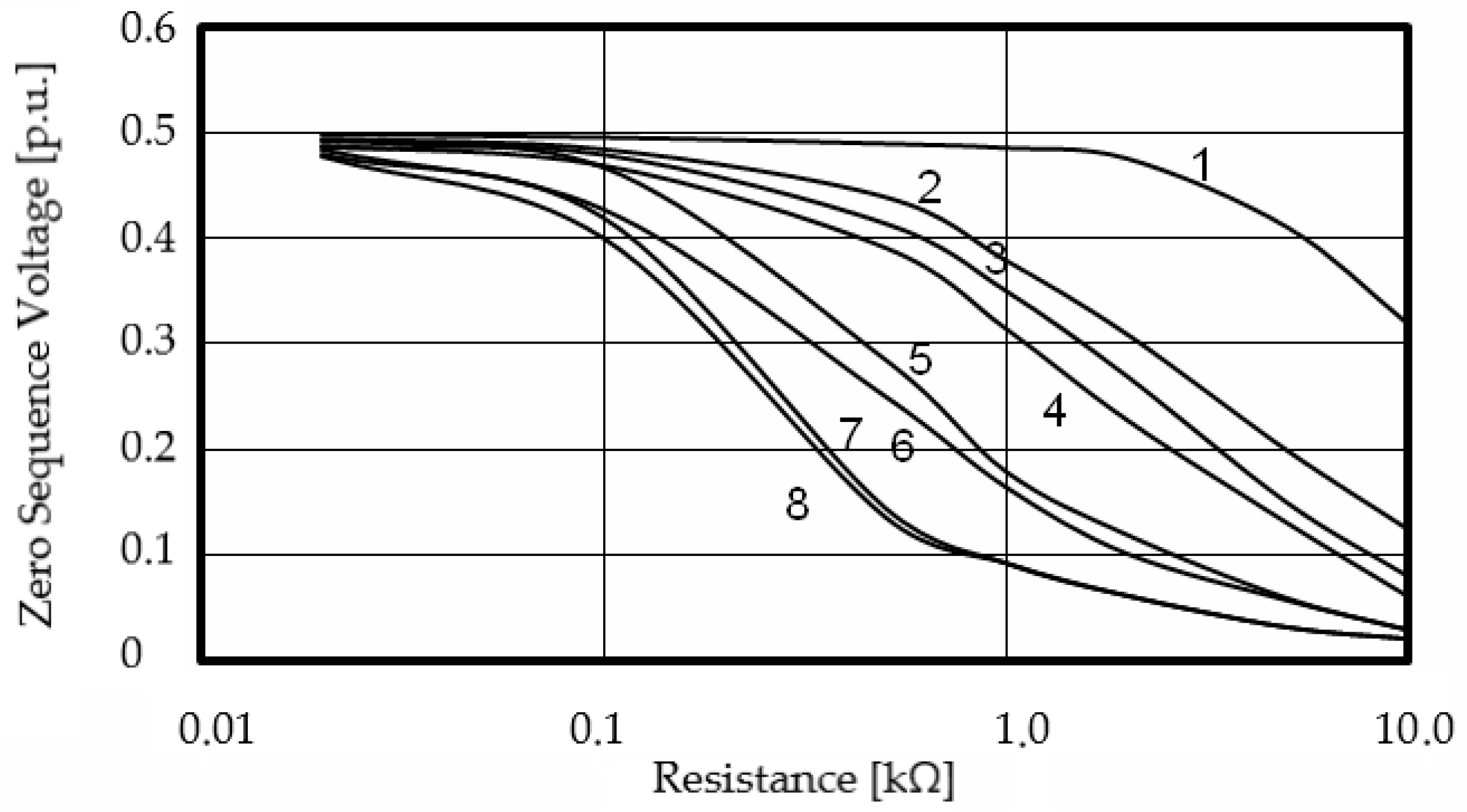
Figure 4. Changing the voltage of the zero sequence in case of damage on the part of the power receiver at C (μF) and R (kΩ), respectively, equal to: 1—0.1 and 100.0; 2—0.1 and 10.0; 3—1.0 and 100.0; 4—1.0 and 10.0; 5—3.0 and 100.0; 6—3.0 and 10.0; 7—6.0 and 100.0; 8—6.0 and 10.0.

Figure 4. Changing the voltage of the zero sequence in case of damage on the part of the power receiver at C (μF) and R (kΩ), respectively, equal to: 1—0.1 and 100.0; 2—0.1 and 10.0; 3—1.0 and 100.0; 4—1.0 and 10.0; 5—3.0 and 100.0; 6—3.0 and 10.0; 7—6.0 and 100.0; 8—6.0 and 10.0.

The parameter r denotes the transient (fault) resistance at the point of a single-phase ground fault and is expressed in kiloohms (kΩ). It reflects the quality of electrical contact between the damaged phase conductor and the grounding medium. At low resistance values (r = 0.02–0.1 kΩ), the fault path exhibits high conductivity, characteristic of solid or metallic ground faults. In this regime, the capacitive component of the fault current dominates, and the voltage-current phase approaches 360°, indicating an almost purely reactive response. At intermediate resistance levels (r = 0.2–0.5 kΩ), the fault becomes transient or semi-conductive. The resistive current component increases, resulting in a perceptible phase shift and a reduction in the zero-sequence voltage magnitude. At high resistance values (r = 1.0–2.0 kΩ), the fault path is weakly conductive, typical of arc-type or surface-leakage faults occurring through contaminated or moist insulation. In this range, the zero-sequence voltage decreases sharply, while the phase angle drops to 280–300°, indicating that the active component of the current becomes comparable to the capacitive one.

The characteristics obtained show that for r < 0.1 kΩ the zero-sequence voltage remains nearly constant across all insulation parameter configurations, confirming the predominance of capacitive leakage currents. As r increases, the voltage declines steeply, particularly at higher capacitance values, reflecting stronger attenuation of the capacitive current. For r > 1.0 kΩ, the zero-sequence voltage asymptotically approaches zero, indicating that the fault current becomes negligible and the system tends to restore symmetrical operating conditions. The nonlinear voltage decay highlights the significant influence of both insulation capacitance and transient resistance on zero-sequence voltage behavior underground-fault conditions. This tendency demonstrates the transition of the network behavior from capacitive to mixed resistive–capacitive as the fault resistance rises. The variation in the zero-sequence voltage phase angle in the event of a fault on the power receiver side for different values of network insulation parameters C (μF) and R (kΩ) is presented in Figure 5.

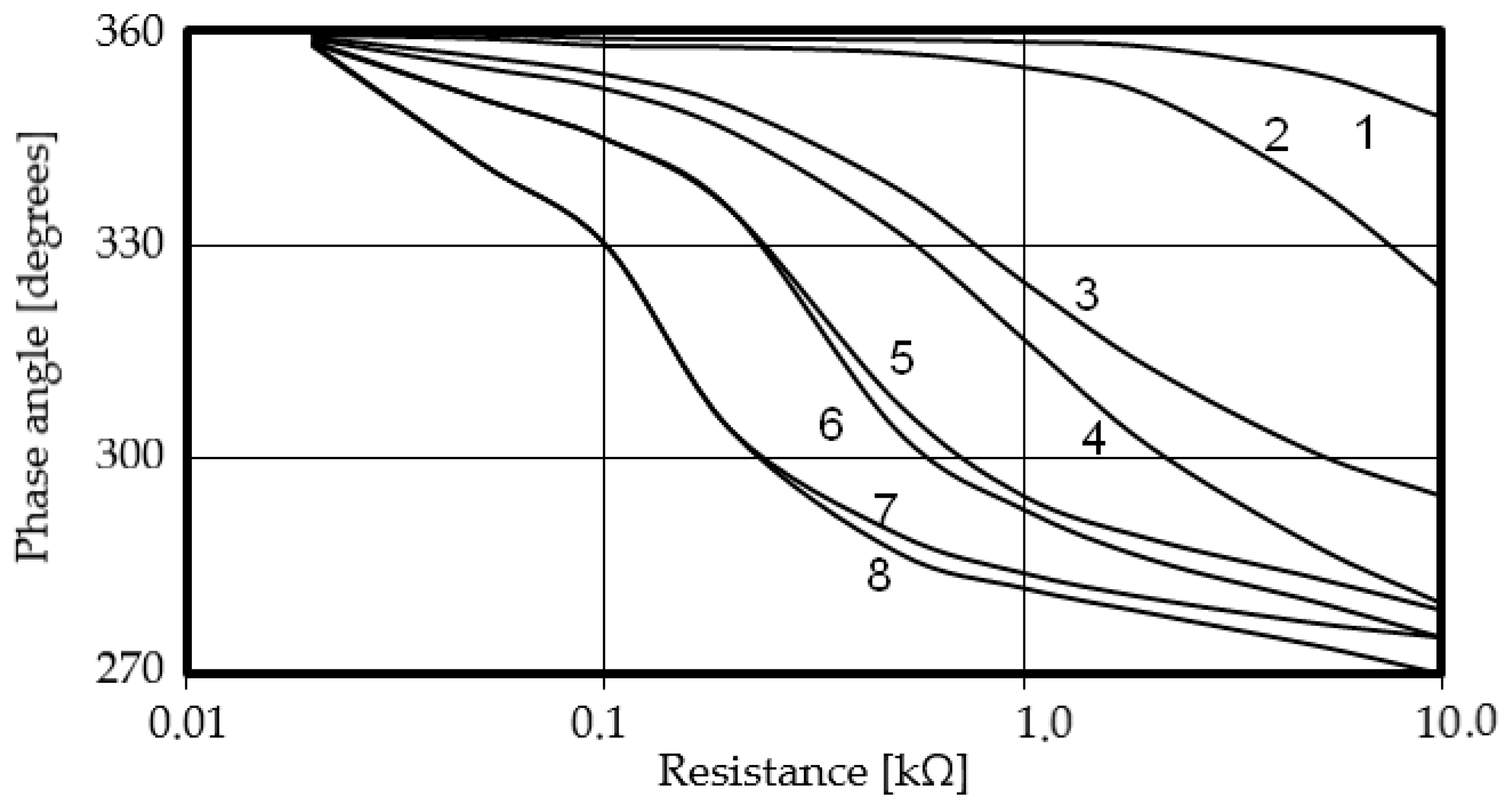
Figure 5. Changing the phase of the zero-sequence voltage in case of damage on the part of the power receiver at C (μF) and R (kΩ), respectively, equal to: 1—0.1 and 10.0; 2—0.1 and 100.0; 3—1.0 and 10.0; 4—1.0 and 100.0; 5—3.0 and 10.0; 6—3.0 and 100.0; 7—6.0 and 10.0; 8—6.0 and 100.0.

Figure 5. Changing the phase of the zero-sequence voltage in case of damage on the part of the power receiver at C (μF) and R (kΩ), respectively, equal to: 1—0.1 and 10.0; 2—0.1 and 100.0; 3—1.0 and 10.0; 4—1.0 and 100.0; 5—3.0 and 10.0; 6—3.0 and 100.0; 7—6.0 and 10.0; 8—6.0 and 100.0.

The dependencies demonstrate a nonlinear inverse relationship between the transient resistance and the zero-sequence voltage magnitude. At low resistance values (below 0.1 kΩ), the voltage remains practically constant (≈0.5 p.u.) for all parameter sets, which indicates that the fault current is dominated by the capacitive component and the system retains quasi-symmetrical behavior. For high resistance values (above 1.0 kΩ), the zero-sequence voltage approaches near-zero values, corresponding to a weak current flow through the fault path. In this region, the influence of insulation parameters becomes less significant, and the system gradually transitions toward a symmetrical steady-state regime. The higher insulation capacitance (curves 5–8) leads to a faster decay of voltage with resistance, while networks with lower capacitance (curves 1–2) retain a higher zero-sequence voltage at equivalent fault conditions.

The obtained numerical results clearly illustrate the sensitivity of the zero-sequence voltage phase characteristics to both the insulation parameters and the transient resistance, which is essential for accurate fault localization and for assessing the degree of insulation degradation in isolated neutral systems.

4.3. Zero-Sequence Currents

To assess the performance of earth fault protection system it is essential to investigate the amplitude and phase dependencies of the zero-sequence currents. For single-phase earth fault on the power receiver’s side two cases of damage should be considered:

-

the earth fault on the side of the power receiver in the monitored line;

-

the earth fault on the side of the power receiver outside the monitored line (in the external network).

The current of the zero sequence in the monitored line in the event of damage at the same connection is defined as the sum of all currents flowing in the line and according to the replacement scheme Figure 2 is described by the expression:

$${\dot{I}}_0={\dot{I}}_{A1}+{\dot{I}}_{B1}+{\dot{I}}_{C1}+{\dot{I}}_{BH}+{\dot{I}}_{CH} ,$$

where İ_A1, İ_B1, İ_C1—currents in phases A, B, C, respectively, of the protected connection; İ_BH and İ_CH—the load currents, respectively, in phase B and C, in phase A the load current is zero due to a circuit break.

Given that the currents between phases B and C, determined by the magnitude of the linear voltage and the load resistance, are equal in value and counter-directed, the zero-sequence current is determined by:

$${\dot{I}}_0={\dot{I}}_{A1}+{\dot{I}}_{B1}+{\dot{I}}_{C1}+{\dot{I}}_{BE}+{\dot{I}}_{CE}$$

where İ_BE and İ_CE—the earth fault currents of the phase B and C through the load resistance and transient resistance.

Performing the appropriate substitutions and transformations, we obtain the expression for the current of the zero sequence:

$${\dot{I}}_0=-3{\dot{U}}_0\cdot \left(Y-Y_1\right)=-3{\dot{U}}_A\left(Y-Y_1\right){\displaystyle \frac{y}{3Y+2y}} ,$$

where Y—the conductivity of the whole network phase insulation relative to the ground; y—conductivity (taking into account the power receiver) of undamaged phases of the network relative to the ground in the place of damage; Y₁—insulation conductivity of the protected connection.

To express the current of the zero sequence through the parameters of the network installation and monitored connection, replace the conductivities with their values Y = 1/R + jωC, Y₁ = 1/R₁ + jωC₁, y = 1/(r + jωL_H) and after the corresponding transformations we obtain:

$${\dot{I}}_0=-{\displaystyle \frac{3{\dot{U}}_A}{R_1}}\cdot {\displaystyle \frac{P\left(R_1-R\right)+Q\omega \left(C-C_1\right)R{R}_1+j\left[P\omega \left(C-C_1\right)R{R}_1-Q\left(R_1-R\right)\right]}{P^2+Q^2}} ,$$

where R₁—insulation resistance of the protected connection; P = 3r + 2R − 3ω²CL_HR and Q = 3ω (L_H + CRr)—additional symbols entered to simplify the expression.

The effective value of the current of the zero-sequence expressed through the phase voltage U and the installation parameters of the network of the protected connection of the power receiver and the value of the transient resistance at the point damage determined by the formula:

$$I_0={\displaystyle \frac{3U}{R_1}}\cdot {\displaystyle \frac{\sqrt{{\left[P\left(R_1-R\right)+Q\omega \left(C-C_1\right)R{R}_1\right]}^2+{\left[P\omega \left(C-C_1\right)R{R}_1-Q\left(R_1-R\right)\right]}^2}}{P^2+Q^2}}$$

The angle between the zero-sequence current vector and the voltage vector of the damaged phase:

$${\phi }_2=180°+\mathrm{arctg}{\displaystyle \frac{P\omega \left(C-C_1\right)R{R}_1-Q\left(R_1-R\right)}{P\left(R_1-R\right)+Q\omega \left(C-C_1\right)R{R}_1}}$$

Figure 6 and Figure 7 show the characteristic dependencies of the change in the effective value of current of zero sequence and the value of the angle between the vector of the investigate current and the vector of the voltage of the damaged phase, corresponding to the normal mode of a symmetrical three-phase system.

In case of closure outside the monitored line, the self-connection current based on the replacement scheme (Figure 3) is defined:

$${\dot{I}}_{0C}={\dot{I}}_{A1}+{\dot{I}}_{B1}+{\dot{I}}_{C1}$$

Performing the appropriate substitutions and transformations, we obtain the expression for self-current of connection:

$${\dot{I}}_{0C}=3\cdot {\dot{U}}_0\cdot Y_1=3\cdot {\dot{U}}_A\cdot Y{\displaystyle \frac{y}{3Y+y}}$$

By replacing the conductivities with their values, we obtain:

$${\dot{I}}_0=3{\dot{U}}_A{\displaystyle \frac{R}{R_1}}\cdot {\displaystyle \frac{P+Q\omega C_1{R}_1+j\left(P\omega C_1{R}_1-Q\right)}{P^2+Q^2}}$$

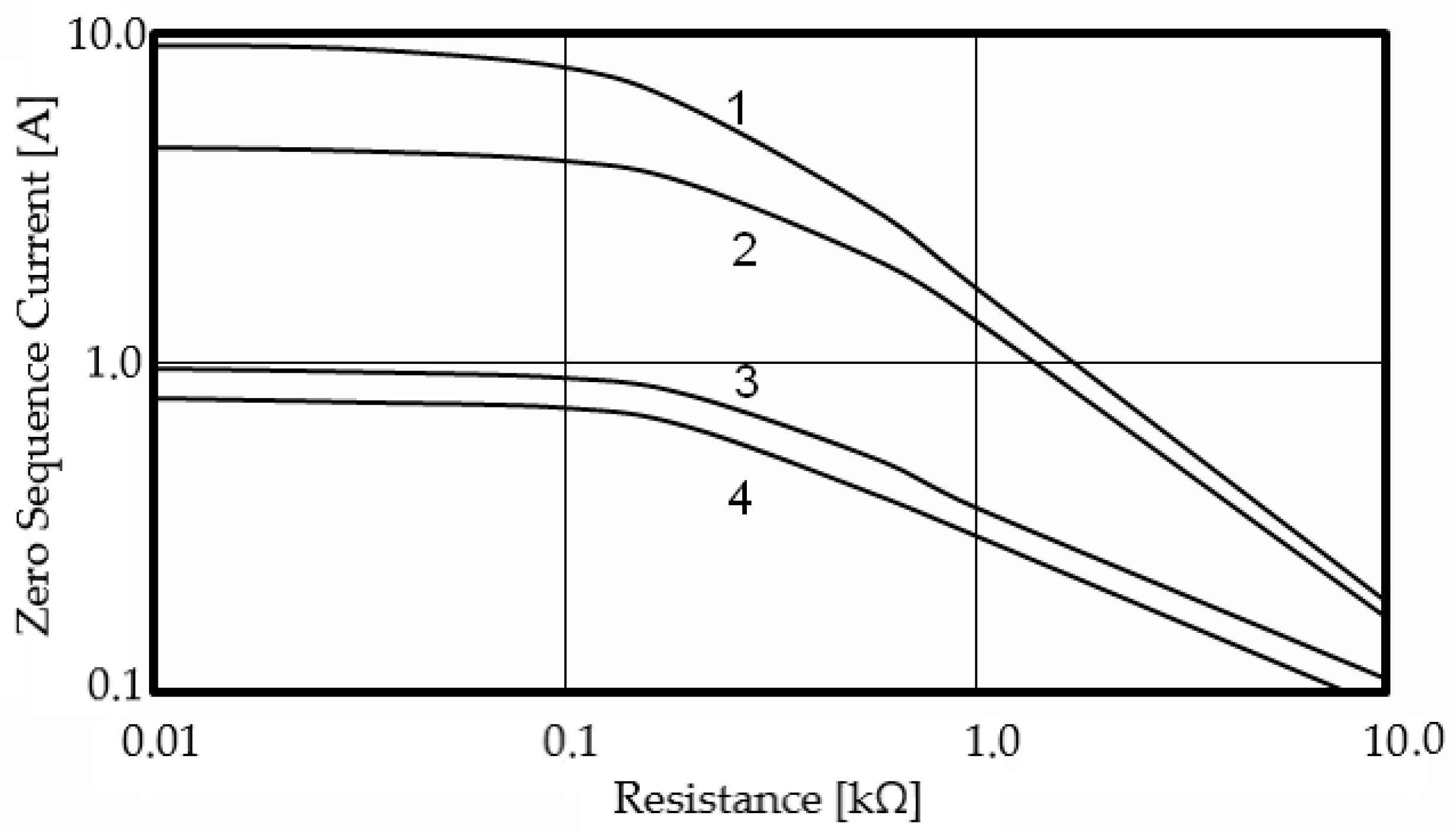
Further research presents the calculated values of the zero-sequence current amplitude under conditions of a single-phase ground fault on the power receiver side. The parameter r represents the transient resistance (kΩ) at the fault location, which corresponds to different combinations of insulation capacitance C and resistance R. The data show a monotonic decrease in the zero-sequence current magnitude as transient resistance r increases. At very low resistance (r = 0.01–0.03 kΩ), the current reaches its maximum values, about 9.2 A for case 1 and 4.5 A for case 2, indicating a strong capacitive coupling and low impedance of the fault path.

As the resistance increases to r = 0.2–1.0 kΩ, the current declines significantly, and for r > 1.0 kΩ, it becomes nearly negligible, with values below 0.4 A. This behavior reflects the transition from a capacitive to a resistive–capacitive fault regime, in which the leakage current through the insulation decreases sharply due to reduced charge–discharge effects of the line-to-ground capacitance. At the highest resistance value (r < 10.0 kΩ), the zero-sequence current stabilizes at minimal levels (0.09–0.19 A), confirming that the system approaches a symmetrical state with almost no current flow through the ground path.

Figure 6 presents the variation in the zero-sequence current magnitude as a function of the transient resistance r for several combinations of insulation capacitance C and resistance R. The results reveal a pronounced nonlinear inverse dependence between the zero-sequence current and the transient resistance.

Figure 6. Changing the current of the zero-sequence depending on the transient resistance in case of damages on the side of the power receiver at C (μF) and R (kΩ), respectively, equal to: 1—6.0 and 10.0—100.0; 2—3.0 and 10.0—100.0; 3—1.0 and 10.0; 4—1.0 and 100.0.

Figure 6. Changing the current of the zero-sequence depending on the transient resistance in case of damages on the side of the power receiver at C (μF) and R (kΩ), respectively, equal to: 1—6.0 and 10.0—100.0; 2—3.0 and 10.0—100.0; 3—1.0 and 10.0; 4—1.0 and 100.0.

At very low resistances (r ≤ 0.03 kΩ), the zero-sequence current reaches its maximum value, determined primarily by the capacitive leakage through the network insulation. In this region, the network behaves as a strongly capacitive system, and the current amplitude for the highest capacitances significantly exceeds that of configurations with smaller insulation capacitance.

As the transient resistance increases beyond 0.1 kΩ, the current decreases rapidly. This decline is caused by the diminishing capacitive coupling between the damaged phase and ground, with the rate of decay strongly influenced by the value of the insulation capacitance:

-

networks with larger capacitance exhibit higher initial currents and a slower decrease,

-

while networks with smaller capacitance show both lower initial currents and a steeper attenuation.

For high transient resistances (r ≥ 1.0 kΩ), the zero-sequence current approaches near-zero values, corresponding to weakly conductive or intermittent faults. In this region the contribution of the fault path to the overall current flow becomes negligible, and the system gradually approaches a symmetrical state. These findings confirm that zero-sequence current amplitude is highly sensitive to both insulation parameters and transient resistance, making it a reliable diagnostic indicator for ground-fault detection in isolated-neutral systems.

Figure 7 illustrates the dependence of the zero-sequence current phase angle on the transient resistance for the same insulation parameter sets. The results show a monotonic decrease in the phase angle as the transient resistance increases.

Figure 7. The dependence of the phase of the zero-sequence current from the transient resistance in case of damages on the side of the power receiver at C (μF) and R (kΩ), respectively, equal to:1—6.0 and 10.0—100.0; 2—3.0 and 10.0—100.0; 3—1.0 and 10.0; 4—1.0 and 100.0.

Figure 7. The dependence of the phase of the zero-sequence current from the transient resistance in case of damages on the side of the power receiver at C (μF) and R (kΩ), respectively, equal to:1—6.0 and 10.0—100.0; 2—3.0 and 10.0—100.0; 3—1.0 and 10.0; 4—1.0 and 100.0.

The results reveal a monotonic nonlinear decrease in the phase angle with increasing transient resistance. At low resistance values (r ≤ 0.05 kΩ), the phase angle remains close to 260–270°, indicating that the zero-sequence current is predominantly capacitive and lags the voltage of the damaged phase by approximately 90°.

As the transient resistance increases to the range of 0.1–1.0 kΩ, the phase angle gradually decreases to 210–240°, reflecting the transition from a capacitive to a mixed resistive–capacitive regime of current flow.

For high resistance values (r ≥ 2.0 kΩ), the phase angle stabilizes around 185–190°, which corresponds to a predominantly resistive behavior of the fault current and indicates that the reactive component becomes almost negligible. Overall, the figure demonstrates that the phase displacement between zero-sequence current and voltage depends strongly on both the insulation capacitance and the transient resistance.

Higher capacitance values (curves 3–4) lead to larger phase angles and a slower decline with increasing r, while lower capacitances (curves 1–2) result in smaller phase angles and a faster transition toward resistive behavior. These dependencies quantitatively describe the dynamic evolution of fault current characteristics in isolated-neutral networks and provide a theoretical basis for identifying the fault regime and estimating insulation condition.

The effective value and the angle between the zero-sequence current vector and the voltage vector of the damaged phase are defined by the expressions:

$$I_{0C}={\displaystyle \frac{3U_{P}R}{R_1}}\cdot {\displaystyle \frac{\sqrt{{\left(P+Q\omega C_1{R}_1\right)}^2+{\left(P\omega C_1{R}_1-Q\right)}^2}}{P^2+Q^2}}$$

$${\phi }_3=\mathrm{arctg}{\displaystyle \frac{P\omega C_1{R}_1-Q}{P+Q\omega C_1{R}_1}}$$

Figure 8 and Figure 9 show the characteristic dependencies of the effective value and the angle between the zero-sequence current vector for damage outside the monitored line and the voltage vector of the damaged phase.

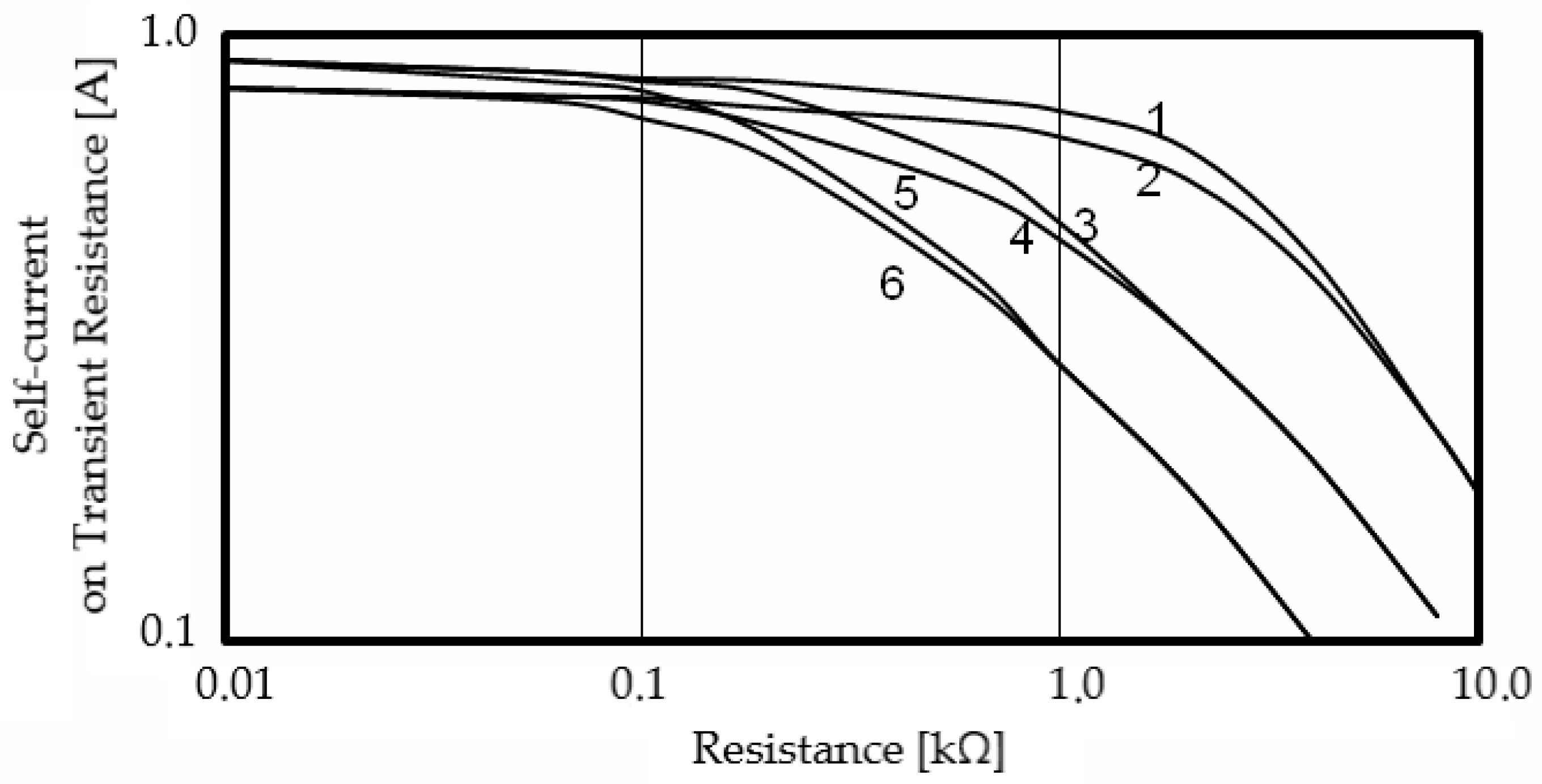
Values of the self-current amplitude depending on the transient resistance r at the point of fault for different combinations of insulation capacitance C, resistance R, and equivalent resistance of the adjacent line R₁ shows that, at low resistance values (r = 0.01–0.1 kΩ), the self-current reaches its maximum amplitude (0.8–0.9 p.u.), which indicates a strong conductive coupling between the faulted phase and the ground. As transient resistance increases (r = 0.2–1.0 kΩ), the self-current decreases gradually, reflecting a reduction in capacitive leakage and a shift toward resistive current flow. At r > 1.0 kΩ, the current amplitude drops sharply and becomes almost negligible for r ≥ 4.0 kΩ, where values fall below 0.2 p.u. This trend demonstrates a nonlinear inverse relationship between the transient resistance and the self-current magnitude. Moreover, the results show that higher insulation capacitance (C = 3.0–6.0 μF) leads to greater initial current values and slower attenuation, while higher insulation resistance (R = 100 kΩ) causes a faster decline of current with increasing r.

Overall, the data provides a quantitative assessment of the current attenuation mechanism under different insulation conditions. The observed dependencies confirm that the self-current magnitude is primarily governed by the interplay between transient resistance and insulation capacitance, which defines the system’s response to ground faults in isolated neutral networks. The dependence of the self-current on transient resistance for different combinations of network insulation parameters C (μF), R (kΩ), and R₁ (kΩ), is presented in Figure 8.

Figure 8. Dependence of the self-current on the transient resistance at C (μF), R (kΩ) and R₁ (kΩ), respectively, equal to: 1—1.0; 10.0 and 50.0; 2—1.0; 100.0 and 200.0; 3—3.0; 10.0 and 50.0; 4—3.0; 100.0 and 200.0; 5—6.0; 10.0 and 50.0; 6—6.0; 100.0 and 200.0.

Figure 8. Dependence of the self-current on the transient resistance at C (μF), R (kΩ) and R₁ (kΩ), respectively, equal to: 1—1.0; 10.0 and 50.0; 2—1.0; 100.0 and 200.0; 3—3.0; 10.0 and 50.0; 4—3.0; 100.0 and 200.0; 5—6.0; 10.0 and 50.0; 6—6.0; 100.0 and 200.0.

The observed dependencies exhibit a strong nonlinear inverse relationship between transient resistance and self-current amplitude. Curves corresponding to higher capacitance values (5–6) display greater initial current levels and a slower attenuation rate, while systems with higher insulation resistance (curves 1–2) show smaller initial currents and a steeper decline with increasing r. These patterns highlight the dominant influence of the network’s insulation parameters on fault current behavior, providing an analytical basis for evaluating ground fault severity and insulation condition in isolated neutral power systems.

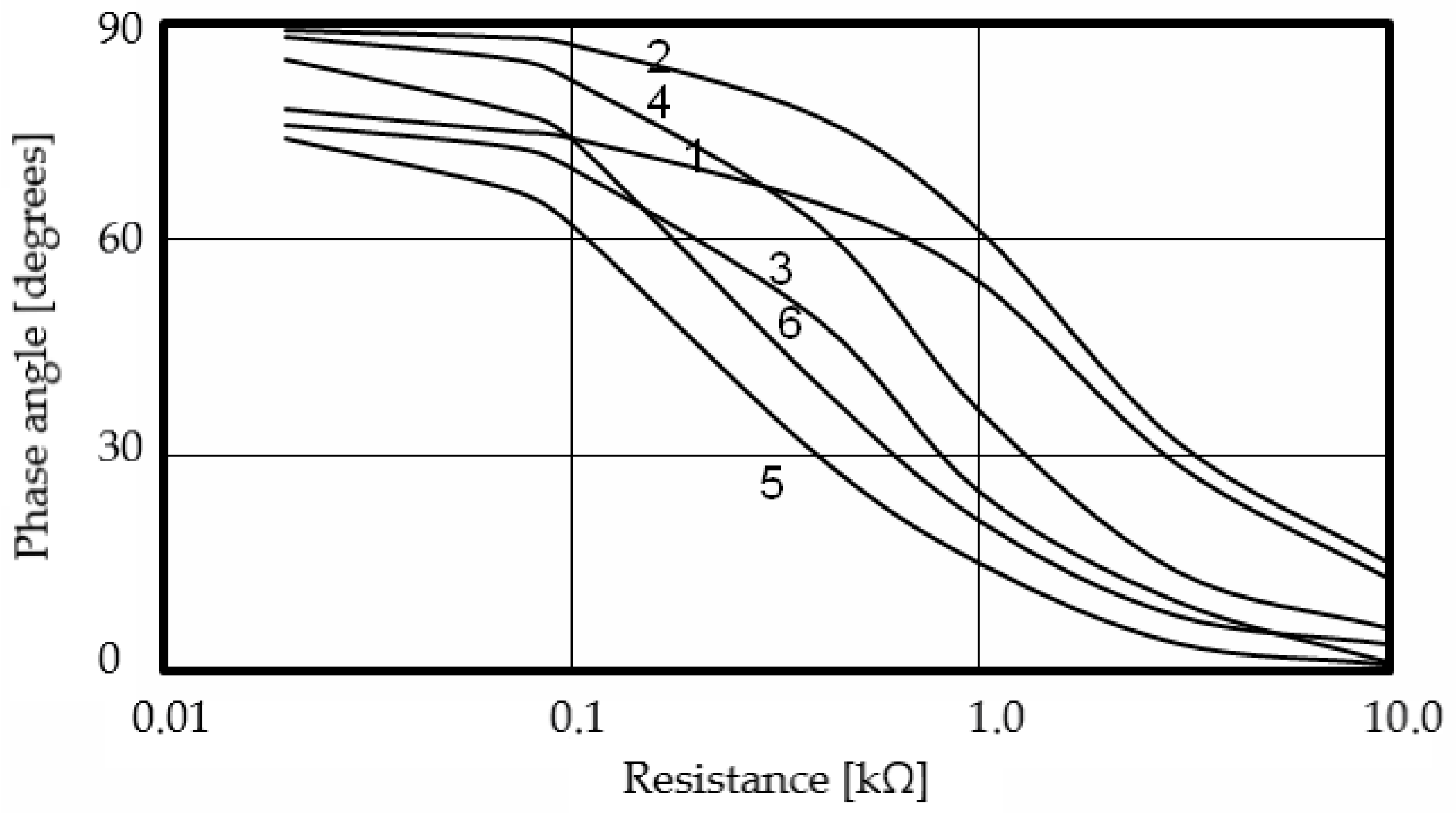
Values of the phase angle of the self-current φ3 (in degrees) as a function of the transient resistance r at the fault location shows, that at low transient resistance values (r = 0.02–0.1 kΩ), the phase angle remains relatively high (74–89°), indicating a predominantly capacitive character of the self-current. In this range, the current vector leads the voltage vector by approximately 90°, which corresponds to the behavior of an isolated neutral network dominated by capacitive leakage currents. As the resistance increases (r = 0.4–0.1 kΩ), the phase angle decreases sharply to 30–77°, reflecting a transition from capacitive to resistive–capacitive behavior. The rate of decrease depends on the capacitance C: higher capacitance leads to faster phase reduction, as the capacitive reactance becomes comparable to the fault resistance.

At high transient resistances (r ≥ 3.0 kΩ), the phase angle drops below 20° and eventually approaches 1–6° for r = 10.0, kΩ, confirming that the current becomes almost purely resistive, and the reactive component is negligible. Overall, the data show a strong nonlinear relationship between the transient resistance and the phase angle of the self-current.

This behavior highlights the sensitivity of the fault current phase to both the insulation parameters and the coupling resistance. The observed dependencies are crucial for identifying the transition from capacitive to resistive fault regimes and for developing diagnostic models of ground-fault dynamics in isolated neutral systems. The variation in the phase angle φ3 with transient resistance for different combinations of insulation parameters C (μF), R (kΩ), and R₁ (kΩ), is presented in Figure 9.

Figure 9. Change angle φ3 from the transient resistance at C (μF), R (kΩ) and R₁ (kΩ), respectively, equal to: 1—1.0; 10.0 and 50.0; 2—1.0; 100.0 and 200.0; 3—3.0; 10.0 and 50.0; 4—3.0; 100.0 and 200.0; 5—6.0; 10.0 and 50.0; 6—6.0; 100.0 and 200.0.

Figure 9. Change angle φ3 from the transient resistance at C (μF), R (kΩ) and R₁ (kΩ), respectively, equal to: 1—1.0; 10.0 and 50.0; 2—1.0; 100.0 and 200.0; 3—3.0; 10.0 and 50.0; 4—3.0; 100.0 and 200.0; 5—6.0; 10.0 and 50.0; 6—6.0; 100.0 and 200.0.

Overall, the figure demonstrates a strong nonlinear relationship between transient resistance and the phase angle of the self-current. Higher capacitance values (curves 5–6) cause a faster decline in φ3, whereas higher insulation resistance (curves 1–2) stabilizes the phase angle at larger values. These dependencies reveal the gradual transformation of the system’s behavior from capacitive to resistive with increasing fault resistance, offering valuable insight into the diagnostic assessment of insulation and transient fault dynamics in isolated neutral networks.

The analytical and computational results demonstrate that insulation parameters and transient fault resistance critically govern the behavior of zero-sequence voltage, zero-sequence current, and self-current in isolated-neutral distribution networks. The derived dependencies indicate a distinctly nonlinear relationship between the transient resistance and both the magnitude and phase angle of the resulting fault currents. At low resistance values, the network operates in a quasi-capacitive mode, characterized by high current amplitudes and phase angles approaching 90°, which reflects the predominance of displacement currents through insulation. As the transient resistance increases, the system response shifts toward a mixed resistive–capacitive regime, accompanied by rapid current attenuation and a corresponding reduction in phase angle.

These results confirm that the combined effects of insulation capacitance, insulation resistance, and fault-path impedance dictate the electrical response of the network ground-fault conditions. The characteristic curves obtained for zero-sequence and self-currents (Figure 6, Figure 7, Figure 8 and Figure 9) provide a solid theoretical basis for diagnosing insulation degradation, evaluating protection sensitivity, and optimizing ground-fault detection settings in isolated and compensated neutral systems. The proposed models and identified patterns can be effectively applied to enhance the reliability of open-pit mining power networks, enabling more accurate identification of fault regimes and improving the resilience of electrical infrastructure operating under harsh industrial conditions.

5. Conclusions

The performed analytical and computational investigations confirm that the parameters of insulation and transient resistance exert a decisive influence on the zero-sequence voltage and current behavior in isolated-neutral distribution networks. Under single-phase earth-fault conditions on the power receiver side, the electrical response of the network is characterized by nonlinear amplitude-phase dependencies, which are closely correlated with the insulation capacitance and the fault resistance at the damage point. These relationships provide a physical basis for understanding fault processes and serve as reliable indicators for assessing network insulation and the performance of protection systems.

Quantitative analysis shows that as the transient resistance increases from 0.01 kΩ to 10.0 kΩ, the zero-sequence voltage decreases from approximately 0.5 p.u. to 0.05 p.u., while the corresponding current amplitude diminishes from 9.2 A to below 0.2 A. The phase angle of the zero-sequence current varies from about 90° at low resistance to nearly 0° at high resistance, reflecting a gradual transition from capacitive to resistive-capacitive network behavior. The data obtained clearly demonstrates that the magnitude of zero-sequence quantities is inversely proportional to transient resistance and directly dependent on the network insulation capacitance.

Comparative evaluation of fault locations reveals that for realistic network parameters, the zero-sequence voltages and currents during faults on the power receiver side are approximately half those observed for similar faults on the power source side, with a vector displacement of about 180°. This finding highlights the importance of distinguishing between these fault types in diagnostic and protection algorithms. The characteristic dependencies derived from Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 can therefore be used to improve the selectivity and accuracy of protective relays operating in isolated and compensated neutral systems.

The analysis of existing diagnostic and monitoring methods confirms their limited sensitivity to faults occurring on the power receiver side, which may lead to delayed protection activation and prolonged exposure of electrical equipment and personnel to hazardous voltages. Moreover, the increased fault duration and asymmetric load conditions contribute to deterioration of energy efficiency and voltage quality within the distribution network. This emphasizes the need to update diagnostic approaches and integrate zero-sequence analysis into modern protection strategies for open-pit power systems.

Finally, the obtained results provide a theoretical and practical foundation for improving the reliability and electromagnetic compatibility of mining power networks. By accounting for the nonlinear dependencies between insulation parameters, transient resistance, and zero-sequence quantities, the proposed models enable more accurate prediction of insulation degradation, better tuning of fault-protection thresholds, and enhanced assessment of energy losses under poor voltage quality conditions. These developments will ultimately support safer, more efficient, and more resilient operation of electrical systems in open-pit mining environments.

The results of the studies of the amplitude and phase dependencies of zero-sequence currents and voltages made it possible to select the principle of implementing a directional protection device that best suits the specific conditions of mining enterprises, based on an assessment of the relative position of the zero-sequence current and voltage vectors with a narrow angular characteristic and offset from transient processes, on the basis of which the circuits of the first and second stage protection devices were developed. In our subsequent research, we plan to expand the current findings to encompass more complex operating conditions of isolated-neutral and compensated mining distribution networks, with particular focus on the influence of dynamic load variations, harmonic distortion, and switching transients on the amplitude–phase behavior of zero-sequence quantities. Further validation using large-scale electromagnetic transient simulations and targeted field experiments will be undertaken to refine key parameter assumptions and reduce model uncertainties.