Optimization of Virtual Inertia Control for DC Microgrid Based on Model Predictive Control
Abstract
1. Introduction
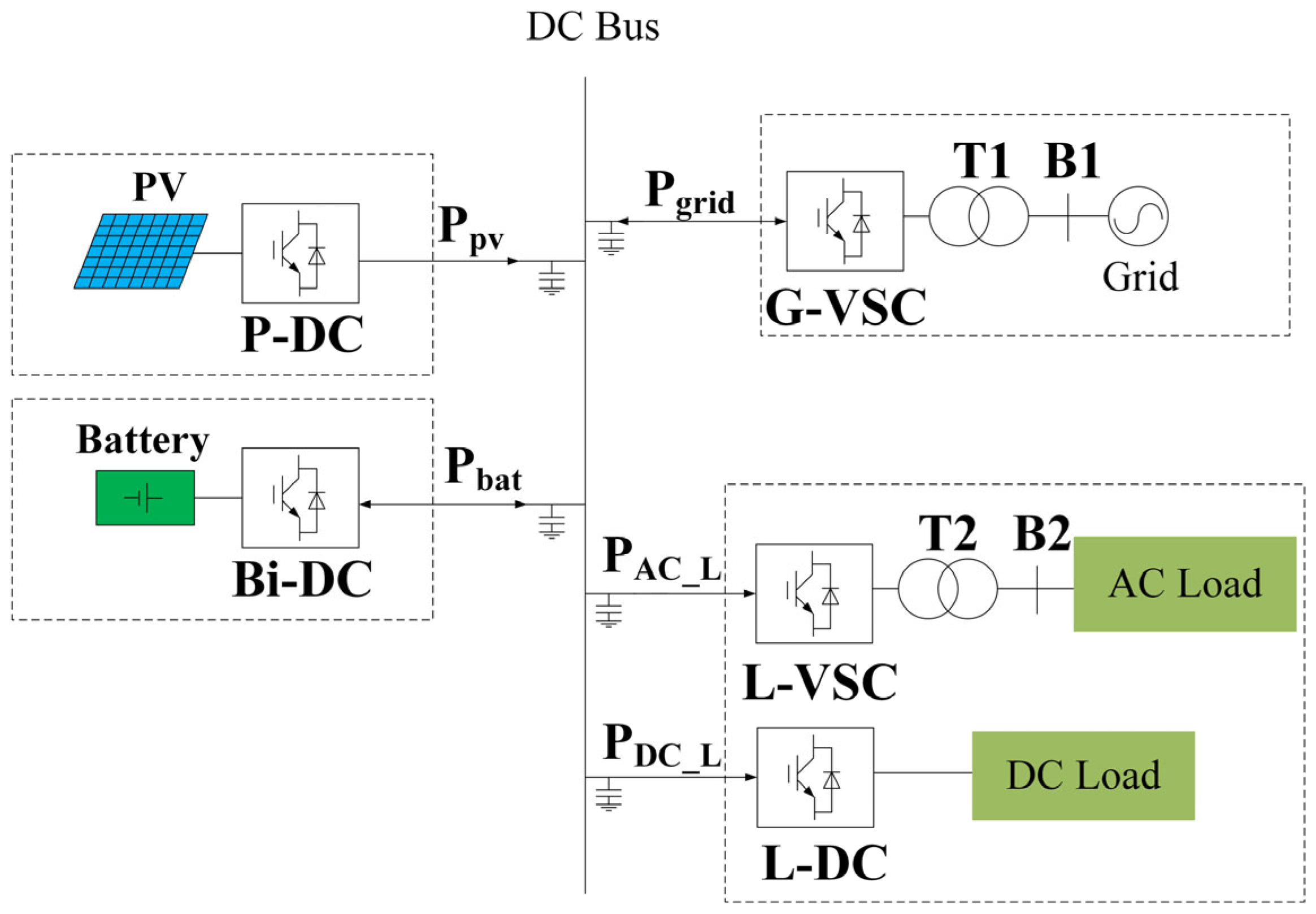
2. DC Microgrid Structure and Modeling
2.1. DC Microgrid Structure
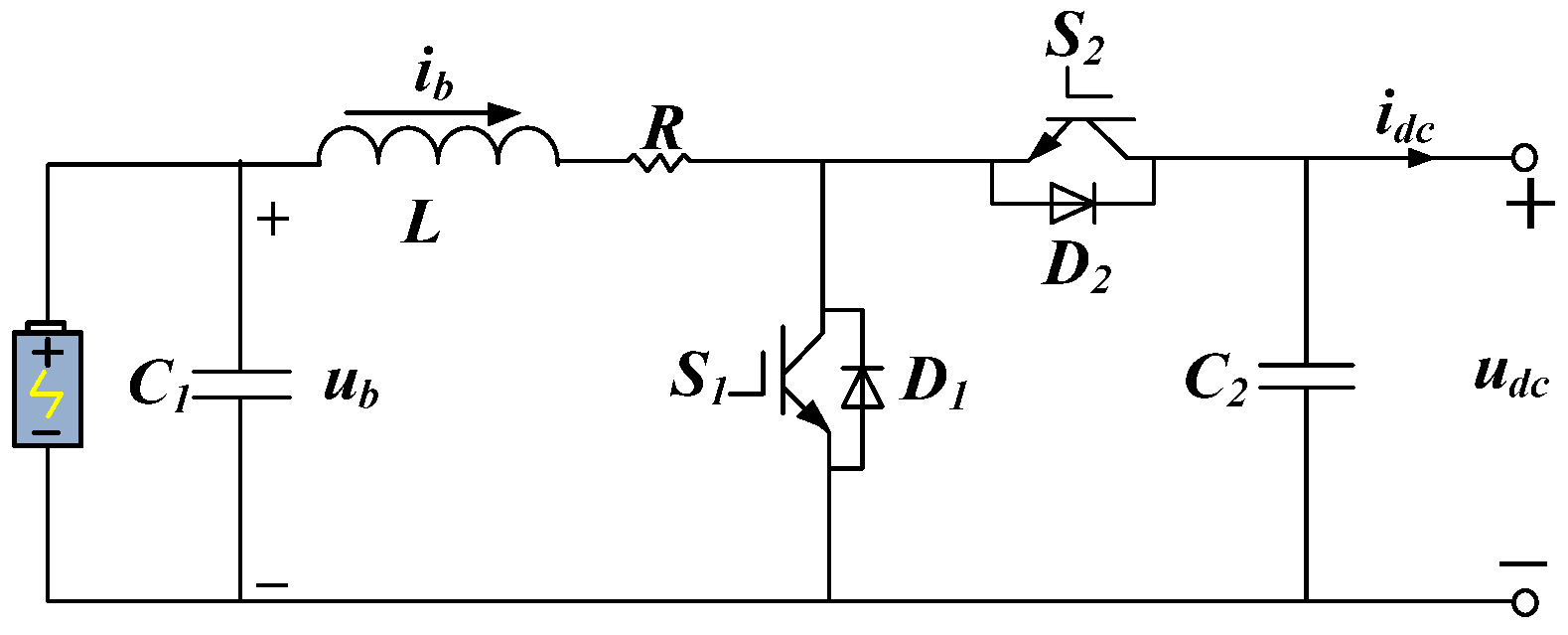
2.2. Energy Storage Unit Interface Converter Modeling
3. Virtual Inertia Optimization of Energy Storage Unit Based on MPC
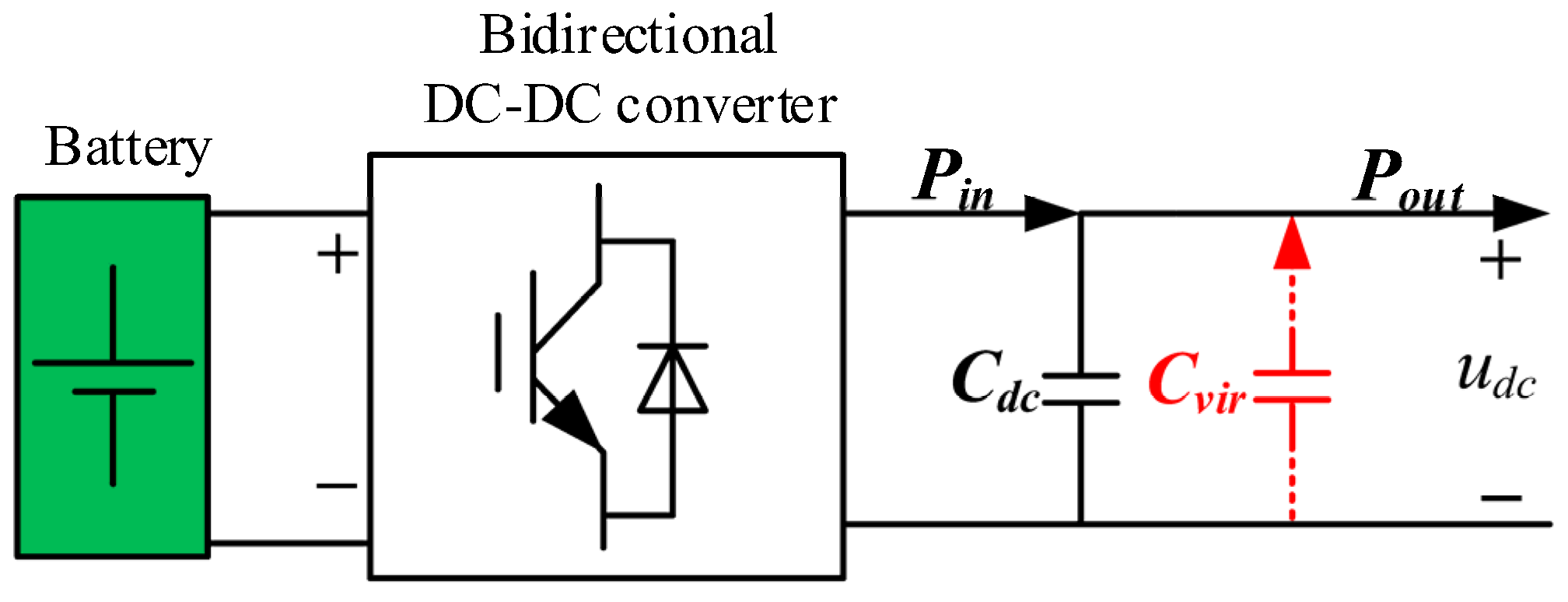
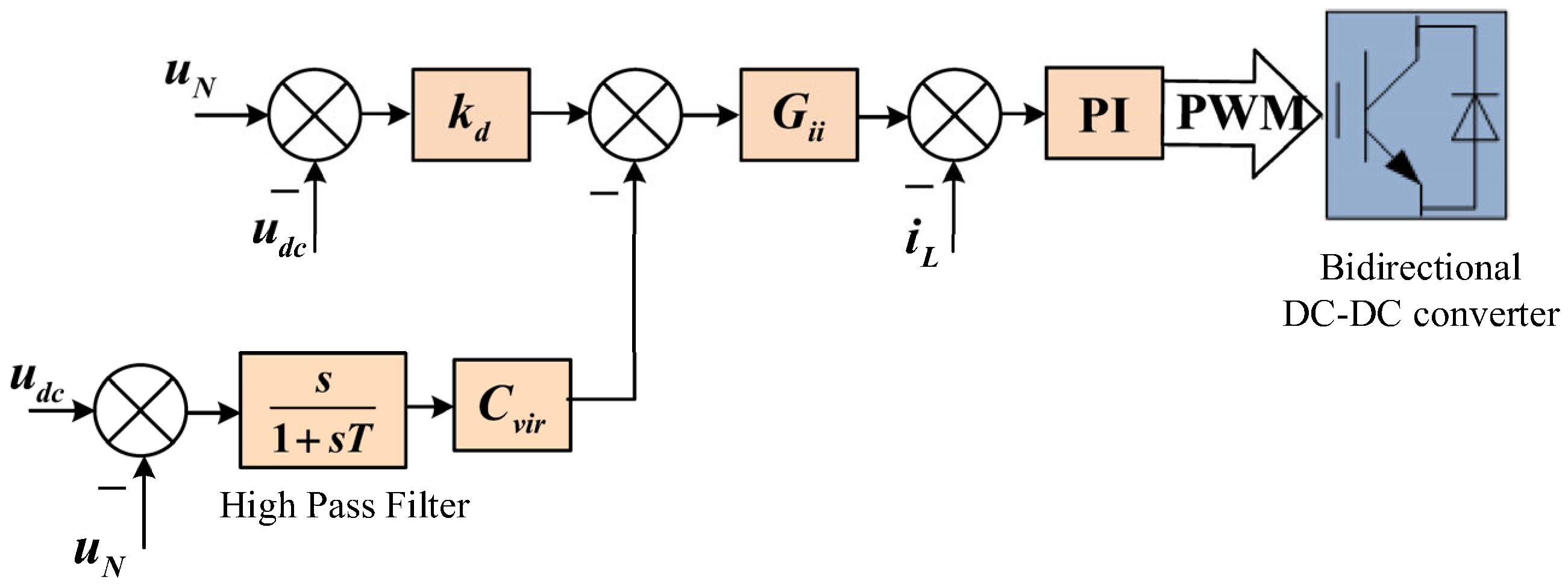
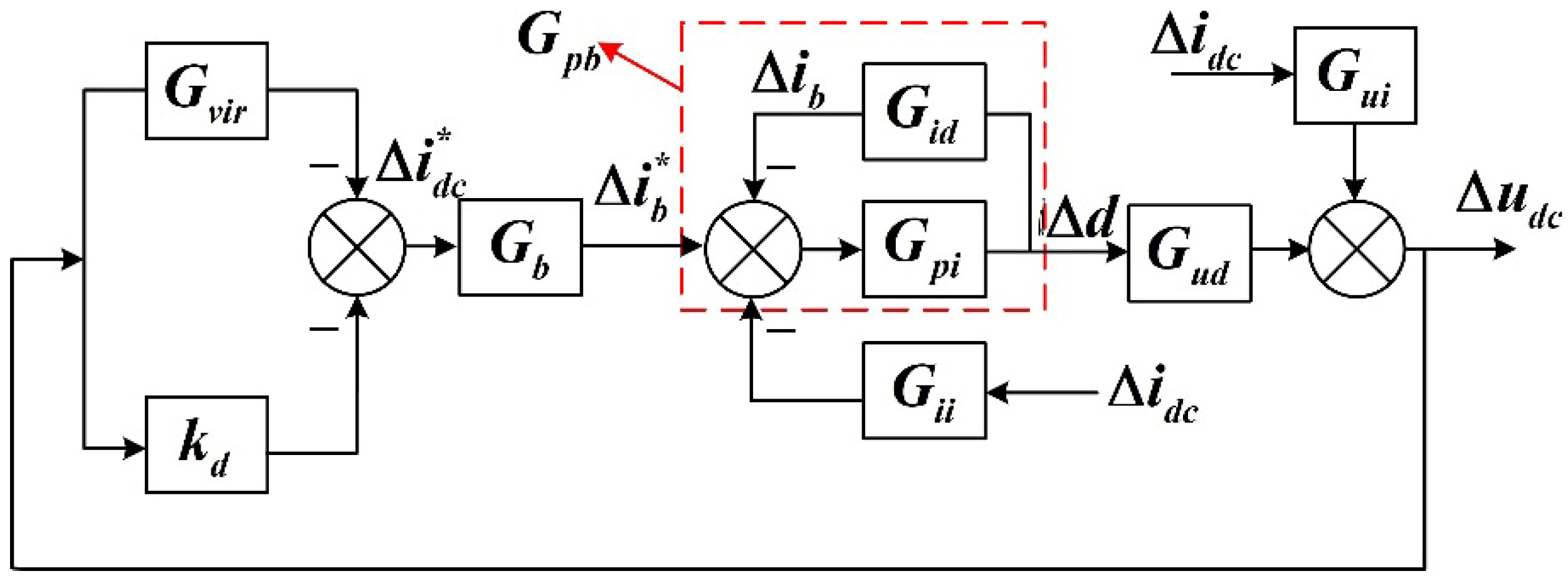
3.1. Virtual Capacitor Attached Inertia Control Principle
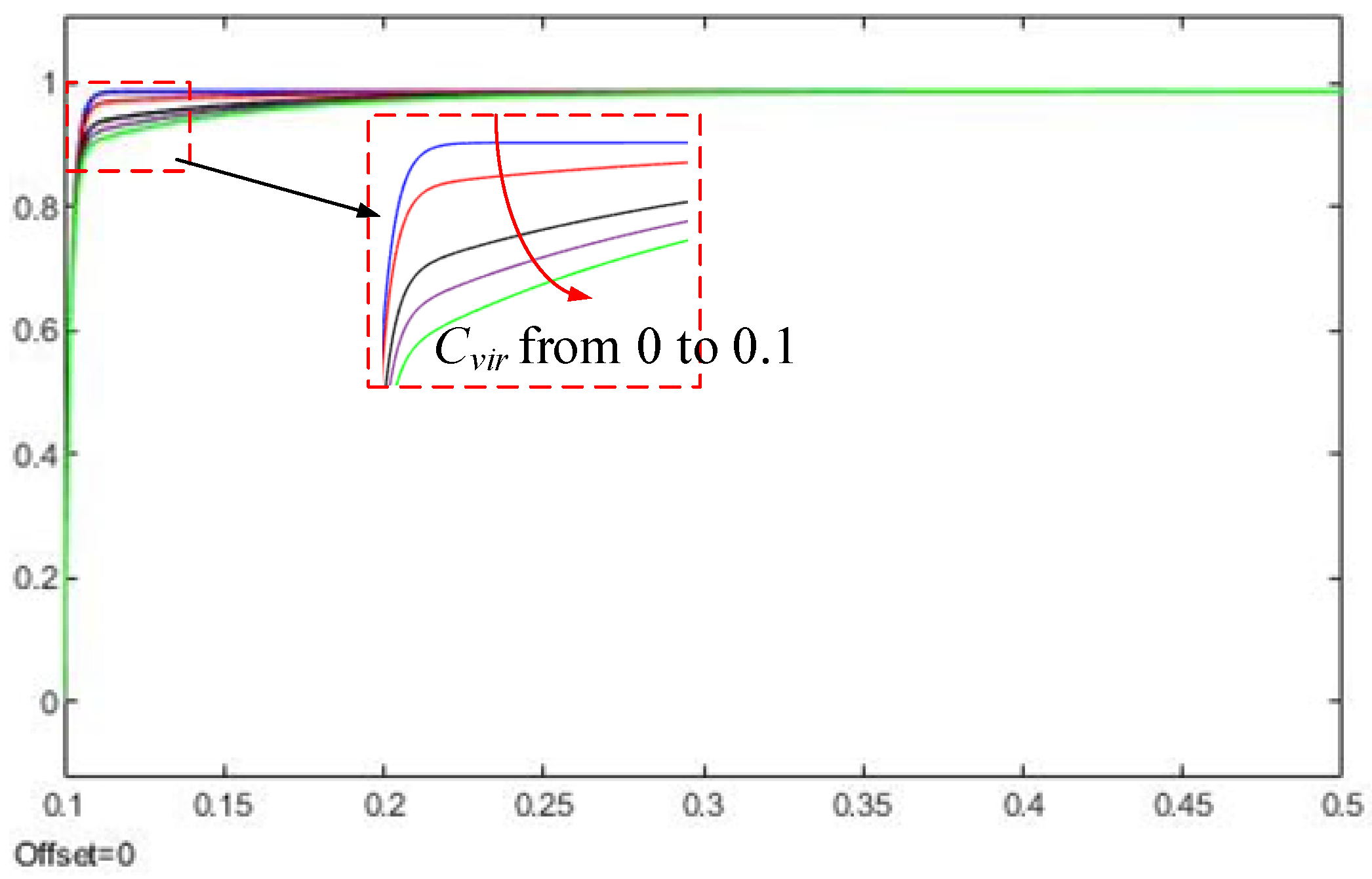
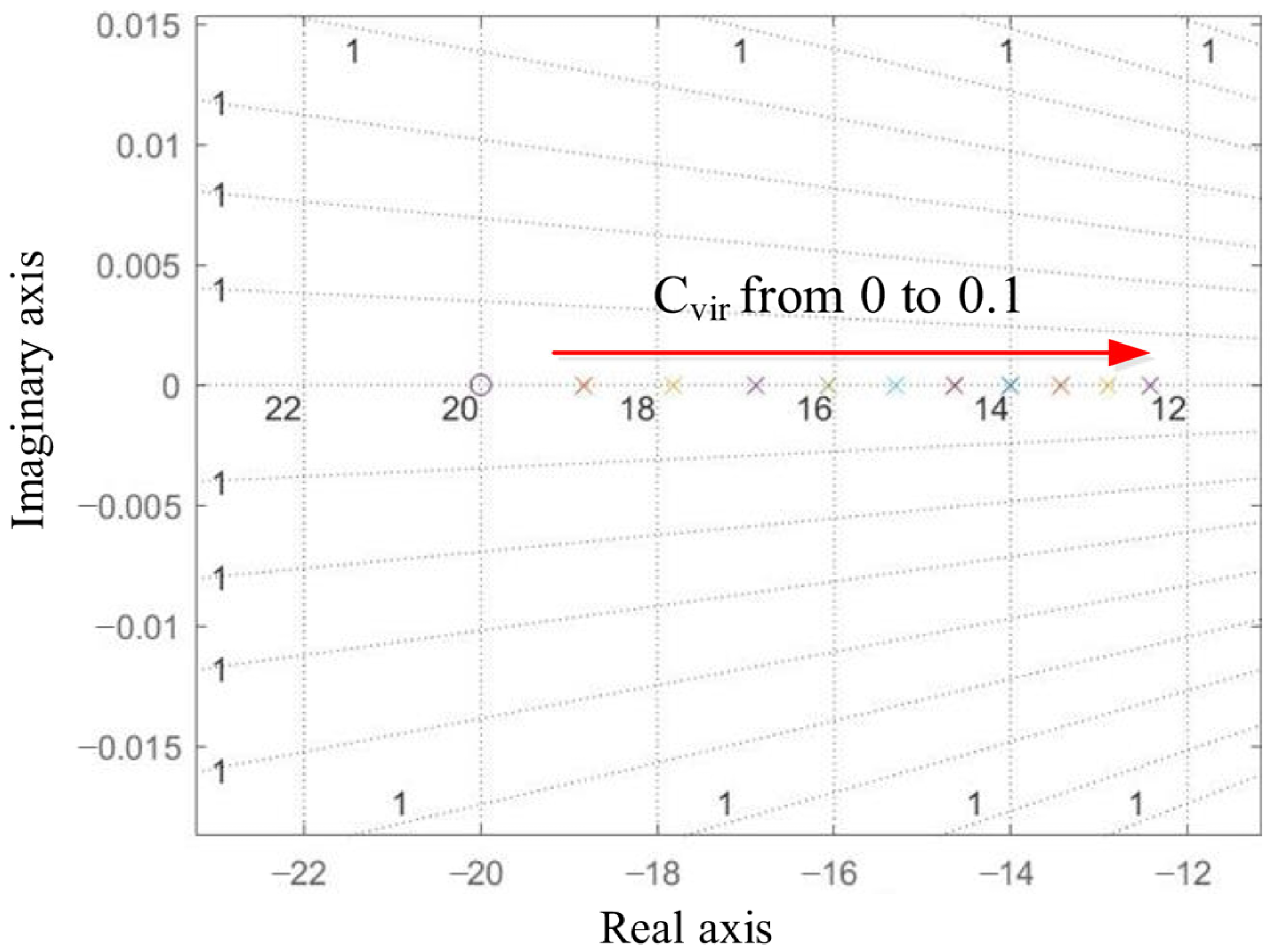
3.2. Modeling and Stability Analysis of Virtual Capacitor Attached Inertial Control
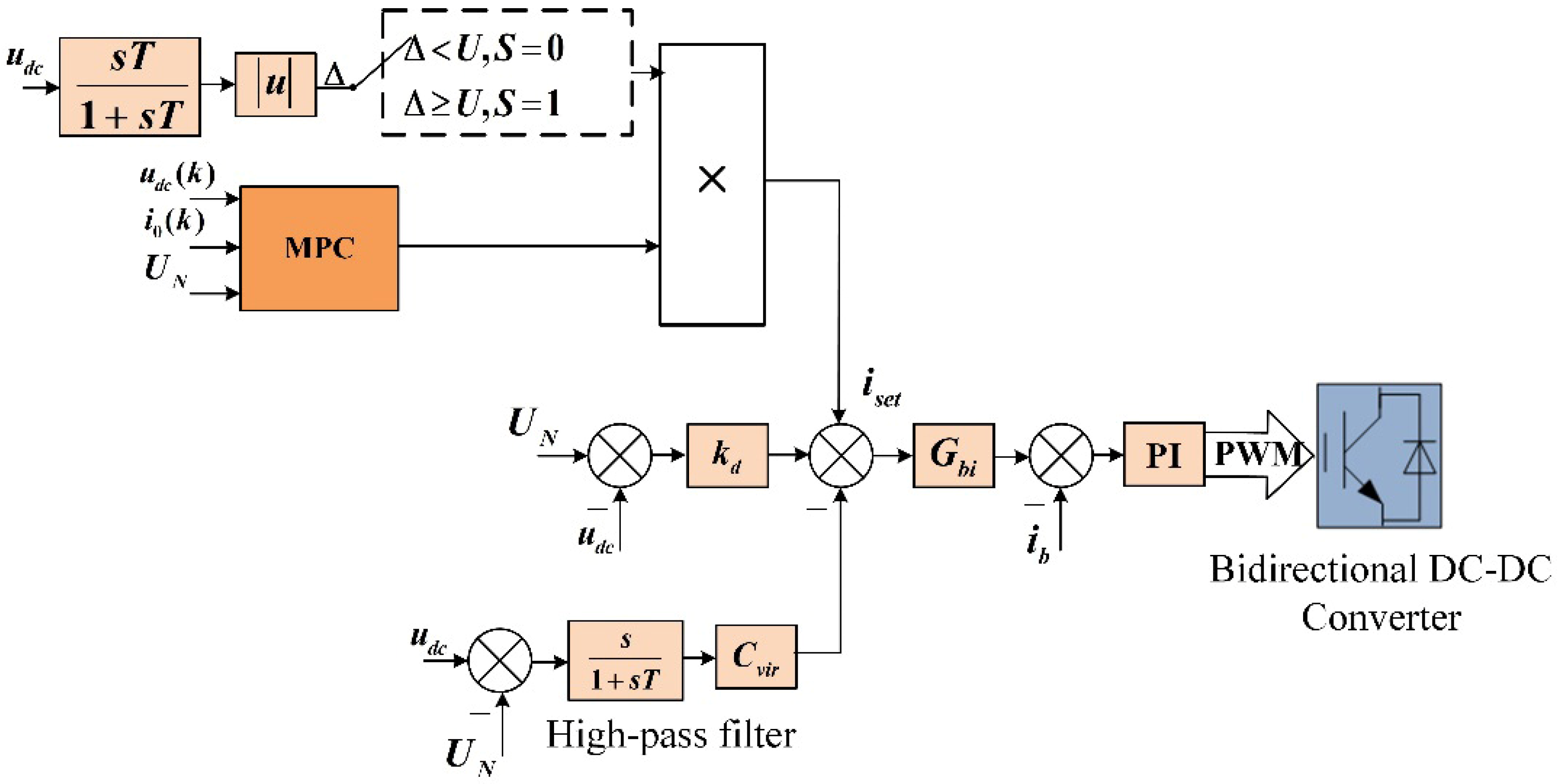
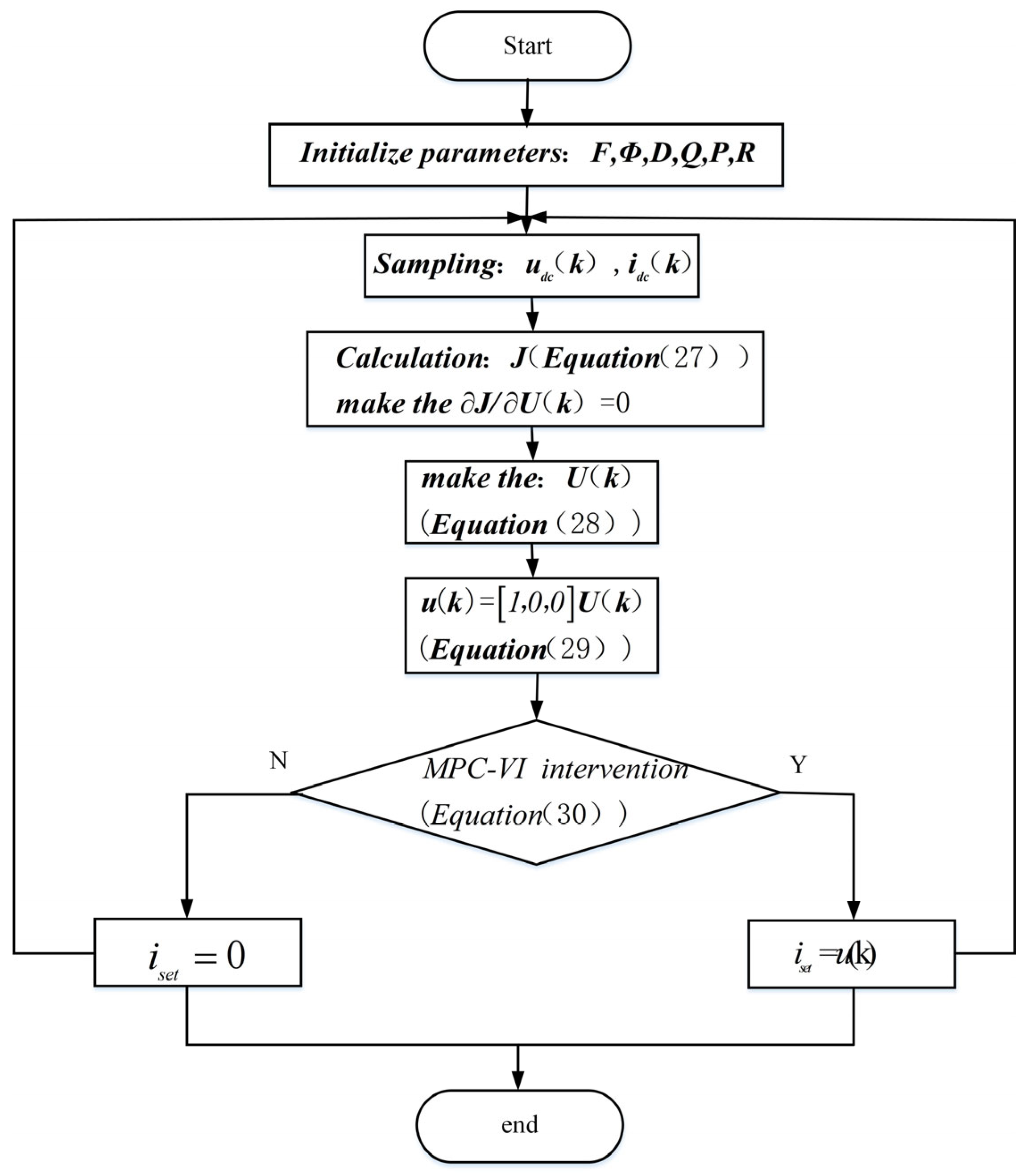
3.3. MPC-VI Control Design
3.3.1. MPC-VI Predictive Model
3.3.2. Objective Function Design
3.3.3. Solution of the Control Quantity
4. Simulation Analysis
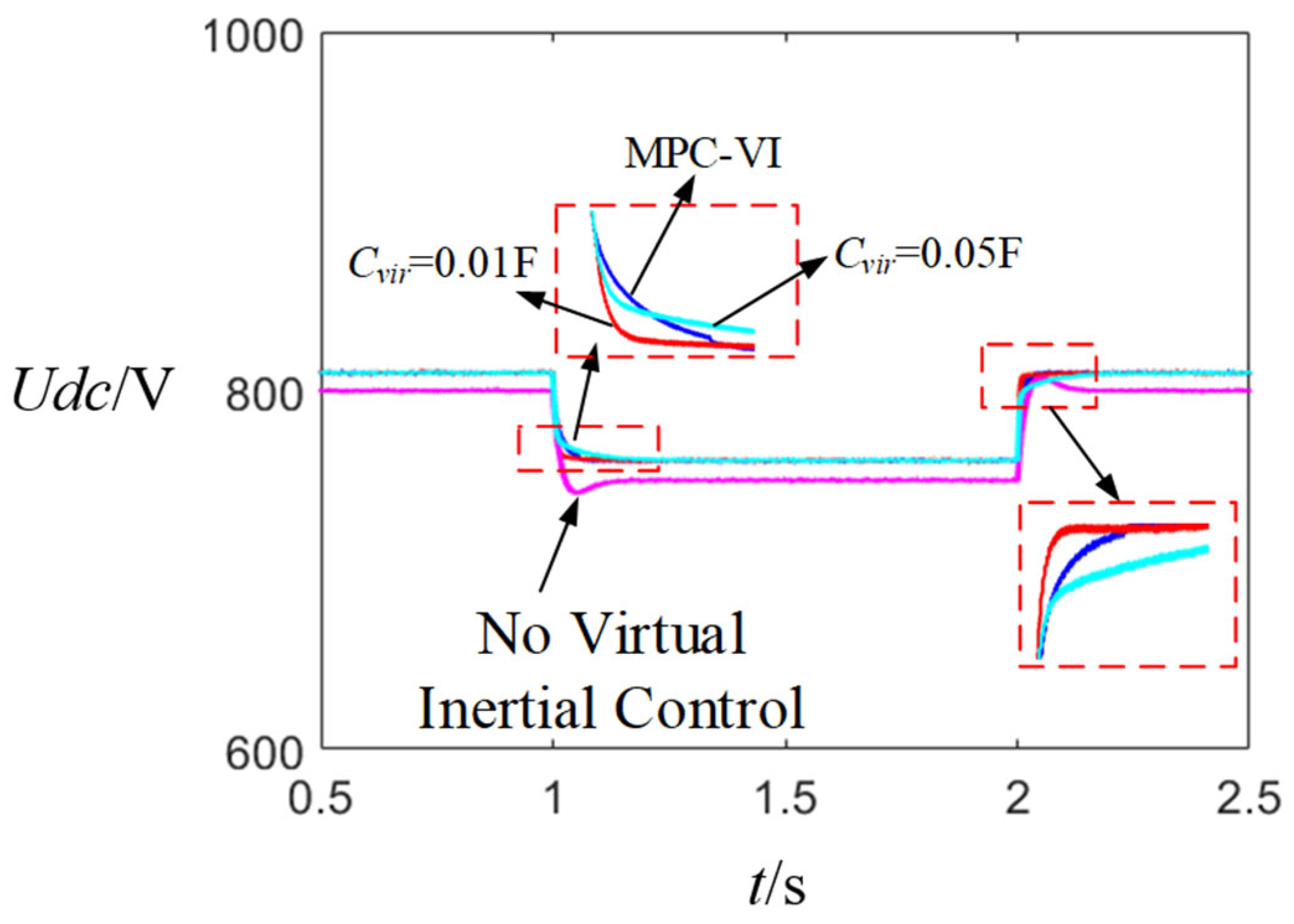
4.1. Step Response Simulation Comparison
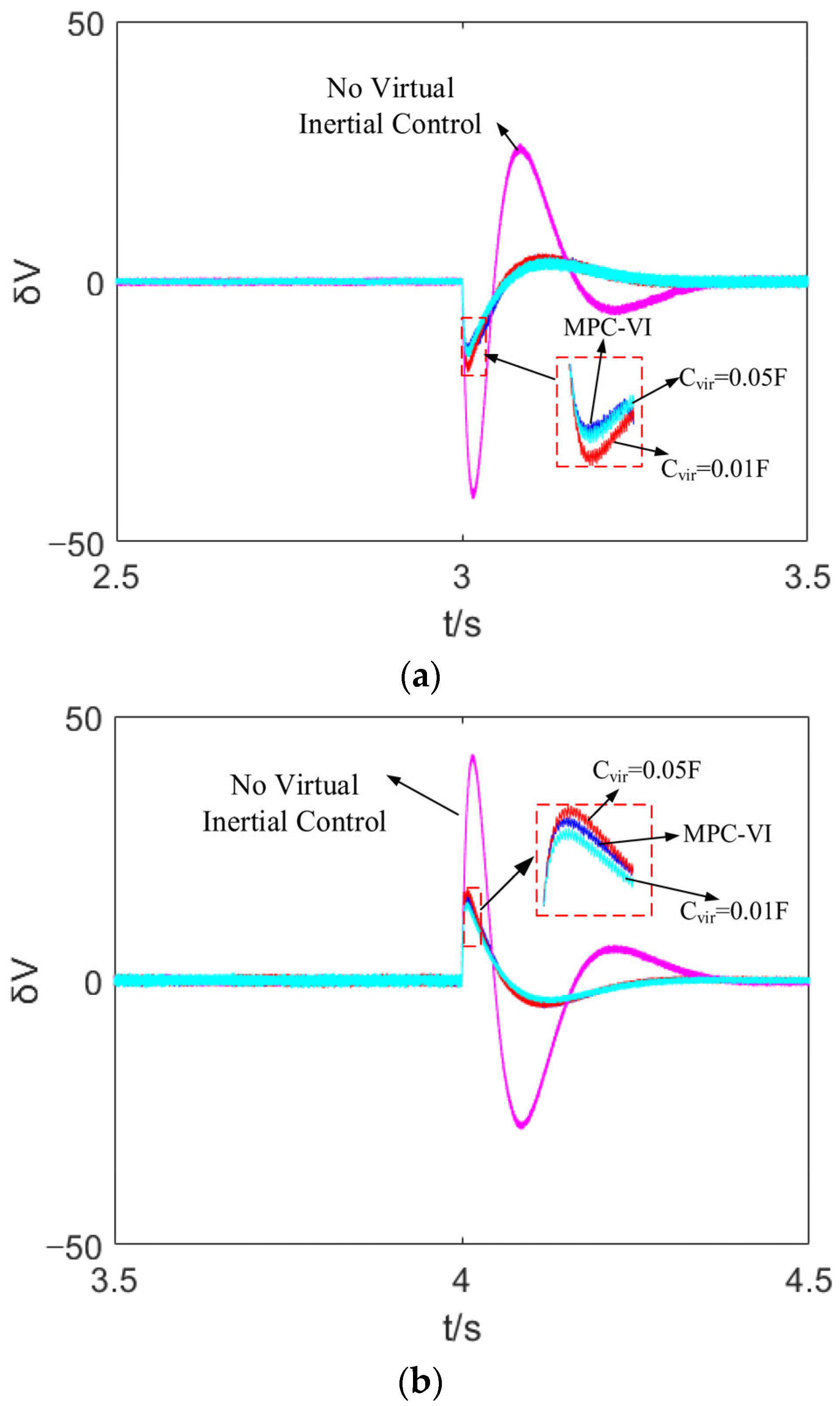
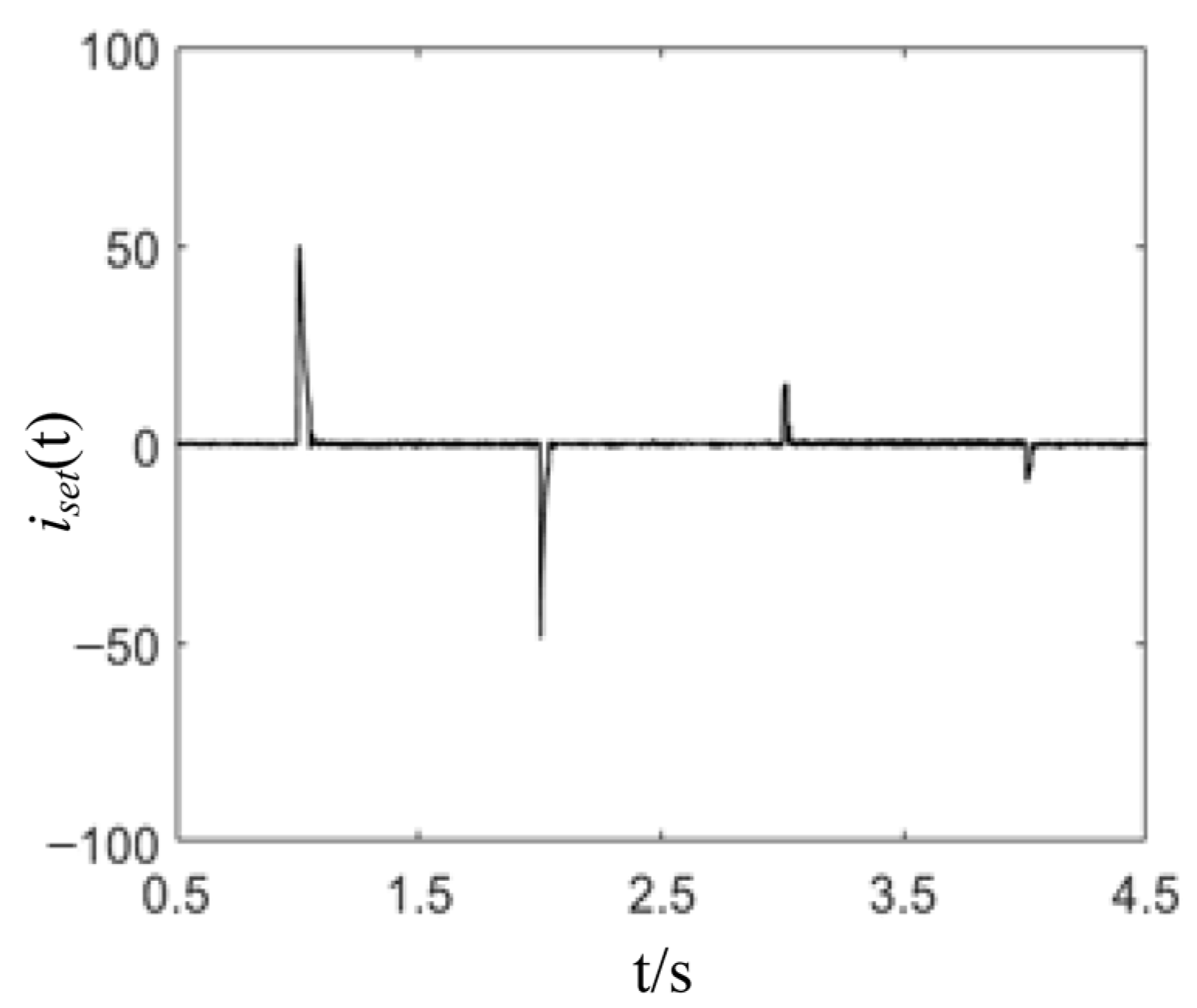
4.2. Load Mutation Simulation Comparison
5. Experimental Verification
5.1. Experimental Platform Construction
5.2. Stability and Dynamic Performance Test
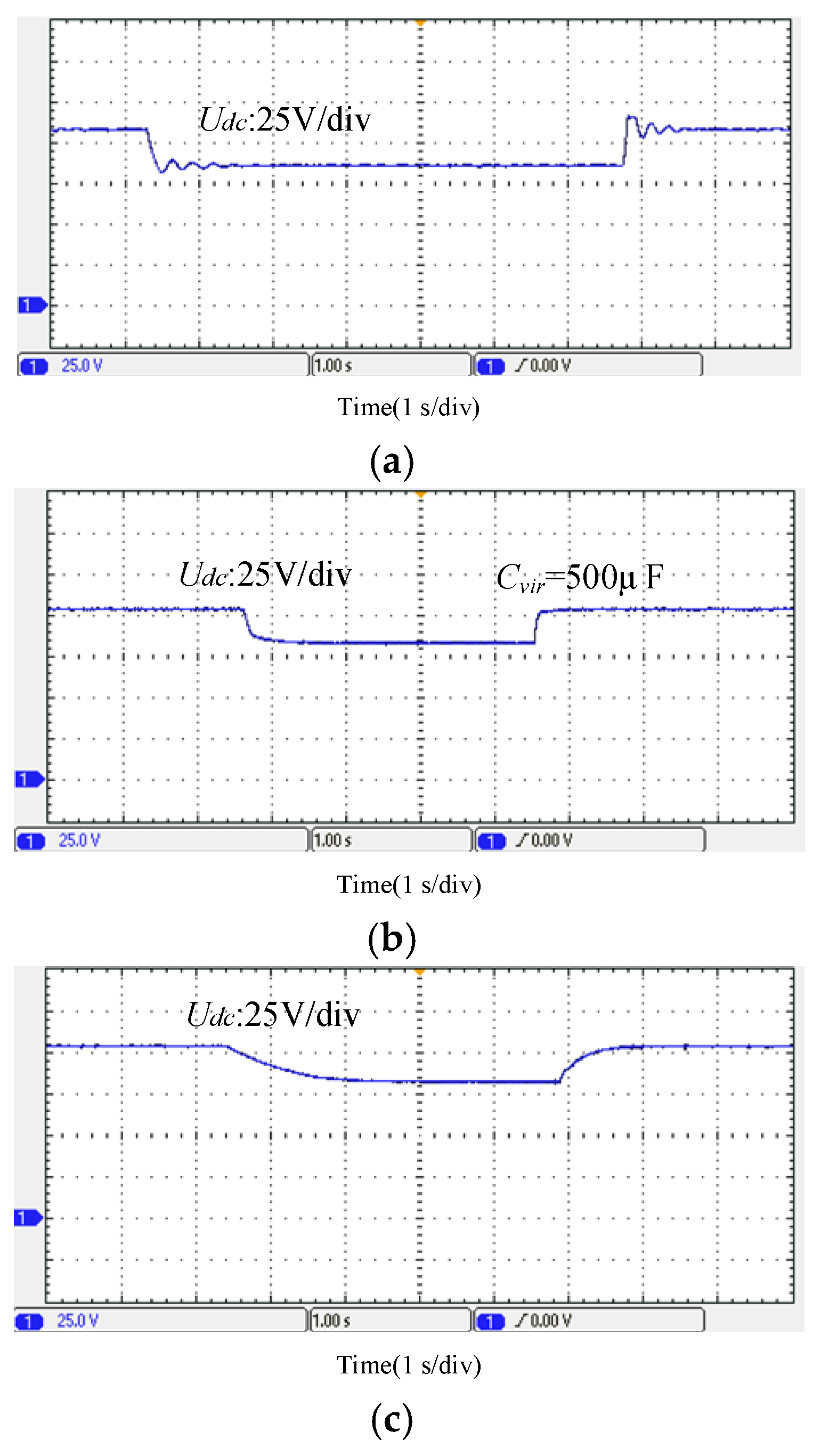
5.2.1. Step Response Comparison
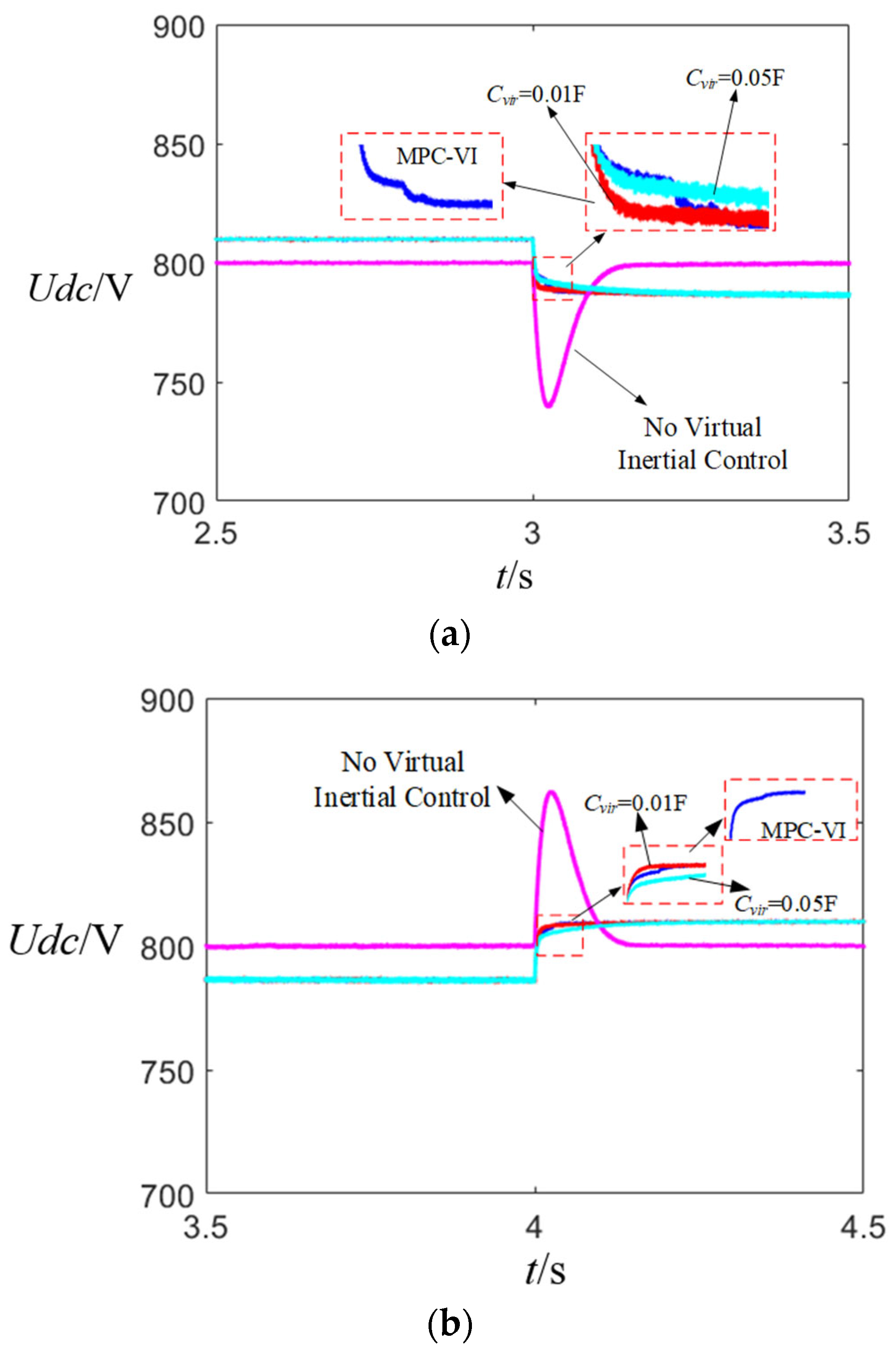
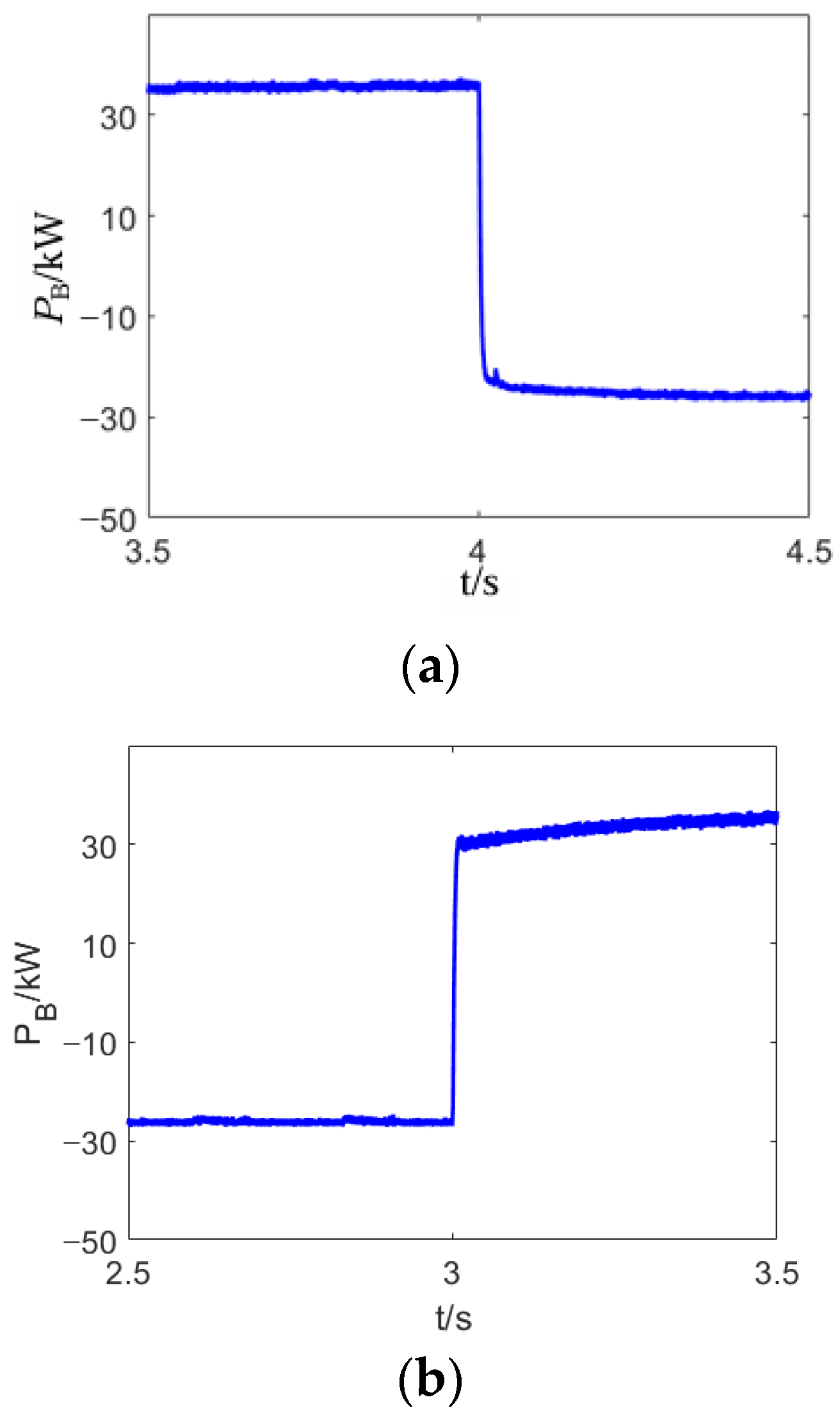
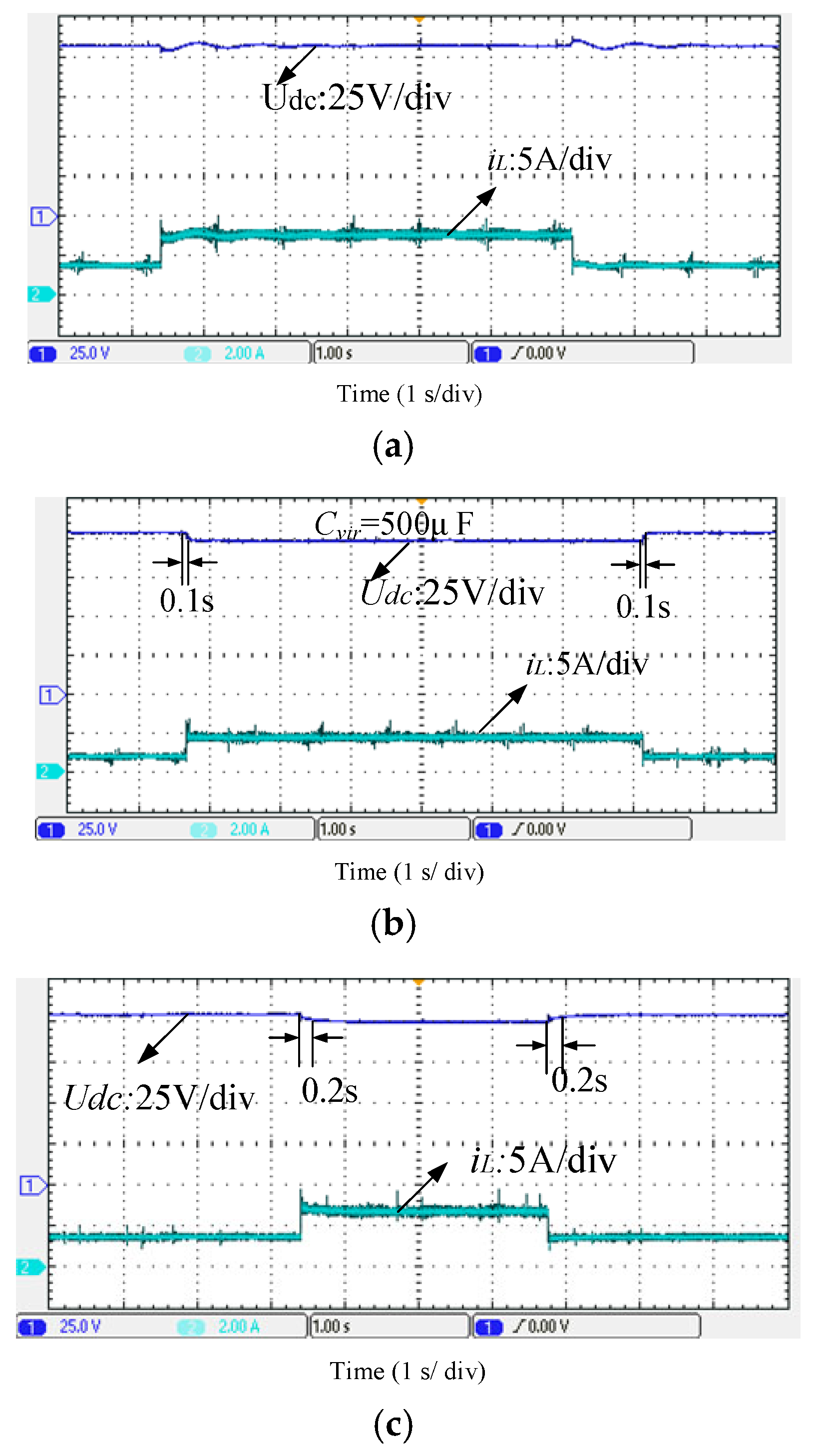
5.2.2. Load Mutation Response Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, X.; Li, Z.; Meng, F. Stability analysis of DC microgrid based on different grid structures. Trans. China Electrotech. Soc. 2021, 36, 166–178. [Google Scholar]
- Peng, Q.; Fang, J.; Yang, Y.; Liu, T.; Blaabjerg, F. Maximum virtual inertia from DC-link capacitors considering system stability at voltage control timescale. IEEE J. Emerg. Sel. Top. Circuits Syst. 2021, 11, 79–89. [Google Scholar] [CrossRef]
- Zhang, M.; Xu, Q.; Zhang, C.; Nordström, L.; Blaabjerg, F. Decentralized coordination and stabilization of hybrid energy storage systems in DC microgrids. IEEE Trans. Smart Grid 2022, 13, 1751–1761. [Google Scholar] [CrossRef]
- Lu, S.; Yu, T.; Liu, H.; Zhang, W.; Sui, Y.; Yang, J.; Zhang, L.; Zhou, J.; Wang, H. Research on Flexible Virtual Inertia Control Method Based on the Small Signal Model of DC Microgrid. Energies 2022, 15, 8360. [Google Scholar] [CrossRef]
- Lu, Z.; Sheng, W.; Liu, H.; Sun, L.; Wu, M.; Li, R. Application and challenge of virtual synchronous machine technology in power system. Proc. CSEE 2017, 37, 349–359. [Google Scholar]
- Zhi, N.; Ding, K.; Huang, Q.; Li, W.; Zhang, H. Control strategy of virtual DC motor based on P-U droop characteristic. Trans. China Electrotech. Soc. 2021, 36, 1238–1248. [Google Scholar]
- Jami, M.; Shafiee, Q.; Bevrani, H. Dynamic improvement of DC microgrids using a dual approach based on virtual inertia. J. Mod. Power Syst. Clean Energy 2020, 10, 667–677. [Google Scholar] [CrossRef]
- Wu, W.; Chen, Y.; Luo, A.; Zhou, L.; Zhou, X.; Yang, L. A virtual inertia control strategy for bidirectional grid connected converters in DC micro-grids. Proc. CSEE 2017, 37, 360–372. [Google Scholar]
- Meng, J.; Zou, P.; Wang, Y.; Wang, C. Small-signal modeling and parameter analysis of the DC microgrid based on flexible virtual inertia control. Trans. China Electrotech. Soc. 2019, 34, 2615–2626. [Google Scholar]
- Zhao, S.; Wang, H.; Tian, N.; Meng, J.; Wang, C.; Tian, Y. Model predictive control based DC microgrid virtual inertia optimal method. Trans. China Electrotech. Soc. 2023, 38, 3264–3276. [Google Scholar]
- Long, B.; Zeng, W.; Rodriguez, J.; Guerrero, J.M.; Chong, K.T. Voltage regulation enhancement of DC-MG based on power accumulator battery test system: MPC-controlled virtual inertia approach. IEEE Trans. Smart Grid 2021, 13, 71–81. [Google Scholar] [CrossRef]
- Zhu, X.; Hou, S.; Li, Z. Voltage Dynamic Response Optimization of DC Microgrid Based on Model Predictive Control. Power Grid Technol. 2020, 44, 2187–2195. [Google Scholar]
- Zhi, N.; Zhang, H.; Xiao, X.; Yang, J. System-level stability analysis of DC microgrid with distributed control strategy. Proc. CSEE 2016, 36, 368–378. [Google Scholar]

| Parameters | Values |
|---|---|
| Sampling Time Ts/μs | 20 |
| Droop Coefficient kd | 3.28 |
| Virtual Capacitance Cvir/mF | 1 |
| Weight Coefficient λ1, λ2, λ3 | 1, 1, 0.02 |
| Predictive Time Domain p | 3 |
| Time Constant T | 0.05 |
| Threshold Value U | 0.2 |
| Parameters | Values |
|---|---|
| Rated voltage of DC bus udc/V | 800 |
| P-DC Nominal capacity PVN/kW | 25 |
| G-VSC Nominal capacity PGN/kW | 50 |
| Bi-DC Nominal capacity PBN/kW | 40 |
| Dc bus capacitance Cdc/mF | 5 |
| Ac grid frequency/Hz | 50 |
| Sampling time/μs | 20 |
| Load L1/kW | 5 |
| Load L2/kW | 8 |
| Load L3/kW | 7.5 |
| Load L4/kW | 30 |
| Load L5/kW | 50 |
| Parameters | Values |
|---|---|
| High voltage side rated voltage udc/V | 110 |
| Low voltage side rated voltage uin/V | 48 |
| Rated power P/W | 150 |
| Inductance L/mH | 2.5 |
| Low-voltage filter capacitor C1/μF | 470 |
| High-voltage filter capacitor C2/μF | 100 |
| Parameters | Values |
|---|---|
| Switching frequency/Hz | 20 k |
| Control frequency/Hz | 40 k |
| Droop coefficient | 0.12 |
| Virtual capacitance Cvir/μF | 20 |
| Threshold value U | 1 |
| Weight coefficient λ1, λ2, λ3 | 1, 1, 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Jin, Z.; Su, X.; Li, S. Optimization of Virtual Inertia Control for DC Microgrid Based on Model Predictive Control. Energies 2025, 18, 6180. https://doi.org/10.3390/en18236180
Yang G, Jin Z, Su X, Li S. Optimization of Virtual Inertia Control for DC Microgrid Based on Model Predictive Control. Energies. 2025; 18(23):6180. https://doi.org/10.3390/en18236180
Chicago/Turabian StyleYang, Guoliang, Zedong Jin, Xiaoling Su, and Songze Li. 2025. "Optimization of Virtual Inertia Control for DC Microgrid Based on Model Predictive Control" Energies 18, no. 23: 6180. https://doi.org/10.3390/en18236180
APA StyleYang, G., Jin, Z., Su, X., & Li, S. (2025). Optimization of Virtual Inertia Control for DC Microgrid Based on Model Predictive Control. Energies, 18(23), 6180. https://doi.org/10.3390/en18236180







