Abstract
The use of non-renewable energy resources is one of the main drivers of climate change. In response, the United Nations established the seventh Sustainable Development Goal, “Affordable and clean energy”, which promotes the transition toward renewable and environmentally friendly sources such as wind and solar energy. However, the intermittent nature of these resources poses challenges for maintaining a stable, continuous power supply, highlighting the need for hybrid technology approaches, such as Hybrid Renewable Energy Systems (HRES), which integrate complementary renewable sources with energy storage. In this context, this study applies a Particle Swarm Optimisation (PSO)-based approach to determine the optimal sizing and operating strategy for a hybrid system comprising photovoltaic, wind, battery storage, and diesel backup units under various synthetic load profiles. The results indicate that diesel-assisted configurations achieve lower levelized costs of energy (0.23–0.35 USD/kWh) and maintain high reliability (LPSP < 0.25%), although at the expense of higher fuel consumption and CO2 emissions. Conversely, fully renewable configurations present higher energy costs (0.29–0.44 USD/kWh), but reduce annual CO2 emissions by up to 50% and create more employment opportunities, particularly in regions with abundant wind resources such as La Guajira, Colombia.
1. Introduction
Global energy demand is increasing faster than human population growth [1]. In 2023, energy demand increased by 2% compared to the previous year, with fossil fuels remaining the dominant contributors to the global energy matrix. Energy generation relies on two types of resources: conventional (coal, oil, natural gas, nuclear, etc.) and unconventional (solar, wind, biomass, hydropower, etc.) resources [2]. Among these, conventional fossil fuels were the most over-exploited during the 20th century as the primary source for human activities [3]. According to the Statistical Review of World Energy 2024 [4] by the Energy Institute, global electricity generation in 2024 increased by 2.5% compared to 2023, a rate about 25% higher than the growth in total global energy consumption. Despite continued expansion of renewable energy, fossil fuels remained the dominant source of electricity, providing about 60% of total generation in 2023. Renewable sources contributed around 30%, while nuclear energy accounted for 9.1%. However, 20% of the world’s population, about 1.4 billion people, still lack access to electricity, limiting their quality of life and access to education and development opportunities [5]. This persistent inequality in electricity access remains a significant barrier to social and economic development, particularly in rural areas where grid extension is often too costly or technically unfeasible due to geographic isolation.
Renewable energy systems have attracted increasing interest in research, implementation, and development in recent years [6]. Solar and wind power have emerged as viable options due to their cost-effectiveness, especially in remote areas with abundant resources [7]. As part of the global energy transition, microgrids have emerged as a practical approach to expand access to renewable energy systems and improve energy efficiency and equity in remote communities [8]. These systems are classified into two categories: grid-connected and off-grid; the latter are mainly used in remote regions without transmission infrastructure, where grid expansion is economically and environmentally costly [9]. Despite their potential, these renewable energy sources face several challenges in ensuring a stable electricity supply, as they depend on natural factors such as solar radiation, wind speed, and cloud cover, as well as local resource availability, leading to power outages during peak demand in off-grid areas [10,11].
To address this issue, researchers have focused on implementing Hybrid Renewable Energy Systems (HRES), which integrate multiple Renewable Energy Sources (RES) with Energy Storage Systems (ESS) to complement each other at times of low energy production [12,13,14]. The integration of diverse Renewable Energy Sources (RES) mitigates the weaknesses of individual technologies by leveraging the strengths of others. Furthermore, accurate resource forecasting contributes to stabilising power distribution and enhancing the balance between supply and demand [15,16,17]. ESS, including batteries, fuel cells, flywheels, supercapacitors, molten salts, compressed air, and pumped hydroelectric storage, helps mitigate supply intermittency by storing energy in electrical, potential, or thermal form for use when demand exceeds supply [18]. In this context, microgrids face challenges such as low inertia, high renewable penetration, and harsh environmental conditions, which can lead to uncertain operating states and reduced stability [19]. Therefore, to ensure continuity of power supply, an Energy Management System (EMS) is essential as a supervisory control layer that governs source–load interactions by coordinating charging, discharging, and surplus allocation according to system demands. Effective control of energy flows among various generation and storage technologies helps reduce operational costs and mitigates instability associated with resource intermittency. Consequently, the ESS must be supported by an appropriate management strategy to ensure supply security [20].
One of the main challenges of an HRES is selecting the equipment in an optimal configuration to achieve the best technical, economic, social, and environmental results while ensuring adequate energy management [10]. Due to the number of variables involved—resources, technologies, and time—there may be multiple combinations whose analysis for implementation is complex and requires thorough examination to achieve the operating objectives that satisfy all constraints. For this reason, numerous studies have employed various optimisation techniques in combination with computational tools to identify the optimal configurations, strategies, or operating parameters for HRES.
Mathematical optimisation is the process of determining the best solution to a problem by maximising or minimising an objective function, subject to given constraints and alternatives [21]. Bamisile et al. [22] indicates that optimisation problems can be divided into those where it is necessary to maximise and those where it is required to minimise, considering the constraints that limit the solutions obtained. Modu et al. [23] identify three approaches for sizing HRES: 1. Classical optimisation techniques based on differential calculus, including iterative, probabilistic, and graphical methods, among others. 2. New optimization methods of soft computing, which use artificial intelligence and hybrid approaches and can determine the global optimum of the system, offering better convergence and accuracy in the search for solutions; notable examples include metaheuristic algorithms such as Genetic Algorithms (GA), Particle Swarm Optimization (PSO), Artificial Bee Colony (ABO), as well as multi-objective, Multi-Objective Particle Swarm Optimization (MOPSO), Genetic Sorting Algorithm (NSGA-II), among others [6,22]. 3. Commercial computer software packages for hybrid systems: these tools are available under commercial licenses, and implement single-objective optimisation strategies to minimise the objective function costs. Some examples includes HOMER (Hybrid Optimisation of Multiple Energy Resources [24], iHOGA (Improved Hybrid Optimisation via Genetic Algorithm) [25] and RETScreen [26].
Among new optimisation methods, stochastic techniques are very popular and effective for managing complex mono- and multi-objective systems, providing accurate solutions in a relatively short time. Numerous studies have employed various metaheuristic techniques, such as MPSO, PSO, GA, NSGA-II, and the Grey Wolf Algorithm (GWA), to assess microgrid systems and determine the optimal size of energy storage systems [27]. Belboul et al. [28] optimised an HRES configuration consisting of PV/WT/BATT/DG by applying the Salpidae Multi-Objective Swarm Algorithm (MOSSA). The optimization considered two objective functions, Loss of Power Supply Probability (LPSP) and Cost of Energy (COE), and a single constraint, the Renewable Factor (RF). Additionally, an EMS strategy was implemented to coordinate energy flow among the microgrid’s components. The algorithm was compared with other algorithms, such as the Multi-Objective Dragonfly Algorithm (MODA), the multi-objective grasshopper algorithm (MOGOA), and the multi-objective ant lion optimiser algorithm (MOALO), demonstrating superior performance by MOSSA with a COE of 0.255 USD/kWh.
On the other hand, Atawi et al. [29] optimised an HRES model comprising PV panels, wind turbines, and storage in batteries and a water reservoir (PHES) technologies using the Multi-Objective Optimisation algorithm African Vultures (MOAVOA). The optimisation considered two objective functions: Total Annual Cost (TAC) and yearly amount of Expected-not-Served Energy (EENS). The performance of MOAVOA was compared with the NSGA-II and MOPSO algorithms, obtaining solutions that were evaluated using mean weighting, entropy, and the importance of criteria using the correlation between criteria method (CRITIC), followed by the decision-making method (TOPSIS) to select the best system design. Adetoro et al. [6] performed a comparative analysis of the performance of three metaheuristic algorithms (ABC, GA, and PSO) in optimising an HRES connected to an unreliable electrical grid. The study defined minimising the Levelized Cost of Energy (LCOE) as its objective function and considered EMS strategies to coordinate dispatch among PV/WT/BATT/DG/BG technologies and the grid. The results showed that the PSO algorithm achieved the best performance, yielding the lowest LCOE, indicating that it maintained a good balance between exploration and exploitation. Mohammed et al. [30] optimised an HRES composed of wind turbines/tidal turbines/PV modules/batteries to supply the electricity demand of a remote area in Brittany, France. They used a modified PSO algorithm to minimise the total net present cost (TNPC). The algorithm achieved high-precision, high-speed solutions with only 20 iterations, resulting in shorter execution time than other conventional techniques.
Ghorbani et al. [31] performed a comparative analysis of metaheuristic algorithms to calculate the cost and reliability of a hybrid PV/WT/Battery system in an isolated dwelling in Tehran. They used GA, PSO, their hybrid version GA-PSO, and MOPSO to determine the sizes of PV/WT/BATT configurations. The study concluded that the PV/WT/Battery configuration had the lowest cost. GA-PSO was identified as the most efficient algorithm, achieving the lowest net present cost and surpassing both HOMER and previous studies. PSO has been widely adopted and applied across various scientific fields, including HRES optimisation, demonstrating its effectiveness as a successful algorithm for solving problems due to its fast convergence [30,32]. This provides evidence of the implementation of metaheuristic algorithms for problem-solving, yielding remarkable results. Additionally, previous studies included a comparative assessment between the Particle Swarm Optimization (PSO) and Genetic Algorithm (GA) approaches applied to similar optimization problems. The results demonstrated that PSO consistently outperformed GA in terms of convergence speed, solution stability, and computational efficiency [33]. Based on these findings, already reported in our earlier publications [34], PSO was selected as the optimisation method for the present work.
The objective of this research is to define the optimal configuration of an HRES by analysing its technical, economic, environmental, and social impacts, using the traditional PSO algorithm, which has demonstrated its effectiveness as a successful optimisation technique due to its fast convergence speed. Based on the analysis of previous works, the main contributions of this paper can be summarised as follows: first, a rule-based EMS is used to ensure the distribution and management of energy, guaranteeing the safety and stability of the systems studied, preventing power outages, and reducing fuel consumption. Second, a single-objective optimisation approach is applied, with the LCOE as the objective function, LPSP and RF as constraints, and proportional penalties to enforce the restrictions alongside key social and environmental indicators. Finally, a comprehensive evaluation of HRES configurations is performed, providing an assessment of different configurations (WT/PV/BATT/DG and WT/PV/BATT) for two renewable energy resources, ensuring robust search performance in various resource scenarios.
The paper is organized as follows: Section 2 presents the methodology, which includes: formulation technologies, indicators, constraints, and objectives, system specifications, the synthetic demand profiles, and data sources. In the same section, it details how the proposed EMS works and finally presents the optimisation method algorithm. Section 3 presents the discussion and obtained results. Finally, Section 4 concludes the study.
2. Methodology
This section presents the strategy for integrating the mathematical formulation, constraints, meteorological data, and algorithms to obtain solutions tailored to the characteristics of the case studies. Additionally, it specifies the parameters of the system components.
2.1. Components Formulation
The HRES microgrid model comprises multiple combinations of components, including photovoltaic (PV) panels, wind turbines (WT), battery banks (BATT), and diesel generators (DG). A key characteristic of HRES systems is their connection to the low-voltage distribution network rather than to transmission lines or high-voltage lines [35] as shown in Figure 1. This section presents the mathematical model for each energy conversion technology involved in this HRES system.
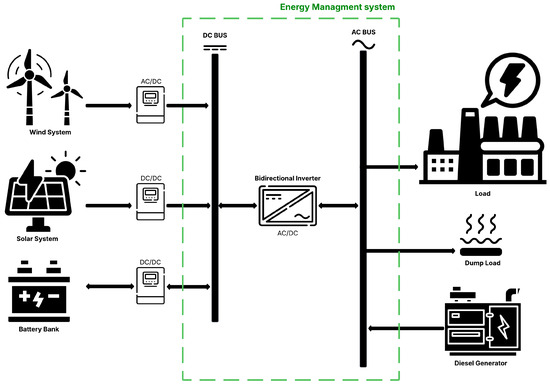
Figure 1.
Hybrid renewable energy system (HRES) for an isolated microgrid configuration.
2.1.1. Wind Energy System
Wind turbines are mechanical devices that harness the kinetic energy of wind and convert it into electrical energy, making wind speed the key determinant of their power output [6]. The wind turbine relies on essential parameters, usually specified by manufacturers, including speed characteristics: cut-in or starting (), rated (), and furling or cut-off (). When this limit is exceeded, the safety system halts blade rotation to prevent structural damage [36]. The output power of the WT is denote as and is calculate as follows [37]:
where is the nominal power (kW) of the wind turbine, while is the wind speed of the air at the wind turbine hub height (m/s) [37]. To use Equation (1), which includes wind speed increase variation with height, it is necessary to extrapolate the recorded wind speeds, commonly normalised to 10 m or 20 m above the Earth’s surface [15]. Converting the measured wind speed at a given height to the turbine hub speed () is carried out using the power law:
where is the wind speed of the air at measurement height (m/s), is the wind measurement height (m), represents the height required for the calculation (m), and is the friction coefficient. For this study, a value of equal to 0.14 will be used, assuming an ideal case of smooth surface [32,36]. The total power output of the wind energy system is calculated as follows:
where is the total power of the system (kW), and is the number of wind turbines [38].
2.1.2. Solar Photovoltaic System
The output power of a photovoltaic generation system is directly related to irradiation and ambient temperature as input parameters [38]. The power generation of a PV panel is shown by Equation (4) [28]:
being the solar cell’s or module’s operating temperature at a given time, expressed as
where is the output power (W), is the nominal power (W) of the PV module under standard test conditions (STC), is the solar radiation perpendicular to the panel surface (), is the solar radiation at STC ( = 1000), is the panel temperature coefficient (°C−1), is the ambient temperature (°C), and is the solar cell operating temperature (°C) [28]. The total power output of the solar photovoltaic system is calculated as follows:
where is the total power of the system (kW), is the number of solar panels.
2.1.3. Battery Bank System
The use of battery banks is essential in HRES, as they store surplus energy during low-demand periods and release it when required [38,39]. The capacity of the battery bank is given by Equation (7) [40]:
where is the number of autonomous days of the battery bank (days), the maximum daily load consumption in a year (kWh/day), is the efficiency of the inverter (%), is the battery efficiency (%), and is the maximum depth of discharge (%). The number of batteries required to provide autonomy for the specified number of days is determined by dividing the total capacity of the system by the capacity of each battery, as follows [40]:
where is the number of batteries connected in parallel, and is the nominal capacity of each battery (kWh). Additionally, the number of batteries connected in series is determined by the DC bus voltage of the system and the voltage of each battery, as given by the equation below [40]:
Therefore, the number of batteries required to meet the electricity demand during periods of low production can be determined as follows [40]:
The state of charge characterises the dynamic behaviour of batteries over time and is determined by the difference between generation and demand. It is expressed for the charge and discharge processes as follows [41]:
where is the previous state of the battery, is the self-discharge rate of the battery (%/h), is the efficiency during charging (%), is the efficiency during discharging (%) [41]. represents the energy difference between production and electricity demand, which depends on the technologies used in the HRES and is calculated as follows [10]:
where is the efficiency of the photovoltaic panel inverter (%), is the efficiency of the wind turbine inverter (%), is the efficiency of the inverter (%), and is the system electricity demand [10]. In addition, the operating conditions of the battery are defined by and , which represent the minimum or lowest charge level and the maximum or nominal charge level of the battery, respectively. Furthermore, the charge and discharge rates established by the manufacturer (C-Rate) are the battery’s capacity to operate over time [34]. The discharge rate is the unit of measurement for the charging or discharging speed relative to its nominal capacity, and it changes over time. For example, a discharge rate of 1C indicates that the battery will charge or discharge its nominal capacity in one hour. In contrast, a discharge rate of 0.5C indicates that the battery will discharge its nominal capacity in two hours [42].
Finally, corresponds to the nominal capacity value of the battery (kWh), while the lower limit is determined by the DOD, which affects the battery’s service life [10]. The lower limit is calculated using the following equation [41]:
2.1.4. Diesel Generators System
The diesel generator serves as a backup source when renewable energy and the battery bank are insufficient to meet the minimum electricity demand. It ensures demand–supply adequacy and can also recharge the battery bank since the generator’s fuel consumption depends on the demand it supplies [10,28]. Hourly fuel consumption of a diesel generator can be expressed by the following formula [43]:
where is fuel consumption (L/h), is power generated over time (kW), is the nominal power of the diesel genset (kW), is the slope coefficient of the fuel curve (L/h/kW), and is the intercept coefficient of the fuel curve (L/h/kW) [43]. For this case study, the values are set at and [10,32].
2.1.5. Power Converter System
The inverter is an essential component in any system that uses direct current (DC), as it converts it into alternating current (AC). These devices are crucial for converting stored energy so that electrical devices can use it. It is important to note that the sinusoidal waveform of the output voltage is critical for maintaining the quality of the electrical network, as it prevents harmonic distortions that could cause inefficiencies or damage to devices [32,44]. The efficiency of an inverter can be calculated using the equations below:
where , and k are determined using Equations (16)–(18):
where is the nominal power of the inverter (kW), and and are the efficiencies of the inverter at 10% and 100% of its capacity, respectively [44,45]. The maximum demand value determines the number of inverters in one hour, because the inverter must be able to handle the system demand while avoiding overload [46]. The number of inverters is determined by Equation (19):
where is the maximum demand value (kW).
2.2. Objectives and Constraints Formulation
The evaluation of an HRES system is defined by constraints and the objective function, determined by the adjusted complexity to be implemented in the sizing process [22]. In addition, several indicators are considered for assessment without forming part of a specific objective within the optimisation algorithm [21]. Based on previous studies, indicators can be classified into technical, social, environmental, and economic [21,22,23]. The low-cost design of an HRES with high technical reliability and high renewable penetration is essential for the implementation of these technologies, as it increases the speed of the energy transition in areas of interest, ensures reliability, reduces greenhouse gas emissions, and helps combat climate change. For these reasons, in this study, the LCOE is employed as the function to be minimised, together with technical constraints such as the LPSP and an environmental constraint such as the RF. The search space is defined by the decision variables—the number of wind turbines, the number of panels, the diesel generator power, and the battery bank’s autonomy—which together form the optimisation problem for the HRES system. To assess the social impact of the proposed solutions, the JC indicator will be used to evaluate the socioeconomic effects, especially in areas where access to energy is closely linked to local development. Finally, the LCA indicator will be used for its ability to quantify greenhouse gas emissions resulting from the use of different renewable and non-renewable technologies in the microgrid, thereby assessing their environmental impact, which is directly related to the RF.
2.2.1. Loss of Power Supply Probability
The Loss of Power Supply Probability (LPSP) is a technical indicator that utilises statistical averaging to estimate the probability that the electricity supply will be unable to meet load demand due to insufficient renewable generation capacity [14,28]. The LPSP can be calculated using the following expression [44]:
where the value of LPSP must be in the range [0, 1], corresponding to zero when demand is met, and a value of one when it is not satisfied; the subscript corresponds to the value of demand, to the value of generation by solar panels, to wind turbines, to the diesel generator, and T, which will be evaluated hourly during the simulation year. For the study, LPSP will be assessed using the worst condition when the load is greater than the total generation energy, as established in Equation (21) [28,44]:
where is the sum of the power generated by all sources available in t.
2.2.2. Renewable Factor
The Renewable Factor (RF) is an environmental indicator used as a constraint to limit the use of non-renewable energy, such as diesel generators [45]. The main goal of this constraint is to increase the proportion of energy generated from renewable sources, thereby reducing reliance on non-renewable energy, ensuring the penetration of clean energy into microgrids, and supporting the energy transition [40]. The RF is calculated using the following formula [32]:
where an RF value must be in the range [0, 1]; an RF of 1 indicates that the system is independent of the diesel generator. Meanwhile, a value of 0 indicates that the energy produced by the generator is equivalent to that from renewable sources.
2.2.3. Life Cycle Assessment
Life Cycle Assessment (LCA) evaluates environmental impact and resource use throughout the entire life cycle, covering extraction, processing, use, and disposal [47]. However, in the case of HRES, although renewable energy sources emit negligible amounts of pollutants during operation, they produce considerable emissions throughout their life cycle, including material acquisition, manufacturing, and transportation [48]. The LCA allows the quantification of CO2 for each kWh generated by the equipment in the HRES (-eq/kWh), following
where are the equivalent CO2 emissions over the lifetime of each component, and U (kWh) is the energy generated or stored by each component. is given only when the storage system delivers electricity to the hybrid system [48]. The values for CO2 equivalent emissions of each component are presented in Table 1.

Table 1.
Environmental and social specifications of system components.
2.2.4. Jobs Creation
Since the early 2000s, several attempts have been made to quantify the employment generated by climate policies, particularly those driven by renewable energy technologies. These typically use a standard metric to assess the social factor, particularly the potential employment in future scenarios, such as jobs (or jobs-years) created per unit of installed capacity for different technologies [51]. The units of the Job Creation (JC) factor for diesel generation systems are jobs/GW-h/year, which are appropriate because the useful life of a generator (including operating and maintenance costs) depends on the number of hours of operation and, therefore, on the energy generated. Dufo-López et al. [50] proposes a value of 0.14 jobs/GW-h/year for electricity generation through DG.
For the analysis of jobs created by renewable energy sources, two job groups are defined: 1. Construction, installation, and manufacturing, and 2. Operation and maintenance. The first group is usually expressed in jobs-year per MW nominal (jobs·year/MW), while the second group is expressed in jobs per MW peak over the lifetime of the plant (jobs/MW) [52]. In RES and ESS, a job creation factor is considered that integrates both labour groups, allowing it to be applied simply by a multiplicative operation. In the case of photovoltaic systems, the JC range is 0.41–2.48 jobs/MW; on the other hand, for wind power systems, the JC range is 0.39–0.8 jobs/MW; finally, for battery storage systems, a JC value of 0.01 jobs/MW-h is estimated [53]. In this sense, for the HRES system, the job creation index can be calculated using the equation below [53]:
where , , and are the job creation factors of the photovoltaic system (jobs/MW), wind system (jobs/MW), storage system (jobs/MWh), and diesel backup system (jobs/GWh/year), respectively. While , are the nominal powers of the photovoltaic system and wind systems (MW), is the annual energy generated by the diesel system (GWh/year), and is the nominal capacity of the storage system (MWh). The job creation values presented in Table 1 for this research include the manufacturing, installation, operation, and maintenance stages. In addition, it considers direct and indirect jobs throughout the project’s useful life, based on global studies [50,54].
2.2.5. Levelized Cost of Energy
The Levelized Cost of Energy (LCOE) is one of the best-known and most widely used economic indicators for assessing the economic profitability of HRES [44]. It is defined as the cost per unit of energy produced (USD/kWh), and is evaluated over time to assess the economic feasibility of a project [32,55]. The Total Net Present Cost (TNPC) must be considered over the system’s lifetime, as it captures the overall expenditure, including capital, replacement, and maintenance costs [32]. The LCOE is calculated using Equation (25) [56]:
where TNPC can be calculated using Equation (26):
in which, , , , , and represent the total cost for each technology. The total cost of each technology is divided into investment costs () and operation and maintenance costs () over the life of the project. For batteries and diesel generators, the replacement cost of the equipment is also included (). In addition, the cost of diesel fuel must be included in the cost of the diesel generator (). For the study, the total lifespan of the panel and turbine equipment has been equated to the project lifespan (20 years), which is why the replacement cost is considered zero. The total cost of WT and PV is defined by [57]:
where represents the cost of equipment ($/kW), is the maintenance cost ($/kW), is the nominal power per unit (kW), is the lifespan of the project (years). In contrast, is the time scaling used to adjust costs over time for future increments (%), and is the interest rate (%) [57]. For this case study, the values are set at , [30]. The cost estimate for the diesel generator is calculated by Equations (30)–(35) [56,57]:
where represents the cost per hour of use ($/h), represents the number of operating hours in the year (h), is the cost of fuel ($/L) [56,57]. For the battery storage system, the costs are obtained from Equations (36)–(39) [56,57]:
For the inverter system, the costs are obtained from Equations (40)–(42) [57]:
where represents the cost of equipment ($), is the maintenance cost ($/kW), is the nominal power per unit (kW), is the useful lifespan of the project (years) [57].
Finally, the capital recovery factor (CRF) is calculated using Equation (43):
2.2.6. Technology Specifications
The specification of the parameters used in the HRES optimisation process is essential, as it enables the assessment of technologies based on their technical, economic, and environmental characteristics. This study does not consider the degradation of photovoltaic panels, wind turbines, and batteries, assuming their performance remains constant over the lifespan. Though the batteries are replaced at the end of their lifespan as defined in Section 2.2.5. The data used for each technology is specified in Table 2.

Table 2.
Economic and technical specifications of system components [41,43,58].
2.3. Energy Management System
The Energy Management System (EMS) is one of the most important features in the design of an HRES due to the inherent variability of natural resources [43]. Figure A1 in Appendix A illustrates the algorithm of the rule-based control system, which ensures energy distribution and management, thereby guaranteeing the safety and stability of the systems studied, minimising power supply losses, and reducing fuel consumption. The methodology can be summarized as follows [28,36,44]:
- When the electricity generated by renewable systems (, ) is sufficient to meet demand, surplus is used to charge the battery bank.
- If the electrical energy generated by renewable systems is capable of meeting electrical demand and the battery bank has already reached its maximum charge, the excess will be discharged into the dump load.
- When demand exceeds the renewable generation capacity, the battery bank will supply the deficit.
- If the electricity demand exceeds renewable generation and the stored energy of the battery bank, the diesel generator is activated under three conditions:
- –
- If the demand is within the nominal capacity of the diesel generator, it will vary its power as long as the demand is not less than the minimum load percentage defined by the manufacturer (). If demand does not require the generator’s full nominal power, the surplus will be used to charge the battery bank. The diesel genset will shut down if the energy of the battery bank can supply the demand and the is less than ().
- –
- If demand exceeds the generator’s capacity, the battery system will turn on to make up the shortfall if the stored energy is available.
- –
- If the battery bank is fully charged, instead of being less than zero, the diesel genset will shut down.
2.4. Description of the Case Studies
This section describes the meteorological and electricity demand data used to parameterise the algorithm. The profiles, along with the selected technologies, define the different case studies. These allow observation of the algorithm’s search process and solutions across various scenarios.
2.4.1. Meteorological Data
The study uses the Data Access Viewer (DAV) database from the National Aeronautics and Space Administration (NASA) [59], which, through an Application Programming Interface (API), provides wind speed, wind direction, ambient temperature, and solar irradiance in a selected area with a resolution of one hour for each data sample. Two regions of Colombia are chosen as case studies based on data from the Institute of Hydrology, Meteorology, and Environmental Studies (IDEAM, by its Spanish acronym) [60,61]. The resources in the selected zones are considered due to their complementarity and the high diversity of renewable resources in Colombia. These areas are also chosen as representative examples of Non-Interconnected Zones (NIZ), where access to electricity is limited and diesel generators are often used as the primary power source, enabling an assessment of how these approaches can support the energy transition. One of them is in Uribia in the department of La Guajira, due to its average surface wind speed between 7.0–8.0 m/s, and an average global solar radiation between 5.5–6.0 , being an area with high energy resources. On the other hand, near the municipality of Arauca in the department of Arauca, it was selected due to its average surface wind speed between 0.5–1.0 m/s and average global solar radiation between 5.5–6.0 , which represents low wind resources but high solar irradiance. Figure 2a shows the probability distribution of wind speed for the year 2023 for both selected regions, while Figure 2b shows the wind speed with a resolution of one hour for the same year. Finally, Figure 3 shows a solar radiation heatmap with an hourly resolution in the year 2023.
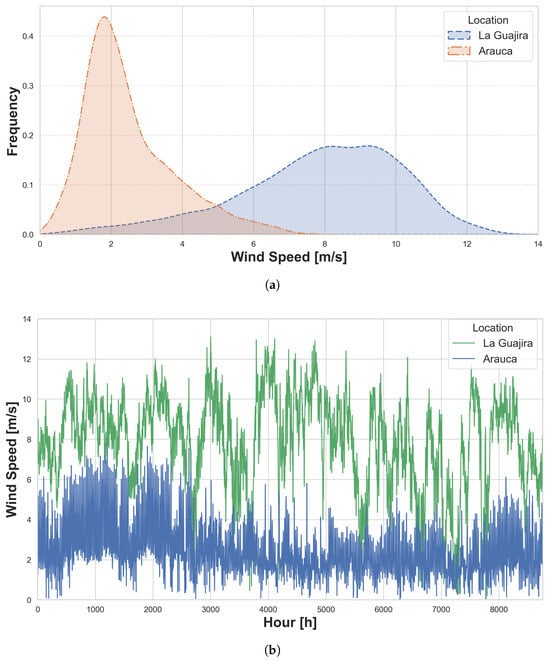
Figure 2.
Wind resource characterisation for 2023 in the selected regions: (a) Kernel density estimation (KDE) of the wind speed distribution. (b) Hourly wind speed profile used for system simulation [59].
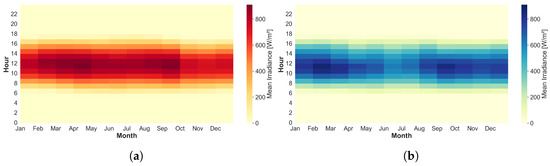
Figure 3.
Solar irradiance in selected areas for the year 2023: (a) La Guajira Heatmap. (b) Arauca Heatmap.
2.4.2. Load Demand Profiles
Many studies have used community demand profiles to guide research, aiming to provide electricity to underserved populations [36,44,57]. One key profile used is the household demand profile, which helps assess microgrid performance and ensure reliable service. Similarly, it is crucial to evaluate the development capacity of communities in light of industry introductions and to assess the feasibility of using microgrids as an electricity supply service. That is why both electricity demand profiles are used in the different case study configurations presented below. Given the lack of consumption data for some isolated areas and the limited information available on household electrical devices, a standardised load profile will be used for electricity demand modelling. This provides access to standard electricity consumption models based on consumer characteristics, which were developed using case studies of more than 1500 load consumption profiles in homes, businesses, and industries [62]. The code used is an open library proposed by the German Association of Energy and Water Industries (BDEW, by its German abbreviation) [63] in which parameters such as public holidays, annual demand, the date of the year, days off, work coefficients on weekdays and weekends, among others, must be set.
The electricity demand profile for a group of homes is shown in Figure 4a; to obtain consumption data, weighted data will be extracted from the department of Guainía in the municipality of Inírida in Colombia, which is presented by the Institute for Planning and Promotion of Energy Solutions for Non-Interconnected Areas (IPSE, by its Spanish abbreviation) in its monthly telemetry report [64]. For which an average annual consumption of 94,800 is assumed, due to its similarity in demand profile to the synthetic model.
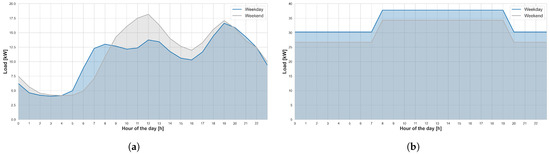
Figure 4.
Electricity demand profiles for weekdays and weekends: (a) Household demand profile-Load (1). (b) Industrial demand profile-Load (2) [62].
For the industrial electricity demand profile case study, a schedule from 8:00 a.m. to 7:00 p.m., every day of the week, is defined. The annual electricity demand is 290,000 kWh, based on measurement data [1]. The maximum demand during the day reaches , while the minimum is on weekends. The average weekday load profile is shown in Figure 4b.
2.5. Particle Swarm Optimisation Algorithm
Particle Swarm Optimisation (PSO) is a meta-heuristic optimisation technique widely used to solve complex optimisation problems [45]. In the PSO algorithm, each particle has a position representing the value of the variables and a velocity that directs the particle towards the individual and global bests. Three elements determine the particle velocity and, based on that, the position: the first is the individual best, which is the best value that the particle has achieved and stored. The second one is obtained by the PSO optimiser among the population; this is called the global best. These three elements: the current position, the individual best, and the global best are used to update the particle velocity and, consequently, its position [44]. During each iteration, the algorithm tracks the position of the particles and updates both the individual () and global () best position values. Each solution is evaluated based on its fitness value using the fitness function. In the iteration process, both the position and velocity of particles are updated. Each particle adjusts its position, moving toward a more optimal solution with every iteration, guided by its velocity [40]. The process is repeated until a stopping criterion, such as the number of iterations or predefined target fitness values, is met. The velocity and position of each iteration are calculated following [6,65]:
where is the velocity of the particle, x is the position, i is the number of the particle, and j the iteration. In the other hand, is a constant confidence in its own movement or inertia, and are cognitive and social parameters; and are random numbers between that generate independence between particles [40,44,66]. Clerc [65] indicated it is possible to show that a good convergence can be ensured by making and (Confidence in other) dependent, using the parameter , for this studio the value will correspond to . The fitness function for the optimisation problem is summarised below:
where is the objective function with external penalty, which can be divided into two main components. The first one, , is the aim of the base function, which in this case is the LCOE, with () as the solution vector. In contrast, the second component is a quadratic penalty term, applied to the technical and environmental indicators LPSP and RF. Additionally, denotes the penalty factor, and q indicates the proportion to the power of the amount by which the restrictions are violated [67]. These penalties can be described as follows:
then, they can be expressed as
therefore, the Equation (47) can be expressed as follows:
To solve the sizing problem, the proposed procedure of action is defined in Appendix A, Figure A2. It starts with the initialisation of the particles positions, which places them in a random search landscape. Continue loading the meteorological data, component characteristics, and constraints, and randomly select particles positions and velocities to generate the initial population. Then, apply these values to the objective functions to find the optimum fitness value. The particle evaluates the indicators LPSP and RF; if those values exceed the limit constraints, the objective function LCOE will be penalised. Continue to assess each particle in the swarm and find the best fitness value among the whole swarm (minimum LCOE). The particle with the lowest electricity cost is chosen as the global best. Before that, the algorithm updates the iteration variable, velocities, position, and inertia using Equations (44)–(46). If the number of iterations exceeds the maximum, stop the algorithm. Multiple studies have shown that PSO demonstrates continuous improvement with the number of iterations, establishing that for HRES design problems, 100 iterations and 50 particles are sufficient to achieve convergence of the objective function [6,31,44,68].
The penalty coefficients are set as = 5000 for both constraint violations. These values were empirically selected to balance the indicators LPSP and RF within the range 0–1, consistent with the LCOE objective scale. The convexity of the minimisation problem depends on the penalty coefficient: the higher it is, the more convex the problem becomes, allowing a smaller search space to be explored more easily. However, if the penalty coefficient is too high, the search space becomes reduced, limiting exploration [69]. Increasing values beyond 10,000 sometimes produced excessively penalised solutions, disproportionately affecting the objective function and masking the algorithm’s performance, particularly with limited exploration. Therefore, = 5000 was selected after testing different coefficient values (1000, 5000, 10,000, and 50,000) as a reasonable trade-off, enforcing LCOE compliance while preserving fair comparability among the constraints [68]. This allows the algorithm to softly penalise solutions that violate the constraints, without immediately discarding them, thus allowing nearby regions to be explored sensitively and guiding the particles through the search space. To ensure convergence, the parameters for this study are defined as follows: problem dimension = 4; number of runs per case = 5; population size = 60; and maximum iterations = 120. The size of each HRES component was allowed to vary between zero and a specific upper boundary (UB) defined in Equation (52) [6,58].
3. Results and Discussion
In this study, optimisation was employed for a single-objective non-interconnected microgrid using various generation and storage technologies, controlled by a rule-based EMS that managed power flow distribution and ensured the stability and security of the electrical grid. The optimisation factor was the LCOE, designed to be optimal, with LPSP and RF as constraints, and JC and LCA used as post-processing indicators. As mentioned in Section 2.4.1 and Section 2.4.2, the optimisation model was implemented in two scenarios, each using a different meteorological data set and load demand profile. Table 3 shows the combinations for the study cases assessed in this work. For the simulation process, the limits and variables of the PSO algorithm were defined; these included an of 2% for Load 1 and of 0% for Load 2 and an of 85% for both, in addition to lower LB and upper UB limits for each technology, as shown in Section 2.5. The study was programmed and executed on an Intel Core-i5-12500H and 16 GB RAM using the Python 3.12.3 programming language.

Table 3.
Study cases: configuration, demands (Load (1): Household demand profile; Load (2): Industrial demand profile-Load), and meteorological resources.
For each WT/PV/BATT/DG or WT/PV/BATT configuration case, five runs of 120 iterations were simulated. This resulted in more than 40 runs and over 4800 particles evaluated to observe the solution’s behaviour in response to technical, economic, environmental, and social factors under the EMS strategy. The convergence curves of global best LCOE values for Case 1 are shown in Figure 5, indicating that the solutions tend to reach their convergence within 100 iterations. In the detailed view, the relative error () is analyzed respect to the best solution obtained (Run 4). This analysis shows a deviation of less than 3% among Runs 1–4, except for Run 5, which shows a deviation of 7.41%. This behavior is attributed to the LCOE’s sensitivity to representative variations across solutions, with a maximum difference of 0.018 between the highest value (Run 5) and the best solution (Run 4). However, when analysing the mean () and standard deviation (), values of 0.2601 USD/kWh and 0.0076 USD/kWh, respectively, are obtained, indicating a variability of less than 3% among the solutions obtained for Case 1, which demonstrates the consistency of the runs. For each run, a solution particle (HRES configuration) was obtained that met or approximated the established LPSP and RF constraints, allowing the calculation of the JC and LCA indicators. In this way, the first section presents an analysis of the results from the sizing methodology, focusing on economic performance—using LCOE as the objective function—and on operational performance under LPSP and RF constraints. Furthermore, an analysis of the EMS behaviour in response to resource variations throughout the simulation year is presented, using Case 1 as an example. Subsequently, in the second section, a comparative analysis is presented, highlighting the performance among the cases listed in Table 3.

Figure 5.
Convergence of the global best LCOE value for the proposed PSO-based model: Case 1.
3.1. Economic and Technical Analysis of HRES Sizing
The WT/PV/BATT/DG configuration was the most economical configuration obtained for Case 1. The solution vector of the configuration includes 21 wind turbines, 38 solar photovoltaic panels, 13 kW of nominal power for Diesel Genset, and 0.029 Autonomy days or one battery, achieving the lowest LCOE = , respecting the established restrictions with values corresponding to an LPSP of 0.87%, and an RF of 85%. In addition to the LCA and JC indicators, with values of 14.24 -eq and 0.096 jobs/year, respectively.
Figure 5 shows how the LCOE indicator tends to stabilise at values below 0.30 USD/kWh, which corresponds to a feasible solution within the set of results obtained [28,32,40]. Additionally, this range of LCOE values is consistent with those reported by García-Vera et al. [70] for the Puerto Estrella community, located in La Guajira, Colombia. Their techno-economic analysis yielded LCOE values between 0.27 and 0.31 USD/kWh for similar hybrid configurations under comparable resource conditions. Given that the present study evaluates a higher energy demand (257 kWh/day vs. 52 kWh/day), the resulting LCOE remains within the expected range.
A detailed analysis of the configuration for Case 1 reveals that wind power is the primary source of electricity generation, utilising turbines with an installed capacity of 42 kW. This is complemented by a photovoltaic system with an installed capacity of 17.5 kW, whose contribution, although smaller, is significant in terms of energy input. A 40 kWh battery storage system is also incorporated, capable of supplying between one and two hours of backup power at peak demand. Finally, the HRES system is supported by a diesel generator with a nominal power of 13 kW, which guarantees continuity of supply in conditions of low renewable availability and if the storage system reaches its lower limit. In terms of annual energy production (AEP), it consists of 124.45 MWh from the wind system, 35.19 MWh from the solar system, 12.93 MWh from the diesel system, and 7.03 MWh from the battery bank, as shown in Figure 6a. Based on this, Figure 6b shows the monthly production of each system during the year, revealing that between August and October, there is less renewable wind and solar energy available, which is why the battery system cannot store the energy needed to provide backup; as a result, the diesel system is used more frequently to meet electricity demand. However, in general, there is an excess of energy from the wind system, which is dumped because it is not used to meet electrical load demand.

Figure 6.
Annual energy production for Case 1: (a) Annual energy contribution by source. (b) Monthly breakdown of energy production by generation source.
The distribution of investment costs by technology shows that the wind power system has the largest share, with a TNPC value of USD 64,979, accounting for 39% of the total configuration cost of USD 166,855.38 (see Table 4). This is due to two factors: the cost per kW and the number of installed wind turbines (). The diesel generator has a TNPC value of USD 39,610, with diesel fuel consumption per operating hour accounting for 63% of its total cost, as shown in Figure 7b. The photovoltaic system costs USD 36,731, which represents 22% of the total configuration costs. Support components, such as the battery bank (USD 13,205) and inverter (USD 12,330), represent a smaller percentage of the total system cost as shown in Figure 7a.

Table 4.
Result comparison of different configurations for HRES optimization.

Figure 7.
Distribution of system costs by technology for the optimised configuration of Case 1: (a) Breakdown of the TNPC by system technology. (b) Cost structure of the HRES components considering capital, O&M, replacement, and fuel expenses.
The obtained system guarantees 99% of the electricity demand, indicating high reliability of the hybrid system, with approximately 824 kWh of unmet demand during the year, due to low resource availability. This is illustrated in Figure 8a, where the red dots represent the hours when the system was unable to provide sufficient energy, in contrast to the green dots, which represent the fulfilment of demand. Similarly, Figure 8b presents a histogram of the system power balance, ranging from 0 kW to 5 kW, demonstrating that the configuration can meet the load’s energy demand without excessive surplus production.
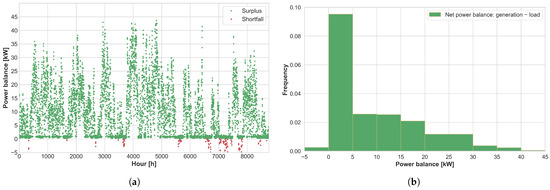
Figure 8.
Power balance analysis () for the optimized configuration over one year for Case 1: (a) Hourly power mismatch between load and generation. (b) Histogram of the power balance illustrating the frequency distribution of the net power.
Finally, Figure 9 shows the behaviour of the EMS in response to variations in solar and wind resource availability over seven days in June. These days were selected to demonstrate the complete rule-based EMS strategy. Based on the control logic, the diesel generator is activated only when the energy supplied by renewable sources and the battery system is insufficient to meet the load demand, ensuring that it remains the backup system with the lowest priority. This behaviour occurs between 1–5 June, when wind and solar production are low in the afternoon, and the battery reaches its lower discharge limit. On the other hand, during 6–7 June, the combined solar and wind production exceeds load demand, keeping the diesel generator off while the excess energy is stored in the battery system. Once the battery reaches its upper charge limit, the surplus energy is discarded through the dump load.

Figure 9.
Annual generation mix using different sources of energy for Case 1.
Additionally, during the night of the first day, the battery system is unable to meet demand, and insufficient wind generation is observed, so the diesel system is started up. Since the demand is lower than the generator’s rated power, the excess is used to charge the battery until it can again support the load. The figure also shows the battery system’s charging and discharging behaviour utilising the state of charge (SOC) axis, expressed as percentage values. It demonstrates how the battery delivers power when needed and stores energy when there is excess generation, validating its DOD restrictions defined by the control logic of the EMS.
An evaluation was conducted using the HOMER Pro tool and compared with the PSO algorithm. HOMER Pro delivered the following results: 17 wind turbines, 44 solar panels, a diesel generator with a nominal power of 19 kW, and four batteries for the backup system, accumulating a TNPC of USD 192,218. Comparing this with the results obtained in Case 1, it was observed that there were notable differences in the number of turbines, the nominal power of the diesel generator, and the number of batteries, resulting in a 13.2% reduction in net present cost compared to HOMER Pro. This reduction is due to the established EMS rules algorithm, which allows the battery to operate simultaneously with the generator during periods of high electricity demand. On the other hand, if this rule is modified and the generator system is not allowed to work in parallel with the battery system, the PSO algorithm search is modified, obtaining the following configuration as the optimal solution for Case 1: 16 turbines, 45 solar panels, a 20 kW nominal power generator, and two batteries with a TNPC of USD 174,361, LPSP of 0% and RF of 86.43%, which shows that the algorithm implementation allows similar and satisfactory solutions to be achieved in terms of results and convergence when compared to software such as HOMER Pro 3.18.4. In summary, the PSO algorithm proved to be capable of achieving reliable and economically competitive configurations when compared with commercial software such as HOMER Pro.
3.2. Comparative Analysis
This section compares the optimized configurations obtained for the different case studies. Section 3.2.1 analyzes the influence of load demand profiles, while Section 3.2.2 examines the effect of renewable resource availability on system performance.
3.2.1. Load Demand Analysis
Figure 10 illustrates how each case study seeks to satisfy or approximate the constraints while optimising the objective function. Additionally, it displays all indicators and highlights the solution with the lowest LCOE, emphasising that this is the best outcome. In general, it can be observed that for Load 1, the restrictions were met with slight differences in percentages. In the case of the LPSP, whose maximum limit was 2%, the search algorithm allowed the limit to be exceeded by 0.10% (shown in Figure 10c) for Case 4. This was due to a soft penalty, which allows the limit value to be approached without altering the LCOE value. Thus, it avoids discarding feasible low-cost solutions that do not precisely meet the constraint. For the RF restriction, all solutions fully complied with the defined limit, ensuring that RF values remained above the minimum of 85%. Cases 3 and 4 are made only by renewable energy sources, resulting in RF values at their maximum possible level for this setup, specifically 100% (see Figure 10c,d). In contrast, Cases 1 and 2 utilise a combination of energy sources. At the same time, while they comply with the RF limits, these cases require increased use of the diesel generator to offset periods of low wind and solar resource availability.
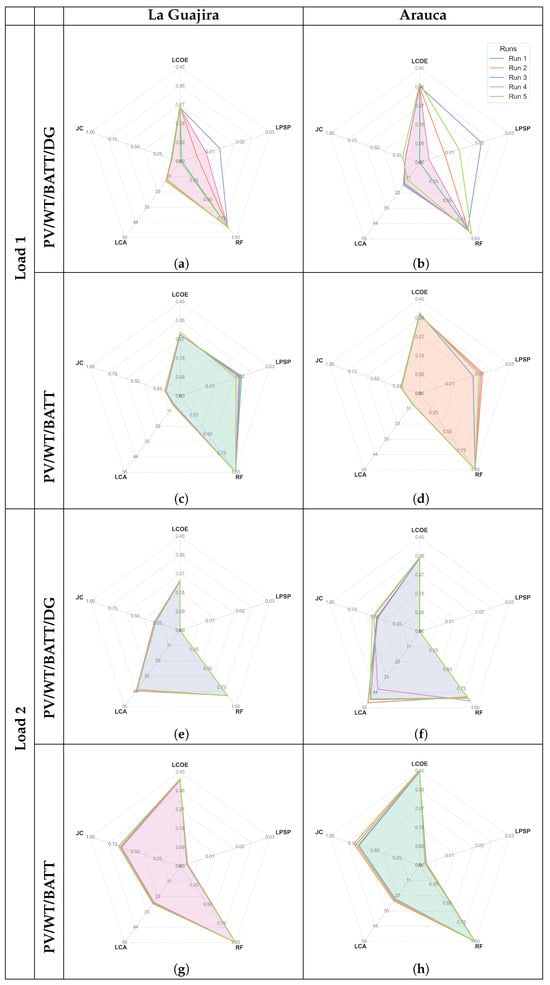
Figure 10.
Radar chart indicator for study cases: (a) Case 1. (b) Case 2. (c) Case 3. (d) Case 4. (e) Case 5. (f) Case 6. (g) Case 7. (h) Case 8.
For Load 2, the restrictions were met with slight percentage differences in the LPSP indicator with a maximum difference value of 0.25% for Case 7 and Case 8 (see Figure 10g,h). This indicates that the system is unable to meet the electrical demand of the load due to its consistently high consumption, even with large-capacity battery systems of 880 kWh for Case 7 and 1080 kWh for Case 8, resulting from prolonged periods of low solar and wind resources. This implies the need to implement an emergency backup system in situations where an industry cannot afford energy deficits. Regarding the RF indicator constraints, the solutions fully complied with the limits in all four cases, indicating that the algorithm aims to ensure compliance with the established regulations.
The results demonstrated, for each case study, that the solutions satisfy the objective function, achieving the lowest LCOE value, allowing controlled deviations in constraints that do not significantly compromise the results. However, electricity demand is a critical parameter, which, as a result, creates the need to evaluate the capacities of renewable and storage sources in relation to the energy resource of the area, to guarantee a continuous supply when required, in this case, for the industrial load that requires a high electricity supply permanently. Table 4 shows the best HRES configuration based on the lowest LCOE value among the five runs of the algorithm. Additionally, the LPSP, RF, JC, LCA, and TNPC factors are presented. A comparison is made between solutions with and without diesel generators for loads by region. This provides a perspective based on the designer’s metrics of interest, whose relevance stems from the needs of each location.
3.2.2. Resource and Configuration Assessment
The results shown in Figure 11 indicate that the best combinations of solutions for both resources, La Guajira and Arauca, for household load (Load 1), involve the use of the diesel system. For the La Guajira region, the most cost-effective solution is a combination of WT/PV/BATT/DG technologies, offering a lower cost of USD 166,855.38 compared to the WT/PV/BATT arrangement, which costs USD 190,815.43. The cost increase is primarily due to the use of batteries. Furthermore, although the system in Case 3 has a higher cost, it does not guarantee that the electricity supply will meet demand, with a 2.06% LPSP indicator, unlike Case 1, which has a lower LPSP of 0.87%. Moreover, the RF value for Case 1 remained within the defined minimum limit. However, based on the LCA indicator, it can be estimated that the use of fuel for the diesel generator proportionally increases carbon dioxide emissions, producing 14.24 -eq in one year, in contrast to the 6.02 -eq emitted by Case 3 (see Figure 12); that is, Case 3 avoids the release of almost 8 -eq, equivalent to a reduction of about 60% compared to Case 1. Regarding the JC value, Case 3 shows 0.156 jobs/year, which falls within the range of standard values for job creation in one year [50,53]. Finally, the increase in job creation compared to Case 1 is due to the rise in the number of solar panels, whose multiplier factor is greater than that of wind turbines.
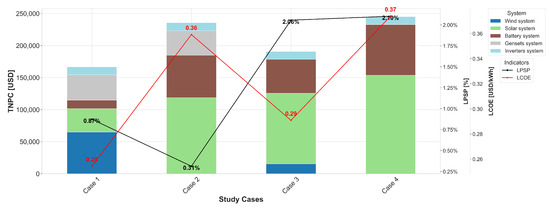
Figure 11.
Comparison among case studies: TNPC breakdown, applied constraints, and objective function for the household load profile.
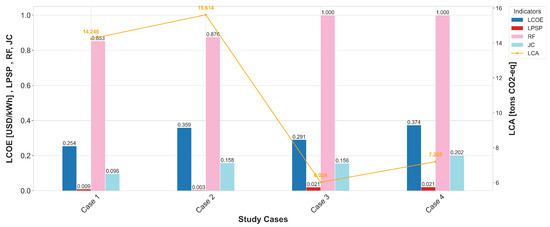
Figure 12.
Comparison of case studies based on economic, technical, social, and environmental indicators for household load profile.
In the Arauca region, the search algorithm ruled out the use of WT due to low wind resources, as shown in Figure 2a,b, where the average wind speed is about 2.5 m/s. As a result, only PV remains as a renewable generation source for the systems. The solution in Case 2, which involves PV/BATT/DG, is more economical in terms of LCOE than the solution in Case 4. However, the LCOE difference is not significant compared to the PV/BATT system; the notable difference lies in the LPSP indicator. For Case 2, LPSP is 0%, indicating that the entire electricity demand for the design year is met. In contrast, Case 4 has an LPSP of 2.10%, indicating a deficit due to prolonged low solar resources, despite backup support from a battery with a nominal capacity of 240 kWh. For the RF indicator, the value remained above the limit for Case 2 at 88%, compared to 100% for Case 4. Once again, a lower RF results in a higher system LCA. Case 2 obtained 15.34 -eq, compared to 7.24 -eq for Case 4, representing about a 50% reduction in carbon emissions. For the JC indicator, Case 4 yielded a value of 0.203 jobs/year, which can be considered a standard value for job creation (see Figure 12). Note that its increase over Case 2 is due to the larger number of solar panels.
Looking at Figure 13, for the industrial load profile (Load 2), the most cost-effective solutions that fully satisfy the operational constraints are those that incorporate diesel technology as a backup system. In the La Guajira region, the optimal configuration corresponds to the WT/PV/BATT/DG system (Case 5), with a TNPC of USD 467,272.13, compared to the alternative without a diesel generator, which amounts to USD 822,318.53. The latter increases significantly (approximately 75% more than the cost of Case 5) due to the increase in the nominal capacity of the battery system. In addition to the high cost, the solutions for Case 7 do not guarantee that they will fully meet the electrical demand of the load, presenting an LPSP of 0.24%; i.e., there are periods during the year when there is an electricity deficit due to high demand and a decrease in renewable energy production, not allowing the battery bank to be charged to its nominal power for discharge periods. Another relevant difference is that Case 7 excludes wind turbines from the microgrid design, despite the site recording average wind speeds of 7.86 m/s during that year. This behaviour is explained by the stochastic nature of the resource, which under these load conditions leads to higher LPSP values and non-compliance with the established constraints, demonstrating that the algorithm prioritises minimising cost while respecting predefined limits. For the RF indicator, Case 5 yielded 86% compared to 100% in Case 7. On the other hand, this is directly proportional to the amount of produced by each system, where the solution in Case 5 released 42.59 -eq, meanwhile 25.96 -eq in Case 7, for LCA values, which means a 39% reduction in production compared to the system with a diesel generator. For its part, the JC index increases considerably for the solutions in Case 7 due to the increased use of solar panels, with 408 more photovoltaic panels than in the HRES configuration for Case 5 (see Figure 14).
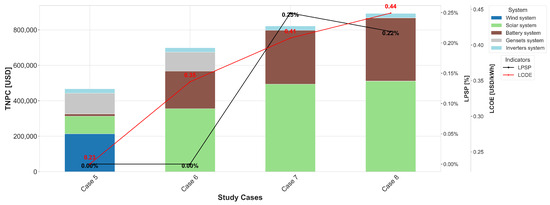
Figure 13.
Comparison among case studies: TNPC breakdown, applied constraints, and objective function for the industrial load profile.

Figure 14.
Comparison of case studies based on economic, technical, social, and environmental indicators for industrial load profile.
In the Arauca region, due to low wind energy production resulting from poor wind resources, the algorithm utilises only the photovoltaic panel system in the HRES configuration, which provides all the renewable energy. The solution obtained for Case 6, consisting of PV/BATT/DG, is more economical, with a TNPC value of USD 699,032.8, compared to Case 8, which does not consider a diesel system (PV/BATT), with a value of USD 892,538.91, a higher value due to the number of batteries used in this configuration (27 units) with an approximate nominal capacity of 1080 kWh (see Table 4). Even with the increase in batteries, the solution in Case 8 cannot meet 100% of the electricity demand. This is due to periods of low solar resource availability between June and July, resulting in an LPSP indicator value of 0.21%, compared to 0% for the configuration in Case 6. The best configuration for Case 6 is estimated to emit 48.76 -eq in one year, while Case 8 emits 24.17 -eq, representing nearly a 50% reduction in emissions but requiring a 27% increase in cost to achieve it (see Figure 14).
Based on the results shown in the comparison between demand profiles and resources by region, the LPSP and LCOE indicators reveal a strong dependence on weather variations and the electricity demand profile. For this analysis, cases with the same system configuration and electricity demand are compared. In the comparison between Case 1 and Case 2, the LCOE increases from 0.2543 to 0.3592 USD/kWh, reflecting higher investment costs due to lower wind and solar resources. However, the LPSP improves from 0.87% to 0.31%, suggesting that, although the generation cost increases, the system operates with greater reliability, attributable to the sizing of diesel backup and storage that compensate for resource limitations. For Case 3 vs. Case 4, the LCOE sensitivity is higher, increasing from 0.2908 to 0.3738 USD/kWh. The LPSP remains similar, confirming that weather conditions in Arauca directly affect the LCOE, indicating that more funds need to be invested to ensure similar technical performance. In contrast, in Case 5 compared to Case 6, the LCOE increases from 0.2328 to 0.3483 USD/kWh, once again demonstrating the dependence of costs on resource availability. The LPSP remains at 0%, indicating that the EMS guarantees complete reliability despite lower renewable production, albeit at a significantly higher cost, which increases the LCOE. Finally, Case 7 vs. Case 8 shows that to achieve similar technical performance in the Arauca region, investment needs to be increased due to meteorological uncertainty, resulting in more solar panels, longer autonomy, and a higher nominal power of the diesel generator. The comparison between regions and load types shows that configurations with diesel generation achieve lower LPSP and LCOE, providing greater reliability at the cost of increased emissions. In contrast, fully renewable configurations have higher costs and occasional supply deficits when resource availability is low. This reveals that reducing LPSP values generally results in a higher LCOE in most system configurations. While this cost reduction improves economic efficiency, it comes at the expense of the technical reliability of the system.
4. Conclusions
A single-objective optimal sizing approach using the PSO algorithm is proposed for a non-interconnected HRES microgrid that integrates solar photovoltaic panels, wind turbines, batteries, and diesel generators while considering technical, economic, environmental, and social criteria. Two microgrid configurations, PV/WT/BATT/DG and WT/PV/BATT, were examined under two different energy resource conditions and electricity demand profiles. The primary objective of the optimisation was to determine the levelized cost of energy and identify the most suitable system under various conditions, including meteorological data, electricity demand profiles, energy management, and installation and implementation costs.
The results showed that optimal solutions that respect the established constraints can be obtained with 120 iterations and 60 particles. This enables configurations to be tailored to the site’s specific needs, yielding solutions that meet electricity demand while being highly productive and environmentally friendly. This means obtaining an HRES configuration applicable to isolated or non-interconnected areas. It is essential to characterise not only the electricity demand and resource profiles, but also the management system that describes how the electricity service is provided to users, as this will determine the optimal configuration. Additionally, the diesel generation system remains a priority for non-interconnected networks due to its stability and ability to supply energy during periods of low production. This behaviour is explained by the stochastic nature of the resource, which under these load conditions leads to higher LPSP values and non-compliance with the established constraints, demonstrating that the algorithm prioritises minimising cost while respecting predefined limits. This is reflected in its expenses and in indicators of electricity supply loss, and it is evident that the most economically viable solutions continue to include it in their PV/WT/BATT/DG configurations. The diesel system is the primary contributor to CO2 emissions among the configurations evaluated, as it is used to supplement periods of low generation.
When comparing configurations, it is notable that those without diesel technology reduced CO2 emissions by up to 50% in one year of service, highlighting a significant environmental advantage. However, it should also be considered that diesel-based configurations consolidate technical and economic viability. In contrast, systems with a greater share of renewable technologies (wind turbines and photovoltaics) show improved job creation indicators compared to those relying on diesel backup. This trend occurs because solar photovoltaic and wind energy provide more stable employment over the project’s lifetime, while diesel-based employment fluctuates with fuel consumption and run hours. Finally, while batteries remain essential for system reliability, they contribute less directly to job creation since their impact is mainly limited to installation capacity and minimal maintenance needs.
Analysis of the different cases shows that the hybrid system configuration and demand level directly influence the microgrid’s technical, economic, environmental, and social indicators. Upon evaluation, solutions that include a diesel generator have lower energy costs with LCOE in the range of 0.23–0.35 USD/kWh and reduce the technical indicator (LPSP), making them more reliable alternatives in high-load contexts such as industrial loads in conditions of lower renewable resource availability, as is the case in the region of Arauca. However, this advantage is achieved at the expense of higher fuel consumption, increased environmental emissions, and lower local job creation. On the other hand, configurations that only consider renewable generation maximise the renewable fraction and promote job creation by increasing installed capacity, although with higher LCOEs of 0.29–0.44 USD/kWh in both regions, La Guajira and Arauca. For the different electricity demand profiles used—industrial and household—both cases showed deviations in the LPSP restriction, with up to 0.10% for case 4 in the region of Arauca, which had a household demand profile, and 0.24% for La Guajira, which had an industrial demand profile. The comparison between loads reveals that, as consumption increases, system costs (TNPC) and the required storage capacity also grow significantly, demonstrating that the most sustainable solutions are more sensitive to demand increase.
The comparison between the resources available in the Arauca and La Guajira regions confirms the influence of available resources on the feasibility of implementing a microgrid. In Arauca, where wind resources are lower, the presence of a diesel generator guarantees stability, while in La Guajira, with abundant wind resources, configurations that complement renewable technologies achieve better relative technical and economic performance, reducing the need for a generator. Overall, the results indicate that diesel generator solutions are more competitive in high-load scenarios with limited renewable resources. In contrast, configurations without generators excel in social contexts and regions with abundant resources, such as La Guajira. This must be evaluated according to the needs of the design to be implemented, since in the latter case, environmental and social benefits, especially in terms of job creation, become the main differentiating factor. However, diesel systems remain a highly viable technical and economic option, ensuring compliance with environmental indicators when balancing cost and sustainability is sought. Additionally, this method can serve as a support to provide an overview of solutions in response to the need for isolated microgrid projects, offering a starting point and a tool to promote energy transition and formulate electrification projects by generating solutions in a short period.
As part of future work, the EMS could be enhanced by incorporating Artificial Intelligence (AI), Machine Learning (ML), or optimisation algorithms to optimise energy flows and respond to changes in demand and resource availability, thereby improving energy efficiency and reducing operating costs. Similarly, AI can be used to generate electricity consumption patterns that can be projected and scaled over the project’s lifespan. In future analyses, it will also be essential to examine the effects of component degradation—particularly of solar PV modules, wind turbines, and batteries—on the overall performance and reliability of the system. This allows for a more sensitive analysis of microgrid technical performance and more accurate economic evaluations. In addition, future research should include comparisons with other optimisation algorithms to validate the effectiveness of the PSO-based approach used in this study. Finally, the research can also be geared towards the assessment of microgrids connected to the electricity grid, analysing combined electricity demand profiles from the industrial, residential, commercial, and electric vehicle charging sectors, as a contribution to the energy transition process.
Author Contributions
Conceptualization, J.L.T.-M. and C.N.-L.; Formal analysis, L.J.T., J.L.T.-M. and C.N.-L.; Funding acquisition, C.N.-L., L.M.C. and M.J.; Investigation, L.J.T., J.L.T.-M. and C.N.-L.; Methodology, J.L.T.-M. and C.N.-L.; Project administration, C.N.-L., L.M.C. and M.J.; Software, L.J.T. and J.L.T.-M.; Supervision, J.L.T.-M. and C.N.-L.; Validation, L.J.T. and J.L.T.-M.; Visualization, L.J.T. and J.L.T.-M.; Writing—original draft, L.J.T. and J.L.T.-M.; Writing—review & editing, C.N.-L., L.M.C. and M.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by Instituto Colombiano de Crédito Educativo y Estudios Técnicos en el Exterior (ICETEX)—under the ICETEX scholarship scheme “Programa de reciprocidad para extranjeros en Colombia”, as a beneficiary student under file number 1663. The authors acknowledge the Research Project “Strengthening National Capacities for the Utilization of Non-Conventional Energy Sources (FNCE) through the Development and Use of a Multicriteria Technological Platform that Supports a Just Energy Transition,” with code 1210-951-110321, funded by the Ministry of Science, Technology, and Innovation (Minciencias) and the National Hydrocarbons Agency (ANH) of the Government of Colombia through the call “951-2024 Call for Strengthening Geoscientific and Technological Knowledge of Non-Conventional Energy Sources and the Capture, Storage, and Use of CO2,” under contract No. 049-2025.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Flowcharts
Appendix A.1. Energy Management System
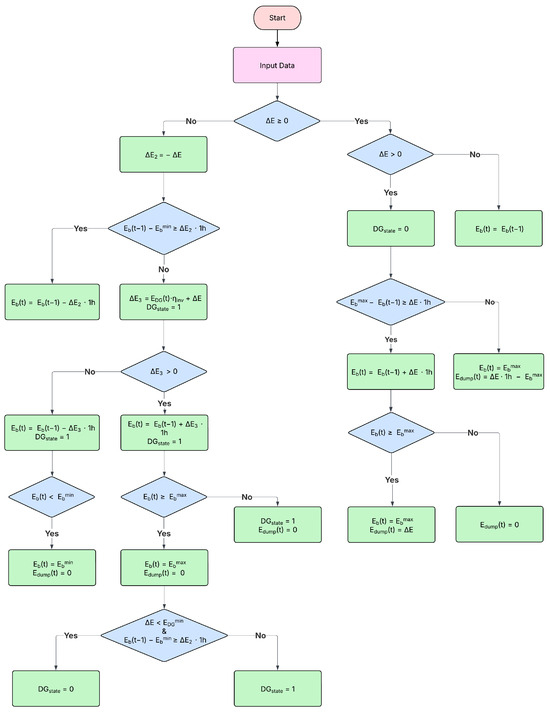
Figure A1.
Energy management system (EMS) strategy for HRES [28,36,44].
Appendix A.2. Particle Swarm Optimization

Figure A2.
PSO Algorithm flowchart [45].
References
- Malheiro, A.; Castro, P.M.; Lima, R.M.; Estanqueiro, A. Integrated sizing and scheduling of wind/PV/diesel/battery isolated systems. Renew. Energy 2015, 83, 646–657. [Google Scholar] [CrossRef]
- Saha, S.; Saini, G.; Mishra, S.; Chauhan, A.; Upadhyay, S. A comprehensive review of techno-socio-enviro-economic parameters, storage technologies, sizing methods and control management for integrated renewable energy system. Sustain. Energy Technol. Assessments 2022, 54, 102849. [Google Scholar] [CrossRef]
- Olabi, A.G.; Elsaid, K.; Obaideen, K.; Abdelkareem, M.A.; Rezk, H.; Wilberforce, T.; Maghrabie, H.M.; Sayed, E.T. Renewable energy systems: Comparisons, challenges and barriers, sustainability indicators, and the contribution to UN sustainable development goals. Int. J. Thermofluids 2023, 20, 100498. [Google Scholar] [CrossRef]
- Energy Institute. Statistical Review of World Energy, 73rd ed.; Energy Institute: London, UK, 2024. [Google Scholar]
- Masinga, F.; Madzivhandila, T. Loadshedding Impact on Food Spoilage: An Analysis of Household Experiences in South Africa. Afr. J. Gov. Dev. 2023, 12, 182–197. [Google Scholar] [CrossRef]
- Adetoro, S.A.; Olatomiwa, L.; Tsado, J.; Dauda, S.M. A comparative analysis of the performance of multiple meta-heuristic algorithms in sizing hybrid energy systems connected to an unreliable grid. E-Prime—Adv. Electr. Eng. Electron. Energy 2023, 4, 100140. [Google Scholar] [CrossRef]
- Ridha, H.M.; Hizam, H.; Mirjalili, S.; Othman, M.L.; Ya’acob, M.E.; Ahmadipour, M.; Ismaeel, N.Q. Multi-objective optimization and multi-criteria decision making aided by numerical method: Framework and a case study of Malaysia and South Africa. Energy Convers. Manag. 2022, 274, 116468. [Google Scholar] [CrossRef]
- Gao, K.; Wang, T.; Han, C.; Xie, J.; Ma, Y.; Peng, R. A Review of Optimization of Microgrid Operation. Energies 2021, 14, 2842. [Google Scholar] [CrossRef]
- Šimunović, J.; Radica, G.; Barbir, F. The effect of components capacity loss on the performance of a hybrid PV/wind/battery/hydrogen stand-alone energy system. Energy Convers. Manag. 2023, 291, 117314. [Google Scholar] [CrossRef]
- Coban, H.H. A multiscale approach to optimize off-grid hybrid renewable energy systems for sustainable rural electrification: Economic evaluation and design. Energy Strategy Rev. 2024, 55, 101527. [Google Scholar] [CrossRef]
- Chauhan, A.; Saini, R. Techno-economic feasibility study on Integrated Renewable Energy System for an isolated community of India. Renew. Sustain. Energy Rev. 2016, 59, 388–405. [Google Scholar] [CrossRef]
- Houssein, E.H.; Ibrahim, I.E.; Kharrich, M.; Kamel, S. An improved marine predators algorithm for the optimal design of hybrid renewable energy systems. Eng. Appl. Artif. Intell. 2022, 110, 104722. [Google Scholar] [CrossRef]
- Tariq, R.; Cetina-Quiñones, A.J.; Cardoso-Fernández, V.; Daniela-Abigail, H.L.; Soberanis, M.A.; Bassam, A.; Lille, M.V.D. Artificial intelligence assisted technoeconomic optimization scenarios of hybrid energy systems for water management of an isolated community. Sustain. Energy Technol. Assessments 2021, 48, 101561. [Google Scholar] [CrossRef]
- Khan, A.; Alghamdi, T.; Khan, Z.; Fatima, A.; Abid, S.; Khalid, A.; Javaid, N. Enhanced Evolutionary Sizing Algorithms for Optimal Sizing of a Stand-Alone PV-WT-Battery Hybrid System. Appl. Sci. 2019, 9, 5197. [Google Scholar] [CrossRef]
- Gonzalez, A.; Riba, J.R.; Esteban, B.; Rius, A. Environmental and cost optimal design of a biomass-Wind-PV electricity generation system. Renew. Energy 2018, 126, 420–430. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Li, J.; Liu, Y.; Yao, L.; Wang, Y.; Wang, C.; Pei, S.; Zhou, J. Short-term optimal operation of wind-solar-hydro hybrid system considering uncertainties. Energy Convers. Manag. 2020, 205, 112405. [Google Scholar] [CrossRef]
- Farhat, O.; Khaled, M.; Faraj, J.; Hachem, F.; Taher, R.; Castelain, C. A short recent review on hybrid energy systems: Critical analysis and recommendations. Energy Rep. 2022, 8, 792–802. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Sultan, H.M.; Kuznetsov, O.N. Optimal sizing of hybrid solar/wind/hydroelectric pumped storage energy system in Egypt based on different meta-heuristic techniques. Environ. Sci. Pollut. Res. 2019, 27, 32318–32340. [Google Scholar] [CrossRef]
- Huang, S.; Wang, L.; Xiong, L.; Zhou, Y.; Gao, F.; Huang, W.; Li, Y.; Guo, H.; Wang, F. Hierarchical Robustness Strategy Combining Model-Free Prediction and Fixed-Time Control for Islanded AC Microgrids. IEEE Trans. Smart Grid 2025, 16, 4380–4394. [Google Scholar] [CrossRef]
- Ibrahim, M.M. Energy management strategies of hybrid renewable energy systems: A review. Wind Eng. 2024, 48, 133–161. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Sawle, Y.; Lala, H. A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renew. Sustain. Energy Rev. 2023, 176, 113192. [Google Scholar] [CrossRef]
- Bamisile, O.; Cai, D.; Adun, H.; Dagbasi, M.; Ukwuoma, C.; Huang, Q.; Johnson, N.; Bamisile, O. Towards Renewables Development: Review of Optimization Techniques for Energy Storage and Hybrid Renewable Energy Systems. Heliyon 2024, 10, e37482. [Google Scholar] [CrossRef]
- Modu, B.; Abdullah, M.P.; Bukar, A.L.; Hamza, M.F. A systematic review of hybrid renewable energy systems with hydrogen storage: Sizing, optimization, and energy management strategy. Int. J. Hydrogen Energy 2023, 48, 38354–38373. [Google Scholar] [CrossRef]
- HOMER Energy. Available online: https://homerenergy.com/ (accessed on 4 May 2025).
- IHOGA (Instituto de Investigación en Recursos y Agrotecnología). Características. Available online: https://ihoga.unizar.es/caracteristicas/ (accessed on 4 May 2025).
- Natural Resources Canada. RETScreen Clean Energy Management Software; Technical Report; Government of Canada: Ottawa, ON, Canada, 2025. [Google Scholar]
- Hossain Lipu, M.; Rahman, M.A.; Islam, Z.U.; Rahman, T.; Rahman, M.S.; Meraj, S.T.; Hossain, M.Y.; Mansor, M. Review of energy storage integration in off-grid and grid-connected hybrid renewable energy systems: Structures, optimizations, challenges and opportunities. J. Energy Storage 2025, 122, 116629. [Google Scholar] [CrossRef]
- Belboul, Z.; Toual, B.; Kouzou, A.; Mokrani, L.; Bensalem, A.; Kennel, R.; Abdelrahem, M. Multiobjective Optimization of a Hybrid PV/Wind/Battery/Diesel Generator System Integrated in Microgrid: A Case Study in Djelfa, Algeria. Energies 2022, 15, 3579. [Google Scholar] [CrossRef]
- Atawi, I.E.; Abuelrub, A.; Al-Shetwi, A.Q.; Albalawi, O.H. Design of a wind-PV system integrated with a hybrid energy storage system considering economic and reliability assessment. J. Energy Storage 2024, 81, 110405. [Google Scholar] [CrossRef]
- Mohammed, O.H.; Amirat, Y.; Benbouzid, M. Particle Swarm Optimization Of a Hybrid Wind/Tidal/PV/Battery Energy System. Application To a Remote Area In Bretagne, France. Energy Procedia 2019, 162, 87–96. [Google Scholar] [CrossRef]
- Ghorbani, N.; Kasaeian, A.; Toopshekan, A.; Bahrami, L.; Maghami, A. Optimizing a hybrid wind-PV-battery system using GA-PSO and MOPSO for reducing cost and increasing reliability. Energy 2018, 154, 581–591. [Google Scholar] [CrossRef]
- Bilal, M.; Oladigbolu, J.O.; Mujeeb, A.; Al-Turki, Y.A. Cost-effective optimization of on-grid electric vehicle charging systems with integrated renewable energy and energy storage: An economic and reliability analysis. J. Energy Storage 2024, 100, 113170. [Google Scholar] [CrossRef]
- Torres-Madroñero, J.L.; Nieto-Londoño, C.; Sierra-Pérez, J. Hybrid energy systems sizing for the colombian context: A genetic algorithm and particle swarm optimization approach. Energies 2020, 13, 5648. [Google Scholar] [CrossRef]
- Torres-Madroñero, J.L.; Nieto-Londoño, C.; Arenas-Castiblanco, E.; Zapata-Benabithe, Z.; Jouhara, H. Multi-objective optimisation of hybrid renewable energy systems for Colombian non-interconnected zones. Therm. Sci. Eng. Prog. 2024, 55, 102927. [Google Scholar] [CrossRef]
- Salameh, Z. Chapter 1—Factors Promoting Renewable Energy Applications. In Renewable Energy System Design; Salameh, Z., Ed.; Academic Press: Boston, MA, USA, 2014; pp. 1–32. [Google Scholar] [CrossRef]
- Farh, H.M.; Al-Shamma’a, A.A.; Alaql, F.; Omotoso, H.O.; Alfraidi, W.; Mohamed, M.A. Optimization and uncertainty analysis of hybrid energy systems using Monte Carlo simulation integrated with genetic algorithm. Comput. Electr. Eng. 2024, 120, 109833. [Google Scholar] [CrossRef]
- Belfkira, R.; Zhang, L.; Barakat, G. Optimal sizing study of hybrid wind/PV/diesel power generation unit. Sol. Energy 2011, 85, 100–110. [Google Scholar] [CrossRef]
- Ma, X.; Deveci, M.; Yan, J.; Liu, Y. Optimal capacity configuration of wind-photovoltaic-storage hybrid system: A study based on multi-objective optimization and sparrow search algorithm. J. Energy Storage 2024, 85, 110983. [Google Scholar] [CrossRef]
- Teixeira, T.P.; Borges, C.L.T. Operation Strategies for Coordinating Battery Energy Storage with Wind Power Generation and Their Effects on System Reliability. J. Mod. Power Syst. Clean Energy 2021, 9, 190–198. [Google Scholar] [CrossRef]
- Bilal, M.; Bokoro, P.N.; Sharma, G. Hybrid optimization for sustainable design and sizing of standalone microgrids integrating renewable energy, diesel generators, and battery storage with environmental considerations. Results Eng. 2025, 25, 103764. [Google Scholar] [CrossRef]
- Jia, K.; Liu, C.; Li, S.; Jiang, D. Modeling and optimization of a hybrid renewable energy system integrated with gas turbine and energy storage. Energy Convers. Manag. 2023, 279, 116763. [Google Scholar] [CrossRef]
- LG Energy Solution. Battery Glossary—C-Rate (Current Rate). 2022. Available online: https://inside.lgensol.com/en/2022/09/battery-glossary-c-rate-current-rate/ (accessed on 6 May 2025).
- Omotoso, H.O.; Al-Shaalan, A.M.; Farh, H.M.H.; Al-Shamma’a, A.A. Techno-Economic Evaluation of Hybrid Energy Systems Using Artificial Ecosystem-Based Optimization with Demand Side Management. Electronics 2022, 11, 204. [Google Scholar] [CrossRef]
- Borhanazad, H.; Mekhilef, S.; Gounder Ganapathy, V.; Modiri-Delshad, M.; Mirtaheri, A. Optimization of micro-grid system using MOPSO. Renew. Energy 2014, 71, 295–306. [Google Scholar] [CrossRef]
- Mokhtara, C.; Negrou, B.; Settou, N.; Settou, B.; Samy, M.M. Design optimization of off-grid Hybrid Renewable Energy Systems considering the effects of building energy performance and climate change: Case study of Algeria. Energy 2021, 219. [Google Scholar] [CrossRef]
- Nkalo, U.K.; Inya, O.O.; Obi, P.I.; Bola, A.U.; Ewean, D.I. A modified multi-objective particle swarm optimization (M-MOPSO) for optimal sizing of a solar–wind–battery hybrid renewable energy system. Sol. Compass 2024, 12, 100082. [Google Scholar] [CrossRef]
- Ali, A.R.; Bartie, N.; Husmann, J.; Cerdas, F.; Schröder, D.; Herrmann, C. Simulation-based life cycle assessment of secondary materials from recycling of lithium-ion batteries. Resour. Conserv. Recycl. 2024, 202, 107384. [Google Scholar] [CrossRef]
- Mandal, S.; Das, B.K.; Hoque, N. Optimum sizing of a stand-alone hybrid energy system for rural electrification in Bangladesh. J. Clean. Prod. 2018, 200, 12–27. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory (NREL). Life Cycle Greenhouse Gas Emissions from Electricity Generation: Update; Fact Sheet, NREL/FS-6A50-80580; NREL: Golden, CO, USA, 2020. [CrossRef]
- Dufo-López, R.; Cristóbal-Monreal, I.R.; Yusta, J.M. Optimisation of PV-wind-diesel-battery stand-alone systems to minimise cost and maximise human development index and job creation. Renew. Energy 2016, 94, 280–293. [Google Scholar] [CrossRef]
- Shi, B.; Wu, W.; Yan, L. Size optimization of stand-alone PV/wind/diesel hybrid power generation systems. J. Taiwan Inst. Chem. Eng. 2017, 73, 93–101. [Google Scholar] [CrossRef]
- Wei, M.; Patadia, S.; Kammen, D.M. Putting Renewables and Energy Efficiency to Work: How Many Jobs Can the Clean Energy Industry Generate in the US? Technical Report RAEL Report 2010-01; University of California: Berkeley, CA, USA, 2010. [Google Scholar]
- Sawle, Y.; Gupta, S.; Bohre, A.K. Socio-techno-economic design of hybrid renewable energy system using optimization techniques. Renew. Energy 2018, 119, 459–472. [Google Scholar] [CrossRef]
- Cameron, L.; van der Zwaan, B. Employment factors for wind and solar energy technologies: A literature review. Renew. Sustain. Energy Rev. 2015, 45, 160–172. [Google Scholar] [CrossRef]
- Roy, D.; Zhu, S.; Wang, R.; Mondal, P.; Ling-Chin, J.; Roskilly, A.P. Techno-economic and environmental analyses of hybrid renewable energy systems for a remote location employing machine learning models. Appl. Energy 2024, 361, 122884. [Google Scholar] [CrossRef]
- Kharrich, M.; Kamel, S.; Abdeen, M.; Mohammed, O.H.; Akherraz, M.; Khurshaid, T.; Rhee, S.B. Developed Approach Based on Equilibrium Optimizer for Optimal Design of Hybrid PV/Wind/Diesel/Battery Microgrid in Dakhla, Morocco. IEEE Access 2021, 9, 13655–13670. [Google Scholar] [CrossRef]
- Anand, P.; Rizwan, M.; Bath, S.K. Sizing of renewable energy based hybrid system for rural electrification using grey wolf optimisation approach. IET Energy Syst. Integr. 2019, 1, 227–238. [Google Scholar] [CrossRef]
- Marocco, P.; Ferrero, D.; Lanzini, A.; Santarelli, M. The role of hydrogen in the optimal design of off-grid hybrid renewable energy systems. J. Energy Storage 2022, 46, 103893. [Google Scholar] [CrossRef]
- NASA. POWER Data Access Viewer. Available online: https://power.larc.nasa.gov/data-access-viewer/ (accessed on 15 May 2025).
- Unidad de Planeación Minero Energética (UPME); Instituto de Hidrología, Meteorología y Estudios Ambientales (IDEAM). Atlas de Viento y Energía Eólica de Colombia, 1st ed.; Ministerio de Minas y Energía: Bogotá, Colombia, 2006. [Google Scholar]
- Unidad de Planeación Minero Energética (UPME); Instituto de Hidrología, Meteorología y Estudios Ambientales (IDEAM). Atlas de Radiación Solar de Colombia, 2nd ed.; UPME & IDEAM: Bogotá, Colombia, 2005. [Google Scholar]
- Meier, H.; Fünfgeld, C.; Adam, T.; Schieferdecker, B. Repräsentative VDEW-Lastprofile; Technical Report; Materialien M-32/99; Verband der Elektrizitätswirtschaft (VDEW), BTU Cottbus: Frankfurt am Main, Germany, 1999. [Google Scholar]
- Group Demandlib: Load Profile Generation Library; Version 0.2.2, MIT License. 2025. Available online: https://demandlib.readthedocs.io/en/latest/ (accessed on 30 September 2025).
- Instituto de Planificación y Promoción de Soluciones Energéticas para las Zonas No Interconectadas (IPSE). Informe Mensual de Telemetría: Enero 1–31 de 2024; Informe técnico; Fecha del informe: 20 de febrero de 2024; Centro Nacional de Monitoreo, IPSE: Bogotá, Colombia, 2024. [Google Scholar]
- Clerc, M. Particle Swarm Optimization; First published in France in 2005 by Hermes Science/Lavoisier under the title L’Optimisation par Essaims Particulaires; ISTE Ltd: London, UK; Newport Beach, CA, USA, 2006. [Google Scholar]
- Mohammadi, A.; Sheikholeslam, F. Intelligent optimization: Literature review and state-of-the-art algorithms (1965–2022). Eng. Appl. Artif. Intell. 2023, 126, 106959. [Google Scholar] [CrossRef]
- Rao, S.S. Engineering Optimization: Theory and Practice, 4th ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Vadi, S.; Bildirici, M.; Kaplan, O. Performance Comparison of Metaheuristic and Hybrid Algorithms Used for Energy Cost Minimization in a Solar–Wind–Battery Microgrid. Sustainability 2025, 17, 8849. [Google Scholar] [CrossRef]
- Prajapati, R.; Dubey, O.P. Analysing the Impact of Penalty Constant on Penalty Function Through Partice Swarm Optimiz ation. Int. J. Stud. Res. Technol. Manag. 2018, 6, 01–06. [Google Scholar] [CrossRef]
- García-Vera, Y.E.; Dufo-López, R.; Bernal-Agustín, J.L. Techno-Economic Feasibility Analysis through Optimization Strategies and Load Shifting in Isolated Hybrid Microgrids with Renewable Energy for the Non-Interconnected Zone (NIZ) of Colombia. Energies 2020, 13, 6146. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).