Investigations on Output Impedance Measurement of Digitally Controlled Power Converters with Wide Bandwidth Signals †
Abstract
1. Introduction
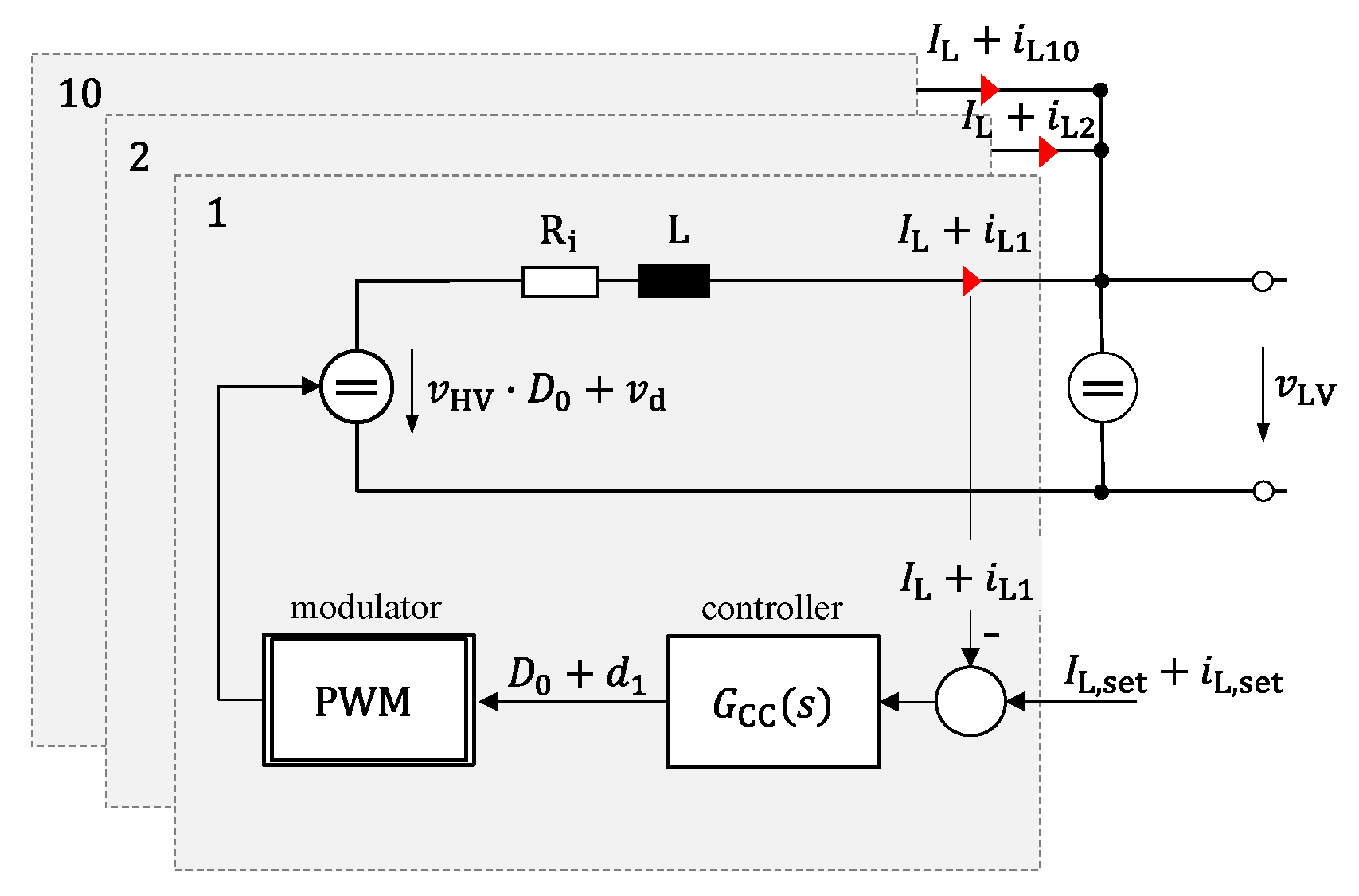
2. Digitally Controlled Power Converters
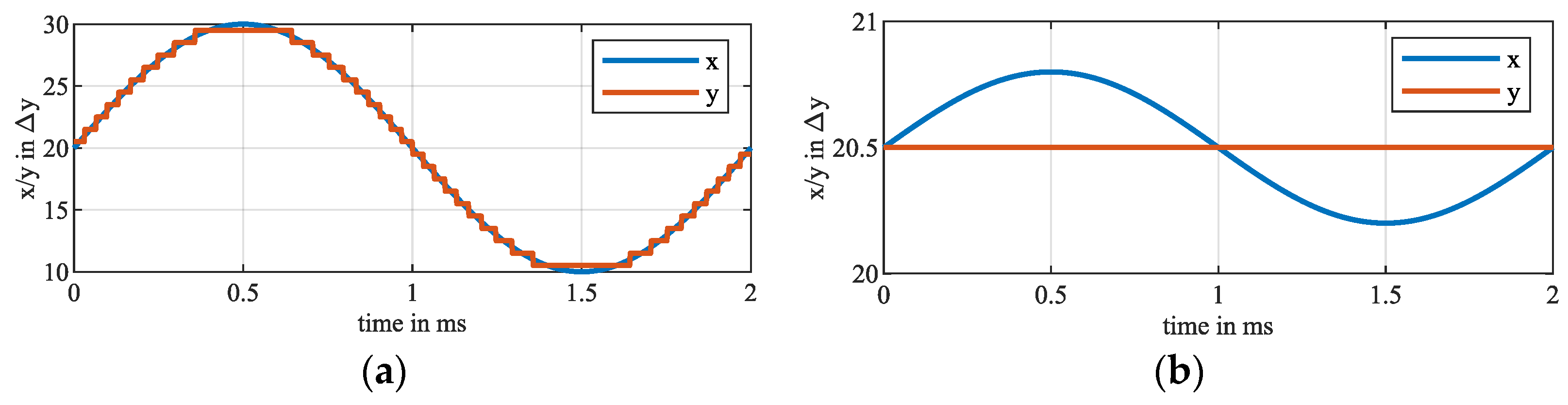
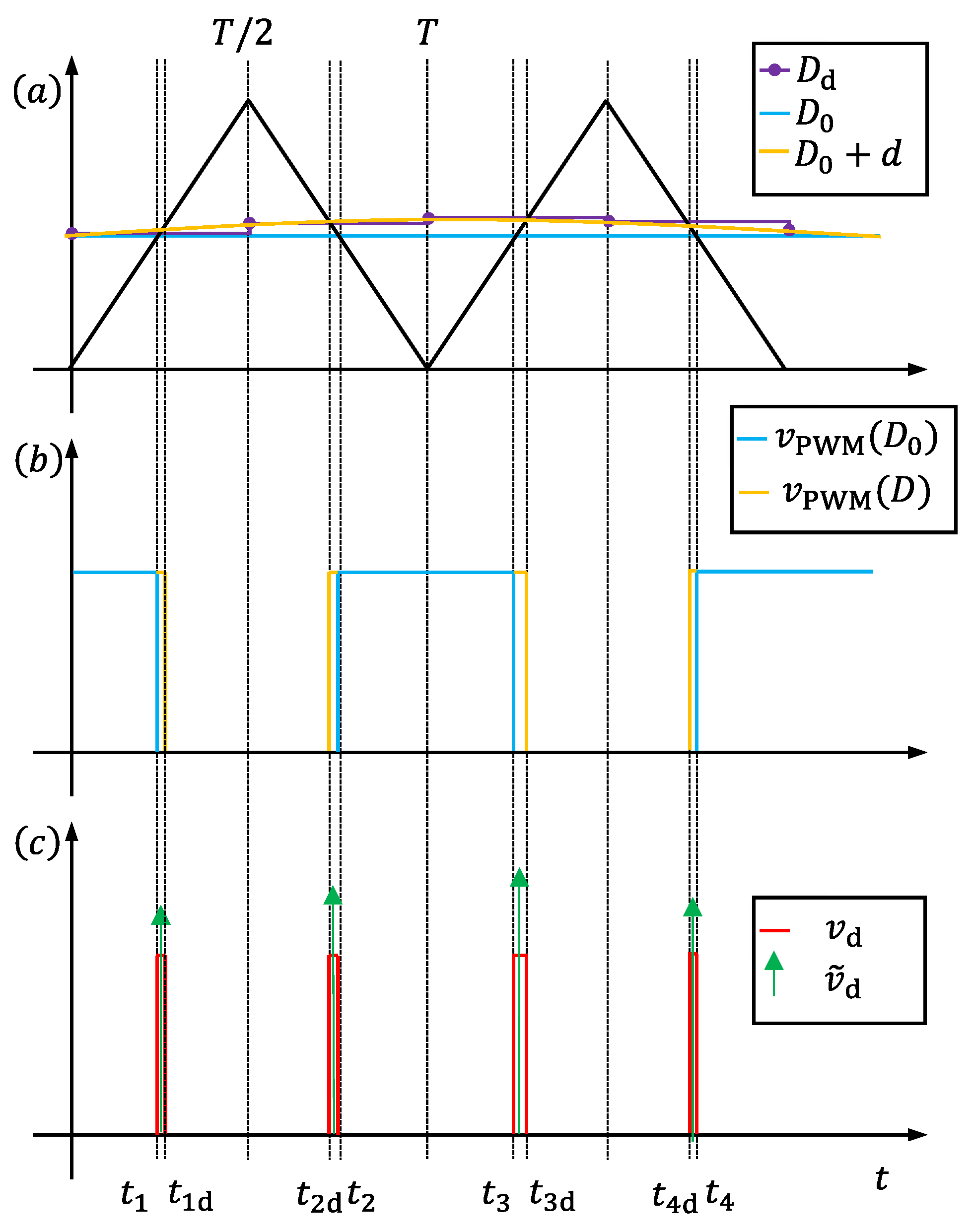
2.1. Value Discretization
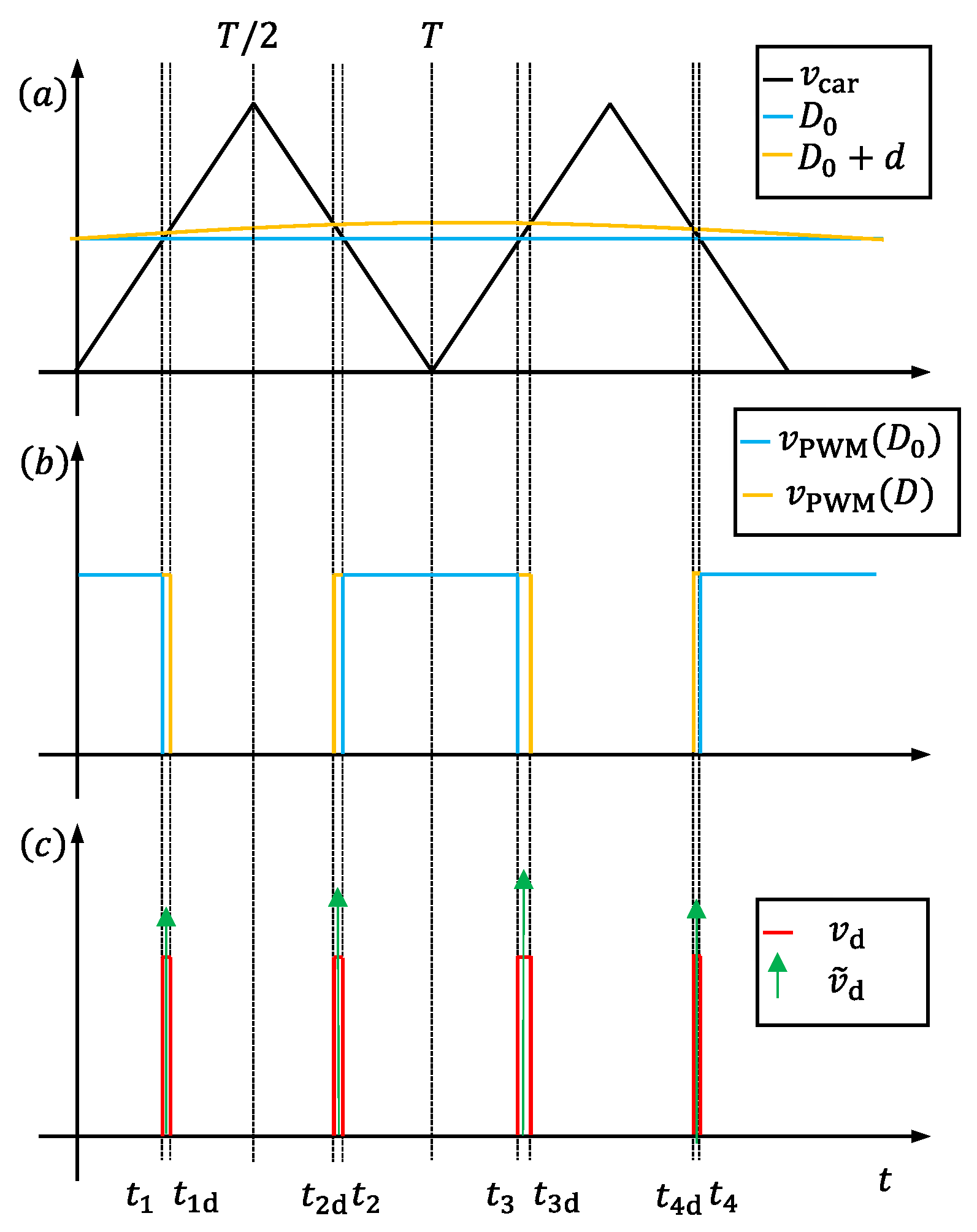
2.2. Time Discretization
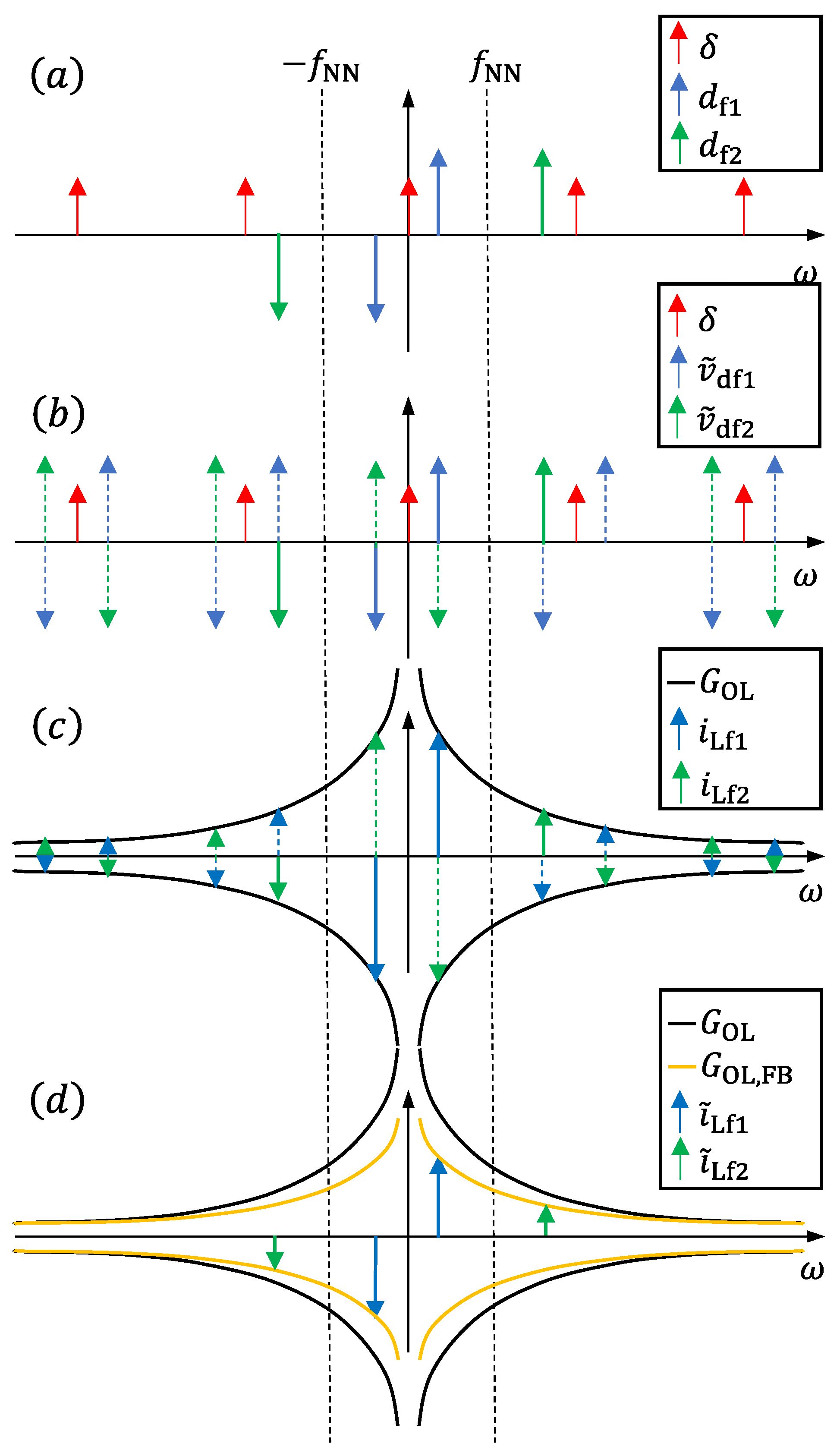
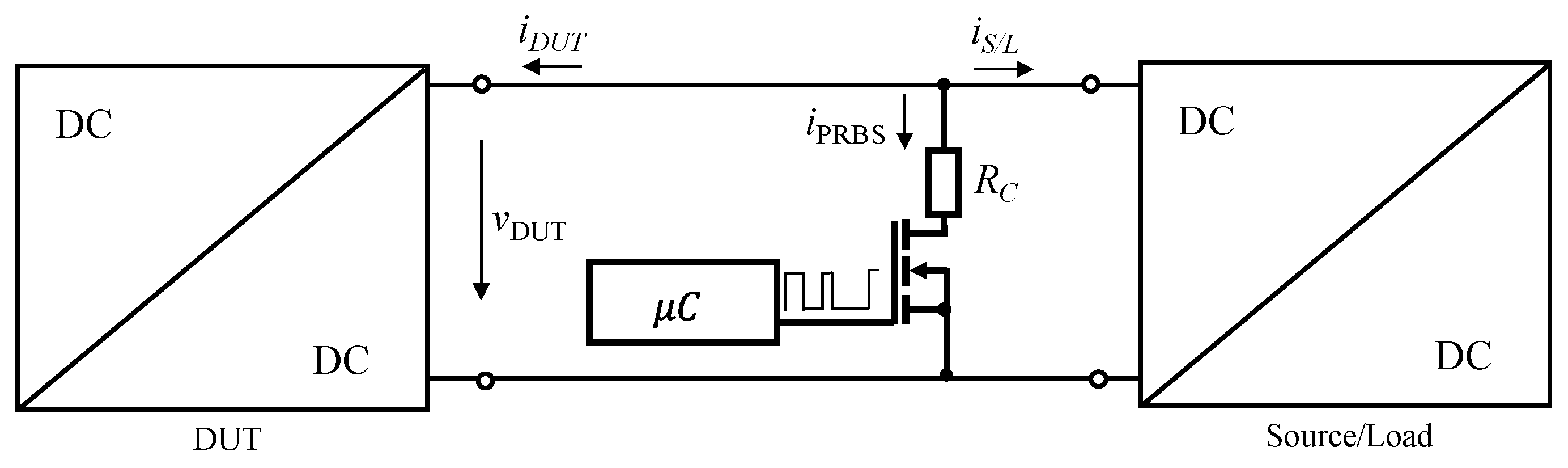
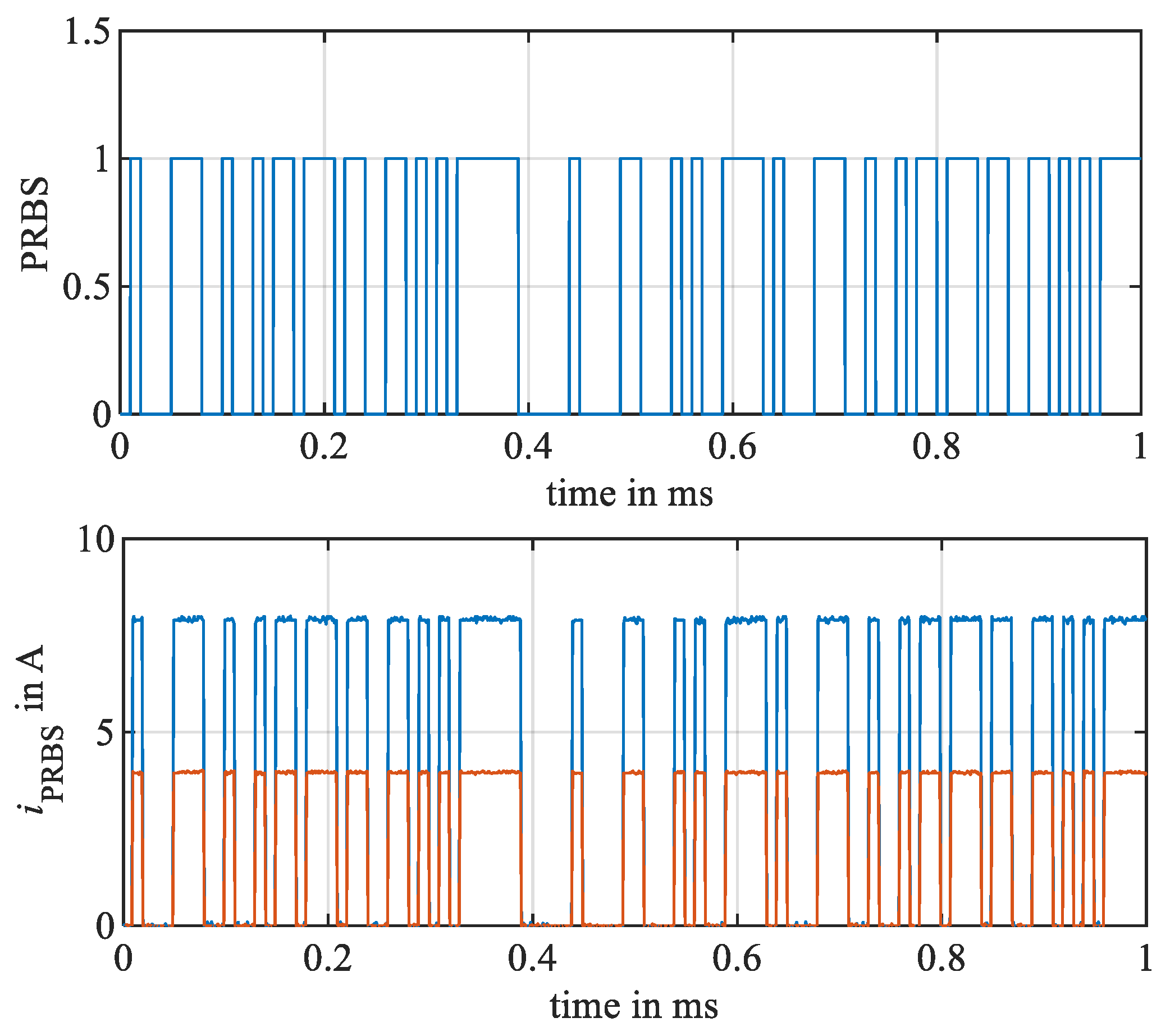
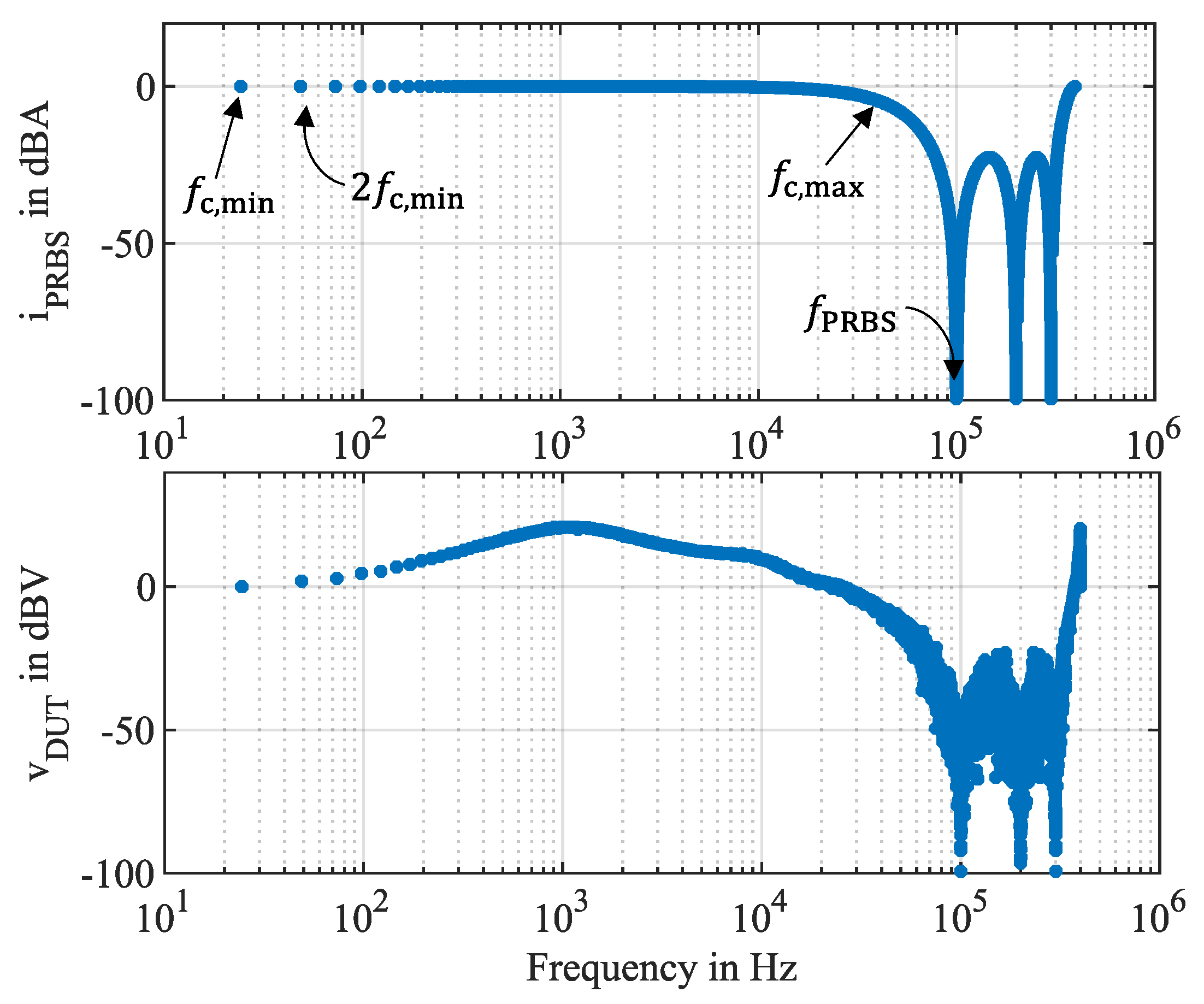
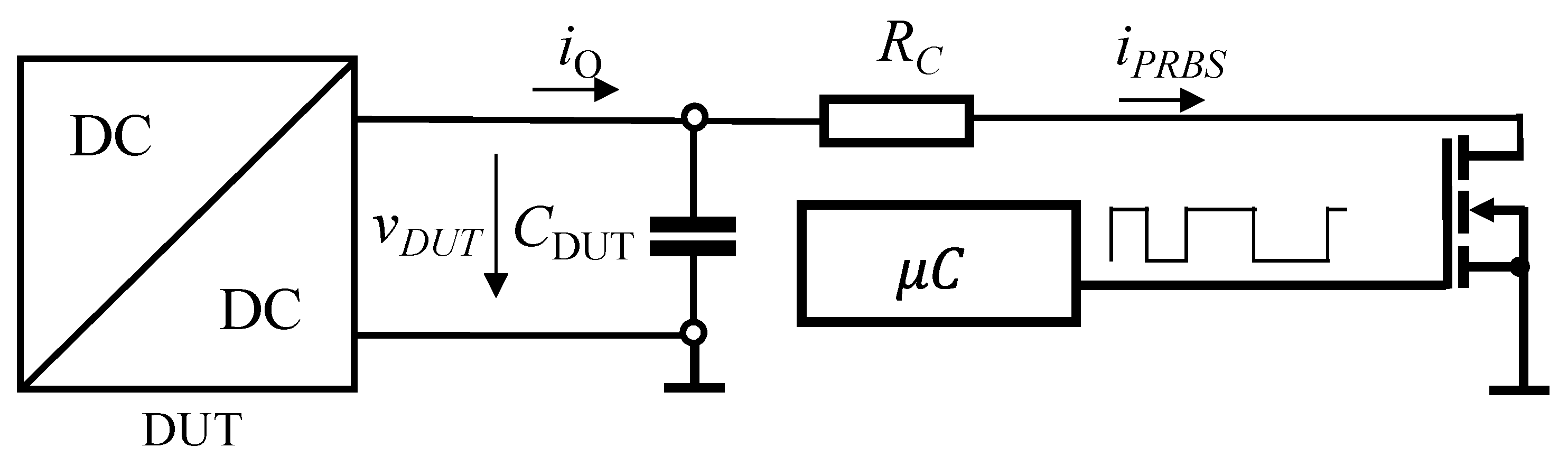
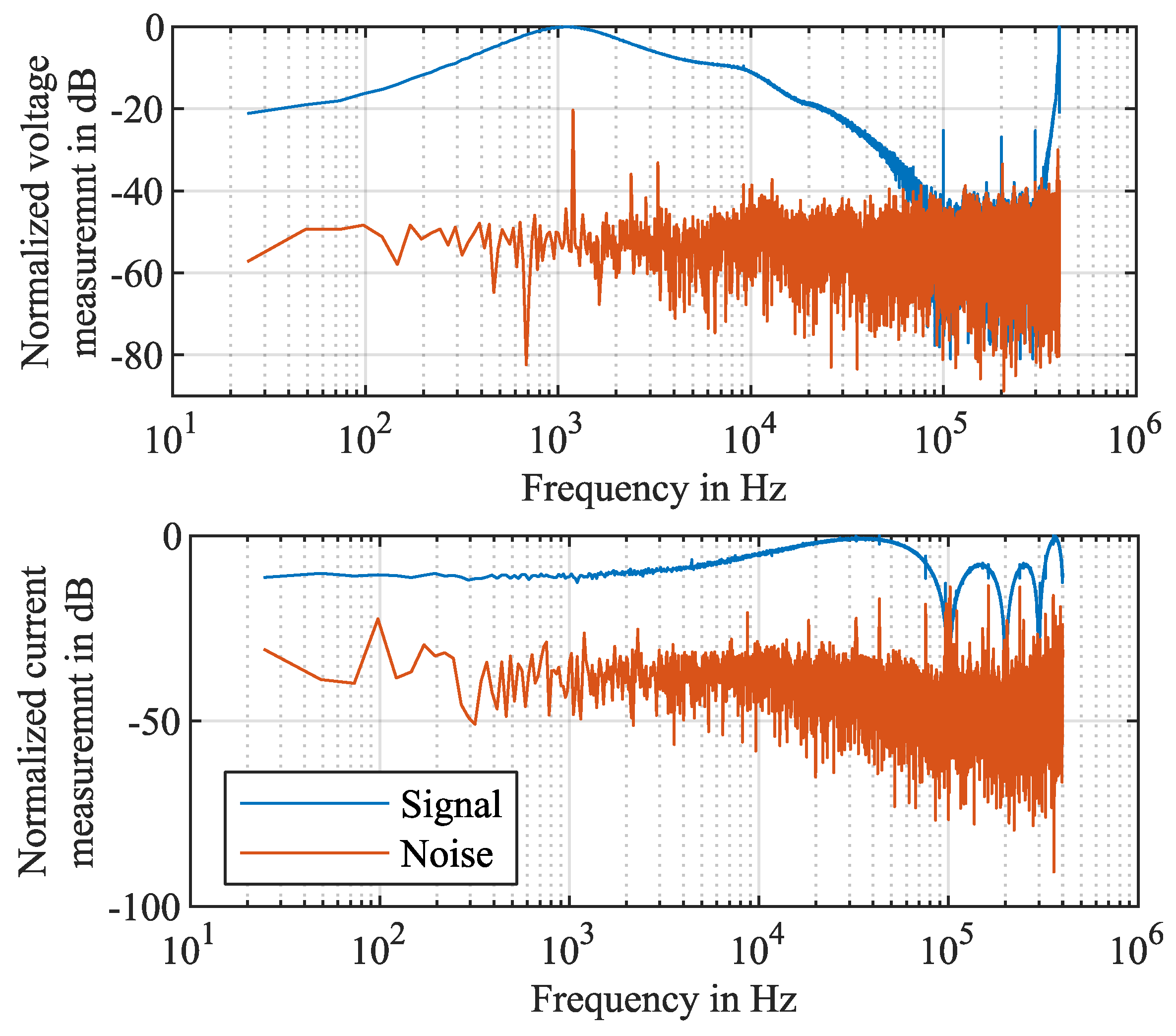
3. Wide Bandwidth Measurement System
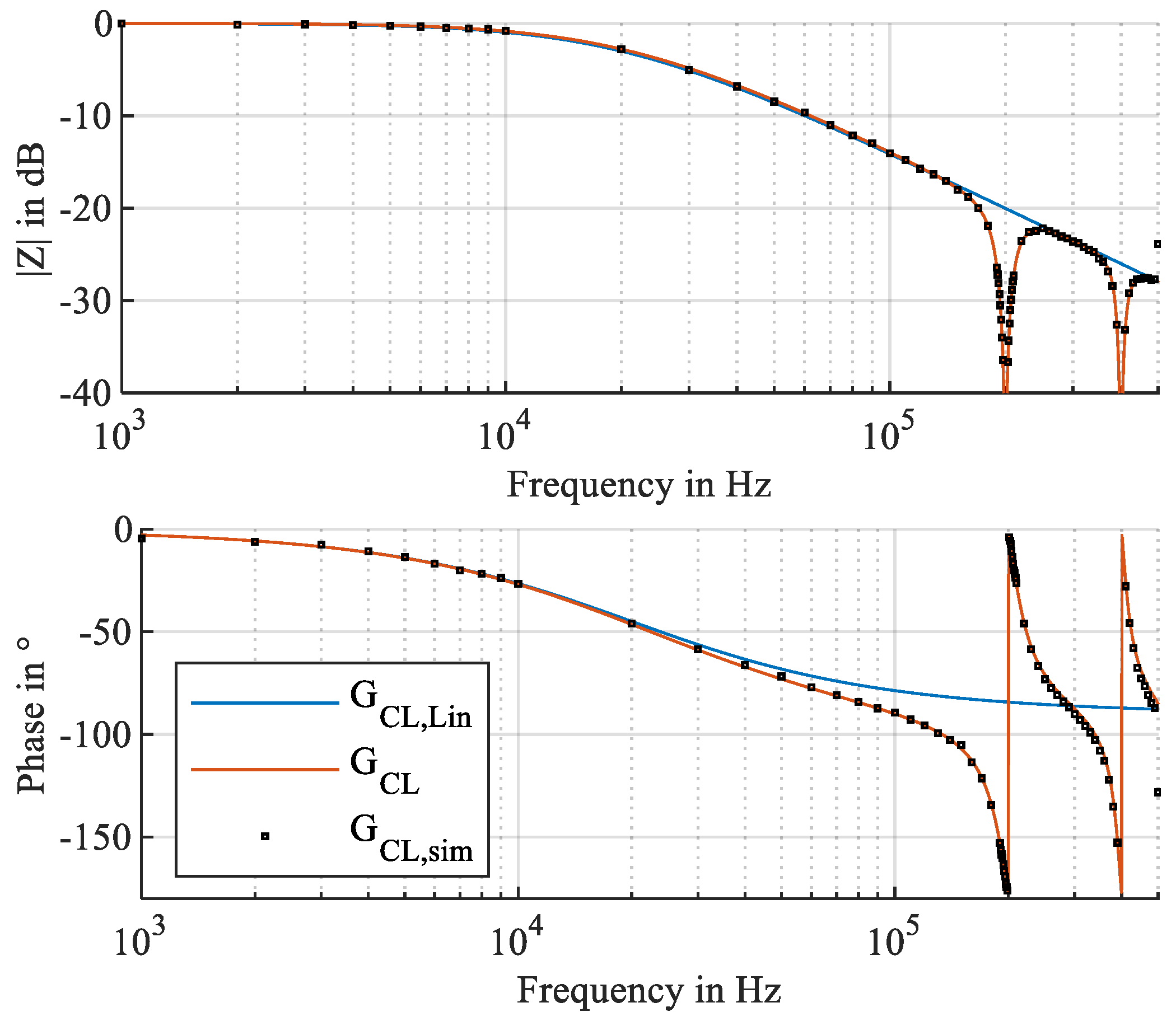
4. Simulation Results
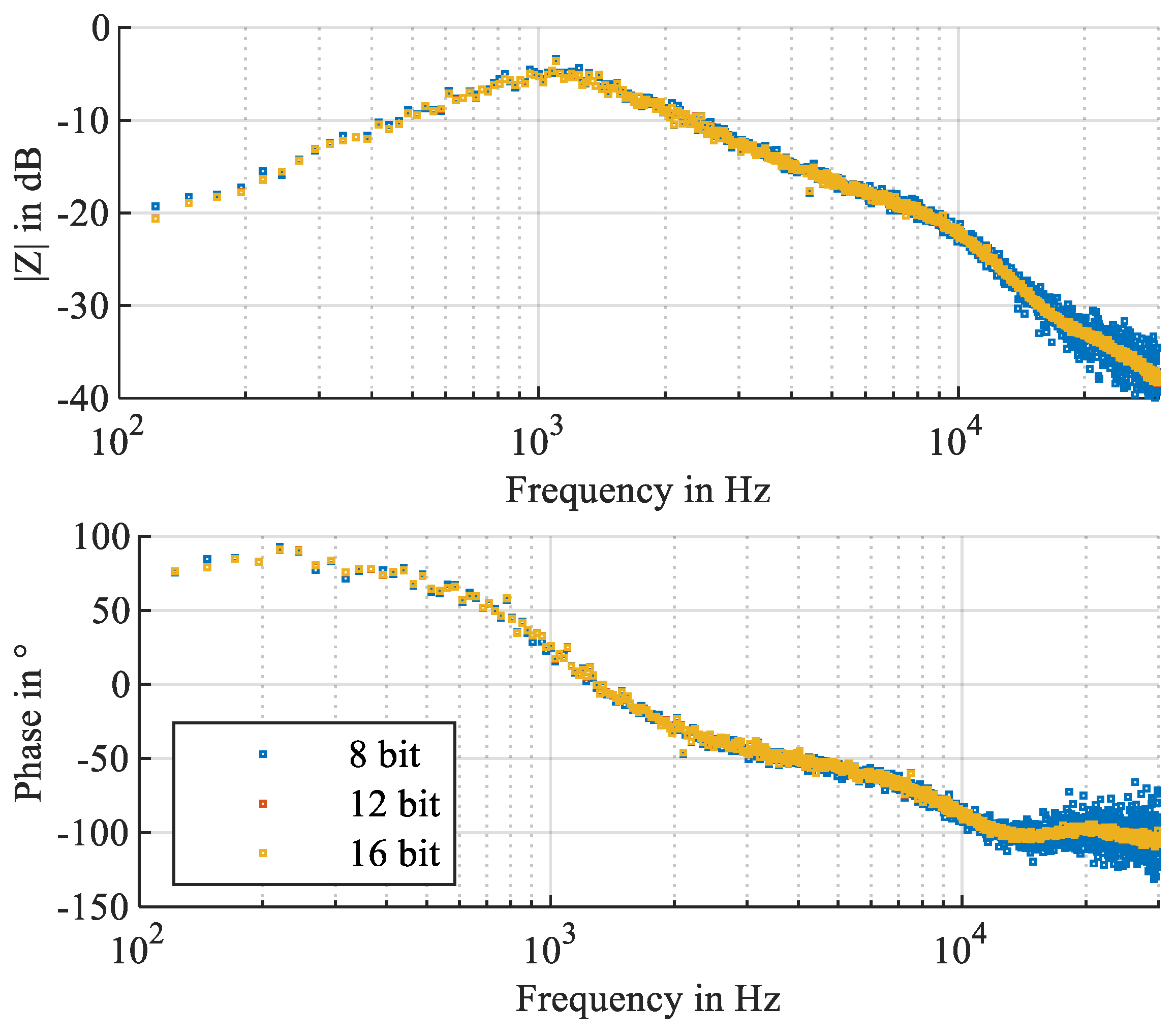
4.1. Value Discretization
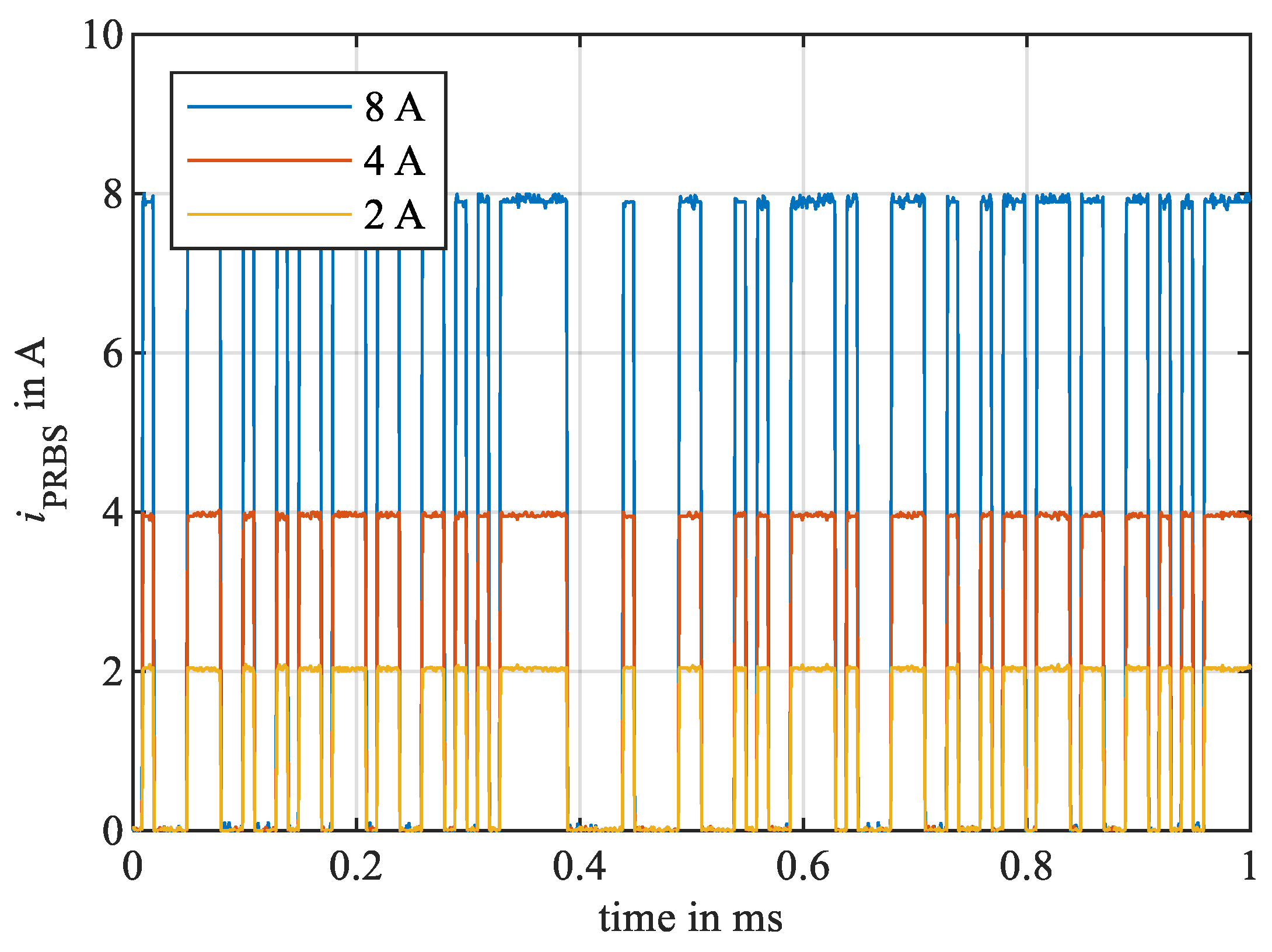
4.2. Time Discretization
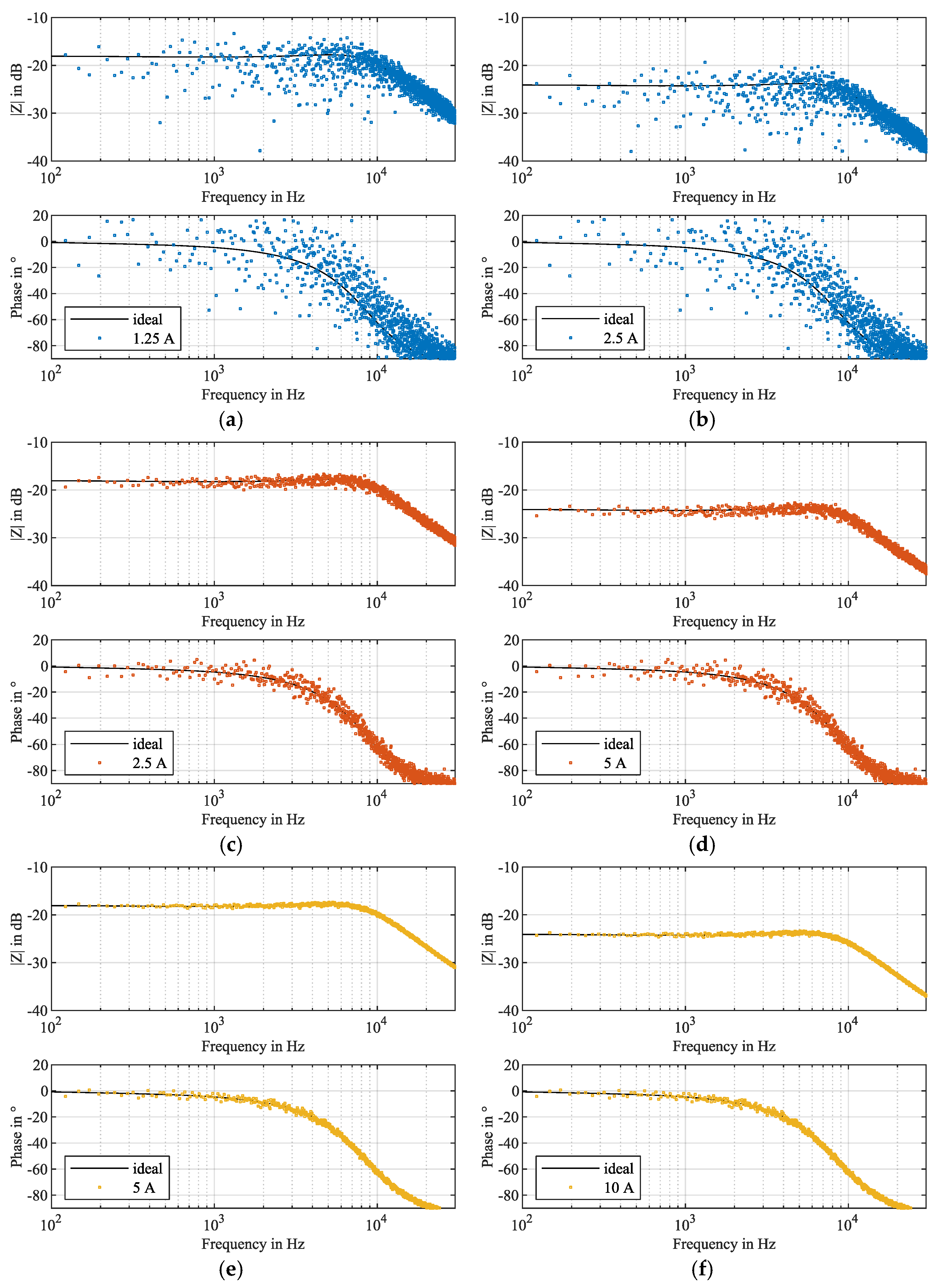
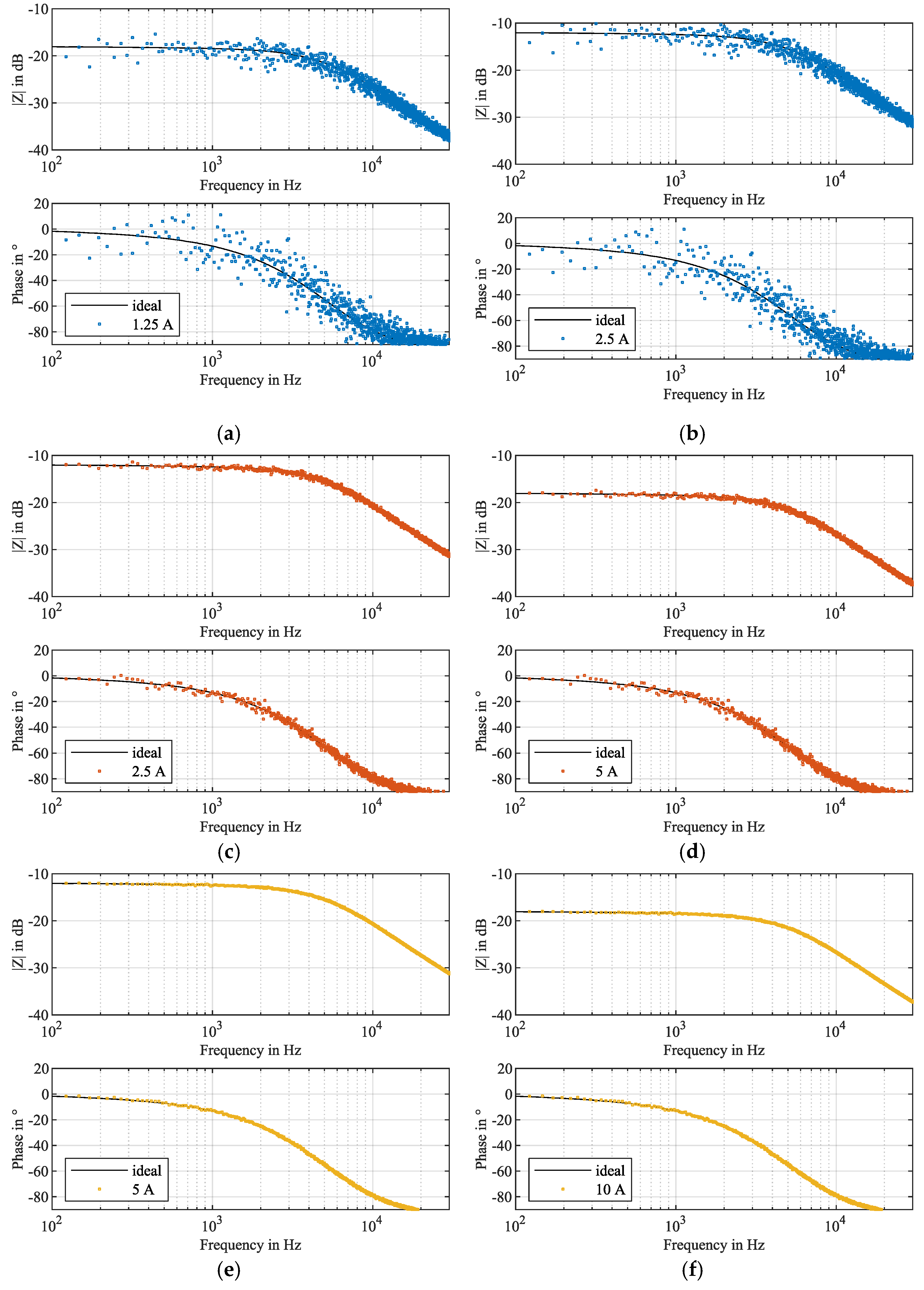
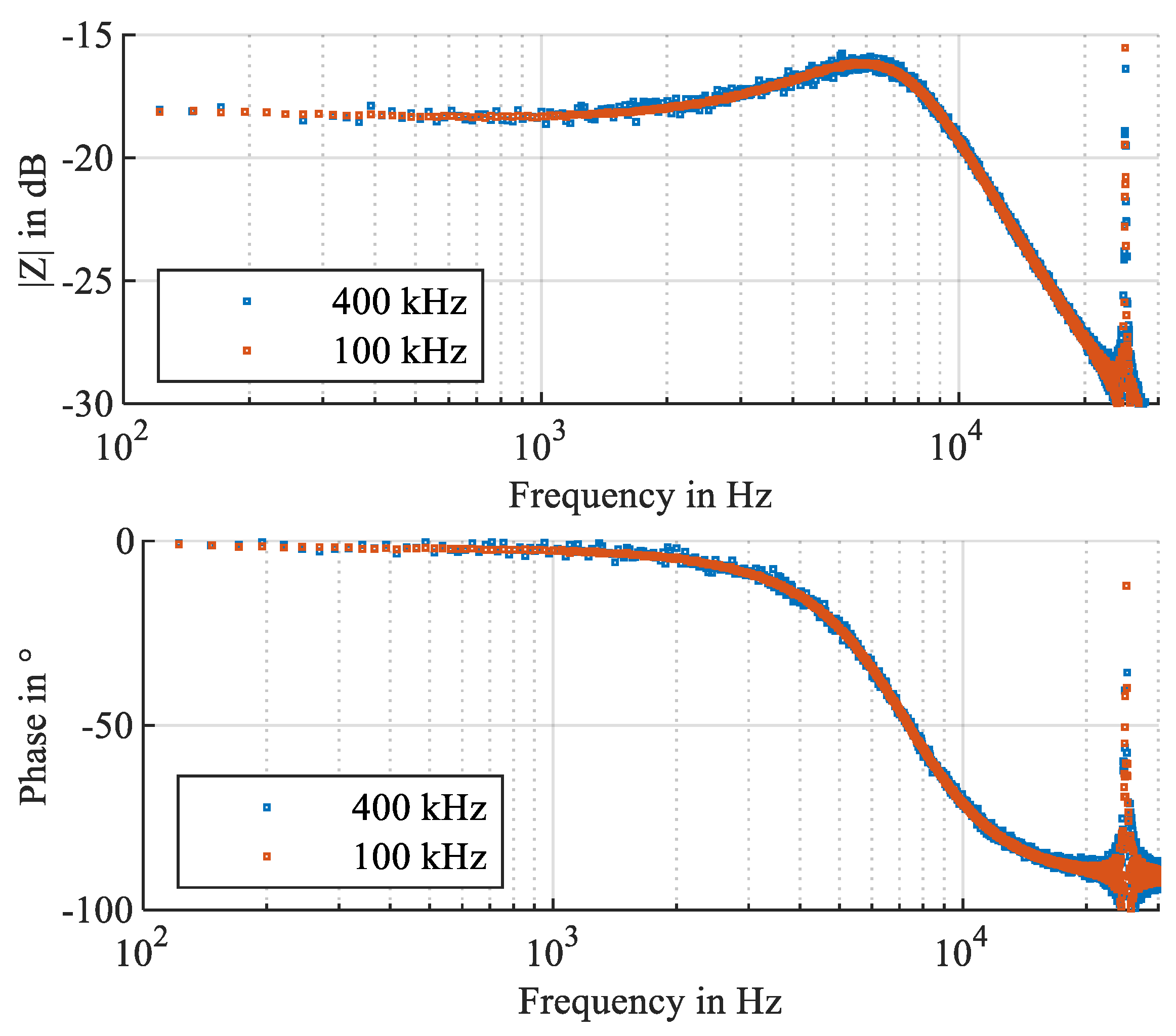
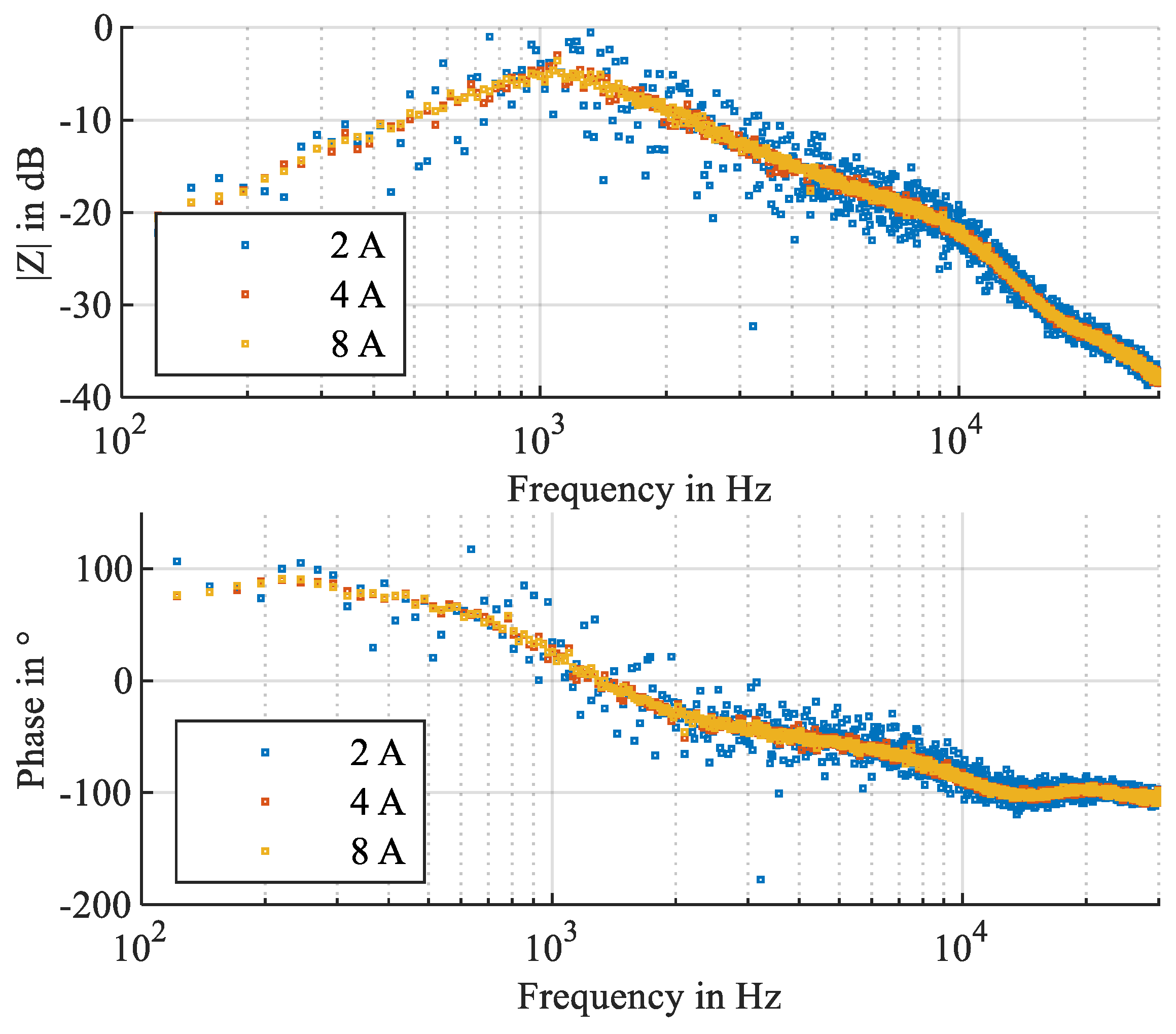
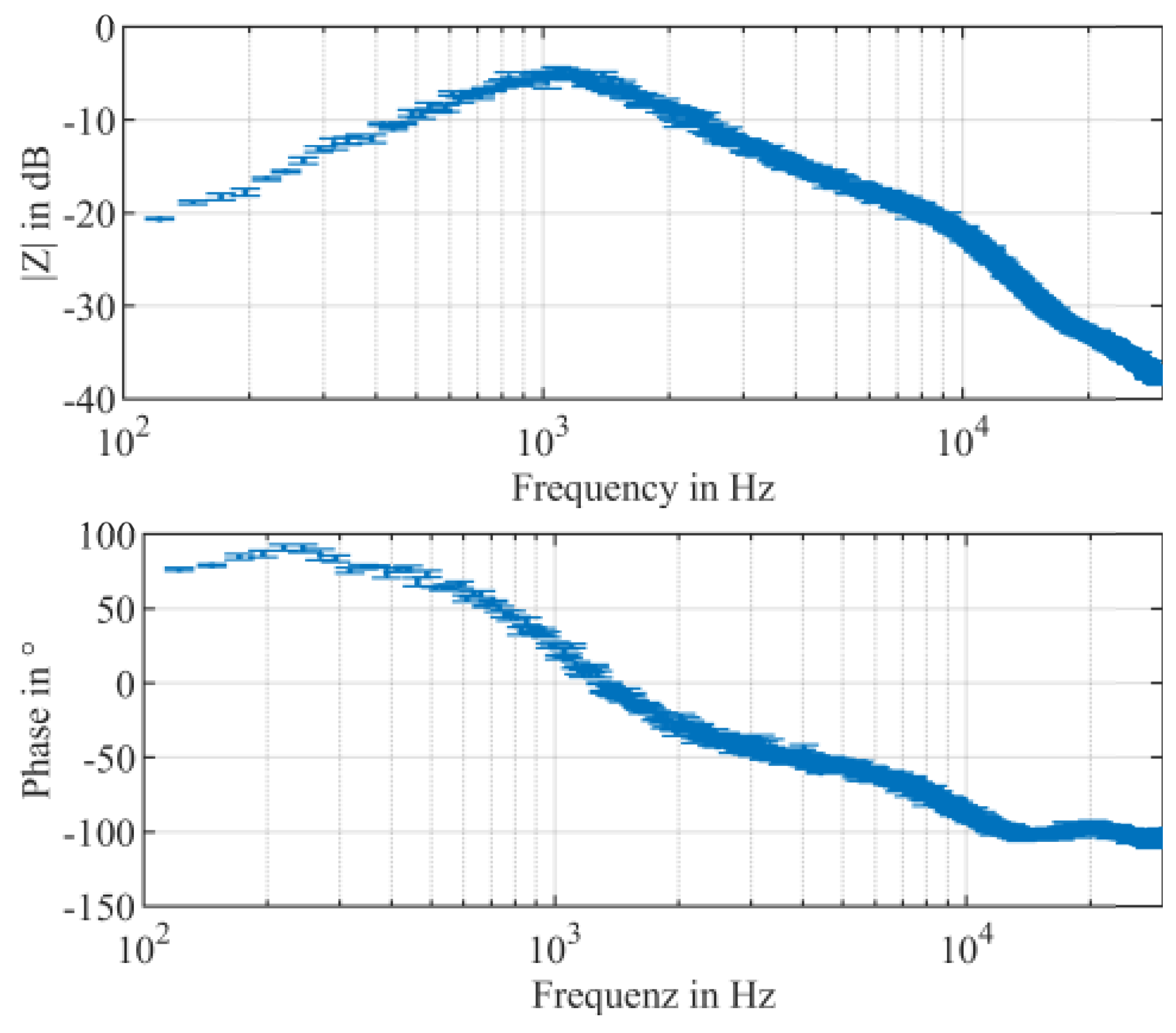
5. Measurement Results
6. Discussion on Measurement Procedure
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dragicevic, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids—Part II: A Review of Power Architectures, Applications, and Standardization Issues. IEEE Trans. Power Electron. 2016, 31, 3528–3549. [Google Scholar] [CrossRef]
- Boroyevich, D.; Cvetkovic, I.; Dong, D.; Burgos, R.; Wang, F.; Lee, F. Future electronic power distribution systems a contemplative view. In Proceedings of the 2010 12th International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 20–22 May 2010; pp. 1369–1380. [Google Scholar]
- Hou, N.; Ding, L.; Gunawardena, P.; Wang, T.; Zhang, Y.; Li, Y.W. A Partial Power Processing Structure Embedding Renewable Energy Source and Energy Storage Element for Islanded DC Microgrid. IEEE Trans. Power Electron. 2023, 38, 4027–4039. [Google Scholar] [CrossRef]
- Santos, P.; Fonte, P.; Luis, R. Improvement of DC Microgrid Voltage Regulation Based on Bidirectional Intelligent Charging Systems. In Proceedings of the 2018 15th International Conference on the European Energy Market (EEM), Lodz, Poland, 27–29 June 2018; pp. 1–6. [Google Scholar]
- Schmidt, H.; Gutierrez, A.J.C.; Romani, A.; Crescentini, M.; Borger, K.; Chacon, R.; Forster, A.; Schwanninger, R.; Eberle, T.; März, M. The PROGRESSUS project—Highly efficient and trustworthy electronics, components and systems for the next generation energy supply infrastructure. In Proceedings of the 2023 AEIT International Conference on Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE), Modena, Italy, 17–19 July 2023; pp. 1–6. [Google Scholar]
- Schwanninger, R.; Friedrich, J.; Lavery, M.; Maerz, M. Investigation of a Decentralized Energy Management System for Undersupplied EV Charging Parks. In Proceedings of the 2024 IEEE Sixth International Conference on DC Microgrids (ICDCM), Columbia, SC, USA, 5–8 August 2024; pp. 1–7. [Google Scholar]
- Barth, M.; Gutwald, B.; Russwurm, E.; Lavery, M.; Schwanninger, R.; März, M.; Franke, J. Holistic Concept for Simulation-based Planning and Design of Hybrid AC/DC Energy Grids for Production Systems. SNE Simul. Notes Eur. 2024, 34, 61–70. [Google Scholar] [CrossRef]
- Schwanninger, R.; Schmitt, D.; Lavery, M.; Maerz, M. Output Impedance Measurement of Digitally Controlled Power Converters in LVDC-Grids. In Proceedings of the 2024 IEEE Sixth International Conference on DC Microgrids (ICDCM), Columbia, SC, USA, 5–8 August 2024. [Google Scholar]
- Enslin, J.; Heskes, P. Harmonic Interaction Between a Large Number of Distributed Power Inverters and the Distribution Network. IEEE Trans. Power Electron. 2004, 19, 1586–1593. [Google Scholar] [CrossRef]
- Dragicevic, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids—Part II: A Review of Power Architectures, Applications, and Standardization Issues. In Proceedings of the 2009 IEEE Electric Ship Technologies Symposium, Baltimore, MD, USA, 4 August 2009; pp. 428–432. [Google Scholar]
- Yang, X.; Pohlenz, S.; Schwanninger, R.; Schleippmann, N.; Wunder, B.; März, M. Modelling and Design of a Droop-Based Cascaded Controller for LLC Resonant Converter. In Proceedings of the 2023 IEEE Fifth International Conference on DC Microgrids (ICDCM), Auckland, New Zealand, 15–17 November 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Lavery, M.; Schwanninger, R.; März, M. Use-Case-Dependent Modeling Approach for Computer Simulation of Hybrid AC-DC Grids. In Proceedings of the 2023 IEEE Fifth International Conference on DC Microgrids (ICDCM), Auckland, New Zealand, 15–17 November 2023; pp. 1–6. [Google Scholar]
- Ott, L.; Han, Y.; Wunder, B.; Maerz, M.; Bodensteiner, F. Evaluation of DC-DC-Converter Impedance Passivity Using Pseudo-Random Test Signals. In Proceedings of the 2018 International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management (PCIM), Nuremberg, Germany, 5–7 June 2018. [Google Scholar]
- Zhang, X.; Ruan, X.; Zhong, Q.-C. Improving the Stability of Cascaded DC/DC Converter Systems via Shaping the Input Impedance of the Load Converter With a Parallel or Series Virtual Impedance. IEEE Trans. Ind. Electron. 2015, 62, 7499–7512. [Google Scholar] [CrossRef]
- Ye, Q.; Mo, R.; Shi, Y.; Li, H. A unified Impedance-based Stability Criterion (UIBSC) for paralleled grid-tied inverters using global minor loop gain (GMLG). In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 5816–5821. [Google Scholar]
- Hassan, R.; Wang, H.; Rehman, M.M.U.; Riar, B.; Zane, R. Nodal Impedance-Based Stability Analysis of Dc Nanogrids. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padua, Italy, 25–28 June 2018. [Google Scholar]
- Schwanninger, R.; Roeder, G.; Wienzek, P.; Lavery, M.; Wunder, B.; Schellenberger, M.; Lorentz, V.; Maerz, M. Experimental Assessment of LVDC-Grid Stability Optimization using Circuit Simulation and Machine Learning. In Proceedings of the 2023 IEEE Fifth International Conference on DC Microgrids (ICDCM), Auckland, New Zealand, 15–17 November 2023; pp. 1–6. [Google Scholar]
- Bakhshizadeh, M.K.; Blaabjerg, F.; Hjerrild, J.; Kocewiak, L.; Bak, C.L. Improving the Impedance-Based Stability Criterion by Using the Vector Fitting Method. IEEE Trans. Energy Convers. 2018, 33, 1739–1747. [Google Scholar] [CrossRef]
- Riccobono, A.; Santi, E. A novel Passivity-Based Stability Criterion (PBSC) for switching converter DC distribution systems. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 2560–2567. [Google Scholar] [CrossRef]
- Vesti, S.; Suntio, T.; Oliver, J.A.; Prieto, R.; Cobos, J.A. Impedance-Based Stability and Transient-Performance Assessment Applying Maximum Peak Criteria. IEEE Trans. Power Electron. 2013, 28, 2099–2104. [Google Scholar] [CrossRef]
- Zhang, C.; Molinas, M.; Rygg, A.; Cai, X. Impedance-Based Analysis of Interconnected Power Electronics Systems: Impedance Network Modeling and Comparative Studies of Stability Criteria. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2520–2533. [Google Scholar] [CrossRef]
- Zhang, X.; Ruan, X.; Tse, C.K. Impedance-Based Local Stability Criterion for DC Distributed Power Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 916–925. [Google Scholar] [CrossRef]
- Middlebrook, R.D. Input filter considerations in design and application of switching regulators. Conf. Rec. IEEE IAS Annu. Meet. 1979, 11, 366–382. [Google Scholar]
- Miao, B.; Zane, R.; Maksimovic, D. A modified cross-correlation method for system identification of power converters with digital control. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; pp. 3728–3733. [Google Scholar]
- Barkley, A.; Santi, E. Improved Online Identification of a DC–DC Converter and Its Control Loop Gain Using Cross-Correlation Methods. IEEE Trans. Power Electron. 2009, 24, 2021–2031. [Google Scholar] [CrossRef]
- Shirazi, M.; Morroni, J.; Dolgov, A.; Zane, R.; Maksimovic, D. Integration of Frequency Response Measurement Capabilities in Digital Controllers for DC–DC Converters. IEEE Trans. Power Electron. 2008, 23, 2524–2535. [Google Scholar] [CrossRef]
- Roinila, T.; Vilkko, M.; Taskinen, A. Improved fast frequency response measurements of switched-mode power supplies using Dirac-ideal PRBS excitation. In Proceedings of the 2009 2nd International Conference on Adaptive Science & Technology (ICAST), Accra, Ghana, 14–16 January 2009; pp. 175–181. [Google Scholar]
- Martin, D.; Santi, E.; Barkley, A. Wide bandwidth system identification of AC system impedances by applying pertubations to an existing converter. In Proceedings of the 2011 IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 17–22 September 2011; pp. 2549–2556. [Google Scholar]
- Pan, P.; Hu, H.; He, Z.; Li, Y. Rapid Impedance Measurement Approach Based on Wideband Excitation for Single-Phase Four-Quadrant Converter of High-Speed Train. IEEE Trans. Instrum. Meas. 2021, 70, 9004611. [Google Scholar] [CrossRef]
- Roinila, T.; Abdollahi, H.; Arrua, S.; Santi, E. Online measurement of bus impedance of interconnected power electronics systems: Applying orthogonal sequences. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 5783–5788. [Google Scholar]
- Roinila, T.; Messo, T.; Luhtala, R.; Scharrenberg, R.; de Jong, E.C.W.; Fabian, A.; Sun, Y. Hardware-in-the-Loop Methods for Real-Time Frequency-Response Measurements of on-Board Power Distribution Systems. IEEE Trans. Ind. Electron. 2019, 66, 5769–5777. [Google Scholar] [CrossRef]
- Roinila, T.; Abdollahi, H.; Arrua, S.; Santi, E. Real-Time Stability Analysis and Control of Multiconverter Systems by Using MIMO-Identification Techniques. IEEE Trans. Power Electron. 2019, 34, 3948–3957. [Google Scholar] [CrossRef]
- Roinila, T.; Messo, T.; Santi, E. MIMO-Identification Techniques for Rapid Impedance-Based Stability Assessment of Three-Phase Systems in DQ Domain. IEEE Trans. Power Electron. 2018, 33, 4015–4022. [Google Scholar] [CrossRef]
- Berg, M.; Alenius, H.; Roinila, T. Rapid Multivariable Identification of Grid Impedance in DQ Domain Considering Impedance Coupling. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2710–2721. [Google Scholar] [CrossRef]
- Mohammed, N.; Ciobotaru, M.; Town, G. Performance Evaluation of Wideband Binary Identification of Grid Impedance Using Grid-connected Inverters. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ‘19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. 1–10. [Google Scholar]
- Riccobono, A.; Mirz, M.; Monti, A. Noninvasive Online Parametric Identification of Three-Phase AC Power Impedances to Assess the Stability of Grid-Tied Power Electronic Inverters in LV Networks. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 629–647. [Google Scholar] [CrossRef]
- Mohammed, N.; Zhou, W.; Bahrani, B.; Hill, D.; Blaabjerg, F. PRBS-Based Impedance Measurement Tool for Stability Analysis of Black-Box EMT Models in PSCAD. In Proceedings of the 2024 4th International Conference on Emerging Smart Technologies and Applications (eSmarTA), Sana’a, Yemen, 6–7 August 2024; pp. 1–8. [Google Scholar]
- Sihvo, J.; Stroe, D.-I.; Messo, T.; Roinila, T. Fast Approach for Battery Impedance Identification Using Pseudo-Random Sequence Signals. IEEE Trans. Power Electron. 2020, 35, 2548–2557. [Google Scholar] [CrossRef]
- Roinila, T.; Messo, T. Online Grid-Impedance Measurement Using Ternary-Sequence Injection. IEEE Trans. Ind. Appl. 2018, 54, 5097–5103. [Google Scholar] [CrossRef]
- Basnet, H.; Tran, M.; Santi, E.; Roinila, T. Dynamical Characterization of STATCOM Application: Applying Computer-Optimized Orthogonal Perturbations. In Proceedings of the 2024 IEEE Sixth International Conference on DC Microgrids (ICDCM), Columbia, SC, USA, 8 August 2024. [Google Scholar]
- Sawma, J.; Khatounian, F.; Monmasson, E. A modified cross-correlation method for the identification of systems with large bandwidth. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 2121–2126. [Google Scholar]
- Texas Instruments. TMS320F2837xD Dual-Core Real-Time Microcontrollers Datasheet (Rev. P); Texas Instruments: Dallas, TX, USA, 2024; pp. 109–110. [Google Scholar]
- LEM. Current Transducer LA 130-P datasheet (Version 5); LEM: Geneva, Switzerland, 2024; pp. 1–4. [Google Scholar]
- Analog Devices. LT1809/1810 Single/Dual 180 MHz, 350 V/µs Rail-to-Rail Input and Output Low Distortion Op Amps Datasheet (Rev. A); Analog Devices: Osaka, Japan, 2000; pp. 1–24. [Google Scholar]
- Al Attar,, H.; Hamida, M.A.; Ghanes, M.; Taleb, M. Review on Modeling and Control Strategies of DC–DC LLC Converters for Bidirectional Electric Vehicle Charger Applications. Energies 2023, 16, 3946. [Google Scholar] [CrossRef]
- Long, X.; Chen, D. Small Signal Modeling of LLC Converter with LED Load and Quasi-Resonant Controller Based Active Ripple Rejection. Energies 2023, 16, 3773. [Google Scholar] [CrossRef]
- Schwanninger, R.; Stöcklein, N.; Weitz, N.; Yang, X.; März, M. A Path to Configurable Solid State Transformers and Energy Routers: Introduction to Modular Active Cell Control. In IEEE Transactions on Power Electronics; IEEE: Piscataway, NJ, USA, 2025; pp. 1–18. [Google Scholar] [CrossRef]
- Marxgut, C.; Krismer, F.; Bortis, D.; Kolar, J.W. Ultraflat Interleaved Triangular Current Mode (TCM) Single-Phase PFC Rectifier. IEEE Trans. Power Electron. 2013, 29, 873–882. [Google Scholar] [CrossRef]
- Niu, P.; Guo, J.; Gao, Z.; Yan, J.; Gao, S. Research on Improved Technology of Totem-Pole Bridgeless PFC Circuit Based on Triangular Current Mode. Energies 2025, 18, 3886. [Google Scholar] [CrossRef]

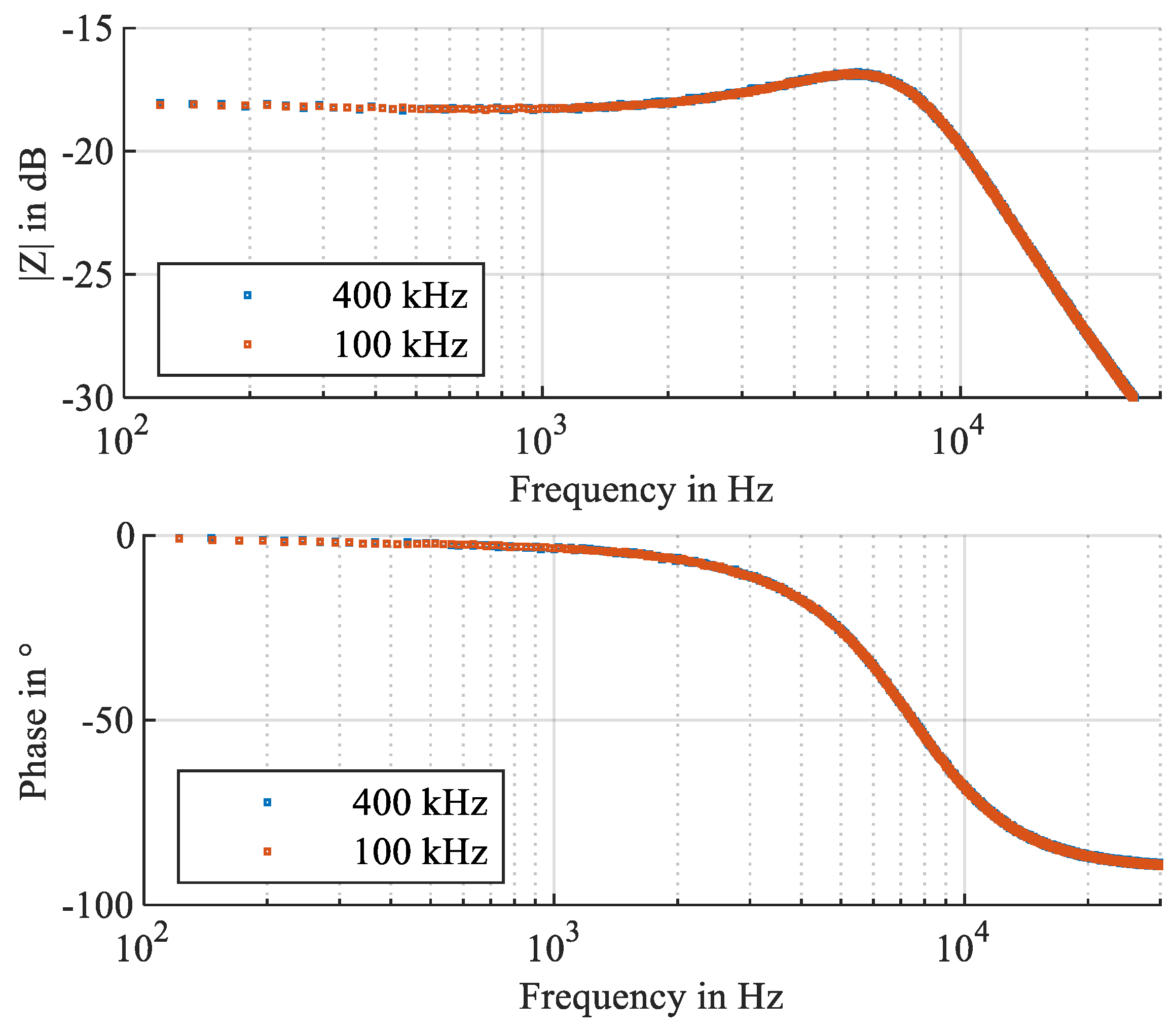
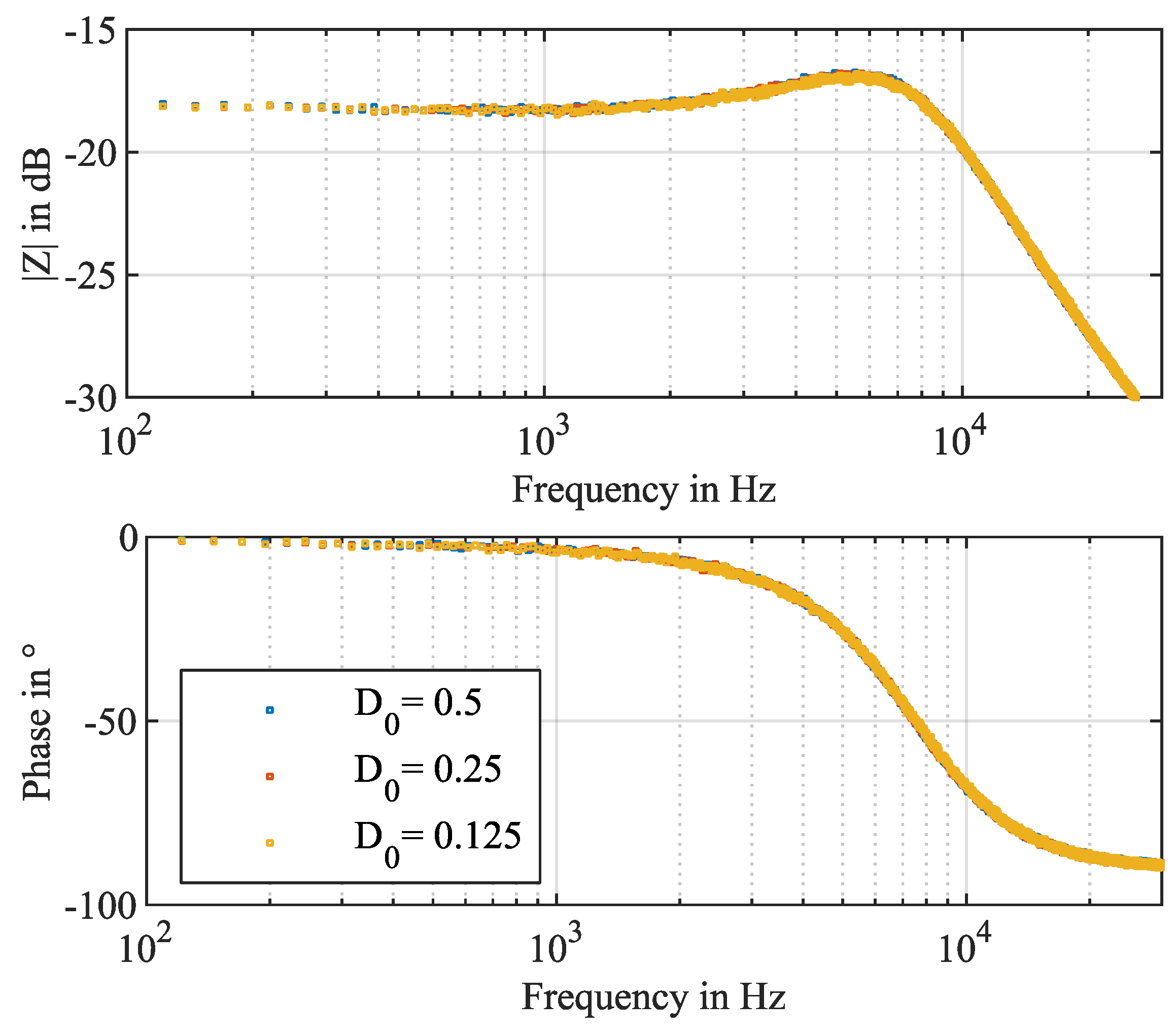
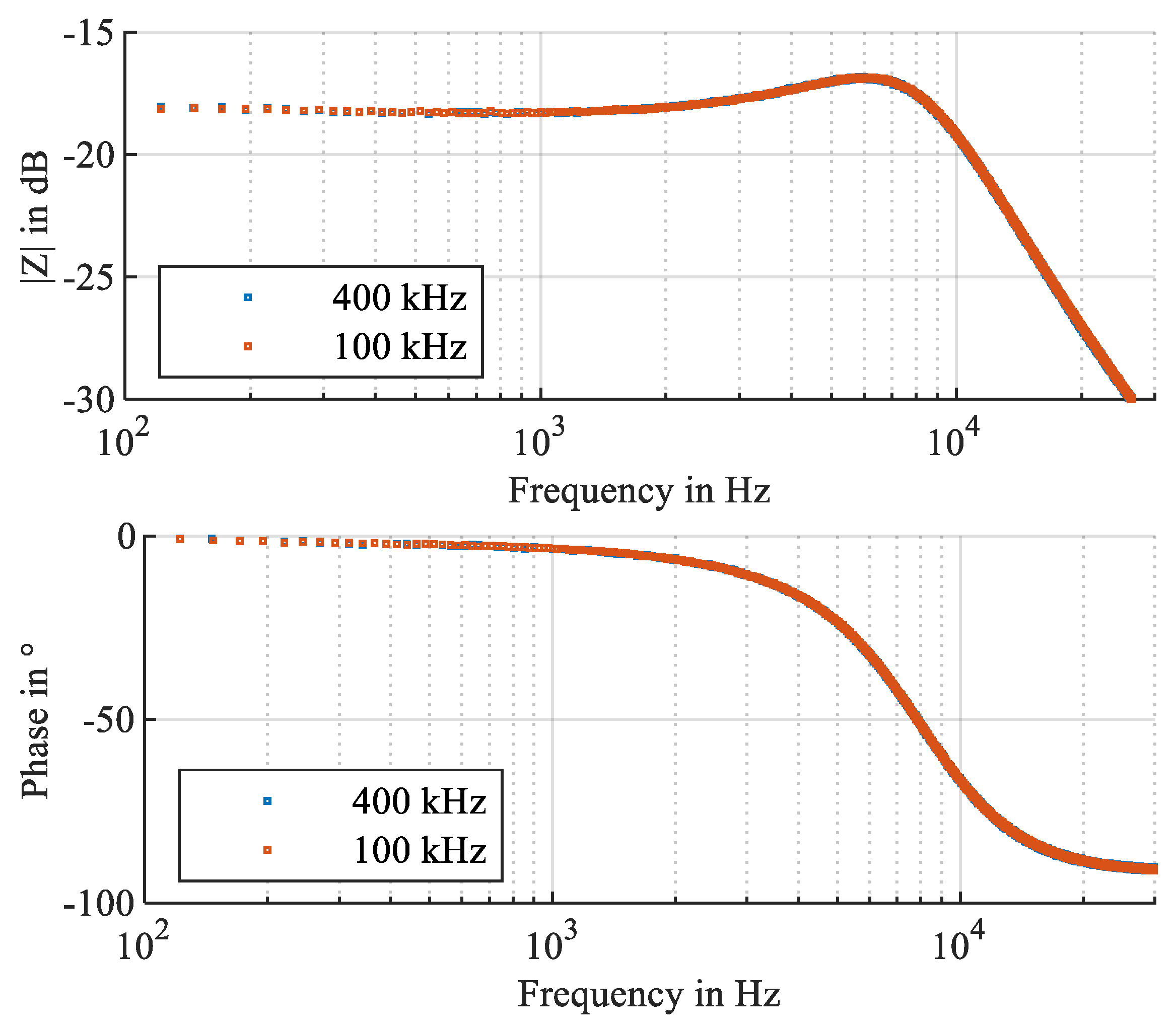
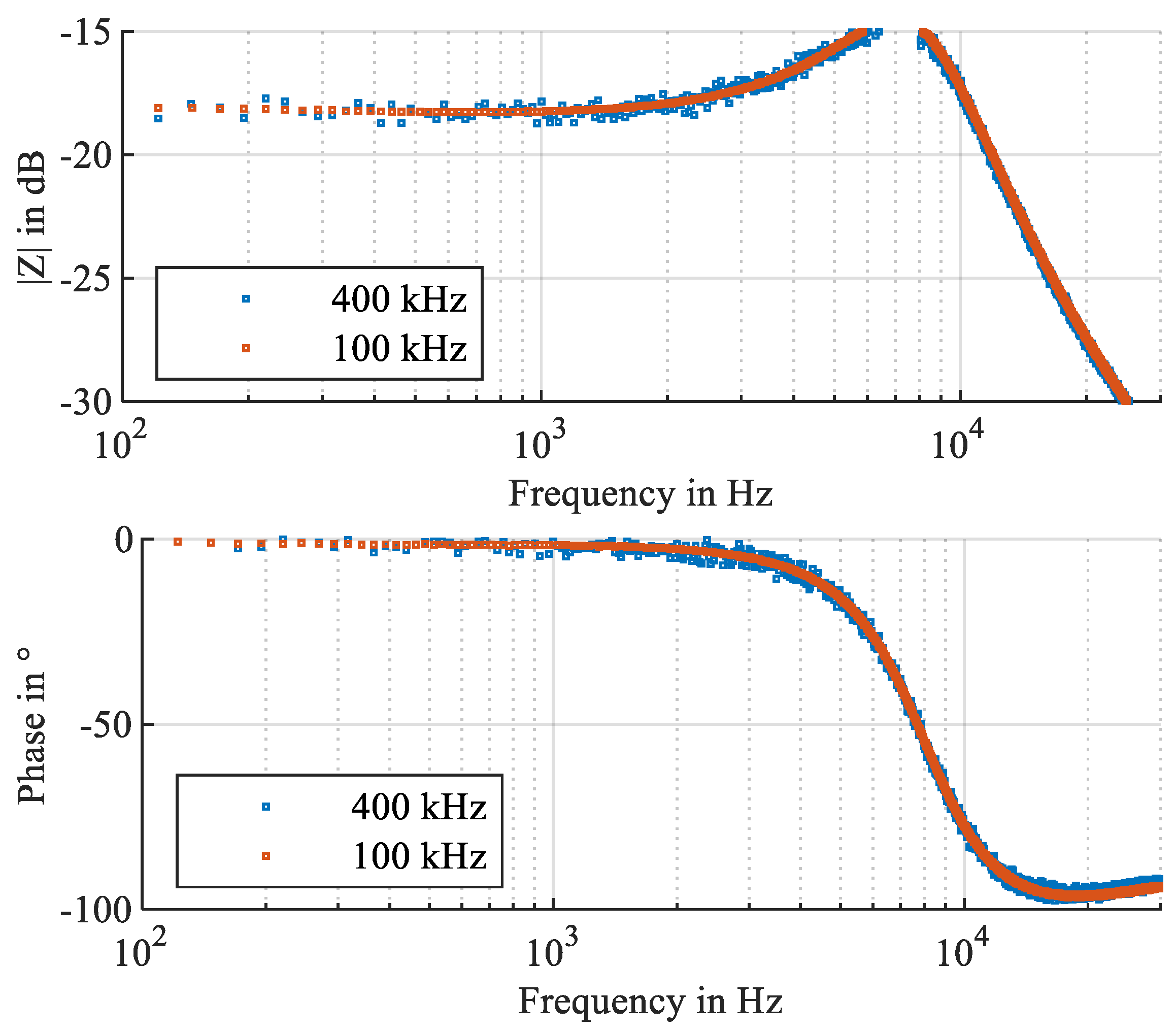
| Component | Parameter | Value |
|---|---|---|
| ADC [42] | Sampling frequency | |
| Resolution | ||
| Gain error | ||
| Offset error | ||
| SNR (at 10 kHz) | 90.2 dB | |
| Current Sensor [43] | Nominal current | |
| Turns ratio () | ||
| Linearity error | ||
| Bandwidth (−1 dB) | DC—150 kHz | |
| Shunt Resistor | Resistance | |
| Tolerance | ||
| Temperature coefficient | ||
| Measurement Amplifiers [44] | Unity gain bandwidth | 320 MHz |
| Slew rate | ||
| Common mode rejection ratio | 78 dB (@ 3 V) | |
| Power supply rejection ratio | 87 dB | |
| Input voltage range | 0 V–3 V | |
| Input noise voltage density | ||
| Voltage Bandpass | Frequency range | 10 Hz–50 kHz |
| Passband attenuation | ||
| Shunt Current Bandpass | Frequency range | 10 Hz–50 kHz |
| Passband attenuation |
| Parameter | Value |
|---|---|
| MOSFET resistance | |
| Inductance | |
| Inductor resistance | |
| Proportional current controller gain | |
| Integral current controller gain | |
| Input voltage | |
| Output voltage | |
| Output capacitance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwanninger, R.; Bosch, M.; Wunder, B.; März, M. Investigations on Output Impedance Measurement of Digitally Controlled Power Converters with Wide Bandwidth Signals. Energies 2025, 18, 6121. https://doi.org/10.3390/en18236121
Schwanninger R, Bosch M, Wunder B, März M. Investigations on Output Impedance Measurement of Digitally Controlled Power Converters with Wide Bandwidth Signals. Energies. 2025; 18(23):6121. https://doi.org/10.3390/en18236121
Chicago/Turabian StyleSchwanninger, Raffael, Moritz Bosch, Bernd Wunder, and Martin März. 2025. "Investigations on Output Impedance Measurement of Digitally Controlled Power Converters with Wide Bandwidth Signals" Energies 18, no. 23: 6121. https://doi.org/10.3390/en18236121
APA StyleSchwanninger, R., Bosch, M., Wunder, B., & März, M. (2025). Investigations on Output Impedance Measurement of Digitally Controlled Power Converters with Wide Bandwidth Signals. Energies, 18(23), 6121. https://doi.org/10.3390/en18236121






