Nanofluid Cooling Enhances PEM Fuel Cell Stack Performance via 3D Multiphysics Simulation
Abstract
1. Introduction
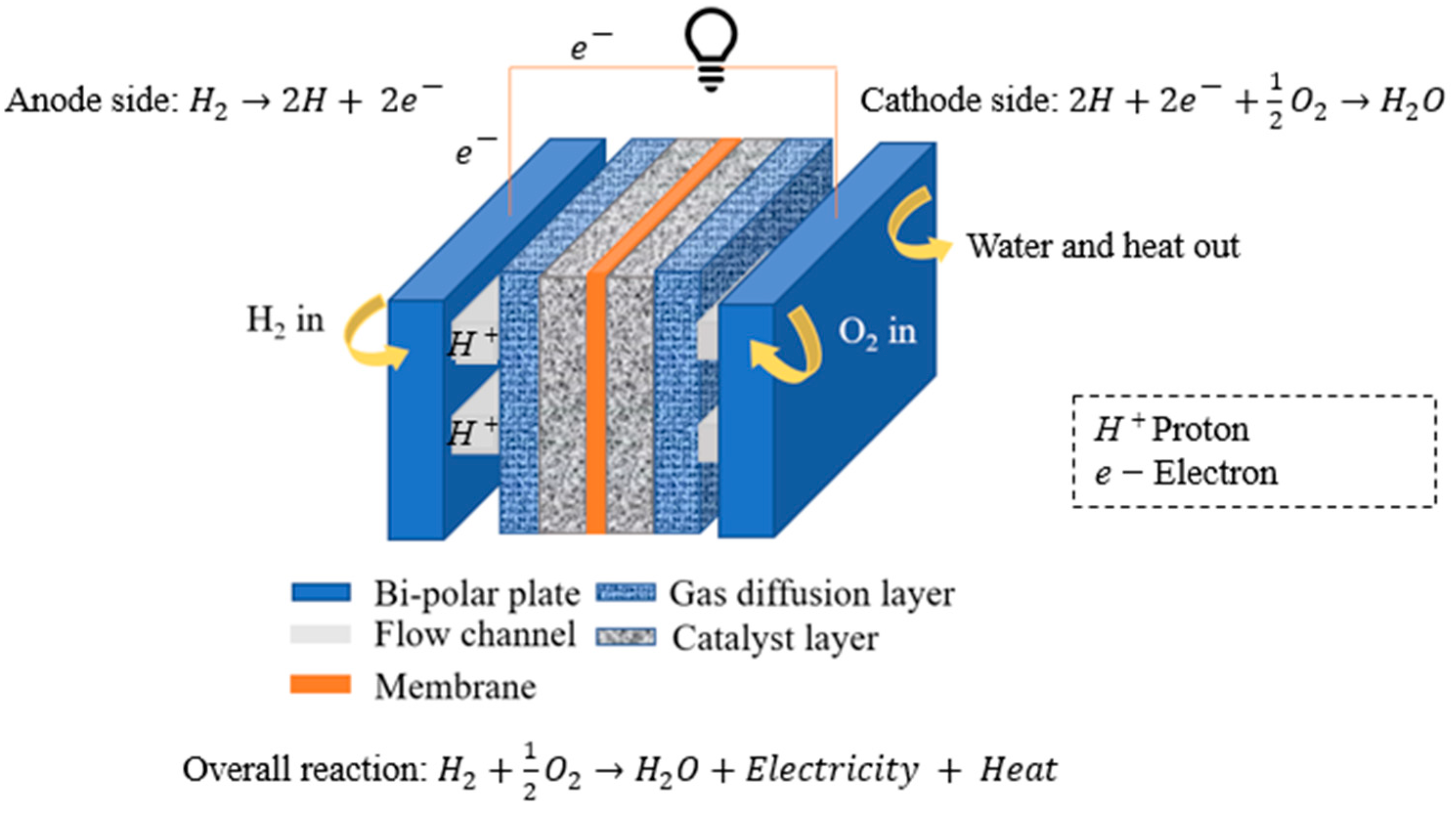
2. Numerical Modeling
2.1. Governing Equations and Solution Procedure
- PEMFC operations are assumed to be under steady-state conditions.
- The gases are modeled as ideal, incompressible, flowing laminar in the channels.
- The gas diffusion layer (GDL) and catalyst layer (CL) are considered isotropic and homogeneous porous layers, with constant values for porosity, tortuosity, and permeability.
- Reactants are assumed to be dry gases.
- The operating temperature is fixed at 300 K to prevent membrane hydration.
- The cooling channel is assumed to be well-insulated, rendering current leakage negligible despite the higher electrical conductivity of nanofluids. In this simulation, the electrical conductivity of the coolant materials is considered to be zero.
- The three-cell model is assumed to represent the thermal and flow behavior of the full nine-cell stack, based on symmetry and uniform boundary conditions, allowing for a reduced computational cost while maintaining accuracy in predicting representative temperature and performance trends.
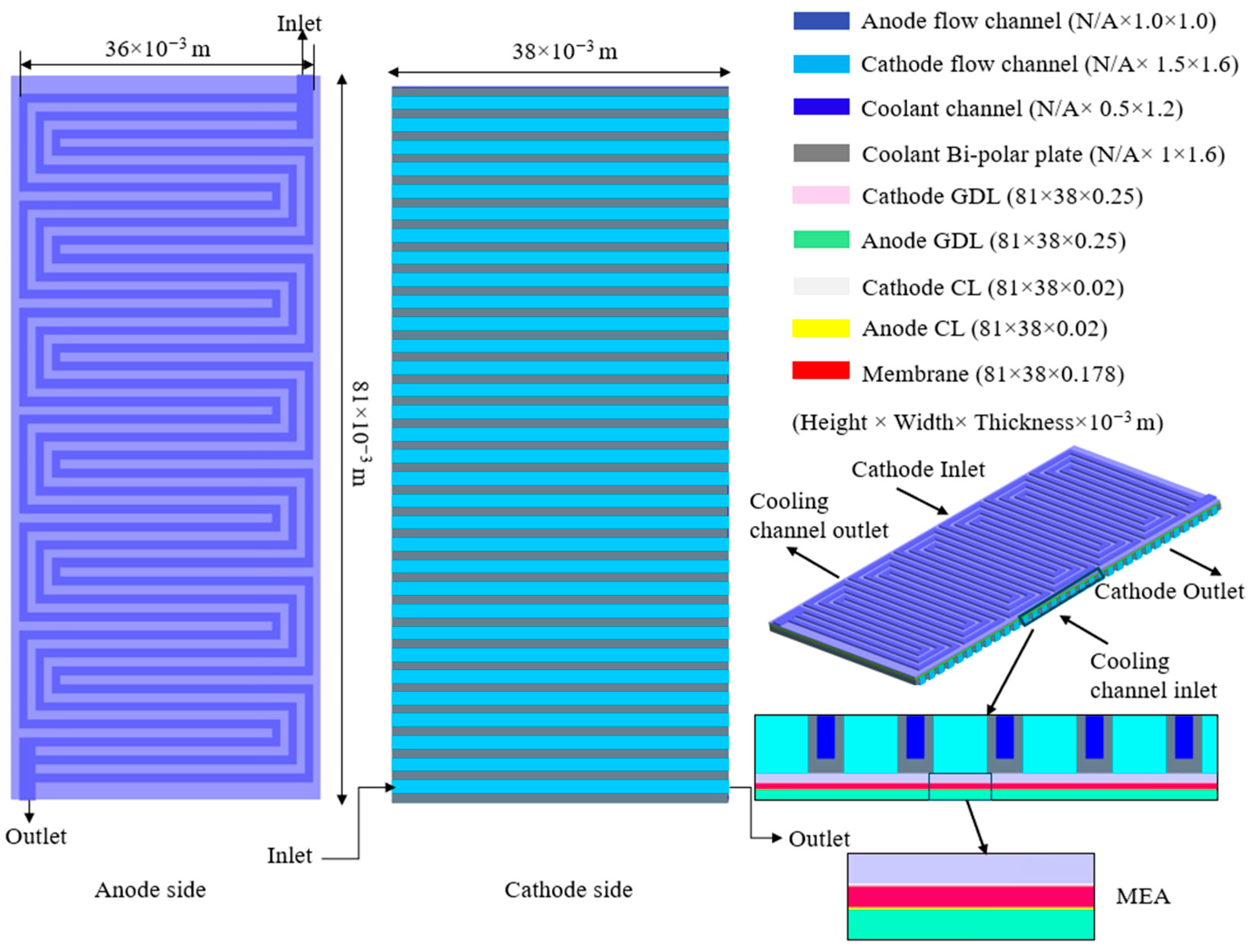
2.2. Flow Channel Design and Computational Domain
2.3. Boundary Conditions and Coolant Properties
3. Simulation Results and Discussion
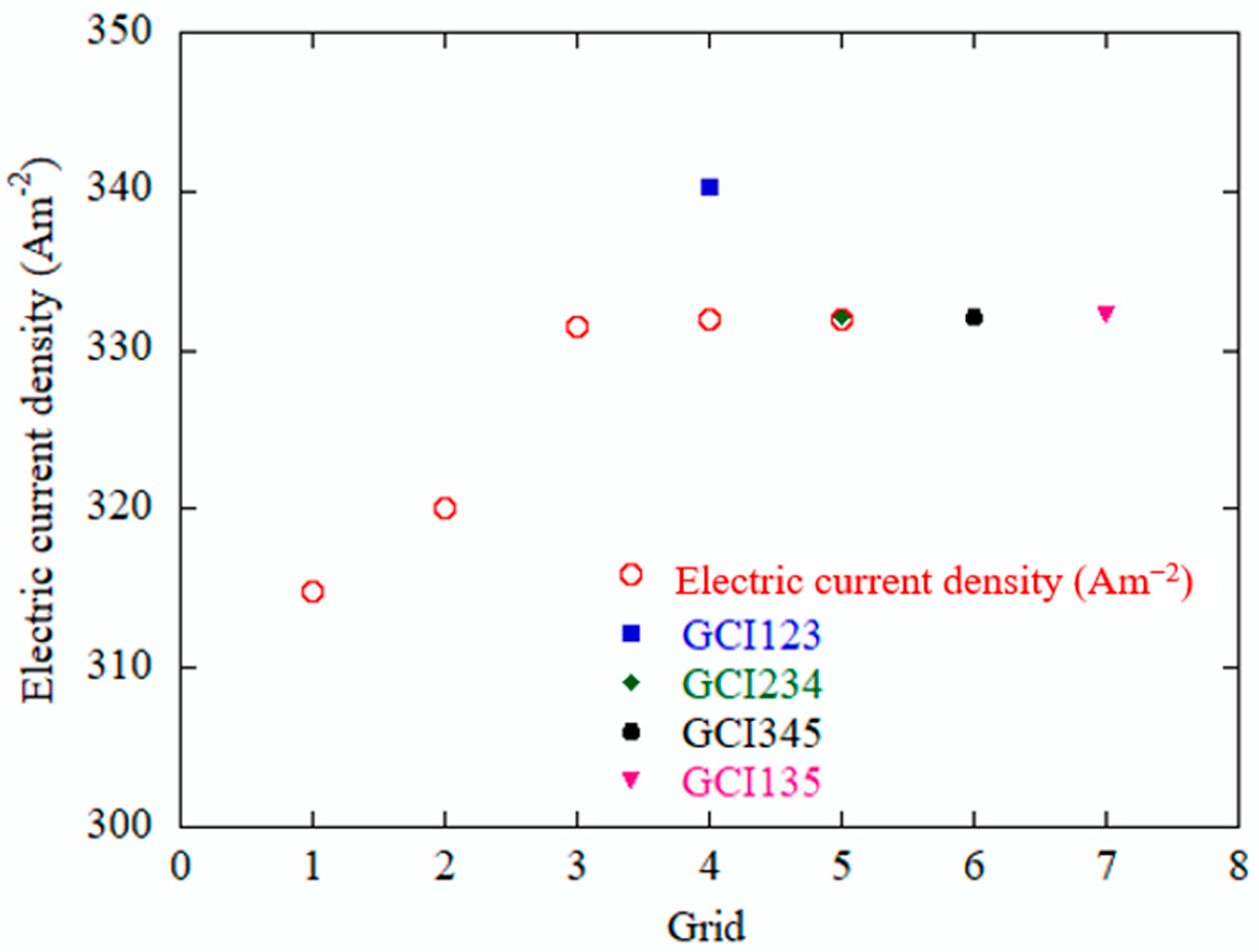
3.1. Grid Uncertainty Analysis
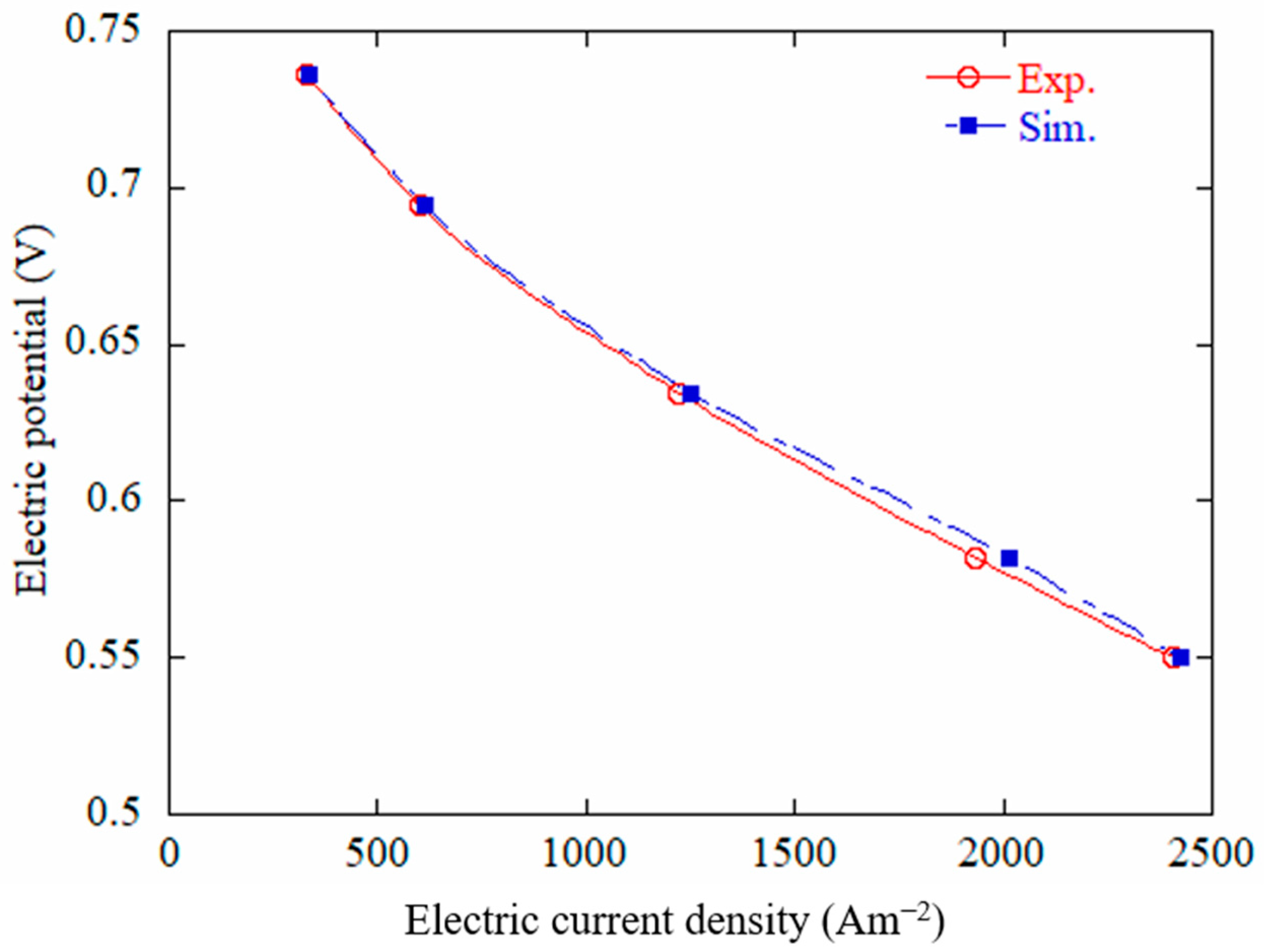
3.2. Experimental Validation
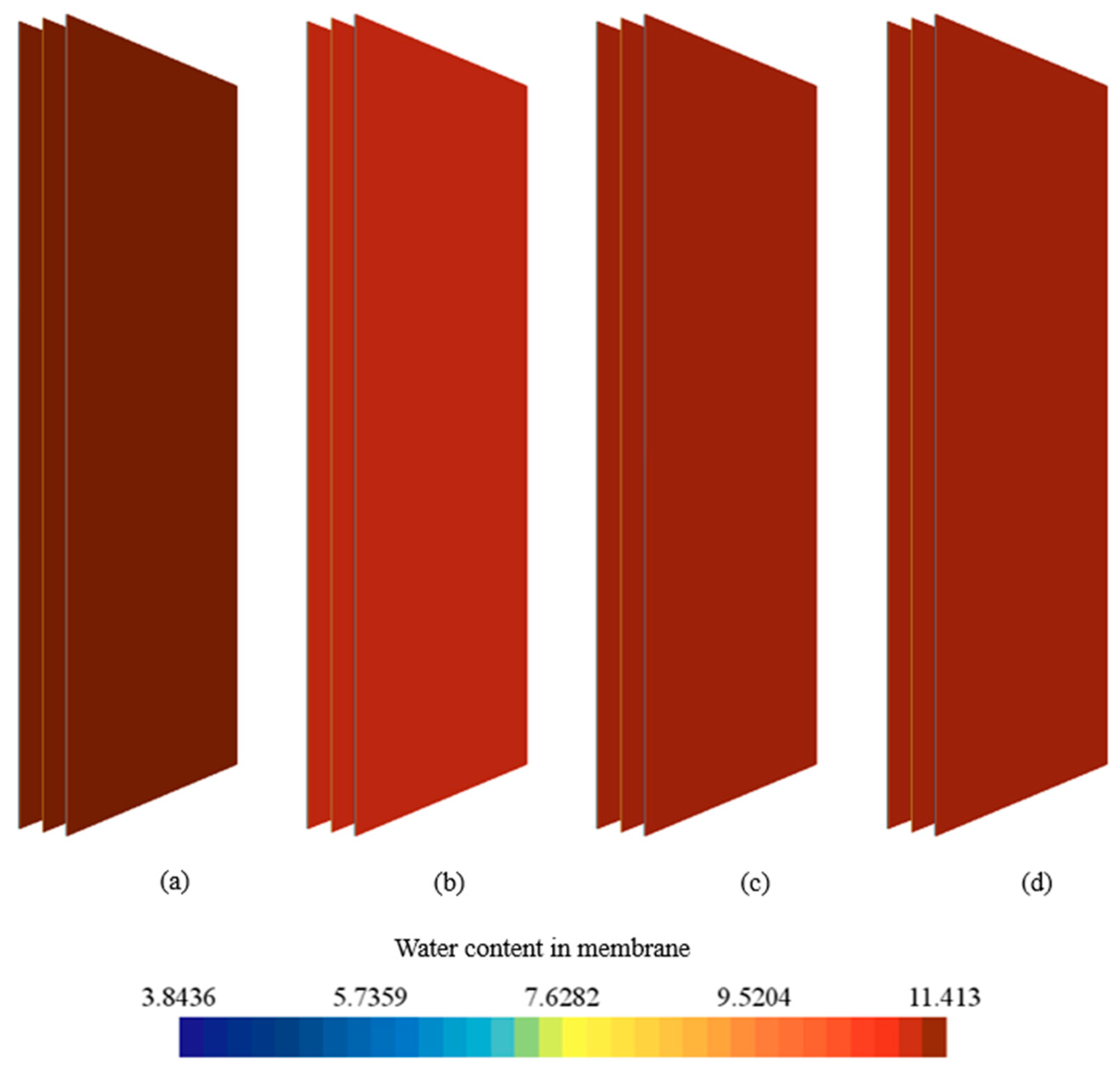
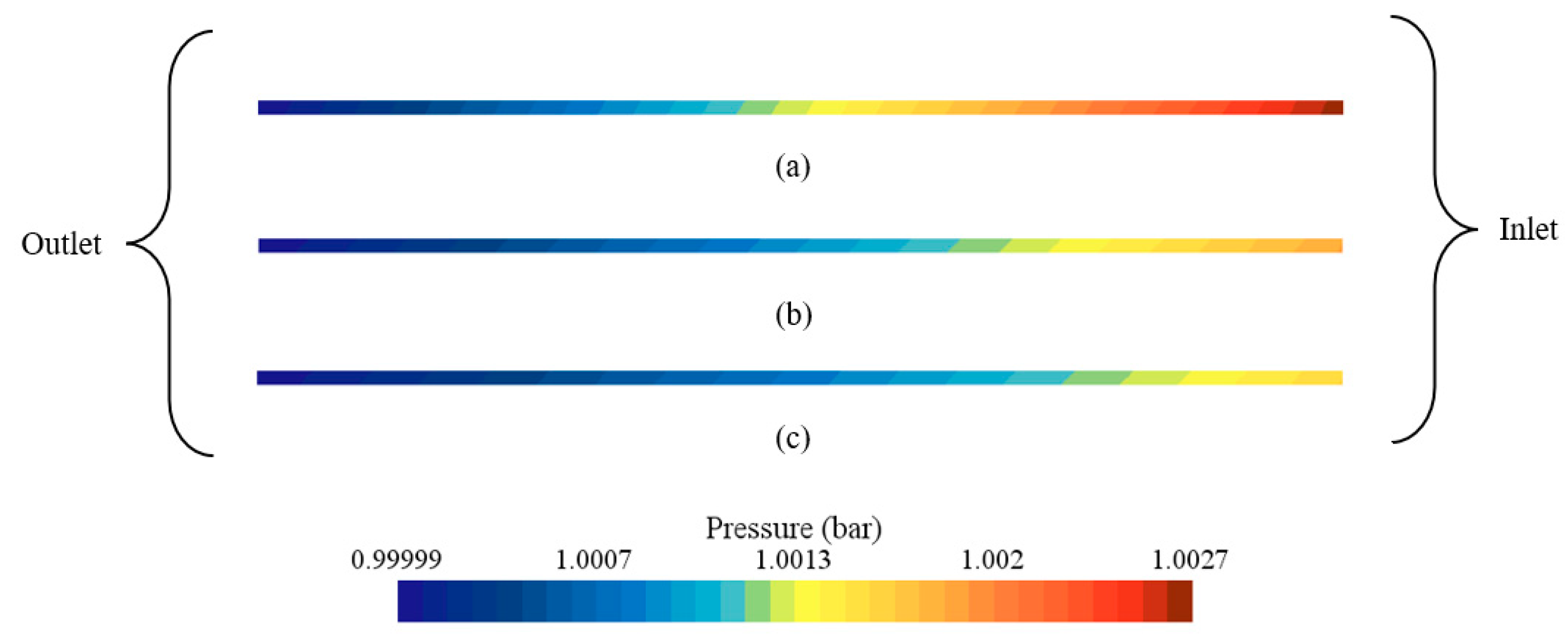
3.3. Effect of Coolants
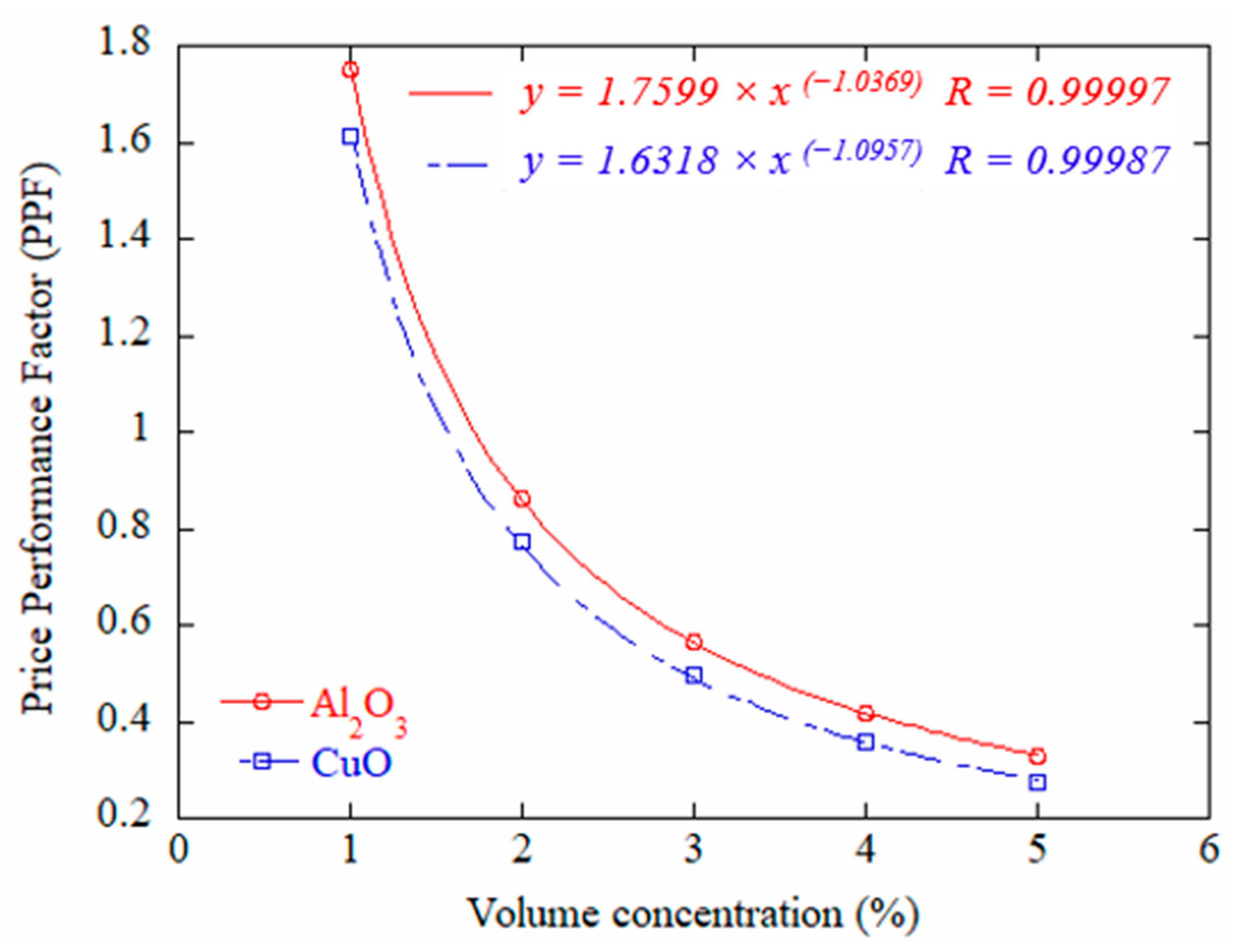
3.4. Performance Price Factor for Nanofluids and Economic Challenges
4. Conclusions and Future Works
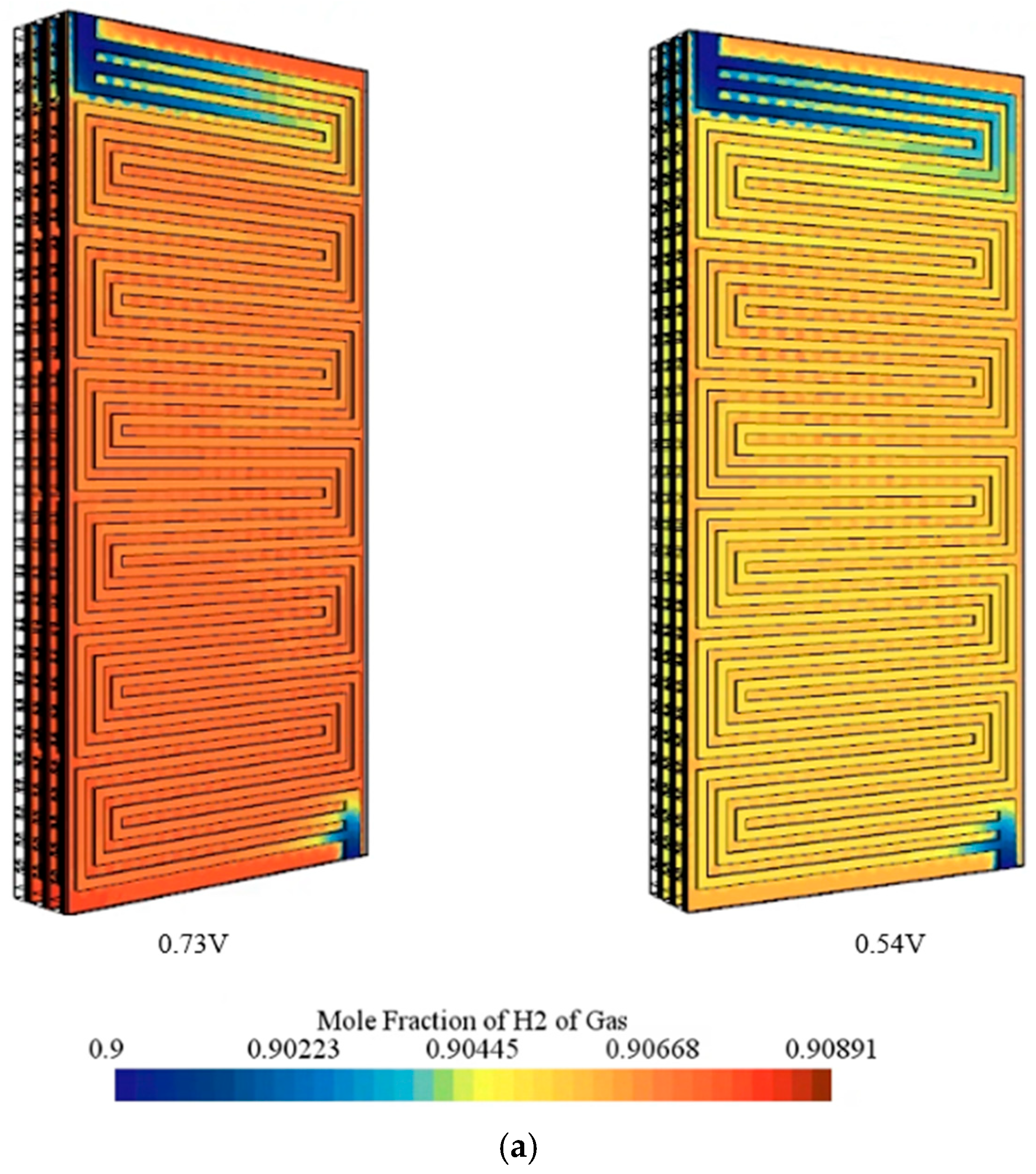
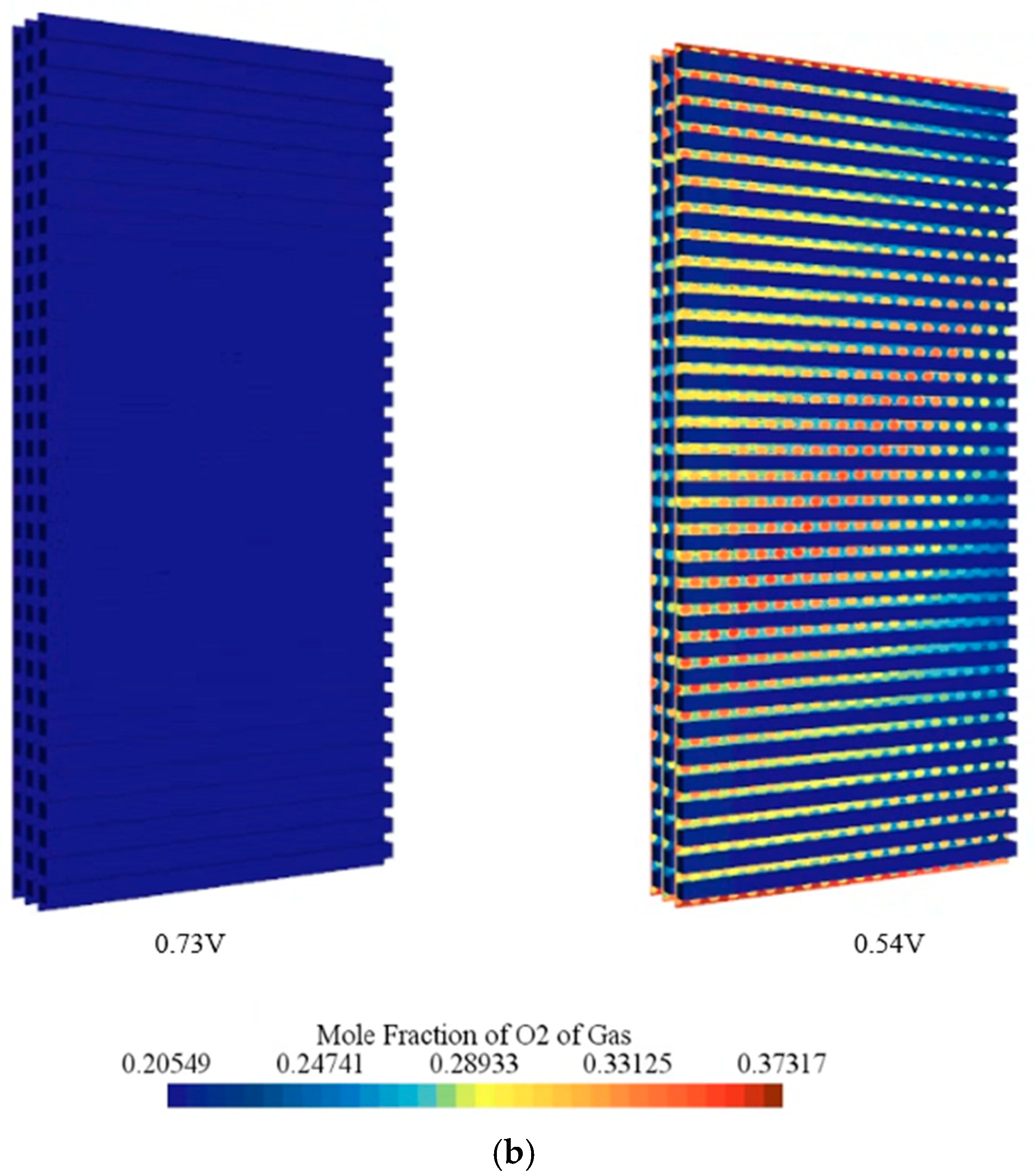
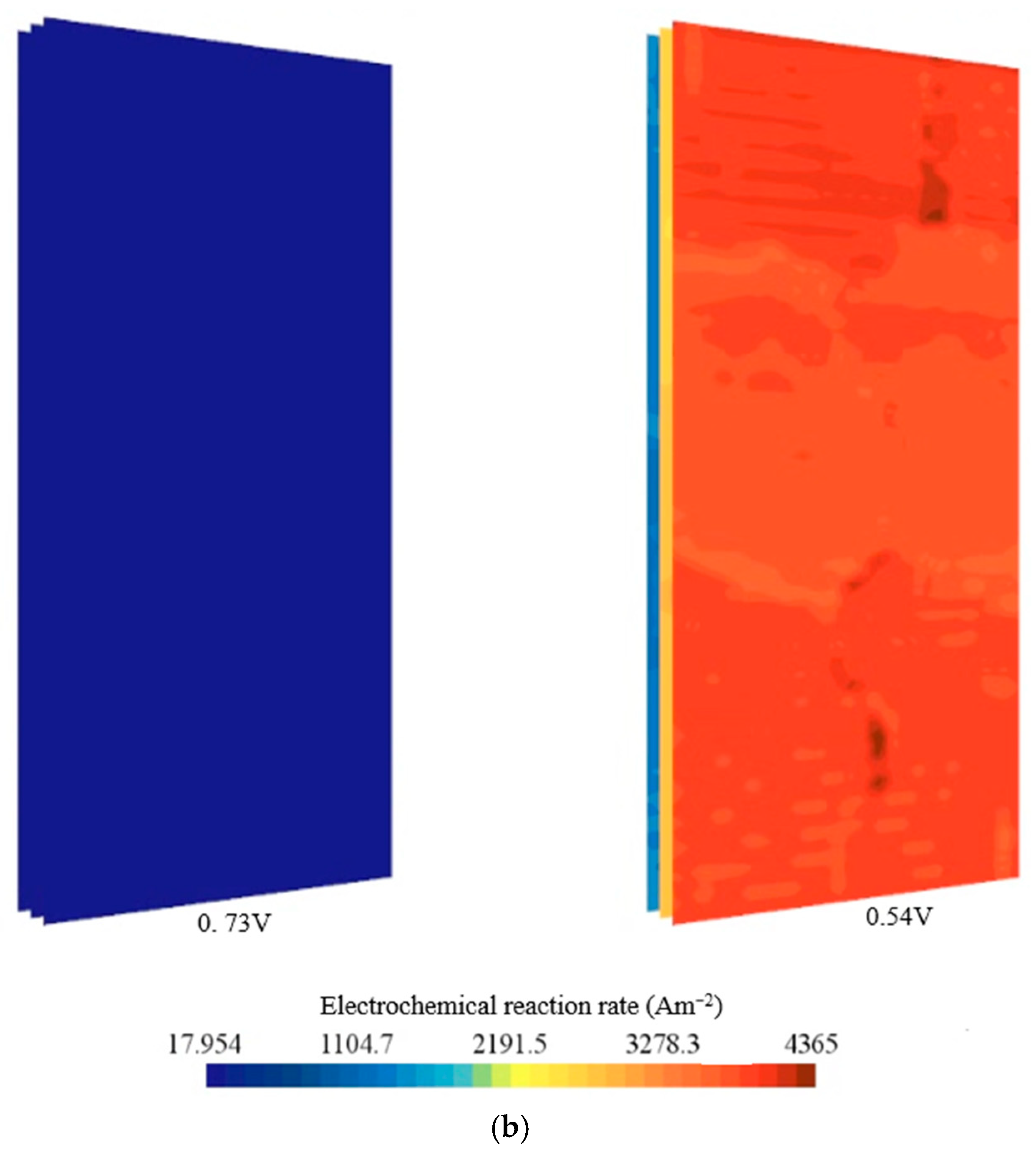
- At high voltage of 0.73 V, the hydrogen and oxygen fields were predicted to remain nearly uniform, whereas at 0.54 V, strong outlet-side gradients and local starvation were observed, indicating mass-transport limitation.
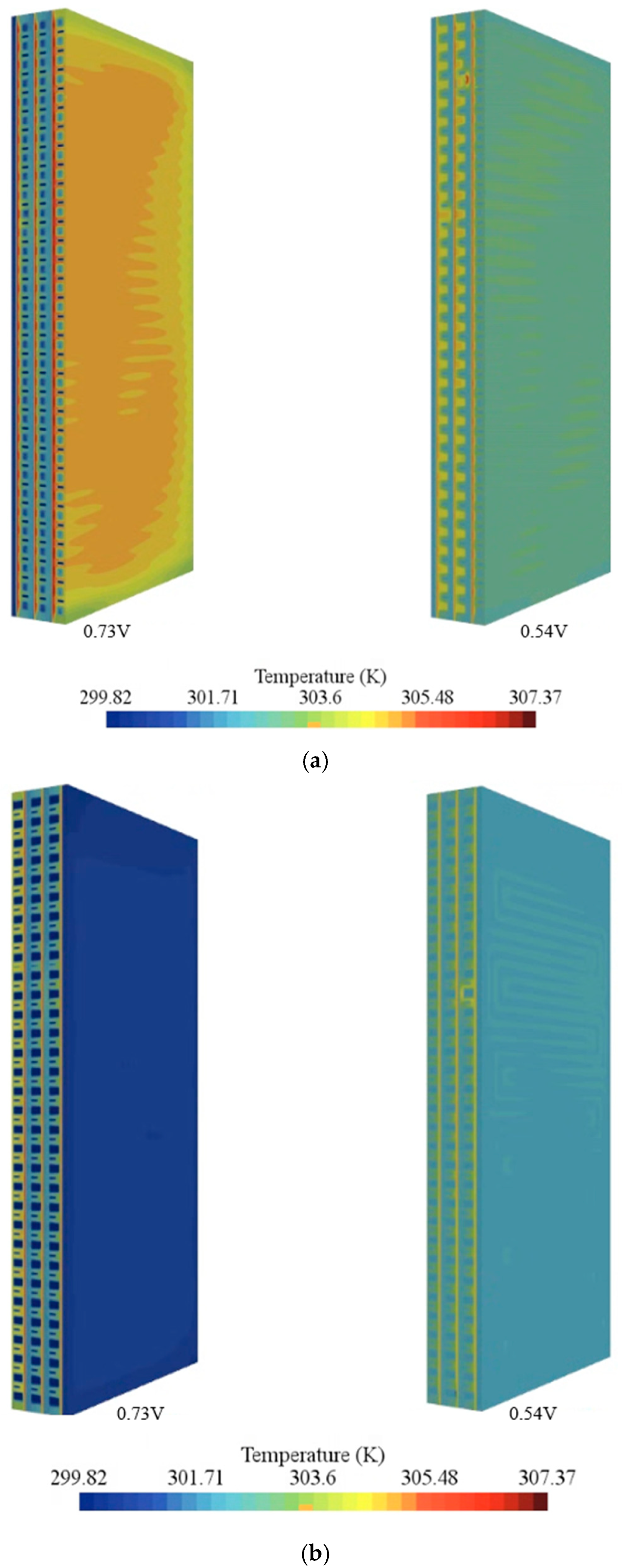
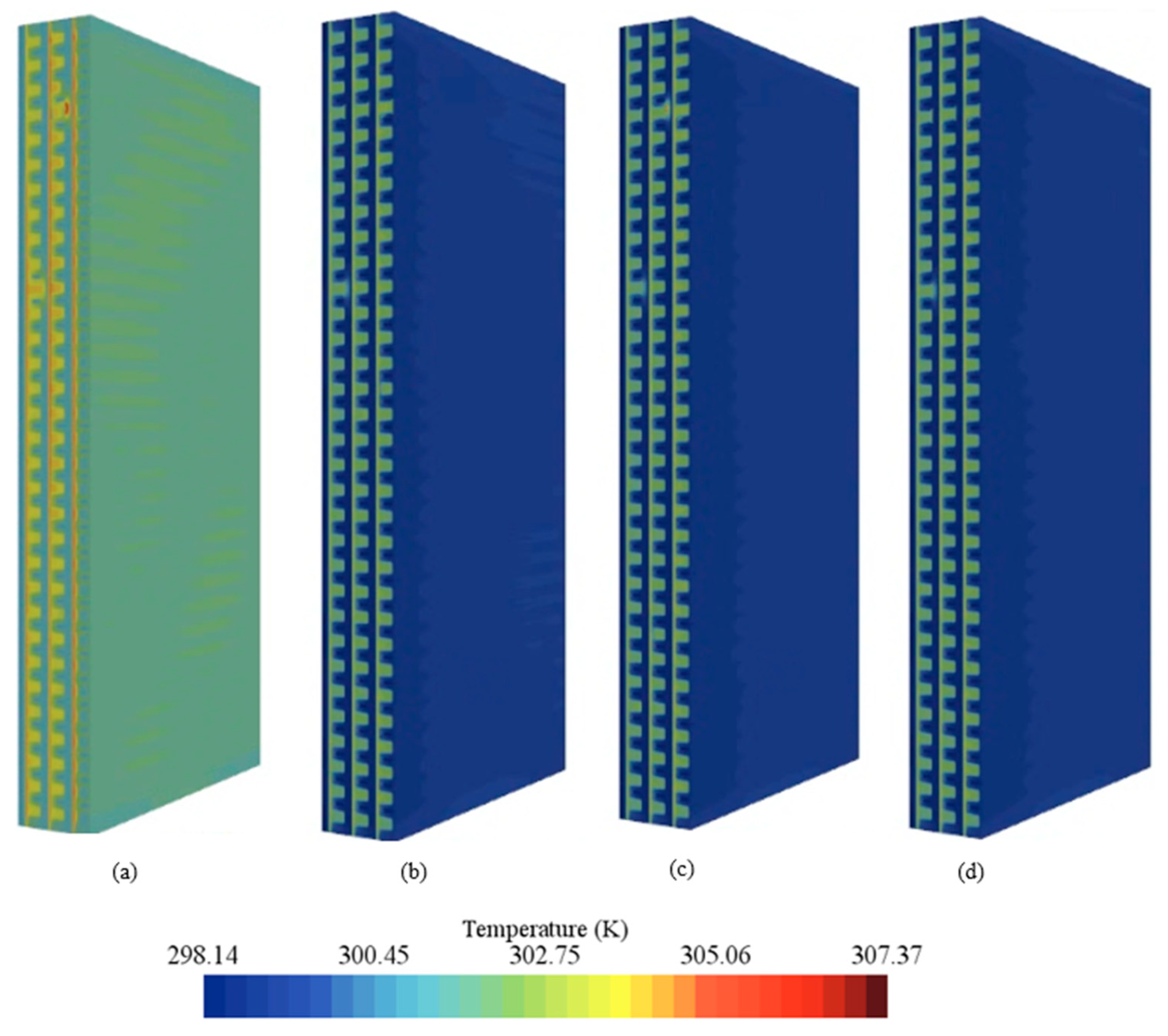
- Temperature fields were uniform at 0.73 V and exhibited hot regions at 0.54 V, especially near cathode outlets without active cooling.
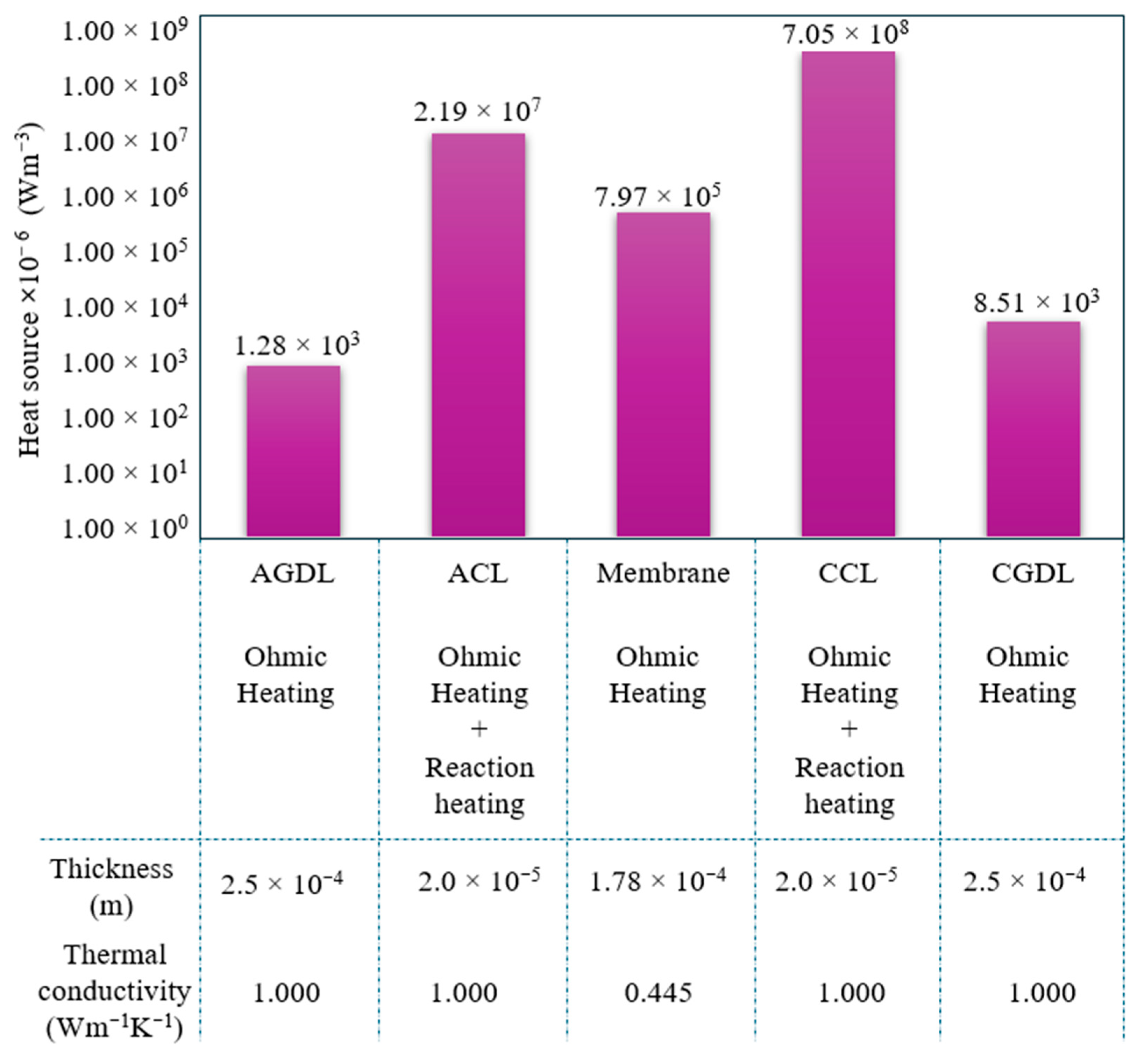
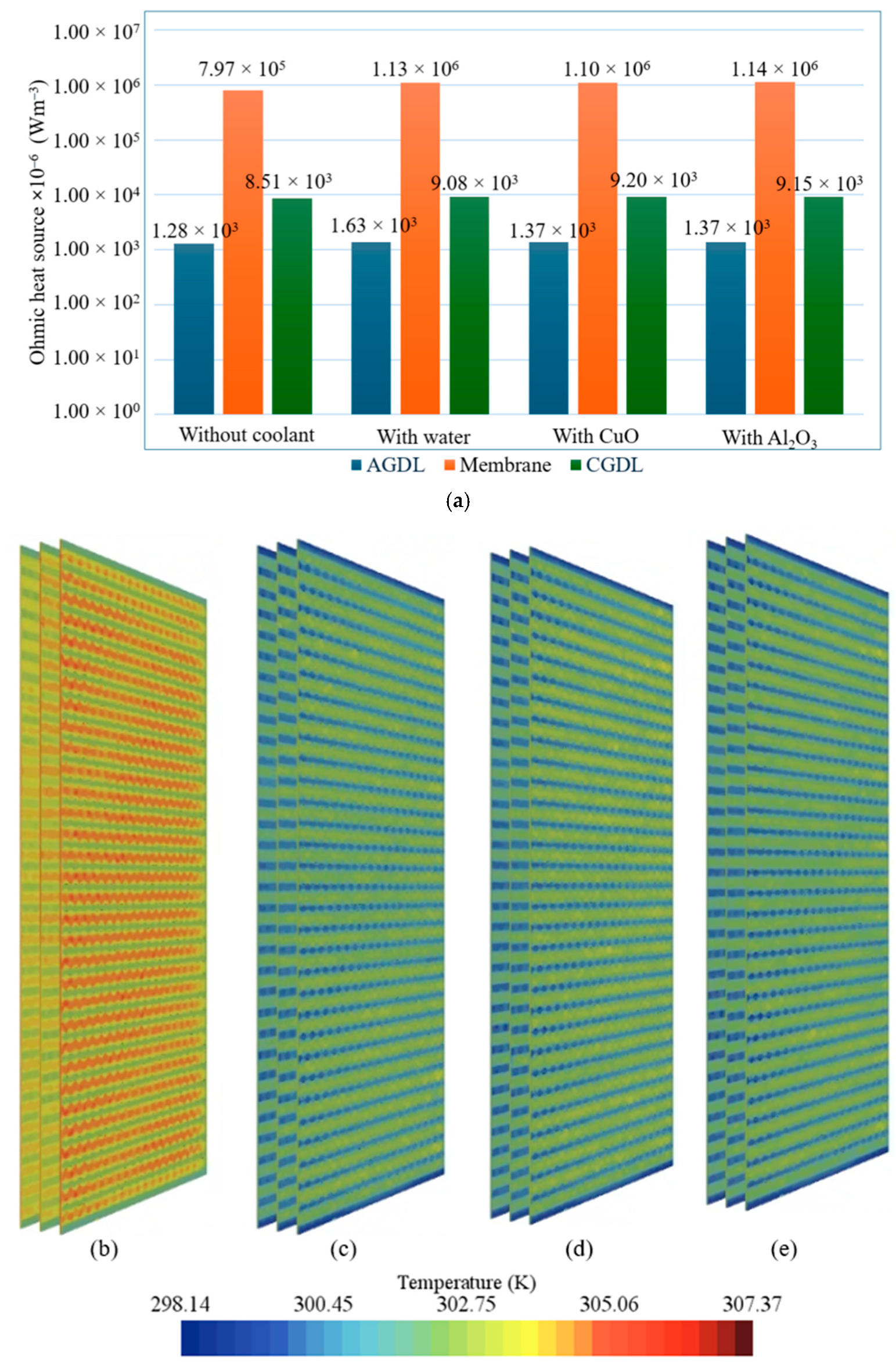
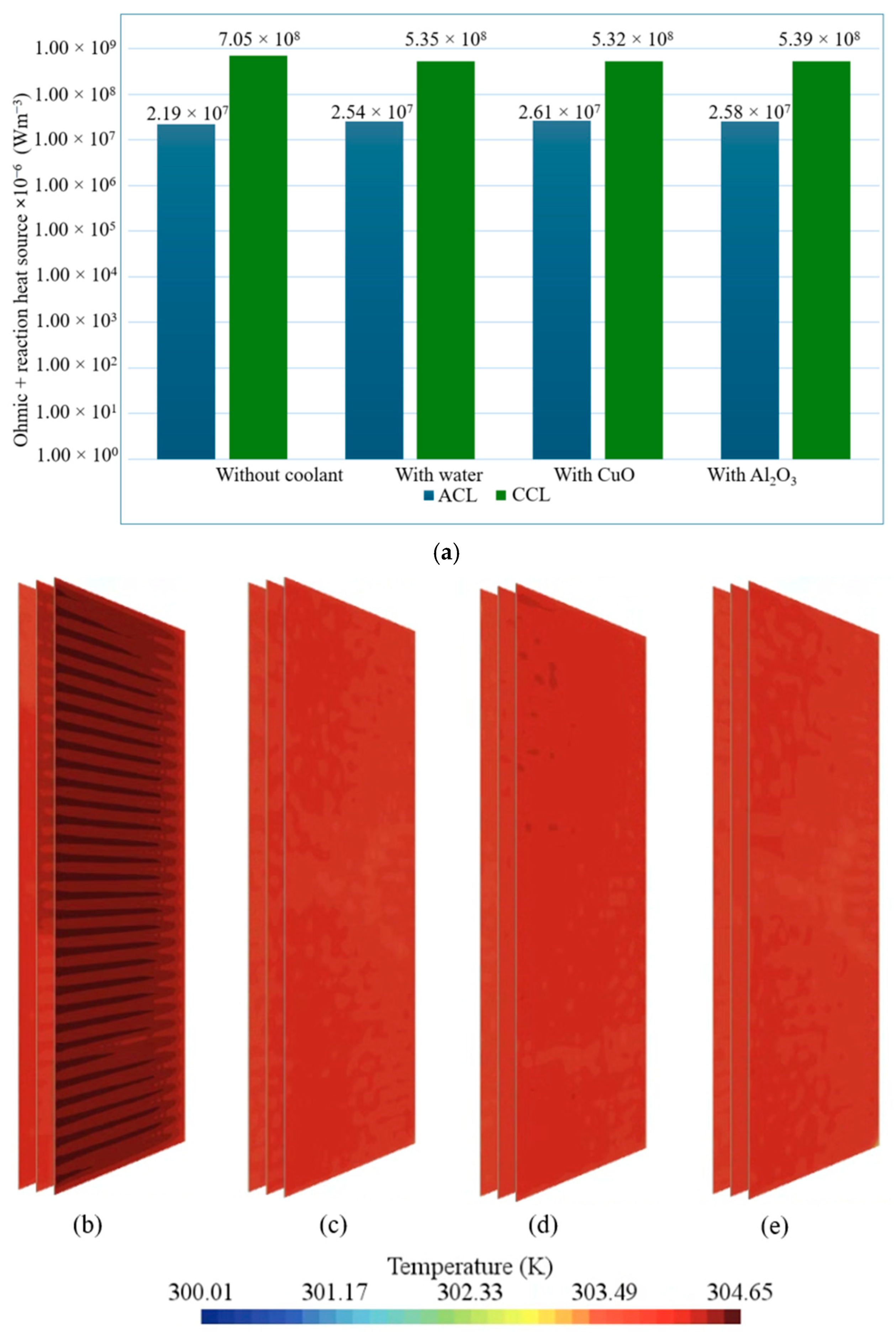
- Component-wise analysis showed that heat generation was concentrated in the catalyst layers, particularly the cathode catalyst layer, while gas-diffusion layers contributed marginally; the membrane produced moderate ohmic heating and acted as a thermal bottleneck.
- Introducing coolant channels increased the area-averaged current density from 2426 A m−2 without coolant to 2613, 2678, and 2702 A m−2 with water, CuO, and Al2O3, corresponding to gains of 7.77%, 10.38%, and 11.37%.
- Among the examined coolants, Al2O3 provided the lowest peak temperature and a favorable pressure drop owing to its higher thermal conductivity and lower viscosity, whereas water yielded the most uniform temperature field.
- Enhanced cooling with nanofluids supported higher oxygen reduction activity at the cathode catalyst layer and thus increased reaction heat while sustaining higher current density, whereas water maintained more stable hydration and uniformity, highlighting a performance–durability trade-off.
- A price to performance analysis indicated that Al2O3 at one percent volume fraction achieved a more favorable balance than CuO under the assumed prices, while deionized water remained attractive when long-term stability and cost are prioritized.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACL | anode catalyst layer |
| AGDL | anode gas diffusion layer |
| BPL | bi-polar plate |
| CC | coolant channel |
| CFD | computational fluid dynamics |
| CL | catalyst layer |
| CBPL | cathode bi-polar plate |
| CCL | cathode catalyst layer |
| CGDL | cathode gas diffusion layer |
| FCL | flow channel |
| GDL | gas diffusion layer |
| MEA | membrane electrode assembly |
| ORR | oxygen reduction reaction |
| PEMFC | proton exchange/polymer electrolyte membrane fuel cell |
| PPF | performance price factor |
| RH | relative humidity |
| Symbols | |
| a | water activity (m−1) |
| c | molar concentration, kmol m−3 |
| D | mass diffusivity (m2 s−1) |
| E | cell potential, V |
| F | Faraday’s constant |
| m | mass |
| M | molecular weight, g/mol |
| electroosmotic drag coefficient | |
| p | partial pressure, atm |
| R | ideal gas constant, 8.3143 Jmol−1K−1 |
| S | source term |
| s | liquid volume fraction |
| T | temperature, K |
| velocity vector, cm s−1 | |
| Greek letters | |
| transfer coefficient, water transport coefficient kmol2 (J·m·s)−1 | |
| porosity | |
| overpotential, V | |
| contact angle | |
| ionic conductivity of the membrane, S/cm | |
| λ | water content |
| dynamic viscosity, kg m−1s−1 | |
| μw | membrane water chemical potential |
| velocity, m s−1 | |
| ρ | density, kg m−3 |
| σ | standard conductivity in the electronically conducting phase, S/cm |
| tortuosity | |
| κ | thermal conductivity, Wm−1 K−1 |
| ϕ | source term of charge |
| Subscripts and superscripts | |
| act | activation |
| an | anode |
| ca | cathode |
| e | electrolyte |
| eq | equilibrium |
| G | gas phase |
| H2 | hydrogen |
| H2O | water |
| O2 | oxygen |
| ref | reference |
| s | solid |
References
- Wang, Y.; Chen, K.S.; Mishler, J.; Cho, S.C.; Adroher, X.C. A review of polymer electrolyte membrane fuel cells: Technology, applications, and needs on fundamental research. Appl. Energy 2011, 88, 981–1007. [Google Scholar] [CrossRef]
- Lai, J.-S.; Ellis, M.W. Fuel cell power systems and applications. Proc. IEEE 2017, 105, 2166–2190. [Google Scholar] [CrossRef]
- Sun, L.; Jin, Y.; Pan, L.; Shen, J.; Lee, K.Y. Efficiency analysis and control of a grid-connected PEM fuel cell in distributed generation. Energy Convers. Manag. 2019, 195, 587–596. [Google Scholar] [CrossRef]
- Alaswad, A.; Omran, A.; Sodre, J.R.; Wilberforce, T.; Pignatelli, G.; Dassisti, M.; Baroutaji, A.; Olabi, A.G. Technical and commercial challenges of proton-exchange membrane (PEM) fuel cells. Energies 2020, 14, 144. [Google Scholar] [CrossRef]
- Wang, Y.; Diaz, D.F.R.; Chen, K.S.; Wang, Z.; Adroher, X.C. Materials, technological status, and fundamentals of PEM fuel cells—A review. Mater. Today 2020, 32, 178–203. [Google Scholar] [CrossRef]
- Wright, S. Comparison of the theoretical performance potential of fuel cells and heat engines. Renew. Energy 2004, 29, 179–195. [Google Scholar] [CrossRef]
- Gittleman, C.; Jorgensen, S.; Waldecker, J.; Hirano, S.; Mehall, M. Automotive fuel cell R&D needs. In DOE Fuel Cell Pre-Solicitation Workshop; Department of Energy: Lakewood, CO, USA, 2010. [Google Scholar]
- James, B.D.; Kalinoski, J.A.; Baum, K.N. Mass Production Cost Estimation for Direct H2 PEM Fuel Cell Systems for Automotive Applications: 2008 Update; Contract No. GS-10F-0099J; U.S. Department of Energy: Washington, DC, USA, 2009.
- Weihai, J.; Zhongwen, Z.; Cheng, L.; Minxin, K.; Chong, Z.; Boqi, S. Model-based fuzzy control for the thermal management of PEM fuel cells. In Proceedings of the 2020 Chinese Automation Congress (CAC), Shanghai, China, 6–8 November 2020. [Google Scholar]
- Baroutaji, A.; Arjunan, A.; Ramadan, M.; Robinson, J.; Alaswad, A.; Abdelkareem, M.A.; Olabi, A.-G. Advancements and prospects of thermal management and waste heat recovery of PEMFC. Int. J. Thermofluids 2021, 9, 100064. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, M.; Zaman, S.; Xing, S.; Wang, M.; Wang, H. Thermal management system for liquid-cooling PEMFC stack: From primary configuration to system control strategy. eTransportation 2022, 12, 100165. [Google Scholar] [CrossRef]
- Marappan, M.; Palaniswamy, K.; Velumani, T.; Chul, K.B.; Velayutham, R.; Shivakumar, P.; Sundaram, S. Performance studies of proton exchange membrane fuel cells with different flow field designs—review. Chem. Rec. 2021, 21, 663–714. [Google Scholar] [CrossRef]
- Zhang, G.; Kandlikar, S.G. A critical review of cooling techniques in proton exchange membrane fuel cell stacks. Int. J. Hydrogen Energy 2012, 37, 2412–2429. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Lu, Z. Thermal management issues in a PEMFC stack—A brief review of current status. Appl. Therm. Eng. 2009, 29, 1276–1280. [Google Scholar] [CrossRef]
- Daud, W.; Rosli, R.; Majlan, E.; Hamid, S.; Mohamed, R.; Husaini, T. PEM fuel cell system control: A review. Renew. Energy 2017, 113, 620–638. [Google Scholar] [CrossRef]
- Yuan, J.; Faghri, M.; Sundén, B. On heat and mass transfer phenomena in PEMFC and SOFC and modeling approaches. In Transport Phenomena in Fuel Cells; WIT Press: Southampton, UK, 2005; Volume 19, p. 133. [Google Scholar]
- Ramousse, J.; Lottin, O.; Didierjean, S.; Maillet, D. Heat sources in proton exchange membrane (PEM) fuel cells. J. Power Sources 2009, 192, 435–441. [Google Scholar] [CrossRef]
- Lai, Y.-H.; Rapaport, P.A.; Ji, C.; Kumar, V. Channel intrusion of gas diffusion media and the effect on fuel cell performance. J. Power Sources 2008, 184, 120–128. [Google Scholar] [CrossRef]
- Kandlikar, S.; Lu, Z.; Lin, T.; Cooke, D.; Daino, M. Uneven gas diffusion layer intrusion in gas channel arrays of proton exchange membrane fuel cell and its effects on flow distribution. J. Power Sources 2009, 194, 328–337. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Zaffou, R.; Yi, J.S.; Kunz, H.R.; Fenton, J.M. Temperature-driven water transport through membrane electrode assembly of proton exchange membrane fuel cells. Electrochem. Solid-State Lett. 2006, 9, A418. [Google Scholar] [CrossRef]
- Kim, S.; Mench, M.M. Investigation of temperature-driven water transport in polymer electrolyte fuel cell: Thermo-osmosis in membranes. J. Membr. Sci. 2009, 328, 113–120. [Google Scholar] [CrossRef]
- Rodatz, P.; Büchi, F.; Onder, C.; Guzzella, L. Operational aspects of a large PEFC stack under practical conditions. J. Power Sources 2004, 128, 208–217. [Google Scholar] [CrossRef]
- Bargal, M.H.; Abdelkareem, M.A.; Tao, Q.; Li, J.; Shi, J.; Wang, Y. Liquid cooling techniques in proton exchange membrane fuel cell stacks: A detailed survey. Alex. Eng. J. 2020, 59, 635–655. [Google Scholar] [CrossRef]
- Han, J.; Yu, S. Ram air compensation analysis of fuel cell vehicle cooling system under driving modes. Appl. Therm. Eng. 2018, 142, 530–542. [Google Scholar] [CrossRef]
- Yu, S.; Jung, D. A study of operation strategy of cooling module with dynamic fuel cell system model for transportation application. Renew. Energy 2010, 35, 2525–2532. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, G.; Zhang, X.; Sun, C.; Jiao, K.; Wang, Y. Thermal management of polymer electrolyte membrane fuel cells: A review of cooling methods, material properties, and durability. Appl. Energy 2021, 286, 116496. [Google Scholar] [CrossRef]
- Sasmito, A.P.; Birgersson, E.; Mujumdar, A.S. Numerical evaluation of various thermal management strategies for polymer electrolyte fuel cell stacks. Int. J. Hydrogen Energy 2011, 36, 12991–13007. [Google Scholar] [CrossRef]
- Soupremanien, U.; Le Person, S.; Favre-Marinet, M.; Bultel, Y. Tools for designing the cooling system of a proton exchange membrane fuel cell. Appl. Therm. Eng. 2012, 40, 161–173. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Feng, Y. Experimental and theoretical studies of nanofluid thermal conductivity enhancement: A review. Nanoscale Res. Lett. 2011, 6, 229. [Google Scholar] [CrossRef] [PubMed]
- Godson, L.; Raja, B.; Lal, D.M.; Wongwises, S. Enhancement of heat transfer using nanofluids—An overview. Renew. Sustain. Energy Rev. 2010, 14, 629–641. [Google Scholar] [CrossRef]
- Wong, K.V.; De Leon, O. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010, 2, 519659. [Google Scholar] [CrossRef]
- Wang, X.-Q.; Mujumdar, A.S. A review on nanofluids-part II: Experiments and applications. Braz. J. Chem. Eng. 2008, 25, 631–648. [Google Scholar] [CrossRef]
- Najafi, B.; Mamaghani, A.H.; Baricci, A.; Rinaldi, F.; Casalegno, A. Mathematical modelling and parametric study on a 30 kWel high temperature PEM fuel cell based residential micro cogeneration plant. Int. J. Hydrogen Energy 2015, 40, 1569–1583. [Google Scholar] [CrossRef]
- Islam, M.; Shabani, B.; Rosengarten, G.; Andrews, J. The potential of using nanofluids in PEM fuel cell cooling systems: A review. Renew. Sustain. Energy Rev. 2015, 48, 523–539. [Google Scholar] [CrossRef]
- McMullen, P.; Mohapatra, S.; Donovan, E. Advances in PEM fuel cell nano-coolant. In Fuel Cell Seminar & Energy Exposition; Curran Associates Inc.: Columbus, OH, USA, 2013. [Google Scholar]
- Xuan, Y.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Madheswaran, D.K.; Vengatesan, S.; Varuvel, E.G.; Praveenkumar, T.; Jegadheeswaran, S.; Pugazhendhi, A.; Arulmozhivarman, J. Nanofluids as a coolant for polymer electrolyte membrane fuel cells: Recent trends, challenges, and future perspectives. J. Clean. Prod. 2023, 424, 138763. [Google Scholar] [CrossRef]
- Zakaria, I.; Mohamed, W.; Bin Mamat, A.; Saidur, R.; Azmi, W.; Mamat, R.; Sainan, K.; Ismail, H. Thermal analysis of heat transfer enhancement and fluid flow for low concentration of Al2O3 water-ethylene glycol mixture nanofluid in a single PEMFC cooling plate. Energy Procedia 2015, 79, 259–264. [Google Scholar] [CrossRef]
- Zakaria, I.; Azmi, W.; Mamat, A.; Mamat, R.; Saidur, R.; Abu Talib, S.; Mohamed, W. Thermal analysis of Al2O3–water ethylene glycol mixture nanofluid for single PEM fuel cell cooling plate: An experimental study. Int. J. Hydrogen Energy 2016, 41, 5096–5112. [Google Scholar] [CrossRef]
- Bargal, M.H.S.; Souby, M.M.; Abdelkareem, M.A.A.; Sayed, M.; Tao, Q.; Chen, M.; Wang, Y. Experimental investigation of the thermal performance of a radiator using various nanofluids for automotive PEMFC applications. Int. J. Energy Res. 2021, 45, 6831–6849. [Google Scholar] [CrossRef]
- Johari, M.N.I.; Zakaria, I.A.; Azmi, W.; Mohamed, W. Green bio glycol Al2O3-SiO2 hybrid nanofluids for PEMFC: The thermal-electrical-hydraulic perspectives. Int. Commun. Heat Mass Transf. 2022, 131, 105870. [Google Scholar] [CrossRef]
- Khalid, S.; Zakaria, I.; Azmi, W.H.; Mohamed, W.A.N.W. Thermal–electrical–hydraulic properties of Al2O3–SiO2 hybrid nanofluids for advanced PEM fuel cell thermal management. J. Therm. Anal. Calorim. 2021, 143, 1555–1567. [Google Scholar] [CrossRef]
- Mei, B.; Barnoon, P.; Toghraie, D.; Su, C.-H.; Nguyen, H.C.; Khan, A. Energy, exergy, environmental and economic analyzes (4E) and multi-objective optimization of a PEM fuel cell equipped with coolant channels. Renew. Sustain. Energy Rev. 2022, 157, 112021. [Google Scholar] [CrossRef]
- Ma, H.; Liu, J.; Liang, W.; Li, J.; Zhao, W.; Sun, P.; Ji, Q. Effects of PEMFC cooling channel insulation coating on heat transfer and electrical discharge characteristics of nanofluid coolants. Appl. Energy 2024, 357, 122514. [Google Scholar] [CrossRef]
- Sahin, F.; Acar, M.C.; Genc, O. Experimental determination of NiFe2O4-water nanofluid thermophysical properties and evaluation of its potential as a coolant in polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2024, 50, 1572–1583. [Google Scholar] [CrossRef]
- Kaiser, R.; Ahn, C.-Y.; Kim, Y.-H.; Park, J.-C. Performance and mass transfer evaluation of PEM fuel cells with straight and wavy parallel flow channels of various wavelengths using CFD simulation. Int. J. Hydrogen Energy 2024, 51, 1326–1344. [Google Scholar] [CrossRef]
- Kaiser, R.; Ahn, C.Y.; Lee, S.Y.; Kim, Y.H.; Park, J.C. Numerical Analysis of Water Management and Reactant Distribution in PEM Fuel Cells with a Convergent 5-Channel Serpentine Flow Field for Emission-Free Ships. Int. J. Nav. Archit. Ocean Eng. 2025, 17, 100649. [Google Scholar] [CrossRef]
- Kaiser, R.; Ahn, C.-Y.; Kim, Y.-H.; Park, J.-C. Towards Reliable Prediction of Performance for Polymer Electrolyte Membrane Fuel Cells via Machine Learning-Integrated Hybrid Numerical Simulations. Processes 2024, 12, 1140. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer electrolyte fuel cell model. J. Electrochem. Soc. 1991, 138, 2334. [Google Scholar] [CrossRef]
- Tawfik, H.; Hung, Y.; Mahajan, D. Metal bipolar plates for PEM fuel cell—A review. J. Power Sources 2007, 163, 755–767. [Google Scholar] [CrossRef]
- Karimi, S.; Fraser, N.; Roberts, B.; Foulkes, F.R. A review of metallic bipolar plates for proton exchange membrane fuel cells: Materials and fabrication methods. Adv. Mater. Sci. Eng. 2012, 2012, 828070. [Google Scholar] [CrossRef]
- Macedo-Valencia, J.; Sierra, J.; Figueroa-Ramírez, S.; Díaz, S.; Meza, M. 3D CFD modeling of a PEM fuel cell stack. Int. J. Hydrogen Energy 2016, 41, 23425–23433. [Google Scholar] [CrossRef]
- Hernández-Herrera, C.; Sierra, J.; Ordoñez, L.; Figueroa-Ramírez, S.; Mandujano-Ramírez, H. Numerical assessment of heat transfer on a PEM fuel cell stack with different refrigeration systems: Heat source management. Int. J. Electrochem. Sci. 2022, 17, 220554. [Google Scholar] [CrossRef]
- Chaudhari, S.; Chakule, R.; Talmale, P. Experimental study of heat transfer characteristics of Al2O3 and CuO nanofluids for machining application. Mater. Today Proc. 2019, 18, 788–797. [Google Scholar] [CrossRef]
- Tlili, I.; Rabeti, M.; Shadloo, M.S.; Abdelmalek, Z. Forced convection heat transfer of nanofluids from a horizontal plate with convective boundary condition and a line heat source embedded in porous media. J. Therm. Anal. Calorim. 2020, 141, 2081–2094. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Lu, Z. Fundamental research needs in combined water and thermal management within a proton exchange membrane fuel cell stack under normal and cold-start conditions. J. Fuel Cell Sci. Technol. 2009, 6, 044001. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Lu, Z.; Trabold, T.A. Current status and fundamental research needs in thermal management within a PEMFC stack; Keynote Paper. In Proceedings of the 10th UK Heat Transfer Conference, Edinburgh, UK, 10–12 September 2007. [Google Scholar]
- Ge, N.; Banerjee, R.; Muirhead, D.; Lee, J.; Liu, H.; Shrestha, P.; Wong, A.; Jankovic, J.; Tam, M.; Susac, D.; et al. Membrane dehydration with increasing current density at high inlet gas relative humidity in polymer electrolyte membrane fuel cells. J. Power Sources 2019, 422, 163–174. [Google Scholar] [CrossRef]
- Dannenberg, K.; Ekdunge, P.; Lindbergh, G. Mathematical model of the PEMFC. J. Appl. Electrochem. 2000, 30, 1377–1387. [Google Scholar] [CrossRef]
- Işıklı, F.; Işıklı, H.; Sürmen, A. Effect of Number of Channels on Performance of PEM Fuel Cells for Serpentine Type Channel Configuration. Arabian J. Sci. Eng. 2025, 50, 2595–2612. [Google Scholar] [CrossRef]
- Khan, S.S.; Shareef, H.; Ibrahim, A.A. Improved semi-empirical model of proton exchange membrane fuel cell incorporating fault diagnostic feature. J. Mod. Power Syst. Clean Energy 2020, 9, 1566–1573. [Google Scholar] [CrossRef]
- Alirezaie, A.; Hajmohammad, M.H.; Ahangar, M.R.H.; Esfe, M.H. Price-performance evaluation of thermal conductivity enhancement of nanofluids with different particle sizes. Appl. Therm. Eng. 2018, 128, 373–380. [Google Scholar] [CrossRef]
- Sergis, A.; Hardalupas, Y. Anomalous heat transfer modes of nanofluids: A review based on statistical analysis. Nanoscale Res. Lett. 2011, 6, 391. [Google Scholar] [CrossRef] [PubMed]




| Equations | |
|---|---|
| Mass | |
| Momentum | |
| Species | |
| Energy | |
| Charge |
| BP | FCL/CC | CL | GDL | Membrane | |
|---|---|---|---|---|---|
| Mass | |||||
| Momentum | |||||
| Species (gas) | |||||
| Energy | Anode CL: Cathode CL: | ||||
| Charge | ; | , | Anode CL: ; Cathode CL: ; | ; | ; |
| Component | Mesh Operations | No. of Cells |
|---|---|---|
| Anode BPL | Automated Polyhedral Mesher | 18,390 |
| Anode GDL | Directed Polygonal Mesher | 22,533 |
| Anode CL | Directed Polygonal Mesher | 32,190 |
| Membrane | Directed Polygonal Mesher | 32,190 |
| Cathode Cl | Directed Polygonal Mesher | 32,190 |
| Cathode FCL | Directed Polygonal Mesher | 1580 |
| Cathode GDL | Directed Polygonal Mesher | 22,533 |
| Cooling BPL | Automated Polyhedral Mesher | 3716 |
| Cooling FCL | Directed Polygonal Mesher | 2748 |
| Parameters | Values |
|---|---|
| Membrane density | 1970 kg m−3 |
| Equivalent weight of membrane, EW | 1100 kg kmol−1 |
| Membrane specific heat | 903 Jk−1 K−1 |
| CL Porosity/Contact Angle | 0.2/145° |
| CL tortuosity | 1.1 |
| CL thermal conductivity | 1.0 Wm−1 K−1 |
| CL electrical conductivity | 2000 S m−1 |
| GDL Porosity/Contact Angle | 0.4/145° |
| GDL tortuosity | 1.2 |
| GDL Resistivity | 8 mΩ cm2 |
| GDL thermal conductivity | 1.3 Wm−1 K−1 |
| GDL electrical conductivity | 5000 S m−1 |
| BPL density | 2250 Kg m−3 |
| BPL thermal conductivity | 24.0 Wm−1 K−1 |
| BPL specific heat | 707.68 JKg−1 K−1 |
| BPL electrical conductivity | 125,000 S m−1 |
| Permeability of anode/cathode gas diffusion layers, K | 8.7 × 10−14 |
| 695 × V−3.638 (A m−2) | |
| 0.695 × V−3.638 (A m−2) | |
| Anode apparent charge transfer coefficient | 2 |
| Cathode apparent charge transfer coefficient | 2 |
| H2 diffusivity | 1.10 × 10−4 |
| H2O diffusivity | 7.35 × 10−5 |
| O2 diffusivity | 3.30 × 10−5 |
| O2 diffusivity | 4.00 × 10−5 |
| Anode FCL | Cathode FCL | Coolant Channel | |
|---|---|---|---|
| Species mole fraction | H2: 0.90|H2O: 0.10 | O2: 0.21|N2 = 0.79 | |
| Mass flow rate | 3.42 × 10−7 (kg s−1) | 3.26 × 10−5 (kg s−1) | 1.38 × 10−4 (kg s−1) |
| Temperature | 300.15 K | 300.15 K | 300.15 |
| Pressure at the outlet | Atmospheric | Atmospheric | Atmospheric |
| Wall treatment | No-slip | No-slip | No-slip |
| Nano Particle/Base Fluid | Thermal Conductivity κ, Wm−1 K−1 | Density ρ, kg m−3 | Specific Heat JKg−1 K−1 | Dynamic Viscosity Pa s |
|---|---|---|---|---|
| Deionized water | 0.613 | 999 | 4179 | 0.000844 |
| CuO | 0.736 | 1052.2 | 3966.50 | 0.00068 |
| Al2O3 | 0.765 | 1007.4 | 4154.7 | 0.000612 |
| Mesh | 123 | 234 | 345 | 135 |
| r | 1.33 | 1.33 | 1.33 | 1.7689 |
| f1 | 331.479 | 331.934 | 331.915 | 331.915 |
| f2 | 320.096 | 331.479 | 331.934 | 331.479 |
| f3 | 314.89 | 320.096 | 331.479 | 314.89 |
| p | 2.743222 | 11.28968 | 331.934 | 6.379947 |
| Electric current density (A m−2) | 341.0726 | 331.9529 | 331.915 | 331.9268 |
| −0.03434 | −0.00137 | 5.72 × 10−5 | −0.00131 | |
| GCIfine | 3.617739 | 0.007134 | 5.55 × 10−44 | 0.004432 |
| GCIcoarse | 8.191542 | 0.178723 | 0.007155 | 0.168853 |
| R | 2.186516 | 0.039972 | −0.04176 | 0.026282 |
| Coolant | Avg. Temp. (K) | Max. Temp. (K) | Surface Standard Deviation of Temp on Cathode CL. | Pressure Drop on Cathode Side, Top Channel, Pin − Pout (Bar) | Pressure Drop on Cathode Side, Bottom Channel Pin − Pout (Bar) |
|---|---|---|---|---|---|
| Without | 301.48 | 307.37 | 3.25 × 10−1 | −8.91 × 10−2 | 1.85 |
| With water | 301.31 | 303.91 | 3.01 × 10−1 | −8.85 × 10−2 | 1.86 |
| With CuO | 301.29 | 303.98 | 1.64 × 10−1 | −1.22 × 10−1 | 1.85 |
| With Al2O3 | 301.28 | 303.81 | 1.19 × 10−1 | −9.25 × 10−2 | 1.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaiser, R.; Jeong, S.-M.; Park, J.-C. Nanofluid Cooling Enhances PEM Fuel Cell Stack Performance via 3D Multiphysics Simulation. Energies 2025, 18, 5824. https://doi.org/10.3390/en18215824
Kaiser R, Jeong S-M, Park J-C. Nanofluid Cooling Enhances PEM Fuel Cell Stack Performance via 3D Multiphysics Simulation. Energies. 2025; 18(21):5824. https://doi.org/10.3390/en18215824
Chicago/Turabian StyleKaiser, Rashed, Se-Min Jeong, and Jong-Chun Park. 2025. "Nanofluid Cooling Enhances PEM Fuel Cell Stack Performance via 3D Multiphysics Simulation" Energies 18, no. 21: 5824. https://doi.org/10.3390/en18215824
APA StyleKaiser, R., Jeong, S.-M., & Park, J.-C. (2025). Nanofluid Cooling Enhances PEM Fuel Cell Stack Performance via 3D Multiphysics Simulation. Energies, 18(21), 5824. https://doi.org/10.3390/en18215824







