Generalized Extreme Value Statistics for Scaling Oil Recovery from Water-Wet and Mixed-Wet Carbonate Rock
Abstract
1. Introduction
2. Materials and Methods
2.1. Brines
2.2. Oils
2.3. Core Plugs
2.4. Core Plug Saturation and Aging
2.5. Spontaneous Imbibition Experiments
2.6. GEV Modeling of Oil Production Dynamics
3. Results and Discussion
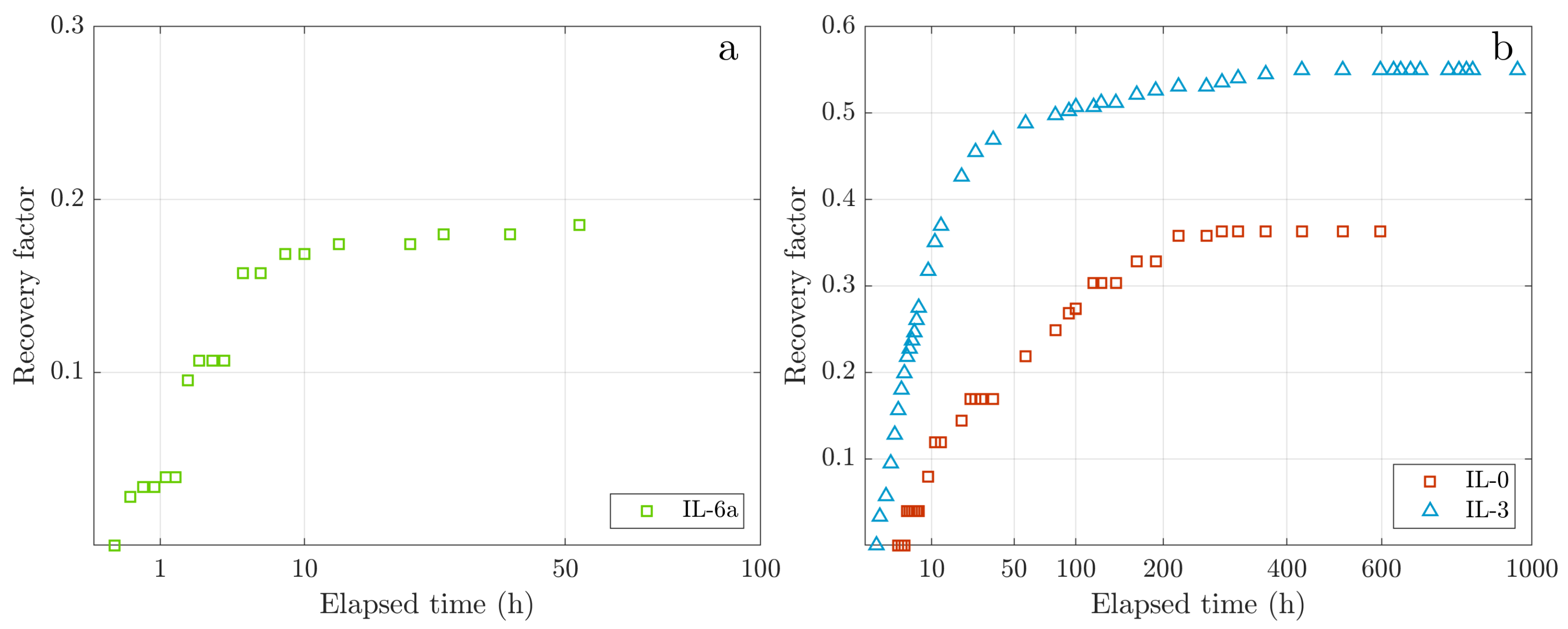
3.1. Artifacts of the Classic Amott-Cell Experiment
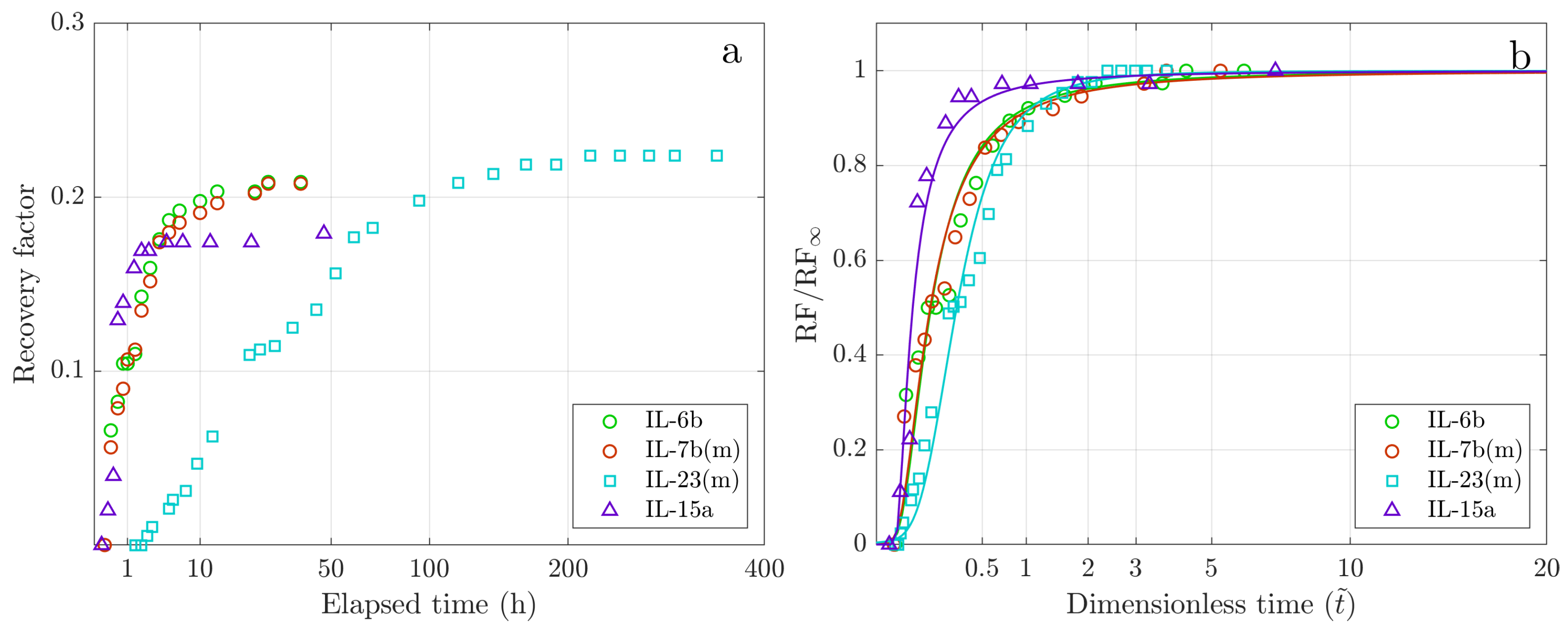
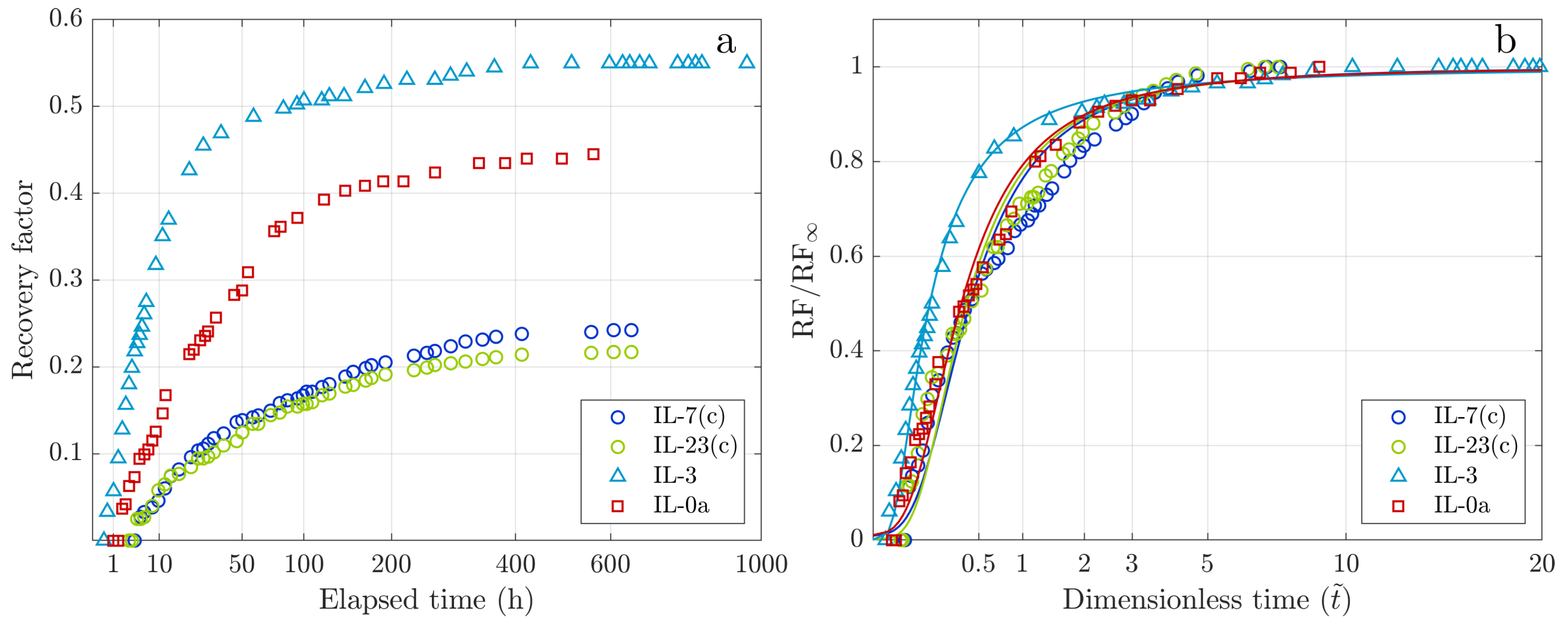
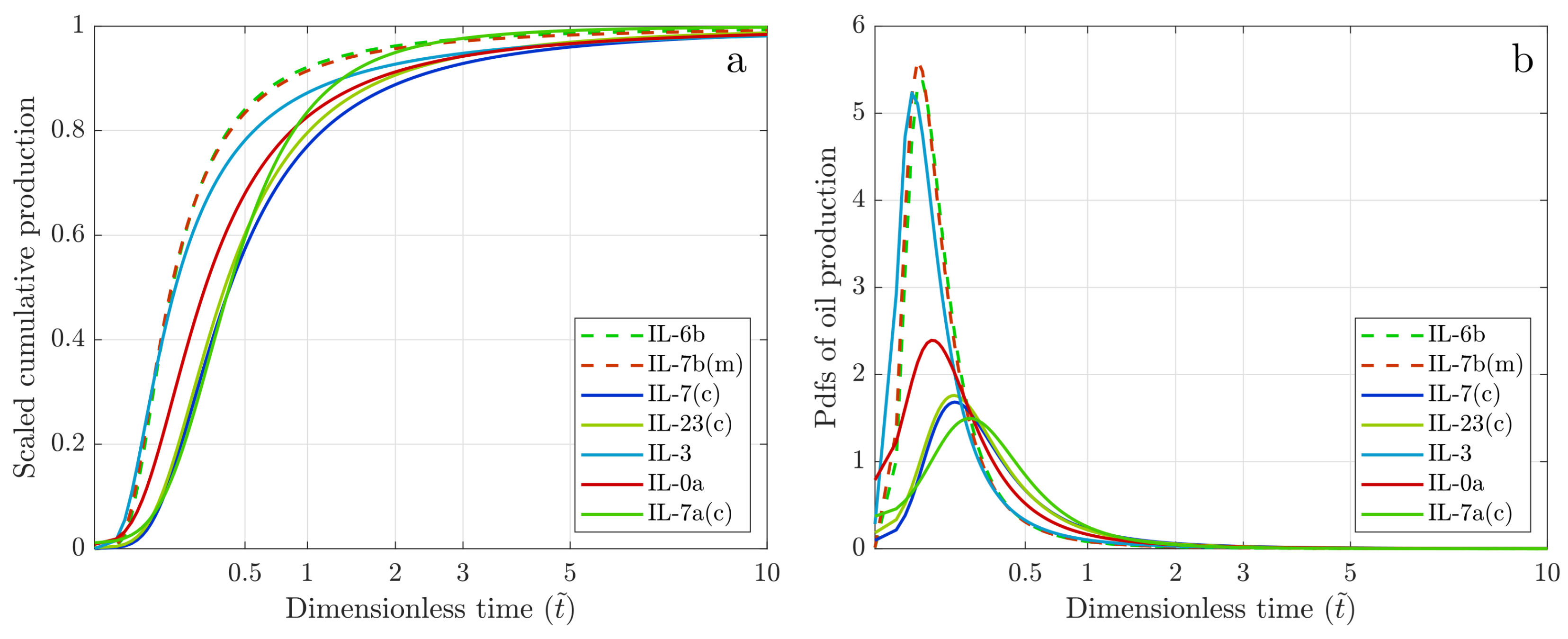
3.2. Spontaneous Imbibition and GEV Modeling Results
3.2.1. Mineral Oil/Indiana Limestone Rock
3.2.2. Crude Oil/Indiana Limestone Rock
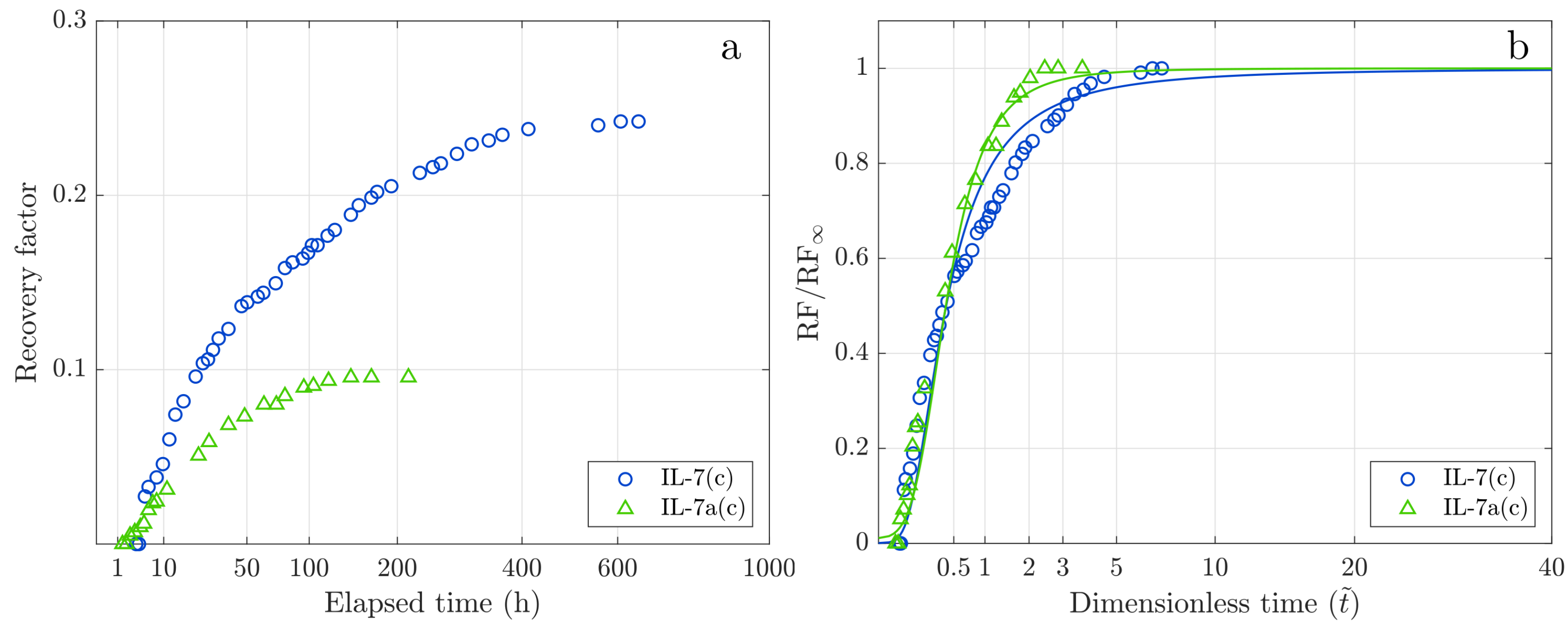
3.2.3. Core Plug Contamination
3.2.4. Summary of Spontaneous Imbibition and GEV Modeling
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Barenblatt, G.I.; Patzek, T.W.; Silin, D.B. The Mathematical Model of Non-Equilibrium Effects in Water-Oil Displacement. SPEJ 2003, 8, 409–416. [Google Scholar] [CrossRef]
- Jadhunandan, P.P.; Morrow, N.R. Effect of Wettability on Waterflood Recovery for Crude-Oil/Brine/Rock Systems. SPE Reserv. Eng. 1995, 10, 40–46. [Google Scholar] [CrossRef]
- Morrow, N.; Ma, S.; Zhou, X.; Zhang, X. Characterization of Wettability from Spontaneous Imbibition Measurements. J. Can. Pet. Technol. 1999, 38. [Google Scholar] [CrossRef]
- Salathiel, R. Oil Recovery by Surface Film Drainage In Mixed-Wettability Rocks. J. Pet. Technol. 1973, 25, 1216–1224. [Google Scholar] [CrossRef]
- Kovscek, A.R.; Wong, H.; Radke, C.J. A Pore-Level Scenario for the Development of Mixed Wettability in Oil Reservoirs. AIChE J. 1993, 39, 1072–1085. [Google Scholar] [CrossRef]
- Clerke, E.A.; Mueller, H.W., III; Phillips, E.C.; Eyvazzadeh, R.Y.; Jones, D.H.; Ramamoorthy, R.; Srivastava, A. Application of Thomeer Hyperbolas to Decode the Pore Systems, Facies and Reservoir Properties of the Upper Jurassic Arab D Limestone, Ghawar Field, Saudi Arabia: A “Rosetta Stone” Approach. GeoArabia 2008, 13, 113–160. [Google Scholar]
- Hosseinzadehsadati, S.; Bonto, M.; Mokhtari, R.; Eftekhari, A.A.; Feilberg, K.L.; Nick, H.M. Modified salinity waterflooding in chalk reservoirs: A journey from rock and fluid interfaces to field scale applications. Fuel 2024, 356, 129461. [Google Scholar] [CrossRef]
- Marquez, R.; Ding, H.; Barrios, N.; Vera, R.E.; Salager, J.L.; Al-Shalabi, E.W.; Mettu, S. Recent Advances in Enhanced Oil Recovery with Low-Salinity Waterflooding and Its Hybrid Methods in Carbonate Reservoirs. Energy Fuels 2025, 39, 8769–8799. [Google Scholar] [CrossRef]
- Zhang, P.; Tweheyo, M.T.; Austad, T. Wettability Alteration and Improved Oil Recovery by Spontaneous Imbibition of Seawater into Chalk: Impact of the Potential Determining Ions Ca2+, Mg2+, and SO42−. Colloids Surf. A Physicochem. Eng. Asp. 2007, 301, 199–208. [Google Scholar] [CrossRef]
- Song, J.; Wang, Q.; Shaik, I.; Puerto, M.; Bikkina, P.; Aichele, C.; Biswal, S.L.; Hirasaki, G.J. Effect of salinity, Mg2+ and SO42− on “smart water”-induced carbonate wettability alteration in a model oil system. J. Colloid Interface Sci. 2020, 563, 145–155. [Google Scholar] [CrossRef]
- Mushabe, R.; Azizov, I.; Adejumo, G.; van der Net, A.; Berg, C.F. Ion Composition Effect on Spontaneous Imbibition in Limestone Cores. Energy Fuels 2022, 36, 12491–12509. [Google Scholar] [CrossRef]
- Akindipe, D.; Saraji, S.; Piri, M. Carbonated Water Injection in Oil-Wet Carbonate Rock Samples: A Pore-Scale Experimental Investigation of the Effect of Brine Composition. Energy Fuels 2022, 36, 4847–4870. [Google Scholar] [CrossRef]
- Khan, M.A.I.; Torrijos, I.D.P.; Algazban, S.H.A.; Strand, S.; Puntervold, T. Polysulphate: A New Eor Additive to Maximize the Oil Recovery from Carbonate Reservoirs at High Temperature. In Proceedings of the ADIPEC, Abu Dhabi, UAE, 31 October 2022. [Google Scholar] [CrossRef]
- Khan, M.A.I.; Pinerez Torrijos, I.D.; Ullah, H.; Puntervold, T.; Strand, S. Comparing Inexpensive, customized brine compositions for enhanced oil recovery in high temperature outcrop and reservoir chalk. Fuel 2025, 396, 135337. [Google Scholar] [CrossRef]
- Zahedi, M.; Dehaghani, A.H.S. Mechanistic evaluation of surfactant assisted smart water flooding with sulfate and phosphate anions. Sci. Rep. 2025, 15, 31594. [Google Scholar] [CrossRef]
- Morrow, N.R.; Mason, G. Recovery of Oil by Spontaneous Imbibition. Curr. Opin. Colloid Interface Sci. 2001, 6, 321–337. [Google Scholar] [CrossRef]
- Mason, G.; Morrow, N.R. Developments in Spontaneous Imbibition and Possibilities for Future Work. J. Pet. Sci. Eng. 2013, 110, 268–293. [Google Scholar] [CrossRef]
- Meng, Q.; Liu, H.; Wang, J. A critical review on fundamental mechanisms of spontaneous imbibition and the impact of boundary condition, fluid viscosity and wettability. Adv.-Geo-Energy Res. 2017, 1, 1–17. [Google Scholar] [CrossRef]
- Karimova, M.; Kashiri, R.; Pourafshary, P.; Hazlett, R. A Review of Wettability Alteration by Spontaneous Imbibition Using Low-Salinity Water in Naturally Fractured Reservoirs. Energies 2023, 16, 2373. [Google Scholar] [CrossRef]
- Xiao, Y.; You, Z.; He, Y.; Du, Z.; Zheng, J.; Wang, L. Capillary-dominated imbibition in heterogeneous-wet reservoirs: Mechanisms, characterizations, and critical insights. Geoenergy Sci. Eng. 2025, 246, 213606. [Google Scholar] [CrossRef]
- Patzek, T.W. Verification of a Complete Pore Network Model of Drainage and Imbibition. SPEJ 2001, 6, 144–156. [Google Scholar] [CrossRef]
- Akin, S.; Schembre, J.M.; Bhat, S.K.; Kovscek, A.R. Spontaneous Imbibition Characteristics of Diatomite. J. Petroleum Sci. Eng. 2000, 25, 149–165. [Google Scholar] [CrossRef]
- Amott, E. Observations Relating to the Wettability of Porous Rock. Pet. Trans. AIME 1959, 216, 156–162. [Google Scholar] [CrossRef]
- Graue, A.; Viksund, B.G.; Eilertsen, T.; Moe, R. Systematic Wettability Alteration by Aging Sandstone and Carbonate Rock in Crude Oil. J. Pet. Sci. Eng. 1999, 24, 85–97. [Google Scholar] [CrossRef]
- Babadagli, T. Dynamics of Capillary Imbibition When Surfactant, Polymer, and Hot Water Are Used as Aqueous Phase for Oil Recovery. J. Colloid Interface Sci. 2002, 246, 203–213. [Google Scholar] [CrossRef]
- Clerke, E.; Funk, J.; Shtepani, E. Spontaneous Imbibition of Water into Oil Saturated M_1 Bimodal Limestone. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2013. [Google Scholar] [CrossRef]
- Bartels, W.B.; Rücker, M.; Boone, M.; Bultreys, T.; Mahani, H.; Berg, S.; Hassanizadeh, S.M.; Cnudde, V. Imaging Spontaneous Imbibition in Full Darcy-Scale Samples at Pore-Scale Resolution by Fast X-ray Tomography. Water Resour. Res. 2019, 55, 7072–7085. [Google Scholar] [CrossRef]
- Cobos, J.E.; Sandnes, M.; Steinsbo, M.; Brattekas, B.; Sogaard, E.G.; Graue, A. Evaluation of Wettability Alteration in Heterogeneous Limestone at Microscopic and Macroscopic Levels. J. Pet. Sci. Eng. 2021, 202, 108534. [Google Scholar] [CrossRef]
- Tang, G.Q.; Firoozabadi, A. Effect of Pressure Gradient and Initial Water Saturation on Water Injection in Water-Wet and Mixed-Wet Fractured Porous Media. SPE Reserv. Eval. Eng. 2001, 4, 516–524. [Google Scholar] [CrossRef]
- Fernø, M.A.; Torsvik, M.; Haugland, S.; Graue, A. Dynamic Laboratory Wettability Alteration. Energy Fuels 2010, 24, 3950–3958. [Google Scholar] [CrossRef]
- Zhou, X.; Morrow, N.; Ma, S. Interrelationship of Wettability, Initial Water Saturation, Aging Time, and Oil Recovery by Spontaneous Imbibition and Waterflooding. SPE J. 2000, 5, 199–207. [Google Scholar] [CrossRef]
- Kaprielova, K.M.; Yutkin, M.P.; Mowafi, M.; Gmira, A.; Ayirala, S.; Yousef, A.; Radke, C.J.; Patzek, T.W. Improved Amott Method to Determine Oil Recovery Dynamics from Water-Wet Limestone Using GEV Statistics. Energies 2024, 17, 3599. [Google Scholar] [CrossRef]
- Kashchiev, D.; Firoozabadi, A. Analytical Solutions for 1D Countercurrent Imbibition in Water-Wet Media. SPE J. 2003, 8, 401–408. [Google Scholar] [CrossRef]
- Schmid, K.S.; Geiger, S. Universal scaling of spontaneous imbibition for water-wet systems. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Schmid, K.; Geiger, S. Universal scaling of spontaneous imbibition for arbitrary petrophysical properties: Water-wet and mixed-wet states and Handy’s conjecture. J. Pet. Sci. Eng. 2013, 101, 44–61. [Google Scholar] [CrossRef]
- Schmid, K.S.; Alyafei, N.; Geiger, S.; Blunt, M.J. Analytical Solutions for Spontaneous Imbibition: Fractional-Flow Theory and Experimental Analysis. SPE J. 2016, 21, 2308–2316. [Google Scholar] [CrossRef]
- Guen, S.S.L.; Kovscek, A.R. Nonequilibrium Effects During Spontaneous Imbibition. Transp. Porous Media 2006, 63, 127–146. [Google Scholar] [CrossRef]
- Schembre, J.M.; Kovscek, A.R. Estimation of Dynamic Relative Permeability and Capillary Pressure from Countercurrent Imbibition Experiments. Transp. Porous Media 2006, 65, 31–51. [Google Scholar] [CrossRef]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar] [CrossRef]
- Arias-Ortiz, D.; Patzek, T.W. Physics-based, data-driven production forecasting in the Utica and Point Pleasant Formation. Geoenergy Sci. Eng. 2025, 246, 213491. [Google Scholar] [CrossRef]
- McPhee, C.; Reed, J.; Zubizarreta, I. Chapter 7—Wettability and Wettability Tests. In Core Analysis; McPhee, C., Reed, J., Zubizarreta, I., Eds.; Developments in Petroleum Science; Elsevier: London, UK, 2015; Volume 64, pp. 313–345. [Google Scholar] [CrossRef]
- Patzek, T.W.; Male, F.; Marder, M. Gas Production in the Barnett Shale Obeys a Simple Scaling Theory. Proc. Natl. Acad. Sci. USA 2013, 110, 19731–19736. [Google Scholar] [CrossRef] [PubMed]
- Schechter, D.; Zhou, D.; Orr, F. Low IFT Drainage and Imbibition. J. Pet. Sci. Eng. 1994, 11, 283–300. [Google Scholar] [CrossRef]


| Parameter | Chlor0.1 | Chlor2.5 | Carb0.5 | Bicarb0.5 |
|---|---|---|---|---|
| NaCl, g/L | 5.85 | 87.75 | 87.75 | 117.0 |
| CaCl2·2H2O, g/L | - | 73.50 | - | - |
| Na2CO3, g/L | - | - | 53.0 | - |
| NaHCO3, g/L | - | - | - | 42.0 |
| TDS, ppm | 5850 | 143,250 | 140,750 | 159,000 |
| pH 1 | 8.3 | 6.8 | 10.7 | 8.3 |
| Interfacial tension 2, mN/m | 52 | 26 | 5 | 18 |
| Parameter | Mineral-1 | Mineral-2 | Crude |
|---|---|---|---|
| Density at 22 °C, g/cc | 0.850 | 0.884 | 0.889 |
| Density at 60 °C, g/cc | 0.825 | 0.859 | 0.855 |
| Viscosity at 22 °C, cP | 28.3 | 178.4 | 19.5 |
| Viscosity at 60 °C, cP | 7.3 | 23.5 | 6.4 |
| Asphaltenes, wt % | - | - | 2.1 |
| Total acid number, mg KOH/g | - | - | 2.1 |
| Total base number, mg KOH/g | - | - | 1.5 |
| Sample Code | Core Length, mm | Core Diameter, mm | , % | , MD | Oil Code | , Fraction | RF, Fraction | Saturation/ Aging Brine | Imbibition Brine |
|---|---|---|---|---|---|---|---|---|---|
| IL-6b | 74.2 | 38.0 | 14.8 | 19 | Mineral-1 | 0.73 | 0.209 | Chlor0.1 | Chlor0.1 |
| IL-7b(m) | 73.6 | 38.0 | 15.1 | 41 | Mineral-1 | 0.70 | 0.208 | Chlor0.1 | Chlor0.1 |
| IL-23(m) | 74.4 | 37.9 | 16.0 | 49 | Mineral-2 | 0.72 | 0.224 | Chlor0.1 | Chlor0.1 |
| IL-15a | 76.1 | 38.1 | 16.5 | 635 | Mineral-2 | 0.70 | 0.179 | Chlor0.1 | Chlor0.1 |
| IL-7(c) | 73.6 | 38.0 | 15.1 | 41 | Crude | 0.74 | 0.242 | Chlor2.5 | Chlor2.5 |
| IL-23(c) | 74.4 | 37.9 | 16.0 | 49 | Crude | 0.79 | 0.217 | Chlor2.5 | Chlor2.5 |
| IL-3 | 76.8 | 37.7 | 16.2 | 270 | Crude | 0.76 | 0.550 | Carb0.5 | Carb0.5 |
| IL-0a | 76.8 | 37.7 | 15.3 | 250 | Crude | 0.77 | 0.450 | Bicarb0.5 | Bicarb0.5 |
| IL-7a(c) | 73.6 | 38.0 | 15.1 | 41 | Crude | 0.81 | 0.096 | Chlor2.5 | Chlor2.5 |
| Sample Code | GEV , h | GEV | GEV | GEV | Peak Rate mL/h |
|---|---|---|---|---|---|
| IL-6b | 6.3 | 0.092 | 0.094 | 0.910 | 1.62 |
| IL-7b(m) | 7.2 | 0.088 | 0.094 | 0.968 | 1.44 |
| IL-23(m) | 92 | 0.215 | 0.182 | 0.457 | 0.05 |
| IL-15a | 6.6 | 0.044 | 0.034 | 0.981 | 4.22 |
| IL-7(c) | 91.4 | 0.286 | 0.285 | 0.790 | 0.04 |
| IL-23(c) | 83.1 | 0.294 | 0.289 | 0.736 | 0.04 |
| IL-3 | 41.8 | 0.091 | 0.116 | 1.160 | 0.73 |
| IL-0a | 66.3 | 0.223 | 0.259 | 0.886 | 0.13 |
| IL-7a(c) | 58.6 | 0.293 | 0.270 | 0.461 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaprielova, K.M.; Yutkin, M.P.; Gmira, A.; Ayirala, S.; Yousef, A.; Radke, C.J.; Patzek, T.W. Generalized Extreme Value Statistics for Scaling Oil Recovery from Water-Wet and Mixed-Wet Carbonate Rock. Energies 2025, 18, 5771. https://doi.org/10.3390/en18215771
Kaprielova KM, Yutkin MP, Gmira A, Ayirala S, Yousef A, Radke CJ, Patzek TW. Generalized Extreme Value Statistics for Scaling Oil Recovery from Water-Wet and Mixed-Wet Carbonate Rock. Energies. 2025; 18(21):5771. https://doi.org/10.3390/en18215771
Chicago/Turabian StyleKaprielova, Ksenia M., Maxim P. Yutkin, Ahmed Gmira, Subhash Ayirala, Ali Yousef, Clayton J. Radke, and Tadeusz W. Patzek. 2025. "Generalized Extreme Value Statistics for Scaling Oil Recovery from Water-Wet and Mixed-Wet Carbonate Rock" Energies 18, no. 21: 5771. https://doi.org/10.3390/en18215771
APA StyleKaprielova, K. M., Yutkin, M. P., Gmira, A., Ayirala, S., Yousef, A., Radke, C. J., & Patzek, T. W. (2025). Generalized Extreme Value Statistics for Scaling Oil Recovery from Water-Wet and Mixed-Wet Carbonate Rock. Energies, 18(21), 5771. https://doi.org/10.3390/en18215771








