Total Energy Balance During Thermal Charging of Cylindrical Heat Storage Units: Thermodynamic Equilibrium Limit

Abstract

The local energy balance at the liquid-solid front has been widely used in the literature. However, depending on the initial state of the system, the boundary conditions, and the thermodynamic properties of the phase change material, the local energy balance can lead to inaccuracies. The total energy balance has been applied to phase change processes; however, discrepancies have been reported regarding the dynamics of the melting front obtained through this approach. In this work, the concept of thermodynamic equilibrium is used to determine the exact liquid-solid coexistence state in adiabatic systems. Thermodynamic equilibrium of saturated mixtures is used to validate the proposed energy balance. We found that the melting front position obtained from a local energy balance can be underestimated by as much as $37.4\%$ when compared with the equilibrium value. In contrast, the interface position estimated by the total energy balance was in good agreement with equilibrium, with relative differences between $0.082\%$ and $0.11\%$. Finally, a melting experiment using paraffin RT50 was conducted in a thermally insulated cylindrical unit. The experimental front position was underestimated by the local energy balance, with differences between $2.4\%$ and $6.9\%$, while the total energy balance showed smaller discrepancies between $0.28\%$ and $5.71\%$.

1. Introduction

Thermal energy storage (TES) represents a technological option for renewable energy supply through solar energy harvesting. In general, this type of energy storage is focused on mitigating greenhouse gas emissions in several types of non-mobile technologies, such as cold energy storage [1], air conditioning supply [2], medium-temperature energy storage for domestic hot water applications [3], and high-temperature thermal storage for thermoelectric generation [4]. Two types of thermal storage have been studied: sensible and latent heat storage. The latter is more appealing because latent heat helps to improve the energy density of TES units. Latent heat thermal energy storage (LHTES) represents its own challenges since this type of storage involves one or more phase transitions, mainly solid-solid and solid-liquid [5]. Energy storage involving these types of phase transitions has been mostly studied in systems where, in general, the phase transition is out of thermodynamic equilibrium [2,6]. Additionally, volume changes resulting from a melting and solidification process require the incorporation of proper mass and energy balance into the phase transition dynamics of models in the thermodynamic limit [7,8,9,10].

The problem related to the dynamics of phase transitions is extremely relevant since two key challenges are involved in practice: heat transfer rates and energy storage capacity. Due to the high intermittency of solar radiation, both challenges are related to the need for reducing melting times and improving the balance between energy supply and demand [11]. The main goal is to achieve complete melting of the solid phase within a limited time window, typically 4–6 h a day, in order to maximize the latent heat storage capacity of TES units. The LHTES capacity that can be achieved in real applications has a great impact on the cost of energy stored and the capacity factors [11]. The low thermal conductivity of materials typically used in LHTES applications represents a technological challenge when seeking to reduce melting rates. Consequently, a great amount of experimental and theoretical work has been carried out to address this problem. Ferromagnetic nanoparticles were used in a numerical study to enhance heat transfer rates in a paraffin-based TES unit, such as in [12]. Heat transport through natural convection in a mixture of liquid paraffin and Fe₃O₄ nanoparticles was enhanced by the interaction of a magnetic field with the iron oxide particles. However, the authors treated the liquid-iron composite as a ferromagnetic fluid instead of considering the viscous flow of the paraffin and its interaction with the solid nanoparticles [12]. Rotational kinetic energy has been applied in a triplex-tube configuration, where the centripetal force was used to accelerate the melting process [13]. Horsetail stem-type fins have been proposed in a cylindrical unit to enhance heat transfer rates [14]. The proposed heat exchange mechanism achieved lower melting times compared with traditional straight fin-based configurations [14]. Effective enthalpy methods have been used to study superheating and supercooling effects in experiments under several heating and cooling rates [2]. Heat transfer was improved using a typical tube-straight fin heat exchanger in a rectangular unit [2]. Aluminum and copper foams have also been used to exploit the high thermal conductivity of metallic foams and accelerate the melting process [15,16]. Finally, confinement of materials in metallic shells has also been used to enhance heat transport [1,5,17,18,19].

Numerical and analytical models of phase transitions in the thermodynamic limit have been proposed. The mathematical treatment of liquid-solid front dynamics in many applications is often, but not exclusively, based on a local energy balance (LEB) at the interface [1,6,7,9,17,18,19,20]. The LEB proposed for different applications, geometries, and experimental conditions is generally not consistent with the first law of thermodynamics and, hence, energy conservation. The LEB is not entirely incorrect and can offer relatively accurate solutions, depending on the material and experimental conditions. Enthalpy methods and front tracking methods commonly found in the literature use an LEB approach. The volume expansion that results from a melting process depends on the relative density ${\rho }_{r_0}-1$ of the phase change material (PCM), where ${\rho }_{r_0}={\rho }_{s_0}/{\rho }_{{𝓁}_0}$ is the relation between the solid and liquid densities. Several studies found in the literature incorporate volume changes by applying a total mass balance [7,17,19,21]. However, the relative density change can also affect the energy balance in a more subtle manner [8].

Total energy conservation has been imposed through an energy balance over the entire system [8,9,10]. Recent studies have applied a total energy balance (TEB) to ice-water pipes, where heat conduction is applied along the axial direction through the pipe [9,10]. The authors estimated the front position by considering the contribution of latent and sensible heats absorbed by the ice and liquid water. The sensible heat contributions to the front dynamics were obtained by considering the time change of the total enthalpy. The energy balance was performed over the entire ice-water system instead of applying an LEB close to the front position (saturated region), where only the latent heat affected the time evolution of the interface. The authors established a non-parabolic motion of their model in contrast with the Neumann solution in semi-infinite domains, where the moving front followed the classic linear relation with the square root of time. Additionally, the energy balance discussed in these studies was compared with a TEB model which was originally applied to PCM wallboards [8]. The TEB model proposed in [8] was adapted to the geometry and boundary conditions of the ice-water pipes discussed in [9,10]. Comparisons between the two models in the conduction regime (Stefan-like problem) were performed for the moving front in a finite ice-water pipe of a length $𝓁=1.0\mathrm{m}$. Differences between the two TEB models for the time evolution of the front position could be the result of how the TEB models were applied. Thge relative difference percentages between these two models for the moving front position in a time window of 27.78 days were between 6.97% at $t^{1/2}=200\min$ and 16.39% at $t^{1/2}=50\min$ [9].

The two-phase solutions for the interface motion and obtained through the models just mentioned were compared in [9,10]. The relative percent differences mentioned earlier should not have been present since both models were applied to the same ice-water system with isothermal boundary conditions and within the conductive regime. Interface dynamics are a consequence of energy conservation and should not be the main criterion for model validation. Total energy conservation must lead to a unique solution in the conductive regime, independent of the boundary conditions, initial conditions, thermodynamic properties of the PCM, and the system’s geometry. The physics of phase transitions close to saturation and in the conductive regime should not depend on the model or how the model is applied. In this work, the proposed TEB is not validated through the interface motion but rather by probing the time evolution of the thermal energy, which must be a constant of the motion. This work represents an attempt to build consensus on the TEB and LEB models by demonstrating that total energy is conserved in a cylindrical heat storage unit.

The TEB model proposed in this work is applied to an annular region where the melting front moves radially outward in a cylindrical unit. The TEB leads to an equation of motion for the liquid-solid front that depends on the relative density change. Additionally, and in contrast to the LEB, the equation of motion for the interface also depends on the net thermal flux at the boundaries, where the entire system exchanges heat with its surroundings. Furthermore, and more importantly, the concepts of thermodynamic equilibrium and pseudothermodynamic equilibrium are used to validate the TEB model and reveal deficiencies regarding energy conservation when applying an LEB approach. Liquid-solid coexistence at thermodynamic equilibrium is an incredibly difficult thermodynamic state to achieve in practice. However, thermodynamic equilibrium can be used as a conceptual framework to test energy conservation in models and propose corrections. We find that the TEB proposed in this work is in agreement with thermodynamic equilibrium. The TEB model reproduces energy conservation and the interface position predicted through the analysis of saturated mixtures at thermodynamic equilibrium. Additionally, when comparing the solutions obtained through the LEB with the thermodynamic equilibrium limit, the deficiencies of the LEB are highlighted. Finally, melting experiments were performed in a cylindrical LHTES unit with medium-temperature paraffin as the PCM to further validate the proposed model.

2. Total and Local Energy Balance

The system under consideration is a cylindrical thermal storage unit, as illustrated in Figure 1. Heat is transferred through a metallic pipe of a radius $r_0$ and a negligible thickness. Liquid water is used as the heat transfer fluid (HTF). The unit has an external radius R that is constant in time and surrounded by a thick layer of insulating material with a thickness ${\delta }_{\mathrm{ins}}$. Thermal insulation is used to minimize heat loss to the surroundings. The space between $r=r_0$ and $r=R$ is filled with a medium-range temperature PCM. During the melting process, the PCM expands freely along the axial direction, as illustrated in Figure 1. The change in volume during the melting of the solid produces an excess volume of liquid that is removed continuously. In practice, this volume of liquid is spread over the top surface of the unit. Consequently, the phase transition from solid to liquid is taking place at a constant pressure. The most important aspect of this work is to present an equation of motion for the liquid-solid front that is designed to conserve thermal energy by considering the interaction of the entire system with its surroundings. The model belongs to the class of Stefan-like problems in the conductive regime where, in general, the proposed energy balance leads to dynamics that differ significantly from those predicted through a local thermal balance at the interface. The focus is to highlight the deficiencies of applying a local balance instead of a global balance, at least in the conductive regime and close to the saturation point. Consequently, the following assumptions were made:

• The thermodynamic properties of the liquid and solid phases were constant and equal to their values at the saturation point $\left(T_{m_0},P_0\right)$;
• The transformed solid expanded freely over the top surface, and the melting process was isobaric;
• The phase transition was close to equilibrium, and the solid close to the melting point was not superheated during the melting process. The melting temperature was equal to its liquid-solid coexistence value at thermodynamic equilibrium $T_{m_0}$;
• Heat transfer from the scattered liquid on the top surface had negligible effects on the melting process at the bottom part of the unit;
• The melting front was radially uniform, and heat transfer was radially symmetric;
• The process took place in the conductive regime. Thermal transport through natural convection was not considered when performing a total energy balance;
• The thermal conductivity of the cooper wall was much higher than the thermal conductivity of the PCM and insulating material. Consequently, the temperature within the copper wall was assumed to be equal to the temperature of the HTF.

The set of assumptions just mentioned resulted from the specific conditions used in the experiments performed in this work. The second assumption limits the applicability of the models to regions far from the top surface. The fifth assumption results from the uniform temperature distribution of the HTF. The latter is heated in a heat bath fixed at the desired temperature. During the heating process, the mass flow of the HTF is continuous and constant, compensating for thermal energy losses by circulation through the heat bath. The HTF enters the unit from the top surface and leaves the unit from the bottom surface. Consequently, the temperature of the HTF decreases only along the axial direction and from top to bottom, as shown in Figure 1. Consequently, it was assumed that the temperature of the copper surface—transporting the HTF—was uniform along the azimuthal direction. This assumption implies the formation of a circular melting front with annular layers of liquid PCM, whose temperature decreases with the depth. The top liquid layers are less dense due to thermal expansion and buoyant forces being greater than those acting on the lower layers. Consequently, the liquid was stratified and steady along the axial direction, and buoyancy-driven convection was not considered. The melted solid is allowed to expand freely along the axial direction, as illustrated in Figure 1. Therefore, the absolute pressure within the unit and during the melting process is constant. The latter implies that there are no pressure differences along the radial direction and the fluid is radially steady. Finally, pressure gradients in the azimuthal direction are not present due to the uniform temperature distribution along this direction. As a result, tangential forces that result from thermal expansion of the liquid layers are canceled, minimizing the effects of natural convection associated with the azimuthal flow in the liquid phase.

The model proposed in this work is also limited to the specific geometry and the manner in which the PCM is allowed to expand. The melted solid expands along the axial direction, as shown in Figure 1. The excess volume of liquid is removed constantly during the phase transition. The latter implies that the total mass of the PCM is not conserved. Consequently, the proposed model was applied to a specific configuration where the mass of the PCM was not constant. Alternatively, cylindrical heat storage units have been used where the expansion during the melting process is radially outward instead of along the axial direction. The top and bottom surfaces are fixed and rigid. Initially, the PCM is in its solid state and in direct contact with these surfaces. Expansion is allowed by introducing a thin air layer between the PCM and the container’s wall. The expansion of the PCM is along the radial direction, with an increasing internal pressure produced by the compression of the air layer [22]. An absolute pressure increase is practically negligible due to the high compressibility of air. In contrast to the configuration studied in this work, the scenario just described involves a total energy balance model where the total energy of the system and total mass are conserved. In this case, the total energy balance can also be applied to obtain a different equation of motion for the interface, as opposed to the equation proposed in this work. Furthermore, the total mass is a constant of the motion and imposing mass conservation leads to an additional equation of motion for the total radius of the PCM. Consequently, the radius $R\left(t\right)$ becomes a dynamic variable of motion in this particular case. Finally, in other geometries such as spherically encapsulated PCMs, the total energy balance model must also incorporate mass conservation. Configurations exist where a highly compressible layer or sacrificial layer between the PCM and the inner surface of a spherical shell is used to allow for volume expansion and minimize the inner pressure increments [23,24]. The radius of the PCM becomes a dynamic variable due to mass conservation. Additionally, spherical shells without a sacrificial layer have been used. In this case, the growth of the inner pressure due to the low compressibility of the PCM introduces complications to the thermodynamics at the liquid-solid saturation line [25]. Similar to the previous case, total mass conservation must also be applied. The inner and outer radii of the shell encapsulating the PCM become dynamic variables. The motion of the outer surface is coupled to the inner surface by the elastic properties of the PCM and spherical shell [19].

2.1. Melting Dynamics: Local Energy and Total Energy Balance

The melting point of the PCM during the solid-liquid phase transition depicted in Figure 1 was close to its value at thermodynamic equilibrium. The temperature of the HTF was relatively close to the melting point of the PCM to maintain low heating rates during the melting process. Consequently, superheating of the solid phase will be neglected in this approximation. Additionally, thermal expansion induced by temperature changes was not considered for the type of paraffin used in this work. The liquid phase, for example, showed small changes in density $[805.429-789.818]\mathrm{kg}/{\mathrm{m}}^3$ when the liquid was heated between 52 °C and 65 °C [26]. Finally, the PCM was allowed to expand along the axial direction only and through the void between the PCM’s surface and the top cover of the unit.

The solid-liquid interface dynamics will be obtained through an energy balance over the entire system. The isothermal boundary condition at the copper-PCM interface represents the thermal energy supplied by the HTF, and the isothermal boundary condition at the insulator-air interface represents the thermal losses. The difference between these energies is equal to the energy absorbed by the PCM and insulating material. The rate of energy supplied by the HTF and thermal losses at the insulator-air interface are expressed as follows:

$${\displaystyle \frac{d{Q}_{\mathrm{in}}}{dt}}=-2\pi L{r}_0{k}_{𝓁}{\displaystyle \frac{\partial T_{𝓁}}{\partial r}}{|}_{r=r_0}\mathrm{and}{\displaystyle \frac{d{Q}_{\mathrm{out}}}{dt}}=-2\pi L\left(R+{\delta }_{\mathrm{ins}}\right)k_{\mathrm{ins}}{\displaystyle \frac{\partial T_{ins}}{\partial r}}{|}_{r=R+{\delta }_{\mathrm{ins}}},$$

(1)

where $r_0$ is the outer radius of the copper tube, R represents the outer radius of the aluminum foil, and ${\delta }_{ins}$ is the thickness of the insulating material. Heat conduction through the thickness of the copper tube that separates the HTF and PCM will not alter the result because of the high thermal conductivity of copper. Similarly, the result will not be altered by considering the thickness of the aluminum foil that lies between the PCM and the insulating material. Consequently, the model does not take into account the contact conditions at the HTF-copper and PCM-aluminum interfaces.

The thermal energy absorbed by the PCM and the insulating material is obtained from the difference between the energy supplied by the HTF and the thermal losses at the insulator-air interface as follows:

$${\displaystyle \frac{d{Q}_{abs}}{dt}}=2\pi L\left(-r_0{k}_{𝓁}{\displaystyle \frac{\partial T_{𝓁}}{\partial r}}{|}_{r=r_0}+\left(R+{\delta }_{\mathrm{ins}}\right)k_{\mathrm{ins}}{\displaystyle \frac{\partial T_{ins}}{\partial r}}{|}_{r=R+{\delta }_{\mathrm{ins}}}\right)$$

(2)

The rate of change in enthalpy in the liquid phase that results from the energy balance shown in the last equation is given by

$${\displaystyle \frac{d{H}_{𝓁}\left(t\right)}{dt}}=2\pi L{\rho }_{{𝓁}_0}{C}_{{𝓁}_0}{\displaystyle \frac{d}{dt}}{\int }_{r_0}^{\overline{r}\left(t\right)}{T}_{𝓁}(r,t)rdr,$$

(3)

where ${\rho }_{{𝓁}_0}$ and $C_{{𝓁}_0}$ are the density and specific heat of the liquid phase at ambient pressure, respectively. Additionally, $\overline{r}\left(t\right)$ represents the radius of the liquid-solid interface shown in Figure 1. Thermal expansion effects could be relevant depending on the type of PCM, which in this case and for this type of paraffin were negligible. The time derivative of the integral shown in the last equation can be expressed more conveniently, applying the Leibniz rule of integration as follows:

$${\displaystyle \frac{d}{dt}}{\int }_{r_0}^{\overline{r}\left(t\right)}{T}_{𝓁}(r,t)rdr=T_{𝓁}(\overline{r}\left(t\right),t)\overline{r}\left(t\right){\displaystyle \frac{d\overline{r}}{dt}}+{\int }_{r_0}^{\overline{r}\left(t\right)}{\displaystyle \frac{\partial }{\partial t}}\left[(T_l(r,t)r\right]dr.$$

(4)

Here, the isothermal condition at the solid-liquid interface $T_{𝓁}(\overline{r}\left(t\right),t)\approx T_{m_0}$ can be applied for a phase change process close to thermodynamic equilibrium. By substituting this result into Equation (3) and using the heat equation in cylindrical coordinates, the following expression for the rate of change in the liquid’s enthalpy is obtained:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{H}_{𝓁}\left(t\right)}{dt}}& =2\pi L\left[{\rho }_{{𝓁}_0}{C}_{{𝓁}_0}{T}_{m_0}\overline{r}\left(t\right){\displaystyle \frac{d\overline{r}\left(t\right)}{dt}}+k_{𝓁}{\int }_{r_0}^{\overline{r}\left(t\right)}{\displaystyle \frac{\partial }{\partial r}}\left(r{\displaystyle \frac{\partial T_{𝓁}}{\partial r}}\right)dr\right]\hfill \\ \hfill & =2\pi L\left[{\rho }_{{𝓁}_0}{C}_{{𝓁}_0}{T}_{m_0}\overline{r}\left(t\right){\displaystyle \frac{d\overline{r}\left(t\right)}{dt}}+k_{𝓁}\left({\left.\overline{r}\left(t\right){\displaystyle \frac{\partial T_{𝓁}}{\partial r}}\right|}_{r=\overline{r}\left(t\right)}-{\left.r_0{\displaystyle \frac{\partial T_{𝓁}}{\partial r}}\right|}_{r=r_0}\right)\right].\hfill \end{array}$$

(5)

Similarly, the rate of change in enthalpy for the solid phase is given by

$${\displaystyle \frac{d{H}_s}{dt}}=2\pi L{\rho }_{s_0}{C}_{s_0}{\displaystyle \frac{d}{dt}}{\int }_{\overline{r}\left(t\right)}^R{T}_s(r,t)rdr.$$

(6)

Here, ${\rho }_{s_0}$ and $C_{s_0}$ are the density and specific heat of the solid phase at ambient pressure, respectively. Additionally, R is the outer radius of the aluminum container. By applying the Leibniz rule of integration and using the heat equation within the domain of the solid phase, the last equation can be written as follows:

$${\displaystyle \frac{d{H}_s}{dt}}=2\pi L\left[-{\rho }_{s_0}{C}_{s_0}{T}_{m_0}\overline{r}\left(t\right){\displaystyle \frac{d\overline{r}\left(t\right)}{dt}}+k_s\left({\left.R{\displaystyle \frac{\partial T_s}{\partial r}}\right|}_{r=R}-{\left.\overline{r}\left(t\right){\displaystyle \frac{\partial T_s}{\partial r}}\right|}_{r=\overline{r}\left(t\right)}\right)\right],$$

(7)

where an isothermal boundary condition at the solid-liquid interface $T_s(\overline{r}\left(t\right),t)\approx T_{m_0}$ was applied. The total amount of thermal energy absorbed by the PCM during the melting process results from adding Equations (5) and (7) as follows:

$${\displaystyle \frac{d{H}_{\mathrm{PCM}}}{dt}}\approx 2\pi L\left({\rho }_{{𝓁}_0}{C}_{{𝓁}_0}-{\rho }_{s_0}{C}_{s_0}\right)T_{m_0}\overline{r}\left(t\right){\displaystyle \frac{d\overline{r}\left(t\right)}{dt}}-\varphi \left(\overline{r}\left(t\right),t\right)+{\displaystyle \frac{d{Q}_{\mathrm{in}}}{dt}}-{\displaystyle \frac{d{Q}_{\mathrm{out}}^{\left(\mathrm{PCM}\right)}}{dt}}.$$

(8)

Here, the net thermal flux at the solid-liquid interface $\varphi \left(\overline{r}\left(t\right),t\right)$ is defined as

$$\varphi \left(\overline{r}\left(t\right),t\right)=2\pi L\overline{r}\left(t\right)\left(-k_{𝓁}{\displaystyle \frac{\partial T_{𝓁}}{\partial r}}{|}_{r=\overline{r}\left(t\right)}+k_s{\displaystyle \frac{\partial T_s}{\partial r}}{|}_{r=\overline{r}\left(t\right)}\right).$$

(9)

Furthermore, the rate of thermal energy supplied by the HTF ${\displaystyle \frac{d{Q}_{\mathrm{in}}}{dt}}$ is given by Equation (2), and the thermal energy released by the PCM to the insulating material ${\displaystyle \frac{d{Q}_{\mathrm{out}}^{\left(\mathrm{PCM}\right)}}{dt}}$ is given by

$${\displaystyle \frac{d{Q}_{\mathrm{out}}^{\left(\mathrm{PCM}\right)}}{dt}}=-2\pi L{k}_{s}R{\displaystyle \frac{\partial T_s}{\partial r}}{|}_{r=R},$$

(10)

Finally, the thermal energy absorbed by the insulating material must also be considered. The expression for this energy is simpler since the solid-insulator interface is not a moving boundary; therefore, the rate of change in enthalpy in the insulating material is given by

$${\displaystyle \frac{d{H}_{\mathrm{ins}}}{dt}}=2\pi L{\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}{\int }_R^{R+{\delta }_{\mathrm{ins}}}{\displaystyle \frac{\partial T_{\mathrm{ins}}}{\partial t}}rdr.$$

(11)

By applying the heat equation in cylindrical coordinates for the insulating material, the above equation is expressed as follows:

$${\displaystyle \frac{d{H}_{\mathrm{ins}}}{dt}}=2\pi L\left(k_{\mathrm{ins}}(R+{\delta }_{\mathrm{ins}}){\displaystyle \frac{\partial T_{\mathrm{ins}}}{\partial r}}{|}_{r=R+{\delta }_{\mathrm{ins}}}-k_{\mathrm{ins}}R{\displaystyle \frac{\partial T_{\mathrm{ins}}}{\partial r}}{|}_{r=R}\right).$$

(12)

The total amount of heat absorbed by the liquid-solid-insulator system is obtained by adding Equations (5), (7) and (12). Consequently, this energy must be equal to the net thermal energy absorbed by the system, shown in Equation (2). The energy balance just described leads to the following equation of motion for the radius of the solid-liquid interface $\overline{r}\left(t\right)$:

$$2\pi L\left({\rho }_{{𝓁}_0}{C}_{{𝓁}_0}-{\rho }_{s_0}{C}_{s_0}\right)T_{m_0}\overline{r}\left(t\right){\displaystyle \frac{d\overline{r}\left(t\right)}{dt}}=\varphi (\overline{r}\left(t\right),t)+\varphi (R,t).$$

(13)

Here, $\varphi (\overline{r}\left(t\right),t$ is given by Equation (9) and represents the net thermal flux at the solid-liquid interface. This flux represents the net amount of heat that is available at time t and absorbed as latent heat by the thin saturated solid layer surrounding the interface. Consequently, this energy produces melting of the thin layer of saturated solid. Similarly, $\varphi (R,t)$ is the net thermal energy absorbed at the PCM-insulator interface and is given by

$$\varphi (R,t)=2\pi LR\left(-k_s{\displaystyle \frac{\partial T_s}{\partial r}}{|}_{r=R}+k_{\mathrm{ins}}{\displaystyle \frac{\partial T_{\mathrm{ins}}}{\partial r}}{|}_{r=R}\right).$$

(14)

Here, $\varphi (R,t)$ represents the net amount of thermal energy absorbed as sensible heat by the insulating layer. This energy produces temperature increments within the insulator.

Finally, the enthalpy changes at a saturation $\Delta h_{𝓁,s_0}=h_{{𝓁}_0}-h_{s_0}$, where $h_{{𝓁}_0}$($h_{s_0}$) represents the specific enthalpy of the liquid (solid) at the saturation point. Therefore, by applying the first law of thermodynamics, $h_{{𝓁}_0}\approx C_{{𝓁}_0}{T}_{m_0}$, and $h_{s_0}\approx C_{s_0}{T}_{m_0}$, the term equal to $\left({\rho }_{{𝓁}_0}{C}_{{𝓁}_0}-{\rho }_{s_0}{C}_{s_0}\right)T_{m_0}$ and shown on the left-hand side of Equation (13) can be expressed in terms of the latent heat at ambient pressure $L_{f_0}=\Delta h_{𝓁,s_0}$ as follows:

$$\left({\rho }_{{𝓁}_0}{C}_{{𝓁}_0}-{\rho }_{s_0}{C}_{s_0}\right)T_{m_0}=({\rho }_{{𝓁}_0}-{\rho }_{s_0})C_{s_0}{T}_{m_0}+{\rho }_{{𝓁}_0}\Delta h_{𝓁,s}.$$

(15)

Consequently, the equation of motion for $\overline{r}\left(t\right)$ is given by

$$2\pi L\left({\rho }_{{𝓁}_0}{L}_{f_0}-\Delta {\rho }_{𝓁,s}{C}_{s_0}{T}_{m_0}\right)\overline{r}\left(t\right){\displaystyle \frac{d\overline{r}\left(t\right)}{dt}}=\varphi (\overline{r}\left(t\right),t)+\varphi (R,t),$$

(16)

Here, $L_{f_0}=\left(C_{{𝓁}_0}-C_{s_0}\right)T_{m_0}$, where $C_{{𝓁}_0}$($C_{s_0}$) represents the liquid (solid) specific heat capacity value close to the solid-liquid saturation point at ambient pressure. The specific capacities correspond to their values at thermodynamic equilibrium and are equal to the specific entropies at saturation.

2.1.1. Contact Condition at the PCM-Insulator Interface

Unlike the solid-liquid interface, the PCM-insulator interface does not undergo a phase transition. The energy balance at the PCM-insulator interface is completely different. While the temperature at the solid-liquid interface is constant due to the nature of first-order phase transitions, the temperature at the PCM-insulator interface changes, while its position is constant in time. Consequently, while the energy balance at the solid-liquid interface is related to the latent heat of the PCM, the energy balance at the PCM-insulator interface must be related to the sensible heat absorbed by the interface. The sensible heat absorbed in a rather small region surrounding the PCM-insulator interface will produce temperature changes at the interface without melting the insulating material. Figure 2 is a schematic illustration of the net thermal flux close to the PCM-insulator interface. The thermal energy balance is similar to a local balance at the solid-liquid interface. The net thermal energy absorbed at the PCM-insulator interface results from the difference between the thermal energy coming from the PCM and the thermal energy absorbed by the insulating material. Consequently, the net amount of thermal energy absorbed at this interface is equal to the thermal flux given by Equation (14). This energy is absorbed by a small region within the PCM and insulating material, as illustrated in Figure 2. The sensible heat absorbed by each of these regions is given by

$$\Delta Q_{\mathrm{PCM}}={\rho }_{\mathrm{PCM}}{C}_{\mathrm{PCM}}L\left[\pi \left(R^2-{\left(R-\Delta r_{\mathrm{PCM}}\right)}^2\right)\right]\left(T_{\mathrm{PCM}}(R,t+\Delta t)-T_{\mathrm{PCM}}(R,t)\right)$$

(17)

and

$$\Delta Q_{\mathrm{ins}}={\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}L\left[\pi \left({\left(R+\Delta r_{\mathrm{ins}}\right)}^2-R^2\right)\right]\left(T_{\mathrm{ins}}(R,t+\Delta t)-T_{\mathrm{ins}}(R,t)\right).$$

(18)

Here, ${\rho }_{\mathrm{PCM}}={\rho }_{s_0}$(${\rho }_{\mathrm{PCM}}={\rho }_{{𝓁}_0}$) and $C_{\mathrm{PCM}}=C_{s_0}$($C_{\mathrm{PCM}}=C_{{𝓁}_0}$) if the PCM is in its solid (liquid) form near the insulating layer. The thickness of each region $\Delta r_{\mathrm{PCM}}\ll R$ and $\Delta r_{\mathrm{ins}}\ll R$; therefore, the above expressions can be reduced as follows:

$$\Delta Q_{\mathrm{PCM}}\approx 2\pi LR\Delta r_{\mathrm{PCM}}{\rho }_{\mathrm{PCM}}{C}_{\mathrm{PCM}}\left(T_{\mathrm{PCM}}(R,t+\Delta t)-T_{\mathrm{PCM}}(R,t)\right)$$

(19)

and

$$\Delta Q_{\mathrm{ins}}\approx 2\pi LR\Delta r_{\mathrm{ins}}{\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}\left(T_{\mathrm{ins}}(R,t+\Delta t)-T_{\mathrm{ins}}(R,t)\right),$$

(20)

after neglecting the terms of $\mathcal{O}\left(\Delta r_{\mathrm{PCM}}^2,\Delta r_{\mathrm{ins}}^2\right)$. The local energy balance at the PCM-insulator interface can be obtained by adding the energy absorbed by the small regions shown in Figure 2 as follows:

$${\displaystyle \frac{d{Q}_{\mathrm{PCM}}}{dt}}+{\displaystyle \frac{d{Q}_{\mathrm{ins}}}{dt}}\approx 2\pi LR\left(\Delta r_{\mathrm{PCM}}{\rho }_{\mathrm{PCM}}{C}_{\mathrm{PCM}}+\Delta r_{\mathrm{ins}}{\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}\right){\displaystyle \frac{\partial T_{\mathrm{ins}}}{\partial t}}{|}_{r=R},$$

(21)

and matching this energy with the net thermal energy absorbed at this interface shown in Equation (14). Consequently, the energy balance at the PCM-insulator interface is then given by

$$2\pi LR\left(\Delta r_{\mathrm{PCM}}{\rho }_{\mathrm{PCM}}{C}_{\mathrm{PCM}}+\Delta r_{\mathrm{ins}}{\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}\right){\displaystyle \frac{\partial T_{\mathrm{ins}}}{\partial t}}{|}_{r=R}=\varphi \left(R,t\right),$$

(22)

where $\varphi \left(R,t\right)$ is shown through Equation (14). Finally, the boundary condition for this interface is related to the continuity of the temperature distribution of the PCM and insulating material at $r=R$ as $T_{\mathrm{PCM}}(R,t)=T_{\mathrm{ins}}(R,t)$.

2.1.2. Finite Difference Approximation to the Contact Condition at the PCM-Insulator Interface

The contact condition given by Equation (22) can be approximated through an explicit finite difference scheme. The PCM region is divided into N nodes separated by a distance $\Delta r_{\mathrm{PCM}}$, and the insulating material is divided into M nodes separated by a distance $\Delta r_{\mathrm{ins}}$. Using an explicit definition for the time derivative, the contact condition can be written as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{T_{1,j+1}^{\left(\mathrm{ins}\right)}-T_{1,j}^{\left(\mathrm{ins}\right)}}{\Delta t}}\left(\Delta r_{\mathrm{PCM}}{\rho }_{\mathrm{PCM}}{C}_{\mathrm{PCM}}+\Delta r_{\mathrm{ins}}{\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}\right)\approx & -k_{\mathrm{PCM}}{\displaystyle \frac{T_{N,j}^{\left(\mathrm{PCM}\right)}-T_{N-1,j}^{\left(\mathrm{PCM}\right)}}{\Delta r_{\mathrm{PCM}}}}\hfill \\ \hfill & +k_{\mathrm{ins}}{\displaystyle \frac{T_{2,j}^{\left(\mathrm{ins}\right)}-T_{1,j}^{\left(\mathrm{ins}\right)}}{\Delta r_{\mathrm{ins}}}},\hfill \end{array}$$

(23)

which must be solved simultaneously with the boundary condition at $r=R$ given by $T_{N,j}^{\left(\mathrm{PCM}\right)}=T_{1,j}^{\left(\mathrm{ins}\right)}$. The thermal flux is discontinuous at the PCM-insulator interface, as stated through Equation (23), and the temperature distribution is continuous at this interface. The approximation given by Equation (22) or (23) was obtained by assuming that the thermal energy coming from the PCM at the interface was greater than the thermal energy released through the insulating material, as illustrated in Figure 2. During a charging process, the temperature of the PCM-insulator interface must increase due to this energy balance. However, Equations (22) and (23) take the same form during a cooling process when the temperature of the PCM-interface decreases. Equation (23) must be used to estimate the temperature at the interface $T_{1,j+1}^{\left(\mathrm{ins}\right)}=T_{N,j+1}^{\left(\mathrm{PCM}\right)}$. When solving for $T_{1,j+1}^{\left(\mathrm{ins}\right)}$, the following expression is obtained:

$$T_{1,j+1}^{\left(\mathrm{ins}\right)}\approx T_{1,j}^{\left(\mathrm{ins}\right)}-{\lambda }_{\mathrm{PCM}}{\displaystyle \frac{T_{N,j}^{\left(\mathrm{PCM}\right)}-T_{N-1,j}^{\left(\mathrm{PCM}\right)}}{1+\frac{{\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}}{{\rho }_{\mathrm{PCM}}{C}_{\mathrm{PCM}}}\frac{\Delta r_{\mathrm{ins}}}{\Delta r_{\mathrm{PCM}}}}}+{\lambda }_{\mathrm{ins}}{\displaystyle \frac{T_{2,j}^{\left(\mathrm{ins}\right)}-T_{1,j}^{\left(\mathrm{ins}\right)}}{1+\frac{{\rho }_{\mathrm{PCM}}{C}_{\mathrm{PCM}}}{{\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}}\frac{\Delta r_{\mathrm{PCM}}}{\Delta r_{\mathrm{ins}}}}}.$$

(24)

Here, ${\lambda }_{\mathrm{PCM}}={\alpha }_{\mathrm{PCM}}\Delta t/\Delta r_{\mathrm{PCM}}^2$(${\lambda }_{\mathrm{ins}}={\alpha }_{\mathrm{ins}}\Delta t/\Delta r_{\mathrm{ins}}^2$) is a dimensionless constant that depends on the thermal diffusivity ${\alpha }_i=k_i/{\rho }_i{C}_i$ of the medium $i=\mathrm{PCM},\mathrm{ins}$. Finally, for slow heating rates where the phase transition is close to thermodynamic equilibrium, the PCM will likely not melt completely, and the PCM close to the insulating material will be in its solid form. Consequently, N represents the number of nodes in the solid phase, and the thermodynamic properties of the PCM in Equation (24) correspond to the properties of the solid phase.

2.1.3. Local Energy Balance at the Solid-Liquid Interface

The local energy balance consists of estimating the mass of melted solid between t and $t+\Delta t$ that results from the net thermal flux at the interface given by Equation (9). The thermal energy that is absorbed at the interface at any time t is shown in Figure 3a and can be obtained through Fourier’s law as follows:

$${\displaystyle \frac{\Delta Q_{𝓁}}{\Delta t}}=2\pi L\overline{r}\left(t\right)k_{𝓁}\left[{\displaystyle \frac{T_{𝓁}\left(\overline{r}\left(t\right)-\Delta \overline{r},t\right)-T_{𝓁}\left(\overline{r}\left(t\right),t\right)}{\Delta r}}\right],$$

(25)

where $2\pi L\overline{r}\left(t\right)$ represents the surface perpendicular to the thermal flux. Similarly, the energy released by the interface at any time t is given by

$${\displaystyle \frac{\Delta Q_s}{\Delta t}}=2\pi L\overline{r}\left(t\right)k_s\left[{\displaystyle \frac{T_s\left(\overline{r}\left(t\right),t\right)-T_s\left(\overline{r}\left(t\right)+\Delta \overline{r},t\right)}{\Delta r}}\right].$$

(26)

Additionally, when $\Delta t$ is extremely small, the above expressions can be written as follows:

$${\displaystyle \frac{d{Q}_{𝓁}}{dt}}=-2\pi L\overline{r}\left(t\right)k_{𝓁}{\displaystyle \frac{\partial T_{𝓁}\left(r,t\right)}{\partial r}}{|}_{r=\overline{r}\left(t\right)}\mathrm{and}{\displaystyle \frac{d{Q}_s}{dt}}=-2\pi L\overline{r}\left(t\right)k_s{\displaystyle \frac{\partial T_s\left(r,t\right)}{\partial r}}{|}_{r=\overline{r}\left(t\right)}.$$

(27)

Melting of a solid implies that the thermal energy absorbed at the interface is larger than the thermal energy released by the interface, as illustrated in Figure 3a. Consequently, the net amount of thermal energy that is available to melt a mass of solid $\Delta M_s$ within a small time interval $\Delta t$ is

$${\displaystyle \frac{dQ}{dt}}={\displaystyle \frac{d{Q}_{𝓁}}{dt}}-{\displaystyle \frac{d{Q}_s}{dt}}.$$

(28)

The energy shown by the last equation is a positive quantity when the solid is melting. Using the last expression and Equation (27), the net amount of thermal energy available for the melting of a solid between t and $t+\Delta t$ is then given by Equation (9). The net amount of thermal energy absorbed at the interface is absorbed as latent heat, since the liquid and solid phases are saturated at $r=\overline{r}\left(t\right)$. Consequently, the latent heat absorbed between t and $t+\Delta t$ is $\Delta Q_f=L_{f_0}\Delta M_s$. The mass solid $\Delta M_s$ in its liquid form is simply given by

$$\Delta M_{𝓁}={\rho }_{{𝓁}_0}\pi L\left({\overline{r}}^2(t+\Delta t)-{\overline{r}}^2\left(t\right)\right).$$

(29)

The radius of the solid-liquid interface has grown from $\overline{r}\left(t\right)$ to $\overline{r}(t+\Delta t)=\overline{r}\left(t\right)+\Delta \overline{r}$ in a rather small time interval $\Delta t$, as illustrated in Figure 3b. When $\Delta t$ is extremely small, this amount of melted solid can be expressed as

$$\Delta M_{𝓁}={\rho }_{{𝓁}_0}\pi L\left(2\overline{r}\Delta \left(t\right)\Delta \overline{r}+\Delta {\overline{r}}^2\right),$$

(30)

and when neglecting the second-order terms in $\Delta \overline{r}$, the latent heat absorbed between t and $t+\Delta t$ is given by

$$\Delta Q_f\approx 2\pi L\overline{r}\left(t\right)\Delta \overline{r}{\rho }_{{𝓁}_0}{L}_{f_0}.$$

(31)

Consequently, the rate of latent heat absorbed and given by

$${\displaystyle \frac{d{Q}_f}{dt}}=2\pi L{\rho }_{{𝓁}_0}{L}_{f_0}\overline{r}\left(t\right){\displaystyle \frac{d\overline{r}\left(t\right)}{dt}}$$

(32)

should be equal to the net amount of thermal energy $dQ/dt$ absorbed at the interface and given by Equation (9). The resulting energy balance at the solid-liquid interface results in the following equation of motion for $\overline{r}\left(t\right)$:

$$2\pi L{\rho }_{{𝓁}_0}{L}_{f_0}\overline{r}\left(t\right){\displaystyle \frac{d\overline{r}\left(t\right)}{dt}}=\varphi (\overline{r}\left(t\right),t),$$

(33)

where $\varphi (\overline{r}\left(t\right),t)$ is shown in Equation (9). The local energy balance (LEB) shown in the last expression represents a more classical approach to the interface dynamics. The LEB at the interface has been used for estimation of the melting (solidification) times in high (low)-temperature applications of confined PCMs [17,18,19,27], in thermal shielding applications through latent heat [28], ice formation in supercooled water [6], etc. Finally, the dynamics of $\overline{r}\left(t\right)$ obtained through the solution of Equation (33) will be compared with the interface dynamics estimated through Equation (16) in melting experiments performed with paraffin.

2.2. Experimental Set-Up

The PCM was subjected to a melting process with the experimental set-up shown schematically in Figure 4. The components used to control the temperature and volume flux of the heat transfer fluid (HTF), heat storage unit, and data processing unit are also shown in Figure 4. Paraffin RT50 from Rubitherm was used as the phase change material. The cylindrical aluminum recipient of $0.5 \mathrm{L}$, shown in Figure 5a, was used as a container for the PCM. Initially, the heat storage unit was filled with paraffin in its solid state at ambient temperature. The paraffin was melted at a high temperature and poured inside the annular region. The system was cooled down long enough for the paraffin to transition to its solid state at ambient temperature. A set of five K-type thermocouples was placed near the bottom of the unit, as shown schematically in Figure 5c. The thermocouples were placed $10 \mathrm{cm}$ below the top surface and distributed at five different radial positions—$r_1=1.28 \mathrm{cm}$, $r_2=2.06 \mathrm{cm}$, $r_3=2.83 \mathrm{cm}$, $r_4=3.6 \mathrm{cm}$, and $r_5=4.38 \mathrm{cm}$—as illustrated by the top view shown in Figure 5c. The HTF was heated at 70 °C and flowed through a $0.5 \mathrm{in}$ copper tube. Additional thermocouples were used to monitor the ambient temperature, the temperature at the inner wall of the copper tube, the inlet and outlet temperatures of the HTF, as well as the temperature of the heat bath. The K-type thermocouples used during the experiments had a temperature measurement uncertainty of $\pm 0.5$ °C. Each thermocouple was calibrated using a constant temperature bath at a working temperature of 70 °C.

The temperature of the HTF was controlled by a thermostatic bath from the brand Lauda with an ECO Silver immersion thermostat and E 10 heating thermostat, as shown schematically in Figure 4. Additionally, the cooper tube was placed along the symmetry axis of the unit as shown in Figure 5a, creating an annular region between the cooper tube and the aluminum layer. The TES unit was thermally insulated with an expansive Sista polyurethane foam with a thickness of $7.35 \mathrm{cm}$. The polyurethane foam provided insulation with a low thermal conductivity of 0.037–0.040 $\mathrm{W}/\mathrm{m}\mathrm{K}$. The space surrounding the heat storage unit, shown in Figure 5a, was completely filled with the polyurethane foam. The polyurethane filling the void shown in Figure 5a formed an insulating layer with an average thickness of $7.35 \mathrm{cm}$. The system was isolated from the surroundings by a medium-density fiber board (MDF), shown in Figure 5b. The MDF enclosure was covered from the inside by a thin, reflective aluminum layer to minimize losses due to thermal radiation. The data acquisition (DAQ) system constituted a National Instruments sourced from Tecnológico de Monterrey, Atizapán de Zaragoza, Mexico, 6062E DAQ PCMCIA for data collection of temperature values registered by the thermocouples, an NI SCXI-1102B thermocouple signal conditioning module with a cold junction compensation sensor for temperature measurements, and the NI SCXI-1303 32-channel isothermal terminal block, which provided a method for connecting and disconnecting signals to the signal processing system. This terminal block provided a solution for large channel count temperature or voltage applications. The NI SCXI-1000 instrument housing rack was used to integrate the components of the data acquisition system just mentioned. The housing rack used constituted a low-noise rack used to feed the SCXI modules and helped handle the timing, activation, and signal routing between the other modules and the SCXI modules. Finally, a laptop was equipped with a custom code developed in LabView for real-time monitoring of temperature values and data storage. LabView National Instruments 2017 version is the graphical programming software environment of choice developed by National Instruments, which allows creating applications for data acquisition, instrument control, and industrial automation.

3. Results and Discussion

This section is focused on comparing the interface dynamics between the LEB at the interface and the dynamics that resulted from the TEB described in Section 2.1. This section starts with the estimation of the thermal energy absorbed by the PCM during a heating process. The discussion is focused on the thermal energy balance of the heat storage unit and the performance of the LEB and TEB models. The TEB was consistent with energy conservation, while the thermal energy absorbed by the unit was underestimated by the LEB at the interface. Some examples will be used to illustrate the concept of energy balance throughout the thermal unit. Additionally, the concepts of thermodynamic and pseudothermodynamic equilibrium are used to find an exact analytical expression for liquid-solid coexistence at thermodynamic equilibrium. The liquid-solid coexistence curve is used to find the interface position (outer radius of the liquid shell) at thermodynamic equilibrium for different initial thermodynamic states. The analysis of liquid-solid coexistence helps reveal the deficiencies of the LEB. Furthermore, these deficiencies are greatly amplified through this analysis. Finally, the experimental results are used to compare the performance of these models and establish the validity of the assumptions described in Section 2.1.

The thermodynamic properties of the paraffin used in this work are summarized in

Table 1. Relevant thermodynamic properties of RT50 and insulating material [26]. The latent heat was determined as the change in enthalpy at saturation $\Delta h_{𝓁,s}=\left(C_{{𝓁}_0}-C_{s_0}\right)T_{m_0}$, where $C_{{𝓁}_0}\left(C_{s_0}\right)$ represents the specific heat capacities close to the saturation point.

Material	Phase	${\mathit{\rho }}_0(\mathbf{kg}/{\mathbf{m}}^3)$	${\mathit{C}}_{{\mathit{p}}_0}(\mathbf{kJ}/\mathbf{kg}\mathbf{K})$	$\mathit{k}(\mathbf{W}/\mathbf{m}\mathbf{K})$	${\mathit{T}}_{{\mathit{m}}_0}\left(\mathbf{K}\right)$	${\mathit{L}}_{{\mathit{f}}_0}\mathbf{kJ}/\mathbf{kg}$
RT50	Solid	904.002	2.031	0.2607	323.15	100.98
	Liquid	798.372	2.343	0.1978
Ins.	Solid	30.0	1674.0	0.035–0.040

. The paraffin used in the examples and in the experimental comparison was RT50. The models presented in this work consider thermodynamic properties close to saturation. Consequently, the density, specific heat capacity, and thermal conductivity of each phase correspond to their values closest to the saturation temperature of the PCM [26]. The curve fitting obtained from the DSC measurements provided in [26] were used. Additionally, the thermodynamic properties of the insulating material are shown in Table 1. The solid-liquid phase change temperature $T_{\mathrm{sol}.-\mathrm{liq}.}$ estimated via differential scanning calorimetry with heating rates of 10 °C/min was obtained from [26] and assumed to be the melting temperature $T_{m_0}$ in this work. The liquid-solid phase change temperature for RT50 was $T_{\mathrm{liq}.-\mathrm{sol}.}=321.65 \mathrm{K}$ with cooling rates of 10 °C/min, which was also estimated in [26]. Consequently the supercooling-superheating range of this PCM was $1.65 \mathrm{K}$ under high heating-cooling rates.

3.1. Thermal Energy Balance Through the PCM-Insulator System

The thermal energy absorbed by the system can be determined from the thermal flux at the copper-PCM interface and the thermal flux at the insulator-air interface, as shown by Equation (2). Consequently, the total amount of thermal energy absorbed by the system from its initial state to any state at some time $\tau$ was obtained through the time integral of Equation (2) as follows:

$$\Delta Q_{\mathrm{abs}}=2\pi L\left(-r_0{k}_{𝓁}{\int }_0^{\tau }{\displaystyle \frac{\partial T_{𝓁}}{\partial r}}{|}_{r=r_0}dt+\left(R+{\delta }_{\mathrm{ins}}\right)k_{\mathrm{ins}}{\int }_0^{\tau }{\displaystyle \frac{\partial T_{ins}}{\partial r}}{|}_{r=R+{\delta }_{\mathrm{ins}}}dt\right)$$

(34)

The thermal energy given by Equation (34) should be distributed into sensible heat absorbed by the PCM-insulator system and the latent heat absorbed by the PCM. The thermal energy absorbed by the PCM is just the change in enthalpy between $t=0$ and $t=\tau$. The enthalpy of the liquid phase at any time instant $\tau$ is

$$H_{𝓁}\left(\tau \right)=2\pi L{\rho }_{{𝓁}_0}{C}_{{𝓁}_0}{\int }_{r_0}^{\overline{r}\left(\tau \right)}{T}_{𝓁}\left(r,\tau \right)rdr$$

(35)

and for the solid phase, it is

$$H_s\left(\tau \right)=2\pi L{\rho }_{s_0}{C}_{s_0}{\int }_{\overline{r}\left(\tau \right)}^R{T}_s\left(r,\tau \right)rdr.$$

(36)

Consequently, the thermal energy absorbed by the PCM $\Delta Q_{\mathrm{PCM}}=H_{\mathrm{PCM}}\left(\tau \right)-H_{\mathrm{PCM}}\left(0\right)$ is given by

$$\begin{array}{cc}\hfill \Delta Q_{\mathrm{PCM}}=& 2\pi L\left\{{\rho }_{{𝓁}_0}{C}_{{𝓁}_0}{\int }_{r_0}^{\overline{r}\left(\tau \right)}{T}_{𝓁}\left(r,\tau \right)rdr+{\rho }_{s_0}{C}_{s_0}{\int }_{\overline{r}\left(\tau \right)}^R{T}_s\left(r,\tau \right)rdr\right.\hfill \\ \hfill & -\left.{\rho }_{{𝓁}_0}{C}_{{𝓁}_0}{\int }_{r_0}^{\overline{r}\left(0\right)}{T}_{𝓁}\left(r,0\right)rdr-{\rho }_{s_0}{C}_{s_0}{\int }_{\overline{r}\left(0\right)}^R{T}_s\left(r,0\right)rdr\right\}.\hfill \end{array}$$

(37)

Here, the enthalpy difference between the saturated phases $\Delta h_{𝓁,s}=\left(C_{{𝓁}_0}-C_{s_0}\right)T_{m_0}$ is included. Finally, the heat absorbed by the insulating material is just sensible heat and is simply given by the difference between the initial enthalpy and the enthalpy at time $\tau$ as follows:

$$\Delta Q_{\mathrm{ins}}=2\pi L{\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}{\int }_R^{R+{\delta }_{\mathrm{ins}}}\left[T_{\mathrm{ins}}\left(r,\tau \right)-T_{\mathrm{ins}}\left(r,0\right)\right]rdr.$$

(38)

The total energy absorbed by the system, constituted by the PCM and insulating shell, is given by the sum of Equations (37) and (38) as $\Delta Q_{\mathrm{PCM}-\mathrm{Ins}}=\Delta Q_{\mathrm{PCM}}+\Delta Q_{\mathrm{ins}}$. Correct energy balance implies that $\Delta Q_{\mathrm{abs}}$ should be equal to $\Delta Q_{\mathrm{PCM}-\mathrm{Ins}}$. The dynamics of the solid-liquid interface given by Equation (16) will be used to estimate $\Delta Q_{\mathrm{PCM}}$, as shown in Equation (37). The thermal energy absorbed and determined in this manner represents the latent and sensible heat absorbed by the PCM $\Delta Q_{\mathrm{PCM}}^{\left(\mathrm{TEB}\right)}$ and conceived through the total thermal balance (TEB) discussed in Section 2.1. Furthermore, the heat absorbed by the PCM $\Delta Q_{\mathrm{PCM}}^{\left(\mathrm{LEB}\right)}$ represents the amount of sensible and latent heat absorbed when applying the local energy balance at the interface (LEB) and given by Equation (33). The system in the following examples is subjected to the following isothermal boundary conditions:

$$T_{𝓁}(r_0,t)=T_H\mathrm{and}{T}_{\mathrm{ins}}(R+{\delta }_{\mathrm{ins}})=T_{\mathrm{amb}}.$$

(39)

Here, $T_H$ represents the temperature of the heat transfer fluid (HTF), and $T_{\mathrm{amb}}$ is the temperature of the surroundings. The energy absorbed by the system can be conceived in two different ways. On the one hand, the heat absorbed by the PCM and insulating material is the result of the net thermal flux through the entire system. The thermal energy obtained in this fashion will depend on the accuracy of the spatial derivatives at $r=r_0$ and $r=R+{\delta }_{\mathrm{ins}}$, as shown in Equation (34). Furthermore, the precision of the calculation will depend on the time step $\Delta t$ used to find the numerical approximations for the time integrals shown in Equation (34). On the other hand, energy can also be determined from the latent and sensible heat absorbed by the system and by using the temperature profile in each phase and the insulating material, as shown in Equations (37) and (38). Figure 6 represents an example where the initial state of the solid phase is close to the saturation temperature $T_{m_0}$ of the paraffin. Initially, quadratic temperature profiles were chosen for each phase, as was a linear temperature distribution for the insulating layer. The initial state of the PCM consisted of a liquid layer between $r_0=0.635 \mathrm{cm}$ and $\overline{r}\left(0\right)=2.0 \mathrm{cm}$, with a quadratic temperature profile between $T_{𝓁}({\overline{r}}_0,0)=50$ °C and $T_{𝓁}(r_0,0)=80$ °C. Initially, the solid phase was a thick shell surrounding the liquid with a quadratic profile between $T_s(R,0)=45$ °C, where $R=7.65 \mathrm{cm}$ and $T_s({\overline{r}}_0,0)=50$ °C. The heating temperature at $r=r_0$ is $T_H=80$ °C, and the ambient temperature $T_{\mathrm{amb}}=40$ °C.

The true value of the thermal energy that is absorbed by the system $\Delta Q_{\mathrm{abs}}$ should be equal to the integral of the net thermal flux given by Equation (34). Alternatively, if the equation of motion for the liquid-solid interface, namely Equation (16) or Equation (33), produces the correct dynamics, then the enthalpy change in the PCM-insulator system should be equal to $\Delta Q_{\mathrm{abs}}$. Figure 6a,b clearly illustrates how the LEB model greatly underestimated the thermal energy absorbed by the PCM, while the energy balance was consistent according to the TEB model. A low thermal conductivity value for the insulating layer $k_{\mathrm{ins}}={10}^{-4} \mathrm{W}/\mathrm{mK}$ was chosen to minimize energy loses from the system to its surroundings. In addition to this type of layer, the boundary conditions and initial thermodynamic state of the PCM used in this example helped exacerbate the observed difference between $\Delta q_{\mathrm{abs}}$ and $\Delta q_{\mathrm{PCM}-\mathrm{ins}}$ in Figure 6b. The effect of these conditions and the system’s properties produced fast melting rates, and they were chosen to reveal possible inconsistencies from the perspective of energy conservation. The thermal energy shown in Figure 6a,b is given in multiples of $\pi L$ and defined as $\Delta q=\Delta Q/\pi L$. Similarly, the enthalpy of the PCM and insulating layer shown in Figure 6c are given in multiples of $\pi L$ and defined as $h\left(t\right)=H/\pi L$. Finally, the resulting dynamics of the liquid-solid interface is shown in Figure 6d according to both models. Here, the time evolution of $\overline{r}\left(t\right)$ for both models is shown within the same time window. The melting front ${\overline{r}}^{\left(\mathrm{TEB}\right)}\left(t\right)$ should get much closer to the solid-insulator interface at $r=R$ than ${\overline{r}}^{\left(\mathrm{LEB}\right)}\left(t\right)$ to preserve thermal energy, according to Figure 6a.

Table 2. RPD values between the radial positions of the interface according to each model considered. The energy balance obtained through the TEB and LEB models was evaluated with the RPD between the energy exchange with the surroundings and the total enthalpy change. Negligible RPD values were observed for the TEB model, in contrast to the high values obtained with the LEB model.

t	${\overline{\mathit{r}}}_{\mathbf{TEB}}$	${\overline{\mathit{r}}}_{\mathbf{LEB}}$	${\mathbf{RPD}}_{\overline{\mathit{r}}}$	$\mathbf{\Delta }{\mathit{q}}_{\mathbf{abs}}^{\left(\mathbf{TEB}\right)}$	$\mathbf{\Delta }{\mathit{h}}_{\mathbf{TEB}}$	${\mathbf{RPD}}_{\mathbf{Engy}}^{\left(\mathbf{TEB}\right)}$	$\mathbf{\Delta }{\mathit{q}}_{\mathbf{abs}}^{\left(\mathbf{LEB}\right)}$	$\mathbf{\Delta }{\mathit{h}}_{\mathbf{LEB}}$	${\mathbf{RPD}}_{\mathbf{Engy}}^{\left(\mathbf{LEB}\right)}$
h	cm		%	kJ/m		%	kJ/m		%
0.50	3.02	2.38	21.13	14.00	14.14	0.97	15.53	3.88	74.99
1.00	3.47	2.62	24.53	27.77	27.92	0.56	31.43	11.73	62.68
1.50	3.85	2.82	26.84	40.55	40.72	0.42	46.40	19.07	58.90
2.00	4.23	3.00	28.95	52.67	52.85	0.35	60.69	25.89	57.34
2.50	4.61	3.18	31.12	64.25	64.45	0.31	74.44	32.20	56.74
3.00	5.02	3.34	33.40	75.40	75.61	0.28	87.73	38.01	56.68
3.50	5.44	3.50	35.69	86.16	86.39	0.26	100.65	43.33	56.95
4.00	5.88	3.66	37.84	96.59	96.83	0.25	113.22	48.19	57.44

shows the radial position of the interface $\overline{r}$ that corresponds to Figure 6d according to the LEB and TEB models discussed in this work. The relative percent difference (RPD) between the LEB value ${\overline{r}}_{\mathrm{LEB}}$ and the TEB value ${\overline{r}}_{\mathrm{TEB}}$ is defined by

$${\mathrm{RPD}}_{\overline{r}}=\left({\displaystyle \frac{{\overline{r}}_{\mathrm{TEB}}-{\overline{r}}_{\mathrm{LEB}}}{{\overline{r}}_{\mathrm{TEB}}}}\right)\times 100\%.$$

(40)

Additionally, to visualize the energy balance according to the TEB and LEB models, the RPD between the net thermal exchange with the surroundings $\Delta q_{\mathrm{abs}}$ and the energy absorbed by the PCM and insulator $\Delta q_{\mathrm{Ins}-\mathrm{PCM}}$ is shown in Table 2. The thermal energy absorbed by the PCM-insulator system corresponds to the total enthalpy change $\Delta q_{\mathrm{Ins}-\mathrm{PCM}}=\Delta h$. The RPD, ${\mathrm{RPD}}_{\mathrm{Engy}}^{\left(\mathrm{LEB}\right)}$(${\mathrm{RPD}}_{\mathrm{Engy}}^{\left(\mathrm{TEB}\right)}$) between $\Delta h_{\mathrm{LEB}}$($\Delta h_{\mathrm{TEB}}$) and $\Delta q_{\mathrm{abs}}^{\left(\mathrm{LEB}\right)}$($\Delta q_{\mathrm{abs}}^{\left(\mathrm{TEB}\right)}$) represents the deviation from total energy balance according to the LEB (TEB) approach. The RPD between these energies is defined as follows:

$${\mathrm{RPD}}_{\mathrm{Engy}}^{\left(\mathrm{M}\right)}=\left|{\displaystyle \frac{\Delta q_{\mathrm{abs}}^{\left(\mathrm{M}\right)}-\Delta h_{\mathrm{M}}}{\Delta q_{\mathrm{abs}}^{\left(\mathrm{M}\right)}}}\right| \times 100\%.$$

(41)

Here, M represents the model used, LEB or TEB, in each case. Additionally, the net thermal exchange with the surroundings $\Delta q_{\mathrm{abs}}$ was considered as the actual amount of thermal energy that should be absorbed by the PCM and insulating material. Table 2 shows extremely low percentages for the TEB results, which can be attributed to errors in the numerical integration of the temperature profiles $T_{𝓁}(r,t)$ and $T_s(r,t)$. In contrast, the RPD estimated when using an LEB was significantly higher, ranging between $57\%$ and $75\%$, well beyond the expected numerical error. Consequently, the energy balance obtained through the LEB approach in this example was clearly inconsistent.

Figure 7 represents an illustration of the energy balance in a system with similar conditions to the experiment performed in this work. Here, the initial temperature of the solid paraffin was 22 °C, and the temperature of the HTF was set to $T_H=70$ °C. Initially, the liquid represented a thin layer with a thickness of $1 \mathrm{mm}$ and a uniform temperature distribution of 70 °C. Additionally, the paraffin was mostly in its solid phase. The insulating layer had a thickness of ${\delta }_{\mathrm{ins}}=1.0 \mathrm{cm}$ with a thermal conductivity of $k_{\mathrm{ins}}=0.035 \mathrm{W}/\mathrm{mK}$ and initially had a uniform temperature distribution of $T_{\mathrm{ins}}(r,0)=22$ °C. The ambient temperature was constant and equal to $T_{\mathrm{amb}}=28$ °C. The initial thermodynamic state in this case, where the solid was well below the saturation temperature of the paraffin, along with the ambient conditions and a much higher thermal conductivity of the insulating layer would result in lower melting rates. The relative difference percentages between the energy exchanged with the surroundings and the thermal energy absorbed by the PCM-insulator system were less pronounced in this case, as shown in Figure 7.

Table 3. Relative percent differences (RPDs) between ${\overline{r}}_{\mathrm{LEB}}$ and ${\overline{r}}_{\mathrm{TEB}}$ and between $\Delta q_{\mathrm{abs}}^{\left(\mathrm{M}\right)}$ and $\Delta h_{\mathrm{M}}$ for each model. Discrepancies between the thermal energies $\Delta q_{\mathrm{abs}}^{\left(\mathrm{LEB}\right)}$ and $\Delta h_{\mathrm{LEB}}$ were less pronounced in this case. The thermal conductivity of the insulating layer, along with the initial state and boundary conditions, resulted in lower relative differences.

t	${\overline{\mathit{r}}}_{\mathbf{TEB}}$	${\overline{\mathit{r}}}_{\mathbf{LEB}}$	${\mathbf{RPD}}_{\overline{\mathit{r}}}$	$\mathbf{\Delta }{\mathit{q}}_{\mathbf{abs}}^{\left(\mathbf{TEB}\right)}$	$\mathbf{\Delta }{\mathit{h}}_{\mathbf{TEB}}$	${\mathbf{RPD}}_{\mathbf{Engy}}^{\left(\mathbf{LEB}\right)}$	$\mathbf{\Delta }{\mathit{q}}_{\mathbf{abs}}^{\left(\mathbf{LEB}\right)}$	$\mathbf{\Delta }{\mathit{h}}_{\mathbf{LEB}}$	${\mathbf{RPD}}_{\mathbf{Engy}}^{\left(\mathbf{LEB}\right)}$
h	cm		%	kJ/m		%	kJ/m		%
0.50	1.14	1.10	3.93	33.83	34.05	0.66	37.06	32.64	11.92
1.00	1.26	1.22	3.68	55.81	56.05	0.42	60.49	54.12	10.53
1.50	1.35	1.30	3.52	74.34	74.58	0.33	80.13	72.30	9.76
2.00	1.41	1.36	3.45	90.25	90.50	0.28	97.00	87.96	9.32
2.50	1.47	1.42	3.48	103.99	104.24	0.24	111.63	101.48	9.09
3.00	1.52	1.47	3.57	115.87	116.13	0.22	124.38	113.18	9.00
3.50	1.57	1.51	3.68	126.16	126.42	0.21	135.51	123.31	9.00
4.00	1.62	1.56	3.80	135.08	135.34	0.20	145.26	132.08	9.07
4.50	1.67	1.60	3.89	142.81	143.08	0.19	153.81	139.68	9.18
5.00	1.71	1.64	3.96	149.51	149.78	0.18	161.32	146.28	9.32

shows the values for $\Delta q_{\mathrm{abs}}$ and $\Delta h=\Delta q_{\mathrm{Ins}-\mathrm{PCM}}$ obtained by the TEB and LEB models. The energy values were estimated from the configuration with the initial thermodynamic state and boundary conditions just described. The ambient conditions, a lower HTF temperature, the initial configuration of the system—PCM in its solid phase, with an initial temperature $T_s\ll T_{m_0}$—and a much higher thermal conductivity $k_{\mathrm{ins}}=0.035 \mathrm{W}/\mathrm{mK}$ produced significantly lower melting rates. The latter was observed through the values of ${\overline{r}}_{\mathrm{LEB}}$ shown in Table 3 when compared with those shown in Table 2. In this case, the change in the radial position of the interface was $\Delta {\overline{r}}_{\mathrm{LEB}}=0.885 \mathrm{cm}$ during the first 4 h of the melting process. In contrast, the scenario illustrated in Figure 6 shows a change of $\Delta \overline{r}=1.66 \mathrm{cm}$ within the same time window. Consequently, the ${\mathrm{RPD}}_{\overline{r}}$ between the LEB and TEB models was significantly lower in this case. The ${\mathrm{RPD}}_{\overline{r}}=37.84\%$ at $t=4 \mathrm{h}$, as shown in Table 2, the relative difference was ${\mathrm{RPD}}_{\overline{r}}=3.8\%$, as shown in Table 3. Consequently, the RPD in the thermal energy at $t=4 \mathrm{h}$ was ${\mathrm{RPD}}_{\mathrm{Engy}}^{\left(\mathrm{LEB}\right)}=9.07\%$ in this example. In contrast, an RPD of $57.44\%$ in the same time window was observed for the scenario shown in Table 2. The behavior just discussed implies that by changing the experimental conditions—initial thermodynamic state, boundary conditions, and thermal conductivity of the insulating material—thermal energy discrepancies can be minimized when using an LEB at the interface. Consequently, the LEB model is not incorrect but limited to low melting rates. The LEB model represents a special case of the more general TEB model.

3.2. Thermodynamic Equilibrium

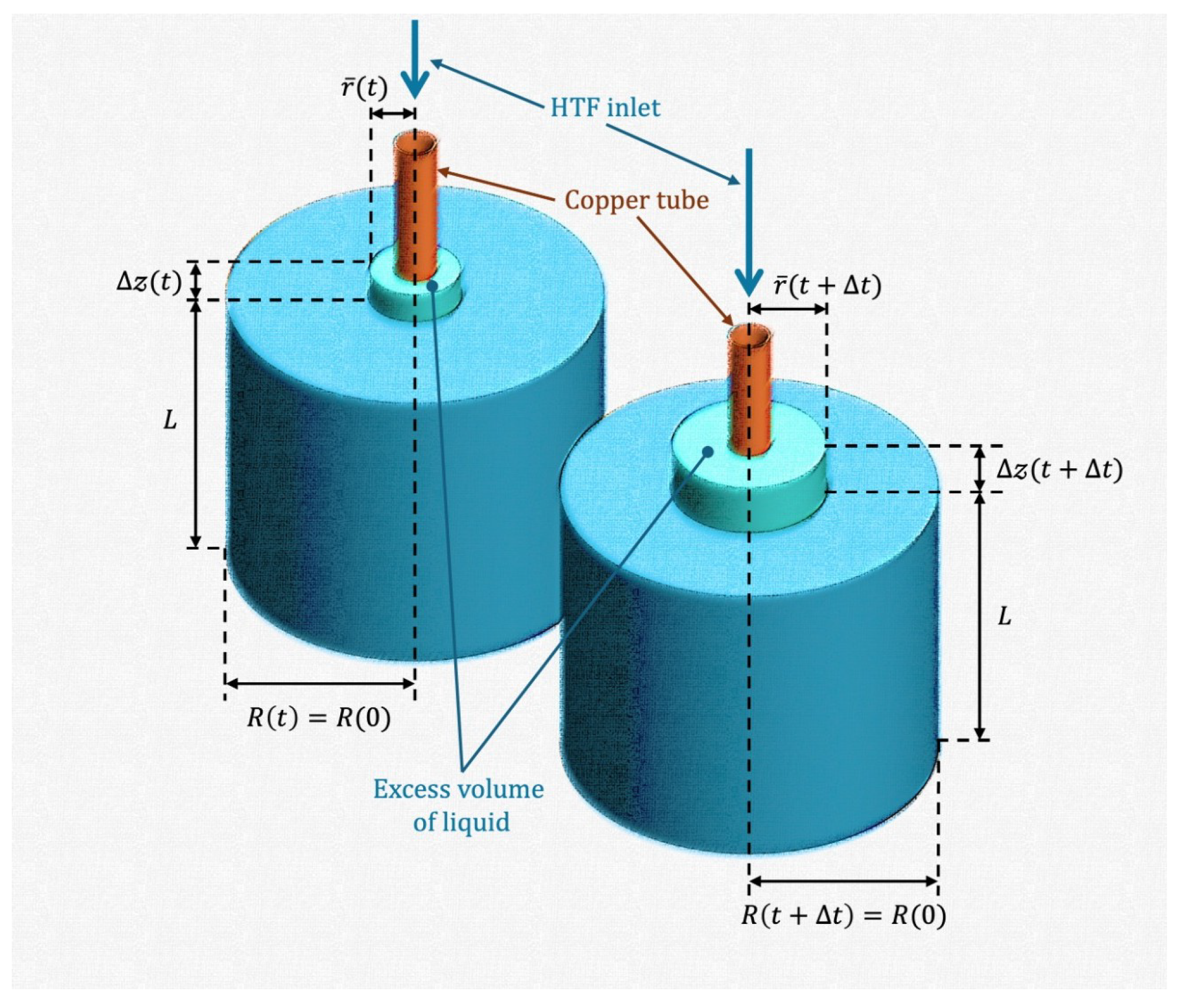
This section is focused on the analysis of energy conservation in liquid-solid mixtures at thermodynamic equilibrium. First, the equation of motion for the interface $\overline{r}$ that results from the LEB and TEB will be solved by applying homogeneous Neumann boundary conditions. Additionally, these equations will be solved in thermally isolated systems, where the liquid-solid mixture will evolve to a pseudothermodynamic equilibrium state.

3.2.1. Thermodynamic Equilibrium: Homogeneous Neumann Boundary Conditions

Adiabatic boundary conditions have been previously applied through homogeneous Neumann boundary conditions to verify energy conservation in liquid-solid mixtures with a sharp planar interface at thermodynamic equilibrium [7,8,29]. The homogeneous Neumann boundary conditions represent a mathematical device to emulate perfect thermal insulation. The thermal flux at the boundaries in contact with the surroundings was set to zero through the following boundary conditions:

$${\displaystyle \frac{\partial T_{𝓁}}{\partial r}}{|}_{r=r0}=0\mathrm{and}{\displaystyle \frac{\partial T_s}{\partial r}}{|}_{r=R}=0.$$

(42)

Here, $r_0$ is the radius of the copper-PCM interface, and R is the radius of the insulator-PCM interface. The boundary conditions shown above represent a liquid-solid mixture without heat exchange with its surroundings. The balance of thermal energy applied to the entire system was simplified to the following equation of motion for the interface in this case:

$$\left({\rho }_{{𝓁}_0}{L}_{f_0}-\Delta {\rho }_{𝓁,s}{C}_{s_0}{T}_{m_0}\right){\displaystyle \frac{d\overline{r}\left(t\right)}{dt}}=-k_{𝓁}{\displaystyle \frac{\partial T_{𝓁}}{\partial r}}{|}_{r=\overline{r}\left(t\right)}+k_s{\displaystyle \frac{\partial T_s}{\partial r}}{|}_{r=\overline{r}\left(t\right)}.$$

(43)

The above equation of motion can be obtained by applying the energy balance described in Section 2.1 with the boundary conditions shown in Equation (42). Alternatively, Equation (43) can be obtained through Equation (16) by replacing $\varphi \left(R,t\right)=0$, since there was no heat exchange with the surroundings in this case. The resulting equation for the liquid-solid interface can be written in the following form:

$${\rho }_{{𝓁}_0}{L}_{f_{\mathrm{eq}}}=-k_{𝓁}{\displaystyle \frac{\partial T_{𝓁}}{\partial r}}{|}_{r=\overline{r}\left(t\right)}+k_s{\displaystyle \frac{\partial T_s}{\partial r}}{|}_{r=\overline{r}\left(t\right)},$$

(44)

where $L_{f_{\mathrm{eq}}}=L_{f_0}-\left({\rho }_{r_0}-1\right)C_{s_0}{T}_{m_0}$ and ${\rho }_{r_0}={\rho }_{s_0}/{\rho }_{{𝓁}_0}$ is a dimensionless variable equal to the ratio between the solid and liquid densities. Equation (44) has the same form as the equation of motion resulting from the local energy balance and given by Equation (33) but with a lower latent heat $L_{f_{\mathrm{eq}}}=L_{f_0}-\left({\rho }_{r_0}-1\right)C_{s_0}{T}_{m_0}$, which depends on the relative difference between the liquid and solid densities ${\rho }_{r_0}-1$. The resulting latent heat $L_{f_{\mathrm{eq}}}$ can be interpreted as an apparent latent heat [8], which will be shown to give the correct liquid-solid coexistence state at thermodynamic equilibrium.

The examples that will be shown were designed through an initial state far from equilibrium, where the exchange of thermal energy was only realized between the liquid and solid phases. The enthalpy of the initial state was chosen so that both phases coexisted at thermodynamic equilibrium and after the system evolved for a large period of time. The homogeneous Neumann boundary conditions were used to artificially isolate the liquid-solid mixture from its surroundings and guarantee that thermal energy exchange was only realized between the liquid and solid phases. The focus of this section is to demonstrate or at least illustrate that TEB applied to this type of boundary condition may reveal the inconsistency of LEB by using energy conservation in isolated systems.

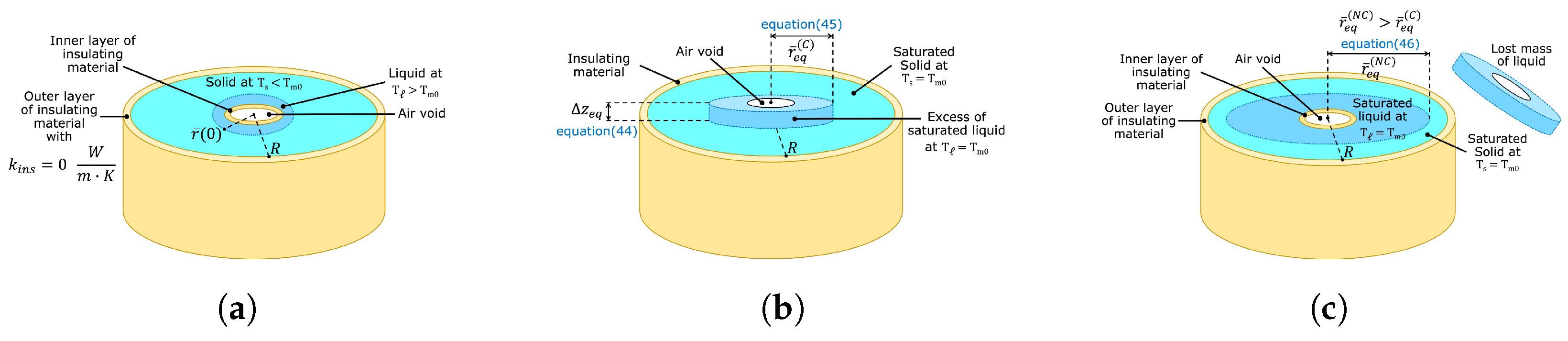
The initial state of the examples shown below consisted of a liquid-solid mixture with an initial arbitrary temperature profile in the liquid and solid phases. The initial temperature distribution was chosen so that the initial enthalpy $h_0$ of the PCM was equal to the enthalpy $h_{\mathrm{eq}}$ of a saturated mixture at thermodynamic equilibrium as shown schematically in Figure 8. Three such initial states were designed, and they are shown in Figure 9a, where the enthalpy of the initial state intersects the coexistence curve at thermodynamic equilibrium. The examples were designed so that the radius of the liquid phase at equilibrium ${\overline{r}}_{\mathrm{eq}}$ was within the physical domain of the PCM $r_0<{\overline{r}}_{\mathrm{eq}}<R$. The exact analytical expression for ${\overline{r}}_{\mathrm{eq}}$ could be found by using energy conservation. The enthalpy $h_0$ of the initial state with arbitrary temperature profiles in the liquid and solid phase is given by

$$h_0=2{\rho }_{{𝓁}_0}{C}_{{𝓁}_0}{\int }_{r_0}^{\overline{r}\left(0\right)}{T}_{𝓁}(r,0)rdr+2{\rho }_{s_0}{C}_{s_0}{\int }_{\overline{r}\left(0\right)}^R{T}_s(r,0)rdr,$$

(45)

where $h_0=H_0/\pi L$ is the initial enthalpy per unit length of the cylindrical container with a height L. The system was artificially isolated from its surroundings through the adiabatic boundary conditions shown in Equation (42).

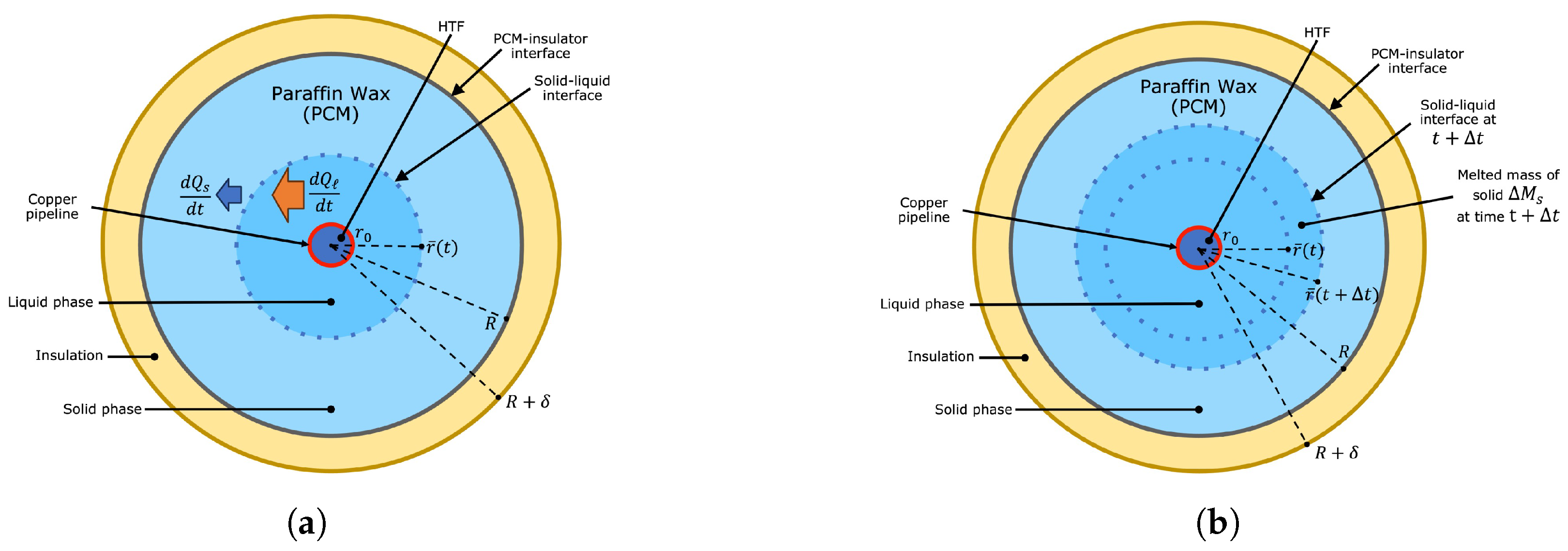
Figure 8a shows an initial state constituted by a liquid-solid mixture far from thermodynamic equilibrium. Initially, the liquid’s temperature was above the saturation point $T_{m_0}$ of the PCM. Similarly, the temperature of the solid phase was below the melting point of the PCM. The mixture was perfectly insulated from the surroundings; therefore, thermal energy exchange only occurred between the liquid and solid phases. The latter implies that thermal energy is constant over time, and the system will evolve to a thermodynamic state where both phases coexist at thermodynamic equilibrium with a uniform temperature distribution equal to $T_{m_0}$, as shown schematically in Figure 8b. Consequently, the enthalpy of the PCM in this steady state $h_{\mathrm{eq}}$ should be equal to the initial enthalpy $h_0$ given by Equation (45). The saturated mixture illustrated in Figure 8b represents a system at thermodynamic equilibrium where the excess volume of liquid is also at the saturation temperature $T_{m_0}$. Figure 8b represents a scenario where the excess volume produced by the melting of solid phase is not removed. The excess volume is dispersed throughout the top surface in reality. Consequently, the thermal energy and total mass of the PCM illustrated in Figure 8b are conserved.

The expression for the enthalpy of the liquid-solid mixture shown in Figure 8b and obtained for a coexistence state with a uniform temperature $T_{m_0}$ is described in Appendix A and given by

$$h_{\mathrm{eq}}={\rho }_{{𝓁}_0}{C}_{{𝓁}_0}\left({\overline{r}}_{\mathrm{eq}}^2-r_0^2\right)\left(1+{\displaystyle \frac{\Delta z_{\mathrm{eq}}}{L}}\right)T_{m_0}+{\rho }_{s_0}{C}_{s_0}\left(R^2-{\overline{r}}_{\mathrm{eq}}^2\right)T_{m_0},$$

(46)

where $\Delta z_{\mathrm{eq}}$ is related to the excess volume of liquid at thermodynamic equilibrium, shown schematically in Figure 8b. The perfect insulation from the surroundings implies that energy was conserved, and $h_{\mathrm{eq}}=h_0$. The result constitutes an equation for the radial position of the liquid-solid interface $r_{\mathrm{eq}}$ and the excess volume of liquid at thermodynamic equilibrium. Although thermal energy was conserved, the liquid-solid mixture shown in Figure 8b had the same mass as the initial state. The total mass of the PCM was constant, since the excess volume of liquid was not removed. Consequently, total mass conservation was applied to the PCM shown in Figure 8a,b. The process is described with more detail in Appendix A, where the following expression for the height of the excess volume of liquid at thermodynamic equilibrium is obtained:

$$\Delta z_{\mathrm{eq}}={\displaystyle \frac{\left({\overline{r}}_{\mathrm{eq}}^2-{\overline{r}}^2\left(0\right)\right)}{\left({\overline{r}}_{\mathrm{eq}}^2-r_0^2\right)}}\left({\rho }_{r_0}-1\right)L.$$

(47)

Through substitution of Equation (47) into Equation (46) and applying energy conservation such that $h_0=h_{\mathrm{eq}}$, the following expression for the radius of the liquid phase at thermodynamic equilibrium is obtained:

$${\overline{r}}_{\mathrm{eq}}^2={\displaystyle \frac{h_0+u_{{𝓁}_v}\left[r_0^2+{\overline{r}}^2\left(0\right)\left({\rho }_{r_0}-1\right)\right]-u_{s_v}{R}^2}{{\rho }_{r_0}{u}_{{𝓁}_v}-u_{s_v}}},$$

(48)

where the expression for ${\overline{r}}_{\mathrm{eq}}$ given by the last equation represents the radial position of the interface ${\overline{r}}_{\mathrm{eq}}^{\left(\mathrm{C}\right)}$ shown in Figure 8b. The upper index represents the radial position at thermodynamic equilibrium in a scenario where the total energy and total mass are conserved. Additionally, $u_{{𝓁}_v}={\rho }_{{𝓁}_0}{C}_{{𝓁}_0}{T}_{m_0}$($u_{s_v}={\rho }_{s_0}{C}_{s_0}{T}_{m_0}$) represents the energy density of the saturated liquid (solid) phase. Alternatively, the saturated state shown in Figure 8c is the result of a system that evolved from the initial state shown in Figure 8a, where the excess volume was constantly removed until the saturated state was reached. The final state was formed by a saturated mixture with less mass. The scenario just described corresponds to a non-conservative case where thermal energy is conserved, but a fraction of the total mass is lost. The radial position of the liquid-solid front at thermodynamic equilibrium is greater than ${\overline{r}}_{\mathrm{eq}}^{\left(\mathrm{C}\right)}$, since the initial energy $h_0$ is distributed throughout a final state with a lower mass. The removed mass of the liquid phase does not absorb thermal energy; therefore, energy conservation leads to a saturated mixture with a larger concentric shell of saturated liquid, as shown in Figure 8.

The TEB model presented in Section 2.1 does not preserve the total mass, since the excess volume of liquid is not considered in this approximation. The model loses mass during melting, and when the system reaches thermodynamic equilibrium, thermal energy is distributed in a system with a lower mass. The exact value at thermodynamic equilibrium of the proposed model in this work ${\overline{r}}_{\mathrm{eq}}$ can be obtained by removing the excess volume of liquid or making $\Delta z_{\mathrm{eq}}=0$ while imposing energy conservation such that $h_0=h_{\mathrm{eq}}$. The process comes down to replacing ${\rho }_{r_0}=1$ in Equation (48) as described in Appendix A. Consequently, the expression for the non-conservative radial position of the interface ${\overline{r}}_{\mathrm{eq}}^{\left(\mathrm{NC}\right)}$, illustrated in Figure 8c, is given by

$${\overline{r}}_{\mathrm{eq}}^2={\displaystyle \frac{h_0+u_{{𝓁}_v}{r}_0^2-u_{s_v}{R}^2}{u_{{𝓁}_v}-u_{s_v}}}.$$

(49)

Here, the difference between energy densities $u_{{𝓁}_v}-u_{s_v}={\rho }_{𝓁}{L}_{f_{\mathrm{eq}}}$ is related to the apparent latent heat $L_{f_{\mathrm{eq}}}$ that results from applying the TEB proposed in this work.

Table 4. Initial conditions necessary to produce three different solid-liquid coexistence states at thermodynamic equilibrium. The corresponding values of ${\overline{r}}_{\mathrm{eq}}$ and excess liquid mass $\Delta m_{\mathrm{eq}}$ at equilibrium and estimated by Equations (49) and (52) are also shown.

	${\mathit{T}}_{\mathit{H}}$ (°C)	${\mathit{T}}_{\mathit{C}}$ (°C)	${\mathit{h}}_0$ (MJ/m)	${\overline{\mathit{r}}}_{\mathbf{eq}}$ (cm)	$\mathbf{\Delta }{\mathit{m}}_{\mathbf{eq}}$ (g/m)
Case 1	90	40	3.4735	4.7646	70.78
Case 2	90	45	3.5015	6.8956	333.26
Case 3	95	45	3.5095	7.3892	407.73

shows the parameters used to elaborate the initial states illustrated in Figure 9a. The liquid-solid coexistence curve shown in Figure 9a was obtained by sweeping the physical domain of the PCM with values of ${\overline{r}}_{\mathrm{eq}}$ within the range $\overline{r}\left(0\right)\le {\overline{r}}_{\mathrm{eq}}\le R$. The corresponding enthalpy at thermodynamic equilibrium for each possible value of ${\overline{r}}_{\mathrm{eq}}$ was obtained by substituting $\Delta z_{\mathrm{eq}}=0$ in Equation (46). Each filled symbol in Figure 9a represents the expected saturated mixture for the initial states with the enthalpy $h_0$ considered. The initial temperature profiles were quadratic functions of the form $T_i(r,0)=a_i\left(r-\overline{r}\left(0\right)\right)+b_i{\left(r-\overline{r}\left(0\right)\right)}^2+T_{m_0}$, where $i=𝓁,s$ represents the phase. The initial radius of the liquid phase $\overline{r}\left(0\right)$ that represents the radial position of the liquid-solid interface was set to 4 cm in all cases. The initial temperature profiles obeyed the isothermal boundary condition at the liquid-solid interface. The constants $a_i$ and $b_i$ were obtained through the initial temperature values at $r_0=0.635 \mathrm{cm}$ and $R=7.65 \mathrm{cm}$ and the corresponding boundary conditions given by Equation (42). Initially, the highest temperature in the liquid phase was $T_{𝓁}(r_0,t)=T_H$, and the lowest temperature value in the solid phase was $T_s(R,0)=T_C$. Sharp temperature changes at the interface were avoided through quadratic profiles, as opposed to constant profiles, in order to start with an initial state not that far from thermodynamic equilibrium and avoid ultrafast heating of the solid phase. Nevertheless, the analysis would also be valid for sharp profiles if superheating effects were neglected. Three initial states were prepared with different temperature values of $T_H$ and $T_C$ at the corresponding boundaries $r=r_0$ and $r=R$. The initial enthalpy values $h_0$ are shown in Table 4 and drawn as horizontal lines in Figure 9a.

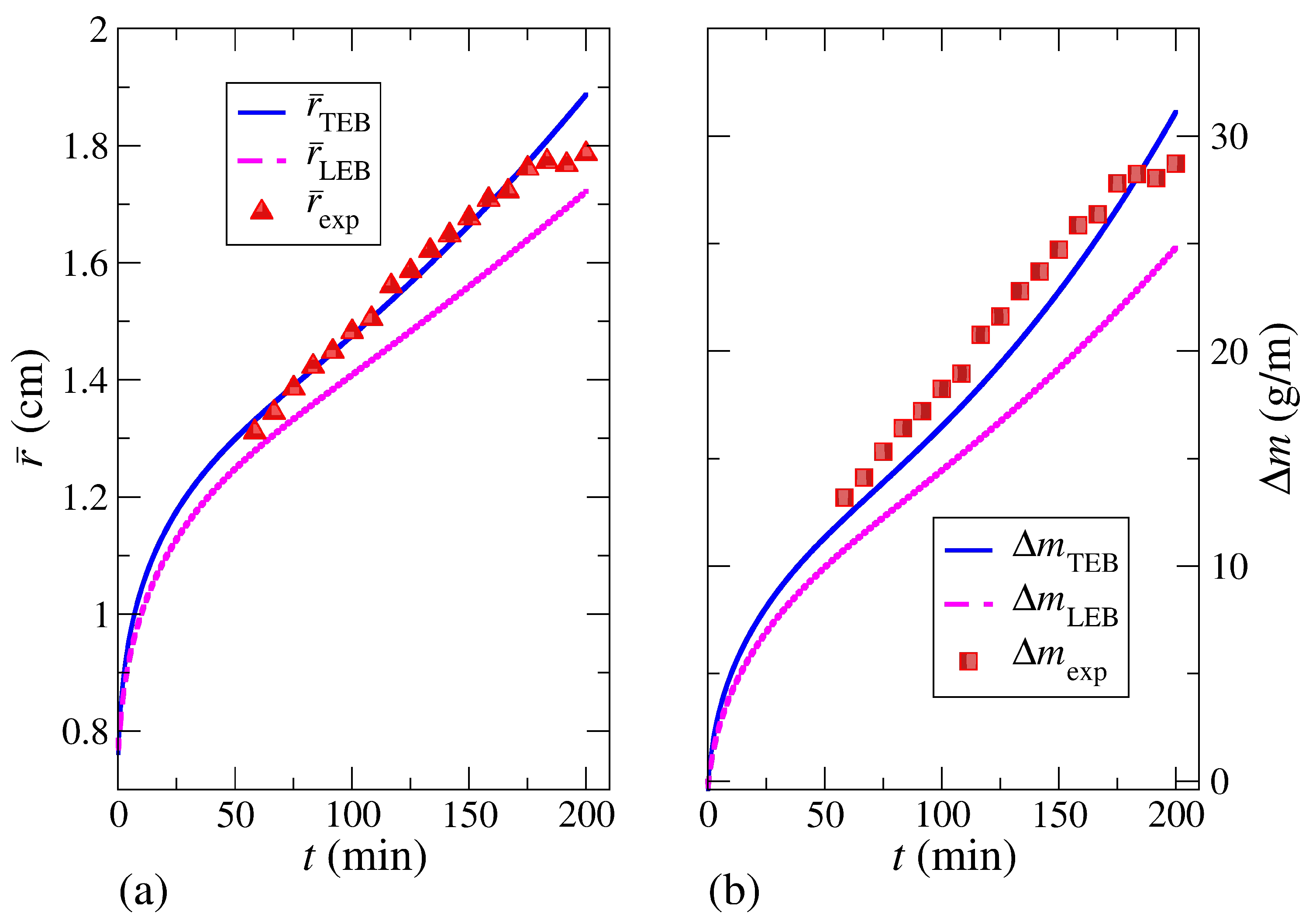
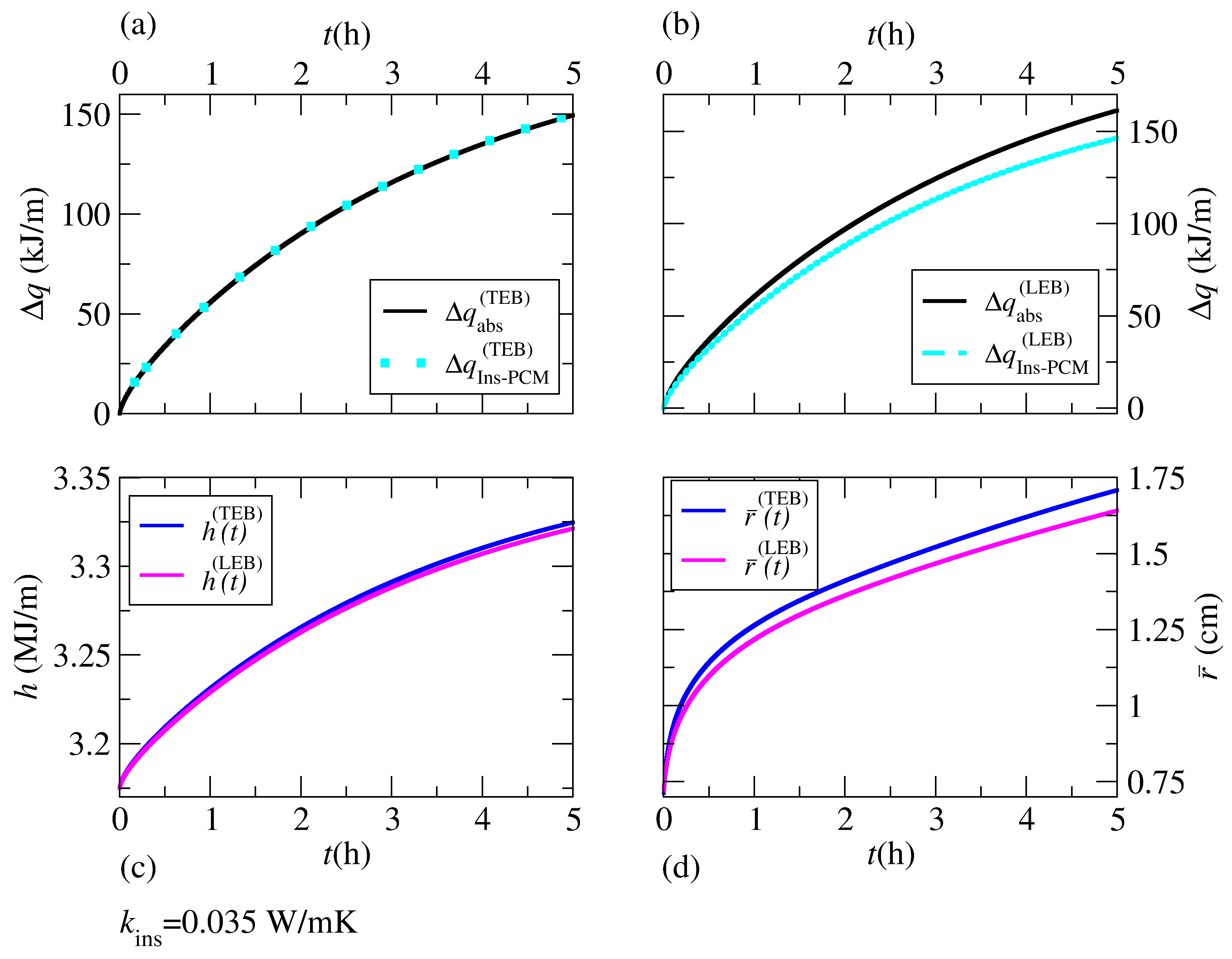
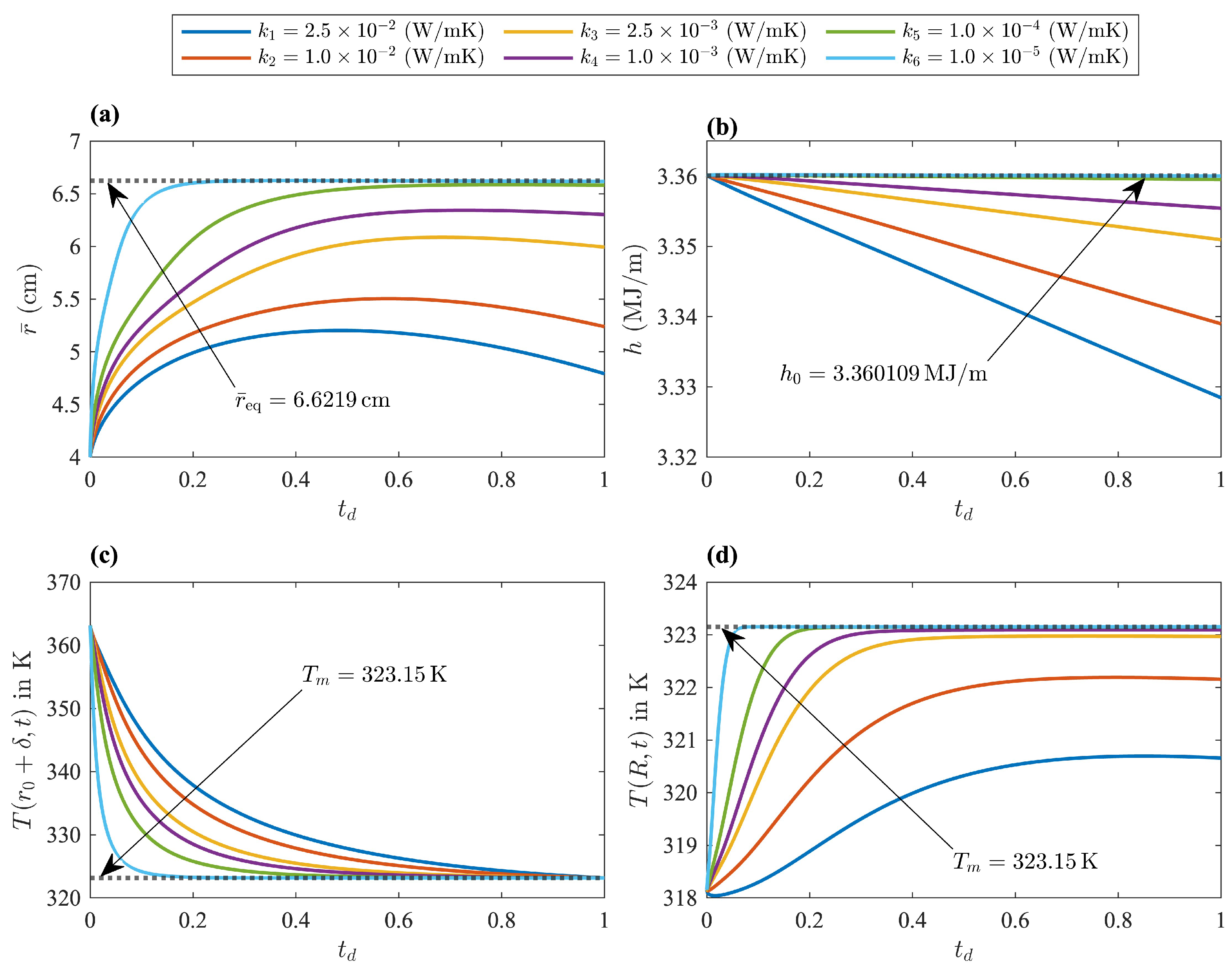
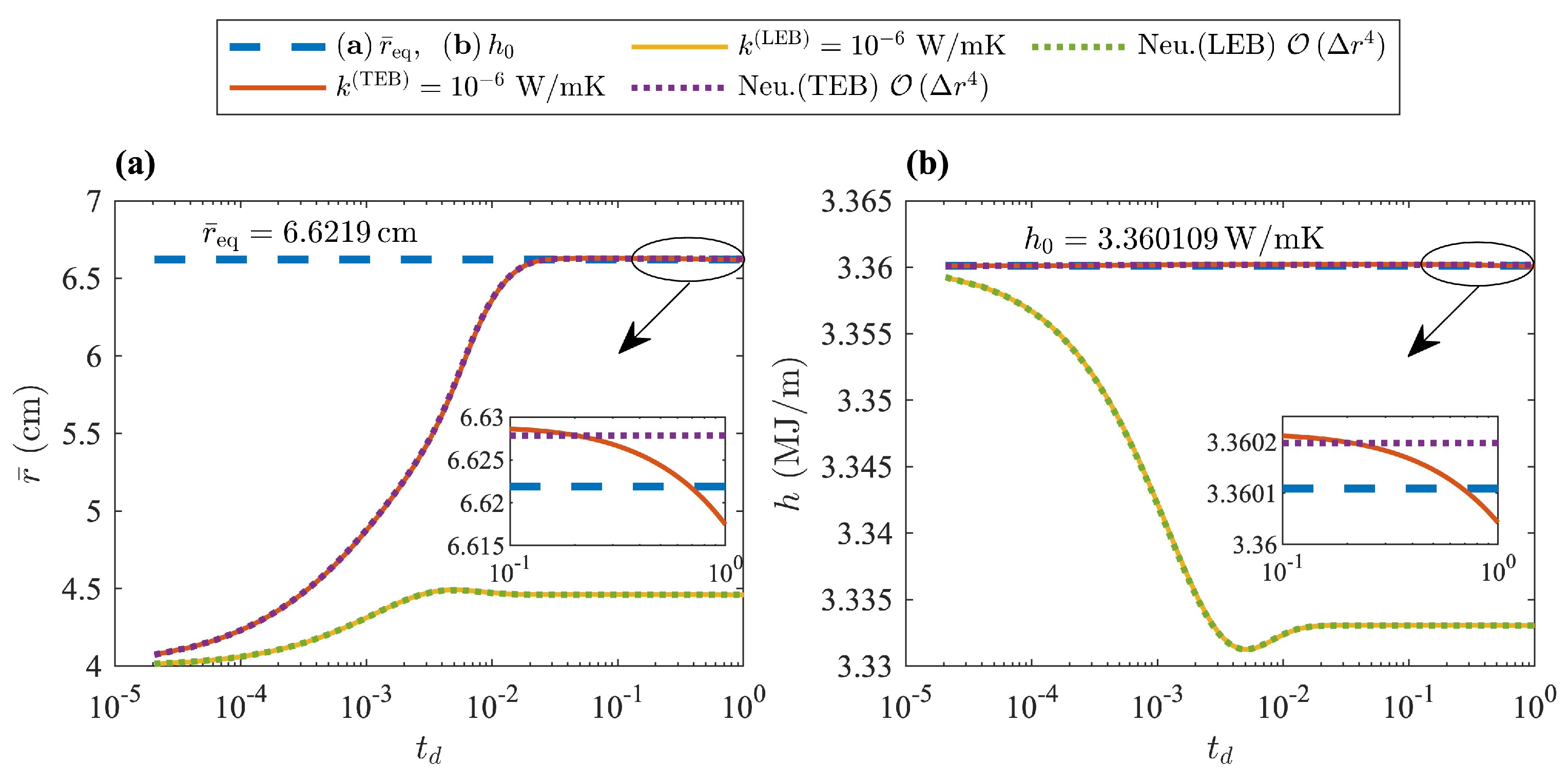
Figure 9b–d shows the time evolution of the liquid-solid front radius $\overline{r}\left(t\right)$ according to the TEB, given by Equation (44), and the LEB, given by Equation (33). The only difference between these equations of motion is the value of the latent heat when applying the homogeneous Neumann boundary conditions. The numerical solutions that show the time evolution of $\overline{r}\left(t\right)$ were obtained by solving the heat equation in each phase, along with the equation of motion for $\overline{r}\left(t\right)$ and under the adiabatic boundary conditions given by Equation (42). The explicit finite difference was used, applying a forward first-order approximation to the time derivatives. The spacial derivatives in the heat equations were calculated through a second-order approximation in $\Delta r$. Additionally, first and fourth order approximations of the spacial derivatives in Equations (42), (44) and (33), were used at each boundary. The precision of the approximation to the derivatives in Equation (42) is incredibly important because they represent perfectly insulated systems. Figure 9b–d represents an illustration of the inconsistencies revealed when applying the LEB at the interface, which can be amplified through the analysis of liquid-solid coexistence at thermodynamic equilibrium.

Figure 9 shows the time evolution of the interface $\overline{r}\left(t\right)$ obtained through the TEB and LEB. The maximum simulation time was $t_{\max }={10}^5 \mathrm{s}$ in all cases, and $t_d=t/t_{\max }$ represents a dimensionless time used in Figure 9b–d. The order of approximation in the spacial derivatives is labeled in each case. First- and fourth-order approximations were used when applying the TEB solution to illustrate improvements with the order of approximation. Additionally, the value of ${\overline{r}}_{\mathrm{eq}}$ was greatly underestimated through the LEB at the interface in all cases. Although in all cases shown in Figure 9, the asymptotic behavior of $\overline{r}\left(t\right)$ was closest to ${\overline{r}}_{\mathrm{eq}}$ when using a fourth-order approximation, the effect is clearer in Figure 9b. The difference between $\overline{r}\left(t_{d_{\max }}\right)$ and ${\overline{r}}_{\mathrm{eq}}$ given by Equation (49) is shown in

Table 5. Relative percent difference between the exact values at thermodynamic equilibrium and the steady state values of $\overline{r}$. according to the TEB with different orders of approximation and according to the LEB with the highest order of approximation.

		TEB-$\mathcal{O}\left(\mathbf{\Delta }\mathit{r}\right)$		TEB-$\mathcal{O}\left(\mathbf{\Delta }{\mathit{r}}^4\right)$		LEB-$\mathcal{O}\left(\mathbf{\Delta }{\mathit{r}}^4\right)$
	${\overline{\mathit{r}}}_{\mathrm{eq}}$	$\overline{\mathit{r}}\left({\mathit{t}}_{{\mathit{d}}_{\max }}\right)$	$\mathbf{RPD}$	$\overline{\mathit{r}}\left({\mathit{t}}_{{\mathit{d}}_{\max }}\right)$	$\mathbf{RPD}$	$\overline{\mathit{r}}\left({\mathit{t}}_{{\mathit{d}}_{\max }}\right)$	$\mathbf{RPD}$
	cm	cm	%	cm	%	cm	%
Case 1	4.7646	4.8185	1.13	4.7685	0.082	4.1158	13.62
Case 2	6.8956	6.9301	0.50	6.9014	0.084	4.5190	34.47
Case 3	7.3892	7.4329	0.59	7.3973	0.110	4.6272	37.38

for the three cases. The relative percent difference (RPD) between $\overline{r}\left(t_{d_{\max }}\right)$ and ${\overline{r}}_{\mathrm{eq}}$, shown in Table 5, had its lowest value, according to the TEB model, when using a fourth-order approximation. The difference was quite small in all cases, and it can be attributed to numerical errors.

The RPDs shown in Table 5 for the radius of the liquid phase $\overline{r}\left(t_{d_{\max }}\right)$ was obtained as follows:

$$\begin{array}{cc}\hfill \mathrm{RPD}& =\left|{\displaystyle \frac{{\overline{r}}_{\mathrm{eq}}-\overline{r}\left(t_{d_{\max }}\right)}{{\overline{r}}_{\mathrm{eq}}}}\right| \times 100\%\hfill \end{array}$$

(50)

Here, ${\overline{r}}_{\mathrm{eq}}$ is given by Equation (49) and represents the interface position at thermodynamic equilibrium. Table 5 also shows the deficiencies of each model and type of approximation.

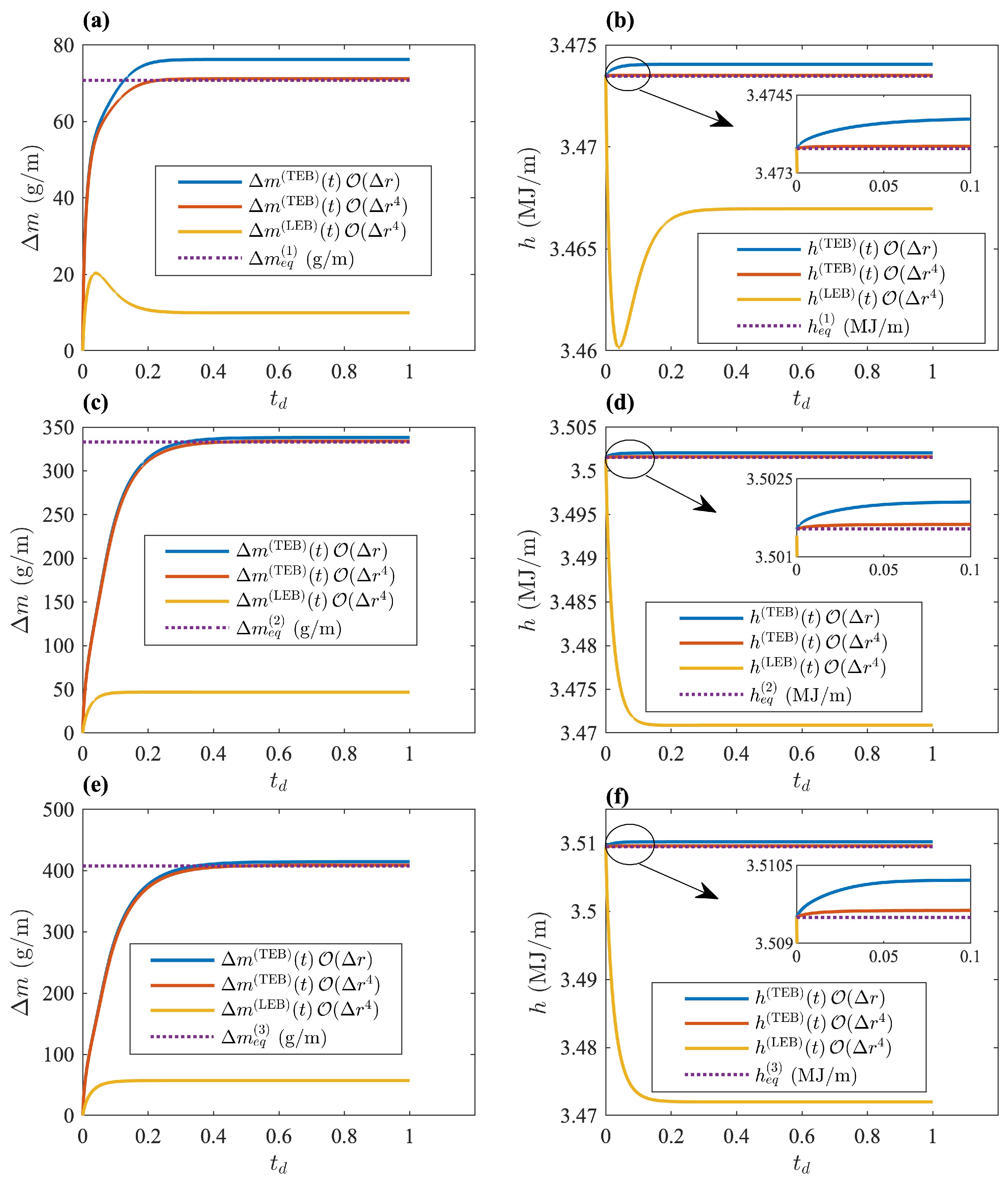
Figure 10 shows the time evolution of the total enthalpy $h\left(t\right)$ and the lost mass of liquid $\Delta m\left(t\right)=m_0-m\left(t\right)$. Here, $\Delta m\left(t\right)$ represents the lost mass per unit length and is defined as $\Delta m\left(t\right)=\Delta M\left(t\right)/\pi L$, where $M\left(t\right)$ is the mass in kilograms at some time t between the initial state and the steady state at thermodynamic equilibrium. The enthalpy is extremely important because this state variable allows verifying energy conservation. The total enthalpy was obtained through numerical integration of the temperature profiles as follows:

$$h\left(t\right)=2{\rho }_{{𝓁}_0}{C}_{{𝓁}_0}{\int }_{r_0}^{\overline{r}\left(t\right)}{T}_{𝓁}(r,t)rdr+2{\rho }_{s_0}{C}_{s_0}{\int }_{\overline{r}\left(t\right)}^R{T}_s(r,t)rdr.$$

(51)

Tracking changes in this variable allowed verifying the following aspects: energy conservation, the effectiveness of artificial insulation given through the boundary conditions and order of approximation, the model’s performance, and the consistency of the temperature profiles. The TEB approach was consistent with energy conservation, as observed in Figure 10b,d,f. The order of approximation was also consistent with energy conservation in all cases, since $h\left(t\right)$ was closer to the initial enthalpy of the system when using a fourth-order approximation. Figure 10b,d,f also helps realize that when applying an LEB at the interface, energy was not conserved.

Finally, the time evolution of the lost mass $\Delta m=m_0-m\left(t\right)$ is shown in Figure 10a,c,e. The exact value at thermodynamic equilibrium was obtained by subtracting the total mass at any time t from the initial mass of the liquid-solid system $m_0={\rho }_{{𝓁}_0}\left({\overline{r}}^2\left(0\right)-r_0^2\right)+{\rho }_s\left(R^2-{\overline{r}}^2\left(0\right)\right)$, where $m_0$ is the initial mass per unit length $m_0=M_0/\pi L$. The exact expression for $\Delta m_{\mathrm{eq}}$ at equilibrium is given by

$$\Delta m_{\mathrm{eq}}={\rho }_{{𝓁}_0}\left({\rho }_{r_0}-1\right)\left({\overline{r}}_{\mathrm{eq}}^2-{\overline{r}}^2\left(0\right)\right),$$

(52)

where ${\overline{r}}_{\mathrm{eq}}$ is given by Equation (49). The LEB at the interface was observed to underestimate the value of $\Delta m_{\mathrm{eq}}$ in all cases, as expected. Additionally, it is important to mention that both models (TEB and LEB) are non-conservative. Volume changes during the melting process were observed as excess volume of liquid and illustrated schematically in Figure 1. The LEB and TEB models assume that excess volume is being removed continuously during the melting process. Consequently, neither approximation conserves mass. The difference relies on energy conservation, as illustrated in Figure 10a,c,e.

3.2.2. PseudoThermodynamic Equilibrium: Thermal Insulation

The homogeneous Neumann boundary conditions constitute an artificial method for emulating perfectly insulated systems, where thermal energy exchange between the system and its surroundings is not present. In reality, such conditions do not exist. In this section, the adiabatic boundary conditions will be replaced by introducing an insulating material. The thermal conductivity of the insulator will be reduced in a series of numerical experiments to produce a liquid-solid mixture as close as possible to a saturated state close to equilibrium. Liquid-solid coexistence close to thermodynamic equilibrium is extremely difficult to reproduce experimentally, as mentioned in Section 1. Open and closed systems in nature are generally far from thermodynamic equilibrium. In this work, we create a closed system with thermal insulation that helps create a simple picture of how coexistence close to equilibrium might be realized. Additionally, the radius of the liquid-solid front close to equilibrium in a coexistence state is a unique solution and does not depend on the type of heat transfer mechanism (e.g., conduction, natural convection, or radiation) present during the transition from an initial state far from equilibrium to the final state close to equilibrium. Consequently, pseudothermodynamic equilibrium becomes a key concept for validating the TEB model proposed in this work. The pseudothermodynamic equilibrium state will also be used as another way to validate the following aspects:

• The performance of the TEB and LEB models;
• Behavior close to equilibrium and shown through Equation (49);
• The validity of the contact condition at the insulator-PCM interface, which is incredibly important for comparison with the experimental results;
• Comparisons with the solutions obtained when using the adiabatic boundary conditions just discussed.

The TEB model proposed in this work must be adapted to this problem by performing energy balancing in a system consisting of insulator-liquid, liquid-solid, and solid-insulator interfaces. The heat storage unit constitutes an air void with a radius $r_0$, an inner layer of insulating material with a thickness ${\delta }_{\mathrm{ins}}$, the PCM confined between $r=r_0+{\delta }_{\mathrm{ins}}$ and $r=R$, and an outer layer of insulating material with the same thickness ${\delta }_{\mathrm{ins}}$. The inner layer of insulating material was placed between the air void and the PCM. In this case, the exchange of thermal energy with the surroundings should be considered. The energy balance must be performed as discussed in Section 2.1 but while adding the energy change of the inner layer just mentioned. The change in thermal energy at the inner layer is given by

$${\displaystyle \frac{d{U}_{\mathrm{ins}}^{\left(1\right)}}{dt}}=2\pi L{\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}{\displaystyle \frac{d}{dt}}{\int }_{r_0}^{r_0+{\delta }_{ins}}{T}_{\mathrm{ins}}^{\left(1\right)}(r,t)rdr$$

(53)

Here, $T_{\mathrm{ins}}^{\left(1\right)}(r,t)$ represents the temperature distribution of the inner insulator. By performing the time derivative of this energy in the same manner as that discussed in Section 2.1, the change in thermal energy at the inner layer is given by

$${\displaystyle \frac{d{U}_{\mathrm{ins}}^{\left(1\right)}}{dt}}=2\pi L\left(k_{\mathrm{ins}}\left(r_0+{\delta }_{\mathrm{ins}}\right){\displaystyle \frac{\partial T_{\mathrm{ins}}^{\left(1\right)}}{\partial r}}{|}_{r=r_0+{\delta }_{\mathrm{ins}}}-k_{\mathrm{ins}}{r}_0{\displaystyle \frac{\partial T_{\mathrm{ins}}^{\left(1\right)}}{\partial r}}{|}_{r=r_0}\right).$$

(54)

Similarly, the thermal energy change at the outer layer of insulating material is given by

$${\displaystyle \frac{d{U}_{\mathrm{ins}}^{\left(2\right)}}{dt}}=2\pi L\left(k_{\mathrm{ins}}\left(R+{\delta }_{\mathrm{ins}}\right){\displaystyle \frac{\partial T_{\mathrm{ins}}^{\left(2\right)}}{\partial r}}{|}_{r=R+{\delta }_{\mathrm{ins}}}-k_{\mathrm{ins}}R{\displaystyle \frac{\partial T_{\mathrm{ins}}^{\left(2\right)}}{\partial r}}{|}_{r=R}\right),$$

(55)

where $T_{\mathrm{ins}}^{\left(2\right)}(r,t)$, represents the temperature profile within the outer layer of insulating material. The total change in thermal energy in this case was obtained by adding Equations (5), (7), (54) and (55). The result must be equal to the net amount of heat exchanged between the insulating layers and the surroundings as follows:

$${\displaystyle \frac{d{Q}_{abs}}{dt}}=2\pi L{k}_{\mathrm{ins}}\left(-r_0{\displaystyle \frac{\partial T_{\mathrm{ins}}^{\left(1\right)}}{\partial r}}{|}_{r=r_0}+\left(R+{\delta }_{\mathrm{ins}}\right){\displaystyle \frac{\partial T_{\mathrm{ins}}^{\left(2\right)}}{\partial r}}{|}_{r=R+{\delta }_{\mathrm{ins}}}\right).$$

(56)

The first term on the right-hand side of the last equation represents the thermal energy released by the liquid phase through the inner layer to the air void. Similarly, the second term on the right-hand side represents the thermal energy released by the solid phase through the outer layer and to the surroundings. The energy balance in this case was obtained as $d{Q}_{abs}/dt=d{U}_{\mathrm{tot}}/dt$, and this is given by the following equation of motion for the liquid-solid interface:

$$2\pi L\left({\rho }_{{𝓁}_0}{L}_{f_0}-\Delta {\rho }_{𝓁,s}{C}_{s_0}{T}_{m_0}\right)\overline{r}\left(t\right) {\displaystyle \frac{d\overline{r}\left(t\right)}{dt}}=\varphi (\overline{r}\left(t\right),t)+\varphi (r_0+{\delta }_{\mathrm{ins}},t)+\varphi (R,t),$$

(57)

with

$$\varphi (r_0+{\delta }_{\mathrm{ins}},t)=2\pi L (r_0+{\delta }_{\mathrm{ins}})\left(-k_{\mathrm{ins}}{\displaystyle \frac{\partial T_{\mathrm{ins}}^{\left(1\right)}}{\partial r}}{|}_{r=r_0+{\delta }_{\mathrm{ins}}}+k_{𝓁}{\displaystyle \frac{\partial T_{𝓁}}{\partial r}}{|}_{r=r_0+{\delta }_{\mathrm{ins}}}\right).$$

(58)

Furthermore, the net thermal fluxes at the liquid-solid interface $\varphi (\overline{r}\left(t\right),t)$ and at the solid-insulator interface $\varphi (R,t)$ have been defined through Equations (9) and (14), respectively. Note that the temperature profile of the insulator in Equation (14) should be replaced by $T_{\mathrm{ins}}^{\left(2\right)}(r,t)$. Following the same procedure discussed in Section 2.1, the contact condition at the insulator-liquid interface must be added. The extra contact condition is quite similar to Equation (23), and in its finite difference form, it is given by

$$\begin{array}{cc}\hfill {\displaystyle \frac{T_{1,j+1}^{\left(\mathrm{PCM}\right)}-T_{1,j}^{\left(\mathrm{PCM}\right)}}{\Delta t}}\left(\Delta r_{\mathrm{PCM}} {\rho }_{\mathrm{PCM}}{C}_{\mathrm{PCM}}+\Delta r_{\mathrm{ins}}{\rho }_{\mathrm{ins}}{C}_{\mathrm{ins}}\right)\approx & -k_{\mathrm{ins}}{\displaystyle \frac{T_{N_i,j}^{\left(\mathrm{ins}\right)}-T_{N_i-1,j}^{\left(\mathrm{ins}\right)}}{\Delta r_{\mathrm{ins}}}}\hfill \\ \hfill & +k_{\mathrm{PCM}}{\displaystyle \frac{T_{2,j}^{\left(\mathrm{PCM}\right)}-T_{1,j}^{\left(\mathrm{PCM}\right)}}{\Delta r_{\mathrm{PCM}}}}.\hfill \end{array}$$

(59)

Here, $N_i$ is the number of spacial nodes within the inner layer of the insulating material. Additionally, during the melting process, the shell of PCM surrounding this layer will be in its liquid form. Similarly, the PCM surrounded by the outer layer of the insulating material, shown in Equation (23), will be in its solid state. Equations (23) and (59) represent a set of equations that describe how the temperature must change at the solid-insulator and liquid-insulator interfaces. The contact conditions in the special case of $k_{\mathrm{ins}}\ll 1 \mathrm{W}/\mathrm{mK}$ are necessary aspects of the model to reproduce states close to thermodynamic equilibrium. Consequently, it is important to analyze the solutions in this type of pseudothermodynamic equilibrium scenario to validate the contact conditions proposed in this work.

The example to be analyzed was initially far from thermodynamic equilibrium and consisted of a liquid-solid mixture with arbitrary quadratic temperature profiles. Initially, the temperature profiles were of the same type previously discussed. The system also consisted of an outer and inner layer of insulating material where the thermal conductivity $k_{\mathrm{ins}}$ was fine-tuned. The thickness of each layer was set to ${\delta }_{\mathrm{ins}}=1.0 \mathrm{cm}$. The initial temperature profiles of each insulating layer were linear. The ambient temperature was constant and set to $T_{\mathrm{amb}}=40$ °C. The ambient temperature represents the temperature of the air void surrounded by the inner layer and the temperature of the surrounding air in contact with the outer layer. The inner and outer surfaces at $r=r_0$ and $r=R+{\delta }_{\mathrm{ins}}$ would be subjected to the following isothermal boundary conditions:

$$T_{\mathrm{ins}}^{\left(1\right)}(r_0,t)=T_{\mathrm{amb}}\mathrm{and}{T}_{\mathrm{ins}}^{\left(2\right)}(R+{\delta }_{\mathrm{ins}},t)=T_{\mathrm{amb}}.$$

(60)

The values of $r_0=0.635 \mathrm{cm}$ and $R=7.65 \mathrm{cm}$ were also used in this case. The initial temperature values at the insulator-liquid interface and at the solid-insulator interface were $T_{\mathrm{ins}}^{\left(1\right)}(r_0+{\delta }_{\mathrm{ins}},0)=90$ °C and $T_s(R,t)=45$ °C, respectively. Furthermore, the initial position of the liquid-solid interface was $\overline{r}\left(0\right)=4.0 \mathrm{cm}$. Consequently, using the quadratic temperature profiles described previously, the initial enthalpy of the liquid-solid mixture obtained from Equation (45) was $h_0=3.360109 \mathrm{MJ}/\mathrm{m}$. The value of $h_0$ just mentioned corresponded only to the enthalpy of the PCM. The thermal energy of the insulating layers was not considered in $h_0$ because for sufficiently low values of $k_{\mathrm{ins}}$, the total enthalpy of the system should be close to $h_0$. The reason for this is that when $k_{\mathrm{ins}}\ll 1 \mathrm{W}/\mathrm{mK}$, heat transfer within the insulating layers is negligible, and the enthalpy changes in the insulating material $\Delta h_{\mathrm{ins}}\approx 0$.

The numerical examples shown in Figure 11 represent a system where the liquid and solid phases were initially far from equilibrium, and the initial enthalpy was the same in all cases. The thermal conductivity of the insulating layers was the only parameter modified in these examples. The real thermodynamic state in all of these examples was the PCM in its solid state at ambient temperature. However, an intermediate state rather close to a saturated mixture at equilibrium could be achieved with sufficiently low values of $k_{\mathrm{ins}}$. Starting with a relatively high conductivity value of $k_{\mathrm{ins}}=0.025 \mathrm{W}/\mathrm{mK}$, it is evident that heat exchange with the surroundings was significant. The PCM was losing too much heat through the inner and outer layers. The maximum amount of liquid phase was quite far from its equilibrium value, which can be appreciated through the maximum displacement of $\overline{r}\left(t\right)$ in Figure 11a. The loss of thermal energy is also evident in Figure 11b. In this case, liquid-solid coexistence close to thermodynamic equilibrium could not be realized. Furthermore, the temperature at the insulator-liquid interface $T_{𝓁}(r_0+{\delta }_{\mathrm{ins}},t)=T_{\mathrm{ins}}^{\left(1\right)}(r_0+{\delta }_{\mathrm{ins}},t)$ was not asymptotically approaching the saturation temperature of $T_{m_0}$, as observed in Figure 11c. The process was stopped at $t_{\max }\approx 8574.5 \mathrm{s}$ when the liquid at this interface reached the saturation temperature $T_{m_0}$. Consequently, beyond this time value, the liquid in contact with the inner layer would transition to its solid phase. The new scenario would be a PCM with an additional solid-liquid interface close to the inner layer and moving outward. Eventually, the system would evolve to its true equilibrium state with the surroundings.

The dimensionless time shown in Figure 11, was obtained as $t_d=t/t_{\max }$, where $t_{\max }$ represents the time when the insulator-liquid interface was cooled down to the saturation temperature of the PCM. Lower values of $k_{\mathrm{ins}}$, translate to larger values of $t_{\max }$ as the PCM closes in on the desired state, with a saturated mixture at thermodynamic equilibrium, where ${\overline{r}}_{\mathrm{eq}}$ is given by Equation (49). Figure 11c illustrates how the temperature of the insulator-liquid interface developed a stronger asymptotic-like behavior with decreasing values of $k_{\mathrm{ins}}$. Additionally, Figure 11b shows a mixture getting closer to its saturated state, which is revealed by decreasing enthalpy changes. Finally, the validity of the contact conditions and the TEB model proposed in this work can be established through the value of ${\overline{r}}_{\mathrm{eq}}$ given by Equation (49) and for sufficiently low values of $k_{\mathrm{ins}}$. Nevertheless, even with extremely low values for $k_{\mathrm{ins}}$, the saturated state obtained in this example does not represent the true equilibrium.

Figure 12 is an illustration of the TEB and LEB solutions applied to insulated systems and using the lowest thermal conductivity $k_{\mathrm{ins}}={10}^{-6} \mathrm{W}/\mathrm{mK}$ considered in this work. The figure is used to illustrate that in these types of systems as well, the deficiencies of the LEB were amplified. Although the system would eventually evolve to its true equilibrium state, the behavior was quite similar to the system with adiabatic boundary conditions previously discussed. The behavior was not identical for two reasons:

• Time was not normalized through the same $t_{\max }$. The maximum value of $t_{\max }$ was ${10}^5 \mathrm{s}$ for the system subjected to adiabatic boundary conditions and $1.213325\times {10}^6 \mathrm{s}$ for the insulated system with $k_{\mathrm{ins}}={10}^{-6} \mathrm{W}/\mathrm{m}·\mathrm{K}$;
• The PCM inside the insulated shell would become quite close to the desired saturated mixture, which is not its real equilibrium state. The effect can be slightly appreciated through the inset in Figure 12b.

Table 6. Improvement in energy conservation and expected quasi-steady state behavior for decreasing $k_{\mathrm{ins}}$ values. Additionally, more realistic asymptotic times are shown than those obtained from systems subjected to artificial adiabatic boundary conditions.

${\mathit{k}}_{\mathbf{ins}}$	${\mathit{t}}_{\mathbf{max}}$	$\mathbf{\Delta }\mathit{h}\left({\mathit{t}}_{\mathbf{max}}\right)$	$\overline{\mathit{r}}\left({\mathit{t}}_{\mathbf{max}}\right)$	$\mathit{T}(\mathit{R},{\mathit{t}}_{\mathbf{max}})$	${\mathbf{RPD}}_{\overline{\mathit{r}}}$
$\times {\mathbf{10}}^{-\mathbf{3}}$W/mK	h	kJ/m	cm	K	%
25.00	2.38	−272.641	4.7914	320.65727	27.643
10.00	3.52	−21.128	5.2381	322.15195	20.897
2.50	5.73	−9.160	5.9932	322.96588	9.494
1.00	7.35	−4.679	6.3022	323.09016	4.828
0.10	11.42	−0.597	6.5816	323.14530	0.609
0.01	35.65	−0.080	6.6166	323.14951	0.080
0.001	337.03	−0.067	6.6175	323.149951	0.066

shows the relative percent difference between the values of $h\left(t_{\max }\right)$ and $\overline{r}\left(t_{\max }\right)$, as well as the exact values at thermodynamic equilibrium for each thermal conductivity $k_{\mathrm{ins}}$ considered in these examples. The data shown in Table 6 were obtained from the solutions of the TEB model applied to an insulated system and given by Equations (57), (59) and (23). The equation of motion for the liquid-solid interface and contact conditions were solved through an explicit finite difference scheme and using a fourth-order approximation of the spacial derivatives. The enthalpy change $\Delta h=h\left(t_{\max }\right)-h_0$ represents the thermal energy lost by the PCM. Table 6 also helps illustrate the concept of pseudo-thermodynamic equilibrium in this problem through the asymptotic growth in $t_{\max }$ with decreasing values for $k_{\mathrm{ins}}$. Furthermore, it is evident that the temperature at the solid-insulator interface $T(R,t)$ shown in Table 6 would never reach the saturation temperature of the PCM for $k_{\mathrm{ins}}>0$. The system released some thermal energy to the surroundings even if $k_{\mathrm{ins}}\ll 1 \mathrm{W}/\mathrm{mK}$, since the real thermodynamic equilibrium in this example consisted of a PCM in its solid phase at ambient temperature and below $T_m$.

Figure 13 provides a visual representation of the temperature profiles in insulated systems with (a) $k_{\mathrm{ins}}={10}^{-2} \mathrm{W}/\mathrm{mK}$, (b) $k_{\mathrm{ins}}={10}^{-4} \mathrm{W}/\mathrm{mK}$, and (c) $k_{\mathrm{ins}}={10}^{-8} \mathrm{W}/\mathrm{mK}$. In this example, the initial temperature distribution in each layer was changed from a linear profile to a constant value of $T_{\mathrm{ins}}=40$ °C. Figure 13 helps qualitatively appreciate the expected behavior of the temperature field with decreasing values for $k_{\mathrm{ins}}$. Additionally, the temperature distribution in the PCM unit offers some insight on how thermal energy is lost to the surroundings during the cooling process. Specifically, during the first $2500 \mathrm{s}$ of the cooling process, the effect of improved insulation was clearer, as observed in the first column of the temperature profiles shown in Figure 13. Finally, the effect of the contact conditions when $k_{\mathrm{ins}}\ll 1 \mathrm{W}/\mathrm{mK}$ can be clearly appreciated in the last row of Figure 13. Here, the deep navy blue color observed across the entire thickness of both layers shows how $T_{\mathrm{ins}}$ was practically constant and equal to 40 °C when $k_{\mathrm{ins}}={10}^{-8}$. In contrast, the boundaries between the layers and the PCM became blurred and hotter (light blue) as time progressed.

3.3. Experimental Comparison Between LEB and TEB

The thermophysical properties of the paraffin used in the experiment are summarized in Table 1. The thermodynamic properties shown in Table 1 correspond to the values of the solid and liquid phases close to the saturation temperature of $T_{m_0}=50$ °C [26]. The HTF was gradually heated to $T_H=70$ °C in a Lauda thermostatic bath. The HTF was allowed to circulate through the copper tube when the thermostatic bath reached the desired temperature value of $T_H=70$ °C. The mass flux of the HTF was fixed at $0.25 \mathrm{L}/\min$ throughout the melting process. Thermal energy was transferred from the HTF to the inner surface of the cooper pipe during a time window of $200 \min$, as shown in Figure 14. The inner radius of the copper tube shown schematically in Figure 5c was equal to $r_0=0.685 \mathrm{cm}$. Additionally, the thickness of the aluminum layer was $2 \mathrm{mm}$ and the outer diameter shown in Figure 5c was $12.11 \mathrm{cm}$. Consequently, the inner radius of the aluminum layer was $R=5.855 \mathrm{cm}$. The thermocouples placed at the radial positions described in Section 2.2 and shown in Figure 5c were used to track the position of the liquid-solid front during the melting process. The experimental value of $\overline{r}\left(t\right)$ was obtained through a linear interpolation of the temperature readings between two adjacent thermocouples. The radial position of the liquid-solid front at some time t during the melting process was estimated as follows:

$$\overline{r}\left(t\right)=r_i+\left(r_{i+1}-r_i\right){\displaystyle \frac{T_i\left(t\right)-T_{m_0}}{T_i\left(t\right)-T_{i+1}\left(t\right)}}$$

(61)

where $T_i\left(t\right)>T_{m_0}$ is the temperature reading at sensor i and time t and above the melting temperature of the PCM. Additionally, $T_{i+1}\left(t\right)<T_{m_0}$ is the temperature reading at the adjacent sensor $i+1$, and below the melting point of the PCM. The linear interpolation method given by the last equation assumes an isothermal phase transition at thermodynamic equilibrium. According to the assumptions described in Section 2, during the melting process, the solid phase is not significantly superheated above its melting temperature at equilibrium $T_{m_0}$. Initially, the paraffin was in its solid phase at $T_s(r,0)=22$ °C, and the ambient temperature surrounding the polyurethane foam was $T_{\mathrm{amb}}=22$ °C. The initial conditions for the numerical solutions shown in Figure 14 consisted of a thin liquid layer of ${\delta }_{𝓁}=0.1 \mathrm{mm}$ surrounding the copper tube at $T_{𝓁}(r,0)=70$ °C and solid and insulating materials initially at 22 °C. Additionally, the isothermal boundary conditions described by Equation (39) with $T_H=70$ °C and $T_{\mathrm{amb}}=22$ °C were applied to each model discussed in this work.

Figure 13. Visual representation of thermal energy conservation in systems with low thermal conductivity insulating layers. The first column illustrates the effects of increasing thermal insulation. The last row shows the expected isothermal behavior of the insulating layers for extremely low values for $k_{\mathrm{ins}}$.

Figure 13. Visual representation of thermal energy conservation in systems with low thermal conductivity insulating layers. The first column illustrates the effects of increasing thermal insulation. The last row shows the expected isothermal behavior of the insulating layers for extremely low values for $k_{\mathrm{ins}}$.

Figure 14. (a) The improvement in the TEB solution for $\overline{r}$ in melting experiments at $T_H=70$ °C. (b) An estimation of the lost mass of liquid obtained from the experimental data and each model discussed in this work.

Figure 14. (a) The improvement in the TEB solution for $\overline{r}$ in melting experiments at $T_H=70$ °C. (b) An estimation of the lost mass of liquid obtained from the experimental data and each model discussed in this work.

Figure 14 shows a comparison between the experimental results and the performance of the LEB and TEB models proposed in this work. The TEB approach was clearly closer to the radial position of the liquid-solid interface, and the relative errors ${\mathrm{RPD}}_{\overline{r}}$ between the experimental results and the predicted values of ${\overline{r}}^{\left(\mathrm{TEB}\right)}\left(t\right)$ and ${\overline{r}}^{\left(\mathrm{LEB}\right)}\left(t\right)$ are shown in

Table 7. Experimental comparison between the TEB and LEB models for the radial position of the interface. Additionally, the energy balance was verified in this case with the RPD between $\Delta Q_{\mathrm{abs}}$, given by Equation (34), and the enthalpy change in the PCM and insulator, shown in Equations (37) and (38).

t	${\overline{\mathit{r}}}_{\mathbf{exp}}$	${\overline{\mathit{r}}}_{\mathbf{TEB}}$	${\overline{\mathit{r}}}_{\mathbf{LEB}}$	${\mathbf{RPD}}_{\overline{\mathit{r}}}^{\left(\mathbf{TEB}\right)}$	${\mathbf{RPD}}_{\overline{\mathit{r}}}^{\left(\mathbf{LEB}\right)}$	${\mathbf{RPD}}_{\mathbf{Engy}}^{\left(\mathbf{TEB}\right)}$	${\mathbf{RPD}}_{\mathbf{Engy}}^{\left(\mathbf{LEB}\right)}$
min	cm			%
58.40	1.3106	1.3314	1.2789	1.59	2.42	0.21	11.35
66.73	1.3437	1.3612	1.3069	1.31	2.74	0.19	11.09
83.39	1.4226	1.4186	1.3591	0.28	4.47	0.17	10.74
100.05	1.4819	1.4761	1.4089	0.39	4.93	0.15	10.55
116.71	1.5600	1.5357	1.4584	1.56	6.51	0.14	10.50
133.38	1.6206	1.5985	1.5086	1.36	6.91	0.13	10.57
150.04	1.6762	1.6649	1.5600	0.67	6.93	0.12	10.72
166.71	1.7220	1.7351	1.6127	0.76	6.35	0.12	10.94
183.37	1.7726	1.8093	1.6668	2.07	5.97	0.11	11.23
200.04	1.7856	1.8875	1.7221	5.71	3.55	0.11	11.57

. The improvement obtained through the TEB model was expected, since this approach is consistent with total energy conservation, as demonstrated by the previous analysis of liquid-solid coexistence at thermodynamic equilibrium. The melting process was monitored over $200\min$, observing just partial melting of the solid phase. The melting fractions were less than $40\%$ to minimize heat transfer through convection and validate the proposed model in the conductive regime. Consequently, the following assumptions could be justified:

• The melting process in the liquid phase was assumed to be in the conductive regime, and thermal transfer through convection was not considered;
• The heat transfer along the axial direction due to the hot liquid at the top surface was not considered. The front position was purposely tracked at the bottom surface of the TES unit to minimize this effect.

Additionally, in Table 7, the relative difference ${\mathrm{RPD}}_{\mathrm{Engy}}$ between the net thermal energy absorbed by the system and the enthalpy change in the PCM and insulating material are also shown for the TEB and LEB models. The relative difference between these energies was calculated for each model to verify that the energy balance predicted by the proposed model was also consistent in this case. Finally, the excess mass $\Delta m$ of liquid shown in Figure 14b was estimated from the experimental values of $\overline{r}\left(t\right)$ and compared with the values predicted by the TEB and LEB models discussed in this work. The experimental value of the excess mass was estimated from the measured values of the liquid-solid front position as $\Delta m=m\left(0\right)-m\left(t\right)$, where $m\left(0\right)={\rho }_{s_0}(R^2-r_0^2)$ and $m\left(t\right)={\rho }_{{𝓁}_0}\left({\overline{r}}_{\exp }^2-r_0^2\right)+{\rho }_{s_0}\left(R^2-{\overline{r}}_{\exp }^2\right)$. According to the results shown in Figure 14b, the RPD between the experimental values and those estimated through the TEB solutions was between ${\mathrm{RPD}}_{\max }^{\left(\mathrm{TEB}\right)}=0.58\%$ and ${\mathrm{RPD}}_{\max }^{\left(\mathrm{TEB}\right)}=8.37\%$. Alternatively, the RPD between the experimental values and the solutions from the LEB fell within ${\mathrm{RPD}}_{\max }^{\left(\mathrm{TEB}\right)}=18.34\%$ and ${\mathrm{RPD}}_{\max }^{\left(\mathrm{TEB}\right)}=20\%$.

4. Conclusions

A total energy balance model applied to cylindrical energy storage units was proposed. Corrections to the equation of motion for the liquid-solid front were found and analyzed. The main goals were to use total energy conservation to construct a model that yielded a new equation of motion for the liquid-solid front and to use thermodynamic equilibrium in saturated mixtures to test the model’s performance in the thermodynamic equilibrium limit. Additionally, a conceptual framework based on energy conservation in adiabatic and pseudo-adiabatic systems was applied to determine the exact distribution of liquid and solid phases at equilibrium. The configuration and distribution of the resulting saturated mixtures provide a basis for validating phase transition models in the thermodynamic equilibrium limit.

Total energy balance was determined by comparing the net thermal energy exchange with the surroundings with the thermal energy absorbed by the insulator-PCM system. The time evolution of each type of energy was estimated by the local and total energy balance models. The evolution of the thermodynamic state estimated by the local energy balance yielded relative differences between thermal energies as high as $75\%$, while the relative difference obtained when applying the total energy balance model fell between $0.25\%$ and $0.97\%$. However, the main finding is related to the models’ performance in the thermodynamic equilibrium limit. The estimated coexistence states were used to show discrepancies related to energy conservation. Relative differences between the radial position of the interface at thermodynamic equilibrium and the value predicted by the local energy balance ranged from $13.6\%$ to $37.4\%$. In contrast, relative differences between $0.082\%$ and $0.11\%$ were found by applying the total energy balance proposed in this work. Additionally, each model was tested against the experimental estimation of the interface position in a cylindrical heat storage unit. The experimental values of the interface position were underestimated by the local energy balance with relative differences that ranged from $2.42\%$ to $6.91\%$. In contrast, relative differences between $0.28\%$ and $5.71\%$ were found by applying the total energy balance. Finally, differences in the lost mass between $18.34\%$ and $20\%$ were found by using the local energy balance approach, while differences ranging from $0.58\%$ to $8.37\%$ were obtained by applying the total energy balance.

The proposed model and the thermodynamic equilibrium of saturated states established in this work were limited to the specific geometrical configuration and the manner in which excess volume was distributed. The total energy balance model is not general, but a conceptual framework was proposed to adapt the idea of total energy balance to different configurations. The limitation consists of applying the energy balance to a cylindrical unit where the melted solid expands during its transformation along the axial direction. The excess volume of liquid is constantly removed, and a fraction of the PCM’s mass is voided from the thermal energy exchange. The specific manner in which the PCM expands during a melting process represents a non-conservative scenario due to the removal of excess volume. The limitation just mentioned is also a result of the geometry. The models studied in this work are also limited to the conductive regime and belong to the class of Stefan-like problems. The framework established in this work, could be generalized to incorporate thermal exchange between the liquid and solid phases that results from natural convection in the liquid phase. The generalization just mentioned could allow the assessment of total balance in melting processes with higher melting fractions and higher melting rates produced by a heat transfer fluid at higher temperatures. The model is also limited to phase transitions close to thermodynamic equilibrium. The model does not consider the superheating of the solid phase produced by higher temperatures for the heat transfer fluid.

Finally, the main implications of this work are twofold. First, the proposed model can be applied to configurations and geometries where the total mass of the PCM is conserved. The result would lead to a different equation of motion for the liquid-solid front and an additional equation of motion for the radius of the PCM-container interface. The result of such a model will also depend on the geometrical shape of the heat storage unit and the presence or absence of sacrificial layers. The absence of such layers, for example, requires incorporating changes in the liquid-solid saturation properties of the PCM—such as the melting temperature and latent heat—into the conceptual framework and model proposed in this work. The second implication involves designing experimental set-ups to test the configurations of saturated mixtures at thermodynamic equilibrium determined by applying energy conservation to storage units of various geometries. Saturated mixtures at thermodynamic equilibrium are extremely difficult to achieve experimentally. In reality, thermodynamic equilibrium is rare, as most heat exchange processes occur under non-equilibrium conditions. Experiments that are able to produce coexistence states as close as possible to a saturated mixture at equilibrium is one of the most relevant and challenging implications. The realization of such experiments would allow verifying the analytical expressions determined by applying energy conservation and testing the proposed models close to the thermodynamic equilibrium limit. For example, one of the main limitations of such experiments is related with the technological development of insulating materials with sufficiently low thermal conductivities.