Maximized Autonomous Economic Operation and Aggregated Equivalence for Microgrids with PVs and ESSs
Abstract
1. Introduction
- Develop a sensitivity-based autonomous economic optimization for an MGPE to minimize electricity exchange while covering internal costs, concurrently lowering outage probability to secure supply reliability.
- Establish aggregated equivalent models of the MGPE to reduce the scheduling complexity of scheduling and enhance the operational efficiency of the main grid.
- Quantify both the physical and economic parameters of the aggregated models to provide valuable information for the main grid, enabling better resource management and improved energy utilization.
2. Autonomous Economic Operation (AEO)
3. Methodology
3.1. Optimization Model
3.1.1. Objective Function
3.1.2. Constraints
- (a).
- Power Balance Constraint
- (b).
- ESS Operation Constraints
- (c).
- Flexible Load Constraints
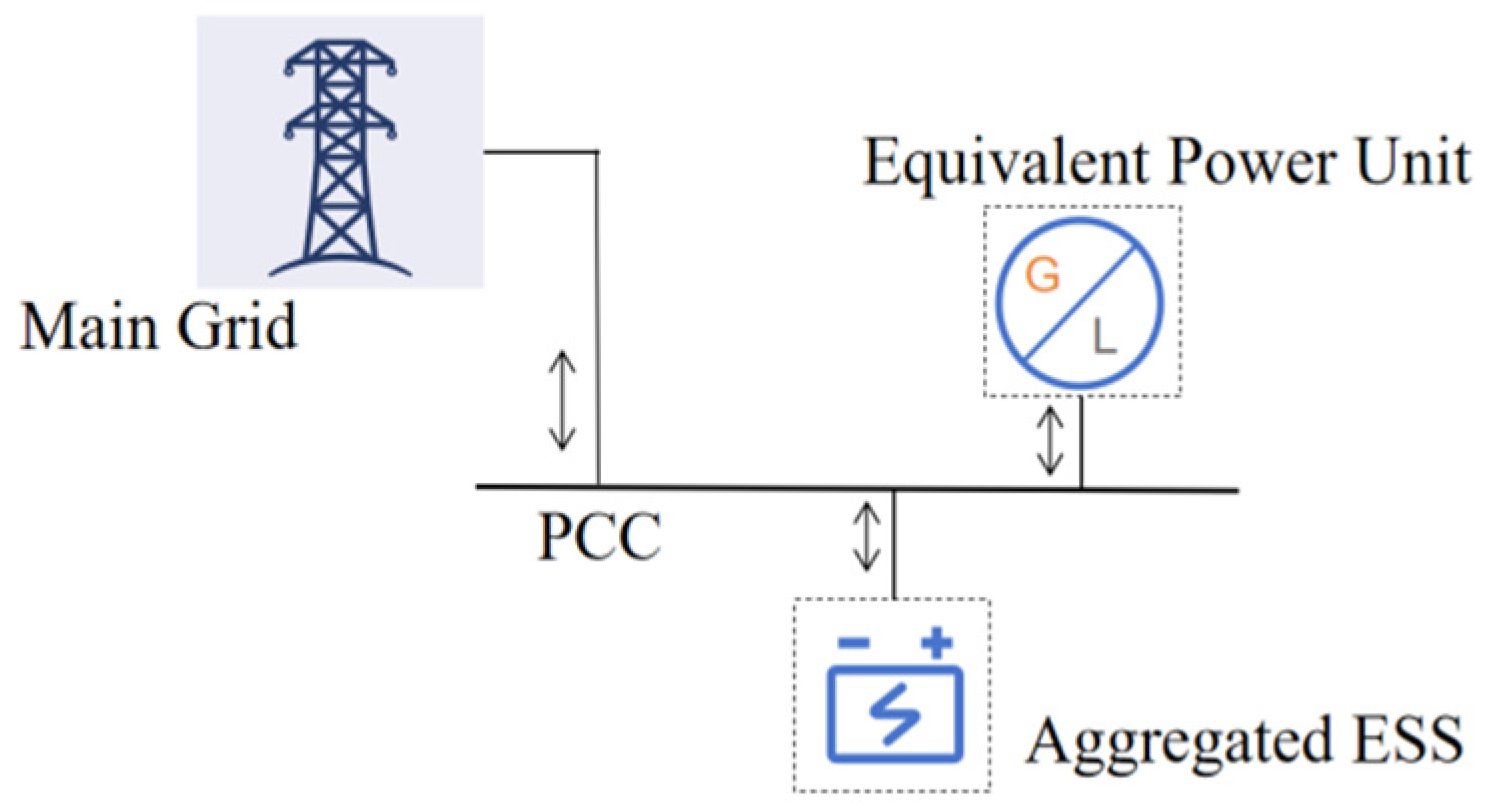
3.2. Aggregation and Equivalence
3.2.1. Residual Regulation Capability
3.2.2. Residual Regulation Capability Residual Surplus Capability
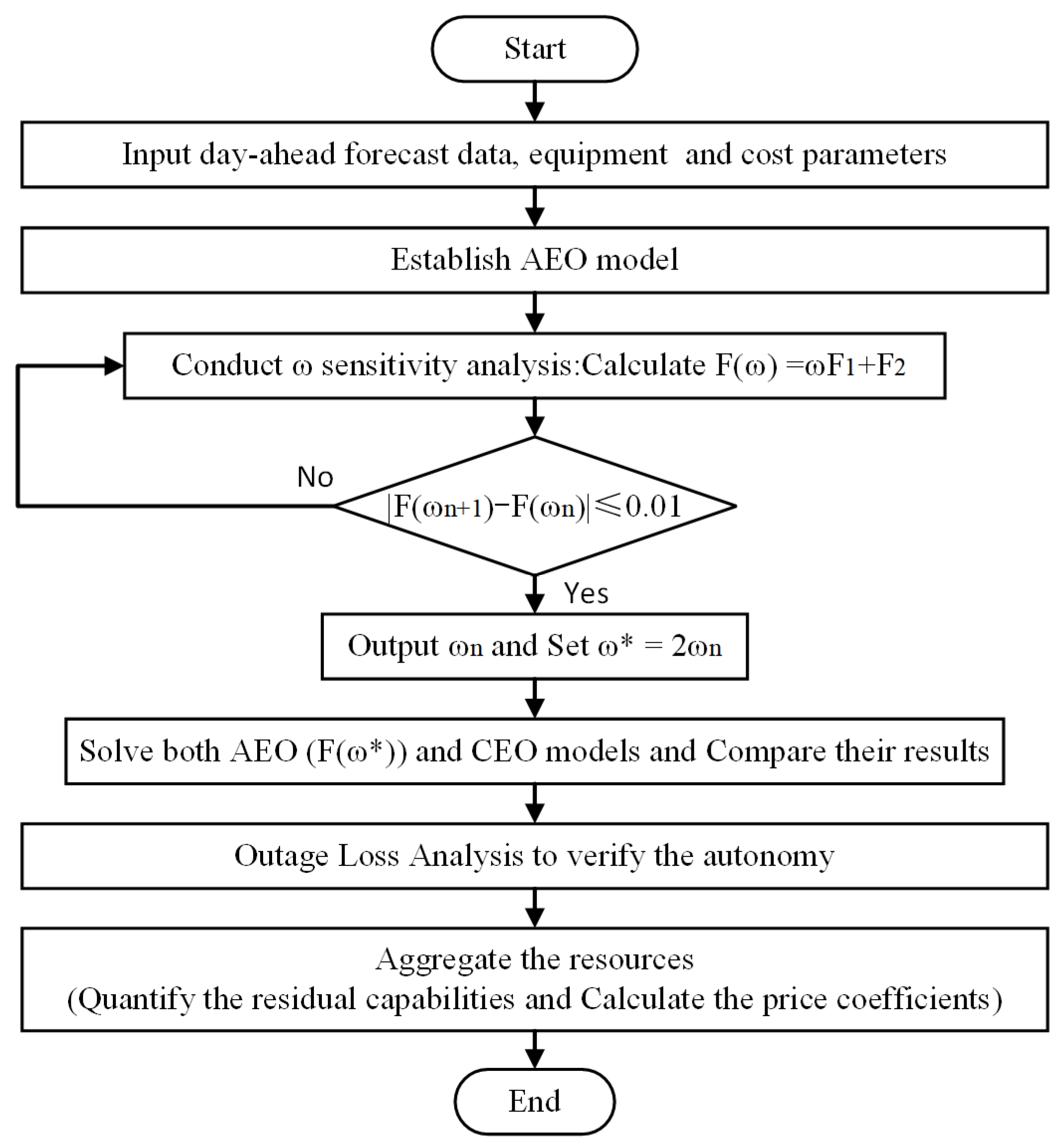
3.3. Procedure
- Data Input: The input set is constructed by reading data of ESSs, PVs, loads, flexible loads, and cost parameters.
- Establish Modeling: The AEO model is constructed using the optimization objective defined by Equations (1)–(3) together with the relevant constraints.
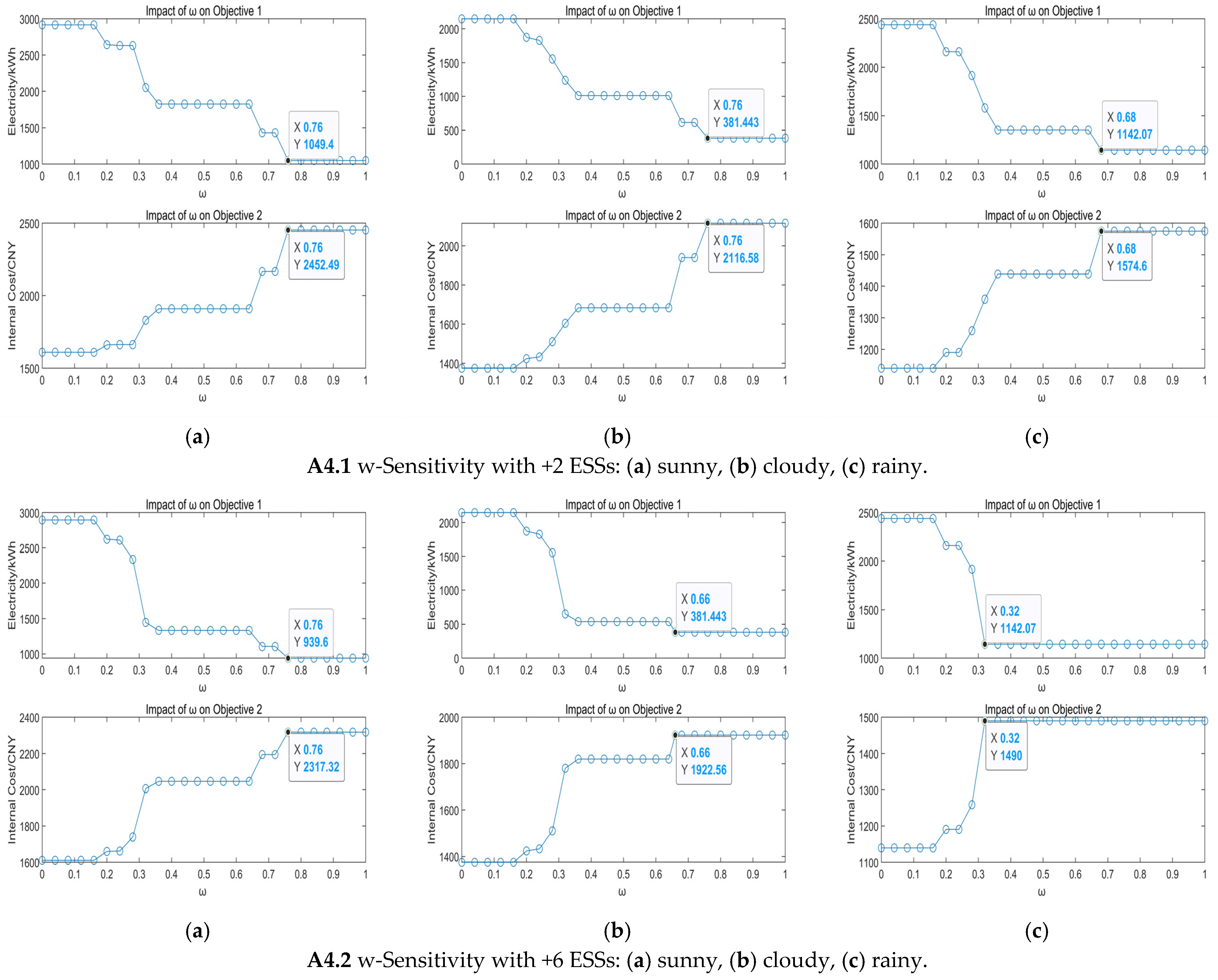
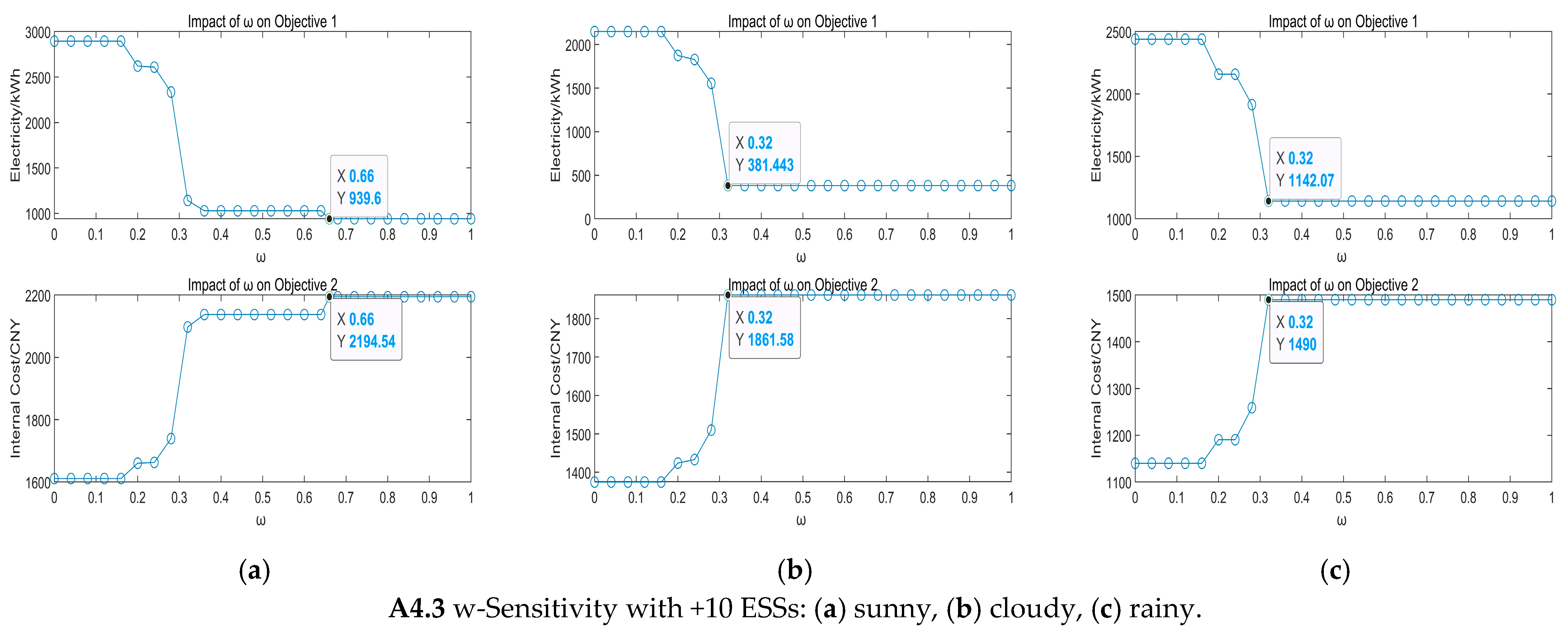
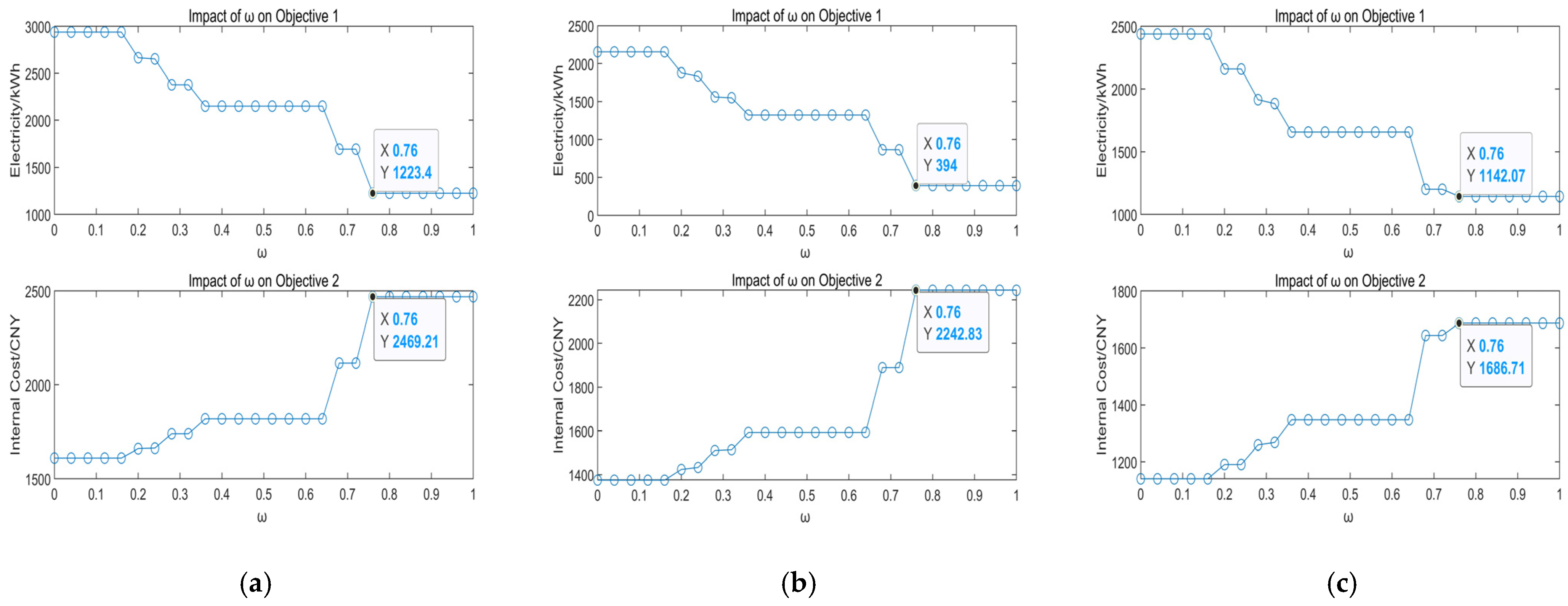
- ω Sensitivity Analysis: the parameter ω is varied from 0 to 1 with a step size of 0.04. At each point, the MIQP is solved using CPLEX and YALMIP, and the F–ω curve is plotted. To maintain an adequate margin, the optimal weight ω* is set to twice the knee-point value.
- Optimization: Optimization with Fixed ω* and Comparison between AEO and the minimized cost economic operation (CEO).
- Substituting ω* the MIQP is solved again to obtain the AEO scheduling result.
- Using the same constraints but minimizing only the cost function (), the CEO scheduling scheme is derived as a benchmark.
- Outage Loss Analysis: the outage probability and outage losses under AEO and CEO scheduling are compared to quantify the autonomy benefits.
- Aggregated equivalence: according to the AEO results, the internal resources are aggregated; the residual external capability and its corresponding price coefficient are then quantified.
4. Case Study Analysis
4.1. Model Verification
- (1)
- Internal consistency
- (2)
- Scalability and sensitivity
- (3)
- Data availability statement
4.2. Basic Data
4.3. Dispatch Analysis
4.3.1. Sensitivity Analysis
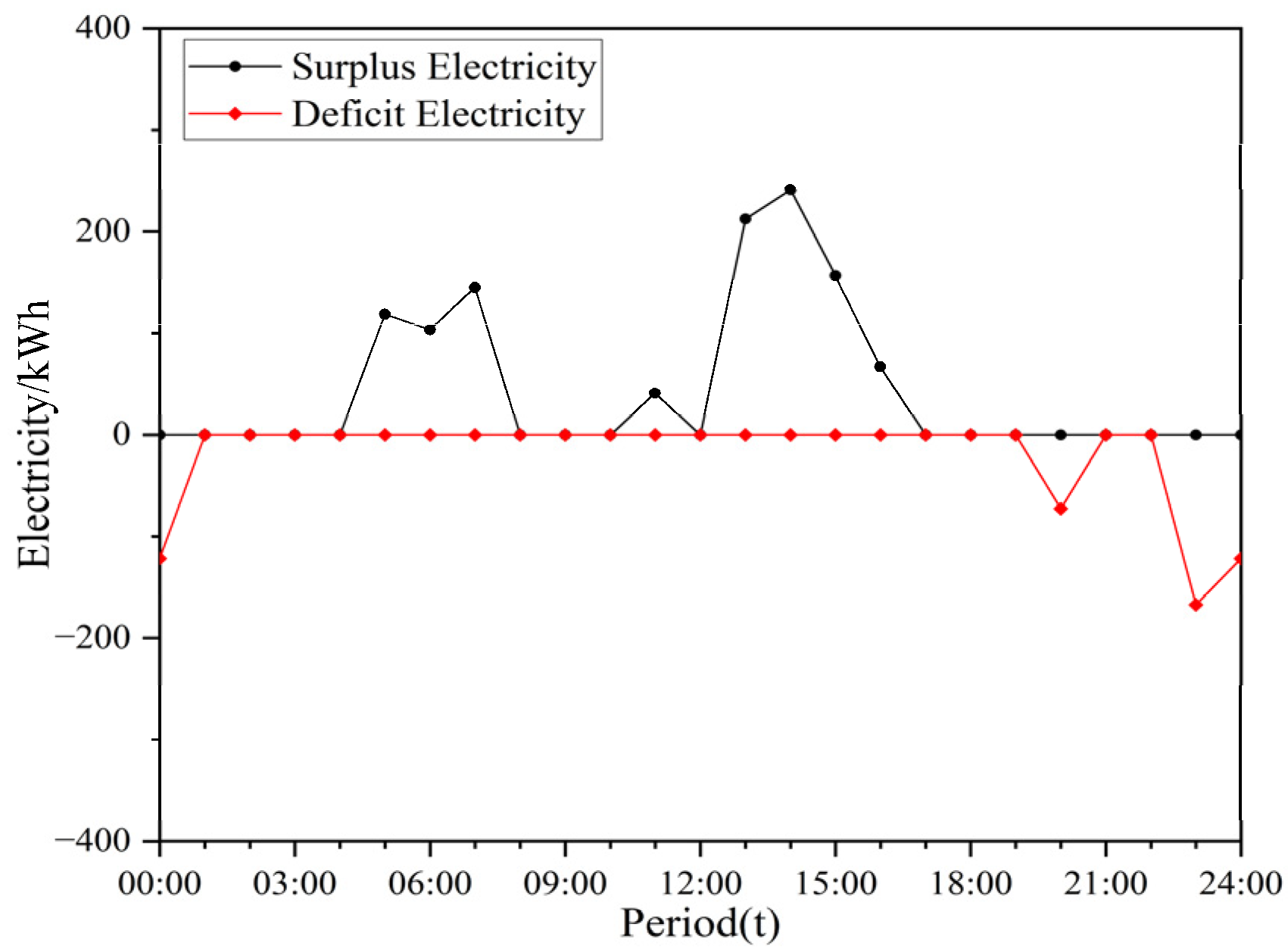
4.3.2. Optimized Scheduling
5. Case Study Improvements
5.1. Comparison of Outage Loss Performance
5.2. Aggregation and Quantification
5.3. Further Experiments
5.3.1. Scalability
5.3.2. Sensitivity Analysis of PV and ESS Capacity
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Algorithm A1: CPLEX-Based Maximized AEO for the MGPE with ω-Sensitivity |
| Input: -Time horizon , step -Fixed load: ; flexible loads: -PV generation: -ESS parameters: -Cost coefficients: Hyperparameters: -Penalty factor set (e.g., 0:0.04:1) -Solver: IBM CPLEX via YALMIP (MIQP model, mipgap = 0.01, timelimit = 60 s) Output: -Optimal schedules: -, , selected * |
| 1. Define Objective |
| 1.1 Objective 1: |
| 1.2 Objective 2: |
| 1.3 Total objective: |
| 2. Constraints |
| 2.1 Power balance: grid exchange, PV generation, ESS charge/discharge must meet total load demand (fixed + flexible) |
| 2.2 ESS operation: SOC dynamics, capacity limits, and mutually exclusive charge/discharge |
| 2.3 Flexible load: shifting and ramp limits, total energy conservation |
| 3. -Sensitivity Analysis |
| For each in : |
| -Update objective F() |
| -Solve MIQP model with CPLEX |
| -CPLEX internally applies Branch-and-Bound for integer vars, Barrier/Simplex for QP relaxation |
| -Presolve, cut generation, heuristics are activated to improve efficiency |
| -Record F(), , and |
| 4. Select |
| 4.1 Choose based on trade-off between grid exchange and internal cost |
| 4.2 Typically select yielding minimal F() under constraints |
| 5. Final Scheduling |
| 5.1 Fix = 2, re-solve MIQP via CPLEX |
| 5.2 Output dispatch |
| Time Period | Flexible Load 1 Cost | Flexible Load 2 Cost |
|---|---|---|
| 01:00–08:00; 19:00–24:00 | 0.18 | 0.28 |
| 12:00–14:00 | 0.25 | 0.35 |
| 09:00–11:00; 15:00–18:00 | 0.20 | 0.30 |



References
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The Role of Renewable Energy in the Global Energy Transformation. Energy Strategy Rev. 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Kroposki, B.; Johnson, B.; Zhang, Y.C.; Gevorgian, V.; Denholm, P.; Hodge, B.-M.; Hannegan, B. Achieving a 100% Renewable Grid: Operating Electric Power Systems with Extremely High Levels of Variable Renewable Energy. IEEE Power Energy Mag. 2017, 15, 61–73. [Google Scholar] [CrossRef]
- Faisal, M.; Hannan, M.A.; Ker, P.J.; Begum, R.A.; Dong, Z.Y. Review of Energy Storage System Technologies in Microgrid Applications: Issues and Challenges. IEEE Access 2018, 6, 35143–35164. [Google Scholar] [CrossRef]
- Dawoud, S.M.; Lin, X.; Okba, M.I. Hybrid Renewable Microgrid Optimization Techniques A Review. Renew. Sustain. Energy Rev. 2018, 82, 2039–2052. [Google Scholar] [CrossRef]
- Muhtadi, A.; Pandit, D.; Nguyen, N.; Yu, D.C. Distributed Energy Resources Based Microgrid Review of Architecture, Control, and Reliability. IEEE Trans. Ind. Appl. 2021, 57, 2223–2235. [Google Scholar] [CrossRef]
- Silva, V.A.; Aoki, A.R.; Lambert-Torres, G. Optimal Day-Ahead Scheduling of Microgrids with Battery Energy Storage System. Energies 2020, 13, 5188. [Google Scholar] [CrossRef]
- Gomes, J.G.; Xu, H.J.; Yang, Q.; Zhao, C.Y. An Optimization Study on a Typical Renewable Microgrid Energy System with Energy Storage. Energy 2021, 234, 121210. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y. Optimal Coordinated Energy Dispatch of a Multi-Energy Microgrid in Grid-Connected and Islanded Modes. Appl. Energy 2018, 210, 974–986. [Google Scholar] [CrossRef]
- Nwulu, N.I.; Xia, X. Optimal Dispatch for a Microgrid Incorporating Renewables and demands Response. Renew. Energy 2017, 101, 16–28. [Google Scholar] [CrossRef]
- Witharama, W.M.N.; Bandara, K.M.D.P.; Azeez, M.I.; Logeeshan, V.; Wanigasekara, C. Advanced Genetic Algorithm for Optimal Microgrid Scheduling Considering Solar and Load Forecasting, Battery Degradation and demands Response Dynamics. IEEE Access 2024, 12, 123456–123470. [Google Scholar] [CrossRef]
- Sun, L.; Xu, Q.; Chen, X.; Fan, Y. Day-Ahead Economic Dispatch of Microgrid Based on Game Theory. Energy Rep. 2020, 6, 633–638. [Google Scholar] [CrossRef]
- Silvente, J.; Kopanos, G.M.; Pistikopoulos, E.N. A Rolling Horizon Optimization Framework for the Simultaneous Energy Supply and Demand Planning in Microgrids. Appl. Energy 2015, 155, 485–501. [Google Scholar] [CrossRef]
- Hou, H.; Xue, M.; Xu, Y.; Xiao, Z.; Deng, X.; Xu, T.; Liu, P.; Cui, R. Multi-Objective Economic Dispatch of a Microgrid Considering Electric Vehicle and Transferable Load. Appl. Energy 2020, 262, 114489. [Google Scholar] [CrossRef]
- Aghajani, G.; Ghadimi, N. Multi-Objective Energy Management in a Micro-Grid. Energy Rep. 2018, 4, 218–225. [Google Scholar] [CrossRef]
- Cao, Y.; Lu, D.; Zhang, Y.; Tang, Q.; Khodaei, A.; Zhang, H.; Han, Z. Optimal Energy Management for Multi-Microgrid under a Transactive Energy Framework with Distributionally Robust Optimization. IEEE Trans. Smart Grid 2022, 13, 599–612. [Google Scholar] [CrossRef]
- Nawaz, A.; Wu, J.; Ye, J.; Dong, Y.; Long, C. Distributed MPC-Based Energy Scheduling for Islanded Multi-Microgrid Considering Battery Degradation and Cyclic Life Deterioration. Appl. Energy 2023, 329, 120168. [Google Scholar] [CrossRef]
- Tan, B.; Chen, H.; Zheng, X. Two-Stage Robust Optimization Dispatch for Multiple Microgrids with Electric Vehicle Loads Based on a Novel Data-Driven Uncertainty Set. Int. J. Electr. Power Energy Syst. 2022, 134, 107359. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, B.; Wang, X.; Pan, Z.; Sun, H.; Liu, Z.; Guo, Q. Active Dynamic Aggregation Model for Distributed Integrated Energy System as Virtual Power Plant. J. Mod. Power Syst. Clean Energy 2020, 8, 831–840. [Google Scholar] [CrossRef]
- Wang, S.; Wu, W. Aggregation Reference Model and Quantitative Metric System of Flexible Energy Resources. Autom. Electr. Power Syst. 2024, 48, 1–9. (In Chinese) [Google Scholar]
- Utkarsh, K.; Ding, F.; Jin, X.; Blonsky, M.; Padullaparti, H.; Balamurugan, S.P. A Network-Aware Distributed Energy Resource Aggregation Framework for Flexible, Cost-Optimal, and Resilient Operation. IEEE Trans. Smart Grid 2021, 13, 1213–1224. [Google Scholar] [CrossRef]
- Wen, Y.; Hu, Z.; You, S.; Duan, X. Aggregate Feasible Region of DERs: Exact Formulation and Approximate Models. IEEE Trans. Smart Grid 2022, 13, 4405–4423. [Google Scholar] [CrossRef]
- Yi, Z.; Xu, Y.; Gu, W.; Yang, L.; Sun, H. Aggregate Operation Model for Numerous Small-Capacity Distributed Energy Resources Considering Uncertainty. IEEE Trans. Smart Grid 2021, 12, 4208–4224. [Google Scholar] [CrossRef]
- He, G.; Huang, Y.; Huang, G.; Liu, X.; Li, P.; Zhang, Y. Assessment of Low-Carbon Flexibility in Self-Organized Virtual Power Plants Using Multi-Agent Reinforcement Learning. Energies 2024, 17, 3688. [Google Scholar] [CrossRef]
- Yang, Z.; Wu, R.; Yang, J.; Long, K.; You, P. Economical Operation of Microgrid with Various Devices via Distributed Optimization. IEEE Trans. Smart Grid 2016, 7, 857–867. [Google Scholar] [CrossRef]
- He, Y.; Chen, Y.; Liu, Y.; Liu, H.; Liu, D.; Sun, C. Analysis on Cost per kWh and Cost per mileage for energy storage technologies. Adv. Technol. Electr. Eng. Energy 2019, 38, 1–10. (In Chinese) [Google Scholar] [CrossRef]
- Hamidieh, M.; Ghassemi, M. Microgrids and Resilience: A Review. IEEE Access 2022, 10, 106059–106080. [Google Scholar] [CrossRef]
- Guangdong Provincial Development and Reform Commission. Implementation Plan for High-Quality Development of Guangzhou Virtual Power Plant (2025); Guangdong Provincial Development and Reform Commission: Guangzhou, China, 2023. [Google Scholar]





| ID | ||||||
|---|---|---|---|---|---|---|
| 1 | 600 | 0.5 | 0.3 | 0.7 | 300 | 300 |
| 2 | 800 | 0.5 | 0.2 | 0.8 | 450 | 450 |
| 3 | 1000 | 0.5 | 0.1 | 0.9 | 500 | 500 |
| Sunny | Cloudy | Rainy | ||||||
|---|---|---|---|---|---|---|---|---|
| Time | AEO | CEO | Time | AEO | CEO | Time | AEO | CEO |
| 1:00–3:00 | 0 | 957.6 | 1:00–3:00 | 0 | 957.6 | 1:00–3:00 | 0 | 649.8 |
| 2:00–4:00 | 0 | 615.6 | 2:00–4:00 | 0 | 615.6 | 2:00–4:00 | 0 | 957.6 |
| 3:00–5:00 | 0 | 285 | 3:00–5:00 | 0 | 285 | 3:00–5:00 | 0 | 653.4 |
| 4:00–6:00 to 17:00–19:00 | 0 | 0 | 4:00–6:00 to 16:00–18:00 | 0 | 0 | 4:00–06:00 | 0 | 334.2 |
| 5:00–7:00 to 14:00–16:00 | 0 | 0 | ||||||
| 15:00–17:00 | 222 | 240 | ||||||
| 16:00–18:00 | 573 | 591 | ||||||
| 17:00–19:00 | 147.6 | 0 | 17:00–19:00 | 573 | 1053.6 | |||
| 18:00–20:00 | 217.8 | 820.8 | 18:00–20:00 | 147.6 | 820.8 | 18:00–20:00 | 1171.8 | 1652.4 |
| 19:00–21:00 | 217.8 | 1607.4 | 19:00–21:00 | 147.6 | 1607.4 | 19:00–21:00 | 1607.4 | 2131.2 |
| 20:00–22:00 | 217.8 | 2041.8 | 20:00–22:00 | 148.2 | 2119.8 | 20:00–22:00 | 2314.2 | 2357.4 |
| 21:00–23:00 | 501.6 | 1722.6 | 21:00–23:00 | 649.8 | 1800.6 | 21:00–23:00 | 1667.6 | 1696.2 |
| 22:00–24:00 | 866.4 | 1300.8 | 22:00–24:00 | 1014.6 | 1378.8 | 22:00–24:00 | 1245.8 | 1259.4 |
| Conditions | Method | SSR | OP | RIP |
|---|---|---|---|---|
| sunny | CEO | 66.7% | 33.3% | - |
| AEO | 91.7% | 8.3% | 75.1% | |
| cloudy | CEO | 66.7% | 33.3% | - |
| AEO | 87.5% | 12.5% | 62.5% | |
| rainy | CEO | 58.4% | 41.6% | - |
| AEO | 66.7% | 33.3% | 24.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Sun, S.; Cheng, Y.; Yu, P.; Xing, J.; Shen, W.; Zhao, J. Maximized Autonomous Economic Operation and Aggregated Equivalence for Microgrids with PVs and ESSs. Energies 2025, 18, 5740. https://doi.org/10.3390/en18215740
Wang Z, Sun S, Cheng Y, Yu P, Xing J, Shen W, Zhao J. Maximized Autonomous Economic Operation and Aggregated Equivalence for Microgrids with PVs and ESSs. Energies. 2025; 18(21):5740. https://doi.org/10.3390/en18215740
Chicago/Turabian StyleWang, Zhiwei, Shumin Sun, Yan Cheng, Peng Yu, Jiawei Xing, Wanting Shen, and Jinquan Zhao. 2025. "Maximized Autonomous Economic Operation and Aggregated Equivalence for Microgrids with PVs and ESSs" Energies 18, no. 21: 5740. https://doi.org/10.3390/en18215740
APA StyleWang, Z., Sun, S., Cheng, Y., Yu, P., Xing, J., Shen, W., & Zhao, J. (2025). Maximized Autonomous Economic Operation and Aggregated Equivalence for Microgrids with PVs and ESSs. Energies, 18(21), 5740. https://doi.org/10.3390/en18215740






