Joint Energy Scheduling for Isolated Islands Considering Low-Density Periods of Renewable Energy Production
Abstract
1. Introduction
- Reflecting the nonlinear characteristics of the diesel generator fuel consumption model;
- Achieving global optimization through mixed-integer linear programming (MILP);
- Quantitatively verifying the economic benefits of scheduling cycle extension based on simulation analysis.
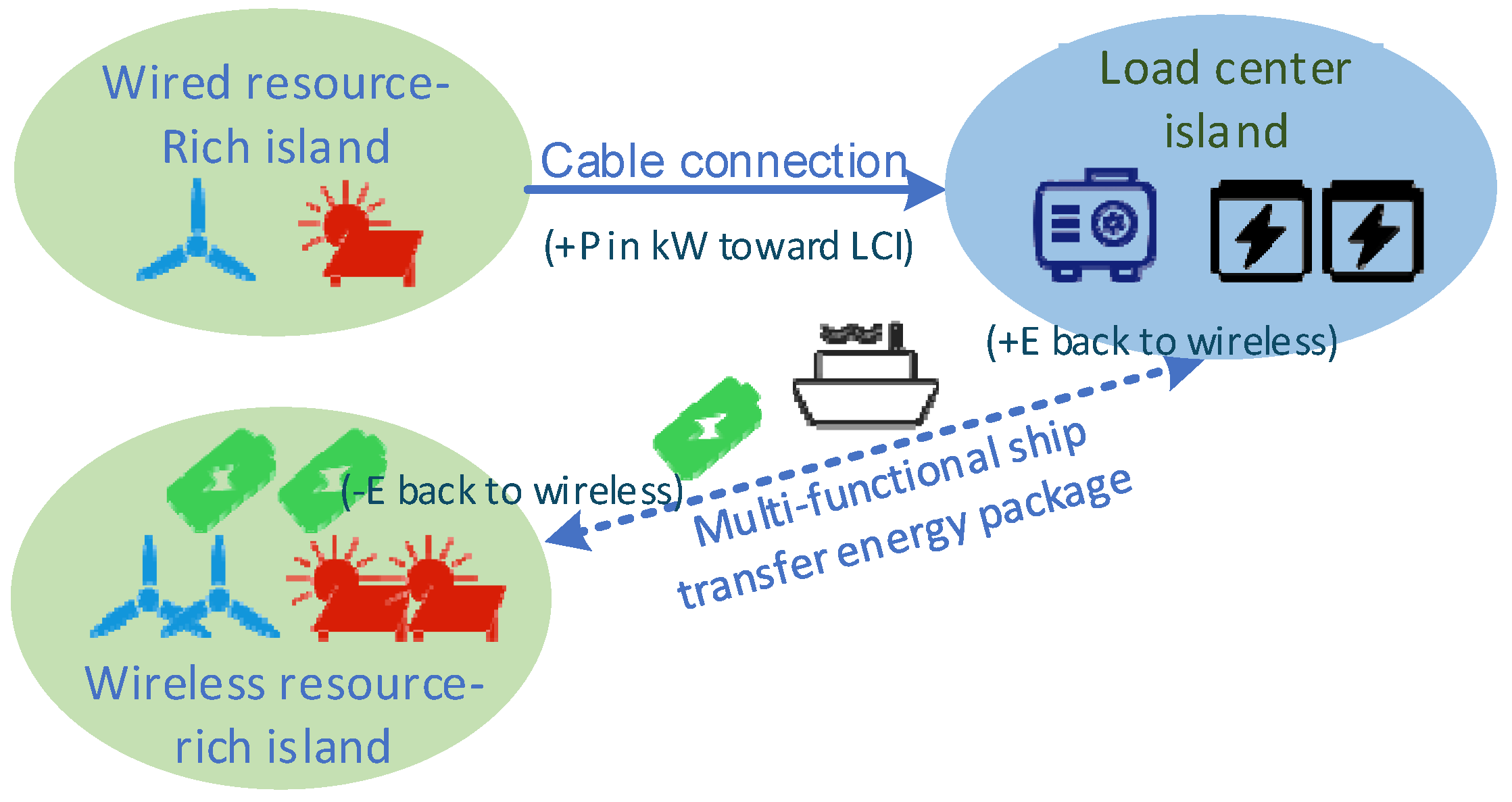
2. Energy Supply System for Isolated Islands
2.1. Refined Modeling of Diesel Generator Set
2.2. Isolated Island Group Multi-Party Cooperative Power Supply Model
3. Optimal Energy Scheduling Model for Isolated Islands
3.1. The Objective Function
3.2. Constraint Conditions
3.3. Linearization of Nonlinear Constraints
4. Analysis of Scheduling Cycle Extension
4.1. Scheduling Cycle
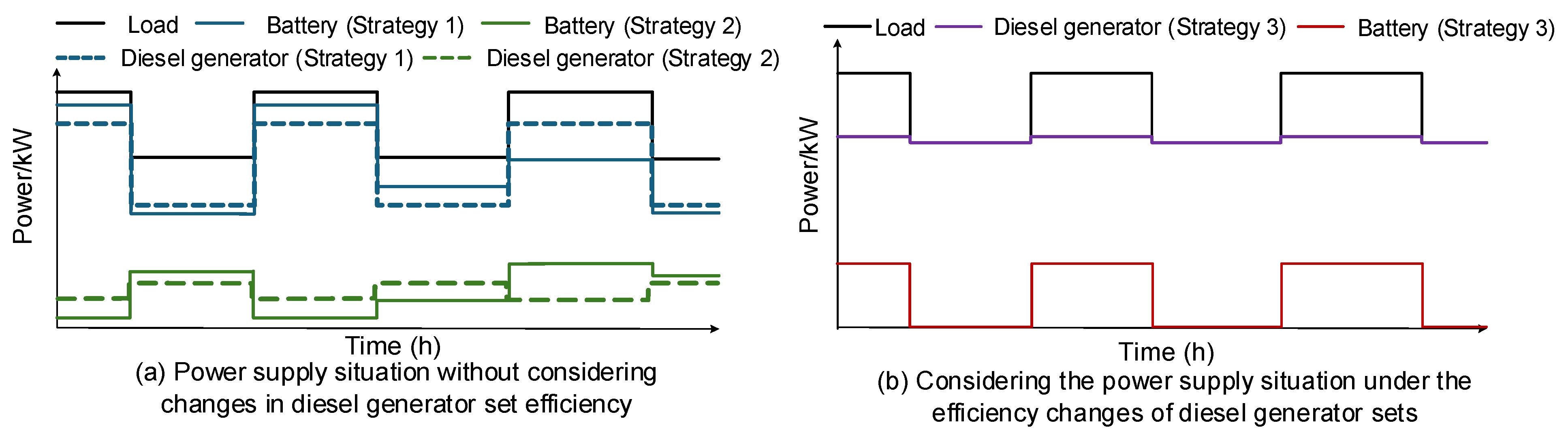
4.2. The Necessity of Improving the Efficiency of Diesel Generators
4.3. The Rationality of Scheduling Cycle Extension
5. Numerical Study
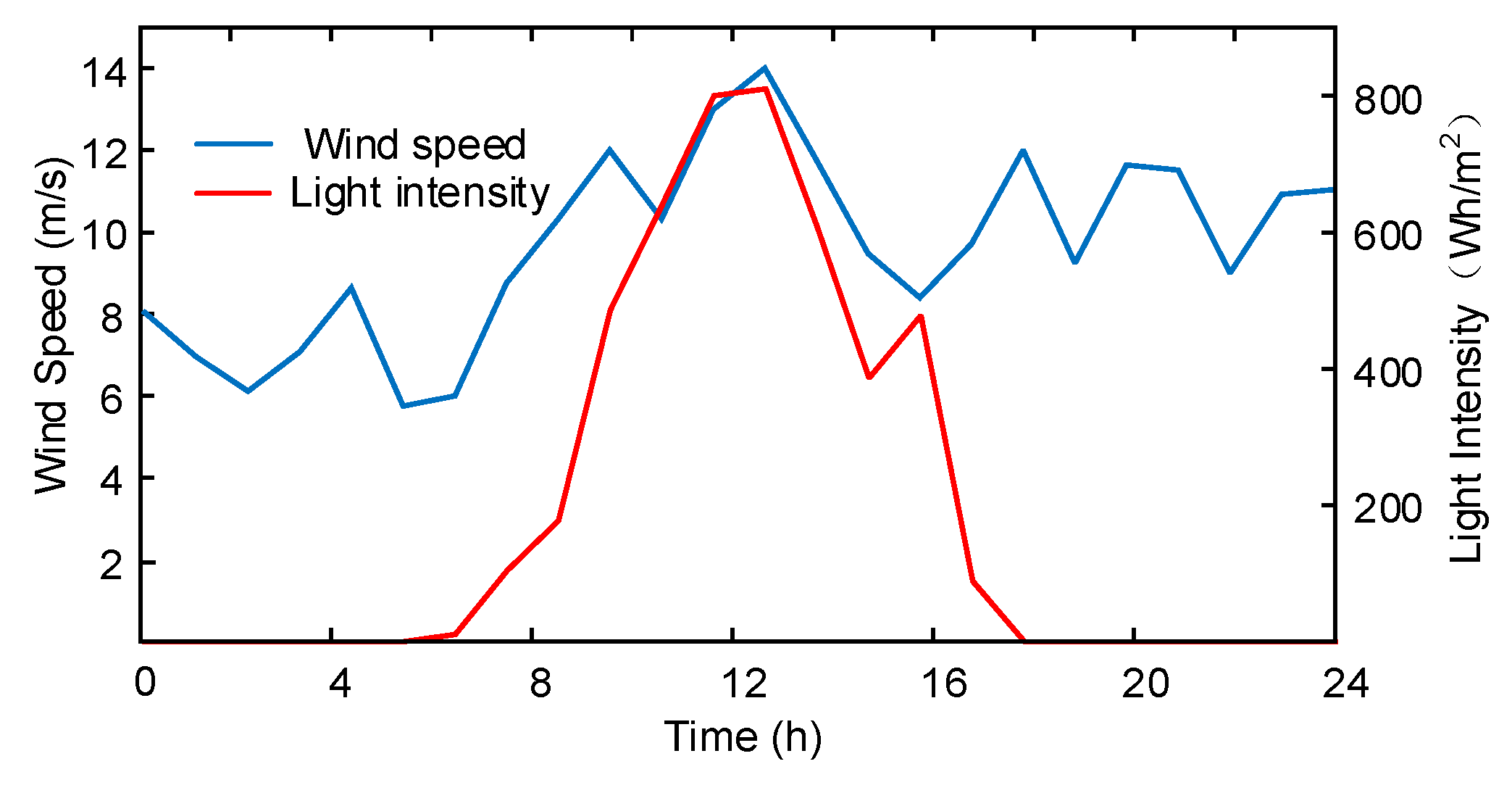
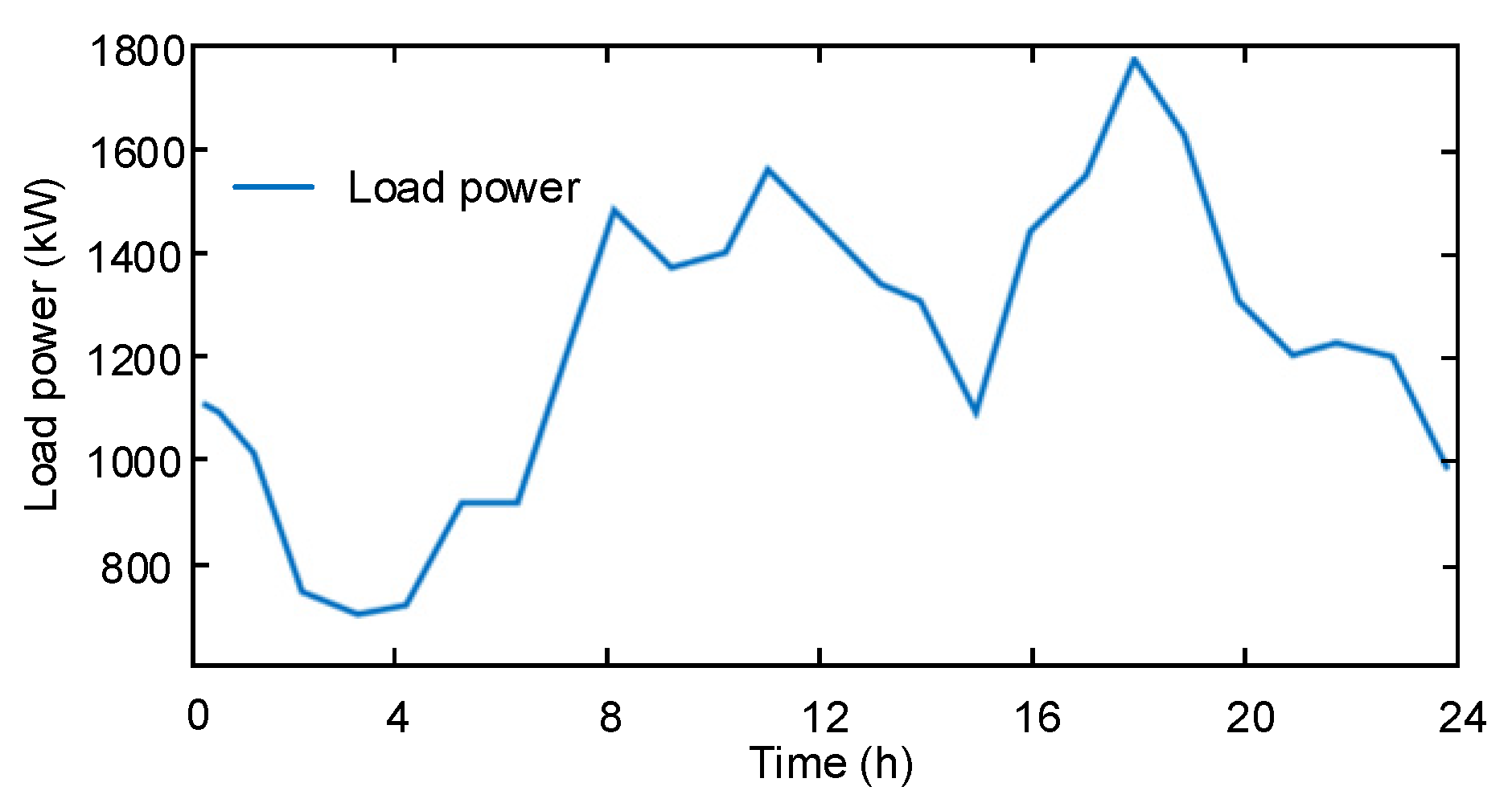
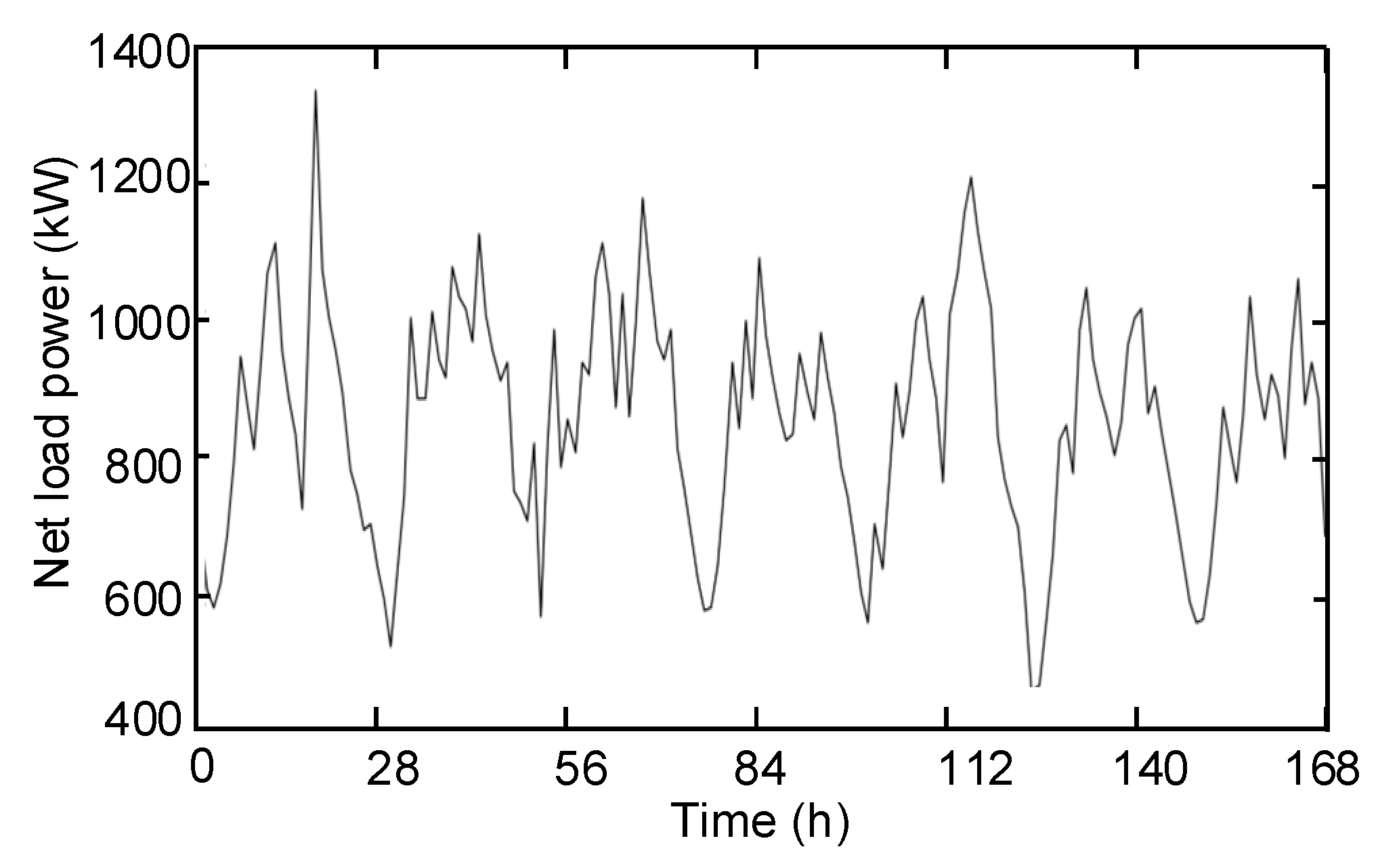
5.1. Simulation Setup
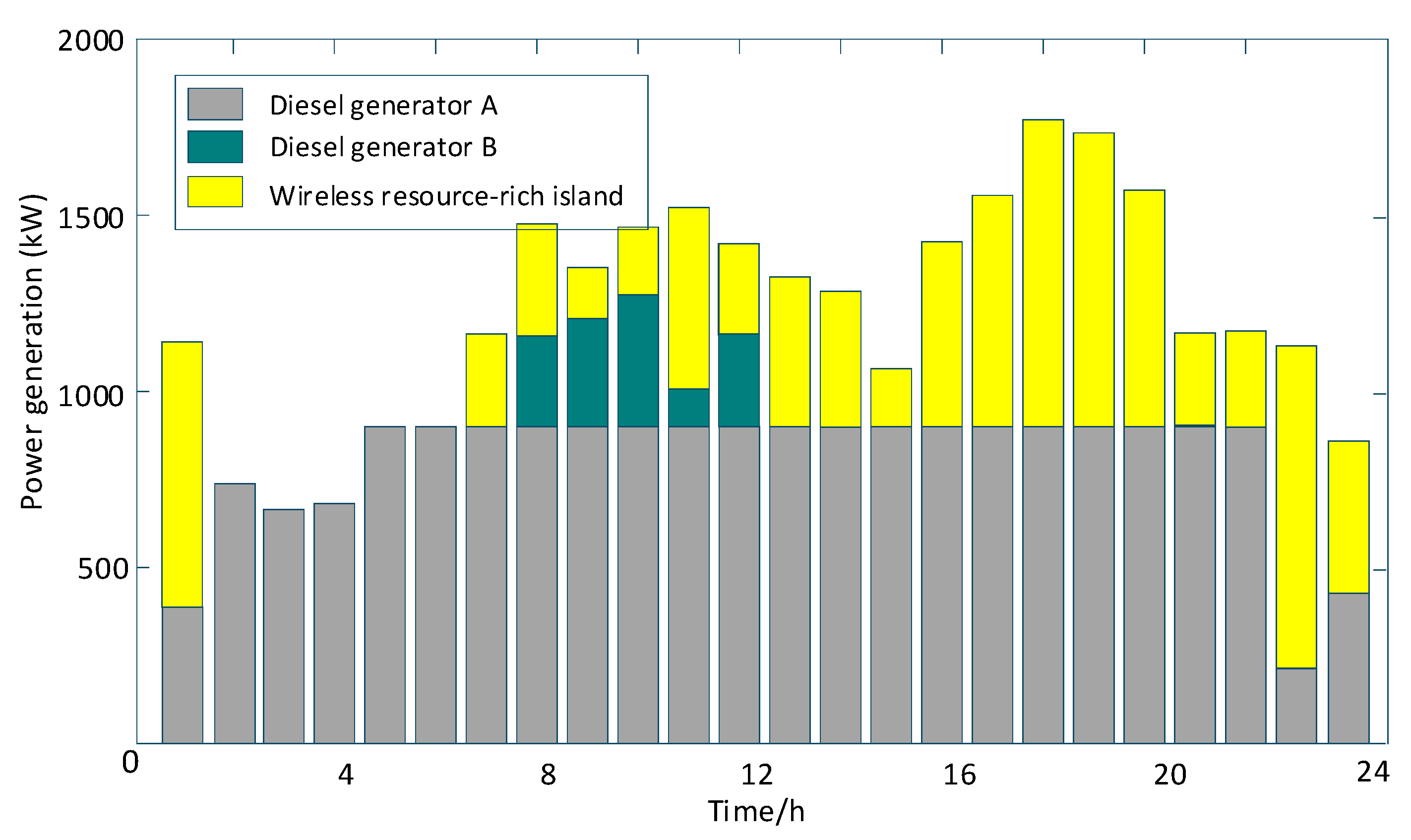
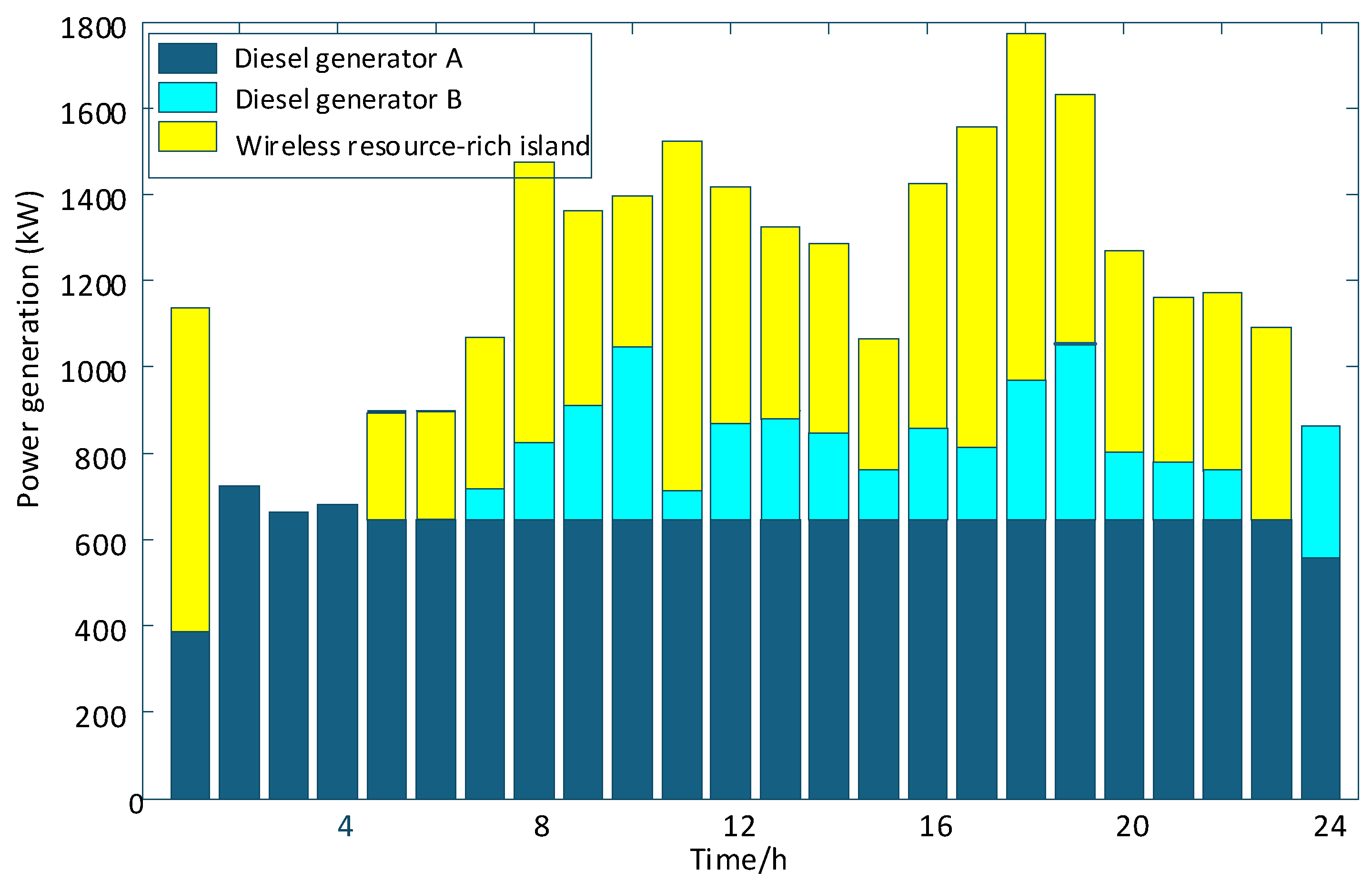
5.2. Necessity Verification of Fine Modeling for Diesel Generators
5.3. Demonstration of Effectiveness of Scheduling Cycle Extension
5.4. Multi-Island Comparative Analysis
5.5. Sensitivity Analysis
6. Conclusions
- Refined efficiency modeling significantly improves the estimation accuracy of diesel generation costs and enhances the coordination between diesel units and energy packages transported from renewable-rich islands. The refined model reduces cost-estimation deviations and improves the stability of optimal dispatch decisions.
- Extending the scheduling cycle from 24 h to 48 h effectively improves long-term operational performance. Comparative simulations show that the proposed approach reduces the total operating cost by approximately 6–9%, increases diesel utilization efficiency by 8–12%, and decreases start–stop events, particularly under low-density renewable output periods.
- The integration of these two improvements—the accurate efficiency model and the extended scheduling horizon—demonstrates clear economic and operational advantages. The former provides a realistic decision foundation, while the latter amplifies its long-term benefits by improving cross-day energy coordination and smoothing diesel generation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Javed, M.S.; Ma, T.; Jurasz, J.; Canales, F.A.; Lin, S.; Ahmed, S.; Zhang, Y. Economic analysis and optimization of a renewable energy based power supply system with different energy storages for a remote island. Renew. Energy 2021, 164, 1376–1394. [Google Scholar] [CrossRef]
- Feio, A.D.; Da Silva, F.C.; Teixeira, M.A.; Lopes Maria, A.C.; Da Silva, G.B.S. Viability of renewable energy integration in isolated systems in Brazil—A case study at Trindade Island (Espírito Santo, Brazil). Renew. Energy 2024, 222, 119805. [Google Scholar] [CrossRef]
- Chen, M.; Song, P.; Chen, G.; Zhang, F.; Qing, X. Multiple criteria analysis for electrifying off-grid island using renewable energy microgrid or submarine cable. Electr. Power Syst. Res. 2023, 224, 109728. [Google Scholar] [CrossRef]
- Jiang, N.; Yang, C.; Xue, H.; Mahseredjian, J. An investigation of electromagnetic transient characteristics on a practical 500 kV submarine cable system. Electr. Power Syst. Res. 2023, 223, 109615. [Google Scholar] [CrossRef]
- Jiang, Z.; Dong, S.; Zhang, Y.; Liu, G.; Dong, T. Corrosion of copper armor caused by induced current in a 500 kV alternating current submarine cable. Electr. Power Syst. Res. 2021, 195, 107144. [Google Scholar] [CrossRef]
- Mustayen, A.G.M.B.; Rasul, M.G.; Wang, X.; Negnevitsky, M.; Hamilton, J.M. Remote areas and islands power generation: A review on diesel engine performance and emission improvement techniques. Energy Convers. Manag. 2022, 260, 115614. [Google Scholar] [CrossRef]
- Zia, M.F.; Nasir, M.; Elbouchikhi, E.; Benbouzid, M.; Vasquez, J.C.; Guerrero, J.M. Energy management system for a hybrid PV-Wind-Tidal-Battery-based islanded DC microgrid: Modeling and experimental validation. Renew. Sustain. Energy Rev. 2022, 159, 112093. [Google Scholar] [CrossRef]
- Jafari, A.; Ganjehlou, H.G.; Khalili, T.; Bidram, A. A fair electricity market strategy for energy management and reliability enhancement of islanded multi-microgrids. Appl. Energy 2020, 270, 115170. [Google Scholar] [CrossRef]
- Sui, Q.; Zhang, R.; Wu, C.; Wei, F.; Lin, X.; Li, Z. Stochastic scheduling of an electric vessel-based energy management system in pelagic clustering islands. Appl. Energy 2020, 259, 114155. [Google Scholar] [CrossRef]
- Wu, C.; Ma, Y.; Chen, C.; Sun, C.; Lin, X.; Wei, F.; Li, Z. Post-Disaster Scheduling Strategy of Island Microgrid with Electric Passenger Ships. In Proceedings of the 2022 4th International Conference on Power and Energy Technology (ICPET), Beijing, China, 28–31 July 2022; pp. 524–529. [Google Scholar] [CrossRef]
- Xia, S.; Tian, Y.; Wang, Z.; Fu, X.; Li, G.; Zhang, F.; Shahidehpour, M. An energy scheduling method for clustering islands with shared power exchanging vessels. Int. J. Electr. Power Energy Syst. 2023, 152, 109200. [Google Scholar] [CrossRef]
- Upadhya, S.; Wagner, M.J. A dispatch optimization model for hybrid renewable and battery systems incorporating a battery degradation model. J. Energy Resour. Technol. 2022, 144, 070907. [Google Scholar] [CrossRef]
- Craparo, E.; Karatas, M.; Singham, D.I. A robust optimization approach to hybrid microgrid operation using ensemble weather forecasts. Appl. Energy 2017, 201, 135–147. [Google Scholar] [CrossRef]
- Hönen, J.; Hurink, J.L.; Zwart, B. Dynamic Rolling Horizon-Based Robust Energy Management for Microgrids Under Uncertainty. arXiv 2023, arXiv:2307.05154. [Google Scholar] [CrossRef]
- Vincent, R.; Houari, A.; Ait-Ahmed, M.; Benkhoris, M.F. Influence of different time horizon-based battery energy management strategies on residential microgrid profitability. J. Energy Storage 2020, 29, 101340. [Google Scholar] [CrossRef]
- Flett, G.; Tuohy, P.; Howarth, G.; Kockar, I. An Optimal Approach to the Pre-Implementation Value Assessment of Smart Energy Systems; a ‘Green’ Hydrogen Case Study. Sustain. Energy Grids Netw. 2025, 44, 101924. [Google Scholar] [CrossRef]
- Boqtob, O.; El Moussaoui, H.; El Markhi, H.; Lamhamdi, T. Energy scheduling of isolated microgrid with battery degradation cost using hybrid particle swarm optimization with sine cosine acceleration coefficients. Int. J. Renew. Energy Res. 2020, 10, 704–715. [Google Scholar] [CrossRef]
- Karatas, M.; Craparo, E.M.; Singham, D.I. Selection of a planning horizon for a hybrid microgrid using simulated wind forecasts. In Proceedings of the Winter Simulation Conference 2014, Savannah, GA, USA, 7–10 December 2014; pp. 1050–1060. [Google Scholar]
- Aaslid, P.; Korpås, M.; Belsnes, M.M.; Fosso, O.B. Stochastic optimization of microgrid operation with renewable generation and energy storages. IEEE Trans. Sustain. Energy 2022, 13, 1481–1491. [Google Scholar] [CrossRef]
- García-Muñoz, F.; Díaz-González, F.; Corchero, C. A Mathematical Model for the Scheduling of Virtual Microgrids Topology into an Active Distribution Network. Appl. Sci. 2020, 10, 7199. [Google Scholar] [CrossRef]
- Sharifpour, M.; Ameli, M.T.; Ameli, H.; Strbac, G. A resilience-oriented approach for microgrid energy management with hydrogen integration during extreme events. Energies 2023, 16, 8099. [Google Scholar] [CrossRef]
- Koholé, Y.W.; Wankouo Ngouleu, C.A.; Fohagui, F.C.V.; Tchuen, G. Optimization of an off-grid hybrid photovoltaic/wind/diesel/fuel cell system for residential applications power generation employing evolutionary algorithms. Renew. Energy 2024, 224, 120131. [Google Scholar] [CrossRef]
- Premadasa, P.N.D.; Silva, C.M.M.R.S.; Chandima, D.P.; Karunadasa, J.P. A multi-objective optimization model for sizing an off-grid hybrid energy microgrid with optimal dispatching of a diesel generator. J. Energy Storage 2023, 68, 107621. [Google Scholar] [CrossRef]
- Iqbal, R.; Liu, Y.; Zeng, Y.; Zhang, Q.; Zeeshan, M. Comparative study based on techno-economics analysis of different shipboard microgrid systems comprising PV/wind/fuel cell/battery/diesel generator with two battery technologies: A step toward green maritime transportation. Renew. Energy 2024, 221, 119670. [Google Scholar] [CrossRef]
- Agga, F.A.; Abbou, S.A.; Houm, Y.E.; Labbadi, M. Short-Term Load Forecasting Based on CNN and LSTM Deep Neural Networks. IFAC-Pap. Online 2022, 55, 777–781. [Google Scholar] [CrossRef]
- Bhuvaneswari, R.; Edrington, C.S.; Cartes, D.A.; Subramanian, S. Online economic environmental optimization of a Microgrid using an Improved Fast Evolutionary programming technique. In Proceedings of the 41st North American Power Symposium, Starkville, MS, USA, 4–6 October 2009; pp. 1–6. [Google Scholar] [CrossRef]
- Mazidi, M.; Zakariazadeh, A.; Jadid, S.; Siano, P. Integrated scheduling of renewable generation and demand response 727 programs in a microgrid. Energy Convers. Manag. 2014, 86, 1118–1127. [Google Scholar] [CrossRef]


| Research Work | Horizon (h) | Alignment | Uncertainty | Finding |
|---|---|---|---|---|
| [12,13,14] | 36 | misaligned | Deterministic (no error) | Higher total cost vs. 48 h |
| [15,16,17] | 48 | aligned | Time-correlated prediction errors | Lowest expected cost |
| [13,18,19] | 60 | misaligned | Deterministic (no error) | Higher total cost vs. 48 h |
| [13,20,21] | 72 | aligned | Time-correlated prediction errors | Higher total cost vs. 48 h |
| This study | 48 | aligned | Time-correlated errors + reserve | Recommended horizon in this study |
| Symbol | Unit | Description |
|---|---|---|
| h | Time step | |
| kW | Power of the i-th diesel generator at hour t | |
| kW | Battery power at hour t | |
| kW | Net load at the load center island at hour t | |
| kW | Minimum/maximum power of the i-th diesel generator at hour t | |
| {0, 1} | battery-swapping selection variable on island k at hour t | |
| kWh | Remaining stored energy on island k at hour t | |
| kWh | Auxiliary variable in linearization | |
| kWh | Hourly energy change on island k | |
| kWh | Lower/upper bounds of stored energy on island k | |
| - | Number of vessels required by wireless island k | |
| kWh | Max energy that one vessel can transport per voyage | |
| h | Travel time of route j | |
| km | Sailing distance of route j | |
| Km/h | Vessel speed | |
| CNY | Start-up/shutdown costs of generator i at hour t | |
| {0, 1} | Start/stop indicators for generator i |
| Operating Parameters | Diesel Generator A | Diesel Generator B |
|---|---|---|
| Rated power (kW) | 900 | 700 |
| a (CNY/kW2·h) | 0.0024 | 0.0029 |
| b (CNY/kW·h) | 0.351 | 0.559 |
| c (CNY/h) | 1.028 | 1.221 |
| Single start-up cost (CNY) | 45 | 35 |
| Single shutdown cost (CNY) | 25 | 22 |
| Scheduling Cycle (h) | Total Cost (CNY) | 95% CI |
|---|---|---|
| 24 | 54,872.60 ± 235.40 | (54,680.20, 55,064.90) |
| 48 | 53,821.50 ± 198.30 | (53,655.40, 53,987.60) |
| 72 | 52,345.80 ± 210.60 | (52,153.10, 52,538.40) |
| Scheduling Cycle (h) | Total Cost (CNY) | 95% CI |
|---|---|---|
| 24 | 55,761.40 ± 262.10 | (55,506.00,56,016.80) |
| 48 | 55,205.30 ± 241.50 | (54,982.20, 55,428.40) |
| 72 | 57,489.60 ± 279.80 | (57,204.30, 57,774.90) |
| 24-h Scheduling Cycle | 48-h Scheduling Cycle | ||
|---|---|---|---|
| Battery Swapping Time | Number of Dispatched Vessels | Battery Swapping Time | Number of Dispatched Vessels |
| 36 h | 1 | 67 h | 1 |
| 84 h | 1 | 160 h | 1 |
| 142 h | 1 | / | / |
| 164 h | 1 | / | / |
| Total Cost (CNY) | |||
| 24-h Scheduling Cycle | 48-h Scheduling Cycle | ||
| 156,780.45 ± 410.72 | 149,950.36 ± 362.84 | ||
| Island | Peak Load | RE Share | Sailing Distance | Battery Packages | Vessel Fee Per Trip |
|---|---|---|---|---|---|
| S | 300 kW | 20% | 30 km | 20 | 700 CNY |
| M | 600 kW | 50% | 60 km | 30 | 900 CNY |
| L | 1000 kW | 80% | 120 km | 50 | 1300 CNY |
| Parameter Change | Δ Total Cost (%) | Change in Diesel Share (%) | Start–Stop Frequency (Times/Day) | Observation |
|---|---|---|---|---|
| a − 20% | −6.1 | +8.1 | increases by 2 | Lower cost, higher load factor |
| a − 10% | −3.0 | +4.0 | increases by 1 | Slight cost reduction |
| a + 10% | +3.1 | −4.2 | decreases by 1 | Slight cost increase; smoother output |
| a + 20% | +6.4 | −8.5 | decreases by 2 | Notable rise; higher storage use |
| b − 20% | −4.1 | +6.0 | virtually zero | Moderate cost decrease |
| b − 10% | −2.0 | +3.0 | virtually zero | Small reduction |
| b + 10% | +2.0 | −2.8 | virtually zero | Linear cost effect |
| b + 20% | +4.5 | −6.1 | virtually zero | Cost increases linearly |
| c − 20% | −1.2 | −2.0 | increases by 3 | Idle loss reduction |
| c − 10% | −0.6 | −1.0 | increases by 1 | Slightly more switching |
| c + 10% | +0.8 | +1.2 | decreases by 1 | Slightly fewer start–stops |
| c + 20% | +1.4 | +2.5 | decreases by 3 | Continuous operation favored |
| Island | Horizon (h) | Total Cost (CNY) | Diesel Share (%) | Start–Stops (Times/Day) | Voyages (Times/Week) | Renewable Utilization (%) |
|---|---|---|---|---|---|---|
| S | 24 | 98,000 | 78 | 9 | 6 | 82 |
| 48 | 95,600 | 74 | 7 | 5 | 85 | |
| 72 | 96,500 | 75 | 8 | 6 | 84 | |
| M | 24 | 152,000 | 56 | 12 | 8 | 88 |
| 48 | 146,700 | 50 | 8 | 6 | 92 | |
| 72 | 149,500 | 53 | 10 | 7 | 90 | |
| L | 24 | 228,000 | 34 | 16 | 12 | 91 |
| 48 | 217,700 | 28 | 10 | 8 | 95 | |
| 72 | 229,100 | 32 | 14 | 11 | 92 |
| Parameter Change | Δ Total Cost (%) | Change in Diesel Share (%) | Observation |
|---|---|---|---|
| Diesel cost −20% | −7.2 | +6.4 | Lower fuel cost; more diesel generation |
| Diesel cost −10% | −3.5 | +3.1 | Moderate cost reduction; reduced storage use |
| Diesel cost +10% | +3.7 | −3.6 | Higher cost; increased renewable dispatch |
| Diesel cost +20% | +7.4 | −7.8 | Strong cost rise; diesel share drops sharply |
| Battery capacity −20% | +3.2 | +4.5 | Insufficient storage; higher diesel cycling |
| Battery capacity −10% | +1.5 | +2.2 | Slight cost increase; limited flexibility |
| Battery capacity +10% | −2.1 | −3.4 | Lower cost; smoother diesel output |
| Battery capacity +20% | −3.9 | −6.1 | Improved renewable utilization; reduced starts |
| Vessel cost −20% | −1.1 | −1.5 | Cheaper logistics; more voyages and renewables |
| Vessel cost −10% | −0.5 | −0.7 | Minor benefit; slightly higher renewable share |
| Vessel cost +10% | +0.8 | +1.1 | Logistics cost dominates; fewer voyages |
| Vessel cost +20% | +1.9 | +2.3 | Reduced voyage frequency; cost rises slightly |
| Forecast error −20% | −1.8 | −2.4 | Improved accuracy; smoother scheduling |
| Forecast error −10% | −0.9 | −1.1 | Slightly lower cost; fewer mismatches |
| Forecast error +10% | +3.6 | +3.9 | Misaligned dispatch; reduced efficiency |
| Forecast error +20% | +6.2 | +7.1 | Cost surge; frequent rescheduling events |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, F.; Weng, H.; Lin, X.; Mansour, D.-E.A. Joint Energy Scheduling for Isolated Islands Considering Low-Density Periods of Renewable Energy Production. Energies 2025, 18, 5702. https://doi.org/10.3390/en18215702
Gao F, Weng H, Lin X, Mansour D-EA. Joint Energy Scheduling for Isolated Islands Considering Low-Density Periods of Renewable Energy Production. Energies. 2025; 18(21):5702. https://doi.org/10.3390/en18215702
Chicago/Turabian StyleGao, Feng, Hanli Weng, Xiangning Lin, and Diaa-Eldin A. Mansour. 2025. "Joint Energy Scheduling for Isolated Islands Considering Low-Density Periods of Renewable Energy Production" Energies 18, no. 21: 5702. https://doi.org/10.3390/en18215702
APA StyleGao, F., Weng, H., Lin, X., & Mansour, D.-E. A. (2025). Joint Energy Scheduling for Isolated Islands Considering Low-Density Periods of Renewable Energy Production. Energies, 18(21), 5702. https://doi.org/10.3390/en18215702







