A Review of the Recent Advances in CH4 Recovery from CH4 Hydrate in Porous Media by CO2 Replacement
Abstract
1. Introduction
2. NGHs and Extraction Methods
2.1. Essential Properties of NGHs
2.2. Formation and Distribution of NGHs
2.3. CH4 Hydrate Extraction Methods
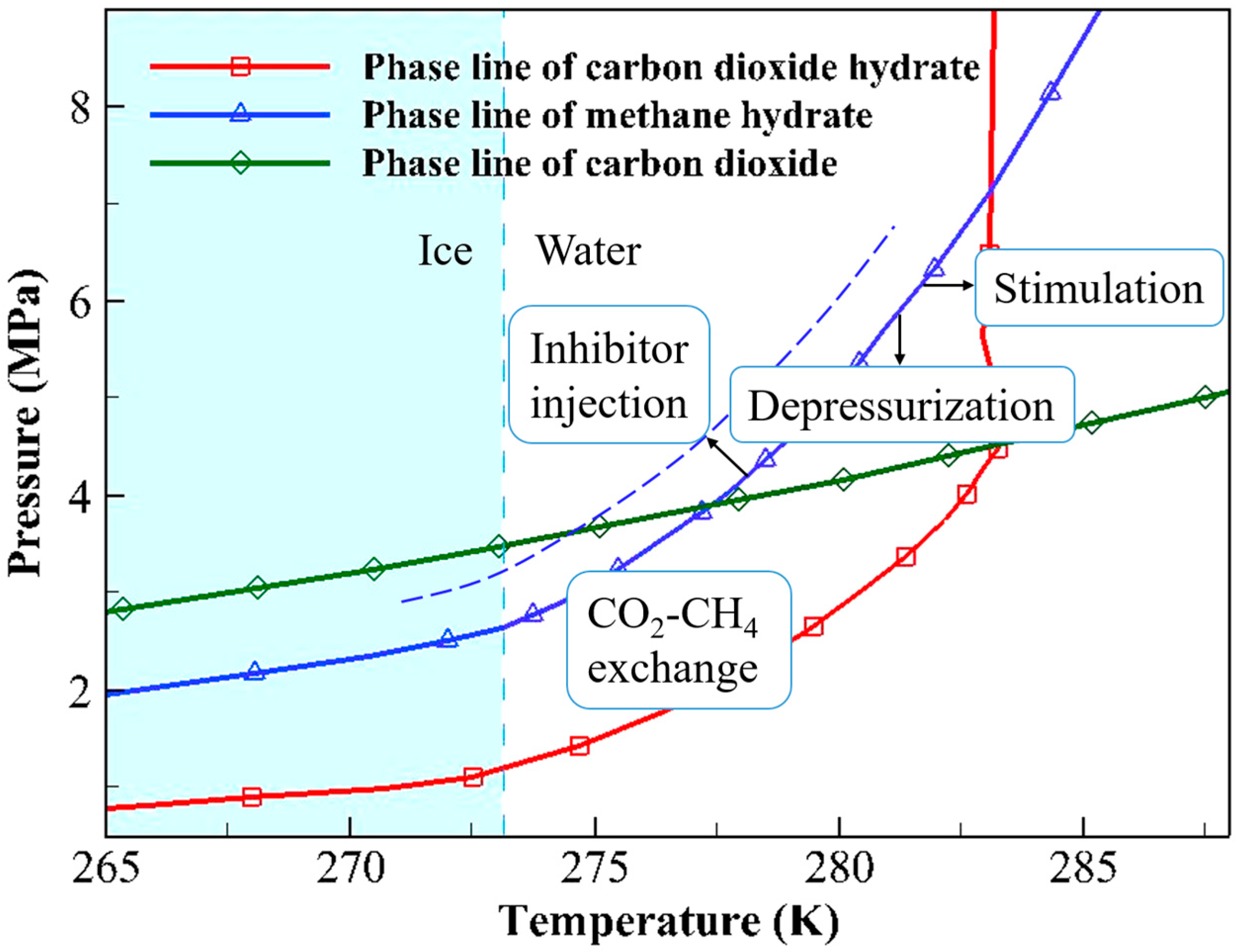
3. Fundamental Theories of CO2-CH4 Hydrate Replacement Extraction
3.1. Current Research on CO2-CH4 Hydrate Replacement Mechanism
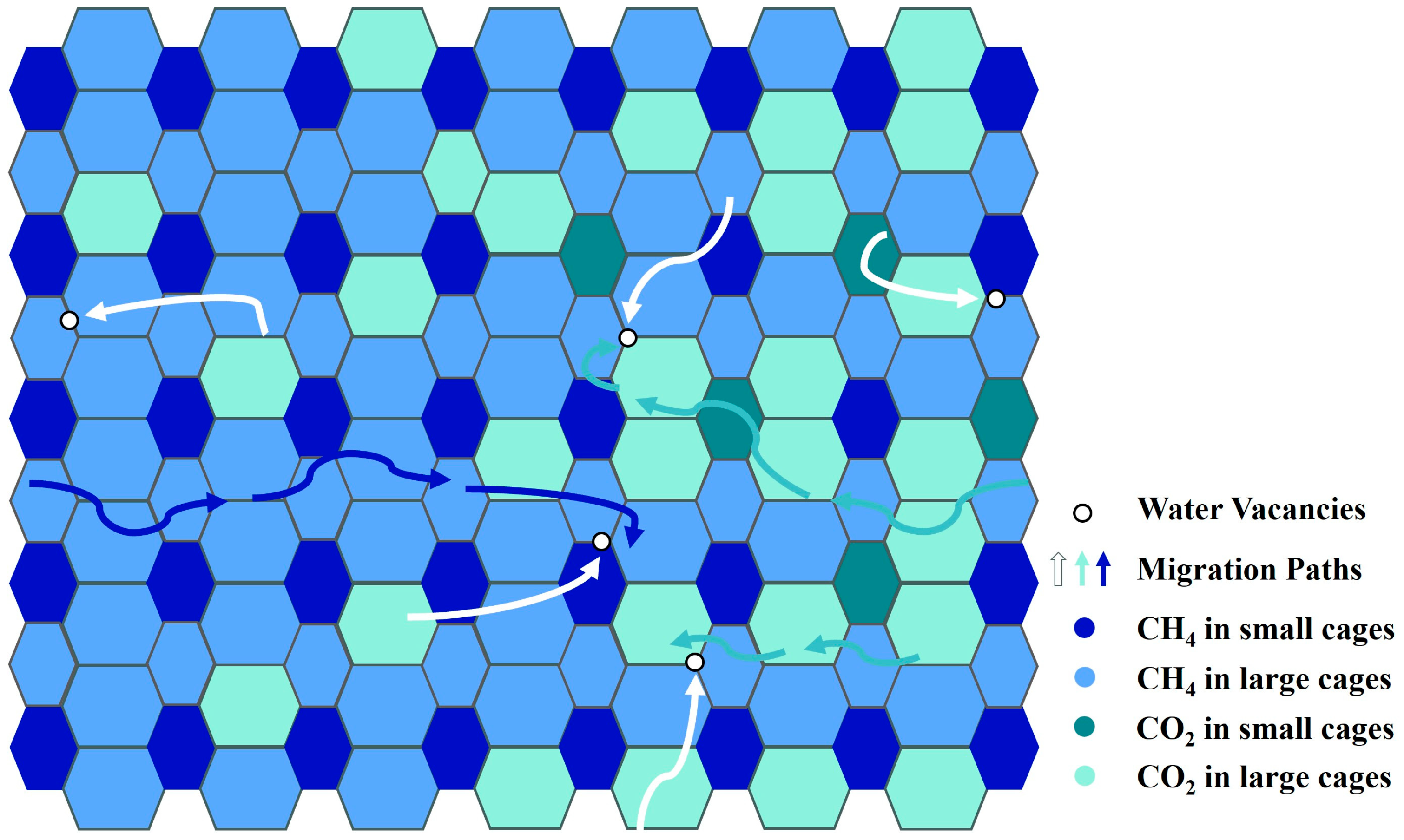
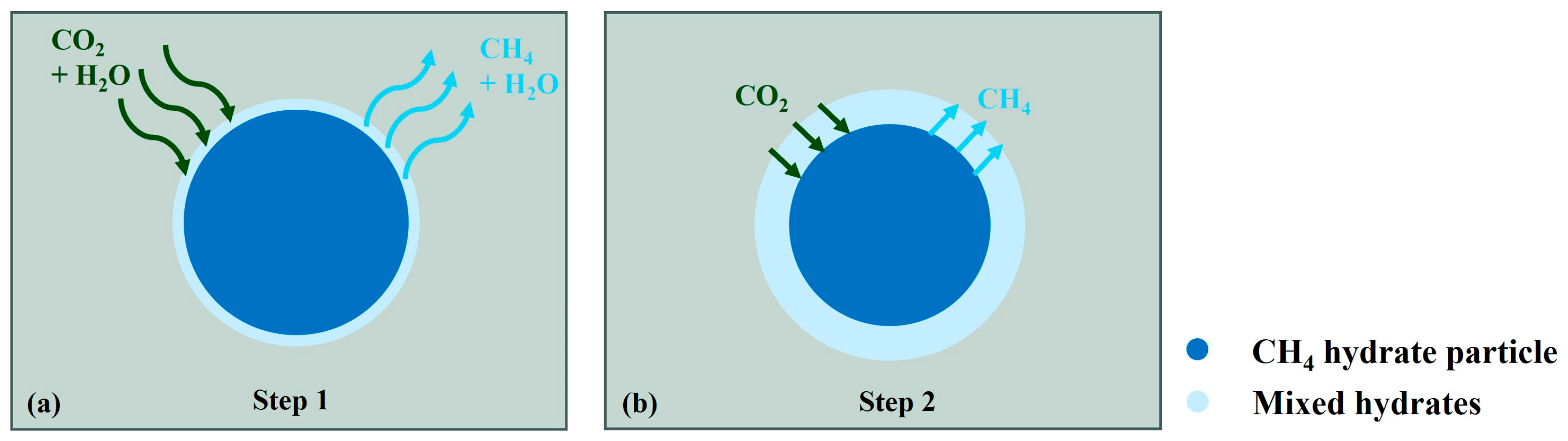
3.1.1. CO2 Replacement with CH4 Hydrate Dissociation
3.1.2. CO2 Replacement Without CH4 Hydrate Dissociation
3.1.3. CH4 Hydrate Dissociation Determined by the CO2-CH4 Hydrate Replacement Environment
3.2. Numerical Models
3.2.1. Kinetic Models
3.2.2. Thermodynamic Models
4. Factors Affecting CO2-CH4 Hydrate Replacement
4.1. Impact of Replacement Methods
4.1.1. Soaking Replacement
4.1.2. Dynamic Replacement
4.2. Effect of Initial Water
4.3. Effect of Other Factors
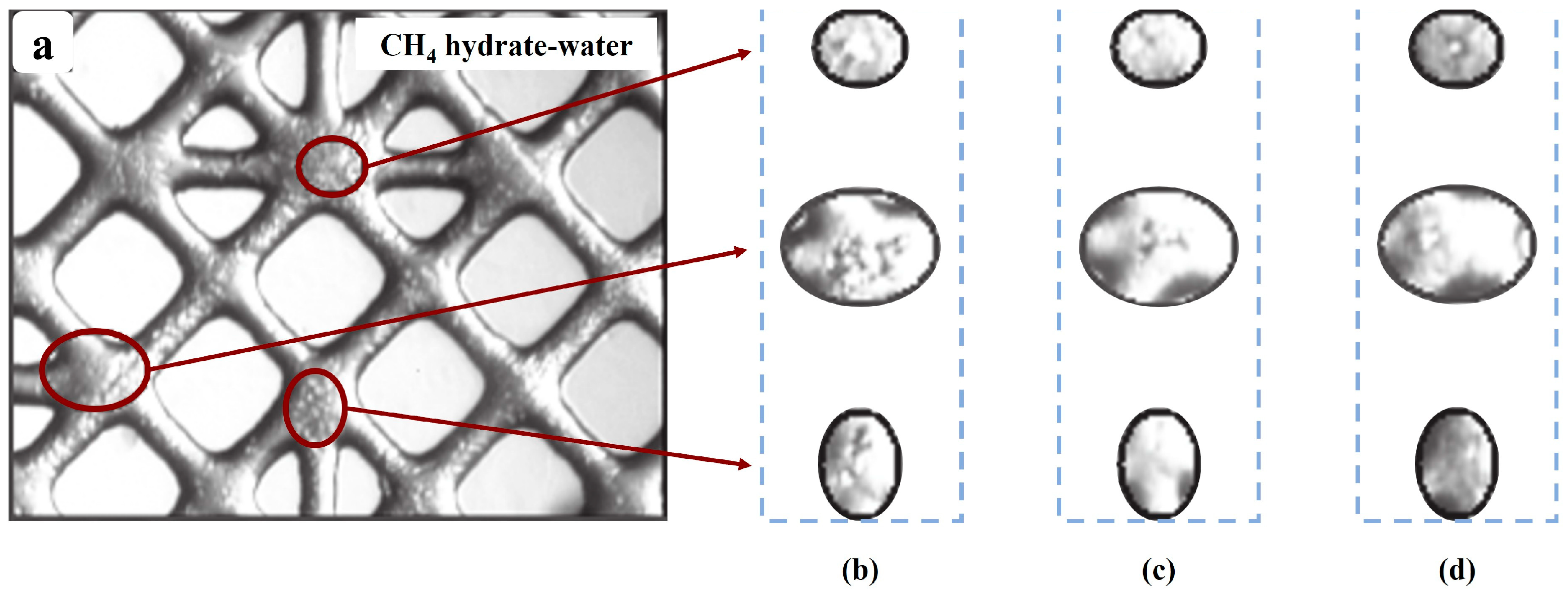
5. Study on Pore-Scale CO2-CH4 Hydrate Replacement
5.1. Pore-Scale Replacement Studies
5.2. Pore-Scale Hydrate Dissociation/Formation Studies
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, J.; Chong, Z.R.; Qureshi, M.F.; Linga, P. Carbon dioxide sequestration via gas hydrates: A potential pathway toward decarbonization. Energy Fuels 2020, 34, 10529–10546. [Google Scholar] [CrossRef]
- Almenningen, S.; Graue, A.; Ersland, G. Experimental investigation of critical parameters controlling CH4-CO2 exchange in sedimentary CH4 hydrates. Energy Fuels 2021, 35, 2468–2477. [Google Scholar] [CrossRef]
- Ryou, J.E.; Al-Raoush, R.I.; Alshibli, K.; Lee, J.Y.; Jung, J. Effects of soaking process on CH4-CO2 replacement efficiency for hydrate-bearing sediments. J. Pet. Sci. Eng. 2021, 196, 107772. [Google Scholar] [CrossRef]
- Lee, H.; Seo, Y.; Seo, Y.T.; Moudrakovski, I.L.; Ripmeester, J.A. Recovering methane from solid methane hydrate with carbon dioxide. Angew. Chem.-Int. Ed. 2003, 42, 5048–5051. [Google Scholar] [CrossRef] [PubMed]
- Salamatin, A.N.; Falenty, A.; Kuhs, W.F. Diffusion model for gas replacement in an isostructural CH4-CO2 hydrate system. J. Phys. Chem. C 2017, 121, 17603–17616. [Google Scholar] [CrossRef]
- Wei, W.N.; Li, B.; Gan, Q.; Li, Y. Le Research progress of natural gas hydrate exploitation with CO2 replacement: A eview. Fuel 2022, 312, 122873. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, L.; Wang, J.; Zhao, J.; Dong, H.; Yang, M.; Liu, Y.; Song, Y. Enhanced CH4 recovery and CO2 storage via thermal stimulation in the CH4/CO2 replacement of methane hydrate. Chem. Eng. J. 2017, 308, 40–49. [Google Scholar] [CrossRef]
- Hirohama, S.; Shimoyama, Y.; Wakabayashi, A.; Tatsuta, S.; Nishida, N. Conversion of CH4 hydrate to CO2 hydrate in liquid CO2. J. Chem. Eng. Jpn. 1996, 26, 1014–1020. [Google Scholar] [CrossRef]
- Song, Y.; Wang, S.; Jiang, L.; Zhang, Y.; Yang, M. Hydrate phase equilibrium for CH4-CO2-H2O system in porous media. Can. J. Chem. Eng. 2016, 94, 1592–1598. [Google Scholar] [CrossRef]
- Ding, Y.L.; Wang, H.Q.; Xu, C.G.; Li, X.S. The effect of CO2 partial pressure on CH4 recovery in CH4-CO2 swap with simulated IGCC syngas. Energies 2020, 13, 1017. [Google Scholar] [CrossRef]
- Kossel, E.; Bigalke, N.K.; Deusner, C.; Haeckel, M. Microscale processes and dynamics during CH4-CO2 guest-molecule exchange in gas hydrates. Energies 2021, 14, 1763. [Google Scholar] [CrossRef]
- Liu, W.; Luo, T.; Li, Y.; Song, Y.; Zhu, Y.; Liu, Y.; Zhao, J.; Wu, Z.; Xu, X. Experimental study on the mechanical properties of sediments containing CH4 and CO2 hydrate mixtures. J. Nat. Gas. Sci. Eng. 2016, 32, 20–27. [Google Scholar] [CrossRef]
- Adisasmito, S.; Frank, R.J.; Sloan, E.D. Hydrates of carbon dioxide and methane mixtures. J. Chem. Eng. Data 1991, 36, 68–71. [Google Scholar] [CrossRef]
- Anderson, G.K. Enthalpy of dissociation and hydration number of methane hydrate from the Clapeyron equation. J. Chem. Thermodyn. 2004, 36, 1119–1127. [Google Scholar] [CrossRef]
- Xu, C.G.; Yan, R.; Fu, J.; Zhang, S.H.; Yan, K.F.; Chen, Z.Y.; Xia, Z.M.; Li, X. Sen Insight into micro-mechanism of hydrate-based methane recovery and carbon dioxide capture from methane-carbon dioxide gas mixtures with thermal characterization. Appl. Energy 2019, 239, 57–69. [Google Scholar] [CrossRef]
- Gray, N.D.; Sherry, A.; Larter, S.R.; Erdmann, M.; Leyris, J.; Liengen, T.; Beeder, J.; Head, I.M. Biogenic methane production in formation waters from a large gas field in the North Sea. Extremophiles 2009, 13, 511–519. [Google Scholar] [CrossRef]
- Davies, S.R.; Boxall, J.A.; Dieker, L.E.; Sum, A.K.; Koh, C.A.; Sloan, E.D.; Creek, J.L.; Xu, Z.G. Predicting hydrate plug formation in oil-dominated flowlines. J. Pet. Sci. Eng. 2010, 72, 302–309. [Google Scholar] [CrossRef]
- Fukumoto, A.; Kamada, K.; Sato, T.; Oyama, H.; Torii, H.; Kiyono, F.; Nagao, J.; Temma, N.; Narita, H. Numerical simulation of pore-scale formation of methane hydrate in the sand sediment using the phase-field model. J. Nat. Gas. Sci. Eng. 2018, 50, 269–281. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, S.; Zhao, J.; Song, Y.; Zhu, J. Research status and prospects of natural gas hydrate exploitation technology. Chin. J. Eng. Sci. 2022, 24, 214. [Google Scholar] [CrossRef]
- Chen, Y.; Gao, Y.; Chen, L.; Wang, X.; Liu, K.; Sun, B. Experimental investigation of the behavior of methane gas hydrates during depressurization-assisted CO2 replacement. J. Nat. Gas. Sci. Eng. 2019, 61, 284–292. [Google Scholar] [CrossRef]
- Yin, Z.; Linga, P. Methane hydrates: A future clean energy resource. Chin. J. Chem. Eng. 2019, 27, 2026–2036. [Google Scholar] [CrossRef]
- Yuan, Q.; Sun, C.Y.; Yang, X.; Ma, P.C.; Ma, Z.W.; Li, Q.P.; Chen, G.J. Gas production from methane-hydrate-bearing sands by ethylene glycol injection using a three-dimensional reactor. Energy Fuels 2011, 25, 3108–3115. [Google Scholar] [CrossRef]
- Goel, N. In situ methane hydrate dissociation with carbon dioxide sequestration: Current knowledge and issues. J. Pet. Sci. Eng. 2006, 51, 169–184. [Google Scholar] [CrossRef]
- Ersland, G.; Husebø, J.; Graue, A.; Kvamme, B. Transport and storage of CO2 in natural gas hydrate reservoirs. Energy Procedia 2009, 1, 3477–3484. [Google Scholar] [CrossRef]
- Tupsakhare, S.S.; Castaldi, M.J. Efficiency enhancements in methane recovery from natural gas hydrates using injection of CO2/N2 gas mixture simulating in-situ combustion. Appl. Energy 2019, 236, 825–836. [Google Scholar] [CrossRef]
- Boswell, R.; Schoderbek, D.; Collett, T.S.; Ohtsuki, S.; White, M.; Anderson, B.J. The Iġnik Sikumi field experiment, Alaska North Slope: Design, operations, and implications for CO2-CH4 exchange in gas hydrate reservoirs. Energy Fuels 2017, 31, 140–153. [Google Scholar] [CrossRef]
- Ebinuma, T. Method for Dumping and Disposing of Carbon Dioxide Gas and Apparatus Therefore. U.S. Patent 5261490A, 16 November 1993. [Google Scholar]
- Deusner, C.; Bigalke, N.; Kossel, E.; Haeckel, M. Methane production from gas hydrate deposits through injection of supercritical CO2. Energies 2012, 5, 2112–2140. [Google Scholar] [CrossRef]
- Yoon, J.H.; Kawamura, T.; Yamamoto, Y.; Komai, T. Transformation of methane hydrate to carbon dioxide hydrate: In situ Raman spectroscopic observations. J. Phys. Chem. A 2004, 108, 5057–5059. [Google Scholar] [CrossRef]
- Ota, M.; Abe, Y.; Watanabe, M.; Smith, R.L.; Inomata, H. Methane recovery from methane hydrate using pressurized CO2. Fluid. Phase Equilibria 2005, 228–229, 553–559. [Google Scholar] [CrossRef]
- Xu, C.G.; Cai, J.; Yu, Y.S.; Yan, K.F.; Li, X. Sen Effect of pressure on methane recovery from natural gas hydrates by methane-carbon dioxide replacement. Appl. Energy 2018, 217, 527–536. [Google Scholar] [CrossRef]
- Salamatin, A.N.; Falenty, A.; Hansen, T.C.; Kuhs, W.F. Guest migration revealed in CO2 clathrate hydrates. Energy Fuels 2015, 29, 5681–5691. [Google Scholar] [CrossRef]
- Iwai, Y.; Nakamura, H.; Hirata, M. Molecular dynamics simulation of replacement of methane hydrate with carbon dioxide. Mol. Simul. 2012, 38, 481–490. [Google Scholar] [CrossRef]
- Liu, B.; Pan, H.; Wang, X.; Li, F.; Sun, C.; Chen, G. Evaluation of different CH4-CO2 replacement processes in hydrate-bearing sediments by measuring P-wave velocity. Energies 2013, 6, 6242–6254. [Google Scholar] [CrossRef]
- Dec, S.F. Surface transformation of methane-ethane sI and sII clathrate hydrates. J. Phys. Chem. C 2012, 116, 9660–9665. [Google Scholar] [CrossRef]
- Kvamme, B.; Qasim, M.; Baig, K.; Kivelä, P.H.; Bauman, J. Hydrate phase transition kinetics from Phase Field Theory with implicit hydrodynamics and heat transport. Int. J. Greenh. Gas. Control 2014, 29, 263–278. [Google Scholar] [CrossRef]
- Ota, M.; Morohashi, K.; Abe, Y.; Watanabe, M.; Lee Smith, R.; Inomata, H. Replacement of CH4 in the hydrate by use of liquid CO2. Energy Convers. Manag. 2005, 46, 1680–1691. [Google Scholar] [CrossRef]
- Yuan, Q.; Sun, C.Y.; Yang, X.; Ma, P.C.; Ma, Z.W.; Liu, B.; Ma, Q.L.; Yang, L.Y.; Chen, G.J. Recovery of methane from hydrate reservoir with gaseous carbon dioxide using a three-dimensional middle-size reactor. Energy 2012, 40, 47–58. [Google Scholar] [CrossRef]
- Xu, C.G.; Cai, J.; Yu, Y.S.; Chen, Z.Y.; Li, X. Sen Research on micro-mechanism and efficiency of CH4 exploitation via CH4-CO2 replacement from natural gas hydrates. Fuel 2018, 216, 255–265. [Google Scholar] [CrossRef]
- Baldwin, B.A.; Stevens, J.; Howard, J.J.; Graue, A.; Kvamme, B.; Aspenes, E.; Ersland, G.; Husebø, J.; Zornes, D.R. Using magnetic resonance imaging to monitor CH4 hydrate formation and spontaneous conversion of CH4 hydrate to CO2 hydrate in porous media. Magn. Reson. Imaging 2009, 27, 720–726. [Google Scholar] [CrossRef]
- Lee, S.; Lee, Y.; Lee, J.; Lee, H.; Seo, Y. Experimental verification of methane-carbon dioxide replacement in natural gas hydrates using a differential scanning calorimeter. Environ. Sci. Technol. 2013, 47, 13184–13190. [Google Scholar] [CrossRef] [PubMed]
- Tung, Y.T.; Chen, L.J.; Chen, Y.P.; Lin, S.T. In situ methane recovery and carbon dioxide sequestration in methane hydrates: A molecular dynamics simulation study. J. Phys. Chem. B 2011, 115, 15295–15302. [Google Scholar] [CrossRef]
- Qi, Y.; Ota, M.; Zhang, H. Molecular dynamics simulation of replacement of CH4 in hydrate with CO2. Energy Convers. Manag. 2011, 52, 2682–2687. [Google Scholar] [CrossRef]
- Liang, S.; Liang, D.; Wu, N.; Yi, L.; Hu, G. Molecular mechanisms of gas diffusion in CO2 hydrates. J. Phys. Chem. C 2016, 120, 16298–16304. [Google Scholar] [CrossRef]
- Peters, B.; Zimmermann, N.E.R.; Beckham, G.T.; Tester, J.W.; Trout, B.L. Path sampling calculation of methane diffusivity in natural gas hydrates from a water-vacancy assisted mechanism. J. Am. Chem. Soc. 2008, 130, 17342–17350. [Google Scholar] [CrossRef] [PubMed]
- Buch, V.; Devlin, J.P.; Monreal, I.A.; Jagoda-Cwiklik, B.; Uras-Aytemiz, N.; Cwiklik, L. Clathrate hydrates with hydrogen-bonding guests. Phys. Chem. Chem. Phys. 2009, 11, 10245–10265. [Google Scholar] [CrossRef]
- Wu, G.; Tian, L.; Chen, D.; Niu, M.; Ji, H. CO2 and CH4 hydrates: Replacement or cogrowth? J. Phys. Chem. C 2019, 123, 13401–13409. [Google Scholar] [CrossRef]
- Shagapov, V.S.; Khasanov, M.K.; Musakaev, N.G.; Duong, N.H. Theoretical research of the gas hydrate deposits development using the injection of carbon dioxide. Int. J. Heat. Mass. Transf. 2017, 107, 347–357. [Google Scholar] [CrossRef]
- Kim, H.C.; Bishnoi, P.R.; Heidemann, R.A.; Rizvi, S.S.H. Kinetics of methane hydrate decomposition. Chem. Eng. Sci. 1987, 42, 1645–1653. [Google Scholar] [CrossRef]
- Englezos, P.; Kalogerakis, N.; Dholabhai, P.D.; Bishnoi, P.R. Kinetics of formation of methane hydrates and gas. Chem. Eng. Sci. 1987, 42, 2647–2658. [Google Scholar] [CrossRef]
- Masuda, Y.; Kurihara, M.; Ochuchi, H.; Sato, T. A field-scale simulation study on gas productivity of formations containing gas hydrates. In Proceedings of the 4th International Conference on Gas Hydrates, Yokohama, Japan, 19–23 May 2002; pp. 40–46. [Google Scholar]
- Zhao, J.F.; Ye, C.C.; Song, Y.C.; Liu, W.G.; Cheng, C.X.; Liu, Y.; Zhang, Y.; Wang, D.Y.; Ruan, X.K. Numerical simulation and analysis of water phase effect on methane hydrate dissociation by depressurization. Ind. Eng. Chem. Res. 2012, 51, 3108–3118. [Google Scholar] [CrossRef]
- Clarke, M.; Bishnoi, P.R. Determination of the activation energy and intrinsic rate constant of methane gas hydrate decomposition. Can. J. Chem. Eng. 2001, 79, 143–147. [Google Scholar] [CrossRef]
- Chun, M.K.; Lee, H. Kinetics of formation of carbon dioxide clathrate hydrates. Korean J. Chem. Eng. 1996, 13, 620–626. [Google Scholar] [CrossRef]
- Clarke, M.A.; Bishnoi, P.R. Determination of the intrinsic kinetics of CO2 gas hydrate formation using in situ particle size analysis. Chem. Eng. Sci. 2005, 60, 695–709. [Google Scholar]
- Yousif, M.H.; Sloan, E.D. Experimental investigation of hydrate formation and dissociation in consolidated porous media. SPE Reserv. Eng. 1991, 6, 69–76. [Google Scholar] [CrossRef]
- Phirani, J.; Mohanty, K.K. Kinetic simulation of CO2 flooding of methane hydrates. Proc.-SPE Annu. Tech. Conf. Exhib. 2010, 3, 1781–1797. [Google Scholar]
- Janicki, G.; Schlüter, S.; Hennig, T.; Lyko, H.; Deerberg, G. Simulation of methane recovery from gas hydrates combined with storing carbon dioxide as hydrates. J. Geol. Res. 2011, 2011, 1–15. [Google Scholar] [CrossRef]
- Gharasoo, M.; Babaei, M.; Haeckel, M. Simulating the chemical kinetics of CO2-methane exchange in hydrate. J. Nat. Gas. Sci. Eng. 2019, 62, 330–339. [Google Scholar] [CrossRef]
- White, M.D.; McGrail, B.P. Numerical simulation of methane hydrate production from geologic formations via carbon dioxide injection. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2008. [Google Scholar]
- Yonkofski, C.M.R.; Horner, J.A.; White, M.D. Experimental and numerical investigation of hydrate-guest molecule exchange kinetics. J. Nat. Gas Sci. Eng. 2016, 35, 1480–1489. [Google Scholar] [CrossRef]
- Liu, Y.; Hou, J.; Zhao, H.; Liu, X.; Xia, Z. A method to recover natural gas hydrates with geothermal energy conveyed by CO2. Energy 2018, 144, 265–278. [Google Scholar] [CrossRef]
- Sridhara, P.; Anderson, B.J.; Garapati, N.; Seol, Y.; Myshakin, E.M. Novel technological approach to enhance methane recovery from Class 2 hydrate deposits by employing CO2 injection. Energy Fuels 2018, 32, 2949–2961. [Google Scholar] [CrossRef]
- Ohgaki, K.; Takano, K.; Sangawa, H.; Matsubara, T.; Nakano, S. Methane exploitation by carbon dioxide from gas hydrates phase equilibria for CO2-CH4 mixed hydrate system. J. Chem. Eng. Jpn. 1996, 29, 478–483. [Google Scholar] [CrossRef]
- Zhu, T.; McGrail, B.P.; Kulkarni, A.S.; White, M.D.; Phale, H.; Ogbe, D. Development of a thermodynamic model and reservoir simulator for the CH4, CO2, and CH4-CO2 gas hydrate system. In Proceedings of the SPE Western Regional Meeting, Irvine, CA, USA, 30 March–1 April 2005; pp. 533–540. [Google Scholar]
- Schicks, J.M.; Luzi, M.; Beeskow-Strauch, B. The conversion process of hydrocarbon hydrates into CO2 hydrates and vice versa: Thermodynamic considerations. J. Phys. Chem. A 2011, 115, 13324–13331. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, F.; Liang, D. Multiscale analysis on CH4-CO2 swapping phenomenon occurred in hydrates. J. Phys. Chem. C 2016, 120, 25668–25677. [Google Scholar] [CrossRef]
- Zhou, X.; Li, D.; Zhang, S.; Liang, D. Swapping methane with carbon dioxide in spherical hydrate pellets. Energy 2017, 140, 136–143. [Google Scholar] [CrossRef]
- Falenty, A.; Qin, J.; Salamatin, A.N.; Yang, L.; Kuhs, W.F. Fluid composition and kinetics of the in situ replacement in CH4-CO2 hydrate system. J. Phys. Chem. C 2016, 120, 27159–27172. [Google Scholar] [CrossRef]
- Chibura, P.E.; Zhang, W.; Luo, A.; Wang, J. A review on gas hydrate production feasibility for permafrost and marine hydrates. J. Nat. Gas. Sci. Eng. 2022, 100, 104441. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, B.; Zhang, L.; Chen, C.; Li, W.; Song, Y.; Liu, Y. Influences of diffusion-limited transport in the crystals and initial water on the gaseous CO2 dynamic replacement in CH4 hydrate. J. Nat. Gas. Sci. Eng. 2022, 106, 104741. [Google Scholar] [CrossRef]
- Baig, K.; Kvamme, B.; Kuznetsova, T.; Bauman, J. Impact of water film thickness on kinetic rate of mixed hydrate formation during injection of CO2 into CH4 hydrate. Aiche J. 2015, 61, 3944–3957. [Google Scholar] [CrossRef]
- Tegze, G.; Gránásy, L.; Kvamme, B. Phase field modeling of CH4 hydrate conversion into CO2 hydrate in the presence of liquid CO2. Phys. Chem. Chem. Phys. 2007, 9, 3104–3111. [Google Scholar] [CrossRef]
- Khasanov, M.K.; Stolpovsky, M.V.; Gimaltdinov, I.K. Mathematical model of injection of liquid carbon dioxide in a reservoir saturated with methane and its hydrate. Int. J. Heat Mass Transf. 2019, 132, 529–538. [Google Scholar] [CrossRef]
- Khasanov, M.K.; Rafikova, G.R.; Musakaev, N.G. Mathematical model of carbon dioxide injection into a porous reservoir saturated with methane and its gas hydrate. Energies 2020, 13, 440. [Google Scholar] [CrossRef]
- Hsieh, P.Y.; Sean, W.Y.; Sato, T.; Seo, Y.W. Mesoscale modeling of exploiting methane hydrate by CO2 replacement in homogeneous porous media. Int. J. Heat Mass Transf. 2020, 158, 119741. [Google Scholar]
- Lee, B.R.; Koh, C.A.; Sum, A.K. Quantitative measurement and mechanisms for CH4 production from hydrates with the injection of liquid CO2. Phys. Chem. Chem. Phys. 2014, 16, 14922–14927. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Zhang, L.; Chen, X.; Zhang, Y.; Liu, Y.; Song, Y. Combined replacement and depressurization methane hydrate recovery method. Energy Explor. Exploit. 2016, 34, 129–139. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, L.; Chen, X.; Fu, Z.; Liu, Y.; Song, Y. Experimental study of conditions for methane hydrate productivity by the CO2 swap method. Energy Fuels 2015, 29, 6887–6895. [Google Scholar] [CrossRef]
- Ota, M.; Saito, T.; Aida, T.; Watanabe, M.; Sato, Y.; Smith, R.L.; Inomata, H. Macro and microscopic CH4-CO2 replacement in CH4 hydrate under pressurized CO2. AIChE J. 2007, 53, 2715–2721. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, L.J.; Li, X.S.; Chen, Z.Y.; Xu, C.G. Replacement of CH4 in hydrate in porous sediments with liquid CO2 injection. Chem. Eng. Technol. 2014, 37, 2022–2029. [Google Scholar] [CrossRef]
- Wang, X.H.; Sun, Y.F.; Wang, Y.F.; Li, N.; Sun, C.Y.; Chen, G.J.; Liu, B.; Yang, L.Y. Gas production from hydrates by CH4-CO2/H2 replacement. Appl. Energy 2017, 188, 305–314. [Google Scholar]
- Khlebnikov, V.N.; Antonov, S.V.; Mishin, A.S.; Bakulin, D.A.; Khamidullina, I.V.; Liang, M.; Vinokurov, V.A.; Gushchin, P.A. A new method for the replacement of CH4 with CO2 in natural gas hydrate production. Nat. Gas Ind. 2016, 36, 40–47. [Google Scholar] [CrossRef]
- Tupsakhare, S.S.; Fitzgerald, G.C.; Castaldi, M.J. Thermally assisted dissociation of methane hydrates and the impact of CO2 injection. Ind. Eng. Chem. Res. 2016, 55, 10465–10476. [Google Scholar] [CrossRef]
- Seo, Y.J.; Kim, D.; Koh, D.Y.; Lee, J.Y.; Ahn, T.; Kim, S.J.; Lee, J.; Lee, H. Soaking process for the enhanced methane recovery of gas hydrates via CO2/N2 gas injection. Energy Fuels 2015, 29, 8143–8150. [Google Scholar] [CrossRef]
- Oldenburg, C.M.; Pruess, K.; Benson, S.M. Process modeling of CO2 injection into natural gas reservoirs for carbon sequestration and enhanced gas recovery. Energy Fuels 2001, 15, 293–298. [Google Scholar] [CrossRef]
- Huneker, R.H. Natural Gas Production and CO2 Sequestration in a Class 2 Hydrate Accumulation: A Numerical Simulation Study; Delft University of Technology: Delft, The Netherlands, 2010. [Google Scholar]
- White, M.D.; Wurstner, S.K.; McGrail, B.P. Numerical studies of methane production from Class 1 gas hydrate accumulations enhanced with carbon dioxide injection. Mar. Pet. Geol. 2011, 28, 546–560. [Google Scholar] [CrossRef]
- Castellani, B.; Rossetti, G.; Tupsakhare, S.; Rossi, F.; Nicolini, A.; Castaldi, M.J. Simulation of CO2 storage and methane gas production from gas hydrates in a large scale laboratory reactor. J. Pet. Sci. Eng. 2016, 147, 515–527. [Google Scholar] [CrossRef]
- Gambelli, A.M.; Rossi, F. Natural gas hydrates: Comparison between two different applications of thermal stimulation for performing CO2 replacement. Energy 2019, 172, 423–434. [Google Scholar] [CrossRef]
- Fan, S.; Wang, X.; Wang, Y.; Lang, X. Recovering methane from quartz sand-bearing hydrate with gaseous CO2. J. Energy Chem. 2017, 26, 655–659. [Google Scholar] [CrossRef]
- Shi, M.; Woodley, J.M.; Von Solms, N. An experimental study on improved production performance by depressurization combined with CO2-enriched air injection. Energy Fuels 2020, 34, 7329–7339. [Google Scholar] [CrossRef]
- Li, G.; Wu, D.M.; Li, X.S.; Lv, Q.N.; Li, C.; Zhang, Y. Experimental measurement and mathematical model of permeability with methane hydrate in quartz sands. Appl. Energy 2017, 202, 282–292. [Google Scholar] [CrossRef]
- Jadhawar, P.; Mohammadi, A.H.; Yang, J.; Tohidi, B. Subsurface carbon dioxide Storage through clathrate hydrate formation. Adv. Geol. Storage Carbon. Dioxide 2006, 65, 111–126. [Google Scholar]
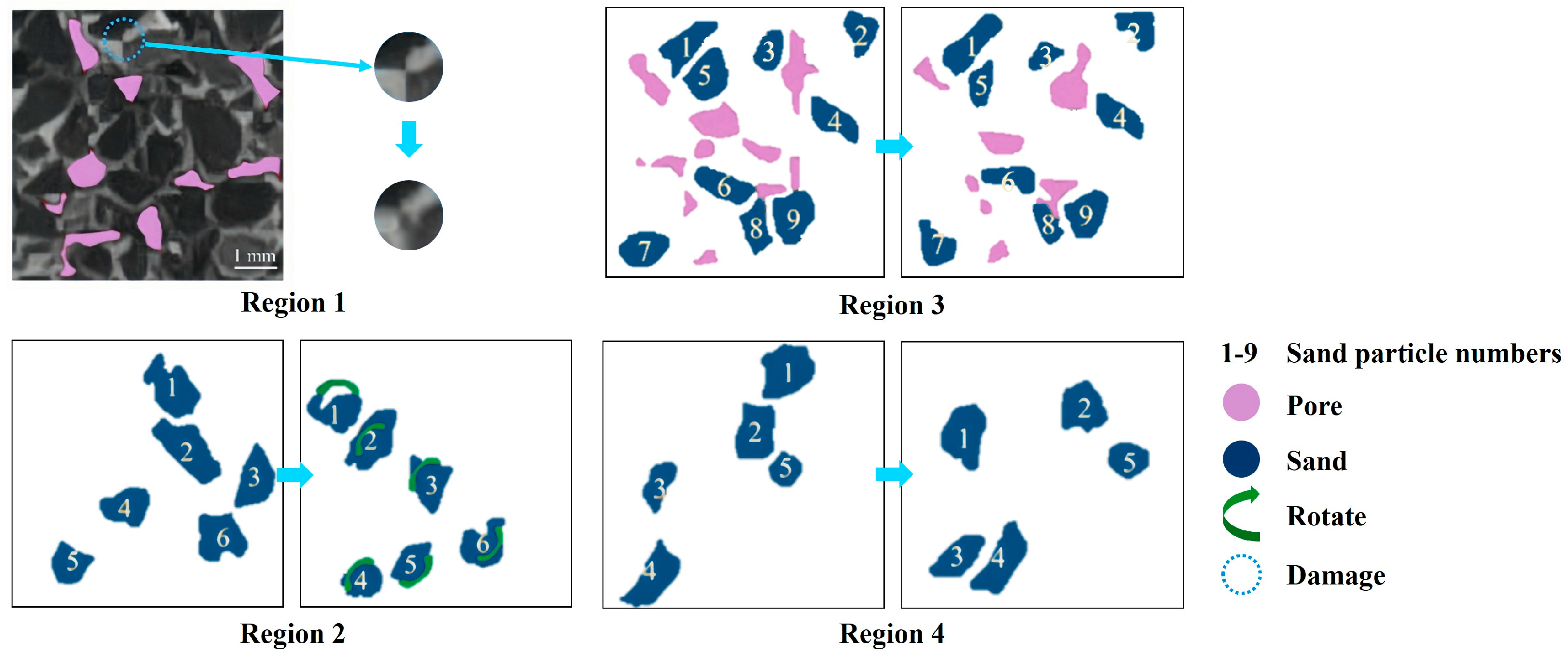
- Huang, L.; Wu, P.; Wang, Y.; Song, Y.; Li, Y. Pore-scale deformation characteristics of hydrate-bearing sediments with gas replacement. Sci. Total Environ. 2024, 954, 176464. [Google Scholar]
- Li, Y.; Huang, L.; Wu, P.; Wang, Y.; Liu, T.; Wang, H.; Song, Y. Investigation on multi-parameter of hydrate-bearing synthetic sediment during hydrate replacement process: A in-situ X-Ray computed tomography study. Sci. Total Environ. 2024, 929, 172621. [Google Scholar] [CrossRef] [PubMed]
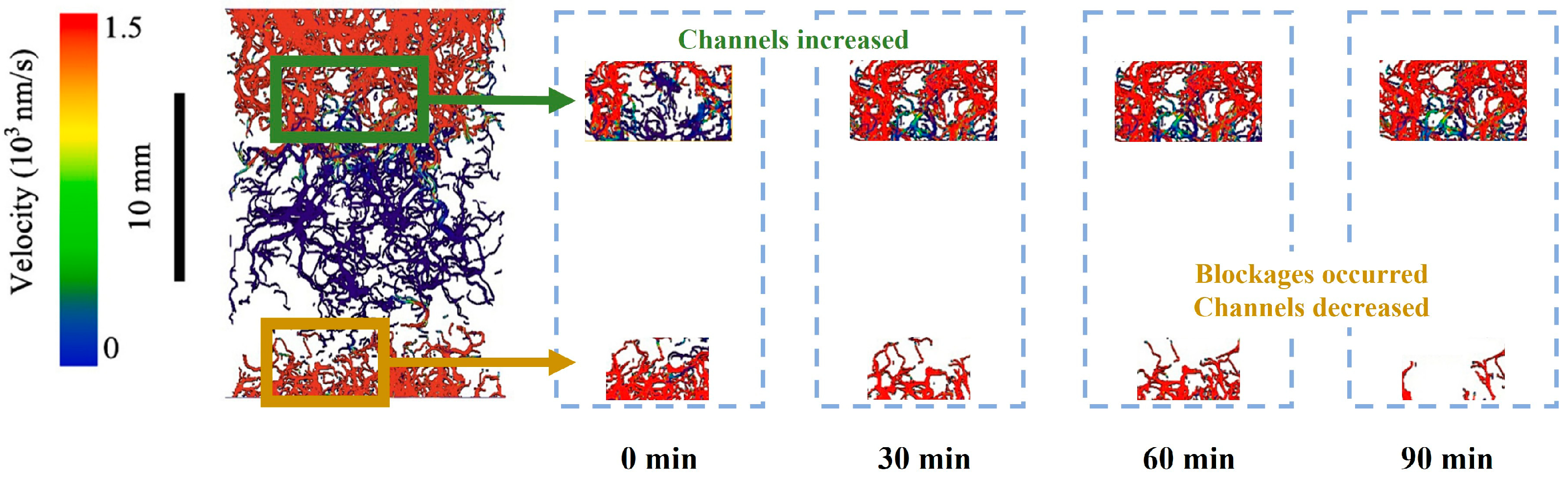
- Wang, H.; Li, Y.; Huang, L.; Liu, T.; Liu, W.; Wu, P.; Song, Y. A pore-scale study on microstructure and permeability evolution of hydrate-bearing sediment during dissociation by depressurization. Fuel 2024, 358, 130124. [Google Scholar] [CrossRef]
- Wang, D.; Wang, C.; Li, C.; Liu, C.; Lu, H.; Wu, N.; Hu, G.; Liu, L.; Meng, Q. Effect of gas hydrate formation and decomposition on flow properties of fine-grained quartz sand sediments using X-Ray CT based pore network model simulation. Fuel 2018, 226, 516–526. [Google Scholar] [CrossRef]
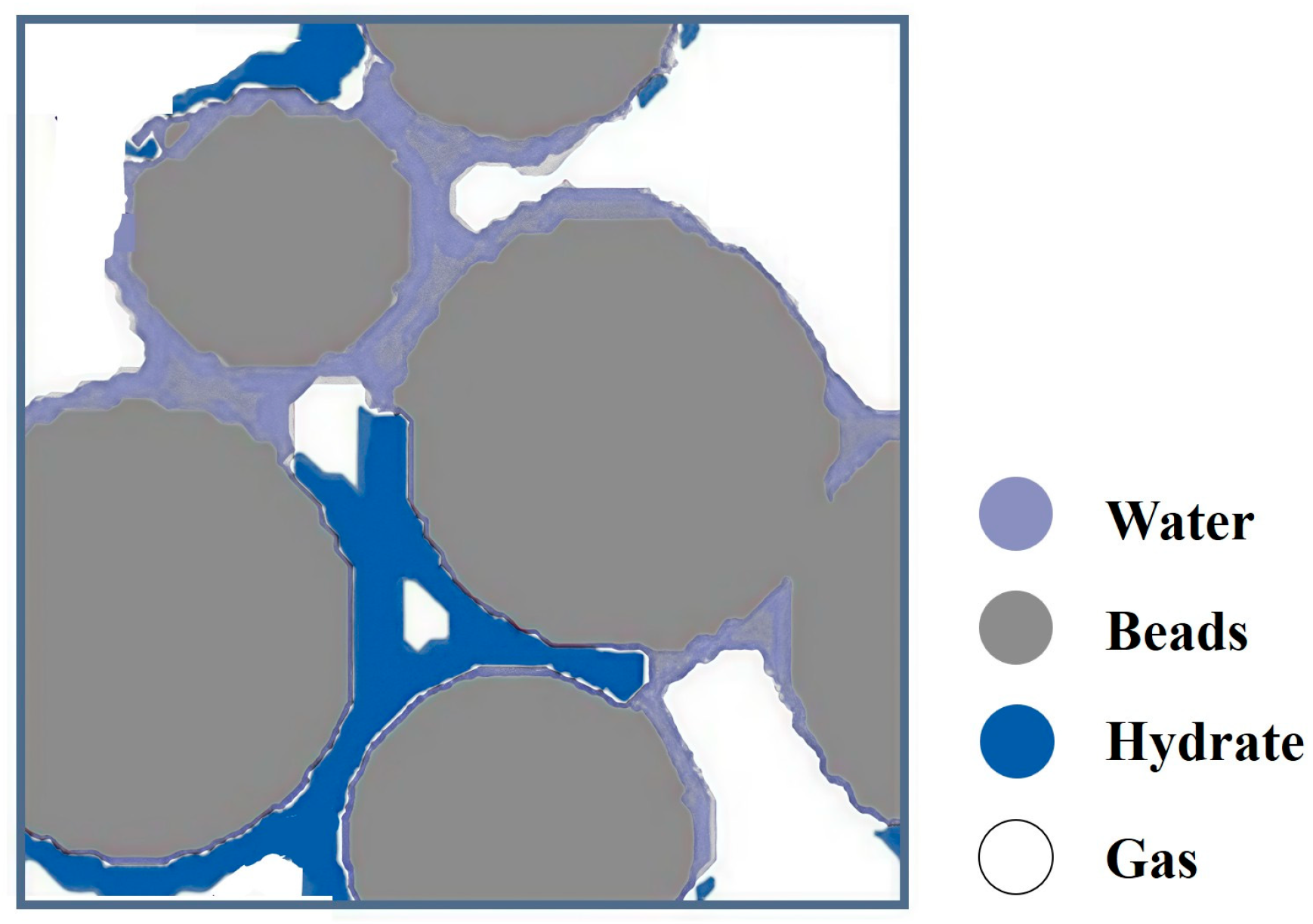
- Habiburrahman, M.; Yu, W.; Ge, K.; Wang, J.; Sultan, A.S. Pore-filling behaviors and lateral propagation of CH4 and CO2 hydrates forming in microfluidic porous media. Chem. Eng. J. 2025, 519, 162234. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Y.; Xu, Q.; Liu, Z.; Dai, X.; Shi, L.; Luo, K.H. Pore-scale visualization of hydrate dissociation and mass transfer during depressurization using microfluidic experiments. Fuel 2024, 368, 131519. [Google Scholar] [CrossRef]


| Model | Fundamental Formula | Viewpoint | Reference |
|---|---|---|---|
| Kinetic model | Hydrate dissociation: Hydrate formation: | CH4 hydrate dissociation and CO2 hydrate formation occur separately. | Kim et al. [49] Englezos et al. [50] |
| Thermodynamic model | Guest molecule diffusion within hydrate crystals is driven by the chemical potential gradient. | Hirohama et al. [8] | |
| Phase-field theory (PFT) | Phase-field transition is related to free energies, concentration fields, and motion mobilities. | Tegze et al. [73] | |
| Multiphase media mechanics model | Kinetic replacement mechanism is associated with diffusion. | Khasanov et al. [74] | |
| Film theory | CH4 hydrate dissociates, then the empty cages are occupied by CO2. | Hsieh et al. [76] | |
| Avrami model Shrinking core model | CH4 hydrate dissociates, then mixed hydrates are formed immediately. | Lee et al. [77] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Li, W.; Wu, X.; Dong, B. A Review of the Recent Advances in CH4 Recovery from CH4 Hydrate in Porous Media by CO2 Replacement. Energies 2025, 18, 5683. https://doi.org/10.3390/en18215683
Wang Y, Li W, Wu X, Dong B. A Review of the Recent Advances in CH4 Recovery from CH4 Hydrate in Porous Media by CO2 Replacement. Energies. 2025; 18(21):5683. https://doi.org/10.3390/en18215683
Chicago/Turabian StyleWang, Yingfei, Weizhong Li, Xiangen Wu, and Bo Dong. 2025. "A Review of the Recent Advances in CH4 Recovery from CH4 Hydrate in Porous Media by CO2 Replacement" Energies 18, no. 21: 5683. https://doi.org/10.3390/en18215683
APA StyleWang, Y., Li, W., Wu, X., & Dong, B. (2025). A Review of the Recent Advances in CH4 Recovery from CH4 Hydrate in Porous Media by CO2 Replacement. Energies, 18(21), 5683. https://doi.org/10.3390/en18215683






