Hybrid Deep Learning for Predictive Maintenance: LSTM, GRU, CNN, and Dense Models Applied to Transformer Failure Forecasting
Abstract
1. Introduction
2. Literature Review
2.1. Data Cleansing and Imputation
2.2. Standardization and Transformation
2.3. Bibliometric Analysis and Review of Recent Literature
- Publication year equal to or later than 2019, in order to focus on recent advances in the state of the art.
- Minimum of 10 total citations, ensuring a basic level of impact and recognition in the scientific community.
- Citations per year used as the main metric of relevance, to highlight influence proportional to the time since publication.
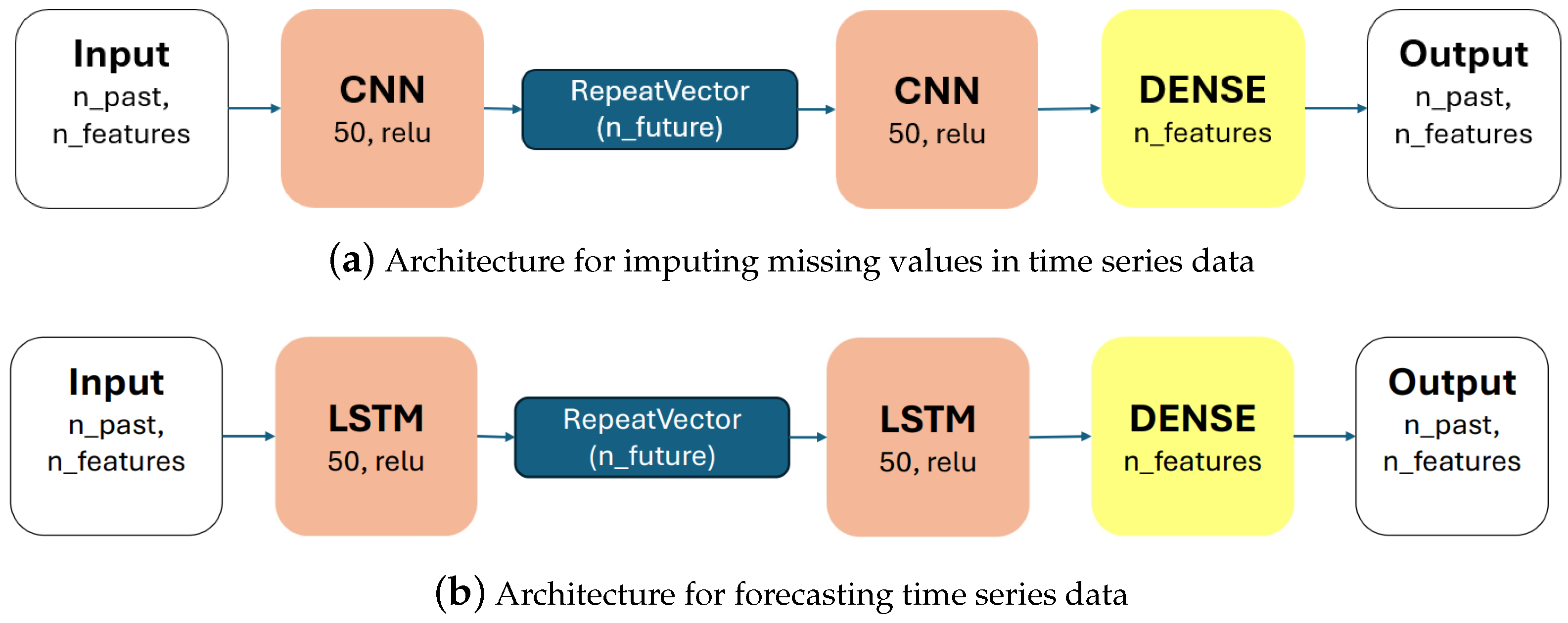
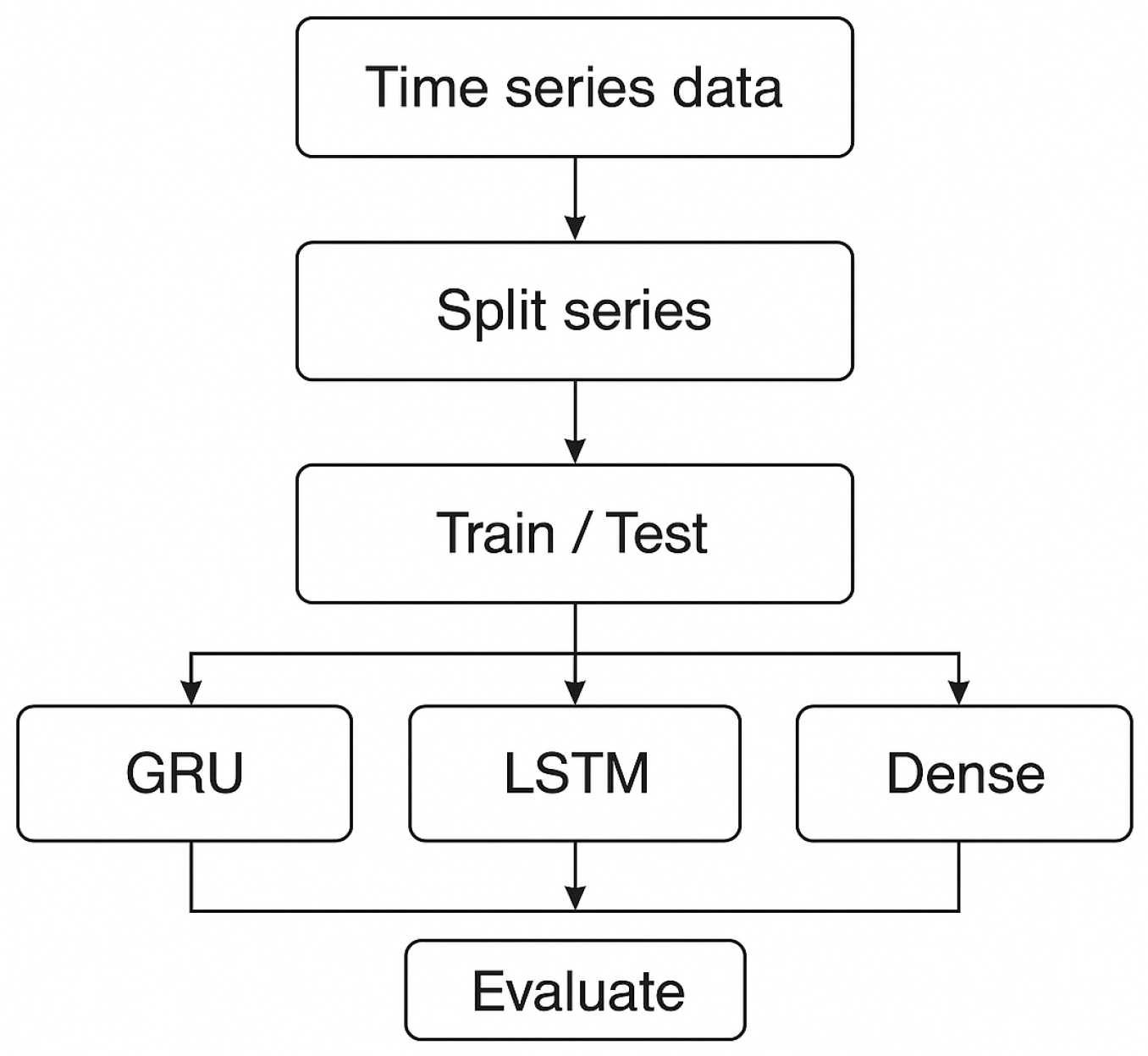
3. Methodology
- -
- GRU encoder–decoder with 64 units;
- -
- LSTM encoder–decoder with 64 units;
- -
- Dense (MLP) network with 128 hidden units.
4. Experiments and Results
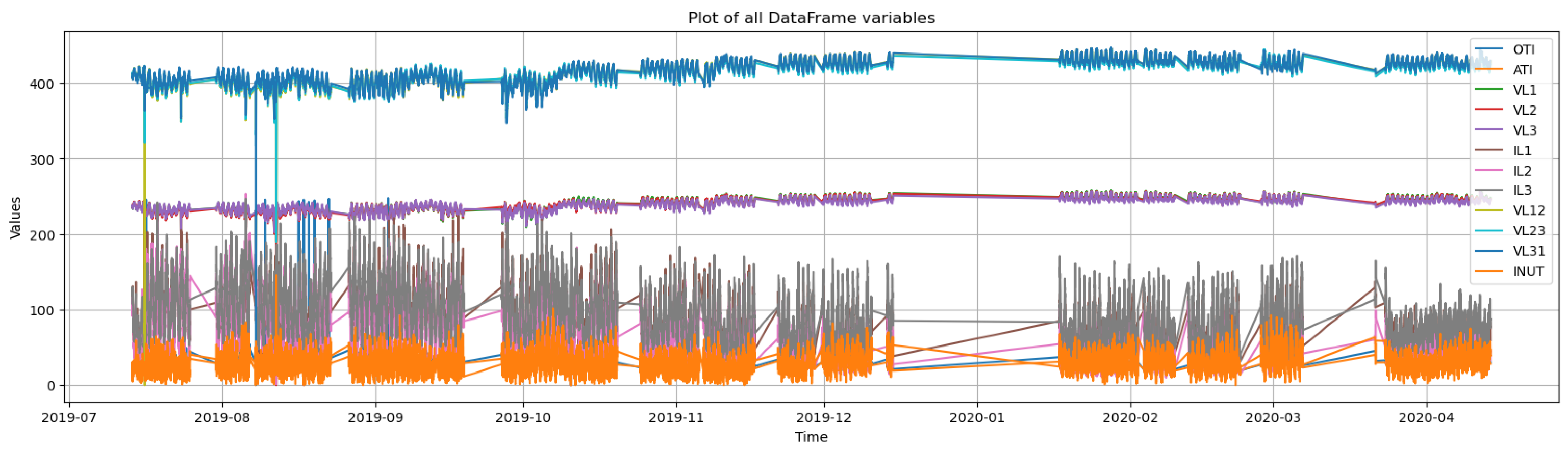
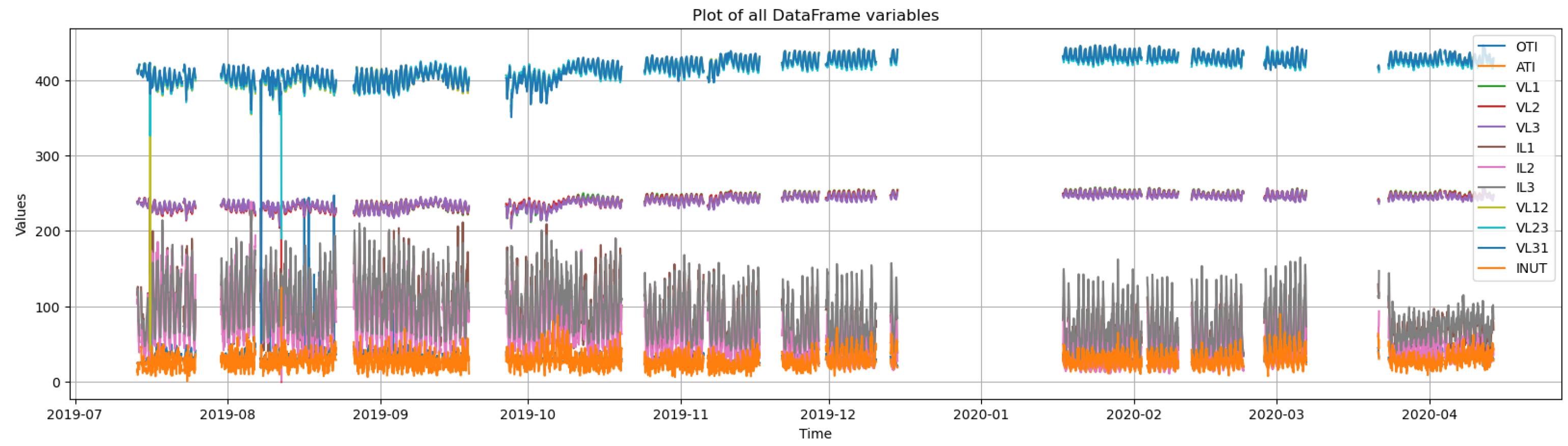
4.1. Power Transformer Data Processing
- LSTM: Final loss = 0.00158.
- GRU: Final loss = 0.00156.
- CNN: Final loss = 0.00120.
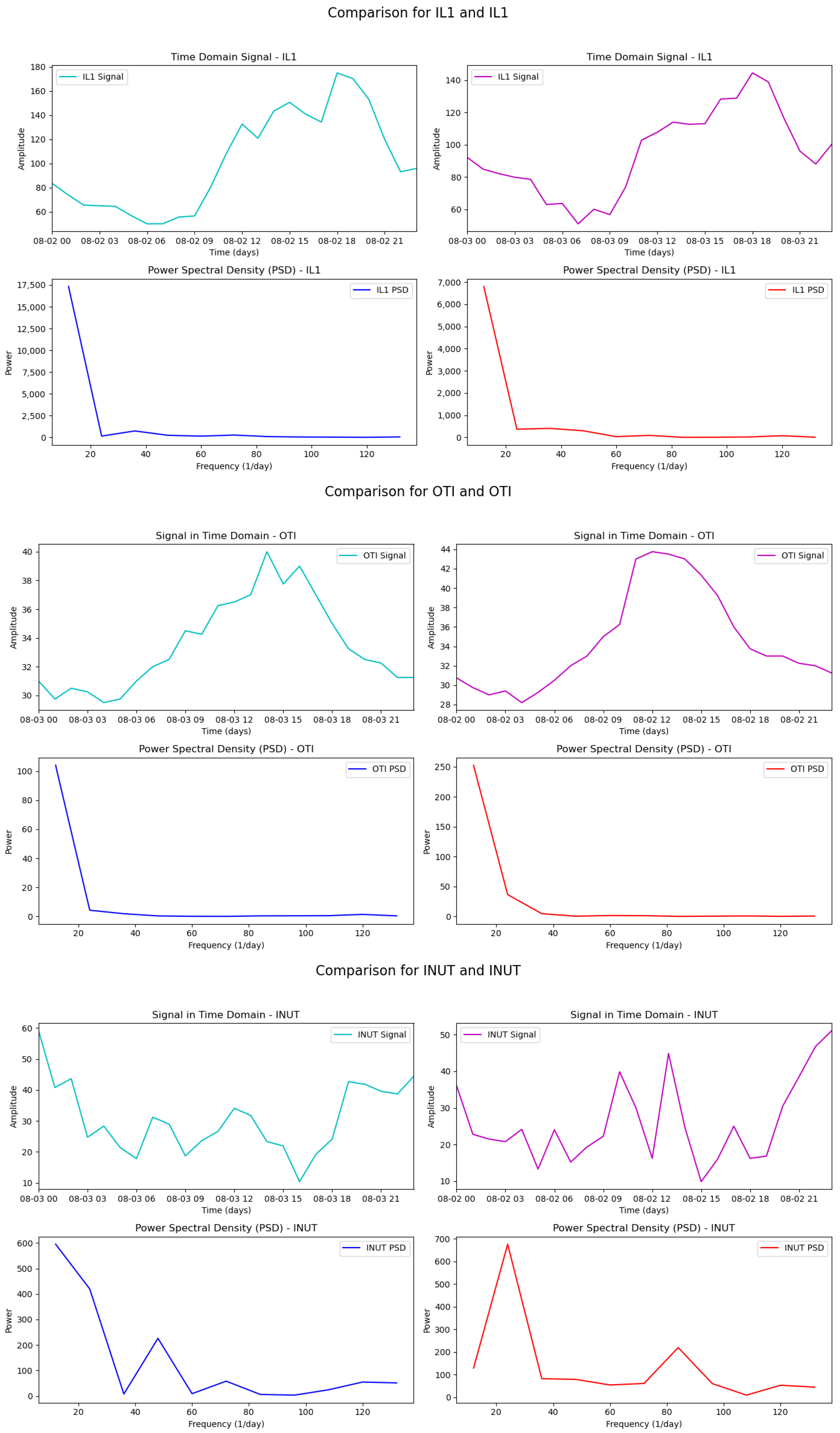
4.2. Clustering and Data Analysis in the Frequency Domain
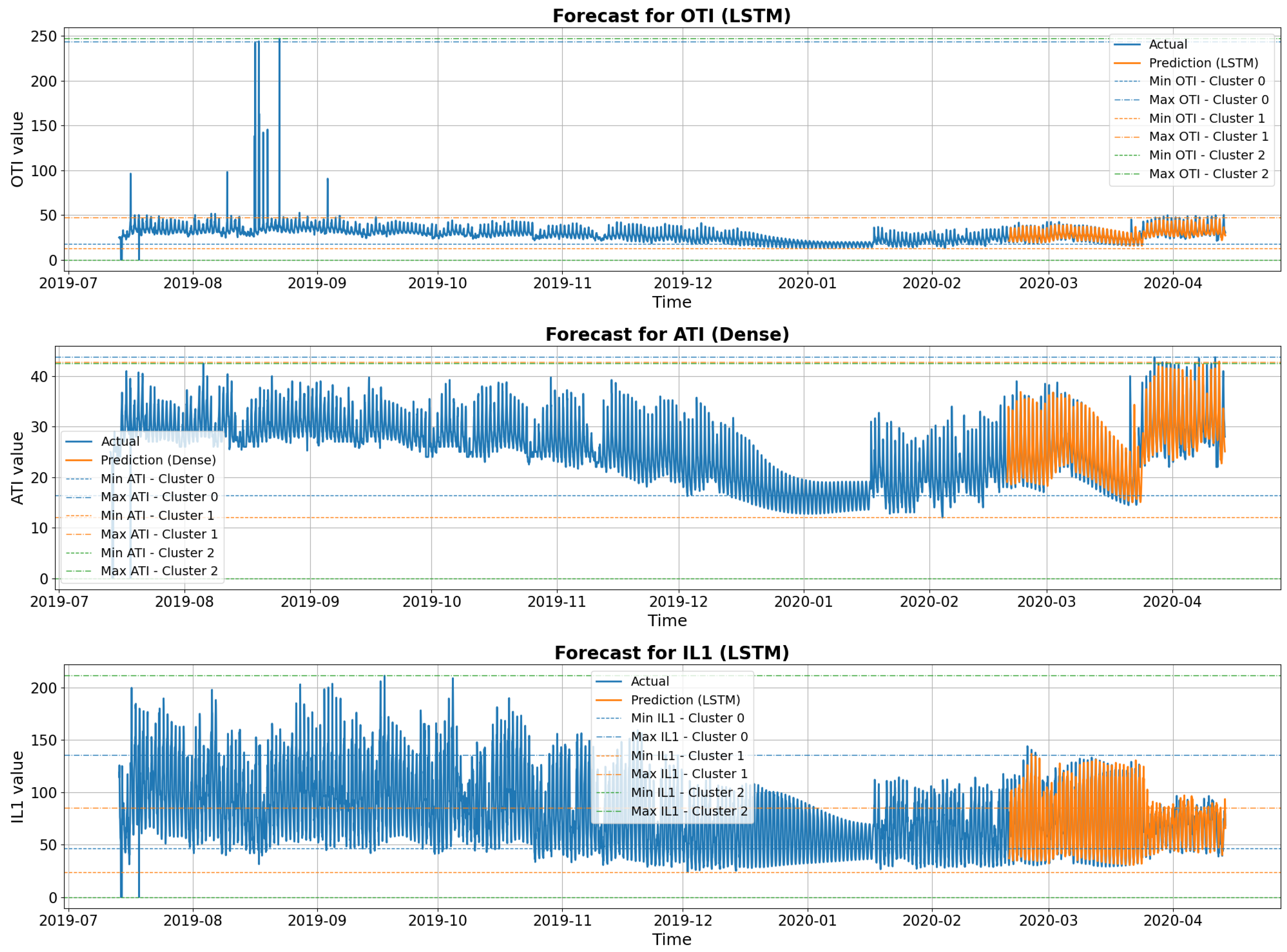
- Cluster 0: Point with high OTI value and high currents.
- Cluster 1: Moderate values, distant but not extreme.
- Cluster 2: Null values in all variables, resulting in the greatest distance proportional to its centroid.
4.3. Prediction of Patterns in Power Transformer Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Description |
| AF | Activation Function |
| ARIMA | Autoregressive Integrated Moving Average |
| ATI | Average Top-Oil Temperature Index |
| CNN | Convolutional Neural Network |
| DNN | Deep Neural Network |
| GRU | Gated Recurrent Unit |
| IL | Current Level |
| INUT | Insulation Utilization Index |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MLP | Multilayer Perceptron |
| OTI | Oil Top Temperature Indicator |
| PM | Predictive Maintenance |
| RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
| Coefficient of Determination | |
| VL | Voltage Level |
References
- Yazdi, M. Maintenance Strategies and Optimization Techniques. In Advances in Computational Mathematics for Industrial System Reliability and Maintainability; Springer Nature: Cham, Switzerland, 2024; pp. 43–58. [Google Scholar] [CrossRef]
- Sandu, G.; Varganova, O.; Samii, B. Managing physical assets: A systematic review and a sustainable perspective. Int. J. Prod. Res. 2023, 61, 6652–6674. [Google Scholar] [CrossRef]
- Farinha, J.M.T. Asset Maintenance Engineering Methodologies, 1st ed.; Taylor & Francis Ltd.: Oxfordshire, UK, 2020; p. 336. [Google Scholar]
- Velmurugan, R.S.; Dhingra, T. Asset Maintenance in Operations-Intensive Organizations. In Asset Maintenance Management in Industry: A Comprehensive Guide to Strategies, Practices and Benchmarking; Springer International Publishing: Cham, Switzerland, 2021; pp. 23–59. [Google Scholar] [CrossRef]
- Farinha, J.T.; Raposo, H.D.N.; de-Almeida-e Pais, J.E.; Mendes, M. Physical Asset Life Cycle Evaluation Models—A Comparative Analysis towards Sustainability. Sustainability 2023, 15, 15754. [Google Scholar] [CrossRef]
- Mirshekali, H.; Santos, A.Q.; Shaker, H.R. A Survey of Time-Series Prediction for Digitally Enabled Maintenance of Electrical Grids. Energies 2023, 16, 6332. [Google Scholar] [CrossRef]
- Balaraman, S.; Kamaraj, N. Cascade BPN based transmission line overload prediction and preventive action by generation rescheduling. Neurocomputing 2012, 94, 1–12. [Google Scholar] [CrossRef]
- Sharma, S.; Srivastava, L. Prediction of transmission line overloading using intelligent technique. Appl. Soft Comput. 2008, 8, 626–633. [Google Scholar] [CrossRef]
- Lee, J.; Ni, J.; Singh, J.; Jiang, B.; Azamfar, M.; Feng, J. Intelligent Maintenance Systems and Predictive Manufacturing. J. Manuf. Sci. Eng. 2020, 142, 110805. [Google Scholar] [CrossRef]
- Sagharidooz, M.; Soltanali, H.; Farinha, J.T.; Raposo, H.D.N.; de-Almeida-e Pais, J.E. Reliability, Availability, and Maintainability Assessment-Based Sustainability-Informed Maintenance Optimization in Power Transmission Networks. Sustainability 2024, 16, 6489. [Google Scholar] [CrossRef]
- Cachada, A.; Barbosa, J.; Leitño, P.; Gcraldcs, C.A.; Deusdado, L.; Costa, J.; Teixeira, C.; Teixeira, J.; Moreira, A.H.; Moreira, P.M.; et al. Maintenance 4.0: Intelligent and Predictive Maintenance System Architecture. In Proceedings of the 2018 IEEE 23rd International Conference on Emerging Technologies and Factory Automation (ETFA), Torino, Italy, 4–7 September 2018; Volume 1, pp. 139–146. [Google Scholar] [CrossRef]
- Parpala, R.C.; Iacob, R. Application of IoT concept on predictive maintenance of industrial equipment. MATEC Web Conf. 2017, 121, 02008. [Google Scholar] [CrossRef]
- Silvestri, L.; Forcina, A.; Introna, V.; Santolamazza, A.; Cesarotti, V. Maintenance transformation through Industry 4.0 technologies: A systematic literature review. Comput. Ind. 2020, 123, 103335. [Google Scholar] [CrossRef]
- Singh, S.; Galar, D.; Baglee, D.; Björling, S.E. Self-maintenance techniques: A smart approach towards self-maintenance system. Int. J. Syst. Assur. Eng. Manag. 2014, 5, 75–83. [Google Scholar] [CrossRef]
- Mateus, B.C.; Farinha, J.T.; Mendes, M. Fault Detection and Prediction for Power Transformers Using Fuzzy Logic and Neural Networks. Energies 2024, 17, 296. [Google Scholar] [CrossRef]
- Martins, A.; Fonseca, I.; Farinha, J.T.; Reis, J.; Cardoso, A.J.M. Prediction maintenance based on vibration analysis and deep learning—A case study of a drying press supported on a Hidden Markov Model. Appl. Soft Comput. 2024, 163, 111885. [Google Scholar] [CrossRef]
- McKinsey & Company. A Smarter Way to Digitize Maintenance and Reliability. 2021. Available online: https://www.mckinsey.com/capabilities/operations/our-insights/a-smarter-way-to-digitize-maintenance-and-reliability (accessed on 23 May 2025).
- Crespo Marquez, A.; Gomez Fernandez, J.F.; Martínez-Galán Fernández, P.; Guillen Lopez, A. Maintenance Management through Intelligent Asset Management Platforms (IAMP). Emerging Factors, Key Impact Areas and Data Models. Energies 2020, 13, 3762. [Google Scholar] [CrossRef]
- Zhang, X.; Li, H.; Wu, P. Data-Driven Construction Safety Information Sharing System Based on Linked Data, Ontologies, and Knowledge Graph Technologies. Int. J. Environ. Res. Public Health 2022, 19, 794. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, H.; Xia, G.; Cao, W.; Li, T.; Wang, X.; Liu, Z. A machine learning-based data-driven method for risk analysis of marine accidents. J. Mar. Eng. Technol. 2025, 24, 147–158. [Google Scholar] [CrossRef]
- Dalzochio, J.; Kunst, R.; Pignaton, E.; Binotto, A.P.D.; Sanyal, S.; Favilla, J.; Barbosa, J.L.V. Machine learning and reasoning for predictive maintenance in Industry 4.0: Current status and challenges. Comput. Ind. 2020, 123, 103298. [Google Scholar] [CrossRef]
- Wan, J.; Tang, S.; Li, D.; Wang, S.; Liu, C.; Abbas, H.; Vasilakos, A.V. A Manufacturing Big Data Solution for Active Preventive Maintenance. IEEE Trans. Ind. Inform. 2017, 13, 2039–2047. [Google Scholar] [CrossRef]
- Roosefert Mohan, T.; Preetha Roselyn, J.; Annie Uthra, R.; Devaraj, D.; Umachandran, K. Intelligent machine learning based total productive maintenance approach for achieving zero downtime in industrial machinery. Comput. Ind. Eng. 2021, 157, 107267. [Google Scholar] [CrossRef]
- NP EN 13306:2007; Maintenance Terminology; Portuguese standard based on EN 13306:2007. Instituto Português da. Qualidade: Caparica, Portugal, 2007.
- Paolanti, M.; Romeo, L.; Felicetti, A.; Mancini, A.; Frontoni, E.; Loncarski, J. Machine Learning approach for Predictive Maintenance in Industry 4.0. In Proceedings of the 2018 14th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Oulu, Finland, 2–4 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Malta, A.; Farinha, T.; Mendes, M. Augmented Reality in Maintenance—History and Perspectives. J. Imaging 2023, 9, 142. [Google Scholar] [CrossRef]
- Compare, M.; Baraldi, P.; Zio, E. Challenges to IoT-Enabled Predictive Maintenance for Industry 4.0. IEEE Internet Things J. 2020, 7, 4585–4597. [Google Scholar] [CrossRef]
- Javaid, M.; Haleem, A.; Singh, R.P.; Rab, S.; Suman, R. Significance of sensors for industry 4.0: Roles, capabilities, and applications. Sens. Int. 2021, 2, 100110. [Google Scholar] [CrossRef]
- Mateus, B.; Farinha, J.T.; Cardoso, A.M. Production optimization versus asset availability—A review. WSEAS Trans. Syst. Control 2020, 15, 320–332. [Google Scholar] [CrossRef]
- Elnahrawy, E.; Nath, B. Cleaning and querying noisy sensors. In Proceedings of the 2nd ACM International Conference on Wireless Sensor Networks and Applications, San Diego, CA, USA, 19 September 2003; WSNA ’03. Association for Computing Machinery: New York, NY, USA, 2003; pp. 78–87. [Google Scholar] [CrossRef]
- McGrath, M.J.; Scanaill, C.N. Sensing and Sensor Fundamentals. In Sensor Technologies: Healthcare, Wellness, and Environmental Applications; Apress: Berkeley, CA, USA, 2013; pp. 15–50. [Google Scholar] [CrossRef]
- Fraden, J. Sensor Characteristics. In Handbook of Modern Sensors: Physics, Designs, and Applications; Springer: New York, NY, USA, 2010; pp. 13–52. [Google Scholar] [CrossRef]
- North, D. An Analysis of the factors which determine signal/noise discrimination in pulsed-carrier systems. Proc. IEEE 1963, 51, 1016–1027. [Google Scholar] [CrossRef]
- Shuai, M.; Xie, K.; Chen, G.; Ma, X.; Song, G. A Kalman Filter Based Approach for Outlier Detection in Sensor Networks. In Proceedings of the 2008 International Conference on Computer Science and Software Engineering, Wuhan, China, 12–14 December 2008; Volume 4, pp. 154–157. [Google Scholar] [CrossRef]
- Tan, Y.L.; Sehgal, V.; Shahri, H.H. Sensoclean: Handling Noisy and Incomplete Data in Sensor Networks Using Modeling. Ph.D. Thesis, University of Kaiserslautern, Kaiserslautern, Germany, 2005; pp. 1–18. [Google Scholar]
- Shao, B.; Song, C.; Wang, Z.; Li, Z.; Yu, S.; Zeng, P. Data Cleaning Based on Multi-sensor Spatiotemporal Correlation. In Machine Learning and Intelligent Communications; Zhai, X.B., Chen, B., Zhu, K., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 235–243. [Google Scholar]
- Liu, H.; Shah, S.; Jiang, W. On-line outlier detection and data cleaning. Comput. Chem. Eng. 2004, 28, 1635–1647. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 3rd ed.; OTexts: Munich, Germany, 2021. [Google Scholar]
- Keogh, E.; Kasetty, S. On the need for time series data mining benchmarks: A survey and empirical demonstration. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, Washington, DC, USA, 24–27 August 2003; pp. 102–111. [Google Scholar]
- Esling, P.; Agon, C. Time-series data mining. ACM Comput. Surv. (CSUR) 2012, 45, 1–34. [Google Scholar] [CrossRef]
- Yoon, J.; Jarrett, D.; van der Schaar, M. Semi-supervised learning with deep generative models for high-dimensional missing data imputation. Adv. Neural Inf. Process. Syst. (NeurIPS) 2020, 33, 8050–8060. [Google Scholar]
- Zhang, Z.; Chen, J.; Yu, T.; Wang, Z. Missing value imputation for microarray gene expression data using a weighted KNN algorithm with truncated normal distribution. BMC Bioinform. 2017, 18, 1–12. [Google Scholar]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–38. [Google Scholar] [CrossRef]
- Schmitt, M.; Zhu, X.X. Missing Data Imputation for Remote Sensing Time Series by Out-of-Sample EM. In Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2019; pp. 347–363. [Google Scholar] [CrossRef]
- Wu, Z.; Li, Z.; Liu, Q. Semi-supervised learning with missing not at random data. arXiv 2023. Available online: https://arxiv.org/abs/2308.08872 (accessed on 1 June 2025).
- Abdalla, H.I.; Altaf, A. The Impact of Data Normalization on KNN Rendering. In Proceedings of the 9th International Conference on Advanced Intelligent Systems and Informatics, Cairo, Egypt, 20–22 September 2023; Hassanien, A., Rizk, R.Y., Pamucar, D., Darwish, A., Chang, K.C., Eds.; Springer Nature: Cham, Switzerland, 2023; pp. 176–184. [Google Scholar]
- Pagan, M.; Zarlis, M.; Candra, A. Investigating the impact of data scaling on the k-nearest neighbor algorithm. Comput. Sci. Inf. Technol. 2023, 4, 135–142. [Google Scholar] [CrossRef]
- Henderi, H.; Wahyuningsih, T.; Rahwanto, E. Comparison of Min-Max normalization and Z-Score Normalization in the K-nearest neighbor (kNN) Algorithm to Test the Accuracy of Types of Breast Cancer. Int. J. Inform. Inf. Syst. 2021, 4, 13–20. [Google Scholar] [CrossRef]
- Ahmed, H.A.; Ali, P.J.M.; Faeq, A.K.; Abdullah, S.M. An investigation on disparity responds of machine learning algorithms to data normalization method. Aro-Sci. J. Koya Univ. 2022, 10, 29–37. [Google Scholar] [CrossRef]
- Abid, A.; Khan, M.T.; Iqbal, J. A review on fault detection and diagnosis techniques: Basics and beyond. Artif. Intell. Rev. 2021, 54, 3639–3664. [Google Scholar] [CrossRef]
- Brito, L.; Susto, G.; Brito, J.; Duarte, M. An explainable artificial intelligence approach for fault detection. Signal Process. Syst. 2022. [Google Scholar] [CrossRef]
- Shakiba, F.; Azizi, S.; Zhou, M.; Abusorrah, A. Application of machine learning methods in fault detection. Artif. Intell. Rev. 2023. [Google Scholar] [CrossRef]
- Azamfar, M.; Singh, J.; Bravo-Imaz, I.; Lee, J. Multisensor data fusion for gearbox fault diagnosis. Signal Process. Syst. 2020. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Abdeljaber, O.; Avci, O.; Gabbouj, M. 1-D convolutional neural networks for signal processing applications. IEEE Trans. Signal Process. 2019. [Google Scholar]
- Chen, Y.; Rao, M.; Feng, K.; Zuo, M. Physics-Informed LSTM hyperparameters selection for fault detection. Signal Process. Syst. 2022. [Google Scholar] [CrossRef]
- Ali, M.; Shabbir, M.; Liang, X.; et al. Machine learning-based fault diagnosis for synchronous motors. IEEE Trans. 2019. [Google Scholar]
- Kumar, P.; Hati, A. Review on machine learning algorithms for fault detection. Arch. Comput. Methods Eng. 2021. [Google Scholar] [CrossRef]
- Yu, J.; Zhang, Y. Challenges and opportunities of deep learning-based predictive maintenance. Neural Comput. Appl. 2023. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S.; Williamson, S. Machine learning-based fault detection in electric vehicles. Electronics 2021. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Javaid, M.; Khan, M.; Lee, J. Signal processing techniques for condition monitoring of electrical machines. IEEE Access 2021, 9, 12034–12050. [Google Scholar]



| Authors | Year | Full Title | Main Technique | Source | Cit./Year |
|---|---|---|---|---|---|
| [50] | 2021 | A review on fault detection and diagnosis techniques using machine learning | Systematic Review | Springer | 101.25 |
| [51] | 2022 | An explainable artificial intelligence approach for fault detection | XAI + ML | Elsevier | 98.33 |
| [52] | 2023 | Application of machine learning methods in fault detection | SVM, DWT, CNN | Springer | 70.00 |
| [53] | 2020 | Multisensor data fusion for gearbox fault diagnosis using deep learning | Data Fusion + CNN | Elsevier | 69.00 |
| [54] | 2019 | 1-D convolutional neural networks for signal processing applications | 1D CNN | IEEE | 66.67 |
| [55] | 2022 | Physics-Informed LSTM hyperparameters selection for robust fault detection | LSTM + Physics Models | Elsevier | 65.33 |
| [56] | 2019 | Machine learning-based fault diagnosis for synchronous motors | Autoencoder + DNN | IEEE | 58.67 |
| [57] | 2021 | Review on machine learning algorithms for fault detection in electrical machines | ML Review | Academia.edu | 55.25 |
| [58] | 2023 | Challenges and opportunities of deep learning-based predictive maintenance | Deep Learning | Springer | 52.00 |
| [59] | 2021 | Machine learning-based fault detection in electric vehicles using vibration signals | Data-Driven ML | MDPI | 48.75 |
| Statistics | OTI | ATI | VL1 | VL2 | VL3 | IL1 | IL2 | IL3 | VL12 | VL23 | VL31 | INUT |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 17,865 | 17,865 | 17,865 | 17,865 | 17,865 | 17,865 | 17,865 | 17,865 | 17,865 | 17,865 | 17,865 | 17,865 |
| mean | 29.77 | 27.06 | 241.04 | 240.42 | 239.76 | 80.75 | 64.61 | 91.25 | 416.72 | 415.69 | 417.27 | 28.88 |
| std | 11.28 | 5.51 | 9.44 | 9.88 | 8.64 | 35.69 | 37.55 | 36.55 | 17.22 | 15.00 | 16.90 | 13.27 |
| min | 11.00 | 12.00 | 112.60 | 0.00 | 90.10 | 0.00 | 0.00 | 0.00 | 0.00 | 189.50 | 0.00 | 0.00 |
| 25% | 25.00 | 24.00 | 234.70 | 234.40 | 234.40 | 52.70 | 37.00 | 62.20 | 406.00 | 406.10 | 406.80 | 19.40 |
| 50% | 29.00 | 27.00 | 243.10 | 242.40 | 241.10 | 73.60 | 53.70 | 85.20 | 420.30 | 418.40 | 420.30 | 27.10 |
| 75% | 33.00 | 30.00 | 247.80 | 246.90 | 245.50 | 103.20 | 86.70 | 117.70 | 428.30 | 426.00 | 428.50 | 36.90 |
| max | 248.00 | 44.00 | 258.10 | 257.00 | 256.50 | 224.10 | 253.60 | 247.30 | 446.50 | 444.80 | 447.30 | 145.80 |
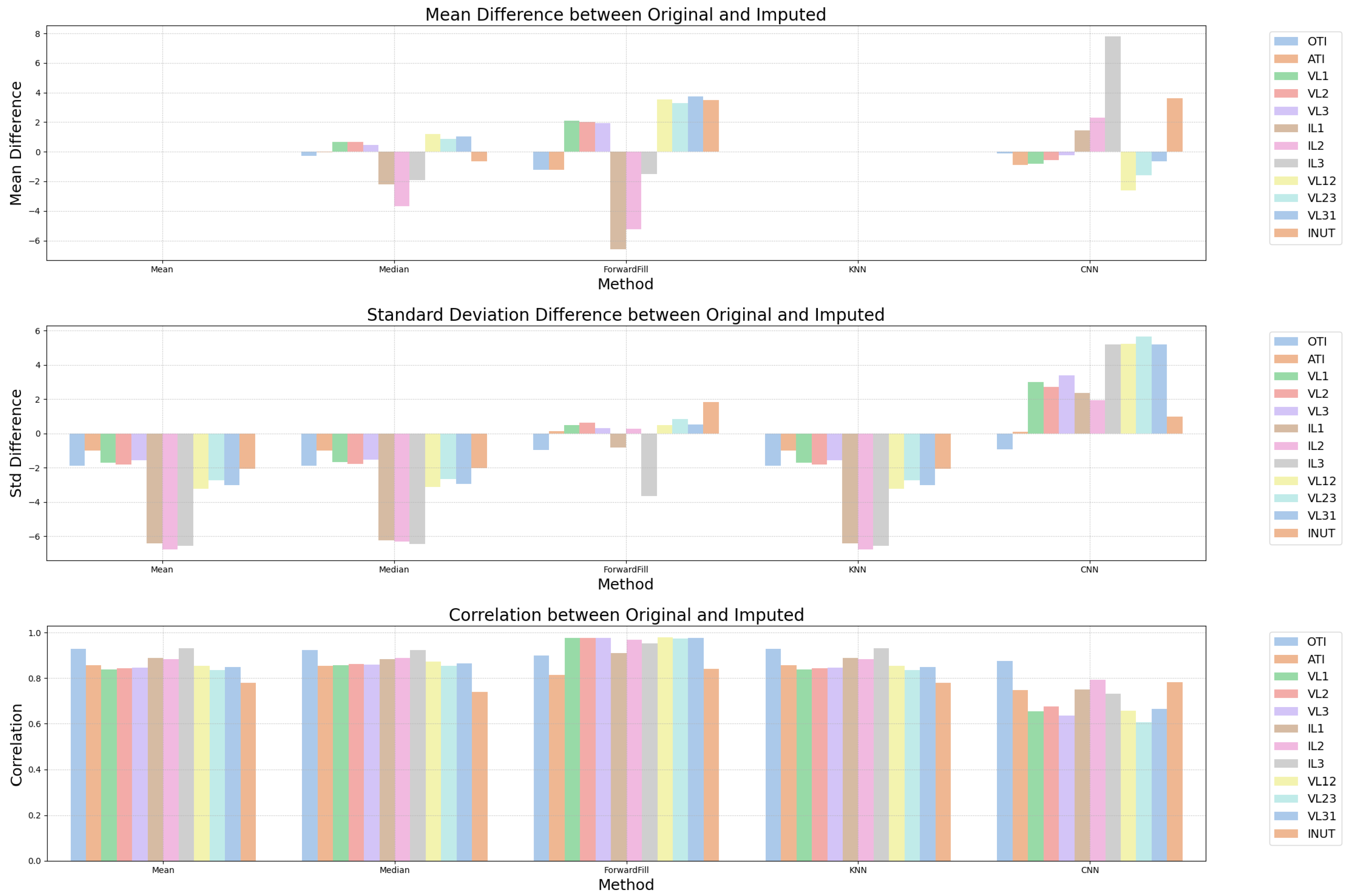
| Method | Mean Diff | Std Diff | Average Correlation | Stability Interpretation |
|---|---|---|---|---|
| CNN | 1.00 | 0.84 | 0.89 | High stability, consistent and accurate imputation with preserved dynamics. |
| KNN | 0.00 | 1.93 | 0.87 | Very stable; minor variability reduction but maintains overall pattern. |
| Mean | 0.00 | 1.99 | 0.86 | Statistically stable but oversmooth; tends to flatten temporal variations. |
| Median | 0.99 | 1.89 | 0.86 | Similar to mean; robust but with slight smoothing effects. |
| Forward fill | 2.54 | 1.00 | 0.93 | Strong correlation but introduces bias and systematic level shifts. |
| Device Time Stamp | OTI | ATI | VL1 | … | IL1 | VL12 | INUT | Cluster | Distance to Centroid |
|---|---|---|---|---|---|---|---|---|---|
| 43,694.46 | 244.00 | 33.25 | 230.88 | … | 68.85 | 398.03 | 14.43 | 0 | 217.97 |
| 43,694.50 | 38.75 | 33.75 | 229.58 | … | 31.43 | 396.15 | 11.13 | 1 | 70.86 |
| 43,660.13 | 0.00 | 0.00 | 0.00 | … | 0.00 | 0.00 | 0.00 | 2 | 823.23 |
| Variable | Best Model | MAPE | RMSE | MAE | R2 |
|---|---|---|---|---|---|
| OTI | Dense | 0.055905 | 2.678454 | 1.664657 | 0.846432 |
| ATI | Dense | 0.051844 | 2.287017 | 1.364484 | 0.876268 |
| VL1 | Dense | 0.007011 | 2.326546 | 1.732341 | 0.745781 |
| VL2 | Dense | 0.007081 | 2.590326 | 1.732341 | 0.682847 |
| VL3 | LSTM | 0.011161 | 3.428184 | 2.736036 | 0.454651 |
| IL1 | Dense | 0.086615 | 8.875986 | 6.088209 | 0.900197 |
| IL2 | Dense | 0.149841 | 8.860712 | 6.012136 | 0.868971 |
| IL3 | Dense | 0.096362 | 11.099322 | 7.388124 | 0.892436 |
| VL12 | Dense | 0.007188 | 4.140241 | 3.042514 | 0.776893 |
| VL23 | LSTM | 0.007763 | 4.513046 | 3.279813 | 0.673239 |
| VL31 | GRU | 0.014124 | 7.268373 | 5.996321 | 0.309541 |
| INUT | Dense | 0.165428 | 6.853638 | 4.934111 | 0.727558 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mateus, B.C.; Mendes, M.; Farinha, J.T.; Martins, A. Hybrid Deep Learning for Predictive Maintenance: LSTM, GRU, CNN, and Dense Models Applied to Transformer Failure Forecasting. Energies 2025, 18, 5634. https://doi.org/10.3390/en18215634
Mateus BC, Mendes M, Farinha JT, Martins A. Hybrid Deep Learning for Predictive Maintenance: LSTM, GRU, CNN, and Dense Models Applied to Transformer Failure Forecasting. Energies. 2025; 18(21):5634. https://doi.org/10.3390/en18215634
Chicago/Turabian StyleMateus, Balduíno César, Mateus Mendes, José Torres Farinha, and Alexandre Martins. 2025. "Hybrid Deep Learning for Predictive Maintenance: LSTM, GRU, CNN, and Dense Models Applied to Transformer Failure Forecasting" Energies 18, no. 21: 5634. https://doi.org/10.3390/en18215634
APA StyleMateus, B. C., Mendes, M., Farinha, J. T., & Martins, A. (2025). Hybrid Deep Learning for Predictive Maintenance: LSTM, GRU, CNN, and Dense Models Applied to Transformer Failure Forecasting. Energies, 18(21), 5634. https://doi.org/10.3390/en18215634








