Numerical Study of Liquid Hydrogen Internal Flow in Liquid Hydrogen Storage Tank
Abstract
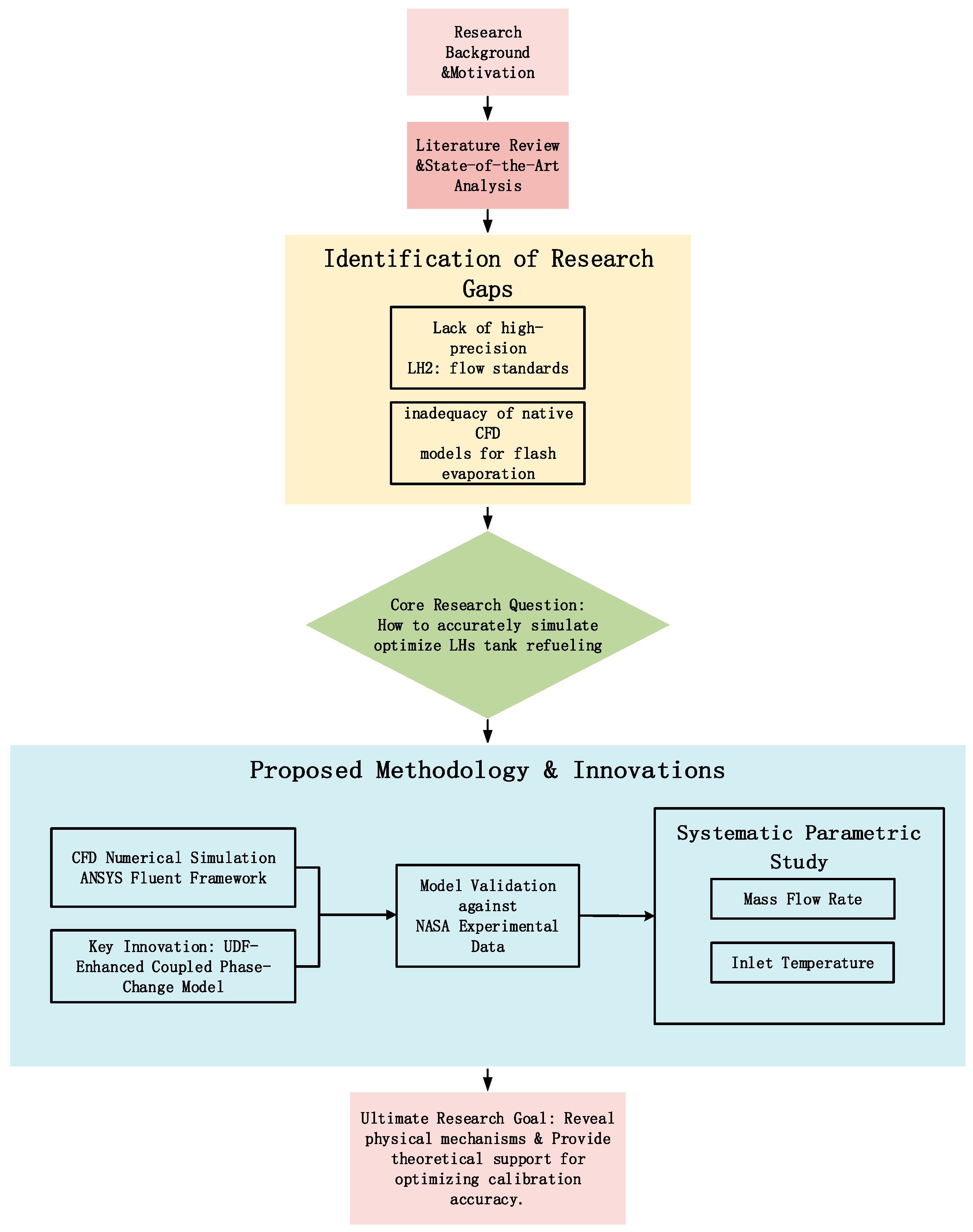
1. Introduction
2. Numerical Methods
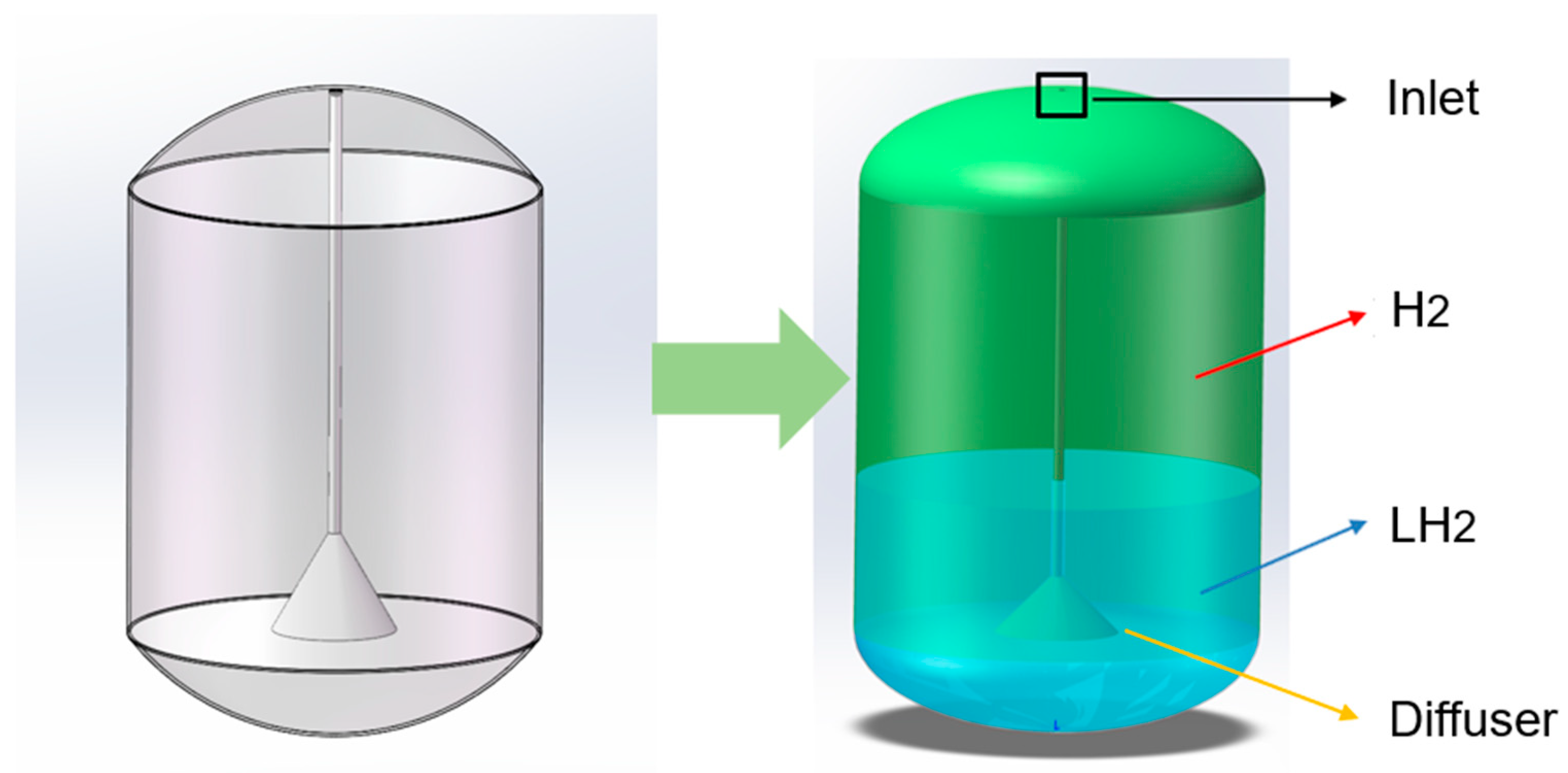
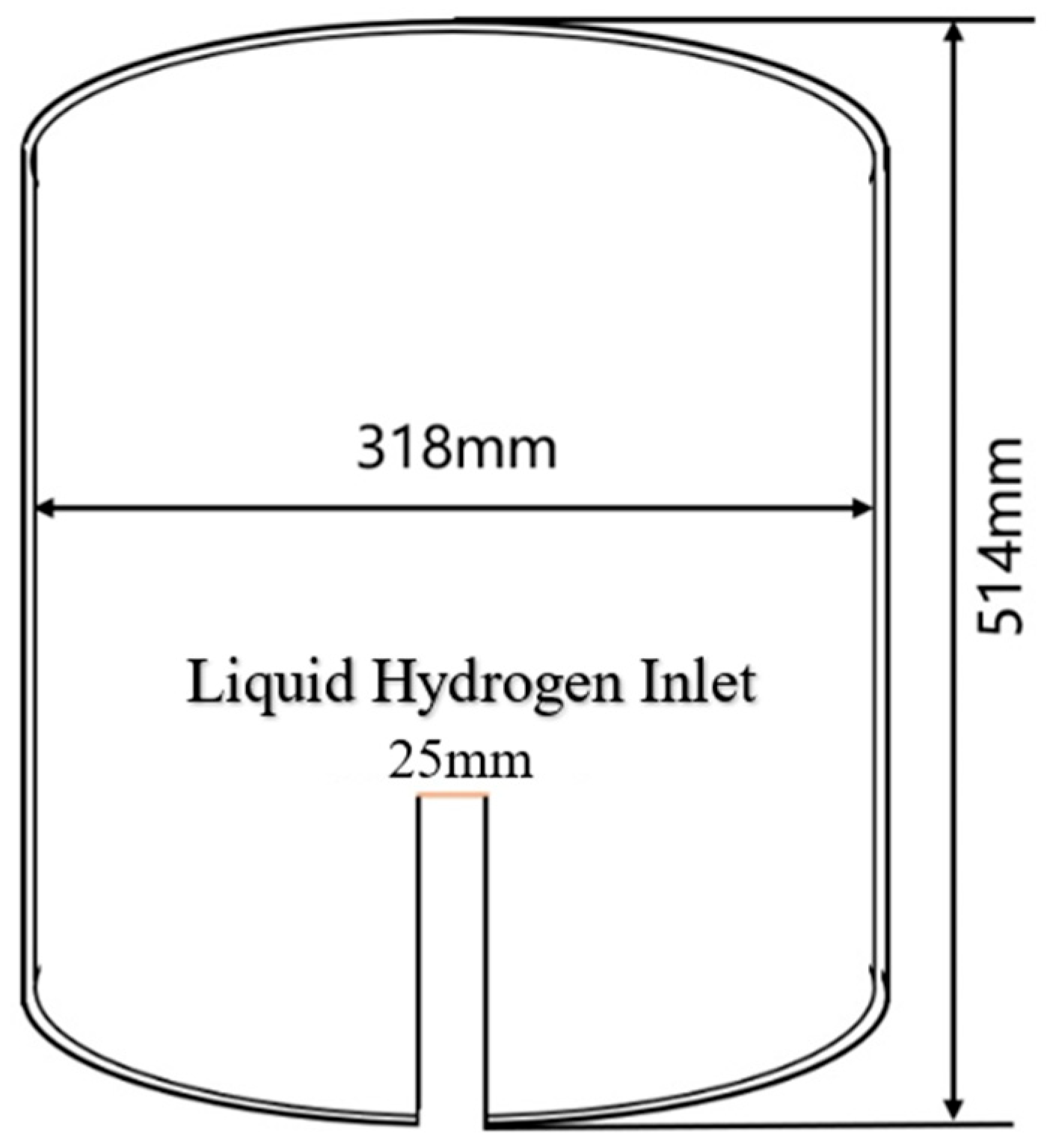
2.1. Geometric Modeling
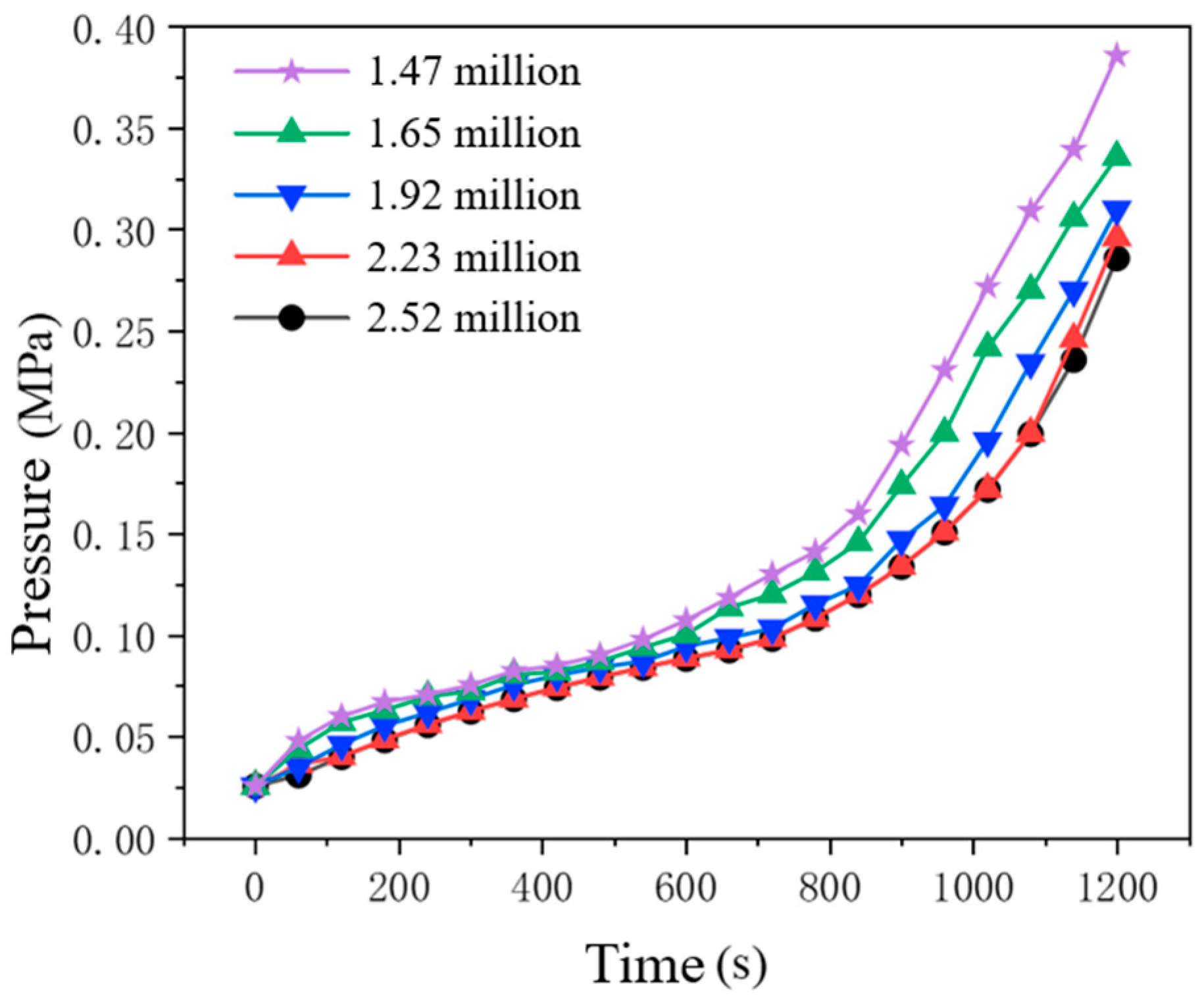
2.2. Meshing and Boundary Conditions
2.3. Thermophysical Properties
2.4. Model Development and UDF Programming
2.4.1. Fundamental Models
2.4.2. UDF Coupled Evaporation–Condensation and Flash Evaporation Models
3. Results and Discussion
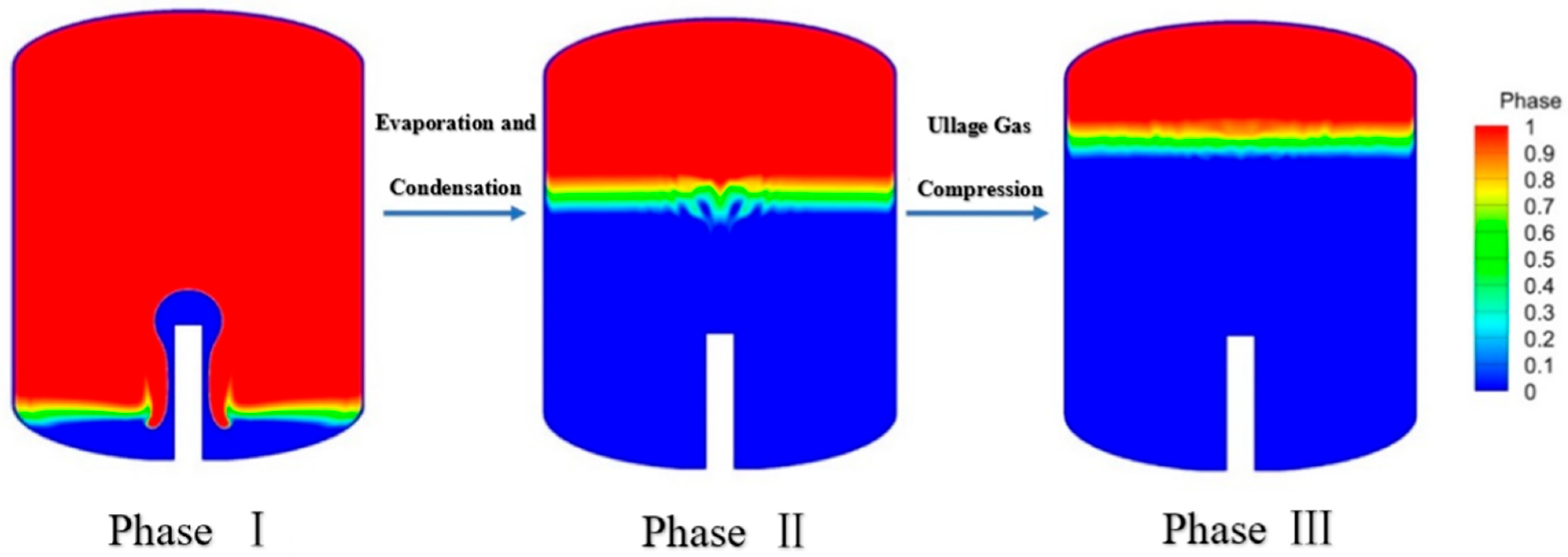
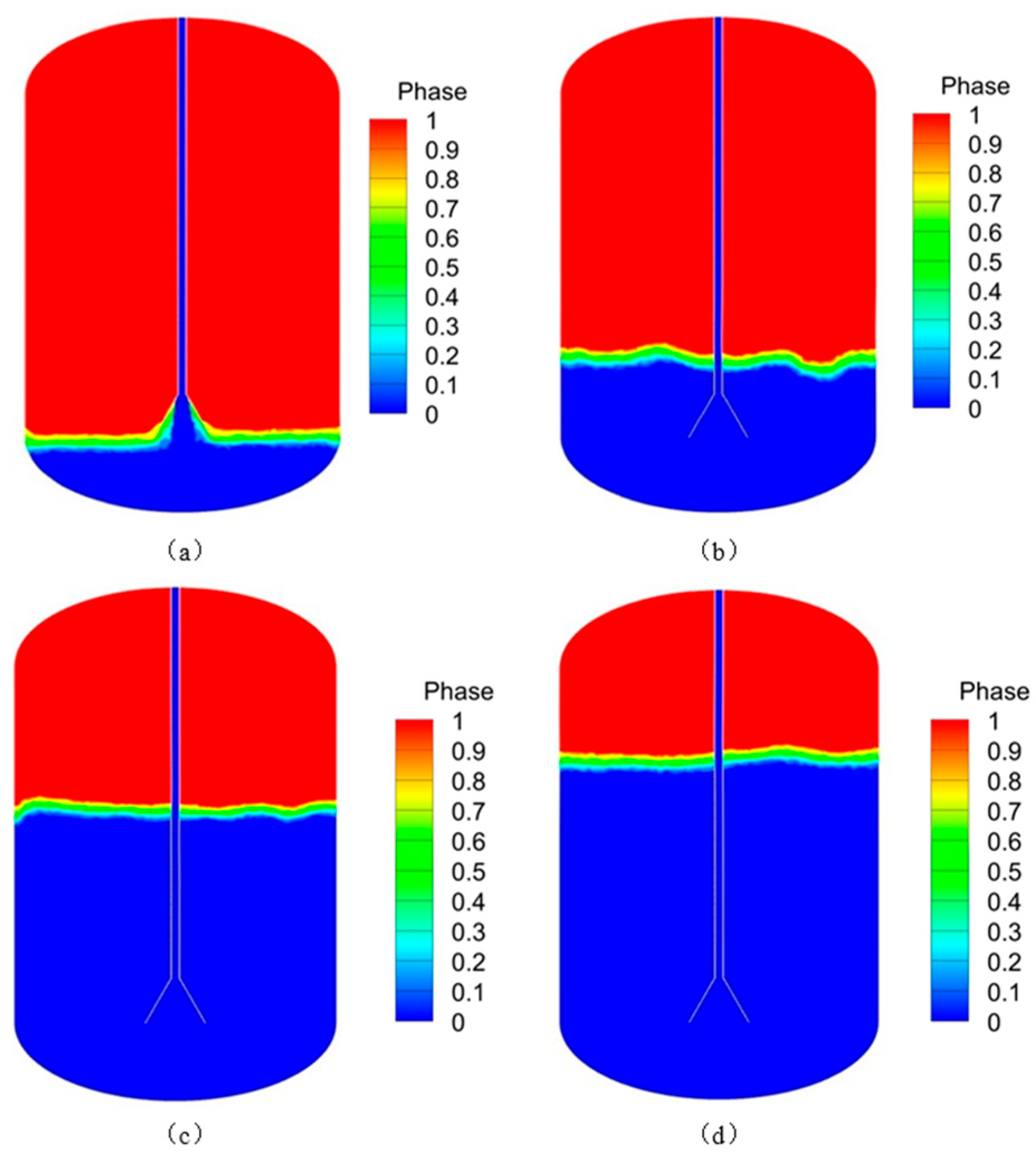
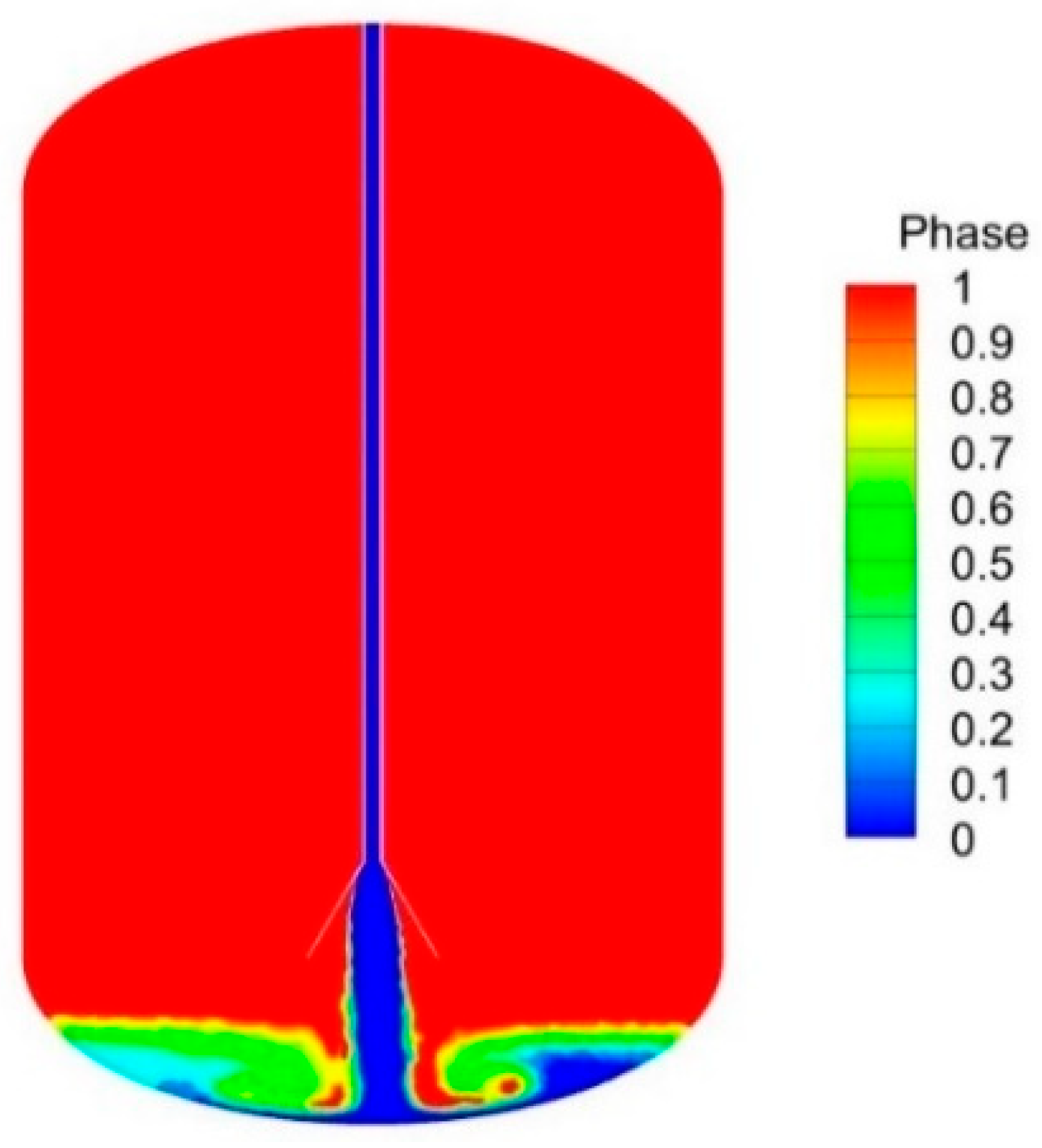
3.1. Model Validation and Comparative Analysis
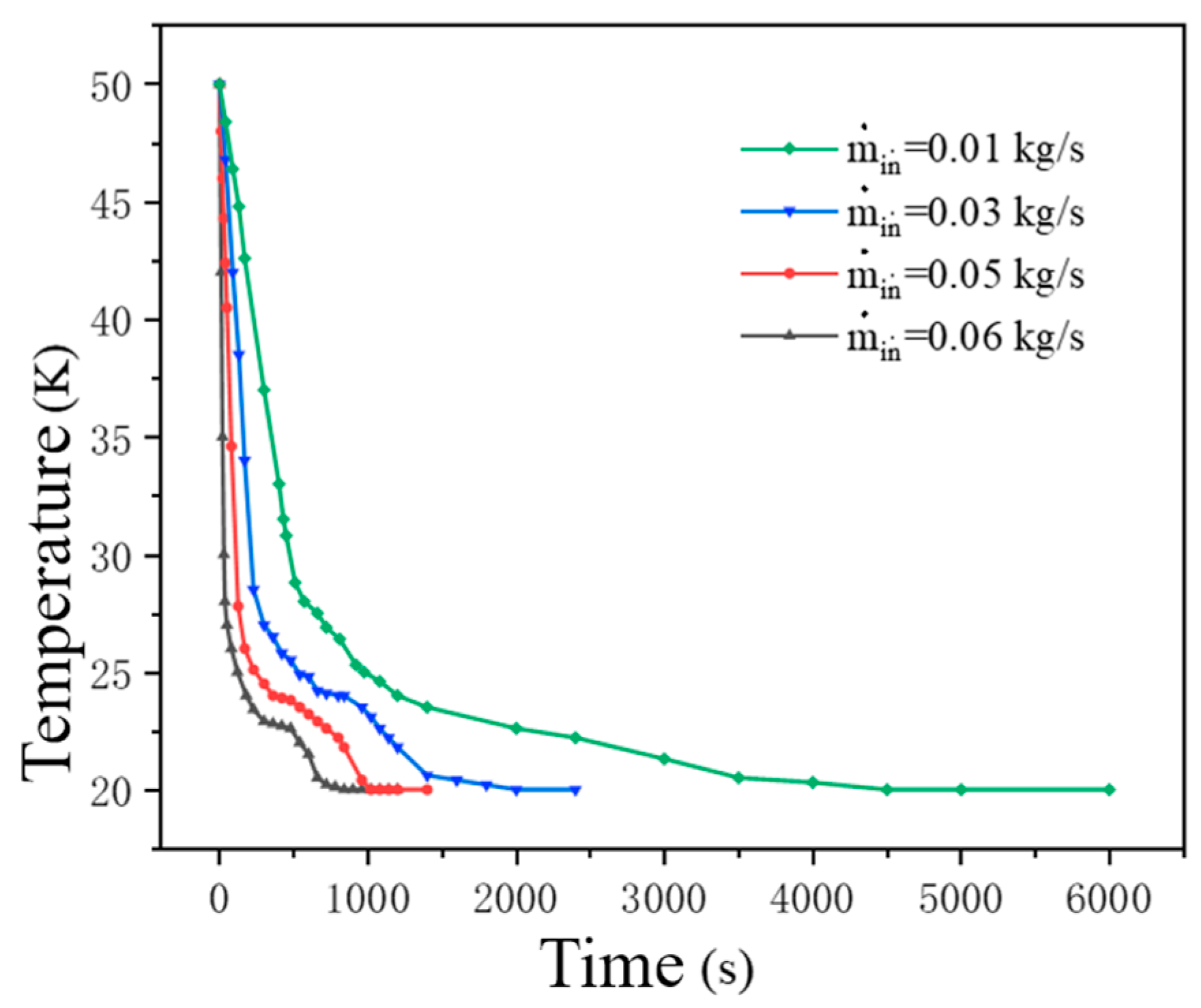
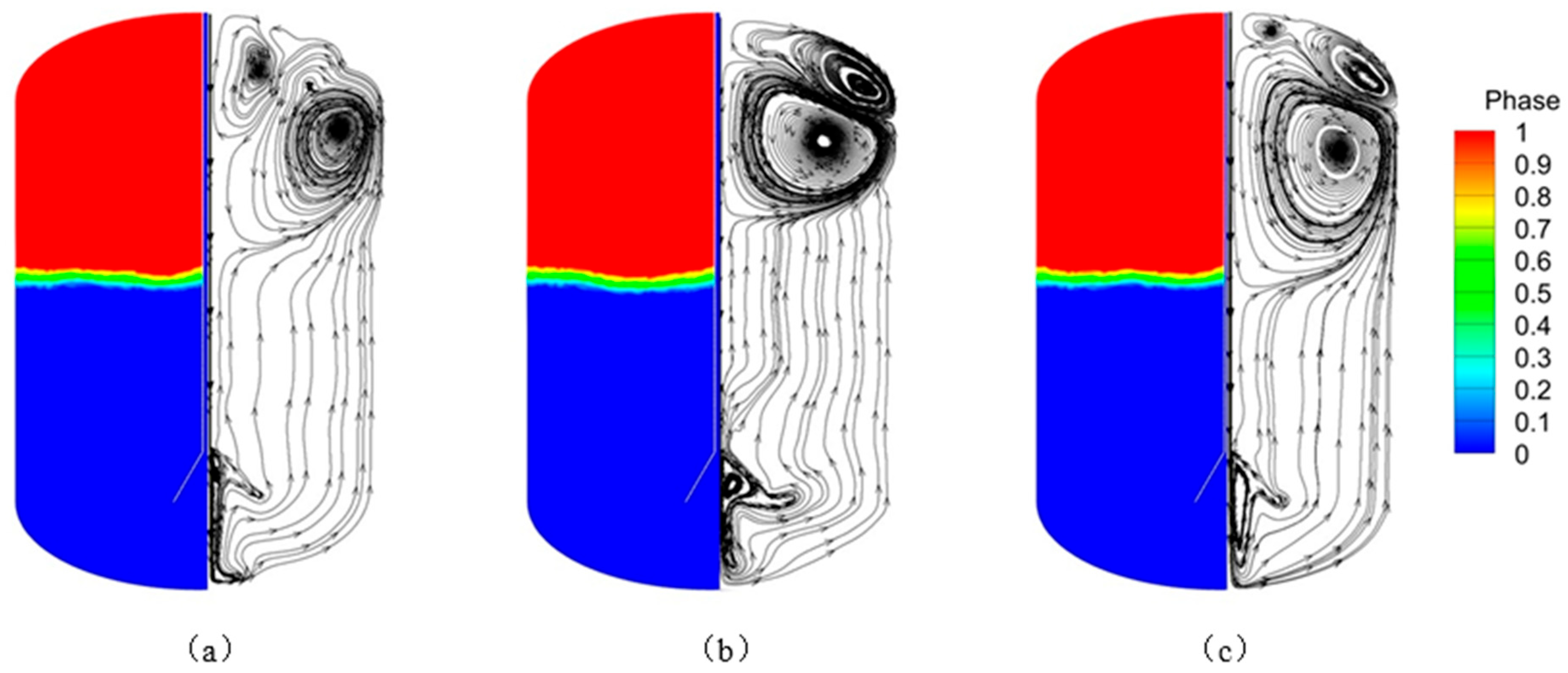
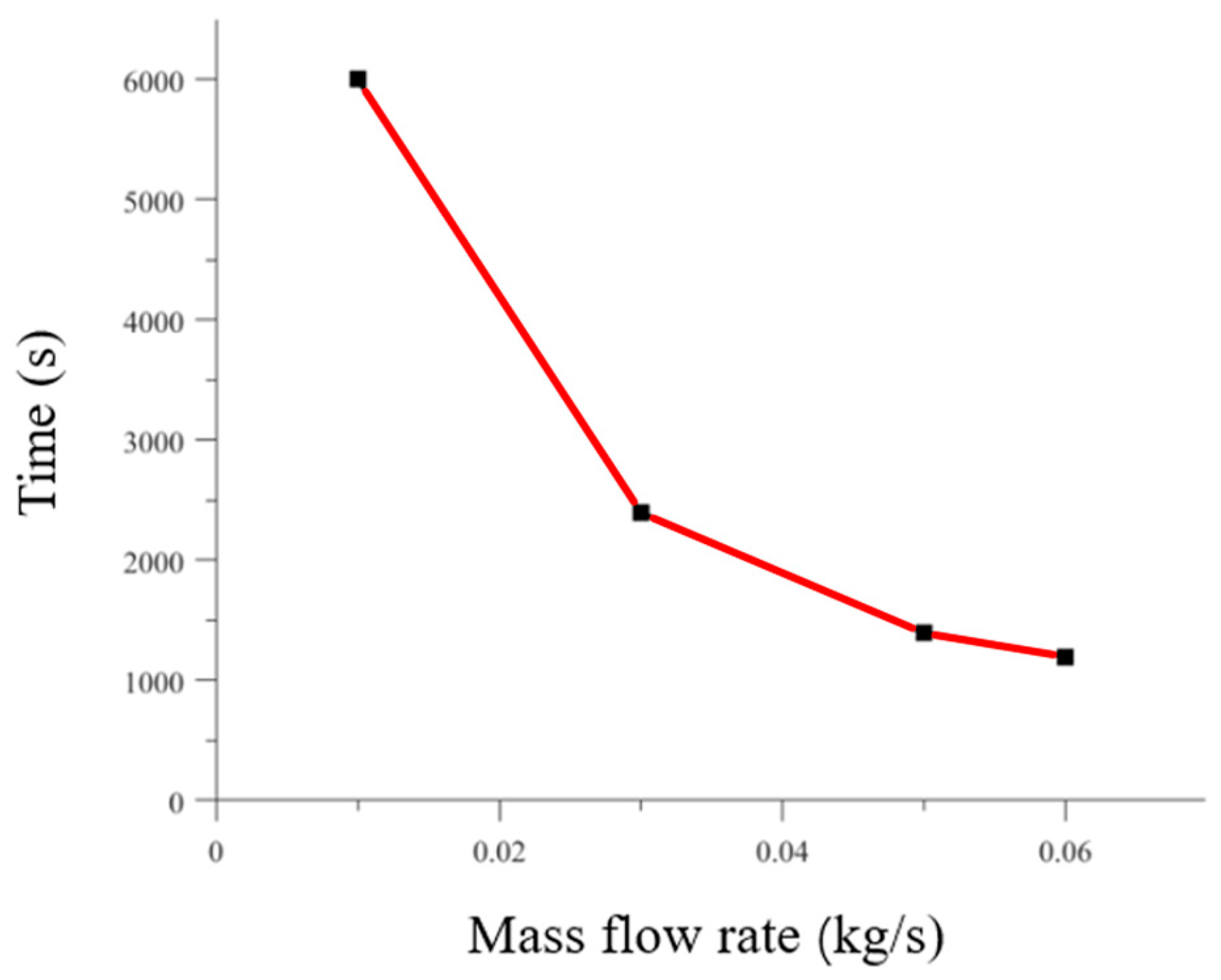
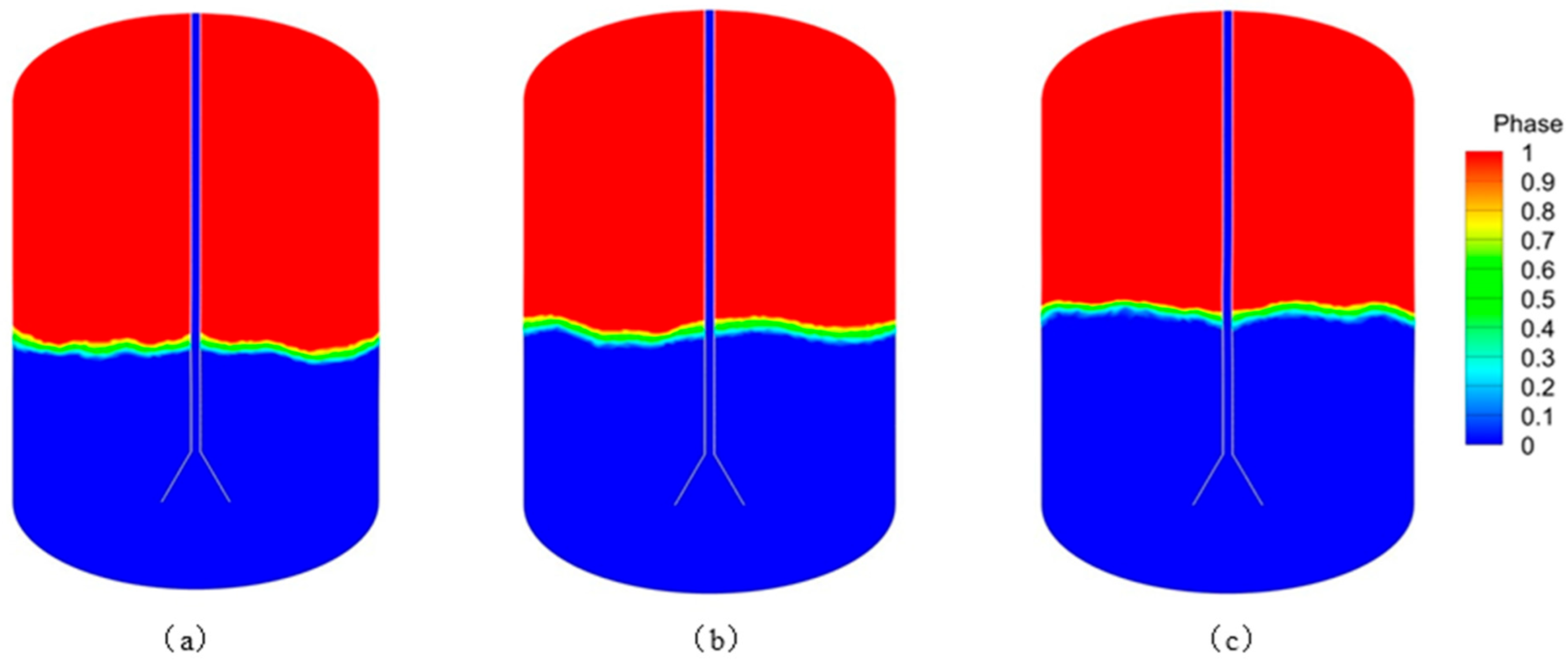
3.2. The Effect of Mass Flow on Tank Filling
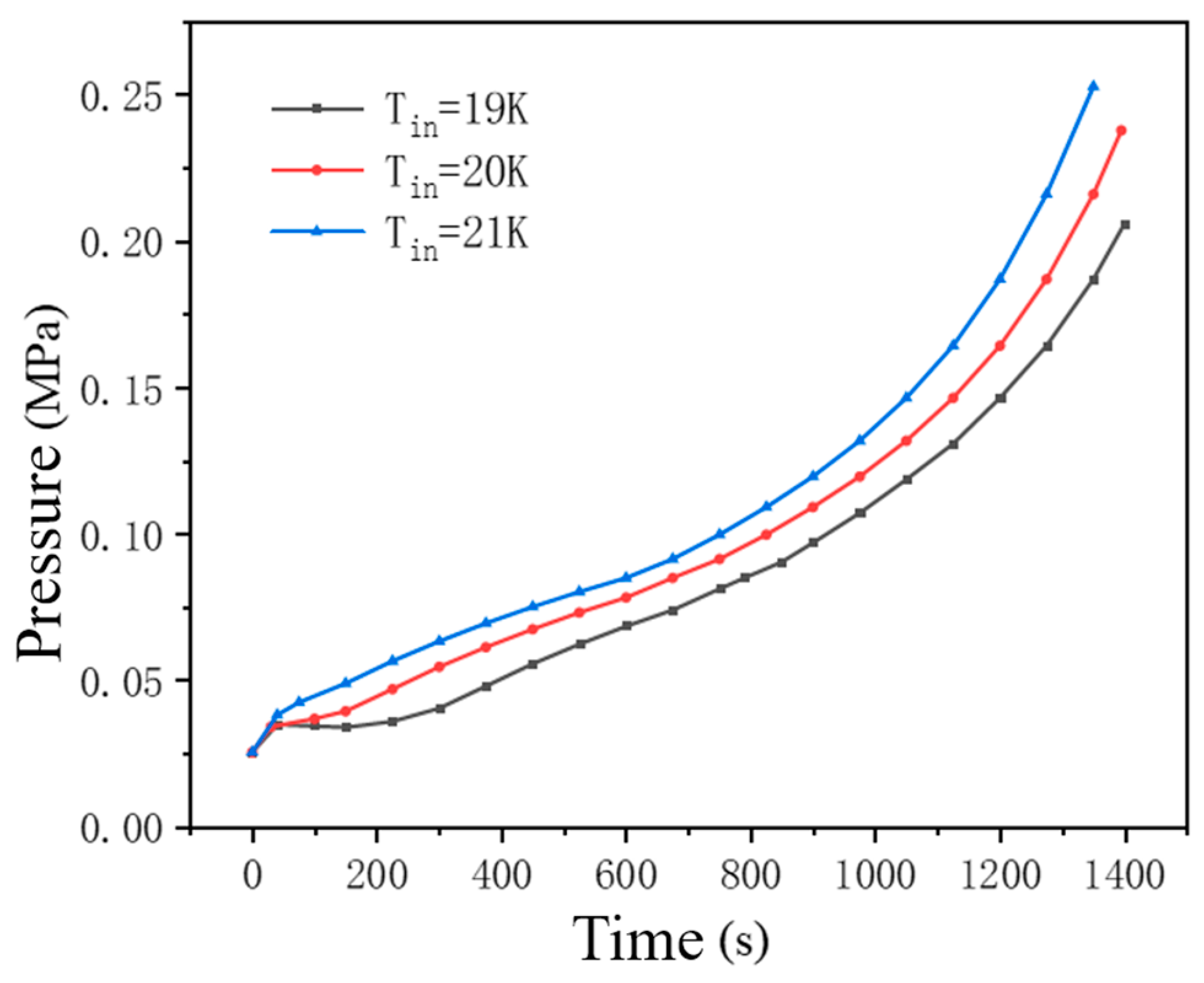
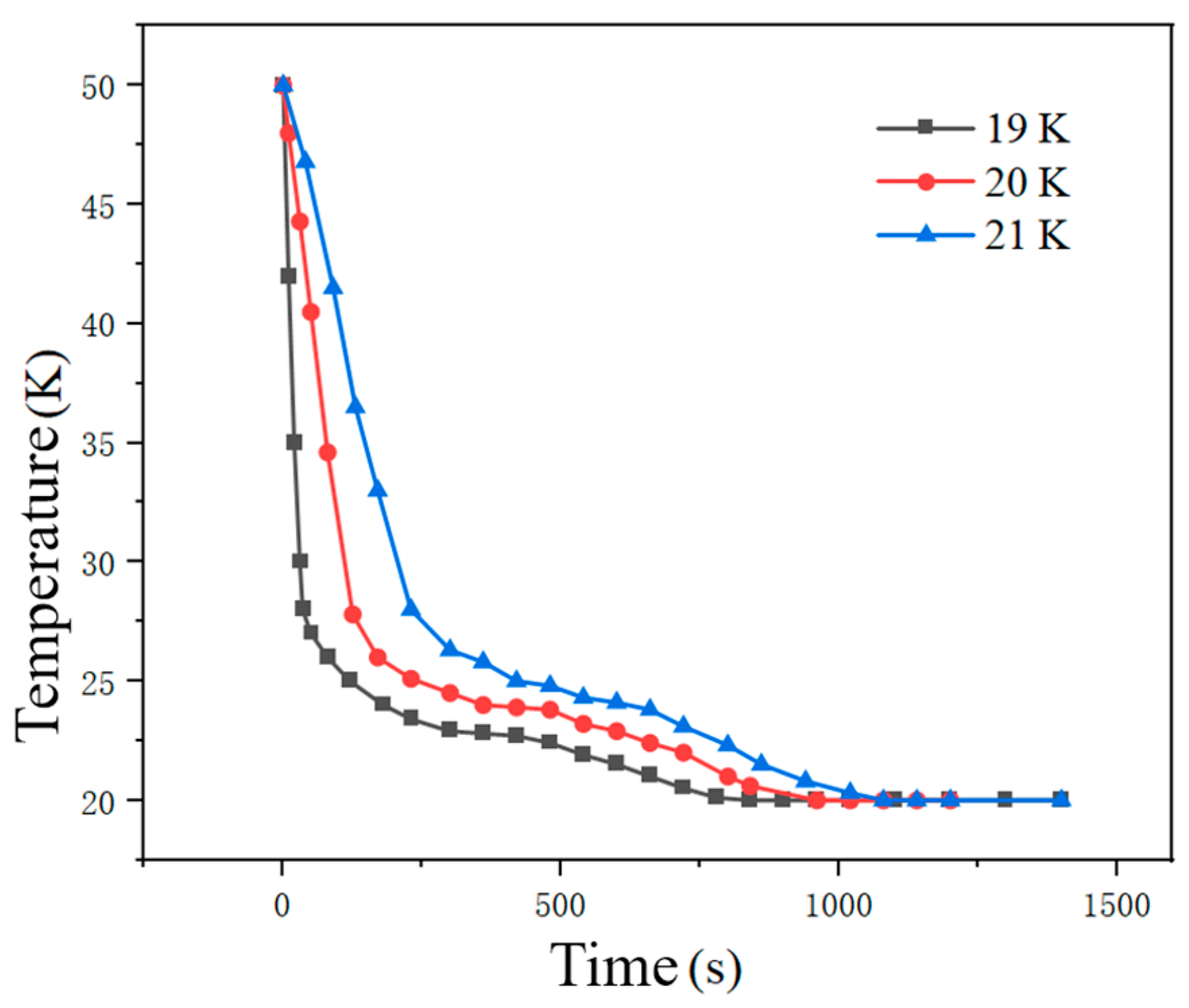
3.3. The Effect of Inlet Liquid Hydrogen Temperature on Tank Filling
4. Conclusions
- (1)
- Validation of the validity of CFD models
- (2)
- The influence mechanism of mass flow
- (3)
- Mechanism of influence of inlet temperature
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| UDF | User-Defined Function |
| LH2 | Liquid Hydrogen |
| m-t method | Mass-Time method |
| LNG | Liquefied Natural Gas |
| BOG | Boil-Off Gas |
| CSF | Continuum Surface Force |
| VOF | Volume of Fluid |
| GRS | Geometric Reconstruction Scheme |
References
- Zhang, T.; Uratani, J.; Huang, Y.; Xu, L.; Griffiths, S.; Ding, Y. Hydrogen liquefaction and storage: Recent progress and perspectives. Renew. Sustain. Energy Rev. 2023, 176, 113204. [Google Scholar] [CrossRef]
- Ma, H.; Sun, Z.; Xue, Z.; Zhang, C.; Chen, Z. A systemic review of hydrogen supply chain in energy transition. Front. Energy 2023, 17, 102–122. [Google Scholar] [CrossRef]
- Beschkov, V.; Ganev, E. Perspectives on the development of technologies for hydrogen as a carrier of sustainable Energy. Energies 2023, 16, 6108. [Google Scholar] [CrossRef]
- Minkin, H.L.; Hobart, H.F. Liquid-Hydrogen-Flowmeter Calibration Facility; Preliminary Calibrations on Some Head-Type and Turbine-Type Flowmeters; National Aeronautics and Space Administration: New York, NY, USA, 1961. [Google Scholar]
- Jin, T.; Tian, H.; Gao, X.; Liu, Y.; Wang, J.; Chen, H.; Lan, Y. Simulation and performance analysis of the perforated plate flowmeter for liquid hydrogen. Int. J. Hydrogen Energy 2017, 42, 3890–3898. [Google Scholar] [CrossRef]
- Schakel, M.D.; van der Beek, M.P.; Rahneberg, I.; Schleichert, J.; Einenkel, T.; Rogge, N.; Fröhlich, T. Improvements to the primary LNG mass flow standard. In Proceedings of the 18th Flow Measurement Conference, Lisbon, Portugal, 26–28 June 2019; LNEC: Lisbon, Portugal, 2019. [Google Scholar]
- Schakel, M.D.; Kerkhof, O.; van der Beek, M.P.; van den Herik, P.; van Hof, R.; Lucas, P.; Wulffers, S. LNG mid-scale loop flow metering–preliminary test results. In Proceedings of the 18th Flow Measurement Conference, Lisbon, Portugal, 26–28 June 2019; LNEC: Lisbon, Portugal, 2019. [Google Scholar]
- Kenbar, A.; Schakel, M. Influence of flow disturbances on the performance of industry-standard LNG flow meters. Flow Meas. Instrum. 2021, 77, 101871. [Google Scholar] [CrossRef]
- Kang, D.; Yun, S.; Kim, B.K.; Kim, J.; Kim, G.; Lee, H.; Choi, S. Numerical Investigation of the Initial Charging Process of the Liquid Hydrogen Tank for Vehicles. Energies 2022, 16, 38. [Google Scholar] [CrossRef]
- Fester, D.A.; Page, G.R.; Bingham, P.E. Liquid fluorine no-vent loading studies. J. Spacecr. Rocket. 1970, 7, 181–185. [Google Scholar] [CrossRef]
- Moran, M.E.; Nyland, T.W.; Papell, S.S. Liquid Transfer Cryogenic Test Facility: Initial Hydrogen and Nitrogen No-Vent Fill Data; National Aeronautics and Space Administration: Washington, DC, USA, 1990. [Google Scholar]
- Moran, M.E.; Nyland, T.W.; Driscoll, S.L. Hydrogen No-Vent Fill Testing in a 1.2 Cubic Foot (34 Liter) Tank; National Aeronautics and Space Administration: New York, NY, USA, 1991. [Google Scholar]
- Chato, D.J. Ground testing on the nonvented fill method of orbital propellant transfer: Results of initial test series. In Proceedings of the 27th Joint Propulsion Conference Exhibit, Sacramento, CA, USA, 24–27 June 1991; American Institute of Aeronautics and Astronautics: Sacramento, CA, USA, 1991. [Google Scholar]
- Flachbart, R.H.; Hedayat, A.; Holt, K.A. Modeling and test data analysis of a tank rapid chill and fill system for the advanced shuttle upper stage (ASUS) concept. AIP Conf. Proc. Wis. 2002, 613, 1284–1291. [Google Scholar]
- Wang, C.; Wang, R. The effects of vertical and horizontal placement on no-vent fill of cryogenic insulated vessels. Cryogenics 2010, 50, 480–485. [Google Scholar] [CrossRef]
- Ma, Y.; Zhu, K.; Li, Y.; Xie, F. Numerical investigation on chill-down and thermal stress characteristics of a LH2 tank during ground filling. Int. J. Hydrogen Energy 2020, 45, 25344–25356. [Google Scholar] [CrossRef]
- Xia, M.; Yuan, W.; Zhang, Q.; Zheng, Y.; Li, P.; Chen, J.; Xie, J. Experimental and numerical analysis of the chill-down process of a large horizontal cryogenic storage tank. Appl. Therm. Eng. 2023, 234, 121246. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Y.; Liu, Y.; Li, Y. Effect of gas injection mass flow rates on the thermal behavior in a cryogenic fuel storage tank. Int. J. Hydrogen Energy 2022, 47, 14703–14713. [Google Scholar] [CrossRef]
- Ayala, E.; Rivera, D.; Ronceros, J.; Vinces, N.; Ronceros, G. Design of a cryogenic duplex pressure-swirl atomizer through cfds for the cold conservation of marine products. Fluids 2023, 8, 271. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- McNaughton, D.J.; Vet, R.J. Eulerian model evaluation field study (EMEFS): A summary of surface network measurements and data quality. Atmos. Environ. 1996, 30, 227–238. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Zhu, X.; Pan, X.; Ma, J.; Mei, Y.; Tang, H.; Zhu, Y.; Liu, L.; Jiang, J.; Chen, T. Dynamic behaviors of in-tank subcooled liquid with depressurization-induced phase change and the impact on primary breakup of flashing jet. Int. J. Therm. Sci. 2023, 186, 108118. [Google Scholar] [CrossRef]
- Majumdar, A.; LeClair, A.; Hartwig, J.; Ghiaasiaan, S.M. Numerical modeling of no vent filling of a cryogenic tank with thermodynamic vent system augmented injector. Cryogenics 2023, 131, 103651. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Y.; Zhu, K.; Wang, Y.; Wang, L.; Tan, H. Investigation on no-vent filling process of liquid hydrogen tank under microgravity condition. Int. J. Hydrogen Energy 2017, 42, 8264–8277. [Google Scholar] [CrossRef]
- Gaertner, J.W.; Kronenburg, A.; Rees, A.; Sender, J.; Oschwald, M.; Lamanna, G. Numerical and experimental analysis of flashing cryogenic nitrogen. Int. J. Multiph. Flow 2020, 130, 103360. [Google Scholar] [CrossRef]
- Aydelott, J.C. Effect of Gravity on Self-Pressurization of SPHERICAL liquid-Hydrogen Tankage; National Aeronautics and Space Administration: New York, NY, USA, 1967. [Google Scholar]


| Completion Time | Institution | Working Medium | Principle | Operating Temperature (°C) | Flow Range (kg/s) | Uncertainty |
|---|---|---|---|---|---|---|
| About 1960 | NASA | Liquid Hydrogen | Volumetric Method | −253~−251 | 0.022~0.45 | 0.25% |
| About 1974 | TNO | Liquid Hydrogen | m-t Method | −253~−251 | /~1.062 | 0.4% |
| 2014 | Kyoto University | Liquid Hydrogen | m-t Method | −252~−249 | / | / |
| About 1960 | NASA | Slush Hydrogen | Volumetric Method | −253~−240 | / | 1~2% |
| 2004 | Tohoku University | Slush Hydrogen | Volumetric Method | −253~−240 | / | / |
| 2012 | VSL | LNG | m-t Method | −175~−123 | 0.625~3.12 | 0.12~0.15% |
| 2018 | VSL | LNG | Master Meter Method | −175~−123 | 0.625~25 | 0.17% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wei, Q.; Yu, L.; Zhang, X.; Zou, Y.; Zhu, Y.; Peng, Y.; Wang, D.; Zhu, Z.; Chen, X.; et al. Numerical Study of Liquid Hydrogen Internal Flow in Liquid Hydrogen Storage Tank. Energies 2025, 18, 5592. https://doi.org/10.3390/en18215592
Li X, Wei Q, Yu L, Zhang X, Zou Y, Zhu Y, Peng Y, Wang D, Zhu Z, Chen X, et al. Numerical Study of Liquid Hydrogen Internal Flow in Liquid Hydrogen Storage Tank. Energies. 2025; 18(21):5592. https://doi.org/10.3390/en18215592
Chicago/Turabian StyleLi, Xiang, Qun Wei, Lianyan Yu, Xiaobin Zhang, Yiting Zou, Yongcheng Zhu, Yanbo Peng, Daolin Wang, Zexian Zhu, Xianlei Chen, and et al. 2025. "Numerical Study of Liquid Hydrogen Internal Flow in Liquid Hydrogen Storage Tank" Energies 18, no. 21: 5592. https://doi.org/10.3390/en18215592
APA StyleLi, X., Wei, Q., Yu, L., Zhang, X., Zou, Y., Zhu, Y., Peng, Y., Wang, D., Zhu, Z., Chen, X., Zhao, Y., Tu, C., & Bao, F. (2025). Numerical Study of Liquid Hydrogen Internal Flow in Liquid Hydrogen Storage Tank. Energies, 18(21), 5592. https://doi.org/10.3390/en18215592








