Flow–Solid Coupled Analysis of Shale Gas Production Influenced by Fracture Roughness Evolution in Supercritical CO2–Slickwater Systems
Abstract
1. Introduction
2. Effect of Supercritical CO2 and Slickwater on Shale Fracture Aperture
2.1. Experimental Equipment and Methods
2.2. Shale Fracture Aperture Variation
3. Numerical Simulation Methods
3.1. Theoretical Model
3.1.1. Model Hypothesis
3.1.2. Non-Linear Medium Models
3.1.3. Shale Fracture Roughness Model
3.1.4. Controlling Equations for Shale Matrix Deformation
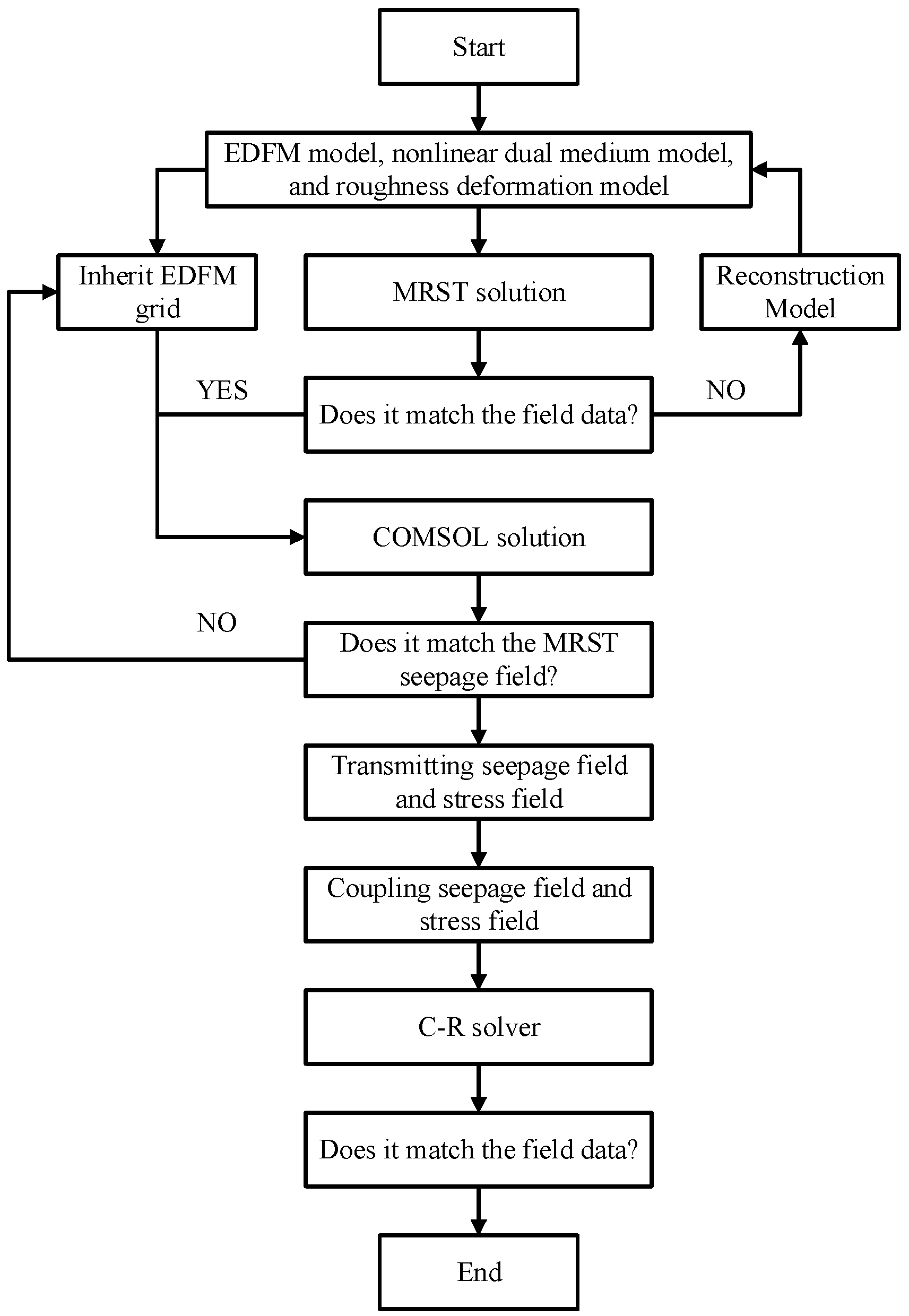
3.1.5. Coupled Solution Methods
3.2. Geometrical Modelling and Boundary Conditions
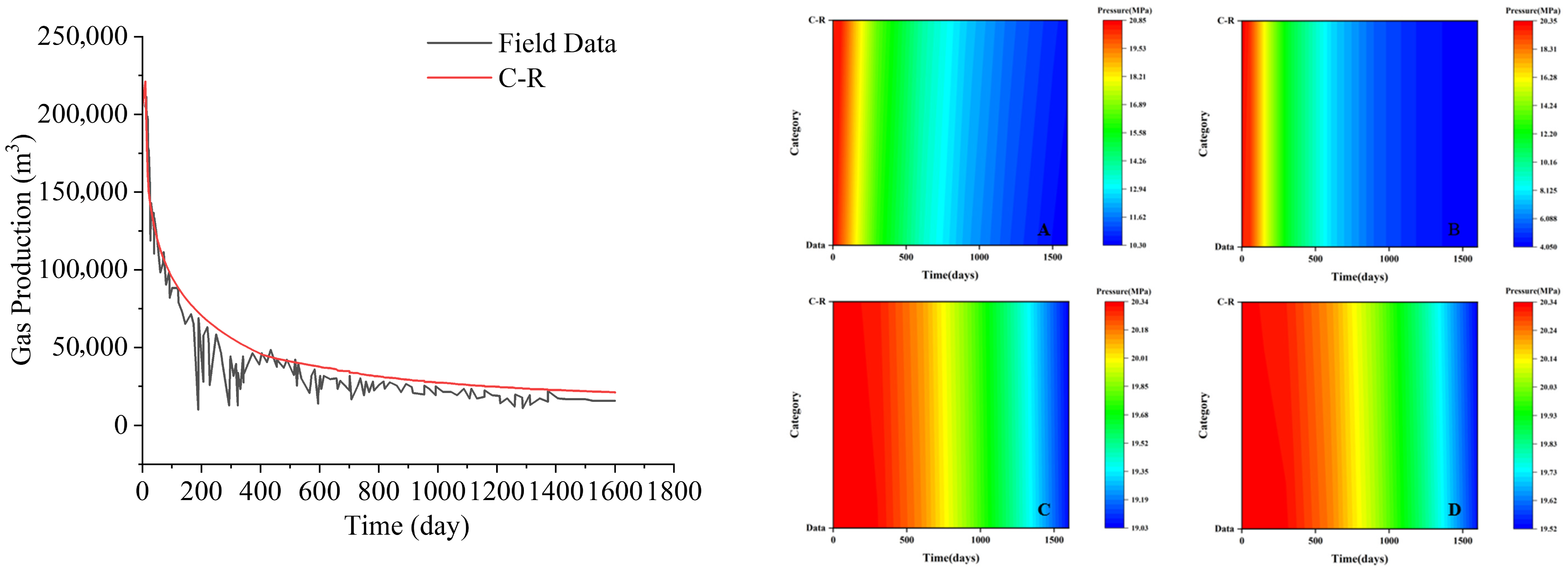
3.3. Validation of the Model
4. Results
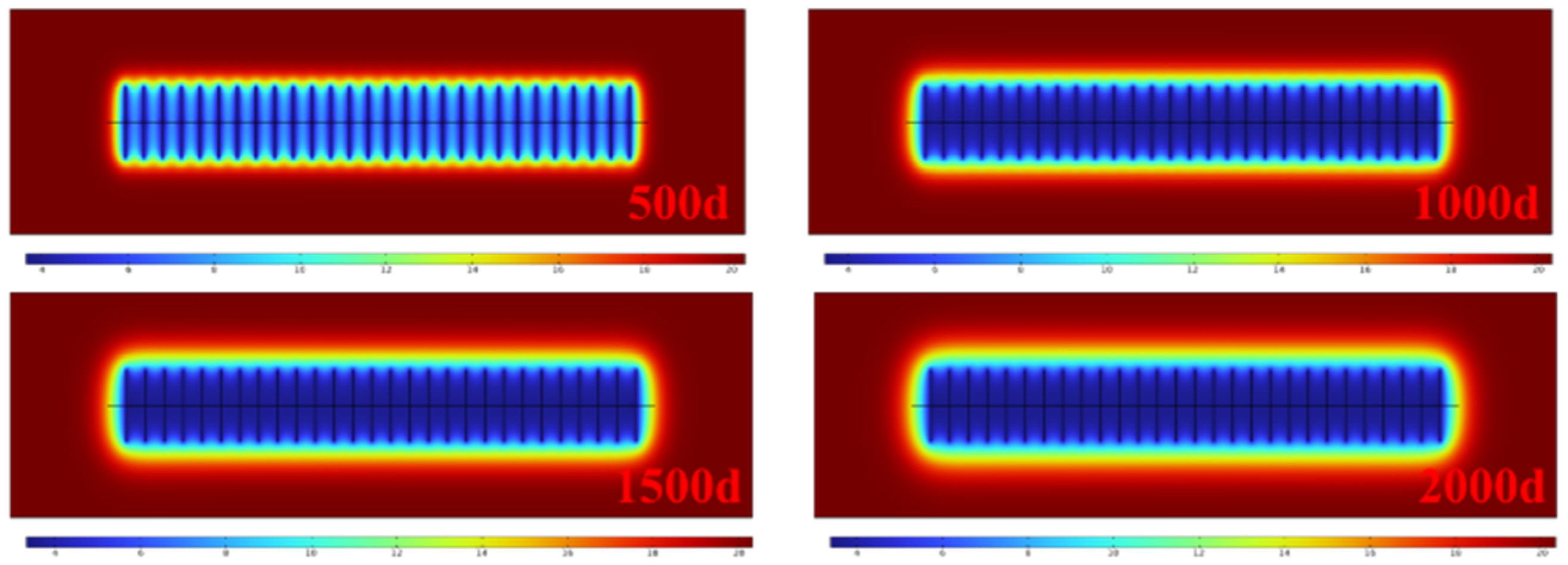
4.1. Reservoir Pressure Evolution
4.2. Multiple Strain Evolution
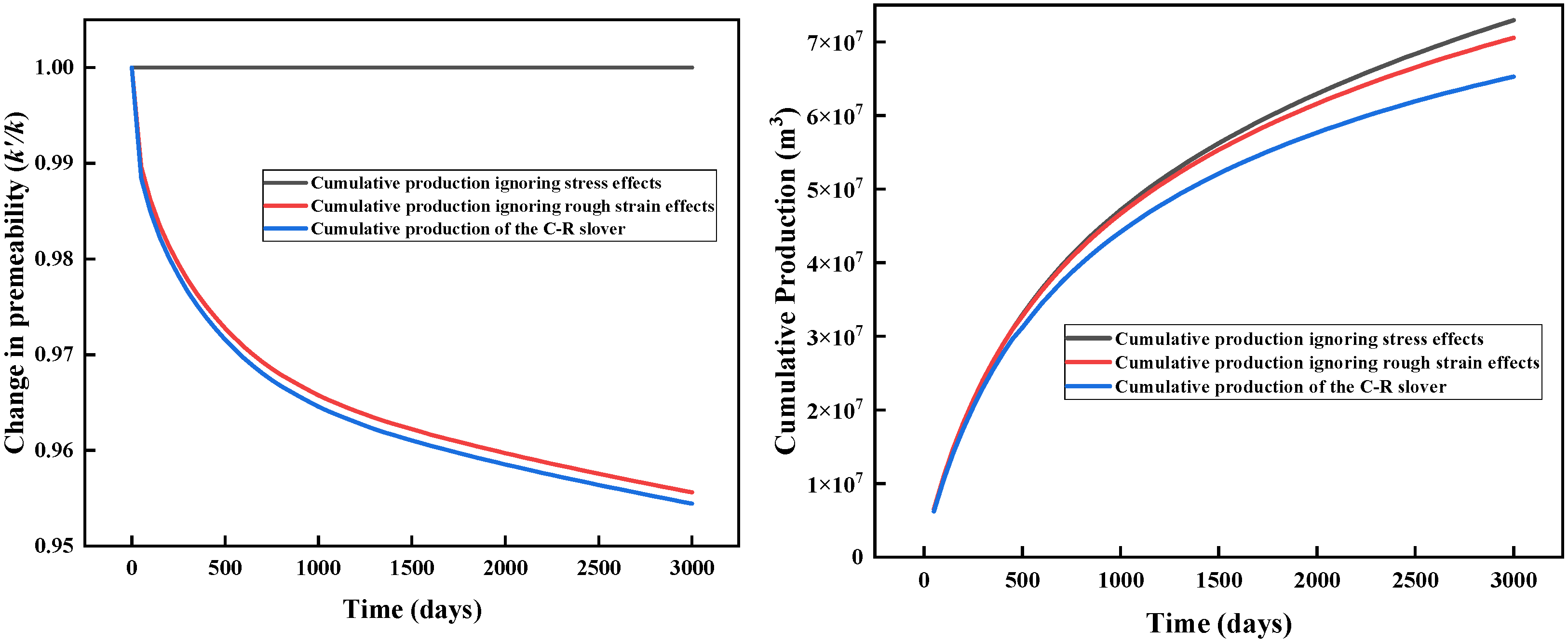
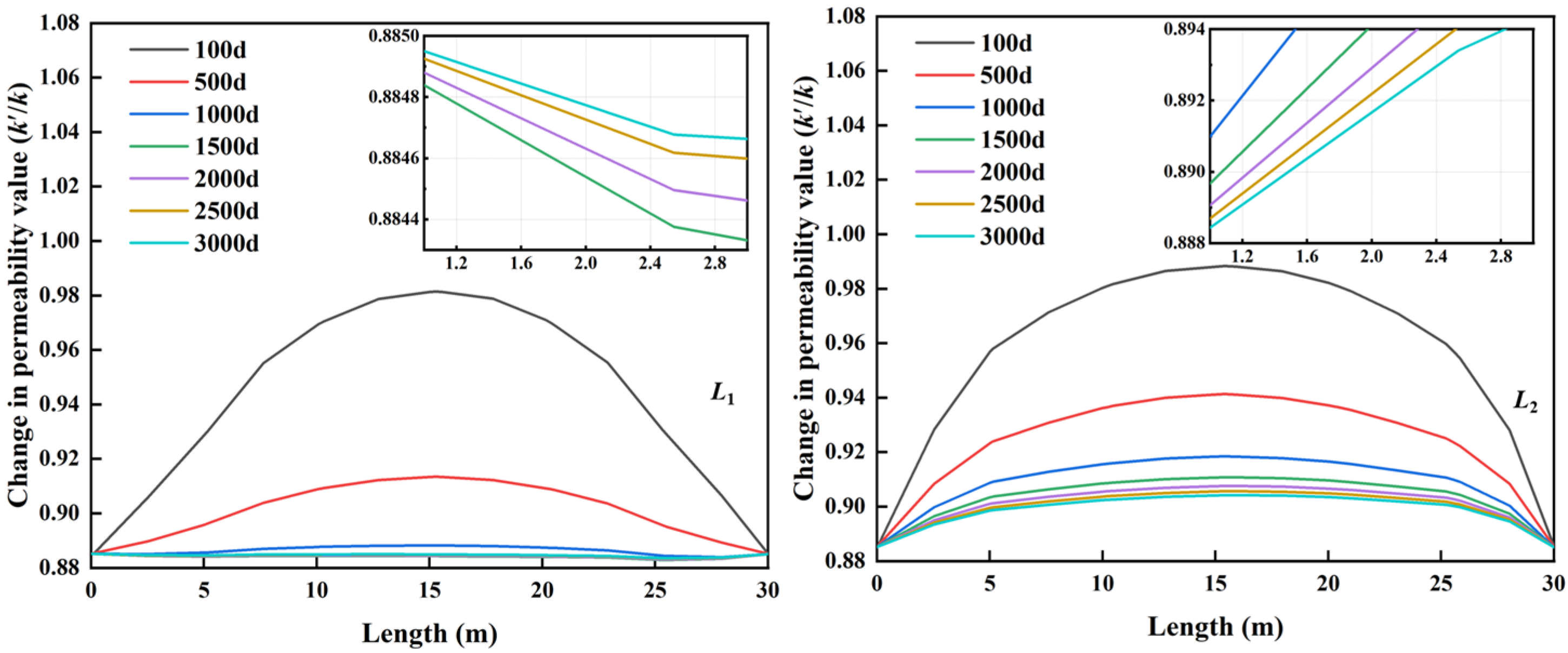
4.3. Permeability Evolution
4.4. Roughness Effects
5. Discussion
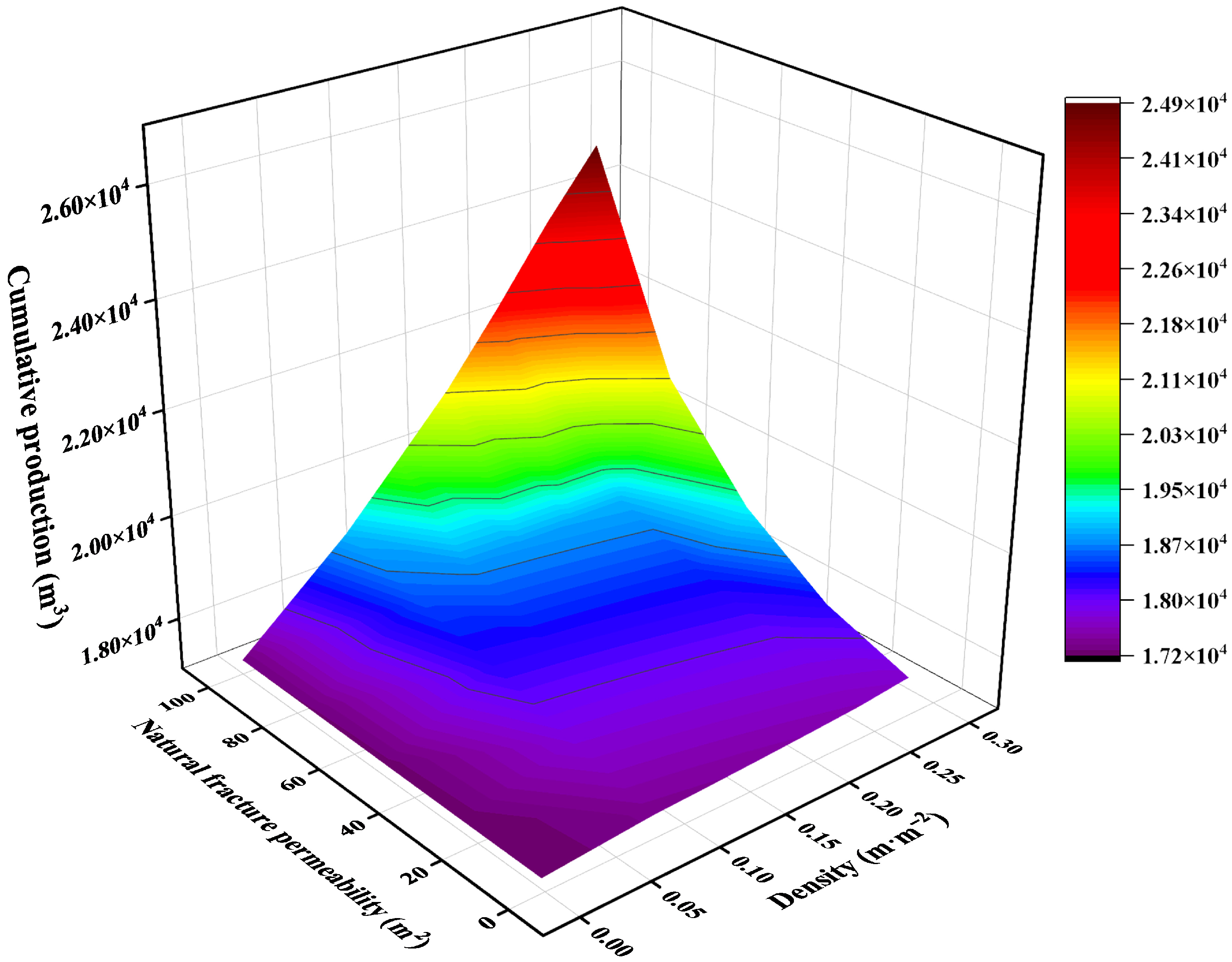
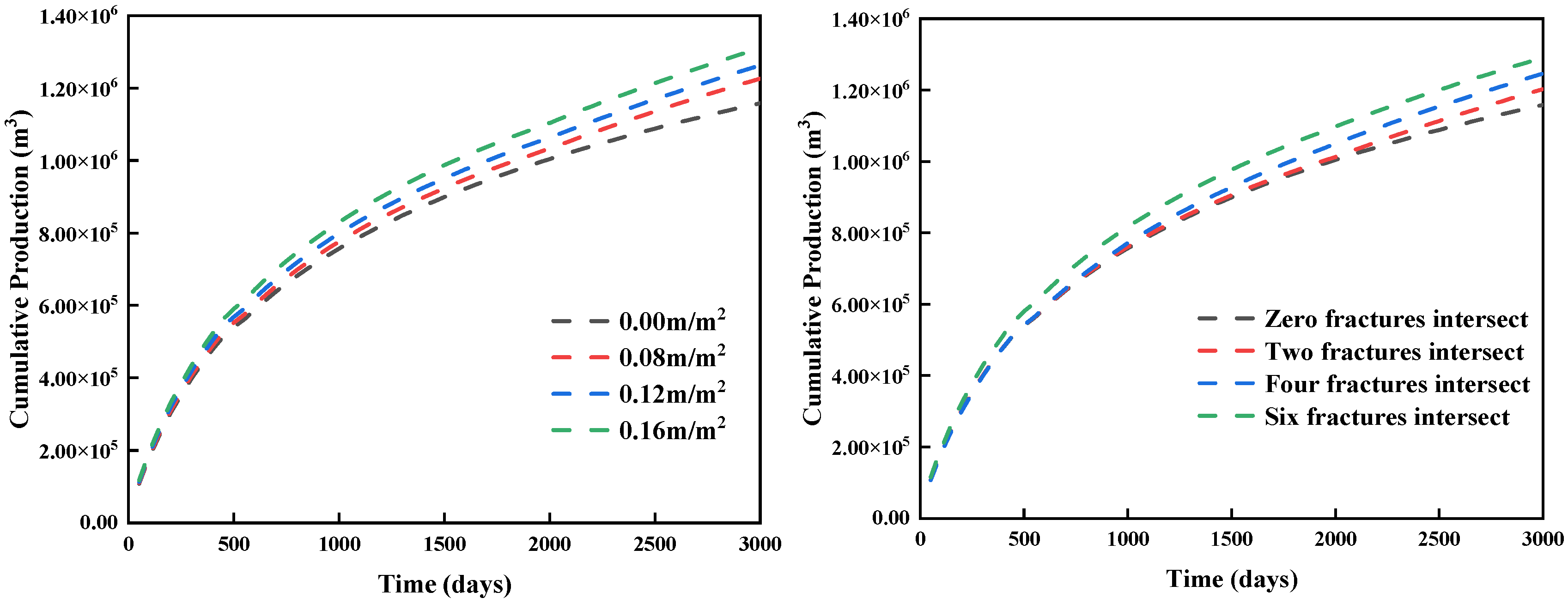
5.1. Effect of Fracture Characteristics on Yield
5.1.1. Fracture Permeability and Fracture Density
5.1.2. Fracture Density and Fracture Inclination
5.1.3. Fracture Permeability and Fracture Inclination Angle
5.1.4. Analysis of the Weighting of Factors
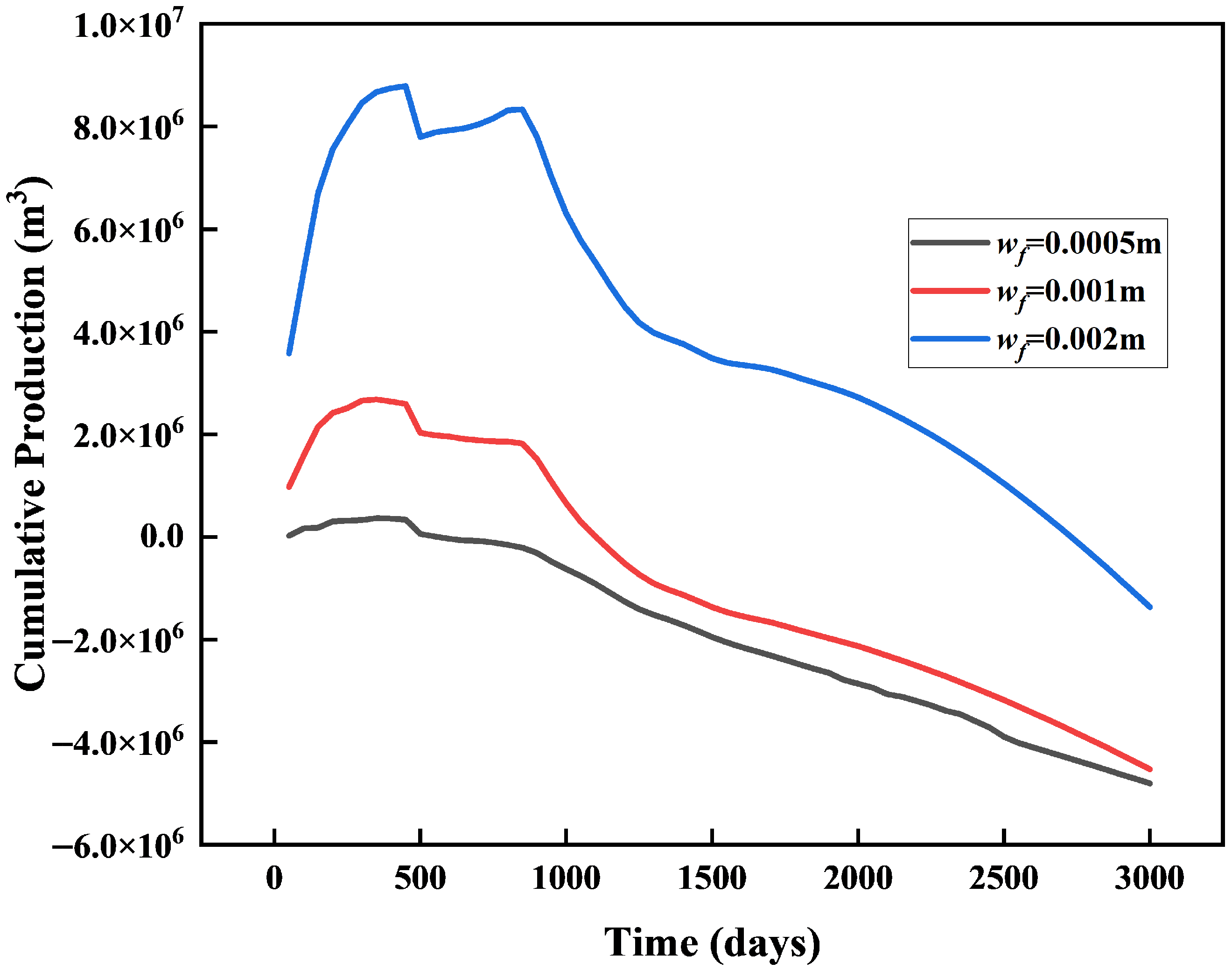
5.2. Extraction Methods’ Impact on Yield
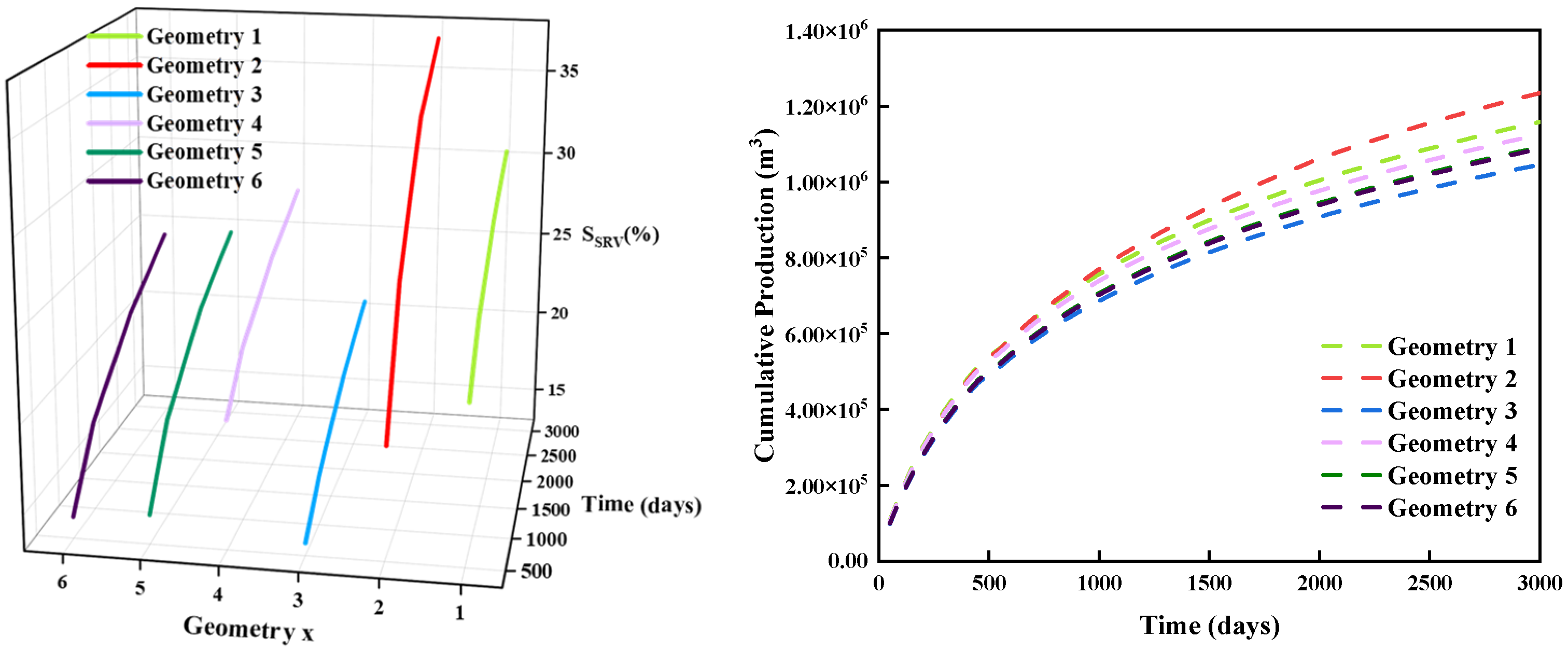
5.2.1. Effect of Hydraulic Fracture Geometry
5.2.2. Effect of Complex Fracture Geometry
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, B.; Wang, H.-Z.; Li, G.-S.; Wang, B.; Chang, L.; Tian, G.-H.; Zhao, C.-M.; Zheng, Y. Fundamental Study and Utilization on Supercritical CO2 Fracturing Developing Unconventional Resources: Current Status, Challenge and Future Perspectives. Pet. Sci. 2022, 19, 2757–2780. [Google Scholar] [CrossRef]
- Zou, C.; Zhao, Q.; Dong, D.; Yang, Z.; Qiu, Z.; Liang, F.; Wang, N.; Huang, Y.; Duan, A.; Zhang, Q.; et al. Geological Characteristics, Main Challenges and Future Prospect of Shale Gas. J. Nat. Gas Geosci. 2017, 2, 273–288. [Google Scholar] [CrossRef]
- Sun, C.; Nie, H.; Dang, W.; Chen, Q.; Zhang, G.; Li, W.; Lu, Z. Shale Gas Exploration and Development in China: Current Status, Geological Challenges, and Future Directions. Energy Fuels 2021, 35, 6359–6379. [Google Scholar] [CrossRef]
- Prasad, S.K.; Sangwai, J.S.; Byun, H.-S. A Review of the Supercritical CO2 Fluid Applications for Improved Oil and Gas Production and Associated Carbon Storage. J. CO2 Util. 2023, 72, 102479. [Google Scholar] [CrossRef]
- Amer, M.W.; Alhesan, J.S.A.; Marshall, M.; Fei, Y.; Jackson, W.R.; Chaffee, A.L. Energy Efficient Method of Supercritical Extraction of Oil from Oil Shale. Energy Convers. Manag. 2022, 252, 115108. [Google Scholar] [CrossRef]
- Jia, B.; Tsau, J.-S.; Barati, R. A Review of the Current Progress of CO2 Injection EOR and Carbon Storage in Shale Oil Reservoirs. Fuel 2019, 236, 404–427. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, X.; Jha, A.N.; Rogers, H. Natural Gas from Shale Formation—The Evolution, Evidences and Challenges of Shale Gas Revolution in United States. Renew. Sustain. Energy Rev. 2014, 30, 1–28. [Google Scholar] [CrossRef]
- Aminu, M.D.; Nabavi, S.A.; Rochelle, C.A.; Manovic, V. A Review of Developments in Carbon Dioxide Storage. Appl. Energy 2017, 208, 1389–1419. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.; Chen, X.; Chen, X.; Wang, L. Increasing Permeability of Coal Seams Using the Phase Energy of Liquid Carbon Dioxide. J. CO2 Util. 2017, 19, 112–119. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Y.; Tang, J.; Zhou, Z.; Liao, Y. Experimental Study on Fracture Initiation and Propagation in Shale Using Supercritical Carbon Dioxide Fracturing. Fuel 2017, 190, 370–378. [Google Scholar] [CrossRef]
- Xie, W.; Chen, S.; Wang, M.; Yu, Z.; Wang, H. Progress and Prospects of Supercritical CO2 Application in the Exploitation of Shale Gas Reservoirs. Energy Fuels 2021, 35, 18370–18384. [Google Scholar] [CrossRef]
- Ozotta, O.; Kolawole, O.; Lamine Malki, M.; Ore, T.; Gentzis, T.; Fowler, H.; Liu, K.; Ostadhassan, M. Nano- to Macro-Scale Structural, Mineralogical, and Mechanical Alterations in a Shale Reservoir Induced by Exposure to Supercritical CO2. Appl. Energy 2022, 326, 120051. [Google Scholar] [CrossRef]
- Lu, Y.; Chen, X.; Tang, J.; Li, H.; Zhou, L.; Han, S.; Ge, Z.; Xia, B.; Shen, H.; Zhang, J. Relationship between Pore Structure and Mechanical Properties of Shale on Supercritical Carbon Dioxide Saturation. Energy 2019, 172, 270–285. [Google Scholar] [CrossRef]
- Zhang, S.; Sheng, J.J.; Shen, Z. Effect of Hydration on Fractures and Permeabilities in Mancos, Eagleford, Barnette and Marcellus Shale Cores under Compressive Stress Conditions. J. Pet. Sci. Eng. 2017, 156, 917–926. [Google Scholar] [CrossRef]
- Wang, B.; Liu, B.; Yang, J.; Bai, L.; Li, S. Compatibility Characteristics of Fracturing Fluid and Shale Oil Reservoir: A Case Study of the First Member of Qingshankou Formation, Northern Songliao Basin, Northeast China. J. Pet. Sci. Eng. 2022, 211, 110161. [Google Scholar] [CrossRef]
- Liu, J.; Ding, W.; Wang, R.; Yin, S.; Yang, H.; Gu, Y. Simulation of Paleotectonic Stress Fields and Quantitative Prediction of Multi-Period Fractures in Shale Reservoirs: A Case Study of the Niutitang Formation in the Lower Cambrian in the Cen’gong Block, South China. Mar. Pet. Geol. 2017, 84, 289–310. [Google Scholar] [CrossRef]
- Wang, L.; Yao, B.; Xie, H.; Winterfeld, P.H.; Kneafsey, T.J.; Yin, X.; Wu, Y.-S. CO2 Injection-Induced Fracturing in Naturally Fractured Shale Rocks. Energy 2017, 139, 1094–1110. [Google Scholar] [CrossRef]
- Figueiredo, B.; Tsang, C.-F.; Rutqvist, J.; Niemi, A. A Study of Changes in Deep Fractured Rock Permeability Due to Coupled Hydro-Mechanical Effects. Int. J. Rock Mech. Min. Sci. 2015, 79, 70–85. [Google Scholar] [CrossRef]
- Lu, C.; Lu, Y.; Gou, X.; Zhong, Y.; Chen, C.; Guo, J. Influence Factors of Unpropped Fracture Conductivity of Shale. Energy Sci. Eng. 2020, 8, 2024–2043. [Google Scholar] [CrossRef]
- Jang, H.-S.; Kang, S.-S.; Jang, B.-A. Determination of Joint Roughness Coefficients Using Roughness Parameters. Rock Mech. Rock Eng. 2014, 47, 2061–2073. [Google Scholar] [CrossRef]
- Lu, Y.; Zhou, J.; Li, H.; Tang, J.; Zhou, L.; Ao, X. Gas Flow Characteristics in Shale Fractures after Supercritical CO2 Soaking. J. Nat. Gas Sci. Eng. 2021, 88, 103826. [Google Scholar] [CrossRef]
- Wang, B.; Fidelibus, C. An Open-Source Code for Fluid Flow Simulations in Unconventional Fractured Reservoirs. Geosciences 2021, 11, 106. [Google Scholar] [CrossRef]
- Zhao, Y.; Borja, R.I. A Continuum Framework for Coupled Solid Deformation–Fluid Flow through Anisotropic Elastoplastic Porous Media. Comput. Methods Appl. Mech. Eng. 2020, 369, 113225. [Google Scholar] [CrossRef]
- Chen, J.; Xu, Z.; Leung, J.Y. Analysis of Fracture Interference—Coupling of Flow and Geomechanical Computations with Discrete Fracture Modeling Using MRST. J. Pet. Sci. Eng. 2022, 219, 111134. [Google Scholar] [CrossRef]
- Xu, Y. Calculation of Unsaturated Hydraulic Conductivity Using a Fractal Model for the Pore-Size Distribution. Comput. Geotech. 2004, 31, 549–557. [Google Scholar] [CrossRef]
- Li, W.; Liu, J.; Zeng, J.; Leong, Y.-K.; Elsworth, D.; Tian, J.; Li, L. A Fully Coupled Multidomain and Multiphysics Model for Evaluation of Shale Gas Extraction. Fuel 2020, 278, 118214. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, G.; Zhang, L.; Wei, Y.; Guo, J.; Chang, C. Numerical Simulation of Shale Gas Reservoirs Considering Discrete Fracture Network Using a Coupled Multiple Transport Mechanisms and Geomechanics Model. J. Pet. Sci. Eng. 2020, 195, 107588. [Google Scholar] [CrossRef]
- Ao, X.; Wang, B.; Rao, Y.; Zhang, L.; Wang, Y.; Tang, H. Effect of CO2 Corrosion and Adsorption-Induced Strain on Permeability of Oil Shale: Numerical Simulation. Energies 2023, 16, 780. [Google Scholar] [CrossRef]
- Du, F.; Wang, K. Unstable Failure of Gas-Bearing Coal-Rock Combination Bodies: Insights from Physical Experiments and Numerical Simulations. Process Saf. Environ. Prot. 2019, 129, 264–279. [Google Scholar] [CrossRef]
- Kong, X.; Wang, E.; Liu, Q.; Li, Z.; Li, D.; Cao, Z.; Niu, Y. Dynamic Permeability and Porosity Evolution of Coal Seam Rich in CBM Based on the Flow-Solid Coupling Theory. J. Nat. Gas Sci. Eng. 2017, 40, 61–71. [Google Scholar] [CrossRef]
- Kong, X. Advanced Seepage Mechanics, 3rd ed.; China University of Science and Technology Press: Hefei, China, 2020; ISBN 978 7312048371. [Google Scholar]
- Yang, S.-Q.; Song, Y.; Du, S.-G.; Huang, Y.-H.; Zhu, Z.-N. Experimental Study on Mechanical and Permeability Characteristics of Rock-Cement Interface in Ultra-Low Temperature Environment. Constr. Build. Mater. 2024, 451, 138790. [Google Scholar] [CrossRef]
- Li, G.; Li, G.; Luo, C.; Zhou, R.; Zhou, J.; Yang, J. Dynamic Evolution of Shale Permeability under Coupled Temperature and Effective Stress Conditions. Energy 2023, 266, 126320. [Google Scholar] [CrossRef]
- Sheng, G.; Javadpour, F.; Su, Y. Dynamic Porosity and Apparent Permeability in Porous Organic Matter of Shale Gas Reservoirs. Fuel 2019, 251, 341–351. [Google Scholar] [CrossRef]
- Lyu, Q.; Ranjith, P.G.; Long, X.; Kang, Y.; Huang, M. A Review of Shale Swelling by Water Adsorption. J. Nat. Gas Sci. Eng. 2015, 27, 1421–1431. [Google Scholar] [CrossRef]
- Cao, P.; Liu, J.; Leong, Y.-K. A Fully Coupled Multiscale Shale Deformation-Gas Transport Model for the Evaluation of Shale Gas Extraction. Fuel 2016, 178, 103–117. [Google Scholar] [CrossRef]





| Sample | Treatment Condition | A1 | A2 | ΔA | Change Rate | ΔH | Change Rate |
|---|---|---|---|---|---|---|---|
| S | Before immersing | 3662.53 | 3821.96 | 1.044 | 26.59% | 5.102 | 21.54% |
| After immersing | 4838.16 | 1.321 | 6.201 |
| Treatment Condition | σ | eh | JRC/eh | Treatment Condition | σ | eh | JRC/eh |
|---|---|---|---|---|---|---|---|
| Before treatment | 1 | 56.917 | 0.24038 | After treatment | 1 | 76.495 | 0.36171 |
| 2 | 46.76239 | 0.29258 | 2 | 61.44677 | 0.4503 | ||
| 4 | 36.60779 | 0.37374 | 4 | 46.39855 | 0.59634 | ||
| 6 | 30.66772 | 0.44613 | 6 | 37.5959 | 0.73596 | ||
| 8 | 26.45318 | 0.5172 | 8 | 31.35032 | 0.88258 | ||
| 10 | 23.18413 | 0.59013 | 10 | 26.50588 | 1.04389 | ||
| 15 | 17.24406 | 0.79341 | 15 | 17.70323 | 1.56295 | ||
| 20 | 13.02952 | 1.05005 | 20 | 11.45765 | 2.41491 | ||
| 25 | 9.76047 | 1.40174 | 25 | 6.61321 | 4.18393 |
| Parameter | Value | Units | Parameter | Value | Units |
|---|---|---|---|---|---|
| Reservoir pressure | 20.34 | MPa | Fracture compressibility | 1.0 × 10−8 | 1/Pa |
| Temperature | 352 | K | Matrix permeability | 2 × 10−19 | m2 |
| Rock density | 2500 | kg/m3 | Fracture permeability | 2 × 10−13 | m2 |
| Langmuir pressure | 4.47 | MPa | Fracture width | 0.003 | m |
| Langmuir volume | 0.00272 | m3/kg | Fracture spacing | 30.5 | m |
| Matrix porosity | 0.03 | Fracture half-length | 47.2 | m | |
| Matrix compressibility | 1.5 × 10−10 | 1/Pa | Well BHP | 3.69 | MPa |
| Gas Viscosity | 0.02 | mPa·s | Gas density | 0.6571 | kg/m3 |
| Name | Position (m, m) | Name | Position (m, m) |
|---|---|---|---|
| Point A | 173.08, 149.53 | Point C | 203.58, 243.93 |
| Point B | 203.58, 149.53 | Point D | 173.08, 243.93 |
| Factor | Square Sum | Freedom | Mean Square | F | p | Variance Contribution Rate |
|---|---|---|---|---|---|---|
| Permeability | 41,069,351.93 | 4 | 10,267,337.98 | 9.04 | 2.16 × 10−6 | 23.76 |
| Density | 51,822,826.89 | 6 | 8,637,137.82 | 8.14 | 2.50 × 10−7 | 29.98 |
| Angle | 22,870,810.14 | 6 | 3,811,801.70 | 2.90 | 0.071 | 13.23 |
| Residual | 57,069,557.71 | 104 | 548,745.75 | 33.02 |
| Sample | Illustration | ||
|---|---|---|---|
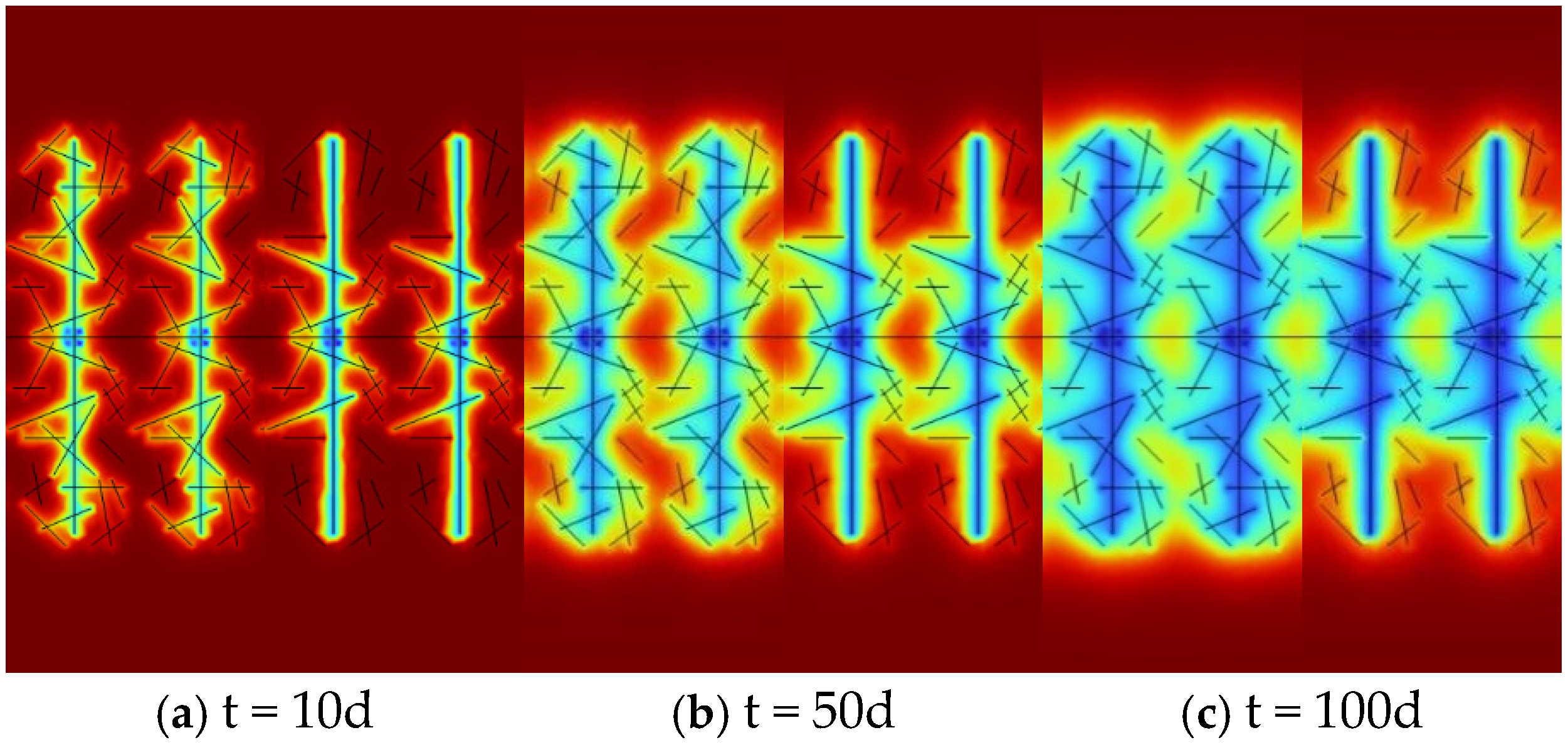
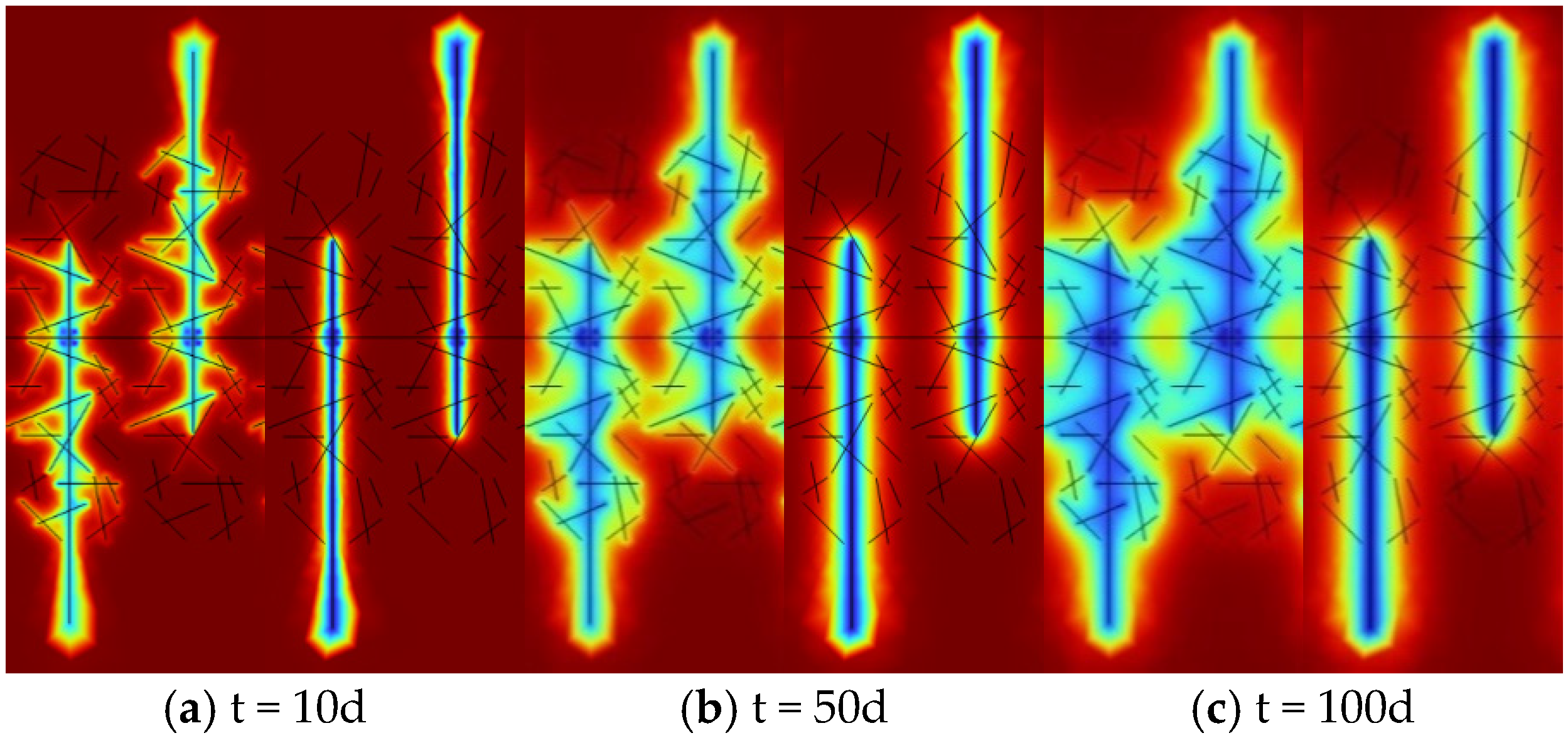
| Different fracture intersection quantities |  a = 2 | 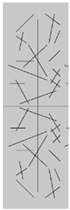 b = 4 | 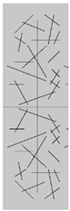 c = 6 |
| Different fracture densities | 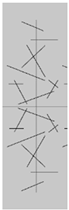 d = 0.08 m/m2 | 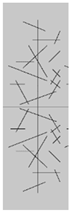 e = 0.12 m/m2 | 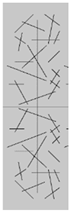 f = 0.16 m/m2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ao, X.; Rao, Y.; Li, H.; Song, B.; Li, P. Flow–Solid Coupled Analysis of Shale Gas Production Influenced by Fracture Roughness Evolution in Supercritical CO2–Slickwater Systems. Energies 2025, 18, 5569. https://doi.org/10.3390/en18215569
Ao X, Rao Y, Li H, Song B, Li P. Flow–Solid Coupled Analysis of Shale Gas Production Influenced by Fracture Roughness Evolution in Supercritical CO2–Slickwater Systems. Energies. 2025; 18(21):5569. https://doi.org/10.3390/en18215569
Chicago/Turabian StyleAo, Xiang, Yuxi Rao, Honglian Li, Beijun Song, and Peng Li. 2025. "Flow–Solid Coupled Analysis of Shale Gas Production Influenced by Fracture Roughness Evolution in Supercritical CO2–Slickwater Systems" Energies 18, no. 21: 5569. https://doi.org/10.3390/en18215569
APA StyleAo, X., Rao, Y., Li, H., Song, B., & Li, P. (2025). Flow–Solid Coupled Analysis of Shale Gas Production Influenced by Fracture Roughness Evolution in Supercritical CO2–Slickwater Systems. Energies, 18(21), 5569. https://doi.org/10.3390/en18215569






