Abstract
Defining compensatory interactions among criteria is a critical yet often subjective step in multi-criteria decision analysis (MCDA). To address this gap, this study proposes a novel model centered around the Inter-Criteria Compensation Index (ICCI), which is a quantitative measure derived from the standard error between normalized criterion values. The ICCI, complemented by correlation analysis and statistical significance testing, provides a structured framework to objectively identify compensatory, non-compensatory, or partially compensatory criteria pairs. The model also includes a method for adjusting criterion weights based on the ICCI and a sensitivity analysis to detect redundancies. We demonstrate the applicability of this framework through a case study ranking the 17 best-selling small electric vehicles in Brazil based on eight technical and economic criteria. The analysis revealed that six of the eight criteria exhibited strong compensatory relationships, while two were identified as non-compensatory. The subsequent ranking, generated using the TOPSIS method with adjusted weights, identified the optimal vehicle choice, and the sensitivity analysis confirmed that all compensatory criteria were essential, as their removal significantly altered the results. The proposed model reduces subjectivity in method selection, enhances the robustness of MCDA, and provides researchers with a verifiable tool for analyzing complex decision problems.
1. Introduction
Multi-criteria decision analysis (MCDA) problems can be characterized as compensatory, non-compensatory, or mixed [1,2]. Consequently, a variety of MCDA methods have been developed, which are each suited to handle one of these specific characteristics. As highlighted by Sousa et al. [3], these methods are widely applied across diverse domains to support structured and transparent decision making. However, selecting the most appropriate method hinges on correctly identifying the nature of the criteria interactions, which is a task that often remains a challenge in practice.
A prerequisite for effectively modeling decision-maker preferences is a clear assessment of the interrelationships among criteria. This assessment is particularly complex in mixed-method problems, where compensatory and non-compensatory logics coexist [4]. The selection of an appropriate MCDA method is therefore contingent upon accurately characterizing the dataset’s compensatory profile. While the existence of such mixed problems is recognized in the literature, the process for systematically discriminating between compensatory and non-compensatory criteria remains underdeveloped. Current approaches often rely on ad hoc judgments or the sequential application of different methods, lacking a unified framework to guide this critical initial phase. This gap underscores the need for a systematic approach to identify compensatory relationships, which is the central focus of this study.
Yu et al. [5] proposed a hybrid approach that integrates compensatory and non-compensatory perspectives to evaluate supplier performance. The analysis was carried out in three stages. In the first stage, the compensatory TOPSIS method was applied to assess performance in economic, environmental, and social dimensions. In the second stage, the weights of the criteria were determined using the Entropy Weight Method (EWM), which was originally proposed by [6].
Kou et al. [7] proposed the use of Spearman correlation coefficient analysis to aggregate the rankings obtained through five methods (namely, TOPSIS, GRA, VIKOR, PROMETHEE II and ELECTRE III) in order to adjust the discrepancies produced by different algorithms. In this context, TOPSIS, GRA (Gray Relational Analysis), and VIKOR were confirmed as compensatory methods, whereas PROMETHEE II and ELECTRE III were identified as non-compensatory. However, the study did not examine the intrinsic nature of the data, focusing just on the application of the methods. Similarly, Banihabib and Shabestari [2] combined compensatory and non-compensatory techniques in a strategic water resource management study that incorporated the SWOT (Strengths, Weaknesses, Opportunities, and Threats) framework. In that approach, the compensatory methods AHP and SAW, along with the non-compensatory method ELECTRE III, were employed to rank strategies evaluated across six criteria.
This discussion highlights that a thorough analysis must consider both data properties and the compensatory interactions among criteria. This is particularly crucial when defining weights, as the presence of two highly influential and mutually compensating criteria can skew the entire decision process. Moreover, a key implication of compensatory behavior is that certain criteria may become redundant; their removal from the model might not significantly impact the results, as their role is effectively covered by other, correlated criteria. Identifying these relationships is therefore essential to build more robust and parsimonious decision models.
One of the most established techniques for assessing the relationships between variables is Pearson’s correlation coefficient [8], which is often complemented by linear regression. These methods remain widely used in statistical analyses and are frequently integrated with other mathematical and statistical approaches. Notwithstanding the considerable diversity of methodologies available for constructing multi-criteria models, the assessment of relationships between criteria often remains subjective. To address this issue, Kheybari [9] proposed a method to better manage trade-offs by decomposing the decision matrix into a primary and a secondary matrix, which is grounded in the concepts of the Kano et al. [10] model. Consequently, identifying the nature of the relationships among criteria can support decision-makers in applying mathematical and statistical tools, beyond subjective judgment, to select the methods that best suit each problem.
The increasing demand for sustainable transportation has become a global priority. Many countries are planning to phase out internal combustion engine vehicles and have implemented policies to encourage the adoption of electric vehicles as a means to reduce greenhouse gas emissions [11]. In this context, significant advancements contributing to transportation sustainability include the development of alternative fuels, electric propulsion systems, and other emerging vehicle technologies [12].
The adoption of electric vehicles (EVs or BEVs) has grown rapidly in recent years [13], making them increasingly competitive with conventional combustion-powered vehicles [14]. However, the pursuit of alternatives to internal combustion engines extends beyond battery electric vehicles to include technologies such as fuel cell electric vehicles (FCEVs), which also aim to achieve zero emissions [15,16]. FCEVs overcome some of the key limitations of BEVs, particularly their restricted driving range and long charging times, by using hydrogen to generate electricity in fuel cells that power the electric motor. The main advantages of FCEVs include longer driving ranges, zero tailpipe emissions, and rapid refueling [17,18].
In this context, the present study proposes the development of a model based on the calculation of an Inter-Criteria Compensation Index (ICCI), which is designed to verify the nature of criteria, adjust weights, and eliminate redundancies. This contribution directly addresses a gap in the literature, as existing methods do not incorporate these elements simultaneously.
The proposed model was applied in a case study to demonstrate its suitability for constructing an electric vehicle (EV) ranking for the Brazilian market. This problem remains unresolved in the current literature, as recently highlighted by De Oliveira et al. [19].
This article is structured as follows. Section 1 has introduced the study’s rationale. Section 2 details the proposed methodology and its application to ranking electric vehicles in Brazil. Section 3 then presents the case study context and results. Finally, Section 4 discusses the findings, their implications, and outlines avenues for future research.
2. Materials and Methods
Although the compensatory or non-compensatory nature of criteria is a well-known factor influencing the selection of multi-criteria methods, a systematic approach for identifying this nature a priori is notably absent from the literature.
In this context, the present study proposes a model to establish compensatory relationships among criteria, thereby supporting researchers in analyzing these interactions. The proposed analyses combine mathematical and statistical techniques while also accounting for the compensatory or non-compensatory reasoning of decision-makers, since subjectivity is an inherent element of multi-criteria problems.
To operationalize this approach, Figure 1 presents a flowchart summarizing the methodology developed in this study. The procedure consists of seven steps, detailed below, which guide the construction and solution of the problems under investigation:
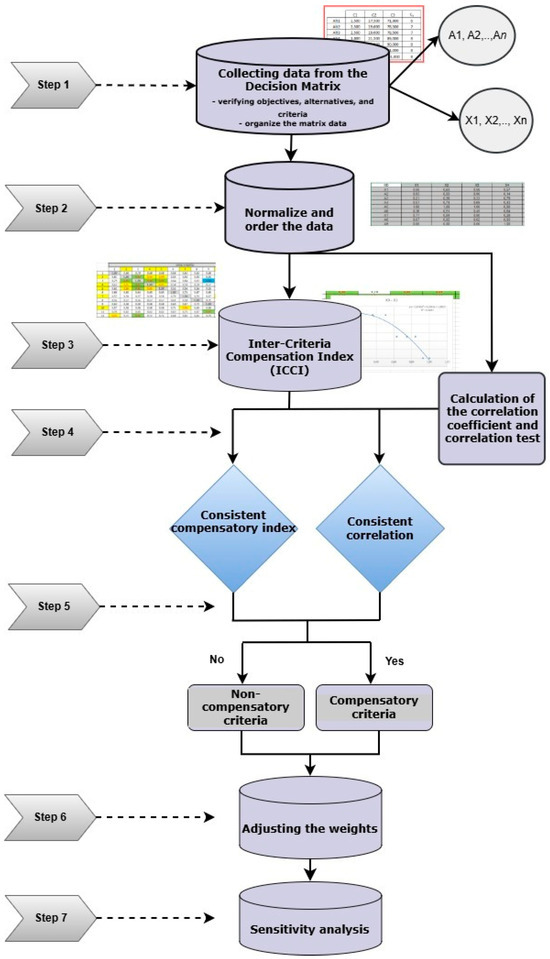
Figure 1.
Flowchart of the proposed Inter-Criteria Compensation Index method.
- Step 1.
- Definition of objectives, alternatives, and criteria; construction of the decision matrix
The first step involves defining the study objectives, alternatives, and criteria and then organizing the data into a decision matrix. This stage is fundamental in multi-criteria decision analysis (MCDA), as it incorporates the preferences and perspectives of relevant stakeholders, such as decision-makers, domain experts, and other affected parties. These may include the opinions of decision-makers, expert evaluations, and the interests of other relevant actors.
The resulting decision matrix, structured with m alternatives evaluated against n criteria, as shown in Equation (1), provides the foundation for analyzing trade-offs among the criteria.
where denotes the performance value of alternative i with respect to criterion j in the decision matrix.
- Step 2.
- Normalization and ordering of data
Data in the decision matrix typically vary in distribution, scale, and measurement units, potentially compromising the fair comparison of alternatives across criteria. Conventional multi-criteria approaches overcome this issue through normalization, which eliminates dimensional differences by transforming all values to a common scale.
In this study, the maximum–minimum normalization method proposed by Chakraborty and Yeh [20] was applied, as described in Equations (2) and (3):
where the following apply:
= normalized value that represents alternative i and criterion j;
= raw value of alternative i and criterion j;
= minimum value observed for criterion j;
= maximum value observed for criterion j.
By performing this normalization, all criteria are standardized to a scale. For cost-type criteria, higher raw values are transformed closer to 0, while lower values are transformed closer to 1. Conversely, for benefit-type criteria, higher values approach 1, and lower values approach 0. This standardization facilitates the subsequent analysis of potential relationships among criteria and the identification of possible trade-offs.
- Step 3.
- Calculation of the Inter-Criteria Compensation Index (ICCI)
To establish potential relationships among criteria and quantify the Inter-Criteria Compensation Index (ICCI), the standard error between criteria pairs was employed, as defined in Equation (4):
where the following apply:
= standard error between criteria j and k;
= value of alternative i for criterion j;
= value of alternative i for criterion k;
= mean value of alternative i for criterion j;
= mean value of alternative i for criterion k;
m = number of alternatives in the matrix decision;
n = number of the criteria in the matrix decision.
Since the standard error yields values between 0 and 1, representing the relative error between the mean values of two criteria, it was transformed into the Inter-Criteria Compensation Index (ICCI). Equation (5) defines this transformation, and when multiplied by 100, it expresses the percentage that quantifies the extent to which one criterion influences (or compensates for) another, which is relative to the sum of the differences between their mean values:
The standard error quantifies differences between criteria relative to their mean values, forming the basis for assessing compensatory relationships. These relationships are determined via the Inter-Criteria Compensation Index (ICCI), strengthened through correlation analysis and hypothesis testing, detailed in the following steps, to provide a more robust identification of compensatory relationships. The corresponding reference values are specified in Step 5.
- Step 4.
- Calculation of correlation coefficients and hypothesis testing
Correlation coefficients, which range from −1 to 1, quantify the strength and direction of relationships between criteria. A value of 1 indicates a perfect positive correlation, −1 signifies a perfect negative correlation, and 0 signifies no correlation.
In this study, Pearson’s method was employed to assess linear trends [8], while Spearman’s method was applied to detect nonlinear associations [21]. Equations (6) and (7) present the formulas for calculating Pearson and Spearman linear correlations, respectively, and Equation (8) shows the Spearman rank correlation formula.
where the following apply:
= Pearson correlation coefficient between criteria j and k;
= mean value of alternative i for criterion j;
= mean value of alternative i for criterion k.
where the following apply:
= Spearman correlation coefficient between criteria j and k;
n = sample size;
= rank of alternative i for criterion j;
= rank of alternative i for criterion k.
Correlation Test
A hypothesis test is conducted to determine whether the correlation coefficient between criteria is statistically significant, thereby assessing whether the null hypothesis (that the correlation is zero) can be rejected. The t-test calculation, as described by Kanji [22], was adapted for this study and is presented in Equations (9) and (10), corresponding to the tests for Pearson and Spearman correlation coefficients, respectively:
where the following apply:
= t value () with degrees of freedom;
= Pearson correlation coefficient between criteria j and k;
= Spearman correlation coefficient between criteria j and k.
The hypothesis test for these correlation coefficients assumes a null hypothesis () that the correlation between the variables (r or ) is equal to 0 with a significance level of , for this study). The null hypothesis is rejected, indicating a statistically significant correlation, if the t-test values exceed the critical values from the t-distribution table. Conversely, if the p-value is greater than 0.05, the null hypothesis is not rejected, indicating that the correlation is not statistically significant.
- Step 5.
- Verification of comparability or non-compensability of criteria
The classification of criteria as compensatory or non-compensatory is multi-faceted. The Inter-Criteria Compensation Index (ICCI) identifies compensatory relationships by considering correlation coefficients (CRs) within the reference range of [0.8, 1.0], where the threshold condition () is satisfied. Furthermore, hypothesis tests are conducted to verify the statistical significance of these correlations. This stringent threshold ensures that only strong and meaningful associations, indicative of a genuine trade-off between criterion pairs, are considered.
It is important to note that the denoted CR values correspond to both Pearson and Spearman correlation coefficients, each of which must individually fall within the specified reference range. Beyond these statistical measures, empirical analysis has identified three additional scenarios in which compensation between paired criteria may occur, as outlined below and further detailed in Figure 2:
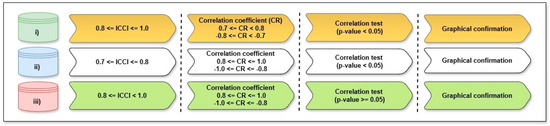
Figure 2.
Flowchart illustrating the procedure for identifying compensatory and non-compensatory criteria based on ICCI values, correlation analysis (Spearman and Pearson), and statistical testing.
- (i)
- Divergent ICCI and Correlation Values with Significance: When the ICCI falls within the reference range [0.8, 1.0] but the correlation coefficients (CRs) are marginal (0.7 to 0.8 or −0.8 to −0.7), and the hypothesis test confirms statistical significance, graphical confirmation is required to establish compensation.
- (ii)
- Marginal ICCI with Strong Correlation and Significance: When the ICCI is marginal [0.7, 0.8] but correlation coefficients are strong (0.8 to 1.0 or −1.0 to −0.8), with statistical significance confirmed, graphical inspection is used to verify the compensatory relationship.
- (iii)
- Strong ICCI and Correlation Values without Statistical Significance: When both ICCI [0.8, 1.0] and correlation coefficients () meet the higher standard range, but the hypothesis test shows lack of statistical significance, graphical analysis determines the final compensatory status.
Scatter plots and related visual tools can reveal compensatory relationships that might be overlooked by relying exclusively on numerical correlation metrics. This graphical dimension provides an intuitive means for decision-makers to incorporate contextual knowledge and nuanced judgment into the final assessment.
For all three scenarios, graphical analysis is considered indicative of a compensatory relationship only when the data trend demonstrates a minimum reliability of 70%. This reliability is quantified by the coefficient of determination of the trendline fitted to the data, which is calculated using the NumPy package’s polyfit function in Python 3. The 70% threshold was calibrated based on the lower bounds of both the Inter-Criterion Compensation Index (ICCI) and the correlation coefficients observed during empirical testing.
The standard thresholds indicating a strong compensatory relationship were established through extensive empirical testing and are supported by the literature [23]. Nevertheless, the judgment of decision-makers remains integral to the process, as visual inspection often yields more robust interpretations of the projected relationship indices.
- Step 6.
- Adjustment of criteria weights
In this step, the criteria weights are adjusted based on their compensatory or non-compensatory nature. The adjustment ensures that the final evaluation reflects the true influence of each criterion, accounting for any compensatory interactions identified in previous steps. The weight adjustment procedure is performed using Equations (11) and (12):
where the following apply:
= Inter-Criteria Compensation Index (ICCI) value for row i of criterion j;
= raw weight of criterion j;
= original weight of criterion j defined by the decision-maker(s);
= adjusted weight of criterion j, accounting for compensatory relationships defined by the ICCI.
The calculations performed for the weights of each criterion, as shown in Equation (11), aim to perform a global adjustment of the criterion weights. To this end, different calculations are performed, considering the raw data of the in comparing the criteria. It is important to note that the values between the criteria may present different values when comparing criterion i with criterion j and criterion j with criterion i.
The first step is to calculate the values of and for each criterion (when compared to the others). After that, the subtraction between and is performed, and the value of this subtraction is divided by the number of criteria. The resulting value is then multiplied by one plus the original weight of the criterion. After performing these calculations for each criteria, the weights’ sum may show a result other than 1. Therefore, the adjusted weights are readjusted proportionally by Equation (12) so that this resulting sum of the criteria weights reaches 1.
It is important to note that for datasets comprising distinct subsets, the weights of the subcriteria should be determined by first partitioning the data and analyzing each subset separately. The overall weights should then be calculated within the decision matrix.
If the decision-maker remains uncertain about defining or adjusting the criteria weights, alternative approaches can be employed. These include calculating weights based on the data distribution within the decision matrix or by comparing results obtained from different weighting methods. It should be noted that changes to the may alter the results and sensitivity analysis. Furthermore, weight adjustments may also influence the sensitivity analysis, which will be explored in step 7.
- Step 7.
- Sensitivity Analysis
The final step involves performing a sensitivity analysis based on the compensatory criteria identified in the normalized decision matrix (Step 2). The analysis is conducted in two stages: the first stage generates individual rankings for each criterion, and the second stage evaluates the impact of removing specific criteria relative to their assigned weights.
The first stage generates individual rankings for each compensatory criterion in the study. If a criterion’s ranking is identical (or approximately 80% similar) to the overall ranking considering all criteria, a hypothesis test is conducted to evaluate whether removing this criterion affects the final ranking. If the ranking remains unchanged, it is assumed that the other criteria compensate for the removed criterion, and it may be excluded from the final analysis (the final ranking should be verified to confirm the removal).
The second stage focuses on removing compensatory criteria, except for the most heavily weighted one, to assess the impact on the overall results. Each criterion’s individual ranking is compared to the original ranking to ensure consistency. If the removal of compensatory criteria does not alter the results, it indicates that the remaining criteria compensate for the removed ones, allowing for their exclusion from the analysis. Figure 3 illustrates this second stage of the sensitivity analysis.
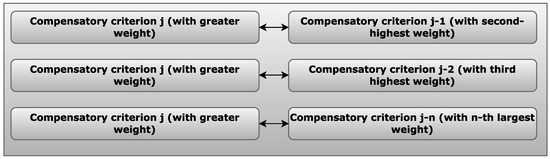
Figure 3.
Sensitivity analysis by removeng compesatory criteria.
When excluding one or more criteria to assess the sensitivity of the results, the weights of the remaining criteria must be adjusted proportionally to ensure that their sum equals 1 (or 100%). In analyses containing both compensatory and non-compensatory criteria, the sensitivity analysis should consider only the removal of compensatory criteria, as non-compensatory criteria do not allow the good performance of one criterion to offset the poor performance of an alternative in another criterion. All cases considered in the sensitivity analysis, as well as in the preceding steps, incorporate the decision-maker’s perspective.
Several empirical tests were conducted to validate the proposed methodology. It is important to note that applying this methodology to different contexts or problems may result in variations in the constraints, which could, in turn, affect the final ranking.
2.1. Methods Used for EV Application
Some studies within the scope of this research already provide criterion weights. However, for the application of the proposed model to rank electric vehicles in Brazil, it was necessary to calculate these weights. In this context, three methods were employed: the Analytic Hierarchy Process (AHP) [24], CRITIC (CRiteria Importance Through Inter-criteria Correlation) [25], and the Entropy Weights Method (EWM) [6].
The AHP-based criterion weights were obtained by constructing a pairwise comparison matrix and calculating the random index (RI) as proposed by Saaty [26], from which the consistency index (CI) is derived.
While the AHP method incorporates the subjectivity of the decision-maker in weighting criteria, the CRITIC and EWM methods rely on the raw values of each alternative relative to the respective criteria.
The final weight assigned to each criterion was computed as the average of the weights obtained from the three methods, according to Equation (13).
Several studies have combined different methods to integrate subjective weighting, based on the decision-maker’s opinion with data-driven approaches [27,28,29]. In this study, the three methods were applied, although the final choice of weighting approach depends on the researchers’ judgment.
In the present study, the TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) method is employed to rank electric vehicles available in the Brazilian market based on the established criteria. The methodology of TOPSIS is described as follows:
R-TOPSIS (Technique for Order Preference by Similarity to Ideal Solution)
The TOPSIS method was originally proposed by Hwang and Yoon [1] and has been noted by several authors to be potentially susceptible to ranking reversal issues [30,31,32]. In this study, R-TOPSIS is applied following the approach of de Farias Aires and Ferreira [30], incorporating the maximum–minimum normalization method proposed by Chakraborty and Yeh [20]. The process begins with the construction of the decision matrix X.
The subsequent step involves multiplying each element of matrix X by the corresponding criterion weight (here, calculated as the average of the weights obtained from the AHP and entropy methods) resulting in a weighted normalized matrix V with elements , as shown in Equation (14).
Next, the ideal () and anti-ideal () solutions are determined, corresponding to the best and worst possible performances among the alternatives, respectively. These solutions are calculated as shown in Equations (15) and (16):
where the following apply:
for benefit criteria;
for cost criteria.
Hwang and Yoon [1] state that the two solutions ( and ) represent, respectively, the most preferable alternative (ideal solution) and the least preferable alternative (negative-ideal solution). The distances of each alternative m from the ideal and anti-ideal solutions can be calculated using the m-dimensional Euclidean distance, as shown in Equations (17) and (18).
The ideal solution is calculated using Equation (19):
Based on the values of , the alternatives can be ranked in descending order, where higher values indicate better performance with respect to the considered criteria.
3. Results and Discussions
The proposed model was applied to generate a ranking of the 17 best-selling small electric vehicles in Brazil. A detailed description of the analyses performed, along with the corresponding results, is presented below:
3.1. Application to the VE Problem
3.1.1. Contextualization of the EV Problem
The escalating climate crisis, driven largely by a transportation sector dependent on fossil fuels, has intensified the global search for sustainable solutions [33]. Electric vehicles (EVs) have thus emerged as a pivotal technology, offering a direct path to cutting greenhouse gas emissions. This urgency stems from over two centuries of reliance on non-renewable energy sources like oil and coal, which have inflicted severe environmental damage and elevated atmospheric CO2 to levels that exacerbate global warming [34,35]. Propelled by government incentives and growing demand for clean energy, the EV industry is now experiencing rapid global expansion [36].
As a cornerstone of sustainable development, EVs present a multi-faceted solution: they mitigate greenhouse gas emissions, curtail fossil fuel consumption, and, with zero tailpipe pollutants, offer a cleaner urban transportation model [37].
Electric vehicles play a critical role in mitigating pollution resulting from fossil fuel consumption. They have the potential to induce a paradigm shift in the transportation sector, as transportation is a major contributor to urban air pollution, making the reduction of emissions a pressing need [38]. Evidence suggests that EVs are advancing successfully, indicating that the automotive industry may soon achieve near-zero emissions [39]. In recent years, the electric vehicle industry has produced high-performance vehicles that do not rely on fossil fuels [38]. Consequently, EVs are crucial for addressing environmental challenges [40].
Multi-criteria decision analysis (MCDA) methods can support researchers in addressing various EV-related decisions, such as determining optimal locations for charging stations and establishing rankings for selecting vehicles and components. Identifying the most sustainable locations for EV charging infrastructure is particularly important in evaluating the full life cycle of electric vehicles [41,42,43].
This process involves multiple conflicting criteria and can therefore be modeled as a multi-criteria decision-making problem [44]. According to [45], current research recognizes that a wide range of MCDA techniques has been extensively applied in vehicle analyses. Specifically, regarding electric vehicle purchases, Ecer [46] highlights that MCDA methods are effective tools for supporting optimal EV selection.
Electric vehicles (EVs) are gaining increasing attention due to growing concerns about sustainability with a rising number of industries focusing on their production. Battery-powered EVs significantly reduce environmental impact [47], prompting many developed countries to transition toward electric mobility as a strategy to mitigate environmental pollution [48,49]. To support this transition, charging infrastructure has been widely implemented across gas stations, buildings, companies, industries, and shopping centers.
3.1.2. EV Ranking Results
In this context, we developed an application to generate a ranking for the selection of electric vehicles sold in Brazil. While similar analyses have been conducted in other countries, few studies are available in the literature [50,51,52]. This study focuses exclusively on small electric vehicles, considering market aspects to identify the optimal purchase choice based on the selected criteria.
We selected seventeen models based on 2022 data from the Brazilian Electric Vehicle Association (ABVE), focusing on the best-selling small electric vehicles in the country. The data were collected in June 2023 and include the 17 models available for sale in Brazil during that period as well as all information published on the ABVE website (https://abve.org.br/, accessed on 15 June 2023).
Eight criteria were considered: Fuel Consumption (kWh/100 km) (C1), Acceleration (0–100 km/h) (C2), Maximum Power (horsepower) (C3), Battery Capacity (kWh) (C4), Price (R$) (C5), Range (km) (C6), Trunk Capacity (L) (C7), and Maximum Speed (km/h) (C8). Criteria 1 (Fuel Consumption) and 5 (Price) are cost-related, while the remaining criteria are benefit-related.
Although a wide range of electric vehicles is currently available on the market, this analysis was restricted to small vehicles (hatchbacks, sedans, and SUVs), since comparing different vehicle categories would not yield meaningful results. The collected data are presented in Table 1.

Table 1.
Collected data.
The decision matrices containing normalized data are presented in Table 2.

Table 2.
Normalized data.
As previously discussed, the criteria values exhibit considerable variation both among themselves and relative to other criteria, making standardization an essential step. Table 3 presents the Inter-Criteria Compensation Index (ICCI) values calculated for the eight criteria considered in this study.

Table 3.
Inter-Criteria Compensation Index (ICCI).
A strong relationship is observed among criteria C1, C2, C3, C4, C5, and C8, whereas criteria C6 and C7 exhibit weak relationships with only a single moderate association observed between C5 and C6. To further validate the relationships indicated by the Inter-Criteria Compensation Index (ICCI) values, Table 4, Table 5, Table 6 and Table 7 present the Pearson and Spearman correlation coefficients along with their corresponding p-values.

Table 4.
Pearson correlation.

Table 5.
Spearman correlation.

Table 6.
Corresponding p-values for Pearson correlation.

Table 7.
Corresponding p-values for Spearman correlation.
Another aspect to consider is that in several cases, the p-value indicates that the correlation between criteria is not statistically significant even when the correlation coefficient is relatively high. Conversely, in some instances, coefficients with moderate values (e.g., 0.5) may be statistically significant. For the purposes of this study, only correlation coefficient values within the predefined ranges are considered relevant.
Upon analyzing the Inter-Criteria Compensation Index (ICCI) values alongside the correlation coefficients and their respective p-values, the relationships between certain criteria, specifically C4–C5, require further verification through graphical analysis. This relationship is illustrated in Figure 4.
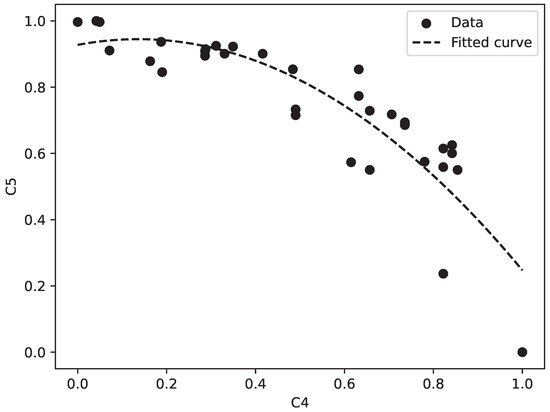
Figure 4.
Relationship between C4 and C5.
For the C4–C5 relationship, the fitted curve is given by the following:
The graphical analysis of this case confirmed the existence of a compensatory relationship between the variables. Table 8 presents the results regarding the compensatory or non-compensatory nature of the criteria.

Table 8.
Compensatory relationship between the variables.
When analyzing the results to determine the compensatory nature of the criteria, only Criteria 6 and 7 were identified as non-compensatory in relation to the others. Based on this finding, the ranking of electric vehicles was constructed using the TOPSIS method, which inherently assumes a compensatory framework. In addition, the weights of the criteria were calculated as the average of three methods (AHP, CRITIC, and EWM). The results of the weight calculation are presented in Table 9, while the adjusted weights are reported in Table 10.

Table 9.
Criteria weights.

Table 10.
Adjusted criteria weights.
The results in Table 9 were obtained from the values in Table 2, following Equations (11) and (12). As an example, the calculation for criterion 1 uses the sum of the values in row 1 and column 1 of Table 2.
Criterion weights may vary depending on the method employed [53]. For this reason, different approaches were adopted, some incorporating the decision-maker’s perspective and others relying exclusively on mathematical and/or statistical tools. The largest variation in adjusted weights was observed for Criterion 5 with a difference of 2.36%. After calculating the weights, the subsequent procedures of the TOPSIS method were applied, as presented in Table 11. The normalization adopted was the max–min approach proposed by Chakraborty and Yeh [20], which is commonly used in TOPSIS to prevent ranking reversal issues, as discussed in de Farias Aires and Ferreira [30].

Table 11.
Alternatives ranking.
In this context, it is important to note that there was little variation in the weights during the adjustments, as all criteria were considered in the final analysis. Consequently, the weight adjustments did not lead to any changes in the final ranking.
The analysis indicates that Electric Vehicle 12 represents the best alternative. Criteria such as purchase price, for instance, show considerable variation, which highlights the usefulness of ranking alternatives in supporting decision making, as demonstrated in this study.
The final stage of applying compensability analysis to electric vehicles involved a sensitivity assessment of the compensatory criteria. As previously discussed, non-compensatory criteria cannot be substituted by others; therefore, excluding them from the analysis would not be meaningful, since no criterion could compensate for their absence. In contrast, compensatory criteria allow for such verification. Accordingly, two procedures were carried out to examine whether removing compensatory criteria (one at a time) would alter the results. The first procedure consisted of constructing rankings based on each individual compensatory criterion. The outcomes of this analysis are presented in Table 12.

Table 12.
Order of alternatives for each criterion.
This analysis revealed that all individual rankings differed from the original one. Consequently, a second stage was carried out in which the compensatory criteria were sequentially removed in descending order of their weights. The results once again produced rankings that diverged from the original. Therefore, it can be concluded that all criteria must be considered in the evaluation of electric vehicles in Brazil.
4. Final Remarks
This study explored two methodologies designed to support researchers and practitioners in multi-criteria decision analysis (MCDA). The lack of studies on these methodologies often makes the analysis subjective [54]. The main objective was to integrate mathematical and statistical techniques to enhance the robustness of both the analysis and the decision-making process.
Determining whether criteria are compensatory or non-compensatory in an MCDA analysis often poses challenges when selecting the most suitable method for problem solving. To address this, the first methodology proposed in this study introduces techniques to objectively determine the compensatory nature of criteria, thereby reducing reliance on the decision-maker’s subjective judgment, even though some degree of subjectivity remains inherent to the process.
The proposed methodology helps reduce subjectivity in both the selection of methods and other stages of the analysis, thereby making the process more reliable and consistent, which is particularly important when multiple stakeholders or managers are directly involved on the decision-making process.
Moreover, the choice of method(s) has a direct impact on the results. For instance, if trade-offs exist among criteria but a non-compensatory method is applied, such trade-offs will not be accounted in the outcome.
The methods for determining the criteria compensation were validated through multiple tests using data from the literature and an application involving the purchase of small electric vehicles in Brazil. Based on this approach with correlation analysis, hypothesis testing of the correlation index, and standard accuracy, which generates the Inter-Criteria Compensation Index (ICCI), were selected as suitable techniques for identifying whether criteria are compensatory or non-compensatory.
An additional contribution of the methodology is the incorporation of sensitivity analysis. This procedure makes it possible to identify whether some criteria could be removed without affecting the results. When criteria are mutually compensatory, one may substitute for another, thus streamlining the study and eliminating redundant criteria.
It is important to note that many decision problems are highly complex, often involving conflicting criteria. Although subjectivity remains an inherent aspect of MCDA, the lack of appropriate techniques for selecting methods highlights the development for systematic approaches, such as the one proposed here, to support the development of robust and reliable solutions.
While this study provides a quantitative framework for analyzing criteria relationships, the decision-maker’s perspective remains indispensable in MCDM. Expert judgment is crucial for interpreting results and contextualizing findings beyond purely computational outputs. The proposed methodology offers a systematic approach for evaluating trade-offs in multi-criteria problems with potential applications across diverse research domains.
It is important to note that although several empirical tests were conducted to validate the proposed methodology, this study presented results only for the electric vehicle case. Future research may extend the application of the methodology to different decision-making problems and explore potential limitations that could influence the final ranking, as variations are expected to depend on the specific context.
While this study demonstrated the practical applicability of the ICCI in a real-world EV scenario, future work should pursue a more rigorous quantitative validation of the index. This may include generating synthetic datasets with predefined compensatory and non-compensatory structures to accurately calibrate the ICCI discrimination thresholds and to assess its classification accuracy against a known ground truth. Such analyses would further strengthen the statistical and theoretical foundations of the proposed method.
Author Contributions
Conceptualization, M.S.d.O. and F.T.; methodology, M.S.d.O. and F.T.; validation, M.S.d.O. and F.T.; formal analysis, M.S.d.O. and F.T.; investigation, M.S.d.O. and F.T.; data curation, M.S.d.O. and F.T.; writing—original draft preparation, M.S.d.O., F.T. and V.S.; writing—review and editing, M.S.d.O., F.T. and V.S.; visualization, M.S.d.O. and V.S.; supervision, F.T.; project administration, F.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hwang, C.L.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making: Methods and Applications a State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Banihabib, M.E.; Shabestari, M.H. Decision models for the ranking of agricultural water demand management strategies in an arid region. Irrig. Drain. 2017, 66, 773–783. [Google Scholar] [CrossRef]
- Sousa, M.; Almeida, M.F.; Calili, R. Multiple criteria decision making for the achievement of the UN sustainable development goals: A systematic literature review and a research agenda. Sustainability 2021, 13, 4129. [Google Scholar] [CrossRef]
- do Carmo Silva, M.; Gavião, L.O.; Gomes, C.F.S.; Lima, G.B.A. Global Innovation Indicators analysed by multicriteria decision. Braz. J. Oper. Prod. Manag. 2020, 17, 1–17. [Google Scholar] [CrossRef]
- Yu, C.; Zhao, W.; Li, M. An integrated sustainable supplier selection approach using compensatory and non-compensatory decision methods. Kybernetes 2019, 48, 1782–1805. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Kou, G.; Lu, Y.; Peng, Y.; Shi, Y. Evaluation of classification algorithms using MCDM and rank correlation. Int. J. Inf. Technol. Decis. Mak. 2012, 11, 197–225. [Google Scholar] [CrossRef]
- Pearson, K. On the Theory of Contingency and Its Relation to Association and Normal Correlation; Cambridge University Press: Cambridge, UK, 1904; Volume 1. [Google Scholar]
- Kheybari, S. Adjusting trade-offs in multi-criteria decision-making problems. Int. J. Inf. Technol. Decis. Mak. 2021, 20, 1499–1517. [Google Scholar] [CrossRef]
- Kano, N.; Seraku, N.; Takahashi, F.; Tsuji, S. Attractive quality and must-be quality. J. Jpn. Soc. Qual. Control 1984, 14, 147–156. [Google Scholar]
- Towoju, O.A.; Ishola, F.A. A case for the internal combustion engine powered vehicle. Energy Rep. 2020, 6, 315–321. [Google Scholar] [CrossRef]
- Mitropoulos, L.K.; Prevedouros, P.D. Conventional, battery-powered, and other alternative fuel vehicles: Sustainability assessment. In Behaviour of Lithium-Ion Batteries in Electric Vehicles: Battery Health, Performance, Safety, and Cost; Springer: Berlin/Heidelberg, Germany, 2018; pp. 101–127. [Google Scholar]
- Alosaimi, W.; Ansari, M.T.J.; Alharbi, A.; Alyami, H.; Ali, S.; Agrawal, A.; Khan, R.A. Toward a unified model approach for evaluating different electric vehicles. Energies 2021, 14, 6120. [Google Scholar] [CrossRef]
- Stamatakis, D.; Tolis, A.I. Coordinated Electric Vehicle Demand Management in the Unit Commitment Problem Integrated with Transmission Constraints. Energies 2025, 18, 4293. [Google Scholar] [CrossRef]
- Pramuanjaroenkij, A.; Kakaç, S. The fuel cell electric vehicles: The highlight review. Int. J. Hydrogen Energy 2023, 48, 9401–9425. [Google Scholar] [CrossRef]
- Jia, C.; Liu, W.; He, H.; Chau, K. Health-conscious energy management for fuel cell vehicles: An integrated thermal management strategy for cabin and energy source systems. Energy 2025, 333, 137330. [Google Scholar] [CrossRef]
- Chandran, M.; Palanisamy, K.; Benson, D.; Sundaram, S. A review on electric and fuel cell vehicle anatomy, technology evolution and policy drivers towards EVs and FCEVs market propagation. Chem. Rec. 2022, 22, e202100235. [Google Scholar] [CrossRef]
- Jia, C.; Liu, W.; He, H.; Chau, K. Superior energy management for fuel cell vehicles guided by improved DDPG algorithm: Integrating driving intention speed prediction and health-aware control. Appl. Energy 2025, 394, 126195. [Google Scholar] [CrossRef]
- De Oliveira, M.; Steffen, V.; Trojan, F. Systematic literature review on electric vehicles and multicriteria decision making: Trends, rankings, and future perspectives. J. Intell. Manag. Decis. 2024, 3, 22–41. [Google Scholar] [CrossRef]
- Chakraborty, S.; Yeh, C.H. A simulation based comparative study of normalization procedures in multiattribute decision making. In Proceedings of the 6th Conference on 6th WSEAS International Conference on Artificial Intelligence, Knowledge Engineering and Data Bases, Corfu Island, Greece, 16–19 February 2007; Volume 6, pp. 102–109. [Google Scholar]
- Spearman, C. Correlation calculated from faulty data. Br. J. Psychol. 1910, 3, 271. [Google Scholar] [CrossRef]
- Kanji, G.K. 100 Statistical Tests; Sage Publications: Thousand Oaks CA, USA, 2006. [Google Scholar]
- Akoglu, H. User’s guide to correlation coefficients. Turk. J. Emerg. Med. 2018, 18, 91–93. [Google Scholar] [CrossRef]
- Saaty, T. The Analytic Hierarchy Process (AHP) for Decision Making; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Liang, M.; Yang, G.; Zhu, X.; Cheng, H.; Zheng, L.; Liu, H.; Dong, X.; Zhang, Y. AHP-EWM Based Model Selection System for Subsidence Area Research. Sustainability 2023, 15, 7135. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, P.; Mu, P.; Wang, M.; Han, L.; Sun, J. A Comprehensive Evaluation Method for the Service Status of Groins in Waterways Based on an AHP-Improved CRITIC Combination Weighting Optimization Model. Sustainability 2022, 14, 10709. [Google Scholar] [CrossRef]
- Xiao, L.; Li, F.; Niu, C.; Dai, G.; Qiao, Q.; Lin, C. Evaluation of Water Inrush Hazard in Coal Seam Roof Based on the AHP-CRITIC Composite Weighted Method. Energies 2023, 16, 114. [Google Scholar] [CrossRef]
- de Farias Aires, R.F.; Ferreira, L. A new approach to avoid rank reversal cases in the TOPSIS method. Comput. Ind. Eng. 2019, 132, 84–97. [Google Scholar] [CrossRef]
- Garcia-Cascales, M.S.; Lamata, M.T. On rank reversal and TOPSIS method. Math. Comput. Model. 2012, 56, 123–132. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Kumar, R. G-TOPSIS: A cloud service selection framework using Gaussian TOPSIS for rank reversal problem. J. Supercomput. 2021, 77, 523–562. [Google Scholar] [CrossRef]
- Hussain, Z.; Marcel, B.; Majeed, A.; Tsimisaraka, R.S.M. Effects of transport–carbon intensity, transportation, and economic complexity on environmental and health expenditures. Environ. Dev. Sustain. 2024, 26, 16523–16553. [Google Scholar] [CrossRef]
- Vieira, S.; Barros, M.V.; Sydney, A.C.N.; Piekarski, C.M.; de Francisco, A.C.; de Souza Vandenberghe, L.P.; Sydney, E.B. Sustainability of sugarcane lignocellulosic biomass pretreatment for the production of bioethanol. Bioresour. Technol. 2020, 299, 122635. [Google Scholar] [CrossRef] [PubMed]
- Consul, S.; Singh, K.V.; Om Bansal, H.; Kim, K.A. Intelligent switching mechanism for power distribution in photovoltaic-fed battery electric vehicles. Environ. Dev. Sustain. 2023, 25, 8259–8278. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, X.; Dong, J.; Yang, X. Optimal allocation of urban new energy vehicles and traditional energy vehicles considering pollution and cost. Environ. Dev. Sustain. 2024, 26, 6007–6026. [Google Scholar] [CrossRef]
- Angeline, P.S.; Rajkumar, M.N. Evolution of electric vehicle and its future scope. Mater. Today Proc. 2020, 33, 3930–3936. [Google Scholar] [CrossRef]
- Ghosh, A.; Ghorui, N.; Mondal, S.P.; Kumari, S.; Mondal, B.K.; Das, A.; Gupta, M.S. Application of hexagonal fuzzy MCDM methodology for site selection of electric vehicle charging station. Mathematics 2021, 9, 393. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Gamal, A.; Hezam, I.M.; Sallam, K.M. Sustainability assessment of optimal location of electric vehicle charge stations: A conceptual framework for green energy into smart cities. Environ. Dev. Sustain. 2024, 26, 11475–11513. [Google Scholar] [CrossRef]
- Ghosh, A. Possibilities and challenges for the inclusion of the electric vehicle (EV) to reduce the carbon footprint in the transport sector: A review. Energies 2020, 13, 2602. [Google Scholar] [CrossRef]
- Zhao, H.; Li, N. Optimal siting of charging stations for electric vehicles based on fuzzy Delphi and hybrid multi-criteria decision making approaches from an extended sustainability perspective. Energies 2016, 9, 270. [Google Scholar] [CrossRef]
- Anthopoulos, L.; Kolovou, P. A multi-criteria decision process for ev charging stations’ deployment: Findings from greece. Energies 2021, 14, 5441. [Google Scholar] [CrossRef]
- Schmidt, M.; Zmuda-Trzebiatowski, P.; Kiciński, M.; Sawicki, P.; Lasak, K. Multiple-criteria-based electric vehicle charging infrastructure design problem. Energies 2021, 14, 3214. [Google Scholar] [CrossRef]
- Karaşan, A.; Kaya, İ.; Erdoğan, M. Location selection of electric vehicles charging stations by using a fuzzy MCDM method: A case study in Turkey. Neural Comput. Appl. 2020, 32, 4553–4574. [Google Scholar] [CrossRef]
- Pradhan, P.; Shabbiruddin; Pradhan, S. Selection of electric vehicle using integrated Fuzzy-MCDM approach with analysis on challenges faced in hilly terrain. Energy Sources Part A Recovery Util. Environ. Eff. 2022, 44, 2651–2673. [Google Scholar] [CrossRef]
- Ecer, F. A consolidated MCDM framework for performance assessment of battery electric vehicles based on ranking strategies. Renew. Sustain. Energy Rev. 2021, 143, 110916. [Google Scholar] [CrossRef]
- Aiello, G.; Quaranta, S.; Certa, A.; Inguanta, R. Optimization of urban delivery systems based on electric assisted cargo bikes with modular battery size, taking into account the service requirements and the specific operational context. Energies 2021, 14, 4672. [Google Scholar] [CrossRef]
- Babar, A.H.K.; Ali, Y.; Khan, A.U. Moving toward green mobility: Overview and analysis of electric vehicle selection, Pakistan a case in point. Environ. Dev. Sustain. 2021, 23, 10994–11011. [Google Scholar] [CrossRef]
- Ziemba, P.; Gago, I. Compromise multi-criteria selection of E-scooters for the vehicle sharing system in Poland. Energies 2022, 15, 5048. [Google Scholar] [CrossRef]
- Puška, A.; Božanić, D.; Mastilo, Z.; Pamučar, D. Extension of MEREC-CRADIS methods with double normalization-case study selection of electric cars. Soft Comput. A Fusion Found. Methodol. Appl. 2023, 27, 7097. [Google Scholar] [CrossRef]
- Ziemba, P. Multi-criteria stochastic selection of electric vehicles for the sustainable development of local government and state administration units in Poland. Energies 2020, 13, 6299. [Google Scholar] [CrossRef]
- Ziemba, P. Selection of electric vehicles for the needs of sustainable transport under conditions of uncertainty—A comparative study on fuzzy MCDA methods. Energies 2021, 14, 7786. [Google Scholar] [CrossRef]
- Mukhametzyanov, I. Specific character of objective methods for determining weights of criteria in MCDM problems: Entropy, CRITIC and SD. Decis. Mak. Appl. Manag. Eng. 2021, 4, 76–105. [Google Scholar] [CrossRef]
- Trojan, F.; Fernandez, P.I.R.; Guerreiro, M.; Biuk, L.; Mohamed, M.A.; Siano, P.; Filho, R.F.D.; Marinho, M.H.; Siqueira, H.V. Class thresholds pre-definition by clustering techniques for applications of ELECTRE TRI method. Energies 2023, 16, 1936. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).