Abstract
Compared with other fossil energy sources, natural gas is characterized by compressibility, low energy density, high storage costs, and imbalanced usage. Natural gas pipeline supply systems possess unique attributes such as closed transportation and a highly integrated upstream, midstream, and downstream structure. Moreover, pipelines are almost the only economical means of onshore natural gas transportation. Given that the upstream of the pipeline features multi-entity and multi-channel supply including natural gas, coal-to-gas, and LNG vaporized gas, while the downstream presents a competitive landscape with multi-market and multi-user segments (e.g., urban residents, factories, power plants, and vehicles), there is an urgent social demand for non-discriminatory and fair opening of natural gas pipeline network infrastructure to third-party entities. However, after the fair opening of natural gas pipeline networks, the original “point-to-point” transaction model will be replaced by market-driven behaviors, making the verification and allocation of gas transmission capacity a key operational issue. Currently, neither pipeline operators nor government regulatory authorities have issued corresponding rules, regulations, or evaluation plans. To address this, this paper proposes a multi-dimensional quantitative evaluation model based on the Analytic Hierarchy Process (AHP), integrating both commercial and technical indicators. The model comprehensively considers six indicators: pipeline transportation fees, pipeline gas line pack, maximum gas storage capacity, pipeline pressure drop, energy consumption, and user satisfaction and constructs a quantitative evaluation system. Through the consistency check of the judgment matrix (CR = 0.06213 < 0.1), the weights of the respective indicators are determined as follows: 0.2584, 0.2054, 0.1419, 0.1166, 0.1419, and 0.1357. The specific score of each indicator is determined based on the deviation between each evaluation indicator and the theoretical optimal value under different gas volume allocation schemes. Combined with the weight proportion, the total score of each gas volume allocation scheme is finally calculated, thereby obtaining the recommended gas volume allocation scheme. The evaluation model was applied to a practical pipeline project. The evaluation results show that the AHP-based evaluation model can effectively quantify the advantages and disadvantages of different gas volume allocation schemes. Notably, the gas volume allocation scheme under normal operating conditions is not the optimal one; instead, it ranks last according to the scores, with a score 0.7 points lower than that of the optimal scheme. In addition, to facilitate rapid decision-making for gas volume allocation schemes, this paper designs a program using HTML and develops a gas volume allocation evaluation program with JavaScript based on the established model. This self-developed program has the function of automatically generating scheme scores once the proposed gas volume allocation for each station is input, providing a decision support tool for pipeline operators, shippers, and regulatory authorities. The evaluation model provides a theoretical and methodological basis for the dynamic optimization of natural gas pipeline gas volume allocation schemes under the fair opening model. It is expected to, on the one hand, provide a reference for transactions between pipeline network companies and shippers, and on the other hand, offer insights for regulatory authorities to further formulate detailed and fair gas transmission capacity transaction methods.
1. Introduction
As the social economy develops rapidly, the demand for energy keeps growing. Natural gas, serving as a clean and efficient transitional energy source, has been playing an increasingly prominent role in the transformation of the energy structure. However, its inherent differences from other energy sources have made the issue of pipeline gas volume allocation a key bottleneck that urgently needs to be broken through. In the past, a “point-to-point” transaction model was applied in gas transmission networks. Specifically, the pipeline gas source, user location, and the daily gas distribution volume of users were relatively fixed, and gas transmission and distribution were strictly implemented in accordance with the plans specified in the purchase and sales contracts. This model has severely restricted the vitality of the natural gas market, failed to give full play to the decisive role of the market in resource allocation, and hindered the efficient operation of the entire natural gas industry supply chain [1,2].
Compared with crude oil and refined oil, which can be conveniently stored in storage tanks, the storage cost of natural gas is extremely high. This is because natural gas is usually stored in the form of Liquefied Natural Gas (LNG), a method that requires a large amount of energy for refrigeration and liquefaction, resulting in poor economic efficiency. For long-distance on-land transportation, pipeline transportation is the only economical option. Tank trucks using the Compressed Natural Gas (CNG) tube bundle storage method do not have the advantage of large-scale transportation, which also determines that the supply of natural gas is highly dependent on pipeline transportation capacity.
For this reason, the current pipeline gas volume allocation method has obvious shortcomings: ① Within the same price region, the longer the transmission distance and the larger the allocated gas volume, the greater the pipeline transmission revenue. This easily leads to a shortage of gas supply in areas near the gas source, implying discrimination against users with short-distance transmission needs; ② The collection of pipeline transmission fees does not take into account costs such as compressor energy consumption, labor, and equipment maintenance. For example, there are differences in energy consumption and gas supply pressure between the inlet and outlet of the compressor, so it is obviously unreasonable to implement the same charging standard; ③ According to the hydraulic and thermal equations of pipeline transmission, different gas volume allocation schemes along the pipeline will have an impact on the pipeline’s own gas transmission capacity and in-pipeline gas storage volume. That is, some users should additionally bear the costs caused by their significant impact on pipeline transportation [3,4,5]. Precisely due to the unique properties of natural gas, the above-mentioned issues indicate that the evaluation of natural gas pipeline gas volume allocation schemes or gas transmission capacity allocation schemes is an urgent task.
To solve these problems and promote the healthy development of the natural gas market, governments and regulatory authorities around the world have successively issued policies to advance fair and open access to oil and gas pipeline networks. In the early 21st century, the European Union took the lead in promoting the third-party access mechanism for natural gas infrastructure and adopted directives such as 2003/55/EC. These directives require that gas transmission, distribution, and storage facilities provide fair and non-discriminatory access to third-party market entities, laying the foundation for the integration and development of the European natural gas market [6]. The 2009 Resolution 715 of the European Commission (EC) has stipulated the Framework Guidelines (FG) and the scope of Network Codes (NC), including: codes for the safety and reliability of pipeline networks, network connection, third-party access specifications, data exchange and settlement, interoperability, operating procedures in emergency situations, capacity allocation and congestion management specifications, specifications related to the technical operation of pipeline network access services and system balancing, transparency specifications, balancing specifications, specifications for unified transmission tariffs, and the energy efficiency of natural gas pipeline networks [7].
In North America, the United States and Canada have also established mature regulatory systems for open access to pipeline networks. The U.S. Federal Energy Regulatory Commission (FERC) introduced a series of regulations requiring pipeline companies to provide transportation services to all users under equal conditions. These rules standardize natural gas pipeline pricing mechanisms and capacity allocation methods, ensuring that pipeline operators serve shippers in a fair and transparent manner. This facilitated a fundamental transformation in the U.S. natural gas industry, transitioning from initial natural monopoly pricing and comprehensive regulation phases to a deregulated stage, further advancing toward full marketization [8,9,10,11].
In Japan, a fair open access system for pipeline facilities was proposed in 2004. However, due to the dominance of regional monopolies and the lack of a unified nationwide management system, the effectiveness of this openness has been limited [12]. These international practices demonstrate that fair and open access to pipeline networks is an effective means of optimizing resource allocation, enhancing market competition, and improving infrastructure utilization efficiency.
In China, following the establishment of the China Oil & Gas Piping Network Corporation (Pipe China) in 2019, a preliminary “X + 1 + X” fair open access system for oil and gas pipelines has taken shape. This system features multi-entity, multi-channel supply of upstream oil and gas resources (X), efficient and unified midstream pipeline transmission (1), and fully competitive downstream sales markets (X). The Chinese government has also issued multiple policy documents requiring pipeline operators to disclose transmission capacity and remaining availability, improve the fair access mechanism for oil and gas pipelines, and promote the fair opening of main and interprovincial pipelines to third-party market entities [13,14].
As global energy market-oriented reform continues to deepen, fair and open access to natural gas pipeline networks has become a common trend. However, in the process of implementing this mechanism, a key challenge has emerged: how to formulate a scientific and reasonable natural gas volume allocation scheme. The gas volume allocation of natural gas pipelines involves the interests of multiple parties, including pipeline operators, shippers, and end-users. It is necessary to take into account not only commercial factors such as pipeline transportation costs and market demand but also technical factors such as pipeline storage capacity, pressure drop, and energy consumption. The stable operation of the pipeline network is the prerequisite and foundation for the production and processing of natural gas in upstream gas fields and the development of the downstream gas-consuming market [15,16]. When the pipeline transmission capacity is limited, an unreasonable allocation scheme may lead to low utilization efficiency of pipeline capacity, unfair distribution of interests among various stakeholders, and even pose a threat to the safe and stable operation of the pipeline network.
The Analytic Hierarchy Process (AHP), with its core advantage of combining qualitative and quantitative analysis, has been widely applied to the optimization and evaluation of multi-objective systems. Wang et al. [17] constructed a corrosion risk assessment model that integrates the improved AHP and Bayesian network for the subsea pipelines of an oil production plant. This model has established a complete assessment system, including 2 first-level indicators (internal and external corrosion), 8 s-level indicators, and 27 fourth-level indicators. By introducing grey relational analysis to quantify the relationship between the corrosion rate and various factors, the dependence of the assessment process on experts’ subjective experience has been effectively reduced, thereby improving the objectivity and accuracy of the results. He et al. [18] developed a model that combines AHP and Fuzzy Comprehensive Evaluation (FCE) to efficiently assess and screen oil and gas reservoirs suitable for conversion into Underground Gas Storage (UGS). This model has established a complete assessment system and standards, including 6 first-level indicators and 44 s-level indicators, which can provide objective and accurate technical support for the screening of UGS targets. To improve the safety management level of LNG receiving terminals, Tian et al. [19] developed a multi-level safety assessment model based on AHP. After identifying key safety factors through literature review and expert interviews, AHP was used to assign weights and sort these factors, ensuring the scientificity and practicality of the model. The results of this study can provide a basis for the formulation of safety policies and the revision of standards, thereby improving the overall safety management level of the industry. Diao et al. [20] adopted a model that combines AHP and fuzzy theory to assess the risk of domino effects caused by pipeline leaks. AHP was used to evaluate the competence of experts, and fuzzy theory was applied to convert their judgments into the occurrence probability of basic events. Qualitative analysis shows that the formation conditions of flammable mixtures account for the highest proportion in terms of structural importance. Quantitative results have verified that this hybrid method can effectively assess the risk of pipeline domino effects and provide support for the risk management and decision-making of petrochemical pipelines. Therefore, in the complex decision-making scenario of the fair and open natural gas pipeline network, it is necessary to establish a gas volume allocation scheme evaluation model. This model should clarify the key influencing factors of the natural gas pipeline network gas volume allocation scheme, their weight proportions, and the calculation method of the optimal gas volume allocation scheme. In this way, the optimal gas volume allocation scheme for natural gas pipelines under the fair and open model can be reasonably determined, and the core problems of complex gas volume allocation indicators and difficult quantification of interest conflicts under the fair and open model can be effectively solved. On the one hand, this can provide a reference basis for transactions between pipeline operators and shippers; on the other hand, it can also provide new ideas for regulatory authorities to formulate more detailed and fair gas transmission capacity transaction rules.
Based on the above background, this paper proposes a multi-dimensional evaluation system that integrates commercial indicators and technical indicators. The relative importance of each indicator is quantified through AHP. The Computational Fluid Dynamics (CFD) numerical method is used to establish and calculate the pipeline network flow model to accurately assess each evaluation indicator [21]. At the same time, a decision-support program for evaluating the natural gas pipeline gas volume allocation scheme based on model and algorithm programming has been developed. This method can not only solve the problem of balancing fairness and economy in traditional gas volume allocation but also provide a standardized evaluation framework for dynamic gas volume transactions after the opening of pipeline network facilities. The following sections will elaborate on the construction process of the evaluation model, the method for determining indicator weights, and the application effect in actual pipeline cases.
2. Establishment of an Evaluation Model for Gas Allocation Schemes
2.1. Model Design
After the fair and open access of pipeline networks is implemented, the evaluation of natural gas pipeline gas volume allocation schemes becomes more important and complex. The gas volume allocation may be affected by six factors, including pipeline transmission fees, line pack, maximum gas storage capacity, gas transmission pressure drop, energy consumption, and user satisfaction [22]. In this study, these six key factors were adopted as the evaluation indicators for the schemes. Mathematical formulas and self-developed software were used to calculate the scores of each evaluation indicator corresponding to different gas volume allocation schemes, and the weight proportion of each evaluation indicator was determined based on the Analytic Hierarchy Process (AHP).
In accordance with the principle of fair and open access, targeted analyses were conducted on each of the six core influencing factors, and the theoretical optimal values of each evaluation indicator were reasonably set based on these analyses. Among them, the theoretical optimal values of pipeline transmission fees and gas storage capacity were set as their respective theoretical maximum values; the theoretical optimal values of pipeline pressure loss and compressor energy consumption were set as their respective theoretical minimum values; the theoretical optimal value of line pack was determined according to boundary conditions such as the maximum operating pressure of the pipeline and the minimum inlet pressure of the compressor; and a score of 100 was set as the theoretical optimal value of user satisfaction. Subsequently, the calculated score of each indicator was determined based on the deviation between each evaluation indicator under different gas volume allocation schemes and its theoretical optimal value. Combined with the weight proportion, the total score of each gas volume allocation scheme was finally determined, thereby obtaining the recommended scheme for the optimal gas volume allocation of the pipeline.
To enhance the applicability of the evaluation method, mathematical fitting is employed to establish functional relationships between the gas volumes allocated to each station and the evaluation indicators. The predetermined indicator weights, along with the derived functional relationships and algorithms, are embedded into the backend database of a computer program. A web-based evaluation tool is developed using HTML for the front-end interface and JavaScript for the core logic. This tool allows users to input proposed gas allocation volumes for each customer, automatically generating an evaluation score for the scheme, thereby streamlining the assessment process. Furthermore, the program can be extended to both pipeline operators and end-users, facilitating data sharing and supporting the fair and open design of pipeline transmission capacity. The evaluation process for gas allocation schemes under the fair and open access mode is illustrated in Figure 1.

Figure 1.
Evaluation process of natural gas pipeline capacity allocation scheme under fair and open access mode.
2.2. Evaluation Index System
For natural gas pipeline capacity allocation, evaluation indicators are determined from both commercial aspects (such as transportation tariffs and user satisfaction) and technical aspects (including line pack, terminal pressure drop, pipeline storage capacity, and energy consumption). Through multiple case studies, various software tools and computational formulas are employed to obtain values for each indicator, thereby establishing a comprehensive evaluation indicator system.
2.2.1. Commercial Indicators
(1) Transportation Tariff
In natural gas pipelines, the transportation tariff serves as a commercial indicator for evaluating pipeline transmission. Its calculation is typically based on the volume of natural gas transported, the transmission distance, and the applicable tariff rate. If the tariff is determined using a zonal pricing method, the fee for Zone 1 is denoted as f1, while that for Zone 2 is denoted as f2. The calculation formula for the transportation tariff is provided in Equation (1).
In the formula, F represents the pipeline transportation cost (in RMB); fi denotes the pipeline transportation cost for each price zone (in RMB/(m3·km)); Qi indicates the unit hourly pipeline transportation volume at different off-take points (in m3); li represents the calculated distance for each off-take point (in km).
(2) User Satisfaction
When evaluating the overall user satisfaction of the pipeline at offtake points, to ensure the objectivity and accuracy of the results, the average value of user satisfaction at all offtake points along the pipeline was calculated and used as the overall satisfaction. This method can fully reflect the actual feelings of users at each offtake point, thereby obtaining a more representative evaluation result of overall satisfaction.
By means of the random sampling method, and based on the statistical data of user satisfaction for the pipeline along the Luntai-Turpan section of the First West-East Gas Pipeline operated by China National Oil and Gas Pipeline Network Group Co., Ltd. (headquartered in Beijing, China), the correlation between different offtake volumes and user satisfaction was fitted, as shown in Figure 2. Its empirical formula is approximately a parabolic function (see Equation (2)), and the R2 value of the fitting formula is 0.9354, which indicates that the empirical formula has a good fitting degree with the actual user satisfaction. It can be known from this formula that the nonlinear relationship between gas transmission volume and user satisfaction leads to the existence of an optimal gas transmission volume. To meet market demand and improve service quality, pipeline operators need to optimize user satisfaction by adjusting the gas transmission volume.
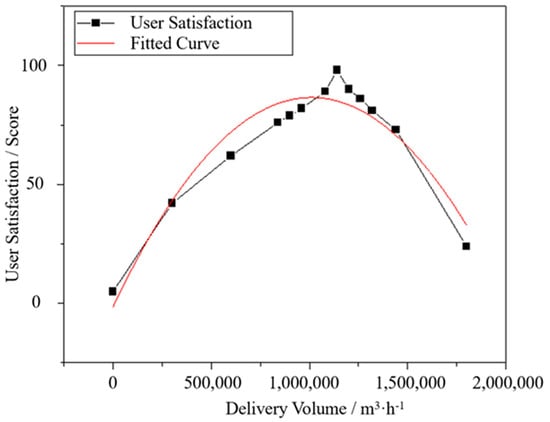
Figure 2.
Analysis diagram of user satisfaction curve.
In the formula, Qi represents the gas delivery volume (m3/h); Ei denotes the satisfaction level of each user (points).
The calculation method for the total user satisfaction score can be referred to in Equation (3).
In the formula, E represents the overall user satisfaction of the pipeline (points); Ei denotes the user satisfaction at different off-take points (points); n indicates the number of users (households).
2.2.2. Technical Indicators
(1) Line pack
Line pack refers to the volume of natural gas stored within the pipeline at a specific moment. The calculation formula is provided in Equation (4) [23]. To ensure the rationality and economy of the line pack, it is necessary to select an appropriate line pack based on actual conditions.
In the formula, LP represents the line pack (m3); V denotes the pipeline volume (m3); P is the actual average pressure of the pipeline segment (MPa); T indicates the actual average temperature of the pipeline segment (K); Z stands for the actual gas compression factor; Psc refers to the pressure under standard conditions (MPa); Tsc is the temperature under standard conditions (K); Zsc represents the ideal gas compression factor.
(2) Pressure Drop in Gas Transmission
The pressure drop in gas transmission is one of the key indicators for evaluating pipeline transportation performance, reflecting the pressure loss during the natural gas delivery process. The starting or ending pressure can be calculated using the Weymouth equation (Equations (5) and (6)) [24].
In the formula, Q represents the volumetric flow rate of the gas pipeline under engineering standard conditions (m3/s); pQ denotes the starting pressure of the calculated pipeline segment (Pa); pZ indicates the ending pressure of the calculated pipeline segment (Pa); D is the internal diameter of the pipeline (m); λ stands for the hydraulic friction coefficient; Z refers to the compression factor of natural gas under pipeline transportation conditions; ∆* represents the relative density of natural gas; T is the gas transportation temperature (K); L denotes the calculated length of the pipeline segment (m); Cw is the coefficient in the Weymouth equation. According to the unit system selected in this paper, its value is set to 0.3967.
By integrating the Sukhov equation and considering the axial temperature drop caused by the Joule-Thomson effect, the thermal calculation equation (see Equations (7) and (8)) can be derived [25].
In the formula, T0 represents the ambient temperature (K); TQ denotes the starting temperature of the pipeline segment (K); K is the overall heat transfer coefficient of the pipeline (W/(m2·K)); M indicates the mass flow rate (kg/s); cp stands for the isobaric specific heat capacity of natural gas (J/(kg·K)); Di refers to the throttling effect coefficient of natural gas.
Based on the fundamental equations of hydraulic and thermal calculations for natural gas, steady-state solutions can be derived to determine the pressure drop during gas transmission.
(3) Pipeline Gas Storage Capacity
Pipeline gas storage capacity is another key indicator for evaluating the performance of a pipeline system, reflecting its buffering capability in response to demand fluctuations. While the gas supply volume from sources remains relatively stable, the gas consumption of users along the pipeline may vary dynamically over time. Therefore, the storage capacity of the pipeline’s last segment serves as an effective solution to balance gas supply and demand imbalances.
The minimum storage capacity is calculated based on the average pressure at the initial moment of gas storage in the pipeline’s last segment (see Equation (9)), while the maximum storage capacity is determined by the average pressure at the end of the storage period (see Equation (10)). The storage capacity of the last pipeline segment can then be derived (see Equation (11)) [26,27]. The calculation process incorporates key evaluation metrics such as pipeline volume, compression factor, temperature, and pressure to ensure the accuracy of the assessment. By applying these formulas, the operational status of the pipeline system under different gas allocation scenarios can be analyzed, thereby evaluating its storage capacity.
In the formula, ppjmin represents the average pressure at the initial moment of gas storage in the pipeline’s last segment (Pa); ppjmax denotes the average pressure at the end of the gas storage period (Pa); Vmin indicates the gas storage volume in the last segment at the initial moment of storage (m3); Vmax stands for the gas storage volume in the last segment at the end of the storage period (m3); V refers to the geometric volume of the last pipeline segment (m3); lZ is the length of the last segment involved in gas storage (m); Z1, Z2 are the compression factors under the average pressure and temperature at the start and end of the storage period, respectively. They can be approximated as Z1 = Z2 = Z; T1, T2 are the average temperatures of the last segment at the start and end of the storage period, respectively. They can be approximated as T1 = T2 = T; p0 is the pressure under engineering standard conditions (Pa); Z0 is the compression factor at pressure p0 and temperature T0; T0 is the temperature under engineering standard conditions (K).
(4) Energy Consumption
Energy consumption is a critical cost evaluation metric in the natural gas transmission process and one of the key indicators for assessing the economic rationality of gas allocation schemes. The energy consumption of compressors during pipeline transportation can be approximated as the total energy consumption of the pipeline system. The compressor energy consumption is calculated using Equation (12) below [28].
In the formula: N represents the compressor shaft power (kW); T1 denotes the inlet gas temperature of the compressor (K); R is the gas constant; Z indicates the gas compression factor; ε stands for the compressor pressure ratio; η refers to the compressor efficiency, with a value of 0.94; M is the natural gas mass flow rate (kg/s); k represents the polytropic index of natural gas, with a value of 1.3.
2.3. Determination of Indicator Weights Based on AHP
2.3.1. Hierarchy Construction and Judgment Matrix Formation
The Analytic Hierarchy Process (AHP) is an effective tool for multi-objective decision analysis. This method decomposes complex problems into different evaluation indicators by constructing a hierarchical structure model, and pairwise comparisons of these indicators are conducted to determine their relative importance in the decision-making process. For long-distance natural gas pipelines: The goal layer consists of different gas transmission schemes; The criterion layer includes pipeline transportation cost, line pack, maximum storage capacity, pressure drop, energy consumption, and user satisfaction; The alternative layer comprises different operation and management schemes. The AHP hierarchical structure is illustrated in Figure 3.
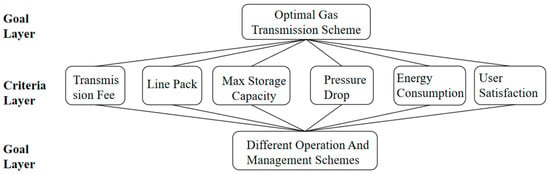
Figure 3.
AHP Hierarchical Structure Diagram.
When constructing the judgment matrix, pairwise comparisons of different elements within the same hierarchy need to be conducted to evaluate their relative importance. In the AHP analysis, an expert group consisting of 5 members was formed, including 1 gas transmission pipeline designer, 2 operation management personnel, 1 financial management personnel, and 1 regulatory authority staff. The experts were invited to conduct pairwise comparisons of the indicators level by level, and the 1–9 scaling method was adopted to assign values to the elements of the judgment matrix. The relative importance between two elements was quantified by numbers: the number 1 indicates that the two elements are equally important; the number 3 means one element is slightly more important than the other; the number 5 represents one element is obviously more important than the other; the number 7 denotes one element is strongly more important than the other; and the number 9 indicates one element is extremely more important than the other.
Taking the evaluation indicators of pipeline transportation cost and line pack as an example, it is generally considered that pipeline transportation cost holds higher importance for the overall operational efficiency of natural gas pipeline transmission. When assigning values to these two indicators, pipeline transportation cost would receive a higher scale value (taken as 2), while line pack would receive a lower scale value (taken as 1/2), reflecting the relative importance of pipeline transportation cost over line pack. Following this approach, the judgment matrix is established as shown in Equation (13).
Here, both i and j represent the evaluation indicators: pipeline transportation cost, line pack, maximum storage capacity, pressure drop, energy consumption, and user satisfaction.
This judgment matrix reflects the relative importance among the evaluation indicators. Use this judgment matrix to calculate the weight vector of each evaluation indicator and conduct a consistency test. This will help determine whether the judgment matrix can be accepted and the relative weights of each evaluation indicator in the decision-making process.
2.3.2. Calculation of Weight Vector and Consistency Check
Calculating the weight vector is an important step in reflecting the relative importance of each evaluation indicator in decision-making. The calculation of the weight vector is usually based on a judgment matrix, by solving for the largest eigenvalue of the judgment matrix and its corresponding eigenvector. The weight vector can be specifically calculated according to the following steps:
Normalize each column of the judgment matrix, i.e., divide each element by the sum of its column, to obtain the normalized matrix Bij (see Equation (14)). Specifically, for the j-th column of the judgment matrix A, the elements are a1,j, a2,j, …, amj. Then calculate the column sum , Subsequently, for each element in the j-th column, the normalized element , After this processing, the elements of each column sum to 1. Next, sum the normalized matrix by rows to obtain a column vector (see Equation (15)). Similarly, normalize this column vector. Finally, calculate the scoring weight matrix Xi for each evaluation indicator, where xi represents the weight of each indicator (see Equation (16)). The calculation results of the weights for each evaluation indicator are shown in Table 1.

Table 1.
Scoring weight table for each evaluation indicator.
Among them, i, j ∈ {1, 2, 3, 4, 5, 6} represent pipeline transportation cost, line pack, maximum gas storage capacity, pressure drop, energy consumption, and user satisfaction, respectively.
These weights reflect the relative importance of each evaluation indicator in the assessment, providing a critical basis for subsequent decision-making analysis. However, it is still necessary to conduct a consistency check on the results. The consistency check is a crucial step in the Analytic Hierarchy Process (AHP), used to evaluate the consistency degree of the judgment matrix and ensure the rationality and reliability of the decision outcomes. By performing the consistency check, it is possible to guarantee the consistency and precision of the decision-making process, thereby promptly identifying and correcting logical contradictions within the judgment matrix. The consistency check is typically carried out by calculating the consistency ratio (CR) of the judgment matrix, as shown in Equation (17).
In the formula, CI is the consistency index that measures the consistency of the judgment matrix; RI is the average random consistency index of the same order (where the order n is identical). The value of RI is typically determined by referring to a predefined table or through calculation.
The formula for calculating CI is shown in Equation (18).
In the formula, λmax is the maximum eigenvalue of the judgment matrix, and n is the order of the judgment matrix (i.e., the number of evaluation indicators, which is set to 6 in this paper).
If the CR value is less than 0.1, the inconsistency level of the matrix is considered acceptable; if the CR value exceeds 0.1, the test fails, and the relative importance of each evaluation indicator must be reassessed until the CR value meets the consistency requirement. For calculating the maximum eigenvalue λmax, various numerical methods can be employed, with the power method being one common approach, and another method involves direct computation using linear algebra software. This paper utilizes the built-in tools of the commercial software MATLAB (R2021 b) to directly compute the value of λmax. For the judgment matrix in the table above, the calculated maximum eigenvalue λmax is 6.3852, and the consistency index CI is 0.07704. The RI value is typically obtained by referring to a standard table; for a 6th-order judgment matrix, this paper adopts a typical RI value of 1.24, resulting in a calculated CR value of 0.06213. Since the CR value is less than 0.1, the consistency test confirms that the consistency of the judgment matrix is satisfactory, and the weight vectors of all elements are reasonable and reliable.
2.4. Objective Function
After completing the weight vector calculation and consistency test, the process moves to the scheme evaluation and selection phase. The objective of this stage is to combine the scheme data with the weight vector to assess the advantages and disadvantages of each scheme and select the optimal one, i.e., to calculate the total score of each scheme by integrating the data and the weight vector. For calculating the total score under various operating conditions, the results of the six evaluation indicators for each condition can first be multiplied by their respective weights to obtain the score for each indicator. Then, the overall score for each condition can be calculated by combining the weight distribution and the results of the six evaluation indicators.
However, due to the differences between the actual data and the ideal state data for scoring, the actual data need to be converted into percentage-based scores. The ideal state is set as follows: the pipeline transmission fee and gas storage capacity are at their maximum values, the line pack is at its theoretical optimal value, the pressure drop and energy consumption are at their minimum values, and the user satisfaction is 100 points. The calculated scores of the six evaluation indicators are computed in accordance with Equation (19), and the total score is calculated based on Equation (20). After the scheme evaluation, the optimal scheme is determined according to the level of the comprehensive score.
In the formula, j takes values of 1, 2, 3, 4, 5, and 6, representing pipeline transportation cost, line pack, maximum gas storage capacity, pressure drop, energy consumption, and user satisfaction, respectively; S denotes the total score; Pj represents the calculated score for each evaluation indicator; xj is the weight of each evaluation indicator; Sj is the result score for each evaluation indicator; and Sjop is the optimal result score for each evaluation indicator.
3. Evaluation Program Development
Establishing a customized evaluation model for pipeline gas distribution allocation schemes can overcome the limitations of fixed allocation methods and provide a more comprehensive assessment of the overall benefits of different gas distribution strategies. This model adopts a multi-objective decision-making approach to form a more holistic and scientific evaluation system. To more accurately assess the gas distribution schemes for different stations, functional relationships between the allocated gas volumes at each station and the evaluation indicators are established [29]. These functional relationships serve as the core component of the gas distribution scheme evaluation model, enabling the assessment of the comprehensive benefits of various allocation strategies. This will help identify the optimal gas distribution scheme to maximize both economic and social benefits [30].
The evaluation program operates through a workflow consisting of user-defined offtake volume settings, computation, result display, and feedback. The user interface design emphasizes friendliness and ease of use, including layout, input prompts, result presentation, and operational feedback. The web design adheres to principles of simplicity, intuitiveness, and efficiency, covering page layout, interactive design, visual design, responsive design, and functional flow. The evaluation program uses HTML as the foundational structure for web pages, combined with JavaScript to implement interactivity and dynamic functionality. This allows users to interact via browsers, while JavaScript handles user inputs, computes results, and updates page content. Program users can also perform data management and report generation-related operations through the interactive interface, such as importing, exporting, editing, and storing data related to natural gas pipeline distribution schemes (including offtake point information, offtake volume settings, pipeline parameters, etc.). Additionally, data can be sorted, filtered, and edited. The program uses pop-up windows to receive user-input data, performs background calculations based on this input, and finally updates and displays the results on the interactive page. The workflow of the customized evaluation model for pipeline gas distribution allocation schemes is illustrated in Figure 4.

Figure 4.
Flowchart of the customized evaluation model for pipeline gas offtake allocation scheme.
The program enables users to input offtake volumes for different compressor stations and automatically obtains an evaluation score for the corresponding gas allocation scheme. This ensures fairness in judgment indicators and transparency in data calculations. The model not only helps decision-makers comprehensively understand the strengths and weaknesses of gas allocation schemes but also provides critical reference for optimizing and improving these schemes.
4. Case Study
In this study, a long-distance natural gas pipeline was selected as the research sample. This pipeline is equipped with 1 gas inlet point, 4 offtake points (marked as A to D), and 1 compressor station. It has a total length of 900 km, an outer diameter of 1016 mm, and a wall thickness of 17.5 mm, with a design pressure of 12 MPa and a minimum pressure requirement of 5 MPa at the offtake points. The pipeline transmission capacity is 1.2 × 106 m3/h, and the relevant parameters of the pipeline are listed in Table 2. The topological structure of the pipeline is shown in Figure 5.

Table 2.
Basic parameters of the pipeline.
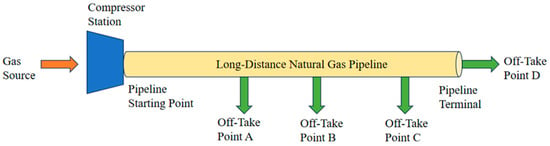
Figure 5.
Schematic diagram of the pipeline topology.
4.1. Gas Allocation Schemes
Under normal operating conditions, the offtake volumes at points A, B, C, and D are 204,000 m3/h, 456,000 m3/h, 252,000 m3/h, and 288,000 m3/h, respectively. Considering a fluctuation range of 80% to 120% for each offtake volume, a total of eight different gas allocation schemes are designed, as shown in Table 3.

Table 3.
Gas allocation at each offtake point under different schemes.
4.2. Calculation Results of Each Indicator
For the eight gas allocation schemes, the basic data of pipeline transmission fee, line pack, maximum gas storage capacity, transmission pressure drop, energy consumption, and user satisfaction for each scheme were obtained by calculating with the above formulas and simulating with TGNET software (V4.0.1), as shown in Table 4.

Table 4.
Evaluation indicator parameters for the eight gas allocation scheme.
The theoretical optimal values of pipeline transmission fee and gas storage capacity are set as theoretical maximum values; the theoretical optimal values of pipeline pressure loss and compressor energy consumption are set as theoretical minimum values; the theoretical optimal value of line pack is determined according to boundaries such as the maximum operating pressure of the pipeline and the minimum inlet pressure of the compressor; and the theoretical optimal value of user satisfaction is set at 100 points. Taking the determination of the theoretical optimal value of line pack as an example, as shown in Figure 6. The line pack is divided into six major control areas. For a certain natural gas pipeline, under the condition of satisfying all constraints such as the compressor operating characteristics of the pipeline system and the minimum pressure requirements of end-users, the maximum line pack can be determined according to the maximum outlet pressure of the compressor (the maximum operating pressure of the pipeline), and the minimum line pack can be determined according to the minimum value of the minimum inlet pressure of the compressor and the minimum pressure of users. The corresponding target line pack, allowable line pack, etc., can all be determined within this range according to the principle of equal division. The theoretical optimal value of line pack is located between the target high line pack and the target low line pack.

Figure 6.
Determination of the theoretical optimal value of line pack.
4.3. Recommended Scheme
After obtaining the specific scores for each of the six evaluation indicators, the total scores and rankings of the eight different schemes were calculated based on the weights of each indicator, as shown in Table 5. The interface of the developed program is illustrated in Figure 7.

Table 5.
Data conclusions for eight different operating conditions.

Figure 7.
Interface of the natural gas pipeline allocation scheme evaluation program under fair open access mode.
From the ranking results, it can be observed that Scheme 6 achieved the highest comprehensive score of 94.40, indicating that it represents the optimal gas allocation strategy. This provides decision-makers with robust support for selecting the most suitable pipeline gas allocation scheme based on specific requirements and conditions in practical applications. Meanwhile, for schemes with lower scores, further analysis is needed to identify the underlying causes, and corresponding optimization measures should be implemented to enhance the overall performance of the gas allocation strategies.
5. Conclusions and Outlook
(1) This study applies the fair open access model to the natural gas market, establishing a weighted scoring framework to evaluate natural gas pipeline allocation schemes. By implementing a fair and open mechanism, it ensures equal opportunities and resources for all parties, promoting healthy competition in the natural gas market.
(2) Six evaluation indicators determining the effectiveness of natural gas pipeline allocation schemes were identified from both commercial and technical perspectives: pipeline transportation cost, line pack, maximum storage capacity, pressure drop, energy consumption, and user satisfaction. Using the Analytic Hierarchy Process (AHP), the weights of these indicators were determined as 0.2584, 0.2054, 0.1419, 0.1166, 0.1419, and 0.1357, respectively.
(3) The six evaluation indicators can be applied in engineering practice to realize the reasonable evaluation of different gas transmission schemes. The self-developed evaluation program for natural gas pipeline gas volume allocation schemes under the fair and open model enables the automatic generation of the evaluation score for a scheme once the allocated gas volume of different offtake stations is input.
(4) To continuously optimize and enhance the effectiveness of the evaluation system, making it adaptable to diverse scenarios and needs, additional evaluation indicators and weight distributions should be incorporated. For example, safety performance indicators such as natural gas leakage risk at stations and environmental impact indicators like waste gas emissions could be included. This would enable a more comprehensive assessment of the advantages and disadvantages of natural gas pipeline allocation schemes.
Author Contributions
Conceptualization, X.L. and D.W.; methodology, D.W.; software, X.L., D.W. and Y.S.; validation, D.W., Y.S. and J.J.; formal analysis, D.W.; investigation, Y.S., J.J. and Z.W.; resources, X.L., D.W. and J.J.; data curation, X.L., D.W. and Y.S.; writing—original draft preparation, X.L., D.W. and Y.S.; writing—review and editing, X.L., D.W. and Y.S.; visualization, X.L., D.W., J.J. and Z.W.; supervision, D.W.; project administration, X.L.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
Supported by the National Natural Science Foundation of China for Regional Fund (52562047); Natural Science Foundation of Xinjiang Uygur Autonomous Region (2023D01A19); Xinjiang Uygur Autonomous Region “Tianchi talents” introduction plan project (TCYC12); Xinjiang Tianshan Innovation Team for Research and Application of High-Efficiency Oil and Gas Pipeline Transportation Technology (2022TSYCTD0002); Xinjiang Uygur Autonomous Region “One Case, One Policy” Strategic Talent Introduction Project (XQZX20240054).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Author Yixun Shi was employed by the company PetroChina. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Tong, X.; Zheng, J.; Fang, B. Strategic analysis on establishing a natural gas trading hub in China. Nat. Gas Ind. B 2014, 1, 210–220. [Google Scholar] [CrossRef][Green Version]
- Bu, Y.; Wu, C.; Zuo, L.; Chen, Q.; Liu, M. Evaluation on gas transmission capacity of gas pipeline network in the open access mode. Nat. Gas Ind. 2021, 41, 129–137. [Google Scholar] [CrossRef]
- Peng, J.; Chen, L.; Liang, G.; Zhou, J.; Li, Z.; Qin, C.; Liu, S. Cooperative operation optimization of natural gas pipeline network and underground gas storage: Economic scheduling and low-carbon control. Geoenergy Sci. Eng. 2025, 257, 214243. [Google Scholar] [CrossRef]
- Zhou, J.; Qin, C.; Liu, S.; He, Y.; Zhang, L.; Peng, J.; Liang, G. A three-model integrated optimization framework for natural gas pipeline capacity operationally efficient and equitable allocation. Appl. Math. Model. 2025, 116416. [Google Scholar] [CrossRef]
- Zhou, J.; Qin, C.; Fu, T.; Liu, S.; Liang, G.; Li, C.; Hong, B. Automatic response framework for large complex natural gas pipeline operation optimization based on data-mechanism hybrid-driven. Energy 2024, 307, 132610. [Google Scholar] [CrossRef]
- Brandao, A.; Soares, I.; Sarmento, P.; Resende, J.; Pinho, J. Regulating international gas transport: Welfare effects of postage stamp and entry–exit systems. Energy 2014, 69, 86–95. [Google Scholar] [CrossRef]
- Hallack, M.; Vazquez, M. European Union regulation of gas transmission services: Challenges in the allocation of network resources through entry/exit schemes. Util. Policy 2013, 25, 23–32. [Google Scholar] [CrossRef]
- Vetter, C.P.; Kuebel, L.A.; Natarajan, D.; Mentzer, R.A. Review of failure trends in the US natural gas pipeline industry: An in-depth analysis of transmission and distribution system incidents. J. Loss Prev. Process Ind. 2019, 60, 317–333. [Google Scholar] [CrossRef]
- Oliver, M.E.; Mason, C.F. Natural gas pipeline regulation in the United States: Past, present, and future. Found. Trends Microecon. 2018, 11, 227–288. [Google Scholar] [CrossRef]
- Mosacula, C.; Chaves-Avila, J.P.; Reneses, J. Reviewing the design of natural gas network charges considering regulatory principles as guiding criteria in the context of the increasing interrelation of energy carriers. Energy Policy 2019, 126, 545–557. [Google Scholar] [CrossRef]
- Oliver, M.E.; Mason, C.F.; Finnoff, D. Pipeline congestion and basis differentials. J. Regul. Econ. 2014, 46, 261–291. [Google Scholar] [CrossRef]
- International Energy Agency. Japan 2021: Energy Policy Review; IEA: Paris, France, 2021; pp. 16–17. [Google Scholar]
- Wang, G.; Cheng, Q.; Zhao, W.; Liao, Q.; Zhang, H. Review on the transport capacity management of oil and gas pipeline network: Challenges and opportunities of future pipeline transport. Energy Strategy Rev. 2022, 43, 100933. [Google Scholar] [CrossRef]
- Wen, W.; Huang, G.; Wu, C.; Yin, Y.; Yang, R.; Sun, M. Design and suggestions on open natural gas infrastructure system based on synergetic supply guarantee responsibilities. Oil Gas Storage Transp. 2024, 43, 614–623. [Google Scholar] [CrossRef]
- Wang, F.; Kobina, F. The Influence of Geological Factors and Transmission Fluids on the Exploitation of Reservoir Geothermal Resources: Factor Discussion and Mechanism Analysis. Reserv. Sci. 2025, 1, 3–18. [Google Scholar] [CrossRef]
- Wu, J.; Ansari, U. From CO2 Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs. Reserv. Sci. 2025, 1, 19–35. [Google Scholar] [CrossRef]
- Wang, W.; Jiang, S.; Liu, J.; Cui, G. An evaluation method for pipeline corrosion risk index weighting in beach and sea oil fields based on combined weighting with improved hierarchical analysis and Bayesian networks. Appl. Ocean Res. 2025, 158, 104522. [Google Scholar] [CrossRef]
- He, Y.; Zhao, G.; Tang, Y.; Song, J.; Chen, Y. Available target evaluation of underground gas storage based on AHP-FCE methods. Geoenergy Sci. Eng. 2024, 242, 213255. [Google Scholar] [CrossRef]
- Tian, L.; Xiao, L.; Song, T. Safety Key Elements and Performance Indicators Analysis of LNG Receiving Stations Based on AHP. Procedia Comput. Sci. 2025, 262, 473–482. [Google Scholar] [CrossRef]
- Diao, X.; Jiang, J.; Mebarki, A.; Ni, L.; Duo, Y.; Chen, S.; Wang, Y.; Zhang, S. Risk analysis of domino effect of leakage accident of petrochemical pipeline based on analytic hierarchy process and fuzzy fault tree analysis. Saf. Sci. 2025, 187, 106852. [Google Scholar] [CrossRef]
- Karpenko, M. Aircraft hydraulic drive energy losses and operation delay associated with the pipeline and fitting connections. Aviation 2024, 28, 1–8. [Google Scholar] [CrossRef]
- Demissie, A.; Zhu, W.; Belachew, C.T. A multi-objective optimization model for gas pipeline operations. Comput. Chem. Eng. 2017, 100, 94–103. [Google Scholar] [CrossRef]
- Marfatia, Z.; Li, X. On steady state modelling for optimization of natural gas pipeline networks. Chem. Eng. Sci. 2022, 255, 117636. [Google Scholar] [CrossRef]
- Amani, H.; Kariminezhad, H.; Kazemzadeh, H. Development of natural gas flow rate in pipeline networks based on unsteady state Weymouth equation. J. Nat. Gas Sci. Eng. 2016, 33, 427–437. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, N.; Wang, B.; Liao, Q.; Qiu, R.; Wei, X.; Zhang, H.; Liang, Y. A mathematical framework for modeling and designing a long distance cryogenic liquefied natural gas pipeline: A practical study and analysis in Shandong, China. Energy Convers. Manag. 2024, 312, 118516. [Google Scholar] [CrossRef]
- Chen, Q.; Wu, C.; Zuo, L.; Mehrtash, M.; Wang, Y.; Bu, Y.; Sadiq, Y.; Cao, Y. Multi-objective transient peak shaving optimization of a gas pipeline system under demand uncertainty. Comput. Chem. Eng. 2021, 147, 107260. [Google Scholar] [CrossRef]
- Chen, Q.; Zuo, L.; Wu, C.; Cao, Y.; Bu, Y.; Chen, F.; Sadiq, R. Supply reliability assessment of a gas pipeline network under stochastic demands. Reliab. Eng. Syst. Saf. 2021, 209, 107482. [Google Scholar] [CrossRef]
- Wei, X.; Qiu, R.; Zhang, B.; Liu, C.; Wang, G.; Wang, B.; Liang, Y. Operation optimization of large-scale natural gas pipeline networks based on intelligent algorithm. Energy 2024, 310, 133258. [Google Scholar] [CrossRef]
- Liang, G.; Li, C.; Zhou, J.; Qin, C.; Peng, J.; Peng, S.; Fu, T.; Ma, J.; Xiong, Z. Intelligent Decision-Making Method and Software for Natural Gas Pipeline Operation Scheme. J. Pipeline Syst. Eng. Pract. 2025, 16, 04025012. [Google Scholar] [CrossRef]
- Schmidt, M.; Steinbach, M.C.; Willert, B.M. High detail stationary optimization models for gas networks: Validation and results. Optim. Eng. 2016, 17, 437–472. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).