Measuring and Simulating Wind Farm Wakes in the North Sea for Use in Assessing Other Regions
Abstract
1. Introduction
2. Methodology
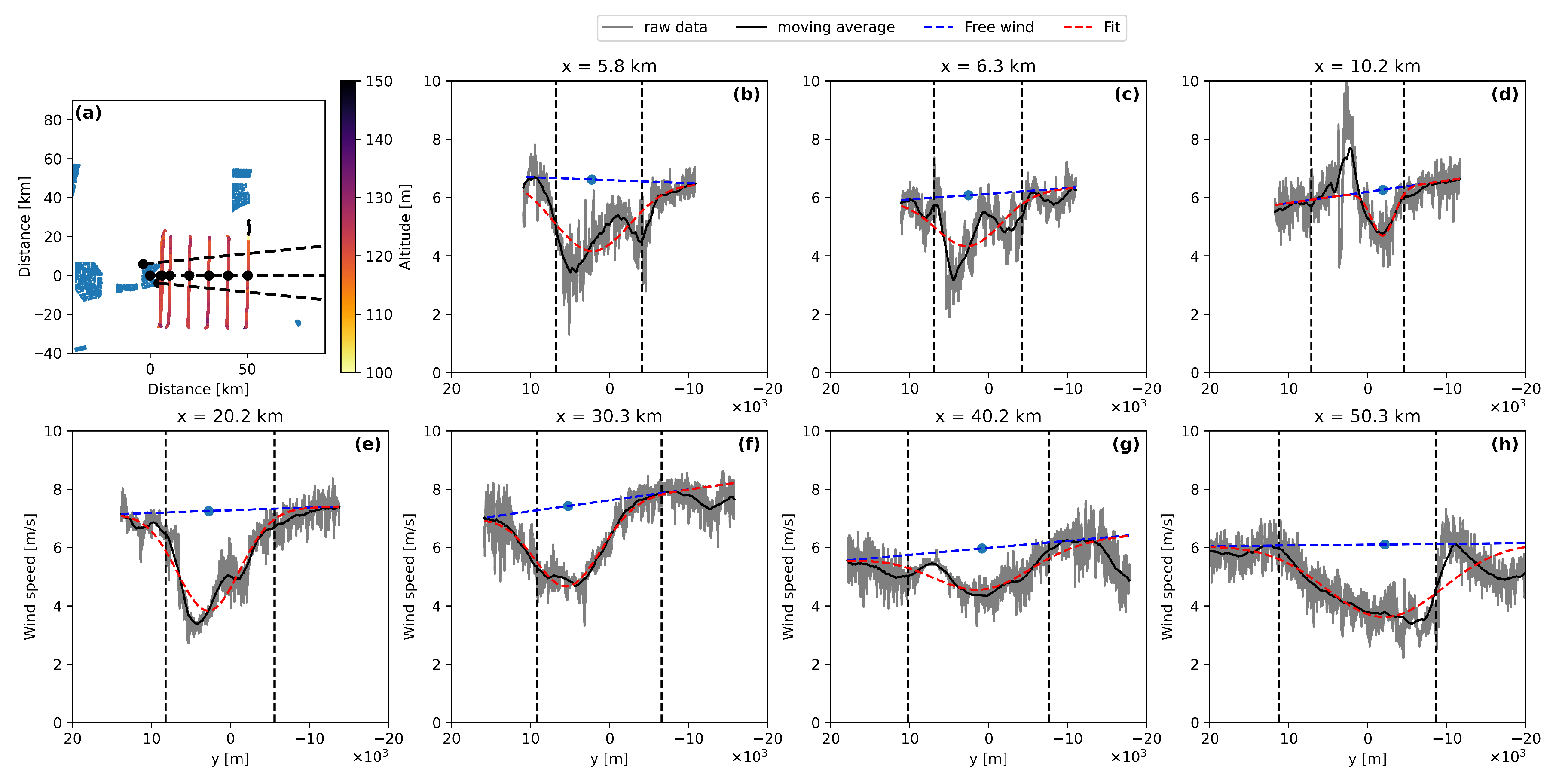
2.1. Flight Measurements of Cluster Wakes
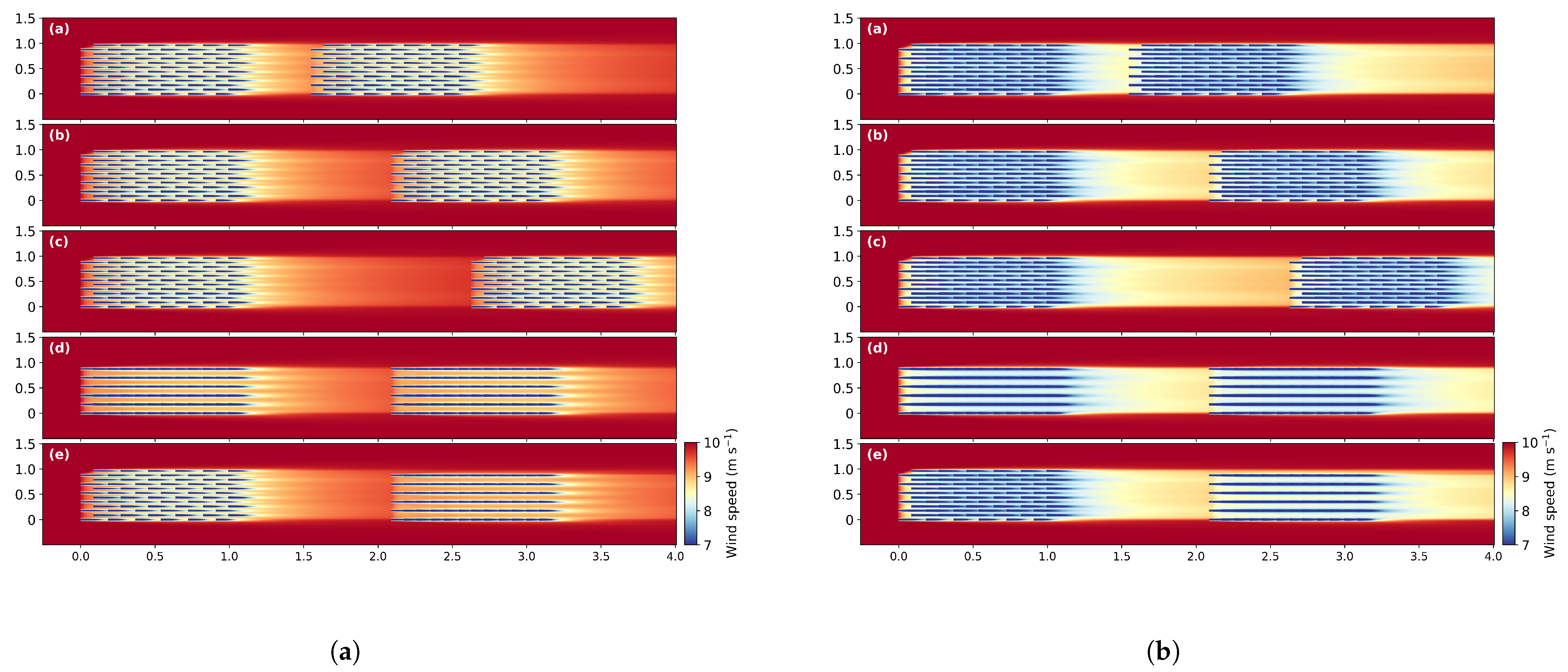
2.2. Engineering Wake Models
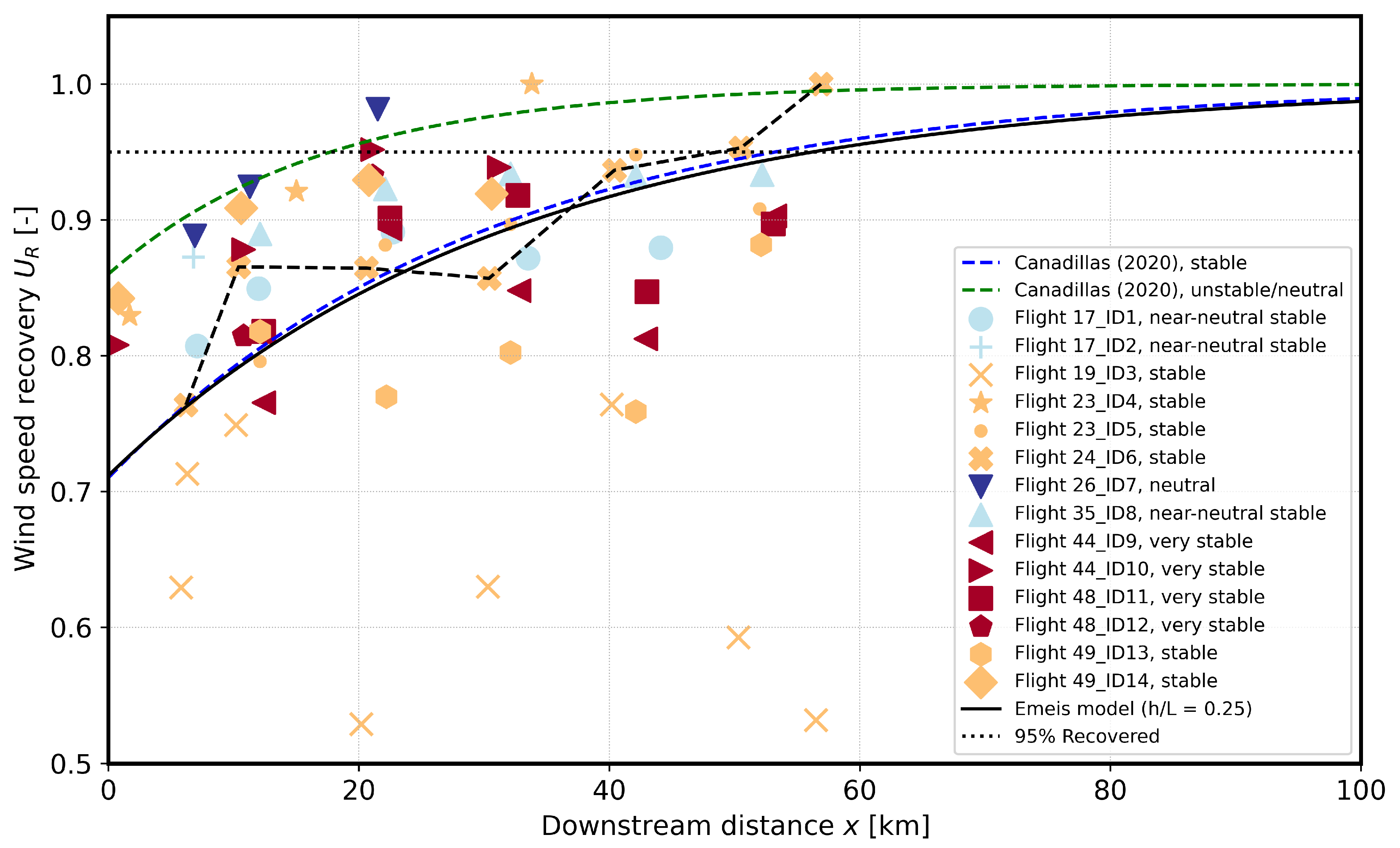
3. Measured and Simulated Cluster Wakes
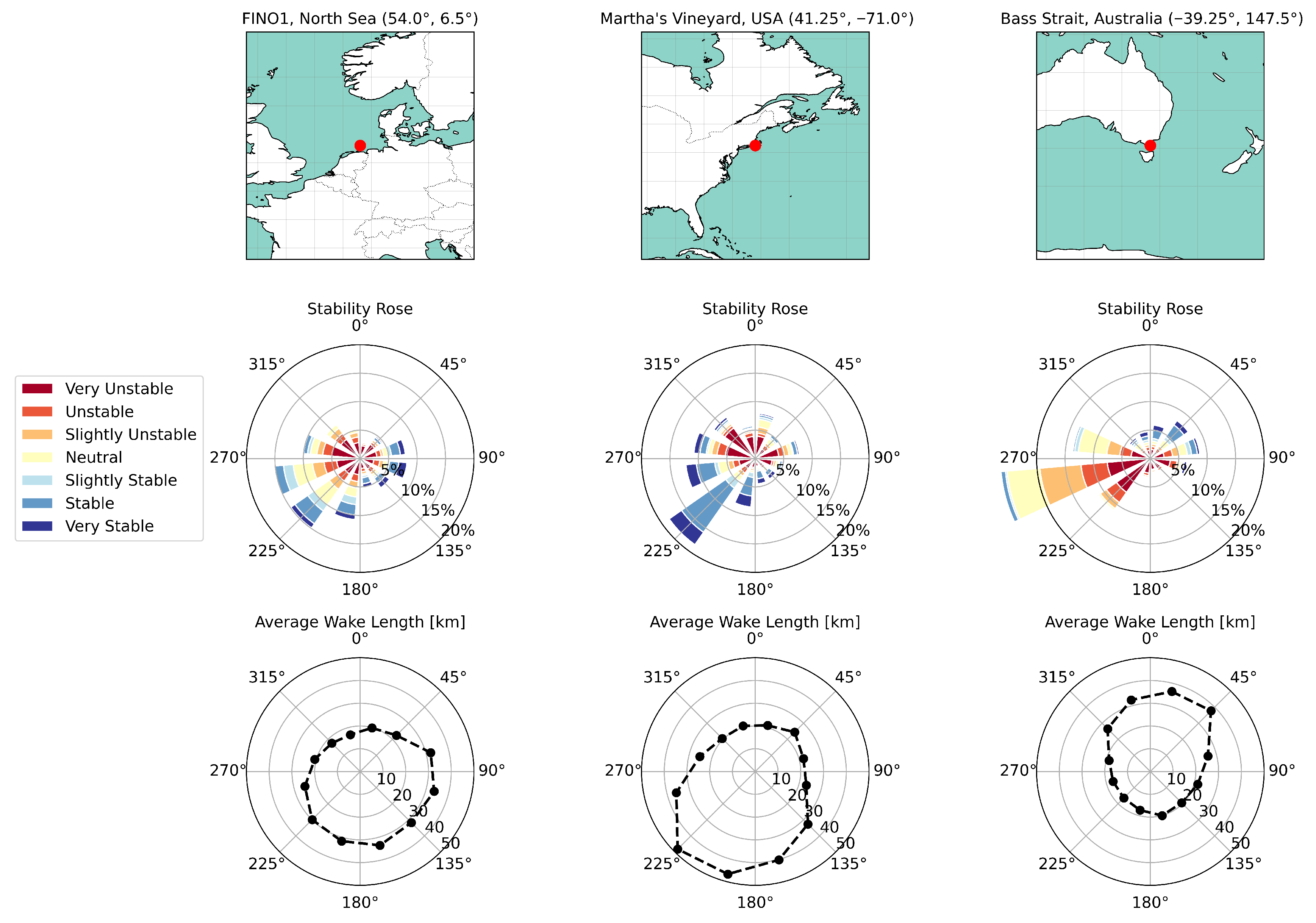
4. Wake Length Scenarios
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
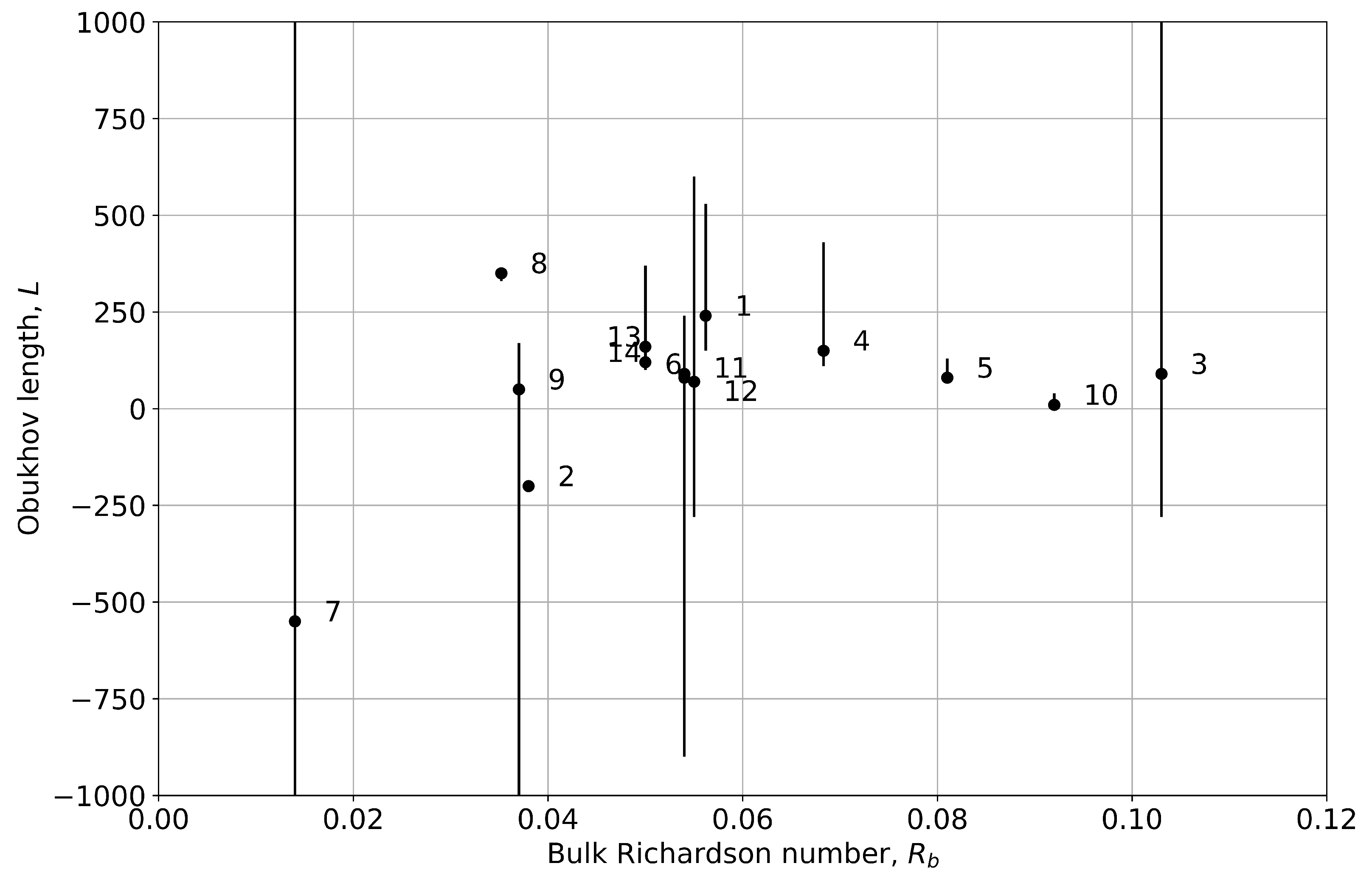
Appendix A. Stability Classification
| Stability | Obukhov Length [m] | Wake Length [km] |
|---|---|---|
| Very stable | 60 | |
| Stable | 60 | |
| Near-neutral stable | 60 | |
| Neutral | 15 | |
| Near-neutral unstable | 15 | |
| Unstable | 15 | |
| Very unstable | 15 |
References
- Pryor, S.C.; Barthelmie, R.J. Wind shadows impact planning of large offshore wind farms. Appl. Energy 2024, 359, 122755. [Google Scholar] [CrossRef]
- Christiansen, M.B.; Hasager, C.B. Wake effects of large offshore wind farms identified from satellite SAR. Remote Sens. Environ. 2005, 98, 251–268. [Google Scholar] [CrossRef]
- Fitch, A.C.; Olson, J.B.; Lundquist, J.K.; Dudhia, J.; Gupta, A.K.; Michalakes, J.; Barstad, I. Local and mesoscale impacts of wind farms as parameterized in a mesoscale NWP model. Mon. Weather Rev. 2012, 140, 3017–3038. [Google Scholar] [CrossRef]
- Nygaard, N.G.; Hansen, S.D. Wake effects between two neighbouring wind farms. J. Phys. Conf. Ser. 2016, 753, 032020. [Google Scholar] [CrossRef]
- Platis, A.; Siedersleben, S.K.; Bange, J.; Lampert, A.; Bärfuss, K.; Hankers, R.; Cañadillas, B.; Foreman, R.; Schulz-Stellenfleth, J.; Djath, B.; et al. First in situ evidence of wakes in the far field behind offshore wind farms. Sci. Rep. 2018, 8, 2163. [Google Scholar] [CrossRef]
- Schneemann, J.; Rott, A.; Dörenkämper, M.; Steinfeld, G.; Kühn, M. Cluster wakes impact on a far-distant offshore wind farm’s power. Wind Energy Sci. 2020, 5, 29–49. [Google Scholar] [CrossRef]
- Akhtar, N.; Geyer, B.; Rockel, B.; Sommer, P.S.; Schrum, C. Accelerating deployment of offshore wind energy alter wind climate and reduce future power generation potentials. Sci. Rep. 2021, 11, 11826. [Google Scholar] [PubMed]
- Cañadillas, B.; Foreman, R.; Barth, V.; Siedersleben, S.; Lampert, A.; Platis, A.; Djath, B.; Schulz-Stellenfleth, J.; Bange, J.; Emeis, S.; et al. Offshore wind farm wake recovery: Airborne measurements and its representation in engineering models. Wind Energy 2020, 23, 1249–1265. [Google Scholar] [CrossRef]
- van der Laan, M.P.; Sørensen, N.N. Why the Coriolis force turns a wind farm wake clockwise in the Northern Hemisphere. Wind Energy Sci. 2017, 2, 285–294. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-turbine and wind-farm flows: A review. Bound.-Layer Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef]
- Stipa, S.; Ajay, A.; Allaerts, D.; Brinkerhoff, J. The multi-scale coupled model: A new framework capturing wind farm–atmosphere interaction and global blockage effects. Wind Energy Sci. 2024, 9, 1123–1152. [Google Scholar] [CrossRef]
- Ouro, P.; Ghobrial, M.; Ali, K.; Stallard, T. Numerical modelling of offshore wind-farm cluster wakes. Renew. Sustain. Energy Rev. 2025, 215, 115526. [Google Scholar] [CrossRef]
- Djath, B.; Schulz-Stellenfleth, J.; Cañadillas, B. Study of Coastal Effects Relevant for Offshore Wind Energy Using Spaceborne Synthetic Aperture Radar (SAR). Remote Sens. 2022, 14, 1688. [Google Scholar] [CrossRef]
- Cañadillas, B.; Beckenbauer, M.; Trujillo, J.J.; Dörenkämper, M.; Foreman, R.; Neumann, T.; Lampert, A. Offshore wind farm cluster wakes as observed by long-range-scanning wind lidar measurements and mesoscale modeling. Wind Energy Sci. 2022, 7, 1241–1262. [Google Scholar] [CrossRef]
- Platis, A.; Bange, J.; Bärfuss, K.; Cañadillas, B.; Hundhausen, M.; Djath, B.; Lampert, A.; Schulz-Stellenfleth, J.; Siedersleben, S.; Neumann, T.; et al. Long-range modifications of the wind field by offshore wind parks - results of the project WIPAFF. Meteorol. Z. 2020, 29, 355–376. [Google Scholar] [CrossRef]
- Lampert, A.; Bärfuss, K.; Platis, A.; Siedersleben, S.; Djath, B.; Cañadillas, B.; Hunger, R.; Hankers, R.; Bitter, M.; Feuerle, T.; et al. In situ airborne measurements of atmospheric and sea surface parameters related to offshore wind parks in the German Bight. Earth Syst. Sci. Data 2020, 12, 935–946. [Google Scholar] [CrossRef]
- Emeis, S. A simple analytical wind park model considering atmospheric stability. Wind Energy 2010, 13, 459–469. [Google Scholar] [CrossRef]
- Emeis, S. Wind Energy Meteorology: Atmospheric Physics for Wind Power Generation; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Cañadillas, B.; Foreman, R.; Steinfeld, G.; Robinson, N. Cumulative interactions between the global blockage and wake effects as observed by an engineering model and large-eddy simulations. Energies 2023, 16, 2949. [Google Scholar] [CrossRef]
- Lampert, A.; Hankers, R.; Feuerle, T.; Rausch, T.; Cremer, M.; Angermann, M.; Bitter, M.; Füllgraf, J.; Schulz, H.; Bestmann, U.; et al. In situ airborne measurements of atmospheric parameters and airborne sea surface properties related to offshore wind parks in the German Bight during the project X-Wakes. Earth Syst. Sci. Data Discuss. 2024, 16, 4777–4792. [Google Scholar] [CrossRef]
- zum Berge, K.; Centurelli, G.; Dörenkämper, M.; Bange, J.; Platis, A. Evaluation of Engineering Models for Large-Scale Cluster Wakes With the Help of In Situ Airborne Measurements. Wind Energy 2024, 27, 1040–1062. [Google Scholar] [CrossRef]
- Foreman, R.J.; Cañadillas, B.; Robinson, N. The atmospheric stability dependence of far wakes on the power output of downstream wind farms. Energies 2024, 17, 488. [Google Scholar] [CrossRef]
- Maas, O.; Raasch, S. Wake properties and power output of very large wind farms for different meteorological conditions and turbine spacings: A large-eddy simulation case study for the German Bight. Wind Energy Sci. 2022, 7, 715–739. [Google Scholar] [CrossRef]
- Stieren, A.; Stevens, R.J. Impact of wind farm wakes on flow structures in and around downstream wind farms. Flow 2022, 2, E21. [Google Scholar] [CrossRef]
- Emeis, S. Analysis of some major limitations of analytical top-down wind-farm models. Bound.-Layer Meteorol. 2023, 187, 423–435. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Bärfuss, K.; Hankers, R.; Bitter, M.; Feuerle, T.; Schulz, H.; Rausch, T.; Platis, A.; Bange, J.; Lampert, A. In-Situ Airborne Measurements of Atmospheric and Sea Surface Parameters Related to Offshore Wind Parks in the German Bight; PANGAEA: Bremen, Germany, 2019. [Google Scholar] [CrossRef]
- Corsmeier, U.; Hankers, R.; Wieser, A. Airborne turbulence measurements in the lower troposphere onboard the research aircraft Dornier 128-6, D-IBUF. Meteorol. Z. 2001, 10, 315–329. [Google Scholar] [CrossRef]
- Rausch, T.; Bärfuss, K.; Hankers, R.; Bitter, M.; Feuerle, T.; Cremer, M.; Angermann, M.; Füllgraf, J.; Lampert, A. In-Situ Airborne Measurements of Atmospheric and Sea Surface Parameters Related to Offshore Wind Parks in the German Bight; PANGAEA: Bremen, Germany, 2023. [Google Scholar] [CrossRef]
- Sathe, A.; Mann, J.; Barlas, T.; Bierbooms, W.A.; van Bussel, G.J. Influence of atmospheric stability on wind turbine loads. Wind Energy 2013, 16, 1013–1032. [Google Scholar] [CrossRef]
- Andreas, E.L.; Mahrt, L.; Vickers, D. A new drag relation for aerodynamically rough flow over the ocean. J. Atmos. Sci. 2012, 69, 2520–2537. [Google Scholar] [CrossRef]
- Fischer, G. Installation and operation of the research platform FINO 1 in the North Sea. In Offshore Wind Energy: Research on Environmental Impacts; Springer: Berlin/Heidelberg, Germany, 2006; pp. 237–253. [Google Scholar]
- Jensen, N.O. A Note on Wind Generator Interaction; Risø National Laboratory: Roskilde, Denmark, 1983. [Google Scholar]
- Nygaard, N.G.; Steen, S.T.; Poulsen, L.; Pedersen, J.G. Modelling cluster wakes and wind farm blockage. J. Phys. Conf. Ser. 2020, 1618, 062072. [Google Scholar] [CrossRef]
- Fleming, P.; Annoni, J.; Scholbrock, A.; Quon, E.; Dana, S.; Schreck, S.; Raach, S.; Haizmann, F.; Schlipf, D. Full-scale field test of wake steering. J. Phys. Conf. Ser. 2017, 854, 012013. [Google Scholar] [CrossRef]
- Nygaard, N.; Poulsen, L.; Svensson, E.; Pedersen, J.G. Large-scale benchmarking of wake models for offshore wind farms. J. Phys. Conf. Ser. 2022, 2265, 022008. [Google Scholar] [CrossRef]
- Munters, W.; Adiloglu, B.; Buckingham, S.; Beeck, J.v. Wake impact of constructing a new offshore wind farm zone on an existing downwind cluster: A case study of the Belgian Princess Elisabeth zone using FLORIS. J. Phys. Conf. Ser. 2022, 2265, 022049. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Dörenkämper, M.; Olsen, B.T.; Witha, B.; Hahmann, A.N.; Davis, N.N.; Barcons, J.; Ezber, Y.; García-Bustamante, E.; González-Rouco, J.F.; Navarro, J.; et al. The making of the new european wind atlas—Part 2: Production and evaluation. Geosci. Model Dev. Discuss. 2020, 2020, 1–37. [Google Scholar] [CrossRef]
- Livingston, H.G.; Lundquist, J.K. How many offshore wind turbines does New England need? Meteorol. Appl. 2020, 27, e1969. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Larsen, G.C.; Pryor, S.C. Modeling Annual Electricity Production and Levelized Cost of Energy from the US East Coast Offshore Wind Energy Lease Areas. Energies 2023, 16, 4550. [Google Scholar] [CrossRef]
- Gao, Q.; Hayward, J.A.; Sergiienko, N.; Khan, S.S.; Hemer, M.; Ertugrul, N.; Ding, B. Detailed mapping of technical capacities and economics potential of offshore wind energy: A case study in South-eastern Australia. Renew. Sustain. Energy Rev. 2024, 189, 113872. [Google Scholar] [CrossRef]
- Davis, N.N.; Badger, J.; Hahmann, A.N.; Hansen, B.O.; Mortensen, N.G.; Kelly, M.; Larsén, X.G.; Olsen, B.T.; Floors, R.; Lizcano, G.; et al. The Global Wind Atlas: A high-resolution dataset of climatologies and associated web-based application. Bull. Am. Meteorol. Soc. 2023, 104, E1507–E1525. [Google Scholar] [CrossRef]
- Emeis, S.; Siedersleben, S.; Lampert, A.; Platis, A.; Bange, J.; Djath, B.; Schulz-Stellenfleth, J.; Neumann, T. Exploring the wakes of large offshore wind farms. J. Phys. Conf. Ser. 2016, 753, 092014. [Google Scholar] [CrossRef]
- Archer, C.L.; Colle, B.A.; Veron, D.L.; Veron, F.; Sienkiewicz, M.J. On the predominance of unstable atmospheric conditions in the marine boundary layer offshore of the US northeastern coast. J. Geophys. Res. Atmos. 2016, 121, 8869–8885. [Google Scholar] [CrossRef]
- Bodini, N.; Lundquist, J.K.; Kirincich, A. US East Coast lidar measurements show offshore wind turbines will encounter very low atmospheric turbulence. Geophys. Res. Lett. 2019, 46, 5582–5591. [Google Scholar] [CrossRef]



| ID a | Flight No. b | Cluster Interaction c | Date | Time d [UTC] | No. Legs | Wind Speed [m/s] e | Wind Speed [m/s] f | Wind Direction [°] g | Obukhov Length L [m] h | Stability i |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 17 | N-3– | 3 Jul 2020 | 11:55–13:05 | 5 | 12 | 11.1 | 240 | 240 | near-neutral stable |
| 2 | 17 | N-2–N-4 | 3 Jul 2020 | 11:10–11:25 | 1 | 12 | 10.9 | 240 | −200 | unstable |
| 3 | 19 | N-2–N-3– | 14 Jul 2020 | 14:05–15:50 | 8 | 8 | 6.4 | 270 | 90 | stable |
| 4 | 23 | N-2–N-4 | 23 Jul 2020 | 12:30–13:30 | 3 | 12 | 10.6 | 240 | 150 | stable |
| 5 | 23 | N-3– | 23 Jul 2020 | 13:20–14:40 | 5 | 11 | 10.6 | 240 | 80 | stable |
| 6 | 24 | N-2–N-3– | 24 Jul 2020 | 9:10–10:50 | 7 | 9 | 9.5 | 270 | 90 | stable |
| 7 | 26 | N-2–N-3 | 28 Jul 2020 | 9:10–10:10 | 3 | 15 | 15.1 | 250 | −550 | neutral |
| 8 | 35 | N-3– | 8 Apr 2021 | 13:40–14:50 | 5 | 17 | 16.5 | 240 | 350 | near-neutral stable |
| 9 | 44 | N-3– | 27 Jul 2021 | 10:45–12:20 | 5 | 10 | 10.2 | 230 | 50 | very stable |
| 10 | 44 | N-4– | 27 Jul 2021 | 12:30–13:45 | 4 | 11 | 10.6 | 230 | 10 | very stable |
| 11 | 48 | N-3– | 30 Jul 2021 | 8:30–10:05 | 5 | 11 | 10.9 | 240 | 80 | stable |
| 12 | 48 | N-4– | 30 Jul 2021 | 10:30–11:05 | 2 | 11 | 12.3 | 240 | 70 | stable |
| 13 | 49 | N-3– | 11 Sep 2021 | 13:25–14:45 | 5 | 9 | 10.0 | 240 | 160 | stable |
| 14 | 49 | N-4– | 11 Sep 2021 | 14:50–15:45 | 4 | 9 | 9.4 | 240 | 120 | stable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Foreman, R.J.; Birzer, C.; Cañadillas, B. Measuring and Simulating Wind Farm Wakes in the North Sea for Use in Assessing Other Regions. Energies 2025, 18, 5538. https://doi.org/10.3390/en18205538
Foreman RJ, Birzer C, Cañadillas B. Measuring and Simulating Wind Farm Wakes in the North Sea for Use in Assessing Other Regions. Energies. 2025; 18(20):5538. https://doi.org/10.3390/en18205538
Chicago/Turabian StyleForeman, Richard J., Cristian Birzer, and Beatriz Cañadillas. 2025. "Measuring and Simulating Wind Farm Wakes in the North Sea for Use in Assessing Other Regions" Energies 18, no. 20: 5538. https://doi.org/10.3390/en18205538
APA StyleForeman, R. J., Birzer, C., & Cañadillas, B. (2025). Measuring and Simulating Wind Farm Wakes in the North Sea for Use in Assessing Other Regions. Energies, 18(20), 5538. https://doi.org/10.3390/en18205538







