The Stochastic Nature of the Mining Production Process—Modeling of Processes in Deep Hard Coal Mines

Abstract

The stochastic and undetermined nature of longwall coal mining results from the complex interaction between geological-mining and technical-organizational factors. This interaction causes variability in key parameters of the production process. This article presents three stochastic models developed on the basis of probability density functions, which describe selected process parameters. These mathematical functions serve as the foundation for effective stochastic models, enabling analysis of complex mining operations. The methodology employed in the study involves empirical data collection, statistical analysis, and stochastic simulation, carried out under both laboratory and field conditions. The results include empirical probability functions for output, delays, and crew-dependent productivity, offering insights into process variability and its impact on performance. Each method is characterized by its theoretical foundations, algorithmic structure, and application areas. The models have been validated through statistical tests and operational field data and can be applied as decision-support tools in both scientific research and industrial management. Given the extensive nature of the described methods, the article provides a comprehensive reference list for readers interested in further exploration and practical implementation in mining engineering.

1. Introduction

Efficient decision-making in mining production is challenged by the inherent stochastic nature of the process, especially in deep hard coal mines [1]. This study addresses the variability in production processes occurring in longwall faces, where despite the repeatability of tasks, fluctuations in key operational parameters are common. These fluctuations arise from the combined influence of geological-mining and technical-organizational factors, which affect the performance of key machines such as shearers, powered supports, and conveyors.

In particular, undetermined behaviors—such as non-uniform shearer advancement—necessitate the use of non-deterministic modeling techniques. Probability density functions (PDFs) are proposed as effective tools to characterize these uncertainties. By integrating such functions into simulation-based models, this approach provides enhanced insight into the performance and planning of mining operations.

The goal of this work is to present and validate a methodology that employs PDFs to model the stochastic characteristics of selected process parameters. The models are supported by empirical data collected from longwall operations and aim to improve forecasting, diagnose delays, and support operational decisions. The influence of key factors affecting output is visualized in Figure 1.

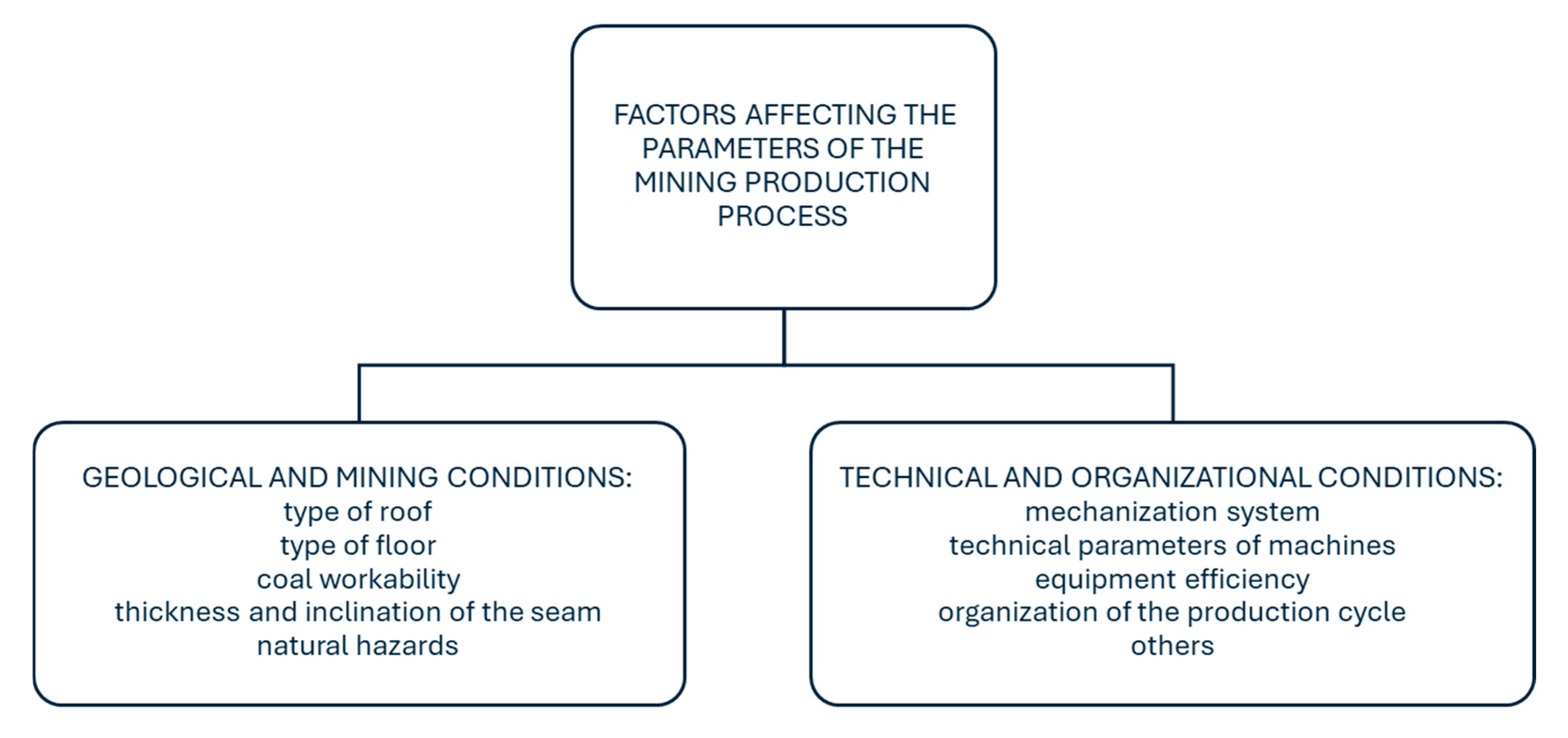
1.1. Factors Influencing the Course of the Production Process Carried out in the Longwall Face

The course of the production process carried out at the coal face in hard coal mining depends on a number of factors. These can be divided into two groups: mining and geological conditions, and technical and organizational conditions.

Mining and geological conditions primarily include the following:

–

Type of roof rock;

–

Type of floor rock;

–

Coal workability;

–

Thickness and inclination of the seam;

–

Natural hazards.

Technical and organizational conditions that significantly affect the production process include the following:

–

Mechanization system;

–

Technical parameters of machines;

–

Equipment failure rate;

–

Organization of the production cycle, which includes the form of work organization, the form of labor organization, and the work system;

–

Training and experience of employees.

The presence of these factors can destabilize the production cycle carried out at the face of the wall.

These phenomena occurring in the rock mass are complex and difficult to precisely determine due to its diverse geological and hydrogeological structure. Improper mining operations can lead to the formation of high-pressure zones, sudden roof collapses, rock bursts, and other hazards. Therefore, in order to ensure the highest level of safety and minimize disruptions to the production cycle at the face of the wall, efforts are made to thoroughly understand the mining and geological conditions of the deposit being exploited.

The type of roof rock is a key criterion when choosing a roof control method. This issue depends mainly on the class of roof and floor rocks, but also on the thickness of the extracted seam and the tendency of the coal to spontaneous combustion [1]. In order to facilitate the selection of the mining system, in particular the roof control method, various classifications of roof rocks have been developed. The most general classification of roof layers occurring in Polish hard coal mines includes the following [2]:

–

Brittle roof rocks, usually forming part of the direct roof, characterized by low cohesion and strength with high deformability, which causes them to fall into the exploited space;

–

Stiff roof rocks, with low deformability and high strength, which collapse in blocks behind the exploitation front;

–

Plastic roof rocks, capable of significant deformations and bending behind the exploitation front.

The bedrock is understood as the lower surface of the coal seam. Just as there are different classes of roof rocks, the floor rocks can also be classified [3]:

–

Class I—direct floor composed of weak rock layers susceptible to exfoliation;

–

Class II—direct floor consisting of strong rock layers;

–

Class III—direct floor consisting of plastic, swelling rocks that are easily extruded into the workings.

The greatest disruptions to the mining process at the face of the wall are caused by brittle roof rocks (e.g., hanging shale layers that collapse immediately upon exposure) and weak floor rocks (e.g., shale or clay that swell upon exposure to water).

Coal workability is a property closely related to the cohesion of coal. The higher the cohesion index, the more difficult the rock is to mine. Workability refers to the rock’s susceptibility to being separated from the solid mass using tools, mining machines, or explosives. It is influenced not only by the hardness and cohesion of the rock but also by the pressure of the rock mass, the cross-sectional dimensions of the working face, and its advance rate [3].

Three groups of coal seams are distinguished based on the value of the workability index, denoted by the letter “f” [4]:

–

Group I—easily workable seams: f from 0.4 to 1.2;

–

Group II—difficult to work seams: f from 1.2 to 2.0;

–

Group III—very difficult to work seams: f above 2.0.

Seam thickness is defined as the shortest distance between the roof and the floor. Depending on the thickness of the deposit, coal seams are conventionally classified as thin or thick [5]. Several classifications exist in the literature, but the most commonly used division in Poland today is as follows [2]:

–

Thin seams—thickness up to 1.5 m;

–

Medium seams—thickness from 1.5 to 4.0 m;

–

Thick seams—thickness greater than 4.0 m.

Seam inclination is related to the dip angle. A coal seam may lie horizontally or at an angle to the horizontal plane. The angle formed between the plane of the seam’s floor or roof and the horizontal plane is called the seam dip angle. Based on the value of this angle, coal seams are classified into the following four groups [2]:

–

Horizontal or nearly horizontal seams—dip angle between 0° and 5°;

–

Gently inclined seams—dip angle between 5° and 30°;

–

Steeply inclined seams—dip angle between 30° and 45°;

–

Very steep seams—dip angle between 45° and 90°.

Natural hazards, including those related to rock and gas outbursts, are among the most dangerous threats in underground mining. The risk of methane and rock outbursts increases with mining depth. As mining operations progress to greater depths, an increase in the methane content of coal seams is observed. At the same time, the gas permeability of coal decreases, which contributes to a higher risk of such hazards. Key factors influencing the occurrence of this threat include the gas content of the deposit (methane content), rock cohesion, pressure and intensity of gas desorption, and mining activities near geological disturbances. There are two categories of methane and rock outburst hazards in underground hard coal mines:

–

Seams prone to methane and rock outbursts—these include coal seams or their parts where methane content exceeds 8 [m³/Mg] (per ton of pure coal substance) and coal cohesion is less than 0.3, or where methane content exceeds 8 [m³/Mg] and cohesion is at least 0.3, but methane desorption intensity is greater than 1.2 kPa.

–

Seams endangered by methane and rock outbursts—these include coal seams or their parts where

• A methane and rock outburst has occurred;
• A sudden methane outflow has occurred;
• Other symptoms indicating increased risk of methane and rock outbursts have been observed.

In summary, the mining and geological conditions in Polish hard coal mines show that seam exploitation involves a number of hazards and difficulties. In addition to typical factors such as seam inclination, roof rock cohesion, seam thickness, or coal workability, there are also particularly dangerous threats, such as rock and gas outbursts and rock bursts [6].

Mining and geological conditions are determined by nature and cannot be changed or modified. However, technical and organizational conditions can be partially controlled—for example, by regulating their variability.

The duration of tasks in the production process is significantly influenced by the mechanization system used. An optimal selection of the shearer–conveyor–support system usually shortens the production cycle time. Nevertheless, this time can still be disrupted by mining and geological factors.

The activities within the production cycle related to the operation of the shearer are limited by the technical parameters of the machine. Although modern shearers operate at increasingly higher speeds and, theoretically, can achieve higher productivity, their actual performance is determined by mining and geological factors—particularly the degree of coal workability and roof conditions.

Machine failure is another factor that can disrupt the production process. It can be assumed that the longer machines and equipment are in use, the more frequently they may fail. Therefore, timely maintenance and rapid repairs are essential. Efforts should be made to minimize failures and downtime.

The organization of the production cycle—which includes the form of work organization, labor organization, and work system—as well as the training and experience of workers are the factors that appear to be the most predictable. A properly trained workforce can be optimally deployed at the longwall face.

In the literature, there are methods for determining the impact of these factors on the duration of tasks performed at the longwall face. These methods use, for example, regression and correlation analysis [6,7].

Recent studies increasingly emphasize the limitations of classical deterministic and purely regression-based methods in the analysis of mining processes—particularly with regard to geological and operational uncertainty as well as short-term variability. For this reason, there is a clear shift toward probabilistic, simulation-based, and stochastic optimization approaches, which better capture uncertainty and enable more robust planning (e.g., short- and long-term planning under deposit, price, or equipment performance uncertainty) [8,9,10,11,12]. At the same time, stochastic modeling is increasingly being integrated with condition monitoring/IoT and process mining, which facilitates model calibration and their in situ decision-making applications [13,14].

In summary, in mining environments dominated by randomness and dynamic disturbances, models based on probability distributions and stochastic simulations prove to be more appropriate than classical deterministic or regression-based models.

1.2. Use of Probability Density Functions as Characteristics of Undetermined Process Parameters

The complex and often difficult to define interactions between the aforementioned factors cause the shearer to move along the longwall in a non-uniform manner, with variable speed.

These same factors can also affect the speed of advancing the powered roof support units and the longwall conveyor. Similar variability may occur in other parts of the technological chain (during the execution of other tasks).

Therefore, when analyzing, for example, the efficiency of the mining production process, it is necessary to consider all the conditions of this process, including the variability of some of its parameters. For this purpose, cause-and-effect models are built, and regression and correlation functions are developed [15,16,17,18,19,20,21].

According to the authors of this study, a better solution is to use probability density functions as characteristics of undetermined process parameters.

The definition of these functions for the conditions of a specific longwall face can be carried out in two stages:

–

The first stage involves collecting time-study data. In the case of the shearer, the data should include the time it takes to traverse a selected section of the longwall (e.g., a section covering two powered roof support units). After accounting for the support unit spacing and performing the necessary calculations, the observed times are converted into shearer advance speeds. This data can be obtained from supervision and monitoring systems installed in shearers, as well as from operational data collection systems in the mine.

–

The second stage involves statistical analysis of these speed values (using, among others, goodness-of-fit tests), which leads to the derivation of a probability density function as an undetermined characteristic of the shearer’s advance speed.

A similar two-stage procedure can be used to obtain characteristics for the speed of advancing powered roof supports, the longwall conveyor, etc.

Describing selected parameters of the mining process using probability density functions necessitates analyzing the process using non-deterministic methods.

Some of these functions are presented in the following sections of this study. Among the non-deterministic methods are the models described in the works of [22,23].

2. Materials and Methods

This section outlines the data sources, procedures, and modeling techniques used to identify the stochastic nature of the mining production process. The applied methodology includes empirical data collection, statistical analysis, and the construction and validation of probabilistic models based on probability density functions (PDFs).

2.1. Study Site and Data Collection

The modeling methods presented in this paper were developed using data obtained from a longwall face in coal seam No. 209 of the Łaziskie beds. The mining process at this site utilized a longwall system with roof cut and fill technology. Key operational parameters of the face include a length of 220 m, seam thickness between 4.0 and 4.4 m, and an exploitation depth ranging from 690 to 710 m.

Table 1. General parameters of the tested longwall face.

Parameters	Value
Longwall length	220 m
Longwall height	4.0–4.4 m
Longwall stopway	1700 m
Maximal web	0.8 m
Longwall inclination	0–2°
Thickness of the coal layer in the roof	up to 0.3 m
Thickness of the coal layer in the floor	up to 0.2 m
Exploitation depth	710–690 m

,

Table 2. Mining and geological conditions of the tested longwall face.

Parameters	Value
Coal seam thickness	4.0–4.4 m
Roof	0.0–6.2 m clayey shale
Basic roof	37.7–43.2 m multi-grained sandstones
Coal seam floor	1.5–2.4 m clayey shale
Coal type	31.2
Coal specific weight (mean)	1.35 g/m3

and

Table 3. Natural hazards of the tested longwall face.

Parameter	Wartość
Coal dust explosion hazard	class “A”
Methane threat	does not occur
Threat of gas and rock outbursts	does not occur
Radiation hazard	does not occur
Fire hazard	group V
Rock burst hazard	level I
Water hazards	level I

summarize the geological conditions, technical specifications, and natural hazard assessments.

Time-study data were collected from the longwall face using monitoring and supervisory systems installed on the shearer. These systems captured real-time movement and operation data, including the time required to traverse segments of the wall. These raw data points were later transformed into performance metrics, such as the shearer’s speed or production cycle duration.

2.2. Data Preprocessing and Statistical Analysis

Raw data were filtered to remove anomalies, including operational downtimes and irregular intervals caused by maintenance or unexpected stoppages. Anomalies were identified using a 1.5 interquartile range (IQR) rule. After cleansing, the data were used to calculate frequency distributions and assess the statistical properties of selected parameters.

To describe the variability in production parameters, probability density functions were fitted to the empirical distributions. The selection of distribution types (e.g., normal, log-normal) was based on the results of Kolmogorov–Smirnov and Anderson–Darling goodness-of-fit tests. Parameters of the distributions were estimated using the method of maximum likelihood.

2.3. Stochastic Modeling Approach

Three types of stochastic models were developed:

• Model 1: Identification of the probability distribution of output obtained from longwall faces.
• Model 2: Stochastic model of coal output from a longwall face using unidirectional shearer-based mining technology.
• Model 3: Shift output characteristic accounting for changes in longwall face crew composition.

Daily output distributions are derived as the convolution of two independent shift-level output distributions, reflecting a two-shift productive schedule within a three-shift workday.

These models are based on previously published and validated methodologies [7,22,23] and have been adapted to the current case study. Model 1 supports diagnostics of task synchronization, model 2 provides a probabilistic benchmark for performance monitoring, and model 3 enables scenario-based planning under varying labor resources.

Each model assumes stationary input distributions and independence between tasks unless explicitly modeled via convolution or conditional PDFs. These simplifications allow practical use in decision-support systems but also highlight areas for future enhancement, such as the inclusion of adaptive elements or drift detection mechanisms.

2.3.1. Identification of the Probability Distribution of Output Obtained from Longwall Faces

The first example concerns a model developed as part of the “Method for identifying the probability distribution of output obtained from longwall faces in hard coal mines” [7]. The model was analyzed using stochastic simulation.

The model introduced elementary probability density functions. It examined whether there are dependencies between them that influence the duration of the production cycle and, consequently, the output obtained from the longwall face.

As a result of the conducted modeling studies, it was found that the following boundary conditions should be satisfied between the elementary probability density functions:

$$\left\{\begin{array}{c}\underset{a}{\overset{+\infty }{\int }}{f}_e\left(t_u\right)d{t}_u-\underset{a}{\overset{+\infty }{\int }}{f}_{e_1}\left(t_1\right)d{t}_1>0\\ \underset{a}{\overset{+\infty }{\int }}{f}_e\left(t_u\right)d{t}_u-\underset{a}{\overset{+\infty }{\int }}{f}_{e_2}\left(t_2\right)d{t}_2>0\\ ⋮⋮⋮\hfill \\ \underset{a}{\overset{+\infty }{\int }}{f}_e\left(t_u\right)d{t}_u-\underset{a}{\overset{+\infty }{\int }}{f}_{e_i}\left(t_i\right)d{t}_i>0\end{array}\right.$$

(1)

For every value “$a$” greater than zero, where

–

$f_e\left(t_u\right)$ is the elementary probability density function of the variable $T_u$, representing the time required for the shearer to cut a 1 m section;

–

$f_{e_1}\left(t_1\right),f_{e_2}\left(t_2\right),\dots ,f_{e_i}\left(t_i\right)$ are the elementary probability density functions for tasks or operations performed simultaneously (in parallel) with the cutting shearer, whose execution affects the shearer’s advance.

By analyzing the relationships between selected elementary probability density functions in the manner defined by Equation (1), one can determine whether the shearer’s movement will be delayed by other simultaneously (parallelly) performed operations within the production cycle. This has clear practical significance and can be helpful in diagnosing the causes of interruptions in the shearer’s advance.

To illustrate the application of Equation (1), an example based on operational data is provided. In this case, the travel time of the shearer over a selected section of the longwall was compared with the parallel task of powered roof support advancement. Probability density functions were fitted to the observed times for both activities. The comparison of these functions makes it possible to estimate the probability that the duration of the supporting task exceeds that of the shearer, which indicates a potential delay. Such an example demonstrates how Equation (1) can be practically applied to identify the likelihood of time conflicts between concurrent operations.

2.3.2. Stochastic Model of Coal Output from a Longwall Face Using Unidirectional Shearer-Based Mining Technology

The next model is a stochastic model of coal output from a longwall face using unidirectional shearer-based mining technology [7].

As in the previous example, it is not possible to present the model’s details or its full analysis. Instead, the results will be presented along with an assessment of their usefulness.

Figure 2 shows the results, which include a histogram (empirical distribution) and a cumulative histogram (empirical cumulative distribution function) of shift-based coal output, along with an approximating function.

The approximating function is a normal distribution with parameters N(1144; 267), for which the value of shift-based coal output W₀ was determined, satisfying the equation

$$\underset{-\infty }{\overset{W_0}{\int }}{\displaystyle \frac{1}{267\sqrt{2\pi }}}{e}^{{\displaystyle \frac{{-(w_z-1144)}^2}{2·{267}^2}}}{dw}_z=F\left(W_0\right)=0.5$$

(2)

where $F\left(W_0\right)$ is the value of the cumulative distribution function of N(1144; 267) at the point $W_0$.

The value of output $W_0$ that satisfies the above equation is, in this case, 1144 Mg/shift. This is the production level for which exceeding or not exceeding it, under the conditions of the given longwall face, is equally probable. Figure 3 presents an interpretation of the relationship between the forecasted value $W_0$ and the actual shift-based output obtained from the given longwall face.

The usefulness of the value $W_0$ determined in this way lies in the fact that it objectifies the actual production capabilities of the longwall face, as it takes into account both upward and downward fluctuations in the achieved output. Therefore, this value can be used at the stage of forecasting or planning production from a given longwall face.

Figure 4 presents the graphs of the density function and the cumulative distribution function of the production cycle duration. These are output quantities in the method of identifying the probability distribution of output obtained from longwall faces in hard coal mines [7].

As is well known, the ratio of effective working time at the longwall face to the duration of the production cycle gives the number of production cycles during a work shift. When this number is multiplied by the output per production cycle, it yields the total output from the longwall face during the shift. In this way—using the functions of production cycle duration (Figure 4)—the shift output characteristic, denoted as $f\left(w_z\right)$, is determined.

The function $f\left(w_z\right)$ links the level of output from a given longwall face with its probability. Knowing this characteristic allows for determining the probability of achieving a certain level of output or, for example, exceeding it.

If this level is $w_0$, then the probability of exceeding this level is

$$P\left(W_z>w_0\right)=1-\underset{w_{min}}{\overset{w_0}{\int }}f\left(w_z\right)d{w}_z$$

(3)

where $w_{min}$ is the lower bound of the range of values that the random variable $W_z$ can take.

2.3.3. Shift Output Characteristic Accounting for Changes in Longwall Face Crew Composition

In the study [7], a model of the process carried out at the longwall face in hard coal mines is presented, in which the output characteristics are expressed as conditional probability density functions. These functions are shown in Figure 5.

If the crew at a given longwall face can vary, then the functions $f_{q_z/LL={ll}_1}\left(q_z\right);f_{q_z/LL={ll}_2}\left(q_z\right);\dots ;f_{q_z/LL={ll}_j}\left(q_z\right);$ are determined for each crew variant, where “LL” denotes the number of workers at the face, and “$j$” is the number of crew variants.

Each of these functions is a conditional probability density function (describing the distribution of outputs for a specific crew coposition at the face). The shift output characteristic that accounts for possible changes in crew composition is therefore the marginal probability density function, calculated using the formula

$$f^b(q_z)\hspace{0.33em}=\hspace{0.33em}{\sum }_{I=1}^j{f}_{q_z/LL=l{l}_I}(q_z) \ast P(LL=l{l}_I)$$

(4)

where

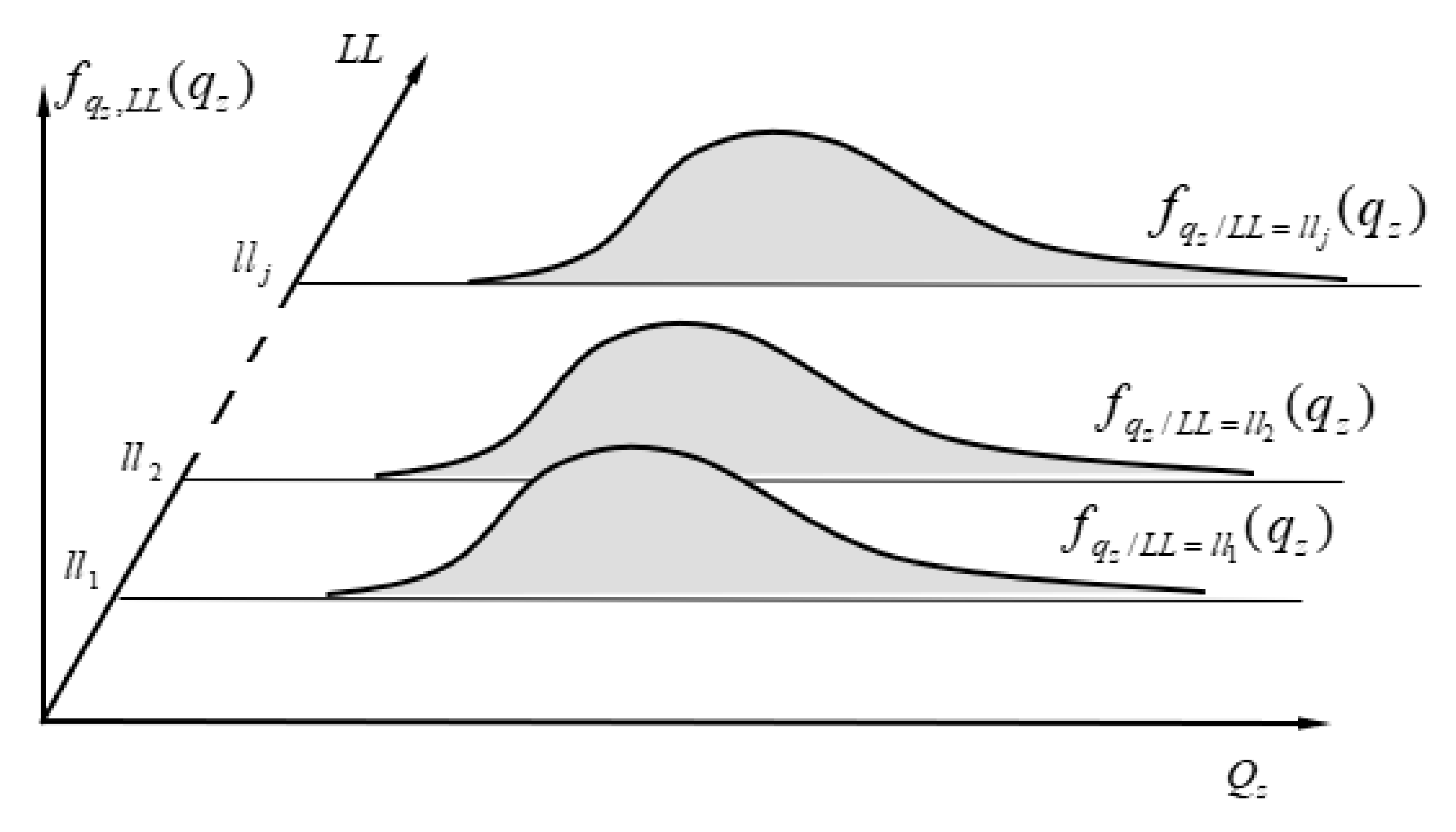
• $f^b(q_z)$—marginal probability density function of the variable Qz (shift output);
• $P(LL={ll}_I)$—probability that the random variable $LL$ (crew composition) takes the value ${ll}_i$.

Probabilities $P(LL={ll}_I)$ were estimated based on shift reports and operational records from the mine’s monitoring and reporting system. The share of shifts with a given crew composition was used as the basis for determining the input probabilities. This ensures that the procedure for calculating the marginal distribution can be reproduced while reflecting the actual variability in workforce allocation in the analyzed longwall face.

Daily output is the sum of the production obtained during individual shifts throughout the day. In a three-shift work system, if two shifts are productive and their outputs are characterized by the probability density functions $f_{q{z}_1}$ and $f_{q{z}_2}$, then the daily output Q_d is described by the probability density function $f_{qd}$ which is the convolution of the two functions: $f_{q{z}_1}$ and, then

$$f_{qd}(q_d)={\int }_{-\infty }^{\infty }{f}_{q{z}_1}(q_{z_1})f_{q{z}_2}(q_d-q_{z_1})d{q}_{z_1}$$

(5)

where $f_{q{z}_1},f_{q{z}_2}$ are the probability density functions of the random variables $Q_{z_1},Q_{z_2}$ representing the output of the two productive shifts.

The usefulness of the daily output characteristic $f_{qd}(q_d)$ lies in its ability to assess the output from a longwall face in probabilistic terms, which can be important both for forecasting and for production planning.

2.4. Model Validation

For all fitted distributions, both Anderson–Darling and Kolmogorov–Smirnov tests yielded p-values exceeding 0.05, indicating that the theoretical distributions adequately represented the empirical data. For example, the normal distribution fitted to shift output data (N(1144; 267)) produced p-values of 0.27 (Anderson–Darling) and 0.33 (Kolmogorov–Smirnov), confirming a good fit. In addition to significance tests (AD, KS), the fit of the normal distribution N(1144; 267) was also evaluated using RMSE and R². The results were RMSE = 112 Mg and R² = 0.91, confirming strong agreement between the theoretical distribution and the empirical data. A sensitivity analysis was also performed for two key parameters: seam thickness and shearer failure frequency. An increase in seam thickness by 10% led to an 8% rise in average output with only a slight increase in variance, while doubling the shearer failure frequency reduced the median output by approximately 12% and increased variance by 25%. This indicates that model stability is particularly sensitive to machine reliability, which is an important practical insight for process management. Similarly, conditional PDFs fitted to crew-specific outputs passed both tests with p-values above 0.10.

Model validation was conducted by comparing the simulated output values with actual historical production data. The fit between modeled and observed distributions was tested statistically, with p-values exceeding 0.05, confirming consistency. This demonstrated the models’ reliability in capturing the stochastic behavior of the mining production process under real-world conditions.

Three models were developed:

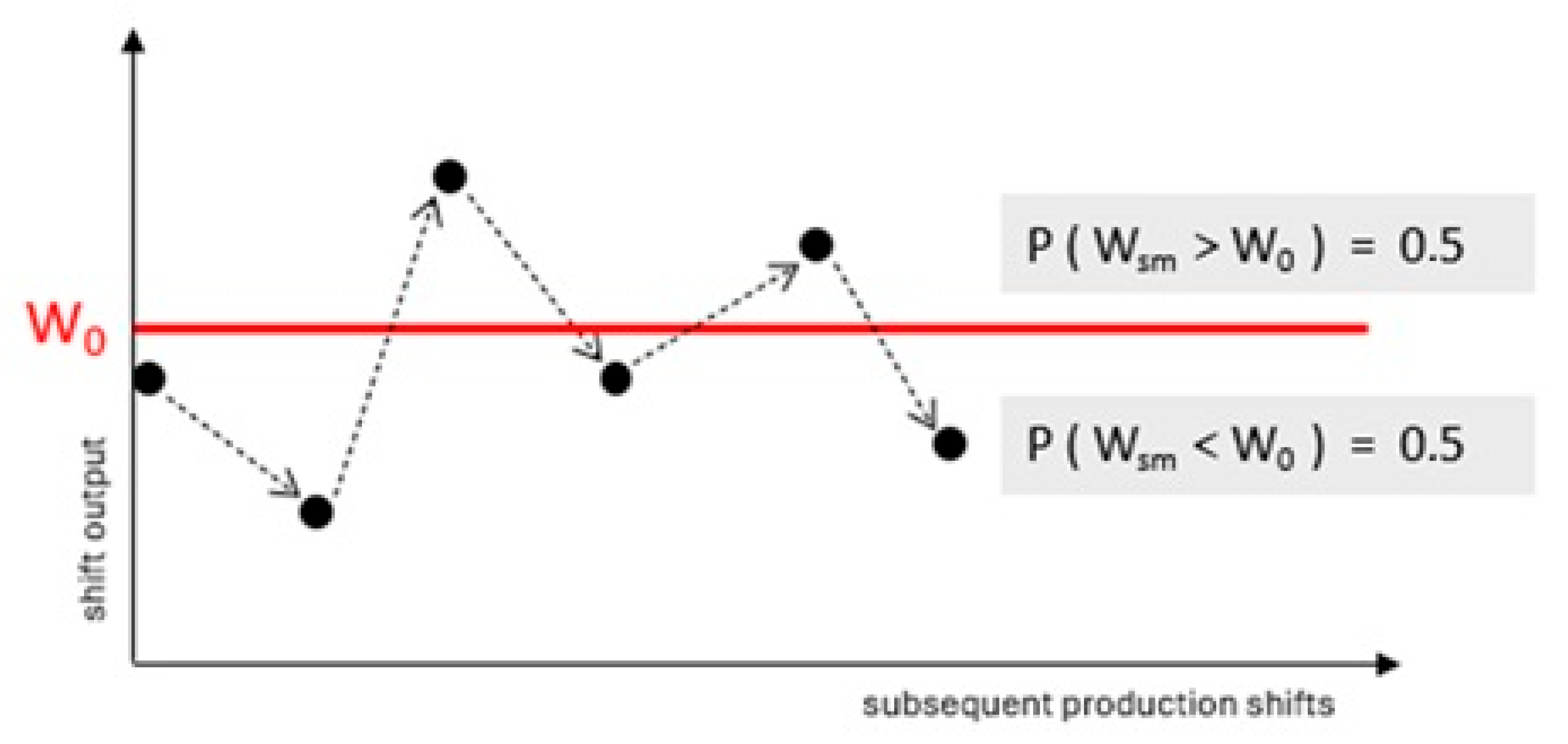
• Model 1: Evaluates delay probability by comparing PDFs of the shearer vs. concurrent tasks. Delay probability is expressed as dla każdego $a>0$ zachodzi zależność $f_{shearer}\left(a\right)<f_{other}\left(a\right)$. The idea of model 1 is presented in Figure 6.
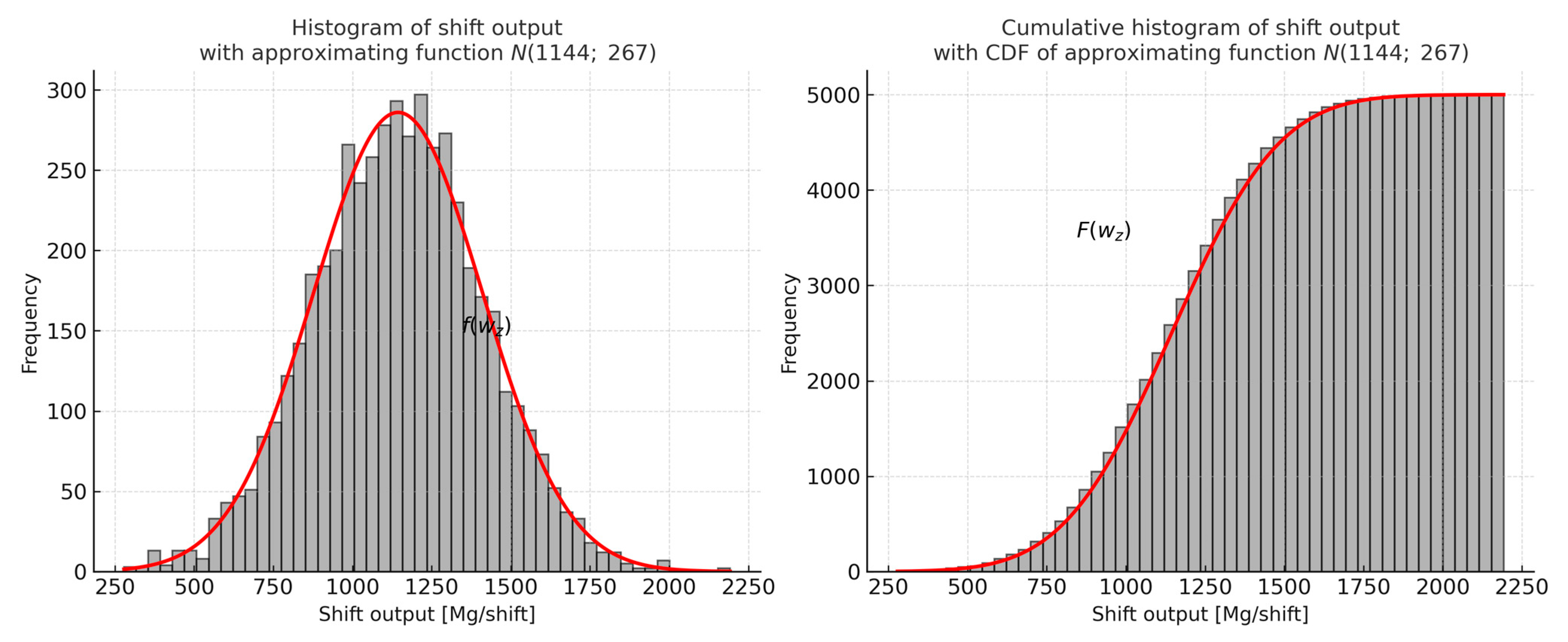
• Model 2: A normal distribution N(1144; 267) describes shift-based output. The cumulative probability $F\left(W_0\right)=0.5$ corresponds to the median output $W_0=1144$ Mg/shift.
• Model 3: Uses conditional PDFs for each crew composition (LL variants) and computes marginal PDF as

  $$f_{Q_z}\left(q\right)=\sum _{j}f(q\left|LL\right.=l_j)·P\left(LL=l_j\right)$$

These functions enable evaluation of output probabilities for both single shifts and full workdays (via convolution).

3. Results

The stochastic models developed in this study yielded results that provide quantitative insights into the mining production process and its variability. Three main models were analyzed using simulation and empirical data: the cycle delay model, the output forecast model, and the crew-dependent model.

3.1. Model 1

Simulation results confirmed that the shearer’s movement is sensitive to delays in concurrently executed tasks such as powered support advancement and conveyor shifting. When the probability density function of a supporting task exceeded that of the shearer at a given duration threshold, a delay in the shearer’s movement was likely. This model enabled identification of process bottlenecks and supported recommendations for optimizing task synchronization.

3.2. Model 2

The output forecast model used a normal distribution with parameters N(1144; 267) to represent the expected shift-based output. The model produced a cumulative distribution function where the median value (W₀ = 1144 Mg/shift) was identified. This value corresponds to the production threshold with an equal likelihood of being exceeded or not. The forecasted output distribution closely matched the empirical histogram of shift production data, demonstrating good agreement between modeled and observed values.

3.3. Model 3

Conditional probability density functions were estimated for different crew configurations, allowing an assessment of how variations in workforce size affect output. The marginal probability density function, computed as the weighted sum of these conditional functions, enabled forecasting of expected output under varying labor resource scenarios. Convolution of two productive shifts was used to estimate daily output distributions.

Collectively, the results validate the usefulness of probability-based modeling in capturing the real-world dynamics of mining operations. All three models provided output distributions that were consistent with historical data, and statistical validation (via p-values > 0.05) confirmed the reliability of the simulations.

4. Discussion

The mining production process takes place under the combined influence of geological-mining and technical-organizational factors. This complexity results in significant variability in key parameters, necessitating analytical approaches capable of capturing undetermined behavior. Traditional methods such as regression or correlation analysis have often proven insufficient in these environments due to multicollinearity and instability in influencing variables.

In contrast, the proposed PDF-based models explicitly account for variability and uncertainty, offering a more realistic representation of mining processes than deterministic or regression approaches [6,7]. This highlights the advantage of stochastic simulation in environments where parameters change dynamically and interdependencies are difficult to capture with traditional models.

To address this, the authors proposed the use of probability density functions (PDFs) as more robust tools for modeling process variability. These PDFs describe operational parameters as random variables, reflecting the stochastic nature of underground mining conditions. Through empirical data collected from a longwall face, the study developed and validated three distinct models: the cycle delay model, the output forecast model, and the crew-dependent output model.

Each model provides targeted decision-making support. The cycle delay model uses PDFs to evaluate the timing of shearer operations against parallel tasks, helping identify production bottlenecks. The output forecast model describes shift-based coal output using a normal distribution (N(1144; 267)), producing a probabilistic reference point for expected performance. The third model applies conditional PDFs to estimate how variations in crew composition (LL variants) influence output, producing marginal distributions and daily forecasts through convolution.

Although time-series records of shearer speed and other operational parameters formed the basis of the analysis, the results are presented in the form of aggregated histograms and probability density functions (Figure 2, Figure 3, Figure 4 and Figure 5). This approach preserves the variability observed in the original time-series while ensuring a concise and interpretable graphical presentation without exposing raw monitoring data.

All three models were tested and statistically validated, demonstrating strong agreement between simulated and actual performance data. The ability to describe uncertainty in a probabilistic framework enhances forecasting and facilitates planning under varying technical and human resource constraints.

Despite these strengths, limitations remain. The models assume stationarity and independence, which may not fully represent dynamic interdependencies or evolving geological conditions. Future research could incorporate adaptive mechanisms such as Bayesian updates, process mining integration, or machine learning to improve responsiveness and predictive power.

The models presented in this study rely on two key assumptions: stationarity of input distributions and independence of tasks. The assumption of stationarity is justified in the short term, when operating conditions remain relatively stable (e.g., constant seam thickness, no significant organizational changes). However, over longer time horizons, it may be weakened by geological variability, the occurrence of natural hazards, or changes in the work schedule.

The assumption of independence implies the absence of strong correlations between the durations of tasks, such as roof support advancement and shearer operation. In practice, however, a failure or slowdown of one element may trigger a domino effect. Therefore, these assumptions should be treated as approximations that enable the construction of decision-support models with high practical usefulness, though with certain limitations. Future research will aim to extend the models by incorporating conditional dependencies and adaptive mechanisms (e.g., Bayesian updating). In addition, dynamic adjustment of probability density functions as new operational data are collected may further enhance model adaptability, ensuring that predictions remain valid under evolving geological and organizational conditions.

Importantly, the modeling approach aligns with ongoing transitions toward digital mining and Industry 4.0. Stochastic modeling. When combined with real-time monitoring systems, they may support intelligent production management systems that automatically adapt to fluctuations in process conditions. These tools represent a significant opportunity to increase operational efficiency, reduce downtime, and enhance safety through more informed and data-driven decision-making.

To emphasize this perspective, a dedicated subsection was added on the integration of stochastic models with real-time monitoring platforms (e.g., IoT-based systems). Such integration enables dynamic updating of input data, on-line recalculation of PDFs, and immediate feedback for operational decision-making, creating a pathway toward adaptive, data-driven mining management systems.

5. Conclusions

The article presents the potential for constructing simulation models that, by design, enable both the analysis of production processes and the evaluation of dynamic changes in terms of process continuity and efficiency. Three models are discussed, each based on the application of probability density functions (PDFs), which allow for the representation of the stochastic nature of production processes carried out in longwall mining operations within hard coal mines.

The randomness inherent in the mining process arises from a number of influencing factors, which—according to the article—can be classified into two main groups: geological-mining factors and technical-organizational factors. The first group, strongly dependent on the geological structure, the location of the seam, and specific conditions within the longwall face, significantly contributes to process variability and operational instability. The second group, although initially perceived as more deterministic, also introduces uncertainty due to the high capital costs and rigidity of technical infrastructure. Given that mining equipment and systems cannot be replaced or modified at will, organizational and technical constraints also exert a destabilizing influence on production workflows.

For the purpose of model development, both deterministic and non-deterministic variables were identified. The deterministic parameters include longwall length, shearer length, spacing between conveyor supports, and the minimum distance between the shearer and the face conveyor. These are key input values which, once defined, remain fixed during the execution of a given mining variant. Their proper selection is critical, not only under in situ conditions but also in the construction of stochastic models. Non-deterministic variables were distinguished according to the specific scope and scale of each model.

According to the authors, the use of stochastic simulation in model development is both justified and economically feasible, offering measurable benefits in process analysis. This approach enables the evaluation of multiple mining scenarios and operational decisions that directly impact production output. The application of probability density functions allows for probabilistic modeling at a level of realism comparable to actual mining conditions—conditions that, for practical and safety reasons, cannot be fully replicated in experimental settings. The effectiveness of the proposed models has been validated through field testing under natural operational conditions. These models, based on probability distributions, can therefore serve as valuable decision-support tools in the context of variable and uncertain mining environments.

In summary, this article demonstrates the application of stochastic methods to model variability in coal mining production processes. It presents three models using probability density functions (PDFs) to quantify uncertainties inherent in the operation of longwall shearers, support systems, and crew configurations. Key conclusions include the following:

–

Mining production variability can be effectively described using probabilistic approaches rather than deterministic or regression-based models.

–

PDFs derived from field data provide a realistic basis for predicting and planning production.

–

The use of conditional and marginal distributions enables analysis of crew impacts and shift variability.

These findings suggest that stochastic simulation offers a practical and realistic method for enhancing production planning and risk assessment in deep hard coal mining. Future research will address model integration with event-driven process mining and adaptive decision systems for dynamic scheduling.

The stochastic models proposed and discussed in this paper can be integrated with real-time monitoring systems. The operational flow for such use would then be as follows: real-time data collection from sensors, then data transmission to a cloud or local server, and then use of stochastic models for calculations and analyses, which would lead to updated predictions and scenarios. Such a flow would be beneficial for decision-making and support, especially when supporting operational decisions: e.g., stopping work or changing production volumes.

Examples of benefits that can directly support decision-making include the following:

–

Production volume is a key element essential to the decision-making process—the proposed method allows for the appropriate preparation of both preparatory and subsequent processing processes.

–

Replacing deterministic variables with random variables allows for the simultaneous consideration of multiple factors influencing the duration of an activity in the form of a probability density function. The probability criterion for achieving the assumed module completion time used in the method allows for rational staffing selection, which supports management processes.

–

The use of the probability criterion in the method for determining staffing at the longwall face of hard coal mines allows for the stochastic nature of the production process carried out at this face to be taken into account, contributing to effective decision-making.

–

It is also possible to support predictive maintenance of machinery.

–

Optimization of the mining and logistics process based on current conditions.