Deep Learning-Based Classification of Transformer Inrush and Fault Currents Using a Hybrid Self-Organizing Map and CNN Model

Abstract

Accurate classification between magnetizing inrush currents and internal faults is essential for reliable transformer protection and stable power system operation. Because their transient waveforms are so similar, conventional differential protection and harmonic restraint techniques often fail under dynamic conditions. This study presents a two-stage classification model that combines a self-organizing map (SOM) and a convolutional neural network (CNN) to enhance robustness and accuracy in distinguishing between inrush currents and internal faults in power transformers. In the first stage, an unsupervised SOM identifies topologically structured event clusters without the need for labeled data or predefined thresholds. Seven features are extracted from differential current signals to form fixed-length input vectors. These vectors are projected onto a two-dimensional SOM grid to capture inrush and fault distributions. In the second stage, the SOM’s activation maps are converted to grayscale images and classified by a CNN, thereby merging the interpretability of clustering with the performance of deep learning. Simulation data from a 154 kV MATLAB/Simulink transformer model includes inrush, internal fault, and overlapping events. Results show that after one cycle following fault inception, the proposed method improves accuracy (AC), precision (PR), recall (RC), and F1-score (F1s) by up to 3% compared with a conventional CNN model, demonstrating its suitability for real-time transformer protection.

1. Introduction

The protection of power transformers is a crucial aspect in maintaining power system reliability and preventing widespread outages [1,2]. Among the various protection methods, differential protection is widely used due to its simplicity and high sensitivity to internal faults [3]. This method operates by comparing the currents at the primary and secondary windings of a transformer, which should ideally be equal under normal operating conditions. Any significant deviation beyond a predetermined threshold is interpreted as a potential internal fault, initiating protective relaying action.

Differential protection schemes are usually implemented using current transformers (CTs) connected at both ends of the transformer winding. A percentage differential relay calculates the operating current as the difference between the two CT currents. It compares this to a restraining current, which is typically defined as the average or sum of their magnitudes [4]. The relay operates according to a characteristic curve in the differential–restraint current plane. This method helps prevent false trips caused by CT saturation or load imbalance, but it can still encounter issues in complex transient conditions [5]. One major challenge in differential protection is its tendency to malfunction during non-fault transients, especially during transformer energization. A typical example is magnetizing inrush current, which occurs when a transformer is first energized [6]. This current has a high amplitude and contains significant harmonic distortion due to the nonlinear magnetization of the transformer core [7]. Its waveform can closely resemble that of a real internal fault, particularly during the first few cycles [8]. Therefore, traditional differential protection may struggle to reliably differentiate between inrush currents and internal faults.

To address this challenge, harmonic restraint techniques have been developed, mainly focusing on the second harmonic component in the differential current [9]. If the ratio of the second harmonic to the fundamental component exceeds a set threshold, the event is usually classified as an inrush rather than a fault. However, with the growing integration of renewable energy sources and power electronic devices, waveform characteristics have become more complex and less predictable [10]. This variability significantly reduces the reliability of fixed-threshold, rule-based approaches under varying operating conditions [11].

The consequences of protection misoperation are not only technical but also operationally serious. False tripping of a transformer can lead to significant downtime, stress on equipment, and cascading effects across the power grid [12]. Therefore, more intelligent and adaptive methods are needed to reliably distinguish between inrush and fault conditions across a broader range of dynamic scenarios. In response, various hybrid and machine learning-based classification approaches have been studied. Supervised learning algorithms, such as artificial neural networks (ANNs), convolutional neural networks (CNNs), and stacked denoising autoencoders (SDAEs), have demonstrated strong performance in experimental settings [13,14]. However, these models generally require large, labeled datasets and lack transparency, making them less suitable for safety-critical applications, such as protective relays [15].

An alternative approach involves unsupervised learning methods, especially the Self-Organizing Map (SOM) introduced by Kohonen [16]. SOMs project high-dimensional input data onto a low-dimensional grid while preserving topological relationships, enabling the clustering and visualization of complex event patterns. Unlike black-box supervised models, SOMs are interpretable and do not need labeled data, making them suitable for practical use in environments with limited ground truth. SOMs have been applied in various power system fields, including load behavior analysis, power quality monitoring, and fault detection [17]. In transformer protection, SOMs help distinguish between inrush and internal fault events based on learned data distributions, eliminating the need for preset thresholds. Their ability to visualize transitions and ambiguous cases further supports their role in detailed decision-making.

This study aims to leverage the clustering and visualization capabilities of SOMs to distinguish between magnetizing inrush and internal faults in transformers effectively. Using simulated differential current waveforms, relevant features are extracted from both the time and harmonic domains and projected onto a two-dimensional SOM grid to enable intuitive clustering of similar events. These clusters serve as a foundation for intelligent decision-making in protective relays.

To validate the approach, extensive simulation data are generated using MATLAB/Simulink (R2022b) for a 154 kV transformer under various energization and fault scenarios, including overlapping inrush-fault events. Unlike supervised models, the SOM-based method requires only signal feature vectors, enhancing its practicality in field applications where labeled data are scarce.

Additionally, two enhancements are proposed to boost classification performance. First, the SOM-based method is quantitatively compared with a comprehensive set of traditional and deep learning classifiers, including support vector machine (SVM), deep neural network (DNN), and convolutional neural network (CNN), all of which use the same input features. Second, an SOM–CNN architecture, representing the proposed model, is designed to convert SOM activation maps into two-dimensional images, which are then fed into a CNN for detailed pattern recognition. This combined approach merges the interpretability of unsupervised clustering with the classification precision of deep learning, effectively bridging the gap between exploratory data analysis and advanced predictive modeling.

• An unsupervised classification method based on SOM is proposed to differentiate between transformer inrush currents and internal faults without requiring labeled data or preset threshold settings;
• A fixed-length feature vector is created using seven statistical and spectral indicators, including RMS, peak value, crest factor, total harmonic distortion, second harmonic ratio, skewness, and kurtosis, extracted from differential current signals;
• The proposed model is created by transforming SOM outputs into two-dimensional images, which are then fed into a convolutional neural network, combining the advantages of unsupervised clustering and pattern-based classification;
• The performance of the proposed model is quantitatively assessed and compared with traditional classification models and deep learning models under identical conditions;
• Extensive simulations are performed using a 154 kV transformer model implemented in MATLAB/Simulink. The proposed model is validated through various scenarios, including inrush, internal faults, and overlapping events, with additional robustness tests under noisy conditions.

The rest of this paper is structured as follows.

Section 2 provides a detailed overview of the SOM, including its fundamental structure, training algorithm, and the process of feature extraction and dataset construction. This chapter outlines the basic concept of SOM and describes how differential current signals are preprocessed and transformed into seven-feature vectors suitable for unsupervised clustering. Section 3 describes the benchmark system used for validation, which is implemented in MATLAB/Simulink based on a 154 kV transformer model, as well as the proposed model and comparison models for analysis of classification performance. Section 4 reports a comprehensive performance evaluation, including (i) SOM training results and visualization (U-matrix, component planes, and label overlay); (ii) comparative analysis of accuracy, precision, recall, and F1 score across XGBoost, SVM, SOM, DNN, CNN, and the proposed model; and (iii) a robustness study under noisy conditions (30 dB SNR). Section 5 concludes the paper with a summary of the key findings and an outlook for future work.

2. Application of the SOM for Classifying Inrush Currents and Internal Faults in Power Transformers

2.1. Basic Principles of the SOM

The SOM is a biologically inspired, unsupervised neural network that projects high-dimensional input data onto a two-dimensional grid, preserving topological relationships [18]. This characteristic makes the SOM highly effective for intuitively visualizing complex data distributions, naturally clustering similar data points, and detecting anomalous patterns. Furthermore, the SOM offers several inherent advantages, including topology preservation, dimensionality reduction and visualization, unsupervised clustering, robustness to noise and outliers, vector quantization, and interpretability [19,20].

In this study, the SOM is used for two main reasons. First, transformer inrush and internal fault currents have subtle waveform differences that make it difficult for traditional supervised methods to detect boundaries. By mapping similar feature vectors to nearby neurons without using labels, the SOM naturally highlights the transition boundaries between clusters. Second, the topology-preserving feature of SOM provides a visual tool for understanding similarity relationships within the feature space and creates structurally meaningful representations for a subsequent CNN classifier.

A 10 × 10 two-dimensional SOM grid with 100 neurons is used. Each neuron contains a weight vector that matches the seven-dimensional input feature vector, which includes (RMS, Peak amplitude, Crest Factor, Total Harmonic THD, Second Harmonic Ratio, Skewness, and Kurtosis). During training, competitive learning assigns similar inputs to their Best Matching Units (BMU), while neighborhood learning updates the weight vectors of nearby neurons. After convergence, the SOM grid naturally forms clusters of transformer events, and each neuron’s activation map is converted into a two-dimensional image, used as input for the CNN.

Therefore, the proposed model combines unsupervised exploration of the data’s inherent distribution with the high classification accuracy of supervised deep learning, providing both interpretability and reliable performance in differentiating between transformer internal faults and inrush currents.

2.2. SOM Training Algorithm

The SOM training algorithm involves the iterative updating of weight vectors based on input patterns. The standard training procedure consists of the following steps:

• Weight Initialization: Each neuron $i$ is initialized with a weight vector $w_i\left(0\right)$, typically using random values within the input data range;
• Input data sampling: At each training step $t$, a random input vector is selected from the dataset. This random sampling promotes better generalization and reduces the risk of overfitting to specific patterns. This step follows an online learning scheme, where weight updates are performed incrementally;
• BMU Identification: For the selected input vector $x\left(t\right)$, the neuron whose weight vector $w_i\left(t\right)$, is closest in terms of Euclidean distance is identified as the BMU, denoted as:

  $$c=\mathrm{a}\mathrm{r}\mathrm{g}\underset{i}{\min }‖x\left(t\right)-w_i\left(t\right)‖$$

  (1)

The BMU determines the location on the map where the input vector is most accurately represented;

4.

Neighborhood Function Calculation: The BMU influences not only itself but also its neighboring neurons through a neighborhood function, typically modeled by a Gaussian distribution:

$$h_{ci}\left(t\right)=\exp \left(-{\displaystyle \frac{{‖r_c-r_i‖}^2}{2\sigma {\left(t\right)}^2}}\right)$$

(2)

Here, $r_i$, and $r_c$ represent the grid locations of neuron $i$ and the BMU, respectively. The neighborhood radius $\sigma \left(t\right)$ decreases over time, progressively focusing updates on a more localized region as learning proceeds;

5.

Weight update: The weight vectors of the BMU and its neighboring neurons are adjusted toward the input vector. The magnitude of this adjustment is proportional to the learning rate $\alpha \left(t\right)$ and the neighborhood function $h_{ci}\left(t\right)$:

$$w_i\left(t+1\right)=w_i\left(t\right)+\alpha \left(t\right)·h_{ci}\left(t\right)·\left(x\left(t\right)-w_i\left(t\right)\right)$$

(3)

Here, $\alpha \left(t\right)$ is the learning rate, which also decays over time, because a high learning rate is beneficial in the early stages for rapid structural adaptation, while a lower learning rate is necessary in later stages to ensure stable convergence and fine-tuning. This process allows the map to gradually conform to the distribution of the input data while maintaining topological order:

$$\alpha \left(t\right)={\alpha }_0·\exp \left(-{\displaystyle \frac{t}{\tau }}\right)$$

(4)

where, ${\alpha }_0$ is the initial learning rate (e.g., 0.1), $t$ is the current iteration step, and $\tau$ is the time constant (decay rate), typically set to one-third to one-half of the total number of iterations;

6.

Iteration and Convergence: Steps 2–5 are repeated for a fixed number of iterations T or until convergence, typically defined as the average quantization error falling below a preset threshold. Over time, α(t) and σ(t) decrease, allowing for the coarse-to-fine tuning of the map.

This process enables the SOM to self-organize, clustering similar patterns together, and the resulting map serves both as a tool for clustering and for visual interpretation.

2.3. Input Data and Feature Extraction

In contrast to end-to-end deep-learning methods that learn features automatically, which often sacrifice transparency and domain alignment, this study prioritizes explainable feature engineering. To classify between inrush currents and internal faults in transformer protection, we extract seven handcrafted features (RMS, Peak Amplitude, Crest Factor, THD, Second Harmonic Ratio, Skewness, and Kurtosis). These were selected based on three criteria:

• Physical interpretability for power system diagnostics: Each feature reflects a specific physical behavior of electrical transients. For example, RMS and Peak Amplitude capture overall energy and transient intensity in the signal, while THD and Second Harmonic Ratio reveal nonlinear magnetization characteristics in transformer cores;
• Empirical validation in prior literature: These features have shown discriminative power in earlier studies on fault detection of power equipment. Particularly, higher-order statistical moments, such as Skewness and Kurtosis, are susceptible to waveform asymmetries and impulse-like distortions typical of fault conditions;
• High compatibility with time-domain simulation data: As the dataset consists of time-domain differential current waveforms, the features can be computed efficiently with standard signal-processing techniques, such as the Fast Fourier Transform (FFT) and moment estimation, without additional domain transformations or complex preprocessing.

Collectively, these seven features capture key temporal, spectral, and statistical characteristics of the waveforms, thereby bridging domain-informed diagnostics with data-driven classification. Their lightweight and interpretable nature not only enhances classification accuracy but also strengthens model explainability.

2.4. Classification Using the SOM

The SOM is inherently an unsupervised clustering algorithm that does not offer direct classification capabilities. In this study, we use a post-labeling approach to leverage the SOM’s clustering ability to distinguish transformer inrush currents from internal fault events. After training, each neuron mapped to training samples is assigned a label of either inrush currents or internal faults based on the dominant class of those samples. In contrast, neurons without mapped samples remain unlabeled. This post-labeling process does not conflict with the unsupervised nature of SOM training, as the network itself learns the topological distribution of input data without prior class information. Instead, it acts as a valuable method to connect unsupervised clustering with supervised decision-making, which is crucial in transformer protection. Similar techniques have been widely used in SOM-based fault diagnosis and pattern recognition studies, where clustered neurons are linked to class labels to enable effective classification. By adopting this approach, the proposed method maintains the interpretability of unsupervised clustering while making it suitable for real-time protection applications [21].

• Training process: Seven feature vectors are extracted from a one-cycle sliding window of differential current signals, and mapped to their BMUs on a 10 × 10 two-dimensional SOM grid using Euclidean distance. Through iterative weight updates, the SOM self-organizes to capture the topological structure of the dataset;
• Post-labeling process: Once training is complete, each neuron is assigned the label inrush or fault based on which class constitutes the majority of its mapped training samples. This step applies a classification criterion to the unsupervised clustering results and thus determines each neuron’s class affiliation;
• Validation process: New test input vectors are projected onto the trained SOM in the same way. The label of the corresponding BMU is then taken as the predicted class. This confirms that the SOM, despite its unsupervised nature, can function effectively as a classifier.

To interpret and evaluate the SOM’s clustering results, we employ the following visualization techniques:

• Label Overlay: displays the dominant class label assigned to each neuron, providing a clear visualization of cluster distributions;
• U-Matrix: highlights the distances between neighboring neurons, revealing cluster boundaries and transition regions;
• Component Planes: visualizes the spatial distribution of each feature across the map, enabling analysis of individual variable influences.

This classification approach preserves both the interpretability and lightweight nature of the SOM, demonstrating its suitability as a protection solution for real-time or edge-computing environments.

2.5. Data Acquisition and Processing

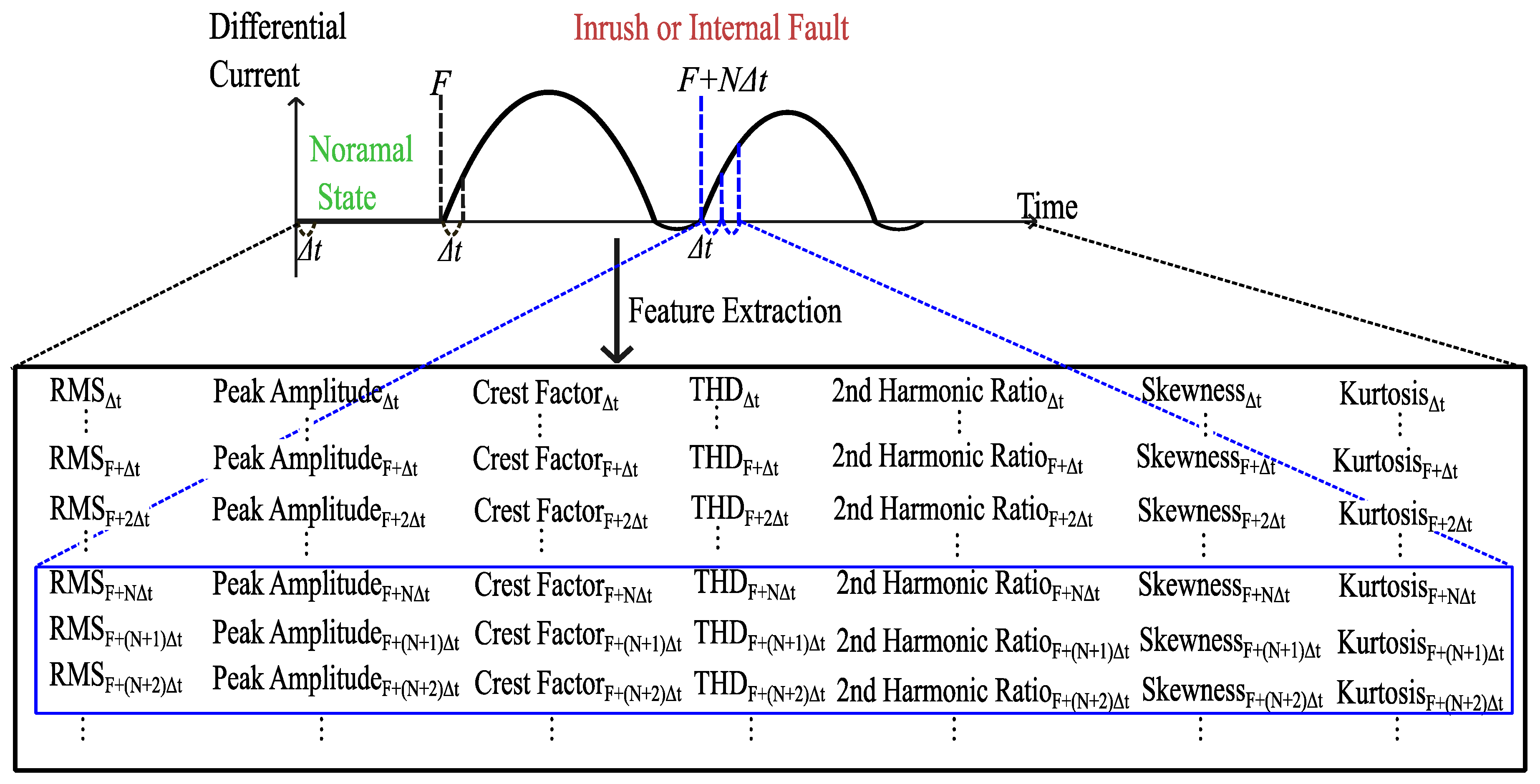
Transformer inrush currents and internal faults change quickly and often last only a few cycles. To effectively capture the time-related details of these short events, the input current signals are divided into segments using a sliding window method. In this study, $N$ represents the number of samples per cycle, and $∆t$ (=1/$N$) denotes the sampling interval.

We define as follows:

• F denotes the instant of fault inception.
• $F+N∆t$ represents the time point corresponding to the first post-fault cycle (i.e., one cycle after the fault occurrence).
• $F+(N+1)∆t$ indicates the subsequent moment, obtained by advancing $∆t$ beyond $F+N∆t$.

Although data acquisition begins at the start of the simulation, only signal segments starting from one complete cycle after the event are used for model training. This approach excludes the initial post-event cycle, which typically contains transient components such as DC offset and harmonic distortion. Therefore, signal segments are selected from stable post-event intervals ($F+N∆t,F+(N+1)∆t$ …) for sliding window-based feature extraction and classification. Each window is independently processed to extract a seven-dimensional feature vector, which is subsequently projected onto the SOM for classification.

Here, $F+N∆t$ indicates the first post-fault cycle immediately after fault inception, while $F+(N+1)∆t$ represents the following cycle. This clarification ensures that the reported results directly reflect the practical relay operating timeline. This approach supports real-time fault detection by allowing the system to monitor how classification confidence changes over time and accurately identify the earliest point at which the SOM can reliably distinguish between inrush and internal fault events. The one-cycle window strikes a balance between temporal detail and computational efficiency. It captures enough signal content to extract meaningful spectral and statistical features, while being short enough for low-latency, real-time protection systems. This windowing method is particularly suitable for intelligent substation environments where quick and understandable decisions are required under strict operational constraints.

Figure 1 illustrates the sliding window-based feature extraction process from differential current signals for transformer event classification. Beginning from the disturbance onset, the current signal is segmented into fixed one-cycle windows. From each segment, a seven-dimensional feature vector is computed, consisting of RMS, peak amplitude, crest factor, THD, second harmonic ratio, skewness, and kurtosis. These time-sequential feature vectors are subsequently projected onto the SOM for classification. The figure visually demonstrates how each segment produces a distinct feature set and how these features change over time, which enables the detection of inrush or internal fault conditions.

2.6. Dataset Preparation

To construct the labeled dataset for classification, fixed-length windows were extracted from the complete set of simulation outputs using a sliding window approach. For each window, the seven input features were calculated and used as descriptive data. All feature vectors were normalized to ensure consistent scaling across the dataset, thereby preventing any individual feature from exerting undue influence. This normalization was applied globally to all samples before training and evaluation.

The resulting dataset included 621,845 labeled cases across four classes: external fault, inrush, internal fault, and overlapping events. While the primary goal of this study is to distinguish inrush currents from internal faults, external faults were included to represent normal operating conditions from the perspective of differential protection. Overlapping events were also added to evaluate the model’s robustness during simultaneous occurrences. A detailed breakdown of each class, along with the corresponding case counts, is summarized in

Table 1. Summary of class type, number of cases, and datasets.

Class Type	Number of Cases (Datatsets)
External Faults (Normal State)	35 (33,253)
Inrush Currents	170 (161,500)
Internal Faults	100 (170,202)
Overlapping Events (Inrush currents + Internal Faults)	270 (256,890)

.

This dataset allowed for a fair and unbiased comparison among different classification models, including both traditional algorithms and the proposed model. Additionally, macro-averaged metrics such as AC, PR, RC, and F1 were calculated to ensure a performance comparison unaffected by class size. The dataset was divided into 80% for training and 20% for validation. To avoid bias from temporal correlation or unintended data leakage, the split was performed at the scenario level, where each event case (defined by a specific combination of fault inception angle, residual flux, and operating condition) was assigned exclusively to either the training or the validation set. This ensured that no sliding windows derived from the same physical scenario appeared in both sets, thereby preserving independence between training and evaluation. All sliding windows derived from the same simulation case (defined by seed, inception angle, and residual flux) were assigned exclusively to either the training, validation, or test set, ensuring no overlap between subsets.

The large size of the dataset results from the high sampling frequency (3840 Hz) and the systematic generation of multiple operating scenarios in MATLAB/Simulink, including various inrush conditions, internal faults with different inception angles, residual flux levels, and overlapping events. For each case, the differential current signals were divided into fixed-length windows following fault inception, thereby increasing the number of training samples. To enhance robustness, additional noise and load variation conditions were added. Although the dataset is simulation-based, its credibility was confirmed by covering a wide range of realistic operating conditions observed in practice.

To ensure reproducibility and consistency in applying machine learning models, all feature vectors and their corresponding class labels were organized in a format compatible with MATLAB’s machine learning environment, including the Statistics and Machine Learning Toolbox and Deep Learning Toolbox. Before training, the distribution of each feature was examined using MATLAB’s visualization and statistical analysis tools to verify inter-class separability and sufficient variance.

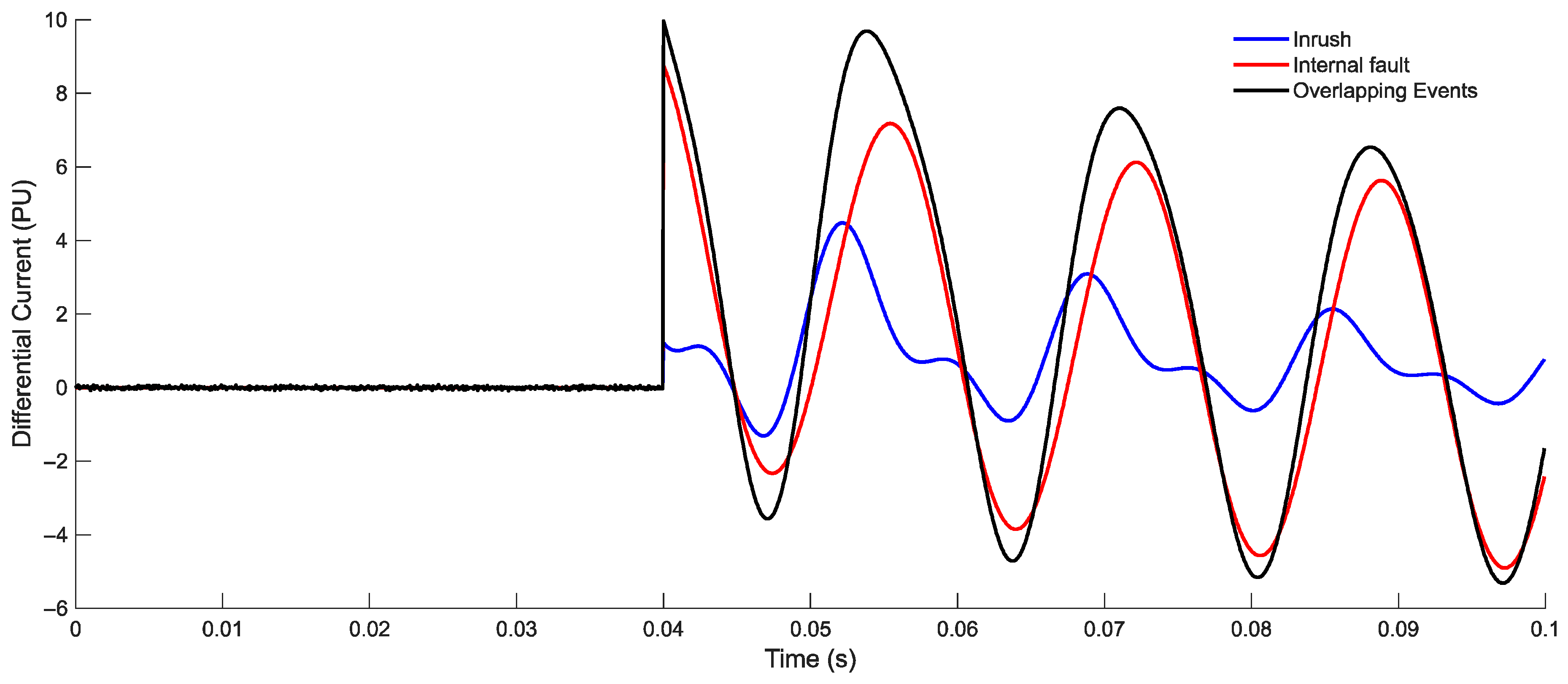
Figure 2 illustrates the differential current waveforms under three representative conditions: inrush, internal fault, and overlapping event. Before 0.04 s, the system remains in the normal operating state or under an external fault condition, during which the differential current stays close to zero. At 0.04 s, the transient events are initiated, and distinct waveform characteristics emerge depending on the event type. The inrush case exhibits a relatively moderate magnitude with an asymmetric pattern. The internal fault shows a higher amplitude due to the fault current contribution, and the overlapping event demonstrates the most severe distortion, with both inrush and fault components superimposed.

3. Simulation Model

The effectiveness of the proposed model depends on the diversity and quality of the dataset used for training and validation. To achieve this, a series of comprehensive simulations was conducted using MATLAB/Simulink, modeling a 154 kV distribution substation transformer under various operating conditions.

3.1. Benchmark Model Configuration and Parameters

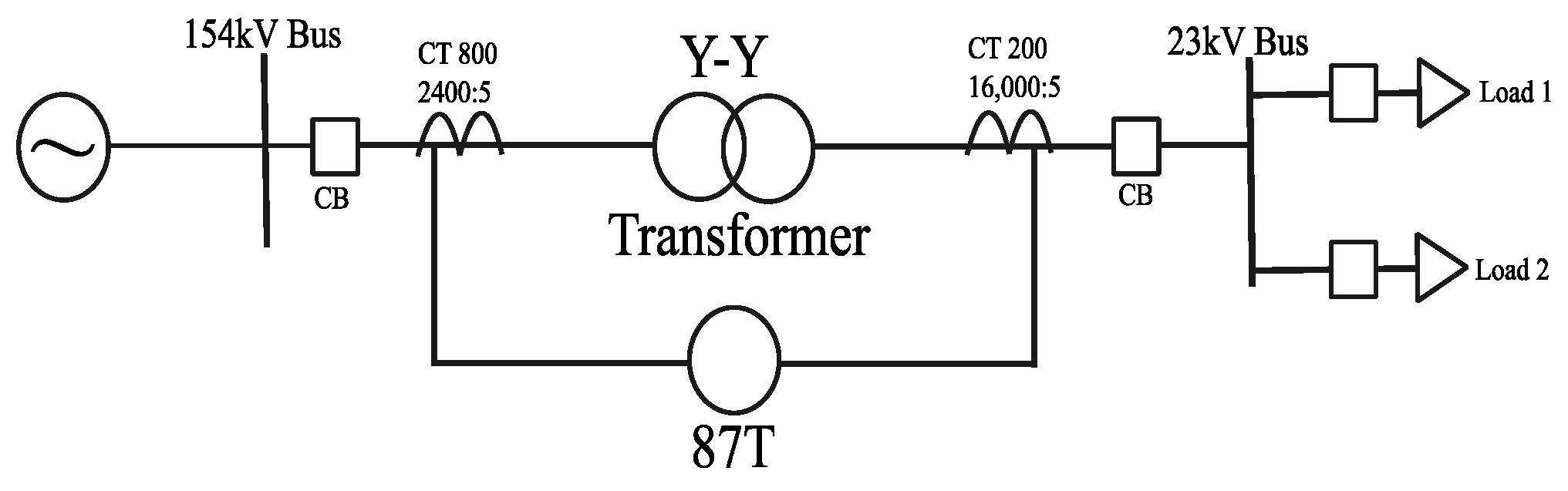
To validate the proposed method, simulations were conducted based on a typical 154 kV distribution substation in South Korea. A 154/23 kV distribution system model was developed in Matlab/Simulink, incorporating a 100 MVA power transformer configured in a Y-Y connection, as schematically represented in Figure 3.

The simulation employed a sampling frequency of 3840 Hz, corresponding to 64 samples per cycle in a 60 Hz system. The source was modeled using the parameters and conditions summarized in

Table 2. Benchmark model parameter and simulation conditions.

Category	Configuration	Parameter
System Configuration	Transformer Rating	100 MVA, 154/23 kV
	System Frequency	60 Hz
	CT Rating	2400/5 (154 kV), 16,000/5 (23 kV)
	Transformer Connection	Y-Y
	Protection Relay	87T (Differential Relay)
	Number of Loads	2 Loads (Load 1, Load 2)
	Sample Frequency	3840 Hz
	Simulation Time	5 s
Modeling Parameters	Source impedance (Positive/Negative)	$R_1$$,R_2$$=0.0419\mathsf{\Omega }$ $L_1$$,L_2$$=0.8921\mathrm{H}$ $C_1$$,C_2$$=0.0128\mathrm{F}$
	Source impedance (Zero)	$R_0$$=0.0293\mathsf{\Omega }$ $L_0$$=2.6657\mathrm{H}$ $C_0$$=0.0042\mathrm{F}$
	Magnetizing Current (%IM)	1
External Faults	Fault Type	Three-phase short circuit
	Fault Inception Angle	0°~90°, in 15° steps
	Fault Resistance	1, 5, 10, 20, 50 $\mathsf{\Omega }$
Inrush Currents	Residual Flux	−80%~80%, in 10% steps
	Switching angle	0°~90°, in 10° steps
Internal Faults	Fault Type	Winding-to-ground fault
	Fault Inception Angle	0°~90°, in 10° steps
	Winding Location	0°~90°, in 10° steps

. This study focuses on winding-to-ground fault scenarios. Faults were introduced by varying the fault location along the transformer’s primary winding from 10% to 90% of the winding length, in 20% increments. The fault inception angles were adjusted from 0° to 90° in 15° steps, with reference to the phase-A current. For inrush current simulations, residual flux levels between 80% and 100% were applied in 10% increments, and various switching angles ranging from 0° to 90° were used in 10° increments.

These variations ensure that the generated signals cover a broad range of operational scenarios, enhancing the SOM’s ability to generalize to unseen system conditions. Each parameter was carefully chosen to reflect realistic transformer dynamics and to introduce distinguishable characteristics in both fault and inrush responses.

3.2. Applications of Classification Models

To effectively distinguish between transformer internal faults and inrush currents in power transformers, this study examines a diverse set of classification models, categorized into two main groups: classification models and deep learning models. These models differ in architectural complexity, learning strategies, and their ability to capture temporal or spatial characteristics of the input signals. This comparative approach enables a robust evaluation of performance under various operational conditions, including changes in residual flux, fault inception angle, and fault location. In this study, the performance of the proposed model for classification between inrush currents and internal faults was validated through comparison with classification models and deep learning models.

Among the classification models, SVM, XGBoost, and SOM were selected for evaluation. These models utilize a predefined seven-dimensional feature vector as input and perform classification based on decision boundaries (SVM), ensemble learning (XGBoost), or unsupervised clustering (SOM). As supervised classifiers, SVM and XGBoost offer fast execution, simple architectures, and ease of interpretation, making them well-suited for distinguishing fault types characterized by clear feature boundaries. The SOM stands out as an unsupervised clustering algorithm that can project feature vectors onto a self-organized two-dimensional lattice. It provides intuitive visualization of data structures through tools such as the U-matrix, component planes, and BMU activation heatmaps. These visualizations facilitate the clear interpretation of class boundaries and distributions, while post-labeling enables effective classification despite the unsupervised nature of the model. These characteristics make the SOM particularly well-suited for real-time fault diagnosis applications where both interpretability and lightweight implementation are critical.

Among deep learning models, DNN and CNN were selected for evaluation. These models can automatically learn from time-frequency features and complex high-dimensional patterns. Particularly, DNN and CNN operate on preprocessed feature vectors or image-like inputs. Owing to their high representational capacity and strong generalization performance, these deep learning models are capable of recognizing intricate fault patterns that conventional classifiers may fail to detect.

Although recurrent architectures such as RNNs, LSTMs, and GRUs are also capable of capturing temporal dependencies in sequential signals, they were not adopted in this work because CNNs offer higher computational efficiency and integrate naturally with the SOM-generated activation maps in image format. Nevertheless, applying recurrent or hybrid sequence–convolutional models remains a promising direction for future work, particularly for handling longer time windows and more complex transient behaviors.

Furthermore, this study proposes a model that integrates the strengths of both the SOM and CNN. In this model, the SOM first performs unsupervised clustering on the input feature space and projects the results onto a two-dimensional grid. This activation map is then converted into a grayscale image, which serves as the input to the CNN for final classification. By combining the visual clustering capability of the SOM with the spatial pattern recognition strength of CNN, the model achieves high classification accuracy while also improving interpretability.

The hyperparameters employed in this study were not arbitrarily assigned but determined through empirical trials and literature references. For XGBoost, tree depths ranging from 2 to 8 were tested, and a max_depth of 4 yielded the most favorable balance between preventing overfitting and maintaining accuracy. For the SOM, a 10 × 10 grid was adopted to balance clustering resolution and interpretability, which aligns with the general guideline that the SOM grid size should be adapted to problem characteristics and dataset scale. For CNN and DNN models, parameters such as the number of layers, neurons, and learning rates were tuned experimentally to achieve both classification performance and computational efficiency.

The model structures and key parameter settings of the classification above and deep learning models are summarized in Figure 4 and

Table 3. Summary of model configuration and parameters.

Model Type	Model	Input Format	Model Structure	Parameters
Classification Model	XGBoost	7 feature vector		100 trees, max_depth = 4
	SVM			C = 1.0, RBF kernel
	SOM			Grid Size = 10 × 10 ${\alpha }_0$ = 0.5 ${\sigma }_0$ = 5
Deep Learning Model	DNN	7 feature vector	Input (7) → Dense (64, ReLU) → Dense (32, ReLU) → Dense (2, Softmax)	ReLU activation, Initial Learning rate = 0.001
	CNN	1 × 7 image map	Conv2D (3 × 3, 32) → Pool → Flatten → Dense → Softmax	Optimizer = SGDM Initial Learning rate = 0.001 Momemtum = 0.95 Min/Max Bitch size = 16/40 Max Epochs = 40
	Proposed Model	10 × 10 SOM Activation Map	SOM (10 × 10) → Activation map → Conv2D (10 × 10, 32) → Pooling → Conv2D (5 × 5, 64) → Pooling → Conv2D (2 × 2, 128) → Pooling → Flatten (128) → Softmax (2)

. Each model differs in terms of input format, architectural design, activation functions, and learning strategies, and has been optimized based on the objectives and characteristics of the dataset used in this study.

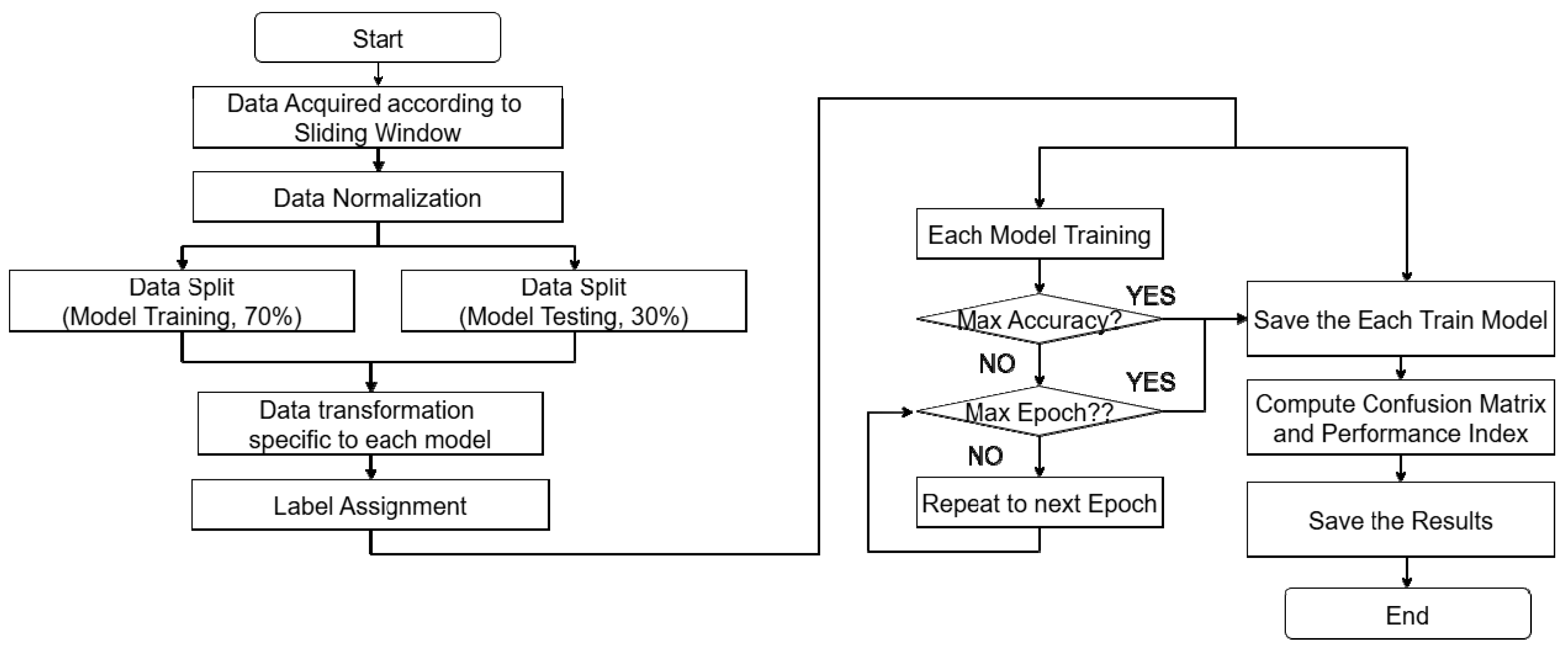
Figure 5 presents the overall process of training and evaluating classification models for distinguishing between inrush currents and internal faults. After acquiring differential current signals, the data were segmented using a fixed-length sliding window and then normalized. The dataset is subsequently split into training and testing sets.

For each model, the data are transformed into the appropriate input format, followed by label assignment and model training. During training, early stopping or a maximum number of epochs is used to control the number of iterations. After training, the model is evaluated on unseen data, using a confusion matrix and standard classification metrics. All results are recorded for subsequent analysis and comparison.

4. Evaluation of the Proposed Model

This chapter presents a comprehensive evaluation of the SOM-based clustering performance using simulation data. It compares the results of the proposed model with those of classification models and deep learning models, including SVM, XGBoost, DNN, and CNN.

4.1. Performance Index

To quantitatively evaluate the performance of the proposed model, a comparative analysis was conducted using the confusion matrix and various performance metrics. Since the SOM is an unsupervised learning model that does not utilize label information during training, a post-labeling strategy was employed to enable fair comparison with supervised classification models.

In the case of the SOM, each neuron was assigned a representative label based on the majority class of the training instances mapped to it during the training process. During testing, each input instance was projected onto the SOM, and the label of the corresponding BMU was treated as the predicted class. This predicted label was then compared with the actual label to construct a confusion matrix, allowing the SOM to be evaluated using the same criteria as supervised models.

In contrast, supervised learning models such as SVM, XGBoost, CNN, DNN, and the proposed model generate class predictions directly from input features. For these models, the confusion matrix was constructed by directly comparing predicted outputs with ground-truth labels. This unified evaluation procedure enables a fair comparison of performance between supervised and unsupervised models under consistent input conditions.

The confusion matrix for the proposed model is presented in

Table 4. Confusion matrix.

Actual Value	Predicted Value
	Positive	Negative
Positive	True Positive (TP)	False Negative (FN)
Negative	False Positive (FP)	True Negative (TN)

, and serves as the basis for calculating various performance metrics such as AC, PR, RC, and F1s. These standardized metrics enable rigorous and consistent evaluation of the model’s classification performance, facilitating direct comparison with other supervised and unsupervised approaches [22].

AC, PR, RC, and F1s are calculated as follows:

$$AC={\displaystyle \frac{TP+TN}{TP+FP+TN+FN}}$$

(5)

$$PR={\displaystyle \frac{TP}{TP+FP}}$$

(6)

$$RC={\displaystyle \frac{TP}{TP+FN}}$$

(7)

$$F1s={\displaystyle \frac{2\times PR\times RC}{PR+RC}}$$

(8)

AC reflects the overall proportion of correctly classified instances, including both inrush and fault events, across the entire dataset. PR measures the proportion of cases that were correctly identified as a specific class, such as fault, among all instances the model predicted as that class. This indicates the model’s ability to minimize false positives. RC quantifies the proportion of correctly identified instances among all actual cases of a given class, demonstrating the model’s effectiveness in detecting relevant events. F1s represents the harmonic mean of PR and RC, providing a balanced evaluation that considers both false positives and false negatives.

In the context of transformer fault and inrush current classification, a model with high PR minimizes the risk of misclassifying inrush events as faults. In contrast, high RC ensures that most fault events are accurately detected. The F1s is especially useful when the class distribution is imbalanced or when both types of errors carry significant consequences. Therefore, a model achieving high AC, PR, RC, and F1s is considered more reliable and robust for practical deployment.

4.2. SOM Training Results and Visualization

The SOM was implemented in MATLAB, utilizing a combination of built-in SOM functions and custom scripts to provide flexibility in training and visualization. Model parameters were empirically selected based on convergence stability and clustering clarity, as determined through a series of preliminary experiments.

• SOM grid (Feature map) size: 10 × 10 neurons;
• Initial learning rate (${\alpha }_0$) = 0.5, decaying to 0.01;
• Initial neighborhood radius (${\sigma }_0$) = 5, gradually decreasing over time;
• Total number of iterations ($T$): 4000.

This configuration was found to provide a good balance between topological preservation and training convergence for the given dataset of transformer inrush and internal fault events. To evaluate the quality of the trained SOM and interpret the resulting feature space, visualization techniques such as the U-Matrix, Component Planes, and Label Overlay were employed.

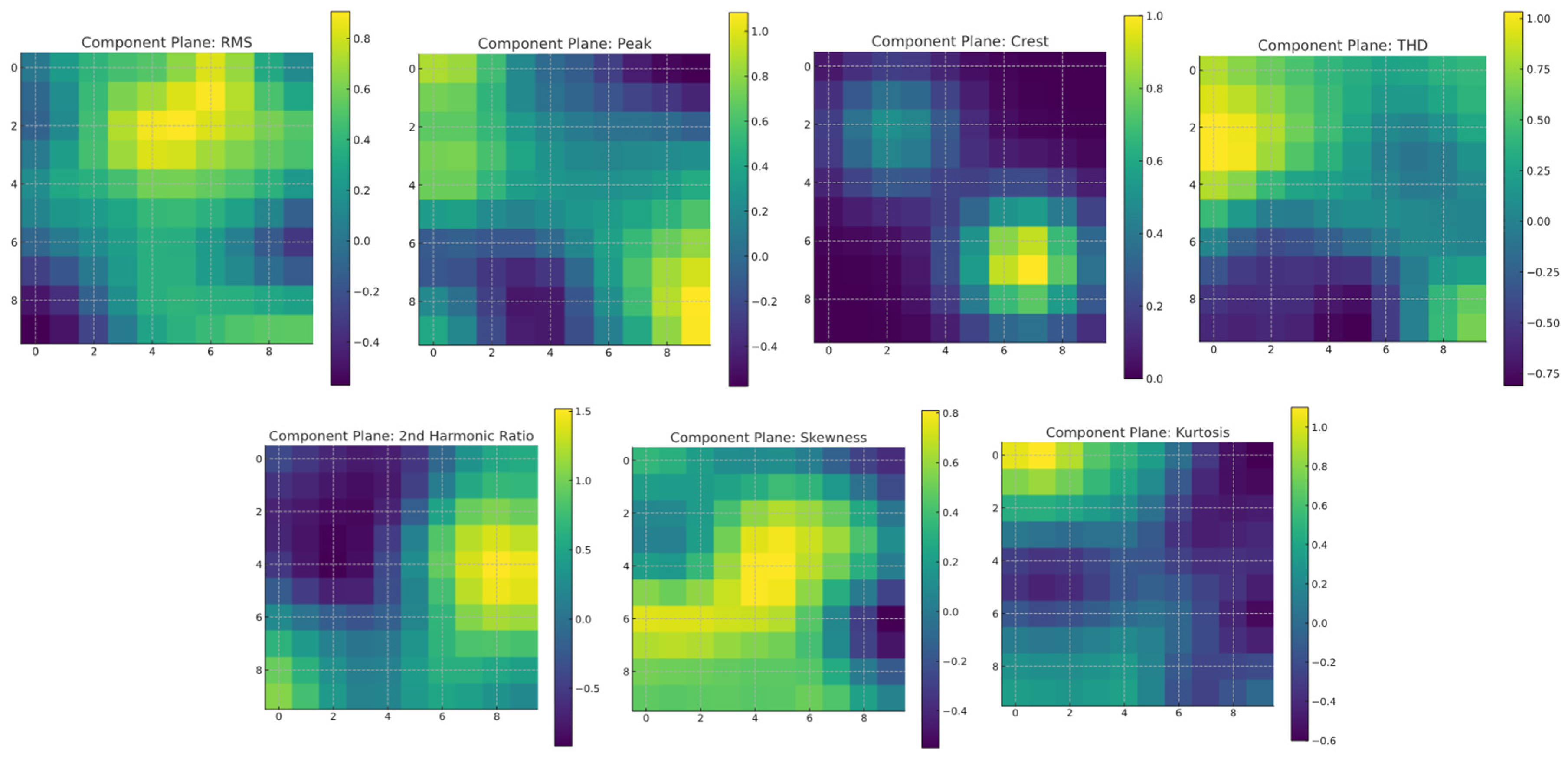
Figure 6 presents the component plane of the seven features mapped onto the 10 × 10 SOM grid. These features include RMS, peak amplitude, crest factor, THD, second harmonic ratio, skewness, and kurtosis. Each component plane visualizes the distribution of a single feature across all neurons using a continuous color scale, providing an intuitive understanding of how each variable contributes to the clustering of transformer events.

In the RMS plane, high values appear in the upper left region, indicating strong energy levels typically associated with inrush current events. This distinction helps separate inrush events from normal operating conditions. The peak amplitude and crest factor planes show high responses in the lower right and central regions, corresponding to internal faults characterized by sharp waveform peaks and asymmetry. Among them, the crest factor plays a particularly critical role in distinguishing internal faults from inrush signals.

The THD plane highlights higher values in the central and upper neurons, suggesting stronger harmonic content during inrush events. The second harmonic ratio plane also shows elevated values in the central and upper right regions, aligning with known characteristics of inrush currents. The skewness component exhibits a smooth gradient along the central axis of the map, reflecting waveform asymmetry that aids in distinguishing between normal and fault conditions. The kurtosis plane highlights sharp transitions and localized peaks in the upper-central region, providing additional cues for detecting abnormal operating conditions such as internal or overlapping faults.

These component planes reveal that the SOM has effectively organized the input feature space and distinguished between different transformer conditions. The clear and distinct activation patterns support the validity of the selected feature set and highlight the SOM’s capability to assist in fault classification tasks.

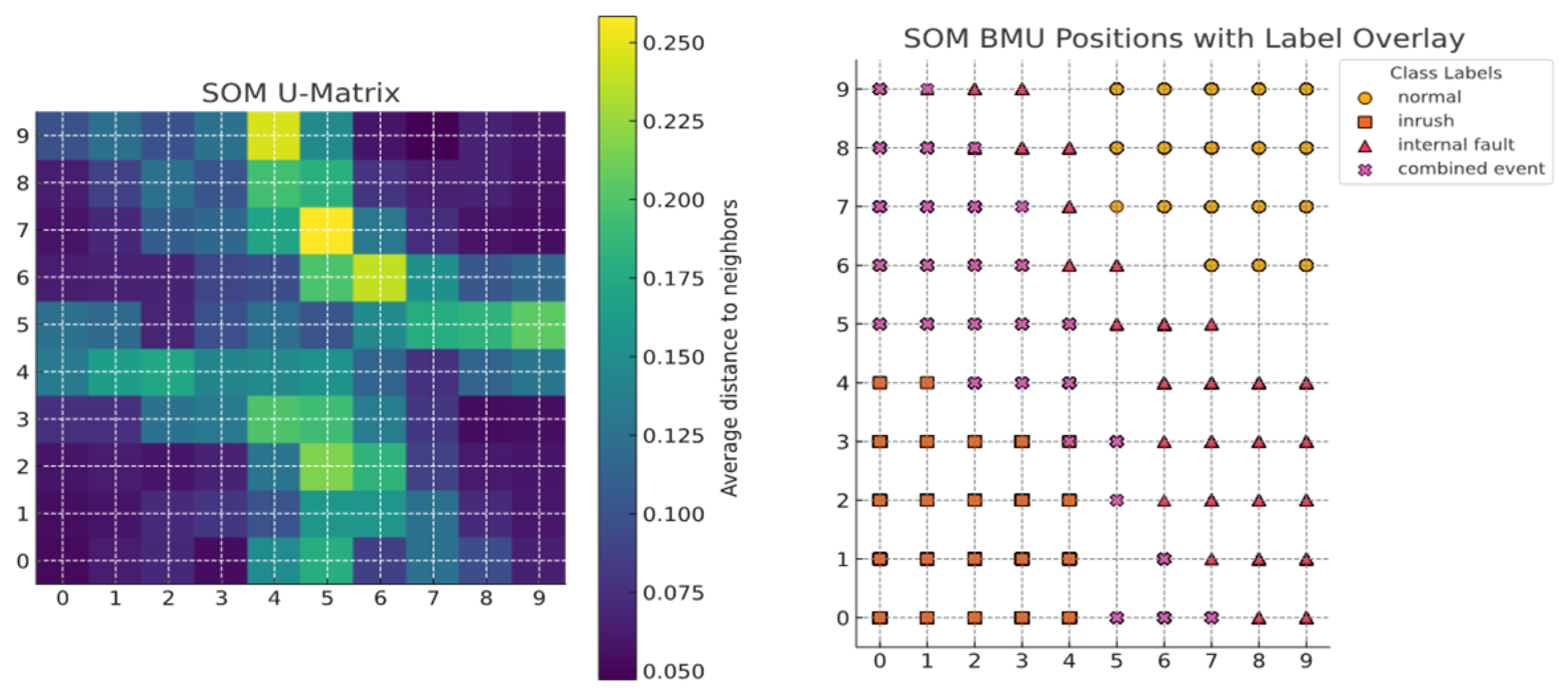
The left side of Figure 7 shows the SOM U-Matrix, which visualizes the average distance between neighboring map units using a continuous color scale. Regions with higher distances indicate boundaries between clusters corresponding to different operating states. The right side overlays class labels on the BMU positions of each instance projected onto the SOM grid. Each marker uses a distinct shape and color to represent the normal, inrush current, internal fault, and overlapping event classes. Instances from the same class tend to cluster together on the grid and remain separated from cases of other classes. This confirms that the SOM effectively distinguishes transformer operating states based on the feature set.

4.3. Simulation Results

To reduce the influence of randomness caused by model initialization and data partitioning and to enhance statistical reliability, each classification model was evaluated through 10 repeated simulation runs under identical experimental conditions. In each run, the same training and testing procedures were applied, and performance metrics (AC, PR, RC, and F1s) were recorded.

To ensure a robust evaluation, each experiment was repeated ten times with different random seeds. The classification performance of AC was then summarized as the mean ± standard deviation (SD) across these runs. To further validate the proposed framework’s superiority, statistical significance tests were performed. Specifically, Wilcoxon signed-rank tests were used to compare the proposed method against each baseline model across 10 independent runs. Significance was assessed using the Wilcoxon signed-rank test across these runs. Pairwise comparisons were made between the proposed SOM–CNN and the comparison models. The resulting p-values consistently fell below 0.05 (with most values being less than 0.01). To supplement p-values, effect sizes were also reported: Cohen’s d ranged from 0.65 to 1.15 (indicating moderate to substantial effects), and Cliff’s delta ranged from 0.55 to 0.78, confirming that the performance improvements are statistically significant.

Initially, the simulations considered five operating scenarios: external fault, normal state, inrush currents, internal faults, and overlapping events. Among these, external faults do not trigger protection relays. They are typically regarded as non-fault conditions in practical power system operations. Accordingly, external faults were categorized under the normal state in this study. As a result, all classification models were trained and evaluated based on four classes: normal state (including external faults), inrush currents, internal faults, and overlapping events. The performance of each model was reported as the average over 10 simulation runs, reducing the impact of stochastic variations and providing a robust basis for performance comparison. This evaluation strategy offers a consistent and statistically sound framework for validating the classification capability of each model. This approach enabled the identification of the earliest time point at which each model achieved 100% classification accuracy, thereby providing a quantitative basis for evaluating model responsiveness and reliability in real-time protection system applications.

Table 5. Results of Performance Index for each Classification Model.

Time	State	Model	AC (%) ± SD	PR (%)	RC (%)	F1s (%)
$F+N$Δ$t$	Normal State + External Fault	2nd Harmonic threshold	$100.0\pm$ 0.00	100.0	100.0	100.0
		XGBoost	$100.0\pm$ 0.00	100.0	100.0	100.0
		SVM	$100.0\pm$ 0.00	100.0	100.0	100.0
		SOM	$100.0\pm$ 0.00	100.0	100.0	100.0
		DNN	$100.0\pm$ 0.00	100.0	100.0	100.0
		CNN	$100.0\pm$ 0.00	100.0	100.0	100.0
		CNN (spectrograms)	$100.0\pm$ 0.00	100.0	100.0	100.0
		Proposed Model	$100.0\pm$ 0.00	100.0	100.0	100.0
	Inrush Currents	2nd Harmonic threshold	$83.1\pm$ 0.14	83.5	84.0	83.7
		XGBoost	$70.4\pm$ 0.24	69.9	70.1	70.0
		SVM	$75.2\pm$ 0.19	74.7	74.9	74.8
		SOM	$80.3\pm$ 0.13	79.8	80.0	79.9
		DNN	$83.2\pm$ 0.12	82.7	82.9	82.8
		CNN	$87.1\pm$ 0.13	86.6	86.8	86.7
		CNN (spectrograms)	$86.9\pm$ 0.15	85.9	86.7	85.9
		Proposed Model	$90.2\pm$ 0.13	89.7	89.9	89.8
	Internal Faults	2nd Harmonic threshold	$85.0\pm$ 0.15	84.5	84.6	84.8
		XGBoost	$72.4\pm$ 0.19	71.9	72.1	72.0
		SVM	$77.2\pm$ 0.19	76.7	76.9	76.8
		SOM	$82.3\pm$ 0.18	81.8	82.0	81.9
		DNN	$85.2\pm$ 0.12	84.7	84.9	84.8
		CNN	$89.1\pm$ 0.13	88.6	88.8	88.7
		CNN (spectrograms)	$89.2\pm$ 0.11	88.9	89.9	88.4
		Proposed Model	$92.2\pm$ 0.10	91.7	91.9	91.8
	Overlapping Events (Inrush Currents + Internal Fault)	2nd Harmonic threshold	$71.2\pm$ 0.41	71.6	71.4	70.9
		XGBoost	$68.4\pm$ 0.31	67.9	68.1	68.0
		SVM	$73.2\pm$ 0.29	72.7	72.9	72.8
		SOM	$78.3\pm$ 0.24	77.8	78.0	77.9
		DNN	$81.2\pm$ 0.20	80.7	80.9	80.8
		CNN	$85.1\pm$ 0.18	84.6	84.8	84.7
		CNN (spectrograms)	$84.8\pm$ 0.17	85.1	83.2	84.9
		Proposed Model	$88.2\pm$ 0.19	87.7	87.9	87.8
	Macro-average	2nd Harmonic threshold	$84.8\pm$ 0.18	84.9	85.0	84.8
		XGBoost	$77.8\pm$$0.19$	77.4	77.5	77.5
		SVM	$81.4\pm$ 0.17	81.1	81.2	81.9
		SOM	$85.2\pm$ 0.13	84.8	85.0	84.9
		DNN	$87.4\pm$$0.11$	87.0	87.1	87.1
		CNN	$90.3\pm$ 0.11	89.9	90.1	90.0
		CNN (spectrograms)	$90.2\pm$ 0.10	89.9	89.9	89.8
		Proposed Model	$92.7\pm$ 0.10	92.2	90.4	92.3
$F+$ $(N+1)$Δ$t$	Normal State + External Fault	2nd Harmonic threshold	$100.0\pm$ 0.00	100.0	100.0	100.0
		XGBoost	$100.0\pm$ 0.00	100.0	100.0	100.0
		SVM	$100.0\pm$ 0.00	100.0	100.0	100.0
		SOM	$100.0\pm$ 0.00	100.0	100.0	100.0
		DNN	$100.0\pm$ 0.00	100.0	100.0	100.0
		CNN	$100.0\pm$ 0.00	100.0	100.0	100.0
		CNN (spectrograms)	$100.0\pm$ 0.00	100.0	100.0	100.0
		Proposed Model	$100.0\pm$ 0.00	100.0	100.0	100.0
	Inrush Currents	2nd Harmonic threshold	$90.4\pm$ 0.12	90.1	89.4	89.1
		XGBoost	$90.1\pm$ 0.16	89.8	89.9	89.9
		SVM	$92.4\pm$ 0.18	92.0	92.2	92.1
		SOM	$94.2\pm$ 0.16	93.9	94.0	94.0
		DNN	$96.0\pm$ 0.13	95.7	95.8	95.8
		CNN	$98.2\pm$ 0.14	98.0	98.1	98.1
		CNN (spectrograms)	$97.9\pm$ 0.14	97.5	97.9	97.5
		Proposed Model	$100.0\pm$ 0.00	100.0	100.0	100.0
	Internal Faults	2nd Harmonic threshold	$90.9\pm$ 0.15	90.1	90.5	90.7
		XGBoost	$91.5\pm$ 0.15	92.1	90.9	91.9
		SVM	$92.5\pm$ 0.16	92.6	92.9	92.9
		SOM	$94.6\pm$ 0.18	94.6	94.5	94.6
		DNN	$97.1\pm$ 0.21	96.0	96.0	96.1
		CNN	$98.9\pm$ 0.16	98.6	98.6	98.9
		CNN (spectrograms)	$99.1\pm$ 0.12	97.9	98.16	98.6
		Proposed Model	$100.0\pm$ 0.00	100.0	100.0	100.0
	Overlapping Events (Inrush Currents + Internal Fault)	2nd Harmonic threshold	$84.5\pm$$0.39$	84.6	84.7	84.9
		XGBoost	$90.7\pm$ 0.24	90.1	88.2	91.2
		SVM	$91.9\pm$ 0.26	92.2	92.7	92.5
		SOM	$94.6\pm$ 0.21	94.0	94.3	94.5
		DNN	$96.5\pm$ 0.15	96.0	96.2	96.0
		CNN	$98.6\pm$ 0.14	98.5	98.6	98.6
		CNN (spectrograms)	$98.7\pm$ 0.17	98.7	98.5	98.2
		Proposed Model	$100.0\pm$ 0.00	100.0	100.0	100.0
	Macro-average	2nd Harmonic threshold	$91.4\pm$ 0.16	91.2	91.1	91.2
		XGBoost	$93.0\pm$ 0.13	93.0	92.2	93.2
		SVM	$94.2\pm$ 0.15	94.2	94.4	94.3
		SOM	$95.8\pm$ 0.13	95.6	95.7	95.7
		DNN	$97.4\pm$ 0.12	96.9	97.0	97.9
		CNN	$98.9\pm$ 0.11	98.7	98.8	98.9
		CNN (spectrograms)	$98.9\pm$ 0.12	98.5	98.6	98.5
		Proposed Model	$100.0\pm$ 0.00	100.0	100.0	100.0

presents the performance indices of each classification model across four operating conditions at successive time steps ($F+N$Δ$t$, $F+(N+1)$Δ$t$, …) following fault inception. It provides quantitative comparisons of AC, PR, RC, and F1s for the four classes at each time.

At the time point $F+N$Δ$t$, all models achieved perfect performance in identifying the normal state, indicating that normal operation, including external faults, is reliably distinguishable from fault-related conditions. However, significant variation in performance was observed among the models for states of inrush currents, internal faults, and overlapping event states. Notably, the proposed model demonstrated the highest AC, PR, RC, and F1s, effectively distinguishing fault types even immediately after the events. CNN and DNN followed with relatively high scores, while SVM and XGBoost exhibited lower performance in early detection. At the time point $F+(N+1)$Δ$t$, corresponding to one cycle after fault occurrences, all deep learning models showed substantial performance improvements. In particular, the proposed model achieved 100% classification accuracy across all states, demonstrating its ability to detect discriminative features rapidly. CNN and DNN also achieved high accuracy, though minor misclassifications remained, particularly in overlapping event scenarios. SVM and XGBoost showed slight improvement but continued to underperform compared to deep learning models. This gap underscores the advantage of hybrid and convolutional architectures in capturing temporal and spatial signal characteristics.

In practical protection settings, transformer differential relays are expected to issue trip signals within approximately 1~2 cycles (≈17~33 ms at 60 Hz, F~$F+2N$Δ$t$), while circuit breakers typically complete interruption within 3~5 cycles ($F+3N$Δ$t$~$F+5N$Δ$t$). The reported results at $F+N$Δ$t$ (≈16.7 ms) and $F+(N+1)$Δ$t$ (≈16.9 ms) therefore fall directly within the operational time budget of protective relays, demonstrating the real-time applicability of the proposed method.

These results confirm the suitability of the proposed model for real-time transformer protection, where fast and accurate classification is crucial. Its ability to achieve perfect classification within one cycle after fault occurrence indicates strong potential for real-world deployment, especially under time-critical constraints. Its superior early-stage performance highlights the effectiveness of integrating unsupervised clustering with spatial feature recognition, enabling precise discrimination even under challenging operational conditions.

In addition to Table 5, the conventional second-harmonic restraint method with a 15% threshold was implemented as a baseline for the industry. For each window, the ratio of the second harmonic to the fundamental component of the differential current was computed; windows with ratios above the threshold were labeled as inrush, and those below were labeled as internal faults. Normal and external fault cases, as well as overlapping scenarios, were handled using the magnitude of the differential current combined with the harmonic rule. Furthermore, a CNN model with spectrogram inputs was implemented to provide a fair comparison among CNN-based methods. The results show that the second-harmonic method provides intense discrimination between inrush and internal faults at the first cycle, but its performance degrades in overlapping cases. Meanwhile, CNN with spectrograms achieved performance similar to CNN on raw sequences, as both methods rely on time-frequency representations of the differential currents. This similarity suggests that the benefit of CNNs lies more in their feature extraction capability than in the specific input representation, reinforcing the advantage of combining the SOM with CNN as proposed in this study.

As shown in Table 5, the classification accuracy for overlapping events at the $F+N$Δ$t$ point is lower than that of other categories, primarily due to the substantial waveform similarity between inrush and fault components during the early cycles. This ambiguity makes it difficult for models to capture clear discriminative features at the initial stage. Nevertheless, the proposed SOM–CNN consistently outperformed the baseline models, achieving higher AC compared to the CNN and the other models. This result indicates that the SOM stage enhances separability, even in ambiguous cases, allowing the CNN to achieve more reliable classification of overlapping events.

4.4. Evaluation of Model Robustness to Signal Noise

To evaluate the practical applicability and robustness of the proposed model, we analyzed its performance under noisy conditions with a signal-to-noise ratio (SNR) of 30 dB. This SNR level was chosen as a conservative scenario that reflects disturbances and sensor noise commonly encountered in actual power systems.

This evaluation focused on three classes, inrush currents, internal faults, and overlapping events, while normal states and external fault states were excluded. This decision was made because normal and external fault conditions are generally well-separated even in noisy environments. In contrast, misclassifications between inrush currents and internal faults are more critical in real-world protection systems due to their similar waveform characteristics. Therefore, the analysis emphasizes scenarios where accurate discrimination is essential for avoiding false trips and ensuring reliable fault detection.

The evaluation procedure was as follows. Additive white Gaussian noise (AWGN) with an SNR of 30 dB was added to the raw current waveforms. From these noisy signals, seven-dimensional feature vectors were extracted at each time step using the same method applied in earlier simulations. These features were then preprocessed for each classification model and used as inputs. The final performance was evaluated based on AC, PR, RC, and F1s.

In noisy environments, classification performance is initially low following fault events but gradually improves as the signal stabilizes and feature extraction is completed. To identify when performance reaches 100%, measurements were taken at three post-fault time points: $F+(N+1)$Δ$t$, $F+(N+3)$Δ$t$, and $F+(N+5)$Δ$t$.

Table 6. Results of Performance Index Comparison of each Classification Model under 30 dB SNR.

Time	State	Model	AC (%)	PR (%)	RC (%)	F1s (%)
$F+$ $(N+1)$Δ$t$	Inrush Currents	XGBoost	88.8	88.7	88.9	88.8
		SVM	89.7	89.7	89.8	89.7
		SOM	91.7	91.6	91.8	91.7
		DNN	93.1	93.0	93.2	93.1
		CNN	94.1	94.0	94.2	94.1
		Proposed Model	99.5	99.5	99.5	99.5
	Internal Faults	XGBoost	89.2	88.9	89.0	89.0
		SVM	90.1	89.8	89.9	89.9
		SOM	92.0	91.8	91.9	91.9
		DNN	93.5	93.2	93.3	93.3
		CNN	94.5	94.2	94.3	94.3
		Proposed Model	99.5	99.5	99.5	99.5
	Overlapping Events (Inrush Currents + Internal Fault)	XGBoost	89.3	89.0	89.0	89.1
		SVM	90.3	89.9	89.8	90.0
		SOM	92.2	91.9	91.8	92.0
		DNN	93.7	93.3	93.2	93.4
		CNN	94.7	94.3	94.2	94.4
		Proposed Model	99.5	99.5	99.5	99.5
$F+$ $(N+5)$Δ$t$	Inrush Currents	XGBoost	93.0	92.8	93.0	92.9
		SVM	94.5	94.3	94.5	94.4
		SOM	96.0	95.8	96.0	95.9
		DNN	97.0	96.8	97.0	96.9
		CNN	98.0	97.9	98.0	98.0
		Proposed Model	100.0	100.0	100.0	100.0
	Internal Faults	XGBoost	93.0	92.8	93.0	92.9
		SVM	94.5	94.3	94.5	94.4
		SOM	96.0	95.8	96.0	95.9
		DNN	97.0	96.8	97.0	96.9
		CNN	98.0	97.9	98.0	98.0
		Proposed Model	100.0	100.0	100.0	100.0
	Overlapping Events (Inrush Currents + Internal Fault)	XGBoost	93.0	92.8	93.0	92.9
		SVM	94.5	94.3	94.5	94.4
		SOM	96.0	95.8	96.0	95.9
		DNN	97.0	96.8	97.0	96.9
		CNN	98.0	97.9	98.0	98.0
		Proposed Model	100.0	100.0	100.0	100.0

summarizes the performance of six models, with only the results at $F+(N+1)$Δ$t$ and $F+(N+5)$Δ$t$ are presented in the table, and the performance at $F+(N+3)$Δ$t$ is described in the main text.

At the time point $F+(N+1)$Δ$t$, the proposed model demonstrated superior performance compared to all other models. While DNN and CNN achieved high accuracies of between 93.1% and 94.1%, and the SOM reached above 91.6%, the proposed model attained 99.5% accuracy across all classes in AC, PR, RC, and F1s. In contrast, XGBoost and SVM yielded accuracies below 90%, showing their limitations in early-stage classification. These results confirm that the proposed model is effective in detecting and distinguishing between inrush currents and internal faults with minimal observation time after a fault occurs.

At the time point $F+(N+3)$Δ$t$, all models showed noticeable performance improvements, reflecting the increased stability and separability between inrush currents and internal faults. The proposed model achieved 99.9% accuracy across all fault types, effectively reaching performance saturation. DNN and CNN also performed well at this stage, attaining accuracies of up to 94.1% and 95.1%, respectively, for overlapping events. The SOM continued to outperform XGBoost and SVM, validating its ability to model non-linear input distributions through topological mapping. Nevertheless, the performance gap between the proposed model and the other models remained evident, particularly in cases of overlapping events.

At the time point $F+(N+5)$Δ$t$, nearly all models reached their peak performance. CNN achieved up to 98.0% accuracy, the SOM reached 96.0% accuracy, and DNN maintained above 97.0% accuracy across all classes. The proposed model consistently outperformed all others, achieving 100% accuracy across all classes. These results indicate that the proposed model is not only robust to noise but also exhibits strong generalization capability.

Overall, these results demonstrate that the proposed model delivers excellent early-stage performance at $F+$Δ$t$, achieves near-perfect accuracy by $F+(N+3)$Δ$t$, and sustains 100% accuracy at $F+(N+5)$Δ$t$, outperforming both traditional machine learning and deep learning baselines.

5. Discussion

The proposed model effectively overcomes the limitations of traditional threshold-based and single-model approaches in distinguishing between magnetizing inrush currents and internal fault currents.

First, it significantly reduces the time required for accurate classification: our model achieves 100% AC, PR, RC, and F1s at the time point $F+(N+1)$Δ$t$, whereas SVM, XGBoost, DNN, and standalone CNN consistently fall below 95% at the same time point.

This improvement stems from the SOM’s topology-preserving clustering, which suppresses transient noise, and the CNN’s hierarchical learning of spatial activation patterns.

Second, the framework demonstrates exceptional robustness to realistic noise conditions. Under an SNR of 30 dB, it maintains over 99% AC at $F+(N+3)$Δ$t$ and restores perfect classification by $F+(N+5)$Δ$t$. Such resilience to electromagnetic interference and waveform distortion suggests that the model can substantially reduce misoperations in protection relays compared to conventional methods that are sensitive to noise.

Third, the SOM-generated activation map offers clear interpretability. Inrush and fault events occupy consistently distinct regions on the SOM grid, providing visual evidence that experts can inspect to understand why and when classification decisions are made. This transparency enhances user confidence relative to black-box deep learning models and supports informed maintenance planning and anomaly investigation. Although the CNN produces the final classification, its input is the SOM activation map, which ensures that the results remain directly associated with the SOM lattice. Thus, each decision can be interpreted by examining the mapped region and its surrounding activation patterns on the SOM grid. Even for misclassified samples, the CNN outputs can be traced back to the underlying SOM representation, allowing experts to analyze the cause of errors. This design mitigates the purely black-box nature of a standalone CNN. It preserves a certain level of interpretability by coupling the SOM’s topology-based structure with the CNN’s discriminative outputs.

Finally, the architecture is inherently scalable. By adjusting the SOM grid resolution or modifying the CNN backbone, the method can accommodate transformers of different voltage classes, varied load conditions, and additional event types. Nonetheless, the two-stage design increases computational load, highlighting the need for future work on model compression, pruning, or quantization to enable deployment on real-time embedded platforms.

The proposed model inevitably introduces higher computational complexity compared to a single CNN due to its two-stage design. In our experimental environment, the average inference time for one input cycle was approximately 25 ms for the standalone CNN and 33 ms for the proposed model, representing about a 29% increase. This measurement was conducted on an Intel i5-8500 CPU, 16GB RAM, (Intel, Santa Clara, CA, USA) and NVIDIA GTX 2060 GPU (NVIDIA, Santa Clara, CA, USA) environment. Nevertheless, this overhead remains well within the typical real-time constraints of protective relay applications, which generally require response times within several tens of milliseconds. Therefore, the proposed model can still meet the real-time requirements in practical systems. Future work will focus on model compression, pruning, and quantization techniques to further optimize its efficiency for embedded environments.

In addition, although the present study primarily compared the proposed model against CNN, DNN, and conventional machine learning baselines, more recent state-of-the-art approaches, such as Transformer-based architectures and signal decomposition–assisted deep learning methods, were omitted. These models have demonstrated strong potential in power system event classification; however, they often involve higher computational costs and additional preprocessing steps. To reflect this, a discussion of these methods has been added, and their integration or direct comparison will be pursued in future work to contextualize the contribution of the proposed framework further.

Despite these advantages in performance and scalability, the fact that this study relies entirely on simulation data remain a significant limitation. This study constructed comprehensive simulation scenarios that considered not only various fault types and transformer operating conditions but also load variations and noise environments. Nevertheless, the complex characteristics of real power grids, such as non-ideal CT saturation, unpredictable background harmonic distortions, and long-term dynamic behaviors, are still challenging to reproduce completely in a simulation environment. In particular, the robustness analysis was limited to additive white Gaussian noise (AWGN) at 30 dB, which should be regarded only as a first-step approximation. Real-world noise sources also include non-Gaussian disturbances, CT saturation, DC offsets, quantization errors, and harmonic pollution that were not fully addressed in this study. Therefore, the results of this study should be interpreted within the scope of simulation-based validation. Future work will extend to robustness testing under these realistic noise conditions, as well as verification using field data.

Moreover, although the proposed framework was comprehensively validated using simulated transformer differential current signals, this reliance on simulation data constitutes a limitation of the present study. Access to extensive real-world fault and inrush datasets is constrained by confidentiality issues; however, small-scale public case studies, such as oscillography records of transformer energization events reported in the open literature, could serve as supplementary validation. Incorporating such data, even in limited quantity, would provide additional external credibility and will be considered in our follow-up work.

In particular, while the proposed model achieved fault detection within one cycle under simulation-based noise conditions, such rapid performance may not be fully guaranteed in real-world environments where additional uncertainties exist. This highlights the potential risk of overfitting to simulation scenarios and reinforces the necessity of validating the model with actual field data.

For practical application in substations, it will be necessary to perform cross-validation using differential current records obtained from actual sites, even in limited quantities, and to subsequently adjust parameters or simplify the model to make it suitable for protective relay applications. Such follow-up research is expected to further enhance the applicability of the proposed model to real power systems.

Finally, the significance of the proposed two-stage architecture lies in the fact that the SOM topologically organizes the input feature space and mitigates local noise. At the same time, the CNN learns spatial patterns from the structured activation maps, thereby improving classification stability. A single-stage CNN may also implicitly learn similar functions with sufficient capacity; however, under limited data conditions, it faces the burden of knowing all tasks simultaneously.

As shown in Table 5 and Table 6, the proposed model achieved improvements of 1.4% and 2.0% in F1 Scores over the single CNN, particularly under noisy conditions and overlapping events, which is consistent with the effect of the SOM in enhancing class separability. More systematic comparisons with stronger single-stage models will be pursued in future work, while this discussion substantiates the practical validity of the current design choice.

In addition, to evaluate the practical applicability of the proposed framework in real protection environments, it is necessary to consider deployment-related metrics. Since this study primarily focused on verifying classification performance using simulated data, important aspects such as inference latency, computational complexity, and compliance with relay operating time constraints were not directly addressed. However, these metrics are critical indicators for assessing whether the model can be operated in real time within protection systems, and they will be incorporated in future research. Furthermore, a comprehensive assessment of deployment feasibility requires experimental validation using hardware-in-the-loop simulation (HILS) or real-time digital simulator (RTDS) platforms, which will be pursued as part of our follow-up work.

6. Conclusions

In this study, we aimed to develop a high-performance classification model capable of detecting abnormal operating conditions in power transformers early and precisely distinguishing between magnetizing inrush currents and internal fault currents. Inrush currents exhibit waveform characteristics similar to those of internal faults, posing a longstanding challenge for the design of protection systems. To address this, we proposed a model that combines an SOM and a CNN. The improved performance of the proposed model results from the effective integration of structured representation by the SOM and deep feature extraction by the CNN through a staged learning approach. The SOM organizes input vectors based on their statistical similarity, spatially separating different event types and generating a representation that is both informative and visually interpretable. This output is then converted into an image format and used as input to the CNN, which performs hierarchical extraction of high-level patterns from the structured input.

Unlike a simple combination of individual models, this sequential architecture enables robust classification even under noisy conditions or waveform distortions by preserving the essential differences between events. It also demonstrates strong adaptability to variations in fault magnitude and operating scenarios, offering clear advantages over conventional threshold-based protection methods.

As a result, the proposed model achieved 100% AC, RC, PR, and F1s at the time point $F+(N+1)$Δ$t$, and under an SNR of 30 dB, it maintained perfect classification at the time point $F+(N+5)$Δ$t$. This demonstrates that the model delivers rapid classification immediately after fault inception while maintaining high reliability in real-world noisy environments.

Given these results, future work should evaluate the model’s real-time applicability under diverse field conditions and system environments. Although the present study validated the framework using simulation data, the trained SOM–CNN model can also be extended to streaming applications by employing a sliding-window scheme to process continuously incoming signals, enabling online classification with low latency. With these follow-up studies, the proposed model is expected to be more widely adopted in power system protection and further extended to fault prediction and preventive maintenance systems. Future research will also explore continual learning strategies and edge-device implementations to enhance real-time applicability.

Furthermore, from a deployment perspective, it is crucial to assess inference latency, computational needs, and compliance with relay operating time limits. Although initial results show that the proposed model meets typical real-time margins, further optimization through model compression, pruning, and quantization will be necessary for embedded implementation. Finally, HILS- and RTDS-based experiments with actual substation data will be essential to fully validate the framework’s practicality in real protection systems.

In addition, special attention will be given to validating the model with differential current records from real substations, as such field data are indispensable to confirm the robustness and practicality of achieving near one-cycle fault detection in real operating conditions.