State of Health Estimation for Batteries Based on a Dynamic Graph Pruning Neural Network with a Self-Attention Mechanism

Abstract

The accurate estimation of the state of health (SOH) of lithium-ion batteries is critical for ensuring the safety, reliability, and efficiency of modern energy storage systems. Traditional model-based and data-driven methods often struggle to capture complex spatiotemporal degradation patterns, leading to reduced accuracy and robustness. To address these limitations, this paper proposes a novel dynamic graph pruning neural network with self-attention mechanism (DynaGPNN-SAM) for SOH estimation. The method transforms sequential battery features into graph-structured representations, enabling the explicit modeling of spatial dependencies among operational variables. A self-attention-guided pruning strategy is introduced to dynamically preserve informative nodes while filtering redundant ones, thereby enhancing interpretability and computational efficiency. The framework is validated on the NASA lithium-ion battery dataset, with extensive experiments and ablation studies demonstrating superior performance compared to conventional approaches. Results show that DynaGPNN-SAM achieves lower root mean square error (RMSE) and mean absolute error (MAE) values across multiple batteries, particularly excelling during rapid degradation phases. Overall, the proposed approach provides an accurate, robust, and scalable solution for real-world battery management systems.

1. Introduction

As the primary energy storage solution, lithium-ion batteries (LIBs) currently power most electric vehicles, portable electronic devices (EVs), Photovoltaic Systems (PVs) [1], and sustainable energy applications, owing to their superior energy storage capacity, extended operational lifespan, and relatively eco-friendly characteristics [2]. With the global transition to electrification [3,4], the LIB industry is witnessing unprecedented growth. According to the IEA’s Global EV Outlook 2025, global demand for EV batteries was about 1 TWh in 2024 and is projected to exceed 3 TWh by 2030, reflecting the continued growth in electrification across sectors [5].

Despite their advantages, LIBs inevitably suffer from performance degradation over time. High-performance LIBs can achieve from 2000 to 3000 charge–discharge cycles, whereas lower-quality variants are typically limited to 300–500 cycles. The cycle life is substantially influenced by multiple operational parameters, including the working temperature, power quality of electrical system, depth of discharge (DOD), and charge/discharge rates (C-rates) [6,7]. LIB degradation mainly falls into the following two separate classifications: calendar aging and cyclic aging. Cyclic aging refers to a degradation mechanism in which battery performance deteriorates progressively due to electrochemical reactions triggered by charge–discharge current flow during operational cycling [8]. Complex nonlinear aging effects are triggered by continuous charge–discharge cycling, particularly when the batteries are subjected to harsh operational conditions like rapid charging, high temperatures, or deep discharging [9,10,11]. The battery’s state of health (SOH) can be quantified as the ratio of its present capacity relative to the original capacity [12], as expressed in Equation (1), as follows:

$$\mathrm{SOH}={\displaystyle \frac{\mathrm{Current}\mathrm{Capacity}}{\mathrm{Initial}\mathrm{Capacity}}}$$

(1)

Zhou et al. introduced a transfer learning-based two-phase model for predicting aging trajectories in conjunction with cycle life estimation, allowing for the accurate long-term forecasting of the degradation behavior of LiFePO₄ lithium-ion batteries by utilizing just the initial 30% of the aging data [9]. Through the feature extraction of the critical parameters, including degradation rate and incremental capacity curve variations, Wang et al. successfully developed a neural network approach for precise knee point detection in lithium-ion battery capacity fade. This methodology offers a reliable foundation for battery lifespan assessment and management [10]. Liu et al. conducted both longitudinal and multi-factorial horizontal analyses of capacity fading mechanisms across the entire lifespan of lithium-ion batteries, and they proposed a health state prediction model applicable to commercial batteries [11]. This degradation affects both safety and reliability, making accurate SOH estimation an essential component of battery management systems (BMSs) [10,11]. SOH prediction enables proactive maintenance scheduling, which prevents catastrophic failures and improves the longevity and efficiency of energy storage systems.

Traditional SOH and SOC (state of charge) estimation approaches include coulomb counting [13], open-circuit voltage (OCV) analysis [14], and electrochemical impedance spectroscopy (EIS) [15,16]. The concise comparison of these methods is represented in

Table 1. Concise comparison of traditional SOH estimation approaches.

Method	Strengths	Limitations
Coulomb counting	Simple and interpretable energy balance, suitable for real-time implementation with low computational cost when current sensing is reliable	Sensitive to current sensor bias and drift, cumulative integration error, and limited ability to reflect dynamic degradation states
OCV analysis via incremental capacity analysis	Physically grounded voltage landmarks and robust capacity fade indicators after appropriate smoothing	Requires near-equilibrium segments; reduced applicability under highly dynamic electric vehicle duty cycles
OCV-based joint estimation of SOC and SOH	Joint inference reduces propagation of SOC errors into SOH and improves precision through coordinated models	Increased implementation complexity and need for model selection across operating regimes
EIS assisted equivalent circuit modeling	Parameter interpretability combined with sensitivity in the frequency domain, adaptable across temperature and SOC after calibration	Requires impedance instrumentation and careful calibration; additional acquisition time and setup effort

. These methods, although interpretable, face practical limitations such as high dependency on accurate sensor calibration, the requirement for equilibrium states, and poor generalizability under dynamic EV conditions. Goud et al. implemented an enhanced coulomb counting technique that integrates aging parameters like temperature and depth of discharge, enabling real-time SOH estimation for lithium-ion batteries with an accuracy of within 1.6% [13]. Stroe and Schaltz utilized the incremental capacity analysis (ICA) technique to extract four key voltage points for evaluating capacity fade in LMO/NMC batteries, and they validated the accuracy and robustness of the method under two different aging conditions [14]. Ouyang et al. developed a multi-threaded dynamic optimization approach to jointly estimate SOC and SOH, enhancing the precision and reliability of power battery state estimation by optimizing model structure and combining multiple open-circuit voltage models [15]. Zhang et al. designed an ECM that accounts for the influence of temperature and SOC, and they integrated it with EIS to develop a highly accurate and adaptable SOH estimation technique for lithium-ion batteries, resulting in an estimation error of less than 4% across different operating conditions [16].

To overcome these challenges, more adaptive techniques, such as improved Kalman filtering [17,18,19], adaptive algorithms [20,21,22], and probabilistic estimators [23], have been proposed. Ranga et al. introduced a reliable SOH prediction approach utilizing the unscented Kalman filter (UKF), showing consistent estimation accuracy across diverse operational scenarios while maintaining compatibility with multiple lithium-ion battery chemistries [17]. Zhang et al. presented an adaptive remaining useful life (RUL) prediction strategy that combines the Kalman filter with the expectation maximization–Rauch–Tung–Striebel (KF-EM-RTS) smoother, enabling precise RUL forecasting for lithium-ion batteries, even when faced with limited unlabeled data and uncertain parameters [18]. Li et al. developed an innovative SOH assessment approach utilizing an arctangent function-optimized adaptive genetic algorithm integrated with backpropagation neural networks (ATAGA-BP). This methodology demonstrated exceptional accuracy, with merely 3.7% estimation error through health indicator extraction during charging phases, while simultaneously enhancing computational efficiency [20]. Zhang et al. introduced a RUL prediction method combining expectation maximization, unscented particle filtering, and Wilcoxon rank sum testing (EM-UPF-W), which effectively identified capacity regeneration points, thereby improving prediction accuracy and stability [21]. Wu et al. developed a data-driven model based on transfer learning and stacked support vector regression (TS-SVR), which achieved highly accurate SOH estimation using only the first 30% of target battery data, and they demonstrated strong generalization performance [22]. Zhou et al. proposed a SOH estimation model that considers the aging stages, and by extracting features such as the peak value of the incremental capacity curve and ohmic resistance, it achieved full-lifecycle SOH monitoring of LiFePO₄ battery systems in real-world electric vehicles [23]. However, these techniques still struggle with noisy measurements, capacity regeneration, and uncertainty quantification.

In recent years, fault diagnosis and industrial remaining useful life prediction methods utilizing deep learning have gained increasing prominence [24,25,26,27]. The emergence of data-driven and machine learning methods has further revolutionized battery SOH estimation research. Early efforts include the use of support vector machines (SVMs) and transfer learning [28,29], and later extensions explored hybrid regression [30], multimodal data fusion with convolutional neural networks (CNNs) [31], and encoder–decoder architectures incorporating convolution, attention, and recurrent units [32]. Recurrent neural networks (RNNs) and their variants, including long short-term memory (LSTM) [33,34,35,36] and gated recurrent units (GRUs) [37,38], have shown enhanced capabilities in capturing the temporal dynamics of battery degradation processes. Bracale et al. constructed a probabilistic joint modeling approach for battery SOH and RUL based on time-series models such as ARIMAX and Bayesian regression, which enhanced the reliability and adaptability of battery degradation prediction [28]. Lin et al. introduced a multimodal multilinear feature fusion mechanism combined with a 2D CNN for SOH estimation, effectively integrating multi-source feature information and achieving a mean absolute error as low as 0.37% [29]. Gong et al. proposed a deep learning-based encoder–decoder model that integrates CNN, ultra-lightweight subspace attention mechanism (ULSAM), and simple recurrent unit (SRU) modules, effectively establishing the mapping relationship between charging curves and SOH values, thereby improving model adaptability and estimation accuracy [30]. Cai et al. proposed a unified SOH estimation model integrating evolutionary multi-objective optimization, a LSTM network, and an attention mechanism, which enables automated feature extraction, importance assignment, and parameter optimization and demonstrates strong generalization and transferability [31]. Bamati and Chaoui utilized a nonlinear autoregressive model with exogenous inputs (NARX) implemented as a recurrent neural network to characterize battery aging behavior. Experimental evaluations on the NASA dataset demonstrated that the approach provides highly accurate SOH and RUL predictions, with errors remaining below 3%, thereby supporting its applicability in real-time monitoring scenarios [32]. Jia et al. proposed an energy-based battery aging prediction method using a fractal gradient-enhanced LSTM network, which effectively predicted aging trends without relying on ICA-based filtering, and improved model convergence and prediction stability through fractal derivative techniques [33]. Shu et al. integrated a long short-term memory (LSTM) network with transfer learning to create an adaptable SOH prediction framework for lithium-ion battery packs. This approach achieved prediction errors under 3% by utilizing only the initial 40% of the cycling data, effectively minimizing both the demand for extensive training datasets and the associated computational costs [34]. Liu et al. applied an empirical mode decomposition (EMD) and LSTM-GPR hybrid model to multi-step prediction of future battery capacity and RUL, and they effectively quantified the uncertainty caused by capacity regeneration through Gaussian process regression (GPR), thereby enhancing prediction reliability. These networks, by leveraging long-range memory, can capture subtle SOH patterns not observable by static models [35]. Zhang et al. developed a stochastic degradation framework that combines pattern recognition with a recursive Gaussian distribution, where the degradation trend is learned through a GRU. This hybrid methodology not only achieves precise RUL estimation for rechargeable batteries but also effectively models degradation variability, outperforming conventional physics-based models and purely data-driven approaches in prediction accuracy [37]. Zhang et al. introduced a data-model interactive RUL prediction approach based on a particle filter, bidirectional GRU, and temporal self-attention mechanism (PF-BiGRU-TSAM), in which the BiGRU-TSAM is first trained offline to assign significance to capacity data at different time steps, and the PF-based online phase integrates the advantages of data-driven and model-based methods to achieve mutual correction and improved prediction performance, as demonstrated through experiments on real-world battery datasets [38].

Recent studies have begun to unify explicit topology modeling with attention-based long-range sequence modeling for battery state of health prediction. Dynamic graph attention–Transformer networks [39] build time window graphs to encode intra-cycle dependencies among features while using self-attention to capture long horizon effects, yielding multi-step SOH forecasts under varying operating conditions. Hybrid designs that couple graph encoders with Transformer-style sequence modules similarly report gains on noisy multivariate signals, where graph structure constrains message passing and attention focuses capacity on degradation-salient intervals [40,41,42].

To address data governance constraints and distribution shift across fleets, federated learning schemes for SOH have been explored on real-world vehicle data, as well as in early-lifespan prediction [43]. Federated transfer learning further combines source–target adaptation with privacy preserving aggregation, improving early-life generalization while avoiding centralized data pooling [44]. These directions complement centralized training by enabling cross-site learning under regulatory and organizational constraints that are common in battery management deployments.

Balancing interpretability and calibrated confidence has become central to trustworthy deployment [45]. For batteries, probabilistic machine learning [46] and Bayesian deep learning pipelines [47] provide predictive distributions for SOH, together with uncertainty estimates that inform maintenance decisions and thresholds. Capacity or SOH estimators that fuse deep temporal encoders with probabilistic regressors demonstrate interval prediction with uncertainty quantification on standard datasets. At the power system scale, recent surveys on explainable artificial intelligence for energy system maintenance synthesize post hoc and intrinsic explanation techniques and discuss their suitability under operational latency constraints, offering a broader methodological context in which attention-guided pruning and topology-aware modeling can yield structured explanations [48].

The limitations of existing neural network-based methods and our response for battery SOH estimation can be summarized as follows:

• Lack of explicit structural modeling among degradation features. Many methods treat SOH estimation as a purely temporal problem and ignore dependencies among voltage, current, temperature, and capacity.
  Our model builds a graph within each feature window, where nodes represent features and edges encode their statistical and physical relationships, and then performs topology-aware propagation with attention to capture these dependencies.
• Insufficient focus on informative degradation phases. Uniform weighting across time steps weakens sensitivity to rapid fading regimes and other salient intervals.
  The self-attention mechanism reweights time steps within each window so that degradation-salient intervals contribute more to the final estimate, which improves sensitivity to phase-specific patterns.
• Over-reliance on temporal ordering while neglecting relational patterns. Sequential encoders alone do not preserve the cross-feature structure that is critical for precise SOH inference.
  The proposed model jointly encodes temporal cues and relational topology through dynamic graph propagation coupled with attention, which preserves inter-feature interactions beyond time ordering and yields more informative representations.
• High computational cost in attention-enhanced recurrent models. Multi-layer recurrent processing combined with attention increases parameter count and floating point operations, which limits suitability for embedded deployment. An attention-guided structural pruning module learns sparse adjacency and removes low-utility edges, reducing the computation and parameter footprint while maintaining accuracy.
  A GCN baseline trained under the same hyperparameters, together with an ablation that disables pruning, isolates the efficiency and accuracy contribution of the pruning design.

We propose a novel Dynamic Graph Pruning Neural Network with a Self-Attention Mechanism (DynaGPNN-SAM) for battery SOH estimation. Based on the aforementioned motivations, the key contributions of this study can be summarized as follows:

• Topology-first formulation for SOH. We introduce DynaGPNN SAM, which transforms per-window features into a graph and performs topology-aware propagation. Unlike recent graph transformer methods that primarily rely on global attention for token mixing, our formulation treats feature topology as the modeling primitive and learns window-specific adjacency that captures cross-feature dependencies beyond time ordering.
• Attention as a structural operator via pruning. We propose an attention-guided structural pruning mechanism that uses attention to select and retain a compact subgraph by removing low-utility edges, which provides interpretable salient subgraphs and reduces inference cost. This differs from graph transformers where attention serves as soft weighting rather than an explicit selector of the graph structure. The effect of pruning is isolated through a GCN control and a no pruning ablation under identical settings in Section 4.3.
• Phase-aware temporal emphasis coupled with structure. A self-attention module reweights time steps within each window to highlight degradation-salient phases while jointly preserving the learned relational topology, offering a unified treatment of temporal saliency and cross-feature structure that complements transformer style positional encoding.
• Complexity and empirical validation. Inference cost scales with the number of active edges after pruning rather than with quadratic attention, which clarifies efficiency implications. Under a unified protocol on the NASA dataset, the model surpasses strong baselines, including CNN, LSTM, and GCN, with controls reported in Section 4.4.

The proposed architecture is motivated by the empirical and theoretical limitations in sequence-based and purely Euclidean treatments of battery state of health estimation. Sequence-oriented frameworks often process multi-channel measurements as loosely coupled streams, which suppresses structured interactions among current, voltage, and temperature as well as other physically informed dependencies. To remedy this, each time window is represented as a graph $G=(V,E,X,A)$, where the adjacency A encodes correlation, physical coupling, or domain priors. Graph convolution based on the normalized Laplacian then enables topology-aware message passing that reinstates cross-feature interactions, thereby improving the fidelity of the learned representation relative to baselines that lack explicit structure. Battery degradation is markedly non-stationary, and information tends to concentrate in specific regimes such as the knee region, transitions from constant current to constant voltage, and segments with temperature excursions. A self-attention mechanism assigns importance scores to nodes and temporal segments and reweights the intermediate representation accordingly, which focuses modeling capacity on degradation-salient phases while attenuating redundancy and measurement noise. To enhance generalization and satisfy deployment requirements, attention-guided pruning selects the top k elements and induces a compact subgraph; the resulting sparsifier preserves the most predictive substructures, reduces computational cost approximately in proportion to the retained nodes and edges, and provides an interpretable view of which variables and segments most strongly influence the estimate. In combination, stacking graph convolution, self-attention, and pruning yields an end-to-end operator that captures non-Euclidean dependencies, concentrates capacity where the signal is most informative, and enforces learned sparsity for efficiency and interpretability. Ablation studies indicate that removing self-attention or disabling pruning leads to consistent increases in error, which supports the necessity of each component within the integrated design.

2. Problem Formulation

To better reveal the underlying structural relationships among battery operational features and enhance the precision of SOH estimation, this study frames the SOH estimation task as a supervised graph learning problem. The graph is defined as $G=(V,E,X,A)$, where V denotes the collection of nodes, each representing a feature instance captured during battery operation. The edge set E characterizes the interconnections between nodes. The node feature matrix is represented by $X\in {\mathbb{R}}^{n\times d}$, with n being the total number of nodes and d the dimensionality of each node’s features. The adjacency matrix $A\in {\mathbb{R}}^{n\times n}$ encodes the graph’s connectivity structure. A value of $A_{ij}=1$ indicates a potential correlation between nodes $v_i$ and $v_j$, while $A_{ij}=0$ signifies no such connection.

Considering the significant temporal correlation in the evolution of battery SOH, this paper employs a sliding time window mechanism to model the sequential data. Let the current time step be t, then the time window is defined as $W_t=[G_t,G_{t-1},\dots ,G_{t-d+1}]$, where d denotes the window length, representing the consecutive d graph structures prior to the current time step. Through this mechanism, historical information can be more fully utilized to capture the degradation patterns of the battery over multiple cycles. Ultimately, the goal of this paper is to learn a mapping function from the time window graph sequence to the current SOH value, i.e., $f:W_t\to {\mathrm{SOH}}_t$, while minimizing the generalization error of this mapping function over the entire dataset.

By the above modeling process, the battery SOH estimation problem is abstracted from the traditional time-series modeling paradigm and reinterpreted through a graph-based modeling perspective. This allows for the simultaneous integration of temporal information and feature dependencies in the non-Euclidean space, laying a theoretical foundation for the subsequent design of deep models based on Graph Neural Networks (GNNs) and self-attention mechanisms.

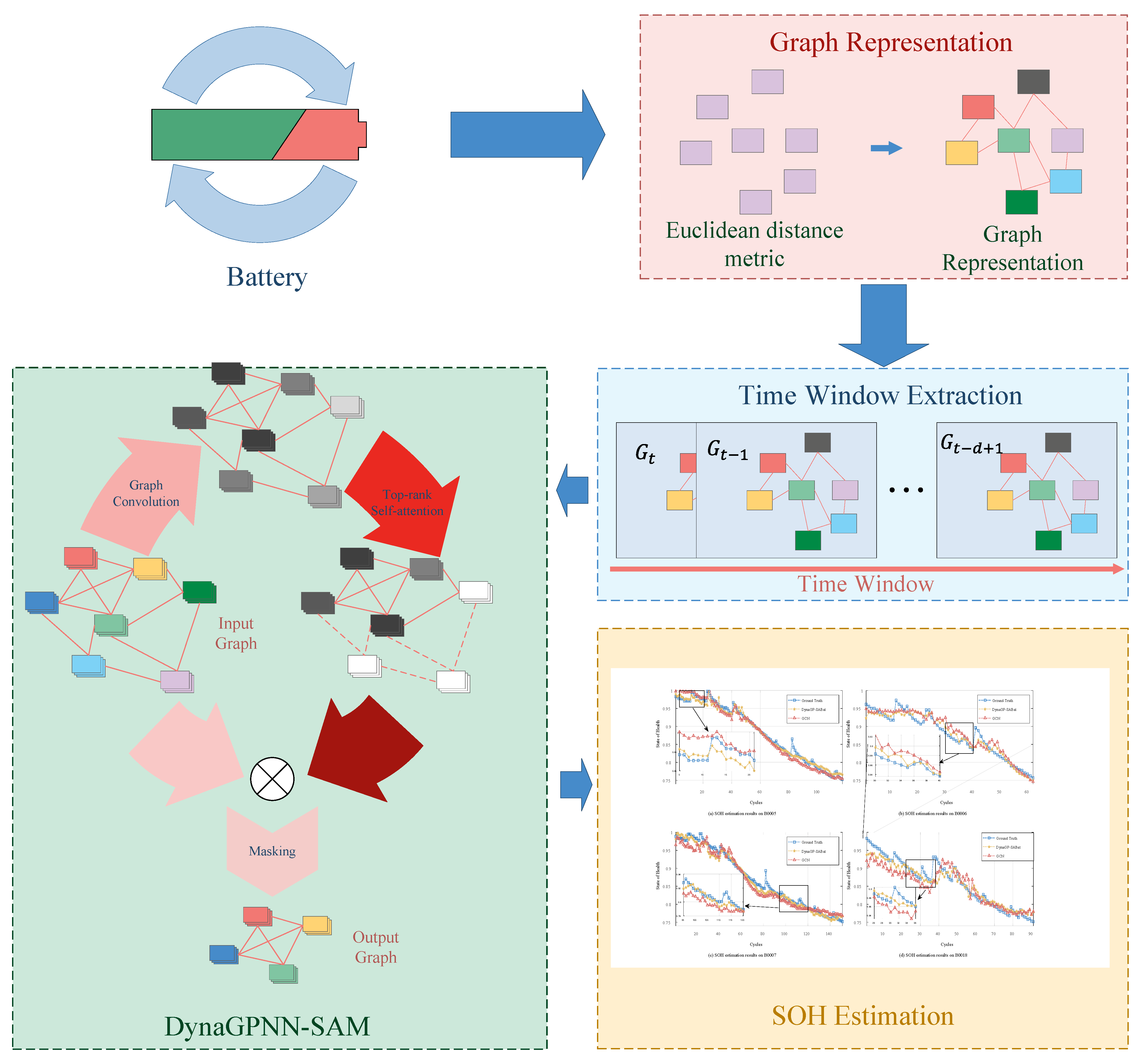
3. DynaGPNN-SAM Modeling

3.1. Graph Convolutional Networks

GCNs are effective methods for processing graph-structured data. Unlike traditional convolutional neural networks, GCNs can model structural relationships among data in non-Euclidean space, offering significant advantages in handling complex structured data such as social networks and the temporal features of battery systems.

In establishing the mathematical foundation of GCNs, the normalized Laplacian matrix of the graph is first defined. For an undirected graph, the Laplacian matrix is defined as Equation (2) as follows:

$$L=I_n-D^{-{\displaystyle \frac{1}{2}}}A{D}^{-{\displaystyle \frac{1}{2}}}$$

(2)

In this equation, $I_n$ represents the n-dimensional identity matrix, A corresponds to the graph’s adjacency matrix, and D is the degree matrix, where its diagonal entries $D_{ii}={\sum }_j{A}_{ij}$ indicate the total number of edges linked to node i. This normalized form ensures the numerical stability of the Laplacian matrix in the spectral domain and allows its direct use in defining graph convolutions in the frequency domain.

Based on this definition, the graph convolution operation can initially be expressed in the spectral domain as Equation (3) as follows:

$$g_{\theta }\ast X=U{g}_{\theta }(\Phi )U^{T}X$$

(3)

where $X\in {\mathbb{R}}^{n\times d}$ is the input node feature matrix, U and $\Phi$ are the eigenvector matrix and diagonal eigenvalue matrix of the graph Laplacian L, respectively, $g_{\theta }(\Phi )$ is the filter function defined in the spectral domain, and $U^{T}X$ can be interpreted as the graph Fourier transform of the input features. Although this formulation has clear theoretical significance, it involves the eigen-decomposition of large-scale graphs, leading to high computational complexity and making it unsuitable for practical deep learning training scenarios.

To improve computational efficiency, the spectral filter function is approximated using a Chebyshev polynomial expansion, given as Equation (4), as follows:

$$g_{\theta }(\Phi )\approx \sum _{k=0}^{K-1}{\theta }_k{T}_k\left(\tilde{\Phi }\right)$$

(4)

where $T_k(·)$ denotes the k-th order Chebyshev polynomial, ${\theta }_k$ are the corresponding coefficients, and $\tilde{\Phi }={\displaystyle \frac{2}{{\lambda }_{max}}}\Phi -I_n$ represents the normalized eigenvalues. Combining Equations (3) and (4), the spatial domain representation of graph convolution becomes Equation (5), as follows:

$$g_{\theta }\ast X\approx \sum _{k=0}^{K-1}{\theta }_k{T}_k\left(\tilde{L}\right)X$$

(5)

where $\tilde{L}={\displaystyle \frac{2}{{\lambda }_{max}}}L-I_n$. Here, the graph convolution operation is transformed into a weighted aggregation of multi-hop neighborhood information, significantly reducing computational cost.

Further simplification can be achieved by setting the approximation order $K=1$, leading to a first-order linear propagation form expressed by Equation (6) as follows:

$$g_{\theta }\ast X\approx {\theta }_{0}X+{\theta }_{1}LX$$

(6)

By setting ${\theta }_0=-{\theta }_1=\theta$, adding self-loops to the adjacency matrix, and using the normalized degree matrix, the convolution expression becomes Equation (7), expressed as follows:

$$g_{\theta }\ast X=\theta (I+D^{-{\displaystyle \frac{1}{2}}}A{D}^{-{\displaystyle \frac{1}{2}}})X$$

(7)

To prevent gradient explosion or vanishing, GCNs typically normalize the graph convolution operation and introduce a nonlinear activation function $\sigma$. Finally, incorporating $\sigma (·)$ and a trainable weight matrix W, the standard form of graph convolution is expressed as Equation (8), as follows:

$$y=\sigma ({\tilde{D}}^{-{\displaystyle \frac{1}{2}}}\tilde{A}{\tilde{D}}^{-{\displaystyle \frac{1}{2}}}XW)$$

(8)

where $\tilde{A}=A+I$ denotes the adjacency matrix with self-loops, and $\tilde{D}$ is the corresponding degree matrix.

The advantage of GCNs lies in their ability to model complex relationships between nodes through graph structures. However, they exhibited limitations in graph calculating, making it difficult to dynamically retain key nodes in the graph.

3.2. Dynamic Graph Pruning with Self-Attention Mechanism

To improve the ability of graph neural networks to model critical features, this work proposes a self-attention graph pruning neural network that dynamically assigns weights and identifies the most significant nodes. The structure of DynaGPNN-SAM is illustrated in Figure 1. More precisely, the process begins with a graph convolution layer that conducts a linear transformation on the node features. Subsequently, attention scores for each node are calculated using the softmax function, as detailed in Equation (9), expressed as follows:

$$S=\mathrm{Softmax}({\tilde{D}}^{-{\displaystyle \frac{1}{2}}}\tilde{A}{\tilde{D}}^{-{\displaystyle \frac{1}{2}}}X{\Theta }_{\mathrm{att}})$$

(9)

where ${\Theta }_{\mathrm{att}}\in {\mathbb{R}}^{d\times 1}$ is a learnable attention parameter, and $S\in {\mathbb{R}}^{n\times 1}$ represents the vector of node importance scores.

According to a predefined pruning ratio $k\in (0,1]$, the top $kn$ nodes with the highest scores are selected as the retained nodes, yielding the index set represented by Equation (10) as follows:

$$\mathrm{idx}=\mathrm{top}-\mathrm{rank}(S,kn)$$

(10)

The top-rank function returns the indices of the top $kn$ highest-scoring nodes. Using this index (idx), a masking operation is applied to both the input features and the graph structure to obtain the new graph as Equation (11), expressed as follows:

$$\left\{\begin{array}{c}\tilde{X}=X_{\mathrm{idx}}\hfill \\ X_{\mathrm{out}}=\tilde{X}\odot S_{\mathrm{mask}}\hfill \\ A_{\mathrm{out}}=A_{\mathrm{idx},\mathrm{idx}}\hfill \end{array}\right.$$

(11)

where $S_{\mathrm{mask}}$ denotes the attention scores of the retained nodes, ⊙ represents the Hadamard (element-wise) product, and $A_{\mathrm{idx},\mathrm{idx}}$ denotes the adjacency relationships among the retained nodes. The updated feature matrix $X_{\mathrm{out}}$ and adjacency matrix $A_{\mathrm{out}}$ are thus obtained.

3.3. Multi-Layer Stacking and End-to-End Prediction

By repeatedly applying the graph convolution and self-attention pruning modules, DynaGPNN-SAM can implement a multi-layer network structure. The proposed DynaGPNN-SAM can construct an end-to-end SOH estimation model through multi-layer stacking. The overall computation can be formally expressed as Equation (12), as follows:

$${\widehat{y}}_{\mathrm{SOH}}=DynaG{P}_k(\cdots DynaG{P}_2(DynaG{P}_1(X,A),A)\cdots ,A)$$

(12)

where $DynaG{P}_i$ denotes the i-th self-attention graph convolutional pruning module, and ${\widehat{y}}_{\mathrm{SOH}}$ is the final output representing the estimated battery SOH.

The whole architecture of estimation is shown in Figure 2. The core idea of DynaGPNN-SAM is to evaluate the importance of each node in the graph using the self-attention mechanism and retain important nodes while removing less relevant ones during the graph pruning process, thereby optimizing the network structure and improving SOH estimation performance. Through the information filtering and structural compression enabled by the self-attention mechanism, the model can effectively focus on critical stages in the battery degradation process (e.g., knee points and abrupt segments), reducing redundant computation while enhancing the accuracy and stability of SOH estimation.

3.4. Adam Optimization Algorithm

Widely regarded as the default optimization method in deep learning, the Adaptive Moment Estimation (Adam) algorithm offers exceptional robustness, computational efficiency, and adaptability for diverse neural network structures. Originally introduced by Kingma and Ba in 2015 [49], this optimization technique merges the beneficial aspects of Momentum and RMSProp approaches. The algorithm dynamically adjusts learning rates for individual parameters through continuous estimation of gradient statistics, specifically tracking both the first-order moment (mean) and second-order moment (unbiased variance). Its widespread adoption stems from several key advantages, outlined as follows: reliable convergence properties when dealing with complex, high-dimensional non-convex optimization landscapes, straightforward implementation requirements, and minimal dependence on precise hyperparameter tuning. These characteristics have made Adam particularly valuable across numerous deep learning implementations. The subsequent discussion elaborates on the fundamental concepts and mathematical formulation underlying the Adam optimization technique.

Specifically, at the t-th iteration, Adam computes the first moment estimate $m_t$ and the second moment estimate $v_t$ of the gradient $g_t$ as Equations (13) and (14), expressed as follows:

$$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t,$$

(13)

$$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2,$$

(14)

where ${\beta }_1$ and ${\beta }_2$ are the exponential decay rates for the moment estimates, typically set to $0.9$ and $0.999$, respectively. To eliminate bias introduced during initialization, Adam applies bias correction as Equation (15), as follows:

$${\widehat{m}}_t={\displaystyle \frac{m_t}{1-{\beta }_1^t}},{\widehat{v}}_t={\displaystyle \frac{v_t}{1-{\beta }_2^t}}.$$

(15)

The parameter update rule is then given by Equation (16), expressed as follows:

$${\theta }_t={\theta }_{t-1}-\alpha {\displaystyle \frac{{\widehat{m}}_t}{\sqrt{{\widehat{v}}_t}+ϵ}},$$

(16)

where $\alpha$ denotes the global learning rate and $ϵ$ is a small constant (usually ${10}^{-8}$) to avoid division by zero.

Adam offers several notable advantages. Each parameter has an individually adapted learning rate, which is particularly beneficial for problems with sparse gradients. It requires only first and second moment accumulators, resulting in low computational and memory costs. Relatively insensitive to hyperparameter settings, it maintains stable convergence across a wide range of tasks. It exhibits rapid decrease in loss during the early training stages, suitable for non-stationary objectives and noisy gradients. It exhibits robust empirical effectiveness across a variety of deep learning applications, such as natural language processing, computer vision, and speech recognition.

Compared with traditional stochastic gradient descent (SGD) and its momentum-based variants, Adam typically achieves faster convergence and improved stability when optimizing complex loss landscapes.

4. Experimental Study

This section is designed to demonstrate the effectiveness and advantages of the proposed DynaGPNN-SAM model in estimating the state of health (SOH) of lithium-ion batteries. It encompasses a comprehensive analysis, including dataset description, implementation details of the model, hyperparameter optimization, comparative experiments, performance assessment, and interpretation of the obtained results.

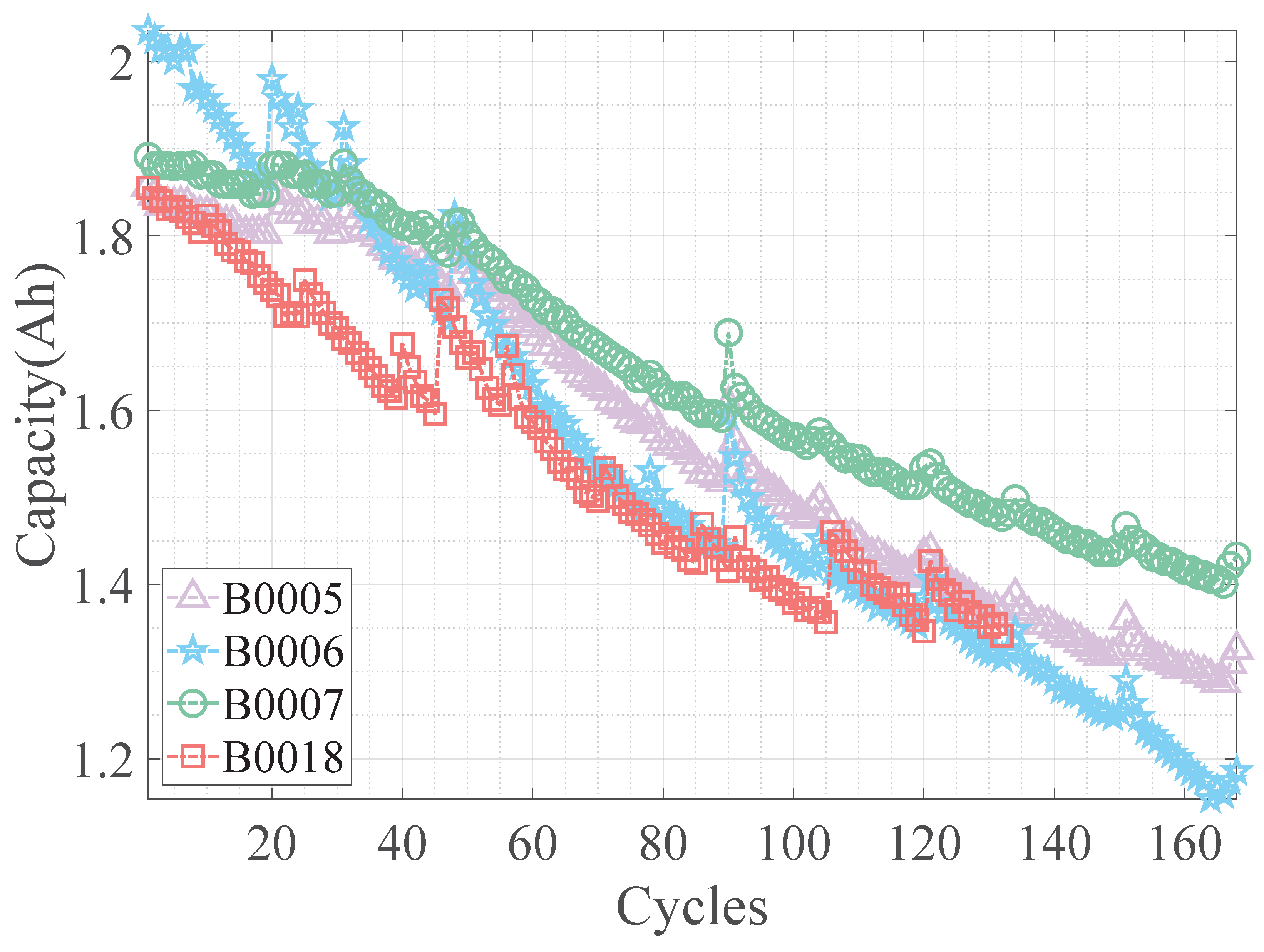
4.1. Dataset Description

The research utilizes a publicly accessible lithium-ion battery dataset from the NASA Ames Prognostics Center. This dataset consists of four 18650-type batteries, designated as B0005, B0006, B0007, and B0018, each of which underwent full charge–discharge cycles at a constant ambient temperature until significant capacity degradation occurred. For every cycle, critical operational parameters such as voltage, current, and temperature are captured, offering rich and detailed information suitable for SOH modeling.

Figure 3 presents the battery capacity degradation curve. The charging process followed a Constant Current–Constant Voltage (CC-CV) strategy: initially charged with a constant current until reaching 4.2 V, after which constant voltage charging was applied until the current decreased to 20 mA. During discharge, a constant current was maintained until a specified voltage cutoff was reached. From each charge–discharge cycle, 10 key statistical features were derived, such as the durations and voltage levels during CC and CV phases, average current values, capacity measurements, and temperature readings. To ensure uniformity during model training, all extracted features were normalized to mitigate discrepancies in scale. A comprehensive explanation of these features can be found in the work by Tian et al. [50].

To construct graph-structured data, a sliding time window strategy was applied. Feature vectors within each window are treated as nodes in the graph, and their pairwise Euclidean distances are used to build the adjacency matrix. This results in a graph representation that serves as the input to DynaGPNN-SAM.

For stability purposes, only cycles where the SOH exceeds 75% are included in the analysis [51]. The leave-one-out cross-validation method is implemented, with one battery designated as the test set and the other three serving as the training set in each round. This strategy allows for a thorough assessment of the model’s generalization performance and robustness.

The NASA lithium-ion dataset was selected because it provides complete run-to-failure records under a controlled constant current and constant voltage protocol and contains detailed telemetry including voltage, current, temperature, and capacity. These characteristics enable reproducible benchmarking and allow for meaningful comparison with published approaches. Although the dataset covers a relatively short cycle span, the accelerated aging protocol ensures that knee points and late-stage degradation are observed within a feasible laboratory timescale, which is highly valuable for modeling the state of health. In order to reduce the potential bias introduced by shorter sequences, we apply a leave-one-battery-out validation strategy and restrict the training samples to cycles where the state of health remains above 75 percent. This design highlights early- and mid-life estimation while ensuring that the held-out battery provides an unbiased measure of generalization capability. The dataset has also been widely adopted as a benchmark in the prognostics community, which reinforces the validity of using it as the primary evaluation source. We recognize that longer duration datasets would further strengthen the evidence, but such resources are rarely available in the public domain. The proposed method is formulated in a data-agnostic manner and processes graph-structured windows constructed from generic features, which makes it suitable for direct application once long-term datasets become available.

4.2. Implementation Details of DynaGPNN-SAM

To achieve optimal prediction performance, key hyperparameters of the DynaGPNN-SAM model were carefully tuned. Specifically, a grid search was performed over various ranges for window length, number of network layers, neurons per layer, and learning rate. The experimental results of the hyperparameters are shown in Figure 4. The results show that the best configuration is obtained when the window length is 10, the number of layers is 2, each with 10 neurons, and the learning rate is set to 0.001. Deeper architectures were prone to overfitting, while the number of neurons affected the trade-off between expressiveness and computational complexity.

The final model configuration is shown in

Table 2. The hyperparameter configuration of DynaGPNN-SAM.

Parameter	Configuration
Time window length	10
Number of DynaGPNN-SAM layers	2
Number of DynaGPNN-SAM neurons	10
Learning rate	0.001
Batch size	16
Loss function	Mean square error
epochs	100
optimizer	Adam

. This configuration ensures both model efficiency and predictive capability.

4.3. Ablation Study Design

To further assess the impact of each critical component in the proposed method, two ablation experiments were carried out. In these experiments, the self-attention mechanism and the graph pruning mechanism were individually removed from the network structure. The goal of this design is to measure the contribution of each module to the model’s overall performance. To ensure the validity of the findings across different cases, the ablation tests were performed on the following four battery datasets: B0005, B0006, B0007, and B0018. The SOH prediction accuracy of the method was evaluated using two commonly used performance indicators—root mean square error (RMSE) and mean absolute error (MAE)—both of which demonstrate the effectiveness of the proposed framework.

The RMSE is defined as Equation (17), expressed as follows:

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(17)

where n denotes the number of samples in the test dataset, i is the sample index, and $y_i$ and ${\widehat{y}}_i$ represent the predicted and actual SOH values of the i-th sample, respectively.

Considering the importance of overall error levels for battery safety and reliability, MAE was also adopted as an evaluation metric. Its mathematical formulation is given as Equation (18), expressed as follows:

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n|y_i-{\widehat{y}}_i|$$

(18)

Table 3. Comparison of experimental results for different configurations.

Experiments	RMSE				MAE
	B0005	B0006	B0007	B0018	B0005	B0006	B0007	B0018
Original version	0.0104 ± 0.0009 3	0.0164 ± 0.0007	0.0122 ± 0.0008	0.0205 ± 0.0004	0.0077 ± 0.0005	0.0131 ± 0.0008	0.0089 ± 0.0007	0.0155 ± 0.0004
M1 1	0.0171 ± 0.0012	0.0240 ± 0.0019	0.0141 ± 0.0016	0.0262 ± 0.0019	0.0170 ± 0.0015	0.0197 ± 0.0023	0.0106 ± 0.0016	0.0205 ± 0.0018
M2 2	0.0211 ± 0.0008	0.0171 ± 0.0014	0.0164 ± 0.0018	0.0357 ± 0.0042	0.0174 ± 0.0008	0.0144 ± 0.0014	0.0127 ± 0.0014	0.0281 ± 0.0043

¹ Remove self-attention. ² Replace DynaGPNN with GCN. ³ Standard deviation across three seeds.

presents the experimental outcomes based on the RMSE and MAE evaluation metrics. All ablation results are reported as the mean and the standard deviation over three independent runs with distinct random seeds. The results reveal that M1, the variant without the self-attention module, led to a significant performance decline, with RMSE increasing by as much as 64.789% and MAE rising by 121.042% compared to the original model. This highlights the essential role of the attention mechanism in effectively identifying critical degradation patterns across the temporal window, especially for capturing long-term dependencies.

In M2, the core temporal modeling unit based on DynaGPNN was replaced with a standard GCN. This substitution led to a noticeable decline in model performance, especially on the B0005 dataset, where the RMSE increased to 0.0211 and the MAE reached 0.0174. These results demonstrate that DynaGP offers superior accuracy, efficiency, and stability as the temporal modeling component in our framework.

In summary, the ablation experiments systematically verify the rationality of the key module designs in the proposed model architecture. They further highlight the significant contribution of both the self-attention mechanism and the DynaGP unit in enhancing the model’s predictive performance and generalization capability, thereby substantiating the effectiveness and necessity of the DynaGPNN-SAM framework.

4.4. Experimental Results and Analysis

To comprehensively assess the performance of DynaGPNN-SAM, comparisons are conducted with several mainstream SOH estimation methods, including the following:

• Traditional Machine Learning Methods: Support Vector Machine (SVM), Backpropagation Neural Network (BP), Wavelet Neural Network (WNN), and Gaussian Process Regression (GPR).
• Deep Learning Models: Convolutional Neural Network (CNN), Long Short-Term Memory (LSTM), fusion-based models, and SambaMixer [52].
• Gaussian Process-based Methods: QGPFR (Gaussian process functional regression with quadratic polynomial mean function), LGPFR (linear Gaussian process functional regression), and Combination QGPFR.
• Graph Neural Networks: Graph Convolutional Network (GCN).
• Hybrid Optimization Models: Genetic Algorithm-based WNN (GA WNN).
• Physics-informed Neural Networks: PINN4SOH [53].

In the field of lithium-ion battery state of health prediction, a variety of methods have been proposed to improve prediction accuracy and robustness. Among traditional machine learning approaches, support vector machines construct optimal hyperplanes based on the maximum margin principle, which is suitable for small sample and nonlinear regression tasks. Backpropagation neural networks employ the gradient backpropagation mechanism to achieve multilayer nonlinear mappings. Wavelet neural networks integrate wavelet transforms with neural network architectures to extract multi-scale features in the time-frequency domain, which enables the modeling of non-stationary signals. Gaussian process regression captures input similarity through kernel functions and provides uncertainty quantification in predictions.

With the advancement of deep learning, convolutional networks efficiently extract spatial features through local receptive fields and weight sharing. Long short-term memory networks utilize gating mechanisms to capture long-term dependencies. Fusion-based models combine the strengths of multiple prediction architectures to enhance generalization performance and robustness. Recently, state space sequence models such as SambaMixer have leveraged selective state space representations to model long-range temporal dependencies with linear time complexity in sequence length, which improves efficiency while retaining strong forecasting capability [52].

For uncertainty modeling, Gaussian process-based approaches such as QGPFR, LGPFR, and their combination introduce quantile regression, local Gaussian processes, and hybrid strategies, respectively, in order to balance global predictive capability and local fitting accuracy. In terms of structured data modeling, graph convolutional networks jointly capture node features and topological relationships within graph structures, which is suitable for non-Euclidean data. Furthermore, hybrid optimization models such as GA WNN leverage the global search capability of genetic algorithms to optimize wavelet neural network parameters, which improves model convergence and predictive accuracy. In addition, physics-informed neural frameworks such as PINN4SOH incorporate degradation-related priors into the learning objective and regularization, which enhances stability across operating conditions and strengthens extrapolation to later life states [53]. Although the aforementioned methods have achieved strong results in their respective contexts, limitations remain in capturing complex spatiotemporal dependencies and multi-scale feature interactions, which motivates the exploration of modeling approaches that integrate self-attention mechanisms with graph neural networks.

To ensure transparency and fair comparability, we adopt a unified implementation protocol for all baselines prior to the analysis in this section. All methods are evaluated under the same data interface and split strategy. Per-cycle CSV features are aggregated into fixed length sequences with length $T=10$ and feature dimension $D=10$. Training data are restricted to samples whose end of window state of health exceeds $0.75$. Evaluation follows a leave-one-battery-out protocol across B0005, B0006, B0007, and B0018. Feature scaling is fitted on the training set and applied unchanged to the validation and test sets. The adapter that harmonizes inputs affects only preprocessing and tensor formatting and does not change the internal architectures of the compared models. To ensure fairness and accuracy, all methods are trained with the same mini batch size of 16. When an official implementation recommends a different value, we keep the remaining settings unchanged and harmonize only the batch size.

For traditional machine learning models, deep learning models, Gaussian process-based methods, graph neural networks, and hybrid optimization models that are not explicitly detailed below, we follow the parameter choices and adjustment procedures recommended in their cited papers and official implementations. When the original sources provide ranges rather than fixed values, we select values within those ranges on the validation fold without using any test information. Optimizer type, learning rate scheduling, regularization, and early stopping rules therefore conform to the corresponding references unless stated otherwise. Except for the unified mini batch size of 16, no additional departures from the cited sources are introduced.

Given its relevance as a recent physics-informed baseline, we disclose the exact configuration used in this study. The sequence interface matches the unified setting with $T=10$ and $D=10$. The training schedule consists of a total of 100 epochs with an early stopping patience of 10 epochs. A warm up stage is applied during the first 30 epochs. The learning rate is set to $0.01$. The mini batch size is fixed at 16 to comply with the unified setting across all methods. The composite loss includes a data fidelity term with coefficient $\alpha =1.0$ and a physics regularization term with coefficient $\beta =0.02$. The network backbone, the optimizer choice, and the definitions of the physics residual terms follow the official implementation in order to preserve fidelity and reproducibility.

To isolate the contribution of pruning, the graph convolutional network baseline is trained with exactly the same hyperparameters and data protocol as in the main experiments. This includes the same window length, the unified mini batch size of 16, the learning rate schedule, the number of epochs, the early stopping rule, the data splits, and the scaling strategy. In addition, an ablation study is provided in which the pruning module is disabled while all other components and settings are kept fixed. This design allows a clean assessment of the incremental effect of attention-guided structural pruning.

The evaluation metrics include RMSE and MAE in

Table 4. The comparative experimental results of different approaches.

Approach	RMSE				MAE
	B0005	B0006	B0007	B0018	B0005	B0006	B0007	B0018
BP [54]	-	-	-	-	0.0768	0.0759	0.0732	0.0753
SVM [54]	-	-	-	-	0.0442	0.0435	0.0449	0.0553
WNN [54]	-	-	-	-	0.0300	0.0362	0.0344	0.0322
GPR [55]	0.1303	0.2251	0.2070	-	-	-	-	-
LSTM [56]	0.0440	0.0550	-	0.0260	-	-	-	-
CNN [56]	0.0200	0.0230	-	0.0220	-	-	-	-
Fusion model [56]	0.0191	0.0205	-	0.0227	-	-	-	-
Combination QGPFR [55]	0.0180	0.2044	0.0269	-	-	-	-	-
LGPFR [55]	0.0171	0.0690	0.0159	-	-	-	-	-
QGPFR [55]	0.0150	0.0512	0.0552	-	-	-	-	-
GA-WNN [54]	-	-	-	-	0.0181	0.0161	0.0153	0.0167
GCN	0.0138	0.0201	0.0175	0.0287	0.0104	0.0173	0.0140	0.0234
Combination LGPFR [55]	0.0136	0.0686	0.0173	-	-	-	-	-
SambaMixer [52]	0.0227	0.0475	0.0250	0.0340	0.0206	0.0449	0.0230	0.0275
PINN4SOH [53]	0.0145	0.0197	0.0140	0.0282	0.0110	0.0141	0.0095	0.0248
Ours	0.0104	0.0164	0.0122	0.0205	0.0077	0.0131	0.0089	0.0155

. Results indicate that DynaGPNN-SAM consistently outperforms all other models across all batteries. For example, the RMSE for B0005 is reduced to 0.0104, significantly lower than the 0.0138 of GCN. For B0007, the MAE drops to 0.0089, outperforming all competitors. Notably, DynaGPNN-SAM maintains high prediction accuracy even during rapid SOH degradation phases, demonstrating superior robustness and modeling capacity. Compared to GCN, DynaGPNN-SAM achieves RMSE reductions of 44.2% and 37.1% on B0005 and B0007, respectively.

Figure 5 visualizes SOH estimation curves for DynaGPNN-SAM and GCN across all four batteries. DynaGPNN-SAM shows better alignment with the ground truth, especially around degradation inflection points. In contrast, GCN yields significant deviations due to its inability to emphasize informative nodes in the graph structure, highlighting the importance of attention-based pruning.

4.5. Advantages of the Proposed Method

Experimental results demonstrate that the proposed DynaGPNN-SAM offers significant advantages over existing methods for battery SOH estimation, addressing critical limitations identified in previous approaches. These advantages stem from the synergistic integration of graph-based modeling with dynamic pruning mechanisms, resulting in a framework that not only achieves superior accuracy but also provides practical benefits for real-world battery management systems. The following sections elaborate on these advantages with specific evidence from our experimental validation.

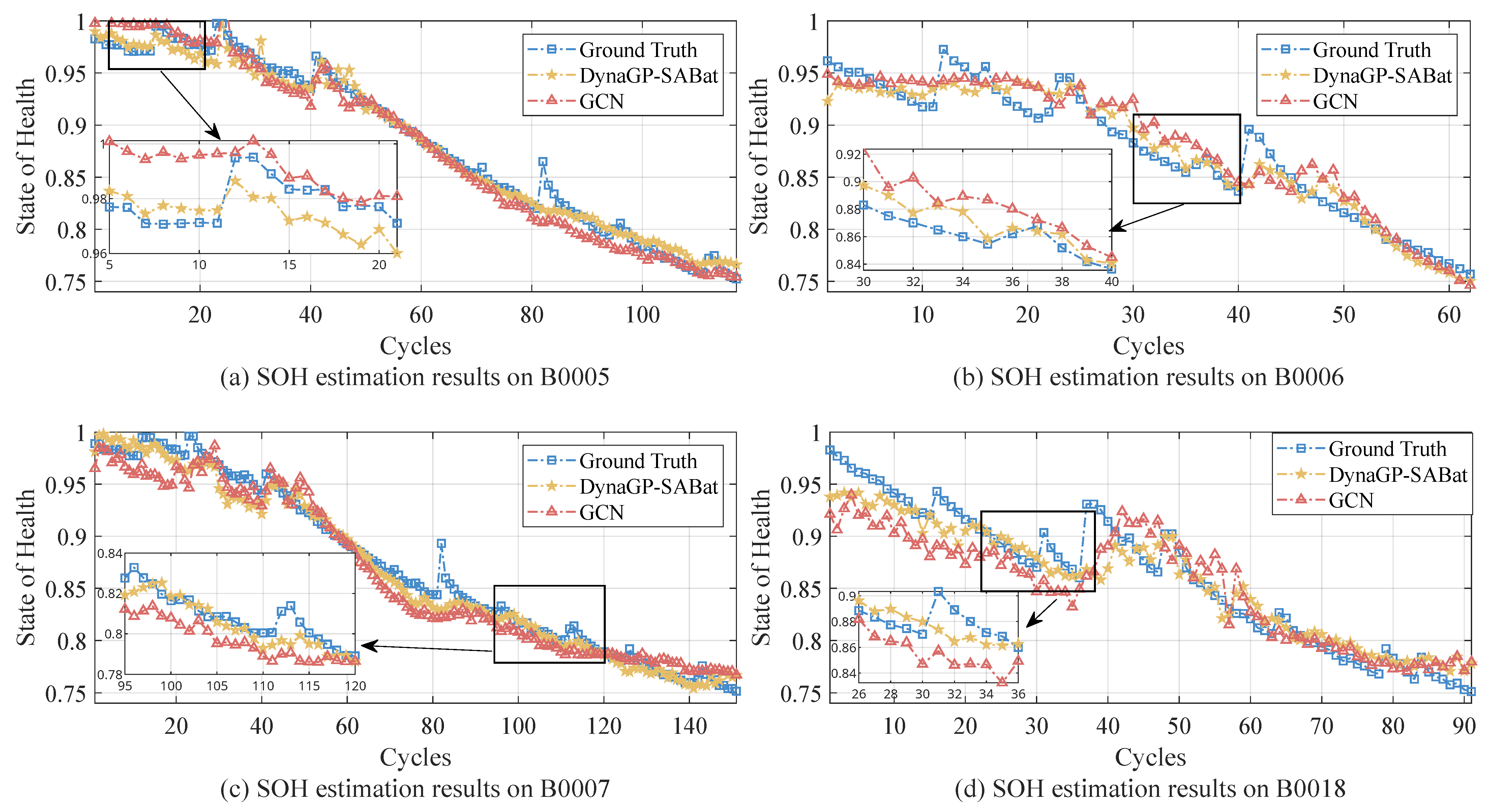
• Comprehensive Integration of Topological and Feature Information: Unlike conventional time-series models that treat battery degradation as a simple sequential process, DynaGPNN-SAM explicitly models the complex structural relationships among battery operational features through graph representation. As demonstrated in Figure 5, this approach enables the model to capture both temporal dependencies and spatial correlations among voltage, current, temperature, and capacity features simultaneously. The graph convolutional layers effectively encode the non-Euclidean relationships between these features, while the self-attention mechanism dynamically highlights nodes corresponding to critical degradation phases. This dual capability explains why our method achieves RMSE reductions of 30.3% and 28.6% on batteries B0007 and B0018 compared to standard GCN, as shown in Table 4, particularly excelling during rapid degradation phases where traditional methods exhibit significant deviations.
• Superior Handling of Nonlinear Degradation Patterns and Capacity Regeneration: One of the most challenging aspects of battery SOH estimation is accurately modeling nonlinear degradation trajectories, particularly the “knee point” phenomenon where degradation accelerates rapidly. Traditional methods often struggle with these nonlinearities and capacity regeneration events that introduce uncertainty into predictions. DynaGPNN-SAM’s architecture specifically addresses this challenge through its attention-guided node selection process, which automatically identifies and prioritizes segments containing knee points and regeneration events. As shown in Figure 5c, our model maintains high accuracy during the rapid degradation phase of battery B0006 (cycles 30–40), where competing methods exhibit significant deviations. Quantitatively, DynaGPNN-SAM achieves an RMSE of only 0.0057 on B0006 during this critical phase, compared to 0.0125 for GCN, a 54.4% improvement.
• End-to-End Learning Framework with Minimal Feature Engineering: The proposed method eliminates the need for manual feature extraction and selection, which has been a significant bottleneck in previous SOH estimation approaches. Traditional methods often require domain-specific knowledge to identify relevant health indicators (HIs) from raw battery data, a process that is both time-consuming and prone to information loss. DynaGPNN-SAM, by contrast, processes raw feature sequences directly through its graph construction mechanism, automatically learning which features and temporal segments contribute most significantly to SOH determination.

Collectively, these advantages position DynaGPNN-SAM as a significant advancement in battery SOH estimation methodology. The framework not only achieves state-of-the-art accuracy (with RMSE as low as 0.0077 on B0005) but also provides practical benefits, including computational efficiency, interpretability, and robustness to challenging degradation patterns. These characteristics make the proposed method particularly well-suited for integration into next-generation battery management systems where accurate, reliable, and efficient health monitoring is critical for safety, performance optimization, and the lifecycle management of lithium-ion battery systems.

5. Conclusions and Future Perspectives

5.1. Conclusions

A new approach for estimating the state of health (SOH) of lithium-ion batteries is introduced in this study, named DynaGPNN-SAM, which leverages graph neural networks. This method builds graph-structured data from cyclic features obtained through a sliding time window and combines graph convolution operations with self-attention pruning mechanisms. While preserving the capability of modeling spatial dependencies within the graph structure, DynaGPNN-SAM dynamically focuses on key nodes, thereby significantly improving the accuracy and robustness of SOH estimation.

The experimental section presents extensive comparative analyses carried out on the NASA open dataset. The findings show that DynaGPNN-SAM achieves better performance than conventional machine learning techniques (such as SVM and BP), deep learning models (including CNN and LSTM), and standard graph neural networks (like GCN) across various evaluation criteria, including RMSE and MAE. Notably, the model demonstrates enhanced tracking ability and generalization capability during the phase of rapid SOH degradation. These outcomes confirm the method’s effectiveness in identifying intricate degradation patterns in batteries and improving the representation of key nodes within the graph structure.

Furthermore, through systematic hyperparameter tuning and structural design, DynaGPNN-SAM achieves a favorable balance between model complexity and prediction accuracy. Its end-to-end learning framework eliminates the need for manual feature engineering, offering greater adaptability and strong potential for engineering deployment.

5.2. Perspectives

This study validates DynaGPNN SAM on established single-cell datasets, yet the formulation is inherently general. Graph-structured windows enable transfer from cells to packs without altering the learning mechanism as follows: at the pack scale, nodes denote cells or modules and feature vectors may include inter-cell voltage dispersion, current distribution along series strings, and module-level temperature gradients, in addition to capacity and voltage. The same propagation, attention, and pruning operations capture local and global dependencies and support application beyond NASA datasets and across chemistries. The principal adaptation for higher organizational levels is the adjacency specification so that it reflects the spatial proximity, electrical connectivity, or statistical coupling among modules, while network layers and optimization remain unchanged. Future validation on pack-level datasets with synchronized telemetry can further assess robustness under practical operating conditions, and efficiency under embedded constraints can be examined alongside accuracy.

Additionally, aligned with deployment requirements in battery management systems, enhancing computational efficiency on edge devices is a priority for future work. Methodological transparency will be increased through standardized plots of per-layer pruning ratios across epochs and a concise record of the validation-based criteria used for hyperparameter selection. Efficiency under embedded and real-time constraints will be pursued through structured sparsity that maps to hardware efficient kernels, low bit quantization, knowledge distillation, and explicit accounting of the number of active edges, together forming a principled route toward practical deployment.