A Fixed-Time Zero Sequence Circulating Current Suppression Strategy Based on Extended Kalman Filter
Abstract
1. Introduction
- (1)
- Firstly, a ZSCC mathematical model and an equivalent ZSCC circuit model incorporating perturbations of the inductor parameters are developed.
- (2)
- Secondly, the inductance parameters are estimated online based on the EKF and the preset inductance parameters in the controller are updated in real time.
- (3)
- Finally, a ZSCC controller is implemented by using the EKF and fixed-time stability theory, which ensures that the system can suppress the ZSCC under different conditions.
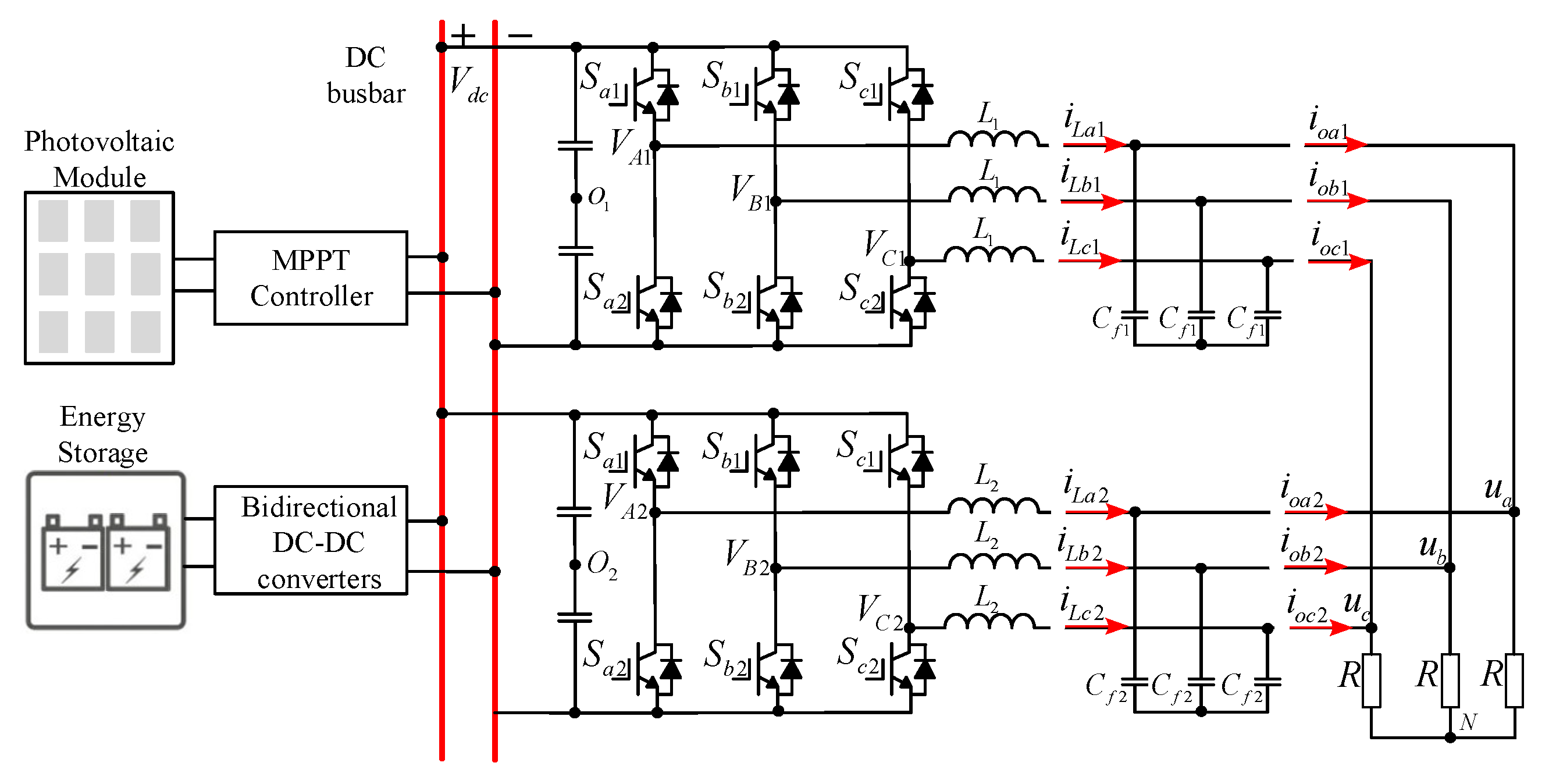
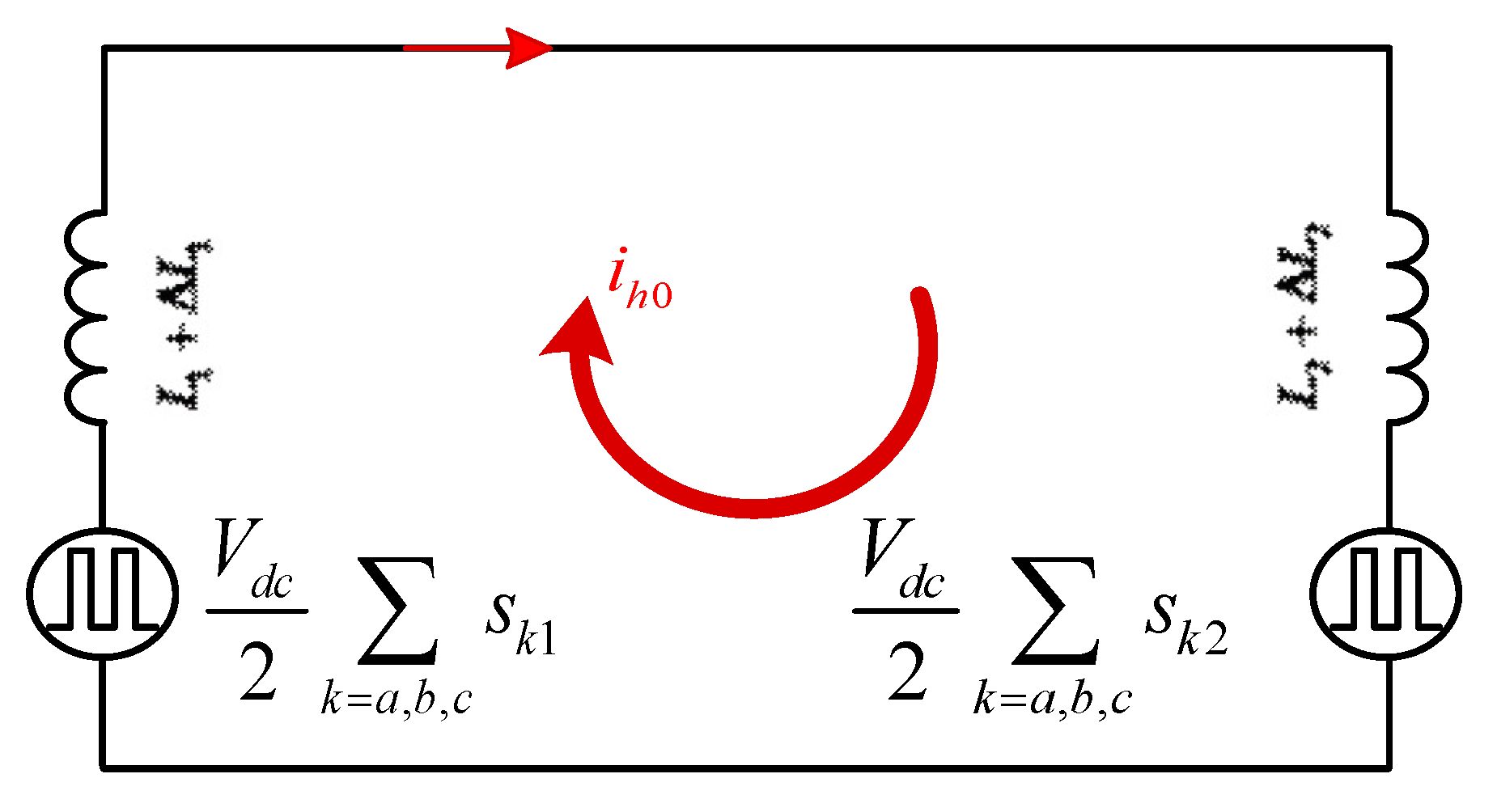
2. ZSCC Mathematical Modeling
2.1. Mathematical Modeling of ZSCC with Consistent Inductive Parameters
2.2. Mathematical Modeling of ZSCC in Case of Perturbation of Inductive Parameters
3. ZSCC Controller Design
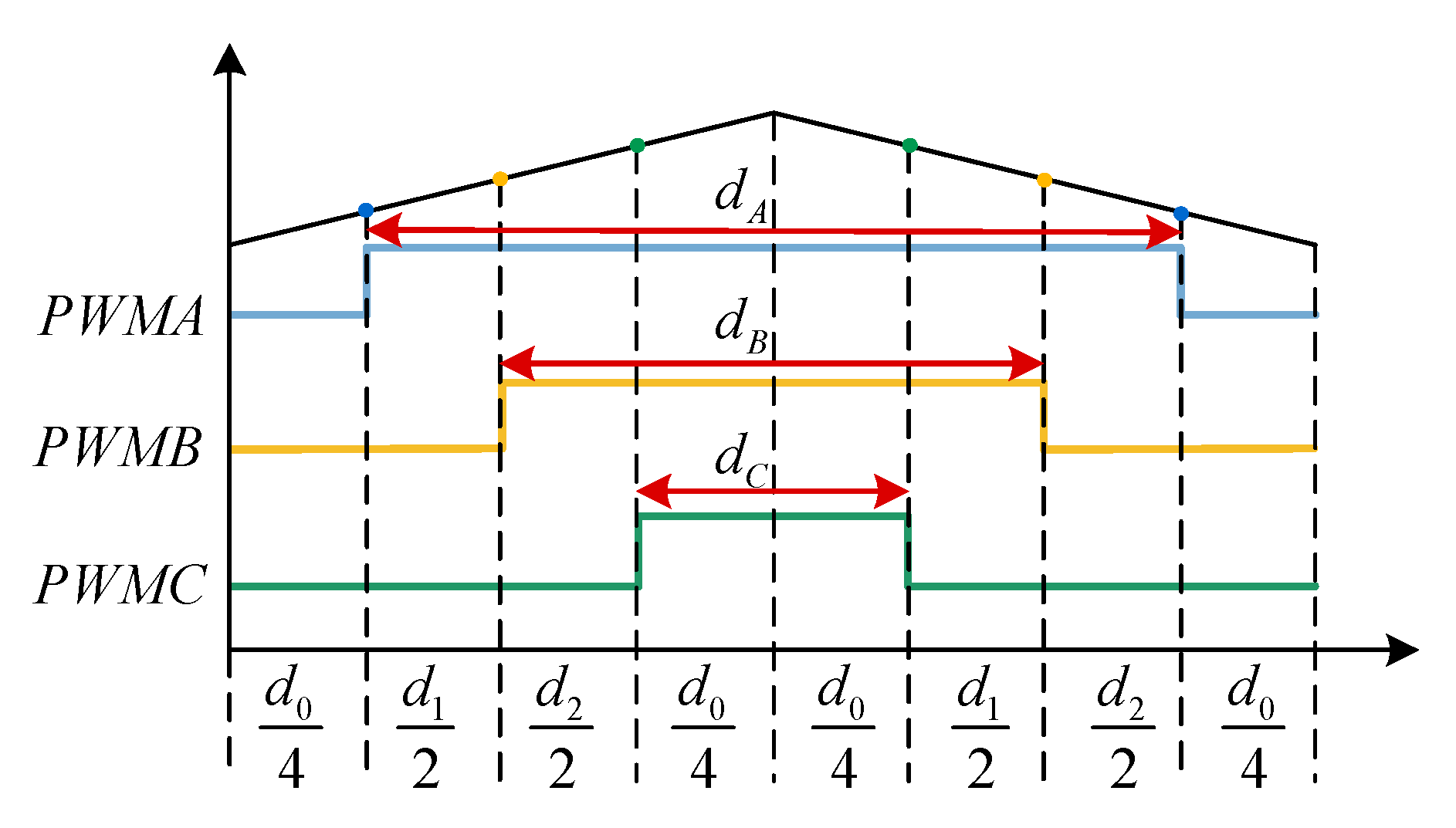
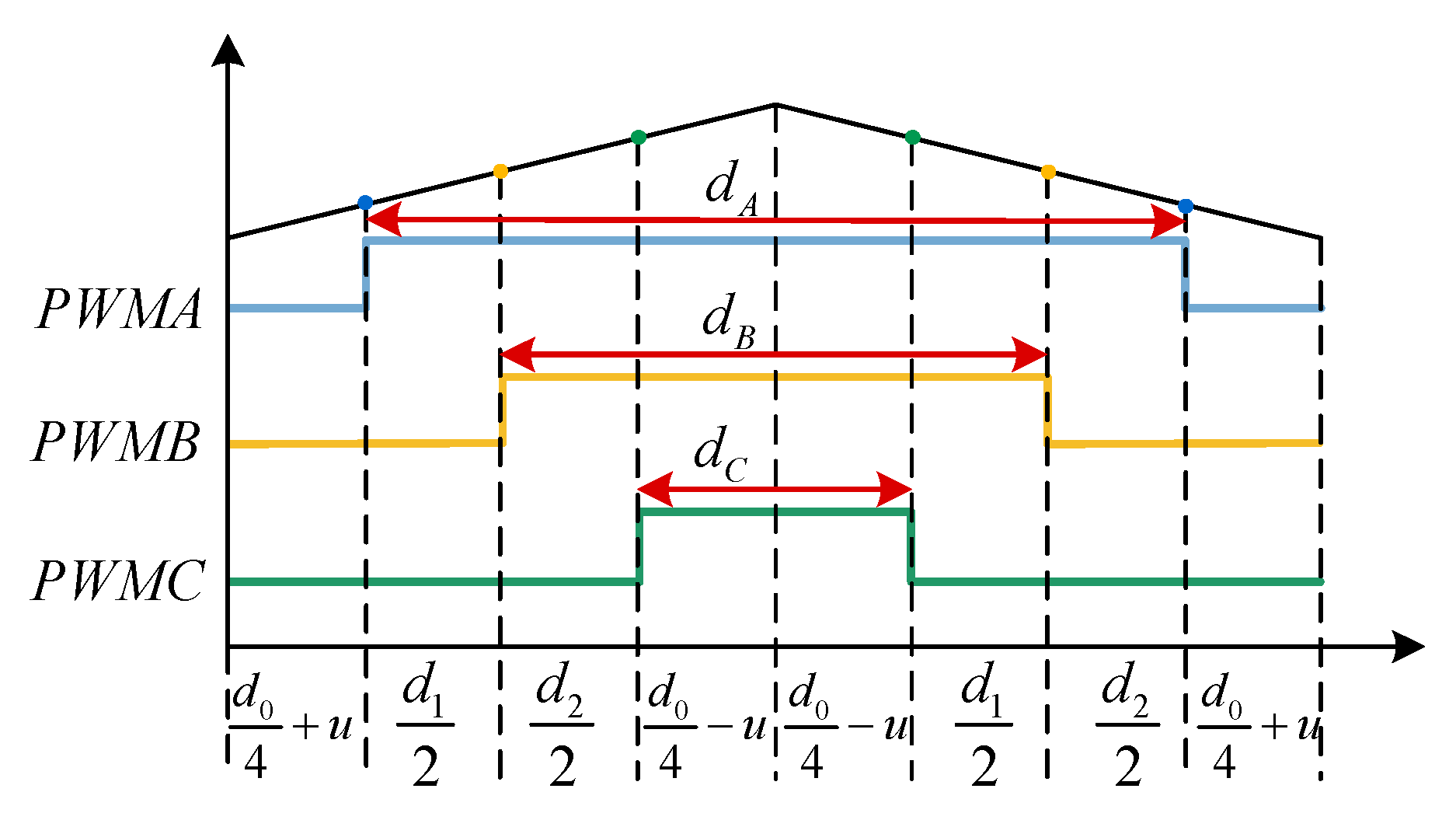
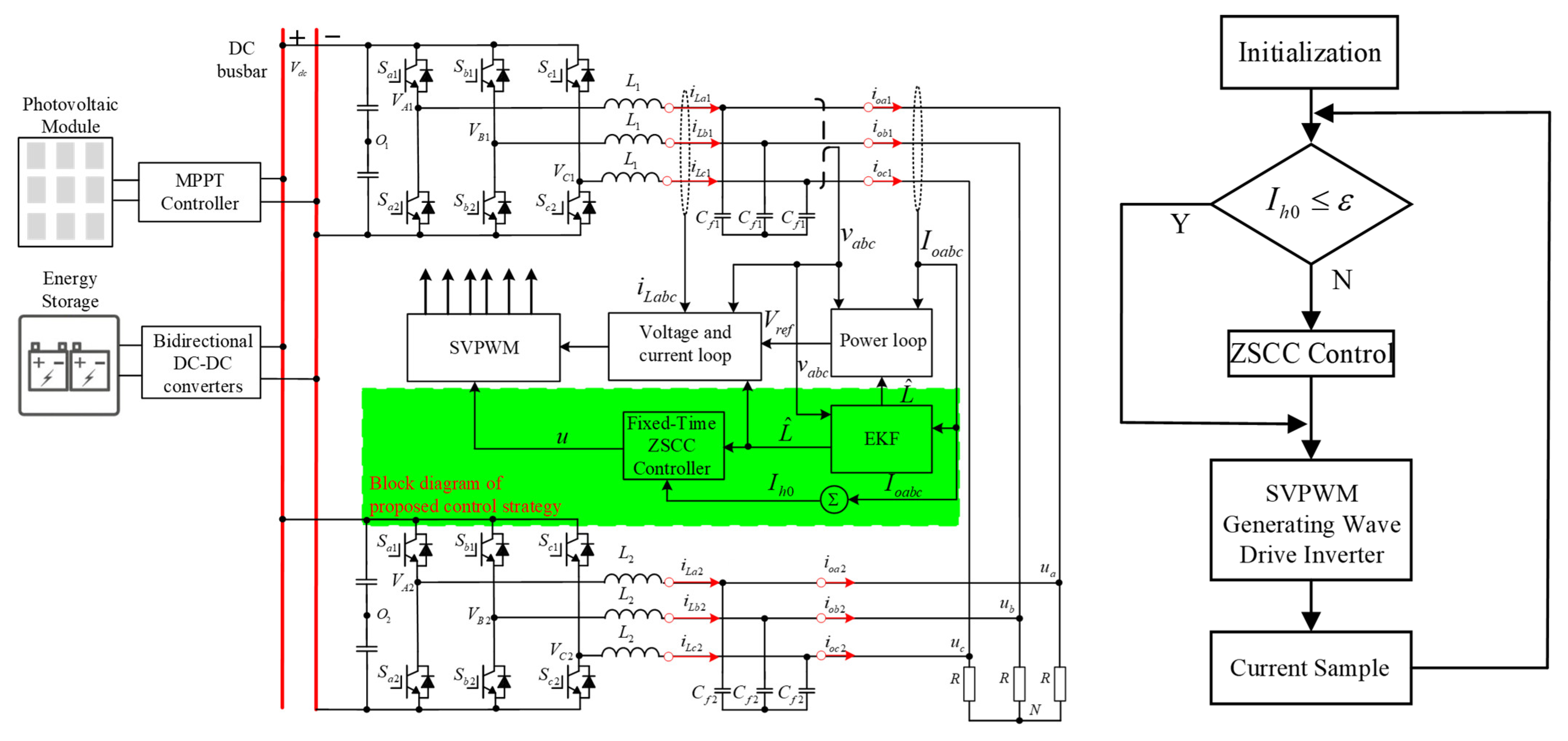
3.1. Control Scheme of the System Under the Control Approach Presented in This Study
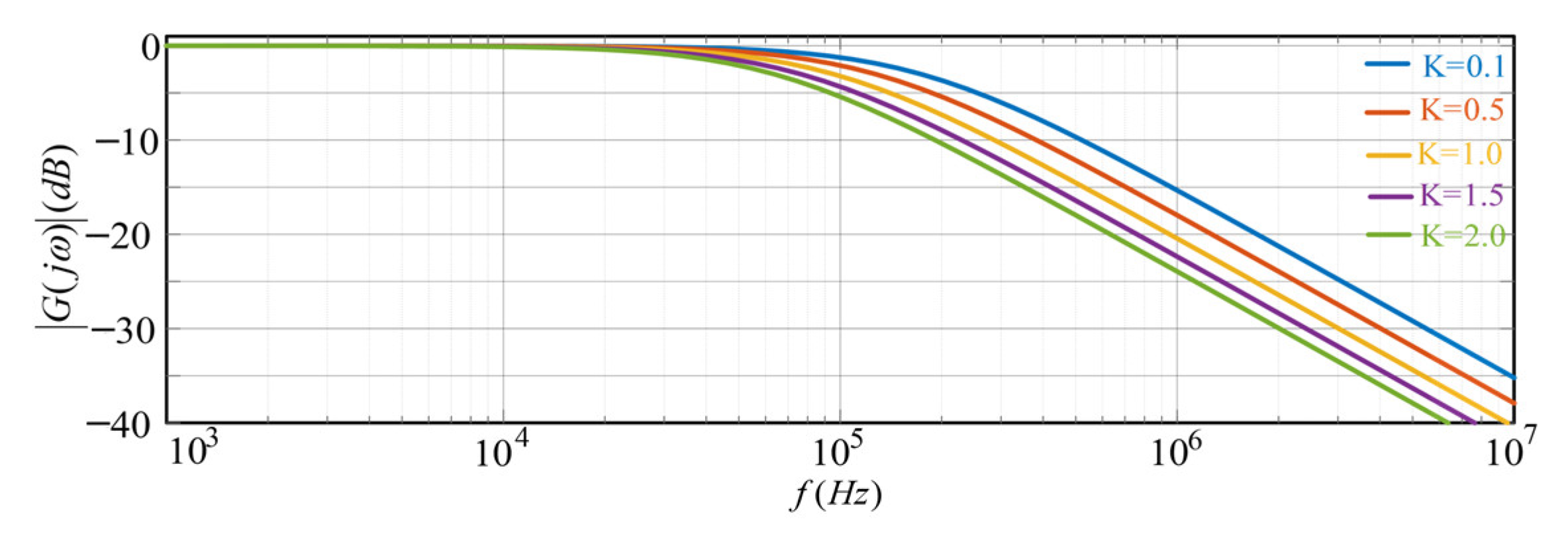
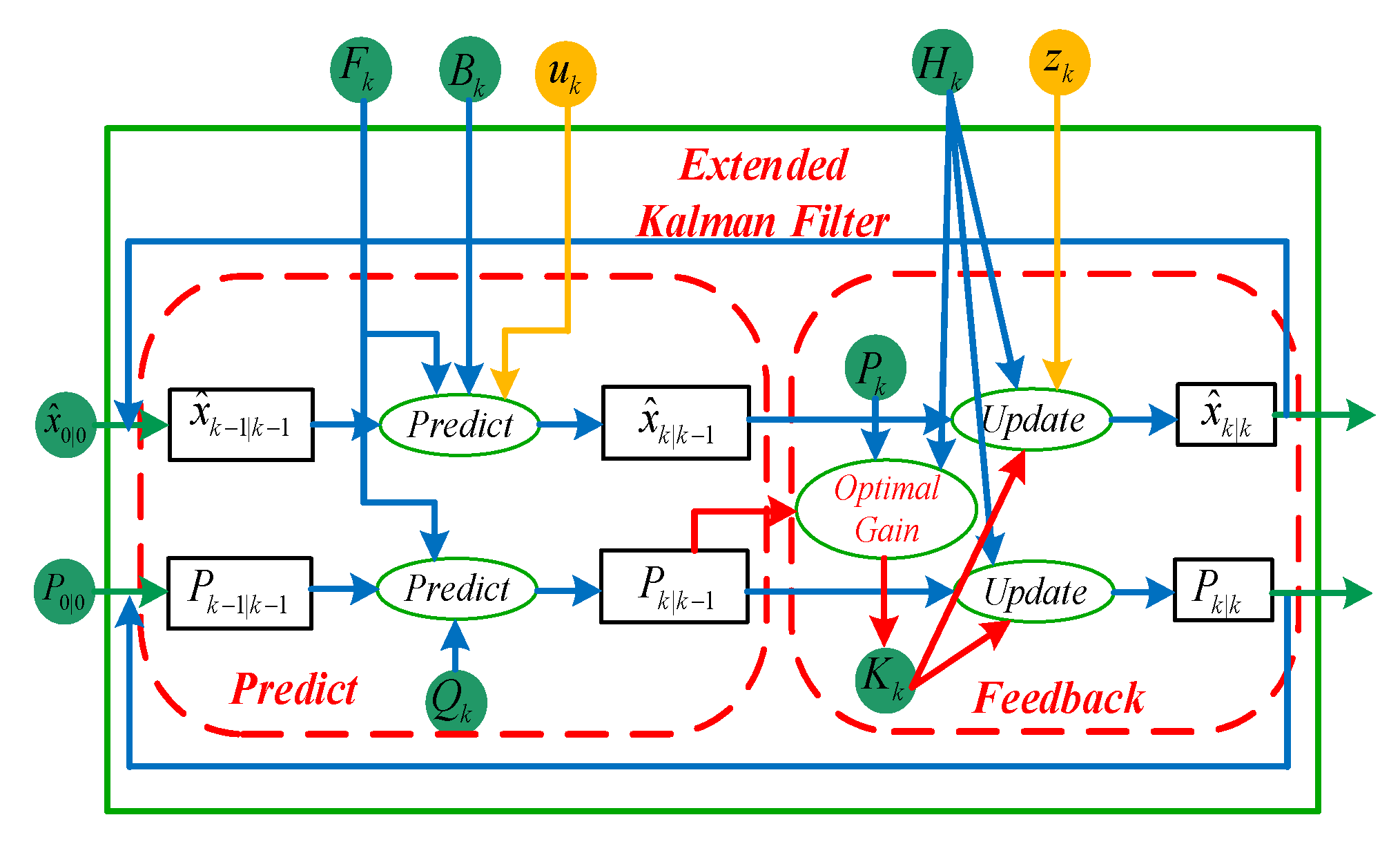
3.2. Extended Kalman Filter-Based Inductor Parameter Identification for Inverters
3.3. Design of ZSCC Controller Based on Fixed-Time Stabilization Theory
3.4. Proven Stability of ZSCC Controller
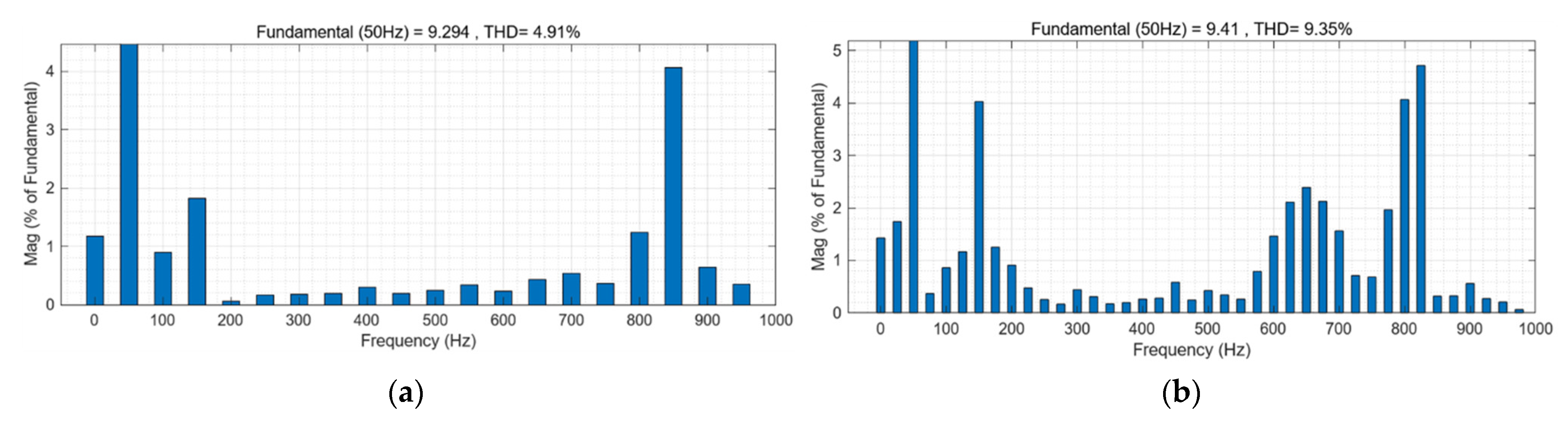
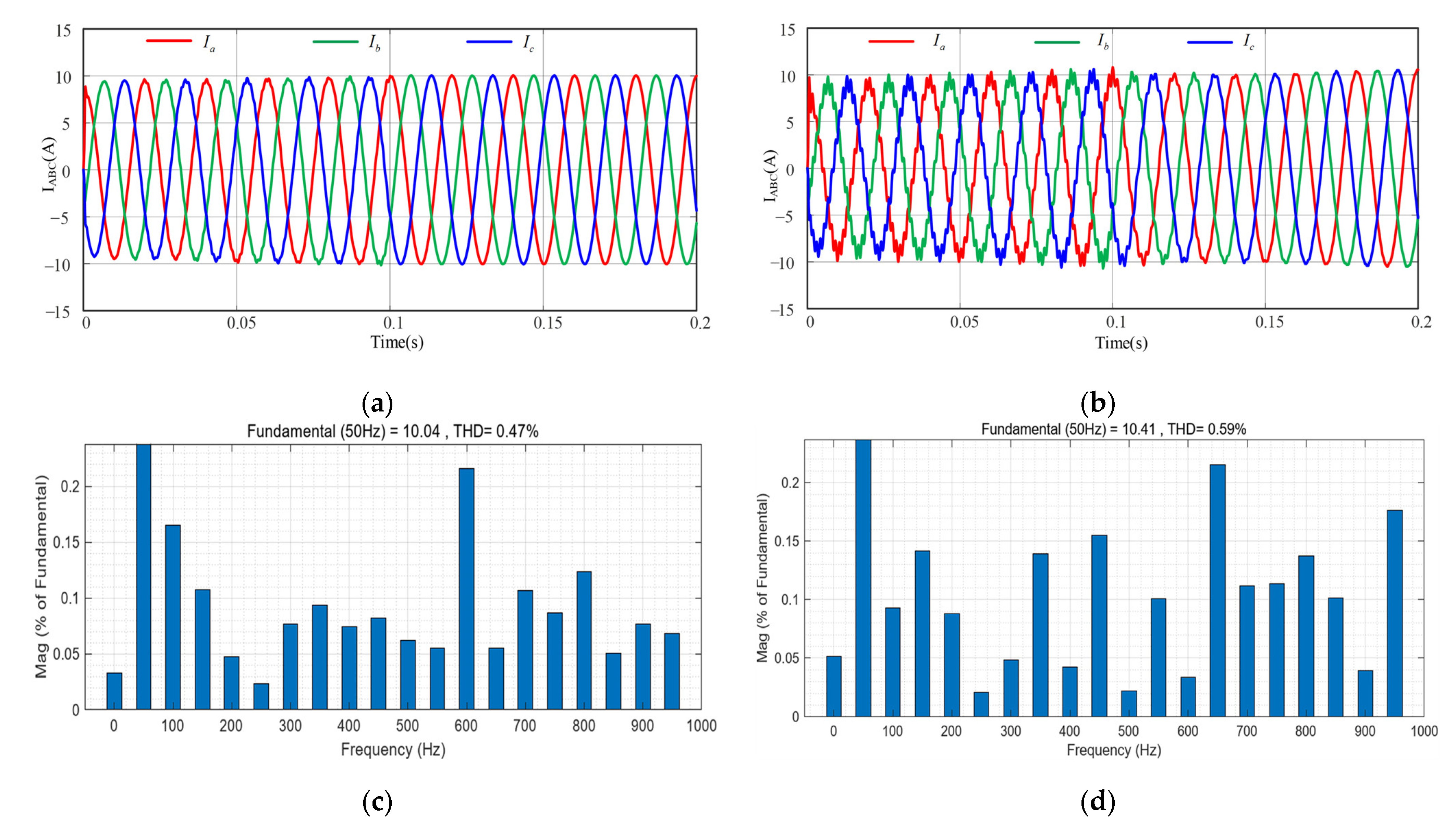
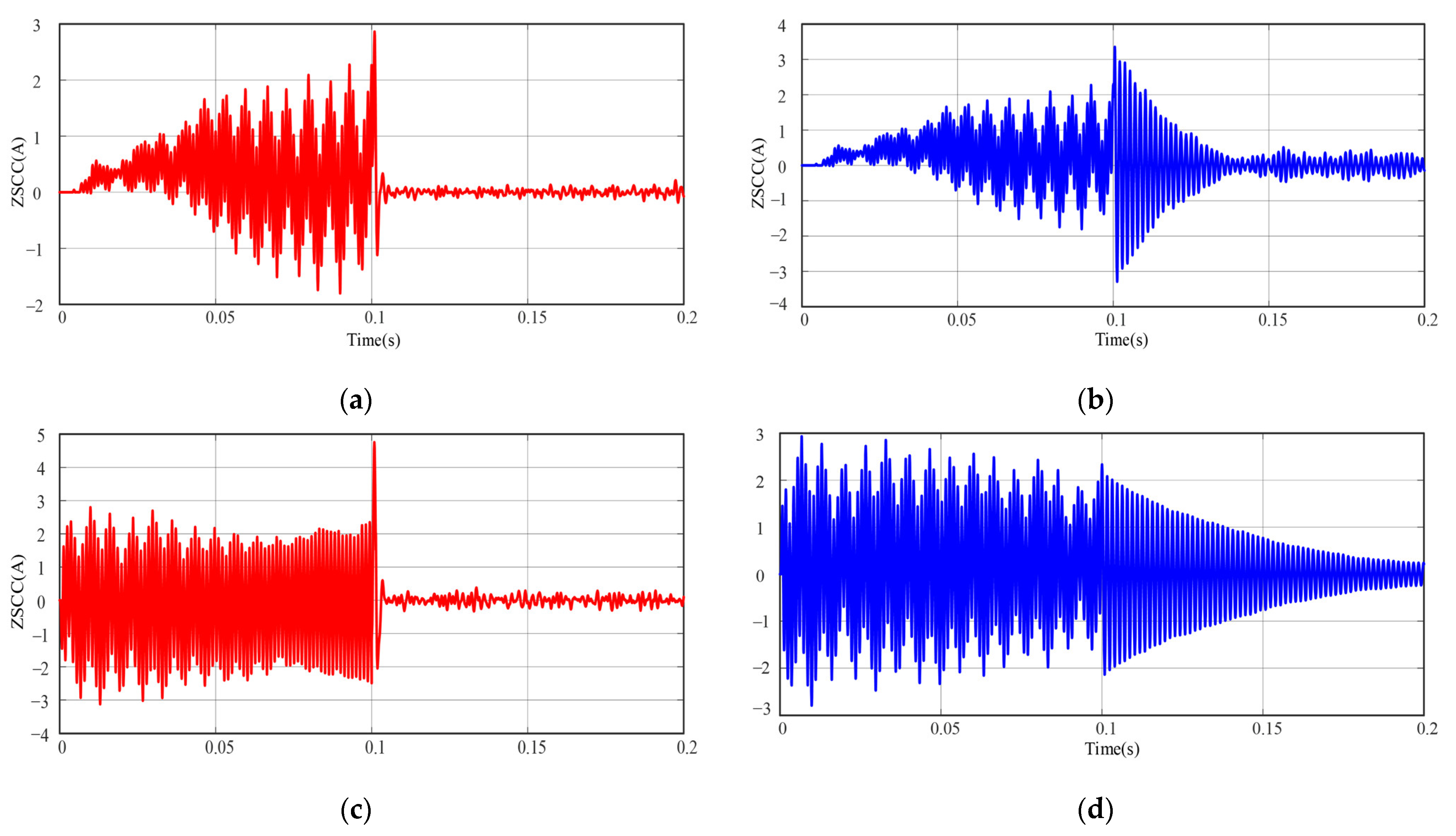
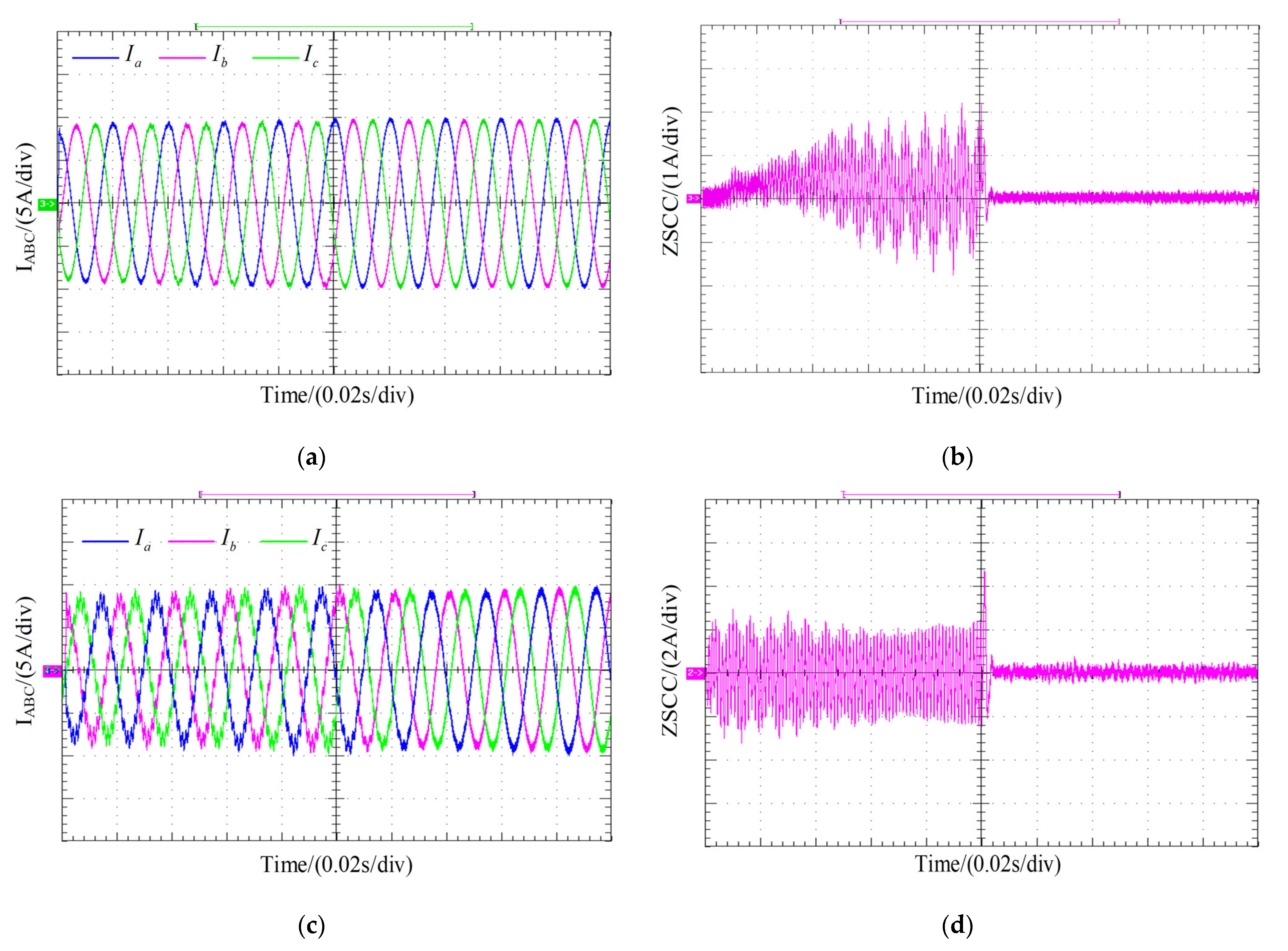
4. Simulation and Experimentation
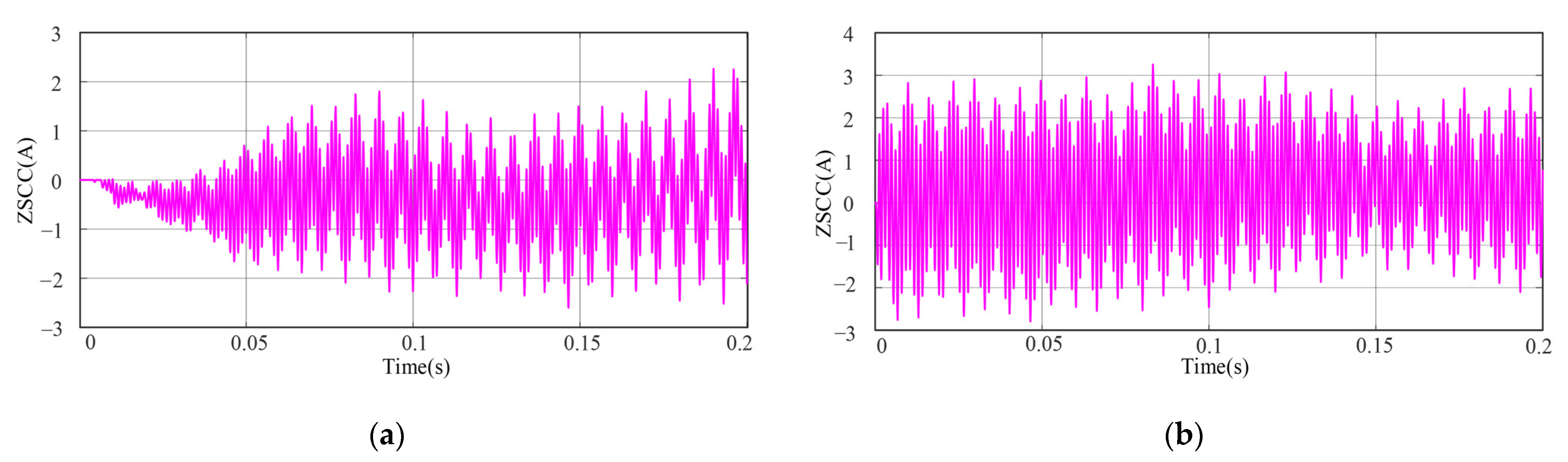
4.1. Simulation Verification
4.2. Experimental Validation
5. Conclusions
- (1)
- Compared with the conventional ZSCC control strategy, the proposed control strategy takes into account the effect of filter parameter perturbations and improves the robustness of the system by extending the Kalman filter to predict the inductance.
- (2)
- The proposed control strategy can suppress the ZSCC in parallel inverters system faster than the traditional ZSCC control strategy.
- (3)
- Under the proposed control strategy, for the ZSCC during parallel operation, the inverter parallel inverters system can respond quickly to the suppression of the ZSCC and the suppression effect of the inverters on the ZSCC, and there is no correlation between the time to stabilization and the state of the system, which improves the dynamic performance of the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Zero Sequence Voltage | ZSV | DC Bus Voltage | Output Current | ||
| Zero Sequence Path | ZSP | The midpoint of the DC bus | Inverter Output Voltage | ||
| Zero Sequence Circulating Current | ZSCC | Filter Capacitor | Load Voltage | , , | |
| Extended Kalman Filter | EKF | Current passing through the inductor | Neutral Voltage | ||
| Distributed Generation system | DGs | Filter Inductor | D-axis Q-axis Voltage | , | |
| Total Harmonic Distortion | THD | Load | D-axis Q-axis Current | , | |
| Zero Sequence Duty Cycle | ZSDC | Initial Covariance Matrix | Process Noise Covariance | ||
| Measurement Noise Covariance | Inductance Estimate | Current Values | |||
| Previous Values | Input to the system | System Noise | |||
| Measurement noise | Output of the system | Control period |
References
- Zhuo, Z.; Zhang, N.; Xie, X.; Li, H.; Kang, C. Key technologies and developing challenges of power system with high proportion of renewable energy. Autom. Electr. Power Syst. 2021, 45, 171–191. [Google Scholar]
- Zhang, H.; Xiang, W.; Lin, W.; Wen, J. Grid Forming Converters in Renewable Energy Sources Dominated Power Grid: Control Strategy, Stability, Application, and Challenges. J. Mod. Power Syst. Clean Energy 2021, 9, 1239–1256. [Google Scholar] [CrossRef]
- Ebinyu, E.; Abdel-Rahim, O.; Mansour, D.-E.A.; Shoyama, M.; Abdelkader, S.M. Grid-Forming Control: Advancements towards 100% Inverter-Based Grids—A Review. Energies 2023, 16, 7579. [Google Scholar] [CrossRef]
- Chen, Z.; Li, X.; Xing, X.; Fu, Y.; Zhang, B.; Pang, X.; Zhang, C. The Tolerance Control Method Based on Zero-Sequence Circulating Current Suppression for Parallel T-Type Three-Level Rectifiers. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 4383–4394. [Google Scholar] [CrossRef]
- Wang, X.; Zou, J.; Zhao, J.; Xie, C.; Li, K.; Munir, H.M.; Guerrero, J.M. A Novel Model Predictive Control Strategy to Eliminate Zero-Sequence Circulating Current in Paralleled Three-Level Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 309–320. [Google Scholar] [CrossRef]
- Pan, C.-T.; Liao, Y.-H. Modeling and Coordinate Control of Circulating Currents in Parallel Three-Phase Boost Rectifiers. IEEE Trans. Ind. Electron. 2007, 54, 825–838. [Google Scholar] [CrossRef]
- Liu, X.; Liu, T.; Chen, A.; Xing, X.; Zhang, C. Circulating Current Suppression for Paralleled Three-Level T-Type Inverters with Online Inductance Identification. IEEE Trans. Ind. Appl. 2021, 57, 5052–5062. [Google Scholar] [CrossRef]
- Li, Z.; Nie, Z.; Ai, S. Nonlinear Modeling and Improved Suppression of Zero-Sequence Circulating Current for Parallel Three-Level Inverters. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 3036–3049. [Google Scholar] [CrossRef]
- Simanjorang, R.; Miura, Y.; Ise, T.; Sugimoto, S.; Fujita, H. Application of Series Type BTB Converter for Minimizing Circulating Current and Balancing Power Transformers in Loop Distribution Lines. In Proceedings of the 2007 Power Conversion Conference—Nagoya, Nagoya, Japan, 2–5 April 2007; pp. 997–1004. [Google Scholar] [CrossRef]
- Inzunza, R.; Sumiya, T.; Fujii, Y.; Ikawa, E. Parallel connection of grid-connected LCL inverters for MW-scaled photovoltaic Systems. In Proceedings of the 2010 International Power Electronics Conference—ECCE ASIA, Sapporo, Japan, 21–24 June 2010; pp. 1988–1993. [Google Scholar] [CrossRef]
- Sato, Y.; Kataoka, T. Simplified control strategy to improve AC-input-current waveform of parallel-connected current-type PWM rectifiers. IEE Proc.-Electr. Power Appl. 1995, 142, 246–254. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, F.; Burgos, R.; Boroyevich, D. Common mode circulating current control of interleaved three-phase two-level voltage-source converters with discontinuous space-vector modulation. In Proceedings of the 2009 IEEE Energy Conversion Congress and Exposition, San Jose, CA, USA, 20–24 September 2009; pp. 2801–2807. [Google Scholar] [CrossRef]
- Ye, Z.; Boroyevich, D.; Choi, J.-Y.; Lee, F.C. Control of circulating current in two parallel three-phase boost rectifiers. IEEE Trans. Power Electron. 2002, 17, 609–615. [Google Scholar] [CrossRef]
- Son, Y.-K.; Chee, S.-J.; Lee, Y.; Sul, S.-K.; Lim, C.; Huh, S.; Oh, J. Suppression of Circulating Current in parallel operation of three-level converters. In Proceedings of the 2016 IEEE Applied Power Electronics Conference and Exposition (APEC), Long Beach, CA, USA, 20–24 March 2016; pp. 2370–2375. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Z.; Xing, X.; Li, X.; Liu, X. Modeling and Suppression of Circulating Currents Among Parallel Single-Phase Three-Level Grid-Tied Inverters. IEEE Trans. Ind. Electron. 2022, 69, 12967–12979. [Google Scholar] [CrossRef]
- Panprasert, D.; Neammanee, B. The d and q Axes Technique for Suppression Zero-Sequence Circulating Current in Directly Parallel Three-Phase PWM Converters. IEEE Access 2021, 9, 52213–52224. [Google Scholar] [CrossRef]
- Stonier, A.A.; Murugesan, S.; Samikannu, R.; Krishnamoorthy, V.; Subburaj, S.K.; Chinnaraj, G.; Mani, G. Fuzzy Logic Control for Solar PV Fed Modular Multilevel Inverter Towards Marine Water Pumping Applications. IEEE Access 2021, 9, 88524–88534. [Google Scholar] [CrossRef]
- Han, W. Research on Control Strategy of Vienna Rectifier and its Parallel System. Master’s Thesis, Shandong University, Jinan, China, 2023. [Google Scholar]
- Mohapatra, S.R.; Agarwal, V. Model Predictive Controller with Reduced Complexity for Grid-Tied Multilevel Inverters. IEEE Trans. Ind. Electron. 2019, 66, 8851–8855. [Google Scholar] [CrossRef]
- Sarrafan, N.; Zarei, J.; Razavi-Far, R.; Saif, M.; Khooban, M.-H. A Novel On-Board DC/DC Converter Controller Feeding Uncertain Constant Power Loads. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 1233–1240. [Google Scholar] [CrossRef]
- Komurcugil, H.; Ozdemir, S.; Sefa, I.; Altin, N.; Kukrer, O. Sliding-Mode Control for Single-Phase Grid-Connected LCL Filtered VSI with Double-Band Hysteresis Scheme. IEEE Trans. Ind. Electron. 2016, 63, 864–873. [Google Scholar] [CrossRef]
- Xu, Q.; Blaabjerg, F.; Zhang, C. Finite-time Stabilization of Constant Power Loads in DC Microgrids. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 2059–2064. [Google Scholar] [CrossRef]
- Ahmad, A.; Ullah, N.; Ahmed, N.; Ibeas, A.; Mehdi, G.; Herrera, J.; Ali, A. Robust Control of Grid-Tied Parallel Inverters Using Nonlinear Backstepping Approach. IEEE Access 2019, 7, 111982–111992. [Google Scholar] [CrossRef]
- He, G.; Zhou, Z.; Zhang, G.; Li, G. Fixed-time fuzzy backstepping control strategy for islanded photovoltaic parallel inverters. Dianli Xitong Baohu Yu Kongzhi/Power Syst. Prot. Control 2023, 51, 147–156. [Google Scholar]
- Zhang, P.; Zhang, G.; Du, H. Circulating current suppression of parallel photovoltaic grid-connected converters. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1214–1218. [Google Scholar] [CrossRef]
- Wang, H.; Dong, Y.; He, G.; Song, W. Fixed-Time Backstepping Sliding-Mode Control for Interleaved Boost Converter in DC Microgrids. Energies 2024, 17, 5377. [Google Scholar] [CrossRef]
- Song, W.; Dong, Y.; He, G.; Zhou, Z. Fixed-Time Robust Fractional-Order Sliding Mode Control Strategy for Grid-Connected Inverters Based on Weighted Average Current. Energies 2023, 17, 4577. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiao, J.; Liu, J. Direct Power Control of PWM Rectifiers with Online Inductance Identification Under Unbalanced and Distorted Network Conditions. IEEE Trans. Power Electron. 2019, 34, 12524–12537. [Google Scholar] [CrossRef]
- Mehreganfar, M.; Saeedinia, M.H.; Davari, S.A.; Garcia, C.; Rodriguez, J. Sensorless Predictive Control of AFE Rectifier with Robust Adaptive Inductance Estimation. IEEE Trans. Ind. Informatics 2019, 15, 3420–3431. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Fu, J.; Li, Y.; Feng, J. Predictive Current Control for Permanent Magnet Synchronous Motor Based on Model Reference Adaptive System Parameter Identification. Electr. Mach. Control Appl. 2017, 44, 48–53. [Google Scholar]
- Song, W.; Ren, H.; Ye, H. Position Sensorless Control of Dual Three Phase Permanent Magnet Synchronous Motor Based on MRAS. Zhongguo Dianji Gongcheng Xuebao/Proc. Chin. Soc. Electr. Eng. 2022, 42, 11641173. [Google Scholar] [CrossRef]
- Liu, X.; Wang, X.; Fu, S.; Liang, L.; Huang, J. Inductance Identification of Permanent Magnet Synchronous Motor Based on Least Square Method. Electr. Mach. Control Appl. 2020, 47, 1–5. [Google Scholar] [CrossRef]
- Pasqualotto, D.; Rigon, S.; Zigliotto, M. Sensorless Speed Control of Synchronous Reluctance Motor Drives Based on Extended Kalman Filter and Neural Magnetic Model. IEEE Trans. Ind. Electron. 2023, 70, 1321–1330. [Google Scholar] [CrossRef]
- Gao, F.; Yin, Z.; Bai, C.; Yuan, D.; Liu, J. A Lag Compensation-Enhanced Adaptive Quasi-Fading Kalman Filter for Sensorless Control of Synchronous Reluctance Motor. IEEE Trans. Power Electron. 2022, 37, 15322–15337. [Google Scholar] [CrossRef]
- Hou, J.; Yang, Y.; Gao, T. A Variational Bayes Based State-of-Charge Estimation for Lithium-Ion Batteries Without Sensing Current. IEEE Access 2021, 9, 84651–84665. [Google Scholar] [CrossRef]
- Li, H.; Xu, H.; Xu, Y. Model prediction torque control of PMSM based on extended Kalman filter parameter identification. Electr. Mach. Control 2023, 19–30. [Google Scholar] [CrossRef]
- Yin, Z.; Li, G.; Zhang, Y.; Liu, J.; Sun, X.; Zhong, Y. A Speed and Flux Observer of Induction Motor Based on Extended Kalman Filter and Markov Chain. IEEE Trans. Power Electron. 2017, 32, 7096–7117. [Google Scholar] [CrossRef]





| Parameter | Value |
| RMS inverter output voltage, Vo | 220 V |
| DC bus voltage, Vdc | 600 V |
| Switching frequency, fsw | 10 kHz |
| Filter’s inductance, L | 3 mH |
| Filter’s capacitor, C | 75 μF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; He, G.; Zhou, Y.; Dong, Y.; Wang, H. A Fixed-Time Zero Sequence Circulating Current Suppression Strategy Based on Extended Kalman Filter. Energies 2025, 18, 408. https://doi.org/10.3390/en18020408
Li X, He G, Zhou Y, Dong Y, Wang H. A Fixed-Time Zero Sequence Circulating Current Suppression Strategy Based on Extended Kalman Filter. Energies. 2025; 18(2):408. https://doi.org/10.3390/en18020408
Chicago/Turabian StyleLi, Xiaopeng, Guofeng He, Yuanhao Zhou, Yanfei Dong, and Hang Wang. 2025. "A Fixed-Time Zero Sequence Circulating Current Suppression Strategy Based on Extended Kalman Filter" Energies 18, no. 2: 408. https://doi.org/10.3390/en18020408
APA StyleLi, X., He, G., Zhou, Y., Dong, Y., & Wang, H. (2025). A Fixed-Time Zero Sequence Circulating Current Suppression Strategy Based on Extended Kalman Filter. Energies, 18(2), 408. https://doi.org/10.3390/en18020408





