Optimal Allocation and Sizing of Battery Energy Storage System in Distribution Network Using Mountain Gazelle Optimization Algorithm

Abstract

This paper addresses the problem of finding the optimal position and sizing of battery energy storage (BES) devices using a two-stage optimization technique. The primary stage uses mixed integer linear programming (MILP) to find the optimal positions along with their sizes. In the secondary stage, a relatively new algorithm called mountain gazelle optimizer (MGO) is implemented to find the technical feasibility of the solution, such as voltage regulation, energy loss reduction, etc., provided by the primary stage. The main objective of the proposed bi-level optimization technique is to improve the voltage profile and minimize the power loss. During the daily operation of the distribution grid, the charging and discharging behaviour is controlled by minimizing the voltage at each bus. The energy storage dispatch curve along with the locations and sizes are given as inputs to MGO to improve the voltage profile and reduce the line loss. Simulations are carried out in the MATLAB programming environment using an Australian radial distribution feeder, with results showing a reduction in system losses by 8.473%, which outperforms Grey Wolf Optimizer (GWO), Whale Optimization Algorithm (WOA), and Cuckoo Search Algorithm (CSA) by 1.059%, 1.144%, and 1.056%, respectively. During the peak solar generation period, MGO manages to contain the voltages within the upper boundary, effectively reducing reverse power flow and enhancing voltage regulation. The voltage profile is also improved, with MGO achieving a 0.348% improvement in voltage during peak load periods, compared to improvements of 0.221%, 0.105%, and 0.253% by GWO, WOA, and CSA, respectively. Furthermore, MGO’s optimization achieves a reduction in the fitness value to 47.260 after 47 iterations, demonstrating faster and more consistent convergence compared to GWO (47.302 after 60 iterations), WOA (47.322 after 20 iterations), and CSA (47.352 after 79 iterations). This comparative analysis highlights the effectiveness of the proposed two-stage optimization approach in enhancing voltage stability, reducing power loss, and ensuring better performance over existing methods.

1. Introduction

Though renewable energy sources bring complexity due to the intermittent nature of their power production in the modern power system, the adoption of renewable resources is increasing day by day. This is due to their environmental benefits over traditional technologies. As renewables are completely dependent on weather conditions, their outputs are uncertain and variable, which makes bi-directional power flow possible across the grid. The existing system is experiencing possible voltage increases during daytime from photovoltaics (PVs), which it has not been designed to tackle [1]. Battery energy storage (BES) technologies can provide flexibility to maintain RESs and loads by charging and discharging operations [2]. Moreover, these devices can be regarded as potential solutions for controlling voltages in distribution systems [3]. BES can also provide different ancillary services such as frequency control [4], peak shaving [5], line loss reduction [6], and peak load shifting [7]. However, most available BES technologies are costly, having their own sustainable challenges. Therefore, to provide reliable and stable grid operation, it is necessary to optimize storage capacity to achieve the maximum benefits from RESs. Moreover, both the size and the locations need to be optimized so that BES technologies can provide the most support to the grid by minimizing energy losses and improving the voltage profile. Researchers have suggested numerous algorithms and strategies to optimally place energy storage along with their optimum sizing due to their evident advantages. Clustering and sensitivity analysis is performed for the optimal placement and sizing of BESs and optimal locations are found irrespective of the clustering sizes [8]. While the method is claimed to be independent of clustering size, this could also be a limitation if a more granular or nuanced analysis of the BES placement would have improved performance. The absence of reliance on clustering sizes suggests that the proposed method does not consider all possible fine-tuning opportunities that could enhance BES placement and sizing in specific scenarios. A strategy was developed to obtain the optimal size and locations of energy storage in the microgrid to minimize the annual electricity cost [9]. The paper likely assumes ideal conditions for the energy storage systems. In reality, the cost of ESS, as well as issues like battery degradation and lifespan, may influence the optimal allocation. These factors should be incorporated to improve the robustness of the model. A two-stage optimization algorithm is proposed for the optimal allocation of BESs by using receding horizon control and a benders decomposition algorithm [10]. By combining the placement and sizing of batteries with real-time control strategies, the authors offer a solution that not only optimizes the design of battery storage but also enhances its operation over time. The ability to update storage management decisions at each time step improves grid flexibility and efficiency. The use of Receding Horizon Control (RHC), while advantageous for dynamic decision-making, can be computationally expensive. The real-time optimization required for each time step might limit the practical application of the approach in large, complex grids, unless efficient algorithms or hardware solutions are utilized. Researchers have proposed a mitigation strategy for overvoltage and undervoltage in distribution networks using energy storage [11]. Each energy storage is connected to the rooftop PV system and an iterative approach is followed for dispatching the battery based on local information. A proper selection of charging and discharging rate is necessary for the effective operation of BESs within distribution network. These analytical approaches cannot provide effective solutions for complex systems. Metaheuristic algorithms can be employed to solve the complex optimization problems. A multilayer optimization algorithm based on genetic algorithm (GA) is proposed for the optimal sizing and allocation of 25 BESs in a distribution network [12]. The main objective is to minimize the power losses and voltage deviation. They have proposed a relationship between BES locations and capacity variables and voltage index. The scenarios used to assess BESS allocation are based on local load and generation conditions. However, there is a risk that the model may be overfitted to these specific scenarios, which may not generalize well to other conditions or broader system contexts. Mixed integer linear programming along with a stochastic algorithm are proposed to obtain the optimal sizes and locations of BESs by minimizing the system cost and maximizing energy arbitrage [13]. Given the already complex nature of energy storage optimization models, the need for new computationally tractable solution techniques may lead to an increase in computational time and resource requirements, which could reduce the feasibility of applying the model in larger-scale systems or for real-time operations. The genetic algorithm has also been proposed in [14,15] to minimize network cost. A short literature review on the optimized variables of BESs based on different algorithms is summarized in

Table 1. A literature review on optimal allocation and sizing of BESs.

Ref.	Optimized Variables	Algorithms	Objective Function
[16]	Size + Location	Modified non-dominated sorting genetic algorithm (NSGA)	Minimize power loss and improve voltage profile
[17]	Size + Location + Scheduling	Mixed integer linear programming (MILP)	Minimize power loss
[8]	Number + Size + Location	Voltage sensitivity analysis	Improve voltage profile
[18]	Size + Location	Whale optimization algorithm (WOA)	Minimize power loss
[19]	Size + Location	Improved Cayote optimization algorithm (ICOA)	Minimize power loss
[20]	Location	Multi-objective evolutionary algorithm (MOEA)	Minimize energy not supplied, load loss, load cost, voltage drop.
[21]	Size + Location	Improved non-dominated sorting genetic algorithm-II (NSGA-II)	Minimize power loss and voltage fluctuations
[22]	Location	Voltage sensitivity index factor (VSIF)	Minimize annual energy loss and overvoltage
[23]	Size + Location	Binary Grey wolf optimization (BGWO)	Improve voltage and frequency stability
[24]	Size + Location	Genetic algorithm(GA)	Minimize cost
[25]	Location	Genetic algorithm (GA)	Minimize cost
[26]	Size + Location	Genetic algorithm (GA)	Minimize power loss and cost
[27]	Size + Location	Hybrid multi-objective particle swarm optimization	Minimize cost and improve voltage profile
[28]	Size + Location	Enhanced opposition firefly algorithm (EOFA)	Minimize power loss and voltage deviation
[29]	Size	Improved bat algorithm (IBA)	Minimize cost
[30]	Location	Artificial bee colony algorithm (ABCA)	Minimize power loss, voltage deviation, line loading
[31]	Size	Improved harmony search algorithm (IHSA)	Minimize cost

.

2. Contributions

This paper presents a novel approach for optimizing the placement, sizing, and operation of Battery Energy Storage Systems (BESSs) in distribution networks, addressing key technical challenges such as voltage regulation and power loss reduction. While the existing literature has primarily focused on BESS sizing and placement, it often neglects the optimization of charging and discharging strategies, particularly in dynamic grid conditions. This work aims to fill this gap by offering a more robust method for improving the reliability and efficiency of the distribution network.

The key contributions of this research are as follows:

• This study introduces the Mountain Gazelle Optimizer (MGO), a novel metaheuristic optimization technique inspired by the behaviour of mountain gazelles, to solve the BESS placement and sizing problem in distribution networks. The algorithm effectively identifies optimal BES locations and sizes while considering real-time grid conditions.
• A hybrid approach combining MGO with MILP is proposed to address the technical constraints of BES optimization, such as power balance and voltage regulation. This integration ensures the solution is both optimal in terms of BES sizing and placement as well as feasible from an operational standpoint within the distribution network.
• Unlike existing studies that focus on static placement and sizing, this research incorporates dynamic control of BES charging and discharging strategies over a 24 h period. The proposed strategy mitigates reverse power flow during peak solar generation, improves voltage regulation, and reduces system losses during peak load periods.
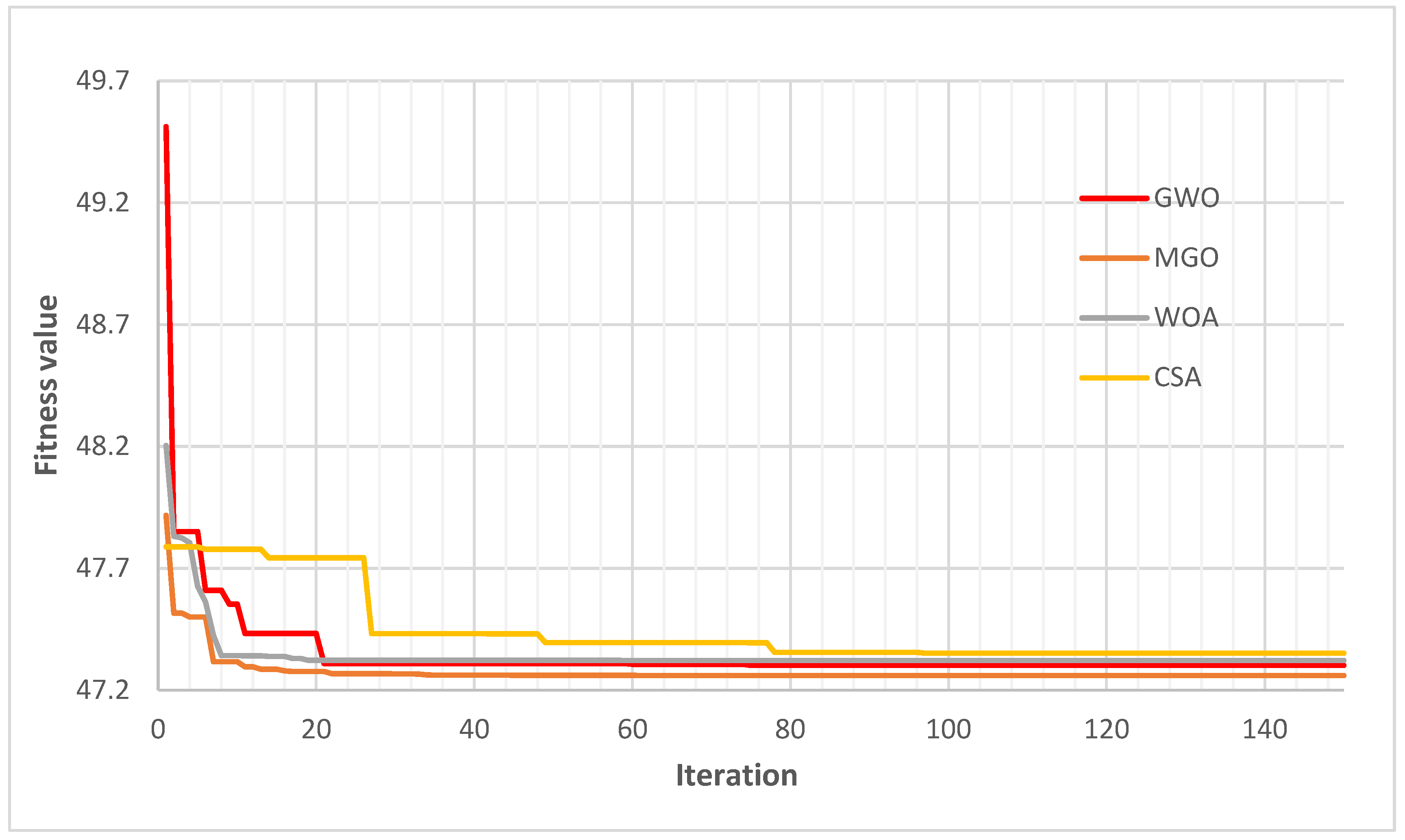
• Although the MGO algorithm was introduced in 2022 [32], it has not yet been applied to BES placement and sizing problems in the literature. The implementation of the MGO is relatively straightforward, necessitating only fundamental mathematical programming skills to adapt the algorithm to a variety of optimization problems. The results presented demonstrate that MGO outperforms other established optimization algorithms, such as Grey Wolf Optimizer (GWO) and Whale Optimization Algorithm (WOA), in terms of convergence speed and overall optimization performance, offering a more effective solution for large-scale, dynamic distribution networks.

These contributions significantly advance the field of distribution network management and energy storage integration by providing a comprehensive approach to BES optimization, which not only focuses on optimal placement and sizing but also integrates dynamic charging and discharging strategies to enhance grid reliability and performance.

3. Mathematical Modelling

This section of the article formulates the problem regarding the optimal allocation and sizing of battery energy storage systems in electrical distribution networks as a mixed integer linear programming (MILP) model. The integer variables represent the locations where BESs will be allocated, and the real variables are their respective capacities.

3.1. Objective Function

The objective function consists of the sum of two functions: one of them represents the voltage deviation ($f_1$) and the other one represents the line losses ($f_2$). These objective functions are as follows:

$$f_1=\sum _{t=1}^{24}\sum _{i=1}^M{(V_r-V_{i,t})}^2$$

(1)

$$f_1=\sum _{t=1}^{24}\sum _{i=1}^M{\left|I_{i,t}\right|}^2{R}_i$$

(2)

where $V_r$ is the reference voltage and $V_i$ is the voltage at $i$th bus, $M$ is the number of buses; $I_i$ is the current at $i$th line, $R_i$ is the resistance of $i$th line, $K$ is the number of lines. $V_i$ and $I_i$ are the function of line parameters, loads, PVs outputs and charging/discharging scheduling of BES, and can be written as:

$$\left[V_{i,t} I_{i,t}\right]=f(R,X,P_{L,t},Q_{L,t},P_{PV,t},P_{BES,t})$$

(3)

where $R$ and $X$ are the vectors of line resistance and reactance, respectively; $P_L$, $Q_L$ are vectors of active and reactive load power, respectively; $P_{PV}$ is the real power of PV and $P_{BES}$ is the real power of BES. The inverters for PV and BES are considered to supply only real powers. Therefore, Equation (3) can be solved by a load flow programme.

The overall objective function can be defined as:

$$\sum _{min}f=f_1+f_2$$

(4)

The two functions, $f_1$ and $f_2$, involve squared terms, which make them nonlinear functions. Again, they have quadratic terms, which make them convex. Metaheuristic algorithms can deal with these complex, nonlinear, convex, and multidimensional problems [33].

3.2. Set of Constraints

Determining the locations and sizes of battery energy storage systems in radial distribution networks requires various constraints related to the network’s physical operation. Some of these have to do with active power balance, voltage grid regulation characteristics, thermal characteristics, and the sizes of BES devices. These constraints are defined below:

$$P_{S,t}+\sum _{i=1}^M{P}_{L,i,t}+\sum _{i=1}^{M_{PV}}{P}_{PV,i,t}+\sum _{i=1}^{M_{BES}}{P}_{BES,i,t}+P_{loss,t}=0$$

(5)

$$Q_{S,t}+\sum _{i=1}^M{Q}_{L,i,t}+\sum _{i=1}^{M_{PV}}{Q}_{PV,i,t}+\sum _{i=1}^{M_{BES}}{Q}_{BES,i,t}+Q_{loss,t}=0$$

(6)

$$V_{min}\le \left|V_{i,t}\right|\le V_{max} \mathrm{where} i=1\dots M$$

(7)

$$0\le I_{i,t}\le I_{max} \mathrm{where} i=1\dots K$$

(8)

where $P_S$ is the real power of the substation; $M_{PV}$ is the number of allocated PVs; $M_{BES}$ is the number of BESs; $P_{PV,max}$ is the allowable maximum PV output power; $Q_S$ is the reactive power of the substation; $Q_L$, $Q_{PV}$ and $Q_{BES}$ are the reactive power from loads, PV system and energy storage; $Q_{loss}$ is the reactive power loss; $V_{min}$ and $V_{max}$ are the allowable minimum and maximum voltage; $I_{max}$ is the allowable maximum line current.

The constraint equations can be interpreted as follows: Equation (5) defines the power balance constraints at each bus of the network for each period. These are also known as power flow constraints [34]. Inequality constraints (6) and (7) refer to the allowable voltage and current limits imposed by the regulatory entities for the operation of distribution network.

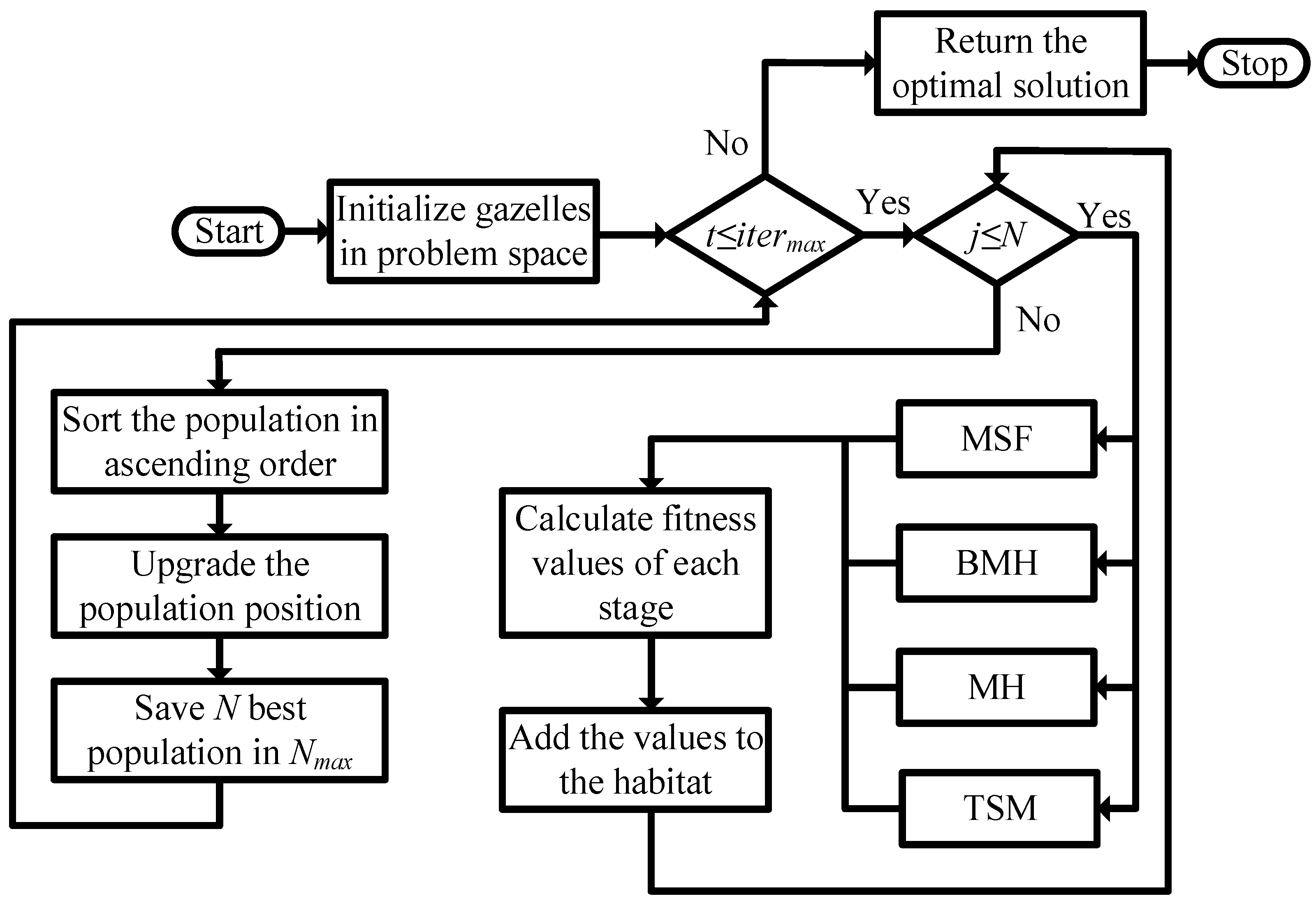
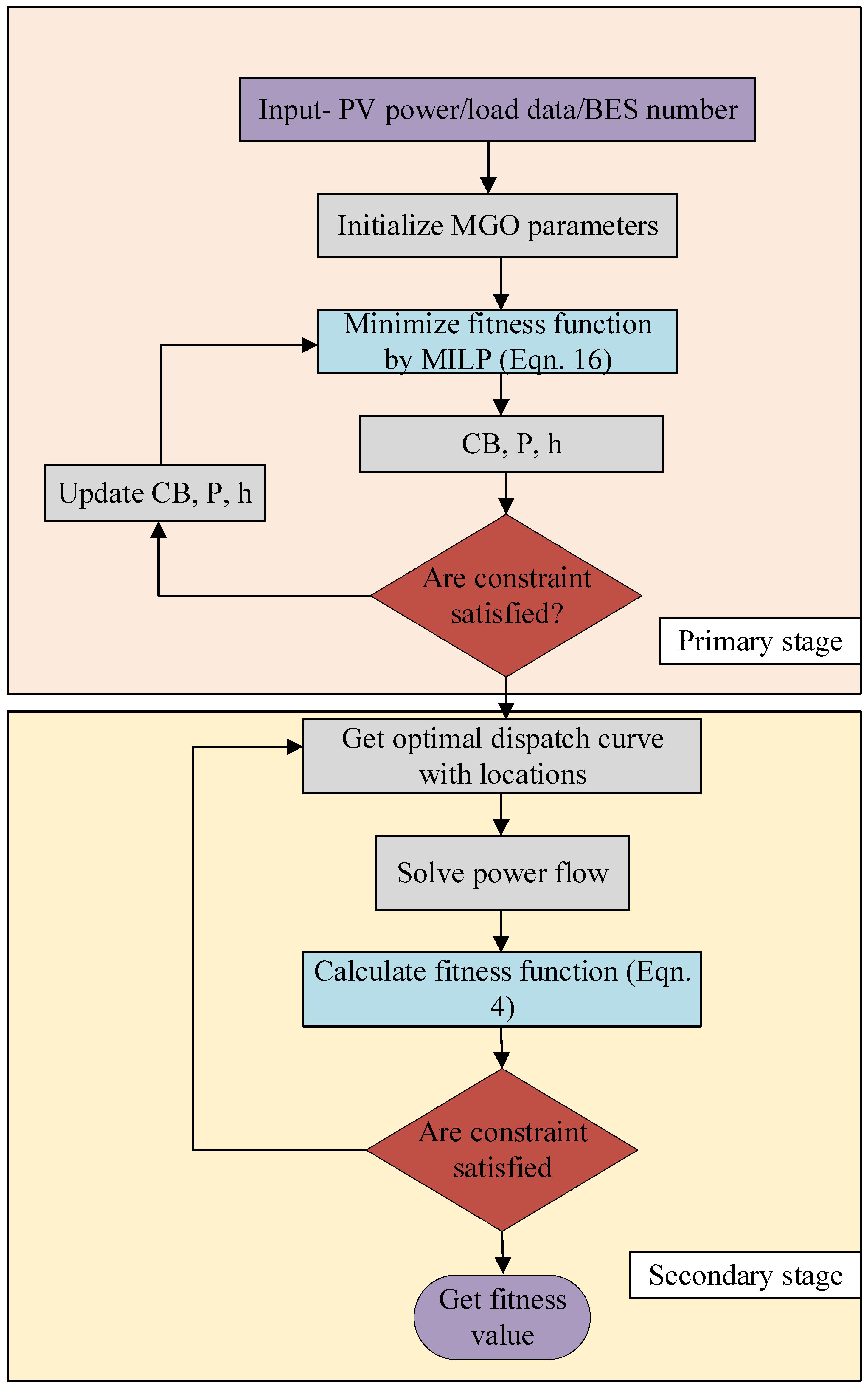
3.3. Proposed Solution Method

3.3.1. Primary Stage: MILP

A battery energy system consists of an inverter and a battery pack. The overall efficiency of BES (${\eta }_{BES}$) can be calculated as [35]:

$${\eta }_{BES}={\eta }_{INV}\ast {\eta }_B$$

(9)

where

${\eta }_{INV}$ = Inverter efficiency

${\eta }_B$ = Battery efficiency

In general, the charging and discharging efficiency of the battery is considered to be the same. Then, the battery efficiency can be written as [35]:

$${\eta }_B=\sqrt{{\eta }_r}$$

(10)

where ${\eta }_r$ is the round-trip efficiency. Again, storage efficiency, which represents the relation between energy retrieved from the battery and the energy supplied to the battery, is also related to the battery efficiency. However, storage efficiency represents a higher value for a short time horizon [36]. That is why it is neglected here.

Table 2. BES efficiencies for different technologies.

Battery Technology	${\mathit{\eta }}_{\mathit{I}\mathit{N}\mathit{V}}$	${\mathit{\eta }}_{\mathit{B}}$	${\mathit{\eta }}_{\mathit{B}\mathit{E}\mathit{S}}$
Lead-acid	>0.97	0.9220	0.8943
Lithium-ion	>0.97	0.9487	0.9202
LiFePO4	>0.97	0.9747	0.9454

shows a summary of energy storage efficiency for three different technologies. The inverter efficiency is greater than 97% for each of these [37]. A battery manufactured with LiFePO₄, or higher technologies, can achieve battery efficiency of 0.9747 whereas Lead-acid and Lithium-ion can achieve only 0.9220 and 0.9487, respectively. Therefore, LiFePO₄ or higher technologies can achieve higher overall efficiency than the other technologies.

Charging/Discharging Strategy

When the power generated from the PV system ($P_{PV}$) is greater than the load power ($P_L$), the excess power $\left(P_{chr}\right)$ is used to charge the battery which can be represented as [38]:

$$P_{chr}(t)={\displaystyle \frac{({SOC}_{t+1}-{SOC}_t)C_B}{{\eta }_{BES}\mathsf{\Delta }t}}$$

(11)

where $\mathsf{\Delta }t$ is the time interval. In this study, $\mathsf{\Delta }t=1 \mathrm{h}$ is considered. $SOC$ is the state of charge of the battery and $C_B$ is the battery capacity in kWh.

When there is no PV or it generates a very small amount of energy, the BESs start to be discharged by supplying the demand. The discharging power ($P_{dch}$) can be expressed as [38]:

$$P_{dch}(t)={\displaystyle \frac{({SOC}_t-{SOC}_{t+1})C_B{\eta }_{BES}}{\mathsf{\Delta }t}}$$

(12)

The optimal battery dispatch curve is determined by minimizing the following objective function:

$$minimize\sum _{h\in N}\sum _{t=1}^{24}\left(P_{dch,h}\right(t)-P_{chr,h}(t\left)\right)V_{i,h}$$

(13)

$$\sum _{h\in N}\sum _{t=1}^{24}{\displaystyle \frac{({SOC}_{t,h}-{SOC}_{\left(t+1\right),h})C_{B,t,h}}{\mathsf{\Delta }t}} \left({\eta }_{BES}+{\displaystyle \frac{1}{{\eta }_{BES}}}\right).V_{t,h}$$

(14)

Matrix Formulation

To solve the optimization problem by mixed integer linear programming, it is important to formulate the function in matrix notation. The solution vector is represented by:

$$x=\left[C_B;P;h;\right]$$

(15)

The vector co-efficient for the objective function is represented by:

$$f=\left({\eta }_{BES}+{\displaystyle \frac{1}{{\eta }_{BES}}}\right).{\displaystyle \frac{1}{\mathsf{\Delta }t}}.V_{t,\mathrm{h}}$$

(16)

Therefore, the MILP problem can be written in matrix notation as

$$\begin{gathered} \underset{n}{\min }{f}^{T}x \\ subject to \left\{\begin{array}{c}Ax\le b\\ A_{eq}x=b_{eq}\\ l_b\le x\le u_b\end{array}\right. \end{gathered}$$

(17)

where A and b represent inequality constraint; $A_{eq}$ and $b_{eq}$ are the equality constraints; $l_b$ and $u_b$ are the lower and upper bound of decision variables.

The constraints for the MILP problem are as follows:

$$0\le {st}_{chr}+{st}_{dch}\le 1$$

(18)

$$0\le P_{chr}\le {st}_{chr}{P}_{max}$$

(19)

$$0\le P_{dch}\le {st}_{dch}{P}_{max}$$

(20)

$${SOC}_{min}\le SOC\le {SOC}_{max}$$

(21)

$${SOC}_{t=24}={SOC}_{in}$$

(22)

Equation (17) represents charging (${st}_{chr}$) and discharging (${st}_{dch}$) state variables which are binary and also cannot happen simultaneously. Equations (18) and (19) impose limits on the charging and discharging power of the battery energy storage system (BESS), ensuring that they do not exceed the maximum BESs power ($P_{max}$). The state of charge should be limited by its minimum (${SOC}_{min}$) and maximum (${SOC}_{max}$) value and it should return to its initial value after the end of $t$ period.

3.3.2. Secondary Stage

The Mountain Gazelle Optimization (MGO) algorithm is a newly developed meta heuristic algorithm proposed by Abdollahzadeh in 2022 [32]. This algorithm takes inspiration from the social and group behaviour of mountain gazelles in the wild and performs the optimization process based on the four aspects of gazelles’ lives: territory solitary males, maternity herds, bachelor male herds, and migration to search for food. The mathematical formulation of these stages is described in the following sections:

Territory Solitary Males (TSM)

Male mountain gazelles establish solitary territories upon reaching adulthood and gaining strength. Adult males fiercely defend these territories and engage in battles over them or for possession of females. Meanwhile, younger males attempt to occupy these territories or attract females, while the adult males focus on protecting their established environments. A mathematical model depicting the territory of an adult male is given below [32]:

$$TSM={male}_{gazelle}-\left|{\phi }_1\ast V_c-{\phi }_2\ast X\left(t\right)\ast G\right|\ast {Cof}_r$$

(23)

$$V_c=X_n\ast ⌊a_1⌋+POP\ast ⌈a_2⌉, n=\left\{⌈{\displaystyle \frac{N}{3}}⌉\dots ..N\right\}$$

(24)

$$G=N_1\left(D\right)\ast \exp (2-iter\ast ({\displaystyle \frac{2}{{iter}_{max}}}))$$

(25)

$${Cof}_r=\left\{\begin{array}{c}\left(b+1\right)+a_3\\ b\ast N_2\left(D\right)\\ a_3\left(D\right)\\ N_3\left(D\right)\ast {N_4\left(D\right)}^2\ast cos(\left(a_4*2\right)\ast N_3(D\left)\right)\end{array}\right.$$

(26)

$$b=-1+iter\ast ({\displaystyle \frac{-1}{{iter}_{max}}})$$

(27)

where ${male}_{gazelle}$ denotes the position vector of the best global solution; ${\phi }_1$ and ${\phi }_2$ are random integers ranging from 1 or 2; $V_c$ denotes the co-efficient vector for a young male; ${Cof}_r$ is arbitrarily selected co-efficient vector which is updated in each iteration and increases the searching capability; $X\left(t\right)$ denotes the initial position of the gazelle; $X_n$ is a random solution of young male in the range of $n$; $POP$ is the average number of population where $⌈{\displaystyle \frac{N}{3}}⌉$ were selected randomly; $N$ represents the total number of gazelles; $a_1$, $a_2,$ $a_3$ and $a_4$ are randomly selected values ranging from 0 to 1; $N_1$ represents the random number drawn from the standard deviation; $N_2$, $N_3$, and $N_4$ denote the dimensions of the problem and are randomly selected numbers; $iter$ and ${iter}_{max}$ are the current and maximum iterations, respectively.

Maternity Herds (MH)

Maternity herds play an essential role in the life cycle of mountain gazelles, as these types of packs give birth to solid male gazelles. Male gazelles can also play a role in the delivery of gazelles and young males trying to possess females. This behaviour can be formulated as follows [39]:

$$MH=\left(V_c+{Cof}_{1,r}\right)+\left({\phi }_3\ast {male}_{gazelle}-{\phi }_4\ast X_{rand}\right)\ast {Cof}_{2,r}$$

(28)

where ${\phi }_3$ and ${\phi }_4$ are randomly generated integers 1 or 2; ${Cof}_{1,r}$ and ${Cof}_{2,r}$ are randomly selected co-efficient vectors calculated from Equation (4); $X_{rand}$ denotes the randomly selected position vector of a gazelle.

Bachelor of Male Herds (BMH)

As male gazelles mature, they tend to establish territories and seek possession of female gazelles. During this period, young male gazelles enter into competition with adult males for territory and control of females, often resulting in considerable violence. This behaviour can be articulated mathematically as follows [39]:

$$BMH=\left(X\left(t\right)-F\right)+\left({\phi }_5\ast {male}_{gazelle}-{\phi }_6\ast V_c\right)\ast {Cof}_r$$

(29)

$$F=\left(\left|X\left(t\right)\right|+\left|{male}_{gazelle}\right|\right)\ast (2\ast a_5-1)$$

(30)

where $X\left(t\right)$ represents the position vector of gazelle in current iteration; ${\phi }_5$ and ${\phi }_6$ are randomly selected integers from 1 or 2; $a_5$ is the random number ranging from 0 to 1.

Migration in Search of Food (MSF)

Mountain gazelles cover large distances in search of food and are constantly on the lookout for new sources. They are known for their impressive running speed and powerful jumping ability. As a result, they often travel great distances to find food and migrate. The following equation is used to formulate this behaviour as follows [39]:

$$MSF=\left(ub-lb\right)\ast a_6+lb$$

where $ub$ and $lb$ are upper and lower limits of the optimization problem; $a_6$ is the randomly generated number ranging from 0 to 1. The flowchart of the MGO is shown in Figure 1.

During the secondary stage, the power flow is solved by the Newton-Raphson method, which is used by OpenDSS software [40]. This allows the calculation of voltages and system loss at each hour and evaluation of the constraints. After the locations and sizing of the BESs are integrated into the grid from the primary stage, Equation (1) is evaluated by MGO, keeping all the constraints satisfied. The pseudocode for the secondary stage is shown in Algorithm 1.

Algorithm 1: Secondray stage algorithm: MGO

Data: Data reading and assignment of MGO parameters    for $t$ = 1:24 do Load the power demanded by the loads for period $t$; Load the optimal dispatch curve of the energy storage during period $t$; Solve the power flow for period $t$ by Newton Raphson method in OpenDSS software. Calculate the fitness function for period $t$ by using Equation (4); Evaluate the constraint from Equations (5)–(7) for period $t$;    end    Report the best fitness value

To summarize the proposed primary-secondary methodology, a flow diagram is presented in Figure 2.

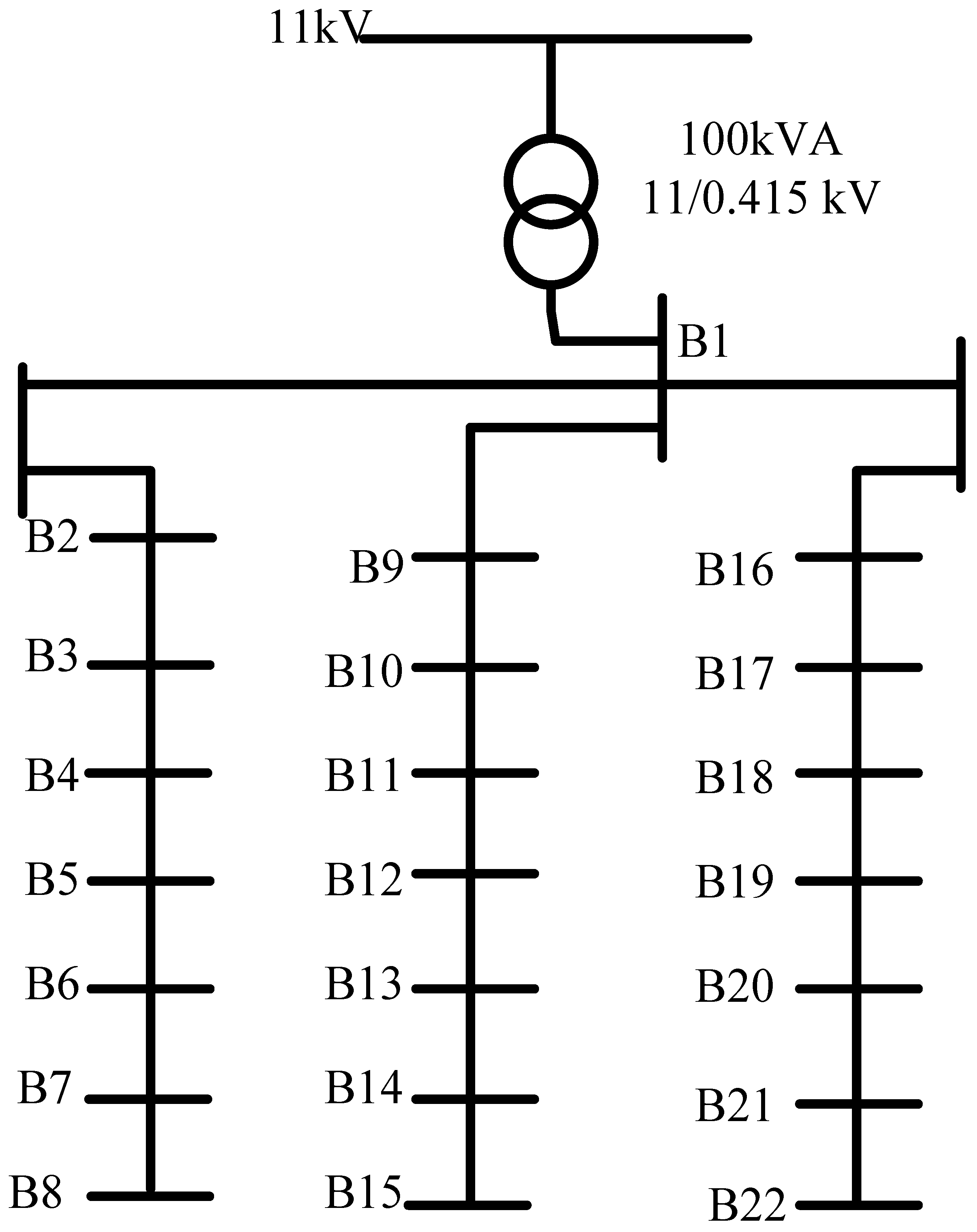
4. Simulation Test System

To verify the efficiency of the proposed solution methodology for placing and sizing battery energy storage systems in radial distribution systems, an Australian distribution network is employed. The electrical configuration of this system is presented in Figure 3. The system has an 11 kV voltage at the substation bus and a 415 kV at the distribution side. The capacity of the transformer is 200 kVA. To connect the buses, a moon conductor has been used. A total of 55 houses are connected to the system and PV is also connected to the buses where the load is connected. Each PV system is equipped with 6 kW. The time resolution of the load and the PV power is 1 h.

Figure 4 shows the transformer loading over a 24 h period with PV and without PV integration. The transformer operates with a consistent loading pattern fluctuating between −97 kW to −167 kW when there is no PV. However, there is a noticeable increase in transformer loading from 8 a.m. to 6 p.m., peaking at 169 kW at around 11 a.m. This peak indicates that PV generation is causing reverse power flow due to excess generation being fed back to the grid.

To validate the proposed solution methodology, the optimization procedure is implemented in MATLAB’s 2023b version on a computer with an Intel Core i9-13900@2.6 GHz and 64.0 GB of RAM running the 64-bit version of Microsoft Windows. In this simulation, 30 search agents and 150 iterations are set to evaluate the performance of MGO, GWO, WOA, and CSA.

Table 3. A comparative analysis among base case scenario and GWO, WOA, CSA, and the proposed methodology.

Method	Buses	Sizes		Fitness Value
		Capacity (kW)	Capacity (kWh)
Base				49.0101
GWO	[19 8 21]	[9.5 2.78 20]	[40 15.3 40]	47.302
WOA	[19 8 16]	[13.36 1.96 0.14]	[40 7.51 38.07]	47.322
CSA	[19 19 16]	[9.4 6.34 7.61]	[40 21.45 16.67]	47.352
Proposed methodology	[19 8 21]	[13.38 15.26 8.98]	[40.00 30.19 40.00]	47.260

shows a comparison among the base case scenario, grey wolf optimization (GWO), whale optimization algorithm (WOA), and the proposed methodology for an Australian distribution configuration for 24 h. Batteries are placed concurrently within the optimization framework.

The optimal dispatch curves and SOC of the battery energy storage systems over a 24 h period are exhibited in Figure 5 and Figure 6, respectively. Bat 1 starts charging around 9 a.m. and peaks at 13 kW. Bat 1 stops charging at 12 p.m., when SOC reaches 1. It starts discharging from 6 p.m. and stops discharging at 8 p.m., when SOC reaches the minimum value 0.2. Bat 2 is charged for only two hours, peaking at 15 kW, and is also discharged for two hours. Bat 2 starts charging at 9 a.m. and continues to charge until 2 p.m. It starts discharging at 6 p.m. and continues to discharge until 10 p.m. A few observations can be made from the above discussion:

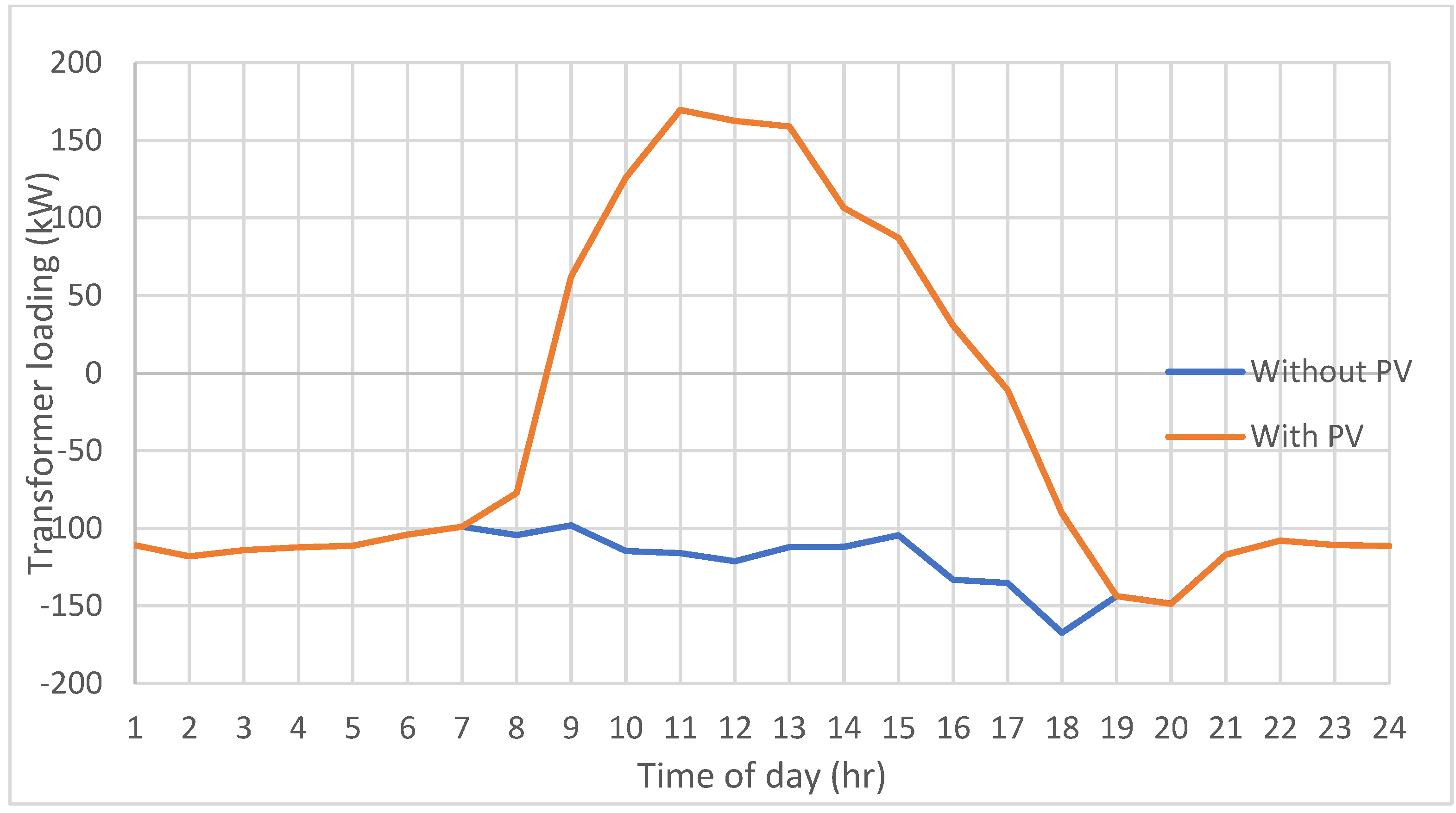
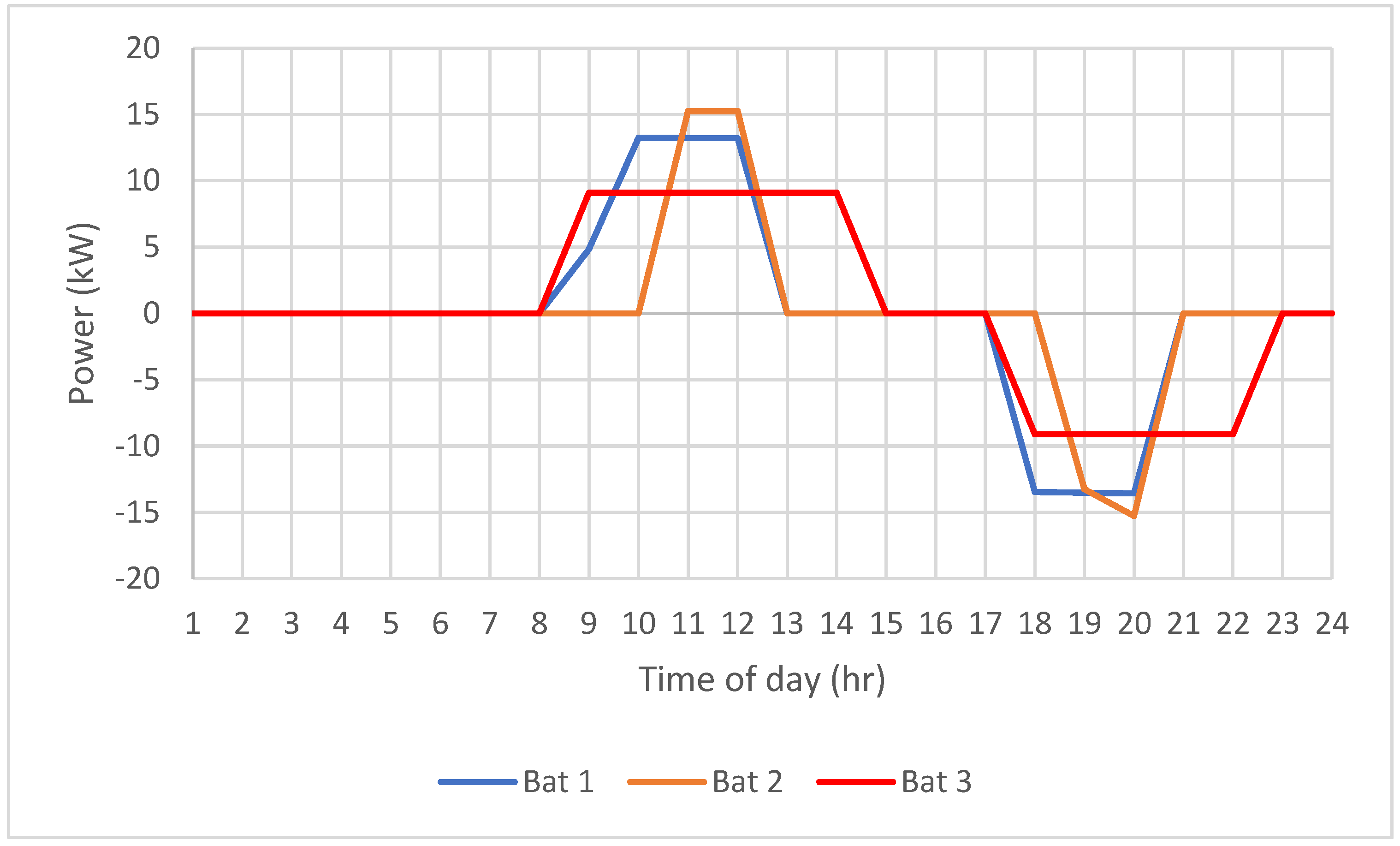
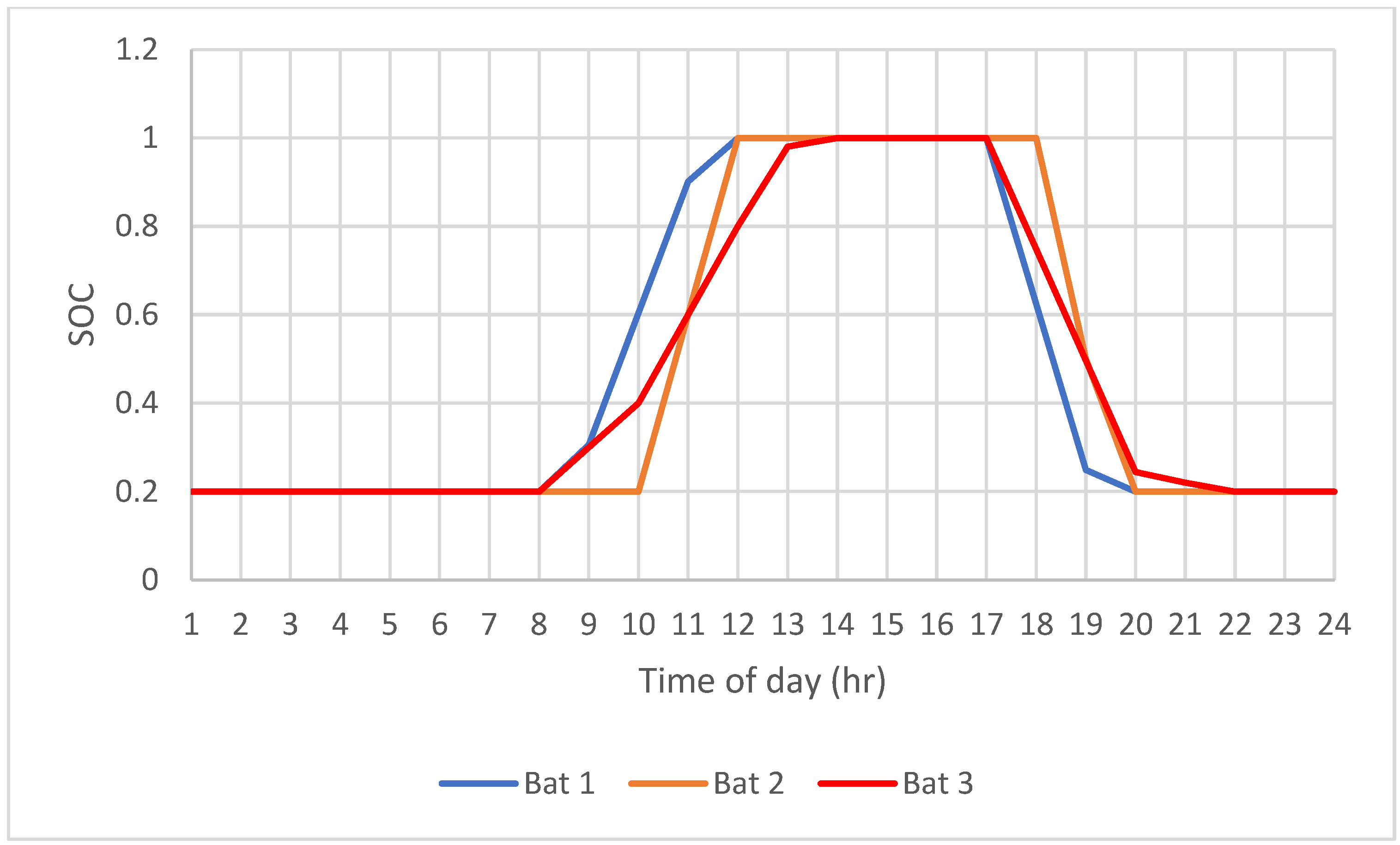
• The batteries are charging in such a way that they charge during peak PV generation to stop the reverse power flow to the grid.
• The batteries collectively discharge during the evening peak load period to support the grid.
• While Bat 1 and Bat 2 have similar profiles of charging and discharging heavily during peak PV and peak demand period, Bat 3 has a more uniform profile.

The bus voltages for a 24 h period for each algorithm are presented in Figure 7.

In the base case scenario at 11 a.m., the voltage at bus number 21 is recorded at 1.0538 p.u. Upon applying the MGO algorithm, the voltage decreases to 1.0463 p.u., resulting in a reduction of 0.712%. Additionally, the voltage values obtained through the WOA, GWO, and CSAs are 1.0505 p.u., 1.0491 p.u., and 1.0488 p.u., respectively. At bus number 21, the percentage reductions in voltages are as follows: 0.313% with the WOA, 0.446% with the GWO algorithm, and 0.475% with the CSA. Similarly, at bus number 19 at 11 a.m., the voltage in the base case scenario is 1.0542 p.u. After applying the MGO, GWO, WOA, and CSAs, the voltages are reduced to 1.0467 p.u. for the MGO and 1.0509 p.u., 1.0495 p.u. and 1.0492 p.u. for the WOA, GWO, and CSAs, respectively, resulting in consistent reductions of 0.712%, 0.313%, 0.446%, and 0.475%. Though the voltage is reduced by 0.313% by WOA, it could not keep the voltages within the upper boundary, which suggests the algorithm might become stuck in local minima. During the peak load period at 8 p.m., the voltage at bus number 8 is recorded at 0.9495 p.u. With the support of energy storage systems dispatching power to the grid, the voltage is improved to 0.9528 p.u. with the MGO algorithm, leading to an improvement of 0.348%. The GWO, WOA, and CSAs yield voltage improvements to 0.9516 p.u., 0.9505 p.u., and 0.9519 p.u., corresponding to improvements of 0.221%, 0.105%, and 0.253%, respectively. Overall, these results indicate that all optimization algorithms except WOA demonstrate a consistent ability to manage voltage levels effectively across various scenarios.

By allocating BESs at optimal locations at their optimal capacities by MGO, the system losses are reduced, as is shown in Figure 8. The total system loss for the base case scenario for 24 h is 49.0701 kW. A reduction in system loss of 8.473% is achieved by MGO. Similarly, GWO, WOA, and CSA can reduce the system loss by 7.414%, 7.329% and 7.417%, respectively.

From the above discussion, it can be concluded that the BESs can minimize the reverse power flow during the high PV generation and also support the grid during peak load period by maintaining the voltage profile within acceptable limits and reducing the system losses while placed at optimal locations and optimal sizing.

The convergence curves of different optimization algorithms are shown in Figure 9. The x-axis shows the number of iterations and the y-axis shows the best fitness value found by the algorithms. The grey wolf optimization algorithm starts with a high fitness value of 49.512 and reaches a stable point of 47.302 after 60 iterations.

The whale optimization algorithm also starts with a high fitness value around 48.203 and quickly reduces to 47.322 within 20 iterations. It converges relatively quickly, suggesting it might be becoming trapped in a local minimum. This finding is also consistent with the results found from WOA discussed in the above section. CSA shows a steplike pattern, suggesting slower convergence and possible oscillations in finding the optimum solution. This algorithm stabilizes at 47.352 after 79 iterations. MGO shows consistent improvement over the iterations and achieves the lowest fitness value of 47.260 after 47 iterations indicating superior performance than other algorithms.

5. Conclusions

This study addresses the optimal siting and sizing of Battery Energy Storage Systems (BESSs) in distribution networks to minimize system losses and improve voltage profiles. The proposed two-stage optimization approach utilizes Mixed Integer Linear Programming (MILP) in the primary stage for determining optimal locations and sizes of BESSs, followed by the application of the Mountain Gazelle Optimization (MGO) algorithm in the secondary stage to optimize daily operation for voltage regulation and system loss reduction.

The key findings of this study are summarized as follows:

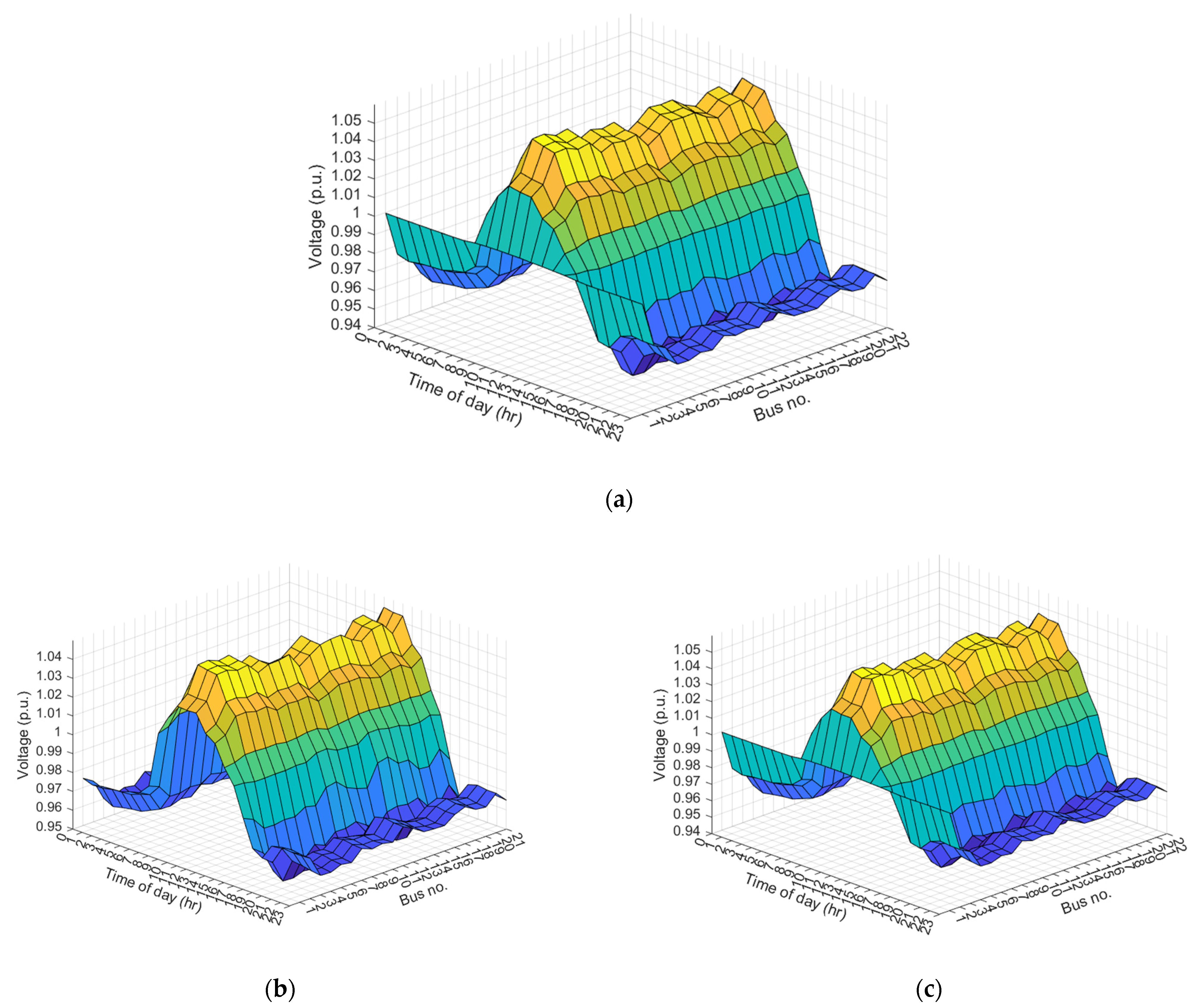
• The proposed methodology significantly improves the voltage profile across the network. For instance, at the peak load period (8 p.m.), the voltage at bus number 8 improves from 0.9495 p.u. (base case) to 0.9528 p.u. using the MGO algorithm, representing a 0.348% improvement. This improvement is superior to that achieved by other optimization algorithms, such as Grey Wolf Optimizer (GWO), Whale Optimization Algorithm (WOA), and Cuckoo Search Algorithm (CSA).
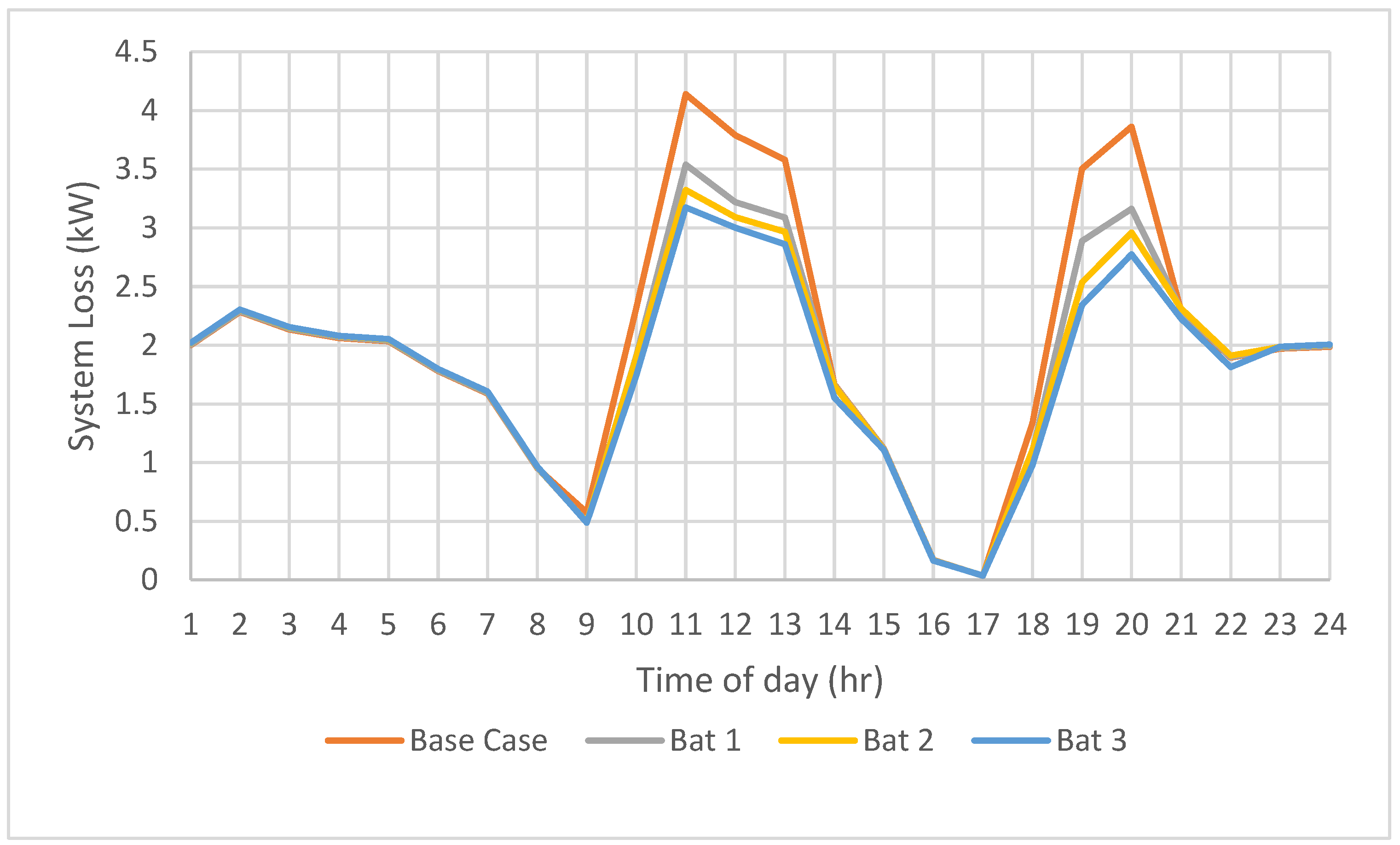
• The integration of BESs optimally located and sized leads to a reduction in system losses. The total system loss for a 24 h period in the base case scenario is 49.0701 kW, which is reduced by 8.473% (4.16 kW) with the application of MGO. Other algorithms (GWO, WOA, and CSA) show reductions in losses ranging from 7.33% to 7.42%.
• The BESs are allocated to buses where voltages exceed predefined limits, ensuring the grid is supported and the voltage remains within acceptable ranges. The optimal locations correspond to areas of the grid that experience overvoltage or undervoltage issues, improving overall network stability.
• MGO demonstrates superior convergence behaviour, achieving a minimum fitness value of 47.260 after 47 iterations, as compared to GWO, WOA, and CSA. In particular, WOA shows signs of becoming trapped in local minima, leading to suboptimal performance.
• MGO outperforms other optimization algorithms (GWO, WOA, CSA) in both voltage profile improvement and system loss reduction. MGO achieves the lowest fitness value (47.260), indicating superior performance in optimizing BES placement, sizing, and operational dispatch.

These results confirm that the proposed MGO-based methodology offers a more effective solution for integrating BESs into distribution networks, ensuring better voltage regulation and lower system losses compared to existing techniques in the literature.

6. Limitations and Future Research Directions

This study proposes an innovative two-stage optimization approach for the optimal siting, sizing, and operational dispatch of Battery Energy Storage Systems (BESSs) in distribution networks. While the proposed methodology demonstrates significant improvements in voltage profile and system loss reduction, there are several limitations and areas for future research that can be explored to enhance the effectiveness and applicability of the approach.

6.1. Limitations

• Single-Stage System: The current methodology is based on a daily operational horizon and does not consider the dynamic nature of BESS dispatch over a longer period (e.g., seasonal variations in load and generation). The study does not account for real-time adjustments in the operation of BESSs.
• Scalability: While the proposed methodology has been tested on an Australian distribution feeder, it may face scalability issues when applied to larger or more complex networks with a higher number of buses and BESSs. The computational complexity of the two-stage optimization approach could increase significantly as the system size grows.
• Grid Stability Under Extreme Conditions: The optimization is performed based on typical grid operation conditions. However, extreme weather events or unexpected load peaks could significantly impact the performance of the proposed methodology in real-world conditions. The current approach does not account for such contingencies.

6.2. Future Research Directions

• Incorporating Uncertainty and Forecasting: Future research can explore incorporating forecasting errors and uncertainties in renewable energy generation and load demands. Stochastic optimization techniques or robust optimization methods could be integrated to account for these uncertainties and provide more reliable solutions.
• Extended Time Horizons and Dynamic Operation: Expanding the methodology to account for longer time horizons, such as weekly, monthly, or even seasonal periods, would allow for more accurate planning and dispatch of BESs. Additionally, dynamic control strategies that can adjust to real-time grid conditions and BESS state of charge could be investigated.
• Hybrid and Advanced Metaheuristic Algorithms: The study utilizes the Mountain Gazelle Optimization (MGO) algorithm for optimization, which shows superior performance compared to other algorithms. However, hybrid optimization techniques that combine MGO with other algorithms, such as Genetic Algorithms or Particle Swarm Optimization, could be explored to further improve the optimization results and robustness, especially in larger networks.
• Integration with Grid Expansion Planning: Future studies could explore the integration of BESS optimization with grid expansion planning, where the placement and sizing of energy storage systems are considered along with other grid infrastructure decisions, such as the placement of transformers and conductors.
• Considering Real-World Constraints: Further research could include additional real-world constraints, such as market-based constraints (e.g., cost of electricity, market participation). This would provide a more realistic framework for the practical implementation of BESSs in distribution networks.